Đề thi học sinh giỏi tỉnh Toán 11 năm 2020 – 2021 sở GD&ĐT Bắc Ninh

UBND TỈNH BẮC NINH
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2020-2021 Môn: Toán - Lớp 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
(Đề thi có 02 trang)
Câu 1. (2,0 điểm) Cho hàm số 2
y  x  (2  m)x  4 có đồ thị là Pvà điểm (
A 5;5). Tìm m
để đường thẳng (d) : y  x
  m cắt đồ thị Ptại hai điểm phân biệt M và N sao cho tứ giác
OAMN là hình bình hành (O là gốc tọa độ).
Câu 2. (2,5 điểm) Cho phương trình 3
4 cos x  cos 2x  m  3cosx 1  0
1. Giải phương trình khi m = 3.
2. Tìm giá trị nguyên của tham số m để phương trình có đúng bốn nghiệm khác nhau thuộc khoảng        ;    2 2 3 2 3
2x − 4x + 3x −1 = 2x (2 − y) 3− 2y
Câu 3. (2,5 điểm) Giải hệ phương trình (
 x 3 − 2y + 2 − x 
)2( x 3−2y +2+ x−1)4 =4 Câu 4. (4,5 điểm)  3 2
 5  x  3x  5 1. Cho hàm số  khi x  1
y  g(x)   , x  1
với m là tham số. Tìm m  mx  2 khi x  1 
để hàm số g(x) liên tục trên .  u   1  1 
2. Cho dãy số u thoả mãn  2u
. Tìm công thức số hạng tổng quát u của n  n u   , n  1  n n 1   u  4  n dãy số đã cho.
3. Có bao nhiêu số tự nhiên có 8 chữ số, trong đó có hai chữ số lẻ khác nhau và ba chữ số chẵn
khác nhau, mà mỗi chữ số chẵn có mặt đúng hai lần.
Câu 5. (1,5 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho hình vuông ABCD có tâm I(1;4), đỉnh
A nằm trên đường thẳng có phương trình 2x  y  1  0 , đỉnh C nằm trên đường thẳng có phương
trình x  y  2  0. Tìm tọa độ các đỉnh của hình vuông đã cho. Câu 6. (5,0 điểm)
1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tất cả các cạnh bên đều bằng a.
Gọi điểm M thuộc cạnh SD sao cho SD = 3SM , điểm G là trọng tâm tam giác BCD .
a) Chứng minh rằng MG song song với mp(SBC ) .
b) Gọi (α ) là mặt phẳng chứa MG và song với CD . Xác định và tính diện tích thiết diện của hình chóp với mp (α ) .
c) Xác định điểm P thuộc MA và điểm Q thuộc BD sao cho PQ song song với SC . Tính PQ theo a.
2. Cho tứ diện SABC có ,
SA SB, SC đôi một vuông góc; SA = a, SB = ,
b SC = c . Lấy một điểm M
nằm trong tam giác ABC . Gọi d ,d ,d lần lượt là khoảng cách từ M đến các đường thẳng , SA SB, SC 1 2 3 2 abc 2 2 2 ( )2
Chứng minh rằng: d + d + d ≥ . 1 2 3 2 2 2 2 2 2
a b + b c + c a Câu 7. (2,0 điểm)
1. Tìm giá trị nhỏ nhất của 2 2 2 5 P = + + + a − b b − c c − a
ab + bc + ac Trong đó a, ,
b c là các số thực thỏa mãn hai điều kiện a + b + c = 1,ab + bc + ca > 0. n  
2. Với mỗi số nguyên dương n ta kí hiệu b là hệ số của 2
x trong khai triển  2 1 x   x    thành n  2 đa thức. Đặt *
u  b  b  b  ...  b , n   . Tìm số hạng tổng quát của dãy số u và n  n 1 2 3 n
tính giới hạn limu . n =====Hết=====
Họ và tên thí sinh:........................................................... Số báo danh .............................. UBND TỈNH BẮC NINH HƯỚNG DẪN CHẤM
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TỈNH NĂM HỌC 2020-2021 Môn: Toán - Lớp 11 Câu
Lời giải sơ lược Điểm
1. (2,0 điểm) Cho hàm số 2
y  x  (2  m)x  4 có đồ thị là Pvà điểm (
A 5;5). Tìm m để đường
thẳng (d) : y  x
  m cắt đồ thị Ptại hai điểm phân biệt M và N sao cho tứ giác OAMN là
hình bình hành (O là gốc tọa độ).
Hoành độ của M và N là nghiệm của pt: 2 2
x  (2  m)x  4  x
  m  x  (3  m)x (m  4)  0 (1)Vì 2
  m  2m  25  0, m   1 nên  
1 luôn có hai nghiệm phân biệt d luôn cắt 0.5
P tại hai điểm phân biệt.
Do các điểm O và A thuộc đường thẳng  : y  x
 nên để OAMN là hình bình hành
thì MN = OA = 5 2
Gọi M(x ; x
  m), N(x ; x
  m) vớix ,x là nghiệm của   1 . 1 1 2 2 1 2 0.5 x
  x  m  3 Ta có  1 2  x  x  (  m  4)  1 2  2 2 2 2 MN 2(x x ) 2 (x x ) 4x x       
 2m  4m  50 1 2  1 2 1 2   m   2 2 MN 5 2 2m 4m 50 50        0.5 m   0  + m  0 thì , O ,
A M,N thẳng hàng nên không thỏa mãn. + m  2 thỏa mãn. 0.5
2. (2,5 điểm) Cho phương trình 3
4 cos x  cos 2x  m  3cosx 1  0
1. Giải phương trình khi m = 3.
2. Tìm giá trị nguyên của tham số m để phương trình có đúng bốn nghiệm khác nhau thuộc khoảng        ;   .  2 2 cos x  0 
Với m = 3 ta có phương trình 3 2
4 cos x  2 cos x  0   1  0.25 cos x   2 2.1  1
cos x  0  x   k điểm 2 0.5 1  cos x 
 x    k2 2 3
Vậy phương trình có các họ nghiệm là   x 
 k , x    k2 . 0.25 2 3 Ta có: 3 x 
x  m   3 2 4 cos cos 2
3 cos x  1  0  4 cos x  2 cos x  m  3cosx  0 cosx  0    2
4 cos x  2 cos x  m  3  0   1 0.5      
cos x  0  x   k ,
 k   không có nghiệm thuộc khoảng   ; . 2  2 2 2.2    
1,5 Đặtt  cosx , vì  x    ;   nên t 0;1  .    điểm 2 2 
Khi đó phương trình   2
1  4t  2t m  3  0 2 . 0.5
Ycbt  phương trình 2 có 2 nghiệm phân biệt t , t thỏa mãn 0  t , t  1. 1 2 1 2   2
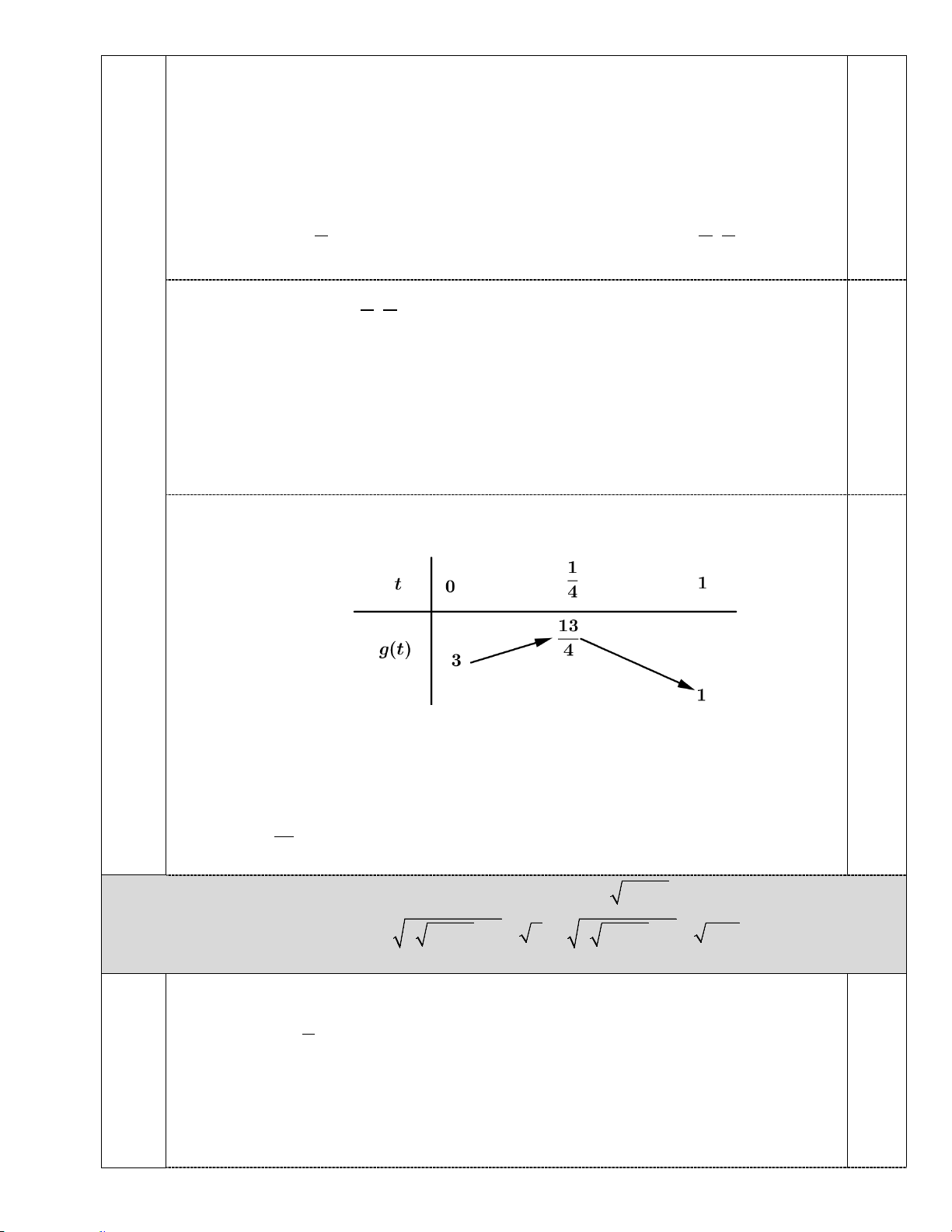
2  m  4t  2t  3  g t
Ta có bảng biến thiên của g t trên t 0;1   . 0.5
Từ bảng biến thiên trên phương trình 2 có 2 nghiệm phân biệt t , t thỏa mãn 1 2
0  t , t  1 1 2 thì 13 3  m 
. Vì m nguyên nên không có giá trị nào. 4 3 2 3
2x − 4x + 3x −1 = 2x (2 − y) 3− 2y
3. (2,5 điểm) Giải hệ phương trình (
 x 3 − 2y + 2 − x 
)2( x 3−2y +2+ x−1)4 =4 x ≥ 1  Điều kiện:  3 y ≤   2
Với điều kiện trên, từ PT đầu ta có: 1.0 4 3 1
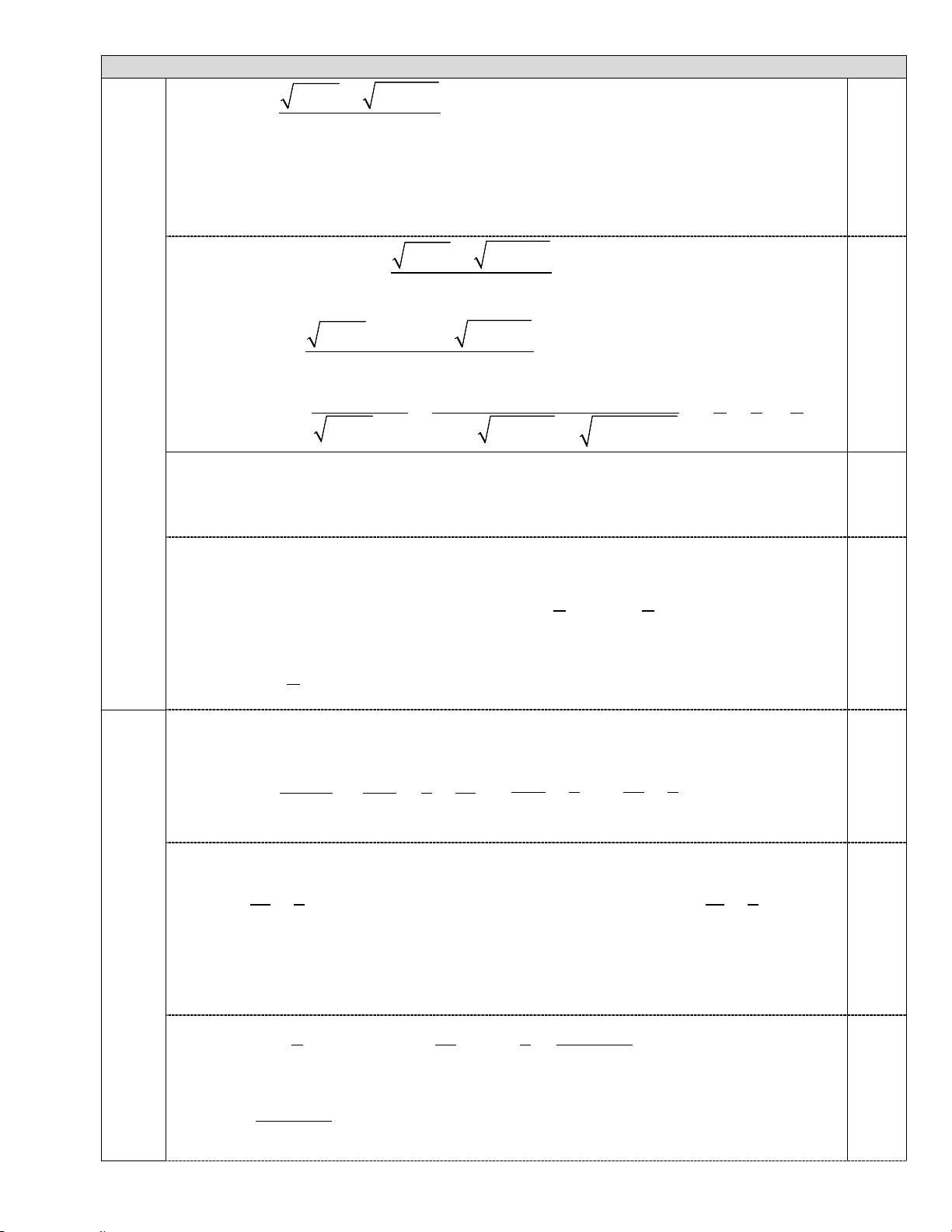
2x − 4x + 3x −1 = 2x (2 − y) 3 − 2y ⇔ 2 − + − = ( 3− 2y )3 3 2 3 + 3 − 2y 2 3 x x x 3  1   1 1 1  ⇔ − + − = ( 3− 2y )3 + 3−     2y  x   x  1 ⇔ 1− = 3 − 2y x 2 4
Thế vào phương trình thứ hai ta có: ( x +1 − x ) ( x +1 + x −1) = 4 (*)
Do x ≥ 1⇒ x +1 − x > 0 , phương trình 0.5
⇔ ( x + − x)( x + + x − )2 (*) 1 1 1 = 2
⇔ 2( x +1 − x)( x +1 + x −1)2 2
= 2 = ( x +1+ x −1)( x +1− x −1) 2
⇔ 2( x +1 − x) = ( x +1 − x −1)2 0.5 2
⇔ x +1 + x −1 = x + x
Bình phương hai vế dương ta có:  1− 5 x = 2 2 3 2
⇔ x +1 x −1 = x x ⇔ (x +1)(x −1) = x ⇔  1+ 5 x =  2 1 5
Kết hợp điều kiện ta có: x + =
. Thay vào trên ta có nghiệm của hệ là: 0.5 2  1+ 5 x =  2   3 5 −1 y =  4 4. (4.5 điểm)  3 2
 5  x  3x  5 1. Cho hàm số  khi x  1
y  g(x)   , x  1
với m là tham số. Tìm m  mx  2 khi x  1 
để hàm số g(x) liên tục trên .  u   1  1 
2. Cho dãy số u thoả mãn  2u
. Tìm công thức số hạng tổng quát u của n  n u   , n  1  n n 1   u  4  n dãy số đã cho.
3. Có bao nhiêu số tự nhiên có 8 chữ số, trong đó có hai chữ số lẻ khác nhau và ba chữ số chẵn
khác nhau, mà mỗi chữ số chẵn có mặt đúng hai lần. 3 2    Hàm 5 x 3x 5 g(x) 
liên tục trên khoảng (1; )  . x  1 0.5
Hàm g(x)  mx  2 liên tục trên khoảng ( ;  1).
Vì thế g(x) liên tục trên  khi và chỉ khi nó liên tục tại điểm x  1. 3 2
5  x  3x  5
Ta có lim g(x)  lim x 1 x 1     x  1 3 2 4.1
5  x  2  2  3x  5  lim 0.5 1.5 x  1 x  1 điểm    1 3(1  x)  1 1 3  lim         .   x  1 3 2 3 2 2  5  x  2       4 2 4 4 2 3x 5 (3x 5) 
Và lim g(x)  lim (mx  2)  2 m; g(1)  2 m. x 1 x 1     0.25
Hàm số g(x) liên tục trên tại điểm x  1 khi và chỉ khi 3 5
lim g(x)  lim g(x)  g(1)  2  m   m  . x 1 x 1     4 4 0.25 5
Vậy với m  thì g(x) liên tục trên .  4
Nhận xét u  0, n  1. n 2u   0.5 Ta có 1 1 2 1 1  1 1 n u        2  . n 1    u  4 u 2 u u 2 u 2 n n 1  n n 1  n Đặt 1 1 1 1 v   thì v
 2v . Suy ra v là cấp số nhân với v   và công n  4.2 n u 2 n 1  n 1 u 2 n 1 1.5 0.5 bội . điểm q  2 n 1  Do đó 3  n 1  n 2  1 1 3.2 1 v  2  3.2   v   . n 2 n u 2 2 n 0.5 Vậy 2 u  , n  1. n n 1 3.2   1
Trường hợp 1: Xét các số có 8 chữ số, trong đó có hai chữ số lẻ khác nhau và ba chữ
số chẵn khác nhau mà mỗi chữ số chẵn có mặt đúng hai lần, coi chữ số 0 có thể đứng đầu.
+ Chọn 2 chữ số lẻ khác nhau và 3 chữ số chẵn khác nhau có 2 3 C C (cách). 5 5
+ Với mỗi cách chọn trên ta có: số có 8 chữ số, trong đó có hai chữ số lẻ khác nhau 0.75
và ba chữ số chẵn khác nhau mà mỗi chữ số chẵn có mặt đúng hai lần là: 8! (số). 2!2!2! Trường hợp này có: 2 3 8! C .C .  504000 (số). 5 5 2!2!2! 4.3
Trường hợp 2: Xét các số có 8 chữ số, trong đó có hai chữ số lẻ khác nhau và ba chữ
1.5 số chẳn khác nhau mà mỗi chữ số chẵn có mặt đúng hai lần, mà chữ số 0 đứng đầu. điểm
+ Chọn 2 chữ số lẻ khác nhau và 2 chữ số chẵn khác nhau có 2 2 C C (cách). 5 4
+ Với mỗi cách chọn trên ta có: số có 8 chữ số, trong đó có hai chữ số lẻ khác nhau 0.5
và hai chữ số chẵn khác nhau mà mỗi chữ số chẵn có mặt đúng hai lần là: 7! (số). 2!2!
Trường hợp này có: 2 2 7! C .C .  75600 (số). 5 4 2!2!
Vậy có: 504000  75600  428400 (số). 0.25
5. (1,5 điểm) Trong mặt phẳng với hệ tọa độ Oxy , cho hình vuông ABCD có tâm I(1;4), đỉnh A nằm
trên đường thẳng có phương trình 2x  y 1  0 , đỉnh C nằm trên đường thẳng có phương trình
x  y  2  0. Tìm tọa độ các đỉnh của hình vuông đã cho.
Gọi C(t;t 2) thì (2
A  t;6  t). Vì A thuộc đường thẳng có phương trình
2x  y  1  0 nên 2(2  t)  (6  t)  1  0  t  3. Dẫn tới (
A 1;3), C(3;5). 0.5 Ta thấy ,
B D là giao điểm của đường tròn đường kính AC và đường trung trực của AC .
Đường tròn đường kính AC có phương trình 2 2
(x  1)  (y  4)  5. 0.5
Đường trung trực của AC có phương trình 2x  y  6  0. 2 2 (
 x 1)  (y  4)  5 x   0;y  6 Ta có     .
2x  y  6  0 x    2;y  2    
Do đó B(0;6),D(2;2) hoặc B(2;2),D(0;6). 0.5
Vậy tọa độ các đỉnh hình vuông là (
A 1;3),B(0;6),C(3;5),D(2;2) hoặc (
A 1;3),B(2;2),C(3;5),D(0;6). 6. (5,0 điểm)
1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tất cả các cạnh bên đều bằng a.
Gọi điểm M thuộc cạnh SD sao cho SD = 3SM , điểm G là trọng tâm tam giác BCD .
a) Chứng minh rằng MG song song với mp(SBC ) .
b) Gọi (α ) là mặt phẳng chứa MG và song với CD . Xác định và tính diện tích thiết diện của hình chóp với mp (α ) .
c) Xác định điểm P thuộc MA và điểm Q thuộc BD sao cho PQ song song với SC . Tính PQ theo a.
2. Cho tứ diện SABC có ,
SA SB, SC đôi một vuông góc; SA = a, SB = ,
b SC = c . Lấy một điểm M
nằm trong tam giác ABC . Gọi d ,d ,d lần lượt là khoảng cách từ M đến các đường thẳng , SA SB, SC . 1 2 3 2 abc 2 2 2 ( )2
Chứng minh rằng: d + d + d ≥ . 1 2 3 2 2 2 2 2 2
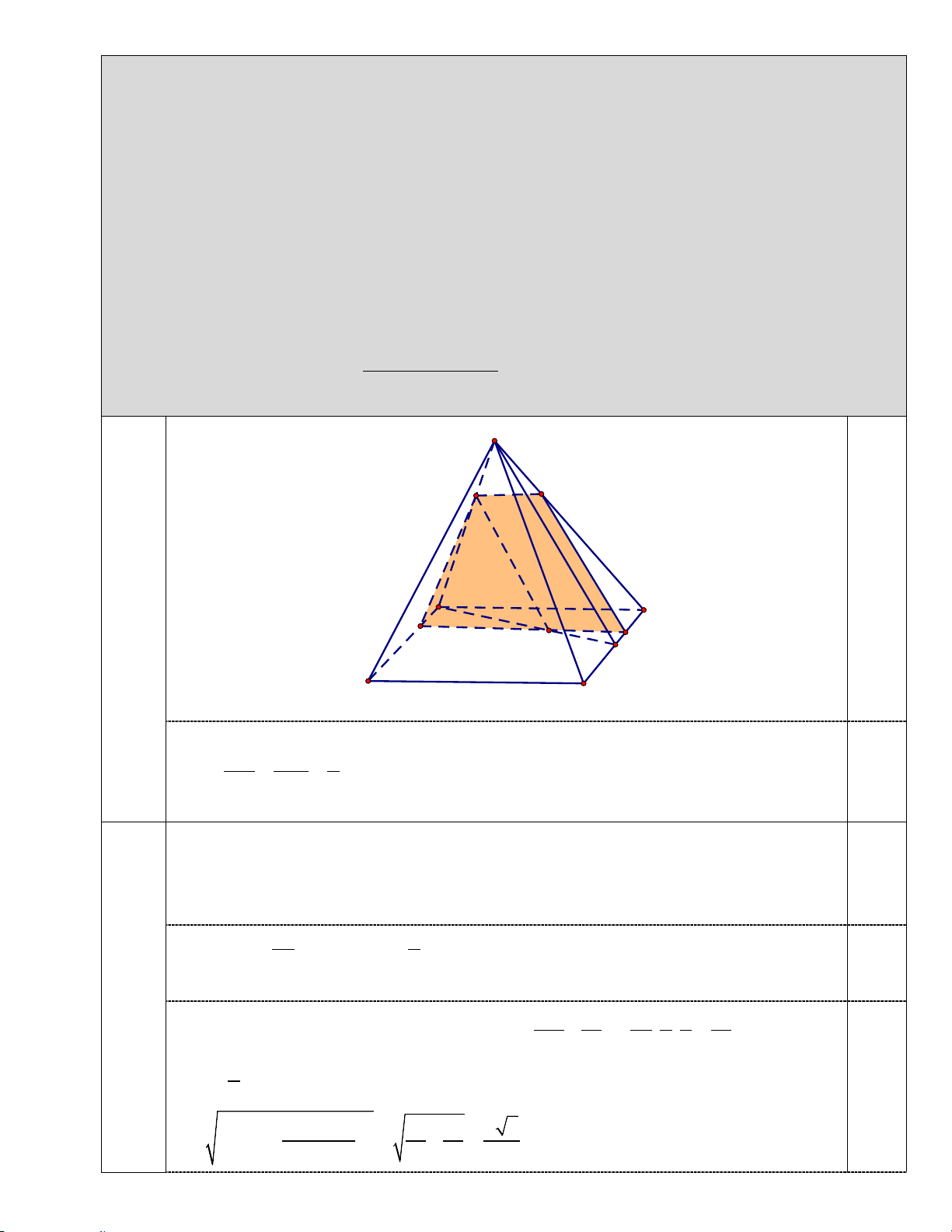
a b + b c + c a S M H 0.25 D C E 6.1.a G F 1,0 I điểm A B
a) Gọi I là trung điểm của BC Ta có DG DM 2 =
= ⇒ MG / /SI mà SI ⊂ (SBC) nên MG / / (SBC) . 0.75 DI DS 3
Qua G kẻ đường thẳng song song với CD cắt AD và BC lần lượt tại E và F . Qua
M kẻ đường thẳng song song với CD cắt SC tại H . Thiết diện của hình chóp với mp(
α ) là tứ giác EFHM . 0.5
Ta có HM / /EF vì cùng song song với CD 2
MD = HC = a
DE = CF = a  MDE =  0 , ,
HCF = 60 nên tam giác DME bằng tam 3 3 0.5
giác CHF suy ra ME = HF do đó EFHM là hình thang cân 6.1.b 2 2 2 a a a a a 1,5 Ta có 2 2 2 0 4 2 1
EM = DM + DE − 2DM.DE. os c 60 = + − 2 . . = 9 9 3 3 2 3 điểm = a MH
,EF = a .Gọi h là độ dài đường cao của hình thang ta có 0.5 3 2 2 2 2  EF − HM  a a a 2 h = EM − = − =    2  3 9 3 2
Diện tích thiết diện là 1
1 a 2 4a 2a 2 S = h HM HM . .(EF + ) = . . = EF 2 2 3 3 9
Qua M dựng đường thẳng song song với SC cắt CD tại N. Nối A với N cắt BD tại Q. S M P 0.5 D C N Q A B
6.1.c Trong mp (AMN) từ Q dựng đường thẳng song song với MN cắt AM tại P.
1,5 Ta có PQ//MN, MN//SC nên PQ//MN 0.5
điểm Suy ra hai điểm P, Q thỏa mãn điều kiện bài toán. Ta có MN DM 2 AQ AB 3 AQ 3 = = , = = ⇒ = SC DS 3 QN DN 2 AN 5 PQ AQ 3 PQ PQ MN 3 2 2 = = , = . = . = 0.5 MN AN 5 SC MN SC 5 3 5 Suy ra 2 = a PQ 5 A
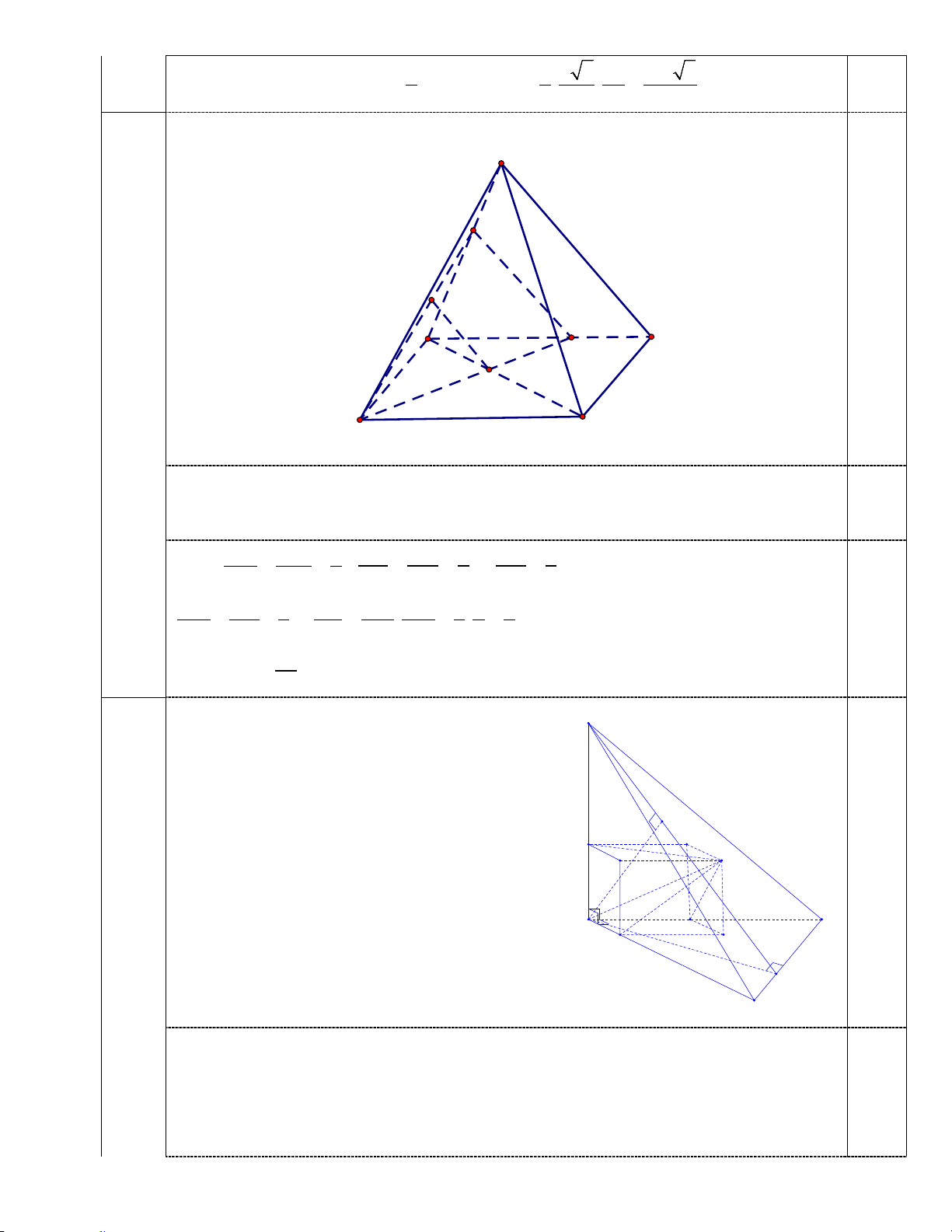
Dựng hình hộp chữ nhật MNP . Q IJSH như hình vẽ
⇒ SP ⊥ (MNPQ) ⇒ SP ⊥ MP ⇒ MP = d 1
Tương tự ta có MH = d ;MJ = d 2 3 K Q P M 0.25 N S B H J I D C
Trong hình chữ nhật MNPQ có: 2 2 2 2
d = MP = MN + MQ 1 6.2 Tương tự: 2 2 2
d = MQ + MI ; 2 2 2
d = MN + MI 2 3 1,0 Ta có: 2 2 2 2 2 2
SM = MP + SP = MQ + MN + MI 0.25 điểm 2 2 2 2
⇒ d + d + d = 2SM (1) 1 2 3
Dựng SD ⊥ BC, SK ⊥ AD ⇒ SK ⊥ ( ABC) ⇒ SK ≤ SM (2)
Trong tam giác ASD có 1 1 1 = + 2 2 2 SK SA SD
Trong tam giác SBC có 1 1 1 = + 2 2 2 SD SB SC 0,25 Từ đó suy ra 1 1 1 1 1 1 1 = + + = + + 2 2 2 2 2 2 2 SK SA SB SC a b c (abc)2 2 ⇒ SK = (3) 2 2 2 2 2 2
a b + b c + c a 2 abc 2 2 2 ( )2
Từ (1), (2), (3) suy ra : d + d + d ≥ (đpcm). 0,25 1 2 3 2 2 2 2 2 2
a b + b c + c a 7. (2,0 điểm)
1. Tìm giá trị nhỏ nhất của 2 2 2 5 P = + + + a − b b − c c − a
ab + bc + ac Trong đó a, ,
b c là các số thực thỏa mãn hai điều kiện a + b + c = 1,ab + bc + ca > 0. n  
2. Với mỗi số nguyên dương n ta kí hiệu b là hệ số của 2
x trong khai triển  2 1 x   x    thành n  2 đa thức. Đặt *
u  b  b  b  ...  b , n   . Tìm số hạng tổng quát của dãy số u và tính n  n 1 2 3 n giới hạn limu . n
Không mất tính tổng quát giả sử a >b >c. Khi đó 2 2 2 5 P = + + + a − b b − c a − c
ab + bc + ac
Với 2 số dương x,y ta có BĐT tổng quát sau 0.25 1 1 4 2 2 + ≥ ≥ + 2 2 x y x y x + y   Ta có 1 1 2 5 8 2 5 P = 2  +  + + ≥ + +
 a − b b − c  a − c
ab + bc + ac a − c a − c
ab + bc + ac 10 10 20 2 7.2 = + ≥ − 2 a c 0.25 1
2 ab + bc + ac
(a −c) + 4(ab +bc +ac) điểm 20 2 20 2 = =
(a +c)(a +c + 4b) (1−b)(1+ 3b) 2
 3 − 3b + 1 + 3  Lại có 3(1 − ) (1 + 3 ) b b b ≤   = 4  2  Suy ra ( 0.25
− b) ( + b) 2 3 1 1 3 ≤ 3 Do đó P ≥ 10 6 .  2 + 6 a  = a
 − b = b − c  6  Dấu bằng xảy ra khi  1 3
 − 3b = 1 + 3b ⇔ b  = .   3
a + b + c = 1   2 − 6 c =   6 0.25  2 + 6 a  =  6 Vậy  1
MinP = 10 6 khi b  = .  3  2 − 6 c =   6 n n k  n k  n n k       Ta có  2 1 k 2 k 1   k j 1 x
  x    C (x  x)      C C        
(1)kj kj x . 2 n n k         k0 2 k0 j0 2 Số hạng chứa 2
x ứng với k  j  2, 0  j  k  n , hay j  0,k  2 hoặc 0.25 j  k  1. n 2  n 1  2     Do đó 2 0 1   2 1 1 1   0 n
b  C C   (1) C C     (1)  . n n 2 n 1     n 1 2 2 2  n 1 x   1 Xét hàm số 2 ( )  1    ... n f x x x
 x thì f (x)  với x  1. x  1 Ta có  n 1      nx (n 1) n x n n 1 2 2 1
f '(x)  1  2x  3x  ...  (n  1)x  nx  , x  1; 7.2 2 0.25 (x  1) 1 2 n 2
f ' (x)  2.1  3.2x  4.3x  ...  n(n  1)x  điểm n 1  n n 1
n(n  1)x
 2(n  1)(n  1)x  n(n  1)x   2  , x  1; 3 (x  1) 2 2 2 2 2 n 1
 f '(x)  xf ' (x)  1  2 x  3 x  ...  n x  2 n 2  2 n 1  2 n x
 (2n  2n  1)x  (n  1) n x  x  1  , x  1; 3 (x  1) 0.25 2 2 2 2 2 1 2 3 n 2n  8n  12     ...   12  . 0 1 2 n 1 2 2 2 2  2n 2 Vậy 2n  8n  12 * u  12  , n   . n 2n
Với mọi số nguyên dương n  3 ta thấy   n n 0 1 2 3 n 3 n(n 1)(n 2)
2  (1  1)  C C C C  ... C  C  . n n n n n n 6 Suy ra 2 2 2n  8n  12
6(2n  8n  12) * 0  
, n   ,n  3. 2n
n(n  1)(n  2) 2 8 12 2 6(   ) 0.25 Hơn nữa 2 3
6(2n  8n  12) lim 0  0, lim  lim n n n  0.
n(n  1)(n  2) 1 2 (1  )(1  ) n n 2 Dẫn tới 2n  8n  12 lim  0. 2n 2   Vậy  2n  8n  12 lim u  lim 1  2     12. n    2n 
Document Outline

• Đề Toán 11
  • Câu 5. (1,5 điểm) Trong mặt phẳng với hệ tọa độ , cho hình vuông có tâm , đỉnh nằm trên đường thẳng có phương trình , đỉnh nằm trên đường thẳng có phương trình Tìm tọa độ các đỉnh của hình vuông đã cho.
• Đáp án Toán 11