Đề thi học sinh giỏi tỉnh Toán 11 năm 2020 – 2021 sở GD&ĐT Hà Tĩnh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI TỈNH LỚP 10 & 11 THPT HÀ TĨNH NĂM HỌC 2020 - 2021 TOANMATH.com Môn thi: TOÁN LỚP 11
Đề thi có 01 trang - gồm 05 câu
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Câu 1. (5,0 điểm)    3sin x  cos 2x  2sin  x    1 3  2
a. Tìm số nghiệm của phương trình 
 1 trên đoạn 0;2021 . 2cos x  3 n b. Tìm hệ số của 4
x trong khai triển biểu thức P   3
1 x  3x  thành đa thức, biết n là số nguyên dương thỏa mãn 2 2 2 2 C  C  C  A . n  2 3 2 3 n 1  Câu 2. (4,0 điểm)
a. Tìm tất cả các giá trị của m để phương trình 3 x    m 2 1 2
x  m  3 x  3m  3  0 có ba nghiệm phân biệt
lập thành một cấp số cộng. f  x  4 f  x  4
b. Cho đa thức f  x thỏa mãn lim  5. Tìm lim . x2 x  2
x2  3 3x  2  2 2 f (x) 1  3 Câu 3. (2,0 điểm)
Một chuồng có 3 con thỏ trắng và 4 con thỏ xám. Người ta bắt ngẫu nhiên lần lượt từng con ra khỏi chuồng
cho đến khi bắt được cả 3 thỏ trắng thì mới dừng lại. Tính xác suất để người đó phải bắt ít nhất 5 lần. Câu 4. (5,0 điểm)
a. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng  ABC . Gọi M là   
trung điểm SB, N là điểm thỏa mãn NS  2NC  0 . Tính độ dài SA biết AN vuông góc với CM.
b. Cho hình lăng trụ ABC.A' B 'C ' . Gọi I là trung điểm B 'C ' và M là điểm thuộc cạnh A'C ' . Biết AM cắt 2
A'C tại P, B ' M cắt A' I tại Q. Tìm vị trí điểm M trên cạnh A 'C ' sao cho diện tích tam giác A' PQ bằng 9 diện tích tam giác A'CI . Câu 5. (4,0 điểm)
a. Cho các số thực x, y, z không âm thỏa mãn 2 2 2
x  y  z  2xyz  1. Tìm giá trị lớn nhất của biểu thức
P  x x  2  y  z . x  3, x  7 n 1
b. Cho dãy số  x thỏa mãn 1 2
. Đặt y   . Chứng minh dãy  y có giới n  n   2 2 * x  x  x  x , n     n  x n2 n 1  n n k 1 k
hạn và tìm giới hạn đó.
_______________ HẾT _______________ https://toanmath.com/
Thí sinh không được sử dụng tài liệu và máy tính cầm tay. Giám thị không giải thích gì thêm./.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . . . LỜI GIẢI TOÁN 11   x   k2  Điều kiện: 3 6 cos x    , k,l  (*). 2 
x    l2  6
Với điều kiện trên, phương trình đã cho tương đương:    2
3sin x  cos 2x  2sin
 x 1 3  2cos x  3  3sin x  2sin x  2  0    2    sin x  2  x   k2   6  1    sin x   5  x   k2 2   6 
Đối chiếu điều kiện ta có 5 x   k2 6 5 5 12121 0 
 k2  2021    k 
 k 0;1;2;...;101  0 6 12 12
Vậy phương trình có 1011 nghiệm trên đoạn đã cho
Áp dụng công thức k k 1 C   C
 Ck ,  k   ta có n n 1  n n 1  1 1 3 2 C  C 3 2 3 2 3
C  C  C 4 3 3 3 2 3
C  C  C 5 4 4 .................. 3 2 3 C  C  C n n 1  n 1  3 2 3 C  C  C n 1  n n
Cộng vế theo vế các đẳng thức trên ta được 3 2 2 2 C
 C  C  ...  C . n 1  2 3 n   3 2
n 1nn 
Kết hợp giả thiết suy ra 1 C 2  3A   . 3 1 n  2 n 1    n 1  n n 3 n 1   3  n  10 . 3
Theo công thức Newton ta có
A  1 x1 3x  10 2  0 C  1 10 10 C x1 2 3x  2 2 10
C x 1 3x 2 2  3 3 10
C x 1 3x 3 2  4 4        10 C x 1 3x 4 2 5 5 10 C x 1 3x 5 2 10 10 ... 10 C x  2 1 3x 10 . Vậy hệ số của 4 x là 2 C . 1 C 3 . 1 4
 C  270 210  480 10 2 10 3
x    m 2 1 2
x  m  3 x  3m  3  0 (1)  x   2 (
1) x  2mx  3m  3  0 x 1  0   2
x  2mx  3m  3  0 (2)
Phương trình (1) có ba nghiệm phân biệt  phương trình (2) có hai nghiệm phân biệt x  1  . 2 '  0 
m  3m  3  0 2        f    m (*) 1  0 5  m  2  0 5 Giả sử x  1
 , còn x , x là nghiệm của (2). Ta xét các trường hợp sau: 1 2 3
TH1: x , x , x lập thành một cấp số cộng  x  x  2x  2m  2   m  1  2 1 3 2 3 1
TH2: x , x , x lập thành một cấp số cộng  x  x  2x  x  2x 1 1 2 3 1 3 2 3 2  4m  1 x   3  Kết hợp Viet: 3
x  x  2m   . 2 3 2m 1 x  2  3 m  2   Lại theo Viet: 4m 1 2m 1 
x x  3m  3 2  .
 3m  3  8m  29m  26  0  2 3 13 3 3 m   8 Đối 13
chiếu điều kiện ta có: m  1
 ; m  2 ; m  . 8 f  x  4 Nếu lim  f
 x  4  L  0  thì lim
  , trái giả thiết x2 x2 x  2 Do đó lim  f
  x  4  0 
hay lim f  x  4 x2 x2          f  x 3 3x 22 3 2 3x 2 4 f      x 4 4   P  lim  lim
x2  3 3x  2  2 2 f x 1  3 x2
3x  6 2 f x13       f  x 3 3x 22 3 2 3x 2 4  4   5 12 10  lim .lim  . 
x2 3 x  2 x2
 f x   3 6 3 2 1 3
Gọi A là biến cố thỏa mãn bài toán thì A là biến cố “người đó bắt hết thỏ trắng trong 3
hoặc 4 lần”. Ta tính PA:
TH1: Cần 3 lần để bắt được hết thỏ trắng. Xác suất TH này là 3! 1  . 3 A 35 7
TH2: Cần 4 lần để bắt được hết thỏ trắng. Khi đó trong 3 lần đầu phải có 1 con thỏ xám,
lần thứ 4 bắt được thỏ trắng. Xác suất TH này là 4.3.3! 3 
. (Có 4 cách chọn thỏ đen, 3 4 A 35 7
cách chọn vị trí cho thỏ đen, 3! hoán vị 3 thỏ trắng). 3! 4.3.3! 4 Vậy P A   
, nên xác suất cần tìm là P    P  31 A 1 A  3 4 A A 35 35 7 7
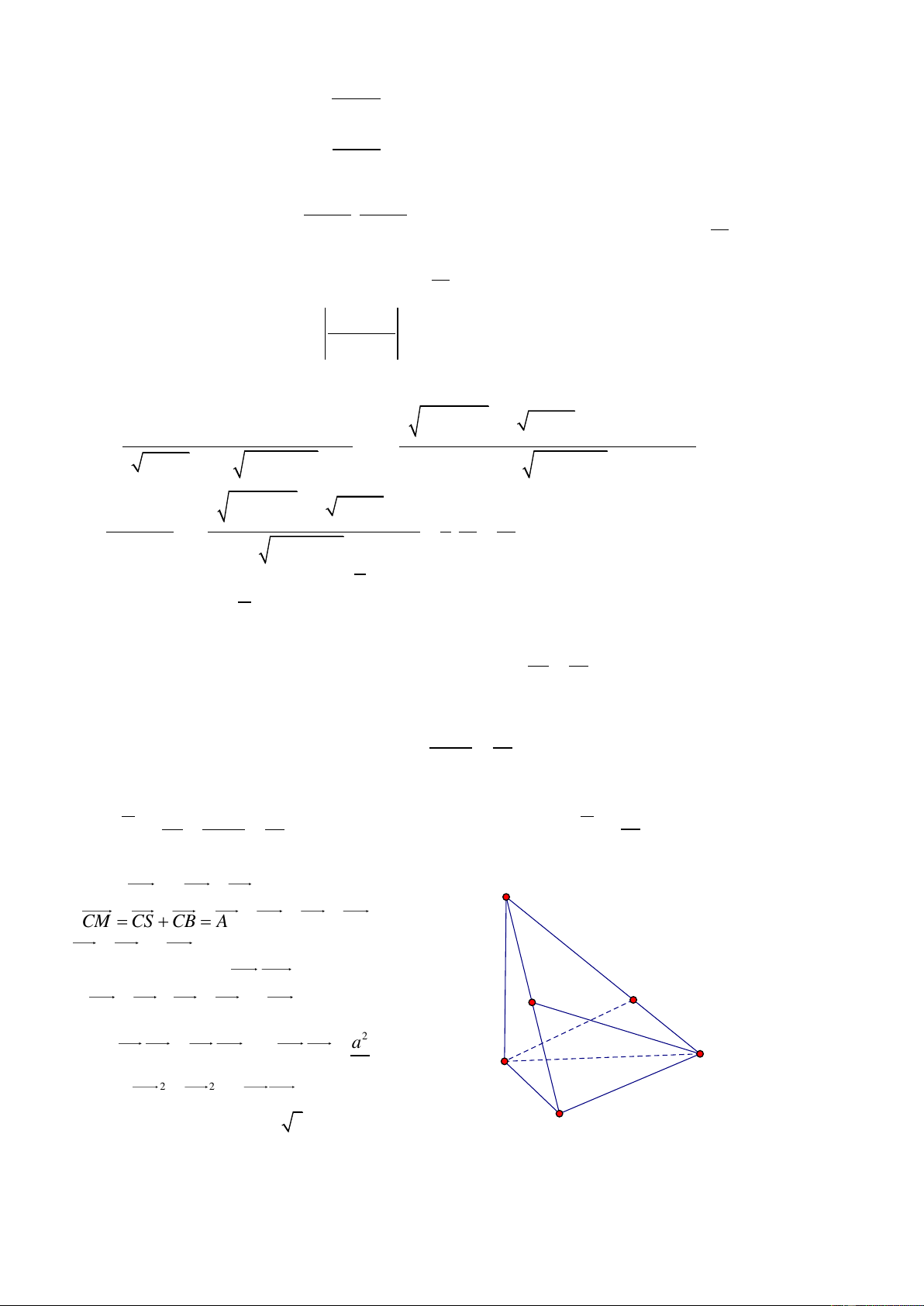
Ta có 3AN  2 AC  AS S
2CM  CS  CB  AS  AC  AB  AC 
AS  AB  2AC
Do đó AN  CM  AN.CM  0   M N
2AC  AS  AS  AB  2AC  0 (1) (1,5 điểm) 2 Để ý a
AS.AB  AS.AC  0; AC.AB  nên từ (1) C 2 A 2 2 ta có 4
 AC  AS  2ABAC  0 2 2
 AS  3a  0  AS  a 3 (1 điểm) B
Gọi I là trung điểm B’C’ và K là giao điểm của AC’ A C
với A’C. Ta thấy ba mặt phẳng ( AB 'C ') , ( A' IC) ,
( AB ' M ) đôi một cắt nhau theo ba giao tuyến là:
AB ', PQ, IK nên ba giao tuyến ấy đồng qui hoặc B đôi một song song. Mà
AB ' / / IK nên K
AB ' / / IK / / PQ. (1.0 điểm) P S A  ' PQ A' P A'Q
1 A' P A'Q  .  . .  M S A'C A' I 2 A' K A' I A' A  'CI C' . (1 điểm) 2 1  A'Q  2 A'Q 2 Q .      I 2  A' I  9 A'I 3 B'
Suy ra Q là trọng tâm A
 ' B'C '.Vậy M là trung
điểm của cạnh A'C' . (0,5 điểm)
Từ giả thiết suy ra tồn tại tam giác ABC không tù sao cho x  cos ,
A y  cos B, z  cosC B  C B  C 2
P  cos A  2 cos B  cosC   cos .
A cos A  2 2 cos cos  2 2 A cos .
A cos A  2 2 sin 2
Do tam giác ABC không tù nên 0  cos A  1  cos .
A cos A  cos A , do đó 2 A A A  A  2
P  cos A  2 2 sin  1 2sin  2 2 sin  2  2 sin 1  2   2 2 2  2    A   Đẳng thức xảy ra khi 2 1  . Vậy    
max P  2 khi x 0, y z  2 B  C   4 Ta có x  2 x  x  x  2
x  x  ...  x  2
x  x  1 , suy ra: n  2 n 1 n 1 n 1 n n 2 1 1 x  2 x  x  1 . n 1 n n 1 1 1 Ta được:   . x x  1 x  1 k k k 1
Cho k chạy qua các giá trị 1, 2, ..., n và lấy tổng, được: y  1  1 . n x  1 x  1 1 n 1 2 Ta có x
 x  x  1  0, suy ra x là dãy tăng . n  n 1 n  n 
Giả sử x bị chặn trên thì x có giới hạn hữu hạn. n  n 
Đặt L  limx , ta có: L  2
L  L  1 , suy ra L  1, vô lí. Do đó L  lim x    . n n Vậy: y  1 lim . n 2
Document Outline

• de-thi-hoc-sinh-gioi-tinh-toan-11-nam-2020-2021-so-gddt-ha-tinh
• LỜI GIẢI TOÁN 11