Đề thi học sinh giỏi Toán 11 cấp tỉnh năm 2016 – 2017 sở GD&ĐT Lai Châu

UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 11 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2016 – 2017 Môn thi: Toán ĐỀ 01
Thời gian: 180 phút (Không kể thời gian giao đề)
(Đề thi có 01 trang) Ngày thi:…. /4/2017
Câu 1: ( 3 điểm) Giải phương trình sau: sin 2x + 2cos2x =1+ sin x − 4cos .x
Câu 2: ( 3 điểm) Cho số nguyên dương n thỏa mãn điều kiện: n−3 2 1 n+2 C − C = . − C − C n n 1 n 1 n+3 n
Tìm hệ số của số hạng chứa  − n 11
x trong khai triển 3 n 8 x x  −  với x ≠ 0. 3x   
Câu 3: (4 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt
bên SAD là một tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Gọi
M, N, P lần lượt là trung điểm của các cạnh SB, BC và CD. Biết góc giữa đường
thẳng SB và mặt phẳng (ABCD) bằng 0 30 .
a) Chứng minh rằng BP ⊥ ( AMN ) .
b) Tính khoảng cách giữa hai đường thẳng AB và SC. 2
x + 3 xy + x − y − y = 5y + 4
Câu 4: (4 điểm) Giải hệ phương trình  (x, y∈). 2
 4y − x − 2 + y −1 = x −1 u  =1 1
Câu 5: (3 điểm) Cho dãy số {u xác định như sau:  2  u . n} n u = + =  + u n n n , 1,2,... 1  2017   Tính: u u u 1 2 lim n  + + ⋅⋅⋅ + . n→+∞  u u u 2 3 n 1 + 
Câu 6: ( 3 điểm) Cho ba số thực dương a, b, c thỏa mãn 3
a + b + c = . 4 Chứng minh rằng: 1 1 1 + + ≥ 3. 3 3 3 a + 3b b + 3c c + 3a
…………………..HẾT……………………
- Thí sinh không sử dụng tài liệu
- Cán bộ coi thi không giải thích gì thêm. UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 11 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2016 - 2017 Môn thi: Toán HƯỚNG DẪN CHẤM ĐỀ THI SỐ 1
Thời gian: 180 phút (không kể thời gian phát đề) (Gồm có 05 trang) Ngày thi: 4/2017 HƯỚNG DẪN CHẤM Câu Đáp án Thang điểm
Câu 1 sin2x + 2cos2x = 1+ sin x − 4cos x (3 điểm) ⇔ 0,5
2sin x cos x −1 + 2
4 cos x − 2 − sin x + 4 cos x = 0 ⇔ x x − + 2 sin (2 cos
1) 4 cos x + 4 cos x − 3 = 0 0,5
⇔ sin x(2 cos x −1) + (2 cos x −1)(2 cos x + 3) = 0 0,5
⇔ (2 cos x −1)(sin x + 2 cos x + 3) = 0 0,5  1 π
cos x = ⇔ x = ± + k π  2 ⇔  2 3 0,5
sin x + 2 cos x + 3 = 0(VN) π
⇔ x = ± + k π 2 0,5 3 Câu Đáp án Thang điểm Câu 2 + n ∈
(3 điểm) n−3 2 1 n+ C − C = C ⋅ 2 C ĐK: n n−1 n−1 n+3  n ≥ 3 0,5 n! (n −1)!
(n −1)! (n + 3)! ⇔ ( n 3) − !3! (n 3) = !2! (n 2) ⋅ − − − !1! (n + 2)!1!
⇔ (n − 2)(n −1)n − 3(n − 2)(n −1) = 6(n −1)(n + 3) 0,5 n = −1 (L) ⇔ 2
n −11n −12 = 0 ⇔  0,5 n =  12 (TM) 12 12 k 12 Với 3  4 4  3 n x x x ∑ k 4 12 C x C 4 k k k k x 0,5 12 ( 4 )12−  −  = ⇒ − = = ∑ 12 (−     ) − 51 5  x  k=1  x  k=1
Theo bải ra ta có: 51− 5k = 11 ⇔ k = 8 0,5
Vậy hệ số cần tìm là: C (4)8 8 0,5 12 Trang 1/5 Câu Đáp án Thang điểm Câu 3 (4 điểm)
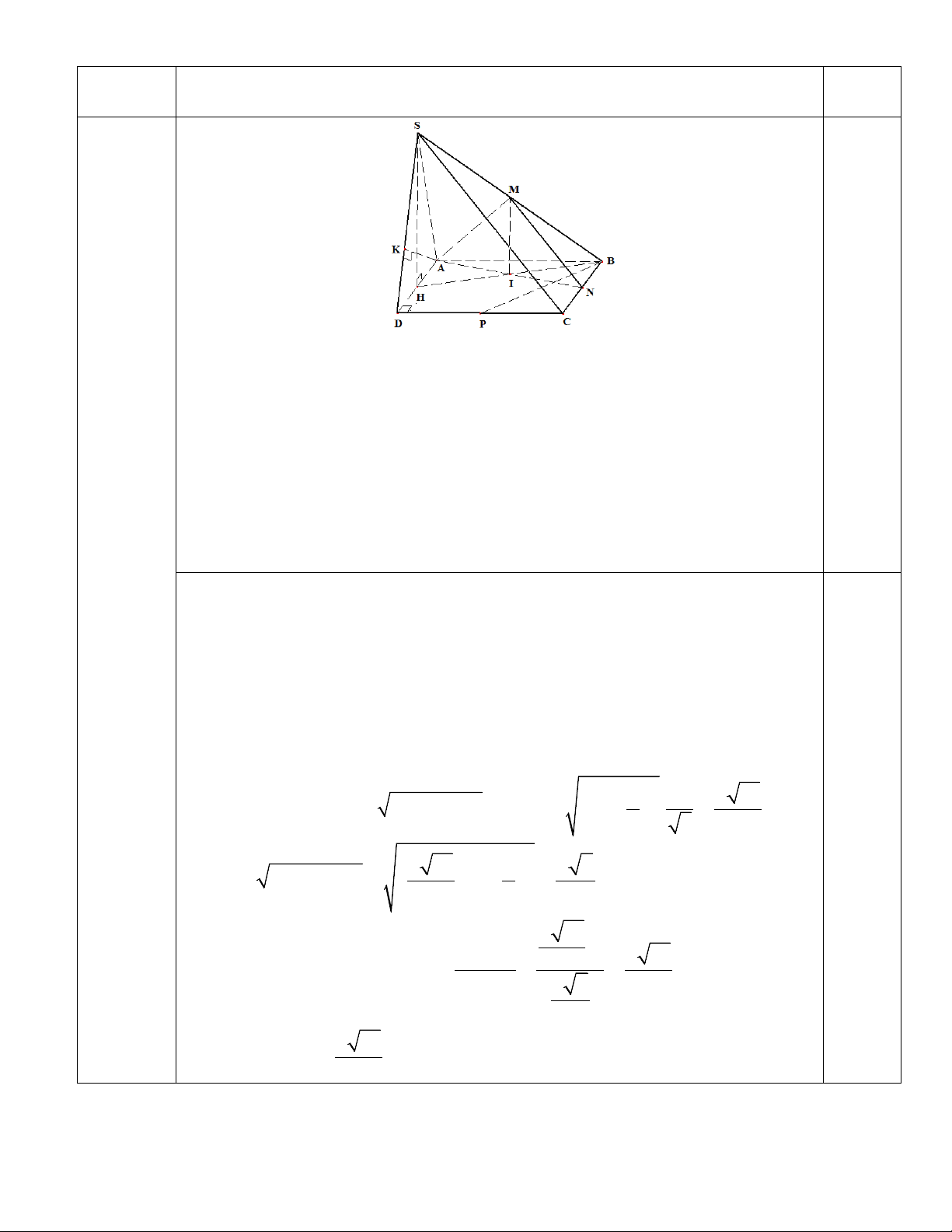
a) Gọi H là trung điểm của AD
(SAD) ⊥ (ABCD) Ta có: 
 ⇒ SH ⊥ ( ABCD) (*) SH ⊥ AD  1,0
Gọi I = AN ∩ BH
Ta có ABNH là hình chữ nhật nên I là trung điểm của BH
⇒ MI / /SH ⇒ MI ⊥ (ABCD) ⇒ MI ⊥ BP (1) Mặt khác  PBC +  BNA =  BAN +  BNA = 0
90 ⇒ BP ⊥ AN (2) 0,5
Từ (1), (2) và MI, AN ⊂ (AMN) ⇒ BP ⊥ (AMN) 0,5 b) Kẻ AK ⊥ ,
SD K ∈ SD
Ta có DC ⊥ AD ⇒ DC ⊥ (SAD) ⇒ DC ⊥ AK ⇒ AK ⊥ (SDC) DC ⊥ SH  1,0 AB / / (SDC) Vì 
 ⇒ d ( AB, SC) = d (AB,(SDC)) = d ( ,
A (SDC)) AK SC ⊂ (SDC) = 
Ta có(SB (ABCD))  =  SBH = 0 , 30 2  2 2 0 2  a  ⇒ = = + = + 1 a SH BH SBH AB AH a . = 15 .tan .tan 30    2  3 6 0,5  a 2 2 2 15  a 2
⇒ SD = SH + HD = a 6   + =      6   2  3 a 15 .a
Ta có SH AD = AK SD ⇒ AK = SH.AD = = a 10 6 . . SD a 6 4 0,5 3
Vậy d(AB SC) = a 10 , 4 Trang 2/5 Câu Đáp án Thang điểm Câu 4 xy + x − 2 y − y ≥ 0
(4 điểm) ĐK :  2
4y − x − 2 ≥ 0 y ≥  1
(1) ⇔ x − y + 3 (x − y)(y +1) − 4(y +1) = 0 0,5
Đặt x − y = u ≥ 0, y +1 = v ≥ 2 u v ⇒ 2 u + uv − 2 3
4v = 0 ⇔ (u − v)(u + 4v)  = = 0 ⇔  u = −4 ( v L)
Với u = v ⇒ x − y = y +1 ⇒ x = 2y +1 0,5
Thay vào phương trình (2) ta được: 0,5 2
4y − 2y − 3 + y −1 = 2y ĐK: + y ≥ 1 13 4 ⇔ 2
4y − 2y − 3 − (2y −1) + ( y −1 −1) = 0 0,5 2(y − 2) y − ⇔ + 2 = 0 0,5 2
4y − 2y − 3 + (2y −1) y −1 + 1   (y − ) 2 + 1 2  = 0(*)  0,5 2
4y − 2y − 3 + (2y −  1) y −1 + 1  Ta có: 2 1 1 + + > ∀y ≥ 13 0, 0,5 2
4y − 2y − 3 + (2y −1) y −1 + 1 4
⇒ PT (*) có nghiệm duy nhất là y = 2 ⇒ x = 5
Vậy tập nghiệm của hệ PT là: S = ( { 2;5)} 0,5 Câu Đáp án Thang điểm Câu 5 2 u u  1 1 
(3 điểm) Ta có: u − u = n , n = 1,2,3,... ⇒ n = 2017 0,5 n 1 n  − +  2017 u u u n+1  n n+1  ⇒ u u u 1 + 2 + ⋅⋅⋅ + n u u u 2 3 n+1  0,5  1 1   1 1   1 1   1 1 
= 2017  −  +  −  + ⋅⋅⋅+  −  +  −   u u u u u u u u 1 2   2 3   n−1 n   n n+1   Trang 3/5  1 1   1  = 2017 −  = 20171 −   u u u 1 n+1   n+1 
Từ công thức xác định của dãy {u , ta có: 1 = u < u < ⋅⋅⋅ < u < ⋅⋅⋅ 0,25 n} 1 2 n+1
Vậy dãy {u là dãy tăng. 0,25 n}
Giả sử dãy {u bị chặn trên. Khi đó tồn tại giới hạn hữu hạn n}
Đặt: lim u = a > 1 →+∞ n n 2 2 Ta có: u  u  u = n
+ u ⇒ lim u = lim n u 0,5 n 1 n n 1  + + + n  n→+∞ n→+∞ 2017  2017  2 ⇔ = a a
+ a ⇔ a = 0 (vô lý) 2017
Do đó {u không bị chặn trên, mà nó lại đơn điệu tăng, nên n} u = +∞ ⇒ 1 lim lim = 0 0,5 →+∞ n n n→+∞ un  u u u   1 
lim  1 + 2 + ⋅⋅⋅ + n  = lim 20171−  = 2017 0,5 n→+∞ n→+∞  u u u u 2 3 n+1   n+1  Câu Đáp án Thang điểm
Câu Áp dụng bất đẳng thức Cô si cho 3 số dương ta có
(6 điểm) (x y z)1 1 1 + + + + ≥ 3 3 3 xyz =   9  x y z  3 xyz ⇒ 1 + 1 + 1 ≥ 9 (*) 1,0 x y z x + y + z Áp dụng (*) ta có P = 1 + 1 + 1 ≥ 9 3 a + 3 3b b + 3 3c c + 3 3a
a + 3b + 3 b + 3c + 3 c + 3a
Áp dụng bất đẳng thức Cô si ta có a 3b 1 1 1 3 (a 3b) + + + + .1.1 ≤ = (a + 3b + 2) 3 3 b 3c 1 1 1 1,0 3 (b 3c) + + + + .1.1 ≤ = (b + 3c + 2) 3 3 c 3a 1 1 1 3 (c 3a) + + + + .1.1 ≤ = (c + 3a + 2) 3 3 Suy ra 1
3 a + 3b + 3 b + 3c + 3 c + 3a ≤ 4(a + b + c) + 6 1,0 3 Trang 4/5 1  3  ≤ 4. + 6 =   3 3  4  Do đó P ≥ 3  3
Đẳng thức xảy ra khi a + b + c = 1  4
⇔ a = b = c =  4
a + 3b = b + 3c = c + 3a = 1
Lưu ý: - Điểm bài thi là tổng điểm của các câu thành phần. Thang điểm toàn bài là
20 điểm, không được làm tròn (điểm lẻ từng ý trong một câu nhỏ nhất là 0,25)
- Thí sinh làm bài bằng cách khác, lập luận chặt chẽ, logic, ra kết quả đúng
vẫn cho điểm tối đa.
……………………….Hết……………………… Trang 5/5
Document Outline

• Đề chon 01
• HDC CHON ĐỀ 1.