Đề thi học sinh giỏi Toán 11 năm 2012 – 2013 trường THPT Thuận An – TT Huế

SỞ GD&ĐT THỪA THIÊN HUẾ
THI HỌC SINH GIỎI TOÁN KHỐI 11
TRƯỜNG THPT THUẬN AN NĂM HỌC 2012-2013
Thời gian làm bài: 120 phút ( không kể thời gian phát đề)
Họ và tên thí sinh :......................................................................... Số báo danh : ......................................... ĐỀ CHÍNH THỨC
Bài 1: (4 điểm) Giải các phương trình sau : 1. 10 2
4sin x.cos x  tan(
)(2sin x 1)  2sin3x 2. x x π 2 2  x 
1 + sin sin x − cos sin x = 2 cos − 3   2 2  4 2 
Bài 2: (2 điểm) Bạn Tùng có 10 người bạn thân, trong đó có Long và Lân. Tùng muốn mời 5 bạn
đến tham dự sinh nhật của mình. Hỏi bạn Tùng có bao nhiêu cách mời, biết rằng hai bạn Long và
Lân rất ghét nhau nên Tùng không thể đồng thời mời cả hai bạn này cùng có mặt. Bài 3: (3 điểm) 1. Chứng minh: 1 2 n n 1 + n+2 2 C + + + = + + + . + C +
C + C + C + C n n ... n n n ... n 2 1 2 1 2 1 2 1 2 1 2n 1 + n
2. Tìm hệ số của số hạng chứa 26
x trong khai triển nhị thức Newtơn  1 7 x  +   , 4  x  biết rằng 1 2 n 20 C + C + + C = − n+ n+ ... n+ 2 1 2 1 2 1 2 1 u   2
Bài 4: (2 điểm) Cho dãy số  1 (u ) :
. Tìm số hạng tổng quát của u theo n. n u   5u 4 n  n 1   n
Bài 5: (2 điểm) Ba số x, y, z theo thứ tự lập thành một cấp số nhân; đồng thời chúng theo thứ tự là
số hạng thứ nhất, số hạng thứ ba và số hạng thứ chín của một cấp số cộng. Tìm 3 số đó biết tổng của chúng bằng 13.
Bài 6: (3 điểm) Trong mặt phẳng Oxy, cho ∆ABC. Biết B,C nằm trên đường thằng d : x  y3 0 ,
A nằm trên đường thẳng d ':3x  y 2  0 , trọng tâm của tam giác ABC là 2 2
G( ; ) và diện tích tam 3 3
giác ABC bằng 10. Tìm tọa độ các đỉnh của tam giác, biết hoành độ của điểm A không âm.
Bài7: (2 điểm) Cho tam giác ABC, về phía ngoài của tam giác, dựng 3 tam giác đều
ABC ,BCA ,CAB . Chứng minh AA ,BB ,CC đồng quy. 1 1 1 1 1 1
Bài 8: (2 điểm) Cho 3 số dương a, b, c thỏa : 1
a  b c  . 2 Chứng minh : 1 1 1    3
a 2b 3c
b 2c 3a
c 2a 3b
--------------------------Hết---------------------
ĐÁP ÁN, BIỂU ĐIỂM Bài Đáp án Điểm 1) 10
1)(2điểm) Giải phương trình:  2
4sin x.cos x tan(
)(2sin x1)  2sin3x (4điểm) 3
Phương trình đã cho tương đương với: sin2x  3cos2x  2sin3x 0,5 1 3  sin 2x 
cos2x  sin3x 0,5 2 2 sin(2x    )  sin3x 0,5 3  x 
   k2  3   k   0,5  4 k2 x     15 5
2)(2điểm) Giải phương trình: x x π 2 2  x 
1+ sin sin x − cos sin x = 2cos  −  2 2  4 2  x x
Phương trình đã cho tương đương với: sin x(sin cos .sin x 1)  0 0,5 2 2 3
 sin (2sin x sin x x 1)  0 0,5 2 2
• sin x  0  x  k 0,5 x x x • 3 2sin
sin 1 0  sin 1  x    k4 0,5 2 2 2 2)
Bạn Tùng có 10 người bạn thân, trong đó có Long và Lân. Tùng muốn mời 5 bạn đến tham dự
sinh nhật của mình. Hỏi bạn Tùng có bao nhiêu cách mời, biết rằng hai bạn Long và Lân rất ghét
(2điểm) nhau nên không thể đồng thời có mặt.
Số cách bạn Tùng chọn 5 người bạn trong 10 người đến dự sinh nhật của mình là : 5 C  252 0,5 10
Số cách bạn Tùng mời 5 người bạn trong 10 người đồng thời có cả Long và Lân là: 3 C  56 0,5 8
Vì hai bạn Long và Lân rất ghét nhau nên không thể đồng thời có mặt, vì vậy bạn Tùng
chỉ có thể mời nhiều nhất là 1 bạn Long hoặc Lân dự sinh nhật. 0,5
Vậy, số cách bạn Tùng mời 5 bạn đến dự sinh nhật là: 25256 196 0,5 3)
1) (1,0 điểm) Chứng minh: 1 2 n n 1 + n+2 2 C + + + = + + + + C +
C + C + C + C n n ... n n n ... n 2 1 2 1 2 1 2 1 2 1 2n 1 + (3điểm) Vì k 2n 1  k C  C
k  ,k  2n 1 nên: 2n 1  2n 1  0,5 1 2n 2 2n 1  n n 1 C  C ;C  C ;............;C  C  2n 1  2n 1  2n 1  2n 1  2n 1  2n 1  Do đó: 1 2 n n 1 + n+2 2 C + + + = + + + (đpcm) + C +
C + C + C + C n n ... n n n ... n 2 1 2 1 2 1 2 1 2 1 2n 1 + 0,5 n
2) (2,0 điểm) Tìm hệ số của số hạng chứa 26
x trong khai nhị thức New tơn  1 7 x  +   , 4  x  biết rằng 1 2 n 20 C + C + + C = − n+ n+ ... n+ 2 1 2 1 2 1 2 1 Theo câu 1) và từ 0 2n 1 C  C  1 ta có: 2n 1  2n 1  0,5 1 2 n 1 0 1 2n 1 C + + + = + + + − (1) + C + C + C + C + C + n n ... n ( n n ... n+ ) 1 2 1 2 1 2 1 2 1 2 1 2 1 2 Mà 2n 1+ 2n 1 + 0 1 2n 1 2 = (1+1) = C + + + (2) + C + C + n n ... 2 1 2 1 2n 1 + 0,5
Do đó, từ (1), (2) và từ giả thiết đã cho suy ra: 1 2n 1  20 2
1 2 1  n 10 0,5 2
Với n 10 , tính được hệ số của số hạng chứa 26
x trong khai nhị thức New tơn 10  1 0,5 7 x  +   là 6 C  210 4  x  10 4) u   2 (2 điểm) Cho dãy số  1 (u ) :
Tìm số hạng tổng quát của u theo n. n  n (2điểm) u 
 5u 4,n 1  n 1   n
Ta có: u  5u 4  (u 1)  5(u 1) n 1 0,5  n n 1  n v 1
Do đó, đặt v  u 1 thì ta được dãy  1 (v ) : n n n  0,5
v  5v ,n 1  n 1   n n
Dãy (v ) là cấp số nhân với công bội q=5 và v 1 nên 5 1 v   0,5 n 1 n 4 n
Vậy số hạng tổng quát theo n của dãy (u )là: 5 5 u   0,5 n n 4 5)
Ba số x, y, z theo thứ tự lập thành một cấp số nhân; đồng thời chúng theo thứ tự là số hạng thứ
nhất, số hạng thứ ba và số hạng thứ chín của một cấp số cộng. Tìm 3 số đó biết tổng chúng bằng (2điểm) 13.
Vì x, y, z theo thứ tự là số hạng thứ nhất, thứ 3 và thứ 9 của một cấp số cộng, do đó nếu
gọi d là công sai của cấp số cộng thì ta có: y  x 2d; z  x 8d 0,5
Tổng của 3 số là 13 nên: x  y  z 13  3x 10d 13 0,5
X, y, z theo thứ tự lập thành 1 cấp số nhân nên: d  0 2 2 2
xz  y  x(x 8d)  (x 2d)  xd d  0   0,5 x  d  • 13
d  0  x  y  z  3 0,5
• x  d  x 1, y  3, z  9 6)
Trong mặt phẳng Oxy , cho ABC . Biết B,C nằm trên đường thằng d : x  y3  0 , A nằm
(3điểm) trên đường thẳng d ':3x  y 2  0 , trọng tâm của tam giác ABC là 2 2
G( ; ) và diện tích tam 3 3
giác là 10. Tìm tọa độ các đỉnh của tam giác, biết hoành độ của A không âm.
Vì A  d ' : 3x  y 2  0 và hoành độ A không âm nên ( A ;
a 3a2), a  0 0,5
B,C  d : x  y3  0 và G là trọng tâm nên: 5 2 d( ,
A BC)  3d(G,BC)  (*) 0,5 2 2a 5 2a 5 5 2 a  0 Mà d( , A BC)  nên ta có :    2 2 2 a 5  0,5
Vì a  0 nên ta nhận giá trị a  0  ( A 0;2)
Ngoài ra, từ (*) và diện tích tam giác ABC bằng 10, ta suy ra được BC  4 2 và tọa độ 0,5
trung điểm I của BC là I(1;2) b  1
B  d : x  y3  0  B( ;3 b b) và 2 2
IB  (b1) (1b)  2 2   0,5 b  3 
• b  1 B(1;4), C(3;0) 0,5
• b  3  B(3;0), C(1;4) 7)
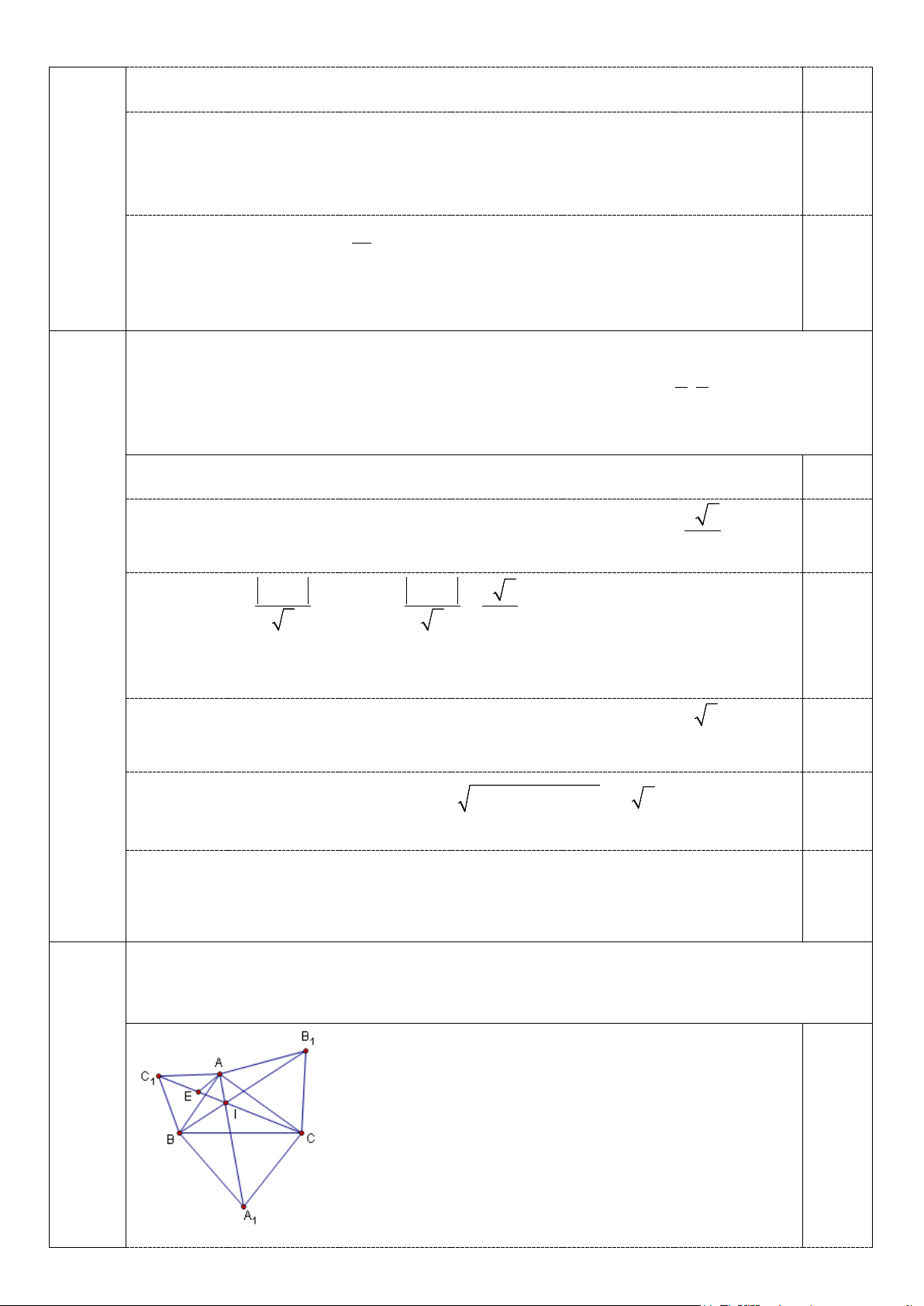
Cho tam giác ABC, về phía ngoài của tam giác, dựng 3 tam giác đều ABC ,BCA ,CAB . Chứng 1 1 1
(2điểm) minh AA ,BB ,CC đồng quy 1 1 1 0,5
Xét phép quay tâm B, góc quay 0 60 , ta có: 0 Q (A )  C, ( Q
A)  C  Q
(A A)  CC  (A , A C C)  60 0 0 0 (B,60 ) 1 (B,60 ) 1 (B,60 ) 1 1 1 1
Gọi I là giao điểm của AA ,CC thì  0 AIC  60 . 1 1 1 0,5
Trên C I , lấy điểm E sao cho IE=IA, suy ra tam giác IAE đều. 1
Xét phép quay tâm A, góc quay 0 60 , ta có 0,5 Q (C)  B , ( Q E)  I, ( Q C )  B 0 0 0 ( A,60 ) 1 ( A,60 ) ( A,60 ) 1
Mà C,E,C thẳng hàng, suy ra B ,I,B thẳng hàng. Vậy AA ,BB ,CC đồng quy tại I 0,5 1 1 1 1 1 8)
Cho 3 số dương a,b,c thỏa : 1
a  b c  . Chứng minh : (2điểm) 2 1 1 1    3
a 2b 3c
b 2c 3a
c 2a 3b
Áp dụng BĐT Cô si cho 3 số ta có: 1 1 1 1
(a2b3c) 3 1
(a2b3c) 3 0,5 .  .     
2 a2b3c 2 a2b3c 2 2
a 2b3c 2 2
b  c  a
c  a  b Tương tự ta có: 1 ( 2 3 ) 3 1 ( 2 3 ) 3   ;   0,5
b 2c 3a 2 2
c 2a 3b 2 2
Cộng các bất đẳng thức trên vế theo vế ta được: 1 1 1 9 0,5  
(3a 3b 3c) 
a 2b 3c
b 2c 3a
c 2a 3b 2 1 1 1     3(đpcm) 0,5
a 2b 3c
b 2c 3a
c 2a 3b
Document Outline

• de thi HSG khoi 11
• Dethi HSG11-2013