Đề thi học sinh giỏi Toán 11 năm 2020 – 2021 trường THPT Đông Hà – Quảng Trị

Đề thi học sinh giỏi Toán 11 năm 2020 – 2021 trường THPT Đông Hà – Quảng Trị gồm 01 trang với 05 bài toán dạng tự luận, thời gian làm bài 180 phút, đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm; kỳ thi được diễn ra vào ngày 15 tháng 04 năm 2021.

30 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Đề thi gồm 1 trang
TRƯỜNG THPT ĐÔNG HÀ
TỔ TOÁN
ĐỀ CHÍNH THỨC
KỲ THI CHỌN HỌC SINH GIỎI LỚP 11
NĂM HỌC 2020 - 2021
Môn: TOÁN
Thời gian: 180 phút (Không kể thời gian giao đề)
Ngày thi: 15 /4/2021
Câu 1. (5,0 điểm).
1. Tìm số nguyên dương
n
biết rằng:
1 3 5 2 1
2 1 2 1 2 1 2 1
... 1024
n
n n n n
C C C C
.
2. Một trường có 50 học sinh giỏi, trong đó có 4 cặp anh em sinh đôi. Cần chọn ra 3 học
sinh trong số 50 học sinh để tham gia trại hè. Tính xác suất để 3 em được chọn không
có cặp anh em sinh đôi.
Câu 2. (2,0 điểm). Giải phương trình
2
2 2
1
x
x
.
Câu 3. (5,0 điểm).
1. Cho ba số
0, 0, 0
a b c
thỏa mãn
2 2 2
3
a b c
. Chứng minh rằng
3 3 3
2 2 2
3
.
2
3 3 3
a b c
b c a
2. Chứng minh dãy số
n
u
với
2 2 2
1 1 1
...
1 2
n
u
n
là một dãy số tăng và bị chặn.
Câu 4. (2,0 điểm). Tìm giá trị nhỏ nhất của biểu thức
2 2 2 2
1 2 9 6
P x y y x y y
trong đó
,
x y
là các số thực thỏa mãn
1
y
x
.
Câu 5. (6,0 điểm).
1. Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật với
, 2 ,
AB a AD a
( )
SA ABCD
và
SA a
, M là trung điểm của
CD
.
a) Tính góc giữa
SM
và mp
( )
SAB
.
b) Tính theo
a
khoảng cách từ
A
đến mp
( )
SBM
2. Cho
, ,
M N P
lần lượt là trung điểm của ba cạnh
, ,
BC CA AB
của
ABC
. Gọi
, ,
H G O
lần lượt là trực tâm, trọng tâm, tâm đường tròn ngoại tiếp
ABC
,
I
là tâm đường tròn ngoại
tiếp
MNP
. Chứng minh
, , ,
H G O I
thẳng hàng.
.........HẾT........
Họ và tên:………………………….……… Lớp:………SBD:……
Đề thi gồm 1 trang
HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI VĂN HÓA LỚP 11 THPT NĂM HỌC 2020-2021.
MÔN TOÁN
Câu Nội dung Điểm
Câu
1.1
(2
điểm)
+Xét khai triển
2 1 0 1 1 2 2 2 1 2 1
2 1 2 1 2 1 2 1
2 1 0 1 1 2 2 2 1 2 1
2 1 2 1 2 1 2 1
(1 ) ... (1)
(1 ) ... (2)
n n n
n n n n
n n n
n n n n
x C C x C x C x
x C C x C x C x
+Trừ từng vế (1), (2) ta có
2 1 2 1 1 1 3 3 5 5 2 1 2 1
2 1 2 1 2 1 2 1
(1 ) (1 ) 2( ... )
n n n n
n n n n
x x C x C x C x C x
(3)
+Thay
1
x
vào (3) rồi chia hai vế cho 2 ta có
1 3 5 2 1 2
2 1 2 1 2 1 2 1
... 2
n n
n n n n
C C C C
+Suy ra
2 10
2 1024 2 2 10 5
n
n n
0.5
0.5
0.5
0.5
Câu
1.2
(3
điểm)
+Số cách chọn 3 học sinh bất kì từ 50 học sinh là
3 3
50 50
19600
C C
+Số cách chọn 3 học sinh trong đó có 1 cặp anh em sinh đôi là 4.48
Gọi biến cố A: “Chọn được 3 học sinh không có cặp anh em sinh đôi”
+Ta có
3
50
4.48 19408
A
C
+
19408 1213
( )
19600 1225
A
P A
1
0,5
1
0.5
Câu 2
(2
điểm)
+Điều kiện
1 1
x x
hoặc
1
x
1
x
Phương trình vô nghiệm
+Xét
1
x
: Đặt
1
, 0;
cos 2
x t
t
Ta có phương trình
1 1
2 2 sin cos 2 2 sin cos
cos sin
t t t t
t t
2 sin 2 sin 2 sin 2 sin
4 4
t t t t
0.5
1
Đề thi gồm 1 trang
2 2
2
4
4
( )
2
2 2
4
4 3
t k
t k
k
t k
t k
+
1
0; 2
2 4
cos
4
t t x
thỏa
1
x
Vậy nghiệm của phương trình là
2
x
0.5
Câu
3.1
(3
điểm)
+Ta có
3 3 2 6
2
3
2 2
3 3 2 6
2
3
2 2
3 3 2 6
2
3
2 2
3 3
3 (1)
16 64 4
2 3 2 3
3 3
3 (2)
16 64 4
2 3 2 3
3 3
3 (3)
16 64 4
2 3 2 3
a a b a
a
b b
b b c b
b
c c
c c a c
c
a a
+Cộng (1), (2), (3) vế theo vế ta có
2 2 2
2 2 2
9 3
( )
16 4
12 9 9 12 3
16 4 4 16 2
a b c
P a b c
P P
Dấu “=” xảy ra khi
1
a b c
1.5
1.5
Câu
3.2
(2
điểm)
Ta có
* *
1 1
2
: ,
( 1)
n n n n
n N u u u u n N
n
Dãy
( )
n
u
tăng
( )
n
u
tăng
*
1
1,
n
u u n N
2 2 2
1 1 1 1 1 1
1 ... 1 ...
1.2 2.3 ( 1).
2 3
1 1 1 1 1 1
1 1 ... 2 2
2 2 3 1
n
u
n n
n
n n n
1 2
n
u
*
,
n N
( )
n
u
bị chặn
0.5
0.25
1.0
0.25
Đề thi gồm 1 trang
Câu 4
(2
điểm)
+Ta có
2 2 2 2
( 1) ( 3)
P x y x y
Đường thẳng
: 2 2 0
x y
+Lấy
( ; )
M x y
, hai điểm
(0; 1), (0; 3)
A B
P AM BM
A, B nằm cùng phía đối với
, lấy A’ đối xứng với A qua
4 7
' ; , '
5 5
A MA MA
+
' ' 2 5
P AM BM A M BM A B
+
min 2 5
P
khi A’, B, M thẳng hàng
Khi
2 2
' ;
3 3
M A B M
Vậy
min 2 5
P
khi
2 2
;
3 3
x y
0.5
0.5
0.5
0.5
Câu
5.1
(4
điểm)
a) +Gọi E là trung điểm AB
/ /
( )
( )
ME AD
ME SAB
AD SAB
Góc giữa SM và (SAB) là góc
0 0
(0 90 )
MSE
+Tính
tan : 2
ME AD a
2
2 2 2
5
4 2
2 4 5
tan tan
5
5
2
a a
SE AS AE a
ME a
MSE
SE
a
1
1
Đề thi gồm 1 trang
b. +
( ) ( )
AN BM SAN SBM
Kẻ
( )
AK SN AK SBM
( ,( ))
AK d A SBM
+Tính
: ( )
ABM ABCD ADM BCM
AK S S S S
2 2 2
2 2
ABCD ADM
S S a a a
+
2
2 2
2
2
2
2
1 2
.
2
2 4
17
4
4
ABM
ABM
S
a
S AN BM AN
BM
BC BM
a a
a
a
2 2 2
1 1 1 4 4
( ,( ))
33 33
a a
AK d A SBM AK
AK SA AN
0.5
0,5
0.5
0,5
Câu
5.2
(2
điểm)
+
1
( , )
2
:
G
V ABC MNP
+Ta có
/ /PN BC
MO PN
MO BC
Tương tự
NO PM
O là trực tâm tam giác MNP
+
1
( , )
2
1
: , ,
2
G
V H O GO GH H G O
 
thẳng hàng
+
1
( , )
2
: , ,
2
G
V O I GI GO I G O
 
thẳng hàng
Vậy
, , ,
H G O I
thẳng hàng.
0.5
0.5
0.5
0.5
.........HẾT........
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT ĐÔNG HÀ
KỲ THI CHỌN HỌC SINH GIỎI LỚP 11 TỔ TOÁN NĂM HỌC 2020 - 2021 ĐỀ CHÍNH THỨC Môn: TOÁN
Thời gian: 180 phút (Không kể thời gian giao đề) Ngày thi: 15 /4/2021 Câu 1. (5,0 điểm).
1. Tìm số nguyên dương n biết rằng: 1 3 5 2n 1 C C C . . C   1024 . 2n 1  2n 1  2n 1  2n 1 
2. Một trường có 50 học sinh giỏi, trong đó có 4 cặp anh em sinh đôi. Cần chọn ra 3 học
sinh trong số 50 học sinh để tham gia trại hè. Tính xác suất để 3 em được chọn không có cặp anh em sinh đôi. x
Câu 2. (2,0 điểm). Giải phương trình x   2 2 . 2 x 1 Câu 3. (5,0 điểm).
1. Cho ba số a  0, b  0, c  0 thỏa mãn 2 2 2
a b c  3 . Chứng minh rằng 3 3 3 a b c 3    . 2 2 2 b  3 c  3 a  3 2 1 1 1
2. Chứng minh dãy số u với u   ..  là một dãy số tăng và bị chặn. n  n 2 2 2 1 2 n
Câu 4. (2,0 điểm). Tìm giá trị nhỏ nhất của biểu thức 2 2 2 2
P  1  x  y  2y  9  x y  6y y
trong đó x, y là các số thực thỏa mãn x   1. 2 Câu 5. (6,0 điểm).
1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB  a, AD  2a,
SA  (ABCD) và SA  a , M là trung điểm của CD .
a) Tính góc giữa SM và mp(SAB).
b) Tính theo a khoảng cách từ A đến mp (SBM )
2. Cho M , N, P lần lượt là trung điểm của ba cạnh BC, C , A AB của A  BC . Gọi H,G,O
lần lượt là trực tâm, trọng tâm, tâm đường tròn ngoại tiếp A
 BC , I là tâm đường tròn ngoại tiếp M
 NP . Chứng minh H,G,O, I thẳng hàng. .........HẾT........
Họ và tên:………………………….……… Lớp:………SBD:…… Đề thi gồm 1 trang HƯỚNG DẪN CHẤM
ĐỀ THI CHỌN HỌC SINH GIỎI VĂN HÓA LỚP 11 THPT NĂM HỌC 2020-2021. MÔN TOÁN Câu Nội dung Điểm Câu +Xét khai triển 1.1 2n 1  0 1 1 2 2 2n 1  2n 1 (1  x)  C C x C x . . C x  (1) (2 2n 1  2n 1  2n 1  2n 1  2n 1  0 1 1 2 2 2n 1  2n 1  0.5 điểm) (1  x)  C C x C x  . .C x (2) 2n 1  2n 1  2n 1  2n 1 
+Trừ từng vế (1), (2) ta có 2n 1  2n 1  1 1 3 3 5 5 2n 1  2n 1 (1  x) (1x)
 2(C x C x C x . . C x  ) (3) 2n 1  2n 1  2n 1  2n 1  0.5
+Thay x  1 vào (3) rồi chia hai vế cho 2 ta có 1 3 5 2n 1 2 C C C .. C   2 n 2n 1  2n 1  2n 1  2n 1  0.5 +Suy ra 2n 10
2  1024  2  2n  10  n  5 0.5 Câu
+Số cách chọn 3 học sinh bất kì từ 50 học sinh là 3 3 C    C  19600 1 1.2 50 50 0,5 (3
+Số cách chọn 3 học sinh trong đó có 1 cặp anh em sinh đôi là 4.48
điểm) Gọi biến cố A: “Chọn được 3 học sinh không có cặp anh em sinh đôi” +Ta có 3   C  4.48  19408 A 50 1  A 19408 1213 P( ) A     19600 1225 0.5 +
Câu 2 +Điều kiện x  1  x  1  hoặc x  1 (2 0.5 điểm) x  1
  Phương trình vô nghiệm 1   +Xét x  1: Đặt x  ,t   0;  cost  2 Ta có phương trình 1 1 
 2 2  sint  cost  2 2 sint cost cost sint      2 sin t   
    2 sin2t  sin2t  sin t    1       4    4 Đề thi gồm 1 trang  2t  k2      t      k2  4      4    (k  )             2  2t k2        4 t     k    4 3      1 + t  0;   t   x   2  thỏa x  1  2 4 cos  4 0.5
Vậy nghiệm của phương trình là x  2 Câu +Ta có 3.1 3 3 2 6 a a b  3 a 3 (3 2 3    3  a (1) điểm) 2 2 2 b  3 2 b  3 16 64 4 3 3 2 6 b b c  3 b 3 2 3    3  b (2) 2 2 2 c  3 2 c  3 16 64 4 3 3 2 6 c c a  3 c 3 1.5 2 3    3  c (3) 2 2 2 a  3 2 a  3 16 64 4
+Cộng (1), (2), (3) vế theo vế ta có 2 2 2 a b c  9 3 2 2 2 P   (a b c ) 16 4 12 9 9 12 3  P    P    1.5 16 4 4 16 2
Dấu “=” xảy ra khi a  b  c  1 Câu 1 3.2 Ta có * * n  N : u  u   u  u , n  N n 1  n 2 n 1 (n 1)  n (2 0.5 điểm)  Dãy (u )tăng n (u )tăng *  u  u  1, n  N n n 1 0.25 1 1 1 1 1 1 u  1   . .   1   . .  n 2 2 2 2 3 n 1.2 2.3 (n 1).n  1 1 1  1 1                 1 1 1 . .  1.0         2   2 2 2 3   n 1 n  n  1  u  2 * , n  N n  (u )bị chặn 0.25 n Đề thi gồm 1 trang Câu 4 +Ta có 2 2 2 2
P  x (y 1)  x (y  3) 0.5 (2
điểm) Đường thẳng  : 2x  y  2  0
+Lấy M(x;y)   , hai điểm ( A 0;1),B(0;3) 0.5  P  AM  BM
A, B nằm cùng phía đối với  , lấy A’ đối xứng với A qua  4 7  A' ;   ,MA'  MA  5 5 0.5
+P  AM  BM  A ' M  BM  A ' B  2 5
+ min P  2 5 khi A’, B, M thẳng hàng 2 2
Khi M  A'B    M  ;     3 3 2 2 0.5
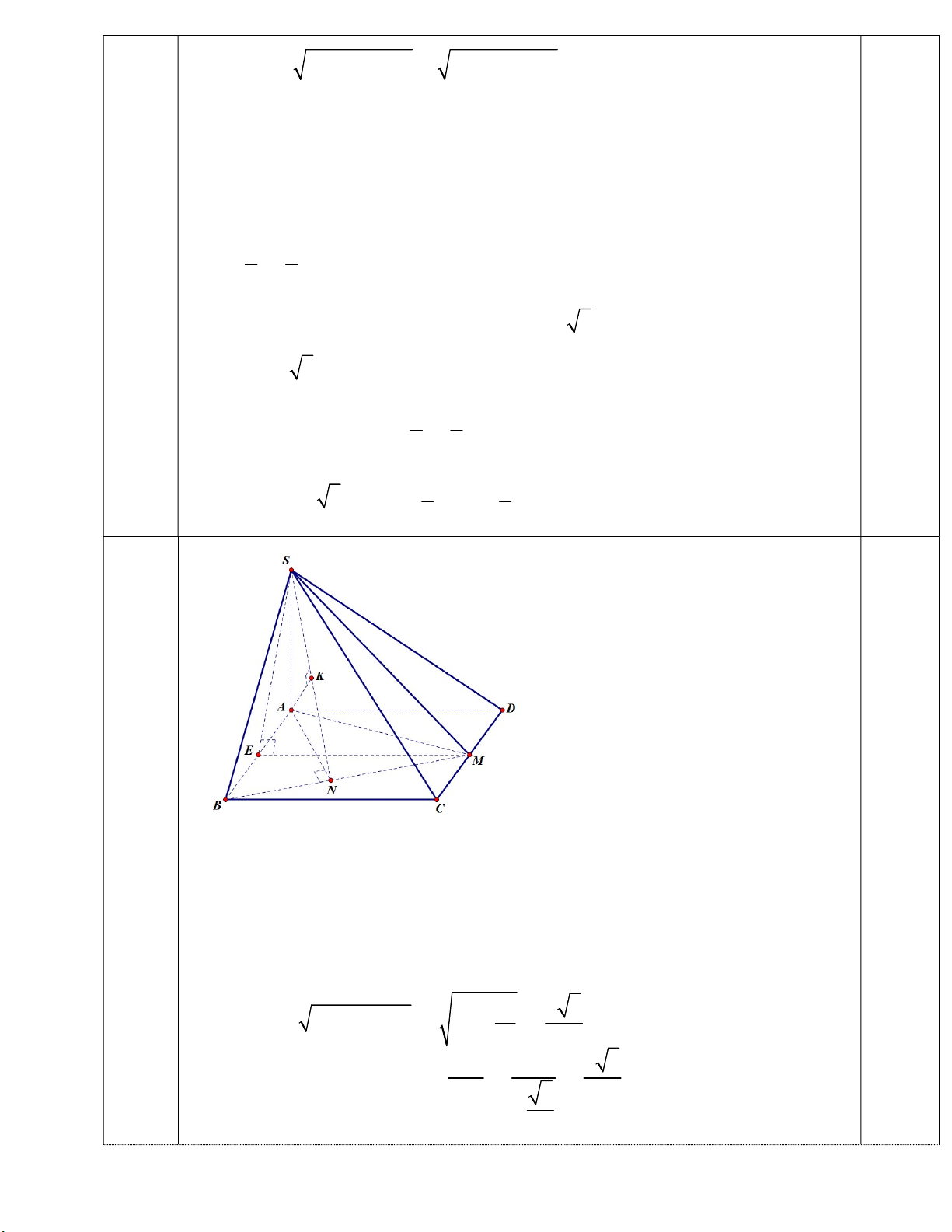
Vậy min P  2 5 khi x  ;y   3 3 Câu 5.1 (4 điểm)
a) +Gọi E là trung điểm AB M  E / /AD     ME  (SAB) A  D  (SAB) 
Góc giữa SM và (SAB) là góc    MSE 0 0 (0    90 ) 1
+Tính tan : ME  AD  2a 2 2 2 2 a a 5 SE  AS  AE  a   4 2  ME 2a 4 5  tan  tanMSE    SE 1 5 5 a 2 Đề thi gồm 1 trang
b. + AN  BM  (SAN )  (SBM )
Kẻ AK  SN  AK  (SBM) 0.5 AK  d( , A (SBM)) +Tính AK : S  S (S  S ) A  BM ABCD A  DM B  CM 2 2 2  S 2S  2a a  a ABCD A  DM 0,5 2 1 2S A  BM 2  . a S AN BM  AN   A  BM 2 2 2 BM BC  BM 0.5 2 2a 4a   2 2 a 17 4a  + 4 1 1 1 4a 4      ( ,( )) a AK d A SBM  AK  2 2 2 AK SA AN 33 33 0,5 Câu V : A  BC  M  NP 0.5 5.2 1 + (G, ) 2 (2  điểm) PN / /BC +Ta có   MO  PN M  O  BC  Tương tự NO  PM  0.5
O là trực tâm tam giác MNP  1  V
: H  O  GO   GH  H,G,O thẳng hàng 1 0.5 G  2 + ( , ) 2  1  V
:O  I  GI   GO  I,G,O thẳng hàng 1 G  2 + ( , ) 2 Vậy H ,G,O, I 0.5 thẳng hàng. .........HẾT........ Đề thi gồm 1 trang