

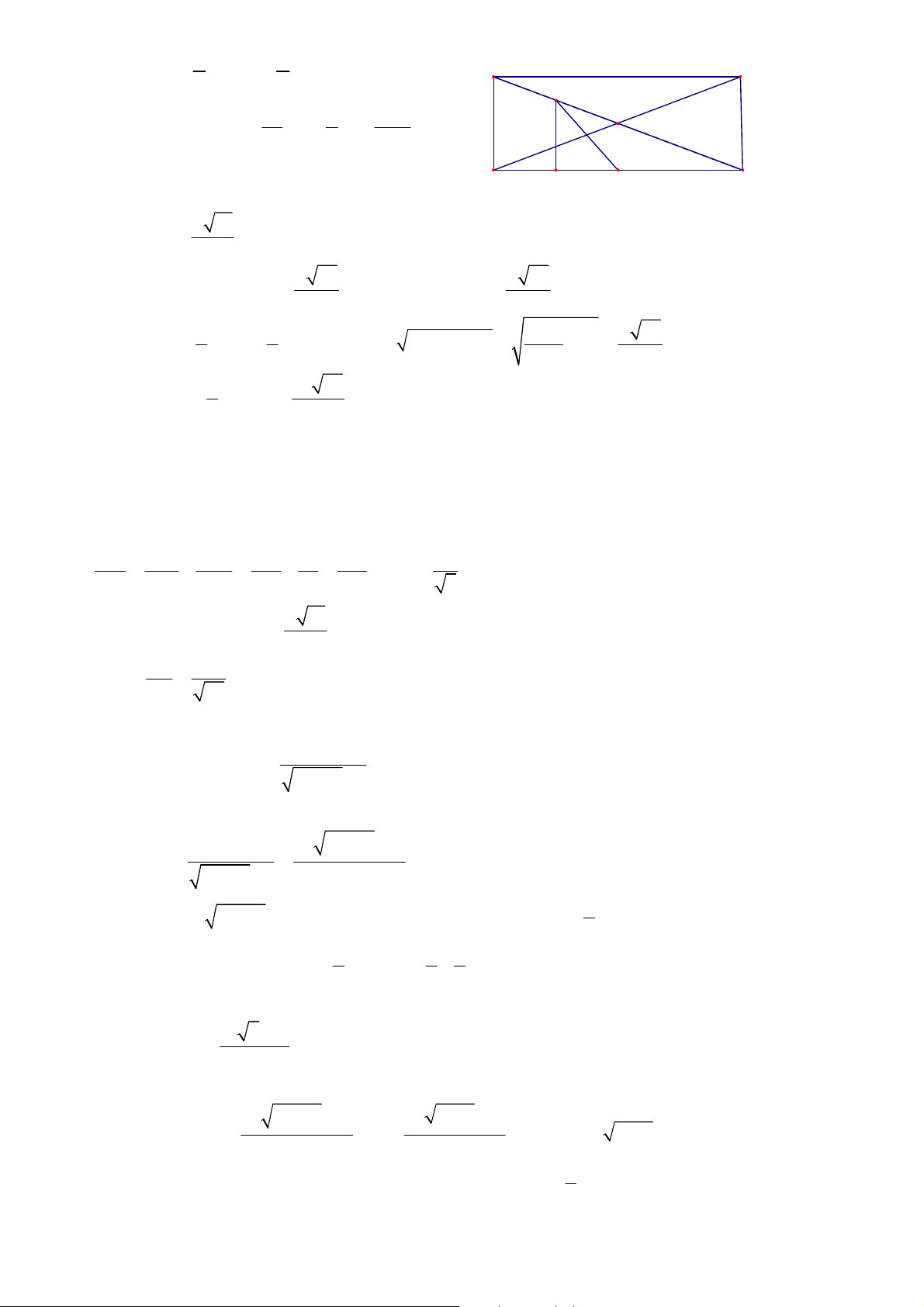
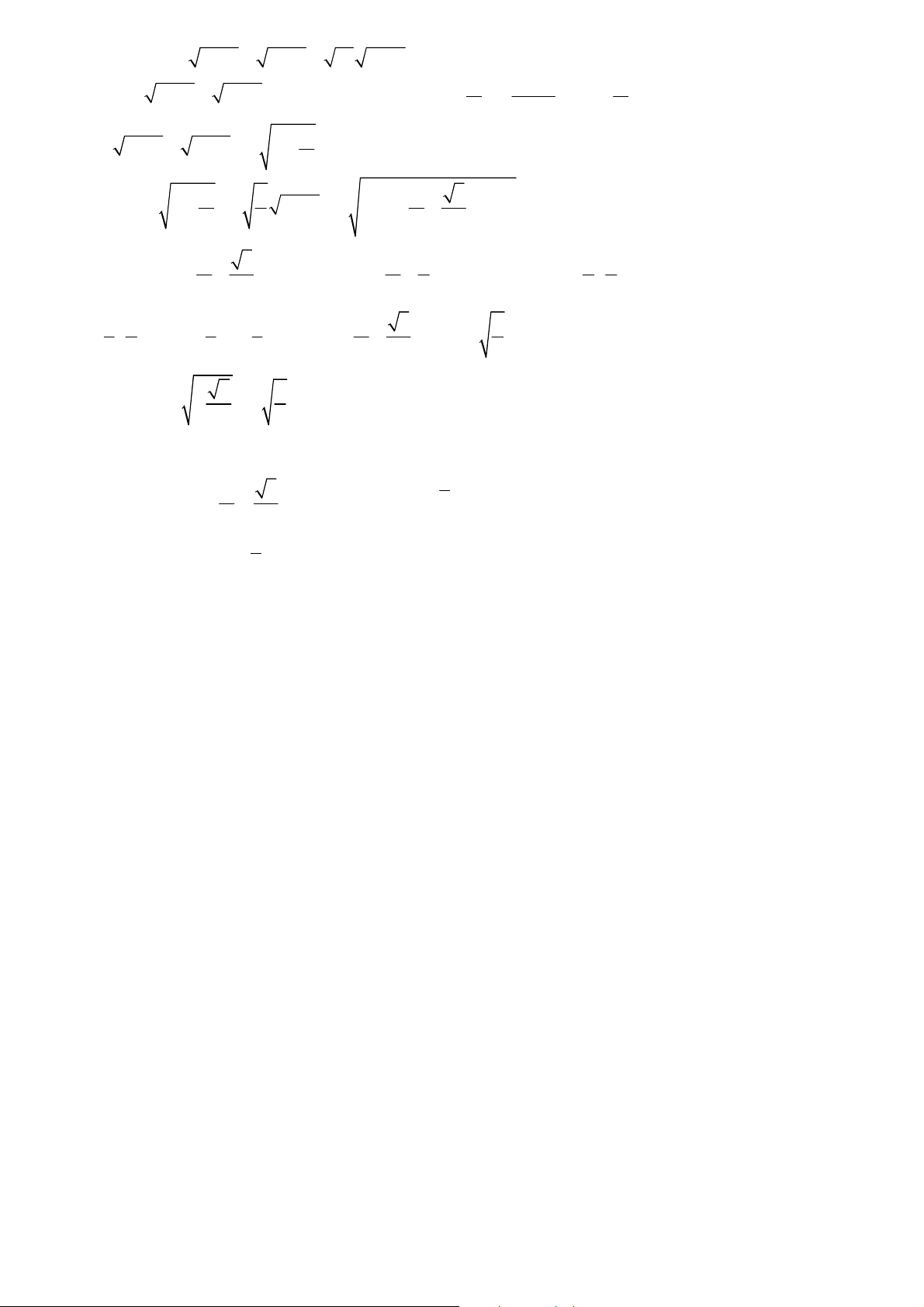
Preview text:
(sinx − o
c sx)(sin 2x − 3) − sin 2x − o c s2x +1
Câu 1. Xét phương trình: = 0 (1) 2 sin x − 2 π x ≠ + k2π Đ 2 4 K sin x ≠ ⇔
(k, l ∈ Z ) 2 3 π x ≠ + l2π 4
Khi đó phương trình (1) ⇔ (sinx − o
c sx)(sin 2x − 3) − sin 2x − o c s2x +1 = 0
⇔ ( x − c x)( x − ) 2 s in os sin 2 3 − 2sin .
x cosx + 2sin x = 0 ⇔ (sinx − o
c sx)(sin 2x − 3) + 2sin (
x s inx − cosx) = 0 ⇔ ( − = x − c x)( x + x − ) s inx o c sx 0 (2) s in os sin 2 2 sin 3 = 0 ⇔
sin 2x + 2sin x − 3 = 0 (3) π π 5π
PT (2) ⇔ sin(x − ) = 0 ⇔ x =
+ kπ , đối chiếu điều kiện ta có x =
+ k2π (k ∈ℤ) . 4 4 4 s in2x=1
PT (3) ⇔ sin2x+2sin x = 3 ⇔ (vn) s in x = 1 5π Vậy x =
+ k2π (k ∈ℤ) . 4 5π 5
x ∈ (−2018π ; 2019π ) ⇔ 2 − 018π <
+ k2π < 2019π ⇔ −2018 < + 2k < 2019 4 4
Do k ∈ ℤ nên k ∈{ −1009, −1008,....,1008} suy ra có 2018 nghiệm. Câu 1b. Tính lim + + − + + + →−∞ ( 3 3 2 2 x 2x 1 4x 2x 3 mx x ) Nếu m = −3 thì lim + + − + + + →−∞ ( 3 3 2 2 x 2x 1 4x 2x 3 mx x ) = lim + + − − + + + →−∞ ( 3 3 2 2 ( x 2x 1 x) ( 4x 2x 3 2x) x ) 2x +1 2 Ta có lim
x + x + − x = = x→−∞ ( 3 2 1 ) 2 3 2 lim x→−∞ 3 2 2 3 2 2 2 3 3
(x + 2x +1) + x (x + 2x +1) + x 3 x + − lim
x + x + + x = = x→−∞ ( 2 3 1 2 4 2 3 2 ) lim x→−∞ 2
4x + 2x + 3 − 2x 2 7 Suy ra lim x + x + −
x + x + + mx = x→−∞ ( 3 3 2 2 2 1 4 2 3 ) 6 Nếu m < 3 − thì lim + + − + + + →−∞ ( 3 3 2 2 x 2x 1 4x 2x 3 mx x ) = lim + + − − + + + + + = +∞ →−∞ ( 3 3 2 2 ( x 2x 1 x) ( 4x 2x 3 2x) (m 3)x x )
Nếu m > −3 thì lim + + − + + + →−∞ ( 3 3 2 2 x 2x 1 4x 2x 3 mx x ) = lim + + − − + + + + + = −∞ →−∞ ( 3 3 2 2 ( x 2x 1 x) ( 4x 2x 3 2x) (m 3)x x ) 2 1 3 1 C − C C − C
Câu 2a. Theo giả thiết ta có 2 1 3 1
C = C + 4d; C = C +14 n n n n d = n n n n 4 14 2 1 3 1 3 2 1
⇔ 7(C − C ) = 2(C − C ) ⇔ 2C − 7C + 5C = 0 n n n n n n n 1 n = 11
n(n −1)(n − 2) n(n −1) 2 2 − 7
+ 5n = 0 ⇔ 2n − 27n + 55 = 0 ⇔ 5 6 2 n = (L) 2
Với n = 11 , thử lại thỏa mãn cấp số cộng 2 2 2 2 1 Ta cần chứng minh ( 0 C ) + ( 2 C ) + ( 4 C ) +....+ ( 22 C ) 23 = C 23 23 23 23 46 2 2 2 2 2 n− 1
Ta sẽ chứng minh bài toán tổng quát ( 0 C ) + ( 2 C ) + ( 4 C ) +....+ ( 1 C ) n
= C với n lẻ n n n n 2 2 n Xét khai triển 2n n n x x x ( 0 1 n n C C x C x )( 0 n 1 n 1 (1 ) (1 ) ( 1) ... C x C x − + = + + = + + + + +... n + C n n n n n n )
Đồng nhất hệ số của n
x của đẳng thức trên ta có
(C )2 +(C )2 +(C )2 +(C )2....+( n C )2 0 1 2 3 n = C (1) n n n n n 2n n 1 − n 1 + Do n lẻ và 0 n 1 n 1 − 2 2
C = C ; C = C ;...C = C ; n n n n n n 2 2 2 2 2 2 2 2 2 nên ( 0 C C C C C C C C C − + + + + = + + + + n )
( 1n) ( 2n) ( 3n)
( nn) ( 0n) ( 2n) ( 4n) ( n 1 .... 2 .... n ) ) 2 2 2 2 n− 1 Thay vào (1) ta có ( 0 C ) + ( 2 C ) + ( 4 C ) +....+ ( 1 C ) n = C (đpcm n n n n 2 2 n A
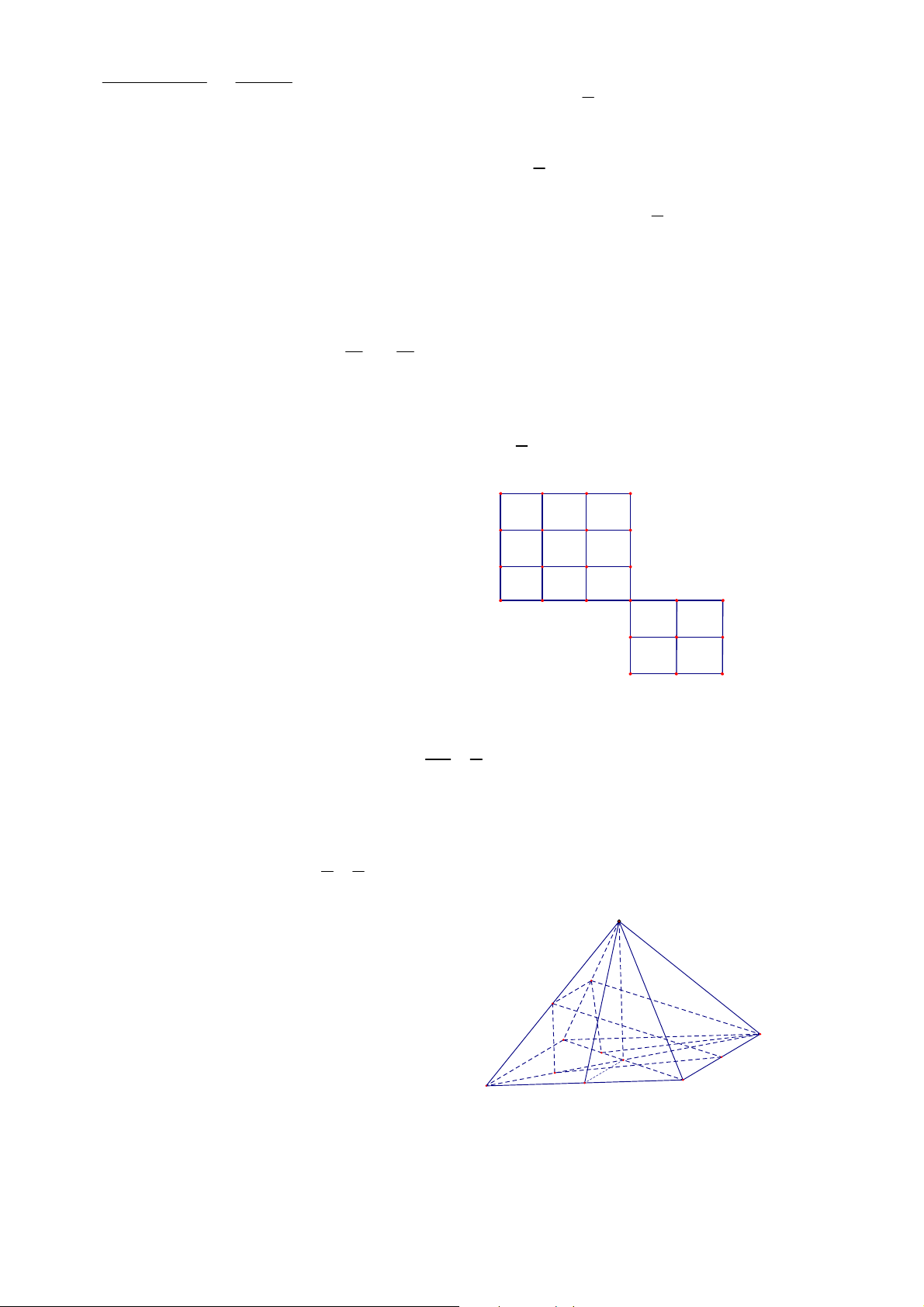
Câu 2b Kiến muốn đi đến B thì bắt buộc phải đi qua D
Gọi m là số cách đi từ A đến D
Gọi n là số cách đi từ D đến B
Gọi k là số cách đi từ D đến B mà không đi D C E qua C I G F H K B
Ta có số cách đi từ A đến B là mn ; số cách đi từ A đến B mà không đi qua C là mk . mk k
Ta có xác suất mà kiến đi được đến B là p = = mn n
Các cách đi từ D đến B mà có đi qua C là: DCEFB; DCIFB; DCIKB; suy ra số cách đi từ D đến B có mà không đi qua C là 3.
Vì tính đối xứng của lưới ô vuông 2x2 nên số cách đi từ D đến B mà không qua C là 3. k 1
Suy ra k = 3, n = 6 . Do đó p = = n 2
Câu 3a Vì SA = SC nên SO ⊥ AC S
Vì SB = SD nên SO ⊥ BD
Do đó SO ⊥ ( ABCD) P Trong tam giác SAC kẻ M
MH ⊥ AC (H ∈ AC) MH SO
MH ⊥ (ABCD) C D Theo giả thiết thì 0 MNH = 60 I N H O A K B 2 3 a Ta có: HQ = ; a QN = D A 4 2 2 2 2 O 3a a 13a H 2 2 2
NH = HQ + QN = + = 4 2 16 B C Q N a 13 Suy ra NH = 4 a 39 a 39 Do đó 0 MH = NH tan 60 =
, suy ra SO = 2MH = 4 2 1 1 2 39a a 43 Ta có S = S = SK.AB ; 2 2 2
SK = SO + KO = + a = S ∆ MB ∆ 2 SAB 4 4 2 2 1 a 43 Suy ra S = SK.AB = S ∆ MB 4 8
Câu 3b Gọi P là trung điểm của SD, ta có tứ giác MPCN là hình bình hành suy ra MN//CP
Gọi α là góc giữa đường thẳng MN và mặt phẳng (SBD), ta thấy α bằng góc giữa đường thẳng CP và mặt phẳng (SBD)
Kẻ CI ⊥ BD CI ⊥ (SBD) α = CPI
Tam giác BCD vuông tại C có CI là đường cao, suy ra 1 1 1 1 1 5 2a = + = + = CI = 2 2 2 2 2 2 CI CB CD 4a a 4a 5 a 13
Ta có CP = MN = 2NH = 2 CI 4 sin α = = CP 65 u =1 1 Câu 4a Xét dãy: 2u . n u = , n ≥ 1 n 1 + 5u +1 +1 n
Bằng quy nạp ta chứng minh được u > 0 n ∀ n 2 u ( 5u +1− n n )1 2 Ta có u = = n 1 + 5u +1 +1 5 n 4 2 2
⇔ 5u + 2 = 2 5u +1 ⇔ 25u + 20u + 4 = 20u + 4 ⇔ u = (u − u ) n 1 + n n 1 + n 1 + n n 1 + n n 1 + 5 4 9 4 2 2 2 2 2
S = u + u + u + .... + u = u + (u − u ) = − u (1) n 1 2 3 n 1 1 5 n 5 5 n
Ta sẽ chứng minh (u ) là dãy giảm. n 2( 6 −1) Thật vậy có u =
< u , giả sử u > u , thay vào công thức xác định dãy ta thấy u > u . 2 1 + + + 5 k k 1 k 1 k 2
Vậy (u ) là dãy giảm, mà u > 0 n
∀ suy ra tồn tại giới hạn limu = l (l ≥ 0) n n n 2 ( 5u +1 − l + − n )1 2 ( 5 1 ) 1 Từ đẳng thức u = l =
⇔ 5l + 2 = 2 5l +1 n 1 + 5 5 9 2
⇔ 25l + 20l + 4 = 20l + 4 ⇔ l = 0 . Thay vào (1) ta có lim S = n 5 3 Câu 4b 4
P = sin A + sin B + 12 sin C C A − B C Ta có ( A + B )2 sin sin
≤ 2(sin A + sin B) = 4cos cos ≤ 4cos 2 2 2 C
sin A + sin B ≤ 2 cos 2 C 3 C 3 4 P ≤ 2 cos + 2 sin C ≤ 2 2 cos + sin C 2 4 2 2 2 C 3 C 3 3 3 Ta lại có 2 2 2 cos + sin C ≤ 2 cos + sin C =1+ o
c sC + - cos C 2 2 2 4 2 2 2 8 3 1 8 C 3 2
= - cos C − ≤ suy ra cos + sin C ≤ 2 3 2 3 3 2 2 3 6 2 Do đó 4 P ≤ 2 4 = 4 3 3 A = B 1 C 3 C = arccos có “ = ” khi cos = sin C ⇔ 3 2 2 A = B 1 cos C = 3 4
Document Outline
- [toanmath.com] - Đề thi học sinh giỏi Toán 11 năm học 2018 – 2019 sở GD&ĐT Hà Tĩnh
- loigiaitoan11 (2)




