Đề thi HSG cấp trường Toán 11 năm 2020 – 2021 trường Cẩm Xuyên – Hà Tĩnh

TRƯỜNG THPT CẨM XUYÊN
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG TỔ: TOÁN – TIN NĂM HỌC 2020 – 2021 (Đề có 8 câu ) MÔN TOÁN LỚP 11
(Thời gian làm bài : 150 Phút)
Câu 1. (4.5 điểm) Giải các phương trình sau:
a) sin 2x  cos x  0. b) 2
3 sin 2x  2cos x  3 . c) x 2 4C  A  70. x2 x3 Câu 2. (3.0 điểm) 13   a) Tìm hệ số của 8
x trong khai triển nhị thức Niutơn 2 3 2x    .  x 
b) Cho hai đường thẳng song song d ,d . Trên d lấy 6 điểm phân biệt và trên d lấy 8 điểm 1 2 1 2
phân biệt. Hỏi từ 14 điểm đã cho tạo được bao nhiêu tam giác?
Câu 3. (1.5 điểm) Trong mặt phẳng Oxy , cho đường thẳng Δ : 2x  3y  6  0 . Gọi Δ ' là ảnh của Δ qua 
phép tịnh tiến theo vectơ u  1;3 . Tính diện tích tứ giác được tạo thành bởi hai đường thẳng Δ,Δ ' và hai trục tọa độ.
Câu 4. (1.5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần lượt là trung SP
điểm SB, SD . Tìm giao điểm P của đường thẳng SC với mặt phẳng  AMN  và tính tỉ số . SC
Câu 5. (2.0 điểm) Tìm m để phương trình : sin 3x  2sin 2x  5  4msin x  0 có đúng ba nghiệm thuộc  π  khoảng   ;π  .  2  Câu 6. (4.0 điểm)
a) Gọi T là tập hợp các số tự nhiên có 7 chữ số khác nhau được lập từ các chữ số
0,1,2,3,4,5,6,7,8 . Chọn ngẫu nhiên một số từ T , tính xác suất để số đó chia hết cho 9. 1 1 1 1 b) Tính tổng: S     ... . 2!.2019! 4!.2017! 6!.2015! 2020!
Câu 7. (2.0 điểm) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều bằng a .
Gọi M là trung điểm của SB . Gọi P là mặt phẳng chứa CM và song song với SA. Tính theo a diện
tích thiết diện tạo bởi P và hình chóp S.ABCD . Câu 8. (1.5 điểm) Cho , A B,C  0
C  90  là ba góc của tam giác ABC . Tìm giá trị lớn nhất của biểu 2 2 2cos A  2sin B 1 thức: P  . sin C 1 -----HẾT-----
Thí sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm.
Họ và tên thí sinh: …………………………...…………………………Số báo danh: .............
TRƯỜNG THPT CẨM XUYÊN KỲ THI HSG CẤP TRƯỜNG NĂM HỌC 2020-2021 TỔ: TOÁN – TIN Đáp án môn: Toán 11
Thời gian làm bài 150 phút Câu Nội dung Điểm
Giải các phương trình sau:
a) sin 2x  cos x  0  cos x2sin x   1  0 0,5  Câu 1a x  k2π (1.5 điểm) cos x  0  π  1    x   k2π  . Vậy ….. 1,0 sin x   6  2  5π x   k2π  6 b) 2
3sin 2x  2cos x  3  3sin 2x  cos 2x  2 0,5 Câu 1b       (1.5 điểm)  sin 2x 
1  2x    k2  x   k   . Vậy…. 1,0  6  6 2 6 c) x 2 4C  A  70 x2 x3 ĐK: x  , x  1. x  2 ! x  3 ! x 2     4C  A  70  4   70 Câu 1c x2 x3 2!.x! x   1 !
(1.5 điểm)  2x  2x  1x 3x  2  70 0,5 x  8Tm 2
 x  x  72  0   . Vậy…. 0,5 x  9   L 13   Tìm hệ số của 8
x trong khai triển nhị thức Niutơn 2 3 2x    .  x  Câu 2a 13  2 3  k 13k k 26 3  k
(1.5 điểm) Số hạng tổng của khai triển 2x    là: k T 1   1 C 32 3 .x 0,5  x  Hệ số của 8
x tương ứng với 26  3k  8  k  6 0,5 Vậy Tìm hệ số của 4
x trong khai triển đã cho là 6 7 6 1 C 3.2 .3 . 0,5
Cho hai đường thẳng song song d ,d . Trên d lấy 6 điểm phân biệt và trên 1 2 1
d lấy 8 điểm phân biệt. Hỏi từ 14 điểm đã cho tạo được bao nhiêu tam giác? 2 Câu 2b TH1: Hai đỉnh thuộc d có 2 1 C .C tam giác. 0,5 1.5 điểm 1 d và một đỉnh thuộc 2 6 8
TH2: Hai đỉnh thuộc d2 và một đỉnh thuộc 1 d có 1 2 6 C . 8 C tam giác. 0,5 Vậy có 2 1 1 2 6 C . 8 C  6 C . 8 C  288 tam giác. 0,5
Trong mặt phẳng Oxy , cho đường thẳng Δ : 2x  3y  6  0 . Gọi Δ ' là ảnh  Câu 3
của Δ qua phép tịnh tiến theo vectơ u  1;3 . Tính diện tích tứ giác được 2,0
1.5 điểm tạo thành bởi hai đường thẳng Δ,Δ' và hai trục tọa độ. x'  x 1
Biểu thức tọa độ của T là: . u   y '  y  3
Lấy A3;0  . Khi đó A'4;3 là ảnh của A qua T  A' '. 0,5 u
 ' đi qua A, song song hoặc trùng    ' : 2x  3y 17  0 .
Ta có: A3;0, B0;2 lần lượt là giao điểm của  với Ox,Oy và 17   17  D ;0 ,C 0;   
 lần lượt là giao điểm của  ' với Ox,Oy . 0,5  2   3  1 1 289 Ta có: S  .O . A OB  3 O  AB , S  .OC.OD  . 2 OAB 2 12 0,5 289 253  S  S  S   3 ABCD OCD OAB  (đvdt). 12 12
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M , N lần
lượt là trung điểm SB, SD . Tìm giao điểm P của đường thẳng SC với mặt SP 1,5
phẳng  AMN  và tính tỉ số . SC S P
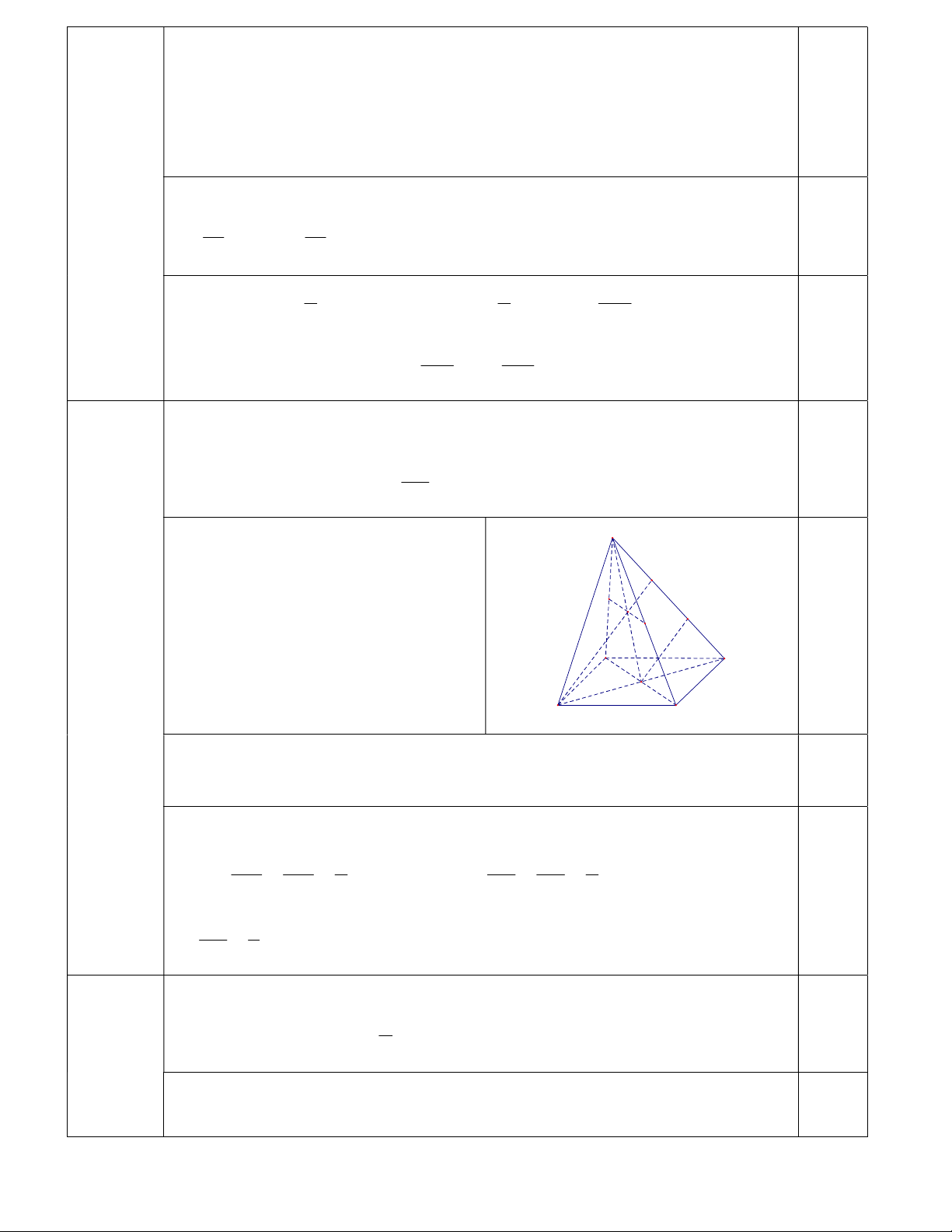
Gọi O là giao điểm của AC và BD . M Q
Trong mặt phẳng SBD có SO cắt I N 0,5 MN tại I . B C Câu 4 1,5 điểm O A D
Trong mặt phẳng SAC  có AI cắt SC tại P . Điểm P chính là giao điểm
của đường thẳng SC với mặt phẳng  AMN . 0,5
Trong mặt phẳng SAC  , kẻ đường thẳng qua O , / / AP cắt SC tại Q . CQ CO 1 SP SI 1 Ta có:    CQ  QP và    SP  PQ CP CA 2 SQ SO 2 0,5 SP 1   . SC 3
Tìm m để phương trình : sin 3x  2sin 2x  5  4msin x  0 có đúng ba  π 
nghiệm thuộc khoảng   ;π . Câu 5   2  (2.0 điểm) sin x  0 PT  sin x 2 cos x  cos x  m   1  0   0,5 2
cos x  cos x  m 1  0  π 
PT: sin x  0 có duy nhất một nghiệm x  0 trên khoảng   ;π  .  2   π  PT đã cho có ba nghiệm thuộc khoảng   ;π    2  0,5 2
cos x  cos x  m 1  0 * có hai nghiệm phân biệt khác 0 thuộc khoảng  π    ;π  .  2   π 
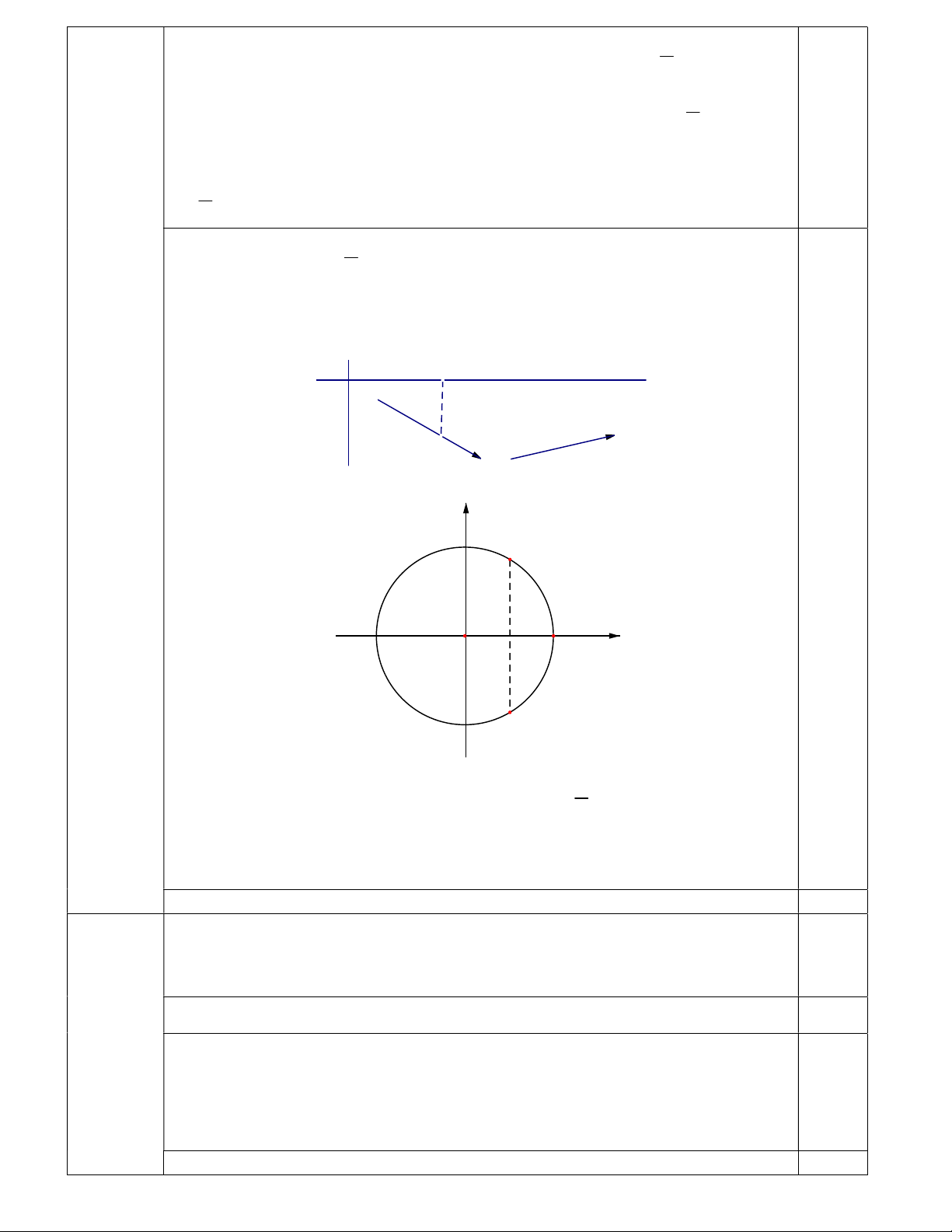
Đặt t  cos x , x    ;π   t  1  ;  1 .   2
*  m  t  t 1 ** .  2  Xét hàm số f t  2  t  t 1, t  1  ;  1 . BBT: x - 1 0 1/2 1 3 y 1 1 3/4 y 0,5 -1 O 1/2 1 x  π 
(*) có hai nghiệm phân biệt khác 0 thuộc khoảng   ; π   (**) có nghiệm  2  kép thuộc 0; 
1 hoặc có duy nhất một nghiệm thuộc 0;  1 và nghiệm còn lại không thuộc  1  ; 
1 hoặc hai nghiệm phân biệt thuộc  1  ;0. Từ BBT  m  3 / 4 . 0,5
Gọi T là tập hợp các số tự nhiên có 7 chữ số khác nhau được lập từ các chữ
số 0,1,2,3,4,5,6,7,8 . Chọn ngẫu nhiên một số từ T , tính xác suất để số đó chia hết cho 9. Câu 6a n 6  8.A  161280 0,5 (2.0điểm) 8 Đặt A  0;1;2;3;4;5;6  ;7;  8
Ta có: 0 1 2  3  4  5  6  7  8  36 chia hết cho 9. Do đó, số cần lập
chia hết cho 9 được tạo thành từ các tập 0,5 sau: A \ 1;  8 , A \ 2;  7 , A \ 3;  6 , A \ 4;  5 . Mỗi tập n
h ư thế tạo thành 6.6! số có 7 chữ số khác nhau chia hết cho 9 0,5  có 4.6.6! 17280 số. 17280 3
Vậy xác suất cần tìm là P   . 0,5 161280 28 1 1 1 1 Tính tổng: S     ... . 2!.2019! 4!.2017! 6!.2015! 2020! Ta có: 2 4 6 2020 S.2021!  C  C  C  ...  C 0,5 2021 2021 2021 2021 Do 0 1 2 3 4 5 2020 2021 2021 C  C  C  C  C  C  ... C  C  2 2021 2021 2021 2021 2021 2021 2021 2021 0,5 Câu 6b và 0 1 2 3 4 5 2020 2021 C  C  C  C  C  C  ... C  C  0 2021 2021 2021 2021 2021 2021 2021 2021 (2.0 điểm) 0 2 4 2020 1 3 5 2021  C2021  2
C 021  C2021  ... C2021  C2021  2 C 021  2 C 021  ...  2 C 021 2021 2 0,5 2020   2 2 2020 2 4 2020 2020 2 1  C2021  2 C 021  ... C2021  2 1  S  . 0,5 2021!
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và các cạnh bên đều
bằng a . Gọi M là trung điểm của SB . Gọi P là mặt phẳng chứa CM và 0,5
song song với SA . Tính theo a diện tích thiết diện tạo bởi P và hình chóp S.ABCD . S
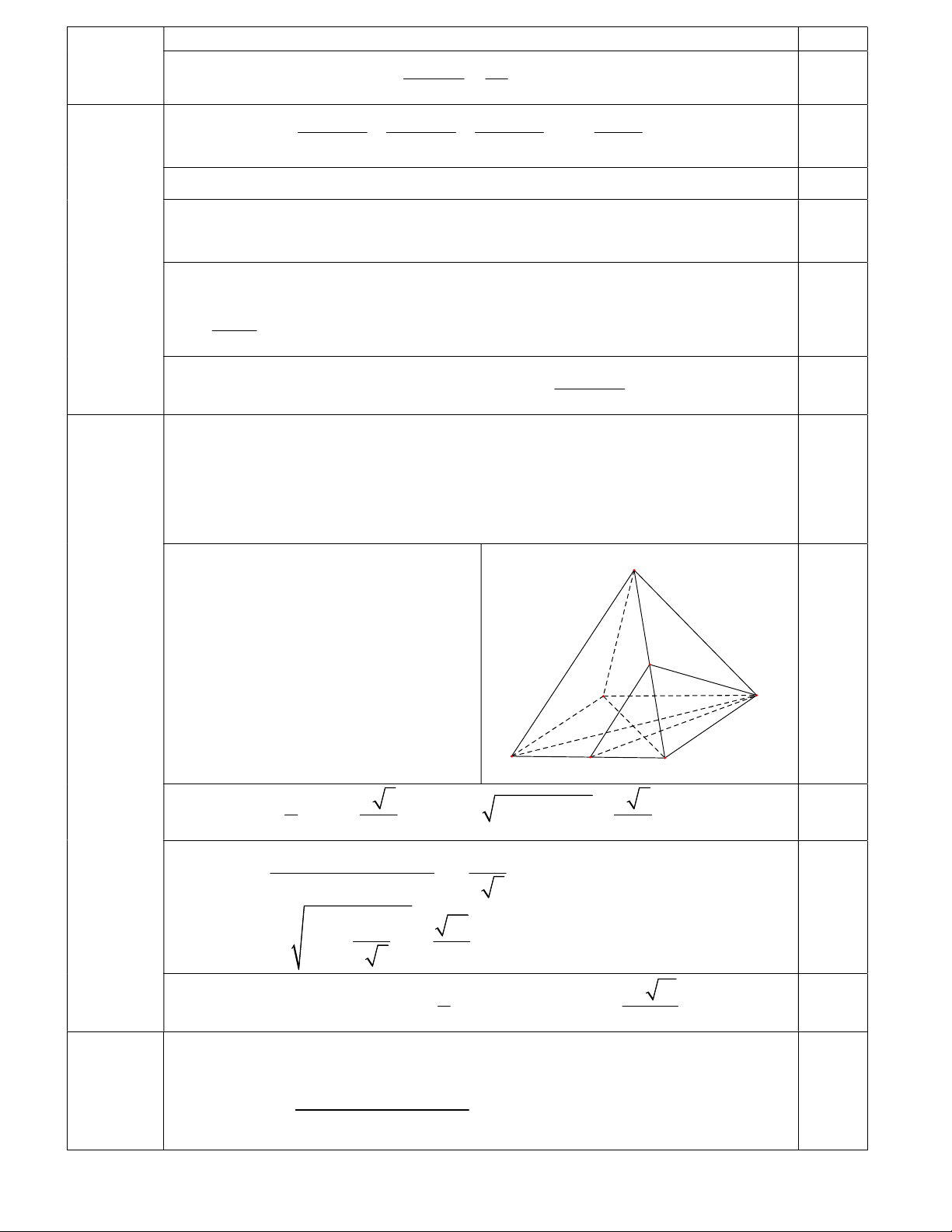
Gọi N là trung điểm của AB ,
 MN / /SA  thiết diện cần tìm là M 0,5 tam giác CMN . D C Câu 7 (2.0điểm) A N B a a 3 a Ta có: MN  , MC  và 2 2 5 CN  BC  BN  0,5 2 2 2  2 2 2 MN  MC  CN 1 cosCMN    2.MN.MC 2 3 2    1  33 sin CMN  1     .  2 3  6 a
Diện tích tam giác CMN là S  MN MC  2 1 11 . . .sin CMN  (đvdt) 2 16 Cho A B C  0 , ,
C  90  là ba góc của tam giác ABC . Tìm giá trị lớn nhất của 2 2 2cos A  2sin B 1  biểu thức: P . sin C 1 Câu 8 cos 2A  cos 2B 1 0,5đ P   PsinC  
1  2cos A  Bcos A  B 1 (1,5điểm) sin C 1  PsinC   1  2
 cosC.cos A  B 1
 Psin C  2cos A  B.cosC  P 1  * (*) có nghiệm 2 2  P 
A B  P  2  P  2 2 4cos 1 1  P  4 0,5đ 3  P  . 2 3 A  B A  B  3 P      với sin   . 0 2 3  sinC  4cosC  5 C   90   5 0,5đ 3 Vậy max P  . 2
Chú ý: Mọi cách giải khác đúng đều cho điểm tối đa.