Đề thi HSG Toán 11 cấp trường năm 2018 – 2019 trường Thuận Thành 2 – Bắc Ninh

Nhằm tuyển chọn các em học sinh khối lớp 11 giỏi môn Toán để thành lập đội tuyển học sinh giỏi Toán 11 THPT, trường THPT Thuận Thành 2, tỉnh Bắc Ninh tiến hành tổ chức kỳ thi chọn học sinh giỏi Toán 11 THPT năm học 2018 – 2019

22 11 lượt tải Tải xuống

Chia sẻ Báo cáo tài liệu

Câu I (4,0 điểm).

1.Giải phương trình

2 2

2cos 2 3 cos 4 4cos 1

x x x



 

   

 

 

2.Cho các số

5 ;5 2 ;8

x y x y x y  

theo thứ tự đó lập thành một cấp số cộng; đồng thời các số

 

( 1) ; 1; 2

y xy x  

theo thứ tự lập thành một cấp số nhân. Hãy tìm

,x y

Câu II (5,0 điểm).

1. Tính tổng

2 3 4 n

n n n n

S 2.1C 3.2C 4.3C ... n(n 1)C

     

2.Chọn ngẫu nhiên một số tự nhiên có sáu chữ số khác nhau. Tính xác suất để chọn được một số có 3

chữ số chẵn và 3 chữ số lẻ.

Câu III (5,0 điểm).

Tìm

lim

4 3 2

n n n

 

2. Giải hệ phương trình

2 2

4 8 17 1

21 1 2 4 3

x x x y y

x y y y x



      





     





Câu IV(2,0 điểm).

Trong mặt phẳng Oxy, cho tam giác ABC có đỉnh A(3; 4), B(1; 2), đỉnh C thuộc đường thẳng

: 2 1 0

d x y

  

, trọng tâm G. Biết diện tích tam giác GAB bằng 3 đơn vị diện tích, hãy tìm tọa độ đỉnh

Câu V (4,0 điểm).

Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn

2BC a

đáy bé

AD a

AB b

. Mặt

bên SAD là tam giác đều. M là một điểm di động trên AB, Mặt phẳng (P) đi qua M và song song với SA, BC.

1. Tìm thiết diện của hình chóp khi cắt bởi

 

mp P

. Thiết diện là hình gì?

2. Tính diện tích thiết diện theo a, b và

 

, 0 .x AM x b

  

Tìm x theo b để diện tích thiết diện lớn

nhất

-----------------Hết-----------------

Họ và tên thí sinh :....................................................... Số báo danh .............................

Họ và tên, chữ ký: Giám thị 1:........................................................................................

Họ và tên, chữ ký: Giám thị 2:........................................................................................

SỞ GIÁO DỤC VÀ ĐÀO TẠO

TRƯỜNG THPT THUẬN THÀNH 2

ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG

NĂM HỌC 2018 – 2019

Môn thi: Toán – Lớp 11

Thời gian làm bài: 150 phút (không kể thời gian giao đề)

ĐỀ CHÍNH THỨC

Huớng dẫn chấm

Câu Nội dung Điểm

Câu I.

2 2

2cos 2 3 cos4 4cos 1

x x x



 

   

 

 

 

12cos124cos34

cos1 













 xxx



xxx 2cos24cos34sin 

0.5

xx 2cos

4cos 

















0.5















kxx

 

















336

1.0



5 ;5 2 ;8

x y x y x y  

theo thứ tự lập thành CSC nên ta có:

 

5 8 2 5 2

2 1

x y x y x y

x y

    

 

0.5



   

2 2

1 ; 1; 2

y xy x  

theo thứ tụ lập thành CSN nên ta có:

       

2 2 2

1 2 1 2

y x xy   

0.5

 Thay (1) vào (2) ta đc:

   

 

2 2

4 2 4 2

1 2 2 2 1

4 2 1 4 4 1

y y y

y y y y

y x

   

     





   



  



  





1.0

Câu II

2 3 4 n

n n n n

S 2.1C 3.2C 4.3C ... n(n 1)C

     

Số hạng tổng quát:

1.0

SỞ GIÁO DỤC VÀ ĐÀO TẠO

TRƯỜNG THPT THUẬN THÀNH 2

ĐÁP ÁN ĐỀ THI CHỌN HỌC SINH GIỎI CẤP

TRƯỜNG

NĂM HỌC 2018 – 2019

Môn thi: Toán – Lớp 11

ĐỀ CHÍNH THỨC

   

 

  

     

   

1 1

! !

1 2 !

2 ! 2 ! 2 !

1 2

k n

u k k C k k

k n k

n n n

k n k

n n C k n



   



 



 

   

 

   

 

0 1 2

2 2 2

1 ...

n n n

S n n C C C



  

    

1.0

 

1 2

n n



 

0.5

Số phần tử của không gian mẫu:

6 5

10 9

136080

n A A



  

0.5

*Số các số tự nhiên có 6 chữ số có3 chữ số chẵn và 3 chữ số lẻ là

TH1: (số tạo thành không chứa số 0)

 Lấy ra 3 số chẵn có:

 Lấy ra 3 số lẻ có:

 Số các hoán vị của 6 số trên: 6!

Suy ra số các số tạo thành:

3 3

4 5

. .6! 28800

C C 

0.5

TH2: ( số tạo thành có số 0)

 Lấy ra hai số chẵn khác 0:

 Lấy ra 3 số lẻ:

 Số các hoán vị không có số ) đứng đầu:

6! 5! 5.5! 

Số các số tạo thành:

2 3

4 5

. .5.5! 36000

C C 

0.5

Gọi biến cố A: “số đuợc chọn có 3 chữ số chẵn và 3 chữ số lẻ”

Suy ra :

28800 36000 64800

n   

Xác suất xảy ra biến cố A:

64800 10

136080 21



  

Câu III









 

4 3 2

lim lim

4 3 2

4 2

4 3 2 2

lim lim

3 1 1

n n n n

n n n

n n n n

n n n

 

 



 

 

  

 

 

 

 

2.0

 

2 2

4 8 17 1 1

21 1 2 4 3 2

x x x y y

x y y y x



      





     





Điều kiện:



 

2 2

1 ( 4) 8 17 1 0

4 0

8 17 1

x y x x y

x y

x x y

        

 

    

   

0.5

 

  

2 2

4 4

4 0

8 17 1

x y x y

x y

x x y

   

    

   

 

2 2

4 (1 ) 0

8 17 1

x y

x x y

y x

 

    

   

  

0.5

Vì:

 

   

2 2 2 2

4 1 4 1

1 0 ,

8 17 1 8 17 1

x x y y

x y

x x y x x y

      

 

   

       

0.5

Thay

y x

 

vào 2 ta đuợc

 

     

2 4 25 1 2 16

4 2 25 5 8 2 16 0

1 1 12

4 2 25 5 8 2 16

x x x x

       

          



 

   

 

      

 

0.5

 

0 4

1 1 12

4 2 25 5 8 2 16

x y

x x x x

  









  



      



0.5

Câu IV

Ta có:

 

2;2 , 2 2

BA AB 



Phuơng trình đuờng thẳng AB:

1 2

1 0

1 1

x y

 

    

0.5

 

: 2 1 0 1 2 ;C d x y C t t

      

Gọi G là trọng tâm của tam giác ABC suy ra:

1 ;2

3 3

G t

 

 

 

 

0.5

Khoảng cách từ G đến AB:

 

;

G AB

d 

0.5

Vì diện tích GAB bằng 3 đơn vị nên ta có:

0.5

 

;

3 7;3

. 3

3 5; 3

G AB

t C

d AB

t C



  

 



   





Câu V

+ Từ M kẻ đuờng thẳng song song với BC và SA lần luợt cắt DC tại N, SB tại Q.

+ Từ Q kẻ đuờng thẳng song song với BC cắt SC tại P.

Thiết diện hình thang cân MNPQ

0.5

+ Tính diện tích MNPQ

Ta tính đuợc

2. .

, ;

b x a x ab ax

MQ NP a PQ MN

b b b

 

   

từ đó tính đuợc

. 3

ab a x





1.5

Suy ra diện tích MNPQ là: x

    

1 3.

. 3

2 4

MNPQ

S MN PQ QK b x b x

    

0.5

  

2 2 2

2 2

3. 3. 3 3. 3. 3.

4 12 2 12

MNPQ

a a b x b x a

S b x b x

b b

  

 

    

 

 

Dấu “=”xẩy ra khi



Bấm Tải xuống để xem toàn bộ.

| 1/5

| | Tải xuống

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT THUẬN THÀNH 2 NĂM HỌC 2018 – 2019
Môn thi: Toán – Lớp 11 Đ Ề CHÍNH THỨC
Thời gian làm bài: 150 phút (không kể thời gian giao đề) Câu I (4,0 điểm).    1.Giải phương trình 2 2 2 cos
 2x  3 cos 4x  4 cos x 1    4 
2.Cho các số x  5 y;5x  2 y;8x  y theo thứ tự đó lập thành một cấp số cộng; đồng thời các số y 
xy   x  2 2 ( 1) ; 1;
2 theo thứ tự lập thành một cấp số nhân. Hãy tìm x, y . Câu II (5,0 điểm). 1. Tính tổng 2 3 4 n S  2.1C
n  3.2Cn  4.3Cn  ...  n(n  1)Cn
2.Chọn ngẫu nhiên một số tự nhiên có sáu chữ số khác nhau. Tính xác suất để chọn được một số có 3
chữ số chẵn và 3 chữ số lẻ. Câu III (5,0 điểm). 2
n  n  n 1. Tìm lim 2
4n  3n  2n 2 2
x  4  x  8x 17  y  y 1 
2. Giải hệ phương trình  x  y 
y  21  1  2 4 y  3x  Câu IV(2,0 điểm).
Trong mặt phẳng Oxy, cho tam giác ABC có đỉnh A(3; 4), B(1; 2), đỉnh C thuộc đường thẳng
d : x  2 y  1  0 , trọng tâm G. Biết diện tích tam giác GAB bằng 3 đơn vị diện tích, hãy tìm tọa độ đỉnh C. Câu V (4,0 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn BC  2a đáy bé AD  a , AB  b . Mặt
bên SAD là tam giác đều. M là một điểm di động trên AB, Mặt phẳng (P) đi qua M và song song với SA, BC.
1. Tìm thiết diện của hình chóp khi cắt bởi mp  P . Thiết diện là hình gì?
2. Tính diện tích thiết diện theo a, b và x  AM ,0  x  b. Tìm x theo b để diện tích thiết diện lớn nhất
-----------------Hết-----------------
Họ và tên thí sinh :....................................................... Số báo danh .............................
Họ và tên, chữ ký: Giám thị 1:........................................................................................
Họ và tên, chữ ký: Giám thị 2:........................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ THI CHỌN HỌC SINH GIỎI CẤP
TRƯỜNG THPT THUẬN THÀNH 2 TRƯỜNG NĂM HỌC 2018 – 2019 Đ Ề CHÍNH THỨC
Môn thi: Toán – Lớp 11 Huớng dẫn chấm Câu Nội dung Điểm Câu I. 1   2  2 2 cos
 2x  3 cos 4x  4 cos x 1    4     0.5 PT 1  cos
 4x   3 cos 4x   2 1  cos 2x 1  6 
 sin 4x  3 cos 4x  2 cos 2x    0.5  cos 4x    cos 2x  6      k 1.0 4x 
 2x  k  2 x   6  36 3     k  Z     4x   2x  k  2 x   k  6  12 2 
x  5y;5x  2 y;8x  y theo thứ tự lập thành CSC nên ta có: 0.5
x  5y  8x  y  25x  2 y
 x  2 y   1 2 2   y  
1 ; xy 1; x  2 theo thứ tụ lập thành CSN nên ta có: 0.5
 y  2  x  2   xy  2 1 2 1 2 2  y  2
1 2 y  22   2 2 y   1 1.0
 Thay (1) vào (2) ta đc:  4 4 2
y  2 y   4 2
1  4 y  4 y 1   3 y   x   3  3 2 2  y    4  3 y   x  3   2 Câu II 1 2 3 4 n S  2.1C
n  3.2Cn  4.3Cn  ...  n(n  1)Cn Số hạng tổng quát: 1.0 n k ! u  k k  C  k k  k   1 n  
1 k !n  k! n n   1 n  2! 
k  2!n  2! k  2!  
 n n   k2 1 C 2  k  n n2  
S  n n   1  0 1 2 C  C  ... n  C  1.0 n2 n2 n2    2 1 2n n n    0.5 2.
Số phần tử của không gian mẫu: 6 5
n  A  A  136080 0.5  10 9
*Số các số tự nhiên có 6 chữ số có3 chữ số chẵn và 3 chữ số lẻ là 0.5
TH1: (số tạo thành không chứa số 0)
 Lấy ra 3 số chẵn có: 3 C 4
 Lấy ra 3 số lẻ có: 3 C 5
 Số các hoán vị của 6 số trên: 6!
Suy ra số các số tạo thành: 3 3
C .C .6!  28800 4 5
TH2: ( số tạo thành có số 0) 0.5
 Lấy ra hai số chẵn khác 0: 2 C 4  Lấy ra 3 số lẻ: 3 C 5
 Số các hoán vị không có số ) đứng đầu: 6! 5!  5.5! Số các số tạo thành: 2 3
C .C .5.5!  36000 4 5
Gọi biến cố A: “số đuợc chọn có 3 chữ số chẵn và 3 chữ số lẻ” 1
Suy ra : n  28800  36000  64800 A n 64800 10
Xác suất xảy ra biến cố A: A P    A n 136080 21  Câu III 1 2.0 n    2 2
4n  3n  2n n n n  lim  lim 2
4n  3n  2n 3n  2
n  n  n 3 2 4   2
4n  3n  2n n 2  lim  lim  3 2
n  n  n  1  3 3 1 1 n   2 2 2  x  4 
x  8x  17  y  y  1    1  x  y 
y  21  1  2 4 y  3x 2 
Điều kiện: y  0   2 2
1  (x  y  4) 
x  8x 17  y 1  0 0.5  x  42 2  y
  x  y  4   0 2 2
x  8x 17  y 1
 x  4  y x  4  y
  x  y  4   0 2 2
x  8x 17  y 1
 x  4  y 0.5
  x  y  4 (1 )  0 2 2
x  8x 17  y 1
 y  x  4 0.5
 x  4  y
 x  42 1   x  4 2  y 1  y Vì:1   0 x  , y 2 2 2 2
x  8x 17  y 1
x  8x 17  y 1
Thay y  x  4 vào 2 ta đuợc 0.5 :
2  x  x  4  x  25 1  2 x 16
  x  4  2   x  25  5   x  8  2 x 16  0  1 1 x 12   x    0    x  4  2 x  25  5
x  8  2 x 16 
x  0  y  4 0.5  1 1 x 12 vn     0 0.5  x  4  2 x  25  5
x  8  2 x 16  Câu IV
Ta có: BA  2; 2, AB  2 2 0.5 x 1 y  2
Phuơng trình đuờng thẳng AB: 
 x  y 1  0 1 1
C  d : x  2 y 1  0  C  1
  2t;t  0.5  2 t 
Gọi G là trọng tâm của tam giác ABC suy ra: G 1 t; 2     3 3  t 0.5
Khoảng cách từ G đến AB: d  G;AB 2
Vì diện tích GAB bằng 3 đơn vị nên ta có: 0.5
t  3  C 7;3 1  d .AB  3    G; AB  2 t  3   C 5; 3     Câu V
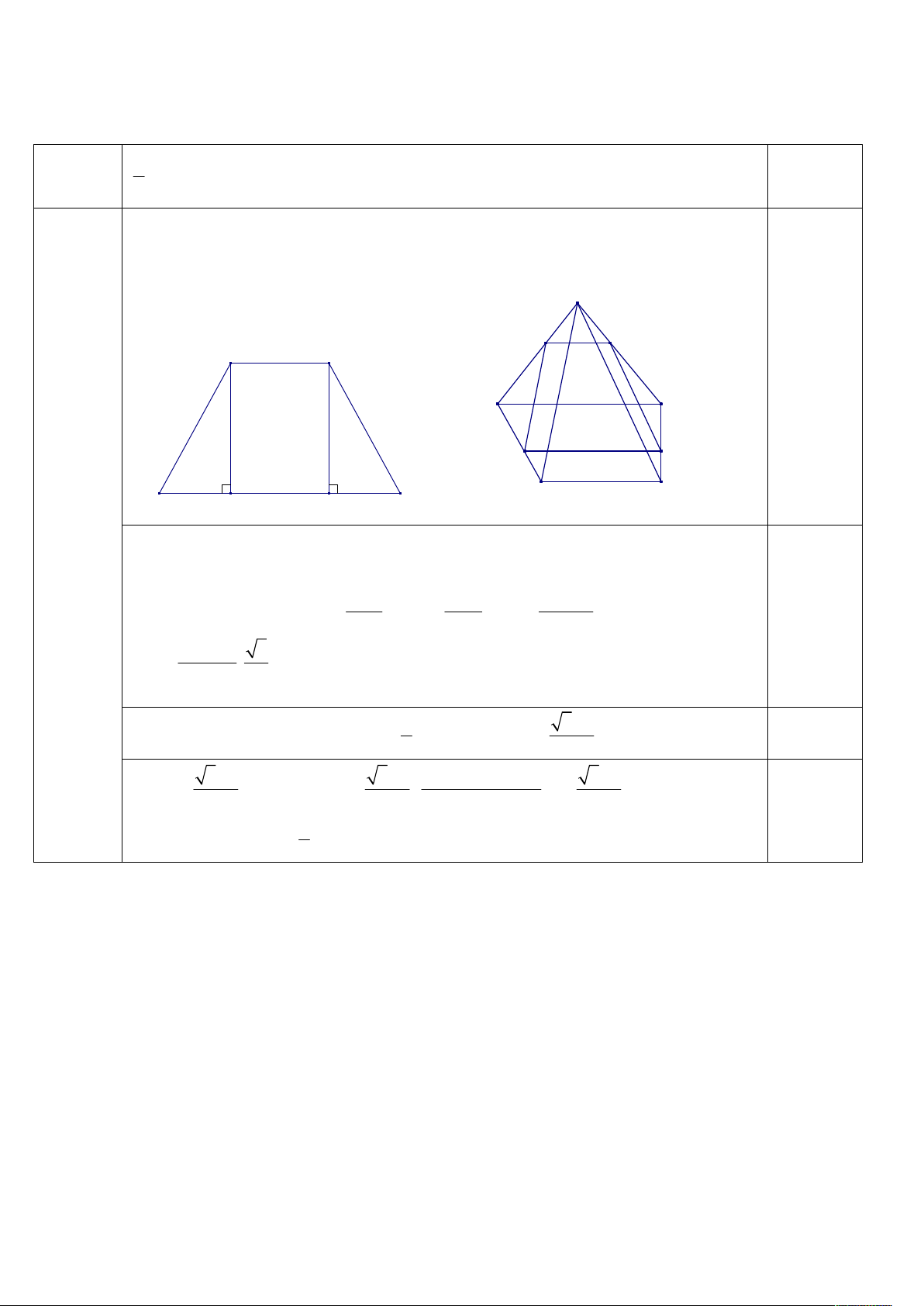
+ Từ M kẻ đuờng thẳng song song với BC và SA lần luợt cắt DC tại N, SB tại Q. 0.5
+ Từ Q kẻ đuờng thẳng song song với BC cắt SC tại P. 0.5
Thiết diện hình thang cân MNPQ S Q P P Q 2a C B b M N x D A N M a H K + Tính diện tích MNPQ 1.5 b  x 2. . a x ab  ax
Ta tính đuợc MQ  NP  a, PQ  ; MN  từ đó tính đuợc b b b ab  . a x 3 QK  . b 2 2 1 3.a 0.5
Suy ra diện tích MNPQ là: x S  MN  PQ QK 
b  x b  x MNPQ  . 3 2    2 4b 2 2 2 2 3.a
3.a  3b  3.x  b  3.x  3.a 1 S 
b  x b  3x   MNPQ 2    2   4b 12b  2  12 b
Dấu “=”xẩy ra khi x  . 3

Đề thi HSG Toán 11 cấp trường năm 2018 – 2019 trường Thuận Thành 2 – Bắc Ninh

Thông tin :

Tài liệu liên quan:

Đề khảo sát tháng 10 Toán 11 năm 2024 – 2025 trường THPT Gia Bình 1 – Bắc Ninh

Đề khảo sát Toán 11 đầu năm 2024 – 2025 trường THPT Thuận Thành 1 – Bắc Ninh

Đề thi Toán học kỳ II lớp 11

Đề khảo sát lần 4 Toán 11 năm 2025 trường THPT Nguyễn Đăng Đạo – Bắc Ninh

Đề khảo sát chất lượng Toán 11 năm 2022 - 2023 trường THPT Yên Lạc 2 - Vĩnh Phúc