Đề thi HSG Toán 11 năm 2019 – 2020 trường Nguyễn Quán Nho – Thanh Hóa

SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA
ĐỀ THI HỌC SINH GIỎI LỚP 11 THPT
TRƯỜNG THPT NGUYỄN QUÁN NHO NĂM HỌC 2019-2020 Tháng 2 MÔN: TOÁN U
(Thời gian làm bài: 180 phút)
Câu 1( 4,0 điểm) U U 1) . Cho hàm số 2
y = x − 4x + 3 có đồ thị là (P = + + 1) và hàm số 2 y x
2x 3 có đồ thị là (P2). Giả sử R R R R
đường thẳng (d): y = m cắt (P1) tại hai điểm phân biệt A, B và cắt (P2) tại hai điểm C, D. Tìm m để R R R R AB = 2CD . 2
1 + 2 x − 2 x + 3x + 1
2) Giải bất phương trình > 1. 2
1 − 2 x − x + 1 Câu 2( 4,0 điểm) U U x
1) Giải phương trình 4cos3x cos x − 2cos 4x − 4cos x + tan tan x + 2 = 0. 2 2  9y + 
(2y +3)( y − x) + 4 xy = 7x
2) Giải hệ phương trình.  2 2
 7x + 25y +19 − x − 2x − 35 = 7 y + 2 
Câu 3( 4,0 điểm) 1) Cho các số thực dương x, y, z. Chứng minh rằng U U 2 2 2 1 + x 1 + y 1 + z 3 + + ≥ . 3 2 3 2 3 2 + + + + + + + + + 5 1 4 1 y 3z 1 4 1 z 3x 1 4 1 x 3y  2 =  1 u  3  , n ∀ ≥ 2.
2) Cho dãy số (u u
n ) xác định như sau n 1 −
Tính tổng của 2019 số u  = n  2  (2n − )1u + n 1 1 −
hạng đầu tiên của dãy số (un ) . Câu 4( 4,0 điểm) U U
1) Xung quanh bờ ao của gia đình bác Nam trồng 20 cây chuối. Do không còn phù hợp bác muốn thay
thế để trồng bưởi, lần đầu bác chặt ngẫu nhiên 4 cây. Tính xác suất để trong 4 cây bác Nam chặt không có hai cây nào gần nhau.
2) Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có ba góc đều nhọn và nội tiếp đường tròn
tâm I. Gọi K là hình chiếu vuông góc của B trên đường thẳng AC, H là hình chiếu vuông góc của C trên
đường thẳng BI. Các đường thẳng AC và KH lần lượt có phương trình là x  y  1  0 và
x  2y  1  0 . Biết điểm B thuộc đường thẳng y  5  0 và điểm I thuộc đường thẳng x  1  0 .
Tìm tọa độ điểm C. Câu 5( 4,0 điểm) U U
1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB  3a và AD  a 3 . Cạnh bên
SA  2a và SA vuông góc với mặt đáy ABCD. Gọi H,K lần lượt là hình chiếu vuông góc của
đỉnh A lên các cạnh SB và SD . Tính góc giữa đường thẳng AC và mặt phẳng AHK.
2. Cho tứ diện OABC có ba cạnh , OA ,
OB OC đôi một vuông góc với nhau tại O. Gọi H là hình
chiếu vuông góc của O lên mặt phẳng ABC  và P là điểm bất kỳ trong tam giác ABC. Chứng minh 2 2 2 2 rằng PA PB PC PH    2  . 2 2 2 2 OA OB OC OH
....................... HẾT ....................... 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN ĐỀ THI HỌC SINH GIỎI LỚP 11 THPT THANH HÓA NĂM HỌC 2019-2020 Tháng 2
MÔN: TOÁN (Thời gian làm bài: 180 phút) U
ĐÁP ÁN ĐỀ CHỌN HSG 2019 - 2020 Câu Đáp án Điểm 1a Xét 2 phương trình: 2
x − 4x + 3 − m = 0 (1) và 2
x + 2x + 3 − m = 0 (2) ∆ = m +1 > 0 ĐK: 1  ⇒ m > 2 ∆ = m − 2 > 0  2 2 2 2 2 AB =
2CD ⇔ AB = 2CD ⇔ (x − x ) = 2(x − x ) 1 2 3 4 2 2
⇔ (x + x ) − 4x x = 2[(x + x ) − 4x x ] ⇔ 16 - 4(3 - m)=2[4 - 4(3 - m)] ⇒ m = 5 1 2 1 2 3 4 3 4 ĐS: m = 5. 2.0 1b
+ Điều kiện x ≥ 0 (2 điểm) 2  1  3 + Ta có 2
2 x − x + 1 = 2 x − + ≥ 3 > 1   nên 2
1 − 2 x − x + 1 < 0  2  4 Do đó bất phương trình 2 2
⇔ 1+ 2 x − 2 x + 3x +1 < 1− 2 x − x +1 2 2
⇔ x + x − x +1 < x + 3x +1 0.5
+ Nếu x = 0 thì bất phương trình trở thành 1 <1 (vô lý) + Nếu 1 1
x > 0 thì bất phương trình ⇔ 1 + x + −1 < x + + 3 x x 0,5 + Đặt 1 x +
= t với t ≥ 2 , bất phương trình trở thành 1+ t −1 < t + 3 x 13
⇔ 2 t −1 < 3 ⇔ t < 4 0.5 − + + Với 13 1 13 13 105 13 105 t < thì 2 x + <
⇔ 4x −12x + 4 < 0 ⇔ < x < 4 x 4 8 8 − +
+ Vậy bất phương trình có nghiệm là 13 105 13 105 < x < 8 8 0.5 2a  x (2 điể  ≠  x ≠ −
m) + Với điều kiện cos 0 cos 1  2 ⇔ 
phương trình tương đương với   cos x ≠ 0 cos x ≠ 0 x sin sin x 2
4 cos 3x cos x − 2 cos 4x − 4 cos x + + 2 = 0 x cos cos x 2 0.5 x x sin sin x + cos cos x ⇔ ( x + x) 2 2 2 cos 2 cos 4
− 2 cos 4x − 4 cos x + +1 = 0 x cos cos x 2 0,5 2 1
⇔ 2 cos 2x − 4 cos x + +1 = 0 2
⇔ 2 cos 2x cos x − 4 cos x + cos x +1 = 0 cos x ⇔ x x + x − ( 2 2 cos 2 cos cos 4 cos x − ) 1 = 0
⇔ 2 cos 2x cos x + cos x − (2cos 2x + ) 1 = 0 0.5  1  π = − = ± + π ⇔ ( cos 2x x k 2 cos 2x + ) 1 (cos x − ) 1 = 0  ⇔  2 ⇔  3  cos x = 1 x = k2π  π = ± + π
+ So sánh với điều kiện ta được x k  3 (k ∈)  x = k2π 0.5 2b 2 9
 y + (2y + 3)( y − x) ≥ 0
(2 điểm)  2
7x + 25y +19 ≥ 0
xy ≥ 0; y ≥ 2; − x ≤ 5 − ∨ x ≥ 7
Từ PT đầu của hệ và kết hợp với điều kiện xác định suy ra x≥7,y≥0. Do đó 2
(1) ⇔ 9 y + (2 y + 3)( y − x) − 3x + 4 xy − 4x = 0
9 y + (2 y + 3)( y − x) − 9x 4 ( 2 2 2 xy − x ) ⇔ + = 0 2
9 y + (2 y + 3)( y − x) + 3x xy + x  
9 x + y + 2 y + 3 4x ⇔ ( y − x) ( )  +  = 0 2
 9y + (2y +3)( y − x) +3x xy + x    ⇔ x = y
+ Thế vào (2), ta được: 2 2 7x + 25x +19 =
x − 2x − 35 + 7 x + 2 2
⇔ 3x −11x − 22 = 7 (x + 2)(x + 5)(x − 7) ⇔ ( 2 x − x −
)+ (x+ ) = (x+ )( 2 3 5 14 4 5 7 5 x − 5x −14) Đặt 2 a =
x − 5x −14 ;b =
x + 5 (a ≥ 0,b > 0) . Khi đó phương trình trở thành 2 2
3a + 4b = 7ab ⇔ a = b ∨ 3a = 4b
Với a = b ⇒ x = 3+ 2 7 (thỏa mãn) và x = 3− 2 7 (loại) Với 61+ 11137 −
3a = 4b ⇒ x = (thỏa mãn) và 61 11137 x = (loại) 18 18
Kết luận: Hệ có 2 nghiệm của hệ là: (  61+ 11137 61+ 11137  3 + 2 7;3 + 2 7 ) và  ;   18 18    0.5 3 3.a 2 2 2 1 + x 1 + y 1 + z (2 điể = + +
m) + Đặt P 3 2 3 2 3 2 1 + 4 1 + y + 3z 1 + 4 1 + z + 3x 1 + 4 1 + x + 3y và 2 2 2
1 + x = a, 1 + y = ,
b 1 + z = c với a, , b c > 1 + Ta có 3 + y = ( + y)( 2 1 1 1 − y + y ) 2 + y 2 2 + y + Theo cô-si
(1+ y)(1− y + y ) 2 2 ≤ 3 ⇔ 1+ y ≤ 2 2 2 2 1 + x 1 + x a + Suy ra ≥ = 1 + 4 1 + y + 3z 2 ( 1 2 1 + y ) + 3( 2 3 2 1 + z ) ( ) 2b + 3c 0.5
+ Hoàn toàn tương tự ta cũng có 2 2 1 + y 1 + y b ≥ = 1 + 4 1 + z + 3x 2 ( 2 2 1 + z ) + 3( 2 3 2 1 + x ) ( ) 2c + 3a 2 2 1 + z 1 + z c ≥ = 1 + 4 1 + x + 3y 2 ( 3 2 1 + x ) + 3( 2 3 2 1 + y ) ( ) 2a + 3b
+ Cộng các bất đẳng thức ( )
1 , (2) , (3) theo vế ta được a b c P ≥ + + 2b + 3c 2c + 3a 2a + 3b 0,5 2 2 2 a b c ⇔ P ≥ + + 2ab + 3ca 2bc + 3ab 2ca + 3bc
(a + b + c)2
⇒ P ≥ 5(ab+bc + ca) 0.5
3(ab + bc + ca) 3 ⇒ P ≥ = ⇒ đpcm
5 (ab + bc + ca) 5
+ Dấu “=” xảy ra khi và chỉ khi x = y = z = 2 0.5 3.b  2 (2 điể = m)  1 u  3  ∀ ≥ Cho dãy số ( , n 2. u u
n ) xác định như sau n 1 − Tính tổng u  = n  2  (2n − )1u + n 1 1 −
của 2019 số hạng đầu tiên của dãy số (un ) . 1 2 (2n − ) 1 u +1 n− 1 1 Ta có 1  2  = = + 4n − 2 =
+ 2 n − (n − )2 1   u  n un 1 u − n 1 u − n 1 − 1 2 1  2  ⇒ − n = + n − (n − )2 2 1 2 2 1 − 2n = − 2(n − )2 1   u  n un 1 u − n 1 −
Tương tự ta sẽ có 1 − (n − )2 1 = − (n − )2 1 2 1 2 2 = .... = − 2 un 1 un 2 1 u − − 2 1 1 3 1 1 4n − 1 Suy ra 2 − 2n = − 2 = − 2 = − ⇒ = u 1 u 2 2 u 2 n n 0,5 4 2 1 1 ⇒ u = = − n
(2n − )1(2n + )1 2n −1 2n + 1 2019 2019  1 1  ⇒ ∑ = ∑ − i u    − +  i 1 = i 1 2i 1 2i 1 = .  1   1 1   1 1   1 1  1 4038 = 1 − + − + − + ... + − = 1− =          3   3 5   5 7   4037 4039  4039 4039 4.a + n(Ω) 4 = C = 4845 (2 điể 20
m) Trường hợp 1: Cả 4 cây được chặt ở gần nhau có 20 cách 0.5
+ Trường hợp 2: Trong 4 được chặt có đúng 3 cây gần nhau
- Chặt 3 cây gần nhau có 20 cách
- Mỗi 3 cây gần nhau có 15 cây không gần 3 cây đó. Vậy trường hợp này có: 20 X 15 = 300 cách 0,5
Trường hợp 3: Trong 4 cây được chặt có đúng 2 cây gần nhau:
- Chặt đúng 2 cây ở gần nhau có 20 cách
- Với mỗi 2 cây gần nhau có 16 cây không ở gần hai cây này. Trong 16 cây lại có 15
cặp cây gần nhau. Chọn hai cây không gần nhau trong 16 cây có: 2 C −15 = 105 16
Vậy trường hợp này có: 20.105 = 2100 cách 0.5
+ Trường hợp 4: Trong 4 cây được chặt có đúng hai cặp cây gần nhau
- Chọn một cặp cây gần nhau có 20 cách
- Mỗi cách chọn một cặp cây gần nhau lại có 15 cặp cây gần nhau được chọn từ 16
cây. Vậy trường hợp này có 20 15 . = 150 cách 2 Vậy n( )
A = 4845 − (20 + 300 + 2100 + ) 150 = 2275 2275 455 Suy ra: P( ) A = = 4845 969 0.5
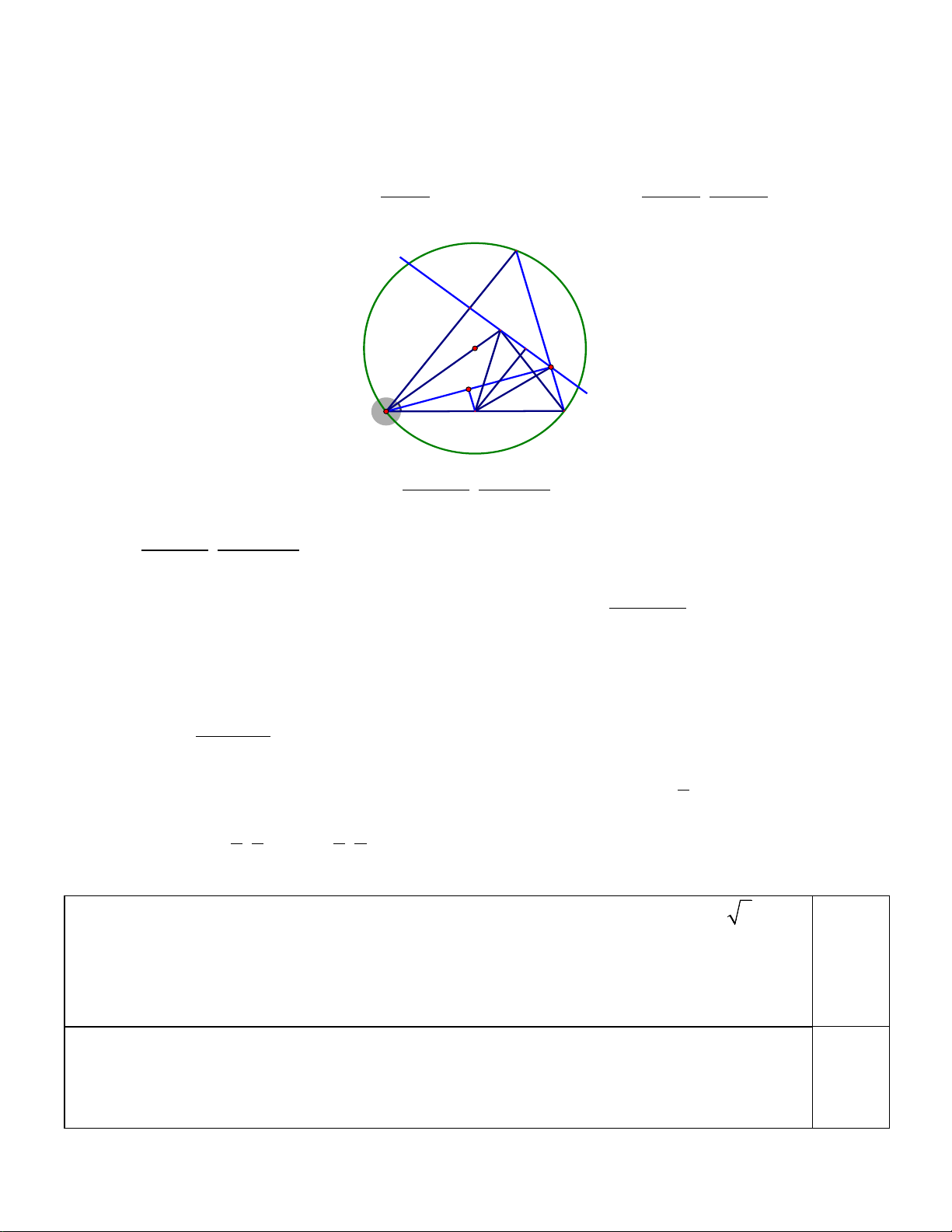
Bài 4 b (2,0 điểm). Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có ba góc đều nhọn và nội tiếp
đường tròn tâm I. Gọi K là hình chiếu vuông góc của B trên đường thẳng AC, H là hình chiếu vuông góc
của C trên đường thẳng BI. Các đường thẳng AC và KH lần lượt có phương trình là x  y  1  0 và
x  2y  1  0 . Biết điểm B thuộc đường thẳng y  5  0 và điểm I thuộc đường thẳng x  1  0 . Tìm tọa độ điểm C. Hướng dẫn.
K là giao điểm của HK và AC nên có tọa độ là K(-3; 2). Đường thẳng BK vuông góc với AC nên có
phương trình: x - y + 5 = 0. Vì B thuộc đường thẳng y - 5 = 0 nên tọa độ B(0; 5).   Gọi 3 7 E   ;  
là trung điểm của BK, M là trung điểm BC thì EM // AC nên phương trình EM là: x + y - 2  2 2
= 0. Suy ra tọa độ của M là: M m;2 m. Do MH = MK nên tam giác HMK cân tại M, có MD là trung 5 x
  m  t
tuyến cũng là trung trực, nên phương trình đường thẳng  MD có dạng:  , thay vào phương y
  2  m  2t 
trình của HK ta có:  6m 3 4 3m  
m  t    m  t m 3 2 2 2  1  0  t  , suy ra tọa độ củ   a D là: D  ; . 5  5 5  A N H D I K E B M C    Từ tọa độ của m    m  
D và K suy ra tọa độ của 12 9 2 6 H  ;  
. Suy ra tọa độ véc tơ BH  là:  5 5  
12m 9 27 6m      BH    ;  
. Mặt khác gọi I 1;n
BI  1;n  5  , ta có 
 cùng hướng với BH nên  5 5   
n   m   
 m  n   m   22m 24 5 12 9 27 6 5 4
3  9  2m  n  (1). 4m  3  
Ngoài ra BM.IM  0 nên ta có: m m  
1  m  32  m  n  0 2
 2m  2m  6  n m  3  0 (2). Thế (1) vào (2) ta được:  2 11m 12
m  m  3 
m  3  0   2 m  m  
3 4m  3  11m  12m  3  0 4m  3 3 2
 m  m  m 
   m   2 m  m   3 4 18 36 27 0 2 3 2 6
9  0  m   . 2     Khi đó tọa độ 3 7   3 7 M   ;  E       ;   C 
nên tam giác ABC vuông tại C.    
3;2  K 3;2 2 2  2 2 Câu 5.
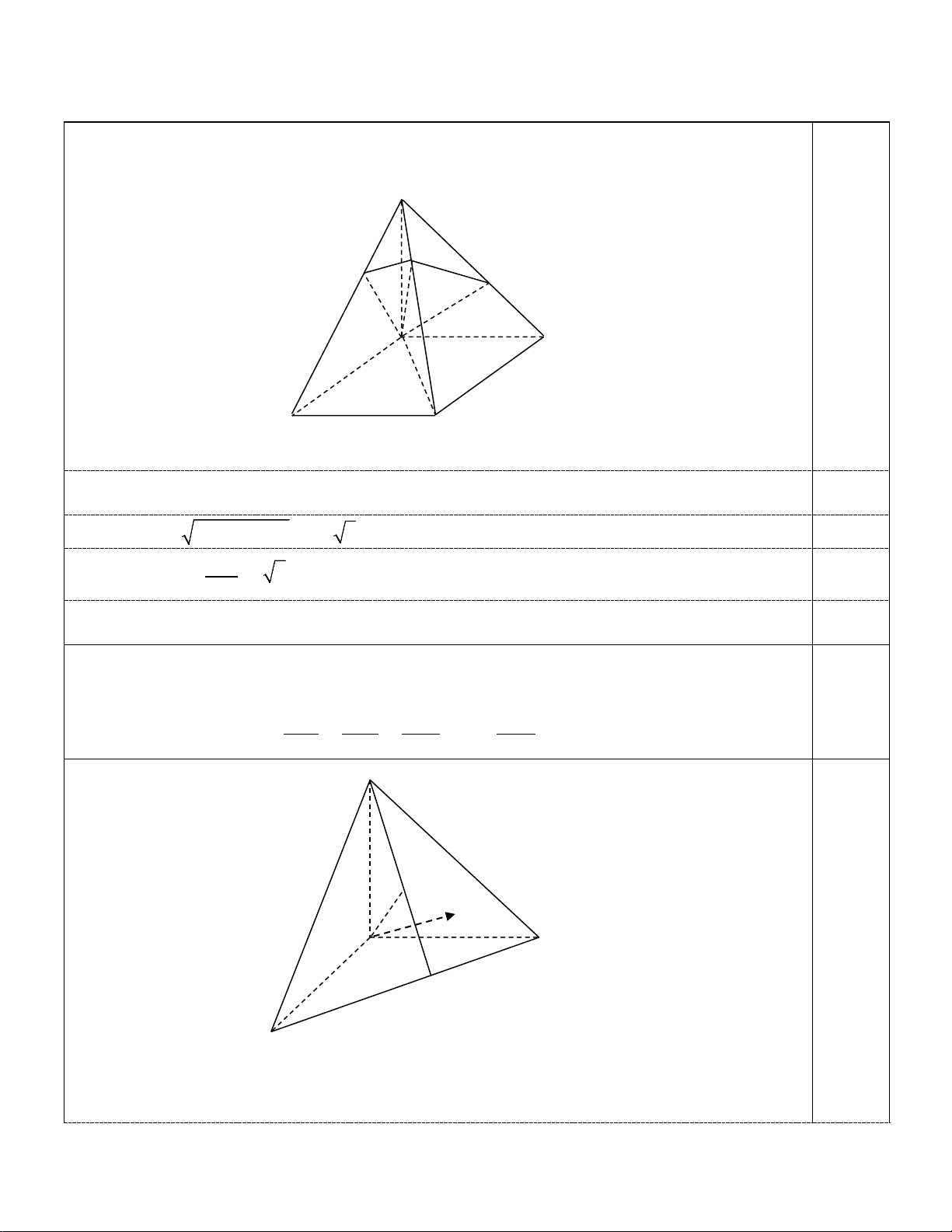
1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB  3a và AD  a 3 . Cạnh
bên SA  2a và SA vuông góc với mặt đáy ABCD. Gọi H,K lần lượt là hình chiếu 2,0
vuông góc của đỉnh A lên các cạnh SB và SD . Tính góc giữa đường thẳng AC và mặt phẳng AHK. BC   SA 
Ta có AH  SB , mà 
 BC  SAB  BC  AH BC   BA  0,50
Suy ra: AH  SBC   AH  SC  1 4 6
Tương tự: AK  SC 2 0,50
Gọi I  SC  AHK , từ  
1 và 2 suy ra: SC  AHIK  S I H K A D B C
Do đó: AC AHK    ,
 CAI  ASC 0,25 Ta có: 2 2
AC  AB  AD  2a 3 0,25  AC  Mà: 0 tan ASC   3  ASC  60 0,25 AS
KL: AC AHK   0 ,  60 . 0,25
2. Cho tứ diện OABC có ba cạnh , OA ,
OB OC đôi một vuông góc với nhau tại O. Gọi H là
hình chiếu vuông góc của O lên mặt phẳng ABC  và P là điểm bất kỳ trong tam giác 2,0 2 2 2 2 PA PB PC PH
ABC. Chứng minh rằng    2  . 2 2 2 2 OA OB OC OH A H P . O C B    
Ta có: OP  xOA  yOB  zOC   1
Do điểm P nằm trong tam giác ABC nên x  y  z  1. 0,25 7  2   Từ  
OP OA  PA
OP OA  PA 1 ta có: x   2 2 2 2 2 2
OA  OP.OA   x  2 2 2OA 0,50 2 2 1  OP PA  Suy ra: x  1      2 2 2   OA OA  2 2   2 2   Tương tự: 1  OP PB 1  OP PC y  1        , z  1     2 2 0,25 2      OB OB  2 2 2  OC OC 
Mà ta có: x  y  z  1 5 2 2 2 2 2 2 1  OP PA  1  OP PB  1  OP PC   1      1        1           1 2 2 2 2      2 2 2  OA OA 2  OB OB  2  OC OC  2 2 2 2 2 2 OP OP OP PA PB PC 0,50  3     2    2 2 2 2 2 2 OA OB OC OA OB OC 2 2 2   2 1 1 1   PA PB PC  1 OP         2 2 2  2 2 2 OA  OB OC  OA OB OC Mặt khác ta có: 1 1 1 1    và 2 2 2
OP  OH  PH 0,25 2 2 2 2 OA OB OC OH 2 2 2 2 2 2 2 Do đó: PA PB PC OP OH  HP PH    1   1   2  2 2 2 2 2 2 OA OB OC OH OH OH 0,25 2 2 2 2 PA PB PC PH KL:    2  (đpcm). 2 2 2 2 OA OB OC OH 8
Document Outline

• 32.-ĐỀ-THI-HSG-THÁNG-2