Đề thi HSG Toán lớp 11 năm 2020-2021 trường Trần Nguyên Hãn vòng 1 (có đáp án)
Đề thi HSG Toán lớp 11 năm 2020-2021 trường Trần Nguyên Hãn vòng 1 có đáp án được soạn dưới dạng file PDF gồm 5 trang giúp các bạn ôn tập, tham khảo và chuẩn bị tốt cho kỳ thi sắp tới. Các bạn xem và tải về ở dưới.
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HẢI PHÒNG
ĐỀ THI CHỌN HỌC SINH GIỎI VÒNG 1
TRƯỜNG THPT TRẦN NGUYÊN HÃN
LỚP 11 - NĂM HỌC 2020-2021 Môn: TOÁN
ĐỀ THI CHÍNH THỨC
(Đề thi có 01 trang)
Thời gian bàm bài: 180 phút, không kể thời gian phát đề
Họ, tên thí sinh: ……………………………………. Số báo danh: ………………
Câu 1 (6 điểm): Giải các phương trình, bất phương trình sau:
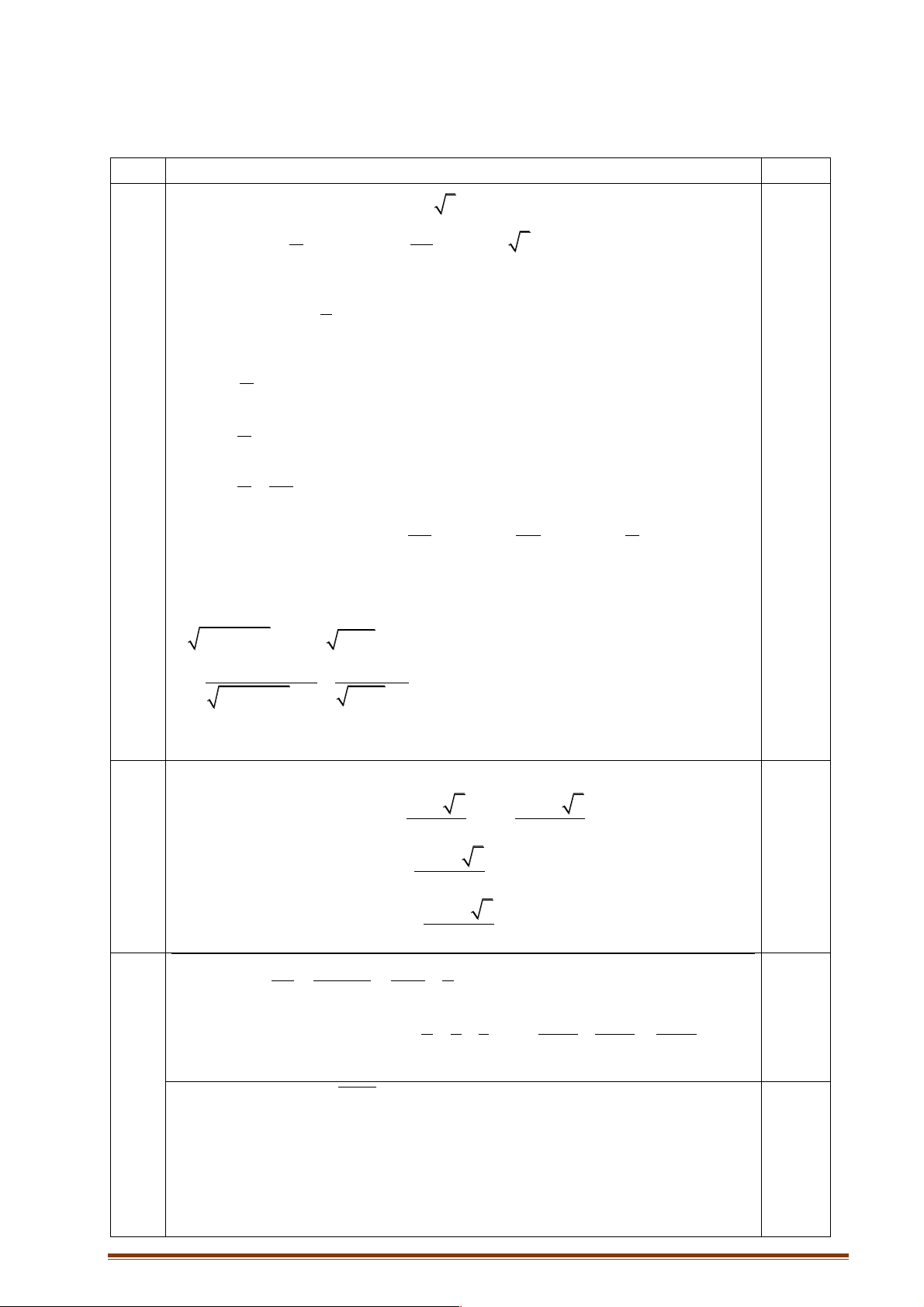
1) 3sin 2x -3+ 6sin x - 3 cos x = 0 p 2 3x 3 2 2sin ( - ) + 3 cos x(1-3tan ) x 2) 2 4 = 1 - 2sin x -1 3) 2
x - x - 2 + x - 2 > 3 2 3sin 2x - 2cos x
Câu 2 (2 điểm): Tìm giá trị nhỏ nhất và lớn nhất của hàm số y =
sin 2x - 2cos 2x + 4
Câu 3 (4 điểm): 1 1 1 1) Tính tổng S = + + ××× × 2 2 2 A A A 2 3 2020
2) Từ các chữ số 1; 2; 3; 4; 5; 6; 7; 8; 9 lập được bao nhiêu số có 4 chữ số đôi một khác
nhau và chia hết cho 11 đồng thời tổng của 4 chữ số của nó cũng chia hết cho 11.
Câu 4 (2 điểm): Trong mặt phẳng Oxy, cho hình bình hành ABCD, hình chiếu của điểm D
lên AB, BC lần lượt là M(-2;2), N(2;-2). Biết rằng đường thẳng DB có phương trình là
3x - 5y + 1 = 0 và hoành độ điểm B lớn hơn 0. Tìm tọa độ điểm B.
Câu 5 (4 điểm): Cho hình chóp S.ABCD, đáy ABCD là hình bình hành, M là trung điểm của
SA và E là trung điểm của SB; P thuộc cạnh SC sao cho SC = 3SP.
1) Dựng giao điểm của DB với mặt phẳng (MPE).
2) Gọi N là một điểm thuộc cạnh SB, mặt phẳng (MNP) cắt SD tại Q. SB SD Chứng minh + = 5 SN SQ
Câu 6 (2 điểm): Cho a, b, c là các số dương thỏa mãn: a + b + c = 3 a b c 3 Chứng minh rằng P = + + ³
ab + 3c bc + 3a ca + 3b 4
------------------ Hết ------------------
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ tên, Chữ kí của cán bộ coi thi:………………………………………………… Trang 1
ĐÁP ÁP ĐỀ THI HSG MÔN TOÁN – KHỐI 11- LẦN1- NĂM HỌC 2020-2021 Câu Đáp án Điểm
1) Biến đổi thành (2sin x -1)( 3 cos x + 3) = 0 1 1 p p giải ta được x= + 5 k2p ; x=
+ k2p ( 3 cos x + 3 = 0vô nghiệm) 1 6 6 1 2)Điều kiện in
s x ¹ và cos x ¹ 0 Biến đổi thành 2 p sin(3x - ) = sinx 3 1 é p x = + kp ê 6 Û êê p kp 1 x = + êë 3 2 7p p - p
Đói chiếu đk pt có nghiệm x = + k2p, x =
+ k2p, x = + kp 6 6 3 3)Đk x ³ 2 Bpt đưa về 2
( x - x - 2 - 2) + ( x - 2 -1) > 0 1 (x - 3)(x + 2) x - 3 Û + > 0 2 x - x - 2 + 2 x - 2 +1 1 Û x > 3
Từ gt ta có (y -3)sin 2x - (2y -1)cos 2x = 1 - - 4y 0,5 9 + 6 5 9 - + 6 5 2 Pt trên có nghiệm cho ta - £ y £ 11 11 1,25 9 - + 6 5
kết luận GTLN của y bằng 11 0,25 GTNN của y bằng 9 - - 6 5 11 1 1 1 1 1) Ta có = = - 2 A k(k -1) k -1 k 1 k 3
Cho k = 2,3,..., 2020 Þ 1 1 1 1 1 S =1- + - + ××× + - 2019 .= 1 2 2 3 2019 2020 2020
2) Gọi số cần tìm là abcd
Þ (a + c) - (b + d) 1 ! 1
suy ra a+c và b+d đều chia hết cho 11
(a + c) + (b + d) 1 ! 1 1
Có 2+9=3+8=4+7=5+6 nên có 4.2.3.2=48 số 1 Trang 2
Gọi I(x;y) là tâm hình bình hành ABCD, do IM=IN nên x=y
có I thuộc BD nên 3x-5y+1=0 từ đó suy ra x=y= 0,5 0,75 34 có IB=ID=IM=
do đó D,B thuộc đường tròn dường kính BD 2 có pt là 1 1 17 2 2
(x - ) + ( y - ) = (1). 2 2 2 4
Lại có tọa độ B,D thỏa mãn 3x-5y+1=0 (2) 0,75
Giải hệ (1),(2) vói hoành độ điểm B lớn hơn 0 ta được B(3;2) 0,5
1) Gọi O là tâm của đáy ,SO cắt MP tại I,IE cắt DB tại J là điểm càn dựng 2
2)Ta c/m bổ đề :cho tam giác SAB ,O là trung điểm của AB.Một
đt cắt SA,SO ,SB tại M,N,P CMR SA SB SO + = 2 (1) 5 SM SP SN
CM : kẻ AH//MN ,BK//MN ( H,K thuộc SO) ta có SA SH SB SK = , = ,OH = OK Þ SM SN SP SN (1) 1
Áp dụng bổ đề trên ta được SB SD SA SC 2SO + = + = ( ) =5 1 SN SQ SM SP SI 1) (1điểm) ta có P= a b c + +
(a + c)(b + c) (b + c)(b + a) (c + a)(c + b) a
a(a + c) a(b + c) 3a + + ³
,tương tự và cộng laị ta được P 1
(a + b)(a + c) 8 8 4 2
9 (a + b + c) + ab + ac + bc 6 ³ - 4 8 2
9 (a + b + c) 1 3 2 ³ - -
(a + b + c) = 4 8 24 4 2 (Do
(a + b + c)
ab + bc + ca £ ) 1 3 Dấu bằng khi a=b=c=1 Trang 3