Đề thi kì 1 Toán 11 năm 2020 – 2021 trường THPT Năng khiếu TDTT Bình Chánh – TP HCM
Đề thi kì 1 Toán 11 năm học 2020 – 2021 trường THPT Năng khiếu TDTT huyện Bình Chánh, thành phố Hồ Chí Minh có đáp án và lời giải chi tiết.
21
11 lượt tải
Tải xuống
sO GIAO DUC
vA
DAO TO TP HO
CHI
MINH
TR
NANG
KHIEU TDTT H.BC
kE
CHINH
THIIJC
TR[JNG
IRUNG 8C U IHONG
__
HANG KKIEII 1011
,
BINH CHANK
*
KIEM TRA
HOC K! I
-
NAM HQC 2020-202 1
MON: TOAN HQC
-
KHOI 11
Thai gian lam bài: 90 phüt
Câu 1: (1,0 dim)
Trong rnt nhOm h9c sinh CO 3 h9c sinh Nam,
5
hc sinh NU.
a)
CO bao nhiêu cách sp xp nhórn hoc sinh nay vào môt bàn an cm dài cO 8 ch.
b)
Chçn ngu nhiên 3 btn di nhn phn ccim cho
Ca
nhóm. HOi cO bao nhiêu cách chQn?
Câu
2: (1,75 dim) Môt hop chüa 12 the do, 9 the xanh và 7 the yang. Ch9n ngâu nhiên tir
hp
5
the. TInh xác sut d:
a)
Trong
5
the duc ch9n cO dung 2 the xanh.
b)
Trong
5
the duçic ch9n có dü ba màu và có It nht 2 the màu yang.
Câu
3: (0,75 dim) Giâi phucng trInh sau:
A
-
5x + 5
=
0 (x
E
N*,x ~ 2).
Câu 4: (1,0 dim)
Khai trin theo cong thirc Nhj thirc Niu-tm biu thirc: (x +
3)4•
Câu 5: (1,0 dim)
TIm s htng chüa x
1°
trong khai trin (x
-
vOi x ~
Câu 6: (1,0 dim)
Cho cp s cong
(u
n
)
cO:
u
1
=
5;
d
=
3.
a)
TIm u
20
.
b)
Hay cho bit s 146 là s hang thir bao nhiêu cüa cp s cong?
Can
7: (3,5
diem)
Trong không gian cho hinh chOp
S. ABCD,
có day
ABCD
là hInh chi:t nht
tam
0.
G9i
M, N
lAn
h19't là trung dim cUa
SA, SD.
a)
Tim giao tuyn cüa hai
mtt phng
(SAD) và (SBC).
b)
Chirng minh rtng:
MN
//
(SBC).
c)
Chirng minh ring:
(OMN)
//
(SBC).
d)
Giâ
sir
AD
=
8;
SB
=
SC
=
6. TIm nhanh thit din cüa hInh chop S.
ABCD
khi ctt
bii mt phâng
(0 MN)
và tinh din tich thit din thu duqc.
...Hêt...
Ho ten HS:
...
S báo danh:
Lop:
DUC VA DAO TAO TP. HCM
T NANG KHIEU TDTT H.BC
E
CH!NH THIIJ'C
O TOAN
ThànhpMH C/il Minh, ngày 13 tháng 12 nãm 2020
7TWJ1D
1
ThLiK6
oc O rHUNC
HANG XHiEU JOlT
8NHCHANH
p
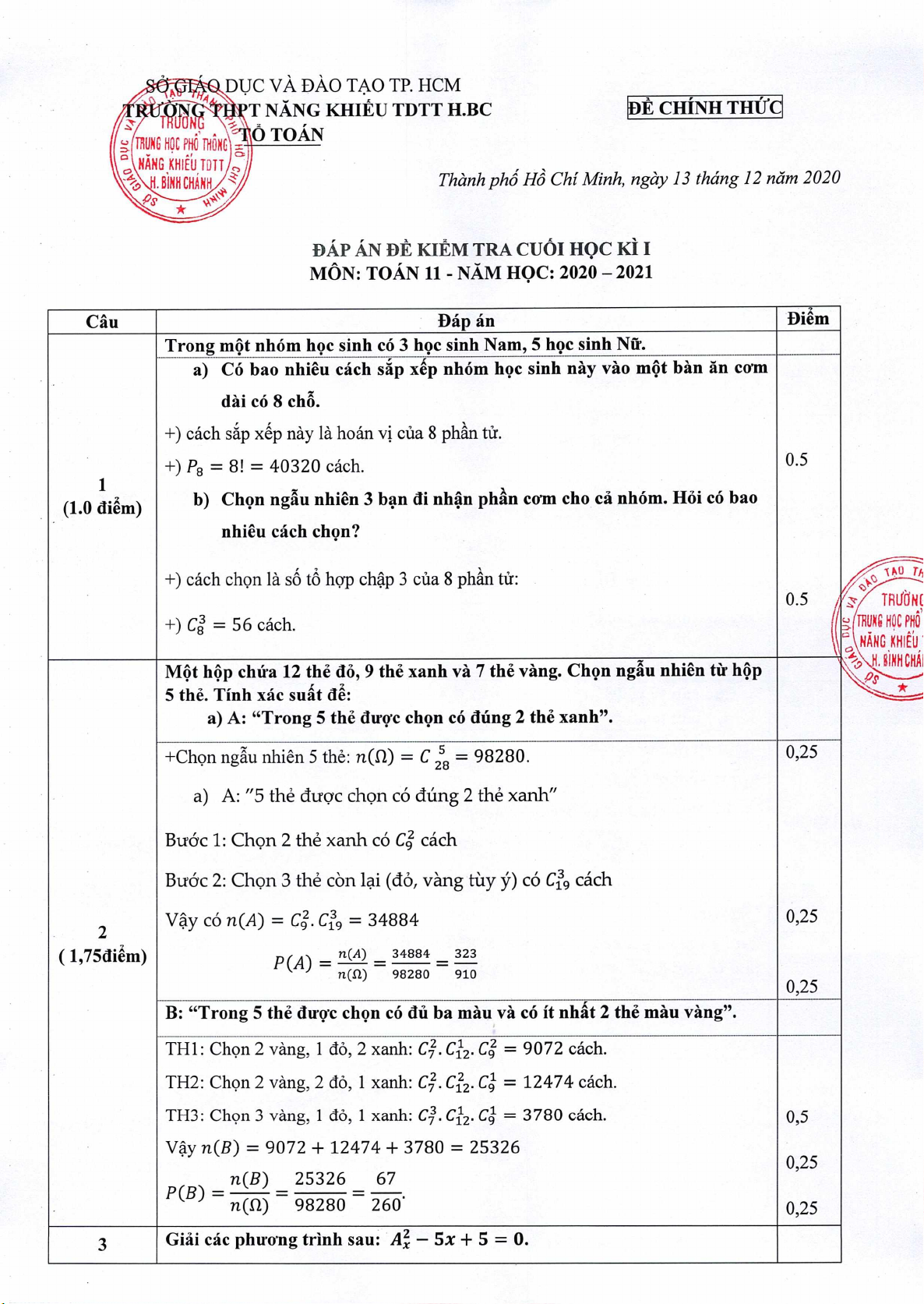
PAP AN BE KIEM TRA CUOI HQC Ki i
MON: TOAN 11-
NAM
HQC: 2020
—
2021
Câu
Pap an
Diem
Trong môt nhóm hoc sinh có 3 h9c sinh Nam, 5 hc sinh Nfr.
a)
Co bao nhiêu cách sp xp nhóm hoc sinh nay vào môt bàn an co'm
dài có 8 ch&
+) cách s.p xp nay là hoán vj cüa 8 ph.n
t1r.
+) P
8
= 8! = 40320 cách.
0.5
-
(1.0 dim)
b)
Ch9n ngâu nhiên 3 bn di nhn phân co'm cho cã nhóm. HOi có bao
nhiêu each chon?
+) each chn là s
t hçTp ch.p 3 cUa 8 phn tü:
0.5
+)
C
= 56 each.
Mt hp chira 12 the do, 9 the xanh và
7
the yang. Ch9n ngu nhiên tr hp
5 the. TInh xác sut dê:
a) A: "Trong 5 the dtrçrc chçn có dung 2 the xanh".
+Chn ngu nhiên
5
the:
n(1) = C
= 98280.
a)
A: "5 the duc chQn có dung 2 the xanh"
0,25
BuOc 1: Ch9n 2 the xanh có C' cách
BuOc 2: Chon 3 the con 1i (do, yang tüy ) có
C
1
%
cách
2
Vy có n(A) = C. C,
9
=
34884
0,25
(1,75dim)
P(A) — n(A) — 34884 — 323
— n(fl) — 98280 — 910
0,25
B: "Trong 5 the du'qc chçn có dü ba màu và cO It nht 2 the màu yang".
TH1:
Chn 2 yang, 1 dO, 2 xanh:
C. C,'
2
. C
= 9072 each.
TH2:
Ch9n 2 yang, 2 do, 1 xanh:
C. C,
2
. C
9
'
= 12474 cách.
TH3:
Chçn 3 yang, 1 do, 1 xanh:
C. C
11
2
. C
9
' = 3780 each.
0,5
Vây
n(B)
=
9072 + 12474 + 3780 = 25326
0,25
—
n(B)
—
25326
67
P(B)
— n(ul) —
98280 =
0,25
Giái cac phu'o'ng trInh sau:
A
— 5x + 5 = 0.
ThUK HOC PHI
NG XHIE
IINHCHA
(0,75dim)
A
4=x
2
.
Vy
— 5x
5
0
X!
5x
5
0
+ =
+ =
0,25
0,25
0,25
(x-2)!
x(x
-1)(x-2)!
5x+5
=0=x(x-1)-5x+5 = 0
-6x+5=0
= 1 (L)
Ix
= 5 (N)
S
=
f5}
Khai trin theo cong thu'c Nhi thuc Niu-to'n biu
thIrc: (x + 3)4
4
(x+3)
4
= C.(x)
4
.3°+C.(x).3' +C.(
x
)
2
.3
2
+C.(
x
)
1
.33 +
0,5
(1.Odiêm)
C
•
.(x)
°
.3
=x
4
+ 12x
3
+ 54x
2
+ 108x + 81.
05
a)
TIm
s
hng chua x
10
trong khai trin
(x
-
4)25, vói x
Tk+l
= C.
a
n_k.bk = C.(
x
)
2
5_k
.
()
0,25
-
c
'
(_
2
k
x
253
k
-
25'
025
(1.0dim)
GT25-3k= 10
k=5
0,25
Vy
s
hang
cn tim là
C
. (-
2)
5
.x
10
.
0,25
Cho cp
s
cong
(u
n
) có: u1
=
5;
d
=
3
a)
TIm
u20
u
20
= u
1
+ 19d
0,25
=5+19.3=62
0,25
(1,0 dim)
b)
Hay cho bik
sI
146 là s hng thü bao nhiêu?
u =u
1
+(n-1).d4= 146=5+ (n-1).3
0,25
=n=48
Vy
u
48
= 146.
0,25
Trong không gian cho hInh chop S.
ABCD,
có
day
ABCD là
hInh chü' nht
tam
0.
G9i
M, N
1n hryt
là
trung dim
cüa
SA, SD.
S
x
N
U
___
_
I
(3,5 diem)
1
\
''
II,
'%'
!\
'
\
D
/
_-'--
--
-/
I
1
I_
,
s
/
1'
,
'
I
_-_(
//
!--
----
O
--
-.
H
F
B'----
-------
a)
TIm giao tuyn cüa hai mt phäng
(SAD)
và
(SB C).
+)S
e
(SAD) n (SB C)
+
fAD c (SAD); BC c (SBC)
0,25
AD//BC
Vy (SAD) n (SB C) = Sx//AD//BC.
0,25
0,25
b)
Chiung minh ring:
MN // (SBC).
MN là dung trung bInh cüa tam giác SAD nen MN
II
AD
0,25
( MN//AD
Ta co:
0,25
AD c (SAD)
0,25
Suy ra MN // (SAD).
c)
Chfrng minh rang:
(OMN)
//
(SBC).
Tt'rcâub:MN//AD//BC
Ta có:
( BCC(SBC) Suy
ra MN
II
(SBC)
0,25
OM là dithng trung blnh cüa tam giác SAC nên OM // SC.
Ta có: [
SC
(SBC) . Suy
ra: OM // (SBC).
0,25
MN // (SAD), OM // (SAC).
VI
MNnOM=M
0,25
MN, OM
C
(OMN)
0,25
Nên
(OMN) // (SBC).
d)
Giã
sfr
AD =
8; SB
=
SC
=
6.
TIm nhanh thit din cüa hInh chop
S. ABCD
khi ct bôi mt phng
(OMN)
và tInh din tIch thiêt din
thu thwc.
+ (OMN)
n
(SAD) = MN.
+ (OMN)
n
(ABCD) = Oy//AD//BC.
Trong(ABCD),
gçi E = Oy
fl
AB; F = Oy
fl
CD.
0,25
Suy ra
(OMN)
n
(ABCD) = EF.
+ (OMN) n (SAB) = ME.
+(OMN) n (SCD) = NF.
+(OMN)
n
(SBC) = 0.
0,25
Suy ra thit din là hInh tir giác MNFE.
Do MN//EF nên MNFE là hInh thang.
Han n1ta SB = SC nên suy ra ME = MF, vy MNFE là hlnh thang can.
0,25
*
Drng NH, MK ltn lu'ot vuông góc vài EF.
VI MNFE là hInh thang can nén FH = EK = 2
NH =
Vy
5
MNFE = . (
MN + EF). NH =
0,25
Bấm Tải xuống để xem toàn bộ.
Preview text:
Document Outline
- Page 1
- Page 2
- Page 3
- Page 4