Đề thi môn Toán 11 giữa học kỳ 2 (có đáp án)

KIỂM TRA GIỮA HỌC KỲ II NĂM HỌC 2020 - 2021 MÔN Toán 11
Thời gian làm bài : 90 phút
(không kể thời gian phát đề)
Họ và tên học sinh :....................................................... Số báo danh : ...................Lớp: 11
Phần I. TRẮC NGHIỆM : 7 điểm (Học sinh trả lời bằng cách khoanh tròn vào đáp án đúng.)
Câu 1: Mệnh đề nào sau đây là đúng ? 1 A. lim = +¥ 1 . B. lim = +¥ 1 C. lim = -¥ 1 . D. lim = 0. n k n k n k n Câu 2: Tính ( 2 lim n - 4)? A. +¥ . B. -¥ . C. 1 - . D. 4 . u
Câu 3: Cho các dãy số (u ), v
limu = a, limv = +¥ lim n n ( n ) và thì bằng n n vn A. 1. B. 0 . C. -¥ . D. +¥ . 2n + 3 Câu 4: Tính lim
được kết quả là 3 + n 1 A. . B. 0 . C. 2 . D. 1. 2
Câu 5: Dãy số nào sau đây có giới hạn bằng 0 ? 1 n æ ö 4 n æ ö æ 5 n - ö 5 n æ ö A. . B. . C. . D. . ç ÷ ç ÷ ç ÷ ç ÷ è 5 ø è 3 ø è 3 ø è 3 ø
Câu 6: Cho hai dãy số (u ), v limu = 7 limv = 4 lim(u .v n n ) n ( n) thỏa mãn và Giá trị của bằng n n A. 7 . B. 28 . C. 11 D. 7 -
Câu 7: Cho dãy số (u limu =15. lim(u +5 n ) n ) thỏa mãn Giá trị của bằng n A.10. B. 30. C. 20. D. 30. -
Câu 8: Cho hai hàm số f (x), g (x) thỏa mãn lim f (x) = 5 và lim g (x) = 2. Giá trị của x 1 ® x 1 ® lim é f
ë ( x).g ( x)ù bằng û x 1 ® A. 3. B. 7. C. 3. - D. 10.
Câu 9: Cho hàm số f (x) thỏa mãn lim f ( )
x = 2004 và lim f ( )
x = 2004. Giá trị của lim f ( ) x x 1+ ® x 1- ® x 1 ® bằng A. 2004 . B. 1. C. 2020 . D. 2021.
Câu 10: Giá trị của lim ( 2 3x - 2x - ) 1 bằng x 1 ® A. 2 . B. 1. C. +¥ . D. 0 .
Câu 11: lim x +16 bằng x®9 A. 25 . B. 4 . C. 5 . D. 9 . Câu 12: 2021 lim x bằng x®+¥ A. . -¥ B. + . ¥ C. 0. D. 1. Trang 1
Câu 13: Cho hai hàm số f (x), g (x) thỏa mãn lim f (x) = 2021 và lim g (x) = + . ¥ Giá trị của x 1 ® x 1 ®
lim é f ( x).g (x)ù ë û x 1 ® bằng A. + . ¥ B. . -¥ C. 2. D. 2. - 1
Câu 14: Hàm số y =
gián đoạn tại điểm nào dưới đây? x - 2022 A. x = 2022 . B. x = 2020 . C. x = 2023 . D. x = 2022 - . 2021
Câu 15: Hàm số y =
liên tục tại điểm nào dưới đây?
(x - )1(x -2)(x -3) A. x = 2 - . B. x = 3. C. x = 1. D. x = 2 .
Câu 16: Hình chiếu của hình chữ nhật không thể là hình nào trong các hình sau? A. Hình thang B. Hình bình hành C. Hình chữ nhật D. Hình thoi
Câu 17: Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AD và BC . Khẳng định nào sau đây sai? !!!" !!!" !!!" !!!" !!!!" !!!" !!!"
A. AB +CD = CB + AD.
B. 2MN = AB + DC . !!!" !!!!" !!!" !!!" !!!!" !!!" !!!" !!!"
C. AD + 2MN = AB + AC.
D. 2MN = AB + AC + AD. !!!" !!!" !!!"
Câu 18: Cho hình hộp ABC . D A¢B C ¢ D ¢ .¢ Ta có '
BA + BC + BB bằng !!!!" !!!" !!!" !!!!"
A. BD ' . B. BD. C. BA '. D. BC '. ! ! ! !
Câu 19: Với hai vectơ u, v khác vectơ - không tùy ý, tích vô hướng u.v bằng ! ! ! ! ! ! ! !
A. u . v .cos(u,v). B. - ! ! ! !
u . v .cos(u,v). C. u . v .cot (u,v). D. - ! ! ! !
u . v .cot (u,v).
Câu 20: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Số đo của góc giữa hai đường thẳng AB và DD¢ là A. 90° . B. 60° . C. 45°. D. 120° . 3n - 2 Câu 21: lim bằng n + 3 2 - A. 3 B. 1 C. 3 D. 2 -
Câu 22: Cho cấp số nhân lùi vô hạn có u = 1
1 và công bội q = - . Tổng S của cấp số nhân lùi vô 1 2 hạn đã cho bằng A. S = 3 2 . B. S = . C. S = 2 1. D. S = . 2 3 3.2n - 3n Câu 23: lim bằng n 1 + n 1 2 + 3 + 1 A. - . B. -¥ . C. 2. D. 1 . 3 Trang 2 Câu 24: ( 3 2
lim -x + x + 20 ) 21 bằng x®+¥ A. 0 . B. -¥ . C. +¥ . D. 2 . x + 2022 Câu 25: lim bằng x 1- ® x -1 A. 0 . B. +¥ . C. 1. D. -¥ . 2 2x + 3x - 2 Câu 26: lim bằng 2 x 2 ®- x - 4 5 5 A. . B. - 1 . C. . D. 2 . 4 4 4 2 x +1
Câu 27: Hàm số f (x) =
liên tục trên khoảng nào dưới đây? 2 x + 5x + 6 A. ( 3; - 2). B. ( 2; - +¥). C. ( ;3 -¥ ). D. (2;3). ì 3x +1 - 2 ï khi x ¹ 1
Câu 28: Cho hàm số f ( x) = í x -1
. Giá trị của tham số m để hàm số f (x ) liên ïîm khi x = 1
tục tại điểm x = 1 bằng A. m = 3 . B. m = 3 1. C. m = 1 . D. m = . 4 2
Câu 29: Hàm số nào dưới đây liên tục trên khoảng (0;202 ) 1 ? x - 2 2x +1 x +1 1 A. y = . B. y = . C. y = . D. y = . x + 2020 x - 25 x - 2020 2 x - 4
Câu 30: Trong các hàm số sau, hàm số nào liên tục trên ( ; -¥ +¥)? 2 x + 3
A. f (x) = tan x +5.
B. f (x) = .
C. f (x) = x - 6 . D. 5 - x + f ( x) x 5 = . 2 x + 4
Câu 31: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Tính góc giữa hai đường thẳng B D
¢ ¢ và A¢A. A. 90° . B. 45°. C. 60° . D. 30° .
Câu 32: Cho tứ diện đều ABCD . Số đo góc giữa hai đường thẳng AB và CD bằng: A. 60° . B. 30° . C. 90° . D. 45°. ! ! ! ! ! ! ! !
Câu 33: Cho hai vectơ a,b thỏa mãn: a = 4; b = 3; a - b = 4. Gọi a là góc giữa hai vectơ a,b.
Chọn khẳng định đúng? 3 1 A. cosa = . B. a = 30° . C. cosa = . D. a = 60°. 8 3
Câu 34: Cho hình tứ diện ABCD có trọng tâm G . Mệnh đề nào sau đây sai. !!!" 2 !!!" !!!" !!!" !!!" 1 !!!" !!!" !!!"
A. AG = ( AB + AC + AD).
B. AG = ( AB + AC + AD). 3 4 !!!" 1 !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" "
C. OG = (OA+OB +OC +OD).
D. GA+GB +GC +GD = 0. 4
Câu 35: Cho tứ diện ABCD Gọi E là trung điểm AD , F là trung điểm BC và G là trọng tâm
của tam giác BCD .Tìm mệnh đề sai trong các mệnh đề sau: !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" "
A. EB + EC + ED = 3EG .
B. GA+GB +GC +GD = 0. !!!" !!!" !!!" !!!" !!!" !!!" !!!"
C. AB + AC + AD = 3AG.
D. 2EF = AB + DC . Trang 3
Phần II. TỰ LUẬN: 3 điểm
Câu 1: (2,0 điểm) Tìm các giới hạn sau: 3x2 - 2x -1 x + 3 a) lim b) lim x® x3 1 -1 x 3- ® x - 3
Câu 2: (1,0 điểm) Xét tính liên tục của hàm số sau tại điểm x = 2: 0 ì x2 2 - 3x - 2 ï khi x ¹ 2 ï f (x) = 2x - 4 í 3 ï khi x = 2 ïî2
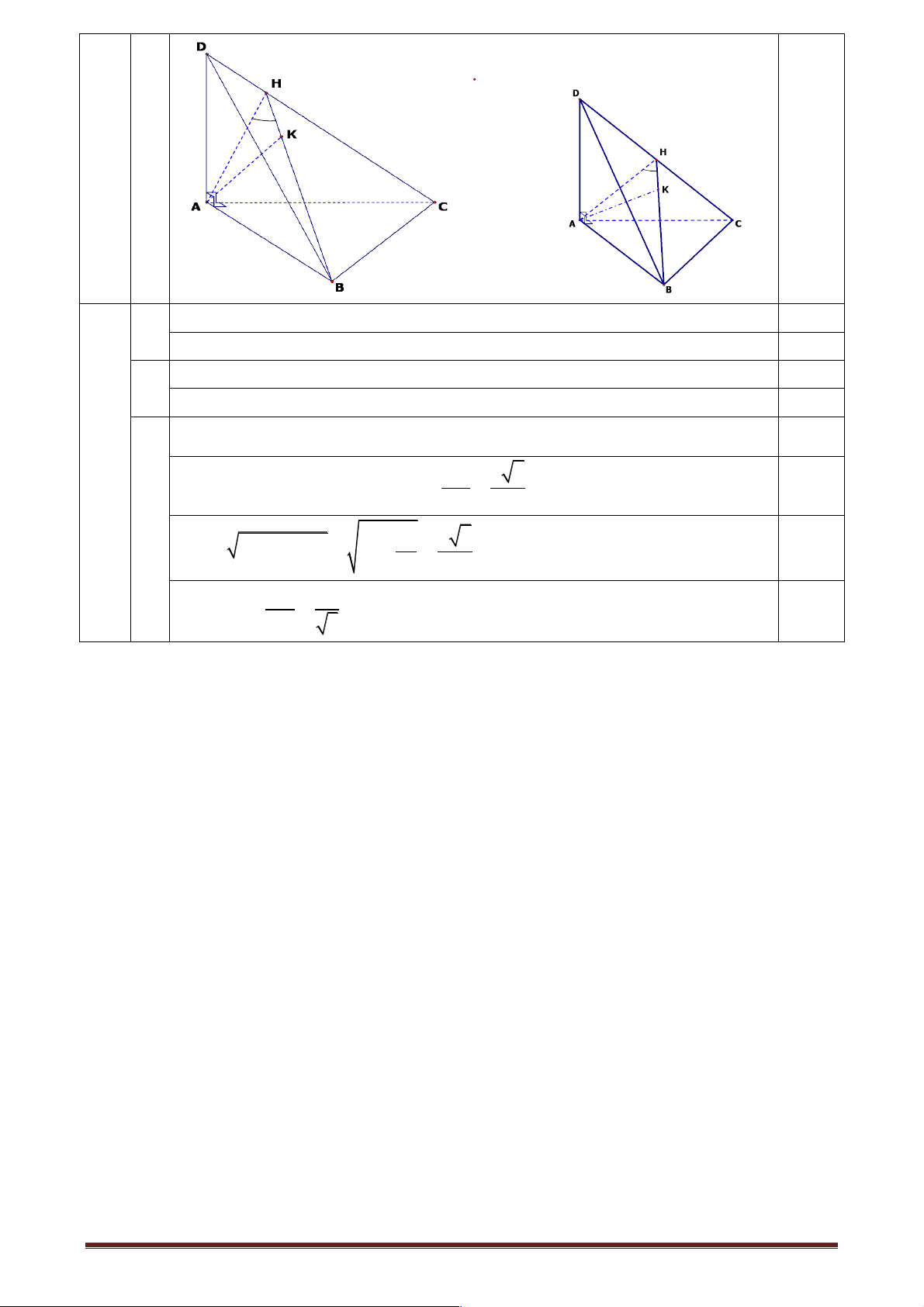
Câu 3: (3,0 điểm) Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc với nhau. Gọi H là chân
đường cao vẽ từ A của tam giác ACD. a) Chứng minh: CD ^ BH.
b) Gọi K là chân đường cao vẽ từ A của tam giác ABH. Chứng minh AK ^ (BCD). ĐÁP ÁN
I.PHẦN TRẮC NGHIỆM 1.D 2.A 3.B 4.A 5.A 6.A 7.A 8.A 9.A 10.D 11.A 12.A 13.A 14.A 15.A 16.A 17.D 18.A 19.A 20.A 21.C 22.D 23.A 24.B 25.D 26.A 27.B 28.C 29.A 30.D 31.A 32.C 33.A 34.A 35.B
* Mỗi câu trắc nghiệm đúng được 0,2 điểm.
II. PHẦN TỰ LUẬN Câu Ý Nội dung Điểm 1 a) 3x2 - 2x -1 (x -1)(3x +1) lim = lim 0,50 x 3 ® x x -1 ® (x -1)(x2 1 1 + x +1) 3x +1 4 = lim = 0,50 x® x2 1 + x +1 3 b) ìlim(x - 3) = 0 x®3- ïï
Viết được ba ý íx ® 3- Û x - 3 < 0 0,75 ïlim(x +3) = 6 > 0 ïx®3- î x + 3 Kết luận được lim = -¥ 0,25 x 3- ® x - 3 2 ì x2 2 - 3x - 2 ï khi x ¹ 2 ï f (x) = 2x - 4 í 3 ï khi x = 2 0,25 ïî2 3
Tập xác định D = R. Tính được f(2) = 2 2x2 - 3x - 2 (x - 2)(2x +1) 2x +1 5 lim f (x) = lim = lim = lim = 0,50 x®2 x®2 2x - 4 x®2 2(x - 2) x®2 2 2
Kết luận hàm số không liên tục tại x = 2. 0,25 Trang 4 3 a) 0,25
a) AB ^ AC, AB ^ AD ÞAB ^ (ACD) Þ AB ^ CD (1) 0,25 AH ^ CD
(2). Từ (1) và (2) Þ CD ^ (AHB) Þ CD ^ BH 0,50
b) AK^ BH, AK ^ CD (do CD ^ (AHB) (cmt) 0,50 Þ AK^ (BCD) 0,50
c) Ta có AH ^ CD, BH ^ CD Þ (( ),( )) ∑ BCD ACD = AHB 0,25 CD a 2
Khi AB = AC = AD = a thì AH = = 0,25 2 2 a2 2 2 2 a 6
BH = AB + AH = a + = 0,25 2 2 ∑ AH 1 cos AHB = = 0,25 BH 3 Trang 5