Đề thi Olimpic Toán 11 Tỉnh Quảng Nam 2016-2017 (có đáp án)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLIMPIC LỚP 11 CẤP TỈNH QUẢNG NAM
Năm học 2016 – 2017 Môn thi : TOÁN ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi : 25/3/2017
Câu 1 (3,0 điểm). Giải các phương trình sau: æ p ö a) 2cos 2x + + 2sin x -1 = 0 ç ÷
b) 3(sin 2x + cos x) - cos 2x - sin x = 2 è 3 ø Câu 2 (4,0 điểm).
a) Chứng minh bất đẳng thức sau bằng phương pháp quy nạp: n 1 + > ( +1)n n n , n " Î N,n ³ 3. ì 2 u ï = b) Cho dãy số (u ) 1 n thỏa: í 3 . *
ï4u + u .u - 6u = 0, n " Î N î n 1+ n 1 + n n
Tìm số hạng tổng quát của (u ) và tính lim u . n n Câu 3 (4,0 điểm).
a) Từ 10 chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên thỏa: là số có 8
chữ số, trong đó có 2 chữ số lẻ khác nhau và 3 chữ số chẵn khác nhau mà mỗi chữ số chẵn có mặt đúng 2 lần.
b) Một đa giác đều có 24 đỉnh, tất cả các cạnh của đa giác sơn màu xanh và tất cả các
đường chéo của đa giác đó sơn màu đỏ. Gọi X là tập hợp tất cả các tam giác có ba đỉnh là các
đỉnh của đa giác đều trên. Người ta chọn ngẫu nhiên từ X một tam giác, tính xác suất để chọn
được tam giác có ba cạnh cùng màu. 3
ì 5x + 3 - 2 - x -1 ï khi x < 1 ï -
Câu 4 (2,0 điểm). Cho hàm số x 1 f (x) = í ï æ p x ö . m sin + 2017p ç ÷ ïî è 2 ø khi x ³ 1
Tìm giá trị của m để hàm số f (x) liên tục tại x = 1. Câu 5 (3,0 điểm).
Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác ABC có trọng tâm G(1;0) và trực
tâm H . Phương trình đường tròn đi qua ba trung điểm của ba cạnh HA, HB , HC là 2 2 æ 5 ö æ 1 ö 25 x - + y - =
. Viết phương trình đường tròn ngoại tiếp tam giác ABC . ç ÷ ç ÷ è 6 ø è 6 ø 18 Câu 6 (4,0 điểm).
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, BC = a 3 ,
SA = 3a . Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABCD); M là trung điểm của OB.
a) Gọi j góc giữa đường thẳng SO và mặt phẳng (SCD). Tính sinj .
b) Tính khoảng cách giữa hai đường thẳng SB và CM theo a . Page 1
–––––––––––– Hết ––––––––––––
Họ và tên thí sinh: …..…………………………………….; Số báo danh: ……………………... Page 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLIMPIC LỚP 11 CẤP TỈNH QUẢNG NAM
Năm học 2016 – 2017
ĐÁP ÁN – THANG ĐIỂM Môn thi: TOÁN
(Đáp án – Thang điểm gồm 06 trang) Câu 1 (3,0 điểm) æ p ö a 2cos 2x + + 2sin x -1 = 0 ç ÷ 1,5 è 3 ø æ p ö æ p p ö 2cos 2x + + 2sin x -1 = 0 ç ÷ Û 2 cos 2 . x cos - sin 2 . x sin + 2sin x -1 = 0 ç ÷ 0.25 è 3 ø è 3 3 ø 2
Û cos 2x - 3.sin 2x + 2sin x -1 = 0 Û 2 - sin x - 2 3 sin .
x cos x + 2sin x = 0 0.25 Û 2
- sin x(sin x + 3.cos x -1) = 0 ésin x = 0 0.25 Û ê
ësin x + 3.cos x -1 = 0
• sin x = 0 Û x = k.p 0.25 p 1
• sin x + 3.cos x -1 = 0 Û sin(x + ) = 3 2 é p x = - + k.2p ê 6 Û ê 0.25 p ê x = + k.2p êë 2 p p
Vậy phương trình có nghiệm là: x = k.p , x = - + k.2p , x = + k.2p 0.25 6 2 b
3(sin 2x + cos x) - cos 2x - sin x = 2 1,5
3(sin 2x + cos x) - cos 2x - sin x = 2 0.25 2 Û + - - - = 3(2.sin .
x cos x cos x) (2cos x 1) sin x 2 2 Û 2 3.sin .
x cos x + 3 cos x - sin x = 1+ 2cos x 2 2
Û (3.cos x - 2. 3 cos .
x sin x + sin x) - ( 3 cos x - sin x) = 0 0.25 2
Û ( 3 cos x - sin x) - ( 3 cos x - sin x) = 0 0.25 Page 3 é
3 cos x - sin x = 0 Û ê
êë 3 cos x -sin x =1 p p 0.25
* 3 cos x - sin x = 0 Û cos(x + ) = 0 Û x = + k.p 6 3 p 1 •
3.cos x - sin x = 1 Û cos(x + ) = 6 2 é p x = + k.2p ê 6 Û ê p 0.25 êx = - + k.2p êë 2 p p p 0.25
Vậy phương trình có nghiệm là: x =
+ k.p , x = + k.2p , x = - + k.2p 3 6 2 Câu 2 (4,0 điểm)
Chứng minh bất đẳng thức sau bằng phương pháp quy nạp: a n 1 + > ( +1)n n n , n
" Î N,n ³ 3 . 2,0
- Xét n = 3: Bất đẳng thức cần chứng minh trở thành 81 > 64 (đúng). 0.25
- Giả sử bất đẳng trên đúng với một số tự nhiên k tùy ý ( k ³ 3) tức là: 0.25 k 1 + > ( +1)k k k
+ Ta đi chứng minh bất đẳng thức đã cho đúng với n = k +1, tức là đi chứng minh k +2 k 1 (k 1) (k 2) + + > + (1) 0.25 k 1 + k +
Từ giả thiết quy nạp ta có: k 1 k > (k +1)k Û > 1 k 0.25 (k +1)
Do đó để chứng minh (1), ta chỉ cần chứng minh: k 1 + + + k k 2 k 1 (k +1) > (k + 2) . (2) 0.25 (k +1)k k 1 + + + k k 1 + Ta có: k 2 k 1 2k +2 (k +1) > (k + 2) . Û (k +1) > k k + k [ ( 2)] 0.25 (k +1) k 1 + k 1 2 + 2 k 1 + 2 k 1 + Û é(k +1) ù > ë û
[k(k + 2)] Û (k + 2k +1) > (k + 2k) (đúng) 0.25
Suy ra (1) đúng, hay bất đẳng thức đã cho đúng với n = k +1.
Vậy bất đẳng thức đã cho đúng với mọi số thự nhiên n thỏa n ³ 3. 0.25 ì 2 u ï =
Cho dãy số (u ) thỏa: 1 í 3 . b n * 2,0 ï + - = " Î 4u u .u 6u 0, n N î n 1+ n 1 + n n
Tìm số hạng tổng quát của (u ) và tính lim u . n n Page 4 6u 0.25 4u
+ u .u - 6u = 0 Û u (4 + u ) = 6 n u Û u = n 1 + n 1 + n n n 1 + n n n 1 + 4 + un
Dễ dàng chứng minh được * u > 0, n " Î N . n æ ö 6u 1 1 2 1 1 Do đó n u = Û - = ç - ÷ (1). n 1 + 0.5 4 + u u 2 3 u 2 n n 1 + è n ø 1 1 n 1 - n 1 2 æ 2 ö æ 2 - ö Đặt v =
- ; khi đó từ (1) suy ra: v = v Þ v = v . = . n n 1 + n n 1 ç ÷ ç ÷ 0.5 u 2 3 è 3 ø è 3 n ø n 1 1 1 æ 2 - ö 1 Suy ra: - = Û u = . ç ÷ n n 1 u 2 è 3 - 0.5 ø n 1 æ 2 ö + ç ÷ 2 è 3 ø æ ö ç ÷ 1 Do đó lim u lim ç ÷ = = 2 0.25 n n 1 ç 1 2 - ÷ æ ö ç + ç ÷ ÷ è 2 è 3 ø ø Page 5 Câu 3 (4,0 điểm)
Từ 10 chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 lập được bao nhiêu số tự nhiên thỏa: là số a 2,0
có 8 chữ số, trong đó có 2 chữ số lẻ khác nhau và 3 chữ số chẵn khác nhau mà
mỗi chữ số chẵn có mặt đúng 2 lần.
* Bước 1: Xét số có 8 chữ số , trong đó có hai chữ số lẻ khác nhau và 3 chữ số chẵn
khác nhau mà mỗi chữ số chẵn có mặt đúng hai lần (kể cả số có chữ số 0 đứng đầu).
- Từ 10 chữ số chọn ra 5 chữ số khác nhau gồm 2 số lẻ và 3 số chẵn có 2 3
C .C cách chọn. 0.25 5 5
+ Với mỗi cách chọn trên ta có: số các số có 8 chữ số trong đó có 2 chữ số lẻ khác nhau 0.5 8!
và 3 chữ số chẵn khác nhau mà mỗi chữ số chẵn có mặt đúng hai lần là số. 2!2!2! 8! + Vậy với 2 3
C .C cách chọn ở trên ta tạo được 2 3 C .C .
= 504000 số (kể cả số 0 0.25 5 5 5 5 2!2!2! đứng đầu tiên)
* Bước 2: Xét các số thoả mãn điều kiện ở bước 1 mà có chữ số 0 đứng đầu .
- Từ 9 số đã cho (bỏ số 0) chọn ra 4 số khác nhau gồm 2 số lẻ và 2 số chẵn (vì đã có số 0 đứng đầu) có 2 2
C .C cách chọn. 0.25 5 4
+ Với mỗi cách chọn trên ta có: số các số có 8 chữ số có số 0 đứng đầu, trong đó có mặt
2 chữ số lẻ khác nhau, 3 chữ số chẵn khác nhau và mỗi chữ số chẵn khác 0 có mặt đúng 0.25 7! hai lần là số. 2!2! 7! + Vậy với 2 2
C .C cách chọn ở trên ta tạo được 2 2 C .C . = 75600 số ( ở bước 2) 5 4 5 4 2!2! 0.25
* Từ 2 bước trên suy ra số các số thoả đề bài là: 504000 - 75600 = 428400 số 0.25
b) Một đa giác đều có 24 đỉnh, tất cả các cạnh của đa giác sơn màu xanh và tất cả các b
đường chéo của đa giác đó sơn màu đỏ. Gọi X là tập hợp tất cả các tam giác có ba đỉnh 2,0
là các đỉnh của đa giác đều trên. Người ta chọn ngẫu nhiên từ X một tam giác, tính xác
suất để chọn được tam giác có ba cạnh cùng màu.
Gọi đa giác là A1A2.....A24
Số phần tử của không gian mẫu là 3 n(Ω)= C =2024 0.25 24
Gọi A là biến cố chọn được tam giác có ba cạnh cùng màu, ba cạnh này cùng màu đỏ. 0.25
Gọi B là biến cố chọn được tam giác có đúng 1 cạnh màu xanh (cạnh đa giác)
Giả sử xét cạnh màu xanh A 0.25
1A2, ta có 20 cách chọn đỉnh Ai ( Ai Î{A4; A5;...;A23})
Nên số phần tử của B là n(B) = 24.20 = 480 . 0.25
Gọi C là biến có chọn được tam giác có hai cạnh màu xanh, như vậy tam giác đó có hai
cạnh là hai cạnh liên tiếp của đa giác, nên n(C) = 24 0.25
Ta có n(A) + n(B) + n(C) = n( W ) 0.25
Suy ra số phần tử biến cố A là
n (A)= n(W) - n(B) - n(C) = 2024 - 480 - 24 =1520 0.25 n(A) 190
Vậy xác suất của biến cố A là P(A)= = n(Ω) 253 0.25 Câu 4 (2,0 điểm) Page 6 3
ì 5x + 3 - 2 - x -1 ï khi x < 1 ï Cho hàm số x -1 f (x) = í ï æ p x ö . m sin + 2017p ç ÷ ïî è 2 ø khi x ³ 1
Tìm giá trị của m để hàm số f (x) liên tục tại x = 1. æ p ö f (1) = . m sin + 2017p = -m ç ÷ 0,25 è 2 ø
lim f (x) = -m 0,25 x 1+ ® 3 3
é( 5x + 3 - 2) - ( 2 - x -1)ù
éæ 5x + 3 - 2 ö æ 2 - x -1öù
lim f (x) = lim ê ú = lim êç ÷ - ç ÷ú 0,25 ç ÷ ç ÷ x 1- x 1- - x 1 x 1 - ® ® ® x ë û ê -1 x -1 ëè ø è øúû 3 5x + 3 - 2 5 + Tính được: lim = - 0,5 x 1 ® x -1 12 2 - x -1 1 + Tính được: lim = - - 0,25 x 1 ® x -1 2 11
Suy ra lim f (x) = x 1- ® 12
Để f (x) liên tục tại x = 1 thì lim f (x) = lim f (x) = f (1) 0,25 x 1+ x 1- ® ® 11 0,25 Suy ra: m = - là giá trị cần tìm. 12 Câu 5 (3,0 điểm)
Trong mặt phẳng với hệ trục tọa độ Oxy, cho tam giác ABC có trọng tâm G(1;0) và trực tâm
H . Phương trình đường tròn đi qua ba trung điểm của ba cạnh HA, HB , HC là 2 2 æ 5 ö æ 1 ö 25 x - + y - =
. Viết phương trình đường tròn ngoại tiếp tam giác ABC . ç ÷ ç ÷ è 6 ø è 6 ø 18 Page 7
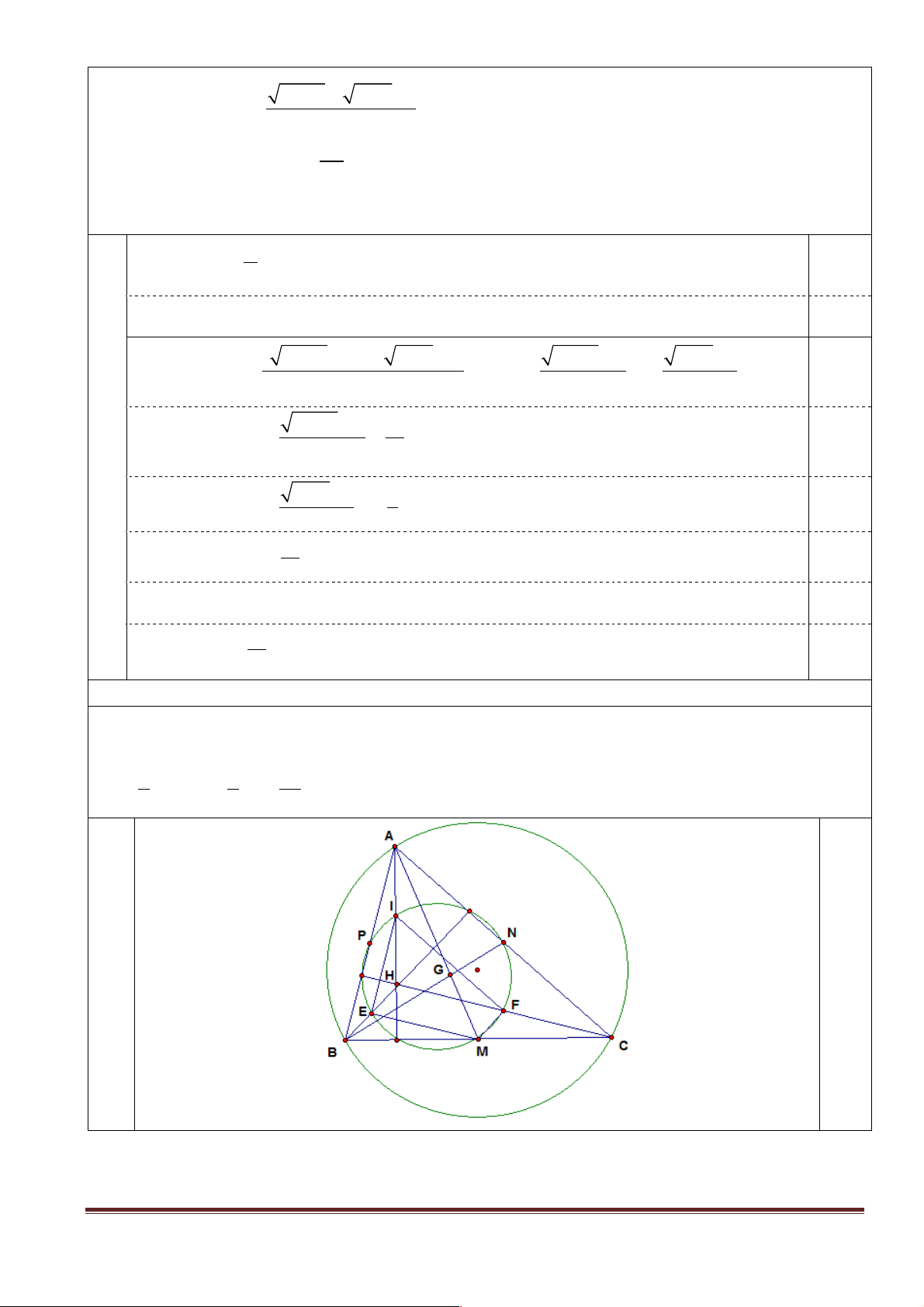
- Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.
- Gọi I, E, F lần lượt là trung điểm của các cạnh HA, HB, HC.
+ CH ^ IE và CH / /ME . Suy ra ME ^ IE (1). 0.5
+ Tương tự, chứng minh được MF ^ IF (2). 0.25
Từ (1) và (2) suy ra M nằm trên đường tròn ngoại tiếp tam giác IEF. 0.25
- Tương tự, N và P nằm trên đường tròn ngoại tiếp tam giác IEF. 0.25
Suy ra sáu điểm: M, N, P, I, E, F cùng nằm trên một đường tròn. 0.25
Như vậy đường tròn qua I;E;F cũng qua ba trung điểm ba cạnh. Do đó xét phép vị
tự tâm G tỉ số k = 2
- biến đường tròn (IEF) thành đường tròn (ABC) 0.25 5 1 5
Ta có đường tròn (IEF) có tâm O ( ; ) bán kính R = . 1 1 0.25 6 6 3 2 !!!!" !!!!" 4 1 - Gọi O 0.5
2 là tâm đường tròn (ABC) ta có: GO = 2
- GO , ta tìm được O ( ' ) 2 1 2 3 3 5 2 Bán kính R =
. Khi đó phương trình đường tròn ngoại tiếp tam giác ABC 0.25 2 3 2 2 æ 4 ö æ 1 ö 50 là: x - + y + = ç ÷ ç ÷ è 3 ø è 3 ø 9 0.25 Câu 6 (4,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, BC = a 3 , SA = 3a .
Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABCD); M là trung điểm của OB.
a) Gọi j góc giữa đường thẳng SO và mặt phẳng (SCD). Tính sinj .
b) Tính khoảng cách giữa hai đường thẳng SB và CM theo a . Page 8
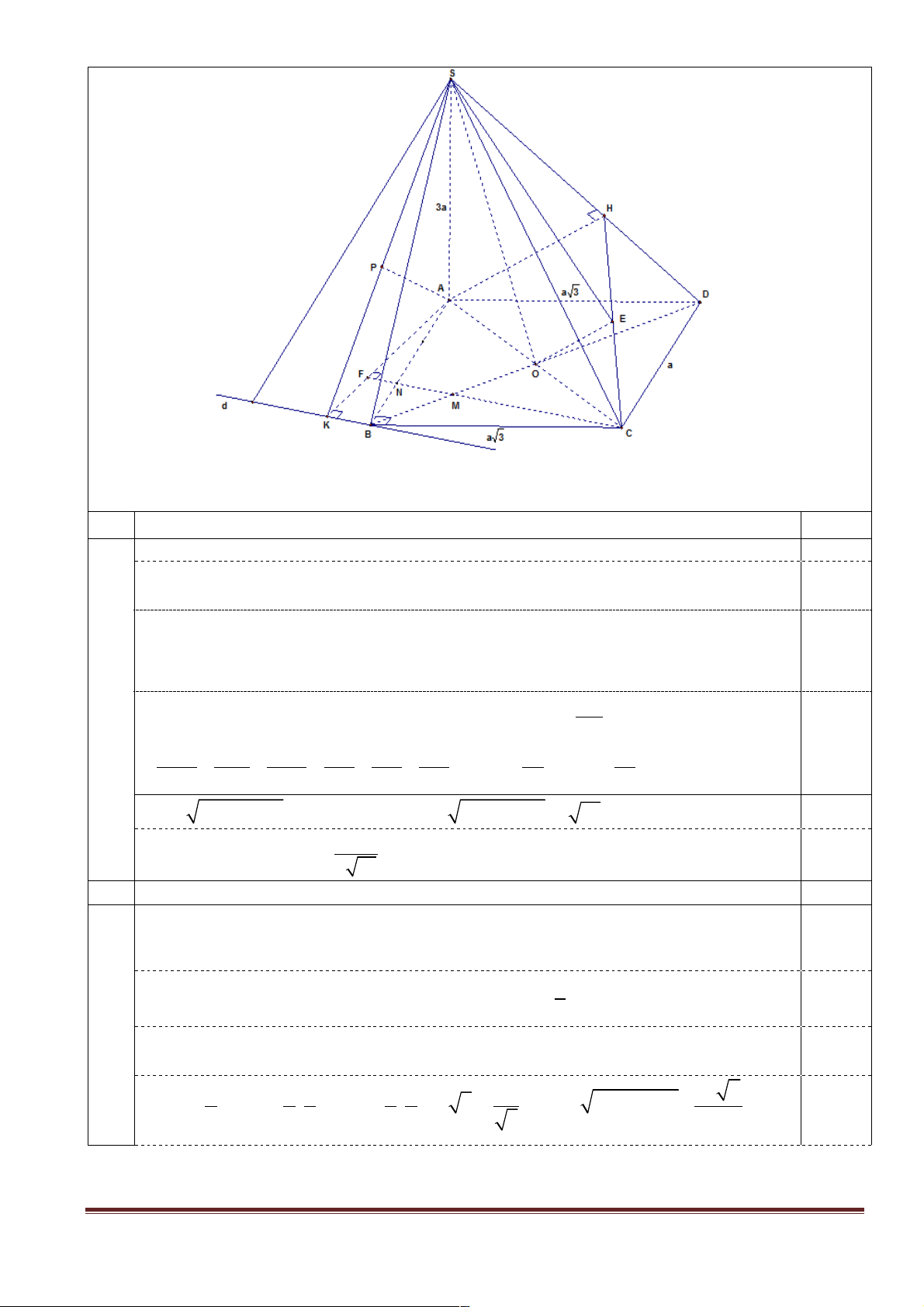
(Hình vẽ phục vụ câu a - 0,5 điểm) a
Gọi j góc giữa đường thẳng SO và mặt phẳng (SCD). Tính sinj . 1,5
+ Lập luận được SA vuông góc với (ABCD). 0,25
+ Gọi H là là hình chiếu vuông góc của A lên SD 0,25
+ Chứng minh được AH vuông góc với (SCD).
+ Gọi E là trung điểm của CH. Suy ra OE ^ (SCD) 0,25
+ Suy ra hình chiếu vuông góc của SO lên (SCD) là SE.
+ Suy ra được góc giữa SO và (SCD) là góc ∑ OSE , hay ∑ j = OSE .
+Trong tam giác vuông SOE tại E có: ∑ sinj = sin = OE OSE OS 0,25 1 1 1 1 1 4 3a 3a + = + = + = Þ AH= Þ OE= 2 2 2 2 2 2 AH AS AD 9a 3a 9a 2 4 2 2 AC= AB +BC =2a Þ AO=a ; 2 2 SO= SA +AO =a 10 0,25 Suy ra ∑ sinj = sin = 3 OSE 0,25 4 10 b
Tính khoảng cách giữa hai đường thẳng SB và CM theo a . 2,0
+ Qua B dựng đường thẳng d song song với CM, hạ AK vuông góc với d tại K .
+ Đường thẳng CM cắt AB và AK lần lượt tại N và F. Chứng minh được NA=2NB. 0,25 + Suy ra: ( ) 1
d CM,SB =d(CM,(SKB))=d(N,(SKB))= .d(A,(SKB)) . 0,25 3
+ Chứng minh được (SKB) ^ (SAK) . Suy ra được d(A,(SKB))=AP 0,25 2 2 2 1 2 1 a S = .S = . S = . .a.a 3 = , 2 2 2a 7 CN= BC +BN = ΔANC ΔABC ABCD 0,25 3 3 2 3 2 3 3 Page 9 a 3 3 3 a 3 3a 3 Suy ra: AF= ; AK= AF= . = 0,25 7 2 2 7 2 7 3a 3 3a 3 Tính được: AP= hay d(A,(SKB))=AP= 0,5 31 31 Suy ra ( ) 1 a 3 d CM,SB = .d(A,(SKB))= 0,25 3 31
Ghi chú: Nếu học sinh có cách giải khác đúng thì Ban Giám khảo thảo luận và thống nhất thang điểm
cho phù hợp với Hướng dẫn chấm. Page 10