Đề thi Olympic 27/4 Toán 11 năm 2017 – 2018 sở GD và ĐT Bà Rịa – Vũng

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI OLYMPIC 27/4 - NĂM HỌC 2017- 2018
TỈNH BÀ RỊA – VŨNG TÀU
MÔN THI: TOÁN LỚP 11
ĐỀ THI CHÍNH THỨC Ngày thi: 06/03/2018
Thời gian làm bài: 180 phút, không kể thời gian giao đề Bài 1 (5,0 điểm): 1) Giải phương trình  4 4
2 cos x  sin x  1 2cos2xsin x  3 cos3x . 9
2) Cho tam giác ABC không tù và thỏa mãn 2 3 3 3
cos A  cos B  cos C   3cos Acos BcosC  . 8
Chứng minh ABC là một tam giác đều.
Bài 2 (2,0 điểm): Cho khai triển sau: 2018 2
 x  2x  2  b b b 2018 2017 1 2 2018    a x  a x
 ...  a x  a    ...  với x  1  . 2018 2017 1 0 x  1 x  1 x  2 1 x  2018 1 Hãy tính hệ số a
S  b  b  ...  b . 0 và tổng 1 2 2018
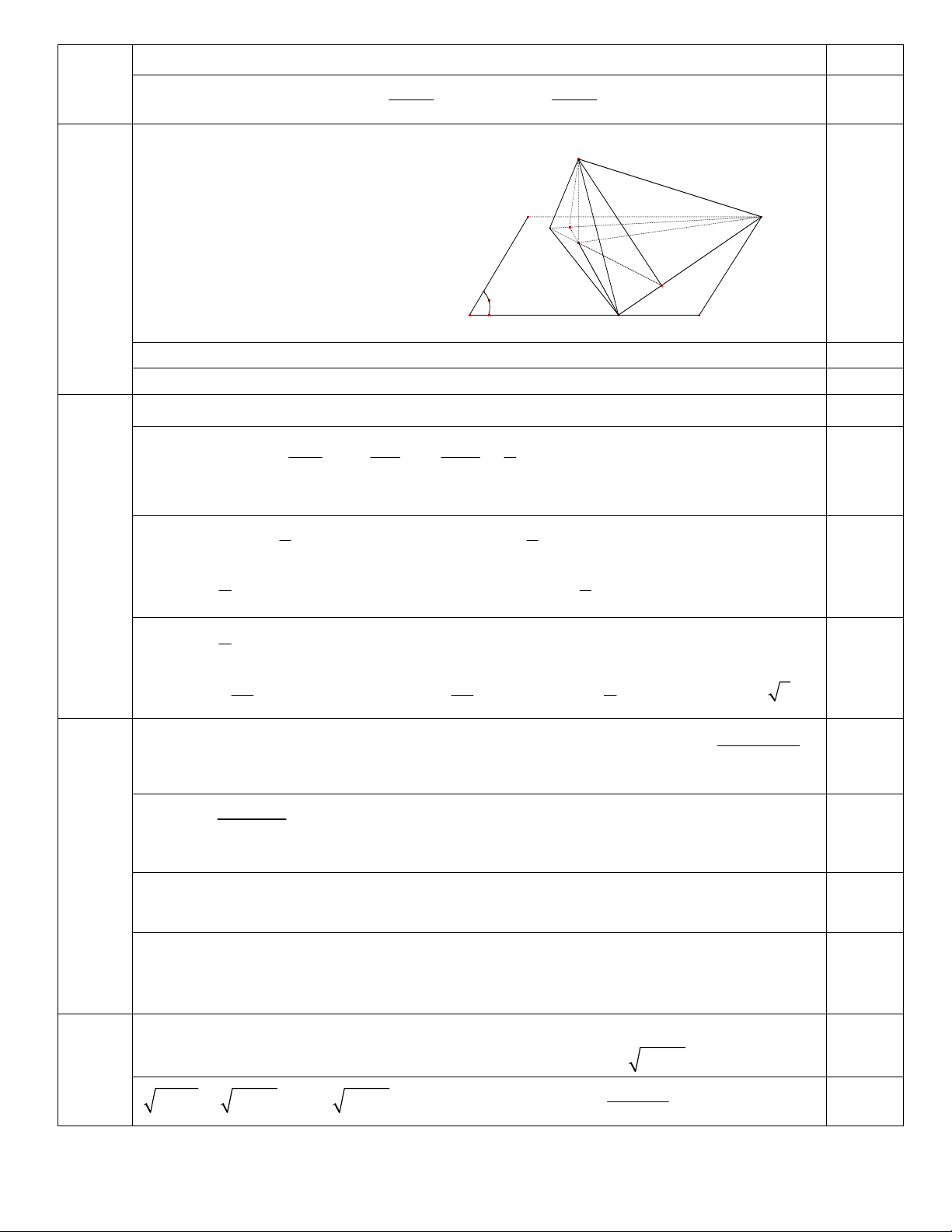
Bài 3 (5,0 điểm): Cho đoạn AB vuông góc mặt phẳng (P) tại điểm B . Trong (P) lấy điểm H thỏa
BH  BA  a (a  0) . Vẽ đường thẳng d nằm trong (P) và qua H , d vuông góc với BH. Hai điểm
M , N di động trên d và thỏa mãn 
MAN  90 . Đường thẳng qua A và vuông góc mặt phẳng (AMN )
cắt (P) tại điểm K.
1) Chứng minh rằng B là trực tâm của tam giác KMN .
2) Gọi ,  lần lượt là số đo các góc tạo bởi BM với mp (AKN ) , BN với mp (AKM ) . Chứng 1 minh 2 2
cos   cos   và tìm giá trị nhỏ nhất của    . 2
Bài 4 (4,0 điểm): Cho dãy số (a ) xác định bởi công thức: n
a  1;a  2; 1 2  na
 (3n  2)a  2(n 1)a ;n  1;2;3; ...  n2 n 1  n
1) Tìm công thức số hạng tổng quát của dãy (a ) . n n(n 1) 2) Chứng minh *
a 1  a 1  ...  a 1  ; n    . 1 2 n 2  a a a  3) Tính 1 2 lim   ... n   . 2   3 3 3n  Bài 5 (4,0 điểm):
1) Tìm tất cả các giá trị của a để giới hạn x     có giá trị hữu hạn.   2 2 lim ax x 2x 2 x x x 
2) Tìm tất cả các hàm số f :    thỏa mãn
f  x  y  f  x f  y  f  xy  f  x  f  y  2xy với mọi x, y  . 
----------------- HẾT -----------------
Họ và tên thí sinh........................................................................... Số báo danh ..................................
Chữ ký của giám thị 1 ...................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI OLYMPIC 27/4 - NĂM HỌC 2017- 2018
TỈNH BÀ RỊA – VŨNG TÀU
MÔN THI: TOÁN LỚP 11
HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC
(Hướng dẫn chấm có 04 trang) Bài Nội dung Điểm 1.1 2 4 4
cos x  sin x  1  2cos 2xsin x  3 cos3x 0,25 (2,5 đ)  2 2 2
cos x  sin x 2 2
cos x  sin x  sin x  2sin xcos 2x  3 cos3x
 2cos 2x  sin x  sin 3x  sin x  3 cos3x 0,5 3 1 0,25 
cos3x  sin 3x  cos 2x 2 2      0,25x2
 cos cos3x  sin sin 3x  cos 2x  cos 3x   cos 2x   6 6  6      3x   2x  k2 x   k2  6  6     k     2 0,5x2  3x 2x k2       x   k  6  30 5 1.2 1      
(2,5đ) Ta có cos Acos B cosC cos 
 A B cos A B cosC 2  0,25 1 0,25 2
  cos C  cos A  Bcos A  B 2   1  1  1 0,25x2 2 
 cos C  cos 2A  cos 2B    2 2 2
cos A  cos B  cos C    1 2  2  2 3 9 0,25 Do đó gt  2 3 3 3
cos A  cos B  cos C    2 2 2
cos A  cos B  cos C   1  2 8   3 2 A  A     3 2 16cos 12cos 1
16cos B  12cos B   1 0,25   3 2
16cos C  12cos C   1  0   A  2  A     B  2 2cos 1 4cos 1 2cos 1 4cos B   1 0,25   C  2 2cos 1 4cosC   1  0 1  0,25x2
cos A  cos B  cosC 
(Do 4cos A  1  0, 4cos B  1  0, 4cosC  1  0 ). 2 0
 A  B  C  60  ABC  đều (đpcm). 0,25 2018 2
 x  2x  2  2
Đặt f (x)    ta có 2018
f (0)  a  b  ...  b  2 . 0 1 2018 0,5 (2,0đ)  x  1  Vậy 2018 a  S  2 . (1) 0 2018 2018  1  0,5 k 2k  2018
f (x)  x  1 
  C (x  1)   2018  x  1 k 0 . 1008 k 2018 C2018 k 2k 2018  
  C (x  1) 20182k 2018  k 0 ( x 1) k 1009 1008 1007 1 0
b  b  ...  b
 0  S  b  b  ...  b  C  C  ...  C  C 0,25 1 3 2017 2 4 2018 2018 2018 2018 2018 1009 1010 2017 2018 1009 a C C ... C C C S,( k n k doC C          ) (2) 0,25 0 2018 2018 2018 2018 2018 n n 2017! 2017! 0,5 Từ (1) và (2) suy ra: 2017 2017 S  2  ; a  2  . 0 1009 1009
- Xác định vị trí M, N trên d: Tam giác 3.1
AMN vuông tại A và có đường cao AH A 0,5
(2,5đ) ( MN  AB, BH ) nên M, N khác phía đối với H. N
- Xác định vị trí K: trong (ABH) dựng K E K thuộc BH và 
KAH  90 (BH = BA = a 0,5 B d
nên B là trung điểm KH),
- Chứng minh: AK  (AMN) . 0,5 H P M
- AM  AN, AK  AM  KN. Mà AB  (P)  KN  AB ,vậy KN  BM . 0,5
- KH  MN (cmt), KH  BM  B nên B là trực tâm tam giác KMN. 0,5 3.2  
AM  (AKN )  (BM , (AKN ))  MEA  MAB   , tương tự  NAB   . 1,0 (2,5đ) 2 2 2  AB   AB  AB 1 2 2 cos   cos         
, (do tam giác ABH vuông cân tại B). 2 0,5  AM   AN  AH 2
(Cách khác: chứng minh, áp dụng hệ thức 2 2 2  0
cos   cos   cos   1,   KAB  45 ) 1 1 2 2 cos   cos    cos(  )  .cos(  )    . 2 2    0,5  1 ,  0;  0  cos(  )   1  
. Vậy cos(  )   .(1)  2  2    ,  0;  0        
và hàm số y  cos x nghịch biến trên (0; )  nên từ (1) ta  2  0,5 2 2  có     . Kết luận: min(  )   đạt khi    
 HM  HN  a 2 . 3 3 3 a  a n  2 n 1 4.1 na  (3n  2)a
 2(n  1)a  n(a
 a )  2(n  1)(a  a )   2 n  2 n 1 n n  2 n 1 n 1 n n  1 0,5 (2,0đ) a  a Đặt n 1 n x  , ta có *
x  a  a  1; x  2x ; n
   .Vậy (x ) là cấp số nhân n n 1 2 1 n 1 n n 0,5
với công bội q = 2, nên n 1 n 1 *
x  x .q  2 ; n    . n 1 Suy ra n 1 * 0 1 2 n  2 a  a  .2 n ; n
    a  a  1.2  2.2  3.2  ...  (n  1)2 n 1 n n 1 1 2 n 2 *  0,5
a  2  [2.2  3.2  ...  (n  1)2 ]; n    . n Xét 2 3 n 2 n 1
2a  4  [2.2  3.2  ...  (n  2)2  (n  1)2 ] n n 1 2 3 n  2 n 1 n 1  0,5
2a  a  (n  1)2
 (2  2  2  ...  2 )  a  (n  1)2  (2  2)  (n n n n 4.2 n 1 n 1 0 1 n 1 2  (1  1)  C  C  ...  C
 1  (n  1)  ; n n   2 n 1 n 1 n 1 (1,0đ) 0,5 n 1 2
 a  (n  2)2
 2  (n  2)n  2  (n  1)  1; n
  2  a  1  n  1; n   2 n n n(n  1) 0,5 *
a  1  a  1  ...  a  1  0  1  2  ...  (n  1)  ; n    . 1 2 n 2 4.3 1 a (k  2)2  2 k  2 k   2 k   1 k k  (1,0đ) Ta có k *   .   2. ; k          3k 3k 2  3   3   3  a a a 1 1 2  2   2   2 n  1 2    ... n 
 S  T  2P , với S  1  2  ...  n ; 1 2       3 3 3n 2 n n n n  3   3   3  1 2 n 1 2  2   2   2   1   1   1 n  T    ...  ; P    ...  ; 0,5 n              3   3   3 n   3   3   3  2 3 n n 1 2  2   2   2   2  Xét S  1  2  ...  (n  1)  n         3 n  3   3   3   3  2 3 n n 1 2 2  2   2   2   2   2 n   S  S     ...   n
 S  3T  2n . n           3 n 3  3   3   3   3 n n   3  a a a 1  2 n  Vậy 1 2   ... n 
 T  2P  n . 1 2   3 3 3n 2 n n  3  2 1 1 3 3 limT   2;lim P   ; n 2 n 1 2 1  1  3 3 n n 2 2  3   1   1   1   1  n(n  1) 0 1 2 2  1   C  C  C  ...  C  ; n   2           0,5  2   2 n n   2 n   2 n   2  8  2 n  8  2 n    a a a  0  n  ; n   2  lim n  0     . Vậy 1 2 lim   ... n   2.    3  n  1  3  1 2  3 3 3n  5.1  2 1 
(2,0 đ) Nếu a  1 thì lim x              2 2 ax x 2x 2 x x  2 lim x a 1 2 1 x x  x x    0,25  khi a  1   .  khi a  1 0,25 Nếu a  1 thì x          0,25   2 2 ax x x x x  x   2 2 lim 2 2 lim x x 2x 2 x x x x  0,25 x             2 x x
x   x  2 lim 2 1 2 1 2 x x x   1  1  0,25  lim x    x 2 2
 x  2x  x  1 2x  1  2 x  x     1 1   0,25x2  1 lim      . x  2 1 1 1  4 1   1  2   2 1   x x x x   
Vậy a  1 là giá trị cần tìm. 0,25 5.2
Giả sử f  x là một hàm số thỏa mãn giả thiết bài toán. (2,0đ)
f  x  y  f  x f  y  f  xy  f  x  f  y  2xy   1
 f x  y  1   f
  x  1  f
   y  1  f 
xy  1  2xy  1. 0,25
Đặt g  x  f  x  1 ta có phương trình
g  x  y  g  x g  y  g  xy  2xy  1, x
 , y   2
Kí hiệu P a,b chỉ việc thay x bởi a và thay y bởi b vào phương trình (2)
P  x,0  g  x  g  x g 0  g 0  1  g
 0  1 g
   x  1  0  3 . 0,25
Nếu g 0  1  0 thì từ (3) suy ra g  x  1, x
   . Thay vào (2) ta thấy hàm số này
không thỏa mãn, do đó g 0  1 . P 1, 
1  g 0  g   1 g   1  g   1  1  g    1  1 g    1  0 0,25 Nếu g  
1  1 thì P  x 
;1  g  x  
1  2x  1  2 x  
1  1  g  x  2x  1, x  . Ta
thấy hàm số này thỏa mãn (2). Nếu g  
1  1 thì g  
1  0 . Đặt a  g   1 . 0,25 P  x 
,1  g  x  
1  ag  x  g  x  2x  1  g  x  
1  1  a g  x  2x  1, x   
P x,  
1  g x  
1  g  x  2x  1  g  x  g x   1  2x   1 . Thay vào (4) ta được 0,25 g  x  
1  1  a g  x   1  2x   1   2x  1  
1  a g x  1  a2x  1, x   
 g  x  1  a g x  a2x   1 , x    5
 g x  1  a g  x  a 2  x   1 , x
   . Thay vào (5) ta được
g  x  1  a 1  a g x  a2x   1   a  2x   1 .   2
a  2a g x 2  2  a x   2
a  2a, x    6
Rõ ràng từ (6) suy ra a  2 . a
Nếu a  0 thì từ (6) suy ra g  x 2   x  1, x    a  2 4 2 a  a  2 0,25 Thay vào (2) ta được xy  0, x
 , y  a  2
 (Vì a  g   1  1 ) a  22
 g x  x  1, x
   . Hàm số này thỏa mãn (2).
Nếu a  0 thì từ (5) suy ra g  x  g x, x    .
P  x x  g    g  x g x  g  2 x  2 , 0  2x  1 2
   g x  g  2 x  2 1  2x  1 7 0,25
P  x x  g  x 2
 g  x  g  2 x  2 , 2  2x  1 (8)
Từ (7) và (8)  g  x 2
 x   g x 2 2 4 1  x  1, x
   . Hàm số này thỏa mãn 2 .
Do f  x  g  x  1 nên các hàm số cần tìm là 0,25
f  x  x f  x  x f  x 2 2 , ,  x , x    .
----------------- HẾT -----------------