Đề thi Olympic 30/04 Toán 11 lần 28 năm 2024 trường chuyên Lê Quý Đôn – BR VT

SỞ GD – ĐT TỈNH BÀ RỊA – VŨNG TÀU
KỲ THI OLYMPIC TRUYỀN THỐNG 30 THÁNG 4
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN
LẦN THỨ XXVIII – NĂM 2024
MÔN THI : TOÁN – KHỐI : 11 ĐỀ CHÍNH
Thời gian làm bài : 180 phút THỨC
Đề thi gồm có 01 trang
Lưu ý : Thí sinh làm mỗi câu trên một tờ giấy riêng và ghi rõ số thứ tự câu ở trang 1 của mỗi tờ giấy thi.
Thí sinh KHÔNG được sử dụng tài liệu và máy tính cầm tay.
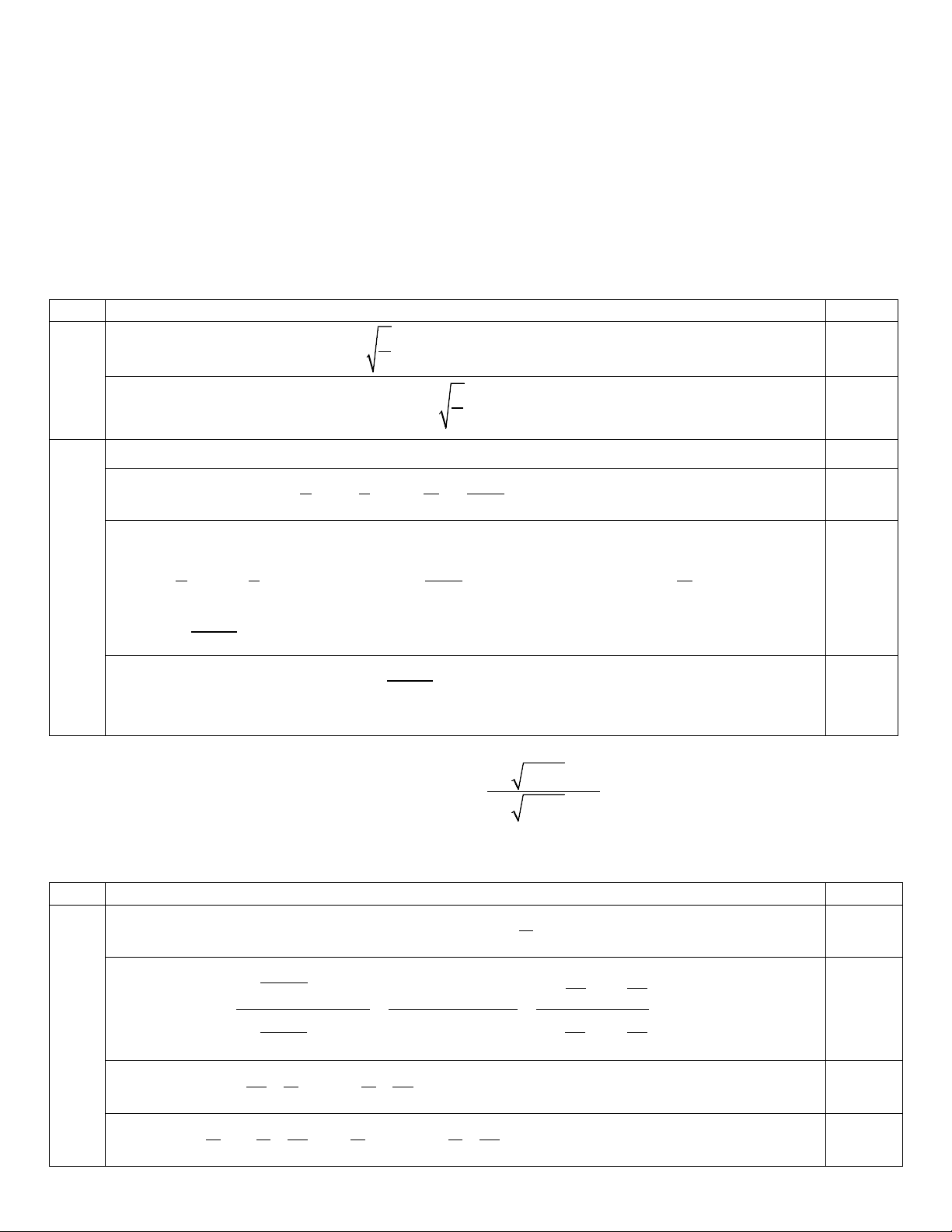
Câu 1 (4,0 điểm). Cho hai đa thức P(x) 4
= x − 2x −1 và Q(x) 6 4 3 2
= x + x − 4x − x −1.
a) Chứng minh đa thức P(x) có đúng hai nghiệm thực phân biệt.
b) Gọi hai nghiệm thực phân biệt của P(x) là u và .v Chứng minh uv là một nghiệm của Q(x). 2 1+ 1+ x − x
Câu 2 (3,0 điểm). Cho dãy số (x xác định bởi x =1; n n x =
với mọi n nguyên dương. Chứng n ) 1 n 1 + 2 1+ 1+ x + x n n
minh dãy số (x có giới hạn hữu hạn và tính giới hạn đó. n )
Câu 3 (4,0 điểm). Cho số nguyên dương m (m ≥ 2). Gọi p là ước nguyên tố của 2
2 m +1. Giả sử = .2n p k +1
với k là số nguyên dương lẻ và n là số nguyên dương.
a) Chứng minh n ≥ m +1. b) Chứng minh n 1 2
k − −1 chia hết cho . p
Câu 4 (5,0 điểm). Cho tam giác ABC nhọn ( AB < AC) nội tiếp đường tròn (O) và có H là trực tâm. Gọi M
là trung điểm cạnh BC. Đường tròn ngoại tiếp tam giác HBC cắt đoạn thẳng AM tại K; tiếp tuyến của (O) tại
A cắt đường thẳng BC ở điểm S. a) Chứng minh 2
MK.MA = MB và SA = SK.
b) Đường thẳng SK cắt hai cạnh AB, AC lần lượt tại P, .
Q Gọi T là tâm đường tròn ngoại tiếp tam giác AP .
Q Chứng minh đường tròn ngoại tiếp tam giác TPQ tiếp xúc với đường tròn (O).
Câu 5 (4,0 điểm). Ban chấp hành Đoàn trường THPT X gồm có n thành viên. Trong năm học, Đoàn trường tổ
chức m chương trình, mỗi chương trình có đúng k thành viên trong ban chấp hành tham gia. Mỗi thành viên
trong ban chấp hành tham gia ít nhất một chương trình.
a) Cho m = 8;k = 3. Biết rằng với hai chương trình bất kỳ luôn có đúng một thành viên trong ban chấp
hành tham gia cả hai chương trình đó. Chứng minh n =17.
b) Cho n = 25;k =10. Biết rằng với hai chương trình bất kỳ luôn có không quá 3 thành viên trong ban
chấp hành cùng tham gia. Chứng minh m ≤ 6.
--------------HẾT--------------
Cán bộ coi thi KHÔNG giải thích gì thêm.
Họ tên thí sinh: ................................................................. SBD: .............................................
Trường: ............................................................................ Tỉnh/TP: ......................................
SỞ GD – ĐT TỈNH BÀ RỊA – VŨNG TÀU
KỲ THI OLYMPIC TRUYỀN THỐNG 30 THÁNG 4
TRƯỜNG THPT CHUYÊN LÊ QUÝ ĐÔN
LẦN THỨ XXVIII – NĂM 2024
ĐÁP ÁN CHÍNH THỨC
MÔN : TOÁN – KHỐI : 11
Câu 1 (4,0 điểm). Cho hai đa thức P(x) 4
= x − 2x −1 và Q(x) 6 4 3 2
= x + x − 4x − x −1.
a) Chứng minh đa thức P(x) có đúng hai nghiệm thực phân biệt.
b) Gọi hai nghiệm thực phân biệt của P(x) là u và .v Chứng minh uv là một nghiệm của Q(x). Câu Nội dung Điểm 1 P '(x) 3
= 4x − 2; P '(x) = ⇔ = 3 0 x . 1,0 1a 2   Mà lim P(x) = ;
+∞ lim P(x) = +∞ và 1 3 P
 < 0 ⇒ P ( x) có đúng hai nghiệm thực. 1,0 x→−∞ x→+∞  2   
Dễ thấy u ≠ 0;v ≠ 0 và 4 4
u = 2u +1;v = 2v +1. 0,5    +
Đặt α = uv, ta có 3 1 1 1 α = + 2
+ 2 = + 2 u v + 4 ⇒ α ( 3 α − 4) =1+ 2(u +    v) (*) 0,5  u  v  α α Lại có ( − ) 4 4 = − = ( − )( 3 3 2 u v u v
u v u + v + uv(u + v)) 1b  1   1     ( ) u + v uv u v α (u v) (u v) 1 2 2 2 4 4 α  ⇒ = + + + + + = + + + = + + +  0,5 u v α  α        2 − α ⇒ u + v = 2 α +1 α Thay vào (*) thu được 4 4 6 4 3 2 α − 4α =1−
⇒ α +α − 4α −α −1 = 0. 2 α +1 0,5
Vậy α = uv là một nghiệm của đa thức Q(x). 2 1+ 1+ x − x
Câu 2 (3,0 điểm). Cho dãy số (x biết rằng x =1; n n x =
với mọi n nguyên dương. Chứng minh n ) 1 n 1 + 2 1+ 1+ x + x n n
dãy số (x có giới hạn và tính giới hạn đó. n ) Cách 1. Câu Nội dung Điểm π 0,5 Từ giả thiết ta thấy * x > n ∀ ∈  ⇒ tồn tại ϕ   ∈ sao cho x = ϕ n tan n. n  0; n 0 2    1 1 + − tan cos ϕ ϕ ϕ n − sin n n ϕ + ϕ − ϕ Ta có cos n 1 cos n sin n 2 2 tanϕ = = = n 1 + 1 1+ cosϕ + ϕ ϕ ϕ 0,5 n sin 1+ + tan n ϕ + n cos n sin n cosϕn 2 2  ϕ π   π ϕ  0,5 ⇒ tanϕ = + = − + cot n   tan n n  . 1  2 4   4 2  2 0,5 Mà  π  π ϕ  π  π ϕ n n * ϕ ∈ ⇒ − ∈ ⇒ ϕ = − ∀ ∈     + n n 0; 0; n  . 1  2  4 2  2  4 2 n 1 π  π  π  π − Khi đó : 1 *  1  * ϕ − = − ϕ − ∀ ∈  ⇒ − = − − ∀ ∈ +   n ϕ ϕ    n n n n  . 1 1 6 2  6  6  6  2  0,5 n 1 π π − Hay  1  * ϕ = + −   n ∀ ∈ n  . 6 12  2  n 1 π π 1 −     π 3 lim x =  + −    = = n lim tan tan .  6 12 2  0,5   6 3   Cách 2. Câu Nội dung Điểm Dễ thấy * x > n ∀ ∈ n 0  . 1 1,0 1+ 2 1+ x + x Ta có n n 1 2 * x = = = + − ∀ ∈ + x x n n 1 n n  . 1 2 2 1+ 1+ x + x + x + x n n 1 n n 2 ( 2 1 x   x  + − + n ) 1 1 1 n 3    2 1 2 ⇒ x − = + − − = = − + x x x n 1 n n . 1 3 3 1  1 n  2 2 3 1+ x + x + n n 3 1+ x + x +  n n  2 3  3  1,0 Mà  2 1   1  * 3 1+ x + x + > + = +    n ∀ ∈  n n 3 1 3 1  .  3   3  Nên 1 2 1 * x − ≤ − ∀ ∈ + x n n n  . 1 3 1+ 3 3 n 1 − Do đó 1  2  1 * x − ≤   x − n ∀ ∈ n .  . 1 3 1+ 3  3 1,0 n 1 − Do  2  1 1 3 lim = 0 ⇒ lim x − = ⇒ x = =   n 0 lim n . 1+ 3  3 3 3
Câu 3 (4,0 điểm). Cho số nguyên dương m (m ≥ 2). Gọi p là ước nguyên tố của 2
2 m +1. Giả sử = .2n p k +1 với
k là số nguyên dương lẻ và n là số nguyên dương.
a) Chứng minh n ≥ m +1. b) Chứng minh n 1 2
k − −1 chia hết cho . p Câu Nội dung Điểm
Dễ thấy p lẻ nên theo định lý Fermat 1 .2 | 2 1 2 n p k p − ⇒ − = −1. 0,5 + + Từ giả thiết m m 1 + − ⇒ ( m1 2 2 2 .2 | 2 1| 2 1 | gcd 2 −1;2 n k p p − )1 0,5 3a m 1 + n Ta có gcd( m 1 2 + −1;2 n k − ) gcd(2 ;k.2 2 .2 ) 1 = 2 −1. Nếu ( m 1 gcd 2 + ≤ ⇒
; .2n ) = 2n | 2 .m n m k 0,5 Khi đó 2n 2 | 2 1| 2 m p − −1 điều này vô lý do 2 | 2 m p
+1. Do đó phải có n ≥ m +1. 0,5 Ta có m 1 2 8 | 2 + ≥ ⇒ | 2n m
| p −1⇒ p ≡1(mod8) 0,5 − p 1 −  2  ⇒ = (− ) p 1 2 2 1 = 1⇒ 2 ≡   1(mod p). 0,5  p  p − Đặt 1
d = ord ⇒ d ⇒ d p − p 2 | 2 | 1. 2
3b Tuy nhiên do 22m ≡ 1
− (mod p) và m 1 2 + ( p) m 1 2 1 mod d | 2 + ≡ ⇒ và d | m m 1 2 d 2 + ⇒ = . 0,5
Đến đây ta thấy n = v p −1 ≥ v 2d = m + 2. 2 ( ) 2 ( ) m 1 + n 1 − n 1 2 2 2 p | 2 1| 2 1 2 − ⇒ − − ⇒ ≡ 1(mod p). 0,5 n 1 − − − n Do đó ( ) n 1 2 ( n k )2
( n12) n1− n1 2 2 1 1 .2 2 .k k − = − ≡ = ≡ (mod p).
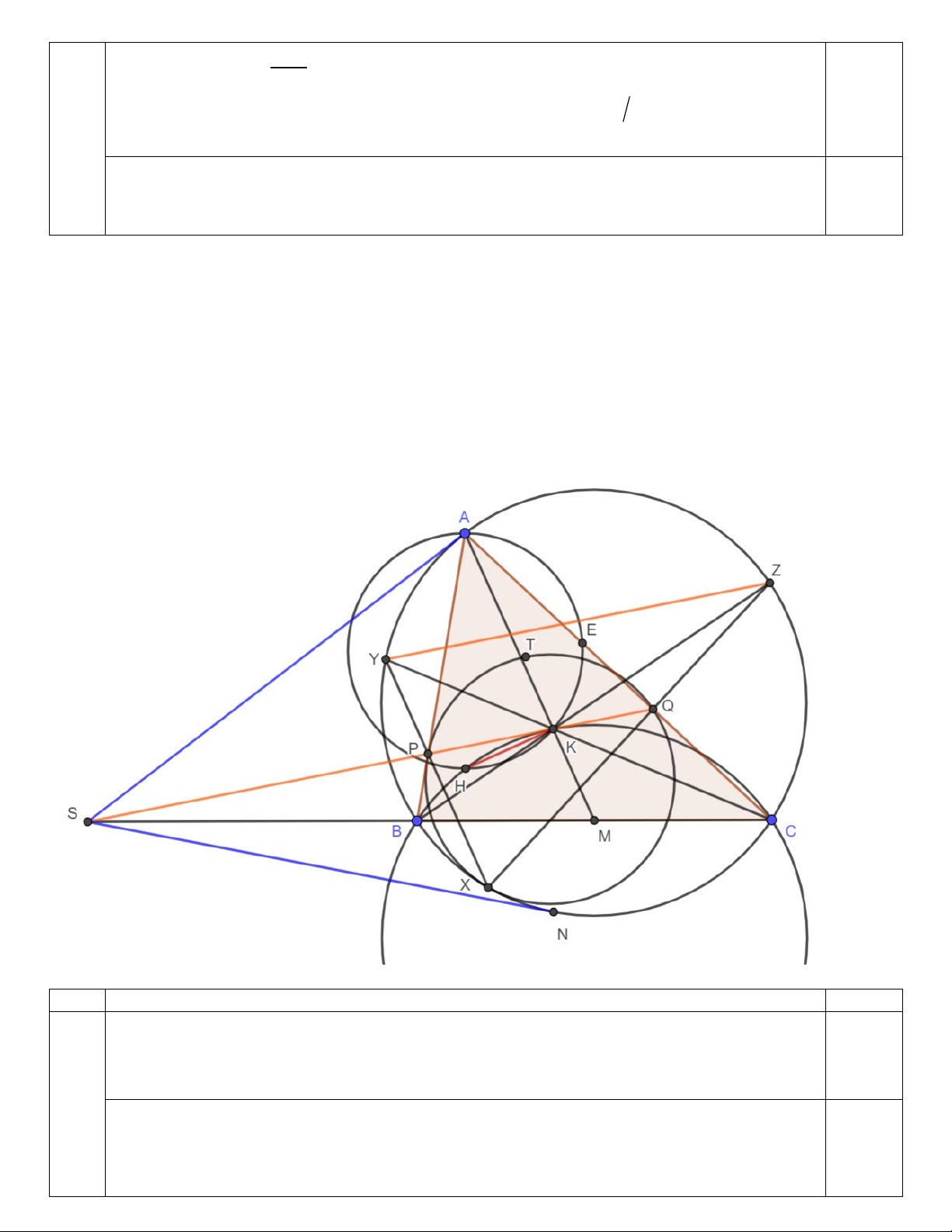
Câu 4 (5,0 điểm). Cho tam giác ABC nhọn ( AB < AC) nội tiếp đường tròn (O) và có H là trực tâm. Gọi M là
trung điểm cạnh BC. Đường tròn ngoại tiếp tam giác HBC cắt đoạn thẳng AM tại K; tiếp tuyến của (O) tại A
cắt đường thẳng BC ở điểm S. a) Chứng minh 2
MK.MA = MB và SA = SK.
b) Đường thẳng SK cắt hai cạnh AB, AC lần lượt tại P, .
Q Gọi T là tâm đường tròn ngoại tiếp tam giác AP .
Q Chứng minh đường tròn ngoại tiếp tam giác TPQ tiếp xúc với đường tròn (O). Câu Nội dung Điểm
Vẽ đường cao BE của tam giác ABC. Dễ thấy ME là tiếp tuyến của ( AHE) tại E. 0,5
Gọi K ' là giao điểm thứ hai của MA và ( AHE). Ta có 2
MK '.MA = ME . 2 2
⇒ MK '.MA = MB = MC .
Hai tam giác MBK ', MAB đồng dạng ⇒  =  MK ' B MB . A 1,0
Hai tam giác MCK ', MAC đồng dạng ⇒  =  MK 'C MC . A
4a Khi đó  =  +  = 
BK 'C MBA MCA BHC ⇒ K '∈(BHC) ⇒ K ' ≡ K. Vậy 2
MK.MA = MB .
Hai tam giác MBK ', MAB đồng dạng KB MK ⇒ = . Tương tự KC MK KB KC = ⇒ = . AB MB AC MC AB AC 0,5
Gọi N là điểm đối xứng của K qua BC ⇒ N ∈(O) (do (HBC);(O) đối xứng nhau qua BC
). Lại có NB KB KC NC = = =
⇒ ( AN, BC) = 1
− ⇒ SN là tiếp tuyến của (O). 0,5 AB AB AC AC
Do đó SA = SN = SK.
Đường thẳng CK, BK cắt lại (O) tại Y,Z khác C, .
B Do ba điểm P, K,Q thẳng hàng nên 0,5
hai đường thẳng YP, ZQ cắt nhau tại X thuộc đường tròn (O). Dễ thấy 2 2 SK = SA = .
SB SC ⇒ SK tiếp xúc ( ) ⇒  =  =  BKC
SKB KCB PXB ⇒ KPBX nội 0,5
tiếp. Tương tự KQCX nội tiếp.
4b Lúc này  =  +  =  +  −  + 
PXQ PBK QCK ABC ACB (KBC KCB) 0 = −  180 2BAC. (Do  +  0 = −  0 = −  = 
KBC KCB 180 BKC 180 BHC BAC ). 1,0 Mà  =  ⇒  +  0 PTQ 2BAC
PTQ PXQ =180 ⇒ X ∈(TPQ). Ta có  =  = 
XPQ XBK XYZ ⇒ PQ ||YZ. Từ đây suy ra hai đường tròn ( XPQ),(O) tiếp xúc 0,5
nhau tại X. Vậy (TPQ) và (O) tiếp xúc nhau.
Câu 5 (4,0 điểm). Ban chấp hành Đoàn trường THPT X gồm có n thành viên. Trong năm học, Đoàn trường tổ
chức m chương trình, mỗi chương trình có đúng k thành viên trong ban chấp hành tham gia. Mỗi thành viên trong
ban chấp hành tham gia ít nhất một chương trình.
a) Cho m = 8;k = 3. Biết rằng với hai chương trình bất kỳ luôn có đúng một thành viên trong ban chấp
hành tham gia cả hai chương trình đó. Chứng minh n =17.
b) Cho n = 25;k =10. Biết rằng với hai chương trình bất kỳ luôn có không quá 3 thành viên trong ban
chấp hành cùng tham gia. Chứng minh m ≤ 6. Câu Nội dung Điểm
Ta đánh số thứ tự các chương trình là 1,2,3,...,8. Giả sử chương trình 1 có ba thành viên tham gia là ,
A B,C. Khi đó mỗi chương trình 2,3,...,8 có đúng một trong ba thành viên 0,5 ,
A B,C tham dự. Theo nguyên lý Dirichlet thì có một trong ba thành viên ,
A B,C tham gia ít
nhất ba trong bảy chương trình 2,3,...,8.
Không giảm tổng quát giả sử A là thành viên tham gia ba chương trình 2,3,4. Khi đó giả sử
5a các thành viên tham dự chương trình 1,2,3,4 lần lượt là ( , A B,C),( , A D, E),( , A F,G), ( ,
A H, I ). Ta chứng minh A có tham dự tất cả chương trình 5,6,7,8. Thật vậy : giả sử A 1,0
không tham dự chương trình 5. Khi đó trong các cặp (B,C),(D, E),(F,G),(H, I ) mỗi cặp
có đúng một thành viên tham dự chương trình 5. Điều này vô lý do chương trình này chỉ có
đúng 3 thành viên tham dự.
Như vậy A có tham dự đủ tám chương trình và ngoài A thì mỗi chương trình còn có thêm 0,5
hai thành viên khác ⇒ n =1+ 2.8 =17.
Gọi S là số bộ ({ ;x }
y ;t) trong đó { ;x }
y là hai chương trình (không có thứ tự) và t là thành
viên tham gia cả hai chương trình. Số cách chọn cặp { ; x } y là 2
C Do hai chương trình có m.
chung không quá ba thành viên nên với mỗi cặp { ; x }
y có không quá 3 cách chọn thành viên 0,5 2 3 m − m 2 ( )
t ⇒ S ≤ 3C = m . 2
Ta đếm S bằng cách khác. Với mỗi thành viên t ∈{1;2;...; }
25 , ta ký hiệu x là số chương t
trình mà thành viên này tham gia. Do mỗi chương trình có 10 thành viên nên 0,5
5b x + x +...+ x =10 . m 1 2 25
Với mỗi thành viên t , số cách chọn cặp { ; x } y là 2 2 2 2
C ⇒ S = C + C + + C x x ... t x 1 2 25 x
x + x +...+ x
x + x +...+ x
x + x +...+ x
x + x +...+ x 1 2 25 1 2 25 ( )2 2 2 2 1 2 25 1 2 25 ⇒ S = − ≥ − 2 2 2.25 2 0,5 (10m)2 10m 3( 2 m − m 2 ) 2 ⇒ S ≥ − = 2m − 5 .
m Do đó 2m − 5m ≤ ⇒ m ≤ 7. 50 2 2
Giả sử m = 7 ⇒ các đẳng thức ở trên phải xảy ra. Khi đó x = x = ... = x và do 1 2 25 70 0,5
x + x +...+ x =10m = 70 ⇒ x =
(vô lý). Vậy ta phải có m ≤ 6. 1 2 25 1 25
-------------------HẾT-------------------
Document Outline

• DE11
• DA11