Đề thi Olympic Toán 11 năm 2018 – 2019 trường THPT Kim Liên – Hà Nội

Giới thiệu đến thầy, cô và các em học sinh khối 11 nội dung đề thi Olympic Toán 11 năm 2018 – 2019 trường THPT Kim Liên – Hà Nội, đề thi gồm 01 trang với 06 bài toán tự luận, học sinh làm bài trong 150 phút 

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Câu 1(3,0 ). :
5
5 2
2cos .sin 2sin .cos sin 4 .x x x x x
Câu 2 (2,0 ).
2
2 6.
3
x
x
x
x
Câu 3 (4,0 ). Cho
(
0;1)
a
và
( )
n
u
xác :
1
3
3
1
1
( ) :
1
n
n
n
u
u
u au a
*
,
.
n
a)
( )
n
v
3
1
n
n
v
u
(
)
n
v
nhân
b)
a
3 3 3
1 2
l
im( ... ) 4
n
u
u u n
.
Câu 4 (3.0
). 25
ó
6
5
,
Toán Anh.
Câu
5 (6.0
). Cho ABC
D.A’B’C’D’
I
AB, E
DD’ sao ch
o
' ,(0 1)AI D E x x
.
IE
'A C
.
b) Tìm
x
'
AC
và
DI
0
,M N
, ' '.
AB A D
K
( )CMN
'
'
B
C
'
.
' '
B K
B C
Câu
6 (2.0
).
,
,
a
b c
2
2 2
3
0
a
b c b
.
2 2 2
1
4 8
1.
1 2 3a b c
-------
------
-
------------
c s d ng tài li i thích gì thêm.
H và tên thí sinh:
……
…………………....................................................….
SBD:
..
.............................
– 2019
Môn: TO
ÁN -
11
: 150 phút
1
TRƯỜNG THPT KIM LI£N
ĐÁP ÁN ĐỀ OLYMPIC MÔN TOÁN LỚP 11
NĂM HỌC 2018 – 2019
C¢U
NỘI DUNG
ĐIỂM
1
(3 điểm)
5 5 2
2 2 2 2 2
22
2cos .sin 2sin .cos sin 4
2cos .sin (cos sin )(cos sin ) sin 4
1
sin 2 .cos 2 sin 4 sin 4 sin 4
2
x x x x x
x x x x x x x
x x x x x

1,5
4
4
sin 4 0
4 2 , .
1
6 24 2
sin 4
2
5
5
42
24 2
6
xk
xk
x
x k x k k
x
xk
xk



1,5
2
(2 điểm)
Điều kiện xác định:
0; 9.xx
2
22
2 6 2(3 ) 2.
3 3 3 3
x x x x
x x x x
x x x x



1,0
2
26
3
8 2 7.
3
1
3
x
xx
x
x
x
xx
x


1,0
3
(4,0 điểm)
a) Ta có

3 3 3 3
11
1 1 1
n n n n
u au a u a u
. Suy ra
1
.
nn
v av
1,0
Như vậy dãy số
n
v
là cấp số nhân với công bội a nên nó là cấp số nhân lùi vô hạn.
1,0
b) Ta được
12
21
...
1
n
n
a
v v v
a
3 3 3
12
21
...
1
n
n
a
u u u n
a
3 3 3
12
lim ... 4
n
u u u n

21
lim 4
1
n
a
a
1,0
Vì
01a
nên
21
2 2 1
lim 4 .
1 1 1 2
n
a
a
a a a
1,0
4
(3,0 điểm)
T là phép thử ‘Chọn ngẫu nhiên 3 học sinh trong số 25 học sinh’. Ta có :
3
25
.C
Gọi A là biến cố : 3 học sinh được chọn luôn có học sinh dự thi môn Toán và học sinh dự thi
môn Anh. Ta có các trường hợp sau thuận lợi cho biến cố A :
0,5
Có 1 học sinh chọn môn Toán, 2 học sinh chọn môn Anh có :
12
65
.CC
khả năng
Có 2 học sinh chọn môn Toán, 1 học sinh chọn môn Anh có :
21
65
.CC
khả năng
Có 1 học sinh chọn môn Toán, 1 học sinh chọn môn Anh, 1 học sinh chọn môn khác
(Văn, Tin, Sinh học, Lịch sử, Vật Lí, Hóa, Địa lý) có :
1 1 1
6 5 14
.C C C
khả năng.
2,0
1 2 2 1 1 1 1
6 5 6 5 6 5 14
..
A
C C C C C C C
Vậy xác suất của biến cố A là
555 111
( ) .
2300 460
A
PA
0,5
2
5
(6,0 điểm)
Đặt
' ' ; ' ' ; ' .A B a A D b A A c
a) Ta có:
'.A C a b c
Lại có:
IE IA AD DE
(1 ) .xa b x c
Xét:
2 2 2
' . . (1 )
(1 ) 1 (1 ) 0.
A C IE a b c xa b x c
xa b x c x x
Suy ra
'.A C IE
F
N
M
A'
A
B'
B
D'
D
C'
C
K
M'
I
E
3.0
b) Ta có:
0
2
. ' ( )( ')
1
cos60
. ' . '
1 . 3
DI AC DA AI AD AB AA
x
DI AC DI AC
x

.
Suy ra:
2
2
1
1
8 1 0 4 15.
2
1 . 3
x
x x x
x

1,5
c) Gọi M’ là trung điểm cạnh A’B’.
Trong
( ' ' ' ') :A B C D
kẻ đường thẳng đi qua
N
và song song với
''CM
cắt đường thẳng
''BC
tại
.K
Khi đó
K
là giao điểm của mặt phẳng
()CMN
với đường thẳng
' '.BC
Áp dụng định lí Ta-lét ta tính được:
'5
.
' ' 2
BK
BC
1,5
6
(2 điểm)
Đặt
2 2 2
1 4 8
1 2 3
P
a b c
.
Ta thấy:
2 2 2
2 2 2
2 4 2 6 1 2 1 0a b c a b c a b c
, theo giả thiết
thì
2 2 2
3a b c b
. Suy ra
3 2 4 2 6 0b a b c
hay
2 2 10 16a b c
.
0,5
Với hai số
,0xy
ta có:
22
2 2 2 2 2
2
2
( )( ) 8 .
( ) 4
x y xy
x y x y x y
x y xy


Do đó:
2
22
1 1 8
(1)
xy
xy

Áp dụng (1) ta có:
2 2 2
1 4 8
12
2
2
ab
b
a






;
2 2 2
1 1 8
3
25
22
c
bb
a a c

.
0,5
2
2 2 2 2
8 8 8 16
8.
3 2 2 10
25
22
P
c a b c
bb
a a c
.
Theo giả thiết và chứng minh trên thì
0 2 2 10 16a b c
,
1P
.
0,5
Khi
1, 2, 1a b c
thì
1P
.
0,5
Học sinh làm theo cách khác, nếu đúng vẫn được đủ điểm tối đa như đáp án qui định.
……………….HÕt………………...
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

– 2019 Môn: TOÁN - 11 : 150 phút Câu 1(3,0 ). : 5 5 2 2 cos . x sin x 2sin . x cos x sin 4 . x 2 x Câu 2 (2,0 ). x 2 x 6. 3 x Câu 3 (4,0 ). Cho a (0;1) và (u ) xác : n u 1 1 (u ) : n 3 3 u au a 1 * , n . n 1 n a) (v ) 3 v u 1 (v ) n n n n nhân b) a 3 3 3 lim(u u ... u n) 4 . 1 2 n Câu 4 (3.0 ). 25 ó 6 5 , Toán Anh. Câu 5 (6.0 ). Cho ABCD.A’B’C’D’ I AB, E DD’ sao cho AI D ' E x, (0 x 1) . IE A'C . b) Tìm x AC ' và DI 0 60 . M , N
AB, A' D '. K B ' K (CMN ) B 'C ' . B 'C ' Câu 6 (2.0 ). a, , b c 2 2 2 a b c 3b 0 . 1 4 8 1. 2 2 2 a 1 b 2 c 3 ------------- ------------- c s d ng tài li i thích gì thêm.
H và tên thí sinh: ………………………....................................................….SBD: ...............................
TRƯỜNG THPT KIM LI£N
ĐÁP ÁN ĐỀ OLYMPIC MÔN TOÁN LỚP 11
NĂM HỌC 2018 – 2019 C¢U NỘI DUNG ĐIỂM 5 5 2
2cos .xsin x  2sin .xcos x  sin 4x 2 2 2 2 2  2cos .
x sin x(cos x sin x)(cos x  sin x)  sin 4x 1,5 2 1 2  sin 2 .
x cos 2x  sin 4x  sin 4x  sin 4x 2 1    x k (3 điểm) 4x k  4 sin 4x  0      1,5  1  
 4x   k2   x   k ,k  . sin 4x   6  24 2  2  5  5  4x   k2 x   k  6  24 2
Điều kiện xác định: x  0; x  9. 2 2 2 x   2  6 x    2(3 )  x x x x x x      2. 1,0 3 x 3 x  3  x  3 x 2 (2 điểm) x  2 3 xx  2  x  6      x  8  2 7. 1,0  x    x x  3 1 3 x a) Ta có 3 u  3
au a 1  3 u 1  3
a u 1 . Suy ra v   av n n. n1 n n1  n  1 1,0
Như vậy dãy số v là cấp số nhân với công bội a nên nó là cấp số nhân lùi vô hạn. n  1,0 21 n a  2 1 n a 3 3 3    3
b) Ta được v v  ... v
u u  ... u n  1 2 n 1 a 1 2 n 1 a ( 4,0 điểm) 1,0 21 n a  lim  3 u  3 u  ... 3 u n 4  lim  4 1 2 n   1 a 21 na  Vì 0  a 1 nên 2 2 1 lim    4  a  . 1,0 1 a 1 a 1 a 2
T là phép thử ‘Chọn ngẫu nhiên 3 học sinh trong số 25 học sinh’. Ta có : 3   C . 25
Gọi A là biến cố : 3 học sinh được chọn luôn có học sinh dự thi môn Toán và học sinh dự thi 0,5
môn Anh. Ta có các trường hợp sau thuận lợi cho biến cố A :
 Có 1 học sinh chọn môn Toán, 2 học sinh chọn môn Anh có : 1 2
C .C khả năng 6 5 4
 Có 2 học sinh chọn môn Toán, 1 học sinh chọn môn Anh có : 2 1
C .C khả năng 6 5 (3,0 điểm) 2,0
 Có 1 học sinh chọn môn Toán, 1 học sinh chọn môn Anh, 1 học sinh chọn môn khác
(Văn, Tin, Sinh học, Lịch sử, Vật Lí, Hóa, Địa lý) có : 1 1 1
C .C C khả năng. 6 5 14  1 2 2 1 1 1 1
  C C C C C C C Vậy xác suất của biến cố A là A 555 111 P( ) A    . A . . 6 5 6 5 6 5 14  2300 460 0,5 1
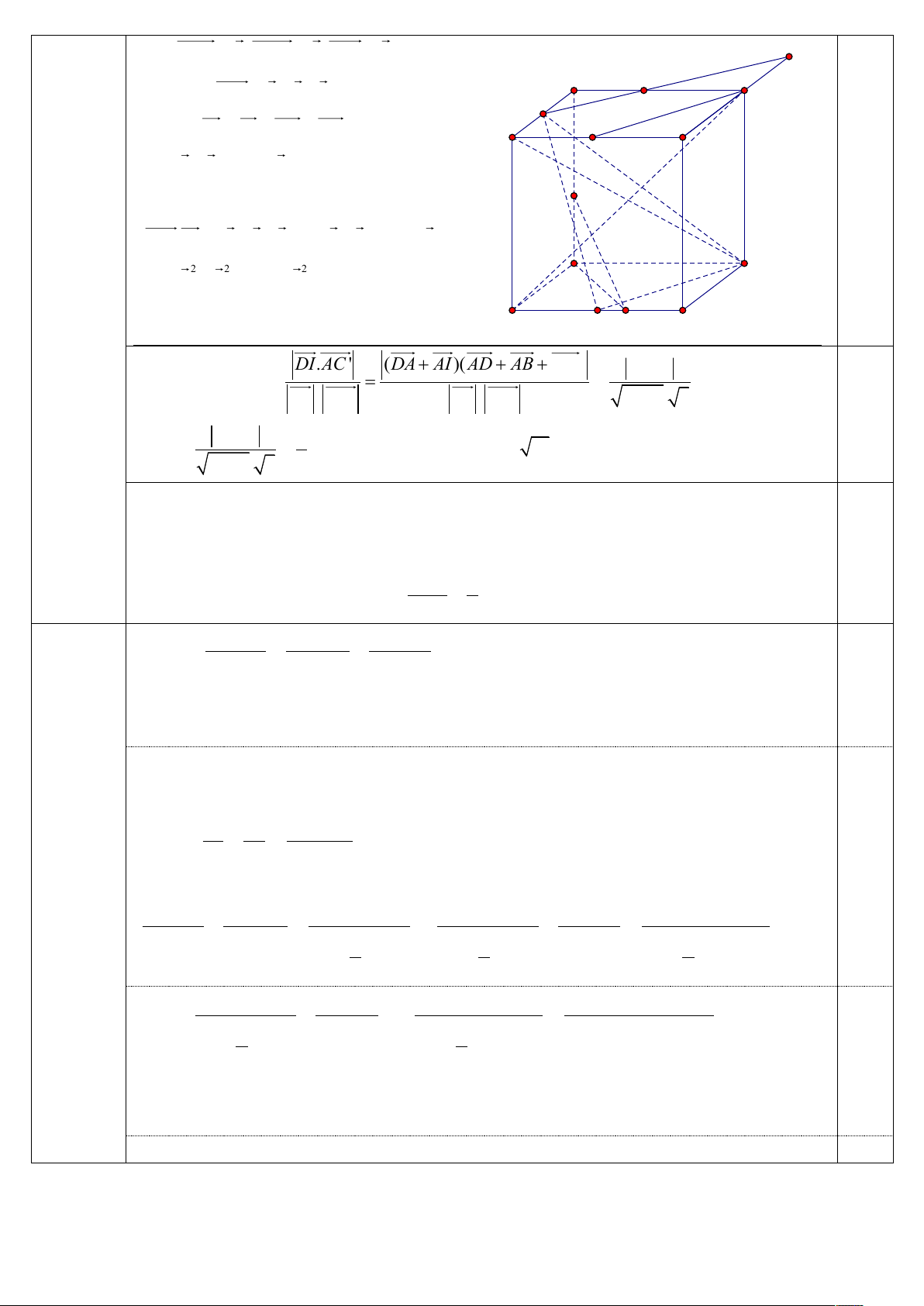
Đặt A'B'  ; a A'D'  ; b A' A  . c K
a) Ta có: A'C a b  . c D' C' F N
Lại có: IE IA AD DE A' B' M'
 xa b  (1 x) . c Xét: E 5 3.0 (6,0 điểm)
A'C.IE  a b c.xa b (1 x)c 2 2 2 C
 xa b  (1 x)c  x 1 (1 x)  0. D
Suy ra A'C IE. A M I B DI.AC '
(DA AI)(AD AB AA') 1   x    b) Ta có: 0 cos60 . 2 DI . AC ' DI . AC ' 1 x . 3 1,5 1   x Suy ra: 1 2
  x 8x 1 0  x  4  15. 2 1 x . 3 2
c) Gọi M’ là trung điểm cạnh A’B’.
Trong (A'B 'C 'D ') : kẻ đường thẳng đi qua N và song song với C 'M 'cắt đường thẳng
B 'C 'tại K. Khi đó K là giao điểm của mặt phẳng (CMN) với đường thẳng B'C '. 1,5
Áp dụng định lí Ta-lét ta tính được: B 'K 5  . B 'C ' 2 Đặt 1 4 8 P    . a  2 1
b  22 c  32 0,5 Ta thấy: 2 2 2
a b c  2a  4b  2c  6  a  2
1  b  22  c  2 1  0 , theo giả thiết thì 2 2 2
a b c  3b . Suy ra 3b  2a  4b  2c  6  0 hay 2a b  2c 10 16. 2 2
x y  2xy
Với hai số x, y  0 ta có: 2 2 2 2 2 
 (x y )(x y)  8x y . 2
(x y)  4xy Do đó: 1 1 8   (1) 2 2 x yx y2 0,5 6 Áp dụng (1) ta có: (2 điểm) 1 4 8   ; 1 1 8   . a  2 1 b  22 2  b 2  b  c  32 2 a 2    b   a   2 a   c     5 2      2   2  2 8 8 8 16  P    8.  . 2  b  c  32 2  b
2a b  2c 102 a   2 a   c     5 2 2      0,5
Theo giả thiết và chứng minh trên thì 0  2a b  2c 10 16, P 1.
Khi a 1, b  2, c 1 thì P 1. 0,5
Học sinh làm theo cách khác, nếu đúng vẫn được đủ điểm tối đa như đáp án qui định.
……………….HÕt………………... 2
Document Outline

  • khối 11 Đề thi OLYMPIC Kim liên năm học 2018-2019.pdf
  • [TRUNGTRINH]Khối 11 Đề thi OLYMPIC Kim liên năm học 2018-2019.pdf
    • Dap_an_thi_Olympic_lop11_2019