Đề thi Olympic Toán 11 năm 2023 – 2024 cụm Hà Đông & Hoài Đức – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
CỤM TRƯỜNG THPT HÀ ĐÔNG – HOÀI ĐỨC LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024 Môn thi: TOÁN 11 ĐỀ CHÍNH THỨC Ngày thi: 28/3/2024
Thời gian làm bài: 150 phút Câu I. (4 điểm)  5   7 
1) Tìm số nghiệm của phương trình sin 2x   3cos x   1  2 sin x    
trên khoảng 0,3 .  2   2 
cos A  cos B  cos C 1 C
2) Cho tam giác ABC. Chứng minh  tan .
sinA  sin B  sin C 2 Câu II. (4 điểm)
1) Cứ vào đầu mỗi tháng, ông A đến gửi tiết kiệm ngân hàng số tiền 10 triệu đồng với lãi suất là
0, 5% / tháng theo hình thức lãi kép. Hỏi sau đúng 5 năm thì ông A nhận được số tiền cả gốc và
lãi là bao nhiêu, biết rằng trong suốt quá trình gửi, ông A không rút tiền ra và lãi suất của ngân hàng không thay đổi. 1 1
2) Cho hai số thực a , b đều lớn hơn 1. Tìm giá trị nhỏ nhất của biểu thức . S   log a log b 4 ab ab Câu III. (4 điểm) 1) Tìm các giới hạn sau 3 2x 1 1
1 x1 2x1 3x...110x 1 a) A  lim . b) . B  lim x 1  2 1  2  x x0 x
2) Cho dãy số u là một cấp số nhân có số hạng đầu u 1, công bội q  2. Chứng minh n  1 1 1 1 1 2    ...   . u  u u  u u  u u  u 3 3 1 4 2 5 3 2024 2022 Câu IV. (6 điểm)
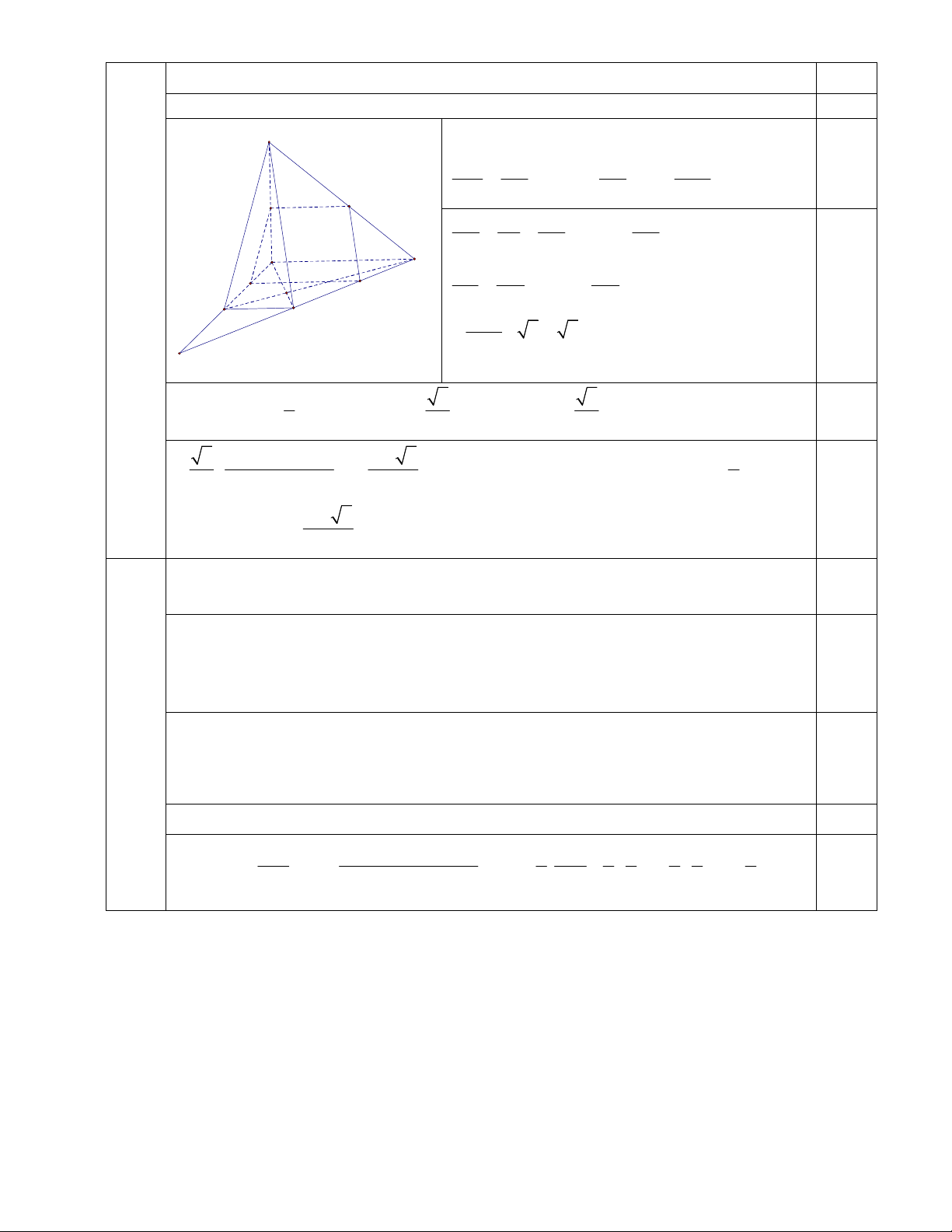
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, AB  BC  a, AD  2a . Biết SA
vuông góc với đáy ( ABCD) và SA  a .
1) Tính sin của góc giữa đường thẳng BD và mặt phẳng (SAC).
2) Gọi M là một điểm thay đổi trên cạnh C ,
D (M khác C và D). Mặt phẳng qua M và song song
với mặt phẳng (SBC ) cắt các cạnh AB, S ,
A SD lần lượt tại N , P và .
Q Chứng minh tứ giác
MNPQ là hình thang vuông.
3) Khi M thay đổi, tìm giá trị lớn nhất của diện tích tứ giác MNPQ.  u  1
Câu V. (2 điểm) Cho dãy số u xác định bởi 1
. Tìm số hạng tổng quát u n   n * u
 4u  3.4  6, n  n   n 1  n u và tính giới hạn n . lim n . n 4n
........................HẾT.....................
Họ và tên thí sinh………………………………………………… Số báo danh……………………...........
Chữ ký cán bộ coi thi số 1………………………… Chữ ký cán bộ coi thi số 2……………………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI OLYMPIC DÀNH CHO HỌC SINH
CỤM TRƯỜNG THPT HÀ ĐÔNG – HOÀI ĐỨC LỚP 10, LỚP 11
NĂM HỌC 2023 – 2024 Môn thi: TOÁN 11 Ngày thi: 28/3/2024 HƯỚNG DẪN CHẤM Câu Nội Dung Điểm I
1) Tìm số nghiệm của phương trình … 2,0 (4,0đ)  5   7  sin 2x   3cos x   1 2 sin x      2   2  0,5
 cos 2x  3sin x  1  2 sin x 2
 1 2 sin x  sin x 1  0 0,5
 sin x 2sin x   1  0  x  k sin x  0       x 
 k 2 (k  ). 1 0,5 sin x   6  2  5 x   k 2  6
Với x  k  0;3  0  k  3  k  1;2  x  ;  2      13  x 
 k 2 0;3  k  0;1 x   ;  6  6 6  0,5 5 5 17  x 
 k2 0;3  k  0;1 x   ;  6  6 6 
Vậy phương trình có 6 nghiệm thuộc 0;3.
cos A  cos B  cos C 1 C
2) Cho tam giác ABC. Chứng minh  tan .
sinA  sin B  sin C 2 2,0 A  B A  B
Ta có cos A  cos B  cos C 1  2 cos  cos  cos C 1 2 2 C A  B C C  A  B C 2   2 sin  cos  2 s n i  2 sin cos  sin   2 2 2 2 1,0  2 2  C  A  B A  B  A B C  2 sin cos  cos  4 sin sin sin .   2  2 2  2 2 2 A  B A  B
Lại có sin A  sin B  sin C  2sin cos  sin C 2 2 0,5 C A  B C C C  A  B C   2 cos  cos  2 cos sin  2 cos cos  sin   2 2 2 2 2  2 2  1 C  A  B A  B  A B C  2 cos cos  cos    4 sin sin  cos . 2  2 2  2 2 2
cos A  cos B  cos C 1 C Suy ra  tan . 0,5
sinA  sin B  sin C 2 II
1) Đầu mỗi tháng, ông A đến gửi tiết kiệm ngân hàng… 2,0
(4,0đ) Số tiền ông A nhận được cả gốc lẫn lãi từ số tiền 10 triệu đồng gửi ở tháng thứ n là: n 0,5 S   (triệu đồng). n  61 10. 1 0, 5%
Do đó, sau đúng 5 năm thì ông A nhận được số tiền cả gốc và lãi là 60 k 0,5 T  10. 1 0, 5% 60    k 1    60 60 1 0, 5% 1    1, 005 1  10.1 0,5%   10.1, 005.  701, 2 (triệu đồng). 1,0  0, 5%  0, 005  
2) Cho hai số thực a , b đều lớn hơn 1… 2,0 1 1 Ta có S    ab  ab a   4 log log log a log b b 4 ab ab 1 1 5 0,5  1 log b  a   log b   . a logb  1 4 a 4 log b 4 a 1 5
Đặt x  log b . Do a , b  1 nên x  0 . Khi đó S  x   . a 0,5 4x 4 1 5 1 5 9
Ta có S  x    2 . x   0,5 4x 4 4x 4 4  1 x  1 Dấu "  " xảy ra   4x  x  . 2 x  0  0,5 9 1 Vậy min S  tại log b   b  a . 4 a 2 III
1) Tìm các giới hạn sau … 2.0 (4,0đ) 2x  2 0,5    2 3 1 2 2 1 1  x x  a) A  lim  lim x 1  2 x 1 1 2  x  x   3 1 2x    2 2 3 1  2x 1   1 2 0,5 2 1 2  x  2  lim  x 1  2 3 3 3  x   1 2x    1  2x 1   1
b) Gọi a là hệ số của i
x trong khai triển của đa thức i
1 x1 2x1 3x...110x 1;i  0;1; 2;...;10 0,5 a  0 0  
a  1 2  ... 10  55.  1 2 10
55x  a x  ...  a .x Suy ra 2 10 9 B  lim
 lim(55  a x  ...  a x )  55. 0,5 2 10 x0 x 0 x  2
2) Cho dãy số u là một cấp số nhân có số hạng đầu u  1, công bội q  2... 2,0 n  1 1 1 1 1 Ta có VT     ...  u  2 q   1 u  2 q   1 u  2 q   1 u  2 q 1 1 2 3 2022  0,5 1  1 1 1 1      ...  2   q 1 u u u u  1 2 3 2022  1  1 1 1 1  1 1  1 1 1      ...   . 1   ...  2  2 2021    q 1 u u q u q u q 2 2 2021 0,5  q 1 u q q q 1 1 1 1  1   2022 2022  1   1 1     1 2022   1 1 q 1    2 2  1     2 1,0  . .  .  1   . 2   q 1 u 1 3 1 3  2     3 1 1 1   q 2 IV
1) Tính sin của góc giữa đường thẳng BD và mặt phẳng (SAC). 2.0 (6,0đ) S
Gọi BD  AC    O .
Chứng minh CD  AC 0.5
mà CD  SA  CD  SAC 
 C là hình chiếu của D lên mặt phẳng SAC  A D
  BD SAC    BD OC   , ;  CO . D 0.5 O B C OD AD 2 2a 5 Ta có:   2  OD  BD  ; CD  a 2 0.5 OB BC 3 3  CD 3 10  sin COD   . OD 10 0.5 3 10
Vậy sin của góc giữa đường thẳng BD và mặt phẳng (SAC) là . 10
2) Gọi M là một điểm thay đổi trên cạnh C ,
D (M khác C và D)... 2.0 S
 là mặt phẳng qua M và song song với SBC.    
   ABCD  MN 0.5   MN ∥ BC∥ A . D Q P SBC 
   ABCD  BC     
  SAD  PQ A D   PQ∥ A . D N   ∥ AD  0.5 M Suy ra MN ∥ PQ. B C 
 AD   SAB Có 
 MN  SAB  MN  N . P 1,0  AD MN  ∥ 3
Vậy tứ giác MNPQ là hình thang vuông.
3) Khi M thay đổi, tìm giá trị lớn nhất của diện tích tứ giác MNP . Q 2,0 S
Đặt BN  x, 0  x  a. Gọi AB  CD  E. MN EN EN a  x 0.5   MN  .AD  .2a  a  . x AD EA EA 2a Q P PQ SP BN BN    PQ  .AD  2 . x AD SA AB AB A D NP AN AN N   NP  .SB M SB AB AB 0.5 O B C a  x  .a 2  2 a  x. a E 1 2 2 Suy ra S  MN  PQ NP  x  a a  x  x  a a  x MNPQ  . 3   3 3 3  0.5 2 2 6 2 2
2  3x  a  3a  3x  2a 2 a   .  
Dấu “=” xảy ra khi 3x  a  3a  3x  x  . 6  2  3 3 0,5 2 2a 2 Vậy MaxS  . MNPQ 3 V  u  1
(2,0đ) Cho dãy số xác định bởi: 1  … n * 2,0 u  4u  3.4 6, n     n 1  n n Ta có u  4u  3.4  6 n 1  n  u  3 .
n 4n  2  4u  3 n 1 .4n  8 n 1  n   0.5  u  3 .
n 4n  2  4 u  3 n     n   n n   n 1 1 .4 2 , 1; 2;3... 1   n
Đặt v  u  n   n   n n   1 3 1 .4 2, 1; 2;3... v  3 0.5 Suy ra 1   v  3n v  3v , n   1; 2;3... n  n 1  n u n       n   0.5 n   n 1 3 1 4 3n 2, 1; 2;3...  u
3n   n 1 1 4  3n  2 n n  3 n 1 1 3 2 1       3 Suy ra n . lim  lim  lim  .         n . n 4n n . n 4n n 4 n n 0,5   4  n  4  4  
Các cách giải khác đáp án, nếu đúng vẫn cho điểm tối đa tương ứng.
---------------HẾT---------------- 4