Đề thi Olympic Toán 11 năm 2023 – 2024 cụm Hoàn Kiếm & Hai Bà Trưng – Hà Nội

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI OLYMPIC NĂM HỌC 2023-2024 CỤM TRƯỜNG THPT Môn Toán - Lớp 11
HOÀN KIẾM – HAI BÀ TRƯNG
Thời gian làm bài: 150 phút ĐỀ CHÍNH THỨC
(Không kể thời gian giao đề)
Bài I (4,0 điểm) Giải các phương trình sau: 1)
sin x  cos x2sin x   1  2  2 sin 2 . x 1 sin x 2)   1 2sin . x tan x cos x 1
Bài II (2,0 điểm) Tính các giới hạn sau: 1)  2 2 lim
n  n 1  4n  2n 1  3n  . n 3
1 x 1 2x 1 2) . lim x0 x
Bài III (3,0 điểm) Cho bất phương trình 2 log x  2  log  2
3x  x  m  1  0. 1 2  2
1) Giải bất phương trình đã cho khi m  2.
2) Tìm các giá trị của m để bất phương trình đã cho nghiệm đúng với mọi x thuộc khoảng 2;3.
Bài IV (1,0 điểm) Gọi S là tập hợp các số tự nhiên có 7 chữ số sao cho trong mỗi số đó chữ số 0 xuất
hiện đúng 3 lần. Chọn ngẫu nhiên một số thuộc S, tính xác suất để số đó chia hết cho 5. a 6
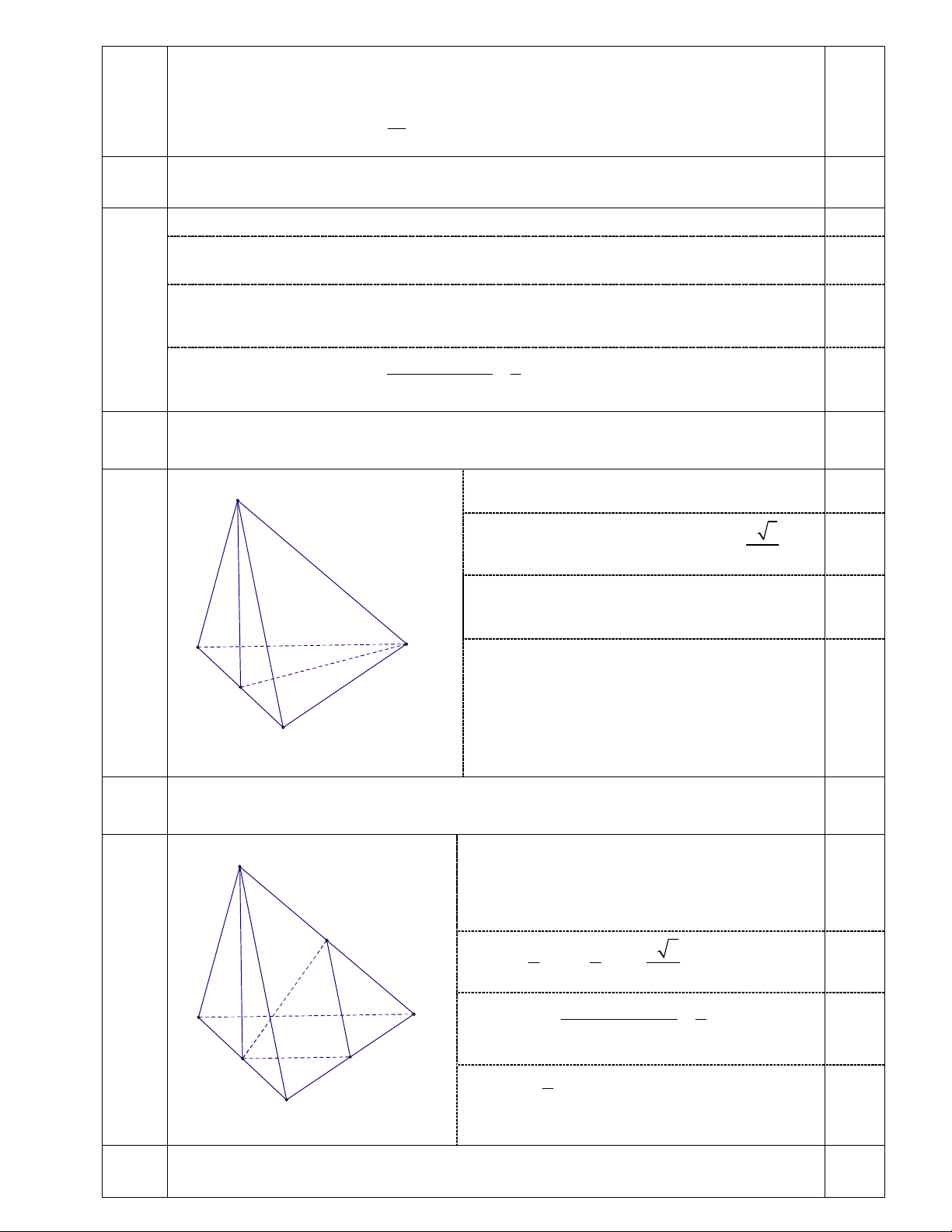
Bài V (6,0 điểm) Cho hình chóp S.ABC có cạnh SB 
, các cạnh còn lại của hình chóp bằng . a 2
Gọi I là trung điểm AC.
1) Chứng minh SI vuông góc với đường thẳng BC.
2) Tính cosin của góc giữa hai đường thẳng AB và SC.
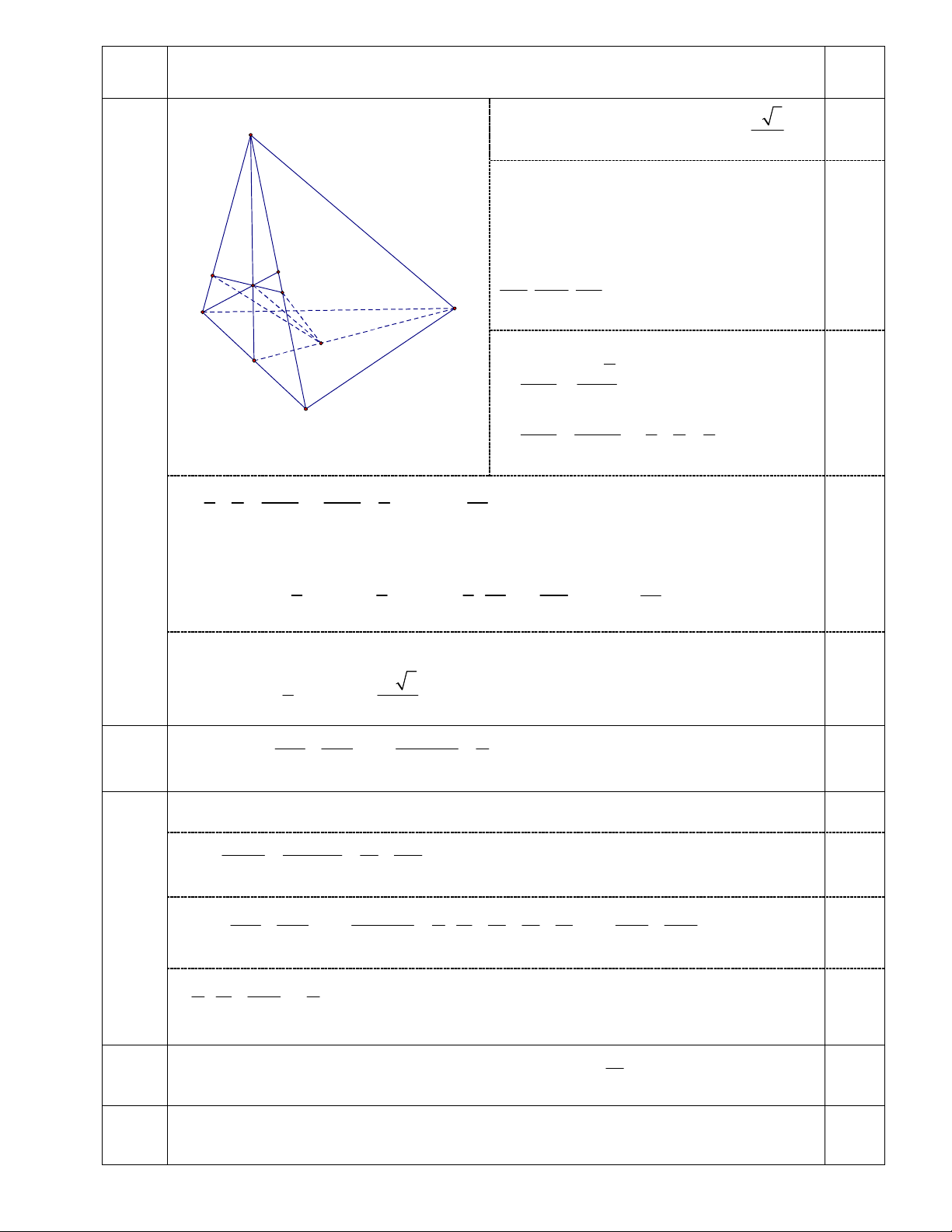
3) Gọi G và G ' lần lượt là trọng tâm của tam giác ABC và tam giác SAC. Một mặt phẳng đi qua
G và G ' cắt hai cạnh S ,
A SC lần lượt tại M và N. Khi MN đạt giá trị nhỏ nhất, tính diện tích của tam giác GMN.
Bài VI (4,0 điểm)
1) Cho cấp số cộng u thỏa mãn u  1 và công sai d  0. Chứng minh n  1 1 1 1 1   ...   . u u u u u u d 1 2 2 3 2023 2024 u   3
2) Cho dãy số u được xác định như sau 1 n 
u  2u  n 1, n   1, 2, 3,...  n 1  n u
Tìm công thức số hạng tổng quát của dãy số u . Tính n . lim n  3n n
-----------------HẾT-----------------
Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh:……………………………………………………………Số báo danh:………………..
Họ tên và chữ kí của cán bộ coi thi số 1:
Họ tên và chữ kí của cán bộ coi thi số 2:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI OLYMPIC NĂM HỌC 2023-2024 CỤM TRƯỜNG THPT Môn Toán - Lớp 11
HOÀN KIẾM – HAI BÀ TRƯNG
Thời gian làm bài: 150 phút ĐỀ CHÍNH THỨC
(Không kể thời gian giao đề) HƯỚNG DẪN CHẤM Câu Nội dung Điểm Bài I.1 1)
sin x  cos x2sin x   1  2  2 sin 2x 2,0đ
Ta có sin x  cos x2sin x  
1  2 1 2sin x cos x 0,5   x  x x     x  x2 sin cos 2 sin 1 2 sin cos 0,5     sin x   0
sin x  cos x  0     4      0,5
2 sin x 1  2 sin x  cos x   1 cos x   2   x    k  4   k  . 0,5 
x    k2  3 Bài I.2 1 sin x 2)   1 2sin x 2,0 đ tan x cos x 1 s  in x  0  k
Điều kiện cos x  0  x  k   2 0,25 cos x  1  1 sin x cos x sin x Ta có   1  2 sin x    1 2 sin x tan x cos x 1 sin x cos x 1 0,5 x  x   2 cos cos 1  sin x 1 cos x   1 2 sin x   1 2 sin x
sin x cos x   1
sin x cos x   1 1 2 
 2 sin x 1  2 sin x  sin x 1  0 0,5 sin x   x   k2   2 s  in x  1      1  x  
 k 2 k   0,5 s  in x    6  2  7 x   k 2  6  7
Kết hợp điều kiện, phương trình có 2 họ nghiệm là x  
 k 2 , x 
 k 2 k  . 0,25 6 6 Bài       1,0 đ   2 2 lim n n 1 4n 2n 1 3n n  II.1 Ta có               0,25   2 2 lim n n 1 n 4n 2n 1 2n n    2 2 lim n n 1 4n 2n 1 3n n   n  1 2n 1   lim    0,5 n 2 2
 n  n 1  n
4n  2n 1  2n  1 1    1 2 2 0,25 Bài 3
1 x 1 2x 1 II.2 lim 1,0 đ x0 x  1 x  3 3 1 2x  x x     1 1 1 2 1 1 x 1 Ta có lim lim     0,25 x0 x0 x  x x      2 1 x 1 lim     0,5 x     x 2 0 3 3 1 x  1 1 2  1 2x 1    2 1 7    0,25 3 2 6 Bài
Giải bất phương trình đã cho khi m  2. 2,0 đ III.1
Với m  2 , bất phương trình đã cho trở thành: 2 log x  2  log  2
3x  x  2 1  0 (điều kiện: x   ) 0,5 1 2  2  log  2
x  2 1  log  2
3x  x  2   2 x   2 2
2  3x  x  2 2 2  0,5 x  1 2
 x  x  2  0   x  2 0,5 
Vậy tập nghiệm của bất phương trình là S   ;  2    1; . 0,5 Bài
Tìm m để bất phương trình đã cho nghiệm đúng với mọi x thuộc khoảng 2;3. 1,0 đ III.2 Ta có 2 log x  2  log  2
3x  x  m 1  0 0,25 1 2  2  log  2
x  2 1  log  2
3x  x  m 2 2    2 x   2 2
2  3x  x  m 0,25 2
 m  x  x  4   *
Xét hàm số f  x 2
 x  x  4 trên 2;3 ta có bảng biến thiên x 1 2  3 2 f  x 17 0,25 4 2  8
Bất phương trình đã cho nghiệm đúng x    2
 ;3 khi và chỉ khi bất phương trình * nghiệm đúng x    2  ;3 . 0,25 17
Suy ra m  Max f  x  m  . 2;3 4
Bài IV Gọi S là tập hợp các số tự nhiên có 7 chữ số sao cho trong mỗi số đó chữ số 0 xuất hiện 3 1,0 đ
lần. Chọn ngẫu nhiên một số thuộc S, tính xác suất để số đó chia hết cho 5.
Số STN có 7 chữ số trong đó chữ số 0 xuất hiện 3 lần là: 3 4 C .9 (số). 0,25 6
Số STN có 7 chữ số không chia hết cho 5 và trong đó chữ số 0 xuất hiện 3 lần là: 0,25 3 3 C .9 .8 (số). 5
Suy ra số STN có 7 chữ số chia hết cho 5 và trong đó chữ số 0 xuất hiện 3 lần là: 3 4 3 3
C .9  C .9 .8 (số). 0,25 6 5 3 4 3 3 C .9  C .9 .8 5
Vậy xác suất cần tính là 6 5 P   . 3 4 0,25 C .9 9 6 Câu
Chứng minh SI  BC. 2,0 đ V.1 S
Từ giả thiết suy ra SAC, ABC đều. 0,5 a 3
Do I là trung điểm AC  SI  BI  . 0,5 2 Xét SBI có 2 2 2
SI  BI  SB 0,5
Suy ra SBI vuông cân tại I . A B  SI  I . B
Do SAC đều nên SI  AC. I
Suy ra SI   ABC   SI  BC. 0,5 C Câu
Tính cosin của góc giữa hai đường thẳng AB và SC. 2,0 đ V.2 0,5 S
Gọi E, F lần lượt là trung điểm của BC, S . B IE∥ AB Suy ra 
  AB, SC    EI , EF   .  EF ∥ SC  F 0,5 a a a 6 Có IE  ; EF  ; IF  2 2 4 0,5 A B  2 2 2
IE  EF  IF 1  cos IEF   2EI.EF 4 I E 1 0,5  cos   . 4 C Câu
Tính diện tích của tam giác GMN . 2,0 đ V.3 0,25 S a 3
Nếu M  A hoặc N  C thì MN  . 2 0,25 Nếu M khác , A N khác .
C Gọi P là trung
điểm SC . Đặt SM  ;
x SN  y 0  x, y  a.
Áp dụng định lý Menelauyt cho SAE ta có M G' P MS G ' A NP N . .  1 A B MA G ' P NS 0,5 G a y  I x 2  .2.  1 a  x y C a  x 2 y  a 1 1 3      x y x y a 1 1 4 4 3 4a 0,5 Do      x  y  . x y x  y x  y a 3
Áp dụng định lý cosin ta có: 2 2 2
MN  SM  SN  2SM .SN.cos 60 2 2 1 3 1  4a  4a 2a
 x  y  xy 
 x  y2   x  y2 2 2      MN  . 4 4 4  3  9 3
Dấu “=” xảy ra khi và chỉ khi x  y  MN ∥ C
A  GG '  MN. 0,5 2 1 a 6 Suy ra S  GG '.MN  . G  MN 2 18 Câu 1 1 1 1 2,0 đ Chứng minh   ...   . VI.1 u u u u u u d 1 2 2 3 2023 2024
Do d  0 nên u là dãy số tăng, suy ra u  0, n  n  n 0,5 d u  u 1 1 Ta có k 1  k    , k   1, 2,... u u u u u u 0,5 k k 1  k k 1  k k 1  1 1 1 1  1 1 1 1 1 1  Do đó:   ...       ...     u u u u u u d u u u u u u 0,5 1 2 2 3 2023 2024  1 2 2 3 2023 2024  1  1 1  1    .   d u u d 0,5  1 2024  Câu u
Tìm công thức số hạng tổng quát của dãy số u . Tính lim n . n n 2,0 đ VI.2 n 3 Ta có u
 2u  n  1  u
 n 1  2 u  n n 1  n n 1   n  0,5
Đặt v  u  n, n   1, 2, 3... n n v  2 0,5 Suy ra 1 
 v  2n , n   1, 2, 3... v  2 n v  n 1  n
 u  2n  , n n   1, 2, 3... n 0,5 n u 2.2n n n  2  Do 2  1  * 1  n, n     0 n    2. .   3n 3n  3  0,5 n  2  u Mà lim 2.  0  lim n  0.     3   3n n n
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.