Đề thi thử HSG tỉnh Toán 11 năm 2019 – 2020 trường Nguyễn Duy Trinh – Nghệ An

SỞ GD&ĐTNGHỆ AN
ĐỀ THI THỬ HỌC SINH GIỎI TỈNH
TRƯỜNG THPT NGUYỄN DUY TRINH
LỚP 11- NĂM HỌC 2019-2020 Môn thi: Toán
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (7,0 điểm). Giải các phương trình sau: 2 x a) ( x + x) 2 sin cos + 2sin
= sin x(2 3sin x + 4− 3) 2 b) 2
x + 4 + 3 − x + 12 − x − x = x −1+ 2x + 5
Câu 2 (7,0 điểm).
a) Có bao nhiêu số tự nhiên có 4 chữ số sao cho trong mỗi số đó có một chữ số xuất hiện hai
lần, các chữ số còn lại xuất hiện không quá một lần.
x + 3 = 2 (3y − x)( y + ) 1 
b) Giải hệ phương trình  (x, y ∈ ) x + 5  3y − 2 −
= xy − 2y − 2  2
Câu 3 (4,0 điểm).
a) Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC vuông tại C , có phân giác 7 7
trong AD với D( ; − ) thuộc BC . Gọi E và F lần lượt thuộc các cạnh AB và AC sao cho 2 2 3 5
AE = AF. Đường thẳng EF cắt BC tại K . Biết E( ; − ) , F có hoành độ nhỏ hơn 3 và phương 2 2
trình đường thẳng AK là x − 2y −3 = 0.Viết phương trình các cạnh của tam giác ABC.
b) Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng d : x − y = 0 và đường tròn
(T ) (x − )2 +( y + )2 : 1 4
= 5 . Từ điểm M thuộc đường thẳng d kẻ hai tiếp tuyến , MA MB ( , A B là các
tiếp điểm) và cát tuyến MCD đến đường tròn (T ) với C nằm giữa M và D ; AB cắt CD tại N . 5
Tìm tọa độ điểm M biết rằng CD = 1 và ND = . 9
Câu 4 (2,0 điểm). Cho x, y, z là các số thực dương thỏa mãn x + y + z = 3. Chứng minh rằng:
x ( y + z)
y ( z + x)
z ( x + y) + + ≥ 2xyz 4 − yz 4 − zx 4 − xy ----- HẾT -----
Họ và tên thí sinh: ..................................................................... Số báo danh: ........................
HƯỚNG DẪN CHẤM ĐỀ THI THỬ Môn: TOÁN Câu Đáp án Điểm 1 2 x 2
(7,0đ) a) (3,5đ) Giải phương trình(sin x + cos x) + 2sin
= sin x(2 3sin x + 4− 3) (1) 2 (1) 2
⇔ 1+ 2sin x cos x +1− cos x = 2 3 sin x + 4sin x − 3 sin x 0,5 ⇔ ( − x) + ( x x − x) = ( 2 2 4 sin 2 sin cos cos
2 3 sin x − 3 sin x) 1,0
⇔ 2(1− 2sin x) + cos x(2sin x − )
1 = 3 sin x (2sin x − ) 1 2sin x −1 = 0 ⇔ ( 1,0 2 sin x − )
1 ( 3 sin x − cos x + 2) = 0 ⇔ 
 3 sin x − cos x + 2 = 0  π 
+) 3 sin x − cos x + 2 = 0 ⇔ sin x − = 1 −    6  π π π 0,5
⇔ x − = − + k2π ⇔ x = − + k2π , k ∈ . 6 2 3  π x = + k2π 1  6
+) 2sin x −1 = 0 ⇔ sin x = ⇔  (k ∈). 2 5π x = + k2π  6 0,5
Vậy phương trình đã cho có nghiệm π π 5π x = −
+ k2π , x = + k2π , x =
+ k2π (k ∈) 3 6 6
b) (3,5đ) Giải phương trình 2
x + 4 + 3 − x + 12 − x − x = x −1+ 2x + 5 2 ĐK: 5 − − ≤ t 7 x ≤ 3 . Đặt 2 t =
x + 4 + 3 − x ⇒ 12 − x − x = , (t > 0) 0,5 2 2 2 Khi đó phương trình trở t − 7 thành:
+ t = x −1+ 2x + 5 1,0 2
Suy ra t2 + 2t = a2 + 2a với a = 2x + 5, (a ≥ 0) ⇒ (t − a)(t + a + 2) = 0 ⇒ t = a 1,0 P P P P +
Với t = a ta có 2
x + 4 + 3 − x = 2x + 5 ⇔ 12 − x − x = x −1 ⇔ 1 89 x = 1,0 4 2
a) (3,5đ) Có bao nhiêu số tự nhiên có 4 chữ số sao cho trong mỗi số đó có một chữ số
(7,0đ) xuất hiện hai lần, các chữ số còn lại xuất hiện không quá một lần.
+TH1: Chữ số 0 xuất hiện 2 lần Có 2
C cách chọn 2 vị trí cho chữ số 0 3 1,0 Có 2
A cách xếp 2 chữ số trong 9 chữ số vào 2 vị trí còn lại 9 Vậy có 2 2
C .A số có 4 chữ số thỏa mãn trường hợp này. 3 9
+TH2: Chữ số a (khác 0) xuất hiện 2 lần và a ở vị trí đầu tiên (vị trí hàng nghìn) Có 9 cách chọn a
Có 3 cách chọn thêm một vị trí nữa cho a 1,0 Có 2
A cách xếp 2 chữ số trong 9 chữ số vào 2 vị trí còn lại 9 Vậy có 2
9.3.A số có 4 chữ số thỏa mãn trường hợp này. 9
+TH3: Chữ số a (khác 0) xuất hiện 2 lần và a không xuất hiện ở vị trí hàng 1,0 nghìn Có 9 cách chọn a Có 2
C cách chọn 2 vị trí cho chữ số a 3
Có 8 cách chọn một chữ số (khác 0 và khác a) vào vị trí hàng nghìn
Có 8 cách chọn một chữ số vào vị trí còn lại Vậy có 2
9.8.8.C số có 4 chữ số thỏa mãn trường hợp này. 3 Vậy có 2 2 2 2
C .A + 9.3.A + 9.8.8.C = 3888 số thỏa mãn đề bài. 0,5 3 9 9 3
x + 3 = 2 (3y − x)( y + ) 1 (1) b) (3,5đ) 
Giải hệ phương trình  x + 5  3y − 2 −
= xy − 2y − 2 (2)  2 ĐK: 2 y ≥ ; x ≥ 5; − 3y ≥ x 3 x = 6 − y − 9 1,0 2
PT (1) ⇔ (x + 3) = 4(3y − x)( y +1) ⇔ (x + 6 y + 9)(x − 2 y +1) = 0 ⇔  x = 2y −1 TH1: x = 6 − y − 9 0,5 Từ PT (1), x ≥ 3 − → 6 − y − 9 ≥ 3 − ⇔ y ≤ 1
− . Suy ra hệ PT vô nghiệm
TH2: x = 2 y −1. Thay vào PT (2) ta có 2( y − 2) 2 3y − 2 −
y + 2 = 2 y − 3y − 2 ⇔
= (2y +1)(y − 2) 1,0 3y − 2 + y + 2  y = 2  ⇔ 2  = 2 y +1
 3y − 2 + y + 2  1,0 2 2 3 7 PT
= 2y +1 vô nghiệm vì ≤ ; 2 y +1 ≥ 3y − 2 + y + 2 3y − 2 + y + 2 2 3
Vậy hệ PT có nghiệm (x; y) với x = 3, y = 2 3
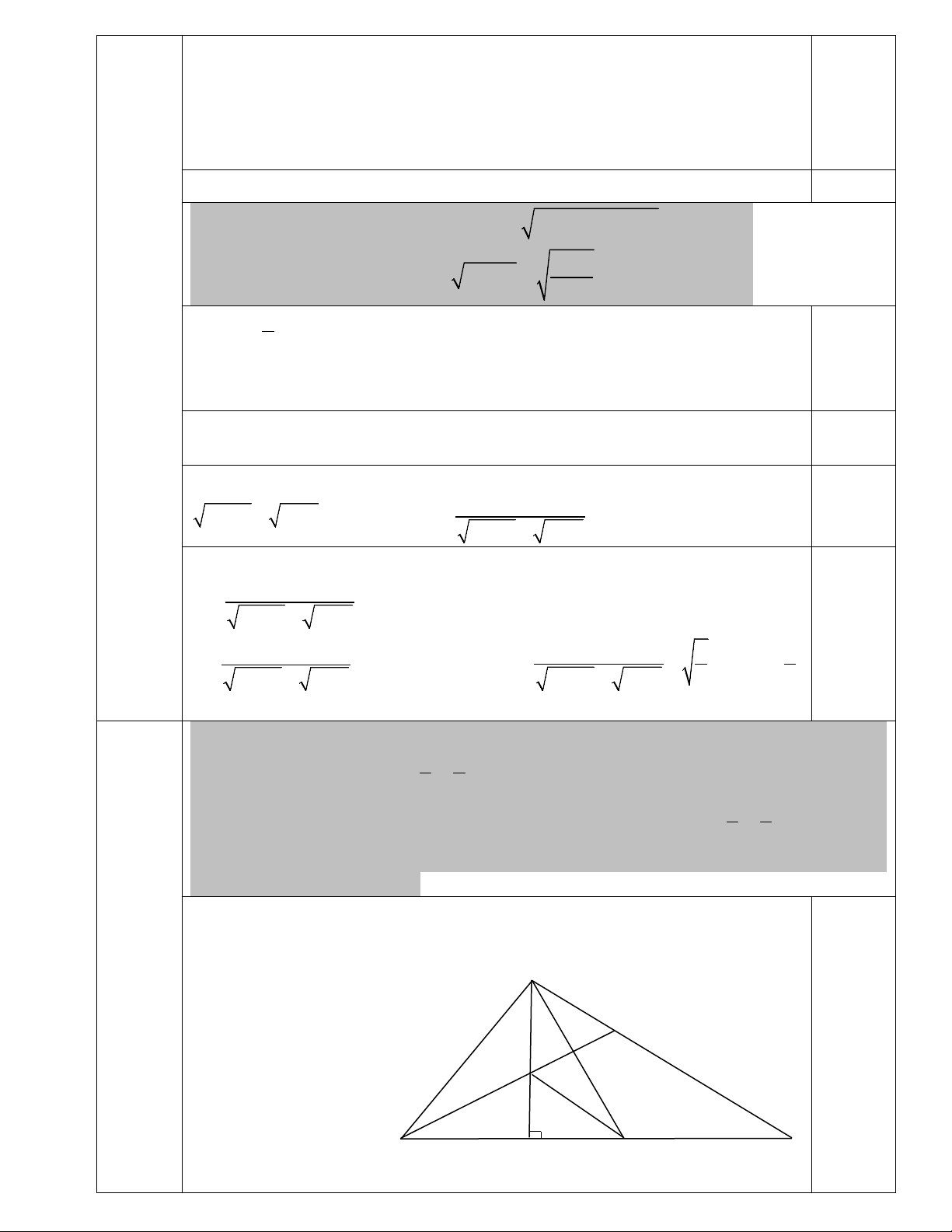
a) (2,0đ) Trong mặt phẳng với hệ trục tọa độ Oxy , cho tam giác ABC vuông tại C , có (4,0đ) 7 7
phân giác trong AD với D( ; − ) thuộc BC . Gọi E và F lần lượt thuộc các cạnh AB 2 2 3 5
và AC sao cho AE = AF Đường thẳng EF cắt BC tại K . Biết E( ; − ) , F có hoành 2 2
độ nhỏ hơn 3 và phương trình đường thẳng AK là x − 2y −3 = 0 . Viết phương trình
các cạnh của tam giác ABC .
Gọi I là giao điểm của AD và EF , suy ra I là trung điểm của EF
Chứng minh DF ⊥ AK A E 0,5 F I B K C D
Phương trình của DF là: 4x + 2y − 7 = 0 7 2t + 3 1− 2t  − t  − t
Gọi F (t; − 2t) ⇒ 3 2 11 2 I ( ; ) ⇒ IE = ( ; 3 − + t), ID = ( ; 4 − + t) 2 4 2 4 4  
Do IE.ID = 0 ⇒ (3 − 2t)(11− 2t) +16(t − 3)(t − 4) = 0  9 t =  1,0 2 2
20t −140t + 225 = 0 ⇔  5 t =  2
Vì F có hoành độ nhỏ hơn 3 nên 5 3
F ( ; − ) ⇒ I (2; 2 − ) 2 2
Do đó đường thẳng AD có phương trình x + y = 0 ⇒ ( A 1; 1 − )
Vậy phương trình đường thẳng chứa các cạnh của tam giác ABC là: 0,5
AC : x + 3y + 2 = 0; AB : 3x + y − 2 = 0; BC : 3x − y −14 = 0
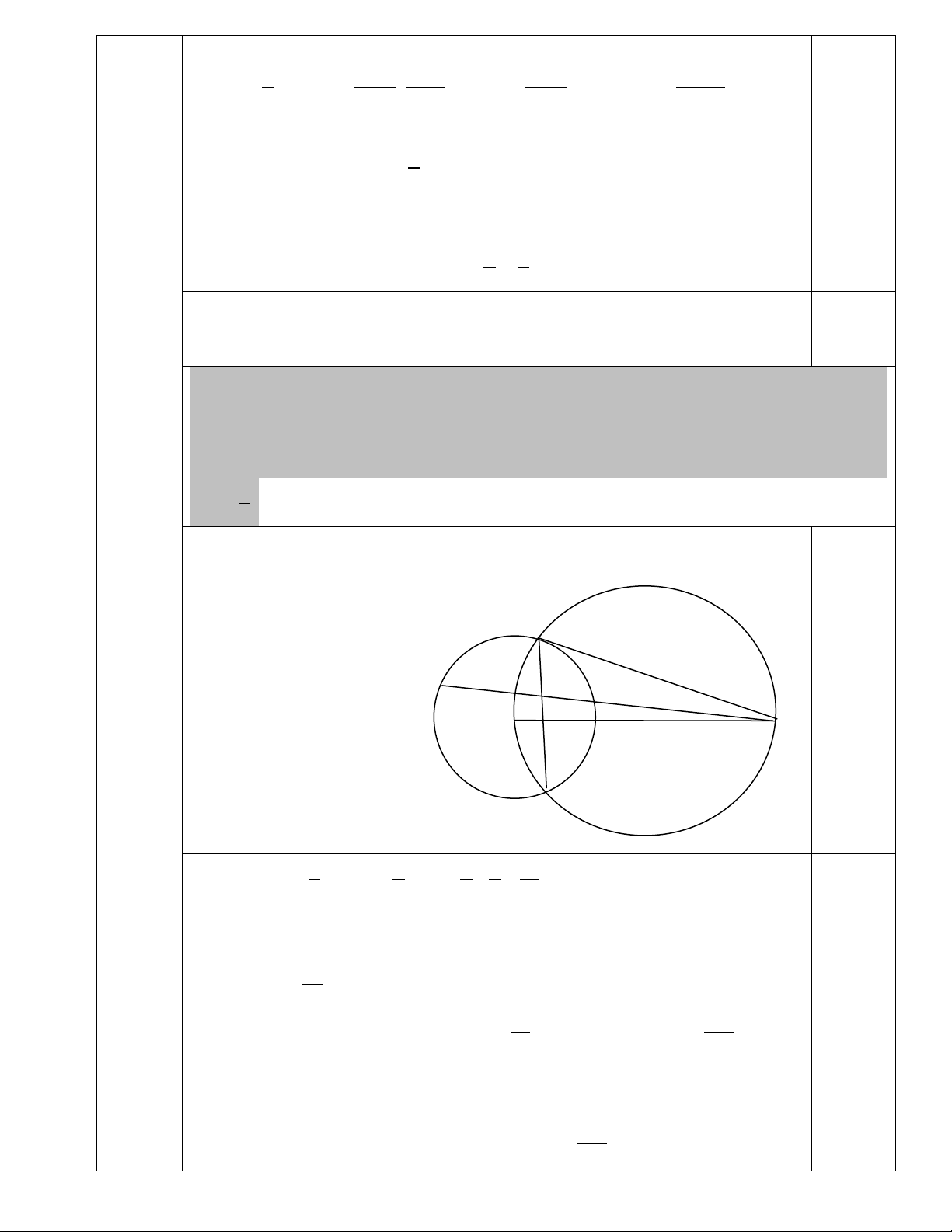
b) (2,0đ) Trong mặt phẳng với hệ trục tọa độ Oxy , cho đường thẳng d : x − y = 0 và
đường tròn (T ) (x − )2 + ( y + )2 : 1 4
= 5 . M là điểm thuộc d , qua M kẻ hai tiếp tuyến ,
MA MB đến (T ) ( ,
A B là các tiếp điểm) và cát tuyến MCD đến đường tròn (T ) với
C nằm giữa M và D ; AB cắt CD tại N . Tìm tọa độ điểm M biết rằng CD = 1 và 5 ND = . 9
+ Gọi K trung điểm DC, I là tâm đường tròn (T), khi đó IK vuông góc CD.
Mà IA vuông góc MA suy ra đường tròn đường kính MI đi qua I, K, A,B.
(Kí hiệu là đường tròn (T’)).
Đường tròn (T) tâm I(1;-4), R2=5. A P P D K N C 0,5 M I B 5 4 1 4 1 + CD = 1, DN =
⇒ NC = , NK = − = . 9 9 2 9 18
N là điểm trong ( T) ta có: ND.NC=NA.NB=20/81
Tương tự vì N trong (T’) : NK.NM=NA.NB=20/81 0,5 40 Suy ra NM = . 9 19 385 Mặt khác 2 2 2 2 2 2 2 2
IK = ID − KD = R − KD =
⇒ IN = IK + KN = 4 81
+ Sử dụng định lý cosintrong tam giác INM ta có: 2 2 2 = + −  2 2 = + +  IM IN NM
2IN.NM .cos(INM ) IN NM
2IN.NM .cos(INK ) (*) 0,5 KN Với cos  = π −  = −  (INM ) cos( INK ) cos(INK ) = − , thay vào (*) ta IN 385 1600 40 2025 có:IM2=IN2+NM2+2NK.NM= + + = = 25 .Vậy IM = 5. P P P P P P 81 81 81 81
Vậy giao của đường tròn (I;5) và (d) cho ta 2 điểm M cần tìm là (1;1) và (- 0,5 4;-4). 4
Cho x, y, z là các số thực dương thỏa mãn x + y + z = 3. Chứng minh rằng: (2,0đ)
x ( y + z)
y ( z + x)
z ( x + y) + + ≥ 2xyz (1) 4 − yz 4 − zx 4 − xy 2
Ta có ( yz + zx + xy ) ≤ ( x + y + z)2 = 9 ⇒ yz + zx + xy ≤ 3 ( ) ( y + z) (z + x) (x + y) 0,5 1 ⇔ + + ≥ (2) yz ( − yz) zx ( − zx) xy ( − xy) 2 4 4 4 Tacó ( y + z) 2 yz 2 2 ≥ = ≥ 0,5 yz (4 − yz)
yz (2 − yz )(2 + yz )  yz 
(2− yz)(2+ yz) 2+ yz Do đó ( y + z) (z + x) (x + y)  1 1 1  + + ≥  + +  ≥ yz ( − yz) zx ( − zx) xy ( − xy) 2 4 4 4
2 + yz 2 + zx 2 + xy   1,0 18 18 ≥ ≥ =
6 + ( yz + zx + xy ) 2 6 + 3
Vậy (2) đúng. Suy ra đpcm.
Ghi chú:Học sinh làm cách khác nếu đúng vẫn cho điểm tối đa.
Document Outline

• Đe-HSG11-Nguyễn-Duy-Trinh-19-20