Đề thi trắc nghiệm ĐS và GT 11 chương 4 (Giới hạn) trường THPT Tô Hiệu – Hà Nội

Đề thi trắc nghiệm ĐS và GT 11 chương 4 (Giới hạn) trường THPT Tô Hiệu – Hà Nội gồm 4 mã đề, mỗi đề gồm 3 trang với 25 câu hỏi trắc nghiệm, thời gian làm bài 45 phút

34 17 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

13 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/13 - Mã đề thi 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
ĐỀ THI TRẮC NGHIỆM
NĂM HỌC 2017 – 2018
M
ôn: Toán - Lớ
p
11
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
105
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..………
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
Câu 1. Xét các mệnh đề sau:
(I).
lim
k
x
x


nếu k là số nguyên dương chẵn.
(II).
lim
k
x
x


với k là số nguyên tuỳ ý.
Trong 2 mệnh đề trên thì
A. Chỉ (II) đúng B. Chỉ (I) đúng C. Cả hai đều sai D. Cả hai đều đúng
Câu 2.
2
3
1
3
lim
2
x
x
x

bằng:
A.
1
B.
2
C.
3
2
D. 2
Câu 3.
2
2
32
lim
1
x
xx
x

bằng:
A. 3 B. 0 C.

D. – 2
Câu 4. Cho dãy số

n
u
thỏa mãn
3
1
2
n
u
n

với mọi
*
nN
. Khi đó:
A.

n
u
không có giới hạn B.
lim 0
n
u
C.
lim 1
n
u
D.
lim 2
n
u
Câu 5. Cho các mệnh đề sau:
(I): Hàm số đa thức liên tục trên tập số thực R
(II): Hàm số

yfx
liên tục tại điểm
0
x
thì

1
fx
liên tục tại điểm
0
x
(III): Nếu hàm số

yfx
liên tục trên

;ab
và

.0fa fb
thì phương trình

0fx
có ít nhất
một nghiệm

;cab
Có bao nhiêu mệnh đề đúng?
A.
2
B.
1
C.
3
D.
0
Câu 6.
1
lim
n
bằng:
A.

B.

C. 0 D. 1
Trang 2/13 - Mã đề thi 105
Câu 7. Cho hàm số
x42
khi x 0
x
f(x)
5
2a khi x 0
4


. Xác định a để hàm số liên tục tại
0
0x ?
A.
3
4
a
B. a = 2 C. a = 1 D. a = 3
Câu 8.
x2
5x 2
lim
x2
bằng:
A.

B.

C. 1 D.
1
Câu 9. Nếu
2
2
45
lim 4
21
x
ax x
xx




thì giá trị của a bằng:
A. Không tồn tại B.
6
C. 4 D.
8
Câu 10. Cho hàm số
2
33
1
()
1
51
xx
khi x
fx
x
khi x
. Hàm số đã cho liên tục?
A.
trên mỗi khoảng
(;5)
và
(5; )
B. Tại x =1
C.
trên mỗi khoảng
(;1)
và
(1; )
D. Trên toàn bộ trục số
Câu 11. Trong các giới hạn sau đây, giới hạn nào bằng -1?
A.
2
32
23
lim .
22
n
nn

B.
5
3
23
lim .
24
n
n

\
C.
2
3
23
lim .
24
n
n

D.
2
2
23
lim .
21
n
n

Câu 12.
Để hàm số
2
2x x 1
khix 1
f(x)
x1
m khix 1

liên tục tại x = 1 thì giá trị của m bằng:
A.
3 B. 4 C. 1 D. 2
Câu 13.
2
x4
x16
lim
x4
bằng:
A.
4 B. 6 C. 8 D. 2
Câu 14.
Cho hàm số

yfx
liên tục trên đoạn

1; 4 và

13f 
;

45f
. Số nghiệm của
phương trình

9fx
trên đoạn

1; 4 là
A.
Có ít nhất một nghiệm B. Có ít nhất hai nghiệm
C.
Không thể kết luận D. Vô nghiệm
Câu 15.
Biết
3
2
1
34
lim , , , 0
34
x
xx a
ab Zb
xx b



. Giá trị nhỏ nhất của
.ab
bằng:
A.
32 B. 12 C. 23 D. 30
Câu 16.
Phương trình
32
23 20xxmx
có ít nhất 1 nghiệm trong khoảng (-1;1) khi:
A.
 33m B.  31;m C.  31m D.
31mm 
Câu 17.
2
3
215
lim
3
x
xx
x

bằng:
A.
-
B. 2 C.
1
8
D. 8
Câu 18.
Số thập phân vô hạn tuần hoàn

1, 7M
được biểu diễn dưới dạng phân số tối giản là
a
b
với
*
;ab N
. Tính
ab
A.
6
B.
25
C.
5
D.
7
Trang 3/13 - Mã đề thi 105
Câu 19. Biết
2
2
0
11
lim
416
x
x
a
x


. Hỏi a là hoành độ đỉnh của parabol nào dưới đây?
A.
2
21616yx x
B.
2
16 16yx x
C.
2
816yx x
D.
2
2816yx x
Câu 20.
Cho hàm số

42
xx
khi x 0
fx
x
mkhix0
.
Với giá trị nào của m thì hàm số đã cho liên tục tại
x0
.
A.
m1
B. Không có m C.
m1
D. m = 1
Câu 21.

x
2
x1
lim
x1
bằng:
A.
1 B. 1 C.
0
D.

Câu 22.
2
2
lim
2
nn
x
x
x
bằng:
A.
1
(n 1).2
n
B.
1
n.2
n
C.
n.2
n
D.
(n 1).2
n
Câu 23.
Biết hàm số

3
111
0
10
ax bx
khi x
fx
x
ab khix


, (a,b là các số thực dương khác 0)
liên tục tại điểm
0x
. Tìm giá trị lớn nhất của biểu thức .Pab .
A.
3
4
B.
36
49
. C.
5
9
. D.
5
.
Câu 24.
Biết

2
2
4133
lim . 4 , 0
1
xa
xx
ba
x
xa
xx






. Trong các mệnh đề sau, mệnh đề nào đúng:
A.
5ba
B.
ba
C.
,0ab
D.
24ab
Câu 25.
Cho tam giác đều
A
BC
có cạnh bằng . Người ta dựng tam giác đều
111
ABC có cạnh bằng
đường cao của tam giác
A
BC
; dựng tam giác đều
222
ABC có cạnh bằng đường cao của tam giác
111
ABC và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích
của tất cả các tam giác đều
111 2 2 2
,, ...ABC A B C A B C bằng 18 3 thì a bằng:
A.
23. B. 2 . C.
32
D. 3.
---------- HẾT ----------
a
S
Trang 4/13 - Mã đề thi 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
ĐỀ THI TRẮC NGHIỆM
NĂM HỌC 2017 – 2018
M
ôn: Toán - Lớ
p
11
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
201
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..………
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
Câu 1.
Trong các dãy số sau đây, dãy số nào có giới hạn bằng 0?
A.


0, 23
n
B.


3
n
C.


1, 99
n
D.


1
n
Câu 2.
Cho hàm số
x3
f(x)
x2
. Hàm số f(x) không liên tục tại điểm nào trong các điểm sau:
A.
x = 2
B.
x = 0
C.
x = 3
D.
x =
3
2
Câu 3. Cho hàm số

yfx
có đồ thị như hình
b
ên: Tính

lim
x
fx

A.

B.
0
C.
2
D.

Câu 4.
Trong các mệnh đề sau, mệnh đề nào sai ?
A.
5
0
1
lim
x
x

B.
0
1
lim
x
x
 C.
0
1
lim
x
x

D.
0
1
lim
x
x

Câu 5.
3
2
lim
x
x

bằng:
A.

B.

C.

D.
0
Câu 6.
3
lim(2 3 )nn
bằng:
A.

B.

C.
2
D.
3
Câu 7.
Tìm khẳng định đúng.
Phương trình:
3
4410xx
:
A.
Chỉ có hai nghiệm phân biệt thuộc

0;1
B.
Có ba nghiệm phân biệt thuộc

0;1
C.
Vô nghiệm trên

0;1
D.
Chỉ có một nghiệm thuộc

0;1
Câu 8.
2
3
lim(5 7 )
x
xx
bằng:
Trang 5/13 - Mã đề thi 105
A.

B.  C. 0 D. 24
Câu 9.
12
lim
12
n
n
bằng:
A.
∞ B.
1 C. 3 D. +
∞
Câu 10.
Cho hàm số
3
3
()
12
3
x
khi x
fx
x
mkhix

. Hàm số đã cho liên tục tại x = 3 khi m bằng?
A.
– 4 B. 4 C. – 1 D. 1
Câu 11.

3
x
lim 2x 4x 3


bằng:
A.
- 2 B. 2 C.

D.

Câu 12.
Cho hàm số
2
2x 2x
khi x 1
f(x)
x1
5khix1
. Hàm số đã cho liên tục:
A.
Trên tập R B. trên mỗi khoảng

;5
và

5; 
C.
Tại điểm x = 1 D. trên mỗi khoảng

;1
và

1; 
Câu 13.
Giả sử

0
lim
x
fx

và

0
lim
x
gx

, xét các mệnh đề sau
(I):
 
0
lim
x
fx gx


(II):


0
lim 1
x
fx
gx

(III):
 
0
lim 0
x
fx gx


Có bao nhiêu mệnh đề đúng?
A.
Cả ba mệnh đề đều đúng B. Không có mệnh đề nào đúng
C.
Chỉ có một mệnh đề đúng D. Có hai mệnh đề đúng
Câu 14.
Nếu
2
2017
2017
lim 1
2017
x
xax
x


thì giá trị a bằng:
A.
1009
B.
2016
C.
2020
D.
2017
Câu 15.
Cho hàm số
2
x16
khix 4
f(x)
x4
7khix4
. Chọn khẳng định sai.
A.
Với x4 thì f(4) = 7
B.
Hàm số liên tục tại mọi x thuộc tập R
C.
Phải gán cho f(4) = 8 thì hàm số mới liên tục tại mọi x thuộc tập R
D.
Với x4 thì f(x) = x + 4
Câu 16.
Số thập phân vô hạn tuần hoàn 0,5111… được biểu diễn bằng phân số:
A.
43
90
B.
47
90
C.
6
11
D.
46
90
Câu 17.
Biết hàm số

2
0
2
10
xx
khi x
fx
x
mkhix

liên tục tại điểm
0
x
khi
0
mm . Tính

0
f
m
A.
1
2
B.
5
4
C.
1
2
D.
3
2
Trang 6/13 - Mã đề thi 105
Câu 18.
23 11
6
11
( 1).( 1).(x 1)...(x 1)
lim
(11 ) 1
x
xx
x




bằng:
A.
1
66
B.
66
11 C.
11
1
66
D.
66
1
11



Câu 19.

3
3
11 1
lim .
3
3
x
x
x



A.
không tồn tại B.  C.  D. 0
Câu 20.
Số nghiệm của phương trình:
11 1
0
xxaxb


với
;0ab
là:
A.
2 B.
3
C. 1 D.
0
Câu 21.
Cho hàm số

23
2
4
x
fx
x
. Tìm khẳng định đúng:
A.
không tồn tại

0
lim
x
f
x
B.

0
lim
x
fx

C.

0
lim 1
x
fx
D.

0
lim 0
x
fx
Câu 22.
22
x
lim x 3x 3 x 8x


bằng:
A.

B. 5 C.
5
2
D.

Câu 23.
Nếu phương trình:

2
0,ax b c x d e

,,,abcd R
có nghiệm
0
1x thì phương
trình:

0fx với

432
f
xaxbxcxdxe
cũng có nghiệm. Khi đó, mệnh đề nào sau đây
đúng:
A.


2
000
.1fxf x x
B.

00
.0fxf x
C.

00
.0fxf x
D.


2
0000
.1
f
xf x x bxd
Câu 24.
Tổng
15 32
... ...
636 6
nn
n
S




có giá trị bằng:
A.
1
2
B. 1 C.
3
4
D.
2
3
Câu 25.
Nếu

2
5
lim 2
2
x
fx
x
thì
 
3
2
1. 5 2 6
lim
2
x
fx fx
x

bằng:
A.
21 B.
63
2
C. Đáp số khác D.
67
18
---------- HẾT ----------
Trang 7/13 - Mã đề thi 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
ĐỀ THI TRẮC NGHIỆM
NĂM HỌC 2017 – 2018
M
ôn: Toán - Lớ
p
11
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
302
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..………
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
Câu 1.
23
3
3
lim
252
nn
nn

bằng:
A.
1
5
B.
3
2
C. 0 D.
1
2
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng:
A. Hàm số đa thức liên tục trên toàn bộ tâp số thực
B. Hàm số phân thức hữu tỉ liên tục trên toàn bộ tâp số thực
C. Hàm số lượng giác liên tục trên toàn bộ tâp số thực
D. Hàm số đa thức không liên tục trên toàn bộ tâp số thực
Câu 3. Trong các mệnh đề sau, mệnh đề nào sai?
A.
k
x
1
lim 0vôùi k nguyeândöông
x

B.
k
x
lim x vôùiknguyeândöông


C.
k
x
lim x vôùiknguyeândöông

 D.
k
x
1
lim 0vôùi k nguyeândöông
x

Câu 4. Trong các mệnh đề sau, mệnh đề nào sai?
A.
0
1
lim
x
x

B.
0
1
lim
x
x

C.
0
1
lim
x
x

D.
5
0
1
lim
x
x

Câu 5. Cho c là hằng số, k là số nguyên dương khác không. Tìm khẳng định sai.
A.
lim
k
x
x


B.
lim
k
x
x


C.
0
0
lim
xx
xx
D.
0
lim
xx
cc
Câu 6.
2
lim
3n
bằng:
A.
+
∞
B.
2
C.
2
3
D.
0
Câu 7. Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Trong các mệnh đề sau, mệnh đề nào đúng:
A. Hàm số liên tục trên khoảng

;2; 2;2
và
2; 
B. Hàm số liên tục trên khoảng

;2
C. Hàm số liên tục trên khoảng
2;
D. Hàm số lên tục trên

\2
Trang 8/13 - Mã đề thi 105
Câu 8. Tổng của cấp số nhân lùi vô hạn
(u )
n
với
1
u
3
n
n
là:
A.
1 B. 2 C.
1
2
D.
1
3
Câu 9.
Hàm số

1
2
3
fx x
x

liên tục trên
A.
3; 2 B.
3; 2 C.

;3 2;  D.

3; 2
Câu 10.
Cho hàm số
3
11
()
11
x
fx
x


chưa xác định tại x = 0. Tìm f(0) để hàm số trên liên tục tại điểm x
= 0?
A.
1
2
B.
3
2
C.
0 D. Không tồn tại f(0)
Câu 11.
53
54
x
3x 7x 11
lim
xx3x



bằng:
A.
0 B. 3 C.

D. -3
Câu 12.
4
1
lim
32
x
x
x
bằng:
A.
3 B.
2 C.
1
3
D.
1
2
Câu 13.
1
31
lim
1
x
x
x

bằng:
A.

B.

C.
2
D.
2
Câu 14.
2
32
2
56
lim
2
x
xx
xxx


bằng:
A.
0 B.
1
7
C. -7 D.

Câu 15.
33
lim
2
nn
n
bằng:
A.
2 B. 0 C.
1
2
D. 1
Câu 16.
Cho hàm số
1
f(x)
x1
.Chọn kết quả
sai:
A.
x3
2
limf(x)
2
B. Hàm số liên tục tại mọi điểm x1
C.
Hàm số liên tục tại mọi

x1;
D.
x2
limf(x) 1
Câu 17.

32
lim 3 5 7 ?
x
xx


A.

B.

C. 3 D. 0
Câu 18.
Cho hàm số

22
32 1fx ax x x
. Tìm tất cả các giá trị của tham số để
lim
x
fx


.
A.
. B.
;2a 
. C.
2;a 
. D.
2a
Câu 19.
Cho hàm số:
2
2
ax 2
()
12
khi x
fx
xx khix

để f(x) liên tục trên R thì a bằng?
a
a
Trang 9/13 - Mã đề thi 105
A.
5
4
B. 4 C. 3 D. 2
Câu 20.
Tìm các giá trị của a để hàm số

2
43
3
xx
fx
x
a

khi
khi
3
3
x
x
liên tục tại
3
x
A.
1
B.
2
C.
4
D.
2
Câu 21.

2
x1
2x 1
lim
x1
bằng:
A.

B.

C. 2 D. 1
Câu 22. Biết
2
2
1
21
lim
1
x
xx
a
x

. Hỏi a không là nghiệm của bất phương trình nào sau đây:
A.
2
10xx
B.
210
x

C.
2
560xx
D.
2
30xx
Câu 23.
Biết hàm số

3
111
0
20
ax bx
khi x
fx
x
ab khix


, (a,b là các số thực dương khác 0)
liên tục tại điểm
0x . Tìm giá trị lớn nhất của biểu thức
.Pab
.
A.
3
4
B.
36
49
. C.
5
9
. D.
3
.
Câu 24.
Biết

2
2
18121
lim . 8 10 2 1
16
21
xa
xx x
xx
xa

 



và

2
2
4
lim . 2 2
xb
x
xxc
xb

với a,b,c là các số thực. Trong các mệnh đề sau, mệnh đề nào sai:
A.
abc
B.
22
54ab c
C.
10ac b
D.
bc a
Câu 25.
Cho hình vuông
1
C
có cạnh bằng
a
. Người ta chia mỗi cạnh của
hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích
hợp để có hình vuông
2
C (Hình vẽ). Từ hình vuông
2
C lại tiếp tục làm
như trên ta nhận được dãy các hình vuông
123
, , ,..., ,...
n
CCC C .Gọi
i
S
là diện tích của hình vuông

1; 2; 3; ...
i
Ci
. Tính tổng

123
... ...
n
SS S S S
A.
2
2.a
B.
2
22.a
C.
2
8
3
a
D.
2
5
.
2
a
---------- HẾT ----------
Trang 10/13 - Mã đề thi 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
ĐỀ THI TRẮC NGHIỆM
NĂM HỌC 2017 – 2018
M
ôn: Toán - Lớ
p
11
ĐỀ CHÍNH THỨC Thời gian: 45 phút (Không kể thời gian phát đề)
Mã đề thi
401
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..………
1
6
11
16
21
2
7
12
17
22
3
8
13
18
23
4
9
14
19
24
5
10
15
20
25
Câu 1. lim
n
q bằng:
A. +
∞ n
ếu |q| ≥ 1 B. 0 nếu |q| < 1 C. 0 nếu |q| > 1 D. 0 nếu |q| ≤ 1
Câu 2. Chọn mệnh đề sai trong các mệnh đề sau.
A.
lim cc
với c là hằng số B.
1
lim 0
k
n
với k nguyên dương
C.
1
lim 0
n
D.
lim 0
k
n
với k nguyên dương
Câu 3. Chọn khẳng định đúng
A.
 
0
0
lim lim
xx
xx
fx a fx a

B.
 
0
0
lim lim
xx
xx
fx a fx a

C.
  
0
00
lim lim lim
xx
xx xx
fx a fx fx a



D.
  
0
00
lim lim lim
xx
xx xx
fx a fx fx



Câu 4. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hàm số chứa căn bậc hai liên tục trên toàn bộ tập số thực R.
B. Hàm số đa thức liên tục trên toàn bộ tập số thực R.
C. Hàm số lượng giác liên tục trên toàn bộ tập số thực R.
D. Hàm số phân thức liên tục trên toàn bộ tập số thực R.
Câu 5.
2
65
23
lim
5
x
x
xx

bằng:
A. 0 B.
3
C.
3
5
D. 2
Câu 6. Giới hạn của hàm số:
1
lim(9 )
x
x
bằng:
A. 10 B.
∞ C. +
∞
D. 9
Câu 7. Biết dãy số

n
u
thỏa mãn
n
2
1
u3
n
 với mọi
*
nN
. Khẳng định nào sau đây đúng?
A.
n
lim u 3
B.
n
limu 3
C.
n
lim u 1
D.
n
lim u 2
Câu 8. Nếu
lim 9
n
u
thì
2018
lim
7
n
u
bằng
A.
504,5
B.
126,125
C.
2018
D.
224,2
Câu 9. Cho phương trình:
5
10xx
(1). Trong các mệnh đề sau, mệnh đề nào sai?
A. (1) có nghiệm trên khoảng (-1; 1) B. (1) có nghiệm trên khoảng (0; 1)
C. (1) có nghiệm trên R D. Vô nghiệm
Câu 10.
1
2.3 5
lim
25
nn
nn
bằng:
A.

B.
0
C.
1
D.
5
Trang 11/13 - Mã đề thi 105
Câu 11. Cho hàm số
2
4
2
()
2
2
x
khi x
fx
x
mkhix
. Hàm số đã cho liên tục tại x
0
= 2 khi m bằng:
A.
-1 B. -4 C. 4 D. 1
Câu 12. Câu nào sau đây sai
A.
Hàm số

f
x liên tục trên

;ab nếu nó liên tục tại mọi điểm thuộc

;ab
B.
Cho hàm số
f
x
có miền xác định D,
aD
. Hàm số liên tục tại điểm x = a nếu

lim
xa
f
xfa
C.
Tổng, hiệu, tích, thương của hai hàm số liên tục tại một điểm là một hàm số liên tục tại điểm đó
D.
Các hàm số phân thức hữu tỉ liên tục trên từng khoảng của tập xác định
Câu 13. Chọn khẳng định sai trong các khẳng định sau:
A.
Hàm số

2
x5x2
y lieântuïctreâncaùckhoaûng ;2 , 2;
x2


B.
Hàm số
2
x4
khix 2
f(x)
x2
3 khix 2


liên tục tại điểm x = -2
C.
Hàm số
2
yx8
liên tục tại điểm x= 1
D.
Hàm số
ysinx
liên tục trên R
Câu 14.
32
31
lim
42
n
nn n
n


bằng:
A.
0 B.  C.
1
4
D. 
Câu 15.
Cho hàm số
2
2
65
1
1
()
5
1
2
xx
khi x
x
fx
akhix


. Tìm a để hàm số liên tục tại x = 1.
A.
a = 2 B.
9
2
a

C.
3
2
a
D. a = 0
Câu 16.
Tính
3
0
1.1 1
lim
x
ax bx
x

theo a; b
A.
32
ab
B.
23
ab
C.
32
ab
D.
23
ab
Câu 17.
2
2
4
lim
2
x
x
x
bằng:
A.
Không tồn tại B. 4 C.

D.
0
Câu 18.



x
4
sinx cosx
lim
tan x
4
bằng:
A.
2
B.

C. 0 D.
1
2
Trang 12/13 - Mã đề thi 105
Câu 19. Cho hàm số y = f(x) có đồ thị như hình vẽ
b
ên. Trong các
m
ệnh đề sau, mệnh đề nào sai:
A.
lim 2
x
fx

B.
lim 2
x
fx

C.
1
lim 0
x
fx
D.
4
lim
x
fx

Câu 20.
Cho hàm số
3
f(x) 3x 3x 2
. Trong các mệnh đề sau, mệnh đề nào sai?
A.
Phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (0; 1)
B.
Phương trình f(x) = 0 vô nghiệm trong khoảng (0; 1)
C. Phương trình f(x) = 0 có nhiều nhất là 3 nghiệm
D. Phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (-1; 1)
Câu 21.
Khi x tiến tới  , hàm số
2
() ( 2 )
f
xxxxcó giới hạn bằng:
A.
1 B. 0 C. + D. 
Câu 22.
Biết hàm số

32 32
2
22 4
7
2
200
ab
khi x
xxx xx
fx
a
khi x



liên tục tại điểm
2x
. Tìm hệ
thức liên hệ giữa a và b.
A.
580ab
B.
30ab
C.
230ab
D. 850ab
Câu 23.
Nếu

1
5
lim 2
1
x
fx
x
và

1
1
lim 3
1
x
gx
x
thì
 
1
.43
lim
1
x
fxgx
x

bằng:
A.
17
6
B.
17
C.
7
D.
23
7
Câu 24.
Nếu phương trình:

2
0,ax b c x d e

,,,abcd R
có nghiệm
0
1x thì phương trình:

0fx
với

432
f
xaxbxcxdxe cũng có nghiệm. Khi đó, mệnh đề nào sau đây đúng:
A.

00
.0fxf x
B.


2
0000
.1
f
xf x x bxd
C.


2
000
.1fxf x x
D.

00
.0fxf x
Câu 25.
Một quả bóng tenis được thả từ độ cao

81 m
. Mỗi lần chạm đất, quả bóng nảy lên cao bằng hai
phần ba độ cao của lần rơi trước. Tính tổng các khoảng cách rơi và nảy lên của quả bóng từ lúc thả đến khi
quả bóng không nảy nữa.
A.

524 m
B.

243 m
C.

405 m
D.

486 m
---------- HẾT ----------
Trang 13/13 - Mã đề thi 105
ĐÁP ÁN
Mã đề [105]
1B 2B 3A 4D 5A 6C 7A 8B 9D 10C 11D 12A 13C 14C 15D
16D 17A 18C 19A 20B 21B 22B 23A 24D 25C
Mã đề [201]
1A 2A 3B 4C 5D 6B 7A 8D 9B 10A 11C 12D 13C 14C 15B
16D 17B 18D 19B 20A 21A 22C 23C 24A 25D
Mã đề [302]
1B 2A 3C 4A 5B 6D 7A 8C 9A 10B 11D 12D 13C 14B 15D
16B 17B 18C 19A 20D 21A 22C 23D 24A 25C
Mã đề [401]
1B 2D 3C 4B 5A 6A 7A 8A 9D 10D 11C 12C 13B 14D 15B
16B 17A 18A 19C 20B 21C 22D 23A 24D 25C
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

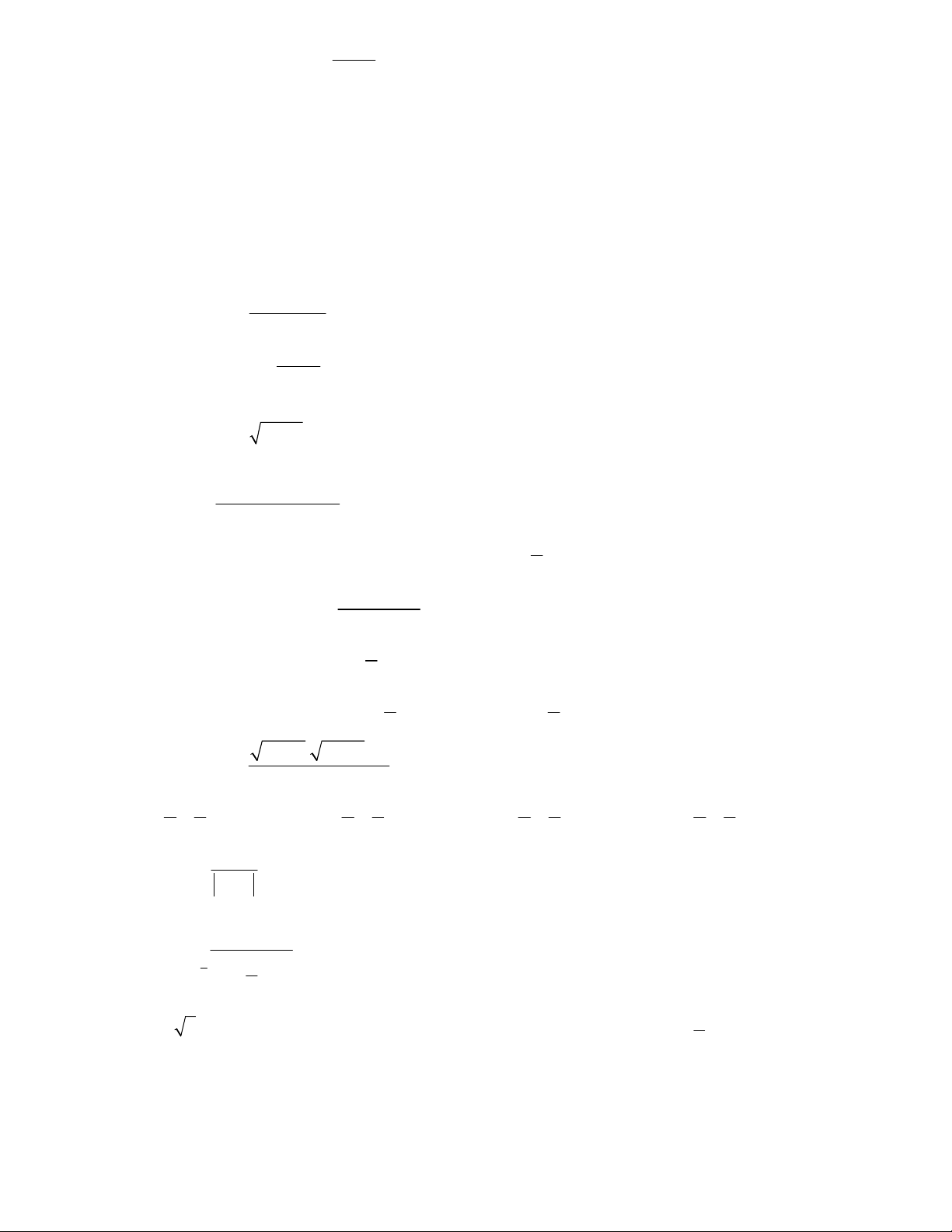
Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI TRẮC NGHIỆM
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
NĂM HỌC 2017 – 2018 Môn: Toán - Lớp 11 ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..……… 105 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25
Câu 1. Xét các mệnh đề sau: (I). lim k
x   nếu k là số nguyên dương chẵn. x (II). lim k
x   với k là số nguyên tuỳ ý. x
Trong 2 mệnh đề trên thì
A. Chỉ (II) đúng
B. Chỉ (I) đúng
C. Cả hai đều sai
D. Cả hai đều đúng 2 x  3 Câu 2. lim bằng: 3 x 1  x  2 3 A. 1 B. 2 C. D. 2 2 2 3x  2x Câu 3. lim bằng: 2 x x 1 A. 3 B. 0 C.  D. – 2 1
Câu 4. Cho dãy số u thỏa mãn u  2  với mọi *
n N . Khi đó: n n 3 n
A. u không có giới hạn
B. limu  0 n n
C. lim u  1
D. lim u  2 n n
Câu 5. Cho các mệnh đề sau:
(I): Hàm số đa thức liên tục trên tập số thực R 1
(II): Hàm số y f x liên tục tại điểm x thì
liên tục tại điểm x 0 f x 0
(III): Nếu hàm số y f x liên tục trên a;b và f a. f b  0 thì phương trình f x  0 có ít nhất
một nghiệm c  ; a b
Có bao nhiêu mệnh đề đúng? A. 2 B. 1 C. 3 D. 0 1
Câu 6. lim bằng: n A.  B.  C. 0 D. 1
Trang 1/13 - Mã đề thi 105  x  4  2  khi x  0  Câu 7. Cho hàm số x f (x)  
. Xác định a để hàm số liên tục tại x  0 ? 5 0 2a  khi x  0  4 3
A. a B. a = 2 C. a = 1 D. a = 3 4 5x  2 Câu 8. lim bằng:  x2 x  2 A.  B.  C. 1 D. 1 2 ax  4x  5 Câu 9. Nếu lim  4
 thì giá trị của a bằng: 2
x 2x x 1
A. Không tồn tại B. 6  C. 4 D. 8  2 3x  3xkhi x  1
Câu 10. Cho hàm số f (x)   x 1
. Hàm số đã cho liên tục?  5 khi x  1
A. trên mỗi khoảng ( ;
 5) và (5;) B. Tại x =1
C. trên mỗi khoảng (;1) và (1; )
D. Trên toàn bộ trục số
Câu 11. Trong các giới hạn sau đây, giới hạn nào bằng -1? 2 2n  3 5 2n  3 2 2n  3 2 2n  3 lim . lim . lim . lim . A. 3 2 2
n  2n B. 3 2  n  4 \ C. 3 2  n  4 D. 2 2  n 1 2 2x  x 1  khi x  1
Câu 12. Để hàm số f(x)   x 1
liên tục tại x = 1 thì giá trị của m bằng:  m khi x  1 A. 3 B. 4 C. 1 D. 2 2 x 16 Câu 13. lim bằng: x4 x  4 A. 4 B. 6 C. 8 D. 2 Câu 14.       Cho hàm số y
f x liên tục trên đoạn  1;4 và f   1
3; f 4 5 . Số nghiệm của
phương trình f x  9 trên đoạn  1;  4 là
A. Có ít nhất một nghiệm
B. Có ít nhất hai nghiệm
C. Không thể kết luận D. Vô nghiệm 3 x  3x  4 a
Câu 15. Biết lim
 ,a,b Z,b 0 . Giá trị nhỏ nhất của . a b bằng: 2 x 1
x  3x  4 b A. 32 B. 12 C. 23 D. 30
Câu 16. Phương trình 3 2
2x  3x mx  2  0 có ít nhất 1 nghiệm trong khoảng (-1;1) khi:
A. 3  m  3
B. 3  m  1;
C. 3  m  1 D. m  3   m  1  2 x  2x 15 Câu 17. lim bằng: x 3  x  3 1 A. -  B. 2 C. D. 8 8 a
Câu 18. Số thập phân vô hạn tuần hoàn M  1,7 được biểu diễn dưới dạng phân số tối giản là với b *
a;b N . Tính a b A. 6 B. 2 5 C. 5 D. 7
Trang 2/13 - Mã đề thi 105 2 x 1 1 Câu 19. Biết lim
a . Hỏi a là hoành độ đỉnh của parabol nào dưới đây? x0 2 4  x 16 A. 2
y  2x 16x 16 B. 2
y x 16x 16 C. 2
y x  8x 16 D. 2
y  2x  8x 16  4  2 x x
Câu 20. Cho hàm số    khi x   0 f x  x .  m khi x  0
Với giá trị nào của m thì hàm số đã cho liên tục tại x  0 . A. m  1 B. Không có m C. m  1 D. m = 1 x 1 Câu 21. lim bằng: x 2 x 1 A. 1 B. 1 C. 0 D.  n x  2n Câu 22. lim bằng: x2 x  2 A. 1 (n 1).2n  B. 1 n.2n C. n.2n D. (n 1).2n 3
ax 1 bx 1 1  khi x  0
Câu 23. Biết hàm số f x   x
, (a,b là các số thực dương khác 0)
a b 1 khi x  0
liên tục tại điểm x  0 . Tìm giá trị lớn nhất của biểu thức P  . a b . 3 36 5 A. B. . C. . D. 5 . 4 49 9 4  x 1 3x  3  Câu 24. Biết lim . 4  
  b, a  0 . Trong các mệnh đề sau, mệnh đề nào đúng:
xa x a2 2  x x 1 x
A. b a  5
B. b a
C. a,b  0
D. 2a b  4 
Câu 25. Cho tam giác đều ABC có cạnh bằng a . Người ta dựng tam giác đều A B C có cạnh bằng 1 1 1
đường cao của tam giác ABC ; dựng tam giác đều A B C có cạnh bằng đường cao của tam giác 2 2 2
A B C và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích S 1 1 1
của tất cả các tam giác đều ABC, A B C , A B C ... bằng 18 3 thì a bằng: 1 1 1 2 2 2 A. 2 3 . B. 2 . C. 3 2 D. 3 .
---------- HẾT ----------
Trang 3/13 - Mã đề thi 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI TRẮC NGHIỆM
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
NĂM HỌC 2017 – 2018 Môn: Toán - Lớp 11 ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..……… 201 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25
Câu 1. Trong các dãy số sau đây, dãy số nào có giới hạn bằng 0? n
A.  0,23n
B.  3 
C.  1,99n D.   1 n x  3
Câu 2. Cho hàm số f(x) 
. Hàm số f(x) không liên tục tại điểm nào trong các điểm sau: x  2 3 A. x = 2 B. x = 0 C. x = 3 D. x =  2
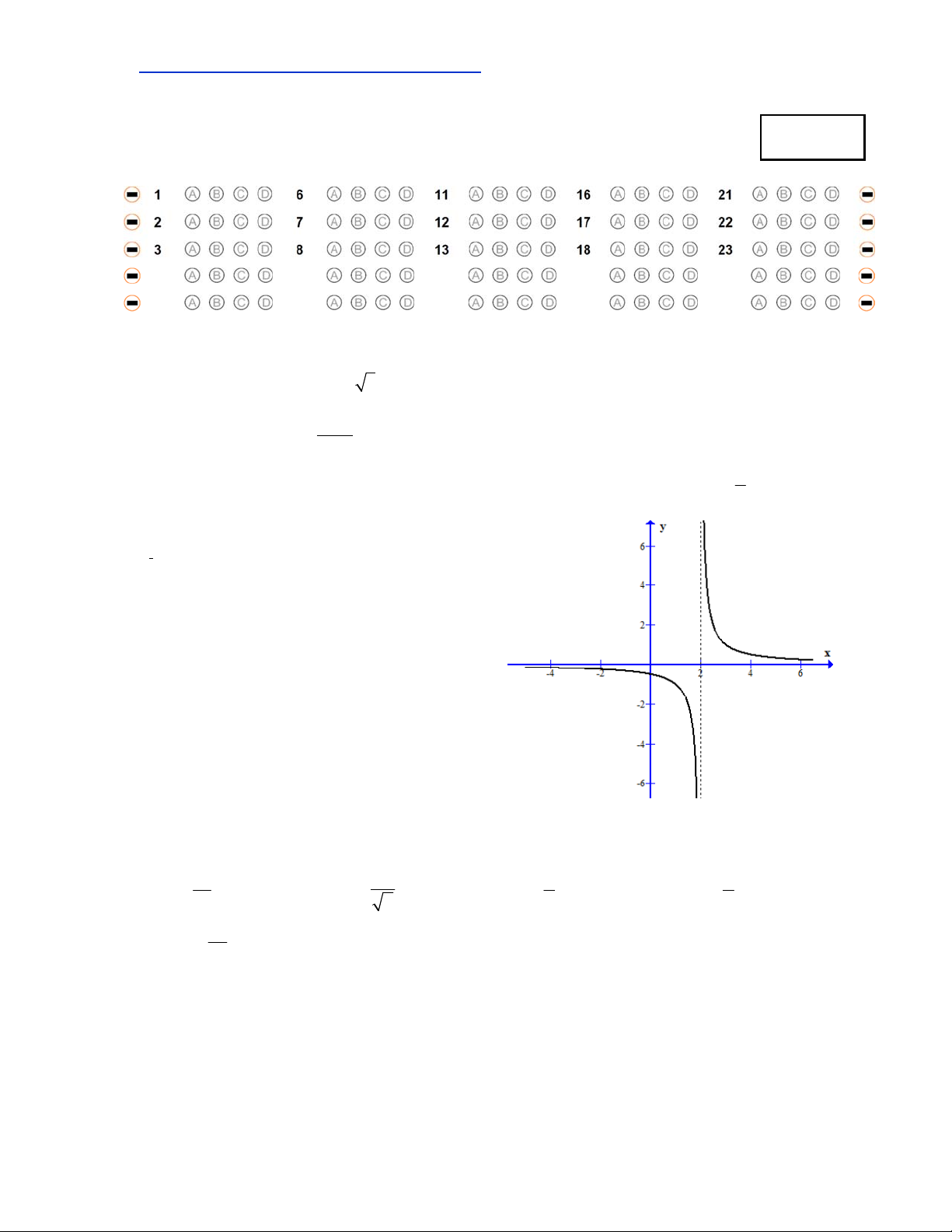
Câu 3. Cho hàm số y f x có đồ thị như hình
bên: Tính lim f xx A.  B. 0 C. 2 D. 
Câu 4. Trong các mệnh đề sau, mệnh đề nào sai ? 1 1 1 1 A. lim   B. lim  
C. lim   D. lim    5 x0 x x 0  x x0 x x 0  x 2 Câu 5. lim bằng: 3 x x A.  B.  C.  D. 0 Câu 6. 3
lim(2n 3n ) bằng: A.  B.  C. 2 D. 3 
Câu 7. Tìm khẳng định đúng. Phương trình: 3 4
x  4x 1  0 :
A. Chỉ có hai nghiệm phân biệt thuộc 0; 
1 B. Có ba nghiệm phân biệt thuộc 0;  1
C. Vô nghiệm trên 0;  1
D. Chỉ có một nghiệm thuộc 0;  1 Câu 8. 2
lim(5x  7x) bằng: x3
Trang 4/13 - Mã đề thi 105 A.   B.  C. 0 D. 24 nCâu 9. 1 2 lim bằng: 1 2n A.  ∞ B.  1 C. 3 D. +∞  3  xkhi x  3
Câu 10. Cho hàm số f (x)   x 1  2
. Hàm số đã cho liên tục tại x = 3 khi m bằng? m khi x  3 A. – 4 B. 4 C. – 1 D. 1 Câu 11. lim  3
2x  4x  3 bằng: x A. - 2 B. 2 C.  D.  2 2x  2x  khi x  1
Câu 12. Cho hàm số f (x)   x 1
. Hàm số đã cho liên tục: 5  khi x  1
A. Trên tập R
B. trên mỗi khoảng  ;5
  và5;
C. Tại điểm x = 1
D. trên mỗi khoảng   ;1
 và 1;
Câu 13. Giả sử lim f x   và lim g x   , xét các mệnh đề sau x 0  x 0  f x
(I): lim  f x  g x     (II): lim  1 x 0  x 0  g x (III): lim  f
  x  g x  0  x 0 
Có bao nhiêu mệnh đề đúng?
A. Cả ba mệnh đề đều đúng
B. Không có mệnh đề nào đúng
C. Chỉ có một mệnh đề đúng
D. Có hai mệnh đề đúng 2
x ax  2017 Câu 14. Nếu lim  1
 thì giá trị a bằng: x2017 x  2017 A. 1009 B. 2016 C. 2020 D. 2017 2 x 16  khi x  4
Câu 15. Cho hàm số f(x)   x  4
. Chọn khẳng định sai.  7 khi x  4
A. Với x  4 thì f(4) = 7
B. Hàm số liên tục tại mọi x thuộc tập R
C. Phải gán cho f(4) = 8 thì hàm số mới liên tục tại mọi x thuộc tập R
D. Với x  4 thì f(x) = x + 4
Câu 16. Số thập phân vô hạn tuần hoàn 0,5111… được biểu diễn bằng phân số: 43 47 6 46 A. B. C. D. 90 90 11 90 2  x xkhi x  0
Câu 17. Biết hàm số f x   2x
liên tục tại điểm x  0 khi m m . Tính f m 0  0
m 1 khi x  0 1 5  1 3 A. B. C. D. 2 4 2 2
Trang 5/13 - Mã đề thi 105 2 3 11
(x 1).(x 1).(x 1)...(x 1) Câu 18. lim bằng: 6 x 11 (11x) 1   1 1 66  1  A. B. 66 11 C. D.   66 11 66 11  1 1  1 Câu 19. lim  .  
x  x 3   x  33 3
A. không tồn tại B.  C.  D. 0 1 1 1
Câu 20. Số nghiệm của phương trình:    0 với ; a b  0 là: x x a x b A. 2 B. 3 C. 1 D. 0 2x
Câu 21. Cho hàm số f x 
. Tìm khẳng định đúng: 2 3 4x x
A. không tồn tại lim f x
B. lim f x   x0 x0
C. lim f x  1
D. lim f x  0 x0 x0 Câu 22. lim     bằng:   2 2 x 3x 3 x 8x x  5 A.  B. 5 C. D.  2
Câu 23. Nếu phương trình: 2
ax  b cx d e  0, a, ,
b c,d R có nghiệm x  1 thì phương 0
trình: f x  0 với   4 3 2
f x ax bx cx dx e cũng có nghiệm. Khi đó, mệnh đề nào sau đây đúng:
A. f x . f  x   x  2 1
B. f x . f x  0 0   0  0 0 0
C. f x . f x  0
D. f x . f x x 1 
bx d 0   0   0  0 2 0   0  1 5
 3n  2n
Câu 24. Tổng S   ... 
 ... có giá trị bằng: 6 36  6n  1 3 2 A. B. 1 C. D. 2 4 3 f x  5 f x 3
1. 5 f x  2  6 Câu 25. Nếu lim  2 thì lim bằng: x2 x  2 x2 x  2 63 67 A. 21 B.
C. Đáp số khác D. 2 18
---------- HẾT ----------
Trang 6/13 - Mã đề thi 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI TRẮC NGHIỆM
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
NĂM HỌC 2017 – 2018 Môn: Toán - Lớp 11 ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..……… 302 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 2 3 n  3n Câu 1. lim bằng: 3 2n  5n  2 1 3 1 A. B. C. 0 D. 5 2 2
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng:
A. Hàm số đa thức liên tục trên toàn bộ tâp số thực
B. Hàm số phân thức hữu tỉ liên tục trên toàn bộ tâp số thực
C. Hàm số lượng giác liên tục trên toàn bộ tâp số thực
D. Hàm số đa thức không liên tục trên toàn bộ tâp số thực
Câu 3. Trong các mệnh đề sau, mệnh đề nào sai? 1 A. lim
 0 vôùi k nguyeân döông B. k
lim x   vôùi k nguyeân döông k x x x 1 C. k
lim x   vôùi k nguyeân döông D. lim
 0 vôùi k nguyeân döông x k x x
Câu 4. Trong các mệnh đề sau, mệnh đề nào sai? 1 1 1 1
A. lim   B. lim   C. lim   D. lim   x0 x x 0  x x 0  x  5 x0 x
Câu 5. Cho c là hằng số, k là số nguyên dương khác không. Tìm khẳng định sai. A. lim k x   B. lim k x  
C. lim x x
D. lim c c x x 0 x  0 x x 0 x 2 Câu 6. lim bằng: n  3 2 A. +∞ B. 2 C. D. 0 3
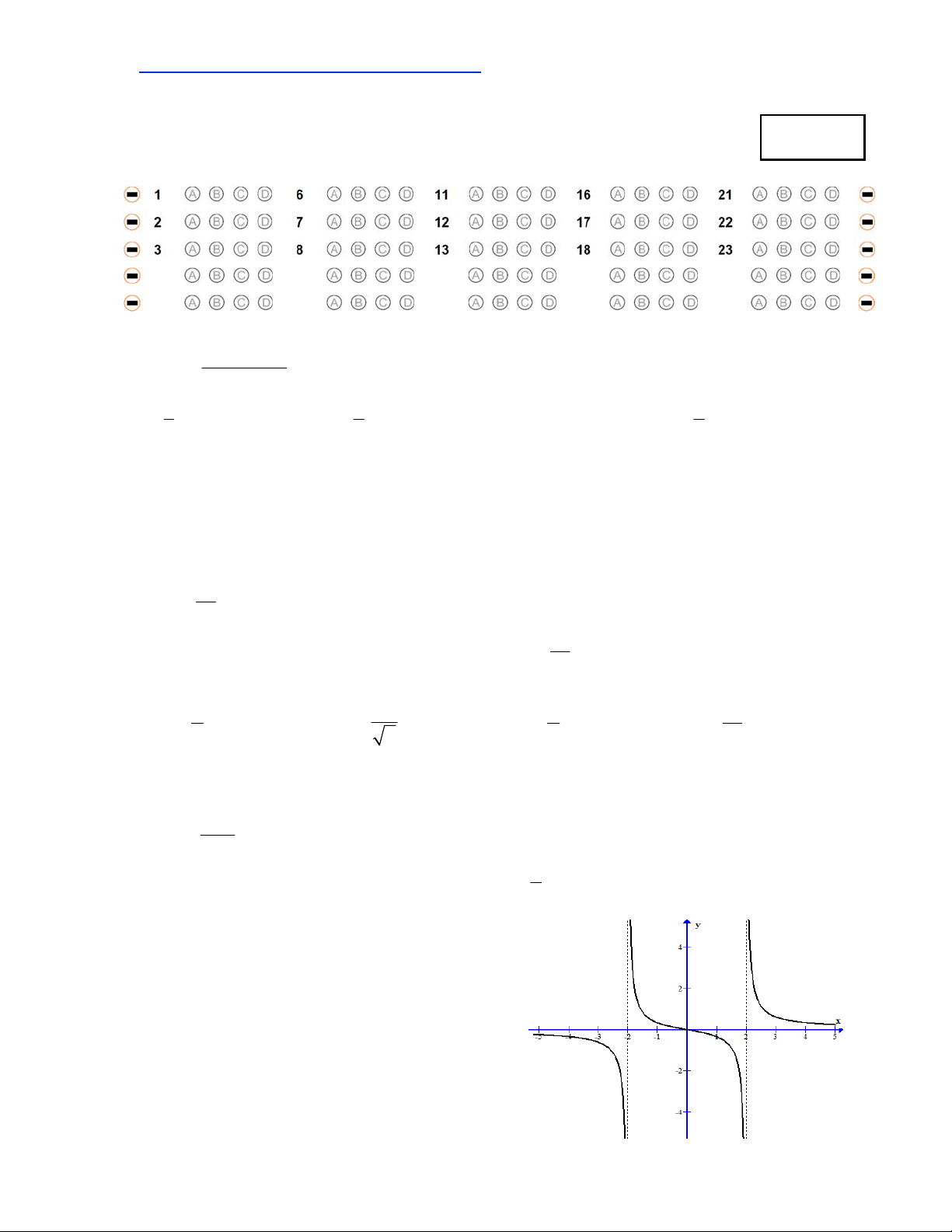
Câu 7. Cho hàm số y = f(x) có đồ thị như hình vẽ bên.
Trong các mệnh đề sau, mệnh đề nào đúng:
A. Hàm số liên tục trên khoảng  ;  2  ; 2  ;2 và 2;
B. Hàm số liên tục trên khoảng  ;2  
C. Hàm số liên tục trên khoảng  2;  
D. Hàm số lên tục trên \  2 
Trang 7/13 - Mã đề thi 105 1
Câu 8. Tổng của cấp số nhân lùi vô hạn (u ) với u  là: n n 3n 1 1 A. 1 B. 2 C. D. 2 3
Câu 9. Hàm số f x 1  2  x  liên tục trên x  3 A.  3;  2 B.  3;  2 C.  ;   
3  2; D. 3;2 1 x 1
Câu 10. Cho hàm số f (x) 
chưa xác định tại x = 0. Tìm f(0) để hàm số trên liên tục tại điểm x 3 1 x 1 = 0? 1 3 A. B. 2 2 C. 0
D. Không tồn tại f(0) 5 3 3  x  7x 11 Câu 11. lim bằng: 5 4 x x  x  3x A. 0 B. 3 C.  D. -3 x 1 Câu 12. lim bằng: x4 3x  2 1 1 A. 3 B.  2 C. D. 3 2 3x 1 Câu 13. lim bằng: x 1  x 1 A.  B.  C. 2  D. 2 2 x  5x  6 Câu 14. lim bằng: 3 2
x2 x x x  2 1 A. 0 B. C. -7 D.  7 3 3 n n Câu 15. lim bằng: n  2 1 A. 2 B. 0 C. D. 1 2 1
Câu 16. Cho hàm số f(x) 
.Chọn kết quả sai: x 1 2 A. lim f(x) 
B. Hàm số liên tục tại mọi điểm x  1 x 3  2
C. Hàm số liên tục tại mọi x 1;
D. lim f(x)  1 x2 Câu 17.  3 2
lim 3x  5x  7  ? x A.  B.  C. 3 D. 0
Câu 18. Cho hàm số f x 2 2
a x x  3  2 x 1 . Tìm tất cả các giá trị của tham số a để
lim f x   . x
A. a  .
B. a  ;2  .
C. a 2; .
D. a  2 2 ax khi x  2
Câu 19. Cho hàm số: f (x)  
để f(x) liên tục trên R thì a bằng? 2
x x 1 khi x  2
Trang 8/13 - Mã đề thi 105 5 A. B. 4 C. 3 D. 2 4 2
x  4x  3  khi x  3
Câu 20. Tìm các giá trị của a để hàm số f x   x  3
liên tục tại x  3 khi x  3 a A. 1 B. 2 C. 4 D. 2 2x 1 Câu 21. lim bằng:  x  2 x 1 1 A.  B.  C. 2 D. 1 2 x  2x 1 Câu 22. Biết lim
a . Hỏi a không là nghiệm của bất phương trình nào sau đây: 2 x 1  x 1 A. 2
x x 1  0 B. 2
x 1  0 C. 2
x  5x  6  0 D. 2
x  3x  0 3
ax 1 bx 1 1  khi x  0
Câu 23. Biết hàm số f x   x
, (a,b là các số thực dương khác 0)
a b  2 khi x  0
liên tục tại điểm x  0 . Tìm giá trị lớn nhất của biểu thức P  . a b . 3 36 5 A. B. . C. . D. 3. 4 49 9 1  81  21 4 Câu 24. Biết 2 lim
. x  8x 10   2 x 1    và lim .       2x x 2 2 x c 2 
xa x a2  x  2 x 1  16
x b x b
với a,b,c là các số thực. Trong các mệnh đề sau, mệnh đề nào sai:
A. a b c B. 2 2
a  5b  4c
C. a c 10b
D. b c a
Câu 25. Cho hình vuông C có cạnh bằng a . Người ta chia mỗi cạnh của 1
hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích
hợp để có hình vuông C (Hình vẽ). Từ hình vuông C lại tiếp tục làm 2 2
như trên ta nhận được dãy các hình vuông C ,C ,C ,...,C ,....Gọi S 1 2 3 n i
là diện tích của hình vuông C i 1;2;3;.. . . Tính tổng i
S S S S  ...  S  ... 1 2 3 n 2 8a A. 2 a 2. B. 2 2a 2. C. 3 2 5a D. . 2
---------- HẾT ----------
Trang 9/13 - Mã đề thi 105
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI TRẮC NGHIỆM
TRƯỜNG THPT TÔ HIỆU – THƯỜNG TÍN
NĂM HỌC 2017 – 2018 Môn: Toán - Lớp 11 ĐỀ CHÍNH THỨC
Thời gian: 45 phút (Không kể thời gian phát đề) Mã đề thi
Họ và tên:………………………………….Lớp:……………. ĐIỂM:……..……… 401 1 6 11 16 21 2 7 12 17 22 3 8 13 18 23 4 9 14 19 24 5 10 15 20 25 Câu 1. lim n q bằng:
A. +∞ nếu |q| ≥ 1
B. 0 nếu |q| < 1
C. 0 nếu |q| > 1
D. 0 nếu |q| ≤ 1
Câu 2. Chọn mệnh đề sai trong các mệnh đề sau. 1
A. lim c c với c là hằng số B. lim
 0 với k nguyên dương k n 1 C. lim  0 D. lim k
n  0 với k nguyên dương n
Câu 3. Chọn khẳng định đúng
A. lim f x  a  lim f x  a
B. lim f x  a  lim f x  a x     0 x xx x  0 x 0 x 0 x
C. lim f x  a  lim f x  lim f x  a D. lim f x  a  lim f x  lim f x x       0 x x  x x   0 x x 0 x 0 x 0 x x 0 x
Câu 4. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hàm số chứa căn bậc hai liên tục trên toàn bộ tập số thực R.
B. Hàm số đa thức liên tục trên toàn bộ tập số thực R.
C. Hàm số lượng giác liên tục trên toàn bộ tập số thực R.
D. Hàm số phân thức liên tục trên toàn bộ tập số thực R. 2 2x  3 Câu 5. lim bằng: 6 5
x x  5x 3 A. 0 B. 3  C. D. 2 5
Câu 6. Giới hạn của hàm số: lim(9  x) bằng: x 1  A. 10 B.  ∞ C. +∞ D. 9 1
Câu 7. Biết dãy số u thỏa mãn u  3  với mọi *
n N . Khẳng định nào sau đây đúng? n  n 2 n A. lim u  3 B. lim u  3  C. lim u  1 D. lim u  2 n n n n 2018
Câu 8. Nếu lim u  9 thì lim bằng n u  7 n A. 504,5 B. 126,125 C. 2018 D. 224, 2
Câu 9. Cho phương trình: 5
x x 1  0 (1). Trong các mệnh đề sau, mệnh đề nào sai?
A. (1) có nghiệm trên khoảng (-1; 1)
B. (1) có nghiệm trên khoảng (0; 1)
C. (1) có nghiệm trên R D. Vô nghiệm n n 1 2.3 5   Câu 10. lim bằng: 2n  5n A.  B. 0 C. 1 D. 5 
Trang 10/13 - Mã đề thi 105 2  x  4  khi x  2
Câu 11. Cho hàm số f (x)   x  2
. Hàm số đã cho liên tục tại x0 = 2 khi m bằng:  m khi x  2 A. -1 B. -4 C. 4 D. 1
Câu 12. Câu nào sau đây sai
A. Hàm số f x liên tục trên  ;
a b nếu nó liên tục tại mọi điểm thuộc  ; a b
B. Cho hàm số f x có miền xác định D, a D . Hàm số liên tục tại điểm x = a nếu lim f x  f a xa
C. Tổng, hiệu, tích, thương của hai hàm số liên tục tại một điểm là một hàm số liên tục tại điểm đó
D. Các hàm số phân thức hữu tỉ liên tục trên từng khoảng của tập xác định
Câu 13. Chọn khẳng định sai trong các khẳng định sau: 2 x  5x  2 A. Hàm số y 
lieân tuïctreân caùc khoaûng ;
 2,2; x  2 2 x  4  khi x  2 
B. Hàm số f(x)   x  2
liên tục tại điểm x = -2  3  khi x  2  C. Hàm số 2
y  x  8 liên tục tại điểm x= 1
D. Hàm số y  s inx liên tục trên R 3 2
n n  3n 1 Câu 14. lim bằng: n 4n  2 1 A. 0 B.  C. D.  4 2
x  6x  5 khi x 1  2   Câu 15. Cho hàm số x 1 f (x)  
. Tìm a để hàm số liên tục tại x = 1. 5 a khi x  1  2 9 3 A. a = 2
B. a  
C. a D. a = 0 2 2 3
1 ax. 1 bx 1 Câu 16. Tính lim theo a; b x0 x a b a b a b a b A. B. C. D. 3 2 2 3 3 2 2 3 2 x  4 Câu 17. lim bằng: x2 x  2
A. Không tồn tại B. 4 C.  D. 0 sinx  cosx Câu 18. lim bằng:  x    4 tan   x  4  1 A.  2 B.  C. 0 D. 2
Trang 11/13 - Mã đề thi 105
Câu 19. Cho hàm số y = f(x) có đồ thị như hình vẽ
bên. Trong các mệnh đề sau, mệnh đề nào sai:
A. lim f x  2
B. lim f x  2
C. lim f x  0
D. lim f x   x x x 1  x 4  Câu 20. Cho hàm số 3
f(x)  3x  3x  2. Trong các mệnh đề sau, mệnh đề nào sai?
A. Phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (0; 1)
B. Phương trình f(x) = 0 vô nghiệm trong khoảng (0; 1)
C. Phương trình f(x) = 0 có nhiều nhất là 3 nghiệm
D. Phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (-1; 1)
Câu 21. Khi x tiến tới  , hàm số 2
f (x)  ( x  2x x) có giới hạn bằng: A. 1 B. 0 C. +  D.  a bkhi x  2
 x  2x x  2 x x  4
Câu 22. Biết hàm số f x 3 2 3 2  
liên tục tại điểm x  2 . Tìm hệ 7a  khi x  2  200
thức liên hệ giữa a và b.
A. 5a 8b  0
B. a  3b  0
C. 2a  3b  0
D. 8a  5b  0 f x  5 g x 1
f x.g x  4  3 Câu 23. Nếu lim  2 và lim  3 thì lim bằng: x 1  x 1 x 1  x 1 x 1  x 1 17 23 A. B. 17 C. 7 D. 6 7
Câu 24. Nếu phương trình: 2
ax  b cx d e  0, a, ,
b c,d R có nghiệm x  1 thì phương trình: 0
f x  0 với   4 3 2
f x ax bx cx dx e cũng có nghiệm. Khi đó, mệnh đề nào sau đây đúng:
A. f x . f x  0
B. f x . f x x 1 
bx d 0   0   0  0 2 0   0 
C. f x . f  x   x  2 1
D. f x . f x  0 0   0  0 0 0
Câu 25. Một quả bóng tenis được thả từ độ cao 
81 m . Mỗi lần chạm đất, quả bóng nảy lên cao bằng hai
phần ba độ cao của lần rơi trước. Tính tổng các khoảng cách rơi và nảy lên của quả bóng từ lúc thả đến khi
quả bóng không nảy nữa.
A. 524m
B. 243m
C. 405m
D. 486m
---------- HẾT ----------
Trang 12/13 - Mã đề thi 105 ĐÁP ÁN Mã đề [105] 1B 2B 3A 4D 5A 6C 7A 8B 9D
10C 11D 12A 13C 14C 15D
16D 17A 18C 19A 20B 21B 22B 23A 24D 25C Mã đề [201] 1A 2A 3B 4C 5D 6B 7A 8D 9B
10A 11C 12D 13C 14C 15B
16D 17B 18D 19B 20A 21A 22C 23C 24A 25D Mã đề [302] 1B 2A 3C 4A 5B 6D 7A 8C 9A
10B 11D 12D 13C 14B 15D
16B 17B 18C 19A 20D 21A 22C 23D 24A 25C Mã đề [401] 1B 2D 3C 4B 5A 6A 7A 8A 9D
10D 11C 12C 13B 14D 15B
16B 17A 18A 19C 20B 21C 22D 23A 24D 25C
Trang 13/13 - Mã đề thi 105