Determination of gravitational acceleration with a reversible pendulum | Báo cáo thí nghiệm môn thí nghiệm vật lý 1 Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh

General Physics Laboratory Report EXPERIMENT 2
DETERMINATION OF GRAVITATIONAL
ACCELERATION WITH A REVERSIBLE PENDULUM
Class: CC19 / Group: 01 Lecturer’s comment Full name: 1. Tăng Gia B o - 2152429 ả 2. Lê D ng Khánh Huy - ươ 2153380 3. Nguy n Lê ễ Anh Tuấn - 2153079 I. Aims/Purposes: Aims/Purposes:
– Calculate the gravitational acceleration. Theory:
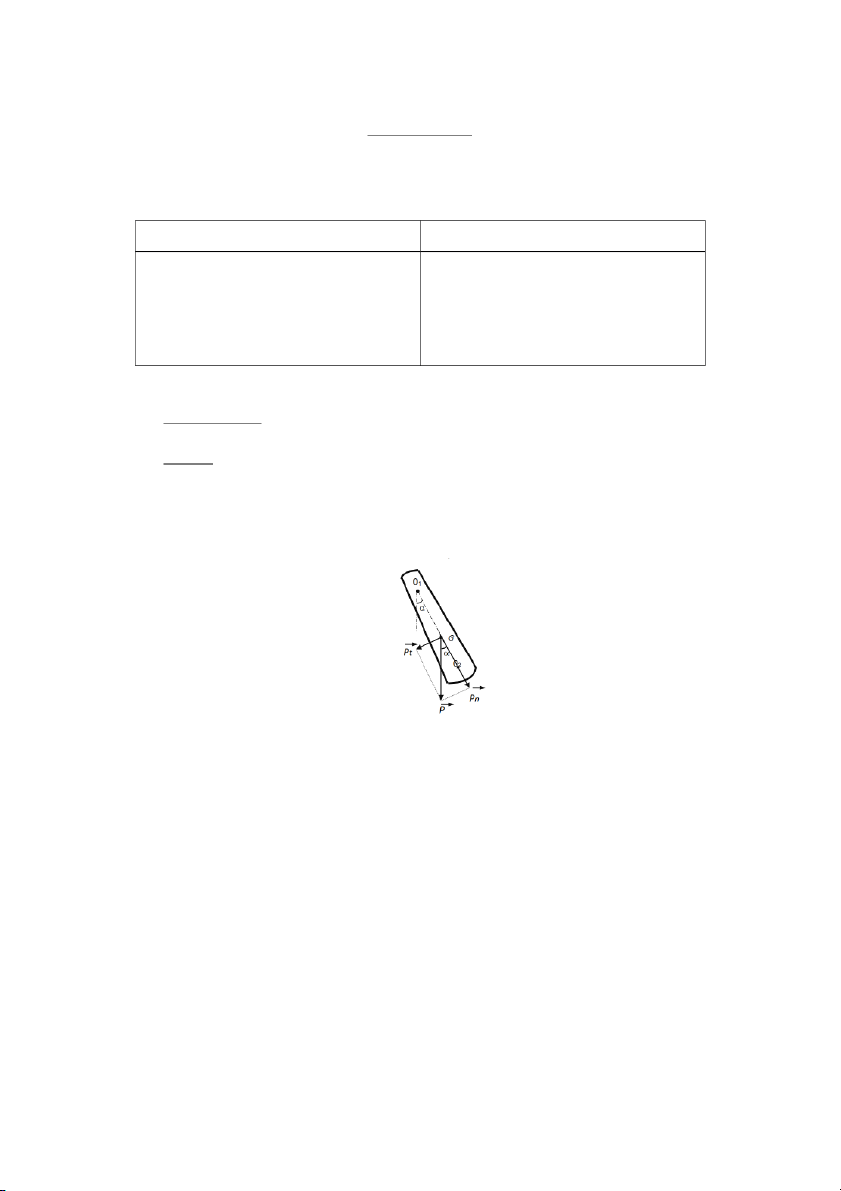
– Physical pendulum is a solid, mass m, that can oscillate around a fixed horizontal axis passing point 0 that 1
is placed higher than its center of mass G (Figure 1). O1 is called the suspension of the pendulum.
– Equilibrium position of the pendulum coincides with the vertical of the line O1G. When
pulling the pendulum out of the equilibrium position, with a small angle , α then release
it, the components Pt of the gravity P = mg acting on the pendulum a torque M1 by: (1)
– Where g is the gravitational acceleration, L1 = O G 1
is the distance from the center O1 to
the center of mass G, (-) indicates torque M1 always pull the pendulum to equilibrium position, meanwhile rotating a reverse angle .
α When α is small, we can consider the approximate: (2)
– Basic equations for the rotation of the pendulum around an axis across 0 : 1 (3) – With β = d 1 2α/dt2 1
is angular acceleration, I is the inertia moment of the pendulum to
which the rotation axis passes through O . Combine (3) and (2) and substitute 1 ω = 12 mg.L /I
1 1, we get the harmonic oscillation equation of the pendulum: – Root of equation (4):. – with as amplitude, is angular frequency
, is the initial phase at time t = 0.
– From (5), Period T1 can determined: (6)
– In the physical pendulum, we can find a point O , located on line through O1 and G so 2
that when the pendulum swings around a horizontal axis passing through O , the 2
oscillation period is equal its period when oscillating around the axis O . T 1 he physical pendulum is called reversible.
– Indeed, we can easily prove that there exists the hanging points O , as follows: 2 When the
oscillation around the axis through point O2 (Figure 1), period T2 of the pendulum is the
same calculation above, and we found: (2)
– G is the distance from the rotation axis through O passing to the center of mass G and I 2 2
is the inertia moment of the pendulum to the rotation axis passing through O2. – IG is moment called the inertia
of the pendulum for the rotating axis through the center of
mass G and parallel to the two axis O1 and O2. According to Huygens-Steiner theorem: (8) (9)
– If the suspension point O2 satisfies T1 = T2 conditions, substitute (9), (8) to (7), (6) we
find equation to determine O2 locate: (10)
– On the other hand, from (6), (7) we can identify gravitational acceleration: (11) – If two point 0 , 0 1
satisfying formula (10), than T 2
1 = T2 = T, and equation to determine the acceleration is: gravitational
II. Method, Equipment and Procedure: Method:
– To determine the local gravitational acceleration we need to determine period T1 and T2,
And then apply the equation to calculate the local gravitational acceleration. Equipment: 1. Physical pendulum. 2. MC-963A meter 3. Optical infrared port. 4. Pendulum suspension. 5. Ruler 1000mm.
6. Caliper 0-150mm, accuracy 0.1 or 0.05mm. 7. Paper 120x80mm. Procedure:
In this experiment, two suspension points (two blades O1, O2) fixed, one must locate
Weighted C (i.e. change the position of the center of mass G, so that (10) is satisfied), to let the
pendulum become irreversible. The following procedure:
1. Turn on the Weighted C closed to the weights 4. Use the caliper to measure the distance
x0 between them. In many cases, the pendulum was created so that the Weighted C was
extremely closed to the weights 4 (x0 = 0). Record the value x0 in table 1. Place the
pendulum on the rack in the forward direction (the word "Forward": toward the people
that are doing the experiment), measuring the time of 50 oscillation periods and recorded
in Table 1, below the columns 50T1.
2. Reverse the pendulum ("Reverse direction": toward the the experiment), people doing and measure the time
period, recording the results in T of the 50 oscillation able 1 below 50T2 column.
3. Set the location Weighted C to weights 4 away a distance x' = x + 40mm, (using calipers 0
to check). Measuring the period of 50 cycle and 50 reverse cycle with this position,
recording the results in Table 1.
4. Performance the measurement results on the graph: vertical axis 120mm, performances
50T1 and 50T2 time, horizontal axis 80mm, shows the position x of C. Connect the 50T1
and 50T2 points together by straight lines, their communication is the approximate
location of x for T1 = T2 (H3). 5. Use calipers to
the weight C on the right position x1. Measured 50T1 and 50T2. place Record results in table 1.
6. Adjust the weight C to the right position: The graph in Figure 4 shows the line 50 T1
slope than the T2, which means to the left of the crossover point than 50T2> 50T1, and
the right of the crossover point than 50T1> 50T2. From the results of measurements 5, at
x1 we can conclude that to obtain the best results, we must shift direction the weight C so that 50T1 = 50T2.
7. Finally, when the best location of Weighted C , we measured each has been identified
direction 3-5 times to get random error, Record results in Table 2.
8. Use a ruler (1000 m) to measure the distance L between the two blades O1, O2. Record in
Table 1. (Only once carefully measured, taking the error ΔL = ±1mm).
9. To complete the experiment, turn
MC-963 meter and unplug it from the power of off the ~ 220V. III. Equations: Calculating the period T: . ⇒ Error T system: Error T total:
Gravitational acceleration IV. Experimental Data: IV.1 Table 1: L= 700 1 (mm) Weighted position 50T1 (s) 50T2 (s) (mm) (mm) x0 = 0 mm 83.35 83.77 x0+40 = 40mm 84.19 84.07 x1 = 30.02 mm 84.04 84.02 IV.2 Raw data: IV.3
Table 2: At the best position x ', physical pendulum becomes T 1 = 1 T = 2 T: Best position x'1 = 30.02 (mm) Data 50T1 (s) Δ (50T1) 50T2 (s) Δ (50T2) 1 84.04 0.007 84.02 0.003 2 84.05 0.003 84.01 0.007 3 84.05 0.003 84.02 0.003 Mean 84.047 0.004 84.017 0.004 V. Calculations:
V.1 Determine the oscillation period of the reversible pendulum:
❖Calculate the mean period T of the reversible pendulum from the values in table 2: ❖ Random error of T: ❖ Systematic error of T: ❖ Absolute error of T:
V.2 Calculate the gravitational acceleration:
❖ Calculate the mean value of gravitational acceleration:
❖ Calculate the relative error of g: ❖ = 4.946 = δ => = 4.946 VI. Conclusions: VII.Questions:
1. What is the same and different between the physical pendulum and mathematical pendulum? Mathematical pendulum Physical pendulum Model A simple pendulum is
A physical pendulum is a considered as an ideal realistic model of the
model because sometimes it
pendulum; it has a finite
is difficult to achieve in body and shape. reality. Suspension
A simple pendulum needs a
A physical pendulum does
tread or a string to suspend
not need any string for the from a rigid support. suspension. Tension
There is a tension force As a physical pendulum
acting on the string, which
does not need any string for
helps the object to suspend.
the suspension, there will be no tension. Time period
The time period depends on The time depends on the
the square root of the ratio
square root of 2/3 ratio of
of length of the pendulum
length and the acceleration
and the acceleration due to due to gravity. gravity. Mechanical energy Mechanical energy is Here also mechanical conserved at every
energy is conserved at every oscillation. oscillation. Oscillation A simple pendulum
The angle of oscillation of
oscillates with a large angle
the physical pendulum is
in a short interval of time. small. Gravity
Gravity acts at the center of Gravity acts towards the
the bob of the pendulum. center of mass of the physical pendulum. Mathematical pendulum Physical pendulum Torque
When a simple pendulum is The physical pendulum
free to rotate, the torque is
rotates freely due to the
due to gravity or angular
torque applied to the center acceleration. of mass.
2. Prove that any physical pendulum hanging given point O1 can be found O2 to let the
pendulum become irreversible.
In the physical pendulum, we can find a point O2, located on line through O1 and G so that when
the pendulum swings around a horizontal axis passing through O2, the oscillation period is equal
to its period when oscillating around the axis O1. The physical pendulum is called reversible.
Indeed, we can easily prove that there exists the hanging points O2, as follows: When the
oscillation around the axis through point O2 (Figure 1), period T2 of the pendulum is the same
calculation above, and we found:
3.Show the way to adjust Weighted C to become a reversible pendulum with two given suspension points O1, O2.
4. Write expressions identify the oscillation period of a reversible pendulum with small amplitude.
5. To determine the oscillation period of a reversible pendulum, we must measure many
periods (50 periods for example), but not measure each period? When such a measure,
which error can be overcome? How to calculate these kinds of errors?
When measuring a certain quantity many times, often no matter how careful you are, the results
between the measurements are almost always different. That proves that in the measured results
there is always an error and the result we get is only its approximate value.
There are many causes of errors, but the main ones are as follows:
Due to the lack of precision measuring machines and tools
Due to the low skill level of the person measuring, the ability of the senses is low
Due to external factors affecting, for example, weather changes, rain and wind, unusual heat and cold, etc.
So that, when we measure it many times, we will collect the approximate value as much as we can.
6. Write a formula to measure the errors by using reversible pendulum? in the formula, determines the number of ? π3.14