
Preview text:
Problem 1:
Suppose that a consumer who uses $60 to buy 2 goods: X and Y. Given
that price of the good X is $3 per unit and price of the good Y is $1 per
unit. Suppose that the utility function of this consumer is TU=XY
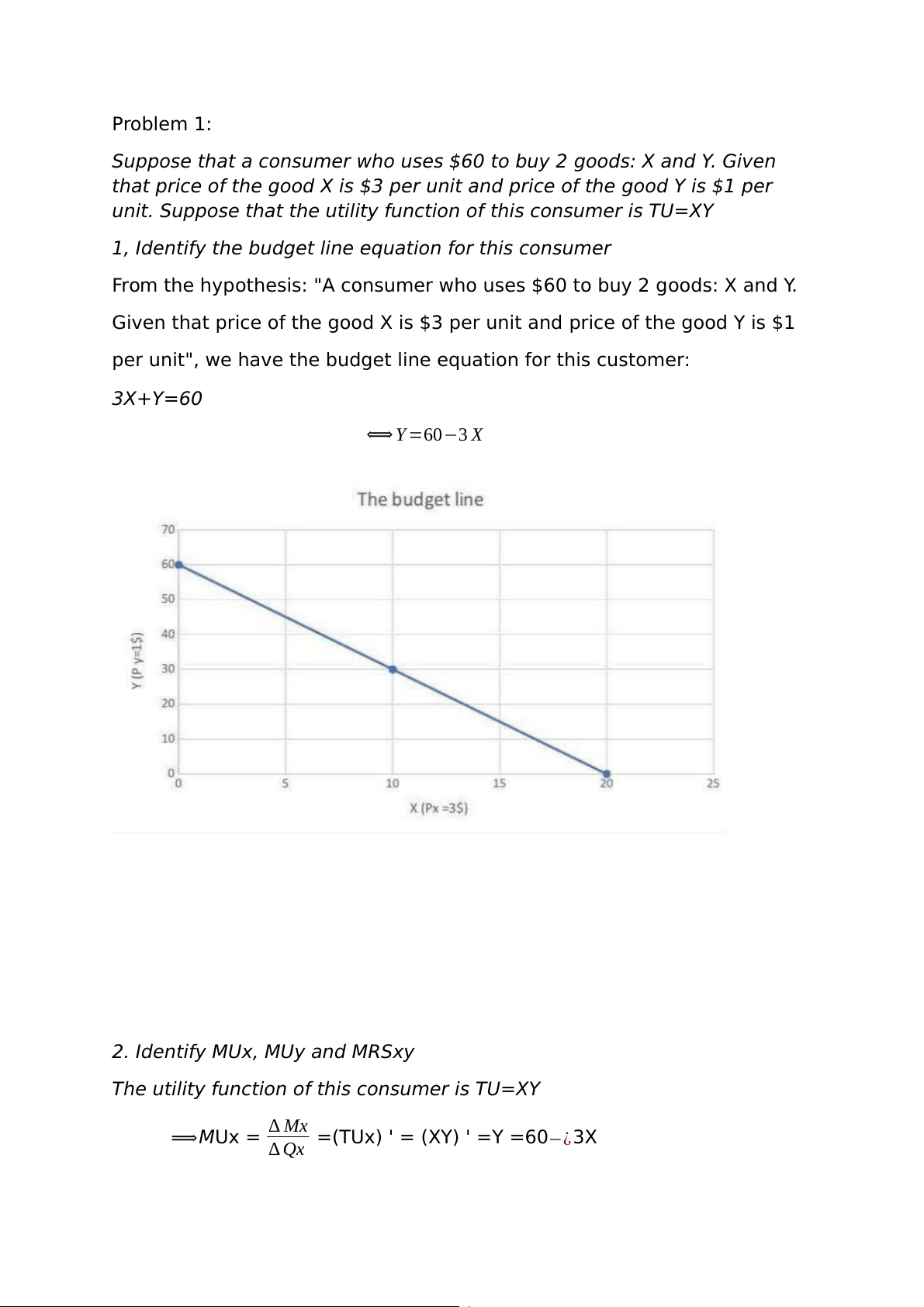
1, Identify the budget line equation for this consumer
From the hypothesis: "A consumer who uses $60 to buy 2 goods: X and Y.
Given that price of the good X is $3 per unit and price of the good Y is $1
per unit", we have the budget line equation for this customer: 3X+Y=60 ⟺ Y =60−3 X
2. Identify MUx, MUy and MRSxy
The utility function of this consumer is TU=XY ∆ Mx ⟹MUx =
=(TUx) ' = (XY) ' =Y =60−¿3X ∆ Qx 60−Y
⟹ MUy= ∆ My =¿(TUy) ' = (XY) ' =X = ∆ Qy 3 180−9 X
⟹MRSxy ¿ MUx = Y = MUy X 60−Y
3. What are optimal quantity of good X (X*) and optimal quantity of good
Y (Y*) that he should buy to maximize his utility Px
To maximize his utility : MRSxy = = MUx Py MUy We have : = MUx {MUx Px Py 3 X +Y =6 = X { Y3 1 3 X +Y =6
{ 3 X=Y ⟺{X=10 3 X +Y =6 Y =30 Problem 2:
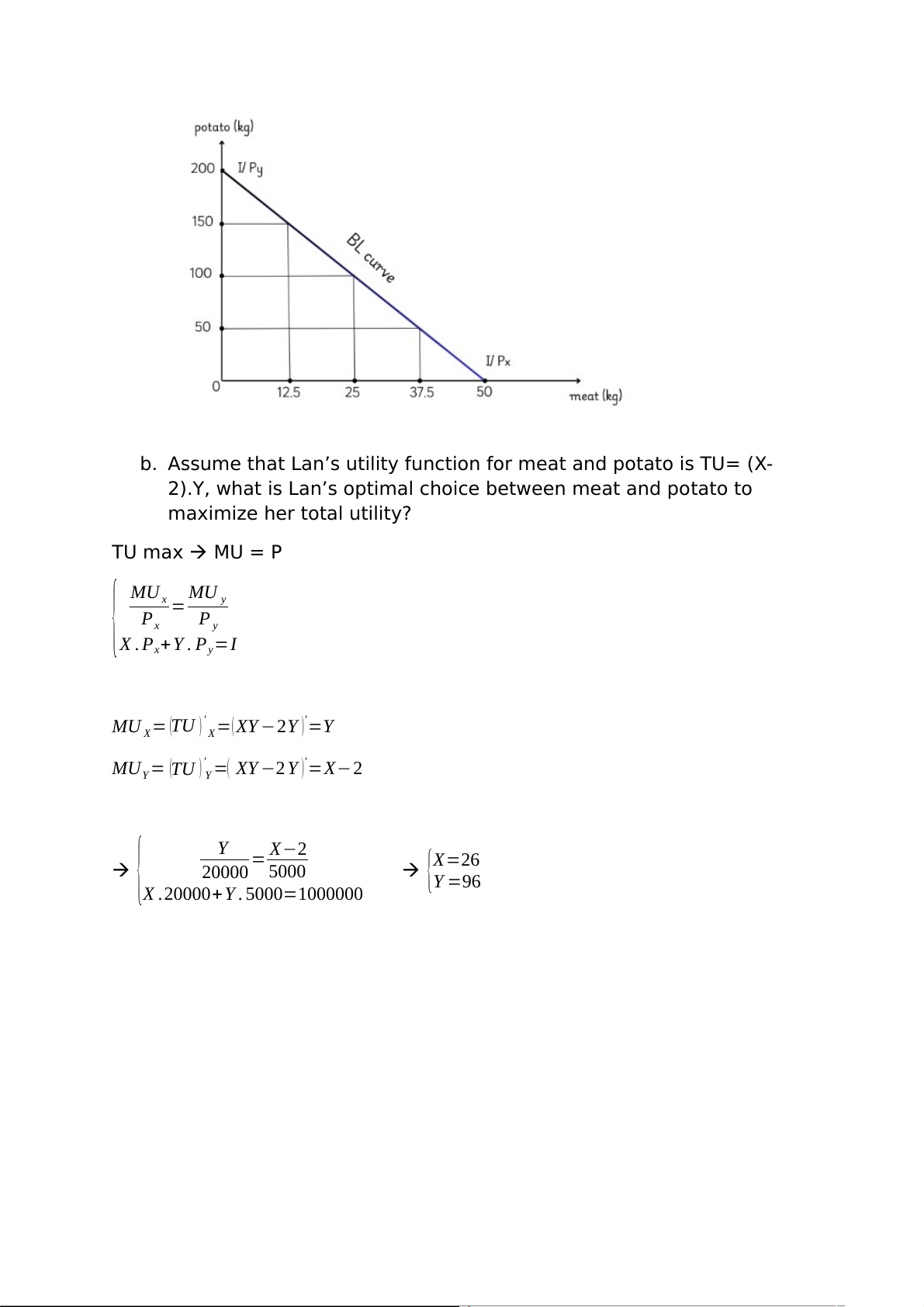
a. Identify Lan’s budget line equation and draw that BL curve
* Identify Lan’s budget line:
X. P + Y. P = I X Y
X. 20000 + Y. 5000 = 1000000 4X + Y = 200 * BL curve:
b. Assume that Lan’s utility function for meat and potato is TU= (X-
2).Y, what is Lan’s optimal choice between meat and potato to maximize her total utility? TU max MU = P { MU MU x = y P P x y X . P + Y . P = y I x
MU = (TU )' =(XY −2Y )'=Y X X
MU = (TU )' =( XY −2 Y )'=X−2 Y Y = X−2 { Y 20000 5000 {X=26 Y =96
X .20000+ Y . 5000 1000000 =




