Econ Review: Probability & Inference Concepts | Môn Econometrics with Financial Application - Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

lOMoAR cPSD| 58583460 lOMoAR cPSD| 58583460 1. Probability 2. Random variables
3. Some important theoretical probability distributions
•Normal distribution, Student’s t-distribution,
•Chi-square distribution, F distribution
4. Statistical Inference: Estimation • Point Estimation
• Interval Estimation (Confidence Interval)
5. Statistical Inference: Hypothesis Testing lOMoAR cPSD| 58583460
1.1 Probabilities and Events
1.2 Conditional Probability
1.3 Random Variables and Expected Values
1.4 Covariance and Correlation lOMoAR cPSD| 58583460 Section 1.1
Probabilities and Events
Consider a random experiment
 The sample space, S, is the set of all possible outcomes of the experiment.
 If there are m possible outcomes of the
experiment then we will generally number them lOMoAR cPSD| 58583460
1 through m. Then S ={1, 2, …, m}
 When dealing with specific examples, we will
usually give more descriptive names to the outcomes. Definitions
Event any collection of results or outcomes of an experiment. lOMoAR cPSD| 58583460
Simple Event an outcome or an event that cannot
be further broken down into simpler components.
Sample Space for an experiment consists of all
possible simple events; that is, the sample space
consists of all outcomes that can not be broken down any further. P denotes a probability. lOMoAR cPSD| 58583460 A, B, C and E denote specific events. P(A)
denotes the probability of event A occurring.
Assume that a given procedure has n different
simple events and that each of those simple events lOMoAR cPSD| 58583460
has an equal chance of occurring. If event A can
occur in s of these n ways, then s Number of Ways A can occur P A( ) = =
n Number of different simple events
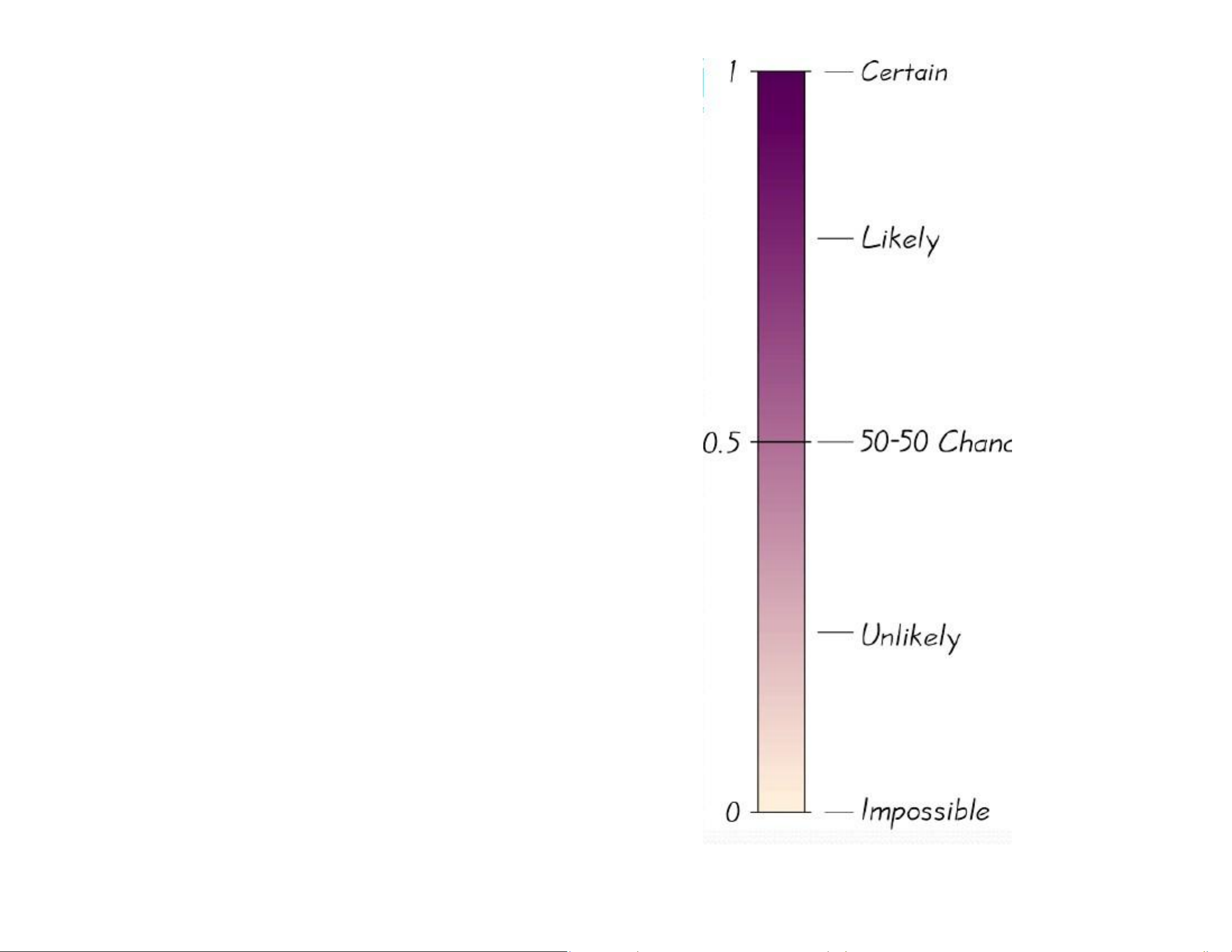
The probability of an impossible event is 0. lOMoAR cPSD| 58583460
The probability of an event that is certain to occur is 1.
For any event A, the probability of A is between 0 and 1 inclusive. That is: 0 P(A) 1
Let S = {1, 2, …, m}. Let be the probability that pi i
is the outcome of the experiment. Then: lOMoAR cPSD| 58583460
0 pi 1, i = 1,2, ... m m pi =1 i=1 For any event A, m
P(A) = pi lOMoAR cPSD| 58583460 i A m
P(S)= pi =1 i=1 lOMoAR cPSD| 58583460
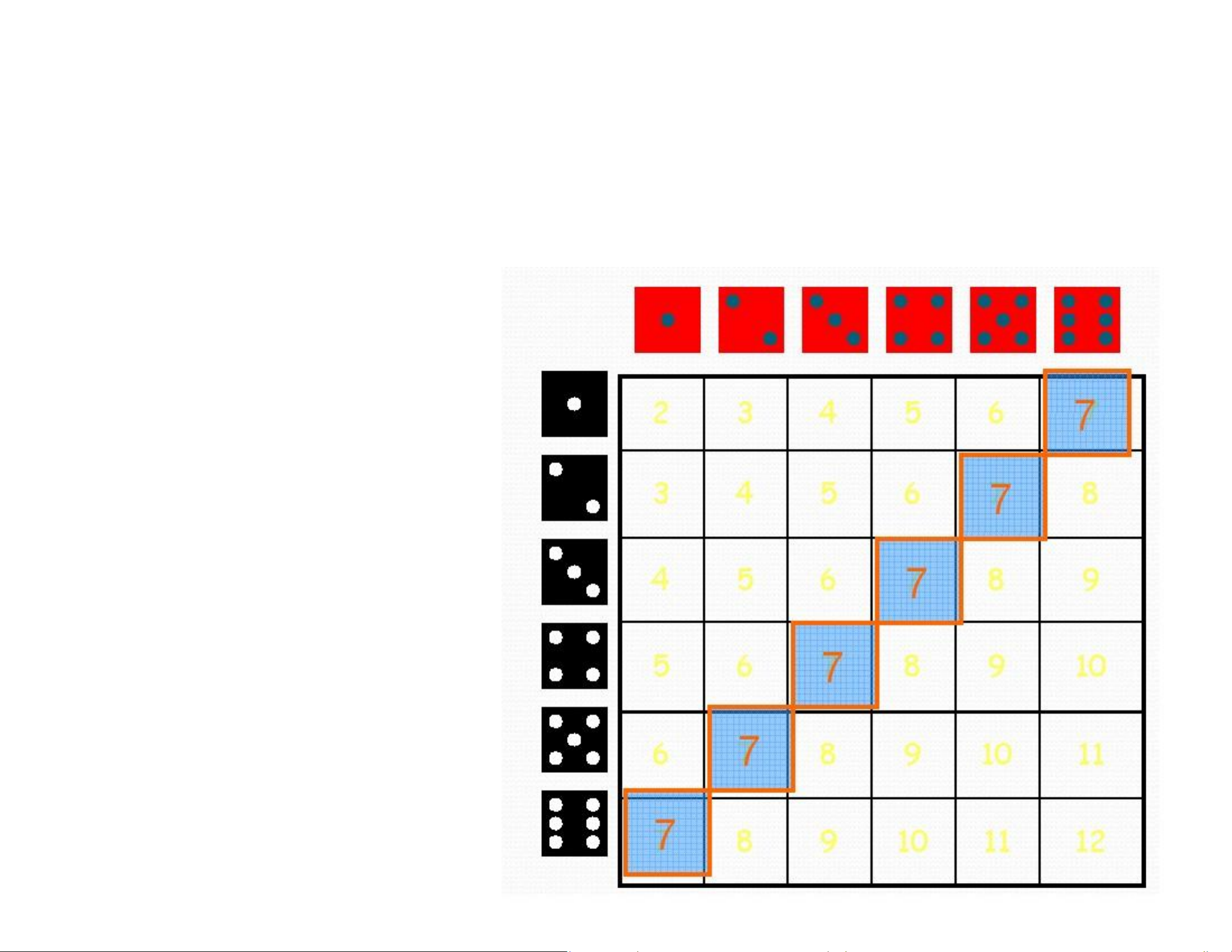
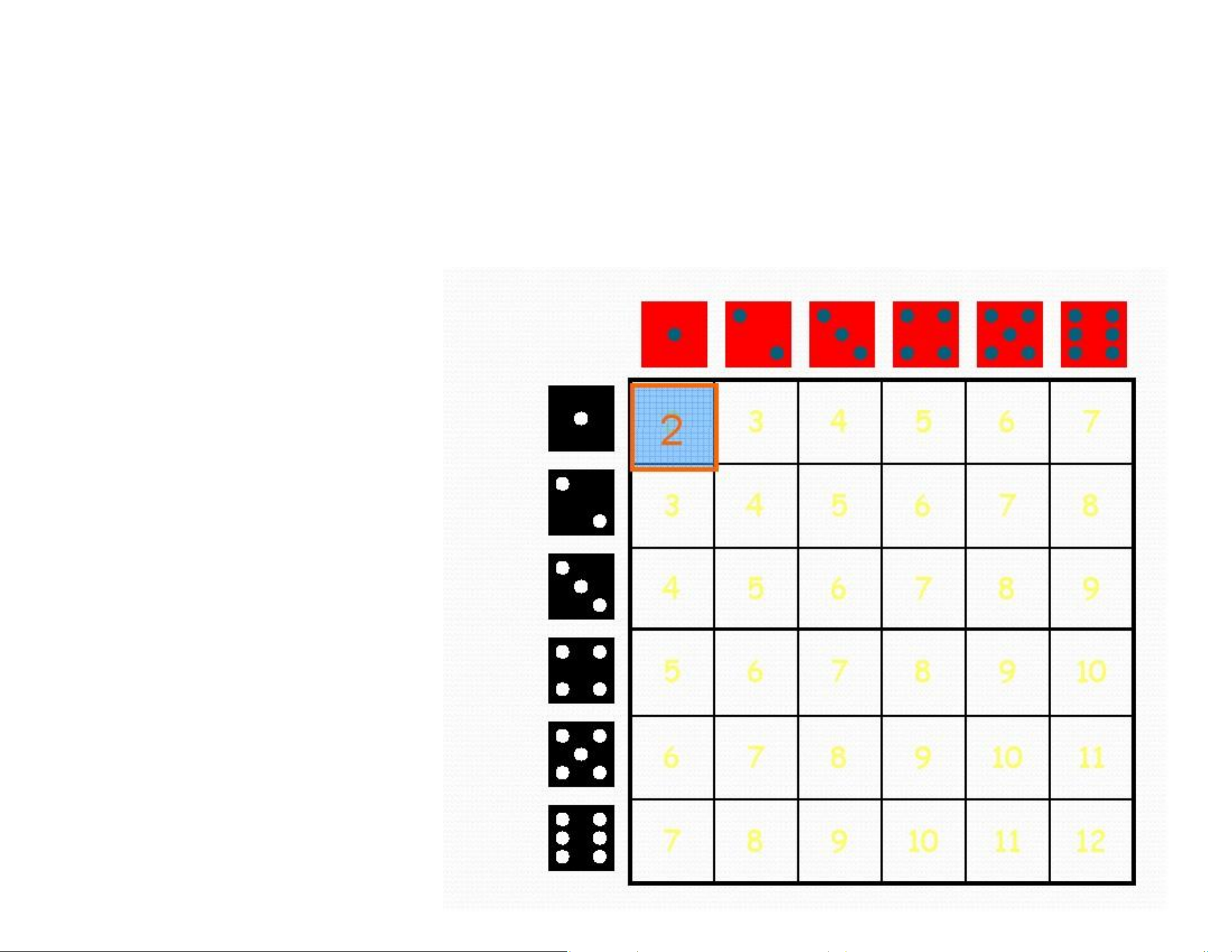
Possible Values for Probabilities lOMoAR cPSD| 58583460 Roll two dice. What is the chance that the sum is: Equal to 7? Equal to 2? Even? Odd? lOMoAR cPSD| 58583460
Example: Sum of two dice Roll two dice. What lOMoAR cPSD| 58583460
Example: Sum of two dice is the chance that the sum is: Equal to 7? lOMoAR cPSD| 58583460
Example: Sum of two dice Roll two dice. What lOMoAR cPSD| 58583460
Example: Sum of two dice is the chance that the sum is: Equal to 7? Equal to 2? lOMoAR cPSD| 58583460
Example: Sum of two dice Roll two dice. What lOMoAR cPSD| 58583460
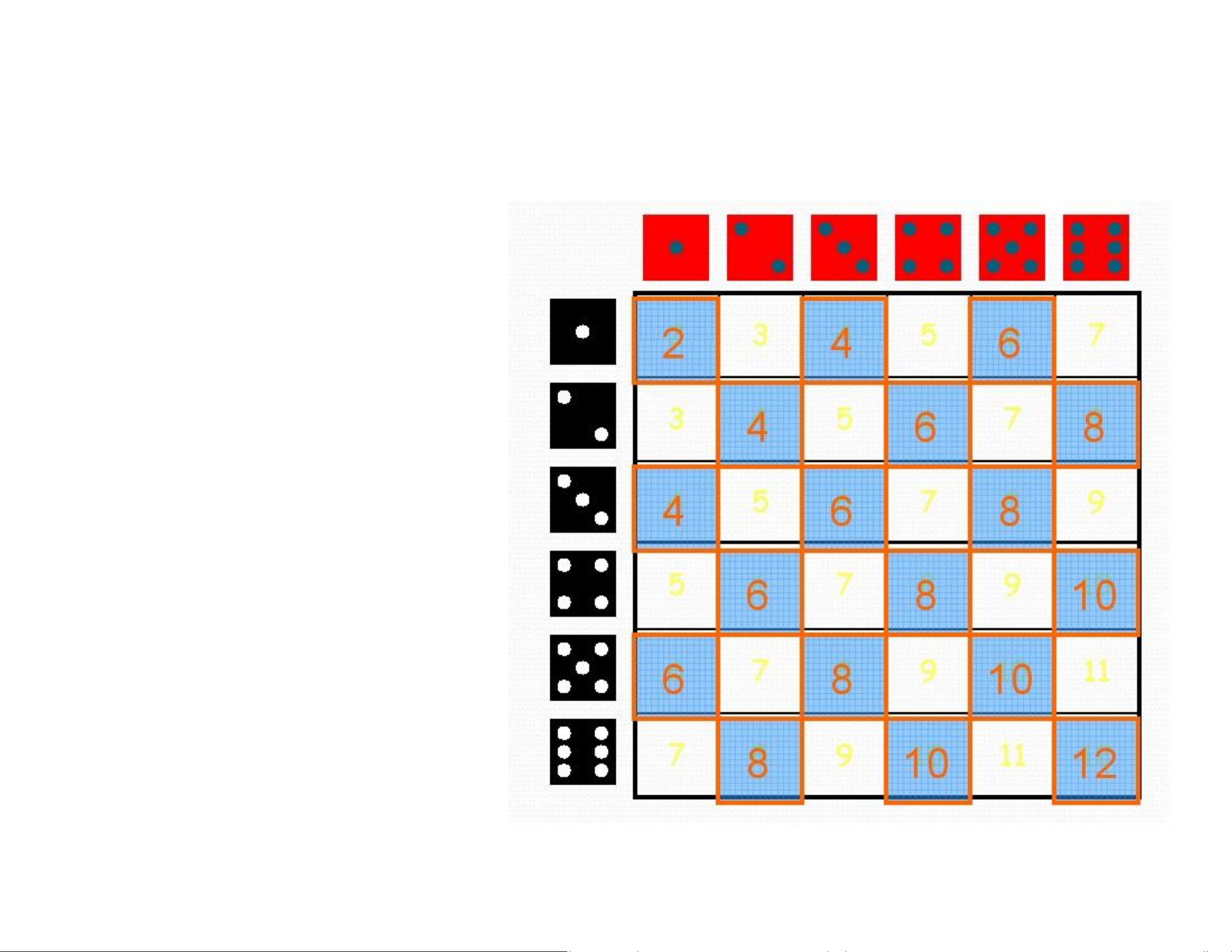
Example: Sum of two dice is the chance that the sum is: Equal to 7? Equal to 2? Even? 18/36 = 1/2 Roll two dice. What is the chance that the sum is: lOMoAR cPSD| 58583460
Example: Sum of two dice Equal to 7? Equal to 2? Even? Odd? 18/36 = 1/2