ECON1006, Introduction to Economic Methods: RevisionQuestions | Tài liệu môn Kinh tế học Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

ECON1006, Introduction to Economic Methods: Revision Questions Question 1
Consider the following set of data, which we can assume to be a sample from a population. 1 1 5 4 12 4 3 1 2 7 6 6 5 1 1 5 8 9 10 2 4 2 6 30 (i)Mean = (ii) Median (iii) Mode = 1
(iv) Calculate (variance) and ‘s’ (standard deviation) for the previous
24 number dataset. [Use calculator for solutions] and
(v) Is the distribution is positively skewed, negatively skewed, not skewed?
Mean > Median > Mode => Right (positively) skewed distribution.
(vi) The coefficient of variation (CV) for the distribution?
CV = s/ = 6.0276/5.625 = 1.0716
(vi) Chebyshev Theorem – Example
For any quantitative population with a finite variance, the proportion
of data points less than ‘c’ standard deviations from the mean is at least , where .
For a non-normal (not Bell shaped) distribution, at least what
proportion of data points would be 1.5 standard deviations of the mean. (55.5%)
By Chebyshev’s theorem, the proportion of weights within s tandard
deviations from the mean would be at least or about 55.5%
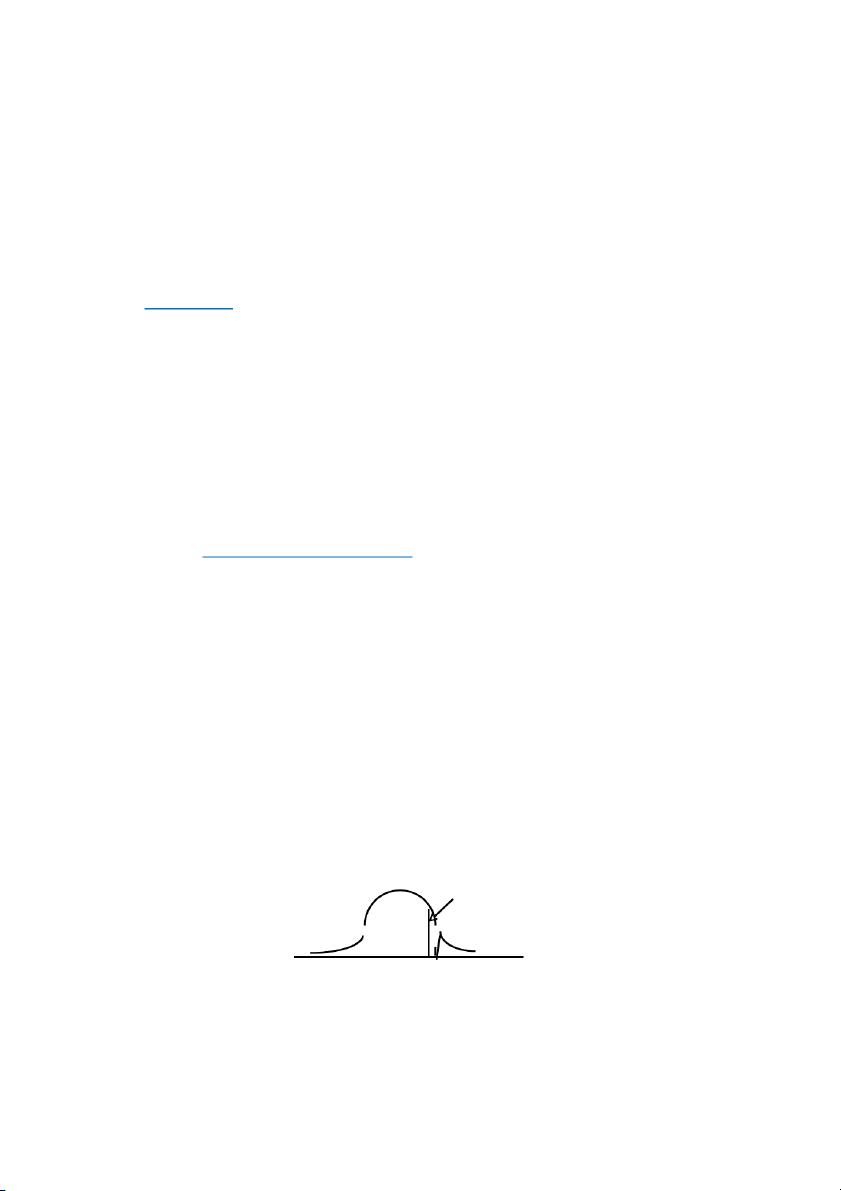
(vii) Empirical rule – Example For a bell-shaped
distribution of sample or population data, it will be approximately true that  68%
of the data points will lie within 1 standard deviation of the mean.  95%
of the data points will lie within 2 standard deviations of the mean.  99.7%
of the data points will lie within 3 standard deviations of the mean. Question 2
(a) Suppose we have the set . Define (i) (ii) (iii)
(iv) B and C are disjoint/mutually exclusive. (b)Suppose .
Where S is the sample space of a statistical experiment and all the
simple events are equally likely. (i) (ii) (c) Suppose that for :
[Note: Simple events not all equally likely] with P(A) P ) 1 (  P( ) 3  P( ) 5  P(6)  1 . 0  1 . 0  . 0 36  1 . 0  . 0 66 P( )
B P(2)  P( )
3  P(4)  P( ) 5  P ) 8 (  1 . 0  1 . 0  . 0 08 36 . 0  . 0 08  . 0 72
P(A  B) P({ , 1 , 3 , 2 } 8 , 6 , 5 , 4 ) P ) 1 (  P( ) 2  P ) 3 (  P(4)  P ) 5 (  P( ) 6  P ) 8 ( 0  .1 . 0 1 . 0 1 0 0 . 8  . 0 36  . 0 1 0.08 0  .92 Question 3
(i) Suppose we select 5 people at random. What is the probability
that they were born on different days of the week, assuming an
individual has an equal probability of being born on any of the seven days of the week?
A simple event here is an ordered sequence of 5 elements, the first
representing the day of the week the first person was born on, the
second the day the second person was born on, and so forth.
The sample space (non-ordered simple events) of this experiment 5      contains 7 7 7 7 7 (7) possible simple events.
The number of simple events in the event of interest (ordered days of birth) is .
Therefore the required probability =
(ii) Consider the numbers 1, 2, 3, 4. How many permutations of
these four numbers taken 2 at a time can be found?
(iii) In how many ways can a committee of 4 people be chosen from a group of 7 people? (35) [ : Ordering does not mat Combinations ter] 7C4 = ways
(iv) Say we have 3 black flags and 2 red flags. How many distinct
ways are there of arranging these flags in a row? (10) 7!/(4!x3!) = 7x6x5/3x2 = 35 Question 4
A company that supplies reverse-cycle air conditioning units has
found from experience that 70% of the units it installs require
servicing within the first 6 weeks of operation. In a given week the
firm installs 10 air conditioning units. Calculate the probability that, within 6 weeks (i) requir 5 of the units e servicing (0.1029 approx.) P(X  ) 5 10C (0 7 . ) 5 5 (0 ) 3 . 5 10!  (0 7 . )5 (0 ) 3 . 5 5 5 ! ! 2  52( . 0 7) 5(0. ) 3 5 0  .1029
(ii) None of the units require servicing (0 approx.) (iii) require s All of the units ervicing (0.0282 approx.) (iv) of the air conditioner less than 8 s require servicing. from the tables (v) of the air conditioner 4 or more s require servicing. from the tables Question 5
(i) The amount of petrol sold daily by a service station (say ) X is
known to be uniformly distributed between 4,000 and 6,000 litres
inclusive. What is the probability of sales on any one day being
between 5,500 and 6,000 litres? (0.25) (ii) If determine the f ~ ollowing probabilities: (0.5) (0.3085) (0.3557) (0.0505) (iii) If , calculat ~
e , and . (0.0021, 0.6853, 0.0401)
(iv) From several years’ records, a fish market manager has
determined that the weight of deep sea bream sold in the market is
approximately normally distributed with a mean of 420 grams and a
standard deviation of 80 grams. Assuming this distribution will
remain unchanged in the future, calculate the expected proportions
of deep sea bream sold over the next year weighing
(a) Between 300 and 400 grams.
(b) Between 300 and 500 grams. (c) More than 600 grams. Question 6
It is known that 60% of cars registered in a given town use unleaded
petrol. A random sample of 200 cars is selected. Determine the
probability that, of the cars in the sample:
(i) 130 use unleaded petrol. (0.021)
(ii) More than 130 use unleaded petrol. (0.0643)
(iii) Less than 130 use unleaded petrol. (0.9147)
Firstly, check that the conditions for the normal approximation are satisfied. Set Let ~ , then on the binomial on the normal Area 0 Z 1.37 1.52 (ii) on the binomial
on the normal with continuity correction (iii) on the binomial on the normal Question 7
a) A cereal manufacturer claims that the mean fat content of its
cereal packets is 2.2 grams. Assume the fat content per packet is
approximately normally distributed with a standard deviation of 0.6
grams. A consumer organisation suspects that the mean fat content
per packet is higher than the manufacturer’s claim. It tests a random
sample of 25 packets of cereal and finds a sample mean fat content
of 2.4 grams. On the basis of this information, test the
manufacturer’s claim against a suitable alternative at the 0.05 level of significance. Step 1:
Label the random variable of interest and formulate the null and alternative hypotheses.
Let the fat content in a packet of cereal. Step 2:
Identify the appropriate sampling distribution of the test statistic under the null hypothesis . ~ ~ ~ Step 3:
Find the critical value(s) of the test statistic. Step 4: State the decision rule. Reject and conclude if Step 5:
Calculate the test statistic based on a realized sample. Step 6:
Compare the realized value of the test statistic and the critical
value(s) to reach a conclusion.
Therefore we reject the null hypothesis and conclude that the mean
fat content is greater than 2.2 grams.
(b) A manufacturer of radial tyres claims the mean tread life of its
tyres is at least 60,000 kilometres. The tyre tread life is known to be
approximately normally distributed. To test the manufacturer’s
claim, 16 of the tyres are selected at random and tested. The sample
yields a mean tread life of 56,000 kilometres and a sample standard
deviation of 5,250 kilometres. Perform the test of the
manufacturer’s claim against a lower tail alternative, assuming . Step 1:
Label the random variable of interest and formulate the null and alternative hypotheses.
Let the tread life in kilometres of a randomly chosen tyre
In this example we are mainly concerned about whether the
manufacturer’s claim is exaggerated, therefore we will choose a lower-tail test. Step 2:
Identify the appropriate sampling distribution of the test statistic under the null hypothesis . ~ Step 3:
Find the critical value(s) of the test statistic. (from the T tables) Step 4: State the decision rule. Reject and conclude if Step 5:
Calculate the test statistic based on a realized sample. Step 6:
Compare the realized value of the test statistic and the critical
value(s) to reach a conclusion. Since we
reject the manufacturer’s claim. Question 8
(b) Suppose the firm manufacturing the machined engine part
considered in the previous example claims its parts have a diameter
variance of no more than 0.0013 (again diameter is measured in
centimetres). Again suppose a random sample of 15 of the parts
from the manufacturer yielded a diameter sample variance of
0.0015. Given this information, perform a test of against at the 5%
level of significance. Again assume the diameter of the part is
approximately normally distributed. Step 1:
Label the random variable of interest and formulate the null and alternative hypotheses. Let = diamet X er of a part in centimetres Step 2:
Identify the appropriate sampling distribution of the test statistic under the null hypothesis . ~ Approximately Step 3:
Find the critical value(s) of the test statistic. Step 4: State the decision rule. Reject and conclude If realised Step 5:
Calculate the test statistic based on a realized sample. Step 6:
Compare the realized value of the test statistic and the critical
value(s) to reach a conclusion.
Since , we do not reject the manufacturer’s claim at the 5% level of significance. Question 9 (i) dy  1   3  1 1 3 4  2 3  ( 5 2)x  2  x    x dx  4  2  3 1  1 3 4  2 3 1  0x  x  x 2 2 (ii) [Product Rule] y d     1 3 1 1 3  x  ) 5 (   ln 5x  ) 3 ( x  2 3  x d  5x   3  3
 x 2 3  (ln5x)(x 2 3) (iii) (iv) (v) 2 x 2 x 2 x dy (ln x)[e ( ) 3  3x(e ) 2 ] 3xe 1 ( x)  2 dx (ln x) 2 x e 3 (ln x  2x ln x  ) 1  2 (ln x) (vi) If , evaluate f (  x) (  x 2  2)2( ) 2  2x( ) 2 (x 2  2)1(2x) 2
 (x2  2)2 8x2 (x2  ) 2  f ) 1 (  1 ( 2  2)2  1 ( 8  2)  6 Question 10
(a) Following the worst cyclone in 50 years, a banana plantation
owner in Northern Queensland has to replant most of his holding.
From research studies conducted in the region the plantation owner
knows that, on average, if 1,760 banana trees are planted per
hectare, the annual yield per tree will be 2 cartons of bananas; in
addition, for every additional tree planted per hectare (over 1,760),
the annual yield per tree falls by a thousandth of a carton. How
many trees should the plantation owner plant per hectare to
maximize the yield per hectare? What is the maximum yield per hectare?
Let ‘x’ be the number of additional trees planted per hectare. Then Total numb er of tre s e per hec a t r e 1  760  x yield per t ree 2   0 0 . 0 x 1 yield per h ectar e y  1 ( 760  x)(2  0 0 . 0 x 1 ) 3  520  0.24x  0 0 . 0 x 1 2
d y 0 2.4 0 0.02x 0  x 1  20 x d 2 d y  0 0.02 x 2 d  
The plantation owner should plant 1760 120 1880 trees per hectare.  Maximum yield per hectare 3534.4 cartons
(b) Suppose the following calculated data refers to a sample
regression of the number of minutes per week spent making mobile
phone calls (Y) on an individual’s annual gross income in thousands of
dollars (X). The regression is estimated with data from a random
sample of 12 individuals. Assume that all assumptions of the
neoclassical simple linear regression model with multivariate
normally distributed random disturbances are satisfied. (sample regression line) (i)
Give a brief interpretation of the sample coefficient of determination valu () e obtained.
About 76% of the variation of the dependent variable in the sample is
explained by the estimated sample regression line. (ii)
Give an interpretation of the estimated slope coefficient .
It is thus estimated that for a
increase in gross annual income $1,000 ,
the mean (and predicted actual) number of minutes spent making
mobile phone calls each week increases by minutes 1.7396 .