

Preview text:
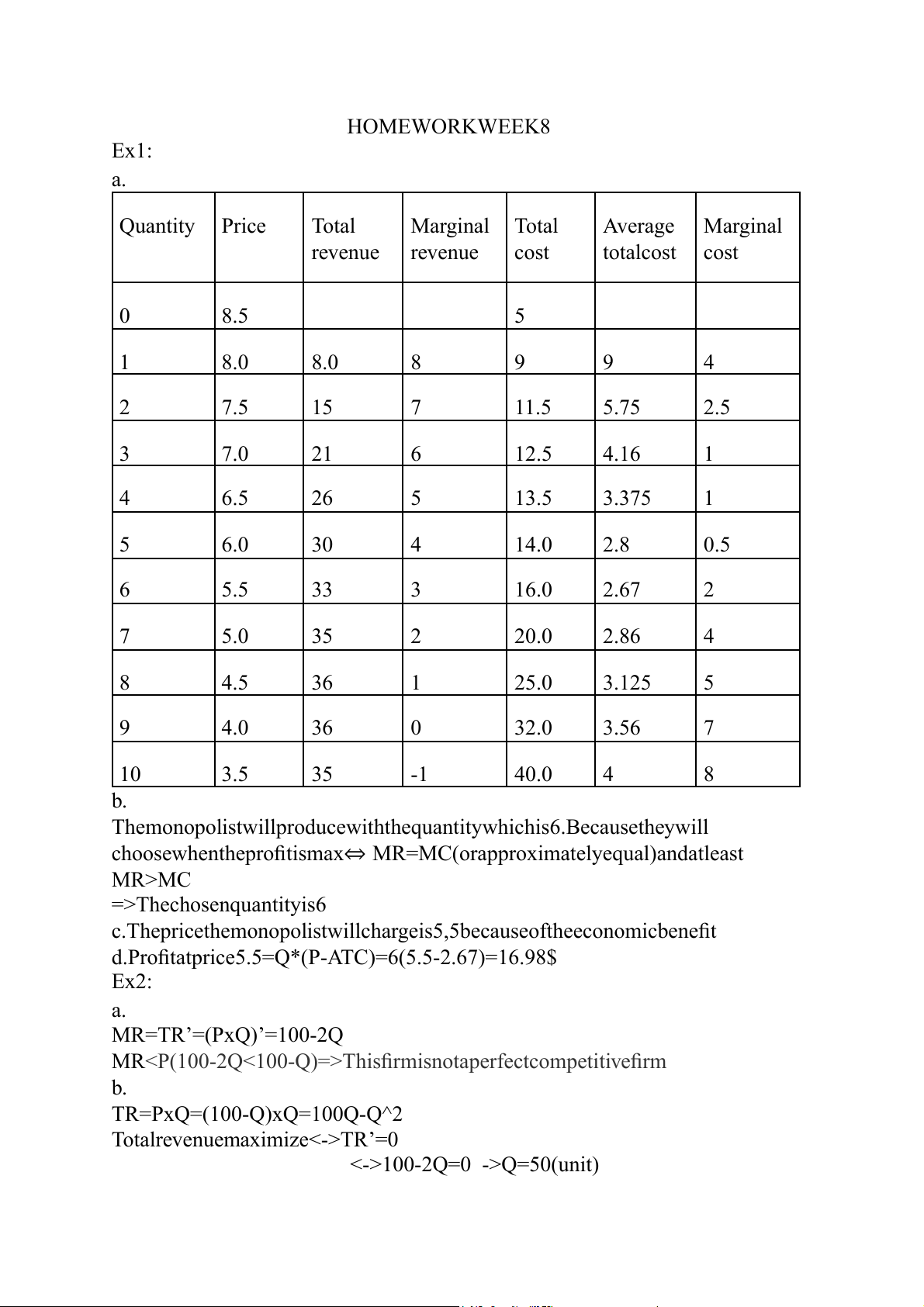
HOMEWORKWEEK8 Ex1: a. Quantity Price Total Marginal Total Average Marginal revenue revenue cost totalcost cost 0 8.5 5 1 8.0 8.0 8 9 9 4 2 7.5 15 7 11.5 5.75 2.5 3 7.0 21 6 12.5 4.16 1 4 6.5 26 5 13.5 3.375 1 5 6.0 30 4 14.0 2.8 0.5 6 5.5 33 3 16.0 2.67 2 7 5.0 35 2 20.0 2.86 4 8 4.5 36 1 25.0 3.125 5 9 4.0 36 0 32.0 3.56 7 10 3.5 35 -1 40.0 4 8 b.
Themonopolistwillproducewiththequantitywhichis6.Becausetheywill
choosewhentheprofitismax⇔ MR=MC(orapproximatelyequal)andatleast MR>MC =>Thechosenquantityis6
c.Thepricethemonopolistwillchargeis5,5becauseoftheeconomicbenefit
d.Profitatprice5.5=Q*(P-ATC)=6(5.5-2.67)=16.98$ Ex2: a. MR=TR’=(PxQ)’=100-2Q
MR
Thisfirmisnotaperfectcompetitivefirm b. TR=PxQ=(100-Q)xQ=100Q-Q^2
Totalrevenuemaximize<->TR’=0
<->100-2Q=0 ->Q=50(unit)
->P=100-Q=100-50=50($) ->TRmax=100x50-50^2=2500($)
-> Tomaximizetotalrevenue,thepriceis50$,thequantityis50unitsandthe maximumtotalrevenueis2500$.
c.Tomaximizeprofit⇔ MR=MC(TR’=TC’) ⇔ 100-2Q*=4+2Q* ⇔ Q*=24(units) =>P*=100-Q*=100-24=76($)
=>profitmax=TR-TC=(100*-Q*^2)-(500+4Q*+Q*^2) =-2Q*+96Q*-500=652($)
So,themaximumprofitof652$isreachedifandonlypriceis76$and optimalquantityis24units d.
- Ifthegovernmentimposesataxof8$perunitofgoodssold,thenew equation oftotalcostis:
TC=500+4Q+Q2 +8QàTC=Q2 +12Q+500($) → MC=2Q+12 TR=P.Q=(100-Q).Q=-Q2 +100Q → MR=-2Q+100
So,thefirmgetmaximizeprofitwhenMR=MC<=>2Q+12=-2Q+100 ⇔ Q=22 P=100–Q=78$ - Themaximumprofitis:
Π =TR–TC=(100Q–Q2)–(Q2 +12Q+500) Π =-2Q2 +88Q–500 Π =468$ e.
Supposingthatgovernmentimposesafixedtaxof100$:
TC=500+4Q+Q^2+100=>MC=TC’=4+2Q(sametoc,)
Accordingtoc,themaximumprofitisachievedwhenpriceis76$andoptimal quantityis24units
However,themaximumprofitwillbechanged:profitmax=TR-TC
=(100Q*-Q*^2)-(600+4Q*+Q*^2)=-2Q*^2+96Q*-600=552($)
Inconclusion,ifgovernmentimposesafixedtaxof100$,thisfirmneedsto
produce24unitsofoutputwiththepriceof76$togetthemaximumprofit thatis552$




