Exercise on Cost Analysis and Profit Maximization | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

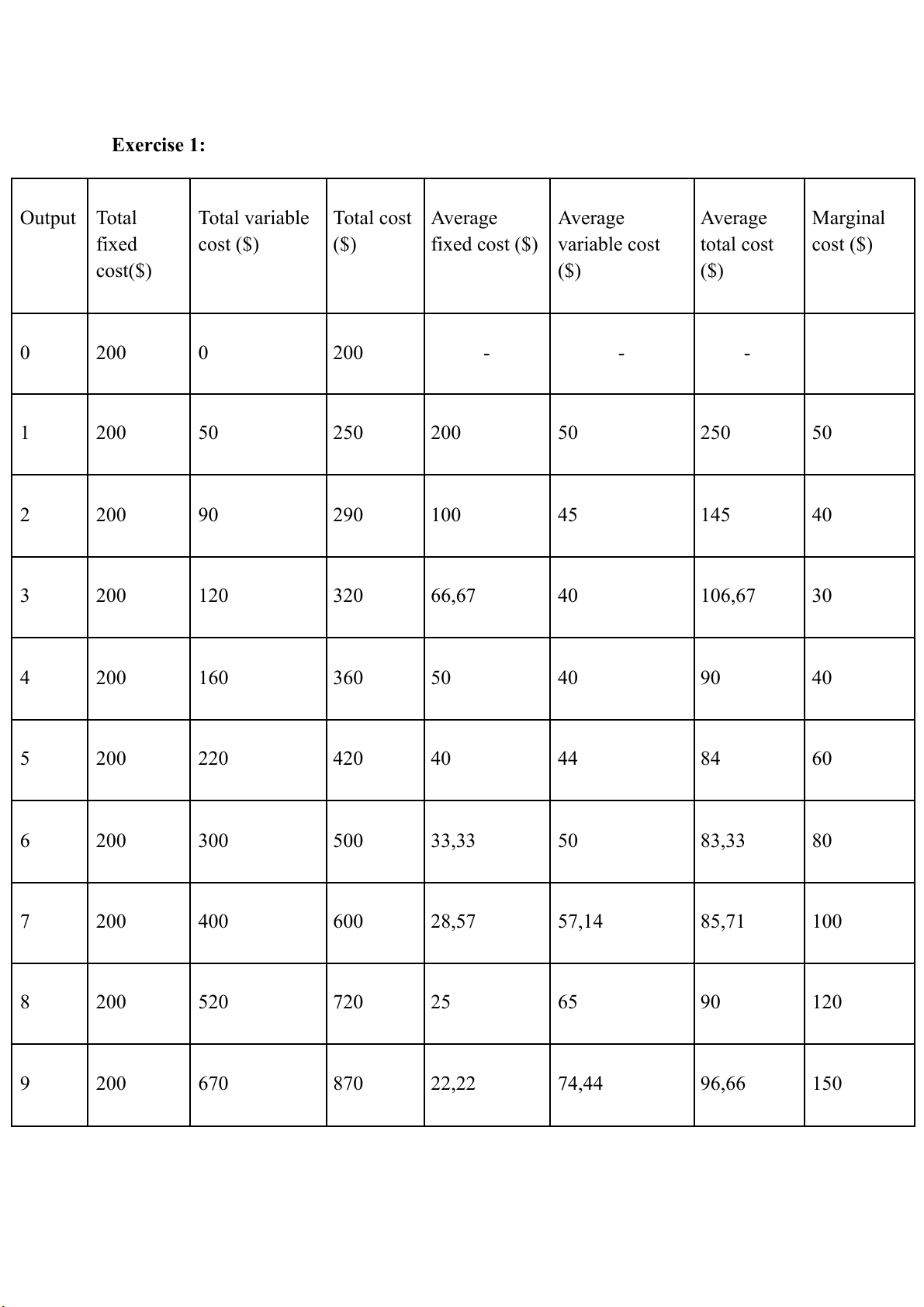
Exercise 1: Output Total
Total variable Total cost Average Average Average Marginal fixed cost ($) ($) fixed cost ($) variable cost total cost cost ($) cost($) ($) ($) 0 200 0 200 - - - 1 200 50 250 200 50 250 50 2 200 90 290 100 45 145 40 3 200 120 320 66,67 40 106,67 30 4 200 160 360 50 40 90 40 5 200 220 420 40 44 84 60 6 200 300 500 33,33 50 83,33 80 7 200 400 600 28,57 57,14 85,71 100 8 200 520 720 25 65 90 120 9 200 670 870 22,22 74,44 96,66 150 10 200 900 1100 20 90 110 230
b. If the price was 100$, what output would the firm produce and what type of
profit (or loss) would the firm make:
- If the price was 100$, MC ≤ R => MC ≤ 100 => Q ≤ 7 when Q = 7 => П = 0
when Q < 7 => П > 0 => profit
- Inverse, MC > R, MC > 100 => Q > 7 => П < 0 => loss
c. The profitable situation in the question b exist in the long – run is false, because:
- When profit increases, many businesses pay attention to this product and
promote industry => increase the supply curve => price decreases until П = 0.
- Therefore, if the profitable situation extends, businesses will receive only zero economic profit. Exercise 2:
1. What are TR, MC, FC, VC, AVC, AFC, ATC ?
- TR is the total revenue, TR = PxQ
- MC is marginal cost, the cost increasing to produce goods/service; MC = ∆TC /ΔQ
- VC is variable cost, VC = AVCxQ
- AVC is average variable cost, AVC = 𝑉𝐶 𝑄
- AFC is average fixed cost, AFC = 𝐹𝐶 𝑄
- ATC is average total cost, ATC = 𝑇𝐶 𝑄
2. Identify optimal output level (Q ) that gives the firm profit *
maximization? What is the maximum profit ?
- At Q = 4, MC = 21 = P = MR => at Q = Q* = 4, the firm profit max - The maximum profit:
PxQ = 21x4 = 84 and TC = 96 => Profit = -12 (actual loss-minimizing)
3. With the above profit (in the question 2), should the firm continue the production? Why?
- The firm should continue the produce, because:
+ FC = 50 (TC = 50 when Q = 0)
=> VC = TC - FC = 96 - 50 = 46 => AVC = 46 = 11,5 < P 4
+ Continuing the production, the firm can continue to pay the
average variable cost and a part of the fixed cost; have no heavy losing.
Exercise 3: A perfect competition firm has a demand equation of P=8 ($) and total cost equation of TC= 2 𝑄 + 2Q+ 4 ($) 1. TR equation: TR = PxQ =8Q
MR equation: MR = ∆𝑇𝑅 = 8 ∆𝑄 2. MC = ∆𝑇𝐶 = 2Q + 2 ∆𝑄
FC = 4 (when Q = 0 => TC = 4) VC = AVC xQ = TC - FC = 2 𝑄 + 2Q AVC = 𝑉𝐶 = Q + 2 𝑄 AFC = 𝐹𝐶 = 4 𝑄 𝑄 ATC = 𝑇𝐶 = Q + 2 + 4 𝑄 𝑄
3. What is optimal output level (Q ) that gives the firm profit *
maximization? What is the maximum profit ?
- The optimal output level: when MC = MR = P ∆𝑇𝐶 ∆𝑇𝑅 ⇔ = = 8 ∆𝑄 ∆𝑄 ⇔ ⇔ 2Q + 2 = 8 Q = 3
- The maximum profit: П = TR - TC = 8x3 - 19 = 5
4. What is break even price and break even quantity?
- Break even occurs when P = ATCP = ATC → TR = TCTR = TC, profit = 0 Q + 2 + 4 = 8 𝑄 ⇔ 2 𝑄 + 2Q+ 4 = 8Q ⇔ Q = 3 + and Q = 3 - 5 5
5. If market price decrease to P= 4$, should the firm continue the production? Why?
- Short-run shutdown rule: produce if P ≥ AVCP ≥ AVC at profit-max Q. - AVC = 𝑉𝐶 = Q + 2 𝑄
- At Q = 1 => AVC = 3 < P (P=4)
=> The firm should continue the production despite the possibility of losing
- At Q = 1 => TR = 4 and TC = 7 П = -3 < FC (FC = 4)
=> should continue producing