Giá trị lớn nhất, giá trị nhỏ nhất và cực trị của hàm trị tuyệt đối Toán 12

Giá trị lớn nhất, giá trị nhỏ nhất và cực trị của hàm trị tuyệt đối Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

43 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 1
GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT
CỰC TRỊ CỦA HÀM TRỊ TUYỆT ĐỐI
Các bài toán về hàm trị tuyệt đối đã bắt đầu xuất hiện trong đề tham khảo năm 2018 của
bộ và sau đó cũng đã trở thành trào lưu trên các diễn đàn, các nhóm, đồng thời xuất hiện
nhiều hơn trong các đề thi thử với các dạng và mức độ khác nhau. Một số có thể chưa phù
hợp với kì thi THPT Quốc Gia, nhưng tuy nhiên trong chuyên đề lần này tôi và các bạn sẽ
cùng nhau bắt tay giải quyết một số dạng toán tiêu biểu đó. Cũng nói thêm để hoàn thành
chuyên đề này tôi rất cảm ơn bên Vted đã có những đề thi vô cùng hay, các bài toán ở đây
đề bài hầu hết được lấy từ Vted và lời giải được thực hiện bởi những người bạn của tôi –
Ngô Nguyên Quỳnh và Nguyễn Hải Linh . Mặt khác cũng vì công việc và thời gian không
có nhiều nên tôi không để đưa thêm nhiều dạng hay khác xuất hiện trong một số đề thi
của các thầy trên mạng được, mong bạn đọc bỏ qua. Mọi ý kiến đóng góp xin gửi về địa
chỉ sau:
NGUYỄN MINH TUẤN – K14 ĐẠI HỌC FPT
Email: tuangenk@gmail.com
Nào bây giờ chúng ta cùng bắt đầu nhé!
I. MỞ ĐẦU.
Bài toán mở đầu
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
3
3f x x x m
trên đoạn
0;2
bằng 3. Số phần tử của S là?
A.
1
B.
2
C.
0
D.
6
Câu 36 – Đề tham khảo THPT Quốc Gia môn toán 2018
Lời giải
Ta có
Xét hàm số
3
3f x x x
trên đoạn
0;2
thì
2
' 3 3f x x
nên
' 0 1f x x
So sánh các số
0 , 1 , 2f f f
ta có
0;2
0;2
min 2,max 2fx
ta có :
33
0;2
0;2
min 3 3 max 3 3 1 1x x m x x m
Đây chỉ là các điều kiện cần của m, ta thử lại như sau
Với
1m
thì với
2x
ta sẽ có
2 1 3yf
Với
1m 
thì với
1x
ta sẽ có
2 1 3yf
Với
0m
thì với
2y f x
nên không thể có giá trị lớn nhất là 3.
Vậy
1;1S 
nên có tất cả 2 giá trị thỏa mãn yêu cầu đề bài.
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
2 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Nhận xét: Đây là một câu trong đề tham khảo thi THPT Quốc Gia 2018 của Bộ , nhìn
chung thì đây là một câu vận dụng cao cần phải có kiến thức về bất đẳng thức trị tuyệt đối
cũng như những phép biến đổi có liên quan.
Bất đẳng thức trị tuyệt đối.
Cho 2 số thực a,b khi đó ta có
a b a b a b
Dấu “=” thứ nhất khi a,b cùng dấu, dấu “=” thứ 2 khi a,b trái dấu.
I. CÁC BÀI TOÁN LIÊN QUAN TỚI ĐIỂM CỰC TRỊ CỦA HÀM SỐ
A. CÁC TÍNH CHẤT LIÊN QUAN TỚI CỰC TRỊ CỦA HÀM TRỊ TUYỆT ĐỐI
Trước khi đi vào các bài toán ta cần nhớ những kiến thức sau.
Số điểm cực trị của hàm số
fx
bẳng tổng số điểm cực trị của hàm số
fx
và số
lần đổi dấu của hàm số
fx
.
Số điểm cực trị của hàm số
f mx n
bằng
21a
, trong đó a là số điểm cực trị lớn
hơn
n
m
của hàm số
fx
Số điểm cực trị của hàm số
fx
bằng
21a
, trong đó a là số điểm cực trị dương
của hàm số.
Cho hàm số có dạng
2
y ax bx c mx
, tìm điều kiện của tham số m để giá trị
cực tiểu của hàm số đạt giá trị lớn nhất, khi đó ta có

max
ct
yc
mb
Câu 1: Biết phương trình
32
0 0ax bx cx d a
có đúng hai nghiệm thực. Hàm số
32
y ax bx cx d
có bao nhiêu điểm cực trị.
A.
3.
B.
5.
C.
4.
D.
2.
Lời giải
Vì phương trình
32
0 0ax bx cx d a
có đúng hai nghiệm thực nên hàm số
32
y ax bx cx d
có hai điểm cực trị.
Mặt khác
2
32
12
ax bx cx d a x x x x
.Do đó phương trình
32
0ax bx cx d
có
một nghiệm đơn và một nghiệm kép.
Vậy số điểm cực trị của hàm số
32
y ax bx cx d
bằng
2 1 3.
Chọn đáp án A.
Câu 2: Có bao nhiêu số nguyên
20;20m
để hàm số
2
2 2 1y x x m x
có ba
điểm cực trị.
A.
17.
B.
16.
C.
19.
D.
18.
Lời giải
Nếu
2
2 0,x x m x
thì
22
2 2 1 1y x x m x x m
có đúng một điểm cực trị
0x
(loại).
Nếu
2
20x x m
có hai nghiệm phân biệt
12
1 0 1x x m m
.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 3
2
2
2
2
2
2
2 2 2 0
0
0
20
2 2 2
2 0 0
2; 0
2
2
2 2 2 0
2
0
20
20
x
x
x
x x m
x x x m
x x m m
yy
x
x
x
x x m
m
x x m
x x m






+) Với
01m
rõ ràng không có số nguyên nào
+) Với
0m
ta có bảng xét dấu của
y
như hình vẽ dưới đây
Lúc này hàm số có 3 điểm cực trị. Vậy
19,...,1 .m
Chọn đáp án C
Câu 3: Biết phương trình
42
0 0ax bx c a
bốn nghiệm thực. Hàm số
42
y ax bx c
có bao nhiêu điểm cực trị.
A.
7.
B.
5.
C.
4.
D.
6.
Lời giải
Vì phương trình
42
0 0ax bx c a
bốn nghiệm thực nên hàm số
2
40
00
0
b ac
b
S ab
a
c
P
a

do đó hàm số
42
0ax bx c
có 3 điểm cực trị
Mặt khác
42
1 2 3 4
ax bx cx d a x x x x x x x x
nên phương trình
42
0ax bx c
có 4nghiệm đơn. Vậy hàm số
42
y ax bx c
có
4 3 7
cực trị.
Câu 4: Cho hàm số
42
2 1 2 3 .y x m x m
Có bao nhiêu số nguyên không âm
m
để
hàm số đã cho có ba điểm cực trị.
A.
3.
B.
4.
C.
5.
D.
6.
Lời giải
Xét hàm số
42
2 1 2 3f x x m x m
4
1 0 1 1m m f x x
có 1 điểm cực trị
0x
và phương trình
0fx
có hai
nghiệm phân biệt. do đó hàm số
y f x
có 3 điểm cực trị (thỏa mãn)
42
1 0 0 2 3m m f x x x
có 1 điểm cực trị
0x
và phương trình
0fx
có 2
nghiệm đơn phân biệt. do đó hàm số
y f x
có 3 điểm cực trị (thỏa mãn)
Ta có
1 0 1mm
khi đó
fx
có ba điểm cực trị. Vậy yêu cầu bài tóan lúc này tương
đương với
0fx
vô nghiệm hoặc có nghiệm kép, tức
22
1 2 3 0 2 0 2m m m m
. Vậy
0, 1, 2m
. Chọn đáp án A
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
4 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 5: Cho hàm số
42
2 1 2 3 .y x m x m
Tập hợp tất cả các giá trị thực của tham
số
m
để hàm số đã cho có đúng
5
điểm cực trị là
A.
3
1; .
2



B.
3
; \ 2 .
2




C.
1; \ 2 .
D.
3
1; .
2


Lời giải
Xét
2
2
2
2
4 2
1
0 1 2 3 02 1 2 3
23
x
f x f x x x mx
xm
m x m


TH1: Nếu
2 3 0m
Do vậy
fx
có 2 điểm đổi dấu
1; 1xx
. Hàm số
y f x
có 5
điểm cực trị
y f x
có ba điểm cực trị
0 2 1 0 1ab m m
Vậy trường hợp này có
3
1
2
m
TH2: Nếu
3
0 2 3 1 2
2
mm
. Khi đó
fx
có bốn điểm đổi dấu
1; 2 3x x m
do đó số điểm cực trị của hàm số
fx
bằng 3 và hàm số
y f x
có
7 cực trị(loại).
TH3: nếu
2
2
2 3 1 2 1m m f x x
khi đó
2
2
1y f x x
có 3 điểm cực trị
(loại).
Chọn đáp án D
Câu 6: Có bao nhiêu số nguyên
20;20m
để hàm số
42
1y x m x m
có 7 điểm
cực trị.
A.
18.
B.
20.
C.
19.
D.
21.
Lời giải
Xét
4 2 2 2
1 1; 1x m x m x mx 
vậy để hàm số
42
1y x m x m
có 7 điểm
cực trị khi và chỉ khi phương trình
1
có 4 nghiệm phân biệt
0
2,...,19
1
m
m
m
. có
18 số nguyên thỏa mãn. Chọn đáp án A
Câu 7: Có bao nhiêu số nguyên
20;20m
để hàm số
22
2y x x m
có đúng 5 điểm
cực trị.
A.
1.
B.
17.
C.
2.
D.
16.
Lời giải
Có
2 2 2 2 4 2
2 2 2 2 .y x x m x x m x m x m
Nếu
42
0 2 2 0,m x m x m x
nên hàm số đã cho có tối đa ba điểm cực trị (loại).
Nếu
4 2 2
0 2 2 0 .m x m x m x m x m
Vậy điều kiện là hàm số
42
22y x m x m
có ba điểm cực trị
2 0 2 3,...,19 .m m m
Có 17 số
nguyên thoả mãn.
Chọn đáp án B.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 5
Câu 8: Có bao nhiêu số nguyên
m
để hàm số
3 2 2 2
2 1 2 2 9 2 9y x m x m m x m
có 5 điểm cực trị.
A.
7.
B.
5.
C.
6.
D.
4.
Lời giải
2 2 2
22
22
3
2 1 2 2 9 2 9
1
1 2 2 9
2 2 9 0
m x m m x m
x
x x mx m
x mx
t
m
ycb x
Có 3 nghiệm phân biệt
22
2
33
2 9 0
2, 1,0,1, 2
1 17
1 2 2 9 0
2
m
mm
m
m
mm




Câu 9: Có bao nhiêu số nguyên
m
để hàm số
3
22
3 3 4 | | 1y x mx m x
có đúng 3
điểm cực trị.
A.
3.
B.
5.
C.
6.
D.
4.
Lời giải
Ta có
3 2 2
3 3 4 1ycbt y x mx m x
có đúng một điểm cực trị dương
22
0 3 6 3 4 0 2; 2y x mx m x m x m
có đúng một nghiệm dương
2 0 2 2 2 1,0,1, 2 .m m m m
Chọn đáp án D.
Câu 10: Có bao nhiêu số nguyên
10;10m
để hàm số
3
22
3 3 4 | | 1y x mx m x
có đúng 5 điểm cực trị.
A.
3.
B.
6.
C.
8.
D.
7.
Lời giải
Ta có
3 2 2
3 3 4 1ycbt y x mx m x
có hai điểm cực trị dương
22
0 3 6 3 4 0 2; 2y x mx m x m x m
có hai nghiệm dương
2 0 3,...,9 .mm
Chọn đáp án D.
Câu 11: Có bao nhiêu số nguyên
m
để hàm số
53
3 15 60y x x x m
có 5 điểm cực trị.
A.
289.
B.
287.
C.
286.
D.
288.
Lời giải
Xét
53
3 15 60y x x x
có
4 2 2
0 15 45 60 0 4 2y x x x x
Vậy hàm số
53
3 15 60y x x x
có đúng 2 điểm cực trị
2; 2xx
Bảng biến thiên
Vậy để hàm số có 5 điểm cực trị
5 3 5 3
3 15 60 0 3 15 60x x x m m x x x
có tổng
số nghiệm đơn và bội lẻ bằng 3, tức
144 144 144 144 143,..,143m m m
.
Có 287 số nguyên thỏa mãn. Chọn đáp án B
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
6 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 12: Có bao nhiêu số nguyên
2019; 2019m
để hàm số
2
4 6 1y x x m x
có
ba điểm cực trị.
A.
2014.
B.
2016.
C.
2013.
D.
2015.
Lời giải
Nếu
2 2 2
4 0, 4 6 21 1x x m x y x x m x x xm 
có đúng 1 điểm cực trị
1x 
(loại).
Nếu
2
40x x m
có hai nghiệm phân biệt
12
4 0 4x x m m
Khi đó
2
2
2
2
2 4 6 0
1
24
5
6; 0
5
24
40
4
4
40
60
5
x x m
x x m
x x m
xx
x
x
x
m
y
x
m
m
y
x






Với
54m
ta có bằng xét dấu của
y
như sau
Hàm số có đúng 1 cực trị
1x 
(loại).
Với
5m 
ta có bằng xét dấu của
y
như sau
Hàm số có 3 điểm cực trị
12
; 5;x x x x x
Vậy
2018,..., 6m
. Có 2013 số nguyên thỏa mãn. Chọn đáp án C
Câu 13: Có bao nhiêu số nguyên
20;20m
để hàm số
2
2 1 1y x m x m
có ba
điểm cực trị.
A.
17.
B.
19.
C.
18.
D.
20.
Lời giải
Ta có
2
2
2 1 1 0 2 2 1 0
2 2 1 0
2 1 1 0
x m x m x m x m x m
yy
x m x m
x m x m x m


Vậy hàm số không có đạo hàm tại điểm
1xm
và
2 2 0
1 0 1 0
1
2 2 0
2
1 0 2 1 0
x m x m
xm
xm
y
x m m
x m x m
x m m
















Vậy để hàm số có 3 điểm cực trị trước tiên phải có
1
2
m
và lúc này bảng xét dấu của
y
như sau
Điều này chứng tỏ với
1
2
m
là các giá trị cần tìm, các số nguyên là
1,...,19m
. Có tất cả
19 số nguyên thỏa mãn.
Câu 14: Có tất cả bao nhiêu số nguyên
m
thuộc đoạn
2017;2017
để hàm số
32
3y x x m
có 3 điểm cực trị ?
A.
4032.
B.
4034.
C.
4030.
D.
4028.
Lời giải
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 7
Ta có
32
3y x x m
có
2
0
3 6 ; 0 0 , 2 4
2
x
y x x y y m y m
x

Yêu cầu đề bài tương đương với
4
0 . 2 0 4 0
0
m
y y m m
m
Do đó
2017,..., 2017m
có
2018 2014 4032
số nguyên thỏa mãn.
Chọn đáp án A
Câu 15: Tìm tất cả các giá trị thực của tham số
m
để hàm số
32
3y x x m
có 5 điểm
cực trị.
A.
4 0.m
B.
4 0.m
C.
0 4.m
D.
4m
hoặc
0.m
Lời giải
Ta có
32
3y x x m
có
2
0
3 6 ; 0 0 , 2 4
2
x
y x x y y m y m
x

Yêu cầu đề bài tương đương với
0 . 2 0 4 0 0 4y y m m m
Chọn đáp án C
Câu 16: Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
42
y x mx m
có 7
điểm cực trị.
A.
4; .
B.
0;1 .
C.
0; 4 .
D.
1; .
Lời giải
Xét hàm số
42
y x mx m
có tối đa 3 điểm cực trị và phương trình
0fx
có tối đa 4
nghiệm. Vì vậy hàm số
y f x
có 7 điểm cực trị khi và chỉ khi
0fx
có 4 nghiệm
phân biệt và
0fx
có 3 nghiệm phân biệt
2
40
0, 0 4
0
m
S m P m m
ab m
Chọn đáp án A
Câu 17: Cho hàm số
32
f x ax bx cx d
thoả mãn
0, 2018, 2018 0.a d a b c d
Tìm số điểm cực trị của hàm số
2018 .y f x
A.
3.
B.
5.
C.
2.
D.
1.
Lời giải
Xét
2018g x f x
ta có
lim ;lim
0 0 2018 2018 0
1 1 2018 2018 0
xx
g x g x
g f d
g f a b c d

 
Do đó đồ thị hàm số
y g x
cắt trục hoành tại ba điểm phân biệt và suy ra hàm số
y g x
có hai điểm cực trị
Do vậy số điểm cực trị của đồ thị hàm số
y g x
là
2 3 5
Chọn đáp án B
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
8 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 18: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2
3 4 12y x x x m
có
7 điểm cực trị ?
A.
3.
B.
5.
C.
6.
D.
4
Lời giải
Hàm số
4 3 2
3 4 12f x x x x m
có ba điểm cực trị là nghiệm của phương trình
3 2 2
0
0 12 12 24 0 12 2 0 1
2
x
f x x x x x x x x
x
Phương trình
0fx
có tối đa 4 nghiệm thực. Do đó hàm số
y f x
có 7 điểm cực trị
khi và chỉ khi phương trình
0fx
có 4 nghiệm thực phân biệt
4 3 2
3 4 12x x x m
có 4 nghiệm thực phân biệt. Lập bảng biến thiên của hàm số
4 3 2
3 4 12y x x x
ta có giá
trị cần tìm
5 0 0 5 1; 2;3; 4m m m
có 4 số nguyên thỏa mãn.
Câu 19: Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4 3 2
5y x x x m
có 7
điểm cực trị.
A.
8.
B.
9.
C.
3.
D.
4
Lời giải
Hàm số
4 3 2
5f x x x x m
có ba điểm cực trị là
5
0; 2; .
4
x x x
Vậy hàm số
y f x
có 7 điểm cực trị
0fx
có bốn nghiệm phân biệt
875 875
0 0 .
256 256
mm
Vậy
1; 2; 3 .m
Chọn đáp án C.
Câu 20: Cho hàm số đa thức bậc bốn
y f x
có ba điểm cực trị
1; 2; 3.x x x
Có bao
nhiêu số nguyên
10;10m
để hàm số
y f x m
có 7 điểm cực trị.
A.
8.
B.
10.
C.
2.
D.
19.
Lời giải
Hàm số
y f x m
có 7 cực trị
f x m
có 3 điểm cực trị lớn hơn
m
Các điểm cực trị của hàm số
y f x m
là
11
22
33
x m x m
x m x m
x m x m





Vậy ta có điều kiện là
1
2 9,...,9
3
mm
m m m m
mm
. Chọn đáp án D
Câu 21: Cho hàm số
3
5.y x mx
Gọi
a
là số điểm cực trị của hàm số đã cho. Mệnh đề
nào dưới đây đúng ?
A.
0.a
B.
1.a
C.
1 3.a
D.
3.a
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 9
Lời giải
Ta có
32
32
5 0 3 0
5 0 3 0
x mx x x m x
yy
x mx x x m x




và hàm số không có đạo hàm tại điểm
0x
Nếu
2
2
3 0 0
0
3 0 0
xx
my
xx

đổi dấu từ âm sang dương khi qua điểm
0x
nê hàm số
có duy nhất 1 điểm cực trị là
0x
Nếu
2
2
30
00
3
3 0 0
x m x
m
m y y x
x m x


chỉ đổi dấu khi đi qua
3
m
x
nên có duy nhất 1 điểm cực trị là
3
m
x
Nếu
2
2
3 0 0
00
3
30
x m x
m
m y y x
x m x

Chỉ đổi dấu khi đi qua
3
m
x

nên có duy nhất 1 điểm cực trị là
3
m
x

Vậy với mọi
m
hàm số có duy nhất 1 điểm cực trị
Chọn đáp án B
Câu 22: Tìm tất cả các giá trị thực của tham số
m
để hàm số
3
2
2 1 3 5y x m x m x
có 5 điểm cực trị.
A.
1
; 1; .
4




B.
11
; 1; .
24



C.
1; .
D.
1
0; 1; .
4




Lời giải
yêu cầu bài toán tương đương hàm số
32
2 1 3 5y x m x mx
có 2 điểm cực trị dương,
tức
2
3 2 2 1 3 0m x mx
có 2 nghiệm dương phân biệt, tức
2
2 1 9 0.
1
2 2 1
0
1
3
0
4
3
0
3
mm
m
m
S
m
m
P


chọn đáp án D
Câu 23: Cho hàm số
32
2 1 2 2.f x x m x m x
Tìm tập hợp giá trị thực của
tham số
m
để hàm số
y f x
có năm điểm cực trị.
A.
5
2.
4
m
B.
5
2.
4
m
C.
1
2.
2
m
D.
5
2.
4
m
Lời giải
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
10 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Ta có
5 2 1 2aa
là số điểm cực trị dương của hàm số
y f x
Ta có
2
2
2 1 3 2 0
2 2 1
5
3 2 2 1 2 0 2.
34
2
0
3
mm
m
f x x m x m S m
m
P

Chọn đáp án B
Câu 24: Tìm tất cả các giá trị thực của tham số
m
để hàm số
3
2
2 1 3 5y x m x m x
có 3 điểm cực trị.
A.
;0 .
B.
1; .
C.
;0].
D.
1
0; .
4


Lời giải
xét
32
2 1 3 5f x x m x mx
và
3
2
2 1 3 5f x x m x m x
ta có
3 2 1 1aa
là số điểm cực trị dương của hàm số
y f x
vậy yêu cầu tương đương với:
fx
có đúng 1 điểm cực trị dương
0fx

có 2 nghiệm
thỏa mãn
12
00x x m
Câu 25: Cho hàm số
4 3 2
, , , ,f x ax bx cx dx e a b c d e
và
0.a
Biết
1 0, 0 0, 1 0.f f f
Số điểm cực trị của hàm số
y f x
bằng
A.
7.
B.
6.
C.
5.
D.
9.
Lời giải
Theo giả thiết ta có:
1 2 3 4
lim
lim . 1 0
10
0 . 1 0
0 0 1 0 1
0 . 1 0
10
lim . 1 0
lim
x
x
x
x
fx
f x f
f
ff
f x x x x
ff
f
f x f
fx











Sao cho
1 2 3 4
0; 0; 0; 0.f x f x f x f x
Điều đó chứng tỏ rằng phương
trình
0fx
có 4 nghiệm phân biệt, do đó hàm số
fx
phải có 3 điểm cực trị. Vì vậy hàm
số
y f x
có
4 3 7
điểm cực trị. Chọn đáp án A
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 11
Câu 26: Cho hàm số
y f x
có đồ thị
như hình vẽ ở bên. Tìm tập hợp tất cả
các giá trị thực của tham số
m
để hàm số
y f x m
có 5 điểm cực trị.
A.
1.m 
B.
1.m 
C.
1.m
D.
1.m
Lời giải
Hàm số
fx
có 2 điểm cực trị
1; 1.xx
hàm số
(| | )f x m
luôn có 1 điểm cực trị
0x
Phá trị tuyệt đối có
0
(| | .
0
f x m x
y f x m
f x m x

Hàm số
f x m
có 2 điểm cực trị là
1; 1 1 ; 1x m x m x m x m
Hàm số
f x m
có 2 điểm cực trị là
1; 1 1 ; 1x m x m x m x m
Vậy điều kiện là
10
10
1.
10
10
m
m
m
m
m


Chọn đáp án A
Câu 27: Có bao nhiêu số nguyên
m
để hàm số
53
3 25 60y x x x m
có 7 điểm cực trị.
A.
42.
B.
21.
C.
44.
D.
22.
Lời giải
Hàm số
53
3 25 60f x x x x m
có 4 điểm cực trị là nghiệm của phương trình
42
0 15 75 60 0 2; 1.f x x x x x
Do đó hàm số
y f x
có 7 điểm cực trị khi và chỉ khi phương trình
0fx
có tổng số
nghiệm đơn và bội lẻ bằng 3. Khảo sát hàm số dễ có
38 m 16 16 38
16 38 38 m 16
m
m



do đó có
21 21 42
số nguyên thỏa mãn. Chọn đáp án A.
Câu 28: Cho hàm số
4 3 2
3 4 12 .f x x x x
Có bao nhiêu số nguyên
10m 
để hàm số
y f x m
có
7
điểm cực trị.
A.
9.
B.
11.
C.
10.
D.
8.
Lời giải
có
3 2 2
0
12 12 24 ; 0 12 2 0 1
2
x
f x x x x f x x x x x
x

O
1
1
x
2
4
y
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
12 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
do đó hàm số
fx
có 3 điểm cực trị
0; 1; 2x x x
hàm số
f x m
luôn có 1 điểm cực trị
0x
phá trị tuyệt đói có
0
.
0
f x m x
y f x m
f x m x

Hàm số
f x m
có 3 điểm cực trị là
1; 0; 2 1; ; 2 .x m x m x m x m x m x m
Hàm số
f x m
có 3 điểm cực trị là
1; 0; 2 1; ; 2.x m x m x m x m x m x m
Do đó hàm số
f x m
có tối đa 7 điểm cực trị là
0; 1; ; 2; 1; ; 2 .x x m x m x m x m x m x m
Điều kiện bài toán tương đương với
10
0
20
1 9, 8,..., 2
10
0
20
m
m
m
mm
m
m
m



Có tất cả 8 số nguyên thỏa mãn. Chọn đáp án D
Câu 29: Có bao nhiêu số nguyên
m
để hàm số
42
4y x x m
có 7 điểm cực trị.
A.
5.
B.
15.
C.
3.
D.
13.
Lời giải
Hàm số
42
4f x x x m
có 3 điểm cực trị. Vậy hàm số
fx
có 7 cực trị khi và chỉ khi
phương trình
0fx
có 4 nghiệm phân biệt, tức
40
0 4 1;2;3
4 0, 0
m
mm
S P m
có 3 số nguyên thỏa mãn. Chọn đáp án D
Câu 30: Cho hàm số
y f x
có đạo hàm
22
1 2 5 .f x x x x mx
Có bao nhiêu giá
trị nguyên
10m 
để hàm số
y f x
có
5
điểm cực trị.
A.
7.
B.
9.
C.
6.
D.
8.
Lời giải
Yêu cầu bài tóan tương đương với
fx
có đúng 2 điểm cực trị dương, tức
2
2 5 0x mx
có 2 nghiệm dương phân biệt, tức
2
50
5 9, 8,..., 3
2 0, 5 0
m
mm
S m P

có tất cả 7 số nguyên thỏa mãn.
Chọn đáp án A
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 13
Câu 31: Cho hàm số
fx
có đạo hàm
3
25
2
1 3 4 3 , .f x x x m m x x
Có bao nhiêu số nguyên
m
để hàm số
y f x
có 3 điểm cực trị.
A.
3.
B.
6.
C.
4
D.
5.
Lời giải
Yêu cầu bài toán tương đương
fx
có một điểm cực trị dương, tức
22
3 4 0x m m
có
nghiệm dương, tức
2
3 4 0 1 4 0,1,2, 3 .m m m m
Chọn đáp án C.
Câu 32: Cho hàm số
2018 4 2018 2 2 2018
1 (2 2 3) 2020.f x m x m m x m
Hàm số
2019y f x
có bao nhiêu điểm cực trị.
A.
7.
B.
3.
C.
5.
D.
6.
Lời giải
Vì
fx
là hàm số trùng phương có
8 2018 2
1 2 2 3 0,ab m m m m
nên hàm số
fx
có 3 điểm cực trị và hàm số
2019fx
cũng có 3 điểm cực trị.
2018 4 2018 2 2 2018
2018 4 2018 2 2 2018
2019 0 (2 2 3) 2020 2019
(2 2 3) 1 0
1
1
f x m x m m x m
m x m m x m
Phương trình này luôn có 4 nghiệm thực phân biệt vì
2
2018 2 2 2018
2018 2
2018
1
0
1
1
(2 2 3) 4 0
2 2 3
0
m m m
mm
S
P
m

Do đó
fx
có 4 nghiệm đổi dấu. vậy số điểm cực trị của đồ thị hàm số
2019y f x
bằng
3 4 7
chọn đáp án A
Câu 33: Cho hàm số
32
2 1 2 1.f x x m x m x
Có bao nhiêu số nguyên
5;5m
để hàm số
y f x
có đúng ba điểm cực trị.
A.
4.
B.
6.
C.
5.
D.
3.
Lời giải
Hàm số
y f x
có đúng 3 điểm cực trị khi và chỉ khi hàm số
y f x
có đúng một điểm
cực trị dương. Điều này tương đương với
2
0 3 2 2 1 2 0f x g x x m x m
có
hai nghiệm phân biệt
12
xx
thỏa mãn
12
3 2 0
3. 0 0
20
02
00
2 2 1
0
0
3
m
g
m
x x m
g
m
S




Vậy
5, 4, 3m
có 3 số nguyên thỏa mãn. Chọn đáp án D
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
14 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Câu 34: Cho hàm số
32
2 1 2 1.f x x m x m x
Có bao nhiêu số nguyên
5;5m 
để hàm số
y f x
có năm điểm cực trị.
A.
4.
B.
6.
C.
5.
D.
3.
Lời giải
Hàm số
y f x
có đúng 5 điểm cực trị khi và chỉ khi hàm số
y f x
có hai điểm cực trị
dương. Điều này tương đương với
2
0 3 2 2 1 2 0f x g x x m x m
có hai
nghiệm phân biệt
12
xx
thỏa mãn
2
12
3 2 0
3. 0 0
0 0 2 1 3 2 0 1
0
2 2 1
0
3
m
g
x x m m m
S
m

Vậy
2, 3, 4, 5m
có 4 số nguyên thỏa mãn. Chọn đáp án A
Câu 35: Có bao nhiêu số nguyên
20;20m
để hàm số
2
2 6 1y x m x m
có ba
điểm cực trị.
A.
17.
B.
16.
C.
18.
D.
15.
Lời giải
Ta có
2
2
2 6 6 0 2 2 6 0
2 2 6 0
2 6 6 0
x m x m x m x m x m
yy
x m x m
x m x m x m


Vậy hàm số không có đạo hàm tại điểm
6xm
và
2 2 0
60
0
3
2 2 0
2 6 0
60
xm
xm
xm
xm
xm
y
x m m
xm
m
xm



Vậy để hàm số có 3 điểm cực trị trước tiên ta phải có
3m
và lúc này bảng xét dấu của
y
như sau: Điều này chứng tỏ với
3m
là giá trị cần tìm, các số nguyên là
4,...,19m
có
tất cả
16
số nguyên thỏa mãn.
Câu 36: Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
32
3x x m
ye

có 5
điểm cực trị.
A.
;0 4; . 
B.
0;2 .
C.
;0] [2; .
D.
0; 4 .
Lời giải
Số điểm cực trị của hàm số
fx
e
bằng số điểm cực trị của hàm số
.fx
Do đó yêu cầu bài toán tương đương với
32
0 3 0f x x x m
có ba nghiệm phân
biệt
4 0 0 4.m m m
Chọn đáp án D.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 15
Câu 37: Có bao nhiêu số nguyên
10m
để hàm số
3
1y x mx
có
5
điểm cực trị.
A.
9.
B.
7.
C.
11.
D.
8.
Lời giải
yêu cầu bài tóan tương đương hàm số
3
1f x x mx
có hai điểm cực trị và phương
trình
0fx
có ba nghiệm thực phân biệt ta có
2
3 ; 0 0 .
3
m
f x x m f x x m

và
33
9 2 3 9 2 3
;
3 9 3 9
m m m m
ff

khi đó điều kiện để có 3 nghiệm phân biệt là
3
3
3
. 0 81 12 0
33
4
mm
f f m m
chọn đáp án D. chú ý các em có thể đưa về xét hàm số
2
1
.mx
x

cho kết quả tương tự
Câu 38: Có bao nhiêu số nguyên
10;10m 
để hàm số
32
3 3 2 2y mx mx m x m
có 5 điểm cực trị.
A.
7.
B.
10.
C.
9.
D.
11.
Lời giải
Yêu cầu đề bài tương đương phương trình
3 2 2
3 3 2 2 0 1 2 2 0mx mx m x m x mx mx m
có ba nghiệm phân biệt
2
0
2 0 0 1, 2,...,10
2 2 0
m
m m m m m
m m m
có tất cả 10 giá trị
Chọn đáp án B
Câu 39: Cho hàm số
y f x
có đạo hàm
3 2 3
2 2 ,f x x x x x
với mọi
.x
Hàm
số
1 2018y f x
có nhiều nhất bao nhiêu điểm cực trị.
A.
9.
B.
2022.
C.
11.
D.
2018.
Lời giải
Có
3
2 2 2 .f x x x x x
Do đó hàm số
fx
có 4 điểm cực trị là
0; 2; 2.x x x
Lập bảng biến thiên của hàm số
fx
suy ra
0fx
có tối đa 5
nghiệm phân biệt. Do đó hàm số
y f x
có tối đa
4 5 9
điểm cực trị.
Mặt khác số điểm cực trị của hàm số
1 2018y f x
bằng số điểm cực trị của hàm số
.y f x
Do đó hàm số
1 2018y f x
có tối đa 9 điểm cực trị. Chọn đáp án A.
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
16 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
II. CÁC BÀI TOÁN LIÊN QUAN TỚI MIN MAX CỦA HÀM TRỊ TUYỆT
ĐỐI
A. CÁC TÍNH CHẤT LIÊN QUAN TỚI CỰC TRỊ CỦA HÀM TRỊ TUYỆT ĐỐI
Bất đẳng thức trị tuyệt đối.
Cho 2 số thực a,b khi đó ta có
a b a b a b
Dấu “=” thứ nhất khi a,b cùng dấu, dấu “=” thứ 2 khi a,b trái dấu.
Tính chất hàm trị tuyệt đối
max ,
2
a b a b
ab
Phương pháp chung
Bước 1: Xét hàm số
y f x
, trên
;ab
.
Tính đạo hàm:
''y f x
.
Giải phương trình
'0fx
và tìm các nghiệm
i
a
thuộc
;ab
.
Bước 2: Giải phương trình
0fx
và tìm các nghiệm
j
b
thuộc đoạn
;ab
.
Bước 3: Tính các giá trị:
; ; ;
ij
f a f b f a f b
. So sánh và kết luận.
Câu 1: Có bao nhiêu số thực m để hàm số
2 3 2
3 4 12y x x x m
có giá trị lớn nhất trên
đoạn
3; 2
bằng 150?
A.
4
B.
0
C.
2
D.
6
Lời giải
Xét
4 3 2
3 4 12u x x x m
trên đoạn
3; 2
ta có:
32
' 0 12 12 24 0 0; 1; 2.u x x x x x x
Khi đó
3;2
3;2
max max 3 , 1 , 0 , 2 3 243
min min 3 , 1 , 0 , 2 2 32
A u x u u u u u m
a u x u u u u u m
Vậy


3;2
243 150
243 32
140
max max 243 , 32 150
93
32 150
32 243
m
mm
m
y m m
m
m
mm
Câu 2: Cho hàm số
2
.y x x m
Tổng tất cả các giá trị thực của tham số sao
cho
2;2
min 2y
bằng?
A.
31
4
B.
8
C.
23
4
D.
9
4
Lời giải
Xét hàm số
2
u x x m
trên đoạn
2; 2
ta có
1
' 0 2 1 0 .
2
u x x
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 17
Do đó



2;2
11
max max 2 , , 2 max 2; ; 6 6
24
A u u u u m m m m
và
2;2
1 1 1
min min 2 , , 2 min 2; ; 6 .
2 4 4
a u u u u m m m m



Nếu
2;2
1 1 9
0 min 2 / .
4 4 4
a m y m m t m
Nếu
2;2
0 6 min 6 2 8 /A m y m m t m
Nếu
2;2
1
. 0 6 min 0 .
4
A a m y l
Vậy tổng các giá trị thực của tham số là
9 23
8.
44
Câu 3: Gọi
,
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 3 2
3 4 12y x x x m
trên đoạn
3; 2
. Có bao nhiêu số nguyên
2019; 2019m
để
2.
A.
3209
B.
3215
C.
3211
D.
3213
Lời giải
Xét
4 3 2
3 4 12u x x x m
trên đoạn
3; 2
ta có:
3 2 3 2
' 12 12 24 ; ' 0 12 12 24 0 0; 1; 2.u x x x u x x x x x x
Khi đó
3;2
3;2
max max 3 , 1 , 0 , 2 3 243
min min 3 , 1 , 0 , 2 2 32
A u x u u u u u m
a u x u u u u u m
Nếu
0 32 0 32 243; 32a m m m m
khi đó giả thiết tương đương
2 32 243 307m m m
Nếu
0 243 0 243 32 ; 243A m m m m
khi đó giả thiết tương
đương
2 243 32 518.m m m
Nếu
243 32 . 0 max 243 , 32 max 243, 32 0; 0m A a m m m m
trường hợp này không thỏa mãn
2
Vậy
2019 518 307 2019 2018;..., 518, 307,...,2018 .m m m
Có tất cả 321 số nguyên thỏa mãn.
Câu 4: Cho hàm số
2
.
2
x m m
y
x

Giá trị lớn nhất M của hàm số trên đoạn
1; 2
có giá trị
nhỏ nhất bằng?
A.
1
6
B.
1
8
C.
1
5
D.
1
7
Lời giải
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
18 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Xét hàm số
2
2
x m m
u
x

ta có
2
2
2
' 0, 1;2 , .
2
mm
u x m R
x

Do đó
22
1;2
1;2
21
max 2 ; min 1
43
m m m m
A u u a u u
Vậy





22
1;2
21
max max , .
43
m m m m
y
Ta có
22
22
2 1 1
7 4 3 2 1 1 .
4 3 7
m m m m
M m m m m M
Dấu bằng xảy ra
22
2 1 1 7 329
.
4 3 7 14
m m m m
m
Câu 5: Cho hàm số
2
.
2
x m m
y
x

Giá trị lớn nhất M của hàm số trên đoạn
1; 2
có giá trị
nhỏ nhất bằng?
A.
26
B.
18
C.
28
D.
26
Lời giải
Xét
3 2 2
1 27u x x m x
trên đoạn
3; 1
ta có
22
' 3 2 1 0, .u x x m x
Do đó


22
3; 1
3; 1
max 1 26 ;a min 3 6 3A u u m u u m
Do đó

22
3; 1
max max 26 , 6 3M y m m
và
22
4 3 26 6 3 72 18.M m m M
Dấu bằng xảy ra
22
26 6 3 18 2 2.m m m
Câu 6: Gọi S là tập hợp giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
3
3y x x m
trên đoạn
0;2
bằng 3. Số phần tử của S là?
A.
1
B.
2
C.
0
D.
6
Lời giải
Xét
3
3u x x m
có
2
' 3 3; ' 0 1 0;2 .u x u x
Khi đó
0;2
0;2
max max 0 , 1 , 2 max , 2, 2 2
min min 0 , 1 , 2 min , 2, 2 2
A u u u m m m m
a u u u u m m m m
Suy ra
0;2
23
22
max max 2 , 2 3 1, 1.
23
22
m
mm
y m m m m
m
mm
Câu 7: Cho hàm số
4 3 2
4 4 .f x x x x a
Gọi M,m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số trên đoạn
0;2
. Có bao nhiêu số nguyên
3;3a
, sao cho
2.Mm
A.
6
B.
3
C.
7
D.
5
Lời giải
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 19
Với
4 3 2 3 2
0
4 4 ' 4 12 8 ; ' 0 1.
2
x
u x x x a u x x x u x
x
Khi đó
1;3
1;3
max max 0 , 1 , 2 1 1
min min 0 , 1 , 2 0
u u u u u a
u u u u u a
Nếu
0 , 1 2 1 1 1; 2;3 .a m a M a a a a a
Nếu
1 1 ; 2 1 2 3; 2 .a m a M a a a a a
Vậy có tất cả 5 số nguyên thỏa mãn.
BÀI TẬP TƯƠNG TỰ.
Cho hàm số
4 3 2
4 4 .f x x x x a
Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số đã cho trên
0;2 .
Có bao nhiêu số nguyên
4; 4a 
sao cho
2?Mm
Câu 8: Cho hàm số
2
2 1 3 .y x x x x m
Khi đó lớn nhất của hàm số đạt giá trị
nhỏ nhất. Mệnh đề nào dưới đây đúng?
A.
1
B.
2
C.
0
D.
6
Lời giải
Điều kiện xác định
1 3 0 1 3.x x x
Đặt
2 2 2
1 3 3 2 2 3.t x x x x x x t
Khi đó ta cần tìm giá trị lớn nhất của hàm số
2
3y t t m
trên đoạn
0;2
Ta có



0;2 0;2
1 13 13
max max 0 , 2 , max 3; 1; 1;max .
2 4 4
u u u u m m m m u m
Do đó






13
13
1
1
4
13 9
4
max max 1 , .
4 2 2 8
mm
mm
y m m
Dấu bằng xảy ra
134 9 17
1.
4 8 8
m m m
Câu 9: Gọi S là tập hợp tất cả các số nguyên m để hàm số
42
1 19
30
42
y x x x m
có giá
trị lớn nhất trên đoạn
0;2
không vượt quá 20. Tổng các phần tử của S bằng?
A.
195
B.
210
C.
195
D.
210
Lời giải
Xét
42
1 19
30
42
u x x x m
trên đoạn
0;2
có
2
5 0; 2
' 19 30; ' 0 3 0;2 .
2 0;2
x
u x x u x
x

Do đó
0;2
max max 0 ; 2 max , 36 26u u u m m m
và
0;2
min um
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
20 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Do đó
0;2
26 20
13 6
max max , 26 20 20 6
20 13
26 20
mm
m
y m m m
m
mm
Vậy
20, 19,..., 6 .m
Vậy tổng các phần tử của S bằng
20
6
195k
BÀI TẬP TƯƠNG TỰ.
Gọi
,ab
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
42
1 19
30
42
y x x x m
trên đoạn
0;2 .
Có bao nhiêu số nguyên
30;30m
để
2ba
Câu 10: Cho hàm số
32
3f x x x m
. Có bao nhiêu số nguyên m để
1;3
min 3.fx
A.
4
B.
6
C.
11
D.
10
Lời giải
Với
22
3u x x m
có
2
' 3 6 ; ' 0 0, 2.u x x u x x
Do đó
1;3
1;3
min min 1 , 3 , 0 , 2 min 2; ; 4 4
1 , 3 , 0 , 2 2; ; 4
u u u u u m m m m
max u max u u u u max m m m m
Nếu
1;3
4 0 4 min 4 3 7 4;5;6;7 .m m f x m m m
Nếu
1;2
0 min 3 3 3; 2; 1;0 .m f x m m m
Nếu
04m
khi đó
1;3 1;3
1;3
min 0; 0 min 0.u maxu f x
( Thỏa mãn )
Vậy
3;...;7m 
có 11 số nguyên thỏa mãn
BÀI TẬP TƯƠNG TỰ.
1. Cho hàm số
32
23f x x x m
. Có bao nhiêu số nguyên m để
1;3
min 3.fx
2. Có bao nhiêu số nguyên m để hàm số
42
2y x x m
có
1;2
min 3.y
3. Cho hàm số
4 3 2
2y x x x a
. Có bao nhiêu số nguyên a để
1;2
max 100.y
4. Cho hàm số
3 2 2
1 4 7 .y x x m x m
Có bao nhiêu số nguyên tố m để
0;2
max 15y
5. Cho hàm số
sin 3 s inx .y x m
Có bao nhiêu số nguyên m để giá trị lớn nhất của
hàm số lớn nhất của hàm số không vượt quá 30.
6. Cho hàm số
2
3 1.f x x x
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của
hàm số
2 sin 1y f x m
không vượt quá 10?
7. Cho hàm số
4 2 3 2 3
11
2.
43
y x m x m x m
Có bao nhiêu số nguyên m để
0;2
max 5.y
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 21
Câu 11: Cho hàm số
3
3.f x x x
Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số
sin 1 2 .y f x
Giá trị biểu thức
Mm
bằng?
A.
4
B.
6
C.
2
D.
8
Lời giải
Đặt
sin 1 0;2 ,tx
khi đó
2
sin 1 2 2 3 2y f x f t t t
Xét
2
32u t t
trên đoạn
0;2
có
2
' 3 3; ' 0 1.u t u t
Do đó
0;2
0;2
max max 0 , 2 , 1 max 2; 4;0 4
min min 0 , 2 , 1 min 2; 4;0 0
u u u
u u u u
Do đó
0;2
0;2
max 4; min 0 0 4M u m u M m a
Câu 12: Cho hàm số
4 3 2
2.y x x x a
Có bao nhiêu số thực a để
1;2
1;2
min 10.y max y

A.
2
B.
5
C.
3
D.
1
Lời giải
Xét
4 3 2
2u x x x a
trên đoạn
0;2
có
32
1
' 4 6 2 ; ' 0 0; 1; .
2
u x x x u x x x












1;2
1;2
1
max max 1 , 2 , 0 , , 1 1 2 4.
2
1
min min 1 , 2 , 0 , , 1 0 1
2
M u u u u u u u u a
m u u u u u u u u a
Trường hợp 1: Nếu
1;2
1;2
0 0 min ;max .m a y m y M
Vậy ta có điều kiện
0
3
4 10
a
a
aa

Trường hợp 2: Nếu
1;2
1;2
, 0 4 min ;max .M m a y M y m
Vậy ta có điều kiện
4
7.
4 10
a
a
aa

Trường hợp 3:
1;2
1;2
, 0 4 0 min 0;max max 4 , max 4; 10.M m a y y a a a a
Suy ra
1;2
1;2
min max 0 10 10yy
( loại)
Câu 13: Cho hàm số
2
2 4 3 .y x a x b
Gọi M là giá trị lớn nhất của hàm số trên
đoạn
2; 3
. Khi đạt giá trị nhỏ nhất, tính giá trị biểu thức
4ab
.
A.
41
B.
30
C.
30
D.
41
Lời giải
Xét
2
2 4 3u x a x b
trên đoạn
2; 3
có
4
' 0 4 4 0
4
a
u x a x
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
22 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Trường hợp 1: Nếu
4
2;3 16 4
4
a
aa
ta có
max 2 , 3 max 2 3 , 3 33
2 3 3 33
2 3 3 33 5 6
25.
2 2 2
M u u a b a b
a b a b
a b a b a
Trường hợp 2: Nếu
4
2;3 16 4
4
a
a
ta có













2
2
2
2
4
max 2 , 3 , max 2 3 , 3 33 , 1
48
2 3 3 33 2 1
2 3 3 33 2 1
8
8
44
1 25 25
6.
16 4 4
aa
M u u u a b a b a b
a
a
a b a b a b
a b a b a b
a
So sánh hai trường hợp có
min
25
.
4
M
Dấu bằng xảy ra
2
6
25
2 3 3 33 1 4 41.
35
84
4
a
a
a b a b a b a b
b


Câu 14: Giá trị lớn nhất của hàm số
2
y x ax b
trên đoạn
,m n m n
có giá trị nhỏ
nhất bằng?
A.
2
1
4
mn
B.
2
1
8
mn
C.
2
1
2
mn
D.
2
1
16
mn
Lời giải
Gọi
,
max
mn
My
.
Nếu
; 2 2
2
a
m n a n a m
ta có
22
2 2 2 2
2
max , max ,
11
.
2 2 2 2
M y m y n m am b n an b
m am b n an b m n a m n
m n m n a m n
Nếu
;
2
a
mn
ta có









2
22
max , , max , ,
24
aa
M y m y n y m am b n an b b
Và
22
2 2 2 2
42
42
aa
M m am b n an b b a m n m n
2 2 2
1 1 1
.
2 2 8
a m n m n M m n
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 23
Dấu bằng đạt tại
2
2
22
1
.
48
a
m am b n an b b m n
Câu 15: Cho hàm số
4
.
1
x ax a
y
x

Gọi M,m lần lượt là giá trị nhỏ nhất của hàm số trên
đoạn
1; 2
. Có bao nhiêu số nguyên a sao cho
2.Mm
A.
15
B.
14
C.
16
D.
13
Lời giải
Xét
4
1
x ax a
u
x

trên đoạn
43
2
34
' 0, 1;2 .
1
xx
ux
x
Do đó
1;2
1;2
16 1
max 2 ;min 1 .
32
u u a u u a
Nếu
1
16
0
1 1 13
2
3
0.
16 1
1
2 2 3
2
32
2
a
Ma
aa
aa
ma









Nếu
1
16
0
2
16 61 16
3
0.
1 16
3 6 3
16
2
23
3
Ma
a
aa
aa
ma











Nếu



1 16 1 16
0 0, max , 2
2 3 2 3
a a m M a a M m
( thỏa mãn) .
Vậy
61 13
10;...;4 .
63
aa
Có 15 số nguyên thõa mãn.
Câu 16: Cho hàm số
2
.f x x ax b
Gọi M là giá trị lớn nhất của hàm số
fx
trên
đoạn
1; 3
. Khi M đạt giá trị nhỏ nhất, giá trị của biểu thức
2ab
bằng?
A.
1
B.
2
C.
4
D.
6
Lời giải
Cách 1.
Xét
2
' 2 ; ' 0 .
2
a
u x ax b u x a u x
Trường hợp 1: Nếu
2
1;3 ,
6
2
a
a
a

khi đó
1
max 1 , 3 max 1 , 9 3 8 4 2 2 4
2
M f f a b a b a a
Trường hợp 2: Nếu
1; 3 6 2,
2
a
a
khi đó
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
24 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor

















2
2
22
max 1 , 3 , max 1 , 9 3 ,
24
11
max 5 , 5 1 4 2.
4 2 4 2 2
aa
M f f f a b a b b
a a a
a b b a
So sánh 2 trường hợp suy ra
min 2M
đặt tại
21ab
Cách 2. Theo giả thiết
1 1 , 1 1 , 3 9 3 .M f a b M f a b M f a b
Suy ra sử dụng bất đẳng thức
x y z x y z
có
4 1 2 1 3 1 2 1 9 3 .
1 2 1 9 3 8 2.
M f f f a b a b a b
a b a b a b M
Vậy giá trị lớn nhất của hàm số trên đoạn
1; 3
có giá trị nhỏ nhất bằng 2 đạt tại
1 2, 1 2, 9 3 2
1 9 3 0
2
2 4.
1
1 2 2 2 0
9 3 2 2 2 0
a b a b a b
a b a b
a
ab
b
a b a b
a b a b



Câu 17: Cho hàm số
2
3 1.f x x x
Có bao nhiêu số nguyên m để giá trị nhỏ nhất của
hàm số
2 sin 1y f x m
không vượt quá 10?
A.
45
B.
41
C.
30
D.
43
Lời giải
Đặt
2 sin 1 1;3tx
ta có
2
3 1 .y f t m t t m
Ta cần tìm m sao cho
1;3
min 10.y
Xét
2
31u t t m
trên đoạn
1; 3
ta có
2
' 0 3 3 0 1.u t t
Vậy
1;3
max max 1 , 3 , 1 max 3, 19, 1 19A u u u u m m m m
và
1;3
min 1.a u m
Trường hợp 1: Nếu
1;3
0 min 10 0 10 0 1 10 1 11.a y a a m a
Trường hợp 2: Nếu
1;3
0 min 10 10 0 10 19 0 29 19A y A A m a
Trường hợp 3: Nếu
1;3
. 0 1 19 0 19 1 min 0 10A a m m m y
( thỏa mãn )
Vậy
29,...,11a
. Có tất cả 41 số nguyên thỏa mãn
Câu 18: Cho hàm số
3
3.f x x x m
Có bao nhiêu số nguyên
20;20m
để với mọi
bộ số ba số thực
, , 2;1a b c 
thì
,,f a f b f c
là độ dài ba cạnh của một tam giác?
A.
30
B.
24
C.
28
D.
26
Lời giải
Xét
3
3u x x m
trên đoạn
2;1
có
3
' 0 3 3 0 1.u x x
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 25
Khi đó
2;1
2;1
max max 2 , 1 , 1 max 2, 2, 2 2
min min 2 , 1 , 1 min 2; 2; 2 2
u u u u m m m m
u u u u m m m m
Để
,,f a f b f c
là độ dài ba cạnh tam giác ta phải có
.f a f b f c
Chọn
2;1
2;1
min ; maxf a f b f x f c f x
ta phải có
2;1
2;1
2 min max .f x f x
Ngược lại
2;1
2;1
2 min max ,f x f x
ta có
2;1
2;1
2 min max 0.f a f b f c f x f x
Vậy điều kiện cần và đủ để
,,f a f b f c
là độ dài ba cạnh tam giác là
2;1
2;1
2 min maxf x f x
Nếu
2;1
2;1
2 2 0 2 min 0 2.0 maxm m f x f x
( loại)
Nếu

2;1
2;1
20
2 0 min 2;max 2 6.
2 2 2
m
m f x m f x m m
mm
2;1
2;1
20
2 0 min 2 ; 2 6.
2 2 2
m
m f x m max f x m m
mm

Vậy
19,.., 7,7,..,19 .m
Có 26 số nguyên thỏa mãn.
Câu 19: Cho hàm số
3
3.f x x x m
. Có bao nhiêu số nguyên
20;20m
để với mọi
bộ ba số thực
, , 2;1a b c 
thì
,,f a f b f c
là độ dài ba cạnh một tam giác nhọn?
A.
30
B.
16
C.
28
D.
12
Lời giải
Xét
3
3u x x m
trên đoạn
2;1
có
2
' 0 3 3 0 1.u x x
Khi đó
2;1
2;1
max max 2 , 1 , 1 max 2; 2; 2 2
min min 2 , 1 , 1 min 2; 2; 2 2
u u u u m m m m
u u u u m m m m
Để
,,f a f b f c
là độ dài ba cạnh tam giác nhọn ta phải nhọn thì
2 2 2
.f a f b f c
Chọn
2;1
2;1
min ; maxf a f b f x f c f x
ta có điều kiện






2
2
2;1
2;1
2 min max .f x f x
Ngược lại với






2
2
2;1
2;1
2 min max ,f x f x
có






2
2
2 2 2
2;1
2;1
2 min max 0.f a f b f c f x f x
Vậy điều kiện cần và đủ để
,,f a f b f c
là độ dài ba cạnh của một tam giác nhọn là






2
2
2;1
2;1
2 min maxf x f x
Nếu



2
2
2;1
2;1
2 2 0 2 min 0 2.0 maxm m f x f x
(loại)
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
26 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Nếu
2;1
2;1
2 0 min 2;max 2m f x m f x m

2
20
6 4 2.
2 2 2
m
m
mm
Nếu
2;1
2;1
2 0 min 2 ;max 2m f x m f x m

22
20
6 4 2.
2 2 2
m
m
mm
Vậy
19,.., 12,12,..,19 .m
Có 16 số nguyên thỏa mãn.
BÀI TẬP TƯƠNG TỰ
Cho hàm số
32
2 9 12 .f x x x x m
. Có bao nhiêu số nguyên
20;20m
để với mọi
bộ ba số thực
, , 2;1a b c 
thì
,,f a f b f c
là độ dài ba cạnh một tam giác nhọn.
Câu 20: Gọi M là giá trị lớn nhất của hàm số
3
4 1 3y ax a x
trên đoạn
1; 1
. Giá trị
nhỏ nhất của M bằng?
A.
1
B.
3
2
C.
8
9
D.
1
2
Lời giải
Xét
3
4 1 3u ax a x
ta có
2
' 0 12 1 3 0.u ax a
Nếu
1;1
0 max 1.a y x M y
Nếu
2
31
0 ' 0 .
12
a
a u x
Nếu
3 1 1
10
31
12 9
1;1 .
3 1 1
12
10
12 15
a
a
a
a
a
a
a
a






Khi đó
8
1 1 .
9
M y a
Nếu
1
3 1 3 1
15
1;1 1 1 .
1
12 12
19
a
aa
aa
a


Khi đó











22
3 1 3 1
31
max 1 , max 1 , .
12 27 27
aa
a
M y y a
a a a
Khảo sát hàm số
2
31
27
a
ga
a
trên
 


11
;;
9 15
D
Ta có



13
min .
62
xD
g a g
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 27
Với





1 5 3 3
max ;
6 6 2 2
aM
(thỏa mãn).
So sánh các trường hợp ta có
min
3
2
M
đạt tại
1
.
6
a 
Câu 21: Cho hàm số
32
,x ax b
gọi M là giá trị lớn nhất của hàm số trên đoạn
3; 2
.
Khi M đạt giá trị nhỏ nhất thì
1
log
a
Tb
có giá trị là ?
A.
0
B.
4026
C.
2
D.
1
2
Lời giải
Xét hàm số
32
h x x ax b
Gọi m,n lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của
hx
trên đoạn
3; 2
.
Suy ra
48
9 27
m a b
n x b
hoặc
9 27
48
m x b
n a b
max ;
2
4 8 9 27 4 8 9 27
2
max
max
m n m n
y m n
a b a b a b a b
y

Vì
4 8 9 27 0a b a b
;
4 8 9 27 0a b a b
Vậy
0.
max
y
Dấu “=” xảy ra khi
7
0
36
0
mn
a
m
b
n


16
log log 36 2.
a
Tb
Câu 22: Cho 2 số thực
1, 0xy
thỏa mãn điều kiện
2
2
22
max 1 ; 2 1
xy
x x y
xy
.
Hỏi biểu thức
2
3 1 2 1P x x y
có tất cả bao nhiêu ước số nguyên dương?
A.
5
B.
6
C.
7
D.
8
Lời giải
Ta có một tính chất cơ bản của hàm trị tuyệt đối
max ;
22
a b a b
ab


Áp dụng ta có
22
2
2 2 2
max 1 ; 2 1
22
x x y x x y
x x y
Sử dụng bất đẳng thức trị tuyệt đối ta có
22
22
2 2 2
2 2 2 2
21
2 2 2 2
x x y x x y
xx
x

Mặt khác theo bất đẳng thức Cauchy – Schwarz ta có
2
22
2
2 2 2 2
2
2
xy
xy
x y x y


MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
28 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Vậy
2VT VP
. Dấu “=” xảy ta khi và chỉ khi
1xy
.
Khi đó
24P
có tất cả 8 ước số nguyên dương.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 29
III. ĐỌC THÊM - ỨNG DỤNG TOÁN CAO CẤP TRONG GIẢI TOÁN SƠ
CẤP
A. ĐA THỨC CHEBYSHEV
Đa thức Chebyshev, được đặt theo tên nhà toán học Nga Pafnuty Chebyshev, là một dãy
đa thức trực giao (tiếng Anh: orthogonal polynomials), và có liên quan đến công thức de
Moivre (de Moivre's formula). Có thể xác định dãy đa thức này bằng công thức truy hồi,
giống như số Fibonacci và số Lucas. Có hai loại: đa thức Chebyshev loại I (ký hiệu là Tn)
và đa thức Chebyshev loại II (ký hiệu là Un). Chữ T được dùng để ký hiệu vì, trong tiếng
Pháp tên của Chebyshev viết là Tchebycheff và trong tiếng Đức là Tschebyscheff. Chữ n
ký hiệu cho bậc của đa thức. Đa thức Chebyshev ý tưởng đơn giản (cũng như bản chất của
nó) chỉ là biểu diễn
cos nx
là đa thức bậc n theo
cos x
. Trong bài viết này ta sẽ cùng tìm
hiểu định nghĩa các tính chất và ứng dụng của nó.
I. ĐỊNH NGHĨA VÀ TÍNH CHẤT ĐA THỨC CHEBYSHEV
1. ĐỊNH NGHĨA
Các đa thức
n
Tx
, n ∈ N xác định như sau:



01
11
1,
2
n n n
T x T x x
T x xT x T x
Gọi là các đa thức Chebyshev loại I.
Các đa thức
n
Tx
, n ∈ N xác định như sau:


01
11
0, 1
2 , 1
n n n
U x U x
U x xU x U x n
Gọi là các đa thức Chebyshev loại II
2. CÁC TÍNH CHẤT CỦA ĐA THỨC LOẠI I
Đa thức Chebyshev có nhiều tính chất hay, được sử dụng rất nhiều trong việc giải quyết
các bài toán đa thức. Sau đây xin được nêu một số tính chất quan trọng (việc chứng minh
rất dễ dàng)
Tính chất 1:
1,1x
,ta có
cos( arccos )
n
T x n x
Tính chất 2:
n
Tx
là đa thức bậc n,
n
,hệ số cao nhất là
1
2
n
Tính chất 3:
n
Tx
là hàm chẵn khi x chẵn và là hàm lẻ khi x lẻ.
Tính chất 4: Đa thức
n
Tx
có đúng n nghiệm phân biệt trong
1, 1
:
21
cos , 1, 2,..., 1
2
k
k
x k n
n
Tính chất 5:
a)
1, 1,1
n
T x x
b)
1
n
Tx
chỉ tại
1n
điểm khác nhau trong
1, 1
là
cos 1,2,...,
k
k
x k n
n
Chú ý là:
1
k
nk
Tx
Các điểm
k
x
gọi là điểm luân phiên Chebyshev.
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
30 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Tính chất 6:
Px
bậc n, hệ số cao nhất bằng 1, ta có
1
1
max
2
n
Px
Đẳng thức xảy ra
1
1
*
2
n
n
P x T x
Một vài đa thức khởi đầu
1.

2
2
21Tx
2.

3
3
43T x x
3.
42
4
8 8 1T x x
3. CÁC TÍNH CHẤT CỦA ĐA THỨC LOẠI II
Tính chất 1:
1,1x
ta có
2
sin arccos
1
n
nx
Ux
x
Tính chất 2:
1
'
nn
U x T x
n
Tính chất 3:
a)
n
Ux
là đa thức hệ số nguyên, bậc
1n
, hệ số cao nhất là
1
2
n
b)
n
Ux
là hàm chẵn nếu x lẻ và là hàm lẻ nếu x chẵn.
Tính chất 4:
, 1,1
n
U x n x
Tính chất 5: Đa thức
n
Ux
có đúng n-1 nghiệm phân biệt khác nhau trong
1, 1
Đặc biệt: Từ tính chất 2 và 4, ta có:
2
' , 1,1
n
T x n x
II. MỘT SỐ BÀI TOÁN MINH HỌA
Một trong những dấu hiệu để nhận biết bài toán đa thức có sử dụng tính chất của đa thức
Chebyshev hay không đó là miền giá trị của đa thức. Các bài toán trên miền
1;1
đều
gợi ra cách giải bằng phương pháp sử dụng tính chất của đa thức Chebyshev. Sau đây ta
xét lớp các bài toán về đa thức có sử dụng tính chất của đa thức Chebyshev.
Bài 1: Cho hàm số
32
4 3 axy x a x
. Tìm a để
1 khi 1yx
.
Lời giải
Vì
1 khi 1yx
nên ta có :









11
7 2 1
11
1 7 2 1
11
1
13
1
11
1
1
44
2 4 2
2
35
13
11
1
1
1
44
2 4 2
2
y
a
y
a
a
aa
y
a
aa
y
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 31


1 7 2 1 4 3
4 1 4 3 5 3
4 3 5 4 1
3
3
aa
a a a
a
a
Ngược lại, khi
3a
thì

3
4 3xyx
. Đặt
cosx
với
0;
thì
os3yc
rõ ràng
thỏa mãn
1 khi 1yx
.
Bình luận: Nếu chỉ xem lời giải và không hiểu rõ nguồn gốc, cội nguồn của bài toán thì
học sinh sẽ thấy lời giải mất tự nhiên ở việc là tại sao ta chỉ xét giá trị của hàm số tại các
giá trị của x là

1
1;
2
mà không phải là các giá trị khác. Thực chất của việc xét giá trị của
hàm số tại các điểm

1
1;
2
chính là xét giá trị của hàm số tại các nghiệm của đa thức
Chebyshev bậc ba.
Bài 2: Cho hàm số

3
4xy x m
. Tìm m để
1 khi 1yx
.
Lời giải
Vì
1 khi 1yx
nên ta có :












11
11
41
1 4 1
53
1
4 1 2 1 2 3
1
31
2
35
1
11
1
1
44
22
1
2
y
y
m
m
m
m m m
y
m
a
m
y
Ngược lại, khi m=-3 thì

3
4 3xyx
. Đặt
cosx
với
0;
thì
os3yc
rõ ràng thỏa
mãn
1 khi 1yx
.
Bài 3: Tìm a, b, c để
32
4 1,x ax bx c
với mọi x thỏa mãn
1x
.
Lời giải
Cách 1.
Điều kiện cần: Vì
1 khi 1yx
nên ta có :












11
5 3 1
11
3 5 2
1
1
6 2 4 2 3
2
2 2 4 6 4
1
1
2
y
a b c
y
a b c
I
y
a b c
a b c
y
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
32 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Từ (1) và (2) ta có:
3
2 6 3 5
3
a b c
bb
a b c
.
Từ (3) và (4) ta có:
2 4 6
4 12 3 6
246
a b c
bb
a b c
Từ (5) và (6) ta được
3b
Thế
3b
vào hệ (I) ta có:

20
0 2 0
0
8 4 0 4 0
0 4 8
ac
a c a c
ac
a c a c
ac
Điều kiện đủ: Khi
0, 3a c b
thì

3
4 3xyx
. Đặt
cosx
với
0;
thì
os 3yc
rõ ràng thỏa mãn
1 khi 1yx
.
Cách 2. Giả sử tồn tại các số a, b, c thỏa mãn điều kiện bài toán.
Đặt

32
1;1
4 ax , max f
x
f x x bx c M x
Ta có
(1) 4 , ( 1) 4 ,
1 1 1 1
,
2 2 4 2 2 2 4 2
f a b c f a b c
a b a b
f c f c
1 1 1 1
6 1 1 2 2 1 1 2 2
2 2 2 2
M f f f f f f f f
4 1 2 1 2
22
aa
a b c a b c b c b c
8 2 6
Vậy
1M
. Dấu “=” xảy ra khi và chỉ khi
11
(1) ( 1) 1
22
f f f f M
, đồng
thời
11
1 , 1 , ,
22
f f f f
đôi một có tích không âm. Điều đó tương đương với
41
41
1
1
2 4 2
11
1
1 1 1
1
22
2 4 2
1 1 4 1
1 1 1
22
41
1
1
2 4 2
1
1
2 4 2
a b c
a b c
ab
c
ab
f f f f
c
a b c
f f f f
a b c
ab
c
ab
c
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 33






2 8 2
0
3
2 4 2 4
0
4 6 2 4
40
b
ac
b
a b c
ac
ac
ac
.
Mặt khác, từ giả thiết thì
1M
, do đó phải có
1M
và xảy ra dấu bằng trong bất đẳng
thức trên tức
0, 3a c b
. Ngược lại, khi
0, 3a c b
thì

3
4 3xyx
. Đặt
os xc
với
0;
thì
os3yc
rõ ràng thỏa mãn
1 khi 1yx
.
Bài 4: Tìm a, b để
42
8 1, 1;1x ax b x
.
Lời giải
Cách 1. Điều kiện cần: Vì
1 khi 1yx
nên ta có :








1 1, 1 1
01
2
1
2
2
2
yy
y
y
y


1
1 1 1 1
8 1 1 8 1 9 7
2 2 4 2 6 2 2
11
8. . 1
42
b
bb
a b a b I a b
a b a b
ab
.
Từ

7
1
26
ab
b
ab
. Lại do
1b
nên
1b
.
Thế
1b
vào hệ
I
ta có



9 1 7 10 8
8
6 2 2 8 4
aa
a
aa
.
Điều kiện đủ: Khi
8, 1ab
thì
42
8 8x 1yx
. Đặt
os xc
với
0;
thì
os 4yc
rõ ràng thỏa mãn
1 khi 1yx
.
Cách 2. Giả sử tồn tại các số a, b thỏa mãn điều kiện bài toán.
Đặt

42
1;1
8 ax , max
x
f x x b M f x
và theo giả thiết
1M
.
Ta có




21
0 , 1 8 , 8.
2 4 2
a
f b f a b f b
.
Do

1;1
max f
x
Mx
nên




0
1
2
2
Mf
Mf
Mf
.
Từ đó ta có:
22
4 4 0 1 2 0 1 2 4
22
M f f f f f f
.
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
34 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Vậy
1M
. Dấu “=”xảy ra khi và chỉ khi




2
0 1 1
2
f f f
, đồng thời
0 , 1ff
,




2
2
f
đôi một cùng dấu. Điều đó tương đương với:









2
0 1 1
2
8
1
2
0 1 1
2
f f f
a
b
f f f
Ngược lại: Khi
8, 1ab
thì
42
8 8 1y x x
. Đặt
cosx
với
0;
thì
cos 4y
rõ ràng thỏa mãn
1 khi 1yx
.
Bình luận. Các giá trị của x mà ta xét ở trên chính là các nghiệm của đa thức Chebyshev
bậc bốn, đó là các nghiệm 0;

2
1;
2
.
Bài 5: Chứng minh rằng nếu với mọi
1;1x
ta có

2
x+cax b h
thì
4a b c h
.
Lời giải
Đặt
2
f x ax bx c
, khi đó theo giả thiết
f x h
và

1 , 1
1 , 1
0 , 0
f a b c f h
f a b c f h
f c f h
Từ đó ta có
1 1 1 1
0 , , 0
22
f f f f
a f b c f
Vậy
1 1 1 1
00
22
f f f f
a b c f f
1 1 1 1
00
2 2 2 2
f f f f
ff
4
2 2 2 2
h h h h
h h h
Như vậy ta có điều phải chứng minh là
4a b c h
.
Bài 6: Cho
2
f x ax bx c
thỏa mãn điều kiện
1 1, 0 1, 1 1f f f
.
Chứng minh rằng

5
1
4
f x khi x
.
Lời giải
Đặt
, A a b c B a b c
, thế thì

,
22
A B A B
a c b
.
Theo giả thiết:
1 1, 1 1, 0 1f A f B f c
.
Ta có

2 2 2 2 2
1
2 2 2 2
A B A B A B
f x ax bx c c x x c x x x x c x
Vậy
2 2 2
11
x + x + 1
22
f x x x x
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 35
Với
01x
, ta có
2 2 2 2 2 2 2
1 1 1 1
x + x + 1 = x + x 1 1
2 2 2 2
f x x x x x x x x x
Với
10x
, ta có
Các kết quả trên chứng tỏ rằng với
1x
thì



2
2
5 1 5
1
4 2 4
f x x x x
.
Bài 7: Chứng minh rằng mọi đa thức
fx
bậc
1n
đều có thể biểu diễn dưới dạng

0
,0
n
i i n
i
f x a T x a
và cách biểu diễn này là duy nhất.
Lời giải
Ta có
n
Tx
là đa thức bậc n có hệ số cao nhất là
1
2
n
nên ta có thể viết
1
2
nn
n
T x x x
với
x
là đa thức bậc nhỏ hơn n.
Suy ra

11
11
22
n
nn
x T x x
Bằng quy nạp ta chứng minh được:
0 1 2 2
...
nn
f x a a T x a T x a T x
Bây giờ ta chứng minh tính duy nhất của cách biểu diễn này
Giả sử
0 1 2 2 0 1 2 2
... ' ' ' ... '
n n n n
f x a a T x a T x a T x a a T x a T x a T x
Khi đó
0
' 0,
n
i i i
i
a a T x x
Vậy
0 0 1 1
' ' ... ' 0
nn
a a a a a a
Hay
0 0 1 1
' , ' ,..., '
nn
a a a a a a
Một trong những dấu hiệu để nhận biết bài toán đa thức có sử dụng tính chất đa thức
Chebyshev hay không đó là miền giá trị đa thức. Các bài toán trên miền
1, 1
đều gợi ra
cách giải bằng phương pháp này.
Ta xét thêm một số ví dụ:
Bài 8: Cho đa thức hệ số thực
32
,0f x ax bx cx d
. Biết rằng
1,1x
ta có
fx
.Tìm max của
, , ,a b c d
Lời giải
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
36 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Đặt







1
.
1
2 8 4 2
1
2 8 4 2
1
0
A f a b c d
b
ac
B f d
a b c
C f d
D f a b c d
E f d
2 4 4 2
3 3 3 3
11
22
1 8 8 1
6 6 6 6
a A B C D
b A D E
c A B C D
dE
. Từ giả thiết:



4
2
3
a
b
c
d
Bằng cách xét:
3
43f x x x
và
2
21g x x
Thì ta có dấu đẳng thức xảy ra. Vậy:



max 4 ,
max 2 ,
max 3 ,
ax
a
b
c
md
Chú ý:
,f x g x
là xét dự trên cơ sở cos2x, cos3x.
Bài 9: Cho đa thức
1n
Px
bậc không vượt quá
1n
có hệ số bậc cao nhất
0
a
, thỏa mãn
điều kiện
2
1
1 1, 1,1
n
x P x x
. Chứng minh rằng
1
0
2
n
a
.
Lời giải
Ta viết đa thức đã cho dưới dạng nội suy Lagrange theo các nút nội suy

21
cos
2
j
j
x
n
là
các nghiệm của đa thức Chebyshev
n
Tx
:



1
1
1
22
1 1 0
11
12
1 1 1 1
j
nn
n
j
n
n j n j j j
jj
j
Tx
P x x P x a x P x
n x x n
Vậy nên

11
21
0
1
22
1 . 2
n
nn
n
jj
j
a x P x n
nn
Bài 10: Giả thiết rằng đa thức
1n
Px
thỏa mãn các điều kiện của Bài 7. Chứng minh rằng
1
, 1,1
n
P x n x
Lời giải
Với các
j
x
được chọn như ở bài toán trên thì do hàm số
cosyx
nghịch biến trong
0;
nên
1 2 1
1 ... 1
nn
x x x x
.
Nếu

1
1xx
thì



2
11
11
11
12
nn
n
n
n j n j
jj
j
j
Tx
Tx
P x x P x
nn
xx
xx
do
0
j
xx
và
n
Tx
có dấu không đổi trên
1
;1x
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 37
Mặt khác thì

1
1
2
n
n
nj
j
T x x x
Nên ta có




1
'1
11
23
n
j
nn
j
n
n
n
kk
kk
xx
Tx
Tx
x x x x
Lại có

'
n
n
Tx
U x n
n
. Nên từ (2) và (3) suy ra
11
, ( ;1]
n
P x n x x
Hoàn toàn tương tự ta cũng có
1
, [ 1, )
nn
P x n x x
Xét

1n
x x x
.Khi đó ta có
22
11
1 1 sin arccos sin
2
x x x
n
Do

sin 2
1
x
x
,


21
sin .
22n n n n
và

2
1
1 x
n
1
1
1
n
P x n
n
Tóm lại ta đã chứng minh được rằng
1
, 1,1
n
P x n x
Bài 11: Cho đa thức lượng giác
12
sin sin 2 ... sin
n
P t a t a t a nt
Thỏa mãn điều
kiện
1, \ ..., 2 , ,0, ,2 ,...P t t
Chứng minh rằng
 , \ ..., 2 , ,0, ,2 ,...
sin
Pt
nt
t
Lời giải
Nhận xét rằng
1
cos
sin
n
Pt
Pt
t
với
1n
Px
là đa thức dạng (1). Đặt
costx
. Khi đó
1x
và

2
11
sin cos 1
nn
P t P t x P x
Ta thấy
Px
thỏa mãn điều kiện của bài toán trước nên
1
, 1,1
n
P x n x
Do đó
 , \ ..., 2 , ,0, ,2 ,...
sin
Pt
nt
t
Bài 12: Cho đa thức lượng giác

0
cos sin
n
jj
j
P x a jx b jx
thỏa mãn điều kiện
1,P x x
. Chứng minh rằng
',P x n x
Lời giải
Cho
0
x
tuỳ ý. Do
0 0 0
0 0 0
cos cos 2 sin sin
sin sin 2 cos sin
x x x x x x
x x x x x x
Nên

00
0
sin
2
n
j
j
P x x P x x
g x c jx

00
''
'
2
P x x P x x
gx
Và
0
' 0 'g P x
.Ta chứng minh rằng
'0gn
.Thật vậy,
gx
là đa thức lượng giác
chứa thuần sin như trong Bài 9 và
00
00
1
22
P x x P x x
P x x P x x
gx
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
38 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Nên theo kết quả của bài 3 thì
sin
gx
n
x
\ ..., 2 , ,0, , 2 ,...x
(4)
Nhưng
00g
suy ra
0
.
0 sin
g x g
x
n
xx
\ ..., 2 , ,0, , 2 ,...x
Nên khi
0x
:
0
'0
0
g x g
g
x
,
1
sin
x
x
Ta nhận được
'0gn
Từ đó ta có
0
'P x n
.Nhưng
0
x
được chọn tùy ý nên suy ra
'P x n
x
Bài 13 (Định lý Berstein-Markov) Cho đa thức
1
01
...
nn
nn
P x a x a x a
. Thỏa mãn
điều kiện
1, 1;1
n
P x x
. Chứng minh rằng khi đó :
2
' , 1;1
n
P x n x
(5)
Lời giải
Đặt
cosxa
.Khi đó theo giả thiết thì
cos 1
n
Pa
.Do
cos
n
Pa
có dạng
0
cos cos sin
n
n j j
j
P a a j b j
Nên ta có thể áp dụng kết quả của Bài 10. Ta được
2
'
sin . ' cos 1 1
n
n
Px
P n x
n
Cũng theo Bài 4, ta có
'
n
Px
n
n
suy ra
2
'P x n
Nhận xét : Dựa vào kết quả của Định lý Berstein-Markov, sau khi áp dụng liên tiếp kết quả
của định lí này, ta sẽ thu được kết quả sau:
Nếu
1, 1;1
n
P x x
thì


2
1 2 ... 1 , 1;1
k
P x n n n n k x
Bài 14: Cho
12
, ,...,
n
a a a
là các số thực không âm và không đồng thời bằng 0.
a) Chứng minh rằng phương trình
1
11
... 0
nn
nn
x a x a x a
(6) có đúng một nghiệm
dương duy nhất.
b) Giả sử R là nghiệm dương của phương trình (6) và



11
,
nn
jj
jj
A a B ja
Chứng minh
rằng khi đó
AB
AR
Lời giải
a) Do
0x
nên (6)
12
2
1 ...
n
n
a
aa
x x x
Đặt
12
2
...
n
n
a
aa
fx
x x x
. Nhận xét rằng
fx
liên tục và
fx
nghịch biến trong khoảng
0,
nên tồn tại duy nhất
0R
sao cho
1fR
.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 39
b) Đặt
j
j
a
c
A
.Suy ra
0
j
c
và
1
1
n
j
j
c
.Do hàm số
lnyx
lõm trong khoảng
0,
Nên teo BĐT Jensen thì
1 1 1
ln ln ln ln ln 1 0
n n n
j
jj
j j j
j j j
a
AA
c c f R
R R R
Suy ra
1
ln ln
n
j
jj
j
c R c A
và


11
ln ln
nn
jj
jj
A c R jc
Hay





11
11
ln ln ; 0
nn
j
j j j
jj
a
a A ja R doc A
A A A
Vậy nên
ln ln
AB
AR
AB
AR
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
40 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
B. ỨNG DỤNG LÝ THUYẾT XẤP XỈ ĐỀU TRONG GIẢI TOÁN.
Lý thuyết xấp xỉ đều tốt nhất là một nhánh của lý thuyết xấp xỉ hàm, có vai trò đặc biệt
quan trọng trong toán lý thuyết cũng như trong các toán ứng dụng. Đặc biệt, nó được
dùng để tìm đa thức có "độ lệch" nhỏ nhất so với hàm số cho trước trên một đoạn xác
định. Từ việc nghiên cứu kĩ lý thuyết xấp xỉ đều tốt nhất chúng ta có thể giải quyết được
một số dạng bài toán tìm giá trị lớn nhất, nhỏ nhất. Tuy nhiên không như đa thức
Chebyshev, đây là một vấn đề khá khó của chương trình toán cao cấp, liên quan tới không
gian mêtric, không gian Banach, không gian Hilbert mà ta sẽ được học trên chương trình
đại học, do đó không thể giới thiệu được cho các bạn THPT . Vì lí do đó nên mình chỉ đưa
ra các bài toán tổng quát từ nguyên lý này để các bạn áp dụng nhé!
Bài toán 1. Cho hàm số
fx
liên tục trên đoạn
;ab
. Tìm m sao cho
;
max
x a b
f x m
đạt
giá trị nhỏ nhất?
Các bước làm
Bước 1: Tìm M là giá trị lớn nhất của hàm số
fx
và n là giá trị nhỏ nhất của hàm
số
fx
trên đoạn
;ab
.
Bước 2: Khi đó
2
Mn
m
là số cần tìm.
Ví dụ. Tìm m để

2
1;2
max 9 4
x
x x a
đạt giá trị nhỏ nhất?
Bước 1. Xét
2
94f x x x
, ta có
4
'0
18
f x x
. Từ đây dễ dàng tìm được
1;2 1;2
4
max , max 28
9
xx
M f x n f x
.
Bước 2. Khi đó ta có
124 124
99
aa
Rất đơn giản và nhanh gọn phải không nào
Bài toán mở rộng – Lục Trí Tuyên
Tìm m sao cho
1.
g m k
với
k
cho trước
H


km
y k m
y k m

;
max
ab
g m f x k m
E
F
yk
A
C
B
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 41
2.
g m k
với
k
cho trước
Đặt
t f x
và gọi
;;
min , max .
a b a b
f x f x
khi đó, do hàm số
y t k m
đồng
biến trên
;
nên ta có:

;
max max ;g m t k m k m k m
Từ đây ta dễ dàng vẽ được đồ thị của hàm
gx
theo biến
m
(ở đây là
km
). Chú ý là lấy
phần đồ thị nằm phía trên trong hai đồ thị
Từ đồ thị của
gm
ta thấy ngay
gm
đạt giá trị nhỏ nhất tại A. do tam giác ABC vuông
cân tại A nên khi đó
2
A
k m x

. Và
1
min
2
RA
g m y

Cũng từ đồ thị ta dễ dàng giải được bất phương trình
g m k
hoặc
g m k
. Chẳng hạn
AA
g m k k m x k y
Khi đó,
g m k
tương đương
km
nằm trong khoảng nghiệm trên,
g m k
tương
đương
km
nằm ngoài khoảng nghiệm trên
Chú ý: trong trường hợp
km
có miền giá trị khác
R
thì hàm
y g k m
xét trên miền
giá trị tương ứng của
km
Bài toán 2. Cho
fx
là hàm luôn lồi(lõm) trên
;
. Tìm a, b để giá trị lớn nhất của hàm
số
y f x ax b
trên
;
đạt giá trị nhỏ nhất?
Các bước làm
Bước 1. Xác định 2 điểm
, , ,A f B f
, viết phương trình đường thẳng
:AB y kx m
Bước 2. Tìm phương trình tiếp tuyến của đồ thị hàm số
y f x
và song song với
AB (tiếp điểm là
xc
với
xc
là điểm cực trị của hàm số, khi đó tiếp tuyến có
dạng
y kx n
Bước 3. Đường thẳng cần tìm là đường song song cách đều 2 đường thẳng AB và
tiếp tuyến trên là
1
2
y kx m n
Bước 4. Kết luận
1
,
2
a k b m n
. Giá trị nhỏ nhất đạt được là
0
11
22
M f k m n f k m n
Ví dụ.
Ngoài ra ta có thể tham khảo thêm một cách khác của thầy Lục Trí Tuyên
Gọi
M
là giá trị nhỏ nhất của hàm số
y f x ax b
trên
;
thì ta có:
.;M y a b f
.M y a b f
và
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
42 | Chinh phục olympic toán Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
. 2 . 2 2
2 2 2 2
M y a b f M a b f
Suy ra



42
2
M f f f
hay



1
2 2 2
ff
M f m
Đẳng thức xảy ra khi



.1
.2
.3
22
a b f m
a b f m I
a b f m
hoặc



.1
.2
.3
22
a b f m
a b f m II
a b f m
Giải
I
: từ phương trình
1
và phương trình
2
của hệ
I
ta giải được
;.
f f f f
a b m
thay 2 giá trị này vào phương trình
3
ta được
















.
22
2
22
2
22
2
22
2*
22
f f f f
m f m
f f f f f f
fm
f f f f
fm
ff
fm
ff
fm
Giải
II
: tương tự giải
I
, ta chỉ cần thay
m
bởi
m
ta được
;.
f f f f
a b m
thay hai giá trị này vào phương trình
3
ta được



2 * *
22
ff
fm
Mà ta thấy
1
2 * * .
2 2 2 2 2
ff
ff
M f m f m
Điều này có nghĩa là một trong hai đẳng thức
*
hoặc
**
luôn đúng, cũng có nghĩa là
một trong hai hệ phương trình
I
hoặc
II
luôn có nghiệm .
Bình luận. Vậy giả thiết lồi(lõm) ở đây sử dụng ở chỗ nào? Liệu chẳng không cần điều
kiện này bài toán vẫn đúng theo cách giải trên?
Câu trả lời như sau:
Nếu M là giá trị lớn nhất của hàm số trên
;
thì nó lớn hơn hoặc bằng một trong
số các giá trị
1
fx
nào đó trong đoạn
;
. Ở lời giải trên ta chỉ lấy ba điểm.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor Chinh phục olympic toán | 43
Nhưng điều ngược lại không đúng. Có nghĩa là M lớn hơn giá trị của hàm số tại 3
điểm chưa chắc nó đã là giá trị lớn nhất.
Điều kiện cần và đủ để cho M là giá trị lớn nhất của hàm số trên
;
là M lớn hơn
hoặc bằng mọi
fx
với x bất kì thuộc
;
. Điều này tương đương với lời giải
trên phải đảm bảo đúng cho mọi
;
ii
;
thay cho
;
ii
ở trên. Cũng có
nghĩa là điều kiện




0
22
ii
ii
ff
f
với mọi
;
ii
;
,
. Điều
kiện này tương đương với
fx
là hàm lồi hoặc lõm trên
;
| 1/43
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
GIÁ TRỊ LỚN NHẤT, GIÁ TRỊ NHỎ NHẤT
CỰC TRỊ CỦA HÀM TRỊ TUYỆT ĐỐI
Các bài toán về hàm trị tuyệt đối đã bắt đầu xuất hiện trong đề tham khảo năm 2018 của
bộ và sau đó cũng đã trở thành trào lưu trên các diễn đàn, các nhóm, đồng thời xuất hiện
nhiều hơn trong các đề thi thử với các dạng và mức độ khác nhau. Một số có thể chưa phù
hợp với kì thi THPT Quốc Gia, nhưng tuy nhiên trong chuyên đề lần này tôi và các bạn sẽ
cùng nhau bắt tay giải quyết một số dạng toán tiêu biểu đó. Cũng nói thêm để hoàn thành
chuyên đề này tôi rất cảm ơn bên Vted đã có những đề thi vô cùng hay, các bài toán ở đây
đề bài hầu hết được lấy từ Vted và lời giải được thực hiện bởi những người bạn của tôi –
Ngô Nguyên Quỳnh và Nguyễn Hải Linh . Mặt khác cũng vì công việc và thời gian không
có nhiều nên tôi không để đưa thêm nhiều dạng hay khác xuất hiện trong một số đề thi
của các thầy trên mạng được, mong bạn đọc bỏ qua. Mọi ý kiến đóng góp xin gửi về địa chỉ sau:
NGUYỄN MINH TUẤN – K14 ĐẠI HỌC FPT
Email: tuangenk@gmail.com
Nào bây giờ chúng ta cùng bắt đầu nhé! I. MỞ ĐẦU.
Bài toán mở đầu
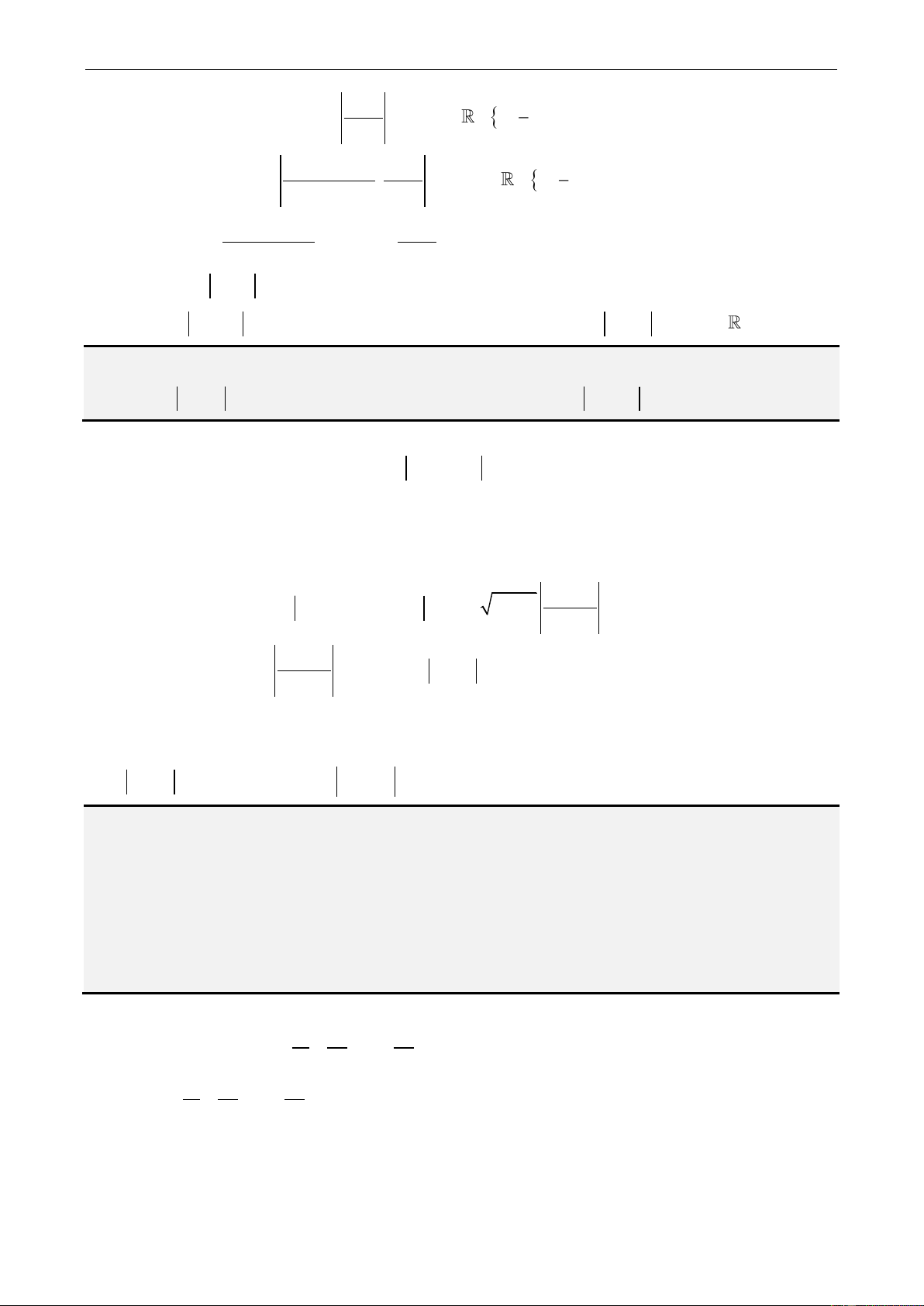
Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số f x 3
x  3x m trên đoạn 0;2 bằng 3. Số phần tử của S là? A. 1 B. 2 C. 0 D. 6
Câu 36 – Đề tham khảo THPT Quốc Gia môn toán 2018 Lời giải 3 m
  x  3x  3 Ta có 3
x  3x m  3, x  0;2 2  3
  x  3x m  3   , x  0;2 3 m     x  3x  3
Xét hàm số f x 3
 x  3x trên đoạn 0;2 thì f x 2 '
 3x  3 nên f 'x  0  x  1 
So sánh các số f 0 , f 1 , f 2 ta có min f x  2  ,max  2 ta có : 0;2 0;2 min 3
x  3x   3  m  max 3
x  3x   3  1   m  1 0;2 0;2
Đây chỉ là các điều kiện cần của m, ta thử lại như sau
 Với m  1 thì với x  2 ta sẽ có y f 2  1  3
 Với m  1 thì với x  1 ta sẽ có y f 2  1  3
 Với m  0 thì với y f x  2 nên không thể có giá trị lớn nhất là 3. Vậy S   1  ; 
1 nên có tất cả 2 giá trị thỏa mãn yêu cầu đề bài.
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 1
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
Nhận xét: Đây là một câu trong đề tham khảo thi THPT Quốc Gia 2018 của Bộ , nhìn
chung thì đây là một câu vận dụng cao cần phải có kiến thức về bất đẳng thức trị tuyệt đối
cũng như những phép biến đổi có liên quan.
Bất đẳng thức trị tuyệt đối.
Cho 2 số thực a,b khi đó ta có a b a b a b
Dấu “=” thứ nhất khi a,b cùng dấu, dấu “=” thứ 2 khi a,b trái dấu.
I. CÁC BÀI TOÁN LIÊN QUAN TỚI ĐIỂM CỰC TRỊ CỦA HÀM SỐ
A. CÁC TÍNH CHẤT LIÊN QUAN TỚI CỰC TRỊ CỦA HÀM TRỊ TUYỆT ĐỐI
Trước khi đi vào các bài toán ta cần nhớ những kiến thức sau.
 Số điểm cực trị của hàm số f x bẳng tổng số điểm cực trị của hàm số f x và số
lần đổi dấu của hàm số f x .
 Số điểm cực trị của hàm số f mx n  bằng 2a  1, trong đó a là số điểm cực trị lớn
hơn  n của hàm số f xm
 Số điểm cực trị của hàm số f x  bằng 2a  1, trong đó a là số điểm cực trị dương của hàm số.
 Cho hàm số có dạng  2 y
ax bx c mx , tìm điều kiện của tham số m để giá trị maxy c ct  
cực tiểu của hàm số đạt giá trị lớn nhất, khi đó ta có  m    b
Câu 1: Biết phương trình 3 2
ax bx cx d  0 a  0 có đúng hai nghiệm thực. Hàm số 3 2
y ax bx cx d có bao nhiêu điểm cực trị. A. 3. B. 5. C. 4. D. 2. Lời giải Vì phương trình 3 2
ax bx cx d  0 a  0 có đúng hai nghiệm thực nên hàm số 3 2
y ax bx cx d có hai điểm cực trị. 2 Mặt khác 3 2
ax bx cx d ax x x x
ax bx cx d  1  
2  .Do đó phương trình 3 2 0 có
một nghiệm đơn và một nghiệm kép.
Vậy số điểm cực trị của hàm số 3 2
y ax bx cx d bằng 2  1  3. Chọn đáp án A.
Câu 2: Có bao nhiêu số nguyên m  20  ;20để hàm số 2
y x  2x m  2x  1 có ba điểm cực trị. A. 17. B. 16. C. 19. D. 18. Lời giải Nếu 2
x  2x m  0, x  thì 2 2
y x  2x m  2x  1  x m  1 có đúng một điểm cực trị x  0 (loại). Nếu 2
x  2x m  0 có hai nghiệm phân biệt x x    1  m  0  m  1 1 2 .
2 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
2x  2  2  0 x  0 x  0     2x  2 2
x  2x m 2 2
x  2x m  0
x  2x m  0 m  0 y   2; y  0    2 
x  2x m
2x  2  2  0 x  2   x  2       2 2
x  2x m  0
x 2x m  0 m  0
+) Với 0  m  1 rõ ràng không có số nguyên nào
+) Với m  0 ta có bảng xét dấu của y như hình vẽ dưới đây
Lúc này hàm số có 3 điểm cực trị. Vậy m  1  9,...,  1 . Chọn đáp án C
Câu 3: Biết phương trình 4 2
ax bx c  0 a  0 bốn nghiệm thực. Hàm số 4 2
y ax bx c có bao nhiêu điểm cực trị. A. 7. B. 5. C. 4. D. 6. Lời giải Vì phương trình 4 2
ax bx c  0 a  0 bốn nghiệm thực nên hàm số  2
  b  4ac  0   b S    0
ab  0 do đó hàm số 4 2
ax bx c  0 có 3 điểm cực trị a   c P   0  a Mặt khác 4 2
ax bx cx d ax x x x x x x x 1   2   3   4  nên phương trình 4 2
ax bx c  0 có 4nghiệm đơn. Vậy hàm số 4 2
y ax bx c có 4  3  7 cực trị. Câu 4: Cho hàm số 4
y x  m   2 2
1 x  2m  3 . Có bao nhiêu số nguyên không âm m để
hàm số đã cho có ba điểm cực trị. A. 3. B. 4. C. 5. D. 6. Lời giải
Xét hàm số f x 4
x  m   2 2
1 x  2m  3
m    m   f x 4 1 0 1
x  1 có 1 điểm cực trị x  0 và phương trình f x  0có hai
nghiệm phân biệt. do đó hàm số y f x có 3 điểm cực trị (thỏa mãn)
m    m   f x 4 2 1 0 0
x  2x  3 có 1 điểm cực trị x  0 và phương trình f x  0có 2
nghiệm đơn phân biệt. do đó hàm số y f x có 3 điểm cực trị (thỏa mãn)
Ta có m  1  0  m  1 khi đó f x có ba điểm cực trị. Vậy yêu cầu bài tóan lúc này tương
đương với f x  0 vô nghiệm hoặc có nghiệm kép, tức
  m  2  m     m  2 1 2 3 0
2  0  m  2 . Vậy m0,1,  2 . Chọn đáp án A
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 3
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI Câu 5: Cho hàm số 4
y x  m   2 2
1 x  2m  3 . Tập hợp tất cả các giá trị thực của tham
số m để hàm số đã cho có đúng 5 điểm cực trị là  3   3   3  A. 1; . B. ;    \  2 .
C. 1;  \  2 . D. 1; .  2   2  2    Lời giải 2 x  1 Xét f x 4
x  2m  1 2
x  2m  3  f x  0   2 x  1 2
x  2m  3  0   2
x  2m  3
TH1: Nếu 2m  3  0  Do vậy f x có 2 điểm đổi dấu x  1; x  1 . Hàm số y f x có 5
điểm cực trị y f x có ba điểm cực trị  ab  0  2
 m  1  0  m  1 3
Vậy trường hợp này có 1  m  2 3
TH2: Nếu 0  2m  3  1 
m  2 . Khi đó f x có bốn điểm đổi dấu 2
x  1; x   2m  3 do đó số điểm cực trị của hàm số f x bằng 3 và hàm số y f x có 7 cực trị(loại).
TH3: nếu m    m   f x  x  2 2 2 3 1 2
1 khi đó y f x  x  2 2 1 có 3 điểm cực trị (loại). Chọn đáp án D
Câu 6: Có bao nhiêu số nguyên m  20  ;20 để hàm số 4
y x  m   2
1 x m có 7 điểm cực trị. A. 18. B. 20. C. 19. D. 21. Lời giải Xét 4
x  m   2 2 2
1 x m x  1; x m1 vậy để hàm số 4
y x  m   2
1 x m có 7 điểm m  0
cực trị khi và chỉ khi phương trình 1 có 4 nghiệm phân biệt    m2,...,1  9 . có m   1
18 số nguyên thỏa mãn. Chọn đáp án A
Câu 7: Có bao nhiêu số nguyên m  20
 ;20để hàm số y   2 x   2
2 x m có đúng 5 điểm cực trị. A. 1. B. 17. C. 2. D. 16. Lời giải Có y   2 x   2
x m   2 x   2 x m 4
x  m   2 2 2 2 x  2m . Nếu 4
m   x  m   2 0
2 x  2m  0, x
 nên hàm số đã cho có tối đa ba điểm cực trị (loại). Nếu 4
m   x  m   2 2 0
2 x  2m  0  x m x   m. Vậy điều kiện là hàm số 4
y x  m   2
2 x  2m có ba điểm cực trị  m  2  0  m  2  m3,...,1  9 . Có 17 số nguyên thoả mãn. Chọn đáp án B.
4 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 8: Có bao nhiêu số nguyên m để hàm số 3
y x   m   2 x   2 m m   2 2 1 2 2
9 x  2m  9 có 5 điểm cực trị. A. 7. B. 5. C. 6. D. 4. Lời giải 3
ycbt x 2m  1 2 x   2
2m  2m  9 2 x  2m  9   x x  1 1 2 2
x  2mx  2m  9   2 2 x  2mx   2m  9  0    2
  m  2 m   3 m 3 2 9  0 
Có 3 nghiệm phân biệt        m 2  , 1  ,0,1,  2 1 17 2
1 2m  2m  9  0 m   2 3
Câu 9: Có bao nhiêu số nguyên m để hàm số 2
y x mx   2 3 3 m  4| | x 1  có đúng 3 điểm cực trị. A. 3. B. 5. C. 6. D. 4. Lời giải Ta có 3 2
ycbt y x mx   2 3
3 m  4x  1 có đúng một điểm cực trị dương 2
y   x mx   2 0 3 6
3 m  4  0  x m  2;x m  2 có đúng một nghiệm dương
m  2  0  m  2  2
  m  2  m1,0,1,  2 . Chọn đáp án D. 3
Câu 10: Có bao nhiêu số nguyên m  10  ;10 để hàm số 2
y x mx   2 3 3 m  4| | x 1 
có đúng 5 điểm cực trị. A. 3. B. 6. C. 8. D. 7. Lời giải Ta có 3 2
ycbt y x mx   2 3
3 m  4x  1 có hai điểm cực trị dương 2
y   x mx   2 0 3 6
3 m  4  0  x m  2;x m  2 có hai nghiệm dương
m  2  0  m3,...,  9 . Chọn đáp án D.
Câu 11: Có bao nhiêu số nguyên m để hàm số 5 3
y  3x  15x  60x m có 5 điểm cực trị. A. 289. B. 287. C. 286. D. 288. Lời giải Xét 5 3
y  3x  15x  60x có 4 2 2
y  0  15x  45x  60  0  x  4  x  2  Vậy hàm số 5 3
y  3x  15x  60x có đúng 2 điểm cực trị x  2; x  2 Bảng biến thiên
Vậy để hàm số có 5 điểm cực trị 5 3 5 3
 3x  15x  60x m  0  m  3x  15x  60x có tổng
số nghiệm đơn và bội lẻ bằng 3, tức 1
 44  m  144  1
 44  m  144  m 1  43,..,143.
Có 287 số nguyên thỏa mãn. Chọn đáp án B
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 5
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
Câu 12: Có bao nhiêu số nguyên m  20
 19;2019 để hàm số 2
y x  4x m  6x  1 có ba điểm cực trị. A. 2014. B. 2016. C. 2013. D. 2015. Lời giải Nếu 2 2 2
x  4x m  0, x
  y x  4x m  6x  1  x  2x m  1 có đúng 1 điểm cực trị x  1(loại). Nếu 2
x  4x m  0 có hai nghiệm phân biệt x x    4  m  0  m  4 1 2
2x  4  6  0 x  1     2x  4 2
x  4x m 2
x  4x m  0 m  5  Khi đó y   6; y  0    2
x  4x m
2x  4  6  0   x  5     2 x 4x    m  0 m  5 
Với 5  m  4 ta có bằng xét dấu của y như sau
Hàm số có đúng 1 cực trị x  1 (loại).
Với m  5 ta có bằng xét dấu của y như sau
Hàm số có 3 điểm cực trị x x ; x  5; x x 1 2 Vậy m  20  18,..., 
6 . Có 2013 số nguyên thỏa mãn. Chọn đáp án C
Câu 13: Có bao nhiêu số nguyên m  20  ;20 để hàm số 2
y x  2m x m  1  1 có ba điểm cực trị. A. 17. B. 19. C. 18. D. 20. Lời giải 2
x  2mx m  1x m  1  0
2x  2mx m  1    0 Ta có y    y   2 x 2m  
x m  1x m  1  0 2x  2m
x m 1  0
Vậy hàm số không có đạo hàm tại điểm x m  1 và
2x  2m  0 x m   x m
x m  1  0 1    0 y       1  
2x  2m  0 x  m
x  mm     2      
x m  1  0  2  m  1  0 1
Vậy để hàm số có 3 điểm cực trị trước tiên phải có m
và lúc này bảng xét dấu của y 2 như sau 1
Điều này chứng tỏ với m
là các giá trị cần tìm, các số nguyên là m 1,...,  19 . Có tất cả 2 19 số nguyên thỏa mãn.
Câu 14: Có tất cả bao nhiêu số nguyên m thuộc đoạn  2017  ; 2017để hàm số 3 2
y x  3x m có 3 điểm cực trị ? A. 4032. B. 4034. C. 4030. D. 4028. Lời giải
6 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN x  0 Ta có 3 2
y x  3x m có 2
y  3x  6x; y  0 
y 0  m,y2  m   4 x   2 m
Yêu cầu đề bài tương đương với y   y     mm   4 0 . 2 0 4  0   m   0 Do đó m  2017 
,..., 2017có 2018  2014  4032 số nguyên thỏa mãn. Chọn đáp án A
Câu 15: Tìm tất cả các giá trị thực của tham số m để hàm số 3 2
y x  3x m có 5 điểm cực trị.
A. 4  m  0.
B. 4  m  0.
C. 0  m  4.
D. m  4 hoặc m  0. Lời giải x  0 Ta có 3 2
y x  3x m có 2
y  3x  6x; y  0 
y 0  m,y2  m   4 x   2
Yêu cầu đề bài tương đương với y 0.y 2  0  m m  4   0  0  m  4 Chọn đáp án C
Câu 16: Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số 4 2
y x mx m có 7 điểm cực trị.
A. 4; . B. 0; 1. C. 0; 4.
D. 1; . Lời giải Xét hàm số 4 2
y x mx m có tối đa 3 điểm cực trị và phương trình f x  0 có tối đa 4
nghiệm. Vì vậy hàm số y f x có 7 điểm cực trị khi và chỉ khi f x  0 có 4 nghiệm 2
  m  4  0 
phân biệt và f x  0 có 3 nghiệm phân biệt  S m  0, P m  0  m  4 
ab  m  0  Chọn đáp án A
Câu 17: Cho hàm số   3 2
f x ax bx cx d thoả mãn
a  0, d  2018, a b c d  2018  0. Tìm số điểm cực trị của hàm số y f x  2018 . A. 3. B. 5. C. 2. D. 1. Lời giải
 lim gx  ;lim gx   x x 
Xét g x  f x  2018 ta có g 0  f 0  2018  d  2018  0
g1  f 12018  abcd2018  0 
Do đó đồ thị hàm số y g x cắt trục hoành tại ba điểm phân biệt và suy ra hàm số
y g x có hai điểm cực trị
Do vậy số điểm cực trị của đồ thị hàm số y g x là 2  3  5 Chọn đáp án B
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 7
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
Câu 18: Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 3 2
y  3x  4x  12x m có 7 điểm cực trị ? A. 3. B. 5. C. 6. D. 4 Lời giải
Hàm số f x 4 3 2
 3x  4x  12x mcó ba điểm cực trị là nghiệm của phương trình x  0 f x 3 2 0 12x 12x 24x 0 12x  2 x x 2 0             x  1  x   2
Phương trình f x  0 có tối đa 4 nghiệm thực. Do đó hàm số y f x có 7 điểm cực trị
khi và chỉ khi phương trình f x  0 có 4 nghiệm thực phân biệt 4 3 2
 3x  4x  12x  m
có 4 nghiệm thực phân biệt. Lập bảng biến thiên của hàm số 4 3 2
y  3x  4x  12x ta có giá trị cần tìm 5
  m  0  0  m  5  m1;2;3; 
4 có 4 số nguyên thỏa mãn.
Câu 19: Có bao nhiêu giá trị nguyên của tham số m để hàm số 4 3 2
y x x  5x m có 7 điểm cực trị. A. 8. B. 9. C. 3. D. 4 Lời giải 5
Hàm số f x 4 3 2
x x  5x m có ba điểm cực trị là x  0;x  2;x   . 4
Vậy hàm số y f x có 7 điểm cực trị  f x  0 có bốn nghiệm phân biệt 875 875 
 m  0  0  m
. Vậy m1; 2;  3 .Chọn đáp án C. 256 256
Câu 20: Cho hàm số đa thức bậc bốn y f x có ba điểm cực trị x  1; x  2; x  3. Có bao
nhiêu số nguyên m  10
 ;10 để hàm số y f x m  có 7 điểm cực trị. A. 8. B. 10. C. 2. D. 19. Lời giải
Hàm số y f x m  có 7 cực trị  f x m có 3 điểm cực trị lớn hơn m  x m  1 x  1  m  
Các điểm cực trị của hàm số  y f x m là x m  2  x  2  m   x m  3 x  3    m
1  m  m
Vậy ta có điều kiện là 2  m  m m   m 9  ,...,  9  . Chọn đáp án D 3  m    m 3
Câu 21: Cho hàm số y x mx  5. Gọi a là số điểm cực trị của hàm số đã cho. Mệnh đề nào dưới đây đúng ?
A. a  0.
B. a  1.
C. 1  a  3.
D. a  3.
8 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN Lời giải 3
x mx  5x  0 2
3x mx  0 Ta có y    y  
và hàm số không có đạo hàm tại điểm 3
x mx  5  x  0 2 3x m  x  0 x  0 2
3x  0x   0
Nếu m  0  y  
đổi dấu từ âm sang dương khi qua điểm x  0 nê hàm số 2 3x  0  x  0
có duy nhất 1 điểm cực trị là x  0 2
3x mx   0 m
Nếu m  0  y  
y  0  x
chỉ đổi dấu khi đi qua 2  3
x m  0  x  0 3 m m x
nên có duy nhất 1 điểm cực trị là x  3 3 2
3x m  0x   0 m
Nếu m  0  y  
y  0  x  2 3x m  x  0 3 mm
Chỉ đổi dấu khi đi qua x  
nên có duy nhất 1 điểm cực trị là x   3 3
Vậy với mọi m hàm số có duy nhất 1 điểm cực trị Chọn đáp án B 3
Câu 22: Tìm tất cả các giá trị thực của tham số m để hàm số y x   m   2 2
1 x  3m x  5 có 5 điểm cực trị. A. B.  1   1       1 1  1; . 0;  1; . ; 1; C.   D.     .  ; 1;   .  4   4   2 4  Lời giải
yêu cầu bài toán tương đương hàm số 3
y x   m   2 2
1 x  3mx  5 có 2 điểm cực trị dương, tức 2
3x  2 2m  1x  3m  0 có 2 nghiệm dương phân biệt, tức
   m 2 2 1  9m   0.      m   m 1 2 2 1 S  0     1 chọn đáp án D 3 0  m    4  3m P   0  3
Câu 23: Cho hàm số f x 3
x   m   2 2
1 x  2  mx  2. Tìm tập hợp giá trị thực của
tham số m để hàm số y f x  có năm điểm cực trị. 5 5 1 5 A.   m  2. B. m  2. C. m  2. D. 2   m  . 4 4 2 4 Lời giải
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 9
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
Ta có 5  2a  1  a  2 là số điểm cực trị dương của hàm số y f x
  2m12 32m   0   2 2m  1 2   5
Ta có f x  3x  2 2m  1 x  2  m S    0   m  2. 3 4   2  m P   0  3 Chọn đáp án B 3
Câu 24: Tìm tất cả các giá trị thực của tham số m để hàm số y x   m   2 2
1 x  3m x  5 có 3 điểm cực trị.  1 
A. ; 0.
B. 1; .
C.  ; 0]. D. 0;  .  4  Lời giải 3 xét f x 3
x   m   2 2
1 x  3mx  5 và f x  x   m   2 2
1 x  3m x  5
ta có 3  2a  1  a  1 là số điểm cực trị dương của hàm số y f x
vậy yêu cầu tương đương với: f x có đúng 1 điểm cực trị dương  f x  0 có 2 nghiệm
thỏa mãn x  0  x m  0 1 2
Câu 25: Cho hàm số f x 4 3 2
ax bx cx dx ea,b,c,d,e và a  0. Biết f  1
   0, f 0  0, f 1  0. Số điểm cực trị của hàm số y f x bằng A. 7. B. 6. C. 5. D. 9. Lời giải
lim f x   x 
lim f x. f 1  0  f  1    0 x  
 f 0.f  1    0
Theo giả thiết ta có:  f 0  0     x
    x   x   x
f 0. f 1 1 0 1 1 2 3 4    f   0 1  0 
lim f x.f 1   f x 0 lim    x x
Sao cho f x  0; f x  0; f x  0; f x  0. 1   2   3  4 
Điều đó chứng tỏ rằng phương
trình f x  0 có 4 nghiệm phân biệt, do đó hàm số f x phải có 3 điểm cực trị. Vì vậy hàm
số y f x có 4  3  7 điểm cực trị. Chọn đáp án A
10 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
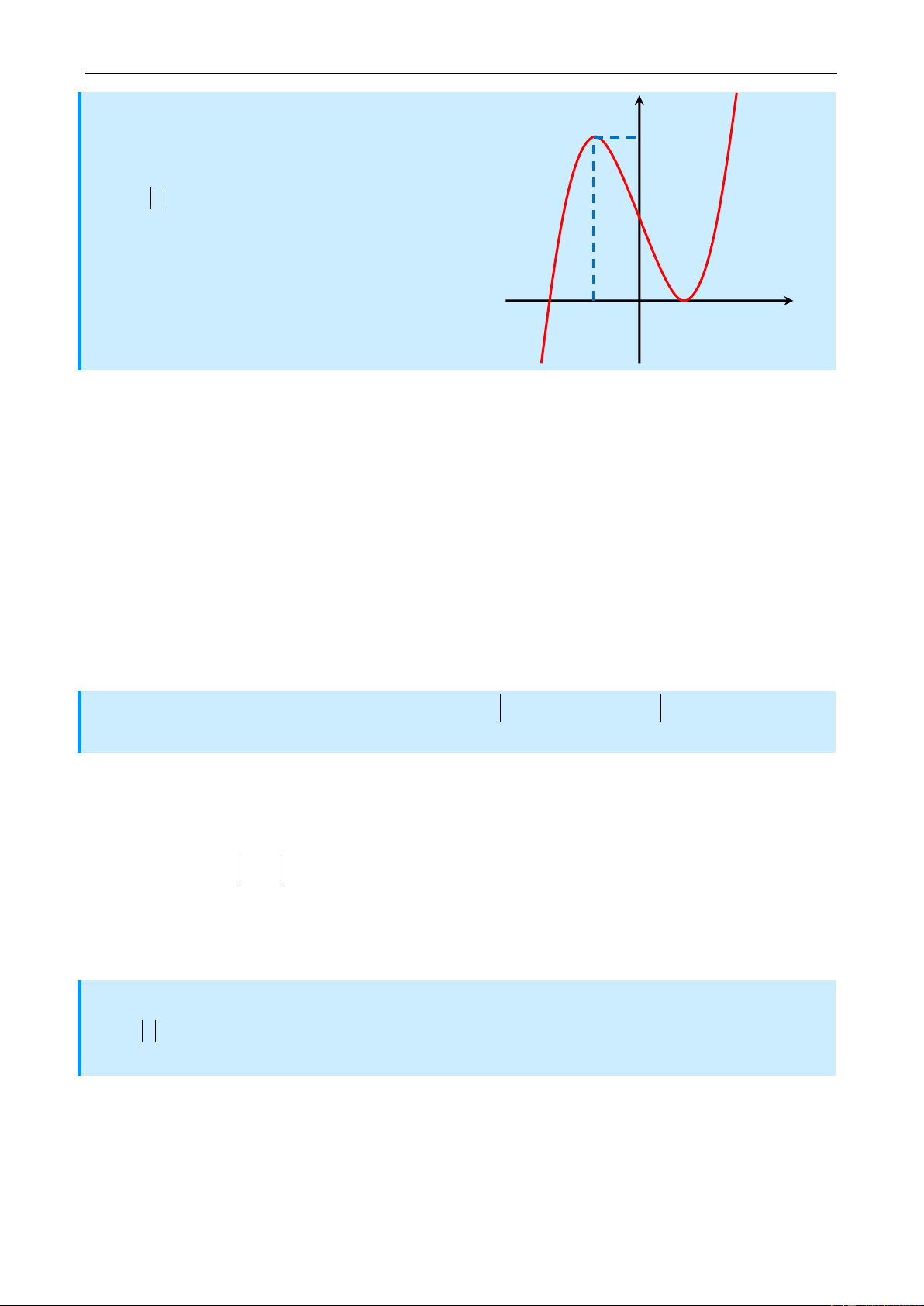
Câu 26: Cho hàm số y f x có đồ thị y
như hình vẽ ở bên. Tìm tập hợp tất cả 4
các giá trị thực của tham số m để hàm số
y f x m có 5 điểm cực trị. 2
A. m  1.
B. m  1.
C. m  1. x
D. m  1. 1 O 1 Lời giải
Hàm số f x có 2 điểm cực trị x  1; x  1. hàm số f (| |
x m) luôn có 1 điểm cực trị x  0
f x mx   0
Phá trị tuyệt đối có y f (| | x m    f
 x mx  . 0
Hàm số f x m có 2 điểm cực trị là x m  1; x m  1  x  1  m; x  1  m
Hàm số f x m có 2 điểm cực trị là x m  1; x m  1  x  1  m; x m  1 m  1  0  m  1  0 Vậy điều kiện là 
m  1. Chọn đáp án A m  1  0  m  1   0
Câu 27: Có bao nhiêu số nguyên m để hàm số 5 3
y  3x  25x  60x m có 7 điểm cực trị. A. 42. B. 21. C. 44. D. 22. Lời giải
Hàm số f x 5 3
 3x  25x  60x mcó 4 điểm cực trị là nghiệm của phương trình f x 4 2
 0  15x  75x  60  0  x  2  ; x  1  .
Do đó hàm số y f x có 7 điểm cực trị khi và chỉ khi phương trình f x  0 có tổng số  3  8  m  1  6 16  m  38
nghiệm đơn và bội lẻ bằng 3. Khảo sát hàm số dễ có   16 m 38     3  8  m  1    6
do đó có 21  21  42 số nguyên thỏa mãn. Chọn đáp án A.
Câu 28: Cho hàm số f x 4 3 2
 3x  4x  12x . Có bao nhiêu số nguyên m  10 để hàm số
y f x m có 7 điểm cực trị. A. 9. B. 11. C. 10. D. 8. Lời giải x  0  có f x 3 2
 12x  12x  24x; f x  0  12x 2
x x  2  0  x  1   x   2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 11
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
do đó hàm số f x có 3 điểm cực trị x  0; x  1; x  2
hàm số f x m luôn có 1 điểm cực trị x  0
f x m x   0
phá trị tuyệt đói có y f x m       f
 x mx  . 0
Hàm số f x m có 3 điểm cực trị là
x m  1; x m  0; x m  2  x  m  1; x  m; x  2  . m
Hàm số f x m có 3 điểm cực trị là
x m  1;x m  0;x m  2  x m  1;x m;x m  2.
Do đó hàm số f x m có tối đa 7 điểm cực trị là
x  0; x m  1; x m; x m  2; x  m  1;x  m;x  2  . m m  1  0 m  0  m  2  0
Điều kiện bài toán tương đương với   m  1   m 9  , 8  ,...,  2 m  1  0  m  0  m  2  0
Có tất cả 8 số nguyên thỏa mãn. Chọn đáp án D
Câu 29: Có bao nhiêu số nguyên m để hàm số 4 2
y x  4x m có 7 điểm cực trị. A. 5. B. 15. C. 3. D. 13. Lời giải
Hàm số f x 4 2
x  4x m có 3 điểm cực trị. Vậy hàm số f x có 7 cực trị khi và chỉ khi
phương trình f x  0 có 4 nghiệm phân biệt, tức
  4  m  0 
 0  m  4  m1;2; 
3 có 3 số nguyên thỏa mãn. Chọn đáp án D
S  4  0, P m   0
Câu 30: Cho hàm số y f x có đạo hàm f x 2
x x   2
1 x  2mx  5.Có bao nhiêu giá
trị nguyên m  10 để hàm số y f x  có 5 điểm cực trị. A. 7. B. 9. C. 6. D. 8. Lời giải
Yêu cầu bài tóan tương đương với f x có đúng 2 điểm cực trị dương, tức 2
x  2mx  5  0 có 2 nghiệm dương phân biệt, tức 2     m  5  0 
m   5  m 9  , 8  ,..., 
3 có tất cả 7 số nguyên thỏa mãn. S    2
m  0, P  5  0 Chọn đáp án A
12 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2 3 5
Câu 31: Cho hàm số f x có đạo hàm f x  x    2 1
x m  3m  4 x  3 , x   .
Có bao nhiêu số nguyên m để hàm số y f x  có 3 điểm cực trị. A. 3. B. 6. C. 4 D. 5. Lời giải
Yêu cầu bài toán tương đương f x có một điểm cực trị dương, tức 2 2
x m  3m  4  0 có nghiệm dương, tức 2
m  3m  4  0  1  m  4  m0,1,2,3. Chọn đáp án C.
Câu 32: Cho hàm số f x   2018 m   4 2018 2 2 2018 1 x (2m
 2m  3)x m  2020. Hàm số
y f x  2019 có bao nhiêu điểm cực trị. A. 7. B. 3. C. 5. D. 6. Lời giải
Vì f x là hàm số trùng phương có ab   8 m   2018 2 1 2m
 2m  3  0, m  nên hàm số
f xcó 3 điểm cực trị và hàm số f x  2019 cũng có 3 điểm cực trị.
f x  2019  0   2018 m  1 4 2018 2 2 2018 x  (2m
 2m  3)x m  2020  2019   2018 m  1 4 2018 2 2 2018 x  (2m
 2m  3)x m  1  0
  (2m  2m  3)  4m 12 2018 2 2 2018  0   2018 2  2m  2m  3
Phương trình này luôn có 4 nghiệm thực phân biệt vì S    0 2018 m  1  P  1  0 
Do đó f x có 4 nghiệm đổi dấu. vậy số điểm cực trị của đồ thị hàm số y f x  2019
bằng 3  4  7 chọn đáp án A
Câu 33: Cho hàm số f x 3
x   m   2 2
1 x  m  2x  1. Có bao nhiêu số nguyên m 5
 ;5 để hàm số y f x  có đúng ba điểm cực trị. A. 4. B. 6. C. 5. D. 3. Lời giải
Hàm số y f x  có đúng 3 điểm cực trị khi và chỉ khi hàm số y f x có đúng một điểm
cực trị dương. Điều này tương đương với f x   g x  2 0
 3x  2 2m  1x m  2  0 có
hai nghiệm phân biệt x x 1 2 thỏa mãn     g  3m 2 0 3. 0  0   m  2  0
x  0  x  g 0  0    m  2 1 2     22m  1 S    0   0  3 Vậy m  5  , 4  , 
3 có 3 số nguyên thỏa mãn. Chọn đáp án D
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 13
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
Câu 34: Cho hàm số f x 3
x   m   2 2
1 x  m  2x  1. Có bao nhiêu số nguyên m 5
 ;5 để hàm số y f x  có năm điểm cực trị. A. 4. B. 6. C. 5. D. 3. Lời giải
Hàm số y f x  có đúng 5 điểm cực trị khi và chỉ khi hàm số y f x có hai điểm cực trị
dương. Điều này tương đương với f x   g x  2 0
 3x  2 2m  1x m  2  0 có hai
nghiệm phân biệt x x 1 2 thỏa mãn  g   3m  2    0 3. 0 0  
0  x x    0   
2m 12  3 m 2  0  m  1 1 2   S 0    2 2m    1  0  3
Vậy m 2, 3, 4, 
5 có 4 số nguyên thỏa mãn. Chọn đáp án A
Câu 35: Có bao nhiêu số nguyên m  20  ;20 để hàm số 2
y x  2m x m  6  1 có ba điểm cực trị. A. 17. B. 16. C. 18. D. 15. Lời giải 2
x  2mx m  6x m  6  0
2x  2mx m  6    0 Ta có y    y   2 x  2m
x m  6x m  6  0 2x  2m
x m  6  0
Vậy hàm số không có đạo hàm tại điểm x m  6 và
2x  2m  0  x m
x m  6  0  x m y  0 
 x  m    
2x  2m  0  x  m  m  3   2m  6    0
x m  6  0
Vậy để hàm số có 3 điểm cực trị trước tiên ta phải có m  3 và lúc này bảng xét dấu của y
như sau: Điều này chứng tỏ với m  3 là giá trị cần tìm, các số nguyên là m 4,...,  19 có
tất cả 16 số nguyên thỏa mãn. 3 2 x 3x m
Câu 36: Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y e    có 5 điểm cực trị.
A. ;0  4; . B. 0; 2.
C.  ;0][2;  . D. 0; 4. Lời giải f x
Số điểm cực trị của hàm số e
bằng số điểm cực trị của hàm số f x .
Do đó yêu cầu bài toán tương đương với f x 3 2
 0  x  3x m  0 có ba nghiệm phân
biệt  mm  4  0  0  m  4. Chọn đáp án D.
14 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 37: Có bao nhiêu số nguyên m  10 để hàm số 3
y x mx  1 có 5 điểm cực trị. A. 9. B. 7. C. 11. D. 8. Lời giải
yêu cầu bài tóan tương đương hàm số f x 3
x mx  1có hai điểm cực trị và phương
trình f x  0 có ba nghiệm thực phân biệt ta có   2 m
f x  3x m; f x  0  x   m  0.và 3 3 3
m  9  2 3mm  9  2 3m f    ; f      3  9  3  9      m   m  3
khi đó điều kiện để có 3 nghiệm phân biệt là 3 f  . f  
  0  81  12m  0  m      3 3 3     4
chọn đáp án D. chú ý các em có thể đưa về xét hàm số 2 1
m x  . cho kết quả tương tự x
Câu 38: Có bao nhiêu số nguyên m  10  ;10 để hàm số 3 2
y mx  3mx  3m  2x  2  m có 5 điểm cực trị. A. 7. B. 10. C. 9. D. 11. Lời giải
Yêu cầu đề bài tương đương phương trình 3 2
mx mx   m  x   m   x   2 3 3 2 2 0
1 mx  2mx m  2  0 có ba nghiệm phân biệt m  0  2
   m mm  2  0  m  0  m1,2,...,1 
0 có tất cả 10 giá trị
m2mm2  0  Chọn đáp án B
Câu 39: Cho hàm số y f x có đạo hàm f x   3 2 x x  3 2
x  2x, với mọi x  . Hàm
số y f 1  2018x có nhiều nhất bao nhiêu điểm cực trị. A. 9. B. 2022. C. 11. D. 2018. Lời giải Có f x 3
x x  2x  2 x  2 .Do đó hàm số f xcó 4 điểm cực trị là
x  0; x  2; x   2. Lập bảng biến thiên của hàm số f x suy ra f x  0 có tối đa 5
nghiệm phân biệt. Do đó hàm số y f x có tối đa 4  5  9 điểm cực trị.
Mặt khác số điểm cực trị của hàm số y f 1  2018x bằng số điểm cực trị của hàm số
y f x . Do đó hàm số y f 1  2018x có tối đa 9 điểm cực trị. Chọn đáp án A.
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 15
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
II. CÁC BÀI TOÁN LIÊN QUAN TỚI MIN MAX CỦA HÀM TRỊ TUYỆT ĐỐI
A. CÁC TÍNH CHẤT LIÊN QUAN TỚI CỰC TRỊ CỦA HÀM TRỊ TUYỆT ĐỐI
Bất đẳng thức trị tuyệt đối.
Cho 2 số thực a,b khi đó ta có a b a b a b
Dấu “=” thứ nhất khi a,b cùng dấu, dấu “=” thứ 2 khi a,b trái dấu.
a b a b
Tính chất hàm trị tuyệt đối max a , b   2 Phương pháp chung
 Bước 1: Xét hàm số y f x , trên a;b .
Tính đạo hàm: y '  f 'x .
Giải phương trình f 'x  0 và tìm các nghiệm a a;b i thuộc   .
 Bước 2: Giải phương trình f x  0 và tìm các nghiệm b a;b j thuộc đoạn   .
 Bước 3: Tính các giá trị: f a ; f b ; f a f b i  ;
j . So sánh và kết luận.
Câu 1: Có bao nhiêu số thực m để hàm số 2 3 2
y  3x  4x  12x m có giá trị lớn nhất trên
đoạn3; 2bằng 150? A. 4 B. 0 C. 2 D. 6 Lời giải Xét 4 3 2
u  3x  4x  12x m trên đoạn3;2 ta có: 3 2
u'  0  12x  12x  24x  0  x  0; x  1  ;x  2.
A  maxux  maxu3,u1,u0,u2  u3  m  243  3;2 Khi đó 
a  min ux  minu3 ,u1 ,u0 ,u2  u2  m  32  3;2
 m  243  150 
 m  243  m   32 m  140
Vậy max y  max m  243 , m  32   150      3;2   m  32  150 m    93  
 m  32  m   243 Câu 2: Cho hàm số 2
y x x m . Tổng tất cả các giá trị thực của tham số sao
cho min y  2 bằng?  2  ;2 31 9 A. D. 4 B. 8 C.  23 4 4 Lời giải 1 Xét hàm số 2
u x x m trên đoạn2;2 ta có u'  0  2x  1  0  x   . 2
16 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN   1    1 
Do đó A  max u  max u2 ,u  
 ,u2  max m  2;m  ;m  6  m  6 và 2;2   2    4        a u  u  1 u    u  1 1 min min 2 ,
, 2   min m  2;m  ;m  6  m  .  2  ;2   2    4  4 1 1 9
Nếu a  0  m
 min y m   2  m  t /m.  2  ;2 4 4 4
Nếu A  0  m  6  min y   m  6  2  m  8 t /m 2;2 1 Nếu . A a  0  6
  m   min y  0l.  2  ;2 4 9 23
Vậy tổng các giá trị thực của tham số là  8   . 4 4
Câu 3: Gọi , lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 3 2
y  3x  4x  12x m trên đoạn 3;2. Có bao nhiêu số nguyên m 20  19;2019 để 2  . A. 3209 B. 3215 C. 3211 D. 3213 Lời giải Xét 4 3 2
u  3x  4x  12x m trên đoạn3;2 ta có: 3 2 3 2
u'  12x  12x  24x;u'  0  12x  12x  24x  0  x  0; x  1  ; x  2.
A  maxux  maxu3,u1,u0,u2  u3  m  243  3;2
Khi đó a  minux  minu3,u1,u0,u2u2 m32  3;2
Nếu a  0  m  32  0  m  32    m  243;  m  32 khi đó giả thiết tương đương
2 m  32  m  243  m  307
Nếu A  0  m  243  0  m  243     m  32 ;   m  243 khi đó giả thiết tương
đương 2 m  243  m  32  m  518.
Nếu 243  m  32  .
A a  0  max m  243 , m  32   maxm  243,32   m  0;  0
trường hợp này không thỏa mãn 2   Vậy 20  19  m  51
 8 307  m  2019  m2018;...,518,307,...,20  18 .
Có tất cả 321 số nguyên thỏa mãn. 2
x m m
Câu 4: Cho hàm số y
. Giá trị lớn nhất M của hàm số trên đoạn1;2 có giá trị x  2 nhỏ nhất bằng? 1 1 1 1 A. B. C. D. 6 8 5 7 Lời giải
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 17
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI 2
x m m 2 2  m m Xét hàm số u  ta có u'   0, x   1;2 , m   . R 2   x  2 x  2 2 m m  2 2 m m  1
Do đó A  max u u2  
; a  min u u1   1;2 1;2 4 3  2 m m  2
2 m m  1  Vậy max y  max  , . 1;2  4 3  2 2 m m  2 m m  1 1 Ta có 2 2 7M  4  3
m m  2  m m  1  1  M  . 4 3 7 2 2 m m  2 m m  1 1 7   329 Dấu bằng xảy ra     m  . 4 3 7 14 2
x m m
Câu 5: Cho hàm số y
. Giá trị lớn nhất M của hàm số trên đoạn1;2 có giá trị x  2 nhỏ nhất bằng? A. 26 B. 18 C. 28 D. 26 Lời giải Xét 3 2
u x x   2
m  1x  27 trên đoạn3; 1   ta có 2 2
u'  3x  2x m  1  0, . x
Do đó A  max u u1  26  2
m ;a  min u u3  6  2 3m 3;1 3;1
Do đó M  max y  max 26  2 m , 6  2 3m và 2 2
4M  3 26  m  6  3m  72  M  18. 3;1 Dấu bằng xảy ra 2 2
26  m  6  3m  18  m  2  2.
Câu 6: Gọi S là tập hợp giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 3
y x  3x m trên đoạn 0;2 bằng 3. Số phần tử của S là? A. 1 B. 2 C. 0 D. 6 Lời giải Xét 3
u x  3x m có 2
u'  3x  3;u'  0  x  10;2. Khi đó
A  max  maxu0 ,u1 ,u2  maxm,m  2,m   2  m  2 0;2
a  min u  minu0 ,u1 ,u2  minm,m  2,m   2  m  2 0;2  m  2  3 
 m  2  m   2
Suy ra max y  max m  2 , m  2   3 
m  1,m  1. 0;2 m2  3  
 m  2  m   2
Câu 7: Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M,m lần lượt là giá trị lớn nhất và giá trị
nhỏ nhất của hàm số trên đoạn0; 2 . Có bao nhiêu số nguyên a  3
 ;3 , sao cho M  2 . m A. 6 B. 3 C. 7 D. 5 Lời giải
18 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN x  0  Với 4 3 2 3 2
u x  4x  4x a u'  4x  12x  8x;u'  0  x  1.  x   2
maxu  maxu0,u1,u2  u1  a   1 1;3 Khi đó 
min u  minu0 ,u1 ,u2  u0  a  1;3
Nếu a  0  m a, M a  1  2a a  1  a  1  a 1; 2;  3 .
Nếu a  1  m   a  1 ; M  a  2 a  1  a a  2  a 3;2.
Vậy có tất cả 5 số nguyên thỏa mãn.
BÀI TẬP TƯƠNG TỰ.
Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ
nhất của hàm số đã cho trên0; 2. Có bao nhiêu số nguyên a  4
 ; 4 sao cho M  2m? Câu 8: Cho hàm số 2
y  2x x  x  13  x  m . Khi đó lớn nhất của hàm số đạt giá trị
nhỏ nhất. Mệnh đề nào dưới đây đúng? A. 1 B. 2 C. 0 D. 6 Lời giải
Điều kiện xác định x  13  x  0  1  x  3.
Đặt t  x    x 2 2 2 1 3
 3  x  2x 2x x t  3.
Khi đó ta cần tìm giá trị lớn nhất của hàm số 2
y t t  3  m trên đoạn0;2   1   13 13
Ta có max u  max u0 ,u2 ,u   max m  3;m  1;m
  m  1;maxu m  . 0;2 0;2   2   4  4 13 13 m  1   mm 1       m  13  4  4  9
Do đó max y  max  m  1 , m      .  4  2 2 8 134 9 17
Dấu bằng xảy ra m  1  m    m  . 4 8 8 1 19
Câu 9: Gọi S là tập hợp tất cả các số nguyên m để hàm số 4 2 y x
x  30x m có giá 4 2
trị lớn nhất trên đoạn0; 2 không vượt quá 20. Tổng các phần tử của S bằng? A. 195 B. 210 C. 195 D. 210 Lời giải x  5  0;2 1 19  Xét 4 2 u x
x  30x m trên đoạn0;2 có 2
u'  x  19x  30;u'  0  x  3  0;2 . 4 2 x  2  0;2
Do đó max u  maxu0 ;u2  maxm,m  3 
6  m  26 và min u m 0;2 0;2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 19
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI m m 26 20  13 m 6
Do đó max y  max m , m  26           20   
 20  m  6 0;2 
m  26  m  20 20  m     13 20 Vậy m  2  0, 1  9,..., 
6 . Vậy tổng các phần tử của S bằng k  195  6
BÀI TẬP TƯƠNG TỰ. 1 19
Gọi a, b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 2 y x
x  30x m 4 2
trên đoạn0; 2. Có bao nhiêu số nguyên m  30
 ;30 để 2b a
Câu 10: Cho hàm số f x 3 2
x  3x m . Có bao nhiêu số nguyên m để min f x  3. 1;3 A. 4 B. 6 C. 11 D. 10 Lời giải Với 2 2
u x  3x m có 2
u'  3x  6x;u'  0  x  0, x  2.
min u  minu1,u3,u0,u2  minm  2;m;m   4  m  4  1;3 Do đó 
max u maxu1 ,u3 ,u0 ,u2  maxm  2;m;m   4   m  1;3
Nếu m  4  0  m  4  min f x  m  4  3  m  7  m4; 5;6;  7 . 1;3
Nếu m  0  min f x  m  3  3
  m m 3  ; 2  ; 1  ;  0 . 1;2
Nếu 0  m  4 khi đó min u  0; max u  0  min f x  0. ( Thỏa mãn ) 1;3 1;3 1;3 Vậy m  3  ;...; 
7 có 11 số nguyên thỏa mãn
BÀI TẬP TƯƠNG TỰ.
1. Cho hàm số f x 3 2
 2x  3x m . Có bao nhiêu số nguyên m để min f x  3.  1  ;3
2. Có bao nhiêu số nguyên m để hàm số 4 2
y x  2x m có min y  3.  1  ;2 3. Cho hàm số 4 3 2
y x  2x x a . Có bao nhiêu số nguyên a để max y  100. 1;2 4. Cho hàm số 3 2
y x x   2
m  1x  4m 7 . Có bao nhiêu số nguyên tố m để max y  15 0;2
5. Cho hàm số y  sin 3x  s inx  m . Có bao nhiêu số nguyên m để giá trị lớn nhất của
hàm số lớn nhất của hàm số không vượt quá 30.
6. Cho hàm số f x 2
x  3x  1. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của
hàm số y f 2 sin x  1  m không vượt quá 10? 1 1 7. Cho hàm số 4
y x   2 m  2 3 2 3
x m x m . Có bao nhiêu số nguyên m để 4 3 max y  5. 0;2
20 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Câu 11: Cho hàm số f x 3
x  3x. Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất
của hàm số y f sin x  1  2 . Giá trị biểu thức M m bằng? A. 4 B. 6 C. 2 D. 8 Lời giải
Đặt t  sin x  10; 2 , khi đó y f
x     f t 2 sin 1 2
 2  t  3t  2 Xét 2
u t  3t  2 trên đoạn0;2 có 2
u'  3t  3;u'  0  t  1. 
max  maxu0,u2,u1  max2;4;  0   4 0;2 Do đó 
min u  minu0 ,u2 ,u1  min2; 4;  0  0  0;2
Do đó M  max u  4; m  min u  0  M m a  0  4 0;2 0;2 Câu 12: Cho hàm số 4 3 2
y x  2x x a . Có bao nhiêu số thực a để min y max y  10.  1  ;2  1  ;2 A. 2 B. 5 C. 3 D. 1 Lời giải Xét 4 3 2
u x  2x x a trên đoạn0;2 có 3 2 1
u'  4x  6x  2x;u'  0  x  0; x  1; x  . 2   1
M max u max u 1 ,u2 ,u0     
,u  ,u1  u1  u2  a  4. 1;2    2       m u  1 min
min u1 ,u2 ,u0  
,u ,u1  u0  u1   a 1;2    2  
Trường hợp 1: Nếu m  0  a  0  min y m; max y M. 1;2 1;2 a  0
Vậy ta có điều kiện   a  3
a a  4   10
Trường hợp 2: Nếu M, m  0  a  4  min y  M; max y   . m 1;2 1;2 a  4 
Vậy ta có điều kiện        a   a 7. 4  a  10
Trường hợp 3: M, m  0  4  a  0  min y  0; max y  max a  4 , a   maxa  4;   a  10. 1;2 1;2
Suy ra min y  max y  0  10  10 ( loại) 1;2 1;2 Câu 13: Cho hàm số 2
y  2x  a  4x b  3 . Gọi M là giá trị lớn nhất của hàm số trên
đoạn2; 3. Khi đạt giá trị nhỏ nhất, tính giá trị biểu thức a  4b . A. 41 B. 30 C. 30 D. 41 Lời giải a  4 Xét 2
u  2x  a  4x b  3 trên đoạn2;3 có u'  0  4x a  4  0  x   4
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 21
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI a  4 Trường hợp 1: Nếu   2
 ;3  a  1
 6 a  4 ta có 4
M  max u2 , u3  max 2a b  3 , 3a b  33
2a b  3  3a b  33
2a b  33a b  33 5 a  6     25. 2 2 2 a  4 Trường hợp 2: Nếu   2  ;3  1
 6  a  4 ta có 4  2  a 4 a
M max  u2 , u3       , u  
   max  2a b  3 , 3a b  33 ,
a b  1    4    8  2 2 a a
2a b  3  3a b  33  2
a b  1
 2a b 3 3a b 33          2  a b   1 8  8    4 4
 1 a  2  25  25 6 . 16 4 4 25
So sánh hai trường hợp có M  . min 4 a  6  2 a 25  Dấu bằng xảy ra  2
a b  3  3a b  33 
a b  1   
35  a  4b  41. 8 4 b    4
Câu 14: Giá trị lớn nhất của hàm số 2
y x ax b trên đoạn m,nm n có giá trị nhỏ nhất bằng? 1 2 1 2 1 2 1 2
A. m n
B. m n
C. m n D.
mn 4 8 2 16 Lời giải
Gọi M  max y . m,n  a
Nếu  m;n  a  2
n a  2  m ta có 2
M  maxy m , y n  max 2 m am  2
b , n an b  2
m am b  2 n an  2 b m  2
n am n  
 1 m n m n a  1 m n2 . 2 2 2 2  a
Nếu  m;n ta có 2  2  a a
M max y m , y n     2 2  , y  
  max  m am b , n an b ,  b    2   4  2 2 a a Và M  2
m am b  2
n an b   b
am n  2 m  2 4 2 n 4 2
 1 a m n2  1 m n2  M  1 m n2 . 2 2 8
22 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2 a 2 Dấu bằng đạt tại 2 2 1
m am b n an b
b  m n . 4 8 4
x ax a
Câu 15: Cho hàm số y
. Gọi M,m lần lượt là giá trị nhỏ nhất của hàm số trên x  1
đoạn1; 2. Có bao nhiêu số nguyên a sao cho M  2 . m A. 15 B. 14 C. 16 D. 13 Lời giải 4
x ax a 4 3 3x  4x Xét u  trên đoạn u'   0, x   1;2 . 2   x  1 x  1 16 1
Do đó max u u2  a
;min u u1  a  . 1;2 1;2 3 2  16  1 M a a   0    1  3  2 1 13 Nếu a   0        a  . 2 1 16  1  2 3 m a   a   2 a    2  3  2    1   16 M     a   a   0   16   2   3 61 16 Nếu a   0        a   . 3   16   1   16  6 3 m   a      a     2  a     3     2   3   1  16   1 16   Nếu a a
 0  m  0, M    
max  a  , a
  M  2m ( thỏa mãn) .  2  3   2 3  61 13 Vậy   a   a 1  0;...; 
4 . Có 15 số nguyên thõa mãn. 6 3
Câu 16: Cho hàm số f x 2
x ax b . Gọi M là giá trị lớn nhất của hàm số f x trên
đoạn1; 3 . Khi M đạt giá trị nhỏ nhất, giá trị của biểu thức a  2b bằng? A. 1 B. 2 C. 4 D. 6
Lời giải Cách 1. a Xét 2
u x ax b u'  2x a;u'  0  x   . 2 aa
Trường hợp 1: Nếu    2 1;3   , khi đó 2 a  6   M
f   f  
 ab ab 1 max 1 , 3 max 1 , 9 3
8  4a  2 a  2  4 2 a
Trường hợp 2: Nếu   1  ;3  6
  a  2, khi đó 2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 23
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI  2  a a
M max  f 1 , f 3     , f  
  max  1  a b , 9  3a b , b     2   4   a  1 a 1  a 2 2 2
 max  a b  5 , b    a   5   1  4    2.  4  2 4 2  2 
So sánh 2 trường hợp suy ra min M  2 đặt tại a  2  b  1
Cách 2. Theo giả thiết M f  1
   1 a b , M f 1  1 a b , M f 3  9  3a b .
Suy ra sử dụng bất đẳng thức x y z x y z có 4M f  1
   2 f 1  f 3  1 a b  2 1 a b  9  3a b .
 1 a b  21 a b  9  3a b  8  M  2.
Vậy giá trị lớn nhất của hàm số trên đoạn 1; 3 có giá trị nhỏ nhất bằng 2 đạt tại
 1  a b  2, 1  a b  2, 9  3a b  2  
 1  a b9  3a b  0 a  2     
a b   1  a b   2
  2a  2b 2 4.  0 b  1  
 9  3ab   2
  2a  2b  0
Câu 17: Cho hàm số f x 2
x  3x  1. Có bao nhiêu số nguyên m để giá trị nhỏ nhất của
hàm số y f 2 sin x  1  m không vượt quá 10? A. 45 B. 41 C. 30 D. 43
Lời giải
Đặt t  2 sin x  11; 
3 ta có y f t 2
m t  3t m  1 .
Ta cần tìm m sao cho min y  10.  1  ;3 Xét 2
u t  3t m  1 trên đoạn1;3 ta có 2
u'  0  3t  3  0  t  1. 
Vậy A  max u  maxu1 ,u3 ,u1  maxm  3,m  19,m  
1  m  19 và a  min u m  1. 1;3  1  ;3
Trường hợp 1: Nếu a  0  min y a  10  0  a  10  0  m  1  10  1  a  11.  1  ;3 Trường hợp 2: Nếu
A  0  min y  A  10  1  0  A  0  1
 0  m  19  0  29  a  19  1  ;3 Trường hợp 3: Nếu .
A a  0  m  1m  19  0  1
 9  m  1  min y  0  10 ( thỏa mãn )  1  ;3 Vậy a  2  9,...,1 
1 . Có tất cả 41 số nguyên thỏa mãn
Câu 18: Cho hàm số f x 3
x  3x m . Có bao nhiêu số nguyên m 20  ;20 để với mọi
bộ số ba số thực a, b,c  2
 ;1 thì f a , f b , f c là độ dài ba cạnh của một tam giác? A. 30 B. 24 C. 28 D. 26 Lời giải Xét 3
u x  3x m trên đoạn2;1 có 3
u'  0  3x  3  0  x  1.
24 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
maxu  maxu2,u1,u1  maxm  2,m  2,m   2  m   2 2;1 Khi đó 
min u  minu2 ,u1 ,u1  minm  2;m  2;m   2  m  2  2;1
Để f a , f b , f c là độ dài ba cạnh tam giác ta phải có f a  f b  f c.
Chọn f a  f b  min f x ; f c  max f x ta phải có 2 min f x  max f x. 2;1 2;  1 2;  1 2;  1
Ngược lại 2 min f x  max f x , ta có f a  f b  f c  2 min f x  max f x  0. 2;  1 2;  1 2;1 2;  1
Vậy điều kiện cần và đủ để f a , f b , f c là độ dài ba cạnh tam giác là
2 min f x  max f x 2;  1 2;  1
 Nếum  2m  2  0  2min f x  0  2.0  max f x ( loại) 2;1 2;  1 m  2  0  
Nếu m  2  0  min f x  m  2;max f x  m  2    m  6. 2;  1 2;  1
2m  2  m  2 m  2  0
m  2  0  min f x  m  2;max f x  m  2    m  6  .  2  ;  1  2  ;  1  2 
 m  2  m  2 Vậy m  19  ,..,7,7,.., 
19 . Có 26 số nguyên thỏa mãn.
Câu 19: Cho hàm số f x 3
x  3x m .. Có bao nhiêu số nguyên m 20  ;20để với mọi
bộ ba số thực a, b,c  2
 ;1 thì f a , f b , f c là độ dài ba cạnh một tam giác nhọn? A. 30 B. 16 C. 28 D. 12 Lời giải Xét 3
u x  3x m trên đoạn2;1 có 2
u'  0  3x  3  0  x  1.
maxu  maxu2,u1,u1  maxm  2;m  2;m   2  m   2 2;1 Khi đó 
min u  minu2 ,u1 ,u1  minm  2;m  2;m   2  m  2  2;1
Để f a , f b , f c là độ dài ba cạnh tam giác nhọn ta phải nhọn thì 2 f a 2  f b 2  f c.  2  2
Chọn f a  f b  min f x ; f c   max f x ta có điều kiện 2  min f x   max f x . 2;1 2;1  2; 1   2; 1   2  2
Ngược lại với 2  min f x   max f x , có  2; 1   2; 1  2 2 2 f a  2 f b  2 f c 
 2min f x 
  max f x  0.  2; 1   2; 1 
Vậy điều kiện cần và đủ để f a , f b , f c là độ dài ba cạnh của một tam giác nhọn là  2 2
2min f x 
  max f x  2;  1   2; 1  2  2  
Nếu m  2m  2  0  2 min f x  0  2.0  max f x (loại) 2;  1  2; 1 
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 25
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
 Nếu m  2  0  min f x  m  2;max f x  m  2 2;1 2;1 m  2   0    m  6  4 2.  2
2 m  2  m  2
 Nếu m  2  0  min f x  m  2;max f x  m  2 2;1 2;1 m  2   0  
m  6  4 2.  2 2
2 m  2  m  2 Vậy m  19  ,..,12,12,.., 
19 . Có 16 số nguyên thỏa mãn.
BÀI TẬP TƯƠNG TỰ
Cho hàm số f x 3 2
 2x  9x  12x m . . Có bao nhiêu số nguyên m 20  ;20để với mọi
bộ ba số thực a, b,c  2
 ;1 thì f a , f b , f c là độ dài ba cạnh một tam giác nhọn.
Câu 20: Gọi M là giá trị lớn nhất của hàm số 3
y  4ax  1  3ax trên đoạn1;1 . Giá trị nhỏ nhất của M bằng? 3 8 1 A. 1 B. C. D. 2 9 2 Lời giải Xét 3
u  4ax  1  3ax ta có 2
u'  0  12ax  1  3a  0.
 Nếu a  0  y x M  max y  1. 1;  1   a Nếu 2 3 1
a  0  u'  0  x  . 12 3a  1  1  1   a  0     3a 1 12a 9 Nếu  1  ;1    
. Khi đó M y   8 1  1  a  . 12a 3a   1  1  1  0  a  9  12a  15  1 a      3a 1 3a 1 15 Nếu  1  ;1  1    1   . 12a 12a  1 a    19  2    3a  1   a   a  2 3 1 3 1
Khi đó M  max y 1     , y  
  max  1  a ,     .   12a   27a  27a   a   1  1 
Khảo sát hàm số g a  2 3 1 
trên D  ;   ; 27a      9  15   1  3
Ta có min g a  g     .  x D  6  2
26 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 1 5 3  3
Với a    M  max  ;   (thỏa mãn). 6 6 2  2 3 1
So sánh các trường hợp ta có Ma   . min đạt tại 2 6
Câu 21: Cho hàm số 3 2
x ax b , gọi M là giá trị lớn nhất của hàm số trên đoạn 3;2.
Khi M đạt giá trị nhỏ nhất thì T  log  b a 1 có giá trị là ? 1 A. 0 B. 4026 C. 2 D. 2 Lời giải Xét hàm số   3 2
h x x ax b
Gọi m,n lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của h x trên đoạn 3; 2 .
m  4a b  8
m  9x b  27 Suy ra  hoặc 
n  9x b  27 
n  4a b  8 
m n m n ym n max max ;  2
4a b  8  9a b  27  4a b  8  9a b  27 ymax 2
Vì 4a b  8  9a b  27  0 ; 4a b  8  9a b  27  0 m n  a  7 Vậy y  m  0   T  log    b a log 36 2. max 0. Dấu “=” xảy ra khi  1 6  b  36  n   0 x y
Câu 22: Cho 2 số thực x  1, y  0 thỏa mãn điều kiện max x  1 ; 2x y  1  2 2  . 2 2 x y
Hỏi biểu thức P  x   2 3
1 x  2y  1 có tất cả bao nhiêu ước số nguyên dương? A. 5 B. 6 C. 7 D. 8 Lời giải a b a b
Ta có một tính chất cơ bản của hàm trị tuyệt đối 
 max a ; b 2 2
x x y
x x y Áp dụng ta có
x xy  2 2 2 2 2 2 max 1 ; 2 1   2 2
Sử dụng bất đẳng thức trị tuyệt đối ta có 2 2 2 2
x  2x y  2
x  2x y 2x  2 2x  2     2x  1 2 2 2 2
    2x y x y 2 2 2 2
Mặt khác theo bất đẳng thức Cauchy – Schwarz ta có   2 2 2 2 2 x y x y
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 27
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
Vậy VT  2  VP . Dấu “=” xảy ta khi và chỉ khi x y  1 .
Khi đó P  24 có tất cả 8 ước số nguyên dương.
28 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
III. ĐỌC THÊM - ỨNG DỤNG TOÁN CAO CẤP TRONG GIẢI TOÁN SƠ CẤP A. ĐA THỨC CHEBYSHEV
Đa thức Chebyshev, được đặt theo tên nhà toán học Nga Pafnuty Chebyshev, là một dãy
đa thức trực giao (tiếng Anh: orthogonal polynomials), và có liên quan đến công thức de
Moivre (de Moivre's formula). Có thể xác định dãy đa thức này bằng công thức truy hồi,
giống như số Fibonacci và số Lucas. Có hai loại: đa thức Chebyshev loại I (ký hiệu là Tn)
và đa thức Chebyshev loại II (ký hiệu là Un). Chữ T được dùng để ký hiệu vì, trong tiếng
Pháp tên của Chebyshev viết là Tchebycheff và trong tiếng Đức là Tschebyscheff. Chữ n
ký hiệu cho bậc của đa thức. Đa thức Chebyshev ý tưởng đơn giản (cũng như bản chất của
nó) chỉ là biểu diễn cos nx là đa thức bậc n theo cos x . Trong bài viết này ta sẽ cùng tìm
hiểu định nghĩa các tính chất và ứng dụng của nó.
I. ĐỊNH NGHĨA VÀ TÍNH CHẤT ĐA THỨC CHEBYSHEV 1. ĐỊNH NGHĨA
T x 1,T x x 0    1    Các đa thức T x
n   , n ∈ N xác định như sau:  T x xT x T x n 2   1   n   n1  
Gọi là các đa thức Chebyshev loại I.
U x 0,U x 1 0    1    Các đa thức T x
n   , n ∈ N xác định như sau:  U x xU x U x n n 2  n n ,    1 1     1  
Gọi là các đa thức Chebyshev loại II
2. CÁC TÍNH CHẤT CỦA ĐA THỨC LOẠI I
Đa thức Chebyshev có nhiều tính chất hay, được sử dụng rất nhiều trong việc giải quyết
các bài toán đa thức. Sau đây xin được nêu một số tính chất quan trọng (việc chứng minh rất dễ dàng)
 Tính chất 1: x 1,1,ta có T x n x n    cos( arccos )  Tính chất 2: T x n
n   là đa thức bậc n,
 ,hệ số cao nhất là 1 2n  Tính chất 3: T x
n   là hàm chẵn khi x chẵn và là hàm lẻ khi x lẻ.
 Tính chất 4: Đa thức T x 1,1
n   có đúng n nghiệm phân biệt trong  : 2k x  1 k n k cos ,  1,2,...,  1 2n  Tính chất 5:
a) T x  1,x 1,1 nk
b) T x  1 n 1,1 x k n k cos  1,2,..., n
chỉ tại  1 điểm khác nhau trong  là   n k Chú ý là: T x
n k    1
Các điểm xk gọi là điểm luân phiên Chebyshev.
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 29
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI  1
Tính chất 6: P x bậc n, hệ số cao nhất bằng 1, ta có max P x   1 2n 1
Đẳng thức xảy ra  P x  T x n *    n1 2
Một vài đa thức khởi đầu 1. T  2 2x  1 2 2. T  3 4x  3x 3 3. T  4 8x  2 8x  1 4
3. CÁC TÍNH CHẤT CỦA ĐA THỨC LOẠI II sin narccos x
 Tính chất 1: x 1,1 ta có U x n      1  2 x  Tính chất 2: U x T x n    1 n '  n  Tính chất 3: a) U x n
n   là đa thức hệ số nguyên, bậc
 1 , hệ số cao nhất là 1 2n b) U x
n   là hàm chẵn nếu x lẻ và là hàm lẻ nếu x chẵn.
 Tính chất 4: U x  n,x 1,1 n
 Tính chất 5: Đa thức U x 1,1
n   có đúng n-1 nghiệm phân biệt khác nhau trong  
Đặc biệt: Từ tính chất 2 và 4, ta có: T x  2 '
n ,x 1,1 n
II. MỘT SỐ BÀI TOÁN MINH HỌA
Một trong những dấu hiệu để nhận biết bài toán đa thức có sử dụng tính chất của đa thức
Chebyshev hay không đó là miền giá trị của đa thức. Các bài toán trên miền 1;  1 đều
gợi ra cách giải bằng phương pháp sử dụng tính chất của đa thức Chebyshev. Sau đây ta
xét lớp các bài toán về đa thức có sử dụng tính chất của đa thức Chebyshev.
Bài 1: Cho hàm số y  3
x  a   2 4
3 x  ax . Tìm a để y  1 khi x  1 .
Lời giải
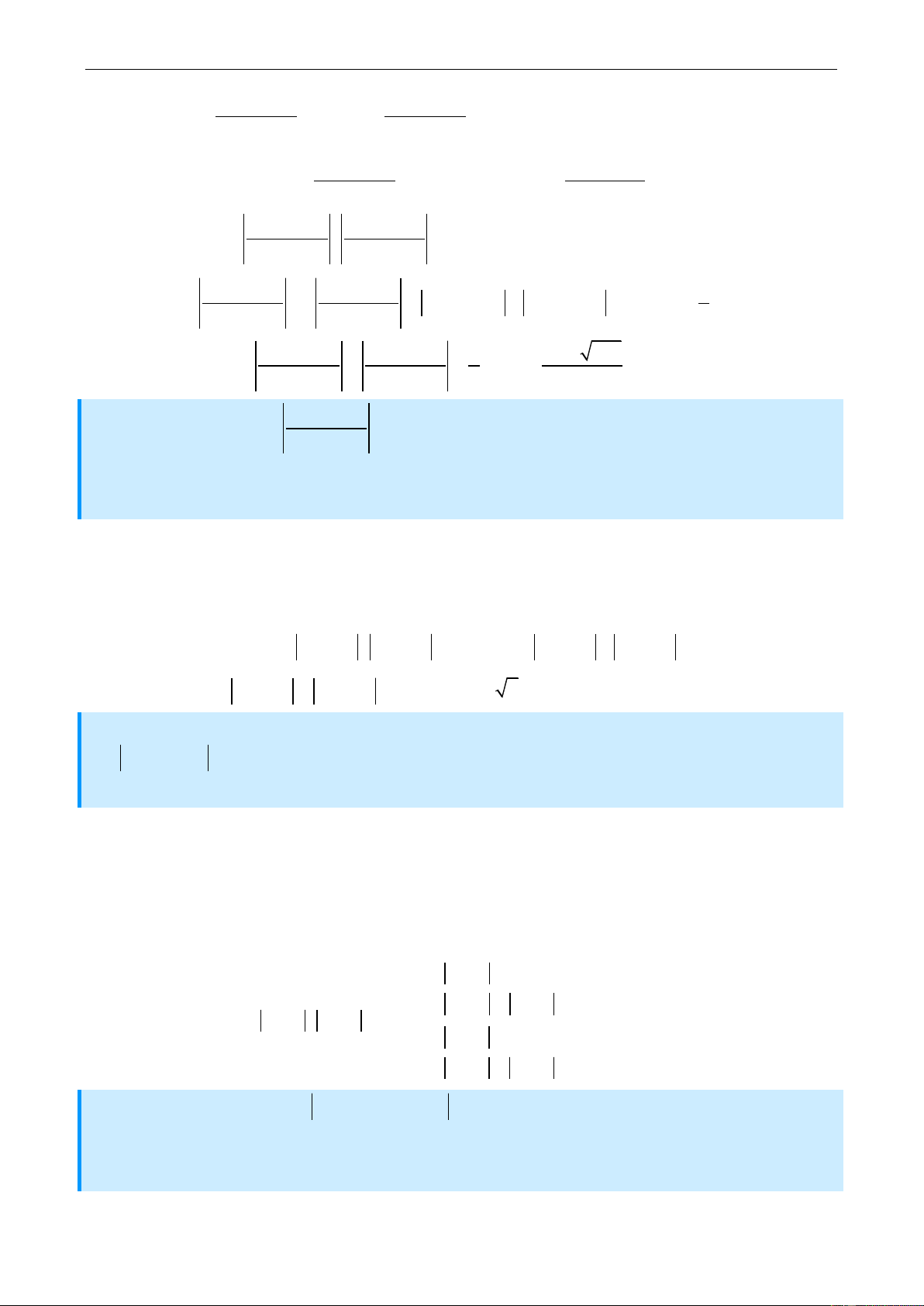
Vì y  1 khi x  1 nên ta có :  y 1  1  7  2a   1   y  1    1 1  1
1  7  2a   1       1  1 a  3 aa 1   y  1       1 1       1   2   2 4 2  4 4    a 1 1 a  3 5   3 a 1      1 y      1 1       4 4   2   2 4 2
30 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 
1  7  2a  1 4  a  3  
 4  a  1  4  3  a  5  a  3   4  3a  5   4   a  1 3  3
Ngược lại, khi a  3 thì y  3
4x  3x . Đặt x  cos  với   0;  thì y  os c  3 rõ ràng
thỏa mãn y  1 khi x  1 .
Bình luận: Nếu chỉ xem lời giải và không hiểu rõ nguồn gốc, cội nguồn của bài toán thì
học sinh sẽ thấy lời giải mất tự nhiên ở việc là tại sao ta chỉ xét giá trị của hàm số tại các
giá trị của x là   1 1;
mà không phải là các giá trị khác. Thực chất của việc xét giá trị của 2
hàm số tại các điểm   1 1;
chính là xét giá trị của hàm số tại các nghiệm của đa thức 2 Chebyshev bậc ba.
Bài 2: Cho hàm số y  3
4x mx . Tìm m để y  1 khi x  1 .
Lời giải
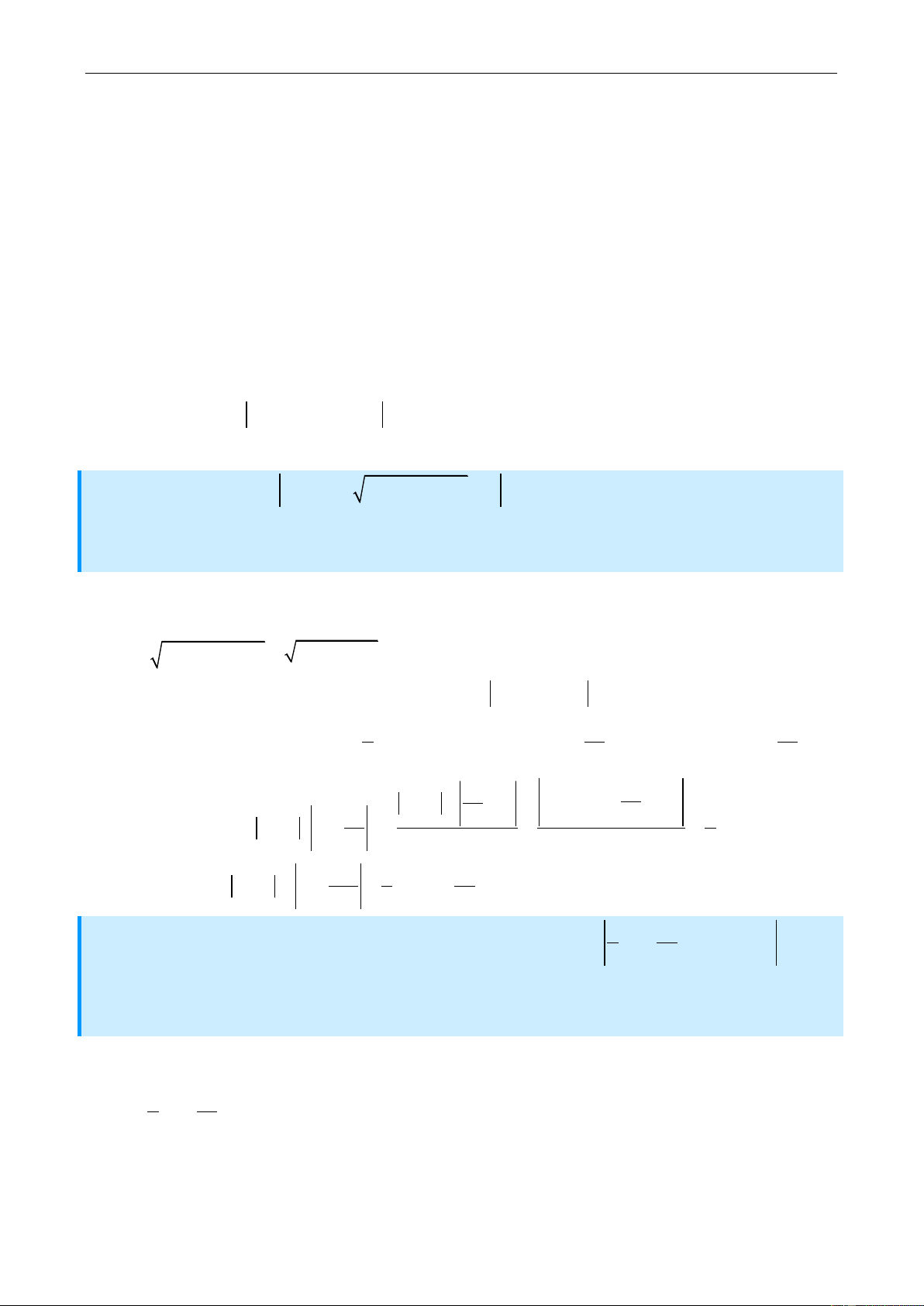
Vì y  1 khi x  1 nên ta có :  y 1  1   y  1     1  4  m  1 1  4  m    1    5  m    1  3   y
 4  m  1  2  m  1  2    m     3 1  3  m        1 2   1 m 3a 5    1 1     1  1   2 2  y   1    4 4   2 
Ngược lại, khi m=-3 thì y  3
4x  3x . Đặt x  cos  với   0;  thì y  os c  3 rõ ràng thỏa
mãn y  1 khi x  1 .
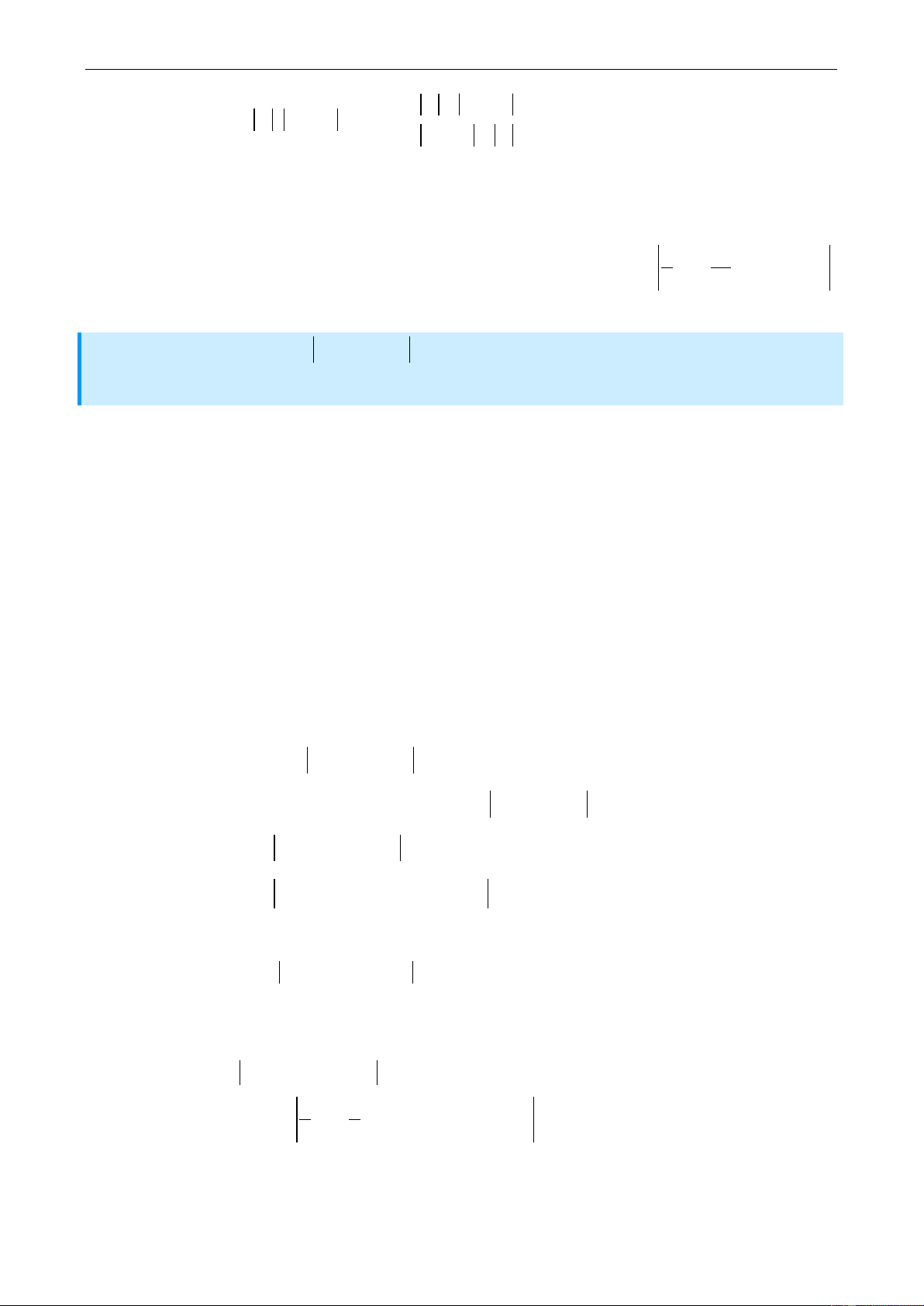
Bài 3: Tìm a, b, c để 3 x  2 4
ax bx c  1, với mọi x thỏa mãn x  1 .
Lời giải Cách 1.
Điều kiện cần: Vì y  1 khi x  1 nên ta có :  y 1  1   y  
5  a b c    31 1 1   
3  a b c  52  1     I y  1     2
6  a  2b  4c      2 3   1
2  a  2b  4c     64  y     1   2 
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 31
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
a b c  3 Từ (1) và (2) ta có: 
 2b  6  b  35.
a b c    3
a  2b  4c  6 Từ (3) và (4) ta có: 
 4b  12  b  36
a  2b  4c   6
Từ (5) và (6) ta được b  3
2  a c  0 
0  a c  2 a c  0
Thế b  3 vào hệ (I) ta có:   
a c  0 
8  a  4c  0 a  4c    0
0  a  4c   8
Điều kiện đủ: Khi a c  0, b  3 thì y  3
4x  3x . Đặt x  cos  với  
0;  thì y c  os 3
rõ ràng thỏa mãn y  1 khi x  1 .
Cách 2. Giả sử tồn tại các số a, b, c thỏa mãn điều kiện bài toán.
Đặt f x  3 4x  2
ax  bx c, M  max f xx   1;1
f (1)  4  a b c , f (1)  4  a b c ,  Ta có   1  1 a b  1      f    1 a b f c ,         c   2  2 4 2  2  2 4 2 6M f 1 f  1  1   1  2 f 2 f
f 1 f  1  1   1            2 f  2 f           2   2   2   2   a a
4  a b c  a b c  1  b  2c   1 b  2c  8  2  6 2 2  1   1 
Vậy M  1 . Dấu “=” xảy ra khi và chỉ khi f (1)  f (1)  ff   M      1 , đồng  2   2  1 1
thời f 1 , f  1       , f , f    
 đôi một có tích không âm. Điều đó tương đương với  2   2 
 4  a b c  1
 4 abc    1   1 a b
     c  1   2 4 2  1 1 1 a bf 1 f  1            ff       1
    c   1  2   2      2 4 2  1 1 4 a b c 1
f 1   f 1             ff        1    2   2 
4  a b c    1 
 1  a b c    1   2 4 2   1 a b
    c    1  2 4 2
32 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2b  8  2 ac   0  b  3
 a  2b  4c  2  4   . a c    0
a  4c  6  2   4 a  4c   0
Mặt khác, từ giả thiết thì M  1 , do đó phải có M  1 và xảy ra dấu bằng trong bất đẳng
thức trên tức a c  0, b  3 . Ngược lại, khi a c  0, b  3 thì y  3
4x  3x . Đặt x cos  với   0;  thì y  os c
3 rõ ràng thỏa mãn y  1 khi x  1 .
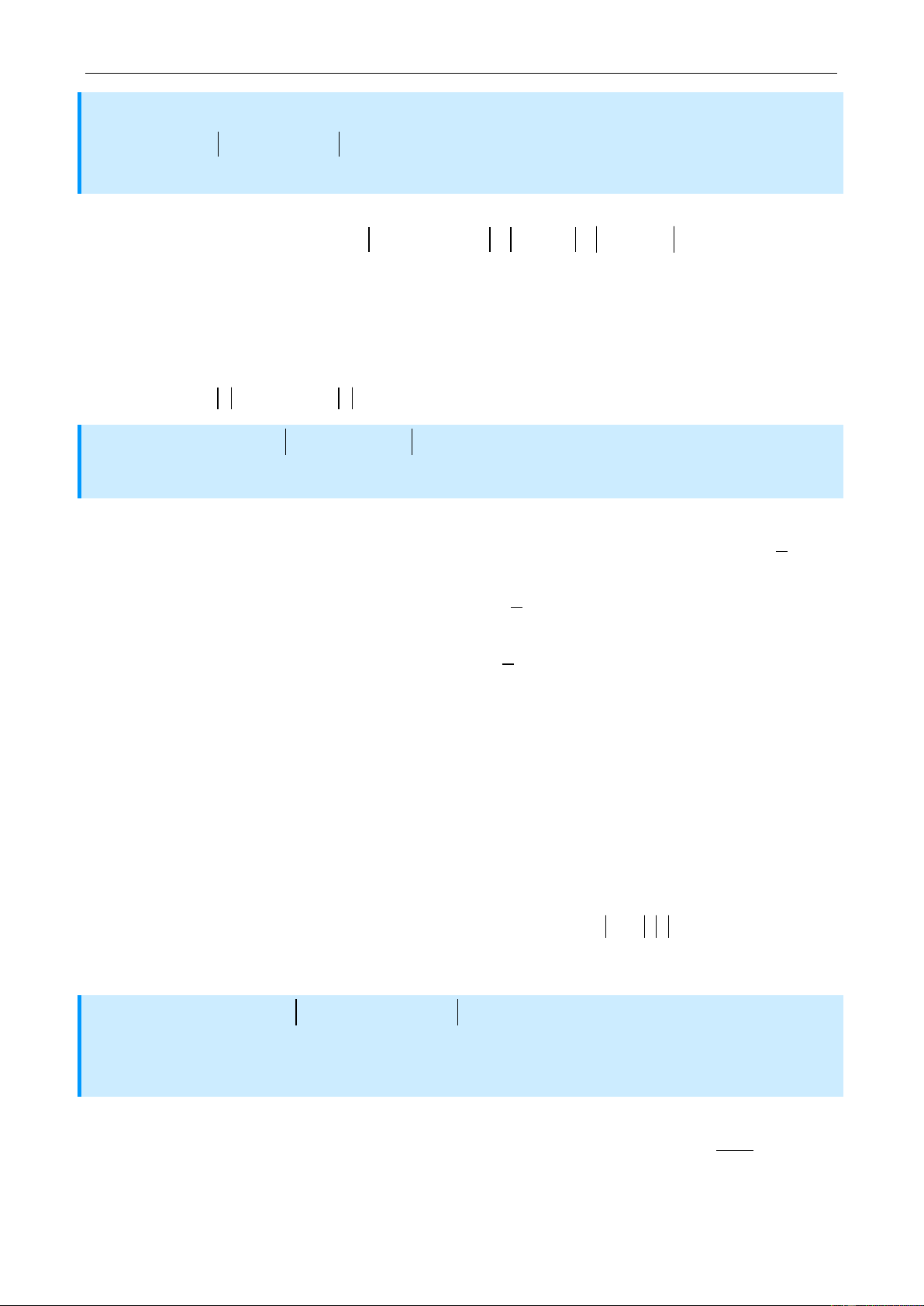
Bài 4: Tìm a, b để 4 x  2 8
ax b  1,x 1;1 .
Lời giải
Cách 1. Điều kiện cần: Vì y  1 khi x  1 nên ta có :
y 1  1, y 1  1   y 0  1    b  1 1  b  1 1  b  1   2      y      1
  8  a b  1
 1  a b  8  1  I9  a b  7 .   2      1 1
2  a  2b  4  2
6  a  2b      2  8.  . a b  1 2   y      4 2      2 
a b  7 Từ 
b  1. Lại do b  1 nên b  1 . a  2b    6
9  a  1  7 10  a  8
Thế b  1 vào hệ I  ta có     a  8  . 6  a  2  2 8  a     4
Điều kiện đủ: Khi a  8, b  1 thì y  4 x  2 8
8x  1 . Đặt x cos  với  
0;  thì y c  os 4
rõ ràng thỏa mãn y  1 khi x  1 .
Cách 2. Giả sử tồn tại các số a, b thỏa mãn điều kiện bài toán.
Đặt f x  4 8x  2
ax  b, M  max f x và theo giả thiết M  1 . x   1;  1 2 1 a Ta có f 0 b , f 1   
 8  a b , f    8.     b .  2  4 2  
M f 0 
Do M  max f x nên M f 1 . x   1;1    2  M f        2   2   2 
Từ đó ta có: 4  4M f 0  f 1  2 f
  f 0  f 1  2 f        4 .  2   2 
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 33
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI 2
Vậy M  1 . Dấu “=”xảy ra khi và chỉ khi f 0 f 1     f      1 , đồng thời  2   2 
f 0, f 1 ,  f   
 đôi một cùng dấu. Điều đó tương đương với:  2   2
f 0 f 1      f       1   2  a  8     2  b  1
f 0 f 1      f       1   2 
Ngược lại: Khi a  8, b  1 thì y  4 x  2 8
8x  1 . Đặt x  cos  với  
0;  thì y  cos 4
rõ ràng thỏa mãn y  1 khi x  1 .
Bình luận. Các giá trị của x mà ta xét ở trên chính là các nghiệm của đa thức Chebyshev
bậc bốn, đó là các nghiệm 0;   2 1; . 2
Bài 5: Chứng minh rằng nếu với mọi x 1;1 ta có 2
ax bx+c  h thì a b c  4h .
Lời giải
f 1  a b c, f 1  h  Đặt    2 f x
ax bx c , khi đó theo giả thiết f x  h và  f 1  a b c, f 1  h
f 0 c, f 0   h
f 1  f 1 f 1  f 1 Từ đó ta có a   f 0     ,b
,c f 0 2 2
f 1  f 1 f 1  f 1
Vậy a b c   f 0       f 0 2 2 f 1 f 1 f 1 f 1    h h h h f 0      
f 0    h    h  4h 2 2 2 2 2 2 2 2
Như vậy ta có điều phải chứng minh là a b c  4h . Bài 6: Cho    2 f x
ax bx c thỏa mãn điều kiện f 1  1, f 0  1, f 1  1 . 5
Chứng minh rằng f x  khi x  1. 4
Lời giải A B A B
Đặt A a b c, B a b c , thế thì a   c,b  . 2 2
Theo giả thiết: f 1  A  1, f 1  B  1, f 0  c  1 . 2  A B
 2  A B A B
Ta có f x  ax bx c   c x x c
 2x x  2x xc      2 1 x   2   2  2 2 1 1
Vậy f x  2 x  2
x + x  x + 1  2 x 2 2
34 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
 Với 0  x  1, ta có
f x  1 2  1 2 xx  2 1 x  2 x 1 x + x + 1 = x +  2
x  x  1 2
x   1 x  2 x 2 2 2 2
 Với 1  x  0 , ta có
f x  1 2  1 2 xx
 2  1  2  x 1 x + x + 1 x = x +  2
x  x  1 2 x   1 x  2 x 2 2 2 2 2 1 5
Các kết quả trên chứng tỏ rằng với x  1 thì f x 2 5  
 1  x x   x     . 4  2  4
Bài 7: Chứng minh rằng mọi đa thức f x bậc n  1 đều có thể biểu diễn dưới dạng n
f x  a T x a i i  ,  n
0 và cách biểu diễn này là duy nhất. i0
Lời giải Ta có T x
n   là đa thức bậc n có hệ số cao nhất là 1
2n nên ta có thể viết T x x xx n     1 2n
n    với   là đa thức bậc nhỏ hơn n. n 1 1 Suy ra x T x   x n   1 n   1 2 2
Bằng quy nạp ta chứng minh được: f x  a a T x  a T x  ...  a T x 0 1 2 2 n n  
Bây giờ ta chứng minh tính duy nhất của cách biểu diễn này
Giả sử f x  a a T x  a T x  ...  a T x a a T x a T x a T x n n    '  '
  '  ... ' 0 1 2 2 0 1 2 2 n n   n
Khi đó a a T x x i
'i i    0,  i0
Vậy a a'  a a'  ...  a a n '  n 0 0 0 1 1
Hay a a' , a a' ,..., a a n ' 0 0 1 1 n
Một trong những dấu hiệu để nhận biết bài toán đa thức có sử dụng tính chất đa thức
Chebyshev hay không đó là miền giá trị đa thức. Các bài toán trên miền1, 1đều gợi ra
cách giải bằng phương pháp này.
Ta xét thêm một số ví dụ:
Bài 8: Cho đa thức hệ số thực f x  3 ax  2
bx cx d,  0 . Biết rằng x 1,1 ta có
f x   .Tìm max của a , b , c , d
Lời giải
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 35
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
A f 1  a b c d   .   1  a b c  2 4 4 2 B f      
a   A B C D   d  3 3 3 3  a  4   2  8 4 2    1 1   1  a b c
b ADEb  2
Đặt C f       d   2 2 . Từ giả thiết:    2  8 4 2  1 8 8 1 c  3 
D f 1  a b c d
c A B C D    6 6 6 6 d   
E f 0  dd   E   
Bằng cách xét: f x    3
4x  3x và gx   2 2x  1 max a  4,  max b  2,
Thì ta có dấu đẳng thức xảy ra. Vậy:  max c  3  , max d   
Chú ý: f x , g x là xét dự trên cơ sở cos2x, cos3x.
Bài 9: Cho đa thức P x n a
n1   bậc không vượt quá
 1 có hệ số bậc cao nhất 0 , thỏa mãn điều kiện 1  2 x P x x 2n a n 1,    1,1 1     . Chứng minh rằng   1 0 .
Lời giải 2 j  1
Ta viết đa thức đã cho dưới dạng nội suy Lagrange theo các nút nội suy x j cos  là 2n
các nghiệm của đa thức Chebyshev T x
n   : j1 n n1 1 T x 2 n P x 1 1 x P x a 1 j n x P x n j n j 1 1       1       0   1 2  2   jjn j1 x x n j j1 n1 n n1 2 2 Vậy nên a   1 2xP x n jjn  .  1 2 0 n j1 n
Bài 10: Giả thiết rằng đa thức P x
n1   thỏa mãn các điều kiện của Bài 7. Chứng minh rằng P
x n,x    1,1 n 1    
Lời giải Với các x y x 0; 
j được chọn như ở bài toán trên thì do hàm số
 cos nghịch biến trong  
nên 1  x xx x n n ...     1 1 2 1 . 1 n T x 1 n n T x
Nếu x x  1 P x  1 n x P x 2 n 1   2  j n 1 j  1 thì           n j1 x x n j1 x x j   j  do x x T x x ;1 j
0 và n   có dấu không đổi trên  1 
36 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN n x x n    j n n T x ' n1 j1 n   Mặt khác thì T x x x T x n 2   3 n   n  1
2   j  Nên ta có   k1 x x x x k k 1  j1  k ' T x n   Lại có  U x n P
x n,x (x ;1] n   
. Nên từ (2) và (3) suy ra n1   n 1
Hoàn toàn tương tự ta cũng có P
x n,x [ x  1, ) n 1   n
Xét x x x 2 2 1 x 1 x sin arccos x sin n 1 .Khi đó ta có 1  1        2n sin x 2   2 1 1 1 Do 1   , sin  .  và 1  2 x   P x   n n1   x  2n 2n n n n 1 n
Tóm lại ta đã chứng minh được rằng P
x n,x    1,1 n 1    
Bài 11: Cho đa thức lượng giác P t  a sin t a sin 2t  ...  a nt n sin 1 2   Thỏa mãn điều
kiện P t  1,t  \..., 2, ,0, , 2,..  . Chứng minh rằng
Pt  n,t \...,2,,0,,2,... sin t
Lời giải Pt Nhận xét rằng  P P x cos t x x  cost 1 
 với n1   là đa thức dạng (1). Đặt  . Khi đó  1 sin n t
và P t  sin P t x P x n cos  1  2 1   n1  
Ta thấy P x thỏa mãn điều kiện của bài toán trước nên P
x n,x    1,1 n 1     Pt Do đó
n,t  \...,2,,0,,2,.. . sin t n
Bài 12: Cho đa thức lượng giác P x  a cos jx b sin jx j j
 thỏa mãn điều kiện j0
Px  1,x  . Chứng minh rằng P'x  n,x
Lời giải
cosx x cos x x 2sin x sin x 0    0   0 Cho x0 tuỳ ý. Do 
sinx x sin x x 2 cos x sin x 0    0   0
P x x P x n x
P' x x P' x x Nên g x  0   0  
 c sin jx g'x      0 0 2 j j0 2
Và g '0  P 'x g' 0 n g x 0  .Ta chứng minh rằng
   .Thật vậy,   là đa thức lượng giác
chứa thuần sin như trong Bài 9 và gx
Px x P x x P x x P x x 0    0    0     0     1 2 2
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 37
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI gx
Nên theo kết quả của bài 3 thì
n x  \...,2,,0,,2,.. . (4) sin x
gx  g0 x
Nhưng g 0  0 suy ra .
n x  \...,2,,0,,2,.. . x  0 sin x
gx  g0 x Nên khi x  0 :  g'0,  1 x  0 sin x
Ta nhận được g '0  n
Từ đó ta có P 'x   n x P' x n x  0
.Nhưng 0 được chọn tùy ý nên suy ra   
Bài 13 (Định lý Berstein-Markov) Cho đa thức P x a x a x a n   n n   1  ... 0 1
n . Thỏa mãn
điều kiện P x  1,x 1;1 P x  2 '
n ,x  1;1 n
. Chứng minh rằng khi đó : n     (5)
Lời giải
Đặt x  cos a .Khi đó theo giả thiết thì P cos a  1 P a n cos n .Do   có dạng n P a a j b j
n  cos    cos   sin  j jj0
Nên ta có thể áp dụng kết quả của Bài 10. Ta được P x sin .P' n x n  cos  ' 2 n       1   1 n P' x n   Cũng theo Bài 4, ta có
n suy ra P x  2 ' n n
Nhận xét : Dựa vào kết quả của Định lý Berstein-Markov, sau khi áp dụng liên tiếp kết quả
của định lí này, ta sẽ thu được kết quả sau: k 2
Nếu P x  1,x 1;1
P x  nn  1n  2...n k  1 ,x  1;1 n  thì
Bài 14: Cho a , a ,..., a 1 2
n là các số thực không âm và không đồng thời bằng 0.
a) Chứng minh rằng phương trình n nx  1 a x
... a x a n n 0 1 1
(6) có đúng một nghiệm dương duy nhất. n n
b) Giả sử R là nghiệm dương của phương trình (6) và A   a ,B ja jj Chứng minh j1 j1
rằng khi đó A B A R
Lời giải a a a
a) Do x  0 nên (6)  1  1  2  ...  n 2 n x x x a a a
Đặt f x  1  2  ...  n . Nhận xét rằng f x liên tục và f x nghịch biến trong khoảng 2 n x x x
0, nên tồn tại duy nhất R  0 sao cho f R  1.
38 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN a n
b) Đặt c j cc y x 0,  j 1 j .Suy ra  j 0 và
.Do hàm số   ln lõm trong khoảng   A j1 n An A   n a
Nên teo BĐT Jensen thì c  ln  ln c f R j 
j    ln   j j j j    ln    ln1  0 j1 R j1 R j    1 R n n n
Suy ra c ln j
R c ln A
ln A c  ln R jc jj j  và     j j1 j1 j1 1 n 1 naj  Hay a A ja R doc A j ln
   j ln   j ;  0 A j1 A j1  A
Vậy nên ln  A   ln  B A
R   A B A R
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 39
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI
B. ỨNG DỤNG LÝ THUYẾT XẤP XỈ ĐỀU TRONG GIẢI TOÁN.
Lý thuyết xấp xỉ đều tốt nhất là một nhánh của lý thuyết xấp xỉ hàm, có vai trò đặc biệt
quan trọng trong toán lý thuyết cũng như trong các toán ứng dụng. Đặc biệt, nó được
dùng để tìm đa thức có "độ lệch" nhỏ nhất so với hàm số cho trước trên một đoạn xác
định. Từ việc nghiên cứu kĩ lý thuyết xấp xỉ đều tốt nhất chúng ta có thể giải quyết được
một số dạng bài toán tìm giá trị lớn nhất, nhỏ nhất. Tuy nhiên không như đa thức
Chebyshev, đây là một vấn đề khá khó của chương trình toán cao cấp, liên quan tới không
gian mêtric, không gian Banach, không gian Hilbert mà ta sẽ được học trên chương trình
đại học, do đó không thể giới thiệu được cho các bạn THPT . Vì lí do đó nên mình chỉ đưa
ra các bài toán tổng quát từ nguyên lý này để các bạn áp dụng nhé!
Bài toán 1. Cho hàm số f x liên tục trên đoạn a; b . Tìm m sao cho max f x  m đạt x   a;b giá trị nhỏ nhất?
Các bước làm
Bước 1: Tìm M là giá trị lớn nhất của hàm số f x và n là giá trị nhỏ nhất của hàm
số f x trên đoạn a; b . M   n
Bước 2: Khi đó m  là số cần tìm. 2
Ví dụ. Tìm m để max  2
9x  4x a đạt giá trị nhỏ nhất? x   1;2
 Bước 1. Xét f x   2
9x  4x , ta có f x   x  4 ' 0
. Từ đây dễ dàng tìm được 18 M f x  4 max
,n  max f x  28 . x   1;2 x   1;2 9  124 124
Bước 2. Khi đó ta có a    a  9 9
Rất đơn giản và nhanh gọn phải không nào 
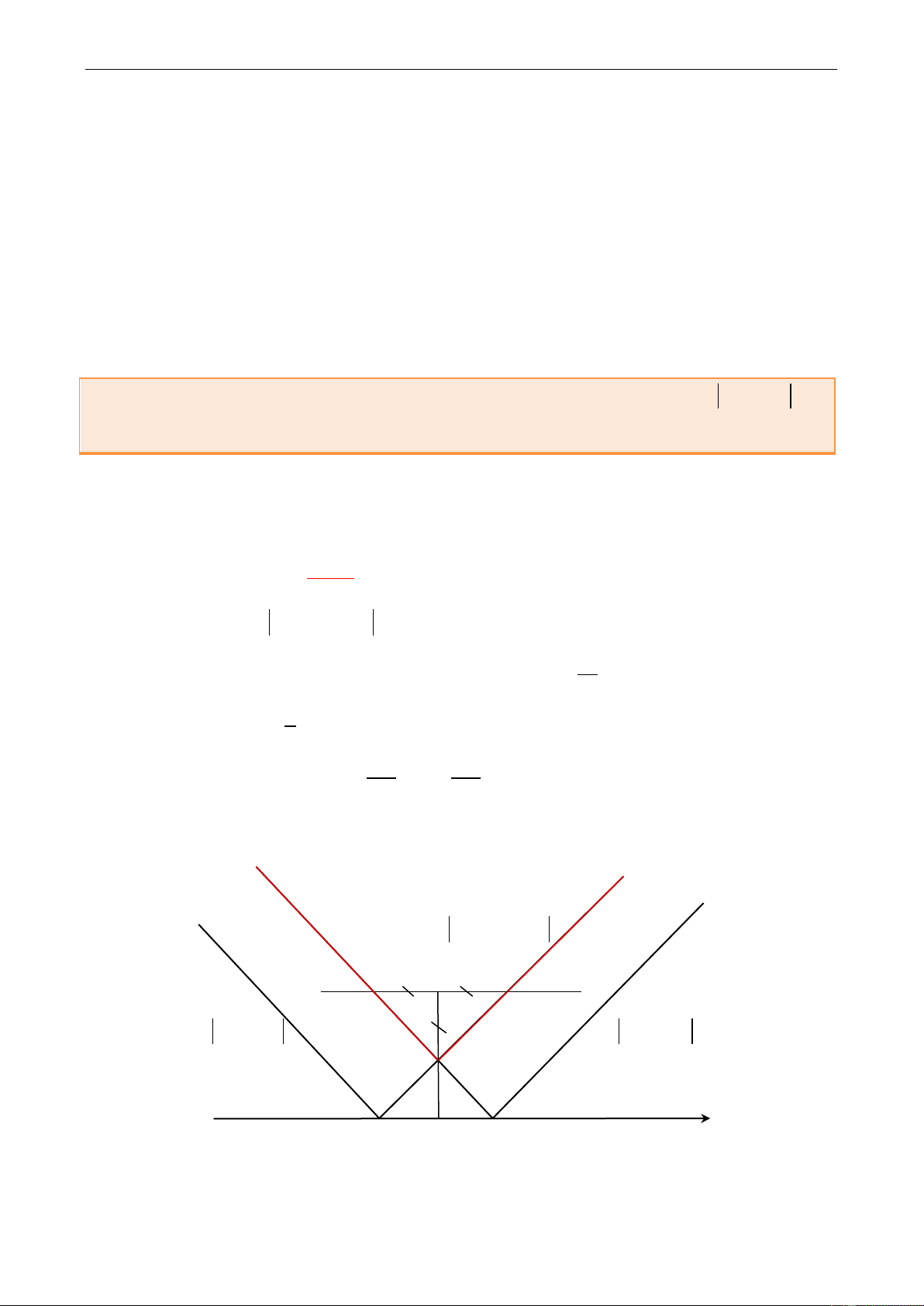
Bài toán mở rộng – Lục Trí Tuyên
gm  max f x  k m a;bE F y k
y k m  
y k m   A B C  H  k m Tìm m sao cho
1. g m  k với k cho trước
40 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
2. g m  k với k cho trước
Đặt t f x và gọi   min f x f x
y t k m b  ,  max . a; a;b       khi đó, do hàm số   đồng
biến trên ; nên ta có: gm  max
t k m  max k m   ; k m   ;          
Từ đây ta dễ dàng vẽ được đồ thị của hàm g x theo biến m (ở đây là k m ). Chú ý là lấy
phần đồ thị nằm phía trên trong hai đồ thị
Từ đồ thị của g m ta thấy ngay g m đạt giá trị nhỏ nhất tại A. do tam giác ABC vuông   
cân tại A nên khi đó k m    x . Và
g m      y R   1 min 2 A 2 A
Cũng từ đồ thị ta dễ dàng giải được bất phương trình g m  k hoặc g m  k . Chẳng hạn
g m  k k m  x k y AA
Khi đó, g m  k tương đương k m nằm trong khoảng nghiệm trên, g m  k tương
đương k m nằm ngoài khoảng nghiệm trên
Chú ý: trong trường hợp k m có miền giá trị khác R thì hàm y g k m xét trên miền
giá trị tương ứng của k m
Bài toán 2. Cho f x là hàm luôn lồi(lõm) trên ; . Tìm a, b để giá trị lớn nhất của hàm
số y f x  ax b trên ; đạt giá trị nhỏ nhất?
Các bước làm
Bước 1. Xác định 2 điểm A, f ,B, f , viết phương trình đường thẳng
AB : y kx m
Bước 2. Tìm phương trình tiếp tuyến của đồ thị hàm số y f x và song song với
AB (tiếp điểm là x c với x c là điểm cực trị của hàm số, khi đó tiếp tuyến có
dạng y kx n
Bước 3. Đường thẳng cần tìm là đường song song cách đều 2 đường thẳng AB và 1
tiếp tuyến trên là y kx  m n 2  1
Bước 4. Kết luận a k, b
mn. Giá trị nhỏ nhất đạt được là 2 1 1 M f k m n f k m n 0                            2   2  Ví dụ.
Ngoài ra ta có thể tham khảo thêm một cách khác của thầy Lục Trí Tuyên
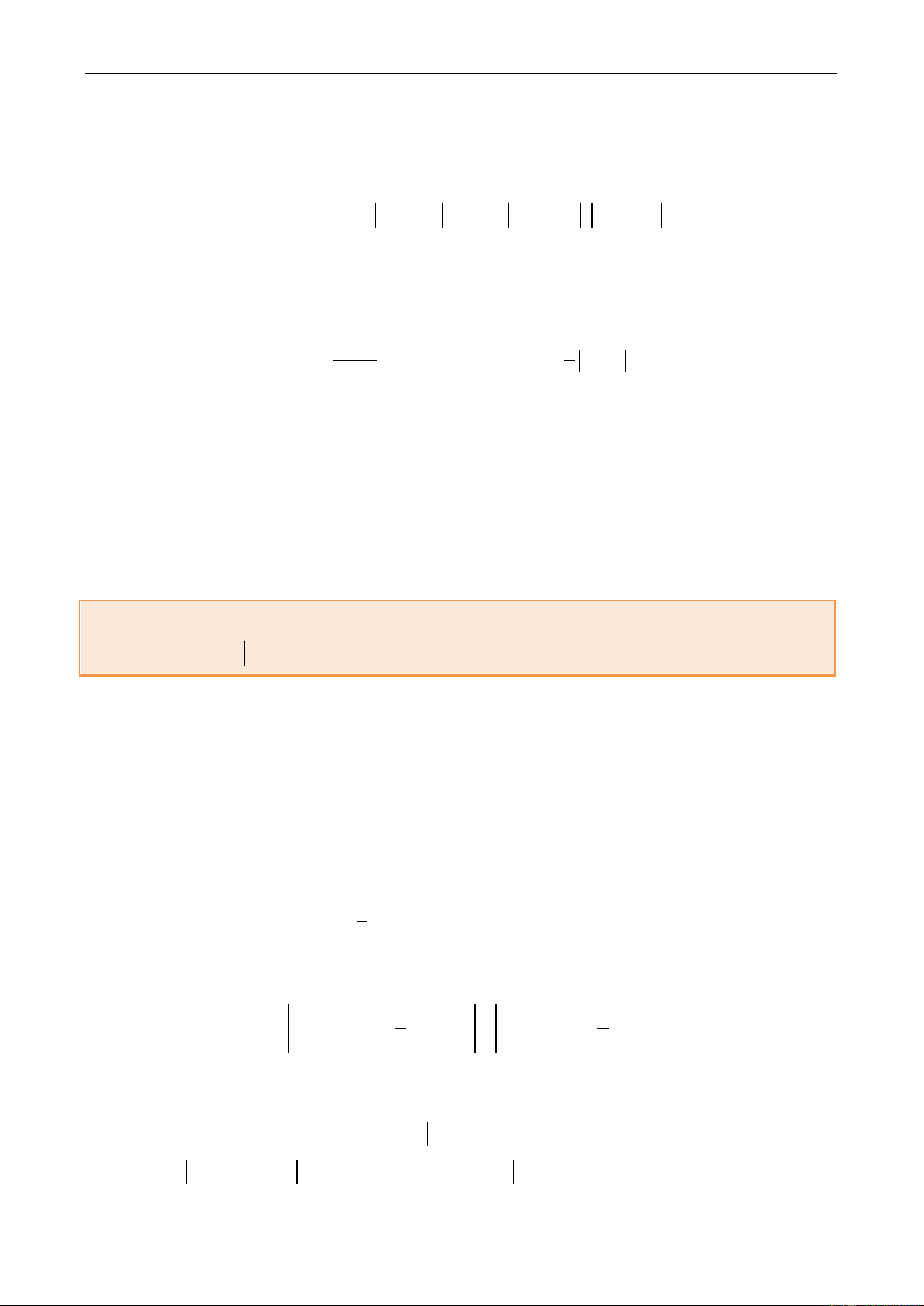
Gọi M là giá trị nhỏ nhất của hàm số y f x  ax b trên ; thì ta có:
M y   .a b f  ; M y   .a b f  và
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 41
MỘT SỐ BÀI TOÁN VỀ HÀM TRỊ TUYỆT ĐỐI              M y .a b f 2M             
     .a  2b      2 f    2  2  2   2      
1       f   f 
Suy ra 4M  2 f
  f   f   
 hay M f     m  2  2  2  2 Đẳng thức xảy ra khi  
.a b f   m1
.a b f   m1    
 .a b f   m2 I hoặc 
 .a b f   m2 II                   
.a b f    m3 
.a b f     m3  2  2   2  2 
Giải I  : từ phương trình 1 và phương trình 2 của hệ I  ta giải được
f   f 
f  f  a  ;b m
. thay 2 giá trị này vào phương trình 3 ta được    
   f   f 
f  f        .  m   f    m 2        2 
f  f   f   f  f  f             f    2m 2        2 
f   f   f   f           f    2m 2     2 
  f   f           f    2m 2     2 
f   f          f    2m* 2  2 
Giải II  : tương tự giải I  , ta chỉ cần thay m bởi m ta được
f   f 
f  f  a  ;b  m
. thay hai giá trị này vào phương trình 3 ta được    
f   f          f    2m* * 2  2 
1       f   f 
f   f       Mà ta thấy M f   m    f       2m* *. 2  2  2 2  2 
Điều này có nghĩa là một trong hai đẳng thức * hoặc * * luôn đúng, cũng có nghĩa là
một trong hai hệ phương trình I  hoặc II  luôn có nghiệm .
Bình luận. Vậy giả thiết lồi(lõm) ở đây sử dụng ở chỗ nào? Liệu chẳng không cần điều
kiện này bài toán vẫn đúng theo cách giải trên? Câu trả lời như sau:
 Nếu M là giá trị lớn nhất của hàm số trên ;thì nó lớn hơn hoặc bằng một trong
số các giá trị f x ;
1  nào đó trong đoạn 
. Ở lời giải trên ta chỉ lấy ba điểm.
42 | Chinh phục olympic toán
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Nhưng điều ngược lại không đúng. Có nghĩa là M lớn hơn giá trị của hàm số tại 3
điểm chưa chắc nó đã là giá trị lớn nhất.
 Điều kiện cần và đủ để cho M là giá trị lớn nhất của hàm số trên ; là M lớn hơn
hoặc bằng mọi f x với x bất kì thuộc ; . Điều này tương đương với lời giải
trên phải đảm bảo đúng cho mọi  ; i ; i ;  i thay cho    i ở trên. Cũng có     f f i i
i  i
nghĩa là điều kiện f     0 với mọi  ; i ;  ,    . Điều  2  2 i
kiện này tương đương với f x là hàm lồi hoặc lõm trên ;
Tinh hoa của toán học nằm ở tự do của nó – Georg Cantor
Chinh phục olympic toán | 43