Giá trị lớn nhất – nhỏ nhất của hàm nhiều biến – Trần Phương Toán 12
Giá trị lớn nhất – nhỏ nhất của hàm nhiều biến – Trần Phương Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số
BÀI 3. GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ
A. GIÁ TRỊ LỚN NHẤT, NHỎ NHẤT CỦA HÀM SỐ
I. TÓM TẮT LÝ THUYẾT
1. Bài toán chung: Tìm giá trị nhỏ nhất hoặc lớn nhất của hàm số f ( x)
Bước 1: Dự ñoán và chứng minh f ( x) ≥ ;
c f ( x) ≤ c
Bước 2: Chỉ ra 1 ñiều kiện ñủ ñể f ( x) = c
2. Các phương pháp thường sử dụng
Phương pháp 1: Biến ñổi thành tổng các bình phương
Phương pháp 2: Tam thức bậc hai.
Phương pháp 3: Sử dụng bất ñẳng thức cổ ñiển: Côsi; Bunhiacôpski
Phương pháp 4: Sử dụng ñạo hàm.
Phương pháp 5: Sử dụng ñổi biến lượng giác.
Phương pháp 6: Sử dụng phương pháp véctơ và hệ tọa ñộ
Phương pháp 7: Sử dụng phương pháp hình học và hệ tọa ñộ.
II. CÁC BÀI TẬP MẪU MINH HỌA:
Bài 1. Tìm giá trị nhỏ nhất của P(x, y) = x2 + 11y2 − 6xy + 8x − 28y + 21
Giải. Biến ñổi biểu thức dưới dạng P(x, y) = (x − 3y + 4)2 + 2(y − 1)2 + 3 ≥ 3 y − 1 = 0 y = 1
Từ ñó suy ra MinP(x, y) = 3 ⇔ ⇔
x − 3y + 4 = 0 x = 1 − 4 4 2 2 Bài 2. x y x y x y
Cho x, y > 0. Tìm giá trị nhỏ nhất của: S = + − − + + 4 4 2 2 y x y x y x 2 2 2 2 2 2 y y x y
Giải. x = − 1 + − 1 − 2 x S + + + + 2 2 2 2 y x y x y x 2 2 2 2 2 y x y x y S x = − 1 + − 1 + − + + − 2 + 2 2 2 y x y x y x 2 2 2 2 2 2 y x y (x − y) S x = − 1 + − 1 + − + + 2 ≥ 2 . 2 2 y x y x xy
Với x = y > 0 thì MinS = 2 1
Chương I. Hàm số – Trần Phương
Bài 3. Tìm giá trị lớn nhất của hàm số 2 2 2
S = sin x + sin y + sin (x + y) 1 − cos 2x 1 − cos 2 y
Giải . 2 2 2
S = sin x + sin y + sin (x + y) = 2 +
+ 1 − cos (x + y) 2 2 S 2 9 1 2
= 2 − cos(x + y) cos(x − y) − cos (x + y) = −
+ cos(x + y) cos(x − y) + cos (x + y) 4 4 2 S 9 1 1 2 9 = −
cos(x − y) + cos(x + y) −
sin (x − y) ≤ . 4 2 4 4 π 9 Với x = y =
+ kπ , (k∈Z) thì Max S = 3 4
Bài 4. Tìm giá trị nhỏ nhất của biểu thức 2 2 2 2
S = x + x + x + ... + x − (x x + x x + ... + x x + x x + x ) 1 2 3 8 1 2 2 3 6 7 7 8 8 2 2 2 2 1 3 2 4 3 5 4
Giải. S = x − x + x − x + x − x + x − x + 1 2 2 3 3 4 4 5 2 4 3 6 4 8 5 2 2 2 2 6 5 7 6 8 7 9 8 4 4 + x − x + x − x + x − x + x − − ≥ − 5 6 6 7 7 8 8 10 6 12 7 14 8 16 9 9 9 1 2 6 7 8 4 Với x = x ; x = x ;...; x = x ; x = x ; x = , thì Min S = − 1 2 2 3 6 7 7 8 8 2 3 7 8 9 9
Bài 5. Cho x, y, z ∈ ℝ . Tìm giá trị nhỏ nhất của biểu thức:
S = 19x2+ 54y2 +16z2 −16xz − 24y +36xy
Giải. Biến ñổi S ⇔ f(x) = 19x2 − 2(8z −18y)x + 54y2 +16z2 − 24y
Ta có ∆′x = g(y) = (8z −18y)2 − (54y2 +16z2 − 24y) = −702y2 +168zy − 240z2
⇒ ∆′y = (84z)2 − 702.240z2 = −161424z2 ≤ 0 ∀z∈R ⇒ g(y) ≤ 0 ∀y, z∈R
Suy ra ∆′x ≤ 0 ∀y, z∈R ⇒ f(x) ≥ 0. Với x = y = z = 0 thì MinS = 0
Bài 6. Cho x2 + xy + y2 = 3. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức:
S = x2 − xy + y2
Giải Xét y = 0 ⇒ x2 = 3 ⇒ S = 3 là 1 giá trị của hàm số.
Xét y ≠ 0, khi ñó biến ñổi biểu thức dưới dạng sau ñây S
x − xy + y ( x / y)2 2 2 2 − (x / y) + 1 t − t + 1 x u = = = = = u với t = 2 2 2 2 3
x + xy + y
(x / y) + (x / y) + 1 t + t + 1 y 2
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số
⇔ u(t2 + t + 1) = t2 − t + 1 ⇔ (u − 1)t2 + (u + 1)t + (u − 1) = 0 (*)
+ Nếu u = 1, thì t = 0 ⇒ x = 0, y = ± 3 ⇒ u = 1 là 1 giá trị của hàm số
+ Nếu u ≠ 1, thì u thuộc tập giá trị hàm số ⇔ phương trình (*) có nghiệm t
⇔ ∆ = (3u − 1)(3 − u) ≥ 0 ⇔ 1 ≤ u ≠ 1 ≤ 3 . 3
Vậy tập giá trị của u là 1 , 3 ⇒ 1 Min u = ; Max u = 3 3 3 x = y Min S = 1 ⇔ 1 Min u = ⇔ t = 1 ⇒ ⇔ x = y = 1 ± 3 2 2
x + xy + y = 3 x = − y
x = 3, y = − 3
Max S = 9 ⇔ Maxu = 3 ⇔ t = −1 ⇒ ⇔ 2 2
x + xy + y = 3
x = − 3, y = 3 Bài 7. 2
Cho x,y∈R thỏa mãn ñiều kiện ( 2 2 x − y + ) 2 2 + x y − ( 2 2 1 4 x + y ) = 0
Tìm giá trị lớn nhất, nhỏ nhất của biểu thức S= 2 2 x + y 2
Giải. Biến ñổi ( 2 2 x − y ) + ( 2 2 x − y ) 2 2 + + x y − ( 2 2 2 1 4 x + y ) = 0 2 2 ⇔ ( 2 2 x + y ) − ( 2 2 x + y ) 2 3 + 1 + 4x = 0 ⇔ ( 2 2 x + y ) − ( 2 2 x + y ) 2 3 + 1 = − 4x 2 3 − 5 3 + 5
Do −4x2 ≤ 0 nên ( 2 2 x + y ) − ( 2 2
3 x + y ) + 1≤ 0 ⇔ 2 2 ≤ x + y ≤ 2 2 3 − 5 −
Với x = 0, y = ± , thì 2 2 3 5 Min(x + y ) = . 2 2 3 + 5 +
Với x = 0, y = ± , thì 2 2 3 5 Max(x + y ) = 2 2
Bài 8. Tìm giá trị nhỏ nhất của hàm số f ( x) 2
= x + 4x + 2x + 1
Giải. Gọi y0 là 1 giá trị của hàm f(x)
⇒ tồn tại x0 sao cho y0 = 2 x + 4x + 2x + 1 0 0 0 ⇔ 2 2 2 2 y − x =
4x + 2x + 1 ⇒ y − 2 y x + x = 4x + 2x + 1 0 0 0 0 0 0 0 0 0 0 ⇔ g(x0) = 2 2
3x + 2(1 + y )x + 1 − y = 0 . Ta có g(x) = 0 có nghiệm x 0 0 0 0 0 ⇔ ∆′ = 2 2 2
(1 + y ) − 3(1 − y ) = 2(2 y + y − 1) = 2( y + 1)(2 y − 1) ≥ 0 0 0 0 0 0 0 3
Chương I. Hàm số – Trần Phương Do y0 = 2 2 2
x + 3x + (x + 1) ≥ x + 3x = x + 3 x ≥ 0 nên 0 0 0 0 0 0 0 1 1 1
∆′ ≥ 0 ⇔ 2y0 − 1 ≥ 0 ⇔ y ≥ . Với x = − thì Minf(x) = 0 2 2 2
Bài 9. Cho y = f ( x) 2
= x − 5x + 4 + m .
x Tìm các giá trị của m sao cho Min y >1 2
x + (m − 5) x + 4 ; x ≤1 ∨ x ≥ 4 : (P1 )
Giải. Ta có f ( x) = 2
−x + (m + 5) x − 4 ; 1 ≤ x ≤ 4 : (P2 )
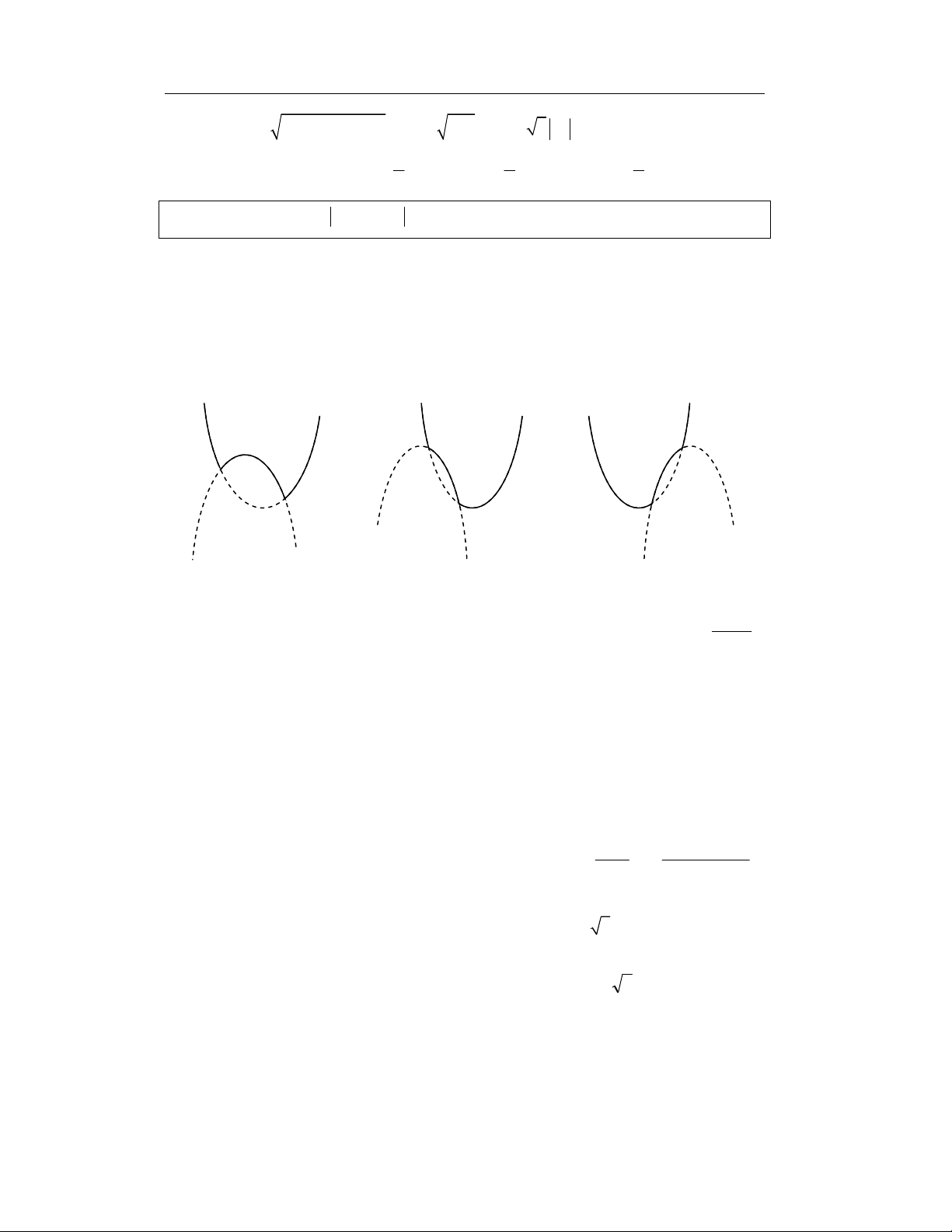
Gọi (P) là ñồ thị của y = f(x) ⇒ (P) = (P1) ∪ (P2) khi ñó (P) có 1 trong các
hình dạng ñồ thị sau ñây P1 A P2 A P1 P1 A P2 P2 B B B C C C
Hoành ñộ của các ñiểm ñặc biệt trong ñồ thị (P): 5 − m
Hoành ñộ giao ñiểm (P1), (P2) xA = 1; xB = 4 ; Hoành ñộ ñỉnh (P1): x = . C 2
Nhìn vào ñồ thị ta xét các khả năng sau:
Nếu xC ∈[xA, xB] ⇔ m∈[ −3, 3] thì Minf(x) = Min{f(1), f(4)}. 3 − ≤ m ≤ 3
Khi ñó Minf(x) > 1 ⇔ f (1) = m > 1 ⇔ 1 < m ≤ 3 (1)
f (4) = 4m >1 5−m 2 m − 1 + 0m−9 Nếu x =
C ∉[xA, xB] ⇔ m∉[ −3, 3] thì Minf(x) = f x f = 1 ( C ) 1 2 4 m ∉[ 3 − , 3]
Khi ñó Minf(x) > 1 ⇔
⇔ 3 < m < 5 + 2 3 (2) 2
m −10m + 13 < 0
Kết luận: Từ (1) và (2) suy ra Minf(x) > 1 ⇔ 1 < m < 5 + 2 3 4
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số
Bài 10. (ðề thi TSðH 2005 khối A)
Cho x, y, z > 0 ; 1 1 1 + + = 4 . Tìm Min của S 1 1 1 = + + x y z
2x + y + z
x + 2 y + z
x + y + 2z
Giải: Sử dụng bất ñẳng thức Côsi cho các số a, b, c, d > 0 ta có:
(a + b + c + d ) (1 1 1 1 + + + ) 4 1 1 1 1 1 16 ≥ 4 4. abcd .4. =16 ⇒ + + + ≥ a b c d abcd a b c d
a + b + c + d 1 1 1 1 16 16 + + + ≥ = x x y z
x + x + y + z
2x + y + z 1 1 1 1 16 16 + + + + ≥ = x y y z
x + y + y + z
x + 2 y + z 1 1 1 1 16 16 + + + ≥ =
x y z z x + y + z + z x + y + 2z 1 1 1 1 1 1 16 = 4 + + ≥ 16 + + ⇒ Min S = 1 x y z
2x + y + z
x + 2 y + z
x + y + 2z
Bài 11. (ðề thi TSðH 2007 khối B) y
Cho x, y, z > 0 . Tìm Min của S x 1 1 z 1 = x + + y + + z + 2 yz 2 zx 2 xy
Giải: Sử dụng bất ñẳng thức Côsi cho 9 số ta có 4 4 4 y y x y z S 1 2 2 2 x x z z 9 9 9 =
x + y + z + + + + + + ≥ .9 = ⇒ Min S = 4 4 4 2 yz yz zx zx xy xy 2 x y z 2 2 x, y > 0 Bài 12. x y Cho
Tìm giá trị nhỏ nhất của S = + x + y = 1 1 − x 1 − y x y
Giải: S = + y + + x −
( x + y ) ≥ 2( x + y ) − ( x + y ) = x + y y x x y 1 − y 1 − x 1 1 Mặt khác, S = + = + = + − ( x + y ) 1 − x 1 − y y x x y 1 1 2 2 Suy ra 2S ≥ + ≥ ≥
= 2 2 ⇒ S ≥ 2 ⇒ MinS = 2 . x y 4 xy x + y 2 xyz ( 2 2 2
x + y + z +
x + y + z )
Bài 13. Cho x, y, z > 0. Tìm Max của: S = ( 2 2 2
x + y + z ) (xy + yz + zx)
Giải: Sử dụng bất ñẳng thức Côsi và BunhiaCôpski ta có 3 ñánh giá sau: 5
Chương I. Hàm số – Trần Phương 2 2 2 3 2 2 2
x + y + z ≥ 3 ⋅ x y z 3 3 2 2 2
xy + yz + zx ≥ 3. xy.y . z zx = 3. x y z ;
x + y + z ≤ ( 2 2 2 + + )( 2 2 2
x + y + z ) 2 2 2 1 1 1
= 3. x + y + z . Từ ñó suy ra xyz (1 + 3 ) 2 2 2 3 3 x + y + z 1 + 3 xyz 1 + 3 xyz 3 + 3 S ≤ = ⋅ ≤ ⋅ = ( 2 2 2
x + y + z ) 3 2 2 2 2 2 2 3 3 3 3. x y z x + y + z 3. xyz 9
Bài 14. (ðề thi TSðH 2003 khối B)
Tìm giá trị lớn nhất, nhỏ nhất của hàm số 2 y = x + 4 − x
Cách 1: Tập xác ñịnh D = [ 2 − ; 2] ; x − 2 2 2 x 2 y′ = 1 −
; y′ = 0 ⇔ x = 4 − x y ′ + 0 − 0 2 4 − x y 2 2 x ≥ 0 max y = 2 2 −2 2 ⇔ ⇔ x = 2 ⇒ 2 2
x = 4 − x min y = 2 − π π
Cách 2: ðặt x = 2 sin u, u ∈ − ; 2 2 ⇒ π y 2 (sin u cos u ) 2 2 sin (u ) 2;2 2 = + = + ∈ −
; max y = 2 2 ; min y = 2 − 4
Bài 15. (ðề dự bị TSðH 2003 khối B)
Tìm giá trị lớn nhất, nhỏ nhất của y = x + ( − x )3 6 2 4 1 trên ñoạn [ 1 − ; ] 1 Cách 1. ðặt 2 u = x ∈[0; ]
1 . Ta có y = u + ( − u )3 3 3 2 4 1 = 3
− u + 12u − 12u + 4 2 2 y′ = 9
− u + 24u − 12 = 0 ⇔ u = ∈[0; ] 1 ; u = 2 > 1 x 0 2 1 1 2 3 3 y ′ 0 − 0 + 0
Nhìn bảng biến thiên ta có 4
max y = 4; min y = 9 4 1 y Cách 2. ðặ 4 t 6 6
x = sin u ⇒ y = sin u + 4 cos u . 9 = ( 6 6 u + u ) 6 + u ≤ ( 2 2 sin cos 3 cos
sin u + cos u ) + 3 = 4
Với x = 0 thì max y = 4 . Sử dụng bất ñẳng thức Côsi ta có: 6 8 8 6 8 8 4 2 3 sin u + + ≥ 3 ⋅ sin u ⋅ ⋅ = sin u 27 27 27 27 3 6 4 4 6 4 4 4 2 3 4 cos u + + ≥ 3 ⋅ 4 cos u ⋅ ⋅ = cos u 27 27 27 27 3 6 6 8 4 y = u + u + ≥ ( 2 2 u + u ) 4 4 sin 4 cos sin cos = ⇒ y ≥ . Với 2 4 x = ⇒ min y = 9 3 3 9 3 9 6
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số Bài 16. +
a) Lập bảng biến thiên và tìm giá trị lớn nhất của hàm số x 3 y = 2 x + 1
b) Cho a + b + c = 1. Chứng minh rằng: 2 2 2 a + 1 + b + 1 + c + 1 ≥ 10 −
Giải. a) TXð: D = ℝ ; 1 3x 1 1 y′ = = 0 ⇔ x = ⇒ y = 10 2 2 ( ) ( x + ) 3 3 1 x + 1 ( x + 3) / x ( x + 3) / x lim = lim = lim = lim x y . x→∞ x→∞ 2 + 1 x→∞ 1 x→∞ x x x 1 + −∞ 1/3 +∞ 2 2 x x y ′ + 0 − 0
Suy ra lim y = 1; lim y = 1 − . Nhìn BBT 10 x→+∞ x→−∞ y + ta có x 3 y = ≤ 10 ⇒ max y = 10 −1 1 2 x + 1
b) Theo phần a) thì y ≤ 10 , x ∀ ⇔ 2
x + 3 ≤ 10. x + 1 , ∀ x .
ðặc biệt hóa bất ñẳng thức này tại các giá trị x = a, x = b, x = c ta có: 2
x = a : a + 3 ≤ 10. a + 1 2
x = b : b + 3 ≤ 10. b + 1 2
x = c : c + 3 ≤ 10. c + 1
a + b + c + ≤ ( 2 2 2 9 10.
a +1 + b +1 + c +1) ⇔ 2 2 2
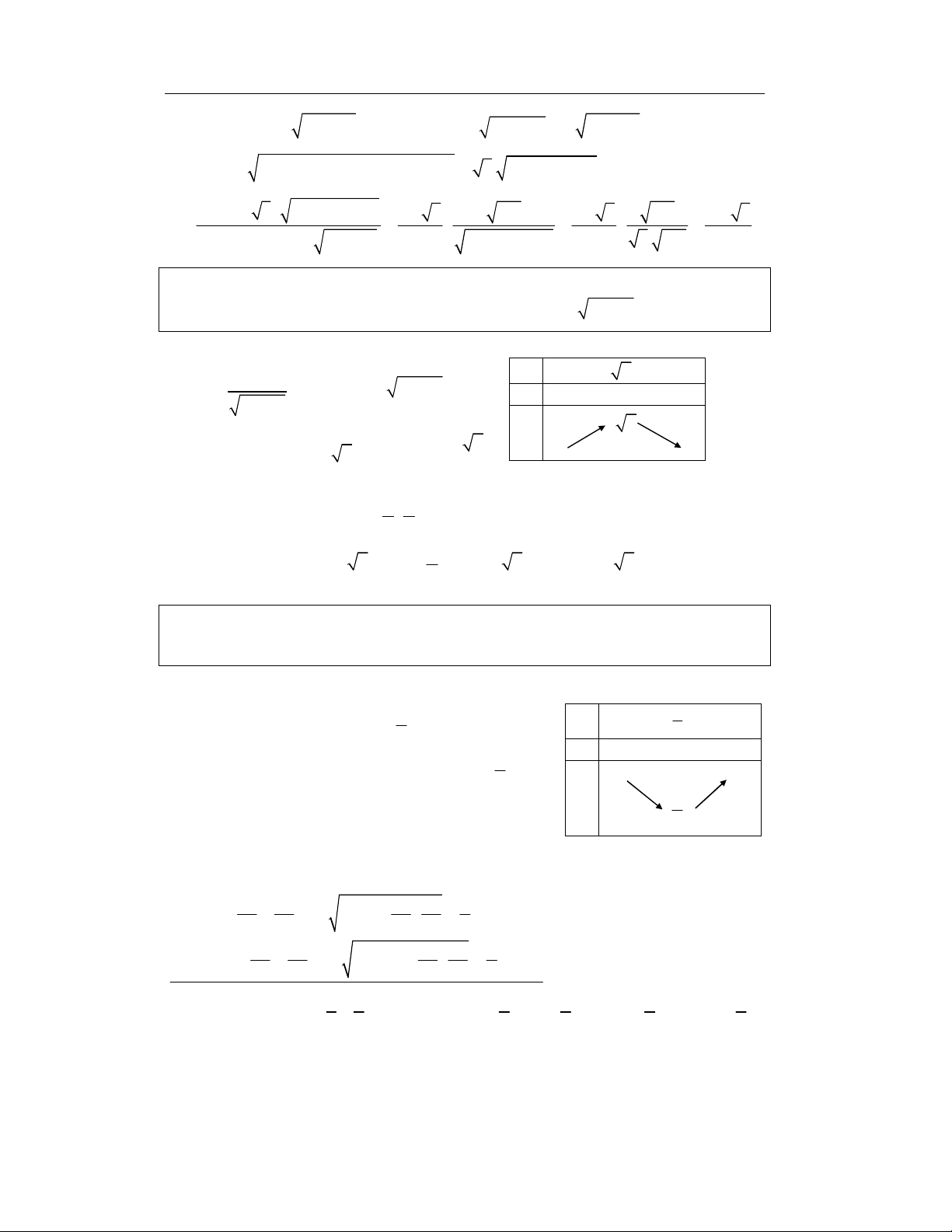
10 ≤ a + 1 + b + 1 + c + 1
Cách 2. Trên mặt phẳng tọa ñộ Oxy ñặt y OA = (a; ) 1 ; AB = ( ; b ) 1 ; BC = ( ; c ) 1 . 3 C
Khi ñó OC = OA + AB + BC = (a + b + c ; 3) . 2 B 1
Do OA + AB + BC ≥ OA + AB + BC = OC A 1 O a x Từ ñó suy ra 2 2 2 a + 1 + b + 1 + c + 1 ≥ 10 a+b a+b+c
Bài 17. (ðề 33 III.2, Bộ ñề thi TSðH 1987 – 1995) Cho 2 2
x + y = 1. Tìm Max, Min của A = x 1 + y + y 1 + x .
Giải. 1. Tìm MaxA: Sử dụng bất ñẳng thức BunhiaCôpski ta có A ≤ ( 2 2
x + y ) ( + y ) + ( + x) = + x + y ≤ + ( 2 2 1 1 2 2 2 x + y ) = 2 + 2 . Với 1 x = y = thì Max A = 2 + 2 2 7
Chương I. Hàm số – Trần Phương
2. Tìm MinA: Xét 2 trường hợp sau ñây
• Trường hợp 1: Nếu xy ≥ 0 , xét 2 khả năng sau:
+) Nếu x ≥ 0, y ≥ 0 thì A>0 ⇒ Min A > 0
+) Nếu x ≤ 0, y ≤ 0 thì |A| ≤ 2 2
(x + y )[(1 + x) + (1 + y)] = 2 + x + y = − x − y ≤ − ( 2 2 2 2 x + y ) = 1
Từ 2 khả năng ñã xét suy ra với xy ≥ 0 thì Min A = −1 2 − • Tr t 1
ường hợp 2: Xét xy < 0 : ðặt x + y = t ⇒ xy = < 0 ⇒ t ∈ ( 1 − , ) 1 2 2 2
A = x ( + y) + xy ( + x) ( + y) 2 1 2 1 1
+ y (1+ x) =1+ xy ( x + y) + 2xy 1 + x + y + xy 2 2 2 2 = − − − − t 1 t 1 t 1 1 + t ⋅ + 2 ⋅ 1 + t + t 1 (1 2 ) t 2 = + + + 1 2 2 2 2 ⇔ 2 A f (t ) 1 (1 2 ) 3 2 t 2 t (1 2 ) t 2 2 = = + + − + + − 2 3(1 + 2 ) 1 + 2 1 + 2
Ta có: f ′ (t ) 2 = t + 2 t −
= 0 ⇔ t = t = − ; t = t = 2 − 1 1 2 2 2 3 2(19 − 3 2 )
Thế t , t vào phần dư của f (t ) chia cho f ′ (t ) ⇒ f (t = ; f t = 0 . 1 ) ( 2 ) 1 2 27
Nhìn bảng biến thiên suy ra: t −1 t 2 1 t2 1
A ≤ f (t
⇒ A ≥ − f t suy ra 1 ) ( 1 ) ƒ′ + 0 − 0 + 2 (19 − 3 2 )
Min A = − f (t = − < −1 f (t 1 ) 1 ) 27 ƒ 1 1 2 t − 1
xảy ra ⇔ x + y = t ; 1 xy = f (t 2 ) 1 2 − (1+ 2 ) ⇒ + − ± 15 − 2 2
x, y là nghiệm của 2 1 2 2 3 u + u + = 0 ⇒ , x y = 3 9 6 2 (19 − 3 2 )
Kết luận: Max A = 2 + 2 ; Min A = − 27
Bài 18. Cho x, y, z ∈[0, ] 1 thoả mãn ñiều kiện: 3
x + y + z = . 2
Tìm Max, Min của biểu thức: S = ( 2 2 2
cos x + y + z ) π
Giải. Do x, y, z ∈[0, ] 1 nên 2 2 2 3
0 < x + y + z < x + y + z = < . 2 2 π
Vì hàm số y = cos α nghịch biến trên (0, ) nên bài toán trở thành. 2 8
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số
1. Tìm MaxS hay tìm Min ( 2 2 2
x + y + z ) 1
x + y + z =
(1 + 1 + 1 )(x + y + z ) ≥ ( x + y + z)2 2 2 2 2 2 2 2 2 2 3 = . 3 4 Với 1
x = y = z = thì MaxS = 3 cos 2 4
2. Tìm MinS hay tìm Max ( 2 2 2
x + y + z )
Cách 1: Phương pháp tam thức bậc hai:
Không mất tính tổng quát giả sử z = Max{x y } 1 , , z ⇒ z ∈ ;1
2 . Biến ñổi và ñánh
giá ñưa về tam thức bậc hai biến z 2 2 2 2 2 2
x + y + z = z + ( x + y) 2
− xy ≥ z + ( 3 − z) 2 9 2 = 2z − 3z + = f ( z ) 2 4
Do ñồ thị hàm y = f(z) là một parabol quay bề lõm lên trên nên ta có: f ( z ) = f ( 1 ) f ( ) { }= f (1 Max Max ; 1 ) = f ( ) 5 1 = . 2 2 4 Với 1 z = 1; x = ; y = 0 thì MinS = 5 cos 2 4
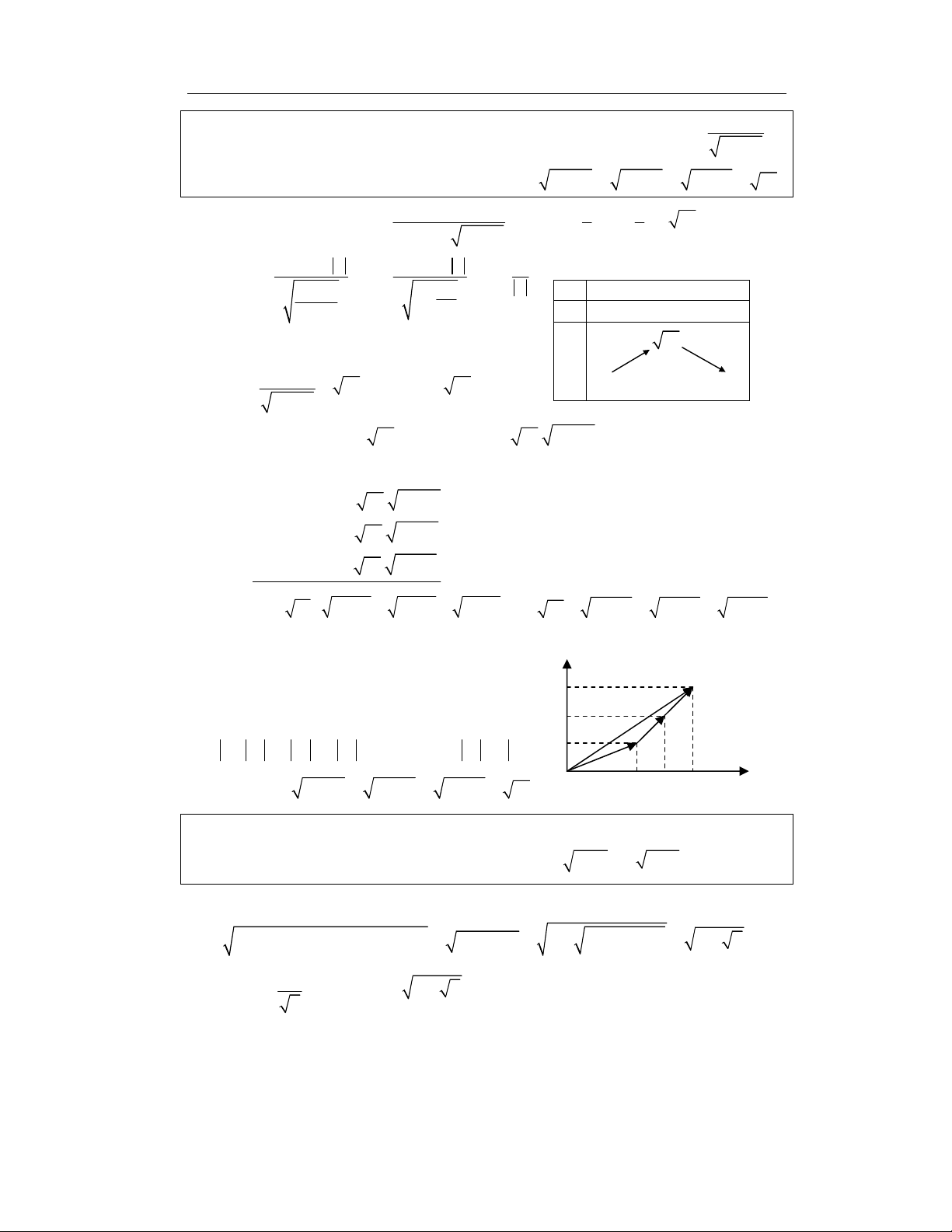
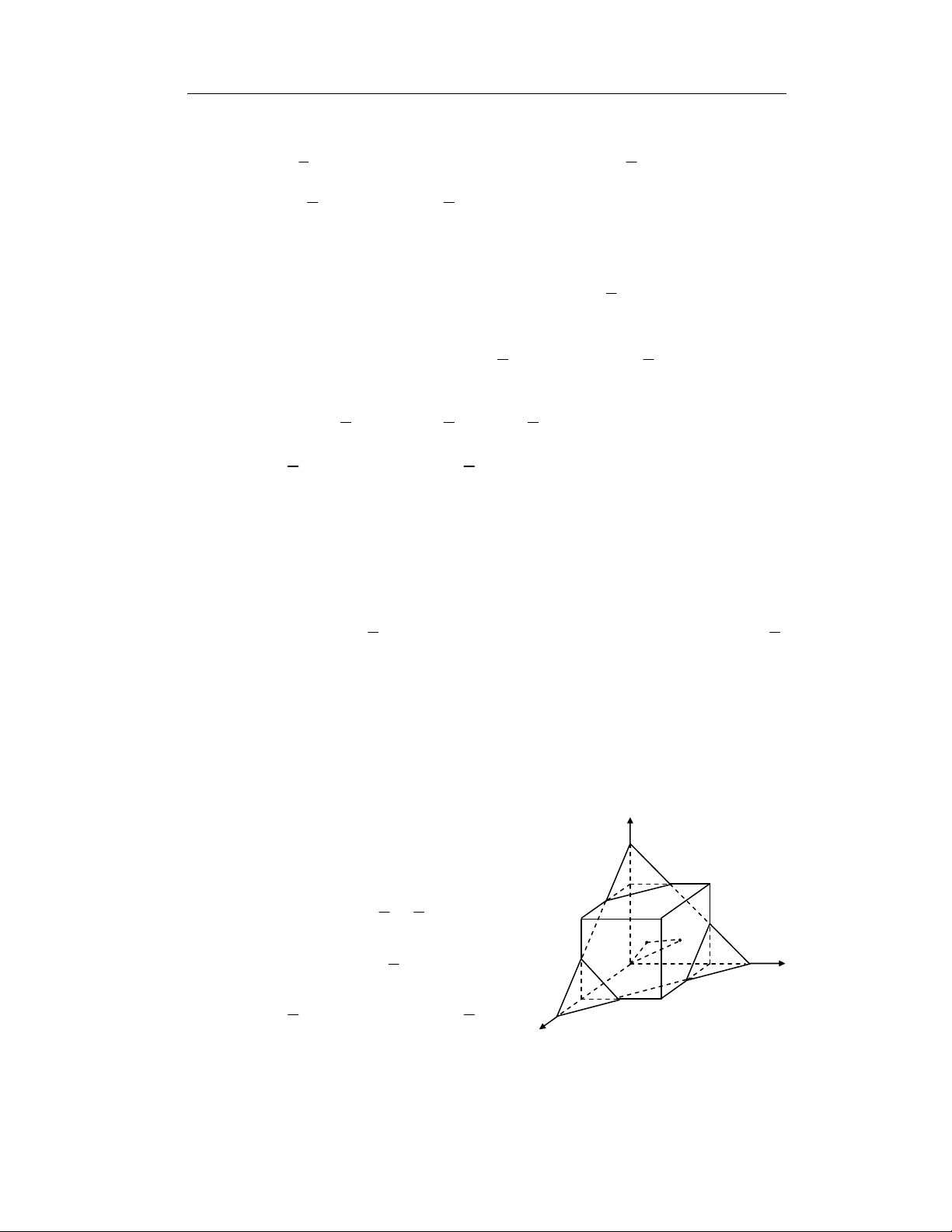
Cách 2: Phương pháp hình học
Xét hệ tọa ðề các vuông góc Oxyz. Tập hợp các ñiểm M ( x, y, z ) thoả mãn
ñiều kiện x, y, z ∈[0, ]
1 nằm trong hình lập phương ABCDA′B′C′O cạnh 1 với
A(0, 1, 1); B(1, 1, 1); C(1, 0, 1); D(0, 0, 1); A′(0, 1, 0); B′(1, 1, 0); C′(1, 0, 0). Mặt khác do 3
x + y + z =
nên M ( x, y, z ) nằm trên mặt phẳng (P): 3
x + y + z = 2 2
Vậy tập hợp các ñiểm M ( x, y, z ) thoả mãn ñiều kiện giả thiết nằm trên thiết
diện EIJKLN với các ñiểm E, I, J, K, L, N là trung ñiểm các cạnh hình lập
phương. Gọi O′ là hình chiếu của O lên EIJKLN thì O′ là tâm của hình lập
phương và cũng là tâm của lục giác ñều EIJKLN. Ta có O′M là hình chiếu của OM lên EIJKLN. Do OM2 = 2 2 2
x + y + z nên OM lớn nhất ⇔ O′M lớn nhất z
⇔ M trùng với 1 trong 6 ñỉnh E, I, J, K, L, N. 3/ 2 Từ ñó suy ra: 1 J K 2 2 2 2
x + y + z ≤ OK = + (1 1 ) 5 = 4 4 I M O′ ⇒ ( 2 2 2
x + y + z ) ≥ (5 cos cos ) L O 1 3/ 2 4 x 1 E Với 1 z = 1; x = ; y = 0 thì MinS = 5 cos 3/ 2 N 2 4 y 9
Chương I. Hàm số – Trần Phương Bài 19. 3
Cho a,b,c > 0 thỏa mãn ñiều kiện a + b + c ≤ 2 1 1 1
Tìm giá trị nhỏ nhất của 2 2 2 S = a + + b + + c + 2 2 2 b c a
Giải. Sai lầm thường gặp: 1 1 1 1 1 1 2 2 2 2 2 2 3 6 S ≥ 3. a + ⋅ b + ⋅ c + = 3. a + b + c + 2 2 2 2 2 2 b c a b c a 1 1 1 2 2 2 6 6 ≥ 3. 2 ⋅ a ⋅ 2 ⋅ b ⋅ 2 ⋅ c ⋅
= 3. 8 = 3 2 ⇒ Min S = 3 2 2 2 2 b c a
• Nguyên nhân: 1 1 1 3
Min S = 3 2 ⇔ a = b = c = = =
=1⇒ a + b + c = 3 > mâu thuẫn với giả thiết a b c 2
• Phân tích và tìm tòi lời giải : 1
Do S là một biểu thức ñối xứng với a, b, c nên dự ñoán Min S ñạt tại a = b = c = 2
Sơ ñồ ñiểm rơi: 2 2 2 1
a = b = c = 1 4 1 4
a = b = c = ⇒ ⇒ = ⇒ α = 16 2 1 1 1 4 4 α = = = 2 2 2 αa αb αc α
Cách 1: Biến ñổi và sử dụng bất ñẳng thức Côsi ta có 1 1 1 1 1 1 2 2 2 S = a + + ... + + b + + ... + + c + + ... + 2 2 2 2 2 2 16b 16b 16c 16c 16a 16a 16 16 16 2 2 2 a b c a b c 17 17 17 17 17 17 ≥ 17⋅ + 17⋅ + 17⋅ = 17 + + 16 32 16 32 16 32 8 16 8 16 8 16 16 b 16 c 16 a 16 b 16 c 16 a a b c 1 3 ≥ 17 17 17 ⋅ ⋅ ⋅ 17 17 3 = 3 17 8 16 8 16 8 16 8 5 5 5 16 b 16 c 16 a 16 a b c 3 17 3 17 3 17 1 3 17 = ≥ ≥
. Với a =b = c = thì Min S = 17 5 ⋅ a b c 2 2 ⋅ (2a+2b+2 2 c )15 2 2 (2 2 2 ) 17 3 10
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số
Cách 2: Biến ñổi và sử dụng bất ñẳng thức BunhiaCôpski ta có 1 1 1 1 4 2 2 a + = ⋅ a + ( 2 2 1 + 4 ) ≥ ⋅ a + 2 2 b 17 b 17 b 1 1 1 1 4 2 2 + b + = ⋅ b + ( 2 2 1 + 4 ) ≥ ⋅ b + 2 2 c 17 c 17 c 1 1 1 1 4 2 2 c + = ⋅ c + ( 2 2 1 + 4 ) ≥ ⋅ c + 2 2 a 17 a 17 a ⇒ 1 4 4 4 1 1 1 1 15 1 1 1 S ≥
⋅ a + b + c + + + =
⋅ a + b + c + + + + + + 17 a b c 17 4a 4b 4c 4 a b c 1 1 1 1 15 1 1 1 1 45 1 6 3 ≥ 6 ⋅ abc ⋅ ⋅ ⋅ + 3 ⋅ ⋅ ⋅ = 3 + ⋅ 3 17 4a 4b 4c 4 a b c 17 4 abc 1 45 1 1 45 3 17 1 3 17 ≥ 3 + ⋅ ≥ 3 + ⋅ 2 =
. Với a = b = c = thì MinS = 17 4 a + b + c 17 4 2 2 2 3
Cách 3: ðặt u = ( 1 a ) v =( 1 b ) w =( 1 , ; , ; c , ) b c a
Do u + v + w ≥ u + v + w nên suy ra : 2 1 1 1 S = a + + b + + c +
≥ ( a + b + c)2 1 1 1 2 2 2 + + + 2 2 2 b c a a b c 2 2 2 1 1 1 1 15 1 1 1
= (a + b + c) + + + + + + 16 a b c 16 a b c 15 ≥
(a + b + c) 1 ⋅ ⋅ ( 1 1 1 + + ) 2 3 1 1 1 2 + 3 ⋅ ⋅ ⋅ 4 a b c 16 a b c 1 135 1 9 135 ≥ 3 3 1 1 1 ⋅ 3 ⋅ abc ⋅ 3 ⋅ ⋅ ⋅ + ⋅ ≥ 1 + ⋅ 2 a b c 16 ( abc )2 3 2 16
(a + b + c)2 3 9 135 18 135 153 3 17 1 3 17 ≥ + ⋅ 4 = + = =
. Với a = b = c = thì Min S = 2 16 4 4 4 2 2 2 11
Chương I. Hàm số – Trần Phương
B. CÁC ỨNG DỤNG GTLN, GTNN CỦA HÀM SỐ
I. ỨNG DỤNG TRONG PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH
Bài 1. Giải phương trình: 4 4 x − 2 + 4 − x = 2
Giải. ðặt f ( x) 4 4 = x − 2 +
4 − x với 2 ≤ x ≤ 4 x 2 3 4 ƒ′ − 0 + f ′ ( x) 1 1 1 = − = 0 ⇔ x = 3 4 ( x − 2)3 (4 − x)3 4 4 ƒ
Nhìn BBT suy ra: f ( x) ≥ f (3) = 2 x ∀ ∈[2, 4] 2
⇒ Phương trình f ( x) 4 4 = x − 2 +
4 − x = 2 có nghiệm duy nhất x = 3
Bài 2. Giải phương trình: 3x + 5x = 6x + 2
Giải. PT ⇔ ( ) = 3x + 5x f x
− 6x − 2 = 0 . Ta có: ′ ( ) = 3x ln 3 + 5 x f x ln 5 − 6 ⇒ 2 2
′ ( ) = 3x (ln 3) + 5 x f x (ln 5) > 0 x
∀ ∈ ℝ ⇒ ƒ′(x) ñồng biến
Mặt khác ƒ′(x) liên tục và
x −∞ 0 x0 1 +∞
f ′(0) = ln 3 + ln 5 − 6 < 0 , f ′( )
1 = 3ln 3 + 5ln 5 − 6 > 0 f ′ − 0 +
⇒ Phương trình ƒ′(x) = 0 có ñúng 1 nghiệm x0 f
Nhìn bảng biến thiên suy ra: ƒ(x0) Phương trình ( ) = 3x + 5x f x
− 6x − 2 = 0 có không quá 2 nghiệm.
Mà f (0) = f ( )
1 = 0 nên phương trình (1) có ñúng 2 nghiệm x = 0 và x = 1
Bài 3. Tìm m ñể BPT: 2
m 2x + 9 < x + m có nghiệm ñúng x ∀ ∈ ℝ
Giải. 2
m 2x + 9 < x + m ⇔ m ( 2 2x + 9 − ) 1 < x ⇔ < ( ) x m f x = 2 2x + 9 − 1 2 9 − 2x + 9
Ta có: f ′ ( x) = = 0 ⇔ 2
2x + 9 = 9 ⇔ x = 6 ±
2x + 9 ( 2x + 9 − )2 2 2 1 x −∞ −6 6 +∞ f ( x) 1 1 lim = lim = ; f ′ − 0 + 0 − x→+∞ x→+∞ 9 1 2 2 + − 2 x x 3 4 1 − − f ( x) 1 1 lim = lim = ƒ 1 − 2 x→−∞ x→−∞ 9 1 2 2 + + 3 2 − 2 x x 4 −
Nhìn BBT ta có f ( x) > m , x ∀ ∈ ℝ ⇔
f ( x) = f (− ) 3 3 Min 6 = −
> m ⇔ m < x∈ℝ 4 4 12
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số Bài 4. π π Tìm m ñể PT: + x = m ( + x)2 2 2 sin 2 1 cos
(1) có nghiệm x ∈ − , 2 2 π π
Giải. Do x ∈ − , x −π π x ∈ ∈ − nên ñặt t = tg [ 1, ] 1 2 2 ⇒ , 2 4 4 2 2 ⇒ − 2 2 1 cos t x = ; 2 sin t x =
. Khi ñó (1) ⇔ 2 (sin x + cos x) = m (1 + cos x) 2 1 + t 2 1 + t 2 2 2 2 2 ⇔ + − − 2t 1 t 1 2 = 1 t m +
⇔ f (t ) = ( 2
2t + 1 − t ) = 2m (2) 2 2 1 + t 1 + t
Ta có: f ′(t ) = ( 2
2 2t + 1 − t )(2 − 2t ) = 0 ⇔ t = 1;t = 1 − 2 ⇒ Bảng biến thiên
Nhìn bảng biến thiên suy ra: t −1 1− 2 1 ƒ′(t) − 0 +
ðể (2) có nghiệm t ∈[ 1 − , ] 1 4 4 ƒ(t)
thì Min f (t ) ≤ 2m ≤ Max f (t ) 0 t [ ∈ 1 − , ] 1 t [ ∈ 1 − , ] 1 ⇔ π π
0 ≤ 2m ≤ 4 ⇔ 0 ≤ m ≤ 2 . Vậy ñể (1) có nghiệm x ∈ − , m ∈ 0; 2 . 2 2 thì [ ] 2
x − 3x ≤ 0
Bài 5. Tìm m ñể hệ BPT:
(1) có nghiệm. 3 2
x − 2x x − 2 − m + 4m ≥ 0 0 ≤ x ≤ 3 2
Giải. (1) ⇔ (2). x 0 2 3 3 f ( x) 3 2
= x − 2x x − 2 ≥ m − 4m f ′ − 0 + + 2 3
x + 4x − 4 x ∀ ∈[0; 2) 21
Ta có: f ′ ( x) = ; f 8 0 2 3
x − 4x + 4 x ∀ ∈ (2; ] 3 CT ƒ′(x) = 0 ⇔ 2 x =
. Nhìn BBTsuy ra: Max f ( x) = f (3) = 21 3 x [ ∈ 0; ] 3
ðể (2) có nghiệm thì Max f ( x) 2
≥ m − 4m ⇔ 2
m − 4m ≤ 21 ⇔ −3 ≤ m ≤ 7 x [ ∈ 0; ] 3 3 2 35
sin x cos y = m − m − 6m + 4
Bài 6. Tìm m ≥ 0 ñể hệ: (1) có nghiệm. 2 33
cos x sin y = m − 6m + 4
Giải 13
Chương I. Hàm số – Trần Phương 3 s
in xcos y + cos xsin y = m −12m +17 s in (x + y) 3 = m −12m +17 (1) ⇔ ⇔ (2) 3 2 1 s
in x cos y − cos xsin y = m − 2m + s
in ( x − y) 3 2 1 = m − 2m + 2 2 Xét f (m) 3
= m − 12m + 17 . Ta có: f ′ (m) 2
= 3m − 12 = 0 ⇔ m = 2 > 0
Nhìn BBT suy ra: ƒ(m) ≥ ƒ(2) = 1,∀m ≥ 0 m 0 2 +∞ ƒ′ − 0 +
kết hợp với sin ( x + y) ≤ 1 suy ra ñểhệ (2) 17 +∞
có nghiệm thì m = 2, khi ñó hệ (2) trở thành: ƒ 1
sin ( x + y) =1 π π có nghiệm x = ; y =
. Vậy (1) có nghiệm ⇔ m = 2. ( x − y) 1 sin = 3 6 2
II. ỨNG DỤNG GTLN, GTNN CHỨNG MINH BẤT ðẲNG THỨC
Bài 1. Chứng minh rằng: + x ( 2 x + + x ) 2 1 ln 1 ≥ 1 + x , x ∀ ∈ ℝ
BðT ⇔ f ( x) = + x ( 2 x + + x ) 2 1 ln 1
− 1 + x ≥ 0 x ∀ ∈ ℝ
Ta có: f ′ ( x) = ( 2
ln x + 1 + x ) = 0 ⇔ x = 0 x −∞ 0 +∞ ⇒ f ′ − 0 + Bảng biến thiên.
Nhìn bảng biến thiên suy ra: f 0
f ( x) ≥ f (0) = 0 ⇒ (ñpcm)
a, b, c > 0 Bài 2. a b c 3 3 Cho CMR: T = + + ≥ 2 2 2 2 2 2 2 2 2
a + b + c = 1 b + c c + a a + b 2 2 2 2 Ta có: T = a b c a b c + + = + + . 2 2 2 − a − b − c a ( 2 − a ) b ( 2 − b ) c ( 2 1 1 1 1 1 1 − c )
Xét hàm số f ( x) = x ( 2
1 − x ) với x > 0 1 x −∞ +∞ 3
Ta có f ′ ( x) 2 1
= 1 − 3x = 0 ⇔ x = > 0 . f ′ + 0 − 3 2 f 3 3
Nhìn bảng biến thiên ⇒ f ( x) 2 ≤ x ∀ > 0 . 3 3 2 2 2 a b c 3 3 3 3 Khi ñó : T = + + ≥ ( 2 2 2
a + b + c ) = f (a) f (b) f (c) 2 2 ðẳng thức xảy ra 1
⇔ a = b = c = . 3 14
Bài 3. Giá trị lớn nhất, nhỏ nhất của hàm số
Bài 3. Cho 3 ≤ n lẻ. Chứng minh rằng: ∀x ≠ 0 ta có: 2 n 2 3 n (1 x + + + ... x + )(1 x x − + − + ... x x x − )<1 2! n! 2! 3! n! 2 n 2 3 n ðặt ( ) = 1 x + + + ... x + ; ( ) = 1 x x − + − + ... x u x x v x x − . 2! n! 2! 3! n!
Ta cần chứng minh f ( x) = u ( x).v ( x) < 1 2 n 1 − n ′( ) =1 x + + + ... x + = ( ) x u x x u x − 2! ( n − ) 1 ! n! Ta có: 2 n 1 − n ′( ) = 1 x − + − + ... x − = − ( ) x v x x v x − 2! (n − ) 1 ! n! ⇒ n n
′ ( ) = ′ ( ). ( ) + ( ). ′( ) = ( ) x − ( ) − ( ) ( ) x f x u x v x u x v x u x v x u x v x + n! n! n n 2 4 n 1 − ⇒ − − ′ ( ) x f x =
[u ( x) + v ( x)] 2x = 1 x x + + + ... x + n! n! 2! 4! (n ) 1 ! −
Do 3 ≤ n lẻ nên ƒ′(x) cùng dấu với (−2x) x −∞ 0 +∞ f ′ + 0 −
Nhìn bảng biến thiên suy ra: 1 f
f ( x) < f (0) = 1 x ∀ ≠ 0 ⇒ (ñpcm) 3 3 4 4 Bài 4. a + b a + b Chứng minh rằng: 3 4 ≤
∀a, b > 0. 2 2 t 0 1 1 a + +∞ 4 4 4 a + b 2 ( )4 4 4 4 4 4 b 1 + t 2 ≥ ⇔ = ≥ f′ − 0 + 3 3 3 3 a + b 2 a + t 1 + ( )3 3 3 3 1 2 3 1 b 1 4 1 f 2 4 4 1 + t ( 4 1 + t ) 4 a Xét f(t) = = với t = > 0 3 2 1 3 3 1 + t ( 3 b 1 + t ) 3 −2 − 1 3 1 −2 2 −3 ( 3 4 2 t ( 3 1 + t ) 1 + t ) 4 3 t ( 3 1 + t ) 3 − ( 4 1 + t ) 4 2 t ( 3 1 + t ) 3 ( 4
1 + t ) 4 (t − ) 1 f′(t) = = 2 2 ( 3 1 + t ) 3 ( 3 1 + t ) 3
f′(t) = 0 ⇔ t = 1 ⇒ Bảng biến thiên của f(t) 4 2 4 4 4 4 2 a + b 3 3 4 4 a + b a + b Từ BBT ⇒
≤ f(t) < 1 ∀t > 0 ⇒ ≤ ⇒ 3 4 ≤ . 3 2 3 3 3 3 2 a + b 2 2
Dấu bằng xảy ra ⇔ a = b > 0. 15
Chương I. Hàm số – Trần Phương
III. BÀI TẬP VỀ NHÀ
Bài 1. Cho ∆ABC có A > B > C . Tìm giá trị nhỏ nhất của hàm số: ( ) x − sin A x − sin B f x = + − 1 x − sin C x − sin C
Bài 2. Tìm Max, Min của: y = 6 6
sin x + cos x + a sin x cos x 4 4 2 2
Bài 3. Cho ab ≠ 0. Tìm Min của a b a b a b y = + − + + + 4 4 2 2 b a b a b a 2 2 Bài 4. x + y Cho 2 2
x + y > 0 . Tìm Max, Min của S = 2 2
x + xy + 4 y
Bài 5. Giả sử phương trình 2 1 x + px + = 0 có nghiệm x 2 1, x2. p Tìm p ≠ 0 sao cho 4 4
S = x + x nhỏ nhất. 1 2 2 x 2 x x x Bài 6.
Tìm Min của y = (2 + 3 ) + (2 − 3 )
− 8 (2 + 3 ) + (2 − 3 )
Bài 7. Cho x, y ≥ 0 và x + y =1. Tìm Max, Min của 3x 9 y S = + . Bài 8. Cho 2 2 2
x + y + z = 1 . Tìm Max, Min của P = x + y + z + xy + yz + zx .
Bài 9. Tìm m ñể PT: 2 − x + 2 + x − (2 − x) (2 + x) = m có nghiệm.
Bài 10 Tìm m ñể PT: 2 x +
9 − x = −x + 9x + m có nghiệm.
Bài 11 Tìm m ñể PT: ( x − x + )3 2 2 2 2 2
− 4 x − 2x + 2 = 2x − 4x + m có 4 nghiệm phân biệt. 2 Bài 12 −
Tìm m ñể PT: 3x
1 = 2x −1 + mx có nghiệm duy nhất. 2x − 1 Bài 13 π
Tìm m ñể PT: m cos 2x − 4 sin x cos x + m − 2 = 0 có nghiệm x ∈(0, ) . 4 Bài 14 π π Tìm m ñể PT: sin . x cos 2 .
x sin 3x = m có ñúng 2 nghiệm x ∈ , . 4 2 2 3
x + 2x −1< 0
Bài 15 Tìm m ñể hệ BPT: có nghiệm. 2
x + 3mx + 1< 0
Bài 16 a. Tìm m ñể: 2
m x + 8 = x + 2 có 2 nghiệm phân biệt.
b. Cho a + b + c =12 . CMR: 2 2 2 a + 8 + b + 8 + c + 8 ≥ 6 6
Bài 17 Chứng minh: ( 3 3 3
x + y + z ) − ( 2 2 2 2
x y + y z + z x) ≤ 3 , x
∀ , y, z ∈[0, ] 1 16