Giải SBT Toán 12 bài 3: Ứng dụng hình học của tích phân
Để giúp các bạn học sinh có kết quả cao hơn trong học tập, mời các bạn học sinh tham khảo tài liệu Giải SBT Toán 12 bài 3: Ứng dụng hình học của tích phân, chắc chắn nội dung tài liệu sẽ là nguồn thông tin hữu ích để phục vụ công việc học tập của các bạn học sinh được tốt hơn.
Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Nguyên hàm - Tích phân và ứng dụng
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
Giải SBT Toán 12 bài 3: Ứng dụng hình học của tích phân
Bài 3.21 trang 184 sách bài tập (SBT) - Giải tích 12
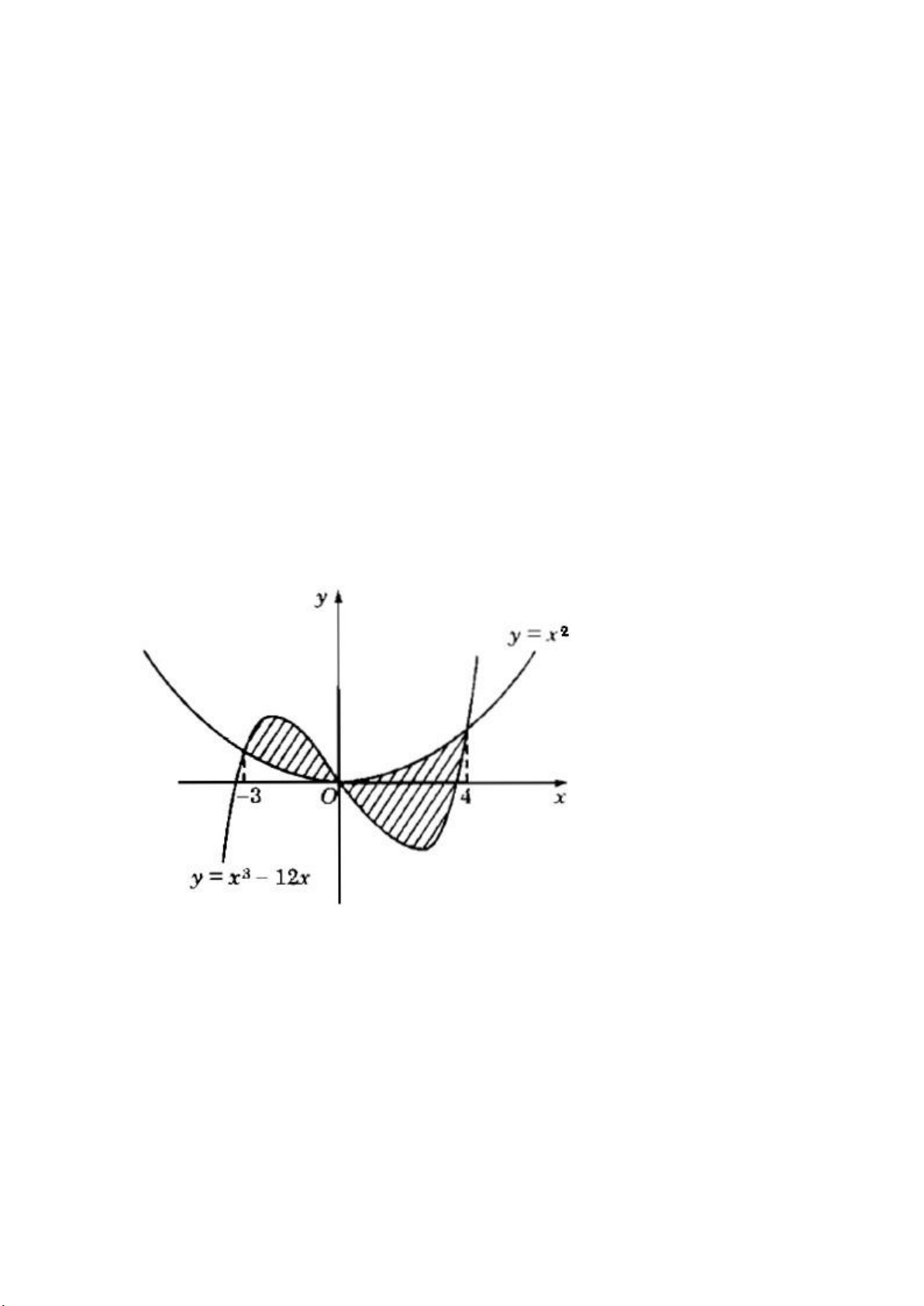
Tính diện tích hình phẳng giới hạn bởi các đường sau: a) y = 2x – x2, x + y = 2; b) y = x3 – 12x, y = x2
c) x + y = 1 ; x + y = -1 ; x – y = 1 ; x – y = -1; d) y=1/1+x2,y=12
e) y = x3 – 1 và tiếp tuyến với y = x3 – 1 tại điểm (-1; -2). Hướng dẫn làm bài a) 1/6
b) 78.1/12 .HD: S=0∫−3(x3−12x−x2)dx+4∫0(x2−x3+12x)dx c) 2; HD: S=41∫0(1−x)dx d) π/2−1
HD: S=21∫0(1/1+x2−1/2)dx=21∫01/1+x2dx−1
Đặt x=tan để tính 1∫01/1+x2dx
e) 27/4 .HD: Phương trình tiếp tuyến tại (-1; -2) là y = 3x + 1. Do đó, diện tích:
S=2∫−1(3x+1−x3+1)dx=2∫−1(3x+2−x3)dx
Bài 3.22 trang 184 sách bài tập (SBT) - Giải tích 12
Tính thể tích vật thể:
a) Có đáy là một tam giác cho bởi: y = x, y = 0, và x = 1. Mỗi thiết diện vuông góc với
trục Ox là một hình vuông.
b) Có đáy là một hình tròn giới hạn bởi x2 + y2 = 1. Mỗi thiết diện vuông góc với trục Ox là một hình vuông. Hướng dẫn làm bài a) 1/3 .
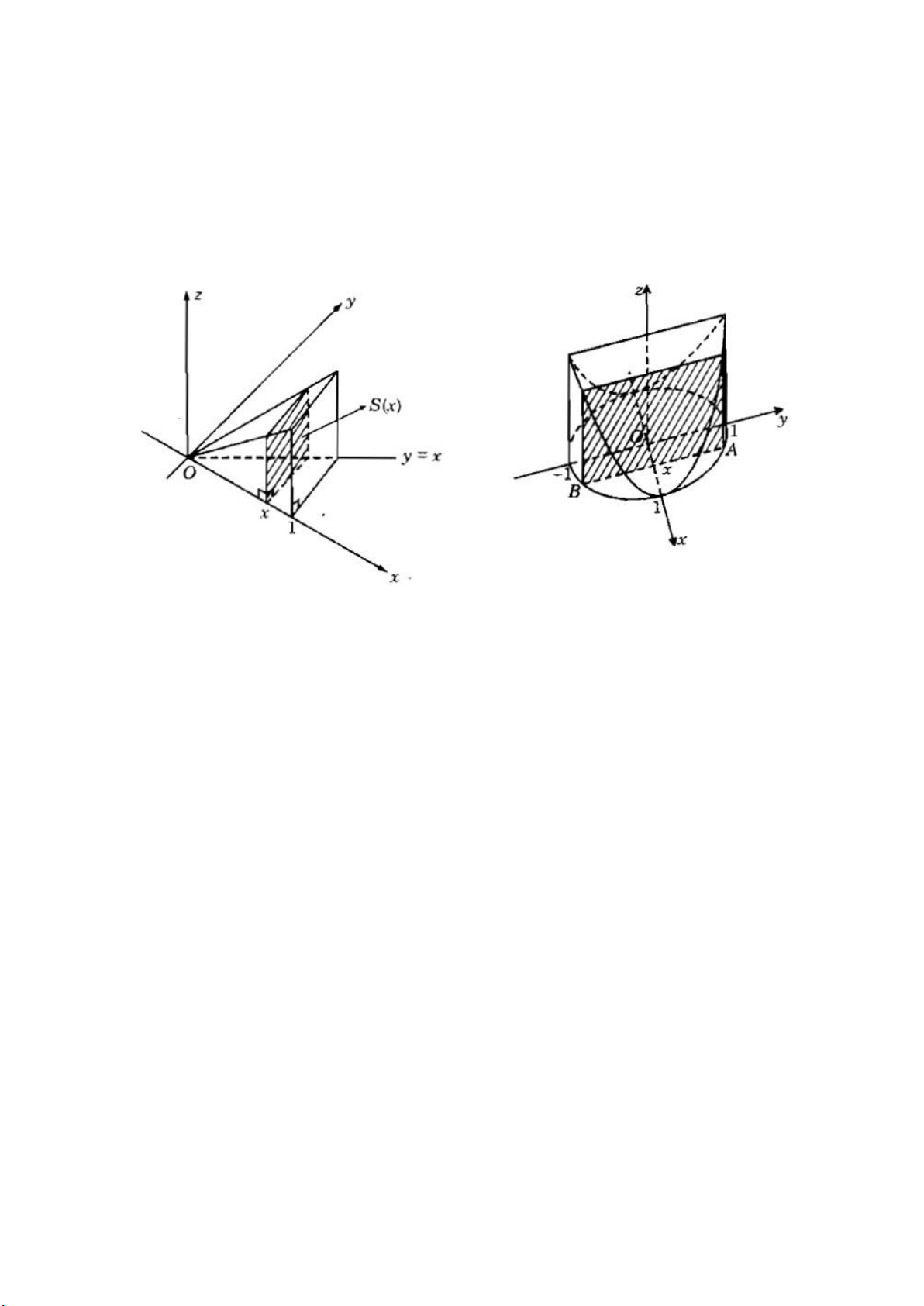
HD: Hình chóp (H.82). Thiết diện tại x∈ [0;1] là hình vuông cạnh bằng x, S(x) = x2.
Vậy V=1∫0S(x)dx=1∫0x2dx=1/3 b) 16/3
HD: (H.83) Thiết diện tại x∈ [−1;1] là hình vuông cạnh AB, trong đó A(x; y) với
y=√1−x2. Khi đó, AB=2√1−x2. Diện tích thiết diện là: S(x)=4(1−x2)
Vậy V=41∫−1(1−x2)dx=81∫0(1−x2)dx=16/3
Bài 3.23 trang 184 sách bài tập (SBT) - Giải tích 12
Tính thể tích các khối tròn xoay khi quay hình phẳng xác định bởi:
a) y = 2 – x2, y = 1, quanh trục Ox.
b) y = 2x – x2, y = x, quanh trục Ox.
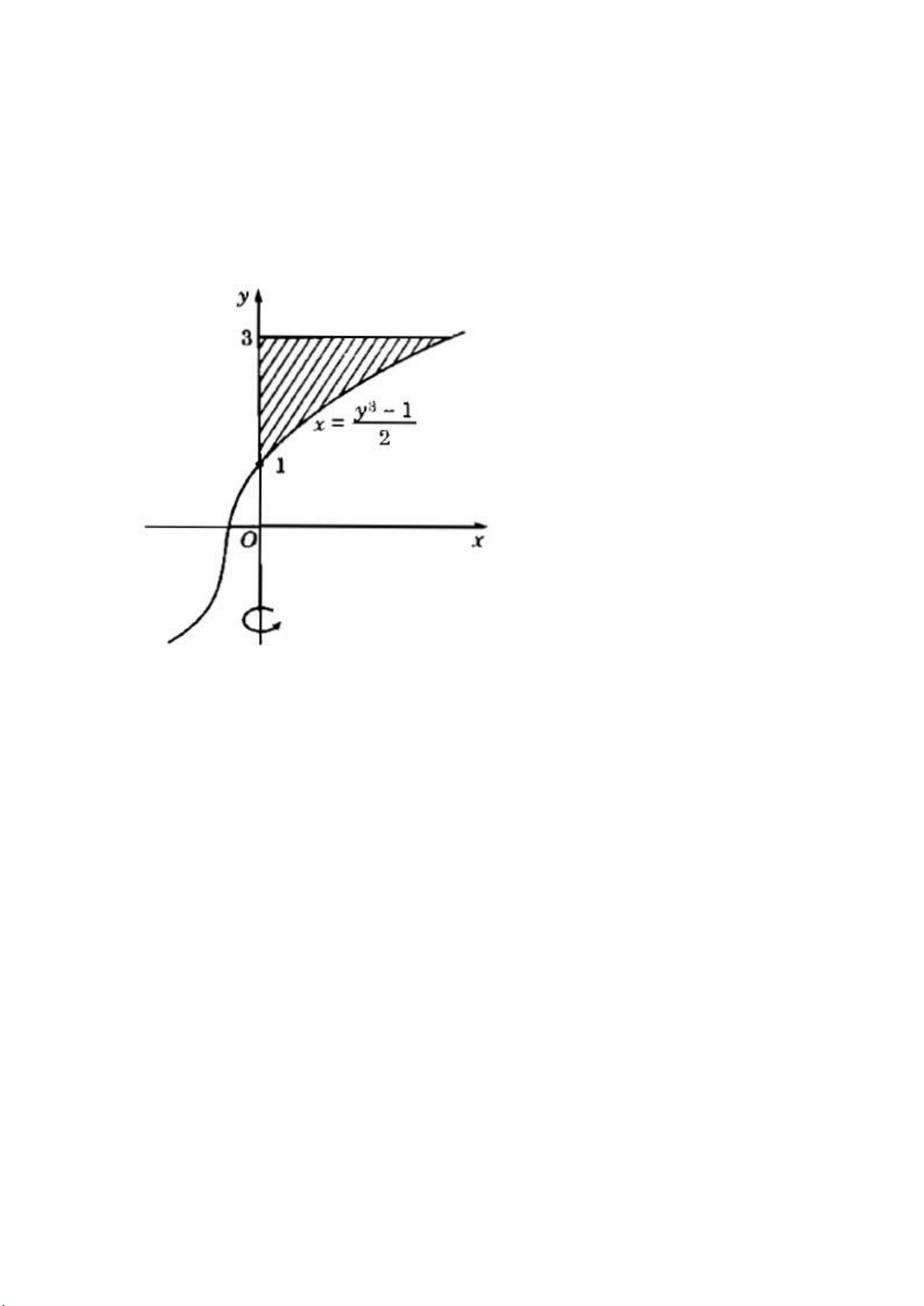
c) y=(2x+1)1/3, x=0, y=3 quanh trục Oy.
d) y = x2 + 1, x = 0 và tiếp tuyến với y = x2 + 1 tại điểm (1; 2), quanh trục Ox.
e) y = ln x, y = 0, x = e, quanh trục Oy. Hướng dẫn làm bài a) 56/15π b) π/5 c) 480/7π. HD: Xem hình d) 8/15π e) e2+1/2π
Bài 3.24 trang 184 sách bài tập (SBT) - Giải tích 12
Tính thể tích khối tròn xoay tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi
các đường y=1/x, y = 0, x = 1 và x = a (a > 1). Gọi thể tích đó là V(a). Xác định thể
tích của vật thể khi a→+∞ (tức là lima→+∞V(a) Hướng dẫn làm bài
V(a)=π(1−1/a) và lima→+∞V(a)=π
Câu 3.25 trang 185 sách bài tập (SBT) - Giải tích 12
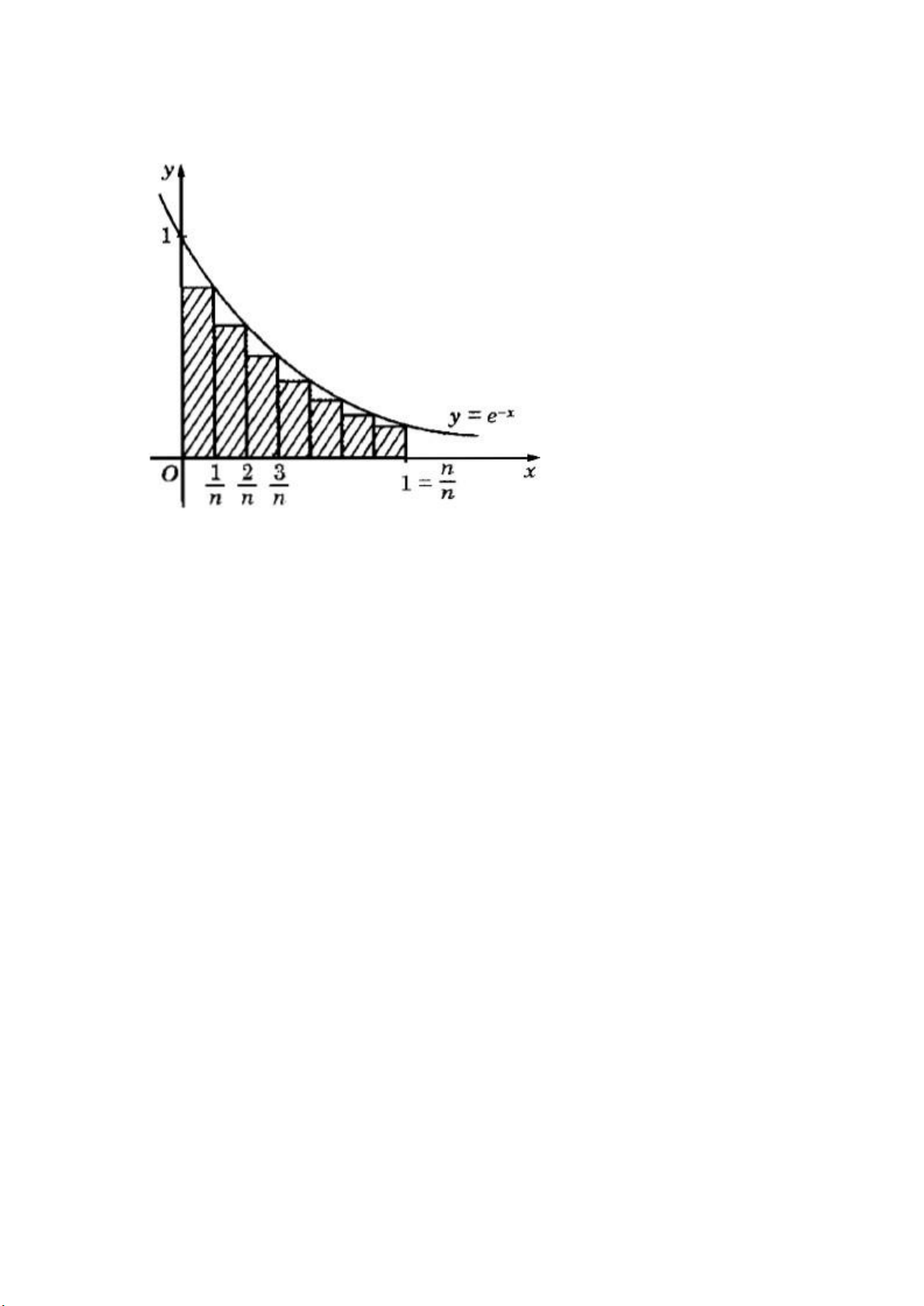
Một hình phẳng được giới hạn bởi y=e−x,y=0,x=0,x=1. Ta chia đoạn [0; 1] thành n
phần bằng nhau tạo thành một hình bậc thang (bởi n hình chữ nhật con như Hình bên).
a) Tính diện tích Sn của hình bậc thang (tổng diện tích của n hình chữ nhật con).
b) Tìm limn→∞Sn và so sánh với cách tính diện tích hình phẳng này bằng công thức tích phân. Hướng dẫn làm bài
a) Sn=1/n(1−e−1)e/1/n−1. HD: Theo hình 80 ta có:
Sn=1/n[e−1/n+e−21/n+...+e−n/n]=1/ne−1/n1−e−1/1−e−1/n=1/n(1−e−1)e1/n−1 b) limn→∞Sn=1−e−1
Mặt khác 1∫0e−xdx=1−e−1
Câu 3.26 trang 185 sách bài tập (SBT) - Giải tích 12
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y=x+sinx,y=x với 0≤x≤π} và {y=x+sinx,y=x với π≤x≤2π};
b) {y=sinx,y=0 với 0≤x≤π} và {y=cosx,y=0 với 0≤x≤π};
c) {y = 2x – x2, y = x} và {y = 2x – x2, y = 2 – x };
d) {y=logx,y=0,x=10} và {y=10x,x=0,y=10};
e) {y=√x,y=x2} và {y=√1−x2,y=1−x} Hướng dẫn làm bài: a) Đúng b) Đúng c) Đúng d) Đúng e) Sai