Giải SBT Toán 12 bài 4: Đường tiệm cận
Xin giới thiệu tới bạn đọc tài liệu Giải SBT Toán 12 bài 4: Đường tiệm cận, với nội dung được cập nhật chi tiết và chính xác sẽ là nguồn thông tin hữu ích để giúp các bạn học sinh đạt kết quả cao hơn trong học tập.
Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
Giải SBT Toán 12 bài 4: Đường tiệm cận
Bài 1.29 trang 22 Sách bài tập (SBT) Giải tích 12
Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau: a) y=2x−1/x+2 b) y=3−2x/3x+1 c) y=5/2−3x d) y=−4/x+1 Hướng dẫn làm bài: a) y=2x−1/x+2 Ta có: lim −
x→−2+2x−1/x+2=−∞,limx→−2 2x−1/x+2=+∞ nên đường thẳng x = 2 là
tiệm cận đứng của đồ thị hàm số.
Vì limx→±∞2x−1/x+2=limx→±∞
=2nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
b) Từ limx→(−1/3)+3−2x/3x+1=+∞;limx→(−1/3)−3−2x/3x+1=−∞ ta có x=−1/3x=−13 là tiệm cận đứng
Vì limx→±∞3−2x/3x+1=limx→±∞
=−2/3 nên đường thẳng y=−2/3 là tiệm cận ngang.
c) Vì limx→(23)+5/2−3x=−∞;limx→(2/3)−5/2−3x=+∞ nên x=2/3 là tiệm cận đứng
Do limx→±∞5/2−3x=0 nên y = 0 là tiệm cận ngang. d) Do lim −
x→−1+−4/x+1=−∞;limx→−1 −4/x+1=+∞ nên x = -1 là tiệm cận đứng.
Vì limx→±∞−4/x+1=0 nên y = 0 là tiệm cận ngang.
Bài 1.31 trang 23 Sách bài tập (SBT) Giải tích 12
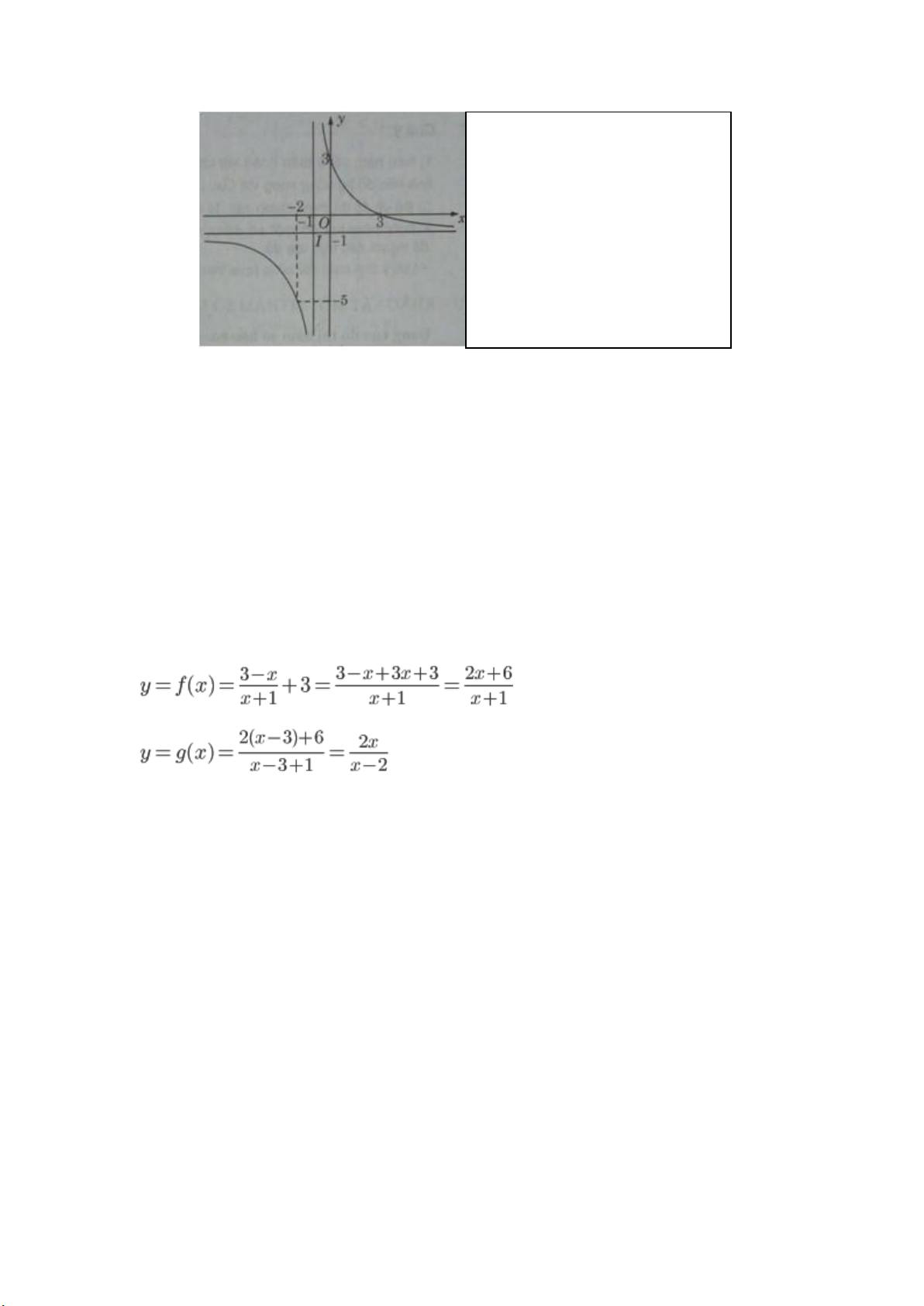
a) Cho hàm số y=3−x/x+1có đồ thị (H)
Chỉ ra một phép biến hình biến (H) thành (H’) có tiệm cận ngang y = 2 và tiệm cận đứng x = 2.
b) Lấy đối xứng (H’) qua gốc (O), ta được hình (H’’). Viết phương trình của (H’’). Hướng dẫn làm bài:
a) Từ đồ thị hàm số (H), để có hình (H’) nhận y = 2 là tiệm cận ngang và x = 2
là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị,
sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương ứng sau:
b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’) có phương trình là:
y=h(x)=2(−x)/(−x)−2=−2x/−2−x=−2x/x+2.