Giải SBT Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng
Xin giới thiệu tới các bạn học sinh tài liệu Giải SBT Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng, với nội dung tài liệu được tổng hợp chi tiết và chính xác sẽ giúp các bạn học sinh có kết quả cao hơn trong học tập. Mời thầy cô và các bạn học sinh cùng tham khảo.
Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng
Môn: Toán 12
Thông tin:
Tác giả:
Thông tin :
Chủ đề:
Chương 3: Nguyên hàm - Tích phân và ứng dụng
Môn:
Tác giả:
Tài liệu liên quan:
Preview text:
Giải SBT Toán 12 ôn tập chương 3: Nguyên hàm - Tích phân và ứng dụng
Câu 3.27 trang 185 sách bài tập (SBT) - Giải tích 12 Tính các nguyên hàm sau:
a) ∫(2x−3)√x−3dx, đặt u=√x−3
b) ∫x/(1+x2)3/2dx, đặt u=√x2+1
c) ∫ex/ex+e−xdx, đặt u=e2x+1 d) ∫1/sinx−sinadx
e) ∫√xsin√xdx, đặt t=√x g) ∫xlnx/1+xdx Hướng dẫn làm bài a) 2/5(x−3)3/2(2x−1)+C b)−1/√1+x2+C c) 1/2ln(e2x+1)+C d) 1/cosaln|
|+C. HD: Ta có: cosa=cos(x−a/2−x+a/2)
e) −2xcos√x+4√xsin√x+4cos√x+C
g) x2/2.lnx/1+x+1/2ln|1+x|−1/2x+C
Bài 3.28 trang 186 sách bài tập (SBT) - Giải tích 12 Tính các tích phân sau:
a) 1∫0(y−1)2√ydy, đặt t=√y b) 2∫1(z2+1) dz, đặt u= c) e∫1
d) π/2∫0(cos5φ−sin5φ)dφ e) π∫0cos3αcos3αdα Hướng dẫn làm bài a) 16/105 b) 2.49/220 c) 38/15 HD: e∫1
=1/5e∫1(4+5lnx)1/2d(4+5lnx) d) 0 e)π/8
HD: Dùng công thức hạ bậc đối với cos3x
Câu 3.29 trang 186 sách bài tập (SBT) - Giải tích 12 Tính các tích phân sau: a) π/4∫0cos2x.cos2xdx b) 1∫1/2ex/e2x−1dx c) 1∫0x+2/x2+2x+1ln(x+1)dx
d) π/4∫0xsinx+(x+1)cosx/xsinx+cosxdx Hướng dẫn làm bài
a) 1/4(1+π/4). HD: 1+cos2x/2=cos2
b) 1/2ln(e−1)(√e+1)/(e+1)(√e−1). HD:ex/e2x−1=1/2(ex/ex−1−ex/ex+1)
c) 1/2(ln22−ln2+1). HD: x+2/x2+2x+1ln(x+1)=ln(x+1)/x+1+ln(x+1)/(x+1)2 d) π/4+ln(1+π/4)−1/2ln2 HD:
xsinx+(x+1)cosx/xsinx+cosx=1+xcosx/xsinx+cosx và d(xsinx+cosx)=xcosxdx
Câu 3.30 trang 186 sách bài tập (SBT) - Giải tích 12
Tính diện tich các hình phẳng giới hạn bởi các đường sau:
a) y=x−1+lnx/x,y=x−1 và x = e;
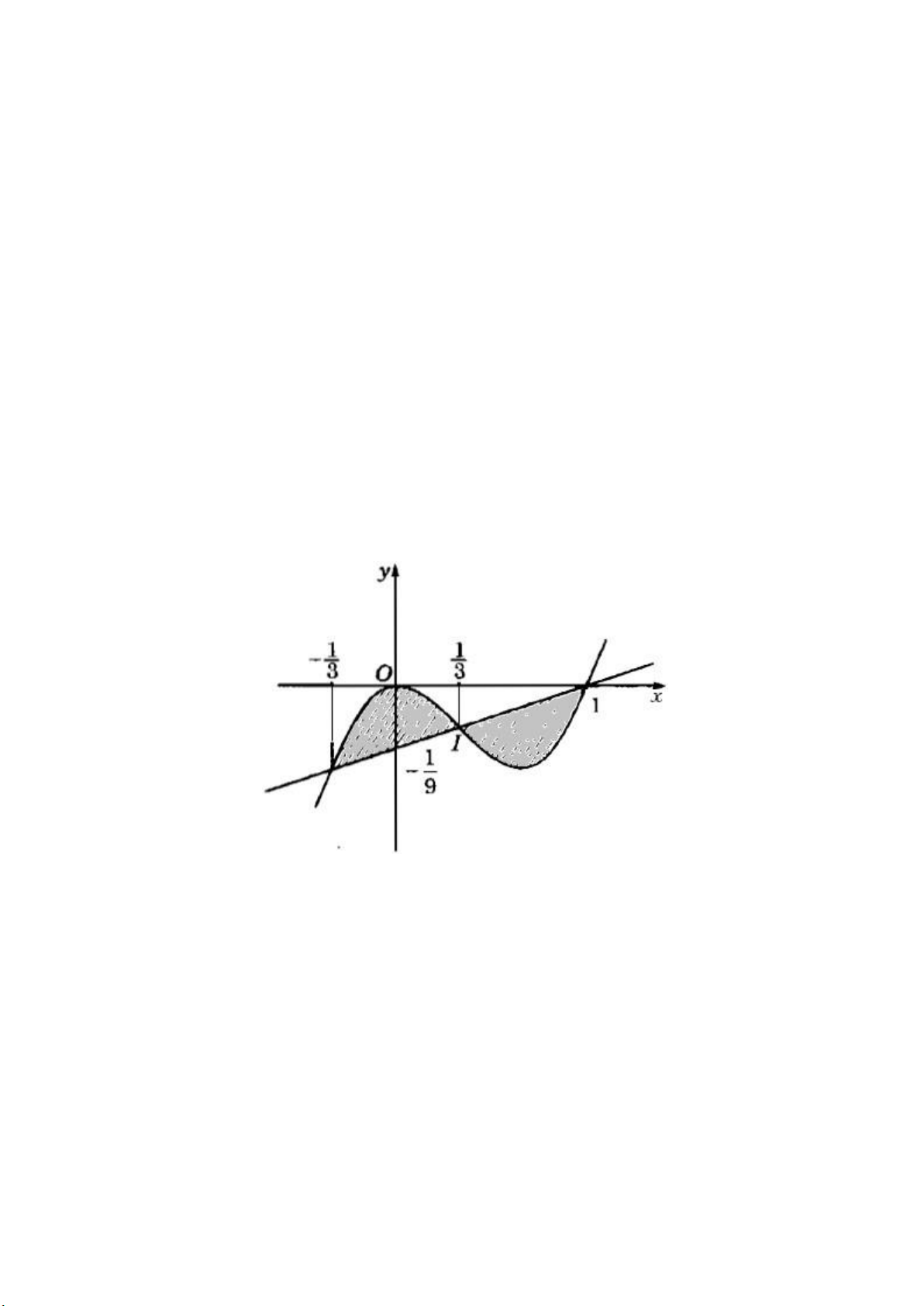
b) y = x3 – x2 và y=1/9(x−1); c) y=1−√1−x2 và y = x2 Hướng dẫn làm bài a) 1/2
b) 8/81. HD: Đường thẳng y=1/9(x−1) đi qua tâm đối xứng I(1/3;−2/27) của hàm số y = x3 – x2.
Do đó, hình phẳng giới hạn bởi hai đường đã cho gồm hai hình vẽ đối xứng
nhau qua điểm I (hình 85).
Vậy : S=21/3∫−1/3[(x3−x2)−1/9(x−1)]dx =41/3∫0(1/9−x2)dx=8/81
(theo bài 3.14. 1/3∫−1/3(x3−1/9x)dx=0 c) π/2−4/3
Câu 3.31 trang 186 sách bài tập (SBT) - Giải tích 12
Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi
a) y=x2/3,x=0 và tiếp tuyến với đường y=x2/3 tại điểm có hoành độ x = 1, quanh trục Oy;
b) y=1/x−1,y=0,y=2x quanh trục Ox
c) y = |2x – x2|, y = 0 và x = 3, quanh: * Trục Ox * Trục Oy Hướng dẫn làm bài a) π/36
Phương trình tiếp tuyến là: y=2/3x+1/3
V=π1∫0y3dy−π1∫1/3(3/2y−1/2)2dy
=π/4−2π/9(3/2y−1/2)3 ∣ 11/3=π/36 b) π(5/3−2ln2)
c) Vx=18/5π và Vy=596πVy=59/6.π
Vy=π{1∫0[(1+√1−y)2−(1−√1−y)2]dy+3∫0[9−(1+√1+y)2]dy}
=π[1∫04√1−ydy+3∫0(7−y−2√1+y)dy]=59π/6
Câu 3.32 trang 187 sách bài tập (SBT) - Giải tích 12
Hãy chỉ ra các kết quả đúng trong các kết quả sau:
a) (1∫0xn(1−x)mdx=1∫0xm(1−x)ndx;m,n∈ N∗
b) 1∫−1t2/et+1dt=1∫0t2dt c) 1∫0sin3xcosxdx=1∫0t3dt Hướng dẫn làm bài a) Đúng
b) Ta có: 1∫−1t2dt/et+1=0∫−1t2dt/et+1+−1∫0t2dt/et+1
Dùng phương pháp đổi biến t = - x đối với tích phân 0∫−1t2dt/et+1, ta được:
0∫−1t2dt/et+1=1∫0x2dx/e−x+1=1∫0t2dt/e−t+1
Thay vào (*) ta có: 1∫−1t2dt/et+1=1∫0t2dt c) Sai.