Giải Toán 8 Bài 35: Định lí Pythagore và ứng dụng | Kết nối tri thức
Giải Toán 8 Bài 35: Định lí Pythagore và ứng dụng | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 5 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Chương 9: Tam giác đồng dạng (KNTT)
Môn: Toán 8
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Tài liệu liên quan:
Preview text:
Toán 8 Bài 35: Định lí Pythagore và ứng dụng Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 2 trang 97 Bài 9.17
Cho tam giác ABC vuông tại A. Trong các khẳng định sau đây, khẳng định nào đúng, khẳng định nào sai a) b) c) d) Đáp án: Khẳng định b, d đúng Khẳng định a, c sai Bài 9.18
Những bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông a) b) c) d) Đáp án: c và d Bài 9.19
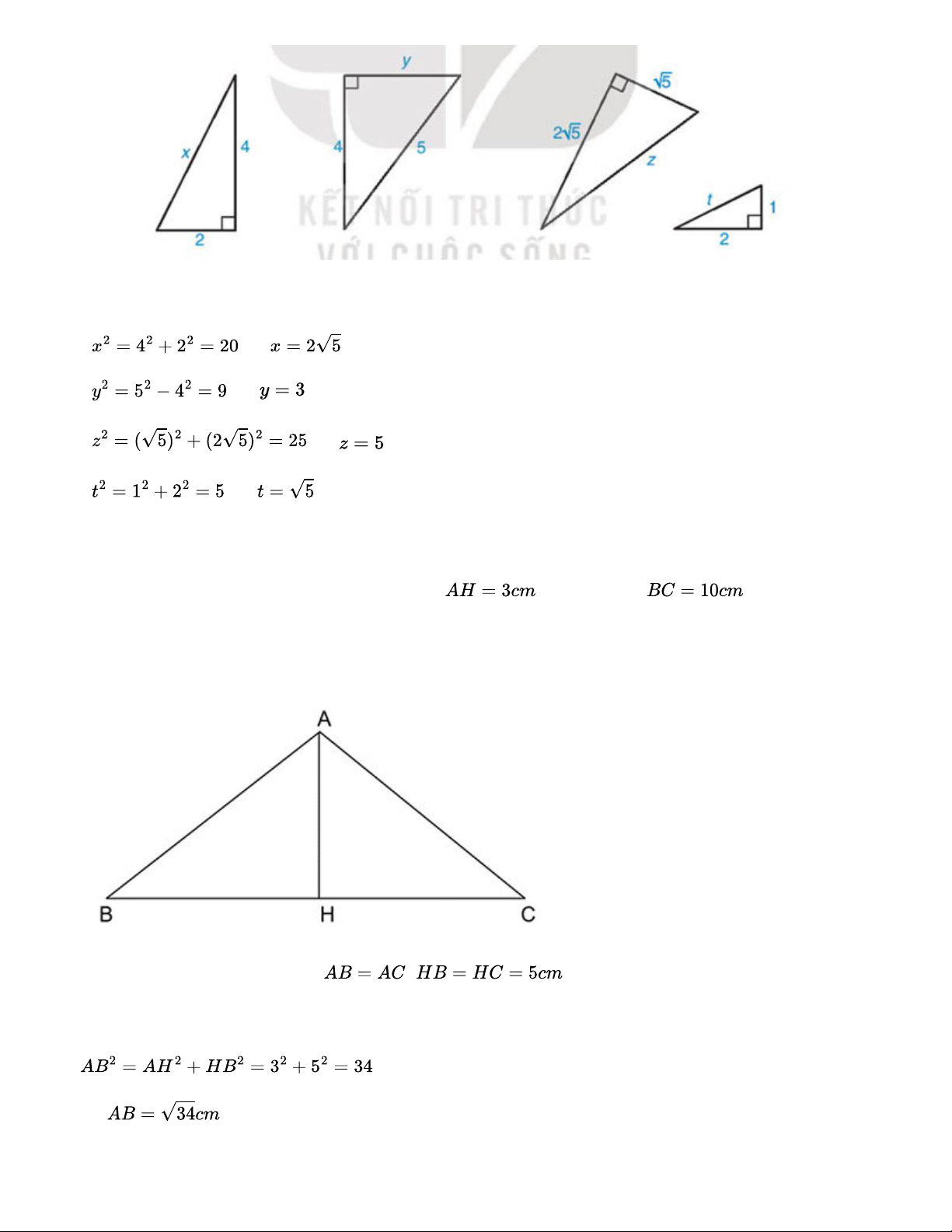
Tính độ dài x, y, z, t trong Hình 9.43 Lời giải: - => - => - => - => Bài 9.20
Cho tam giác ABC cân tại đỉnh A, chiều cao và cạnh đáy . Hãy tính độ dài các cạnh bên AB, AC Lời giải:
Vì tam giác ABC cân tại A => ,
Xét tam giác AHB vuông tại H có => Bài 9.21
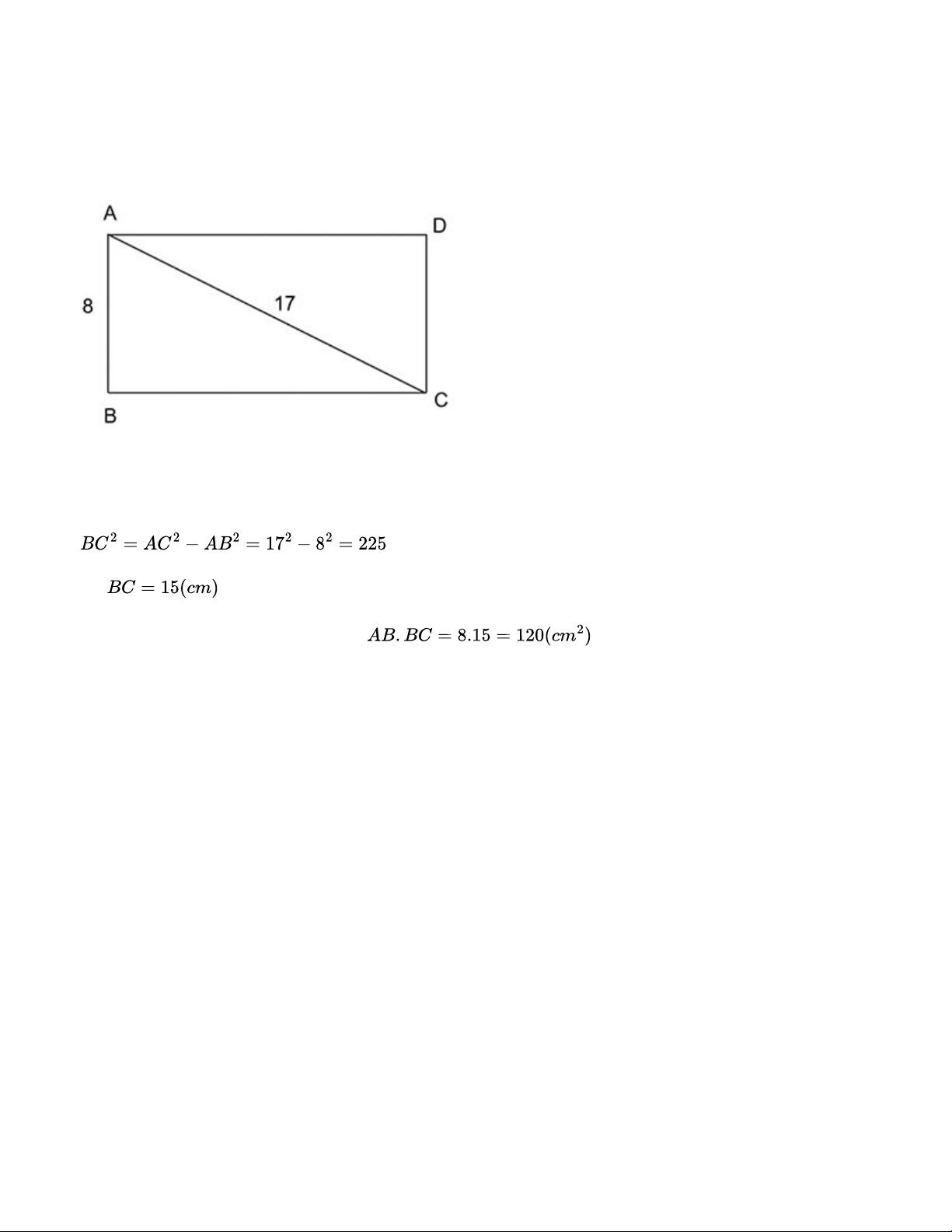
Hãy tính diện tích của một hình chữ nhật có chiều rộng 8cm và đường chéo dài 17cm Lời giải:
Theo đề bài, ta có hình vẽ:
Xét tam giác ABC vuông tại B, có =>
=> Diện tích của hình chữ nhật là: Bài 9.22
Chú cún bị xích bởi một sợi dây dài 6m để canh một mảnh vườn giới hạn bởi các điểm A, B, E,
F, D trong hình vuông ABCD có cạnh 5m như Hình 9.44. Đầu xích buộc cố định tại điểm A của
mảnh vườn. Hỏi chú cún có thể chạy đến tất cả các điểm của mảnh vườn mình phải canh không Lời giải:
- Xét tam giác ABE vuông tại B, có =>
=> Chú chó có thể chạy đến điểm E do khoảng cách AE ngắn hơn sợi dây
- Xét tam giác ADF vuông tại D, có =>
=> Chú chó không thể chạy đến điểm F do khoảng cách AF dài hơn sợi dây
- Xét tam giác ADC vuông tại D, có =>
=> Chú chó không thể chạy đến điểm C do khoảng cách AC dài hơn sợi dây
Vậy chú chó không thể chạy hết tất cả các điểm của mảnh vườn. Chú chó chỉ có thể chạy đến điểm B, D, E.