Giải Toán 8 Luyện tập chung trang 62 | Kết nối tri thức
Giải Toán 8 Luyện tập chung trang 62 | Kết nối tri thức. Tài liệu được biên soạn dưới dạng file PDF bao gồm 5 trang tổng hợp các kiến thức chọn lọc giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Chương 3: Tứ giác (KNTT)
Môn: Toán 8
Sách: Kết nối tri thức
Thông tin:
Tác giả:
Preview text:
Toán 8 Luyện tập chung Kết nối tri thức
Giải Toán 8 Kết nối tri thức Tập 1 trang 63 Bài 3.19
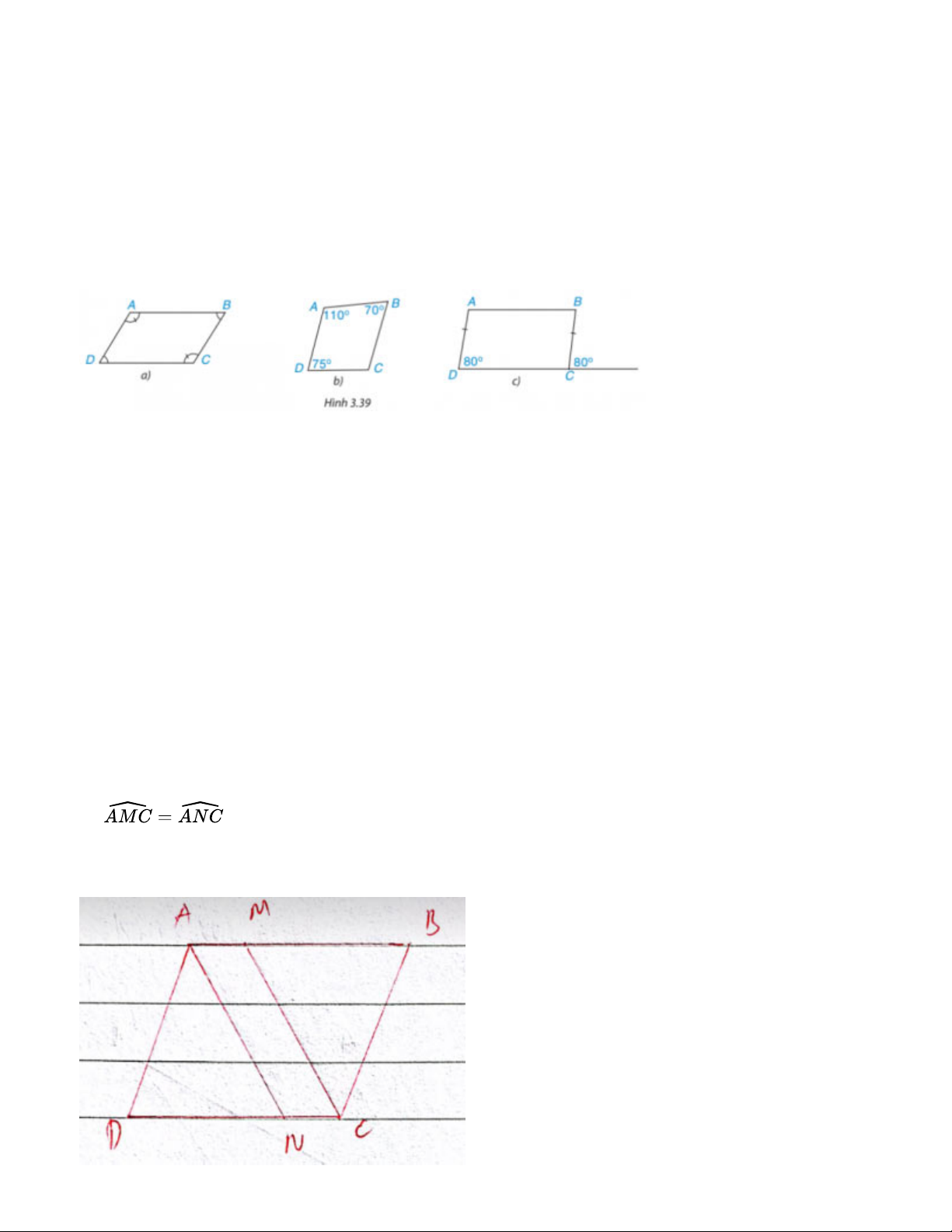
Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao? Bài giải:
a) là hình bình hành vì có các cặp góc đối bằng nhau
b) Không là hình bình hành vì có cặp góc đối không bằng nhau
c) là hình bình hành vì có AD = BC, AD // BC Bài 3.20
Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng: a) AN = CM b) Bài giải:
a) Ta có: AB//CD(hai cạnh đối trong hình bình hành ABCD) mà M∈AB(gt) và N∈CD(gt) nên AM//CN
Xét tứ giác AMCN có AM//CN(cmt) và AM=CN(gt)
nên AMCN là hình bình hành(Dấu hiệu nhận biết hình bình hành)
⇒ AN=MC(hai cạnh đối trong hình bình hành AMCN)
b) AMCN là hình bình hành ⇒ Bài 3.21
Vẽ tứ giác ABCD theo hướng dẫn sau:
Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB Bước 2. Lấy điểm
Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC
Hãy giải thích tại sao tứ giác ABCD là hình bình hành Bài giải: Xét tứ giác ABCD có: AB = CD AB // CD
do đó ABCD là hình bình hành Bài 3.22
Cho hình bình hành ABC có AB = 3 cm, AD = 5 cm
a) Hỏi tia phân giác của góc A cắt cạnh CD hay cạnh BC?
b) Tính khoảng cách từ giao điểm đó đến điểm C Bài giải: a) Cắt cạnh BC
b)Gọi giao điểm của tia phân giác góc A và BC là K Ta có: (so le trong) (AK là tia phân giác ) Suy ra là tam giác cân tại B Bài 3.23
Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C
là trung điểm của DF. Chứng minh rằng:
a) Hai tứ giác AEFD, ABFC là những hình bình hành
b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau Bài giải:
a) Ta có AE = 2AB; DF = 2 CD, AB = CD suy ra AE = DF
Xét tứ giác AEFD có AE = DF. AE//DF suy ra AEFD là hình bình hành
Ta có FC = CD, AB = CD suy ra FC = AB
Xét tứ giác AEFD có FC = AB. FC//AB suy ra ABFC là hình bình hành
b) AEFD là hình bình hành suy ra trung điểm của AF và DE trùng nhau
ABFC là hình bình hành suy ra trung điểm của AF và BC trùng nhau
Do đó các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau Bài 3.24
Cho ba điểm không thẳng hàng.
a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành. Hãy
vẽ hình và mô tả cách tìm
b) Hỏi tìm được bao nhiêu điểm như vậy Bài giải
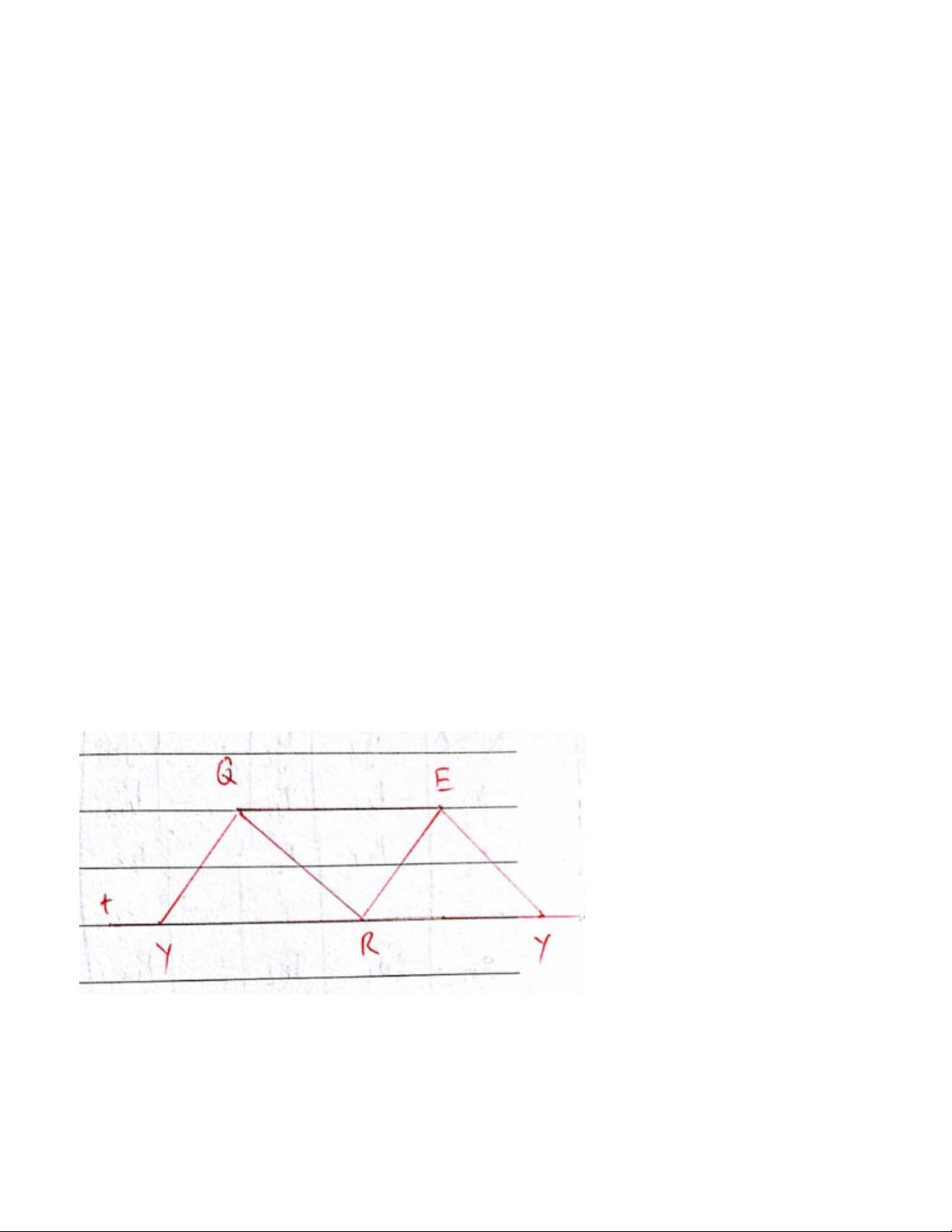
a) Gọi 3 điểm cho trước là Q, E, R
- Nối Q với E, ta được đoạn thẳng QE
- Qua R kẻ đường thẳng t // QE
- Trên t lấy điểm Y sao cho YR=QE
- Nối 4 điểm Q, E, R, Y lại với nhau ta được 1 hình bình hành b) Tìm được 2 điểm