Giải toán tích phân bằng nhiều cách – Nguyễn Thành Long Toán 12

Giải toán tích phân bằng nhiều cách – Nguyễn Thành Long Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

67 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
1
(MỘT PHƯƠNG PHÁP NHẰM PHÁT TRIỂN TƯ DUY CHO HỌC SINH)
Gửi tặng: www.toanmath.com
Bỉm sơn. 13.03.2011
Tải thêm tài liệu môn Toán THPT tại:
+ Trang web: www.toanmath.com
+ Fanpage: www.facebook.com/toanmath
+ Groups: https://www.facebook.com/groups/toanmath
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
2
GIẢI TOÁN TÍCH PHÂN BẰNG NHIỀU CÁCH
(Một phương pháp nhằm phát triển tư duy)
I. TÍCH PHÂN HÀM HỮU TỶ
Bài tập giải mẫu:
Bài 1: Tính tích phân sau:
3
3
2
0
1
x
I dx
x
Giải:
Cách 1: Phương pháp biến đối số
Đặt
2
tan 1 tan
x t dx t dt
Đổi cận
3
3
0
0
t
x
x
t
Khi đó
3 3 3 3
3 2 2
0 0 0 0
tan tan tan 1 1 tan tan 1 tan
I tdt t t dt t t dt tdt
2
3 3
0 0
cos
tan 3
tan tan ln cos ln2
3
cos 2 2
0
d t
t
td t t
t
Nhận xét: Đối với tích phân dạng
2 2
, ,
I R u u a du u u x
thì ta có thể đặt
tan
u a t
Cách 2: Phương pháp tích phân từng phần
Đặt
2
2
2
2
ln 1
1
2
du xdx
u x
x
xdx
dv
v
x
Khi đó
3 3
2 2 2 2 2
0 0
1 13
ln 1 ln 1 3ln2 ln 1 1
2 2
0
J
I x x x x dx x d x

Tính
3
2 2
0
ln 1 1
J x d x
Đặt
2
2
2
2
2
1
ln 1
1
1
1
d x
u x
du
x
dv d x
v x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
3
Khi đó
3
2 2 2
0
1 33
3ln2 1 ln 1 1 ln2
2 2
0
I x x d x
Chú ý: Sở dĩ ta sử dụng được phương pháp này là vì
Khi tính tích phân hàm phân thức mà ta phân tích được về dạng
'
n n
P x f x Q x
I dx dx
Q x Q x
thì
Đặt
'
n
u f x
du
Q x
v
dv dx
Q x
Cách 3: Kĩ thuật tách thành tích kết hợp phương pháp đổi biến số
Nhận xét: Ta có
3 2
x x x
và
'
2
1 2
x x
từ đó ta định hướng giải như sau
Phân tích
3 3
3 2
2 2
0 0
1 1
x x x
I dx dx
x x
Đặt
2
2
1
1
2
x t
t x
dt
xdx
Đổi cận
4
3
1
0
t
x
t
x
Khi đó
4 4
1 1
1
4
1 1 1 1 3
1 ln ln 2
1
2 2 2 2
t
I dt dt t t
t t
Cách 4: Phân tích và đưa vào vi phân
2
3 3 3
2
2 2 2
2 2 2
0 0 0
2
3 3
2
2 2
2
0 0
1 1
1 1 1 1
1 1 1 1
2 2 21 1 1
1
1 33 3
1 ln 1 2ln2
2 2 2
1
0 0
x
x
I d x d x d x
x x x
d x
x
d x x
x
Cách 5: Chia đa thức để tách thành tổng hai tích phân đơn giản hơn
2
3 3 3
3 2
2
2 2 2
0 0 0
1
1 3 1 33 3
ln 1 ln 2
2 2 2 2 2
1 1 1
0 0
d x
x x x
I dx x dx x
x x x
Nhận xét: Đây là tích phân hàm phân thức mà có bậc của tử lớn hơn bậc của mẫu chính vì thế ta chia đa thức
để tách thành tổng các tích phân là phương pháp tối ưu nhất
Cách 6: Phân tích tử thức chứa mẫu thức (thực chất là chia đa thức)
Ta có
3 2
1
x x x x
Khi đó
2
3 3 3
3 2
2
2 2 2
0 0 0
1
1 3 1 33 3
ln 1 ln 2
2 2 2 2 2
1 1 1
0 0
d x
x x x
I dx x dx x
x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
4
Bài 2: Tính tích phân bất định:
3 3
2
3 3
1 2
3 2
x x
I dx dx
x x
x x
Giải:
Cách 1: Phân tích tử thức chứa nghiệm của mẫu thức
Phân tích
3 2 2
3 2 3 3 2 7 1 1
x x x x x x x
Khi đó
2 2
3
2 2
3 2 3 3 2 7 1 1
3
3 2 3 2
x x x x x x
x
I dx dx
x x x x
2
7 1 1
3 3 7ln 2
2 1 2 2 1 2
x
x dx x x dx
x x x x x
2 2
3 7ln 2 ln 2 ln 1 3 8ln 2 ln 1
2 2
x x
x x x x C x x x C
Cách 2: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và kĩ thuật “nhảy tầng lầu”
Phân tích
3 2
3 2 3 1 1 2 3
x x x x x x x
2 2
3 2 3 1 2 3 2 3 3 2 3 1 2 9 1 2 3
x x x x x x x x x x x x x
Khi đó
2
3
2 2
3 2 3 1 2 3 2 3
3
3 2 3 2
x x x x x x
x
I dx dx
x x x x
2
2
2
9 2 3
3 3 9ln 2 ln 3 2
2 3 2 2
x x
x dx dx x x x x C
x x x
Cách 3: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và đồng nhất thức
Phân tích
3 2 2
3 2 3 3 2 7 6
x x x x x x x
Khi đó
2 2
3
2 2
3 2 3 3 2 7 6
3
3 2 3 2
x x x x x x
x
I dx dx
x x x x
2
1
2
7 6
3 3
3 2 2
x x
x dx dx x I
x x
.
Tính
1
I
bằng phương pháp đồng nhất thức….
Cách 4: Chia đa thức để tách thành tổng hai tích phân đơn giản hơn
1
3
2 2 2
3 9 8 9 8
3 3
3 2 3 2 3 2
I
x x x
I dx x dx x dx dx
x x x x x x

Tính
1
I
bằng phương pháp đồng nhất thức….
Bài 3: Tìm nguyên hàm sau:
3 3
2
2
2 1
1
x x
I dx dx
x x
x
Giải:
Cách 1: Phương pháp đổi biến số
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
5
Đặt
1
1
du dx
u x
x u
Khi đó
3
3 2 2
2 2 2
1
3 3 1 3 1 1
3 3 3ln
2
u
u u u u
I du du u du u u C
u u u u u
với
1
u x
Cách 2: Phân tích tử thức chứa nghiệm ở mẫu thức
Phân tích
3 2 2
2 1 2 2 1 3 1 1
x x x x x x x
Khi đó
2 2
3
2 2
2 1 2 2 1 3 1 1
2 1 2 1
x x x x x x
x
I dx dx
x x x x
2
2
3 1 1
2 2 3ln 1
1 2 1
1
x
x dx x x C
x x
x
Cách 3: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và kĩ thuật nhảy tầng lầu
Phân tích
3 2 2
3
2 1 2 2 1 1 2 2
2
x x x x x x x
Khi đó
2 2
3
2 2
3
2 1 2 2 1 1 2 2
2
2 1 2 1
x x x x x x
x
I dx dx
x x x x
2
2
2
1 3 2 2 3
2 2 ln 1 ln 2 1
1 2 2 1 2 2
x x
x dx dx x x x x C
x x x
Cách 4: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và đồng nhất thức
Phân tích
3 2 2
2 1 2 2 1 3 2
x x x x x x x
Khi đó
2 2
3
2 2
2 1 2 2 1 3 2
2 1 2 1
x x x x x x
x
I dx dx
x x x x
2
1
2
3 2
2 2
2 1 2
x x
x dx dx x I
x x
.
Tính I
1
bằng phương pháp đồng nhất thức
Cách 5: Chia đa thức để tách thành tổng các tích phân đơn giản
3 3
2 2 2
2
3 1
2
12 1
1 1
1
2 3ln 1
2 1
x x
I dx dx x dx
xx x
x x
x
x x C
x
Cách 6: Sử dụng phương pháp tích phân từng phần
Đặt
3
2
2
3
1
1
u x
du x dx
dx
dv
v
x
x
Khi đó
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
6
3 2 3 2
3 3 2
1 1
3 3
1 1 1 1
1
3 1 3 ln 1
1 1 1 2
x x x x
I dx dx
x x x x
x x x
x dx x x C
x x x
Bài 4: Tìm nguyên hàm:
2
39
1
x dx
I
x
Giải:
Cách 1: Sử dụng phương pháp đưa vào vi phân
Phân tích
2
2
2
1 1 1 2 1 1
x x x x
2
2
39 39 37 38 39
1 2(1 ) 1
1 2 1
1 1 1 1 1
x x
x
x x x x x
37 38 39 36 37 38
1 1 1 1 1 2 1 1 1
2
36 37 38
1 1 1 1 1 1
I dx dx dx C
x x x x x x
Cách 2:
Đặt
1 1
t x x t dx dt
2
39 39 38 37 38 37 36
1
1 1 1 1 1 2 1 1 1
2
38 37 36
t dt
I dt dt dt C
t t t t t t t
Nhận xét:
Cách 3: Sử dụng phương pháp tích phân từng phần
Đặt
2
39
2
1
38 1
1
du xdx
u x
dx
v
dv
x
x
Khi đó
2
38 38
1 1
19
38 1 1
x
I x dx
x x
…. đến đây các bạn có thể tự làm rồi
Bài 5: Tìm nguyên hàm:
3
10
( 1)
x dx
I
x
Giải:
Cách 1: Sử dụng phương pháp đưa vào vi phân
Sử dụng đồng nhất thức:
3
3 2
3
1 1 1 3 1 3 1 1
x x x x x
3
10 7 8 9 10
1 3 3 1
( 1) ( 1) ( 1) ( 1) ( 1)
x
x x x x x
Khi đó
7 8 9 10
6 7 8 9
3 3
( 1) ( 1) ( 1) ( 1)
1 1 3 1 3 1 1 1
6 7 8 9
( 1) ( 1) ( 1) ( 1)
dx dx dx dx
I
x x x x
C
x x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
7
Cách 2: Sử dụng phương pháp biến đổi số
Đặt
1
t x
ta có:
1
x t
nên
dx dt
3
3 2
7 8 9 10
10 10
1
( 3 3 1)
3 3
t dt
t t t dt
A t dt t dt t dt t dt
t t
6 7 8 9
1 1 3 1 3 1 1 1
6 ( 1) 7 ( 1) 8 ( 1) 9 ( 1)
C
x x x x
Cách 3: Sử dụng phương pháp tích phân từng phần
Đặt
3 2
10 9
3
1
1 9 1
u x du x dx
dx
dv v
x x
Khi đó
1
2
3
9 9
1 1
...
3
9 1 1
I
x
I x dx
x x
đến đây rùi ta có thể tính
1
I
bằng phương pháp tích phân từng phần hoặc phân tích
2 2
1 1 1 1 1
x x x x
Nhận xét :
- Đối với bài 3, bài 4 và mà ta sử dụng phương pháp đồng nhất thức thì giải hệ quả thật là nan giải phải không,
chính vì thể mà lựa chọn phương pháp nào mà hiệu quả và nhanh về đích nhất
Qua bài 3, bài 4 và bài 5 ta chú ý
- Đối với tích phân hàm phân thức có dạng
n
P x
I dx
x a
thì đặt
t x a
là một phương pháp hiệu quả nhất
- Khi tính tích phân hàm phân thức mà ta phân tích được về dạng
'
n n
P x f x Q x
I dx dx
Q x Q x
thì ta sử
dụng phương pháp tích phân từng phần nhưng nên làm khi bậc của
x a
là
1,2
n
Đặt:
'
n
u f x
du
Q x
v
dv dx
Q x
Bài 11: (ĐHDB – B 2004) Tính tích phân sau:
3 3
3
2
0 0
1
dx dx
I
x x
x x
HD:
Cách 1: Biến đổi số
Nhân cả tử và mẫu cho
2
x
3 3 3
3
2 2 2
0 0 0
1 1
dx dx xdx
I
x x
x x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
8
Đặt
2
2
1
1
2
x t
t x
dt
xdx
Cách 3: Biến đổi số
Đặt
tan
x u
… Bạn đọc tự giải
Cách 4: Đưa vào vi phân
Phân tích tử
2 2
1 1 –
x x
Khi đó
2
3 3
2
2
00 0 0
3 3
2
1
13 3
ln ln 1
2
1
1 6
ln
2
0
2
1
0
dx x dx
I dx
d x
x x
x
x x
x
Bài 12: Tính tích phân sau:
2
5 3
1
dx
I
x x
Giải:
Cách 1: Sử dụng phương pháp phân tích
Cách 1.1: Phân tích:
2 2
1 1
x x
2 2 2 2
3 2 3 2 3 2 3 2
3 2
1 1 1 1 1 1 1 1
( 1) ( 1) ( 1) 1
1
x x x x x
x
x x x x x x x x x x
x x
Khi đó
2
2
3 2
2 2
2
1 1 1
2
1 1 1 1 1
ln
3 1 5
ln2 ln
8
ln 1
2
1
2
2
2
1
x
I dx dx dx x x
x
x x x
Cách 1.2: Phân tích:
4 4 4 2 2
1 1 1 1
x x x x x
4 2 2
4 4 2
3
3 2 3 2 2 3 2
3 2
1 1
1 1 1 1
( 1) ( 1) 1 1
1
x x x
x x x x x
x
x
x x x x x x x
x x
... tự làm nhé
Cách 2: Kết hợp kĩ thuật tách thành tích và phương pháp biến đổi số
Phân tích
2 2
2
1
3 2 2
1
1 1 1
.
1 1
I dx dx
x
x x x x
Đặt
2
1
1
1
x
t
t
x
dx dt
t
Đổi cận
1
2
2
1
x
t
x
t
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
9
Khi đó
1
1
3
2
2
2 2
2
1
1
2
1
1 1
1
1
...
t
t
I t dt dx
t
t t
đến đây lại trở thành bài 1, các bạn tha hồ mà làm nhé
Cách 3: Sử dụng kĩ thuật nhân trên tử và phương pháp đổi biển số
2 2
3 2 4 2
1 1
1
1 1
x
I dx dx
x x x x
Đặt
2
1
2
dt
t x xdx
Đổi cận
2 5
1 2
x t
x t
Khi đó
5 5
2 2
2 2
5
1 1 1 1 1 1 3 1 5
ln ln 2 ln
2
2 1 2 1 1 8 2 2
1 1
dt t
I dt
t t t t
t t t
Hoặc các bạn có thể đặt
1
u t
hoặc phân tích
1 1
t t
hoặc đồng nhất thức
Cách 4: Sử dụng kĩ thuật nhân trên tử và phương pháp đưa vào vi phân
2 2 2
2
3 2 4 2 4 2
1 1 1
2 2
2 2 2
2 2 2
4
4 2 2 2
1 1 1
1 1 1
1
2
1 1 1
1
1 1 1 1 1
1 1 1
2 2 2
1 1
x
I dx d x
x x x x x x
x x
d x d x d x
x
x x x x
2 2
3
2
1 1
1 1
...
1
dx dx
x
x x
ôi đến đây lại thành cách 1 rùi, lòng vòng quá, bỏ qua thui…
Cách 5: Sử dụng phương pháp đồng nhất thức
3 2 2
3 2
1
1
1
A B C Dx E
x
x x x
x x
đến đây thì đồng nhất thức hai vế để giải hệ tìm
, , , ,
I A B C D E
tuy nhiên
việc giải hệ là phức tạp chính vì thể trong trường hợp này ta nên làm theo cách 1, cách 2 và cách 3 là hiệu quả
nhất
Cách 6: Đặt
2
tan tan 1
x u dx dt
… bạn đọc tự làm
Bài 14: Tính tích phân sau:
1
3
0
1
dx
I
x
Giải:
Nhận xét:
3 2
1 1 1
x x x x
Cách 1: Dựa vào nhận xét trên ta sử dụng đồng nhất thức:
2 2 2
1 1 1 1
x x x x x
Khi đó
1 1
2
1 2
3 2
0 0
1
1 1
x x
I dx dx I I
x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
10
Tính
1
I
bằng cách đặt
3
1
t x
hoặc
3
1
1
3
0
1
1
3
1
d x
I
x
Tính
2
I
phân tích
1 1
1 2 1
2 2
x x
(kĩ thuật nhảy tầng lầu)
Ta có
1 1 1
2
2 2 2
0 0 0
1 1 2 1 1
2 21 1
1 3
2 4
x x dx
I dx dx
x x x x
x
Cách 2: Đồng nhất thức
Xét
2
3 2
1
1 1 1
1
1 1
A Bx C
A x x Bx C x
x
x x x
Đến đây ta có thể đồng nhất hệ số giải hệ tìm A, B, C hoặc cho một số giá trị riêng là
1 2 1
1 ; 0 ; 1
3 3 3
x A x C x B
…Bạn tự giải tiếp nhé
Kết quả ta được
1
ln2
3
3 3
I
Cách 3: Đổi biến số kết hợp kĩ thuật “nhảy tầng lầu”
1 1 1
3
22
0 0 0
1
1
1 1
1 1 3 1 3
dx dx d x
I
x
x x x
x x x
Đặt
1
x t dx dt
Đổi cận
0 1
1 2
x t
x t
2 2 2 2
2 2
2
2 2
1 1 1 1
dt 1 3 3 3 1 dt 3
dt
3 3
3 3
3 3 3 3
t t t t t
dt
t
t t
t t t t t t
2 2 2
2
2 2
1 1 1
2
2
1 dt 1 3 3 3 dt
3
3 2 2
3 3
3
2
4
2
1 1 2 3 1
ln 3arctan ln 2
13 2 3
3 3
3 3 3
d t t
t
t t
t
t t
t t
Bài 15: Tính tích phân bất định:
4 3
50
3 5 7 8
2
x x x
I dx
x
.
Giải :
Cách 1: Biến đổi số
Đặt
2
2
x t
x t
dx dt
Khi đó
4 3
4 3
50 50
3 2 5 2 7 2 8
3 5 7 8
2
t t t
x x x
I dx dt
t
x
Cách 2: Đồng nhất tử thức chứa nghiệm của mẫu thức
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
11
Phân tích
4 3 2
4 3
3 5 7 8 2 2 2 2
x x x a x b x c x d x e
… đồng nhất để tìm a, b, c, d, e
…
Cách 3: Khai triển Taylor (tham khảo)
Đặt
4 3
4
3 5 7 8
P x x x x
Áp dụng khai triển taylor ta có
3 4
2 3 4
4 4 4 4
4 4
2 2 2 2
2 2 2 2 2
1! 2! 3! 4!
P P P P
P x P x x x x
2 3 4
4
66 149 2 48 2 29 2 3 2
P x x x x x
2 3 4
50
50 49 48 47 46
49 48 47 46 45
66 149 2 48 2 29 2 3 2
2
66 2 149 2 48 2 29 2 3 2
66 149 48 29 3
49 2 48 2 47 2 46 2 45 2
x x x x
I dx
x
x x x x x dx
C
x x x x x
Bài 16: (ĐHTN – 2001) Tính tích phân sau:
1 5
22
4 2
1
1
1
x
I dx
x x
Giải:
Ta có
1 5 1 5 1 5
2
2 2 2
2
2
4 2 2
2
1 1 1
2
1
1
1
1
1
1
1
1
1
1
x
x
x
dx dx dx
x x
x
x
x
x
Đặt
2
1 1
1
t x dt dx
x x
.
Đổi cận
1
0
1 5
1
2
x
t
t
x
Khi đó
1
2
0
1
dt
I
t
. Đặt
2
tan 1 tan
t u dt u du
.
Đổi cận
0
0
1
4
u
t
t
u
Khi đó
1
2
4 4
2 2
0 0 0
1 tan
.
4
4
1 1 tan
0
dt u
I du du u
t u
Cách khác:
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
12
Ta có thể gộp hai lần đặt là
2
2
1 1
tan 1 1 tan
x u dx u du
x x
… bạn đọc tự giải
Bài 17: Tính tích phân:
I
2
2
4
1
1
1
x
dx
x
Giải:
Cách 1: Chia cả tử và mẫu cho
2
0
x
ta được
Biến đổi
2 2
2 2
2
2
1 1
2
1 1
1 1
1
1
2
x x
I dx dx
x
x
x
x
Đặt
2
1 1
1
u x du dx
x x
Khi đó
I
5
2
2
2
1 2
ln
2
2 2 2
du u
u
u
5/2
2
1 (5 2 2)(2 2)
ln
2 2 6 2
Cách 2: Phân tích
2
4 2 2 2 2
1 1 2 2 1 2 1
x x x x x x x
và sử dụng đồng nhất thức
2
4
2 2
1
1
2 1 2 1
x Ax B Cx D
x
x x x x
… đồng nhất hệ số tìm A, B, C và D nhưng cách này dài và rất phức tạp
nên không đưa ra
Nhận xét:
- Qua các ví dụ trên ta thấy kĩ thuật chia thực sự rất hiệu quả trong việc chuyển tích phân ban đầu thành tích
phân đơn giản hơn
- Thông thường để sử dụng kĩ thuật chia thì trên tử là một đa thức bậc hai
2
1
P x x
còn mẫu là một đa thức
bậc 4:
4 3 2
Q x ax bx cx dx e
sao cho hệ số
1
a e
- Tích phân trên đưa về dạng
2
1 1
1
I f x dx
x x
đặt
2
1 1
1
t x dt dx
x x
Tương tự ta có thể giải bài toán này
1. Tính tích phân sau
I
2
2
4
1
1
1
x
dx
x
2 2
2 2
2
2
1 1
2
1 1
1 1
1
1
2
x x
I dx dx
x
x
x
x
. Đặt
2
1 1
1
u x du dx
x x
2. (ĐHQGHN – A 2001) Tính tích phân bất định sau:
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
13
2 2
2
2 2
1 1 5 1
ln
8
3 1
5 1 3 1
x x x
I dx C
x x
x x x x
Bài 18: Tính tích phân sau:
1
4
3 4
0
1
I x x dx
Giải:
Cách 1: Sử dụng phương pháp biến đổi số
Đặt
4 3 3
1 4
4
dt
t x dt x dx x dx
Đổi cận
1 2
0 1
x t
x t
Khi đó
1 2
4
3 4 4 5
0 1
2
1 1 31
1 .
1
4 20 20
I x x dx t dt t
Cách 2: Sử dụng phương pháp biến đổi số
Đặt
4 3
4
dt
t x x dx
Đổi cận
1 1
0 0
x t
x t
Khi đó
1 1
5
4
2 3 4 2 3 4
0 0
1
1 1 1 31
1 1 4 6 4 2 2
0
4 4 4 5 20
t
I t dt t t t t dt t t t t
Cách 3: Sử dụng phương pháp biến đổi vi phân
5
4
1 1
4 4
3 4 4 4
0 0
1
1
1 1 31
1 1 1 .
0
4 4 5 20
x
I x x dx x d x
Cách 4: Sử dụng phương pháp phân tích
Phân tích
4
3 4 3 16 12 8 4 19 15 11 7 3
1 4 6 4 1 4 6 4
x x x x x x x x x x x x
Khi đó
1 1
20 16 12 8 4
4
3 4 19 15 11 7 3
0 0
1
31
1 4 6 4
0
20 4 2 2 4 20
x x x x x
I x x dx x x x x x dx
Nhận xét: Mỗi cách giải có một đặc thù riêng nên lựa chọn cách nào là phù hợp hơn, tùy vào mỗi người, theo
tôi cách 1 và cách 3 là hiệu quả nhất
Bài 19: (ĐH KTQD – 1997) Tính tích phân sau:
1
6
5 3
0
1
1
168
I x x dx
Giải:
Ta có
1 1
6 6
5 3 3 3 2
0 0
1 1
I x x dx x x x dx
Cách 1: Đổi biến số
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
14
Đặt
2
3
3
1
3
1
dt
x dx
t x
x t
Đổi cận
1 0
0 1
x t
x t
0 1 1
7 8
6 6 6 7
1 0 0
1 1 1 1 1
1 1
3 3 3 3 7 8 168
t t
I t t dt t t dt t t dt
Cách 2: Đưa vào biểu thức vi phân
1 1 1 1
6 6 6 7
5 3 2 3 3 2 3 2 3
0 0 0 0
7 8
3 3
1 1
6 7
3 3 3 3
0 0
1 1 1 1 1 1
1 1
1 1
1 1 1 1
1 1 1 1 . .
0 0
3 3 7 3 8 168
I x x dx x x x dx x x dx x x dx
x x
x d x x d x
Cách 3: Khai triển
6
3
1
x
thành tổng các đa thức
6
5 3
1
x x
.. cách này không khó nhưng khai triển phức
tạp… chỉ tham khảo thôi
Chú ý: Nếu ta đặt
3
t x
cũng ra nhưng sẽ dài và phức tạp, bạn đọc có thể tham khảo
Bài 20: Tính tích phân sau
2
2
0
1
I x x dx
Giải:
Cách 1: Sử dụng phương pháp phân tích
Ta có
2
2 3 2
1 2 1 2
x x x x x x x x
Khi đó
2
4 3 2
3 2
0
2
2 34
2
0
4 3 2 3
x x x
I x x x dx
Cách 2: Sử dụng phương pháp đưa vào vi phân
Ta có
2 2 3 2
1 1 1 1 1 1
x x x x x x
Khi đó
4 3
2 2 2 2
3 2 3 2
0 0 0 0
1 1
34
1 1 1 1 1 1
4 3 3
x x
I x dx x dx x d x x d x
Cách 3: Đổi biến số
Đặt
1
1
x t
t x
dx dt
Đổi cận
2 3
0 1
x t
x t
Khi đó
3 3
4 3
2 3 2
1 1
3
34
1
1
4 3 3
t t
I t t dt t t dt
Cách 3: Sử dụng phương pháp tích phân từng phần
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
15
Đặt
2
2
2 1
1
2
du x dx
u x
x
dv xdx v
Khi đó
2 2
2 4 3
2
2 3
0 0
2 2
34
1 1 6 6
0 0
2 4 3 3
x x x
I x x x dx x x dx
Bài 21: Tính tích phân sau:
0
9
2
1
1
I x x dx
Giải:
Cách 1: Biến đổi số
Đặt
1
t x dt dx
Đổi cận
1 0
0 1
x t
x t
Khi đó
0 1 1 1
9 2
2 9 2 9 11 10 9
1 0 0 0
12 11 10
1 1 2 1 2
1
1 2 1 1
2
0
12 11 10 12 11 10 660
I x x dx t t dt t t t dt t t t dt
t t t
Cách 2: Phương pháp phân tích
Phân tích
2
2
1 2 1 1
x x x
Khi đó
0 0 0
9 2 9 11 10 9
2
1 1 1
12 11 10
1 1 2 1 1 1 1 2 1 1
1 1 1
0
1
2
1
12 11 10 660
I x x dx x x x dx x x x dx
x x x
Hoặc phân tích
2
x
theo
1
x
như sau
9 9 9 11 10 9
2 2
1 1 1 1 1 1 2 1 1 1 2 1 1
x x x x x x x x x x
Nhận xét:
- Với bài toán này ta sử dụng phương pháp phân tích tức là khai triển
9
1
x
hay phương pháp tích phân từng
phần như bài 20 thì cũng ra nhưng rất dài và phức tạp vì bậc của
1
x
là lớn
Bài 22: Tính tích phân:
1
2 10
0
(1 3 )(1 2 3 )
I x x x dx
Giải:
Cách 1: Đổi biến số
Đặt
2
1 2 3 (2 6 ) 2(1 3 ) (1 3 )
2
dt
t x x dt x dx dt x dx x dx
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
16
Đổi cận:
0 1
1 6
x t
x t
.
10 11 11 11 11
6 6
10
1 1
6
6 1 6
1
1
2 2 22 22 22 22
dt t t
I t dt
Cách 2: Đưa vào vi phân
1
1
10 10 '
2 2 2
0
0
11
2
1
11
10
2 2
0
1
1 3 1 2 3 1 2 3 1 2 3
2
1 2 3
1
1 6
1 2 3 1 2 3 1
0
2 22 22
I x x x dx x x x x dx
x x
x x d x x
Bài tập tự giải có hướng dẫn:
Bài 1: (ĐHV – D 2000) Tính tích phân sau:
2
3
2
0
3
2 1
x
I dx
x x
Đs:
9ln3 8
I
Bài 2: Tính tích phân sau:
2
2
2 2
1
1
3 1 1
x
I dx
x x x x
HD:
Chia cả tử và mẫu cho
2
x
ta được
2
2
1
1
1
1 1
3 1
x
I dx
x x
x x
Cách 1: Biến đổi số đặt
2
1 1
1
t x dt dx
x x
Cách 2: Biến đổi vi phân
2 2
2
1 1
1
1
1
2
1 1 1
ln 1 ln 3
1 1 1 1
1
2
3 1 3 1
1 7
ln
2 10
d x
x
x
I dx dx x x
x x
x x x x
x x x x
Cách 3: Đồng nhất thức
Bài 3: Tính tích phân sau:
1
5
2
0
.
1
x
I dx
x
HD:
Đồng nhất thức:
5 3 2 2
( 1) ( 1)
x x x x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
17
1
1
3 4 2 2
2
0
0
1 1 1 1 1
ln( 1)] ln2 .
4 2 2 2 4
1
x
I x x dx x x x
x
Hoặc chia tử cho mẫu để tách thành tổng các tính phân đơn giản Hoặc đặt
tan
x t
Bài 4: (ĐHKT – 1994) Tính tích phân sau:
1
3
0
1 2
x
I dx
x
HD:
Phân tích
3 2 3
1 1 1 1
1 2 1
2 2
1 2 1 2 1 2
x
x x
x x x
ta được
1
18
I
Hoặc đặt
1 2
t x
Hoặc tích phân từng phần
Bài 10: Tính tích phân:
1
2
4 2
1
2
3 21 13
ln2 ln3
4 4
3 2
x
I dx
x x x
HD:
Cách 1: Nhân cả tử và mẫu cho x rồi đặt
2
t x
Cách 2: Phân tích mẫu
4 2 2 2
3 2 1 2
x x x x x x
và sử dụng đồng nhất thức
Bài 5: Tính tích phân:
1
2 2
0
2 5 1 5
ln
2 4
3 2 7 12
x
I dx
x x x x
HD:
Phân tích
2 2 2 2
3 2 7 12 1 2 3 4 5 4 5 6
x x x x x x x x x x x x
Cách 1: Sử dụng đồng nhất thức khi mẫu số là 4 nghiệm đơn
Cách 2: Sử dụng đổi biến số đặt
2
5
t x x
Cách 3: Sử dụng phương pháp phân tích
2 2
1
2 5 2 5 5 6 5 4
2
x x x x x x
Bài 6: Tính tích phân:
1
2
4 3 2
1
2
2 3
44
2 5 4 4
x
I dx
x x x x
HD:
Phân tích
2
4 3 2 2
2 5 4 4 2
x x x x x x
Cách 1: Đồng nhất thức
Cách 2: Chia cả tử và mẫu cho
2
x
và đặt
2
t x
x
Hoặc đưa vào vi phân
Bài 7: Tính tích phân sau:
0
2
3
2
1
1
x dx
I
x
HD:
Cách 1: Đặt
tan
x t
Cách 2: Sử dụng phương pháp tích phân từng phần
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
18
Đặt
3
2
1
u x
xdx
dv
x
Cách 3: Sử dụng phương pháp phân tích thành hai tích phân đơn gián
Phân tích
2 2
1 1
x x
Khi đó
0 0 0
2
3 2 3
2 2 2
1 1 1
1 1 1
x dx dx dx
I
x x x
II. TÍCH PHÂN HÀM VÔ TỶ
Bài tập giải mẫu:
Bài 1: (ĐHGTVT – 1998) Tính tích phân:
7
3
3
0
1
3 1
x
I dx
x
Giải:
Cách 1: Biến đối số
Đặt
3
3
2
1
3 1
3
u
x
u x
dx u du
Đổi cận
7
2
3
1
0
u
x
u
x
Khi đó
3
2 2
5
2 3 4 2
1 1
1
1
2
1 1 1 46
3
2 2
1
3 3 3 5 15
u
u
I u du u udu u u du u
u
Cách 2: Biến đối số
Đặt
1
3
3 1
3
u
x
u x
du
dx
Đổi cận
7
8
3
1
0
u
x
u
x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
19
Khi đó
5
2 1 2
8 8 8
3
3 3 3
1 1
1 1 1
3 3
1
1
8
1 1 2 1 1 3 46
3
2 3
1
3 9 9 9 5 15
u
u u
I du du u u du u
u u
Cách 3: Đưa vào vi phân
Phân tích
1 2
1 3 1
3 3
x x
Khi đó
7 7 7 7 7
3 3 3 3 3
2 1
3 3
3 3 3
0 0 0 0 0
5 2
3 3
1 2
3 1
1 3 1 2 1 2
3 3
3 1 3 1 3 1 3 1
3 3 9 9
3 1 3 1 3 1
7 7
1 1 46
3 1 3 1
3 3
15 3 15
0 0
x
x dx
I dx dx x d x x d x
x x x
x x
Cách 4: Tính phân từng phần
Đặt
2
3
3
1
1
1
3 1
3 1 2
u x
du dx
dv dx
v x
x
Khi đó
7 7
2
3 3
2 2 1
3
3 3 3
3
0 0
7
3 1
1 1 1 1
1 3 1 1 3 1 3 1 3 1 ...
3
2 2 2 6
3 1
0
x
I x x dx x x x d x
x
bạn đọc tự giải
Bài 2: Tính tích phân:
1
3
2
1
0
1
x
I dx
x
HD:
C1: Đặt
tan
x t
C2: Phân tích
3 2
1
x x x x
C3: Đặt
2
2
1
u x
x
dv dx
x
C4: Đặt
x t
C5: Phân tích
3 2 2 2
1 1 1
x dx x xdx x d x
Bài 3: (ĐHBKHN – 1995) Tính tích phân sau:
2
2
2
1
dx
I
x x
Giải:
Cách 1: Phương pháp biến đổi số
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
20
Đặt
2
1 sin
cos
cos
tdt
x dx
t
t
với
0;
2
t
hoặc
t
x
sin
1
Đổi cận
2
3
2
4
t
x
x
t
Khi đó
3 3 3
2
2
4 4 4
2
sin
sin
3
cos
sin 12
1 cos
4
cos
t
t
t
I dt dt dt t
t
t
t
(vì
; sin 0
4 3
t t
)
Cách 2: Phương pháp biến đổi số
Nhân cả tử và mẫu cho x ta được
2 2
2 2 2
2 2
1 1
dx xdx
I
x x x x
Đặt
2 2
2
1
1
x t
x t
xdx tdt
Đổi cận
2
3
2 1
x
t
x t
Khi đó
3 3
2
2
1 1
1
1
tdt dt
I
t
t t
. Đặt
2
2
1
tan tan 1
cos
t u dt du u du
u
Đổi cận
3
3
1
4
u
t
t
u
Khi đó
2
4 4
2
3 3
tan 1
4
12
tan 1
3
u
I du du u
u
Cách 3: Phương pháp biến đổi số
Đặt
2
2
1
1
1
2
x t
x t
xdx dt
… tương tự như cách 2
Cách 4: Phương pháp biến đổi số
Đặt
2
1 1 dx
x t dt
t x
x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
21
Đổi cận
1
2
2
1
2
2
t
x
x
t
Khi đó
1
1
2
2
2 2
1 1
2
2
1 1
dt dt
I
t t
. Đặt
sin cos
t x dt xdx
Khi đó
4 4
2
6 6
cos
4
4 6 12
1 sin
6
u
I dx du u
u
Cách 5: Phân tích
2 2
1 1
x x
Khi đó
1 2
2 2 2
2
2 2
2 2 2
1
1 1
I I
dx x x
I dx dx
x
x x x

… bạn đọc tự giải
Bài 3: (ĐH – A 2003) Tính tích phân:
2 3
2
5
4
dx
I
x x
Giải:
Cách 1: Phương pháp biến đổi số
Đặt
2 2
2
4
4
x t
t x
xdx tdt
Đổi cận
2 3 4
3
5
x t
t
x
Khi đó
4 4 4
2
3 3 3
4
1 1 2 1 5
ln ln
3
4 2 2 4 2 4 3
4
dt dt dt t
I
t t t
t
Cách 2: Phương pháp biến đổi số
Đặt
2
1 1
x dx dt
t
t
Khi đó
1/2 3 1/2 3
2
2 2
1/ 5 1/ 5
1/ 2 3
1 (2 ) 1 1 5
ln 2 4 1 ln
2 2 4 3
1/ 5
4 1 (2 ) 1
dt d t
I t t
t t
.
Cách 3: Phương pháp biến đổi số
Đặt
2
2tan 2 1 tan
x t dx t dt
với 0 t
2
và
2
2
4x
cost
.
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
22
Đổi cận:
2 3
3
5
5
tan
2
t
x
x
.
Khi đó:
3
1 1 5
ln tan ln
3
2 sin 2 4 3
dt t
I
t
(trong đó
1 cos 1
tan
2 1 cos 5
)
Bài 4: (ĐHDB – A 2003) Tính tích phân sau:
1
3 2
0
1
I x x dx
Giải:
Phân tích
1 1
3 2 2 2
0 0
1 1 .
I x x dx x x xdx
Cách 1: Phương pháp biến đổi số
Đặt
2 2
2
1
1
x t
t x
xdx tdt
Đổi cận
1 0
0 1
x t
x t
Khi đó
1
0 1 1
2 2 2 2 2 4 3 5
1 0 0
0
1 1 2
1 1
3 5 15
I t t dt t t dt t t dt t t
Cách 2: Phương pháp biến đổi số
Đặt
2
2
1
1
2
x t
t x
dt
xdx
Đổi cận
1 0
0 1
x t
x t
Khi đó
1
1 1 1 3 3 30 1 1
2 2 2 2 2 2
1 0 0
0
1 1 1 1 2 2 2
1 1
2 2 2 2 3 3 15
I t t dt t t dt t t dt t t
Cách 3: Đặt
2
2
dt
t x xdx
… tự giải
Cách 4: Lượng giác hóa
Đặt
cos sin
x t dx tdt
Khi đó
2 2
2 3 2 2
0 0
sin cos sin 1 sin cos
I t tdt t t tdt
Cách 4.1.
Đặt
sin cos
t u tdt du
Khi đó
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
23
1
3 5
2 2 2 4
0
(1 )
3 5
u u
I u u du u u du
Cách 4.2.
3 5
2 2
2 2 2 4
0 0
sin sin 2
sin 1 sin sin sin sin sin
2
3 5 15
0
t t
I t t d t t t d t
.
Cách 4.3.
2 2 2 2
2
0 0 0 0
1 1 1 cos4 1 1
sin 2 cos cos cos cos4 cos
4 4 2 8 8
t
I t tdt tdt tdt t tdt
….
Cách 5: Phương pháp đưa vào biểu thức vi phân
1 1
2 2 2 2 2 2
0 0
1 1
3
2 2 2 2
2
0 0
1 1
1 1 1 1 1 1
2 2
1 1
1 1 1 1
2 2
I x x d x x x d x
x d x x d x
….bạn đọc tự giải
Cách 6: Phương pháp tích phân từng phần
Đặt
2
2
2
2
3
2
1
1
1
3
du xdx
u x
v x
dv x x
Khi đó
1 1
2 2 2
2 2 2 2 2
3 3 3
0 0
1
1 2 1
. 1 1 1 1 ...
03 3 3
I x x x x dx x d x
bạn đọc giải tiếp
Bài 5: (ĐH – A 2004) Tính tích phân:
2
1
1 1
x
I dx
x
Giải:
Cách 1:
Đặt
2 2
1 1 1 2
t x t x x t dx tdt
Đổi cận
2 1
1 0
x t
x t
Khi đó
1 1 1
2 3
2
0 0 0
1
3 2
0
1 2
2 2 2 2
1 1 1
1 1 11
2 2 2ln 1 2 2 2ln 2 4ln 2
3 2 3 2 3
t t t
I tdt dt t t dt
t t t
t t
t t
Cách 2:
2
2 1
1 1
1 1
dx t dt
t x
x t
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
24
Đổi cận
2 2
1 1
x t
x t
Khi đó
2
2 2 2
3 2
2
1 1 1
1 1 1
3 4 1 1
2 . 2 . 2 3 4 .
t t
t t t
I dt dt t t dt
t t t
3 2
2
5
2 3 4 ln | | 2ln 2
13 2 3
t t
t t
Tổng quát:
( )
b
a
p x
dx
ax b c
với
p x
là một đa thức chứa x, m, n, c là các hằng số ta đặt
t ax b c
hoặc
t ax b
Bài 6: Tính tích phân sau:
3
2
8 3
2 4
x
I dx
x
Giải:
Cách 1: Dựa vào đạo hàm
Đặt
8 3
2 4
x
f x
x
. Ta biến đổi
f x
về dạng
'
'
8 3 1
4 4 4
2 4 2 4
x
f x x x x x x
x x
Xét hàm số
4
F x x x
vì
'
'
'
4 4
F x x x x x f x
Vậy
4
F x x x C
là một họ nguyên hàm của hàm số đã cho
Khi đó
3
2
3 3
8 3
4 3
2 2
2 4
x
I dx F x x x
x
Cách 2: Sử dụng phương pháp đổi biến số
Đặt
2
4
4
2
x t
t x
dx tdt
Đổi cận
1
3
2
2
t
x
x
t
Khi đó
2
1 2
2 3
1
2
8 3 4
2
3 4 4 3
1
t
I tdt t dt t t
t
Cách 3: Sử dụng phương pháp đổi biến số
Đặt
4
t x
…bạn đọc tự giải
Cách 4: Sử dụng phương pháp tích phân từng phần
Đặt
8 3
3
2 4
4
u x
du dx
dx
dv
v x
x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
25
Khi đó
3
2
3
2 8 3 4 6 4 ....3
2
I x x xdx
Bài 7: Tính tích phân sau:
I
x dx
x x x x
x dx
x x
2
2 2
2
2 2
4 2 2 2 3 1 3 1( ) [ ( ) ] ( )
.
Giải:
Cách 1:
Đặt
2 2
3sin
1 3 cos
3cos 2 3 cos 1
dx tdt
x t
x t t
Khi đó I =
3 3 2 3 1
3 3 3
1
2 3
3 3
2
3 3
2
2
2 2
sin ( cos cos )
( cos ) sin
(
cos
cos cos
)
t t t dt
t t
t
t t
dt
.
Cách 2:
I =
dx
x x
x dx
x x2 2
2 4
3 1 3 1
2 2 2
( )
[ ( ) ] ( )
1 2
I I
Tính
2
I
( )
[ ( ) ] ( ) ( ) ( )
2 4
3 1 3 1
2
3 3
2
3 3
2 2 2 2 2 2
x dx
x x
tdt
t t
dt
t t
1 2
J J
Tính
1
bằng cách đặt
2
3
t u
, tính
2
J
bằng cách đặt
2
3 3
t u t
Bài tập tự giải có hướng dẫn:
Bài 1: (ĐHĐN- 1997) Tính tích phân:
7
2
1
2 4ln2 2ln3
2 1
I dx
x
HD: Sử dụng phương pháp biến đổi số
Đặt
2 1
t x
Hoặc 2
t x
Bài 2: (ĐHSP QN – 1999) Tính tích phân:
2
3
3
0
1 1
28 3 4
10
3 2
x
I
x
Bài 13: (DBĐH 2 – A 2005) Tính tích phân:
7
3
0
2 231
10
1
x
I
x
Bài 14: (DBĐH 1 – A 2008) Tính tích phân:
3
3
1
2
12
5
2 2
x
I dx
x
Bài 15: (DBĐH 1 – A 2007) Tính tích phân:
4
0
2 1
2 ln 2
1 2 1
x
I dx
x
Bài 16: (CĐXD – 2005) Tính tích phân:
3
1
3
3 1 3
x
I dx
x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
26
III. TÍCH PHÂN HÀM SỐ MŨ VÀ LOGARIT
Bài tập giải mẫu:
Bài 1: (PVBCTT – 1999) Tính tích phân sau:
3 2
1
ln . 2 ln
e
x x
I dx
x
Giải:
Cách 1: Phương pháp biến đổi số
Đặt
ln
x u
Cách 2: Phương pháp biến đổi số
Đặt
3 2 3 2 2
3 ln
2 ln 2 ln
2
x
x t t x t dt dx
x
Đổi cận
3
3
3
1
2
x e t
x
t
Khi đó
3 3
3 3
3 3 3
3
4
2 3
3
2 2
3
3
3 3 2
3
3 3 3
. .
2 2 2 4
2
8
2
t
I t t dt t dt
Cách 3: Phương pháp biến đổi số
Đặt
2
ln
2 ln
2
dt x
x t dx
x
Đổi cận
3
1 2
x e t
x t
Khi đó
1 4
3
3
3
3
3
2
2
1 3
.
1
1 3
3 3 2 2
2 2 4 8
t dtI t
Cách 4: Phương pháp đưa vào biểu thức vi phân
1 1
'
2 2 2 2
3 3
1 1
4
2
3
3
3
1 1
2 ln 2 ln 2 ln 2 ln
2 2
1 3 3
. 2 ln 3 3 2 2
1
2 4 8
e e
I x x dx x d x
e
x
Bài 2: (ĐH – B 2004 ) Tính tích phân sau:
1
1 3ln .ln
e
x x
I dx
x
Giải:
Cách 1: Phương pháp biến đổi số
Đặt
2
1
ln
3
1 3ln
2
3
t
x
t x
dx
tdt
x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
27
Đổi cận
2
1 1
x e t
x t
Khi đó
2 2
2 5 3
2 4 2
1 1
2
2 1 2 2 116
( )
1
3 3 9 9 5 3 135
t t t
I t dt t t dt
Cách 2: Phương pháp biến đổi số
Đặt
1
ln
3
1 3ln
3
t
x
t x
dx dt
x
Đổi cận
4
1 1
x e t
x t
... tương tự cách 1
Cách 3: Phương pháp đưa vào biểu thức vi phân
1 1 1
3 1
2 2
1 1
5 3
2 2
1 3ln .ln 1 1
1 3ln .ln 1 3ln 1 3ln 1 3ln 1 1 3ln
3 9
1 1
1 3ln 1 3ln 1 3ln 1 3ln
9 9
1 2 2 116
1 3ln 1 3ln
1
9 5 3 135
e e e
e e
x x
I dx x xd x x x d x
x
x d x x d x
e
x x
Cách 4: ln
dx
t x dt
x
Khi đó
1
0
1 3 . ...
I t tdt
đến đây rùi ta có thể làm bằng nhiều cách như biến đổi số đặt
1 3
u t
hoặc
1 3
u t
hoặc đưa vào vi phân bằng cách phân tích
1 1
1 3
3 3
t t
Bài 3: Tính tích phân sau:
1
1 ln
e
x
I dx
x
Giải:
Cách 1: Phương pháp biến đổi số
Đặt
2
1 ln 1 ln 2
dx
t x t x tdt
x
Đổi cận
1
1
2
t
x
x e
t
Khi đó
2 2
3
2
1 1 1
2 2 2 1
1 ln 2
.2 2 2 .
3 3
1
e
x t
I dx t tdt t dt
x
Cách 2: Phương pháp đưa vào biểu thức vi phân
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
28
Biến đổi
3
1 1
2 2 2 1
1 ln 2
1 ln 1 ln 1 ln .
1
3 3
e e
e
x
I dx xd x x
x
Cách 3: Phương pháp biến đổi số
Đặt
1 ln
t x
hoặc
ln
t x
Bài 4: (ĐH – B 2010) Tính tích phân sau:
2
1
ln
2 ln
e
x
I dx
x x
Giải:
Cách 1: Phương pháp biến đổi số
Đặt ln
dx
t x dt
x
Đổi cận
1
1 0
x e t
x t
Khi đó
1 1 1 1
2 2 2
0 0 0 0
2 2 1
1 2 2 3 1
2 ln 2 ln
0
2 2 2 2 3
2 2 2
d u d u
udu
I du u
u u u
u u u
Cách 2: Phương pháp biến đổi số
Đặt
ln 2
2 ln
x t
t x
dx
dt
x
Khi đó
3 3
2 2
2 2
2
3
1 2 2
ln
2
3 1
ln
2 3
t
I dt dt t
t tt t
Cách 3: Phương pháp đưa vào biểu thức vi phân
2 2 2 2
1 1 1 1 1
ln 2 ln 2 ln 2 2 ln 2 ln
ln
2 ln 2
2 ln
2 ln 2 ln 2 ln 2 ln
2 3 1
ln 2 ln ln
12 ln 2 3
e e e e e
xd x x d x d x
x
I dx d x
x
x x x x x
e
x
x
Cách 4: Phương pháp tích phân từng phần
Đặt
2
1
ln
1
1
2 ln
2 ln
u x
du
x
dv dx
x
x x
x
Khi đó
3
1 1
2 ln
1 1 1 1 1 3
ln . ln 2 ln ln
1 1
2 ln 2 ln 3 2 ln 3 3 2
e
d x
e e
I x dx x
x x x x
Bài 4: Tính tích phân sau:
1
1
1 ln
e
I dx
x x
Giải:
Cách 1: Phương pháp biến đổi số
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
29
Đặt 1 ln
dx
t x dt
x
Đổi cận
1 1
2
x t
x e t
Khi đó
2
1 1
2
1
ln ln 2.
11 ln
e
dt
I dx t
x x t
Cách 2: Phương pháp đưa vào biểu thức vi phân
Biến đổi
1 1
1 ln
1
ln 1 ln ln2
11 ln 1 ln
e e
d x
e
I dx x
x x x
Cách 3: Phương pháp biến đổi số
Đặt:
ln
t x
Bài 5: Tính tích phân sau:
1
sin ln
e
x
I dx
x
Giải:
Cách 1:
Đặt ln
dx
t x dt
Đổi cận
1 0
1
x t
x e t
Khi đó
1
0
1
sin cos cos1 cos0 1 cos1
0
I tdt t
Cách 2: Phương pháp đưa vào biểu thức vi phân
Biến đổi
1 1
sin ln
sin ln ln cos ln 1 cos1
1
e e
x
e
I dx x d x x
x
Bài 6: Tính tích phân sau:
2
5
ln
e
e
dx
I
x x
Giải:
Cách 1: Phương pháp biến đổi số
Đặt ln
dx
t x dt
x
Đổi cận
2
1
2
x e
t
t
x e
Khi đó
2
2
5 5 4
1
2
1 15
.
1
64
ln 4
e
e
dx dt
I
x x t t
Cách 2: Phương pháp đưa vào biểu thức vi phân
Biến đổi
2 2
2
5
5 4
1 15
ln ln
64
ln 4ln
e e
e e
e
dx
I xd x
x x x
e
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
30
Bài 7: Tính tích phân sau:
2
2
1
ln ln 2 1
2 2
x
I dx
x
Giải:
Cách 1: Đổi biến và sử dụng tích phân từng phần
Đặt ln
t
dx
t x e x dt
x
Đổi cận
2 ln2
1 0
x t
x t
Khi đó
ln 2 ln 2
0 0
t
t
t
I dt e tdt
e
Đặt
t t
u t du dt
dv e dt v e
Khi đó
ln 2
0
ln2 ln 2
ln2 ln2 1
0 0
2 2 2
t t t
I te e dt e
Cách 2: Tích phân từng phần
Đặt:
2
2
1
1
ln
ln
2
du
u
x
x
x
x
dv dx
v
x
Khi đó
2 2
2
1 ln 1 ln
.
2
x x
I dx
x x x
Cách 3: Tích phân từng phần
Đặt
2
ln
1
dx
u x
du
x
dx
dv
v
x
x
Khi đó
2 2
2
1 1
2
1 1 1 ln 2 1
ln . ln 2
1
2 2 2
dx
I x x dx
x x x
Bài 8: Tính tích phân sau
1
0
x
x x
e
I dx
e e
Giải:
Cách 1: Sử dụng tích phân liên kết
Liên kết của I là
1
0
x
x x
e
J dx
e e
Ta có
1 1 1
0 0 0
1
x x
x x x x
e e
I J dx dx dx
e e e e
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
31
1 1
2
1
0 0
1
1
ln ln ln 2 ln
0
2
x x
x x
x x
x x x x
d e e
e e e
I J dx e e e e
e
e e e e
Cộng lại ta được
2 2 2
1 1 1 1 1
2 1 ln 1 ln ln
2 2 2 2 2
e e e
I I
e e
Cách 2: Sử dụng phương pháp biến đổi số
Đặt
x x
t e dt e
Đổi cận
1
0 1
x t e
x t
Khi đó
2
2
2
2 2
1 1 1
1
1 1 1 1
ln 1 ln
1
1
2 2 2 2
1 1
e e e
d t
e
dt t e
I dt t
t t
t
t
Cách 3: Phương pháp biến đổi số
2
1 1
.
1
1
e e
x x x
x
x
x
e e e
I dx dx
e
e
e
Đặt
2
2
tan tan 1
cos
x x
dt
e t e dx dt
t
Khi đó
2
2
1
4
tan 1
tan 1 tan ln cos ln2 ln cos
2
tan 1
4
e
x
I dt xdx x
(với
arctan
e
)
Bài 9: (ĐH DB – B 2003) Tính tích phân sau:
ln 5
2
ln 2
1
x
x
e
I dx
e
Giải:
Cách 1: Tách thành tích để sử dụng phương pháp biến đổi số
Đặt
2
1
1
2
x
x
x
e t
e t
e dx tdt
Đổi cận
ln5 2
ln2 1
x t
x t
Khi đó
2
2 2
2 3
1 1
1
2 2
2 20
2 2 1 2
1 1
3 3
t tdt
I t dt t t
t
Cách 2: Tách thành tích để sử dụng phương pháp biến đổi số
Đặt
1
1
x
x
x
e t
e t
e dx tdt
Đổi cận
ln5 4
ln2 1
x t
x t
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
32
Khi đó
1 3 1 5 3
4 4 4
2 2 2 2 2
1
1 1 1
2
1
4 4
2 2 20
1
1 1
5 3 3
t tdt
I t t dt t t dt t t
t
Cách 3: Sử dụng phương pháp tích phân từng phần
Phân tích
ln 5 ln5
2
ln 2 ln 2
.
1 1
x
x x
x x
e e e
I dx dx
e e
Đặt
2 1
1
x
x
x
x
x
u e
du e dx
e
dv dx
v e
e
Khi đó
ln5
ln5 ln 5
ln 2
ln 2 ln 2
ln5
4 20
.2 1 2 1. 16 2 1 1 16 1 1
ln2
3 3
x x x x x x x x
I e e e e dx e d e e e
Hoặc có thế tính nhanh như sau
ln5 ln 5
ln 5
ln 2
ln 2 ln2
2 1 2 1 2 1
x x x x x x
I e d e e e e e dx
ln5
ln5
ln 2
ln 2
4 20
=16 2 1 1 16 1 1
3 3
x x x x
e d e e e
Cách 4: Đưa vào biểu thức vi phân
ln5 ln 5 ln 5 ln 5
2
ln 2 ln 2 ln 2 ln 2
1 1
1
1 1 1
1 1 1 1
x
x x
x x x
x x x x
e
e e
I dx d e dx e d e
e e e e
ln5
3 1
2 2
ln 2
2 20
1 2 1
3 3
x x
e e
Bài 10: (ĐH – D 2009) Tính tích phân sau:
3
1
1
x
dx
I
e
Giải:
Cách 1: Sử dụng phương pháp đồng nhất thức
1 1
x x
e e
Khi đó
3 3 3 3
1 1 1 1
3
2
1
3 3
1
1 ln 1
1 1
1 1 1
1
2 ln 2 ln 1
1
x
x
x
x x x
d e
e
I dx dx dx x e
e e e
e
e e
e
Cách 2: Sử dụng phương pháp biến đổi số
Đặt
1 1
1
x x
dt
t e dt e dx t dx dx
t
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
33
Đổi cận
3
3
1
1
1
x
t e
x
t e
Khi đó
3
1
1
1
e
e
dt
I
t t
…Bạn đọc tự giải tiếp
Chú ý: Có thể đặt
x
t e
Cách 3: Dựa vào đạo hàm
Đặt
1
1
x
f x
e
ta có
'
' '
' '
1 1
1
1 ln 1 ln 1
1 1 1 1
x x x
x
x x
x x x x
e e e
e
x x e x e
e e e e
ln 1
x
F x x e
Khi đó
3
2
1
3 3
ln 1 2 ln 1
1 1
1
x
x
dx
I F x x e e e
e
Bài 11: (ĐH – A 2010) Tính tích phân sau:
1
2 2
0
2 .
1 2.
x x
x
x e x e
I dx
e
Giải:
2
2 2
2
1 2
2 .
1 2. 1 2. 1 2.
x x
x x x
x x x
x e e
x e x e e
x
e e e
Khi đó
1
1 1 1 1
2 2
2 2
0 0 0 0
2 .
1 2 1 2 1 2
x x x x
x x x
I
x e x e e e
I dx x dx x dx dx
e e e
Tính
1
I
bằng các cách như sau đặt
1 2
x
t e
hoặc
x
t e
hoặc
1
1
0
1 2
1
1 1 1 1 2
ln 1 2 ln
02 2 2 3
1 2
x
x
x
d e
e
I e
e
Vậy
1 1 1 2
ln
3 2 3
e
I
Bài 12: (ĐHK D-2004) Tính tích phân sau:
3
2
2
ln
I x x dx
Giải:
Đặt:
xv
dx
xx
x
du
dxdv
xxu
2
2
12
)ln(
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
34
I = xln(x
2
-x)
3
2
3
2
3
2
))1ln(2(2ln26ln3
1
12
xxdx
x
x
= ln216 – ln4 – 2 – ln2 = ln27 – 2.
Hoặc
3 3 3 3
2
1 2
2 2 2 2
ln ln 1 ln ln 1
I x x dx x x dx xdx x dx I I
Áp dụng TPTP là xong
Bài 10: (ĐHDB – 2002) Tính tích phân sau:
ln 3
3
0
1
x
x
e dx
I
e
Giải:
Cách 1: Phương pháp đưa vào biểu thức vi phân
Ta có
ln3
ln 3 ln 3
3 1
2 2
3
0 0
0
1
1 1 2 1 2 1
1
x
x x x
x
d e
I e d e e
e
Cách 2: Phương pháp biến đổi số
Đặt
2
2
1 1 2
x x x
x
tdt
t e t e tdt e dx dx
e
2
3
2
2
1
2 2. 2 1
2
tdt
I
t
t
Hoặc đặt
1
x
t e
Bài tập tự giải có hướng dẫn:
Bài 1: (ĐHDB – D 2005) Tính tích phân sau
2
1
ln 76
15
ln 1
e
x
I dx
x x
HD:
Đặt
ln 1
t x
hoặc
ln
t x
hoặc biến đổi vi phân
2 2
1 1
ln ln
ln
ln 1 ln 1
e e
x x
I dx d x
x x x
hoặc tích phân từng phần
Bài 2: (ĐHBK – 2000) Tính tích phân sau:
ln 2
2
0
1
x
x
e
I dx
e
Đs:
2 2
3
I
Bài 3: (ĐHHH – 98) Tính tích phân: I =
dx
xx
x
e
1
ln1.
ln
HD: Đặt t =
xln1
Đs:
4 2 2
3
I
.
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
35
Bài 4:
2
3
1 2
2
0
1
x
x
I e dx e e
x
HD:
Đặt
2
2
1
2
1
dt x
t x dx
x
Tổng quát:
f x
I e g x dx
mà
'
;
f x kg x k R
đặt
t f x
IV. TÍCH PHÂN HÀM LƯỢNG GIÁC
Bài tập giải mẫu:
Bài 1: Tính tích phân sau:
4
2
0
cos .cos2
I x xdx
Giải:
Cách 1: Tích phân từng phần
Đặt
2
2cos sin sin 2
cos
1
sin 2
cos2
2
du x xdx xdx
u x
v x
dv xdx
Khi đó
4 4 4 4
2 2
0 0 0 0
1 cos4
1 1 1 1 1
cos .sin 2 sin 2 cos4
4
2 2 2 2 4 4
0
1 1 1
sin 4 4
4
4 16 16
0
x
I x x xdx dx dx xdx
x x
Cách 2: Sử dụng tích phân liên kết
Liên kết với I là
4
2
0
sin .cos2
J x xdx
Ta có
4 4
2 2
0 0
sin 2 1
cos sin .cos2 cos2 1
4
2 2
0
x
I J x x xdx xdx
4 4 4
2 2 2
0 0 0
1 cos4 sin 4
cos sin .cos2 cos 2 2
4
2 2 8 8
0
x x x
I J x x xdx xdx dx
Cộng (1) và (2) theo từng vế ta được
1
4
16
I
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
36
Cách 3: Sử dụng phương pháp phân tích
4 4 4 4
2
0 0 0 0
1 cos2 1 1 1
.cos2 cos2 cos 2 cos2 1 cos4
2 2 2 4
1 1 1 1
sin 2 sin 4 4
4
4 4 16 16
0
x
I xdx x x dx xdx x dx
x x x
Bài 2: (ĐHTM – 2000) Tính tích phân sau:
2
3
0
4sin
sin cos
x
I dx
x x
Giải:
Cách 1: Sử dụng đồng nhất thức
3 3 2 3
2 sin cos cos sin
2 cos sin
4sin 2
sin cos sin cos sin cos sin cos
x x x x
x x
x
x x x x x x x x
1
2 2 2
3 2 3
0 0 0
2 cos sin
4sin 2
sin cos sin cos sin cos
I
x x
x
I dx dx dx
x x x x x x

Tính
1
I
bằng cách biến đổi
2
2
sin cos 2cos
4
x x x
hoặc bằng cách đặt
tan
t x
Cách 2: Sử dụng tích phân liên kết
Xét
2
3
0
4cos
sin cos
x
J dx
x x
.
Khi đó
4
I J
và
0
J I
nên
I 2
Cách 3: Đổi biến số theo cận
Phân tích
2
3
0
1 4sin
2 2
cos
4
x
I dx
x
Đặt
4
x t dx dt
Đổi cận
4
2
0
4
t
x
x
t
Khi đó
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
37
4 4 4 4
3 3 3 2 2
4 4 4 4
4sin
cos
1 sin cos 1
4
4
tan 2
cos cos cos cos 2cos
2 2
4
x
d t
t t dt
I dt dt t
t t t t t
Cách 4: Đổi biến số theo cận
Đặt
2
x t dx dt
Đổi cận
0
2
0
2
x
t
x
t
Khi đó
0
2 2
3 3 3
0 0
2
4sin
4cos 4cos
2
cos sin cos sin
sin cos
2 2
t
t x
I dt dt dx
t t x x
t t
2 2 2 2
3 3 2
2
0 0 0 0
4sin 4cos 4 4
2
sin cos sin cos sin cos
2cos
4
x x
I I I dx dx dx dx
x x x x x x
x
2tan 4 2
2
4
0
x I
Cách 5:
Ta có
3 3 3
3 2
sin sin 1
sin cos sin 1 cot sin 1 cot
x x
x x x x x x
Khi đó
2 2
3 3
2
0 0
4sin 1
4
sin cos sin 1 cot
x
I dx dx
x x x x
Đặt
cot
t x
… bạn đọc tự giải
Cách 6:
Ta có
3 3 3
3 2
sin sin tan
sin cos cos tan 1 cos tan 1
x x x
x x x x x x
Khi đó
2 2
3 3
2
0 0
sin tan
sin cos cos tan 1
x x
I dx
x x x x
Đặt
tan
t x
… bạn đọc tự giải
Cách 7:
tan
t x
… bạn đọc tự giải
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
38
Bài 3: Tính tích phân sau:
3
3
4
tan
I xdx
Giải:
Cách 1: Sử dụng phương pháp phân tích kết hợp với phương pháp đưa vào vi phân
Phân tích
3 2
2 2
1 1
tan tan .tan tan 1 tan tan
cos cos
x x x x x x
x x
Khi đó
3 3 3 3
3
2
4 4 4 4
2
1 1
tan tan . tan tan tan cos
coscos
tan 1
3
ln cos 1 ln2
2 2
4
I xdx x x dx xd x d x
xx
x
x
Cách 2: Sử dụng phương pháp phân tích kết hợp với phương pháp đưa vào vi phân
Phân tích
3 3
2
1
tan tan tan tan tan . tan
cos
x x x x x x
x
… trở lại cách 1
Cách 3: Phương pháp đổi biến số
2 2
2
tan 1 tan 1
1
dt
t x dt x dx t dt dx
t
Đổi cận
3
3
1
4
x
t
t
x
Khi đó
2
3 3 3 3 3
3 23
3
2 2 2 2
1 1 1 1 1
4
2
1
1 2 13
tan
2 2 2
1 1 1 1
1
1 1 1 1 1
3
ln 1 ln 2 1 ln 2 .
2 2 2 2 2
1
d t
t t t t
I xdx dt t dt tdt dt
t t t t
t
Cách 4: Phương pháp đổi biến số
Ta có
2
3 3
3
3
4 4
1 cos sin
tan
cos
x x
I xdx dx
x
Đặt
cos sin
t x dt xdx
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
39
Đổi cận
1
2
3
2
4
2
t
x
x
t
Khi đó
1 2
2
2 2
3 3 2
1
2
2
2
1
1
1 1 1 1
2
ln 1 ln2
2
2
2
2
t
I dt dt t
t
t t t
Cách 5: Phương pháp đưa vào biểu thức vi phân
2 23 3 3 3 3
3 3
3 3
4 4 4 4 4
2
(1 cos )sin (cos 1) (cos ) (cos )
tan cos cos
coscos cos
1 1
3 3
ln | cosx | 1 ln 2 .
2
2cos
4 4
x xdx x d x d x
I xdx xd x
xx x
x
Bài 4: Tính tích phân sau:
2
3
0
sin
I xdx
Giải:
Cách 1: Sử dụng phương pháp phân tích
Cách 1.1: Sử dụng công thức hạ bậc và công thức biến đổi tổng thành tích
Ta có
3 2
1 cos 2 sin cos2 .sin
sin sin .sin .sin
2 2 2
x x x x
x x x x
… bạn đọc tự giải tiếp
Cách 1.2: Sử dụng công thức nhân 3
3 3
3sin sin3
sin3 3sin 4sin sin
4
x x
x x x x
Khi đó
2 2 2 2
3
0 0 0 0
1 3 1 3 1 2
sin 3sin sin3 sin sin3 3 cos cos3
2
4 4 12 4 12 3
0
I xdx x x dx xdx xd x x x
Cách 2: Sử dụng phương pháp tích phân từng phần
Đặt
2
2sin cos
sin
cos
sin
du x xdx
u x
v x
dv xdx
Khi đó
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
40
2 2
2 2 3
0 0
2 2
sin cos 2sin cos 2 cos cos cos
2 2
3 3
0 0
I x x x xdx xd x x
Chú ý: Có thể đặt
sin
t x
Cách 3: Dùng phương pháp đưa vào vi phân
3
2 2 2
2 2
0 0 0
cos 2
1 cos sin sin cos cos cos
2
3 3
0
x
I x xdx xdx xd x x
Chú ý: Có thể đặt
sin
t x
Cách 4:
Đặt
2
2
2
2
1
1
tan tan 1
2
2 2 2
sin
1
dt
dx
x x
t
t dt dx
t
x
t
…. Bạn đọc tự giải
Bài 5: Tính tích phân sau:
2
3
3
sin
dx
I
x
Giải:
Cách 1: Sử dụng kĩ thuật nhân trên tử
2 2 2
3 4 2
2
3 3 3
sin sin
sin sin
1 cos
dx xdx x
I dx
x x
x
Cách 1.1: Đổi biến số đưa về tích phân hàm phân thức
Đặt
cos sin
t x dt xdx
Đổi cận
0
2
1
3
x
t
t
x
1 1 1 1
2
2
2 2 2 2
2 2
2
0 0 0 0
1 1
2 2
2 2 2 2 2
0 0
1 1
1 1 1
1 1 4 1 1
1 1
1
1 1 1 2 1 1 1 1 1
4 4 1 1
1
1 1 1 1
t t
dt dt
I dx dt dt
t t t t
t t
t
dt dt
t t
t
t t t t
1
1 1 1 1 1 1
ln ln3
2
4 1 1 1 3 4
0
t
t t t
Cách 1.2: Đưa trực tiếp vào biểu thức vi phân
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
41
2 2 2 2
3 4 2 2
2
3 3 3 3
2
2
2 2
3 3
2
2 2 2
3
cos
sin sin
sin sin
1 cos 1 cos
1 cos
1 cos 1 cos
1 1 1
cos cos
1 cos 1 cos 4 1 cos 1 cos
1 1 1 2
4 1 cos
1 cos 1 cos
d x
dx xdx x
I dx
x x
x x
x
x x
d x d x
x x x x
x
x x
2
cos 1 1 cos 1 1
2 2
cos ln ln 3
2 1 cos 3 42sin
3 3
x x
d x
xx
Cách 2: Đổi biến số
Đặt
2
2
2
2
1
1
tan tan 1
2
2 2 2
sin
1
dt
dx
x x
t
t dt dx
t
x
t
Đổi cận
1
2
1
3
3
t
x
t
x
Khi đó
1 1
2
3 2
2
1 1
3
3 3
2
1
2 1 1 2 1 1 1 1
2ln ln3
1
8
4 4 2 3 4
2
1 .
3
1
dt t
I t dt t
t
t
t t
t
t
Cách 3: Sử dụng phương pháp phân tích và phương pháp tích phân từng phần
2 2 2
2 2 2 2
3 3 3
3 3 3 3
sin cos cos
1
sin
sin sin sin
J
dx x x dx x
I dx dx
x
x x x

Tính
2
2
3
3
cos
sin
x
J dx
x
Đặt
3 2
cos sin
cos 1
sin 2sin
u x du xdx
x
dv dx v
x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
42
Khi đó
2
2
2
3 3
1 1
2
sin
cos 1
2
2si
3 2 sin
3
n
x
dx dx
x
x x
J
Thay vào (1) ta được
2
3
1 1
3 2 sin
K
dx
I
x
Chú ý:
- Để tính
2
2
3
3
cos
sin
x
J dx
x
ta có thể làm như sau
2
2 2 2 2
3 2 3
3 3 3 3
cos 1 1 1 1
1
sin sin
sin sin sin
I K
x
J dx dx dx dx
x x
x x x
- Để tính
2
3
sin
dx
K
x
ta có thể làm như sau
Nhân cả tử và mẫu cho
sin
x
ta được
2 2 2
2 2
3 3 3
sin sin
sin
sin 1 cos
dx xdx xdx
K
x
x x
Đặt cos sin
t x dt xdx
Đổi cận
0
2
1
2
3
t
x
t
x
Khi đó
1 1 1 1
0
2 2 2 2
2 2
1
0 0 0 0
2
1
1 1 1 1 1 1 1
ln 1 ln 1 ln3
2
2 1 1 2 1 2 1 2 2
1 1
0
dt dt dt dt
K dt t t
t t t t
t t
Hoặc
2 2 2 2
2
3 3 3 3
tan
1 1
2
2
ln tan ln3
sin 2 2 2
2sin cos 2tan cos tan
2 2 2 2 2
3
x
d
dx dx dx x
K
x x x x x
x

Hoặc đặt
2
2
2 1
tan
2
2
sin
1
dt
dx
t
x
t
t
x
t
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
43
Cách 4: Tách thành tích ở dưới mẫu và Sử dụng phương pháp tích phân từng phần
Đặt
2
2
1
cos
sin
sin
1
cot
sin
x
u
du dx
x
x
v x
dv dx
x
Khi đó
2
2
3
3
cot cos
2
sin
sin
3
J
x x
I dx
x
x
. Đến đây ta tích phân
2
2
3
3
cos
sin
x
J dx
x
áp dụng (cách 3)
Hoặc có thể tính nhanh như sau
2 2 2
3
3 3 3
2
2 2
2 3
3 3
1 cot 1
cot cot
sin sin sin
sin
cot cos cot cos
2
cot
sin sin
sin sin
3
J
dx x
I d x xd
x x x
x
x x x x
x dx dx
x x
x x
Cách 5: Đưa vào biểu thức vi phân
2
2
2 2 2 2
3 3 3 6 3
3 3 3 3
4
2
3 2
3
1 tan
1
2
tan
4 2sin
2sin cos 8 tan cos tan
2 2 2 2 2
1 2tan tan
1 1 1
2 2
tan 2l
4 2 4
tan 2 tan
2 2
x
dx dx dx x
I d
x
x x x x x
x x
x
d
x x
2
1 1 1
2
n tan tan ln3
2 2 2 3 4
3
x x
Bài 6: Tính tích phân sau:
2
0
sin
sin cos
x
I dx
x x
Giải:
Cách 1:
sin tan tan 1 1 1
1
sin cos tan 1 tan 1 tan 1
x x x
x x x x x
Khi đó
2 2 2 2
0 0 0 0
sin 1 1
1
sin cos tan 1 tan 1
J
x
I dx dx dx dx
x x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
44
từ đó đặt
tan
t x
Cách 2:
Đặt
2
2
2
2
2
1
2
tan sin
2
1
1
cos
1
dt
dx
t
x t
t x
t
t
x
t
… bạn đọc tự giải
Cách 3:
Đặt
2
x t dx dt
Đổi cận
0
2
0
2
t
x
t
x
Khi đó
2 2 2
0 0 0
sin cos cos
sin cos sin cos sin cos
x t x
I dx dt dx
x x t t x x
2 2 2
0 0 0
sin cos
2
sin cos sin cos 2 4
x x
I dx dx dx I
x x x x
Chú ý:
b b
a a
f x dx f t dt
Cách 4: Sử dụng tích phân liên kết
Chọn
2
0
cos
sin cos
x
J dx
x x
là tích phân liên kết của
2
0
sin
sin cos
x
I dx
x x
Khi đó ta có hệ
2 2 2 2
0 0 0 0
2 2 2 2
0 0 0 0
cos sin sin cos
2
sin cos sin cos sin cos 2
0
sin cos
cos sin cos sin
ln sin cos 0
2
sin cos sin cos sin cos sin cos
0
x x x x
I J dx dx dx dx x
x x x x x x
d x x
x x x x
I J dx dx dx x x
x x x x x x x x
cộng theo từng vế ta được 2
2 4
I I
Cách 5: Sử dụng phương pháp đồng nhất thức
Phân tích
1
sin sin cos sin cos
2
x x x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
45
Khi đó
2 2
0 0
sin 1 1 cos sin
.
sin cos 2 2 sin cos
x x x
I dx dx
x x x x
Chú ý: Có thể dựa vào đồng nhất thức sau
sin sin cos cos sin
sin cos sin cos sin cos
1
2
sin sin sin
1
2
x x x x x
A B
x x x x x x
A
x A B x A B x
B
… quay trở lại cách 5
Cách 6: Sử dụng kĩ thuật nhân
Ta có
2 2
1 1 cos2
sin 2
sin (cos sin ) 1 1
2 2
tan2 1
cos2 2 cos2cos sin
x
x
x x x
x
x xx x
Cách 7: Sử dụng phương pháp phân tích
sin
sin 1
4 4
1 cot
sin cos 2 4
2sin
4
x
x
x
x x
x
Cách 8: Biến đổi số theo cận
2 2
0 0
sin sin
sin cos
2 cos
4
x x
I dx dx
x x
x
Đặt
4
t x dx dt
…bạn đọc tự giải
Bài 7: Tìm nguyên hàm:
1 sin
2 ln
sin .sin cos
4 4
x
I dx C
x x x
Giải:
Cách 1: Ta có
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
46
cos
cos
4
4
1 2 cos 2 cos cos sin sin
4 4 4
2
cos
4
2
sin
1 cos
4
2
sin
sin cos cos
4 4
x x
x x x x x x
x
x
x
x x x
cos
sin
4
sin
2 2 2 ln sin 2 ln cos 2 ln
sin 4
cos cos
4 4
d x
d x
x
I x x C
x
x x
Cách 2: Dựa vào đặt thù của hàm số đã cho ta có :
2
(cot 1)
2 2 2 2 ln cot 1
sin (cos sin ) cot 1sin (cot 1)
dx dx d x
I x C
x x x xx x
Tương tự : (ĐHMĐC – 2000) Tính tích phân:
3
6
sin .sin
6
dx
I
x x
HD:
2sin
cos
6
cos
6
2
sin
sin .sin sin .sin sin
6 6 6
x x dx
x
dx x
dx
x
x x x x x
Bài 8: Tìm nguyên hàm: tan tan
4
I x x dx
Giải:
Cách 1:
Ta có:
sin sin cos cos sin sin cos
4 4 4 4
tan tan 1 1
4
cos cos cos cos cos cos
4 4 4
2 1
1
2
cos cos
4
x x x x x x x
x x
x x x x x x
x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
47
Khi đó xét:
cos cos( )
4
dx
J
x x
Sử dụng đồng nhất thức:
sin
4
1 2 sin 2 sin cos cos sin
4 4 4
sin
4
x x x x x x
1
2 tan 2 tan
4
cos cos
4
2 tan 2 tan 2 ln cos 2 ln cos
4 4
x x
x x
J x dx xdx x x C
cos
2 ln
cos
4
x
I x C
x
Cách 2:
2
2 2
cos (cos sin )
cos (1 tan )
cos cos
4
(1 tan )
2 2 ln 1 tan 2 ln 1 tan
1 tan
dx dx dx
J
x x x
x x
x x
d x
x C I x x C
x
Bài 9: (ĐH – B 2003) Tính tích phân sau:
2
4
0
1 2sin
1 sin 2
x
I dx
x
Giải:
Cách 1: Phương pháp biến đổi số
Ta có
2
4 4
0 0
1 2sin cos2
1 sin 2 1 sin2
x x
I dx dx
x x
Đặt
1 sin 2 cos2
2
dt
x t xdx
hoặc
sin 2
x t
Đổi cận
2
4
1
0
t
x
t
x
Khi đó
2
1
2
1 1 1
ln ln 2
1
2 2 2
dt
I t
t
Cách 2: Phương pháp đưa vào biểu thức vi phân
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
48
'
4 4 4
0 0 0
1 sin 2
cos2
1 1 (1 sin 2 ) 1 1
ln 1 sin2 ln 2
4
1 sin 2 2 1 sin2 2 1 sin2 2 2
0
x
x
d x
I dx dx x
x x x
Cách 3: Phương pháp đưa vào biểu thức vi phân
Biến đối
2
1– 2sin cos sin cos – sin
x x x x x
và
2
1 sin 2 cos sin
x x x
2
4 4
0 0
1 2sin cos sin 1
ln cos sin ln 2
4
1 sin 2 cos sin 2
0
x x x
I dx dx x x
x x x
Hoặc đặt
sin cos
t x x
Bài 10: (ĐH – A 2005) Tính tích phân sau:
2
0
sin 2 sin
1 3cos
x x
I dx
x
Giải:
Cách 1: Phương pháp biến đổi số
Ta có:
sin 2 sin sin 2cos 1
x x x x
.
Đặt
1 3cos
t x
ta được
3sin sin 2
3
2 1 3cos 1 3cos
x x dt
dt dx dx
x x
;
2 2
1 2 1
cos 2cos 1
3 3
t t
x x
Đổi cận
0
2
1
2
x
t
t
x
Khi đó
2
2
3
1
2
4 2 4 2 34
1
9 9 27 9 27
t
I dt t t
Cách 2: Phương pháp biến đổi số
Đặt
1 3cos
t x
…bạn đọc tự giải
Cách 3: Phương pháp tích phân từng phần
Đặt
2cos 1
2sin
1 3cos
2
sin
1 3cos
3
1 3cos 3 1 3cos
u x
du x
d x
x
v x
dv dx
x x
Khi đó
2 2
0 0
3
2 4 2 4
2cos 1 1 3cos sin 1 3cos 1 3cos 1 3cos
2
3 3 3 9
0
2 8 34
1 3cos
2
3 27 27
0
I x x x xdx xd x
x
Cách 4: Phương pháp đưa vào biểu thức vi phân
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
49
Phân tích
2 1
1 3cos
sin 2 sin 1 2cos 1 1
3 3
. 1 3cos . 1 3cos
3 3
1 3cos 1 3cos 1 3cos
2 1
1 3cos 1 3cos 1 3cos
9
9 1 3cos
x
x x x
dx d x d x
x x x
xd x d x
x
Tổng quát:
dx
xdc
xbxa
cos
sin2sin.
hoặc
.sin 2
s
a x bcosx
dx
c d inx
ta đặt
cos
c d x t
.
Bài 11: (ĐH – A 2009) Tính tích phân sau:
2
3 2
0
8
cos 1 cos
15 4
I x xdx
HD:
Cách 1:
1 2
2 2
5 2
0 0
cos cos
I I
I xdx xdx
Đặt
sin cos
t x dt xdx
Đổi cận
1
0
0
0
t
x
t
x
Khi đó
1 1
2 2
2 2
5 2 2 2 4 3 5
1
0 0 0 0
1
2 4 8
cos 1 sin cos 1 1 2
0
3 5 15
I xdx x xdx t dt t t dt t t t
2 2 2 2
2
2
0 0 0 0
1 cos2 1 1 1 1
cos cos2 sin 2
2
2 2 2 2 2 4
0
x
I xdx dx dx xdx x x
Vậy
1 2
8
15 4
I I I
Chú ý:
Có thể tính
1
I
như sau
2 2 2
2 2
5 2 2
1
0 0 0
1
2 4 3 5
0
cos 1 sin cos 1 sin sin
2 4 8
1 2sin sin sin sin sin sin
2
3 5 15
0
I xdx x xdx x d x
x x d x x x x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
50
Cách 2:
2
0
cos3 3cos 1 cos2
1
4 2
x x x
I dx
…
Bài 12: (ĐH – A 2006) Tính tích phân sau:
2
2 2
0
sin 2 2
3
cos 4sin
x
I dx
x x
HD:
Cách 1: Phương pháp phân tích kết hợp biến đổi số
2 2
2 2 2
0 0
sin 2 sin 2
1 sin 4sin 1 3sin
x x
I dx dx
x x x
Đặt
2
1 3sin sin 2
3
dt
t x xdx
Đổi cận
4
2
1
0
t
x
t
x
Khi đó
14 4
2
1 1
4
1 1 2 2
1
3 3 3 3
dt
I t dt t
t
Hoặc đặt
2
1 3sin
t x
Cách 2: Phương pháp đưa vào biểu thức vi phân
1
2 2 2
2 2
2
2 2 2
0 0 0
2
sin 2 sin 2 1
1 3sin 1 3sin
3
1 sin 4sin 1 3sin
2 2
1 3sin
2
3 3
0
x x
I dx dx x d x
x x x
x
Cách 3: Phương pháp phân tích kết hợp biến đổi số
2 2
0 0
sin 2 sin 2
1 cos 2 1 cos 2 5 3cos2
4
2 2 2
x x
I dx dx
x x x
Và đặt
5 3cos2
2
x
t
hoặc
5 3cos2
2
x
t
hoặc đưa vào vi phân
Tổng quát: Để tính I =
2
2 2 2 2
0
sin cos
cos
x xdx
a x b sin x
với a, b
0
Ta đặt: u =
2 2 2 2
cos
a x b sin x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
51
Bài 13: (Đề 68 IVa) Tính tích phân sau:
3
2
0
4sin
1 cos
x
I dx
x
Giải:
Cách 1: Phân tích
3 3
3
2
4sin 1 cos 4sin 1 cos
4sin
4sin 4sin cos 4sin 2sin 2
1 cos 1 cos 1 cos
sin
x x x x
x
x x x x x
x x x
x
Khi đó
3
2 2
0 0
4sin
4sin 2sin 2 cos2 4cos 2
2
1 cos
0
x
I dx x x dx x x
x
Cách 2:
3
2 2
2 2
0 0
0 0
2
4sin
4sin 4sin cos 4 sin 4 cos cos
1 cos
4cos 2cos 2
2 2
0 0
x
I dx x x x dx xdx xd x
x
x x
Cách 3:
2
3
2 2
0 0
4 1 cos sin
4sin
1 cos 1 cos
x x
x
I dx dx
x x
Đặt
sin
1 cos
cos 1
dt xdx
t x
x t
Đổi cận
1
2
2
0
t
x
t
x
Khi đó
2
1 2
2
2 1
4 1 1
2
4 8 2 8 2
1
t
I dt t dt t t
t
Chú ý: Có thể đặt
cos
t x
Cách 4:
3 3
3
3
2
32sin cos
4sin
2 2
16sin cos
1 cos 2 2
2cos
2
x x
x x x
x
x
…Quá hay phải không, bạn tự giải tiếp nhé
Cách 5:
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
52
Đặt
2
2
2
2
2
1
2
tan sin
2
1
1
cos
1
dt
dx
t
x t
t x
t
t
x
t
… Chắc chắn sẽ ra cứ yên tâm làm tiếp đi
Chú ý:
3
4sin 4sin (1 cos )(1 cos )
4sin 2sin 2
1 cos 1 cos
x x x x
x x
x x
... Phân tích đến đây rùi thì có những cách nào, bạn đọc
tự khám phá nhé!
Tương tự
3
2
0
4cos
2
1 sin
x
I dx
x
Bài 14: (KTQS – 1997) Tính tích phân sau:
3
2
3
3
sin sin
cot
sin
x x
I xdx
x
Giải:
Cách 1: Phương pháp đưa vào biểu thức vi phân
3 33 3
2 2
3 2
3 3
5 8
2 2 2
3
2
3 3
3
2
3
3 3 3
sin sin sin sin cot
cot
sin
sin sin
1 3 1
2
1 .cot cot cot .cot cot cot cot cot
8
sin
8 3
3
x x x x x
I xdx dx
x
x x
xd x x xd x xd x x
x
Cách 2: Phương pháp biến đổi số
3 3
2 2
3
3 2 2
3 3
sin sin 1 cot
cot 1 .
sin sin sin
x x x
I xdx dx
x x x
Đặt
2
1
cot
sin
t x dt dx
x
Đổi cận
0
2
1
3
3
t
x
t
x
Khi đó
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
53
5 8
0 0
3 2
3 3
3
1 1
3 3
0
3 1
.
1
8
8 3
3
I t tdt t dt t
Cách 3: Phương pháp biến đổi số
Ta có
3 33 3
2 2
3 4
3 3
sin sin cos sin sin
cot
sin sin
x x x x x
I xdx dx
x x
Nhận xét: Hàm dưới dấu tích phân là hàm lẻ đối với cos
Đặt
sin cos
t x dt xdx
Đổi cận
1
2
3
2
3
t
x
t
x
Khi đó
3
1 1
3 3
2
4 3
3 3
2 2
1
1
t t
t
I dt dt
t t
Đặt
3 2
3
2 2 3
1 1 3
1 1
2
dt
u u u du
t t t
Đổi cận
3
1
0
1
3
3
2
t
u
u
t
Khi đó
3
0
4
3
3
1
3
3
0
3 3 1
1
2 2 4
8 3
3
u
I u du
Bài 15: ( Đề 104. IVa) Tính tích phân sau:
3
8
2 2
8
sin cos
dx
I
x x
Giải:
Cách 1: Sử dụng phương pháp phân tích nhờ đồng nhất thức
2 2
sin cos 1
x x
Khi đó
3 3 3
2 2
8 8 8
2 2 2 2 2 2
8 8 8
3
sin cos 1 1
8
tan cot 4
sin cos sin cos cos sin
8
dx x x
I dx dx x x
x x x x x x
Cách 2: Sử dụng công thức nhân đôi
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
54
3 3 3
8 8 8
2
2 2 2 2
8 8 8
3
2
8
4 2 2cot 2 4
sin cos sin 2 sin 2
8
d x
dx dx
I x
x x x x
Cách 3: Phương pháp biến đổi số
Đặt
2
tan
cos
dx
t x dt
x
và
2 2
2 2 2
1 1 tan 1
sin tan
x t
x x t
….
Bài 16: Tính tích phân sau:
2
3
0
cos
sin 3 cos
xdx
I
x x
Giải:
Cách 1: Đồng nhất thức
Ta phân tích:
2 2 2
cos sin cos (sin cos ) sin cos
x A x B x x x C x x
2 2
( 3 ) cos ( 3 )sin cos sin
B C x B A x x A C x
1
4
3 1
3
3 0
4
0
1
4
A
B C
B A B
A C
C
2
cos 1 3 1
sin cos
4 4
sin 3cos 4(sin 3cos )
x
x x
x x x x
Khi đó
1
3
0
1 3 1
cos sin
3
4 4 4
sin 3cos
0
I
dx
I x x
x x

Tính:
3
0
sin 3cos
dx
J
x x
3
1
0
1 1
ln tan
3
2 2 2 6
0
sin
3
dx x
I
x
1 3 1 3ln3 2
cos sin ln tan
3
4 4 8 2 6 8
0
x
I x x
Cách 2: Tích phân liên kết
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
55
Sử dụng tích phân liên kết
2
3
0
cos
sin 3cos
xdx
J
x x
Giải hệ
3ln3 2
3 1
ln3
2
8
I J
I
I J
Tổng quát:
2
cos
sin cos
xdx
I
A x B x
tích phân liên kết thường là
2
sin
sin cos
xdx
J
A x B x
Bài 17: Tính tích phân sau:
6
2
4
4
cos
sin
x
I dx
x
Giải:
Cách 1: Đưa vào vi phân
Phân tích
6 2 4
4 4 2
4 4 2
cos cos .cos 1
1 tan tan tan
sin sin tan
x x x
x x x
x x x
Khi đó
1 2
6
2 2 2 2
4 2 4 2
4
4 4 4 4
cos
tan tan tan tan
sin
I I
x
I dx x x dx xdx xdx
x
Tính
2 2 2 2 2
4 4 2 2 2 2 2
1
4 4 4 4 4
2
2
4
tan tan tan tan 1 1 tan tan 1 tan 1
2 2
tan tan tan
4 4
I xdx x x x dx dx x dx
xd x x x
Tính
2 2 2
2 2
2
4 4 4
2
tan 1 1 tan 1 tan
4
I x dx x dx dx x x
… tự giải nhé
Cách 2:
Phân tích
2
2
6 2 2 2 2 4
2 2 2
4 4 4 2
cos 1 sin
cos cos 2cos sin cos sin 1
cot . 2cot cos
sin sin sin sin
x x
x x x x x x
x x x
x x x x
Khi đó
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
56
2 2 2
2 2 2
2
4 4 4
2 2 2
2
2
4 4 4
3
1
cot . 2 cot cos
sin
1 1
cot cot 2 1 1 cos2
2
sin
cot 1 sin 2 5 23
2
2 cot 1
3 2 2 8 12
4
I x dx xdx xdx
x
xd x dx x dx
x
x x
x x
Cách 3:
Nhận xét: Vì hàm dưới dấu tích phân là hàm chẵn đối với sin va cos nên ta có thể đặt
tan
t x
nhưng cách đó
khá dài và phức tạp nên không nêu ra, bạn đọc tự khám phá nhé!
Bài 18: Tính tích phân sau:
2
6 3 5
0
1 cos .sin .cos
I x x xdx
Giải:
2
6 3 3 2
0
1 cos .cos .sin .cos
I x x x xdx
Đặt
3 6
6
3 3 6
2 5
cos 1
1 cos 1 cos
sin .cos 2
x t
x t x t
x xdx t dt
.
Đổi cận
1
2
0
0
t
x
t
x
Khi đó
1 1
7 13
6 5 6 12
0 0
1
12
2 1 2
0
7 13 91
t t
I t t t dt t t dt
Hoặc : Đặt
3
1 cos
x t
Cách 2: Sử dụng phương pháp đưa vào vi phân
2 2
6 63 3 2 3 3 3
0 0
2
6 3 3 3
0
2 2
6 6
3 3 3 3 3
0 0
1 cos .cos .sin .cos 1 cos .cos 1 cos
1 cos 1 cos 1 1 cos
1 cos 1 cos 1 cos 1 cos 1 cos
I x x x xdx x xd x
x x d x
x x d x xd x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
57
Bài 19: (ĐH – B 2005) Tính tích phân sau
2
0
sin 2 .cos
1 cos
x x
I dx
x
Giải:
Cách 1: Đổi biến số
Phân tích
2
2 2
0 0
sin 2 .cos sin .cos
2
1 cos 1 cos
x x x x
I dx dx
x x
Đặt
sin
1 cos
cos 1
dt xdx
t x
x t
Đổi cận
1
2
2
0
t
x
t
x
Khi đó
2
1 2
2
2 1
1 2
1
2 2 2 2 2 ln 2ln 2 1
12
t
t
I dt t dt t t
t t
Cách 2:
2
2
2 2 2
0 0 0
2
2
0
1 cos 1
sin 2 .cos sin .cos
2 2 cos
1 cos 1 cos 1 cos
1 cos
2 1 cos cos sin ln 1 cos 2ln2 1
2
1 cos 2
0
x
x x x x
I dx dx d x
x x x
x
x d x x x
x
Chú ý:
cos 1 cos
d x d x
và ta có thể đặt
cos
t x
Tổng quát:
sin 2 .cos
.cos
a x x
I dx
b c x
ta đặt
.cos
t b c x
hoặc
cos
t x
Bài tập tự giải có hướng dẫn:
Bài 1: (ĐH – A 2008) Tính tích phân sau:
4
6
0
tan 1 10
ln 2 3
cos 2 2
9 3
x
I dx
x
HD:
Cách 1: Biến đổi
2 2 2 2
cos2 cos sin 1 tan cos
x x x x x
Đặt
tan
t x
Hoặc sử dụng công thức
2
2
1 tan
cos2
1 tan
x
x
x
Tổng quát:
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
58
1.
4
tan
cos2
a x
I dx
b x
với ,a b
Biến đối
2 2 2 2
cos2 cos sin 1 tan cos
b x b x x b x x
đặt
tan
t x
2. Mở rộng hơn
4
2 2
tan
sin sin cos cos
a x
I dx
b x c x x d x
với , , ,a b c d
Biến đổi
2 2 2 2
sin sin cos cos tan tan cos
b x c x x d x b x c x d x
đặt
tan
t x
Bài 2: (ĐH AN– 1998): Tính tích phân sau:
4
4
0
cos
dx
I
x
Cách 1:
4 4 4
2 3
4 2 2
0 0 0
1 4
. 1 tan tan tan tan
4
3
cos cos cos
0
dx dx
I x d x x x
x x x
Cách 2: Biến đổi số
4 4 4
2
4 2 2 2
0 0 0
1
. 1 tan
cos cos cos cos
dx dx dx
I x
x x x x
Đặt
tan
t x
Cách 3: Sử dụng phương pháp tích phân từng phần
2
2
1
cos
cos
u
x
dx
dv
x
Bài 3: (Đề 84.IVa) Tính tích phân sau:
2
4
4
sin
dx
I
x
3
2 2 2
2
4 2
4 4 4
cot
cot 4
2
1 cot cot (cot )
3 3
sin sin
4
d x
dx x
I x d x x
x x
Bài 4: Tính tích phân sau:
2
2 2
0
cos .cos 2
4
I x xdx
HD:
C1: Hạ bậc biến đổi tích thành tổng
C2: Tích phân liên kết
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
59
Bài 5: Tính tích phân sau:
2
4
4
0
1 2sin
sin cos
x
I dx
x x
HD:
2
1 2sin cos2 cos sin cos sin
x x x x x x
và
4 2
4
sin cos 1 sin2 4cos
4
x x x x
Từ đây ta có các cách sau
Cách 1:
Biến đổi
2
4 4
4 2
0 0
1 2sin cos2
sin cos 1 sin2
x x
I dx dx
x x x
đặt
1 sin 2
t x
hoặc
sin 2
t x
hoặc biến đổi vi phân trực tiếp
2
4 4 4
4 2 2
0 0 0
1 sin 2
1 2sin cos2
sin cos 1 sin 2 1 sin 2
d x
x x
I dx dx
x x x x
hoặc đặt
tan
t x
Cách 2:
Biến đổi
2
4 4 4
4 4 4
0 0 0
cos sin cos sin cos sin
1 2sin
sin cos sin cos sin cos
x x x x x x
x
I dx dx dx
x x x x x x
Đặt
sin cos
t x x
hoặc biến đổi vi phan trực tiếp
Cách 3:
Biến đổi
2
4 4
4
4
0 0
1 2sin cos2
sin cos
4cos
4
x x
I dx dx
x x
x
Đặt
4
t x
Bài 6: (ĐHGT TPHCM – 2000) Tính tích phân:
2
3
6
6
sin
cos
x
I dx
x
HD:
Ta có
2
2 2 2
6 2 2
sin 1 1
tan . . tan 1 tan tan
cos cos cos
x
dx x dx x x d x
x x x
Đs:
42 3 8
15
Bài 7: (ĐHĐN – 2000) Tính tích phân:
2
4
sin cos
sin cos
x x
I dx
x x
HD:
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
60
2 2
4 4
cos
2sin
4
1
4
2
ln cos ln 2
4 2
2 cos cos
4 4
4
d x
x
I dx dx x
x x
Bài 8: Tính tích phân sau:
4
6
0
tan
I xdx
HD:
Đặt
2
tan (tan 1)
t x dt x dx
Đổi cận:
0 0
1
4
x t
x t
Vậy
1
1 1
6 5 3
4 4
6 4 2
2 2
0 0 0 0
0
1 13
tan 1
5 3 15 4
1 1
t dt t t
I xdx t t dt t du
t t
Bài 9: Tính tích phân sau:
2
5
0
8
cos
15
I xdx
Bài 10: Tính tích phân sau:
3
2
2
0
sin cos
1 cos
x x
I dx
x
HD:
2
2
2
2
0
1 cos
1 cos
2
1 cos
x
I d x
x
2
2
1
1
1 1 1 1 ln 2
ln
2 2 2
t
dt t t
t
Bài 11: Tính tích phân sau:
4
tan
I xdx
HD:
4 2 2 2 2 2
2
2
2 3
2
1
tan tan sin tan tan 1 cos tan tan 1 tan
1
tan 1 1 1
tan tan tan tan tan
3
1 tan
I xdx x xd x x x d x x d x
tg x
x
xd x d x x x x C
x
Bài 12: (ĐHTL – 2000) Tính tích phân sau:
2
2 2
0
3sin 4cos
3sin 4cos
x x
I dx
x x
Đs:
3
ln3
6
I
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
61
V. BÀI TẬP HỖN HỢP CỦA NHIỀU HÀM SỐ
Bài tập giải mẫu:
Bài 1: (ĐH TL2001) Tính tích phân sau:
4
0
ln 1 tan
I x dx
Giải:
Cách 1:
Đặt
1 tan 2
1 tan 1 tan 1
4
4 1 tan 1 tan
dx dt
x t
t
x t
t t
Đổi cận
0
4
0
4
x t
x t
Khi đó
4 4 4
0 0 0
2
ln ln 2 ln 1 tan (ln2). ln 2
1 tan 4 8
I dt dt t dt I I
t
Cách 2:
Ta có
4 4 4 4
0 0 0 0
4 4
0 0
sin cos
ln 1 tan ln ln sin cos ln cos
cos
ln 2cos ln cos
4
J
x x
I x dx dx x x dx x dx
x
x dx x dx

Tính
4 4 4 4
0 0 0 0
1 1
ln 2 cos ln 2 lncos ln 2 lncos ln 2
4
4 2 4 2 4 8
0
K
J x dx dx x dx x x dx K

Đặt
4
t x dt dx
Khi đó
4 4
0 0
ln cos ln cos
K t dt x dx
Khi đó
ln2
8
I
Cách 3: Tích phân từng phần
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
62
Đặt
ln 1 tan
u x
dv dx
…Bạn đọc tự giải
Bài 2: Tính tích phân:
1
2
0
ln 1
1
x
I dx
x
.
HD:
Đặt
tan
x t
ta được
4
0
ln 1 tan
I t dt
;
đặt
4
t x
ta được
4 4
0 0
2
ln ln2
1 tan
I du du I
u
Bài 3: Tính tích phân sau:
5
2
ln( 1 1)
1 1
x
I dx
x x
Giải:
Cách 1:
Đặt
2
1
2 1
2 1
1 1
1 1
dt dx t dt dx
x
t x
x t
Đổi cận
5 3
2 2
x t
x t
Khi đó
3 3 3
2 2 2
2
2 2 2
3
( 1)ln ln
2 2 2 ln ln ln ln 3 ln 2
2
( 1) 1
t t t
I dt dt td t t
tt t
Cách 2: Đặt
1
t x
... bạn đọc tự giải
Bài 4: Tính tích phân sau:
2
0
1 sin 2
xdx
I
x
Giải:
Cách 1: Đặt
2
t x
Cách 2: Biến đổi
2
1 sin 2 1 cos 2 2cos
2 4
x x x
, tích phân từng phần
2 3 3 3
0
0 0 0
1 1
.sin .cos cos cos cos
3 3
I x x xdx xd x x x xdx
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
63
3
2
0
0
1 1 sin
1 sin sin sin
3 3 3 3 3 3
x
x d x x
Bài 5: (ĐH DHN – A 2000) Tính tích phân sau:
2 2 2
2
2
0 0
1 sin
sin
1 cos 1 cos
2cos
2
x
x x
o
x e
e e x
I dx dx dx e
x
x x
Giải:
Cách 1:
Ta có:
2
1
2 2 2 2 2
2
0 0 0 0 0
1 sin sin 1 sin
. . .
1 cos 1 cos 1 cos 2 1 cos
cos
2
x x
x x x
I
I
x e dx x e dx x
I e dx e dx e dx
x
x x x x
Tính:
2
1
2
0
1
2
cos
2
x
e dx
I
x
Đặt:
2
tan
cos
2
2
x
x
u e
du e dx
dx
dv
x
v
x
Áp dụng công thức tính tích phân từng phần
2 2 2
2
1
2
0 0 0
1
tan tan . tan .
2
2 2 2 2
cos
0
2
x
x x x
e dx x x x
I e e dx e e dx
x
Tính:
2 2 2
2
2
0 0 0
2sin cos
sin
2 2
. . tan .
1 cos 2
2cos
2
x x x
x x
x x
I e dx e dx e dx
x
x
Vậy
2
I e
Cách 2:
Ta có:
2 2 2 2
2
0 0 0 0
sin
. . (tan ) tan .
1 cos 2 2
2cos
2
xx
x x
e x
e x x
I dx dx e d e dx
x
x
2 2
2 2
2
0 0
0 0
tan tan . tan . tan
2 2 2 2
x x x x
x x x x
e e dx e dx e e
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
64
Sử dụng định nghĩa:
Ta có
' '
'
2 2 2
.2sin cos
1 sin
2 2
tan tan tan tan
1 cos 2 2 2 2
2cos 2cos 2cos
2 2 2
x
x
x x
x x x x
x x
e
x e
e e x x x x
e e e e
x x x
x
Hoặc ta biến đổi:
2
sin cos
1 sin
1 1
2 2
1 2tan tan
1 cos 2 2 2 2
cos
2
x x
x
x x
x
x
Vậy
1
2 2
2
0 0
1 1
1 tan tan
2 2 2 2
x
I
x x
I dx e dx
Tính
2
1
0
tan
2
x
x
I e dx
Bài 6: (ĐH GTVT – 1998) Tính tích phân sau:
2
2
1 1
lnln
e
e
I dx
xx
Cách 1:
Đặt
2
1 1
ln
ln
f x
x
x
Ta có
' '
2 2 2
ln ln
1 1 1 ln
ln ln
ln ln n
x x x x
x x
f x F x
x x
x x l x
Khi đó
2
2
2
2
1 1
ln ln 2
ln
e
e
e
x e
I dx e
x xx
e
Cách 2:
2 2 2 2 2
2
2
1 1 1
ln ln ln ln ln ln
ln
e e e e e
e e e e e
e
dx x dx dx
I dx xd
x x x x x x
x
e
Bài 7: Tính tích phân sau
2
0
.sin cos
I x x xdx
Giải:
0 0
1 1
.sin 2 cos . sin3 sin
2 4
I x x xdx x x x dx
Đặt:
1
sin3 sin
cos3 cos
3
du dx
u x
dv x x dx
v x x
.
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
65
Khi đó
0
1 1 1
cos3 cos cos3 cos
0
4 3 3 3
I x x x x x dx
1 1 1 1 5
cos3 cos sin3 sin
2 2
2 3 2 18 2 9
0 0
x
x x x x
.
Cách 2: Đặt
x t
… bạn đọc tự giải
Chú ý: Qua mấy bài toán trên ta có nhận xét
Dựa vào đạo hàm ta có thể tính Nguyên hàm của một các dạng đặc biệt
Dạng 1: Nguyên hàm của các hàm số dạng tích thương
Dạng Cấu trúc hàm số Nguyên hàm
Tổng
'
' '
f x u v u v
F x u v
Hiệu
'
' '
f x u v u v
F x u v
Tích
'
' '
f x u v v u uv
F x uv
Thương
'
' '
2
u v v u u
f x
v
v
u
F x
v
Dạng 2: Các dạng nguyên hàm đơn giản chứa e
x
Đặc trưng Nguyên hàm Hàm số (đạo hàm)
x
e
x
F x u x e
' ' x
F x u x u x e f x
x
e
x
F x u x e
' ' x
F x u x u x e f x
ax b
e
ax b
F x u x e
' ' ax b
F x u x au x e f x
v v
e
v v
F x u x e
' ' '
v x
F x u x v x u x e f x
Ví dụ: Tính tích phân sau:
1
2
2
0
2
x
x e
I dx
x
Giải:
Cách 1: Tích phân từng phần
Đặt
2
2
2
1
2
2
x
x
u x e
du xe x dx
dx
du
v
x
x
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
66
Khi đó
1
1
2
0
1
0
2
x
x
I
x e
I xe dx
x
Tính
1
1
0
x
I xe dx
. Đặt
x x
u x du dx
dv e dx v e
Khi đó
1
1
0
1 1
0 0
x x x x
I xe e dx xe e
Vậy
2
1 1
1
0 0
2
x
x x
x e
I xe e
x
Cách 2:
Phân tích
2
2 2
4 4 4 2 4 2 4 2 4
x x x x x x
Khi đó
2
1 1 1 1 1
2
2 2 2
0 0 0 0 0
2 4 2 4
1
4 4
2
2 2 2
x
x x x
J
x x
x e
I e dx e dx e dx dx dx
x
x x x
Tính J làm xuất hiện tích phân mà làm triệt tiêu một tích phân
Bài tập tự giải có hướng dẫn:
Bài 1: Tính tích phân sau:
1
2 2
2
0
1
x
x e
I dx
x
HD: Sứ dụng tích phân từng phần
1 1
2 2
2 2
2
0 0
1
1
1
x
x
x e
I dx x e d
x
x
1
1 1 1 1
2 2 2 2 2
1
2 2 2 2 2 2
0
0 0 0 0
0
1
2 2 2 2
0
1
2
1 1 2 2 2
1 1
2 2 2 2 2 2
x
x x x x x
x
x e e e e
d x e xe dx xd e xe e dx
x x
e e e e
Bài 2: Tính tích phân sau:
2
2
2 2
0
4 tan 1 tan tan
2 2 8 8
x x
I x x
Bài 3: (ĐHLN – 2001) Tính tích phân sau:
2
1
2
0
1
1
1
x
x e
I dx
x
Bài 4: Tính tích phân sau:
2
sin
0
1 cos
2
x
I e x x dx e
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com
DĐ: 01694 013 498
67
Bài 5: (ĐHTN – 1996) Tính tích phân sau:
2
2
1
2ln 2 2 2
ln
e
e
I x e e
x
LỜI KẾT:
Đây thực sự chưa phải là những bài toán và cách giải hay, chưa có nhiều bài tập phong phú và đa
dạng, song cũng góp phần nhỏ bé nào đó cho các bạn và Tôi hi vọng các bạn sẽ thích thú và tìm thêm
những bài tập hay và những cách giải đặc sắc hơn….
Tuy nhiên năng lực và kinh nghiệm còn thiếu. Rất mong các bạn học sinh và các bạn đồng nghiệp
góp ý kiến, bổ sung thêm giúp tôi và các bạn hoàn thiện hơn … Xin chân thành cảm ơn
Góp ý theo địa chỉ Email: Loinguyen1310@gmail.com hoặc địa chỉ: Nguyễn Thành Long
Số nhà 15 – Khu phố 6 – Phường ngọc trạo – Thị xã bỉm sơn – Thành phố thanh hóa
MỤC LỤC
I. TÍCH PHÂN HÀM HỮU TỶ………………………………………………........................Trang 2
II. TÍCH PHÂN HÀM VÔ TỶ………………………………………………………..............Trang 18
III. TÍCH PHÂN HÀM SỐ MŨ VÀ LOGARIT……………………………………..............Trang 26
IV. TÍCH PHÂN HÀM LƯỢNG GIÁC....................................................................................Trang 35
Tải thêm tài liệu môn Toán THPT tại:
+ Trang web: www.toanmath.com
+ Fanpage: www.facebook.com/toanmath
+ Groups: https://www.facebook.com/groups/toanmath
| 1/67
| | Tải xuống

Có thể bạn quan tâm:

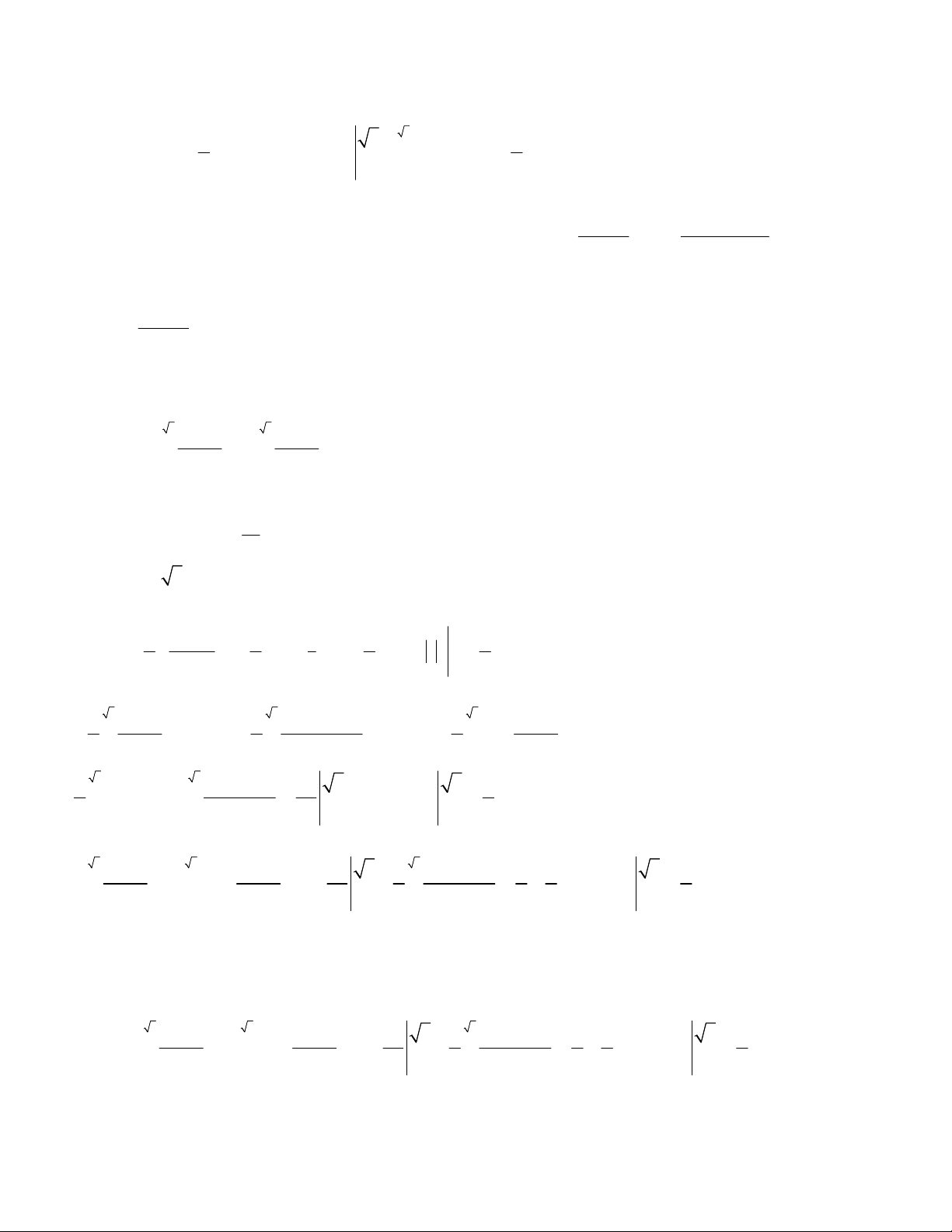
Preview text:

Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
(MỘT PHƯƠNG PHÁP NHẰM PHÁT TRIỂN TƯ DUY CHO HỌC SINH) Gửi tặng: www.toanmath.com
Tải thêm tài liệu môn Toán THPT tại:
+ Trang web: www.toanmath.com
+ Fanpage: www.facebook.com/toanmath
+ Groups: https://www.facebook.com/groups/toanmath Bỉm sơn. 13.03.2011 1
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
GIẢI TOÁN TÍCH PHÂN BẰNG NHIỀU CÁCH
(Một phương pháp nhằm phát triển tư duy)
I. TÍCH PHÂN HÀM HỮU TỶ
Bài tập giải mẫu: 3 3 x
Bài 1: Tính tích phân sau: I dx  2 x  1 0 Giải:
Cách 1: Phương pháp biến đối số Đặt x t dx   2 tan
1  tan tdt  x  3 t   Đổi cận    3 x  0  t   0  Khi đó 3 3 3 3 3
I  tan tdt  tan t    2 tan t  1  1 dt  tan t   2
tan t  1dt  tan tdt  0 0 0 0 3 3 d cos t 2  tan t  3
 tan td tan t     ln cos t     3  ln 2 cos t 2 2 0 0   0
Nhận xét: Đối với tích phân dạng I R   2 2
u, u a du, u u x thì ta có thể đặt u a tan t
Cách 2: Phương pháp tích phân từng phần 2   du  2xdx u x   Đặt  xdx   ln  2 x   1 dv     2 vx  1  2 3 3 1 3 1 Khi đó 2 I x ln  2 x   1  x ln  2 x   1 dx  3ln 2  ln  2 x   1 d  2 x     1 2 0 2 0 0  J 3 Tính J  ln  2 x   1 d  2 x    1 0 2   u     2 x   d x  1 ln 1 du  Đặt 2     dv d x 1 2 x   1  2  v x  1  2
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 1  3  3
Khi đó I  3ln 2   2 x   1 ln  2 x   1  d   2 x   1    ln 2 2  0 2 0  
Chú ý: Sở dĩ ta sử dụng được phương pháp này là vì P xf x ' Q x
Khi tính tích phân hàm phân thức mà ta phân tích được về dạng I dx dxn  thì Q xn Q xu
  f x  du Đặt '  Q x   dv dx v   n Q x 
Cách 3: Kĩ thuật tách thành tích kết hợp phương pháp đổi biến số Nhận xét: Ta có 3 2
x x .x và  x  ' 2
1  2x từ đó ta định hướng giải như sau 3 3 3 2 x x x Phân tích I dx dx  2  2 x 1 x  1 0 0 2 x t 1  Đặt 2
t x  1   dt xdx    2  x  3 t   4 Đổi cận    x  0 t  1   4 1 t   4 1 1  1 1 4 3 Khi đó I dt  1  dt    
t  ln t    ln 2 2 t 2  t  2 1 2 1 1
Cách 4: Phân tích và đưa vào vi phân 2 x  1  1 1 x 1 1  1 2  2 3 3  3  I d   x   1  d   2 x   1  1  d     2 x  1  2 2 2  2 x  1 2 x  1 2  x  1 0 0 0 d x  1 1 x 3 3 3 2  2 3 3  2  d  x   1    ln   2 x 1   2 ln 2 2  2 x  1 2 0 0 2 0 0
Cách 5: Chia đa thức để tách thành tổng hai tích phân đơn giản hơn 3 2 3 d  2 3 3 3 x x x x     1 1 3 1 I dx x dx     ln       3 3 2 x 1   ln 2 2 2 2  x  1  x  1 2 0 2 x  1 2 2 0 2 0 0 0
Nhận xét: Đây là tích phân hàm phân thức mà có bậc của tử lớn hơn bậc của mẫu chính vì thế ta chia đa thức
để tách thành tổng các tích phân là phương pháp tối ưu nhất
Cách 6: Phân tích tử thức chứa mẫu thức (thực chất là chia đa thức) Ta có 3 x x  2 x   1  x 3 2 3 d  2 3 3 3 x x x x     1 1 3 1 3 3 Khi đó I dx x dx     ln       2 x 1   ln 2 2 2 2  x  1  x  1 2 0 2 x  1 2 2 0 2 0 0 0 3
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 3 3x 3x
Bài 2: Tính tích phân bất định: I dx dx  2  x  3x  2  x   1  x  2 Giải:
Cách 1: Phân tích tử thức chứa nghiệm của mẫu thức Phân tích 3 x x  2
x x     2 3 2
3 x  3x  2  7 x   1 1 Khi đó x  2
x  3x  2  3 2 3
x  3x  2  7 x x   1 1 3 I dx dx  2  2 x  3x  2 x  3x  2 2  7 1  x 1   x  3   dx  
 3x  7 ln x  2  dx   x 2  x  1  x 2     2  x   1  x  2   2 2 x x
 3x  7 ln x  2  ln x  2  ln x 1  C
 3x  8 ln x  2  ln x 1  C 2 2
Cách 2: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và kĩ thuật “nhảy tầng lầu” Phân tích 3 x x  2
x  3x  2  3 x   1  x   1  2x   3  x  2
x x     x    x       x    x   2 3 2 3 1 2 3 2 3
x  3x  2  3 x   1  x   2  9 x   1   2x   3 Khi đó x  2 3
x  3x  2  3 x   1 
x  2  3   2x x   3 3   I dx dx  2  2 x  3x  2 x  3x  2 2  9  2x  3 x 2  x  3  dx dx
 3x  9 ln x  2  ln x  3x  2  C    2  x  2  x  3x  2 2
Cách 3: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và đồng nhất thức Phân tích 3 x x  2
x x     2 3 2
3 x  3x  2  7x  6 x x  2
x  3x  2  3 2 3
x  3x  2  7x  6 3 Khi đó I dx dx  2  2 x  3x  2 x  3x  2 2 7x  6 x
  x  3 dx dx   3x I   . 2 1 x  3x  2 2
Tính I bằng phương pháp đồng nhất thức…. 1
Cách 4: Chia đa thức để tách thành tổng hai tích phân đơn giản hơn 3 3x  9x  8  9x  8 I dx x  3  dx      x   3 dx dx 2 2   2 x  3x  2 
x  3x  2  x  3x  2  1 I
Tính I bằng phương pháp đồng nhất thức…. 1 3 3 x x
Bài 3: Tìm nguyên hàm sau: I dx dx  2  x  2x 1  x  2 1 Giải:
Cách 1: Phương pháp đổi biến số 4
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 du dx
Đặt u x 1  x u 1  u  3 3 2 2 1
u  3u  3u 1  3 1  u 1 Khi đó I du du u  3   du
 3u  3ln u   C  2  2  2  u uu u  2 u
với u x 1
Cách 2: Phân tích tử thức chứa nghiệm ở mẫu thức Phân tích 3 x x  2
x x     2 2 1
2 x  2x   1  3 x   1 1 x  2 x  2x   1  2  2 3 x  2x   1  3 x x   1 1 Khi đó I dx dx  2  2 x  2x 1 x  2x 1 2  3 1  x 1  x  2   dx  
 2x  3ln x 1   Cx 1   x  2 1 2 x  1   
Cách 3: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và kĩ thuật nhảy tầng lầu 3 Phân tích 3 x x  2 x  2x   1  2 2 x  2x   1 1  2x  2 2 x  2 x  2x   1  2  2 3 3 x  2x   1 1 2x  2 x Khi đó 2 I dx dx  2  2 x  2x 1 x  2x 1 2  1  3 2x  2 x 3 2  x  2  dx dx
 2x  ln x 1 
ln x  2x 1  C    2  x 1  2 x  2x 1 2 2
Cách 4: Kết hợp phân tích tử thức chứa nghiệm ở mẫu thức và đồng nhất thức Phân tích 3 x x  2
x x     2 2 1
2 x  2x   1  3x  2 x x  2 x  2x   1  2  2 3 x  2x   1  3x  2 Khi đó I dx dx  2  2 x  2x 1 x  2x 1 2 3x  2 x
  x  2dx dx   2x I   . 2 1 x  2x 1 2
Tính I1 bằng phương pháp đồng nhất thức
Cách 5: Chia đa thức để tách thành tổng các tích phân đơn giản 3 3 x x  3 1  I dx
dx   x  2   dx  2   x  2x  1  x  2 1  x  1  x  2 1    2 x 1 
 2x  3ln x  1   C 2 x  1
Cách 6: Sử dụng phương pháp tích phân từng phần 3 2 u   xdu  3x dx   Đặt  dx   1 dv v     x 2 1    x  1  Khi đó 5
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 2 3 2 x x x x  1  1 I    3 dx    3 dx   x  1 x  1 x  1 x  1 3 3 2 x  1  xx     3 x 1  dx    3
x  ln x  1  C     x  1  x  1  x  1 2   2 x dx
Bài 4: Tìm nguyên hàm: I     x39 1 Giải:
Cách 1: Sử dụng phương pháp đưa vào vi phân 2 2 Phân tích 2
x  1  x 1  1  x  21  x  1   x 1 x2 2  2(1 x) 1 1 2 1      1 x39 1 x39
1 x37 1 x38 1 x39 1 1 1 1 1 2 1 1 1 I dx  2 dx dx     C      x37   x38   x39
36   x36 37   x37 38 1 1 1 1 1 1 x38 Cách 2:
Đặt t  1  x x  1  t dx  dt
1 t 2 dt 1 1 1 1 1 2 1 1 1  I     dt 2 dt dt     C  39  39  38  37 38 37 36 t t t t 38 t 37 t 36 t Nhận xét:
Cách 3: Sử dụng phương pháp tích phân từng phần 2 u   xdu  2xdx   Đặt  dx  1 dv v    1 x39  38 x  38 1   1 1 x Khi đó 2 I xdx
…. đến đây các bạn có thể tự làm rồi 38 x  38 1 19  x  38 1 3 x dx
Bài 5: Tìm nguyên hàm: I   10 (x  1) Giải:
Cách 1: Sử dụng phương pháp đưa vào vi phân 3 3 2
Sử dụng đồng nhất thức: 3
x   x  
1 1   x   1  3 x   1  3 x   1  1   3 x 1 3 3 1      10 7 8 9 10 (x  1) (x  1) (x  1) (x  1) (x  1) Khi đó dx dx dx dx I   3  3    7  8  9  10 (x  1) (x 1) (x 1) (x 1) 1 1 3 1 3 1 1 1       C 6 7 8 9 6 (x 1) 7 (x 1) 8 (x 1) 9 (x  1) 6
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
Cách 2: Sử dụng phương pháp biến đổi số
Đặt t x 1 ta có: x t  1 nên dx dt t  3 3 2 1 dt
(t  3t  3t 1)dt 7  8  9  1  0 A    t dt 3  t dt 3  t dt t dt  10  10     t t 1 1 3 1 3 1 1 1       C 6 7 8 9 6 (x 1) 7 (x 1) 8 (x 1) 9 (x 1)
Cách 3: Sử dụng phương pháp tích phân từng phần 3 2 u   xdu  3x dx   Đặt  dx   1 dv v     x 10 1   9 x  9 1   Khi đó 2 1 1 x 3 I  xdx...  9  x  9 1 3  x  9 1  1 I
đến đây rùi ta có thể tính I bằng phương pháp tích phân từng phần hoặc phân tích 1 2 x   2 x  
1 1   x   1  x   1  1 Nhận xét :
- Đối với bài 3, bài 4 và mà ta sử dụng phương pháp đồng nhất thức thì giải hệ quả thật là nan giải phải không,
chính vì thể mà lựa chọn phương pháp nào mà hiệu quả và nhanh về đích nhất
Qua bài 3, bài 4 và bài 5 ta chú ý P x
- Đối với tích phân hàm phân thức có dạng I dx
thì đặt t x a là một phương pháp hiệu quả nhất
x an P xf x ' Q x
- Khi tính tích phân hàm phân thức mà ta phân tích được về dạng I dx dxn  thì ta sử Q xn Q x
dụng phương pháp tích phân từng phần nhưng nên làm khi bậc của  x a là n  1, 2 u
  f x  du Đặt: '  Q x   dv dx v   n Q x  3 3 dx dx
Bài 11: (ĐHDB – B 2004) Tính tích phân sau: I    3  x x x  2 1  x 0 0  HD:
Cách 1: Biến đổi số
Nhân cả tử và mẫu cho 2 x 3 3 3 dx dx xdx I     3   x x x  2 1  x  2 x  2 1  x 0 0 0  7
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 x t 1  Đặt 2
t  1  x   dt xdx    2
Cách 3: Biến đổi số
Đặt x  tan u … Bạn đọc tự giải
Cách 4: Đưa vào vi phân Phân tích tử   2  x  2 1 1 – x 3 3 dx x dx 1 d  2 3 3 1  x  3 1 3 6 Khi đó 2 I   dx    ln x  ln x  1  ln   2   2 x 1  x x 2 1  x 0 2 0 2 0 0 0 0 2 dx
Bài 12: Tính tích phân sau: I   5 3 x x 1 Giải:
Cách 1: Sử dụng phương pháp phân tích Cách 1.1: Phân tích: 2 2
1  x  1  x 2 2 2 2 1 x  1  x 1 1 1 x  1  x 1 1 x          3 x  2 x   3 2 3 2 3 2 3 2 1 x (x  1) x x(x  1) x x(x  1) x x x  1 Khi đó 2 2 2 1 1 x  1 1 1  2 3 1 5 2 I dx dx dx    ln x  ln x 1   ln 2  ln  3   2  2  x x x  1  2 x 2  1 8 2 2 1 1 1
Cách 1.2: Phân tích: 4 4 4
x   x x   2  x  2 1 1 1 1  x  4 x     2 1  x  2 4 4 1 1 1  x x x  2 x 1  x x  1 3        x  3 x  2 x   3 2 3 2 2 3 2 1 x (x  1) x (x  1) x  1 x x  1 x ... tự làm nhé
Cách 2: Kết hợp kĩ thuật tách thành tích và phương pháp biến đổi số 2 2 1 1 1 Phân tích I dx  . dx   3 x  2 x   2 1 x x x  1 1  2 1   1 x  1   t Đặt t    x 1 dx   dt 2   t  1 x  2 t  Đổi cận    2 x  1  t  1  8
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 1 1 2 1 3 2 t Khi đó t I   t dt  . dx ..  
đến đây lại trở thành bài 1, các bạn tha hồ mà làm nhé 2 1  1  t  1 1 1  1 2  2  2 t t
Cách 3: Sử dụng kĩ thuật nhân trên tử và phương pháp đổi biển số 2 2 1 x I dx dx   3 x  2 x   4 1 x  2 x  1 1 1  dt Đặt 2
t x  1   xdx 2 x  2 t  5 Đổi cận    x  1 t  2   5 5 dt 1  1 1 1 1  1 t  5 3 1 5 Khi đó I       dt    ln   ln 2  ln     t t  2 1 2 t  2 1 t  1 t 2 t  1 t  1 2 8 2 2 2 2     
Hoặc các bạn có thể đặt u t 1 hoặc phân tích 1  t  t  
1 hoặc đồng nhất thức
Cách 4: Sử dụng kĩ thuật nhân trên tử và phương pháp đưa vào vi phân 2 2 2 1 x 1 1 I dx   d     2x 1  3 2 4 2 4 2  x x  1 x x  1 2 x x 1 1   1   1    2 x   2 2 2 2 1 1  x 1 1 1 1  d x  1  d x  1  d x  1     4 2  2   2  2 2  2 4  2 x x  1 2 x 2 x x  1 1   1 1   2 2 1 1  dx  . dx ..  3 
ôi đến đây lại thành cách 1 rùi, lòng vòng quá, bỏ qua thui… x x  2 x  1 1 1 
Cách 5: Sử dụng phương pháp đồng nhất thức 1 A B C Dx E    
đến đây thì đồng nhất thức hai vế để giải hệ tìm I  ,
A B, C, D, E tuy nhiên 3 x  2 x   3 2 2 1 x x x x  1
việc giải hệ là phức tạp chính vì thể trong trường hợp này ta nên làm theo cách 1, cách 2 và cách 3 là hiệu quả nhất
Cách 6: Đặt x u dx   2 tan tan  
1 dt … bạn đọc tự làm 1 dx
Bài 14: Tính tích phân sau: I   3 x  1 0 Giải: Nhận xét: 3
x    x    2 1
1 x x   1
Cách 1: Dựa vào nhận xét trên ta sử dụng đồng nhất thức: 2  x   2 x   2 1
1  x   x   1  x   1 1 2 1 x x  1 Khi đó I dx
dx I I  3  2 1 2 x  1 x x  1 0 0 9
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 d  3 1 x   1 1
Tính I bằng cách đặt 3
t x 1 hoặc I  1 1  3 3 x  1 0 1 1
Tính I phân tích x  1  2x   1 
(kĩ thuật nhảy tầng lầu) 2 2 2 1 1 1 x  1 1 2x 1 1 dx Ta có I dx dx  2  2  2  2 x x  1 2 x x  1 2 0 0 0  1  3 x      2  4
Cách 2: Đồng nhất thức 1 A Bx C Xét    1  A 2
x x  1  Bx C x 1 3 2     x  1 x  1 x x  1
Đến đây ta có thể đồng nhất hệ số giải hệ tìm A, B, C hoặc cho một số giá trị riêng là 1 2 1
x  1  A
; x  0  C
; x  1  B   …Bạn tự giải tiếp nhé 3 3 3 1
Kết quả ta được I  ln 2  3 3 3
Cách 3: Đổi biến số kết hợp kĩ thuật “nhảy tầng lầu” 1 1 1 dx dx d x   1 I     3   x  1  x   1  2 x x   1   0 0 0  x   1   x  2 1  3 x   1  3
Đặt x  1  t dx dt x  0 t  1 Đổi cận    x  1 t  2   2 2 dt 1  2
t  3t  3   2 t  3t  2 2 1  dt t  3    dt    dt      t  2
t  3t  3 3 t  2
t  3t  3 2 3 t t  3t  3 1 1  1 1  2 2 1  dt 1 d  2
t  3t  3 2 3 dt         2  3 t 2 t  3t  3 2   3 t      2 2 3 1 1 1 4  2 1  1 t 2t  3  2 1   ln  3 arctan   ln 2  2 3 2 t  3t  3  3 1 3  3 3 4 3
3x  5x  7x  8
Bài 15: Tính tích phân bất định: I dx  .  x  250 Giải :
Cách 1: Biến đổi sốx t  2
Đặt x  2  t   dx dt
3x  5x  7x  8
3t  24  5t  23 4 3
 7t  2  8 Khi đó I dx dt    x  250 50 t
Cách 2: Đồng nhất tử thức chứa nghiệm của mẫu thức 10
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 4 3 2 Phân tích 4 3
3x  5x  7x  8  a x  2  bx  2  cx  2  d x  2  e … đồng nhất để tìm a, b, c, d, e …
Cách 3: Khai triển Taylor (tham khảo)
Đặt P x 4 3
 3x  5x  7x  8 4
Áp dụng khai triển taylor ta có P 2   P  2   3 P  2   4 P  2  
P x  P  2     x  2   x  22   x  23   x  4 4 4 4 4 2 4 4 1! 2! 3! 4!
P x  66 149 x  2  48 x  22  29 x  23  3 x  24 4
66  149 x  2  48 x  22  29 x  23  3 x  24  I dx   x  250     
66 x 2 50 149 x 2 49 48 x 2 48 29 x 2 47 3 x  46 2             dx  66 149 48 29 3       C 49  x  249 48 x  248 47  x  247 46 x  246 45 x  45 2 1 5 2 2 x  1
Bài 16: (ĐHTN – 2001) Tính tích phân sau: I dx  4 2 x x  1 1 Giải: 1 5 1 5 1 1 5  1  1  1  2 2 2 2  2  2 x  1 xx  Ta có dx dx dx  4 2   2 x x  1 1 2 1 1 1  1 x 1    2 x   1 x    x  1  1 
Đặt t x   dt  1  dx  . 2  xx  x  1  t   0 Đổi cận  1  5   x t  1    2 1 dt Khi đó I   . Đặt t u dt   2 tan
1  tan udu . 2 1  t 0 u   0 t   0  Đổi cận    t  1  u    4 1 4 2 4 dt 1  tan u Khi đó I  
du du u 4  .  2  2  1  t 1  tan u 4 0 0 0 0 Cách khác: 11
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 1  1 
Ta có thể gộp hai lần đặt là x   tan u  1  dx     2
1  tan u du … bạn đọc tự giải 2  xx  2 2 x 1
Bài 17: Tính tích phân: I dx  4 x 1 1 Giải:
Cách 1: Chia cả tử và mẫu cho 2
x  0 ta được 1 1 2 1  2 1  2 2 Biến đổi x x I dx dx   2 1 2 1 1  1 x   2 x   2 x    x  1  1 
Đặt u x   du  1  dx  2  xx  5 2 du 1 u  2 5/ 2 1 (5  2 2)(2  2) Khi đó I   ln   ln 2 u  2 2 2 u  2 2 2 2 6  2 2 2 Cách 2: Phân tích 4 x    2 x   2  x   2 x x   2 1 1 2 2
1 x  2x  
1 và sử dụng đồng nhất thức 2 x  1 Ax B Cx D  
… đồng nhất hệ số tìm A, B, C và D nhưng cách này dài và rất phức tạp 4 2 2 x  1 x  2x  1 x  2x  1 nên không đưa ra Nhận xét:
- Qua các ví dụ trên ta thấy kĩ thuật chia thực sự rất hiệu quả trong việc chuyển tích phân ban đầu thành tích phân đơn giản hơn
- Thông thường để sử dụng kĩ thuật chia thì trên tử là một đa thức bậc hai P x 2
x 1 còn mẫu là một đa thức bậc 4:   4 3 2
Q x ax bx cx dx e sao cho hệ số a e  1  1  1  1  1 
- Tích phân trên đưa về dạng I f x  1  dx    
đặt t x   dt  1  dx 2   2   x  x xx
Tương tự ta có thể giải bài toán này 2 2 x 1
1. Tính tích phân sau I dx  4 x 1 1 1 1 2 1  2 1  2 2 x x 1  1  I dx dx  
. Đặt u x   du  1  dx 2 1  2  2 xx  1 1  1 x   2 x   2 x    x
2. (ĐHQGHN – A 2001) Tính tích phân bất định sau: 12
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 2 x  1 1 x  5x  1 I dx   ln  C
  2x 5x  1 2x 3x   2 1 8 x  3x  1 1 4
Bài 18: Tính tích phân sau: 3 I x  4 x    1 dx 0 Giải:
Cách 1: Sử dụng phương pháp biến đổi số dt Đặt 4 3 3
t x  1  dt  4x dx x dx  4 x  1 t  2 Đổi cận    x  0 t  1   1 2 4 1  1  2 31 Khi đó 3 I x   4 x   4 5 1 dx t dt t  .    4  20  1 20 0 1
Cách 2: Sử dụng phương pháp biến đổi số dt Đặt 4 3 t x   x dx 4 x  1 t  1 Đổi cận    x  0 t  0   1 1 5 1 4 1 1  t  1 31 Khi đó I
1 tdt    2 3 4
1  4t  6t  4t t  2 3 4 dt
t  2t  2t t     4 4 4 5 0 20 0 0  
Cách 3: Sử dụng phương pháp biến đổi vi phân 4 4 x  1 1 1 1 31 3 4 4 4  5 4 1 1 I x x   1 dx   x  
1 d x   1  .    4 4 5 0 20 0 0
Cách 4: Sử dụng phương pháp phân tích 4 Phân tích 3 x  4 x   3  x  16 12 8 4
x x x x     19 15 11 7 3 1 4 6 4 1
x  4x  6x  4x x  1 1 20 16 12 8 4 4  x x x x x  1 31 Khi đó 3 I x   4 x   1 dx   19 15 11 7 3 x
 4x  6x  4x x dx         20 4 2 2 4 0 20 0 0  
Nhận xét: Mỗi cách giải có một đặc thù riêng nên lựa chọn cách nào là phù hợp hơn, tùy vào mỗi người, theo
tôi cách 1 và cách 3 là hiệu quả nhất 1 6 1
Bài 19: (ĐH KTQD – 1997) Tính tích phân sau: 5 I x  3
1  x dx   168 0 Giải: 1 1 6 6 Ta có 5 I x   3 1  x  3 dx x   3 1  x  2 x dx 0 0
Cách 1: Đổi biến số 13
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 dt 2   x dx Đặt 3
t  1  x   3 3 x  1  t  x  1 t  0 Đổi cận    x  0 t  1   0 1 1 7 8 1 1 1 1  t t  1 6 I   t 1  t  6 dt
t 1  tdt     6 7
t t dt      3 3 3 3 7 8 168 1 0 0  
Cách 2: Đưa vào biểu thức vi phân 1 1 1 1 I x
 1 x 6 dx x 1   
1 x 1 x 6 dx x
 1 x 6 dx x  1  x 7 5 3 2 3 3 2 3 2 3 dx   0 0 0 0 6 7 1 1 1  x 1 1 1  x 1 1 3 3 3 3  7  8 3 3 1 1
  1 x d 1 x   1 x d 1 x    .  .  3 3 7 0 3 8 0 168 0 0
Cách 3: Khai triển   6 3 1 x
thành tổng các đa thức  x   x 6 5 3 1
.. cách này không khó nhưng khai triển phức
tạp… chỉ tham khảo thôi
Chú ý: Nếu ta đặt 3
t x cũng ra nhưng sẽ dài và phức tạp, bạn đọc có thể tham khảo 2 2
Bài 20: Tính tích phân sau I x x   1 dx  0 Giải:
Cách 1: Sử dụng phương pháp phân tích 2
Ta có x x    x  2 x x   3 2 1 2
1  x  2x x 2 4 3 2  x 2x x  2 34 Khi đó I   3 2
x  2x xdx       4 3 2 0 3 0  
Cách 2: Sử dụng phương pháp đưa vào vi phân 2 2 3 2
Ta có x x   1    x   1 1  x   1   x   1   x   1    x  4 1  x  3 2 2 2 2 3 2 3 2 1 34
Khi đó I   x  
1 dx   x  
1 dx   x  
1 d x   1   x   1 d x   1        4 3 3 0 0 0 0
Cách 3: Đổi biến số x t 1
Đặt t x  1  dx dt  x  2 t  3 Đổi cận    x  0 t  1   3 3 4 3  t t  3 34
Khi đó I  t   2 1 t dt    3 2
t t dt      4 3 1 3 1 1  
Cách 3: Sử dụng phương pháp tích phân từng phần 14
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498    2 du 2  x  1 dx u     x   1  Đặt 2    xdv xdx  v   2 2 2 2 4 3 2 x 2    x x 2 34
Khi đó I   x   2 1
x x   1 dx  6    3
x x dx  6      2 0 4 3 0 3 0 0   0 9
Bài 21: Tính tích phân sau: 2 I x x   1 dx 1 Giải:
Cách 1: Biến đổi số
Đặt t x 1  dt dxx  1  t   0 Đổi cận    x  0 t  1   Khi đó 0 1 1 1 I x x  9
1 dx  t  2 2 9 1 t dt   
 2t  2t   9 1 t dt  11 10 9 t  2tt dt 1 0 0 0 12 11 10  t t t  1 1 2 1 1   2        12 11 10 0 12 11 10 660  
Cách 2: Phương pháp phân tích 2 Phân tích 2
x   x   1  2 x   1  1 Khi đó 0 0 0 I x x  9 1 dx    x  2 1  2 x  
1  1  x  9 1 dx    x  11 1  2 x  10 1   x  9 2 1  dx        1 1  1   x 12 1  x 11 1  x 10 1     0 1    2    12 11 10 1    660   Hoặc phân tích 2
x theo x   1 như sau
x x  9   x      x  9    
x   x       
x  9  x  11   x  10  x  9 2 2 1 1 1 1 1 1 2 1 1 1 2 1 1 Nhận xét:
- Với bài toán này ta sử dụng phương pháp phân tích tức là khai triển  x  9
1 hay phương pháp tích phân từng
phần như bài 20 thì cũng ra nhưng rất dài và phức tạp vì bậc của  x   1 là lớn 1
Bài 22: Tính tích phân: 2 10 I
(1  3x)(1  2x  3x ) dx 0 Giải:
Cách 1: Đổi biến số dt Đặt 2
t  1  2x  3x dt  (2  6x)dx dt  2(1  3x)dx   (1  3x)dx 2 15
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 x  0 t  1 Đổi cận:    . x  1 t  6   10 11 11 11 11 6 6 dt t t 6 6 1 6 10 I tdt     1   1 1 2 2 22 1 22 22 22
Cách 2: Đưa vào vi phân 1 1 10 10 ' 1 I  1  3x   2
1  2x  3x dx   2
1  2x  3x   2
1  2x  3x dx 0 2 0 10 1  2x  3 1 x 1 6 2 2  11 2 1 11 
1 2x  3x d 1 2x  3x     1 2 22 0 22 0
Bài tập tự giải có hướng dẫn: 2 3 3x
Bài 1: (ĐHV – D 2000) Tính tích phân sau: I dx  2 x  2x  1 0
Đs: I  9 ln 3  8 2 2 x 1
Bài 2: Tính tích phân sau: I dx   2 x  3x   1  2 x x  1 1  HD:
Chia cả tử và mẫu cho 2 x ta được 1 2 1  2 x I dx   1  1  1 x   3 x   1      x   x  1  1 
Cách 1: Biến đổi số đặt t x   dt  1  dx  2  xx
Cách 2: Biến đổi vi phân 1  1   d x  2 1 2   2 xx  1   1   1  2 I dx dx  ln x  1  ln x   3        1 1 1 1          2   x   x  1 1 1 x 3 x 1 x 3 x 1                   x   x   x   x  1 7  ln 2 10
Cách 3: Đồng nhất thức 1 5 x
Bài 3: Tính tích phân sau: I d . x  2 x  1 0 HD: Đồng nhất thức: 5 3 2 2
x x (x  1)  x(x 1)  x 16
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 1 1  x  1 1 1  1 1 3 4 2 2
I   x x dx   x x  ln( x 1)]  ln 2  .  2  x  1   4 2 2    2 4 0 0
Hoặc chia tử cho mẫu để tách thành tổng các tính phân đơn giản Hoặc đặt x  tan t 1 x
Bài 4: (ĐHKT – 1994) Tính tích phân sau: I dx    x3 0 1 2 HD: 1 x 1  1 1  1
Phân tích x  1 2x   1    
ta được I  2 1 2x3
2 1 2x2 1 2x3  18  
Hoặc đặt t  1  2x Hoặc tích phân từng phần 1 2 x  3 21 13
Bài 10: Tính tích phân: I dx   ln 2  ln 3  x 4 2 x  3x  2 4 4 1  2 HD:
Cách 1: Nhân cả tử và mẫu cho x rồi đặt 2 t x
Cách 2: Phân tích mẫu x  4 2
x x    x 2 x   2 3 2
1 x  2 và sử dụng đồng nhất thức 1 2x  5 1 5
Bài 5: Tính tích phân: I dx  ln
  2x 3x  2 2x 7x 12 2 4 0  HD: Phân tích  2
x x   2 x x
   x   x   x   x     2
x x   2 3 2 7 12 1 2 3 4 5 4
x  5x  6
Cách 1: Sử dụng đồng nhất thức khi mẫu số là 4 nghiệm đơn
Cách 2: Sử dụng đổi biến số đặt 2
t x  5x
Cách 3: Sử dụng phương pháp phân tích 1 2x  5  2x  5  2
x  5x  6   2
x  5x  4 2   1 2 x  2 3
Bài 6: Tính tích phân: I dx    4 3 2
x  2x  5x  4x  4 44 1 2 HD:
Phân tích x x x x
  x x  2 4 3 2 2 2 5 4 4 2
Cách 1: Đồng nhất thức 2
Cách 2: Chia cả tử và mẫu cho 2
x và đặt t x
Hoặc đưa vào vi phân x 0 2 x dx
Bài 7: Tính tích phân sau: I   x  3 2 1 1 HD:
Cách 1: Đặt x  tan t
Cách 2: Sử dụng phương pháp tích phân từng phần 17
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 u   x  Đặt xdxdv   x  3 2 1 
Cách 3: Sử dụng phương pháp phân tích thành hai tích phân đơn gián Phân tích 2 x   2 x   1 1 0 2 0 0 x dx dx dx Khi đó I         x  3 1   x  2 1   x  3 2 2 2 1 1 1 1
II. TÍCH PHÂN HÀM VÔ TỶ
Bài tập giải mẫu: 7 3 x  1
Bài 1: (ĐHGTVT – 1998) Tính tích phân: I dx  3 3x 1 0 Giải:
Cách 1: Biến đối số 3  u  1 x  Đặt 3 u  3x  1   3 2 dx u du   7 x u   2 Đổi cận  3  u 1 x  0   3 u 1 2 1 2 5 1 1 1  u  2 46 Khi đó 3 2 I u du    3
u  2 udu   4 u  2u 2 du   u    u 3 3 3 5 1 15 1 1  
Cách 2: Biến đối sốu  1 x    3
Đặt u  3x  1   dudx    3  7 x u   8 Đổi cận  3  u 1 x  0   18
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 u  1 5    8 1 8 8 2 1 2 3 1 1 u  2 1    1  3u 8  46 Khi đó 3 3 3 3 I du du   u  2udu   3u   1  1  3 9 9 9  5  1 15 1 3 1 3 1 u u      
Cách 3: Đưa vào vi phân 1 2 Phân tích x  1  3x   1  3 3 Khi đó 7 1 2 7 7 7 7 3 3x   1  3 3 3 2 3 1 1 3x  1 2 dx 1 2 3 3  I dx dx   3x  3
1 d 3x   1  3x   3 1 d 3x   1      3 3 3 3x  1 3 3x  1 3 3x  1 9 9 0 0 0 0 0 7 7 5 2 1 1 46  3x  3 1 3  3x  3 1 3  15 3 15 0 0
Cách 4: Tính phân từng phần u   x  1 du dx   Đặt 2  1   1 dv dx v  3x    3 1 3  3x  1  2 Khi đó 7 7 2 7 2 3 1 1 3x  3 2 3 1 1 1 1 I   x   1 3x  3 1 
dx   x   1 3x  3 1 3  3x  3
1 d  3x   1 ...   bạn đọc tự giải 3 2 2 3x  1 2 6 0 0 0 1 3 x
Bài 2: Tính tích phân: I dx  0  2 1 x  1 HD:
C1: Đặt x  tan t C2: Phân tích 3 x x  2 x   1  x 2 u   xC3: Đặt  x dv dx  2  x  1
C4: Đặt x tC5: Phân tích 3 2
x dx x xdx   2
x     d  2 1 1 x   1   2 dx
Bài 3: (ĐHBKHN – 1995) Tính tích phân sau: I   2 2 x x  1 Giải:
Cách 1: Phương pháp biến đổi số 19
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 1 sin tdt 1 Đặt x   dx  với t  0; hoặc x  2   cos t cos t  2  sin t   2 t x     3 Đổi cận    x  2 t     4 sin t 3 3 3 2 sin cos t t 3    Khi đó I dt
dt dt t     (vì t  ;  sin t  0   ) 2 sin t 12  4 3 1  cos t  4 4 4 2 4 cos t
Cách 2: Phương pháp biến đổi số
Nhân cả tử và mẫu cho x ta được 2 2 dx xdx I     2 2 2 2 x x  1 2 x x  1 2 2 x t 1 Đặt 2
x  1  t   xdx tdt  x  2  t    3 Đổi cận    x  2  t  1  3 3 tdt dt 1 Khi đó I    
. Đặt t  tan u dt du   2 tan u  1 du 2  t  2 t  1 t  1 cos u 1  2 1  u t    3   3 Đổi cận    t   1 u     4 4 2 4 tan u  1 4 Khi đó I
du du u   2  tan u  1 12 3 3 3
Cách 3: Phương pháp biến đổi số 2 x t 1  Đặt 2
x  1  t   1 … tương tự như cách 2 xdx dt   2
Cách 4: Phương pháp biến đổi số 1 1 dx Đặt x    t   dt 2 t x x 20
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498  1 t  x 2     2 Đổi cận    x  2 1  t     2 1 1 2 2 dt dt Khi đó I     
. Đặt t  sin x dt  cos xdx 2 2 1 1  t 1 1  t 2 2 4 4 cos u 4 Khi đó I
dx du u      2 4 6 12 1  sin u 6 6 6
Cách 5: Phân tích    2 x   2 1 1  x    2 2 2 2 dx x  1 x Khi đó I    dx dx    … bạn đọc tự giải 2 2 x 2 x x  1 2 2 x  1
  I I 1 2 2 3 dx
Bài 3: (ĐH – A 2003) Tính tích phân: I   2 5 x x  4 Giải:
Cách 1: Phương pháp biến đổi số 2 2 x t  4 Đặt 2 t
x  4  xdx tdt   x  2 3 t  4 Đổi cận   t  3 x  5   4 4 4 dt 1  dt dt  1 t  2 4 1 5 Khi đó I       ln  ln  2   t  4 4 t  2 t  2 4 t  2 3 4 3 3  3 3 
Cách 2: Phương pháp biến đổi số 1 1 Đặt x   dx   dt 2 t t 1/ 2 3 1/ 2 3 dt 1 d (2t) 1 1 / 2 3 1 5 Khi đó 2 I   
  ln 2t  4t 1  ln   . 2 2 2 2 4 3 1/ 5 4t  1 1/ 5 (2t)  1 1 / 5
Cách 3: Phương pháp biến đổi số 2 Đặt x t dx   2 2 tan
2 1  tan t dt với 0  t  và 2 x  4  . 2 cost 21
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 t   x  2 3   3 Đổi cận:    . x  5 5  tan   2 3 1 dt t 1 5 1  cos 1 Khi đó: I   ln tan 3  ln  (trong đó tan   ) 2 sin t 2 4 3 2 1  cos 5 1
Bài 4: (ĐHDB – A 2003) Tính tích phân sau: 3 2 I x 1  x dx  0 Giải: 1 1 Phân tích 3 2 2 2 I x 1  x dx x 1  x .xdx   0 0
Cách 1: Phương pháp biến đổi số 2 2 x  1  t Đặt 2
t  1  x  xdx tdt  x  1 t  0 Đổi cận    x  0 t  1   1 0 1 1  1 1  2 Khi đó 2 I   t   2 1  t  2 dt t   2
1  t dt   2 4 t t  3 5 dt t t     3 5  15 1 0 0 0
Cách 2: Phương pháp biến đổi số 2 x  1  t  Đặt 2
t  1  x   dt xdx     2 x  1 t  0 Đổi cận    x  0 t  1   1 0 1 1 1 1 1 3 3 3 1 1 1   1  2 2  2 Khi đó 2 I   t 1  t 2 dt t 1  t 2 2 2 2 dt   t t dt   t t      2 2 2 2 3 3 15 1 0 0     0 dt Cách 3: Đặt 2 t x   xdx … tự giải 2
Cách 4: Lượng giác hóa
Đặt x  cos t dx   sin tdt 2 2 Khi đó 2 3 2
I  sin t cos tdt  sin t    2
1 sin t costdt 0 0 Cách 4.1.
Đặt sin t u  cos tdt du Khi đó 22
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 1 3 5  u u  2 2
I u (1  u )du    2 4
u u du     3 5 0   Cách 4.2. 2 2 3 5  sin t sin t  2 2 I  sin t   2
1  sin t d sin t   2 4
sin t  sin td sin t   2    . 3 5 15 0 0   0 Cách 4.3. 2 2 2 2 1 1 1 cos 4t 1 1 2 I
sin 2t costdt  cos tdt  cos tdt   cos 4t costdt     …. 4 4 2 8 8 0 0 0 0
Cách 5: Phương pháp đưa vào biểu thức vi phân 1 1 1 1 2 2 I   x 1  x d   2 1  x    2 1  x   2 1 1  x d  2 1  x  2 2 0 0 ….bạn đọc tự giải 1 3 1 1   1 2
1  x d  2 1  x  2  1  x d   2 2 1  x  2 2 0 0
Cách 6: Phương pháp tích phân từng phần 2 du  2xdx u   x   Đặt 2    1
dv x x  1 v     2 2 x  3 1  3 2 1 2 1 2 1 1 2 1 Khi đó 2 I x .  2 x   1  x  2 x   1 dx    2 x   1 d  2 3 3 3 x    
1 ... bạn đọc giải tiếp 3 0 3 3 0 0 2 x
Bài 5: (ĐH – A 2004) Tính tích phân: I dx 1 x 1 1 Giải: Cách 1: Đặt 2 2 t
x 1  t x 1  x t  1  dx  2tdt x  2 t  1 Đổi cận    x  1 t  0   Khi đó 1 2 1 3 1 t  1 t t  2 2  I  2tdt  2 dt  2
t t  2  dt     1  t t  1  t  1 0 0 0 1 3 2  t t   1 1  11  2 
 2t  2 ln t  1  2   2  2 ln 2   4 ln 2     3 2    3 2  3 0
dx  2 t   1 dt
Cách 2: t  1  x  1  
x  t  2 1  1  23
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 x  2 t  2 Đổi cận    x  1 t  1   t   1 t  2 2   2 1 1 3 2 2  
t  3t  4t  1  1  Khi đó 2 I  2 .dt  2 .dt  2
t  3t  4  .dt     t tt  1 1 1 3 2  t t  2 5  2  3
 4t  ln | t |   2 ln 2   3 2 1 3   b p(x) Tổng quát: dx
với p x là một đa thức chứa x, m, n, c là các hằng số ta đặt t ax b c hoặc
ax b c a t ax b 3 8  3x
Bài 6: Tính tích phân sau: I dx  2 4 x 2 Giải:
Cách 1: Dựa vào đạo hàm 8  3x
Đặt f x 
. Ta biến đổi f x về dạng 2 4  x 8  3x 1  f x   4  x    x
4  x   4  x ' ' x 2 4  x 2 4  x ' '
Xét hàm số F x  x 4  x vì '
F x   x
4  x   4  x x f x
Vậy F x  x 4  x C là một họ nguyên hàm của hàm số đã cho 3 8  3x 3 3 Khi đó I
dx F x  x 4  x  3  2 4  x 2 2 2
Cách 2: Sử dụng phương pháp đổi biến số 2 x  4  t Đặt t
4  x  dx  2  tdt  x  3 t   1  Đổi cận    x  2  t   2  8  3 2 1 4  t  2 2 Khi đó I   tdt     2
3t  4 dt   3 t  4t   3 t 1 2 1
Cách 3: Sử dụng phương pháp đổi biến số
Đặt t  4  x …bạn đọc tự giải
Cách 4: Sử dụng phương pháp tích phân từng phần u   8  3x  du  3dx  Đặt  dx   dv   v  2  4  x   4  x 24
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 3 Khi đó I  2
 8  3x 4  x  6 4  xdx .  ...3  2 2 x2dx x2dx
Bài 7: Tính tích phân sau: I     . (  x x2 )  x x2 [  (x 2  ) ]  (x 2 4 2 2 2 3 1 3  1) Giải: Cách 1:
dx   3 sin tdt Đặt x 1  3 cos t   2 2
x  3cos t  2 3 cos t  1   3 sint(3 2
cos t  2 3 cost  1)dt  2 3 cost 2 Khi đó I =   1 (    )dt . 2  3
(  3cos t) 3 sint 3  3 2 cos t 3  3 2 cos t Cách 2: dx 2 ( x  4 d ) x I =     I I 1 2 2 2x x2 3 [  (x 1 2 ) ] 3 (x 1 2   ) (2x  ) 4 dx 2tdt dt Tính I    2  J J 2    1 2 [3 (x  ) 1 2 ] 3 (x  ) 1 2 (3 2  t ) 3 2  t (3 2  t ) 3 2  t
Tính J bằng cách đặt 2
3  t u , tính J bằng cách đặt 2
3  t u  3  t 1 2
Bài tập tự giải có hướng dẫn: 7 1
Bài 1: (ĐHĐN- 1997) Tính tích phân: I
dx  2  4 ln 2  2 ln 3  2  x  1 2
HD: Sử dụng phương pháp biến đổi số Đặt t
2  x 1 Hoặc t  2  x 2 x  1 1
Bài 2: (ĐHSP QN – 1999) Tính tích phân: I     3 28  3 4 3  3x  2 10 0 7 x  2 231
Bài 13: (DBĐH 2 – A 2005) Tính tích phân: I    3 x  1 10 0 3 x 12
Bài 14: (DBĐH 1 – A 2008) Tính tích phân: I dx   3 2x  2 5 1  2 4 2x  1
Bài 15: (DBĐH 1 – A 2007) Tính tích phân: I dx  2  ln 2  1  2x  1 0 3 x  3
Bài 16: (CĐXD – 2005) Tính tích phân: I dx      3 x 1 x 3 1 25
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
III. TÍCH PHÂN HÀM SỐ MŨ VÀ LOGARIT
Bài tập giải mẫu: e 3 2 ln . x 2  ln x
Bài 1: (PVBCTT – 1999) Tính tích phân sau: I dxx 1 Giải:
Cách 1: Phương pháp biến đổi số
Đặt ln x u
Cách 2: Phương pháp biến đổi số 3 ln x Đặt 3 2 3 2 2
2  ln x t t  2  ln x t dt dx 2 x 3 x e t    3 Đổi cận    3 x  1  t   2  3 3 3 3 4 3 3 3 3 t 3 3 Khi đó 2 3 I t.t dt t dt  .     3 3 3 3  2 2  3 2 2 2 4 8 3 3 2 2 2
Cách 3: Phương pháp biến đổi số dt ln x Đặt 2
2  ln x t   dx 2 xx et  3 Đổi cận    x  1 t  2   3 1 4 1 1 3 2 3 Khi đó 3 3 I t dt  . t    3 3 3 3  2 2  2 2 4 1 8 2
Cách 4: Phương pháp đưa vào biểu thức vi phân e 1 e 1 1 I
2  ln x 2  ln x' 1 2 2 dx   2
2  ln xd  2 3 3 2  ln x 2 2 1 1 4 1 3 e  .  3 2
2  ln x3   3 3 3 3  2 2  2 4 1 8 e 1  3ln x.ln x
Bài 2: (ĐH – B 2004 ) Tính tích phân sau: I dxx 1 Giải:
Cách 1: Phương pháp biến đổi số 2  t  1 ln x    Đặt 3
t  1  3ln x  dx 2   tdt   x 3 26
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 x et  2 Đổi cận    x  1 t  1   2 2 2 5 3 2 t  1 2 2  t t  2 116 Khi đó 2 4 2 I t dt  (t t  )dt        3 3 9 9 5 3 1 135 1 1  
Cách 2: Phương pháp biến đổi số t  1 ln x    3
Đặt t  1  3ln x  dx dt     x 3 x et  4 Đổi cận    ... tương tự cách 1 x  1 t  1  
Cách 3: Phương pháp đưa vào biểu thức vi phân e 1  3ln x.ln x 1 e 1 e I dx
1  3ln x.ln xd 1  3ln x  1  3ln x
 1  3ln x 1d 1  3ln x    x 3 9   1 1 1 e 3 e 1 1 1 
1 3ln x2 d 1 3ln x 
1  3ln x2 d 1  3ln x   9 9 1 1 5 3 1  2 2  e 116 
1 3ln x2  1  3ln x2  9  5 3    1 135 dx
Cách 4: t  ln x   dt x 1 Khi đó I  1  3t .tdt... 
đến đây rùi ta có thể làm bằng nhiều cách như biến đổi số đặt u  1  3t hoặc 0 1 1
u  1  3t hoặc đưa vào vi phân bằng cách phân tích t  1  3t  3 3 e 1  ln x
Bài 3: Tính tích phân sau: I dxx 1 Giải:
Cách 1: Phương pháp biến đổi số dx Đặt 2
t  1  ln x t  1  ln x  2tdt xx  1 t   1  Đổi cận    x et   2  e 2 2 3 2 2 2  1 1  ln x t 2 2   Khi đó I dx t.2tdt 2  t dt 2  .    x 3 1 3 1 1 1
Cách 2: Phương pháp đưa vào biểu thức vi phân 27
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 e e 2 2 2  1 1  ln x 2 3 e   Biến đổi I dx
1  ln xd 1  ln x  1 ln x  .   x 3 1 3 1 1
Cách 3: Phương pháp biến đổi số
Đặt t  1  ln x hoặc t  ln x e ln x
Bài 4: (ĐH – B 2010) Tính tích phân sau: I dx
x 2  ln x2 1 Giải:
Cách 1: Phương pháp biến đổi số dx
Đặt t  ln x   dt xx e t   1 Đổi cận    x  1 t  0   1 1 1 udu  1 2  d 2  u
1 d 2  u  2  1 3 1 Khi đó I     du   2  ln 2  u   ln        2  u2  2  u 2  u2  2  u 2  u2  2  u  0 2 3 0 0 0 0  
Cách 2: Phương pháp biến đổi số
ln x t  2 
Đặt t  2  ln x  dx dt   x 3 t  2 3 1 2   2  3 3 1 Khi đó I dt   dt  ln t   ln   2  2    tt t   t  2 2 3 2 2
Cách 3: Phương pháp đưa vào biểu thức vi phân e ln e x ln 2  ln  e 2  ln   2 e  2  ln  e xd x x d x
d  2  ln xI dx   d 2  ln x   2  2  2  2    
x 2  ln x 2  ln x 2  ln x 2  ln x  2  ln x2 1 1 1 1 1  2  e 3 1
 ln 2  ln x   ln     2  ln x  1 2 3
Cách 4: Phương pháp tích phân từng phần  1 u   ln x du     x Đặt 1   dv dx   1 
x 2  ln x2 x      2  ln x e 3 1 e 1 1
d 2  ln x 1 e 1 3 Khi đó I   ln . xdx     
 ln  2  ln x    ln   2  ln x 1 x 2  ln x 3 2  ln x 3 1 3 2 1   1 e 1
Bài 4: Tính tích phân sau: I dxx 1 ln x 1   Giải:
Cách 1: Phương pháp biến đổi số 28
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 dx
Đặt t  1  ln x dt xx  1 t  1 Đổi cận    x e t  2   e 2 1 dt 2 Khi đó I dx   ln t  ln 2.   x 1  ln x t 1 1   1
Cách 2: Phương pháp đưa vào biểu thức vi phân e 1
e d 1 ln xe Biến đổi I dx   ln 1  ln x  ln 2   x 1  ln x 1  ln x 1 1   1
Cách 3: Phương pháp biến đổi số
Đặt: t  ln x e sin ln x
Bài 5: Tính tích phân sau: I dxx 1 Giải: Cách 1: dx
Đặt t  ln x dt xx  1 t   0 Đổi cận    x e t  1   1 1
Khi đó I  sin tdt   cos t
  cos1  cos 0  1  cos1  0 0
Cách 2: Phương pháp đưa vào biểu thức vi phân e sin ln  e x e Biến đổi I
dx  sin ln xd ln x  cosln x  1  cos1   x 1 1 1 2 e dx
Bài 6: Tính tích phân sau: I   5 x ln x e Giải:
Cách 1: Phương pháp biến đổi số dx
Đặt t  ln xdt xx et  1 Đổi cận    2 x e t  2   2 e 2 dx dt  1  2 15 Khi đó I      .  5  5  4  x ln x t  4t  1 64 e 1
Cách 2: Phương pháp đưa vào biểu thức vi phân 2 2 e e 2 dx  1 e 15 Biến đổi 5 I   ln
xd ln x     5  4 x ln x 4 ln x e 64 e e 29
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 ln x ln 2 1
Bài 7: Tính tích phân sau: I dx     2 x 2 2 1 Giải:
Cách 1: Đổi biến và sử dụng tích phân từng phần dx Đặt t  ln t
x e x dt xx  2 t   ln 2 Đổi cận    x  1 t  0   ln 2 ln 2 t Khi đó t I dt e tdtte 0 0 u   tdu dt Đặt    tt dv e dt v  e   ln 2 ln 2 tt ln 2 ln 2 t ln 2 1 Khi đó I tee dt    e     0 2 0 2 2 0
Cách 2: Tích phân từng phần  1  1 u du     2  xx Đặt:    2 ln x ln xdv dx v      x   2 2 2 1 ln x 1 ln x Khi đó I  .  dx  2 x x 2 x
Cách 3: Tích phân từng phầndx u   ln x du     x Đặt  dx   dv  1  2 v x      x 1 2 2 2  1  dx 1  ln 2 1 Khi đó 2 I   ln x   .   ln 2  x dx        1 1 x 1  x x 2 2 2 1 x e
Bài 8: Tính tích phân sau I dxx x e e 0 Giải:
Cách 1: Sử dụng tích phân liên kết 1  x e
Liên kết của I là J dxxx e e 0 Ta có 1 x 1  x 1 e e I J dx dx dx  1  xxxxe e e e 0 0 0 30
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 1  1 d   xx x x e e e e  2 1    e I J dx   ln x x e e  ln e e    xxxx  1 1  ln 2 ln e e e e 0 2e 0 0 2 2 2 e  1 1  e  1 1 e  1
Cộng lại ta được 2I  1  ln  I  1  ln  ln   2e 2 2e 2 2  
Cách 2: Sử dụng phương pháp biến đổi số Đặt x x
t e dt e x  1 t   e Đổi cận    x  0 t  1   e e e d dt t  2t   2 1 1 1 e 1 e  1 Khi đó I   dt   ln     2t 1  ln 2 2  1 t  1 2 t  1 2 1 2 2 1 1 1 t t
Cách 3: Phương pháp biến đổi số e x e x e e . x e I dx dx   2 1 x x e  1 1 1 e x e dt Đặt x e  tan x t e dx    2 tan  1 dt 2  cos t e tan x 1 Khi đó I    2
tan  1 dt  tan xdx   ln cos x   ln 2  ln cos  ) 2   (với arctan e tan  1 2 1 4 4 ln 5 2 x e
Bài 9: (ĐH DB – B 2003) Tính tích phân sau: I dxx ln 2 e  1 Giải:
Cách 1: Tách thành tích để sử dụng phương pháp biến đổi số x 2  e t 1 Đặt x
e 1  t   xe dx  2tdt  x  ln 5 t   2 Đổi cận    x  ln 2 t  1    2 2 t   2 1 tdt 2 2 2 20 Khi đó I  2  2  2 t   3 1 dt t  2t    t 3 1 1 3 1 1
Cách 2: Tách thành tích để sử dụng phương pháp biến đổi số x  e t  1 Đặt x
e 1  t   xe dx tdt  x  ln 5 t   4 Đổi cận    x  ln 2 t  1   31
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 4 t   4 1 4 3 1 5 3 1 tdt   2 4 2 4 20 Khi đó I   t   2 2 2 2 2
1 t dt   t t dt tt   1   5 1 3 1 3 1 1 1 2 t  
Cách 3: Sử dụng phương pháp tích phân từng phần ln 5 2 x ln 5 x e e . x e Phân tích I dx dx   x x ln 2 e  1 ln 2 e  1 x u   e xdu e dx   Đặt xe   dv dx  v  2 x e 1 x   e  1 Khi đó ln 5 ln 5 ln 5 ln 5 x x x x x I e e   e e dx  
e d x e   4    x e   x 20 .2 1 2 1. 16 2 1 1 16 1 e 1    ln 2 3 3 ln 2 ln 2 ln 2
Hoặc có thế tính nhanh như sau ln 5 ln 5  2 x   x 1 ln 5  2 x x 1  2 x x I e d e e e e e 1dx  ln 2 ln 2 ln 2 ln 5 ln 5 x
e d x e   4    x e   x 20 =16 2 1 1 16 1 e  1   3 3 ln 2 ln 2
Cách 4: Đưa vào biểu thức vi phân ln 5 2 ln 5 ln 5 e e e     xx x x 1 ln 5 1 I dx d   e   x 1 1  dx   e 1   d    x e   1 x x x x ln 2 e  1 ln 2 e  1 ln 2 e  1 ln 2  e  1  ln 5 3 1  2    x e   x 20 2 1  2 e  2 1    3 3   ln 2 3 dx
Bài 10: (ĐH – D 2009) Tính tích phân sau: I   x e  1 1 Giải:
Cách 1: Sử dụng phương pháp đồng nhất thức 1   x   1 x ee Khi đó 3 3 x 3 3 x 1 d e e     1 3 3 I dx  1  
dx   dx   x  ln x e 1  x     e  1 x e  1 x e  1 1 1 1 1   1 1 3 e  1  2  ln  2   ln  2 e e   1 e  1
Cách 2: Sử dụng phương pháp biến đổi số dt Đặt x t e 1 x
dt e dx  t   1 dx   dx t   1 32
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 x  3 t e 1 Đổi cận    x  1  t e  1  3 e 1  dt Khi đó I  
…Bạn đọc tự giải tiếp t  1 t e 1   
Chú ý: Có thể đặt x t e
Cách 3: Dựa vào đạo hàm 1
Đặt f x  ta có x e  1   x e   1 x x xe e 1 1 e '  ' ' '   1     x 
  x'  ln  x e  
1   x  ln  x e   x x x x  1 e 1 e 1 e 1 e 1        
     ln  x F x x e   1 3 dx 3 3 Khi đó I
F x  x  ln   x e      e e x  1 2 ln  2  1 e 1 1    1 1 1 2 x 2
x e  2x . x e
Bài 11: (ĐH – A 2010) Tính tích phân sau: I dx 1  2. x e 0 Giải: 2 2 2 x x   1 2 x x x 2 . e xe x e x e e 2   x  1  2. x e 1  2. x e 1  2. x e Khi đó 1 2 x 2 x 1 x 1 1
x e  2x . x eee 2 2 I dx x dx x dx dx      1  2 x e 1  2 x e 1  2 x e 0 0   0 0  I1
Tính I bằng các cách như sau đặt  1  2 x t e hoặc x
t e hoặc 1 1 x
1 d 1  2e  1 1   e x 1 1 2  I   ln 1  2e  ln 1  x     2 1  2e 2 0 2  3  0 1 1  1  2e  Vậy I   ln   3 2  3  3
Bài 12: (ĐHK D-2004) Tính tích phân sau: I  ln   2
x xdx 2 Giải: 2 1 2  x
u  ln( x x) du dx Đặt:    x 2  xdv dx  v x 33
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 2x 1
I = xln(x2-x) 3 3 
dx  3ln 6  2 ln 2  (2x  ln(  )
1 ) = ln216 – ln4 – 2 – ln2 = ln27 – 2. 2 2  x x 1 2 3 3 3 3 Hoặc I  ln   2
x xdx  ln xx  
1 dx  ln xdx  ln  x  
1 dx I I 1 2    2 2 2 2
Áp dụng TPTP là xong ln 3 x e dx
Bài 10: (ĐHDB – 2002) Tính tích phân sau: I    x e  3 0 1 Giải:
Cách 1: Phương pháp đưa vào biểu thức vi phân d x e   ln 3 ln 3 ln 3 3 1 1   Ta có I      x e   2 1 d x e   1  2   x e   2 1  2 1  x e  3 0 0 0 1
Cách 2: Phương pháp biến đổi số tdt x x x 2 Đặt 2 t
e  1  t e  1  2tdt e dx dx x e 2 2 tdt 1  I  2  2.   2 1  3 2 t t 2 Hoặc đặt x t e  1
Bài tập tự giải có hướng dẫn: e 2 ln x 76
Bài 1: (ĐHDB – D 2005) Tính tích phân sau I dx   x ln x  1 15 1 HD: e 2 e 2 ln x ln x Đặt t
ln x  1 hoặc t  ln x hoặc biến đổi vi phân I dx d ln x   x ln x  1 ln x  1 1 1
hoặc tích phân từng phần ln 2 2 x e
Bài 2: (ĐHBK – 2000) Tính tích phân sau: I dxx 0 e  1 2 2 Đs: I 3 e ln x
Bài 3: (ĐHHH – 98) Tính tích phân: I = dxx. 1  ln x 1
HD: Đặt t = 1  ln x 4  2 2 Đs: I  . 3 34
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 2  x Bài 4: x 1 2 I e
dx e e  2 0 x  1 HD: dt x Đặt 2 t x  1   dx 2 2 x  1 Tổng quát: f xI e
g xdx  mà ' f x
kg x; k R  
đặt t f x
IV. TÍCH PHÂN HÀM LƯỢNG GIÁC
Bài tập giải mẫu: 4
Bài 1: Tính tích phân sau: 2 I  cos . x cos 2xdx  0 Giải:
Cách 1: Tích phân từng phần
du  2 cos x sin xdx   sin 2xdx 2 u   cos x  Đặt    1 dv  cos 2xdx v  sin 2x    2 Khi đó 4 4 1 1 1 1  cos 4x  4 4 1 1 2 2 I  cos . x sin 2x 4  sin 2xdx dx dx  cos 4 xdx     2 2 2 2 4 4 0 0 0 0 0  1 1  1  x  sin 4x   4  4    4 16  16 0
Cách 2: Sử dụng tích phân liên kết 4
Liên kết với I là 2 J  sin . x cos 2xdx  0 4 4 sin 2 x 1
Ta có I J    2 2
cos x  sin x.cos 2xdx  cos 2xdx  4    1  2 2 0 0 0 4 4 4   
I J   1 cos 4 x x sin 4 x 2 2
cos x  sin x 2
.cos 2xdx  cos 2xdx dx   4      2 2  2 8  8 0 0 0 0 1
Cộng (1) và (2) theo từng vế ta được I  4   16 35
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
Cách 3: Sử dụng phương pháp phân tích 4 4 4 4 1  cos 2x 1 I  .cos 2xdx    1 1 2
cos 2 x  cos 2 xdx  cos 2 xdx
1 cos 4xdx   2 2 2 4 0 0 0 0  1 1 1  1  sin 2x x  sin 4x   4   4  4 4 16  16 0 2 4 sin x
Bài 2: (ĐHTM – 2000) Tính tích phân sau: I dx
sin x  cos x3 0 Giải:
Cách 1: Sử dụng đồng nhất thức 4 sin x
2 sin x  cos x  cos x  sin x   2
2 cos x  sin x   
sin x  cos x3
sin x  cos x3
sin x  cos x2
sin x  cos x3 2 2 2 4 sin x 2
2cos x  sin xI dx dx dx   
sin x  cos x3
sin x  cos x2
sin x  cos x3 0 0 0  1 I
Tính I bằng cách biến đổi  x x2 2 sin cos  2 cos x
hoặc bằng cách đặt t  tan x 1    4 
Cách 2: Sử dụng tích phân liên kết 2 4 cos x Xét J dx  .
sin x  cos x3 0
Khi đó I J  4 và J I  0 nên I  2
Cách 3: Đổi biến số theo cận 2 1 4 sin x Phân tích I dx  2 2  3  0 cos x     4  Đặt x
t dx  dt 4  t  x    4 Đổi cận  2   x 0  t       4 Khi đó 36
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 4 sin x  4   4 4 1  4  sin t  cos t d cos t  4 dt  1  4 I dt dt      tan t  2  3  3  3  2  2  2 2 cos t cos t cos t cos t  2 cos t      4 4 4 4 4
Cách 4: Đổi biến số theo cận Đặt x
t dx  dt 2 x  0  t   Đổi cận    2 x   t   0  2    4 sin  t 0   2 2  2  4 cos t 4 cos x Khi đó I   dt dt dx  3       
cost  sin t3
cos x  sin x3 0 0 sin  t  cos  t 2        2   2  2 2 2 2 4 sin x 4 cos x 4 4
I I  2I dx dx dx dx    
sin x  cos x3
sin x  cos x3
sin x  cos x2  2  0 0 0 0 2 cos x     4    2 tan x  
 2  4  I  2  4  0 Cách 5: sin x sin x 1 Ta có  
sin x  cos x3
sin x 1 cot x3
sin x 1  cot x3 3 2 2 2 4 sin x 1 Khi đó I dx  4 dx  
sin x  cos x3
sin x 1 cot x3 2 0 0
Đặt t  cot x … bạn đọc tự giải Cách 6: Ta có sin x sin x tan x  
sin x  cos x3
cos x  tan x  3 1
cos x tan x  3 3 2 1 2 2 sin x tan x Khi đó I dx   
sin x  cos x3
cos x  tan x  3 2 0 0 1
Đặt t  tan x … bạn đọc tự giải Cách 7:
t  tan x … bạn đọc tự giải 37
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3
Bài 3: Tính tích phân sau: 3 I  tan xdx 4 Giải:
Cách 1: Sử dụng phương pháp phân tích kết hợp với phương pháp đưa vào vi phân  1  1 Phân tích 3 2 tan x  tan .
x tan x  tan x 1  tan x  tan x  2  2  cos x  cos x Khi đó 3 3 3 3  1  1 3
I  tan xdx  tan . x  tan x dx  tan xd     tan x  d cos x 2    cos x  cos x 4 4 4 4 2  tan x  3 1   ln cos x  1  ln 2   2 2   4
Cách 2: Sử dụng phương pháp phân tích kết hợp với phương pháp đưa vào vi phân 1 Phân tích 3 tan x   3
tan x  tan x  tan x  tan . x
 tan x … trở lại cách 1 2 cos x
Cách 3: Phương pháp đổi biến số dt
t  tan x dt   2
1  tan xdx   2
1  t dt dx  2 t  1  x    3  t  3 Đổi cận     t  1 x     4 Khi đó 3 3 2 d t  1 tt  1 2t t 3 1 3  2 3 3 3 3 3 
I  tan xdx dt t dt tdt dt     2   2    2  2 t  1  t  1  2 t  1 2  1 2 t 1 1 1 1 1 1 4 1 1   ln  3 1 1 1 2 t   1   ln 2  1 ln 2. 2 2 1 2 2 2
Cách 4: Phương pháp đổi biến số  2 3 3
1  cos x sin x 3 
Ta có I  tan xdx dx   3 cos x 4 4
Đặt t  cos x  dt  sin xdx 38
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498  1 x t     3  2 Đổi cận    2 x t      4   2 Khi đó 1 2 1  2 2 1  t  2  1 1   1  2 1 I   dt   dt    ln t  1  ln 2  3   3   2  tt t   2t  2 2 1 2 2 2 2
Cách 5: Phương pháp đưa vào biểu thức vi phân 3 3 2 3 2 3 3
(1  cos x) sin xdx
(cos x 1)d(cos x) d(cos x) 3 3
I  tan xdx   
 cos xd  cos x   3  3   cos x cos x cos x 4 4 4 4 4 3 1 3 1  ln | cosx |   1  ln 2 . 2   2 cos x  2 4 4 2
Bài 4: Tính tích phân sau: 3 I  sin xdx  0 Giải:
Cách 1: Sử dụng phương pháp phân tích
Cách 1.1: Sử dụng công thức hạ bậc và công thức biến đổi tổng thành tích 1  cos 2x sin x cos 2 . x sin x Ta có 3 2 sin x  sin . x sin x  .sin x  
… bạn đọc tự giải tiếp 2 2 2
Cách 1.2: Sử dụng công thức nhân 3
3sin x  sin 3x 3 3
sin 3x  3sin x  4 sin x  sin x 4 Khi đó 2 2 2 2 1 3 1  3 1  2 3
I  sin xdx
3sin x  sin 3xdx  sin xdx
sin 3xd 3x   cos x  cos 3x 2        4 4 12  4 12  3 0 0 0 0 0
Cách 2: Sử dụng phương pháp tích phân từng phần 2 u   sin x
du  2sin x cos xdx Đặt    dv  sin xdx v   cos x   Khi đó 39
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 2 2 2 2 2
I   sin x cos x 2  2sin x cos xdx  2 
cos xd cos x 3   cos x 2    3 3 0 0 0 0
Chú ý: Có thể đặt t  sin x
Cách 3: Dùng phương pháp đưa vào vi phân 2 2 2 3   I    cos x 2 2 1  cos x 2
sin xdx  sin xdx  cos xd cos x   cos x  2      3 3 0 0 0   0
Chú ý: Có thể đặt t  sin x Cách 4: dt dx  2  2 x 1  x   1  t Đặt 2 t  tan  dt  tan  1 dx     …. Bạn đọc tự giải 2 2  2  2t sin x  2   1  t 2 dx
Bài 5: Tính tích phân sau: I   3 sin x 3 Giải:
Cách 1: Sử dụng kĩ thuật nhân trên tử 2 2 2 dx sin xdx sin x I    dx  3  4  sin x sin x
1  cos x2 2 3 3 3
Cách 1.1: Đổi biến số đưa về tích phân hàm phân thức
Đặt t  cos x  dt  sin xdx x    t   0 2 Đổi cận    t  1 x     3 1 1 1 1 2 dt dt
1  t   1  t 2 2 2 2 2  1  1 1  I dx   dt   dt        1 t 2
1  t 1  t 2 2 1  t 1  t 4   1  t 1  t  0 0 0      0   1 1 2 2 1  1 1 2  1  1 1 1 1      dt      dt   4 1 t 2 1 t 2 2 1  t 4  1  t2
1 t2 1 t 1 t 0 0      1 1  1 1 1  t  1 1    ln 2   ln 3  
4 1  t 1 t 1  t  3 4 0
Cách 1.2: Đưa trực tiếp vào biểu thức vi phân 40
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 2 2 2 dx sin xdx sin x d cos xI    dx    3  4   sin x sin x
1  cos x2
1 cos x 1 cos x 2 2    3 3 3 3 2
 1  cos x  1 cos x 2 2 2  1  1 1    
d cos x   d    cos x     
1 cos x1 cos x 4 1 cos x 1 cos x    3 3 2 1  1 1 2  cos x 2 1 1 cos x 2 1 1    
d cos x    ln   ln 3  4 2     2 sin x  2 1  cos x  3 4 1 cos x2 1 cos x2 2 1 cos x    3 3 3
Cách 2: Đổi biến số dt dx  2  2 x 1  x   1  t Đặt 2 t  tan  dt  tan  1 dx     2 2  2  2t sin x  2   1  t x t   1   2  Đổi cận    1 t  x    3   3 Khi đó 1 1 1 2 2dt 1  1 2  1  1 t  1 1 I     t dt    2 ln t        1   ln 3 3 2  8t 2 4  t t  4 2t 2 3 4 1 t  1 1 .    3  2 1  t 3 3 3
Cách 3: Sử dụng phương pháp phân tích và phương pháp tích phân từng phần 2 2 2 2 2 2 2 dx sin x  cos x dx cos x I   dx   dx 1  3  3   3   sin x sin x sin x sin x 3 3 3 3  J 2 2 cos x Tính J dx 3 sin x 3 u   cos x
du   sin xdx   Đặt  cos x   1 dv dx v    3  2  sin x  2sin x 41
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 2 cos x 2 1 dx 1 1 dx Khi đó J     2   2 sin x  2 sin x 3 2 sin x 3 3 3 2 1 1 dx
Thay vào (1) ta được I    3 2 sin x 3  K Chú ý: 2 2 cos x 2 2 2 2 2 cos x 1  1  1 1
- Để tính J dx
ta có thể làm như sau J dx  1 dx dx dx 3       sin x 3 2 3 sin x sin x  sin x  sin x sin x 3 3 3 3 3    I K 2 dx - Để tính K   ta có thể làm như sau sin x 3
Nhân cả tử và mẫu cho sin x ta được 2 2 2 dx sin xdx sin xdx K      2  2 sin x sin x 1 cos x 3 3 3
Đặt t  cos x dt   sin xdx x  t  0   2  Đổi cận    1 t  x    2   3 Khi đó 1 1 1 1 1 0 2 2 2 2 dt dt 1  1 1  1 dt 1 dt 1 1 K     dt     
ln t 1  ln t 1     2  ln 3 2 2     1  t 1  t 2 1  t 1  t  2 t  1 2 t  1 2 2 1 0 0 0 0 0 2 x d tan 2 2 2 2   dx dx dx 1  2  x 2 1 Hoặc K      ln tan  ln 3     sin x x x x x x 2 2 2 2 2sin cos 2 tan cos tan 3 3 3 3 2 2 2 2 2 3  dt dx   x  2  2 1  t Hoặc đặt tan  t   2  2t sin x   2  1  t 42
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
Cách 4: Tách thành tích ở dưới mẫu và Sử dụng phương pháp tích phân từng phần  1 u   cos x   sin du   dx x Đặt 2    sin x 1 dv dx v    cot x 2    sin x Khi đó 2 2 cot x 2 2 2 cos x cos x I    dx
. Đến đây ta tích phân J dx 3  áp dụng (cách 3) sin x  sin x 3 sin x 3 3  3 J
Hoặc có thể tính nhanh như sau 2 2 2 dx 1 cot x  1  I   
d cot x    cot xd  3     sin x sin x sin x  sin x  3 3 3 2 2 2 cot x cos x cot x 2 cos x    cot x dx    dx  2  3 sin x sin x sin x  sin x 3 3 3  J
Cách 5: Đưa vào biểu thức vi phân 2 x 2  1  tan 2 2 2 2   dx dx dx 1  2   x I     d tan          3 3 3 6 3 sin x x x x   x 4  x   2  2sin cos 8 tan cos tan 3 3   3     3    2 2   2   2   2    x x 4  1  2 tan  tan   2   2 1  2 2   x  1 1 x 1  x  2 1 1  d tan    2 l  n tan tan     ln 3 3   2   4  2 2 2    3 4 x   2  4  x  tan  2 tan  3      2    2  3  2 sin x
Bài 6: Tính tích phân sau: I dx  sin x  cos x 0 Giải: Cách 1: sin x tan x tan x  1 1 1    1  sin x  cos x tan x  1 tan x  1 tan x  1 2 2 2 2 sin x  1  1 Khi đó I dx  1  dx dx dx      sin x  cos x  tan x  1 tan x  1 0 0 0 0    J 43
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
từ đó đặt t  tan x Cách 2:  2dt dx   2 1  tx  2t Đặt t  tan  s  in x  … bạn đọc tự giải 2 2 1  t  2  1  t cos x   2  1  t Cách 3: Đặt x
t dx  dt 2  t   0 x   Đổi cận  2   t  x 0     2 2 2 2 sin x cos t cos x Khi đó I dx dt dx    sin x  cos x sin t  cos t sin x  cos x 0 0 0 2 2 2 sin x cos x  2I dx dx dx   I     sin x  cos x sin x  cos x 2 4 0 0 0 b b Chú ý:
f xdx
f t dt   a a
Cách 4: Sử dụng tích phân liên kết 2 cos x 2 sin x Chọn J dx
là tích phân liên kết của I dx  sin x  cos x sin x  cos x 0 0 Khi đó ta có hệ 2 2 2 2  cos x sin x sin x  cos x I J dx dx dx dx x 2       sin x  cos x sin x  cos x sin x  cos x 2 0 0 0 0  0   2 2 2 2 cos x sin x cos x  sin x
d sin x  cos x I J dx dx dx
 ln sin x  cos x 2  0      sin x  cos x sin x  cos x sin x  cos x sin x  cos x 0 0 0 0  0 
cộng theo từng vế ta được 2I   I  2 4
Cách 5: Sử dụng phương pháp đồng nhất thức 1 Phân tích sin x
sin x  cos x  sin x  cos x 2 44
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 2 sin x  1
1 cos x  sin x  Khi đó I dx   . dx    sin x  cos x  2
2 sin x  cos x  0 0
Chú ý: Có thể dựa vào đồng nhất thức sau sin x sin x  cos x cos x  sin xAB sin x  cos x sin x  cos x sin x  cos x  1 A    
x   A B
x   A B 2 sin sin sin x   1 B     2
… quay trở lại cách 5
Cách 6: Sử dụng kĩ thuật nhân 1  1  cos 2x  sin 2x   
sin x(cos x  sin x) 2  2  1  1  Ta có   tan 2x  1 2 2   cos x  sin x cos 2x 2  cos 2x
Cách 7: Sử dụng phương pháp phân tích  sin x     sin x  4 4  1      1  cot x     sin x  cos x 2   4  2 sin x      4 
Cách 8: Biến đổi số theo cận 2 2 sin x sin x I dx dx   sin x  cos x 0 0 2 cos x     4 
Đặt t x
dx dt …bạn đọc tự giải 4 1 sin x
Bài 7: Tìm nguyên hàm: I dx  2 ln  C    sin . x sin x  cos x       4   4  Giải: Cách 1: Ta có 45
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498    cos cos x   x     4 4            1    2 cos x   x  2 cos x
cos x  sin x  sin x          2  4     4   4 cos   4 2     sin x      1 cos x  4    2       sin x  sin x cos x  cos x       4 4           d cos x d sin x      4    sin xI  2  2 
2 ln sin x  2 ln cos x   2 ln  C     sin x  4    cos x  cos x       4   4 
Cách 2: Dựa vào đặt thù của hàm số đã cho ta có : dx dx d(cot x  1) I  2  2  2
  2 ln cot x  1  C   2 
sin x(cos x  sin x)
sin x(cot x  1) cot x 1 3 dx
Tương tự : (ĐHMĐC – 2000) Tính tích phân: I   sin . x sin x    6  6  HD:        2sin x   x dx   cos x      dx  6  cos x     6    2    dx     sin x  sin . x sin x  sin . x sin x  sin x         6 6  6        
Bài 8: Tìm nguyên hàm: I  tan x tan x dx     4  Giải: Cách 1: Ta có:         sin x sin x  cos x cos x
 sin x sin x  cos x             4   4   4   4  tan x tan x     1   1    4        cos x cos x  cos x cos x  cos xcos x         4   4   4  2 1  1 2   cos x cos x     4  46
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 dx
Khi đó xét: J   cos x cos(x  ) 4 sin         
Sử dụng đồng nhất thức: 4 1   2 sin x   x  2 sin x
cos x  cos x  sin x           4     4   4 sin   4 1     2 tan x   2 tan x      4  cos x cos x     4     J  2 tan x
dx  2 tan xdx   2 ln cos x
 2 ln cos x C        4   4  cos xI  2 ln  x C  cos x     4  Cách 2: dx dx dx J   2  2    2 
cos x(cos x  sin x)
cos x(1 tan x) cos x cos x     4  d (1  tan x)   2
  2 ln 1  tan x C I   2 ln 1  tan x x C  1 tan x 4 2 1  2 sin x
Bài 9: (ĐH – B 2003) Tính tích phân sau: I dx  1  sin 2x 0 Giải:
Cách 1: Phương pháp biến đổi số 4 2 4 1  2sin x cos 2x Ta có I dx dx   1  sin 2x 1 sin 2x 0 0 dt
Đặt 1  sin 2x t  cos 2xdx
hoặc sin 2x t 2  x t   2 Đổi cận  4   t  1 x  0   2 1 dt 1 2 1 Khi đó I   ln t  ln 2  2 t 2 1 2 1
Cách 2: Phương pháp đưa vào biểu thức vi phân 47
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 cos 2x 1 1 sin 2x' 4 4 4 1 d (1 sin 2x) 1 1 I dx dx  
ln 1  sin2 x 4  ln 2    1  sin 2x 2 1  sin 2x 2 1  sin 2x 2 2 0 0   0 0
Cách 3: Phương pháp đưa vào biểu thức vi phân Biến đối 2
1 – 2 sin x  cos x  sin x cos x – sin x và  x   x x2 1 sin 2 cos sin 4 2 4 1  2sin x cos x  sin x 1 I dx
dx  ln cos x  sin x 4  ln 2   1  sin 2x cos x  sin x 2 0 0 0
Hoặc đặt t  sin x  cos x
2 sin 2x  sin x
Bài 10: (ĐH – A 2005) Tính tích phân sau: I dx  1  3cos x 0 Giải:
Cách 1: Phương pháp biến đổi số
Ta có: sin 2x  sin x  sin x  2cos x   1 . 3sin x sin x 2dt
Đặt t  1  3cos x ta được dt dx dx   ; 2 1  3cos x 1  3cos x 3 2 2 t 1 2t  1 cos x   2 cos x  1  3 3 x  0  t   2 Đổi cận    x t  1    2 2 2  4t 2   4 2  2 34 Khi đó 3 I   dt t t      9 9    27 9  1 27 1
Cách 2: Phương pháp biến đổi số
Đặt t  1  3cos x …bạn đọc tự giải
Cách 3: Phương pháp tích phân từng phần u   2 cos x  1 du  2  sin x   Đặt  sin x
d 1  3cos x   2 dv dx   v   1  3cos x    1  3cos x 3 1  3cos x  3 Khi đó 2 2 2 4 2 4
I   2 cos x   1 1  3cos x 2 
sin x 1  3cos xdx  
1  3cos xd 1 3cos x   3 3 3 9 0 0 0 2 8 34  
1 3cos x3 2  3 27 27 0
Cách 4: Phương pháp đưa vào biểu thức vi phân 48
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 Phân tích 2 1 1 3cos x  sin 2x  sin x 1 2 cos x  1 1 dx   d   x 3 3 . 1 3cos   .
d 1  3cos x  1 3cos x 3 1  3cos x 3 1  3cos x 2 1  
1 3cos xd 1 3cos x 
d 1 3cos x 9 9 1  3cos x
a.sin 2x bsin x .
a sin 2x bcosx Tổng quát: dx hoặc dx
ta đặt c d cos x t .
c d cos x
c d s inx 2 8
Bài 11: (ĐH – A 2009) Tính tích phân sau: I   3 cos x   2 1 cos xdx    15 4 0 HD: 2 2 Cách 1: 5 2
I  cos xdx  cos xdx   0 0
  I I 1 2
Đặt t  sin x dt  cos xdx x t   1 Đổi cận  0   t  0 x  0   Khi đó 2 2 1 1  
I  cos xdx  
1 sin x2 cos xdx  1 t 2 2 4 1 8 5 2 2 dt   2 4
1  2t t  3 5 dt t t t  1    3 5  0 15 0 0 0 0 2 2 2 2 1  cos 2x 1 1 1  1  2
I  cos xdx dx dx  cos 2xdx x  sin 2 x  2       2 2 2 2 2  2  4 0 0 0 0 0 8
Vậy I I I   1 2 15 4 Chú ý:
Có thể tính I như sau 1 2 2 2
I  cos xdx  
1 sin x2 cos xdx   1 sin x2 5 2 2 d sin x  1   0 0 0 1    2 4  8 2 4
1  2 sin x  sin xd sin x 3 5  sin x  sin x  sin x 2     3 5  15 0 0 49
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
2  cos3x  3cos x
  1  cos 2x Cách 2: I  1 dx      …  4   2  0 2 sin 2x 2
Bài 12: (ĐH – A 2006) Tính tích phân sau: I dx   2 2 3 0
cos x  4 sin x HD:
Cách 1: Phương pháp phân tích kết hợp biến đổi số 2 2 sin 2x sin 2x I dx dx   2 2 2 0
1  sin x  4sin x 0 1  3sin x dt Đặt 2
t  1  3sin x   sin 2xdx 3  x t   4 Đổi cận  2   t  1 x  0   4 4 1 1 dt 1  2 4 2 Khi đó 2 I   t dt t    3 t 3 3 1 3 1 1 Hoặc đặt 2
t  1  3sin x
Cách 2: Phương pháp đưa vào biểu thức vi phân 2 2 2 1 sin 2x sin 2x 1  I dx dx     2
1  3sin xd  2 2 1 3sin x 2 2 2 3 0
1  sin x  4 sin x 0 1  3sin x 0 2   2 2 1  3sin x 2  3 3 0
Cách 3: Phương pháp phân tích kết hợp biến đổi số 2 2 sin 2x sin 2x I dx dx   1  cos 2x 1  cos 2x 5  3cos 2x 0 0  4 2 2 2 5  3cos 2x 5  3cos 2x Và đặt t hoặc t
hoặc đưa vào vi phân 2 2 2 sin x cos xdx
Tổng quát: Để tính I =  với a, b  0 2 2 2 2 0
a cos x b sin x Ta đặt: u = 2 2 2 2
a cos x b sin x 50
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 3 4 sin x
Bài 13: (Đề 68 IVa) Tính tích phân sau: I dx  1  cos x 0 Giải: Cách 1: Phân tích 3 4sin x
4 sin x 1 cos x 3 3
4 sin x 1 cos x  
 4 sin x  4 sin x cos x  4 sin x  2 sin 2x 1  cos x
1 cos x1 cos x 2 sin x Khi đó 3 4sin x 2 2 I dx
4sin x  2sin 2xdx  cos 2x  4 cos x 2  2   0 0 1  cos x 0 Cách 2: 3 2 2 4sin x 2 2 I dx
4sin x  4sin xcos xdx  4 sin xdx  4 cos xd cos x     0 0 1  cos x 0 0 2
 4 cos x 2  2 cos x 2  2 0 0 Cách 3: 2 2 4  2 3 1  cos x sin 4 sin x x I dx dx   1  cos x 1  cos x 0 0
dt  sin xdx
Đặt t  1 cos x  
cos x t  1   x t   1 Đổi cận  2   t  2 x  0   4 1   t  2 1  2 1 2   Khi đó I   dt   4
t  8 dt     2 2
t  8t  2 t 1 2 1
Chú ý: Có thể đặt t  cos x Cách 4: x x 3 3 3 32sin cos 4sin x 2 2 x x 3   16 sin cos
…Quá hay phải không, bạn tự giải tiếp nhé 1  cos x x 2 2 2 2 cos 2 Cách 5: 51
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498  2dt dx   2 1  tx  2t Đặt t  tan  s  in x
… Chắc chắn sẽ ra cứ yên tâm làm tiếp đi 2 2 1  t  2  1  t cos x   2  1  t Chú ý: 3 4sin x
4 sin x(1  cos x)(1  cos x) 
 4sin x  2 sin 2x ... Phân tích đến đây rùi thì có những cách nào, bạn đọc 1  cos x 1  cos x tự khám phá nhé! 2 3 4 cos x
Tương tự I dx  2  1  sin x 0 2 3 sin x  sin x
Bài 14: (KTQS – 1997) Tính tích phân sau: I  cot xdx  3 sin x 3 Giải:
Cách 1: Phương pháp đưa vào biểu thức vi phân 2 3 3 2 3 3 sin x  sin x
sin x  sin x cot x I  cot xdx dx  3  2 sin x sin x sin x 3 3 2 2 2 5 8 1 3 2 1  1 
.cot xd cot x 3 2 
 cot x.cot xd cot x 3
  cot xd  cot x 3 3   cot x    2   3 sin x 8 8 3 3 3 3 3
Cách 2: Phương pháp biến đổi số 2 3 3 2 sin x  sin x 1 cot x 3 I  cot xdx  1  . dx  3  2 2 sin x sin x sin x 3 3 1
Đặt t  cot x dt   dx 2 sin x x t   0   2  Đổi cận    1 t  x    3   3 Khi đó 52
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 0 0 0 5 8 3 1 3 2 3 3 I   t  .tdt t dt t 1     3 8 1 1 8 3 3 3 3
Cách 3: Phương pháp biến đổi số 2 3 3 2 3 3 sin x  sin x
cos x sin x  sin x Ta có I  cot xdx dx  3  4 sin x sin x 3 3
Nhận xét: Hàm dưới dấu tích phân là hàm lẻ đối với cos
Đặt t  sin x dt  cos xdx x t   1   2  Đổi cận    3 t  x    2   3 1 3 1 1  3 3 1 2 t t t Khi đó I dt dt  4  3 t t 3 3 2 2 1 1 3 dt Đặt 3 2 3 u  1   u  1   u du  2 2 3 t t 2 t t   1 u  0   Đổi cận    1 3 u t      3  2  3 0 0 4 3 3 u 1 Khi đó 3 I u du  1    3 2 2 4  1 8 3 3  3 3 3 3 8 dx
Bài 15: ( Đề 104. IVa) Tính tích phân sau: I   2 2 sin x cos x 8 Giải:
Cách 1: Sử dụng phương pháp phân tích nhờ đồng nhất thức 2 2
sin x  cos x  1 Khi đó 3 3 3 3 8 8 2 2 8 dx sin x  cos x  1 1  8 I   dx  
dx  tan x  cot x  4  2 2  2 2   2 2   sin x cos x sin x cos x cos x sin x    8 8 8 8
Cách 2: Sử dụng công thức nhân đôi 53
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 3 3 3 8 8 8 dx dx d 2x 2 8 I   4  2  2  cot 2x  4  2 2  2  2 sin x cos x sin 2x sin 2x 8 8 8 8
Cách 3: Phương pháp biến đổi số dx 2 2 1 1  tan x 1  t
Đặt t  tan x dt  và   …. 2 cos x 2 2 2 sin x tan x t 3 2 cos xdx
Bài 16: Tính tích phân sau: I  
sin x  3 cos x 0 Giải:
Cách 1: Đồng nhất thức Ta phân tích: 2 x   A x B xx x C  2 2 cos sin cos (sin cos )
sin x  cos x  1 A    4
 3B C  1   2   3  B C x B A x
x   A C 2 ( 3 ) cos ( 3 ) sin cos
sin x  B  3A  0  B  4  A C 0       1 C   4  2 cos x 1 3 1    sin x  cos x
sin x  3 cos x 4 4
4(sin x  3 cos x) 3  1 3  1 dx
Khi đó I   cos x  sin x  3    4 4 
4 sin x  3 cos x   0 0  1 I 3 dx Tính: J  
sin x  3 cos x 0 3 1 dx 1  x I   ln tan  3 1    2   2  2 6  0 sin x  0    3   1 3 1  x   3ln 3  2
I   cos x  sin x  ln tan     3   4 4 8 2 6    8   0
Cách 2: Tích phân liên kết 54
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 2 cos xdx
Sử dụng tích phân liên kết J  
sin x  3 cos x 0
I  3J  1   3ln 3  2 Giải hệ  ln 3  I I J  8   2 2 cos xdx 2 sin xdx
Tổng quát: I  
tích phân liên kết thường là J  
Asin x B cos x
Asin x B cos x 2 6 cos x
Bài 17: Tính tích phân sau: I dx  4 sin x 4 Giải:
Cách 1: Đưa vào vi phân 6 2 4 cos x cos . x cos x  1  Phân tích 4 4 2   1 
tan x  tan x  tan x 4 4  2  sin x sin x  tan x  Khi đó 2 6 2 2 2 cos x I dx     4 2
tan x  tan x 4 2
dx  tan xdx  tan xdx 4   sin x 4 4 4 4
  I I 1 2 Tính 2 2 2 2 2 4
I  tan xdx      4 2
tan x  tan x   2 tan x   2 1  1 dx  tan   2 tan   1 dx   2
tan x  1  dx 1     4 4 4 4 4 2 2  xd x  2 2 tan tan  tan xx   4 4 4 2 2 2 2 Tính I    2  tan x   1 1 dx   2
tan x  1 dx dx  tan x x 2       … tự giải nhé 4 4 4 4 Cách 2: cos x 1 sin  cos x x  2 2 6 2 2 2 2 4  
cos x  2 cos x sin x  cos x sin x 1 Phân tích 2 2 2    cot . x
 2 cot x  cos x 4 4 4 2 sin x sin x sin x sin x Khi đó 55
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 2 2 1 2 2 2 I  cot . x
dx  2 cot xdx  cos xdx  2   sin x 4 4 4 2 2 2  1  1 2
  cot xd cot x  2  1 dx  1 cos 2x dx   2      sin x  2 4 4 4 3  cot x 1  sin 2x  2 5 23    2   cot x   1  x      3 2   2  8 12  4 Cách 3:
Nhận xét: Vì hàm dưới dấu tích phân là hàm chẵn đối với sin va cos nên ta có thể đặt t  tan x nhưng cách đó
khá dài và phức tạp nên không nêu ra, bạn đọc tự khám phá nhé! 2
Bài 18: Tính tích phân sau: 6 3 5 I  1  cos x.sin . x cos xdx  0 Giải: 2 6 3 3 2 I  1  cos x.cos . x sin . x cos xdx  0 3 6 
cos x  1  t Đặt 6 3 3 6
1  cos x t  1  cos x t   . 2 5 s  in .
x cos xdx  2t dt   x t   1 Đổi cận  2   t  0 x  0   1 1 7 13  t t  1 12
Khi đó I  2 t   6 1  t  5 t dt   6 12
t t dt  2     7 13 0 91 0 0   Hoặc : Đặt 3
1  cos x t
Cách 2: Sử dụng phương pháp đưa vào vi phân 2 2 6 3 3 2 6 3 3 I  1  cos x.cos . x sin . x cos xdx
1  cos x.cos xd    3 1  cos x  0 0 2 6 3   1  cos x    3
1  cos x 1 d   3 1  cos x   0 2 2 6 3   1  cos x   3
1  cos xd  3 1  cos x 6 3  1  cos xd   3 1  cos x 0 0 56
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 sin 2 . x cos x
Bài 19: (ĐH – B 2005) Tính tích phân sau I dx  1  cos x 0 Giải:
Cách 1: Đổi biến số Phân tích 2 2 2 sin 2 . x cos x sin . x cos x I dx  2 dx   1  cos x 1  cos x 0 0
dt  sin xdx
Đặt t  1  cos x  
cos x t  1   x t   1 Đổi cận  2   t  2 x  0   t  2 1 2 2 1  1   t  2 Khi đó I  2  dt  2 t  2  dt  2  2t  ln t  2 ln 2 1      tt  2 1 2 1   Cách 2: 2 2 2  2 2 1  cos x   x x x x  1 sin 2 .cos sin .cos   I dx  2 dx  2 d cos x    1  cos x 1  cos x 1  cos x 0 0 0 2 2  1   cos x   2 1  cos x d  
 cos x  sin x   ln 1  cos x   2  2 ln 2 1  1  cos x  2 0   0
Chú ý: d cos x  d 1  cos x và ta có thể đặt t  cos x  a sin 2 . x cos x
Tổng quát: I dx
ta đặt t b  .
c cos x hoặc t  cos x b  . c cos x
Bài tập tự giải có hướng dẫn: 6 4 tan x 1 10
Bài 1: (ĐH – A 2008) Tính tích phân sau: I dx  ln 2  3   cos 2x 2 9 3 0 HD: Cách 1: Biến đổi 2 2 x x x   2  x 2 cos 2 cos sin 1 tan cos x
Đặt t  tan x 2 1  tan x
Hoặc sử dụng công thức cos 2x 2 1  tan x Tổng quát: 57
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 4 a tan x 1. I dx với , a b   b cos 2x Biến đối b x b  2 2 x x  b 2  x 2 cos 2 cos sin 1 tan
cos x đặt t  tan x 2. Mở rộng hơn 4 a tan x I dx với , a b, , c d   2 2
b sin x c sin x cos x d cos x Biến đổi 2 2 b x c x x d x   2 b x c x d  2 sin sin cos cos tan tan
cos x đặt t  tan x 4 dx
Bài 2: (ĐH AN– 1998): Tính tích phân sau: I   4 cos x 0 Cách 1: 4 4 4 dx 1 dx I   .    4 2
1  tan xd  tan x   3
tan x  tan x 4   4 2 2  cos x cos x cos x 3 0 0 0 0
Cách 2: Biến đổi số 4 4 4 dx 1 dx dx I   .     2 1  tan x 4 2 2  2 cos x cos x cos x cos x 0 0 0
Đặt t  tan x
Cách 3: Sử dụng phương pháp tích phân từng phần  1 u   2  cos xdxdv  2   cos x 2 dx
Bài 3: (Đề 84.IVa) Tính tích phân sau: I   4 sin x 4 2 2 dx d cot x 2 3 cot x 2 4 2 I      1
  cot xd cot x   (cot x  )   4  2  sin x sin x   3 3 4 4 4 4 2
Bài 4: Tính tích phân sau: 2 2 I  cos . x cos 2xdx   4 0 HD:
C1: Hạ bậc biến đổi tích thành tổng
C2: Tích phân liên kết 58
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 4 2 1  2 sin x
Bài 5: Tính tích phân sau: I dx
sin x  cos x4 0 4 2  HD: 2
1  2 sin x  cos 2x  cos x  sin xcos x  sin x và  x x    x 4 sin cos 1 sin 2  4 cos x     4 
Từ đây ta có các cách sau Cách 1: 4 2 4 1  2 sin x cos 2x Biến đổi I dx dx  
sin x  cos x4 1 sin 2x2 0 0
đặt t  1  sin 2x hoặc t  sin 2x hoặc biến đổi vi phân trực tiếp 4 2 4 4 1  2 sin x cos 2x
d 1  sin 2xI dx dx    
hoặc đặt t  tan x
sin x  cos x4 1  sin 2x2 1 sin 2x2 0 0 0 Cách 2: 4 2 4 1  2 sin x
cos x  sin xcos x  sin x
4 cos x  sin x Biến đổi I dx dx dx   
sin x  cos x4
sin x  cos x4
sin x  cos x4 0 0 0
Đặt t  sin x  cos x hoặc biến đổi vi phan trực tiếp Cách 3: 4 2 4 1  2 sin x cos 2x
Biến đổi I dx dx  
sin x  cos x4  4  0 0 4 cos x     4 
Đặt t x  4 3 2 sin x
Bài 6: (ĐHGT TPHCM – 2000) Tính tích phân: I dx 6 cos x 6 HD: 2 sin x 1 1 Ta có 2 2 dx  tan . x . dx  tan x 2
1  tan x d tan x 6 2 2    cos x cos x cos x 42 3  8 Đs: 15
2 sin x  cos x
Bài 7: (ĐHĐN – 2000) Tính tích phân: I dx sin x  cos x 4 HD: 59
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498     2 sin x d cos x  2   2     4    4     2 1 I dx  
dx   ln cos x   ln 2             4   2 2 cos x  cos x      4 4  4   4  4 4
Bài 8: Tính tích phân sau: 6 I  tan xdx  0 HD: Đặt 2
t  tan x dt  (tan x  1)dx
x  0  t  0  Đổi cận:  x   t  1   4 1 4 1 6 1 4 5 3 t dt  1   t t  13 Vậy 6 4 2
I  tan xdx  
t t  1  dt    tdu     2  2     t  1  t  1  5 3 15 4 0 0 0   0 0 2 8
Bài 9: Tính tích phân sau: 5
I  cos xdx   15 0 2 3 sin x cos x
Bài 10: Tính tích phân sau: I dx  2 1  cos x 0 HD: 2 2 1 cos x 2 1 t 1 1 2 1 ln 2 I   d   2 1  cos x dt
t  ln t  2   2 1  cos x 1 2 t 2 2 0 1
Bài 11: Tính tích phân sau: 4 I  tan xdx HD:  1  4 2 2
I  tan xdx  tan x sin xd  tan x 2  tan x     2
1  cos xd  tan x 2  tan x 1  d     tan x 2 1  tg x   2 tan x  1  1 1 2
 tan xd tan x  d  tan x 3 
tan x  tan x x C   2 1  tan x 3 2
3sin x  4 cos x
Bài 12: (ĐHTL – 2000) Tính tích phân sau: I dx 2 2
3sin x  4 cos x 0 3 Đs: I   ln 3 6 60
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
V. BÀI TẬP HỖN HỢP CỦA NHIỀU HÀM SỐ Bài tập giải mẫu: 4
Bài 1: (ĐH TL2001) Tính tích phân sau: I  ln 1  tan xdx 0 Giải: Cách 1: dx  dt  Đặt x   t     1 tan t 2 4
1  tan x  1  tan  t  1        4  1 tan t 1 tan t
x  0  t    4 Đổi cận  x   t  0   4 4 4 4  2  Khi đó I  ln
dt  ln 2dt  ln   
1 tan tdt  (ln 2).  I I  ln 2    1  tan t  4 8 0 0 0 Cách 2: Ta có 4 4 4 4
 sin x  cos x
I  ln 1  tan xdx  ln
dx  ln sin x  cos xdx  ln cos xdx         cos x  0 0 0 0 4 4    ln 2 cos  x dx  ln    cos xdx   4  0 0  J 4 4 4 4   1   1  Tính J  ln 2 cos  x dx  ln 2 dx  ln cos  x dx  ln 2x        4  ln cos  x dx  ln 2  K     4  2  4  2  4  8 0 0 0 0 0    K Đặt t
x  dt dx 4 4 4
Khi đó K  ln cos t dt  ln cos xdx   0 0 Khi đó I  ln 2 8
Cách 3: Tích phân từng phần 61
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 u
  ln 1  tan x Đặt  …Bạn đọc tự giải dv dx  1 ln 1 x
Bài 2: Tính tích phân: I dx. 2 1  x 0 HD: 4
Đặt x  tan t ta được I
ln 1  tan t dt  ; 0 4 4 2 đặt t
x ta được I  ln du  ln 2 du I   4 1  tan u 0 0 5 ln( x 1  1)
Bài 3: Tính tích phân sau: I dx
x 1 x 1 2 Giải: Cách 1:  1 dt
dx  2 t   1 dt dx  Đặt t x  1  1 2 x  1 
x  t  2 1  1  x  5 t  3 Đổi cận    x  2 t  2   Khi đó 3 3 3 (t  1) ln t ln t 3 I  2 dt  2
dt  2 ln td ln t 2 2 2  ln t  ln 3  ln 2  2  
(t  1)  t  1 t 2 2 2 2
Cách 2: Đặt t
x 1 ... bạn đọc tự giải 2 xdx
Bài 4: Tính tích phân sau: I   1 sin 2x 0 Giải:
Cách 1: Đặt t   x 2    Cách 2: Biến đổi 2
1  sin 2x  1  cos 2x   2 cos x    
 , tích phân từng phần  2   4  1 1  2 I  . x sin .
x cos xdx   xd    3 cos x 3 3
   xcos x  cos xdx  0 3 3 0 0  0  62
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 3 1    1  sin x 2
1 sin xd sin x   sin x     3 3 3 3 3 3 0   0
Bài 5: (ĐH DHN – A 2000) Tính tích phân sau:
2 1 sin xx 2 x 2 x e e e sin x  2 I dx dx dx e    1  cos x x 2 1  cos x 0 o 0 2 cos 2 Giải: Cách 1: 2 2 x 2 2 x 2 1  sin x e dx x e dx x x sin x 1 sin Ta có: I  .e dx   .e dx   . x e dx      1  cos x 1  cos x 1  cos x 2 x 2 1 cos x 0 0 0 0 0 cos  2 I  2 1 I 2 1 x e dx Tính: I  1  2 x 2 0 cos 2 x u   e xdu e dx    Đặt: dxdv    x x v  tan  2 cos   2   2
Áp dụng công thức tính tích phân từng phần 2 x 2 2 1 e dx x x x x x 2 I   e tan
2  tan .e dx e  tan . x e dx 1    2 x 2 2 2 2 0 0 0 cos 0 2 x x 2 2 2 sin cos 2 sin x x Tính: x 2 2 I  .e dx  . x e dx  tan . x e dx 2    1  cos x x 2 2 0 0 0 2 cos 2 Vậy 2 I e Cách 2: 2 x 2 x 2 2 e e sinx x x Ta có: I  .dx  . x
dx e d (tan ) xe tan .dxx    2 1 cos x 2 2 0 0 0 0 2 cos 2 2 2 2 2 x x x x x x x x 2  e tan  e tan .dx e tan .dx e tan  e   2 2 2 2 0 0 0 0 63
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498
Sử dụng định nghĩa: x x x
1  sin xx x e .2 sin cos ' ' x e ' e e xx xx  Ta có 2 2     tan x e  tan x e  tan    x e xe tan   1  cos x x x x 2 2 2 2  2  2  2 2 cos 2 cos 2 cos  2 2 2
Hoặc ta biến đổi: x x  sin  cos 1 sin x    1  2 2  1  x x 2    1  2 tan  tan   1  cos x 2 x 2  2 2 cos  2 2 2 1  x  1 x Vậy 2 I  1  tan dx  tan x e dx    2  2  2 2 0 0  I1 2 x Tính I  tan x e dx 1  2 0 2 e  1 1 
Bài 6: (ĐH GTVT – 1998) Tính tích phân sau: I   dx   2   ln x ln x e Cách 1: 1 1
Đặt f x   2 ln x ln x 1 1 1  ln x
x' ln x  xln x' x
Ta có f x      F x  2 2 2   ln x ln x ln x l n x ln x Khi đó 2 e 2 2  1 1  x e e I   dx   e    2   ln x ln x  ln x e 2 e Cách 2: 2 2 2 2 2 e e e 2  1 1   1 e edx x e dx dx I   dx xd        2         ln x ln x   ln x  ln x ln x e ln x ln x e e e e e
Bài 7: Tính tích phân sau 2 I  .
x sin x cos xdx 0 Giải: 1 1 I  .
x sin 2x cos xdx  .
x sin 3x  sin xdx   2 4 0 0 du dx u   x   Đặt:    . dv   x x 1 sin 3 sin dx v   
cos3x  cos x   3 64
Giáo viên: Nguyễn Thành Long Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 1  1  1  Khi đó I x cos 3x  cos x
cos 3x  cos x dx       4  3  0  3  3 0 x  1  1  1 1  5  cos 3x  cos x 2  sin 3x  sin x 2       . 2  3  2  18 2  9 0 0
Cách 2: Đặt x t … bạn đọc tự giải
Chú ý: Qua mấy bài toán trên ta có nhận xét
Dựa vào đạo hàm ta có thể tính Nguyên hàm của một các dạng đặc biệt
Dạng 1: Nguyên hàm của các hàm số dạng tích thương Dạng Cấu trúc hàm số Nguyên hàm Tổng        ' ' ' f x u v u v
F x  u v Hiệu        ' ' ' f x u v u v
F x  u v Tích       ' ' ' f x u v v u uv
F x  uv Thương ' ' ' u v v uu u f x   F x  2   v vv
Dạng 2: Các dạng nguyên hàm đơn giản chứa ex Đặc trưng Nguyên hàm
Hàm số (đạo hàm) x e      x F x u x e '   '        x F x u x
u x e f x   x e     x F x u x e  '   '         x F x u x u x ef x   ax b e     ax b F x u x e   '   '     
  axb F x u x au x ef x   vve
F x  u xvve ' F x '
 u x '
v xu xvx  ef x   1 2 x x e
Ví dụ: Tính tích phân sau: I dx   x  2 0 2 Giải:
Cách 1: Tích phân từng phần 2 x x u   x e
du xe x  2 dx   Đặt  dx   1 du v     x 22    x  2  65
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 x 1 x e 1 Khi đó x I    xe dxx  2 0 0  I1 1 u   xdu dx Tính x I xe dx   1  . Đặt  x x dv e dx v e 0   1 1 1 Khi đó x x x x I xe
e dx xe e 1    0 0 0 2 x x e 1 1 Vậy I     x x
xe e   1 x  2 0 0 Cách 2: 2 Phân tích 2 x   2
x  4x  4  4 x  2  4   x  2  4 x  2  4 2 x x   x   e x  22 1 1 4 2 1 1 x 1 4 x x 1 Khi đó I e dx
e dx e dx  4 dx  4 dx       x  22  x  22 x  2  x  22 0 0 0 0 0  J
Tính J làm xuất hiện tích phân mà làm triệt tiêu một tích phân
Bài tập tự giải có hướng dẫn: 1 2 2 x x e
Bài 1: Tính tích phân sau: I dx   x  2 0 1
HD: Sứ dụng tích phân từng phần 1 2 2 x 1 x e x  1 2 2  I dx   x e d      x  2 1  x  1  0 0 1 2 2 x 1 2 1 2 1 2 1 x e 1    d   e e e x x e     2 x xe dx    xd    x e  1 2 2 2 2 2 x 2 x    xee dx  0 x  1 x  1 2 2 2 0 0 0 0 0 1 2 2x 2 2 e e ee 1  1         2 2 2 2 2 2 0   2 2  xx 
Bài 2: Tính tích phân sau: 2 2 I  4x tan  x 1  tan  tan     2 2     8 8 0   2 1   1 x x e
Bài 3: (ĐHLN – 2001) Tính tích phân sau: I dx  1  x  2 0 1 2
Bài 4: Tính tích phân sau: sin x I e
1  x cos xdx e  2 0 66
Giáo viên: Nguyễn Thành Long
Email: Loinguyen1310@gmail.com DĐ: 01694 013 498 2 e  1 
Bài 5: (ĐHTN – 1996) Tính tích phân sau: 2 I  2 ln x   2 2e  2e    x e ln  LỜI KẾT:
Đây thực sự chưa phải là những bài toán và cách giải hay, chưa có nhiều bài tập phong phú và đa
dạng, song cũng góp phần nhỏ bé nào đó cho các bạn và Tôi hi vọng các bạn sẽ thích thú và tìm thêm
những bài tập hay và những cách giải đặc sắc hơn….
Tuy nhiên năng lực và kinh nghiệm còn thiếu. Rất mong các bạn học sinh và các bạn đồng nghiệp
góp ý kiến, bổ sung thêm giúp tôi và các bạn hoàn thiện hơn … Xin chân thành cảm ơn
Góp ý theo địa chỉ Email: Loinguyen1310@gmail.com hoặc địa chỉ: Nguyễn Thành Long
Số nhà 15 – Khu phố 6 – Phường ngọc trạo – Thị xã bỉm sơn – Thành phố thanh hóa MỤC LỤC
I. TÍCH PHÂN HÀM HỮU TỶ………………………………………………........................Trang 2
II. TÍCH PHÂN HÀM VÔ TỶ………………………………………………………..............Trang 18
III. TÍCH PHÂN HÀM SỐ MŨ VÀ LOGARIT……………………………………..............Trang 26
IV. TÍCH PHÂN HÀM LƯỢNG GIÁC....................................................................................Trang 35
Tải thêm tài liệu môn Toán THPT tại:
+ Trang web: www.toanmath.com
+ Fanpage: www.facebook.com/toanmath
+ Groups: https://www.facebook.com/groups/toanmath 67