








Preview text:
CONTENTS
1 VECTOR CALCULUS - GIẢI TÍCH VECTOR 3
1.1 Basic concepts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2 Gradient . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.3 Divergence and curl . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1.3.1
Divergence (Nguồn) . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1.3.2
Curl - Xoáy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 1.3.3
Further properties of 5 . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.4 Line integrals - Tích phân đường . . . . . . . . . . . . . . . . . . . . . . . . 7 1.4.1
Line intergral type 1 -Tích phân đường loại 1 . . . . . . . . . . . . 8 1.4.2
Line intergral type 2 -Tích phân đường loại 2 . . . . . . . . . . . . 10
1.5 Surface integrals − Tích phân mặt . . . . . . . . . . . . . . . . . . . . . . . 14 1.5.1
Surface integrals Type 1 . . . . . . . . . . . . . . . . . . . . . . . . . 14 1.5.2
Surface integrals Type 2 . . . . . . . . . . . . . . . . . . . . . . . . . 17
1.6 Engineering applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26
2 LAPLACE TRANSFOrMS - PHÉP BIẾN ĐỔI LAPLACE 29
2.1 The Laplace transforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 2.1.1
Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29 2.1.2
Definition: Điều kiện tồn tại cho phép biển đổi Laplace . . . . . 30 2.1.3
The property . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30 2.1.4
Table of Laplace Transform . . . . . . . . . . . . . . . . . . . . . . . 31
2.2 The inverse Laplace transform − Biến đổi Laplace ngược . . . . . . . . 32
2.3 Solution of differential equations − Giải phương trình vi phân với điều
kiện ban đầu: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33 2.3.1
Transforms of derivatives − Phép biến đổi đạo hàm . . . . . . . . 33 2.3.2
Giải bài toán điều kiện ban đầu . . . . . . . . . . . . . . . . . . . . 33
2.4 Engineering application . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 2.4.1
Electrical circuits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 2.4.2
Kirchhoff’s laws . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
2.5 Step and inpulse functions − Hàm bước nhảy và hàm xung . . . . . . . 37
2.6 Transfer functions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
3 SYSTEMS OF LINEAR FIRST - ORDER DIFFERENTIAL EQUATIONS
HỆ PHƯƠNG TRÌNH VI PHÂN TUYẾN TÍNH CẤP 1 43
3.1 Preliminary theory − Lý thuyết cơ bản . . . . . . . . . . . . . . . . . . . 43 3.1.1
Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43 3.1.2
Định lý về sự tồn tại và duy nhất nghiệm . . . . . . . . . . . . . . 43 3.1.3
Nghiệm tổng quát của hệ phương trình vi phân . . . . . . . . . . 44 3.1.4
The matrix of linear first − order differential equations . . . . . 44
3.2 Homogeneous linear systems − Hệ tuyến tính thuần nhất . . . . . . . . 45 3.2.1
Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 1 Toán 2E1 ThS. Phạm Kim Thủy 3.2.2
Phương pháp khử: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 45 3.2.3
The characteristic equation − Phương trình đặc trưng . . . . . . 46 3.2.4
The eigenvalue and the eigenvector − Giá trị riêng và vector
riêng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46 3.2.5
Theorem. Distinct real eigenvalues − Giá trị riêng thực đơn . . 48 3.2.6
Theorem. Repeated eigenvalues − Giá trị riêng bội: . . . . . . . . 48 3.2.7
Theorem. Complex eigenvalues − Giá trị riêng phức . . . . . . . 48 3.2.8
Các bước giải hệ phương trình vi phân thuần nhất (Tài liệu sẽ
trình bày cho trường hợp hệ 3 phương trình) . . . . . . . . . . . . 48
3.3 Nonhomogeneous linear systems − Hệ phương trình không thuần nhất: 51 3.3.1
Phương pháp hệ số chưa xác định: . . . . . . . . . . . . . . . . . . . 51 3.3.2
Phương pháp biến thiên tham số . . . . . . . . . . . . . . . . . . . . 52
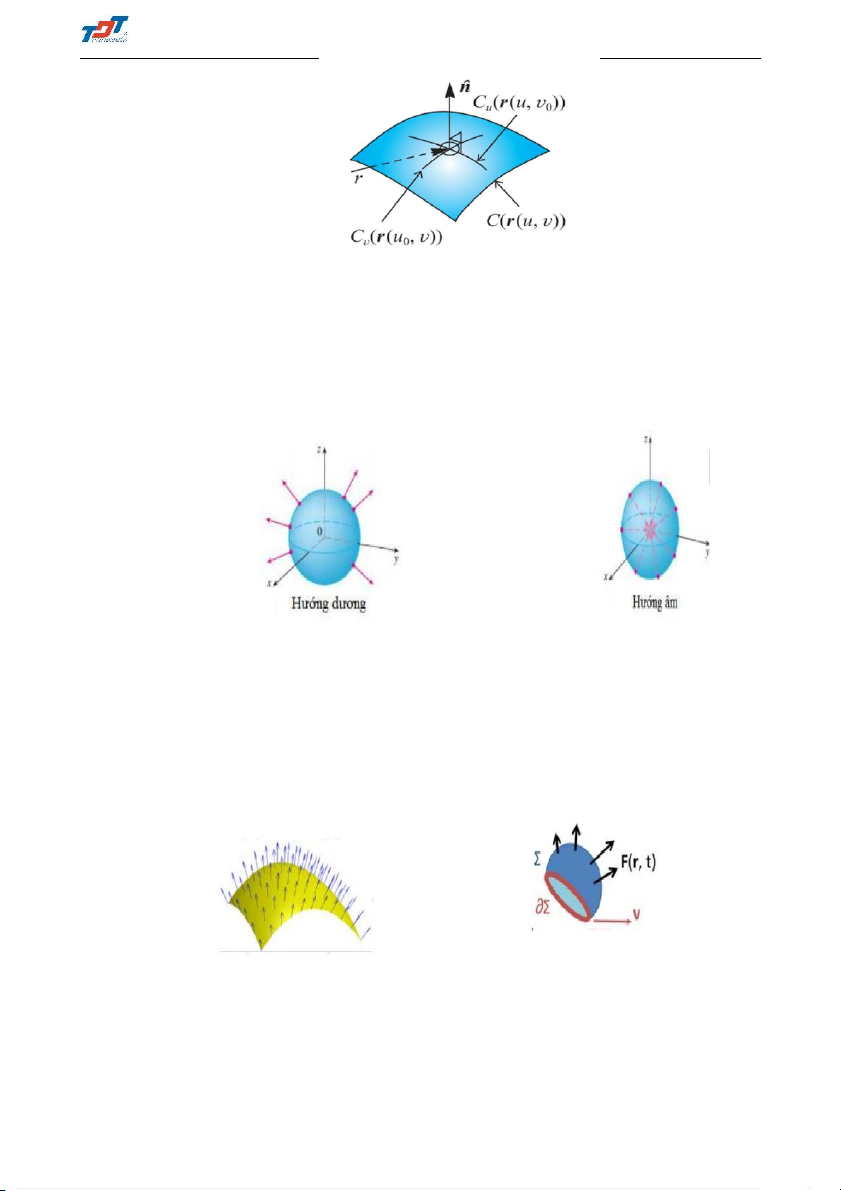
3.4 Matrix exponential − Hàm mũ ma trận . . . . . . . . . . . . . . . . . . . 54 2 CHAPTER 1 VECTOR CALCULUS - GIẢI TÍCH VECTOR 1.1 Basic concepts - Let r = xi + yj + zk
- A scalar point function f is a rule,u = f(r), which assigns to each point with coordinate r in
the domain of the function a unique real number u.
- An alternative name for a scalar point function is scalar field.
- A vector point function F is a rule, v = F (r), which assigns to each r a unique vector v.
- An alternative name for a scalar point function is vector field.
- Consider the transformation or mapping from the from the (x, y) plane to the (s, t) plane defined by s = s(x, y), t = t(x, y)
- The Jacobian of the transformation is defined by ∂(s, t) ∂s ∂s ∂s ∂t J = = ∂x ∂y ∂x ∂x = ∂s ∂t (1.1) ∂(x, y) ∂t ∂t ∂x ∂y ∂ty ∂y Example 1.1.1 ( x = rcosϕ Cho
Xác định định thức Jacobi của phép biến đổi trên. y = rsinϕ
- If u = U(x, y, z); v = V (x, y, z), w = W (x, y, z) represent a transformation in three dimensions
from x, y, z to u, v, w then theo corresponding Jacobian is u x uy u u ∂(u, v, w) z x vx wx J = = v = u (1.2) ∂(x, y, z) x vy vz y vy wy w u x wy wz z vz wz Example 1.1.2 x = rcosϕ
Cho y = rsinϕ Xác định định thức Jacobi của phép biến đổi trên. z = z 3 Toán 2E1 ThS. Phạm Kim Thủy Example 1.1.3 x = rcosϕsinθ Cho
y = rsinϕsinθ Xác định định thức Jacobi của phép biến đổi trên. z = rcosθ 1.2 Gradient
If u = f(x, y, z) represent a transformation in three dimensions then the vector ∂f ∂f ∂f ! , , ∂x ∂y ∂z
is called gradient of the scalar point function f. It’s denoted by gradf or 5f, where 5 is the vector operator. ∂ ∂ ∂ 5 = i + j + k (1.3) ∂x ∂y ∂z Or ∂f ∂f ∂f ∂f ∂f ∂f ! gradf = 5f = i + j + k = , , (1.4) ∂x ∂y ∂z ∂x ∂y ∂z
The gradient of the scalar point function f at the point M0 is ∂f ∂f ∂f ! gradf (M0) = 5f(M0) = (M (M (M (1.5) ∂x 0), ∂y 0), ∂z 0) Example 1.2.1
1. Find gradf, gradf (M) when f(x, y) = x + y , M (2, −3) y x
2. Find gradf, grad(M) if f(x, y, z) = x3 + y3 + z3 + 3xyz, M (1, 2, 3).
3. Find 5f, 5f(M) if f(x, y, z) = ln(x2 + y2 + z2), M(1, 1, 1)
Example 1.2.2 Cho f(x, y) = (3x2 + y)i + (x2 − 3y2)j, tìm hàm số F sao cho F = 5f 1.3 Divergence and curl 1.3.1 Divergence (Nguồn)
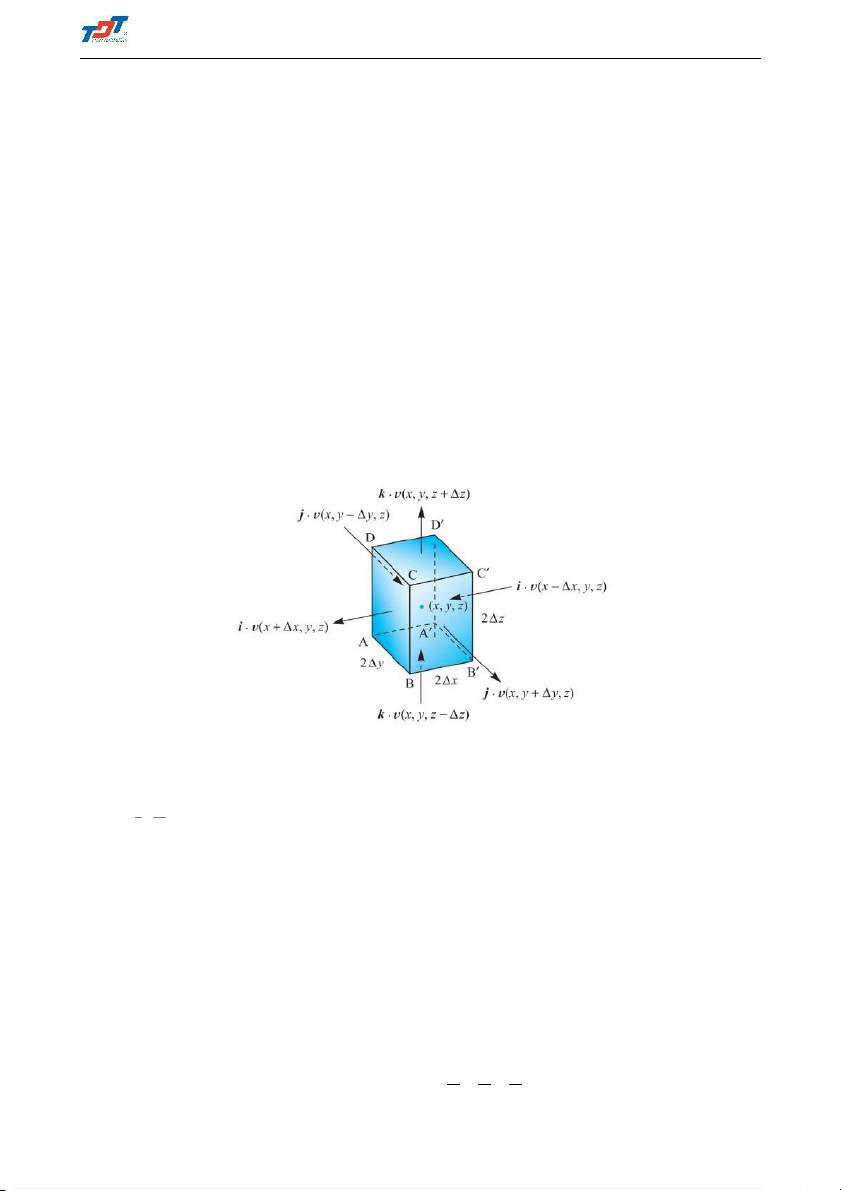
The divergence of the vector field v = (v1, v2, v3), divv = 5.v (1.6) Or ∂ ∂ ∂ ! divv = i + j + k (iv1 + jv2 + kv3) (1.7) ∂x ∂x ∂z Then ∂v ∂v ∂v divv = 1 + 2 + 3 (1.8) ∂x ∂x ∂z
The divergence of a vector field F (r) at the poitn r is f low out of ∆V divF = 5.F = lim (1.9) ∆V →0 ∆V
A vector field F satisfying divF = 0 is sometimes termed solenoidal. Divv là một đại lượng vô hướng. 4 Toán 2E1 ThS. Phạm Kim Thủy Example 1.3.1 Find divv where 1. v(r) = 3x2i + zj + x2k
2. v(r) = (3x + y)i + (2z + x)j + (z − 2y)k
Example 1.3.2 Find the divergence of the vector v = (2x − y2, 3xz + x3, 4y − z2) at the point (2, −1, 3).
Example 1.3.3 Give F = (2xy2 + z2)i + (3x2 + y2 − y2z2)j + (yz2 − 2y)k calculate divF at the point (−1, 2, 3).
Ý nghĩa: Giả sử ~v là vận tốt của chất lỏng, có mật độ S, các thành phần của vector ~ F = ρv
có các đạo hàm riêng liên tục, M là một điểm của chất lỏng. Khi đó:
- Nếu divF (M) > 0 thì thông lượng ra ngoài những mặt cầu khá bé, tâm M là dương, ta nói M là điểm nguồn.
- Nếu divF (M) < 0 thì M là điểm rò.
- Nếu divF (M) = 0 thì thông lượng qua mọi mặt kín đều bằng 0. Khi đó, ta nói rằng trường vector ~
F (M ) có thông lượng bảo toàn - Solenoidal
Example 1.3.4 Cho F = (2xy2+z2)i+(2x2z2−xz3)j+(yz2−xz3)k. Tính divF tại M(−1, 3, 2)
Example 1.3.5 Tìm divF (M), biết F = (exsinycossz)i + (excosycosz)j − (exsinysinz)k, với M (−2, π, 5π ) 2 6
Example 1.3.6 Find the value if the constant λ such that the vector field defined by F =
(2xy2 + z2)i + (3xy3 − x2z)j + (λxy2z + xy)k is solenoid. Example 1.3.7 1.3.2 Curl - Xoáy
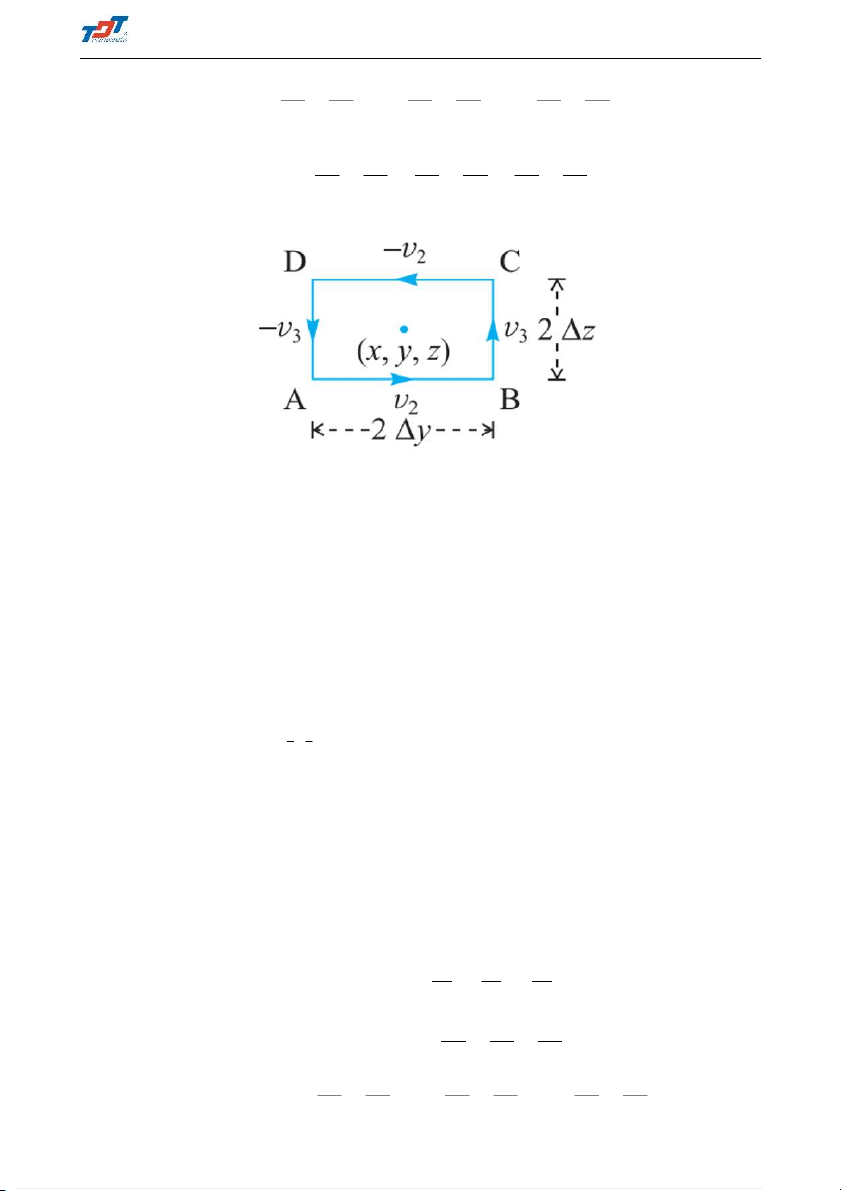
The vector measuring the rotation about a point in the fluid is called the curl of vector field
v (Vector Rota hay vector xoáy), denoted curlv or ~
rot~v Cho trường vcetor v có các toạ độ
v1, v2, v3. Vector Curlv được xác định bởi: i j k curlv = 5 × v = ∂v ∂v ∂v (1.10) ∂x ∂y ∂z v1 v2 v3 5 Toán 2E1 ThS. Phạm Kim Thủy Hoặc ∂v ∂v ! ! ! 2 ∂v1 ∂v3 ∂v2 ∂v1 curlv = 3 − i + − j + − k (1.11) ∂y ∂z ∂z ∂x ∂x ∂y Hoặc ∂v ∂v ∂v ∂v ∂v ∂v ! curlv = 3 − 2; 1 − 3 ; 2 − 1 (1.12) ∂y ∂z ∂z ∂x ∂x ∂y Ý nghĩa của Curl:
- Nếu curlv(M) 6= 0 thì điểm M được gọi là điểm xoáy - Rotation.
- Nếu curl(M) = 0 thì điểm M là điểm không xoáy - Irrotation.
Example 1.3.8 Find the curl of vector v = (2x − y2, 3z + x2, 4y − z2) at the point M(1, 2, 3)
Example 1.3.9 Give F (x, y, z) = sin(yz)i − xzcos(yz)j + xycos(yz)k 1. Find curlF
2. Find curlF (M), M(1, π, π ) 2 4
Example 1.3.10 Cho trường vector, F = (xy2 + z; −xyz2; y2z). Tính Curl(CurlF)
Example 1.3.11 Find constants a, b, c such that the vector field defined by F = (4xy +az3)i+
(bx2 + 3z)j + (6xz2 + cy)k is irrotational. 1.3.3 Further properties of 5
- So far we have used the vector operator in three ways: ∂f ∂f ∂f 5f = gradf = i + j + k (1.13) ∂x ∂y ∂z ∂f ∂f ∂f 5 · 2 3 F = divF = 1 + + (1.14) ∂x ∂y ∂z ∂f ∂f ! ∂f ∂f ! ∂f ∂f ! 5 × 1 2 F = curlF = 3 − 2 i + − 3 j + − 1 k (1.15) ∂y ∂z ∂z ∂x ∂x ∂y 6 Toán 2E1 ThS. Phạm Kim Thủy
- A further application is in determining the directional derivative of a vector field: ∂ ∂ ∂ ! a · 5F = a1 + a + a F (1.16) ∂x 2 ∂y 3 ∂z ∂f ∂f ∂f ! ∂f ∂f ∂f ! ∂f ∂f ∂f ! a·5F = a 1 1 1 2 2 2 3 3 3 1 + a + a i+ a + a + a j+ a + a + a k ∂x 2 ∂y 3 2 3 2 3 ∂z 1 ∂x ∂y ∂z 1 ∂x ∂y ∂z (1.17) df 5 [f(g(r))] = 5 g dg
5 [f(r)g(r)] = g(r) 5 f(r) + f(r) 5 g(r)
5 [u(r) · v(r)] = v × (5 × u) + u × (5 × v) + (v · 5) u + (u · 5) v
5 · [f(r) · u(r)] = u · 5 + f 5 ·u
5 × [f(r)u(r)] = (5f) × u + f 5 ×u ∂2f ∂2f ∂2f div [gradf (r)] = 5 · 5f = + + = 52f ∂x2 ∂y2 ∂z2
Where 52 được gọi là Laplacian operator (somtimes denoted by ∆). When all second -
order derivatives of f(r) are continuous
curl [gradf (r)] = ∇ × ∇f(r) ≡ 0
div [curlv(r)] = ∇ (∇ × v) ≡ 0 ∂ ∂ ∂ ! ∂v ! 1 ∂v ∂v
grad(divv) = ∇ (∇ · v) = i + j + k + 2 + 3 ∂x ∂y ∂z ∂x ∂y ∂z ∂2 ∂2 ∂2 ! ∇2v = + + (v v v ∂x2 ∂y2 ∂z2 1i + 2j + 3k)
curl [curlv(r)] = ∇ × (∇ × v) = ∇ (∇ · v) − ∇2v
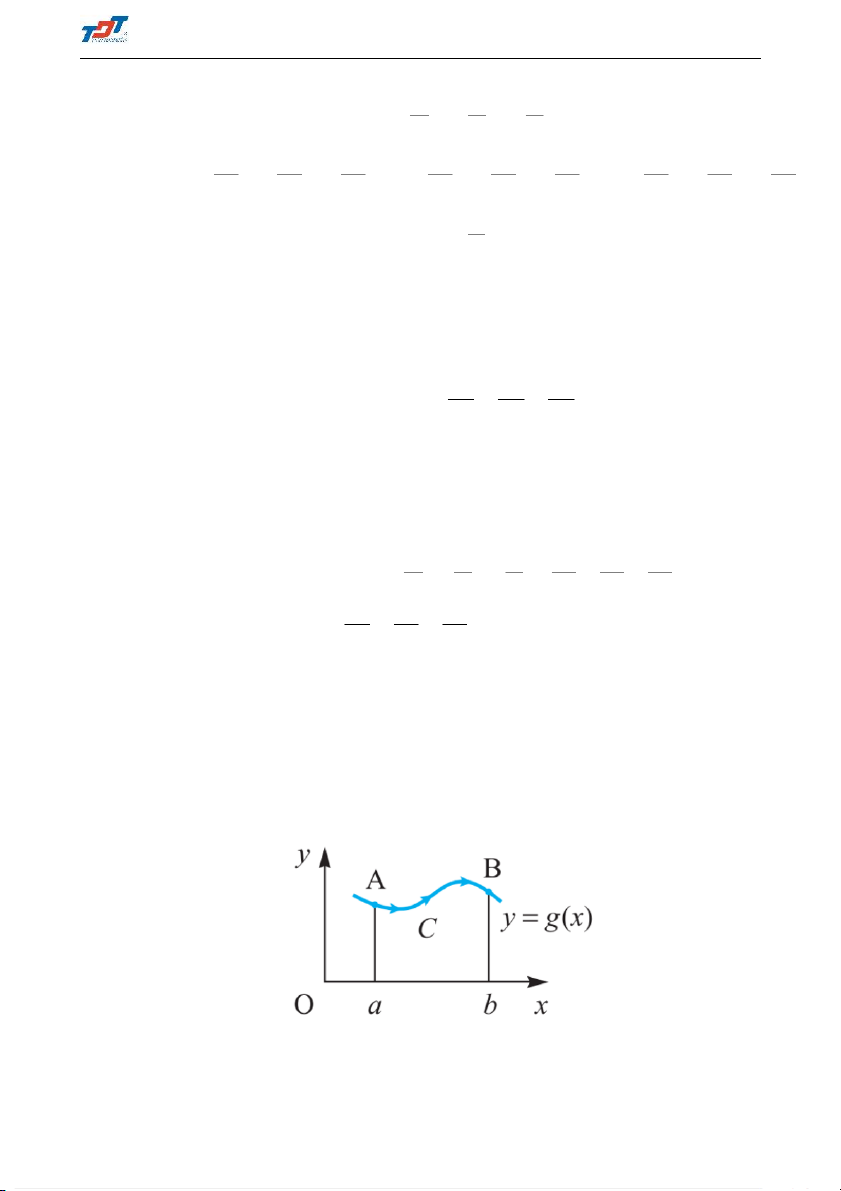
1.4 Line integrals - Tích phân đường - Z b Consider the integral
f (x, y)dx, where y = f (x), x ∈ [a, b] a
- This type of integral is called a line integral. - Z Z
There are many different types of such integrals, for example f (x, y)dy , f (x, y)dS , C C Z Z f (x, y)dt , [f1(x, y)dx + f2(x, y)dy)] C C 7 Toán 2E1 ThS. Phạm Kim Thủy
1.4.1 Line intergral type 1 -Tích phân đường loại 1 _
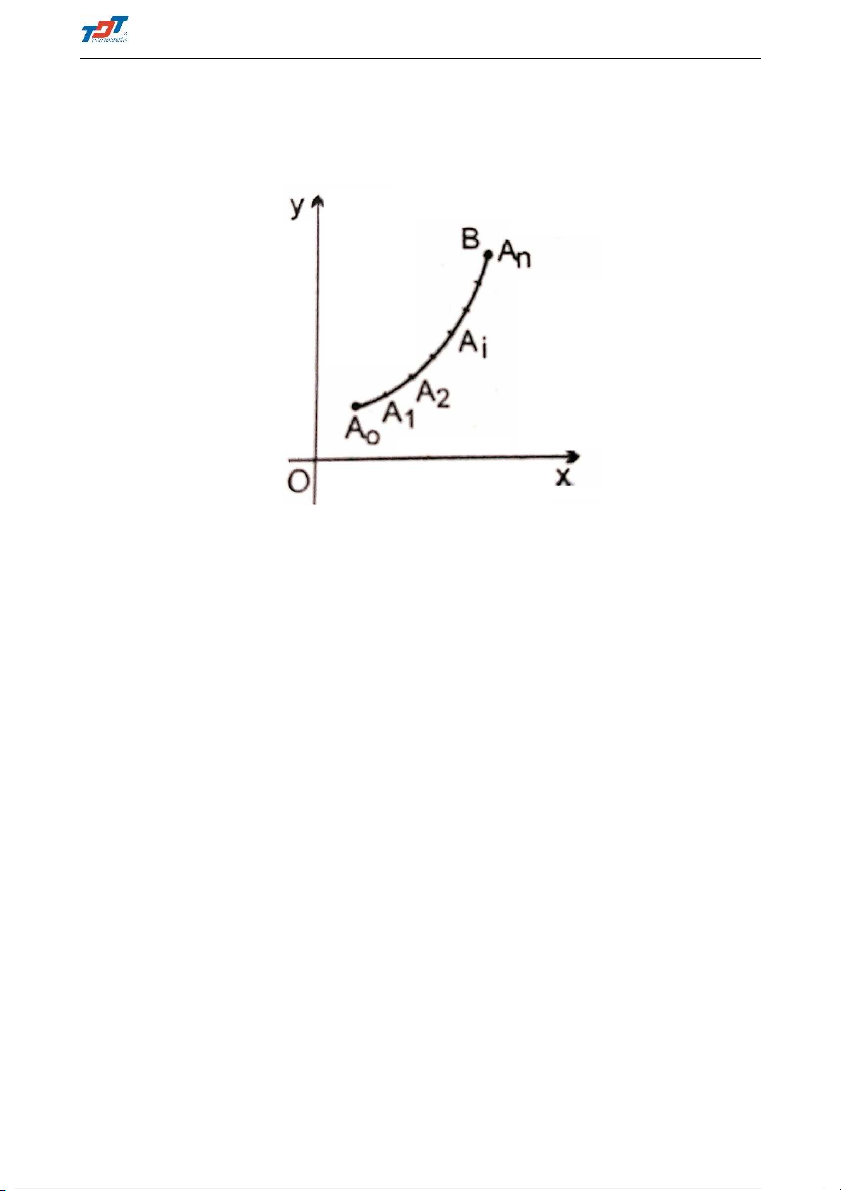
1. Definition Cho hàm số f(M) = f(x, y) xác định trên một cung phẳng AB. Chia cung _ _
AB thành n cung nhỏ bởi các điểm A0 = A, A1, A2, . . . , An = B. Gọi độ dài cung Ai−1Ai _ là ∆si. Trên cung Ai M
−1Ai lấy 1 điểm tuỳ ý i(ξ, ηi). n
Nếu khi n → ∞ sao cho max∆S X i → 0, tổng
f (Mi)∆Si dần đến 1 giới hạn xác định, i=1 _ _
không phụ thuộc vào cách chia cung AB và cách chọn điểm Mi trên cung Ai−1Ai thì giới _
hạn đó được gọi là tích phân đường loại 1 của hàm số f(x, y) dọc theo cung AB và được ký hiệu bởi: Z _ f (x, y)dS AB Tức là, Z n f (x, y)ds = lim X _ f (ξi, ηi)∆Si (1.18) AB max∆si→0 i=1 2. Tính chất: _ _
(a) Nếu AB trơn và hàm số f(x, y) liên tục trên AB thì ta nói hàm số f(x, y) là khả _ tích trên cung AB. _
(b) Trong tích phân đường loại 1, người ta không để ý đến chiều trên cung AB. Z Z f (x, y)ds = f (x, y)ds (1.19) _ _ AB BA _
(c) Nếu cung vật chất AB có khối lượng riêng tại M(x, y, z) là ρ(x, y, z) thì khối lượng _
của cung BA được xác định bởi: Z _ ρ(x, y, z)ds (1.20) AB (d) Chiều dài của cung _
AB được xác định bởi: Z Chiều dài cung _ AB= _ ds (1.21) AB 8 Toán 2E1 ThS. Phạm Kim Thủy _ _ _
(e) Nếu cung C được chia thành hai cung C1 và C2 không dẫm lên nhau thì Z Z Z f ds = f ds + f ds (1.22) _ _ _ C C1 C2
(f) Tích phân đường loại 1 có những tính chất giống tích phân xác định. Z
3. Cách tính tích phân đường loại 1: Giả sử cho tích phân đường loại 1 _ f(x, y)ds, AB _
với f(x, y) liên tục trơn trên AB. ( _ y = y(x) q
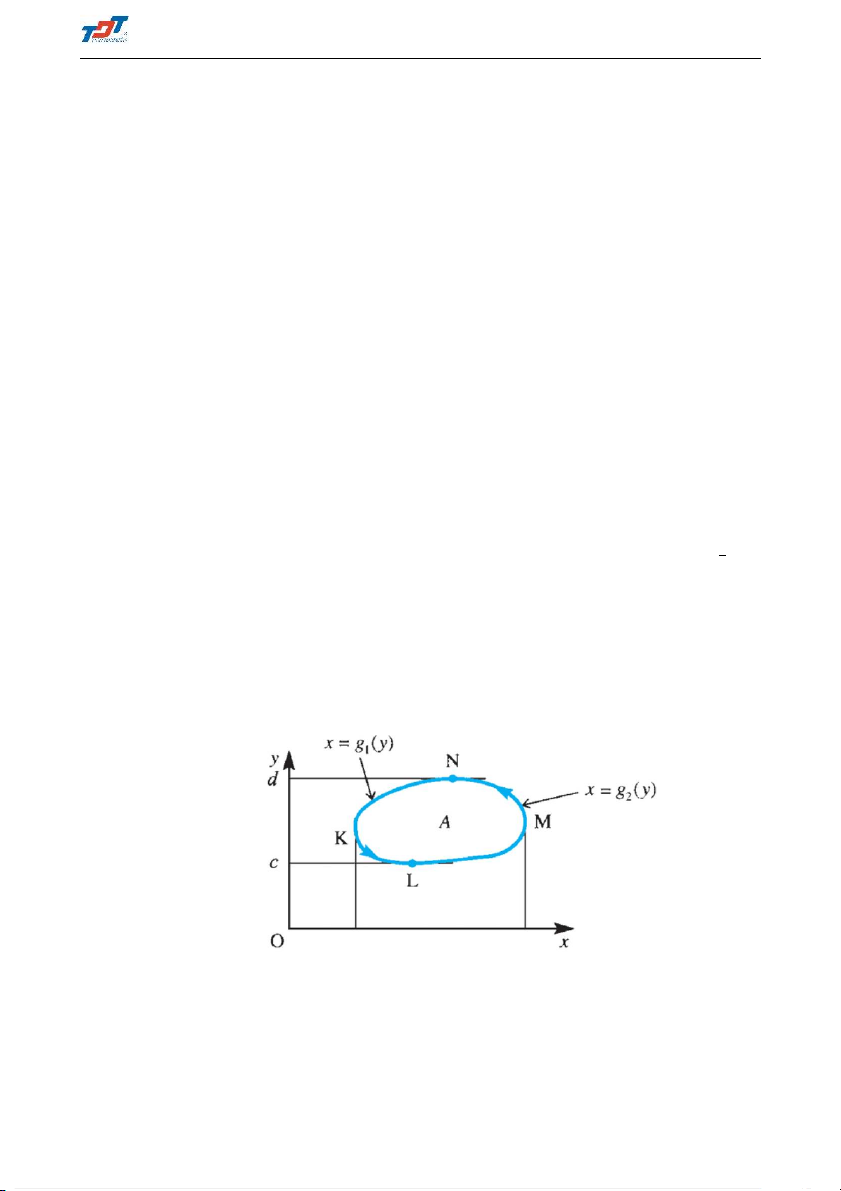
(a) Nếu cung AB trơn được cho bởi thì ds = 1 + [y0(x)]2dx. a ≤ x ≤ b Khi đó: Z Z b q _ f (x, y)ds = f (x, y(x)) 1 + [y0(x)]2dx (1.23) AB a _ ( q (b) Nếu cung x = x(y) AB trơn được cho bởi thì ds = 1 + [x0(y)]2dy. c ≤ y ≤ d Khi đó: Z Z d q f (x, y)ds = f (x(y), y) 1 + [x0(y)]2dy (1.24) _ AB c x = x(t) _ q
(c) Nếu cung AB trơn được cho bởi y = y(t) thì ds = [x0(t)]2 + [y0(t)]2dt. a ≤ t ≤ b Khi đó: Z Z b q _ f (x, y)ds =
f (x(t), y(t)) [x0(t)]2 + [y0(t)]2dt (1.25) AB a x = x(t) _ y = y(t)
(d) Nếu cung AB trong không gian và được cho bởi z = z(t) a ≤ t ≤ b q thì ds =
[x0(t)]2 + [y0(t)]2 + [z0(t)]2dt. Khi đó: Z Z b q _ f (x, y)ds =
f (x(t), y(t), z(t)) [x0(t)]2 + [y0(x)]2 + [z0(t)]2dt (1.26) AB a Example 1.4.1 Z √ (a) Tính
(x3 + y)ds, trong đó C là cung Parabol: y = x2 , 0 3 _ ≤ x ≤ 2 C Z √ √ √ (b) Evaluate
yds along the parabol y = 2 x from A(3, 2 3) to B(24, 4 6). _ C Z (c) Tính
xy2ds, trong đó C là cung Parabol: x = y2 đi từ A(4; 2) đến B(1; _ −1) C Z (d) Tính
ex+2yds, trong đó AB là đoạn thẳng nối hai điểm A( _ −1, 3), B(2, 1) AB Z (e) Tính
(x + 2y)ds, trong đó L là biên của tam giác ABC, A( , B , , C , . _ −1, 3) (2 1) (0 1) L Z (f) Tính
ye−xds, với L là đường được xác định bởi: x = ln(1 + t2), y = 2arctant _ − L t + 3, 0 ≤ t ≤ 3. 9 Toán 2E1 ThS. Phạm Kim Thủy Z q (g) Tính
2yds, với L là đường được xác định bởi: x = t, y = 1 t2, z = 1 t3, 0 _ ≤ 2 3 L t ≤ 1 Z (h) Tính
(2 + x2y)ds, với L là nửa trên của đường tròn x2 + y2 = 4. _ L Z q (i) Tính
x2 + y2ds, với L là đường tròn được xác định bởi x2 + y2 = 2x. _ L _
4. Ứng dụng: Độ dài của cung C được xác định bởi: Z I(C) = ds (1.27) _ C
Example 1.4.2 Hãy tính độ dài của một cung cycloid được xác định bởi: x = t − sint, y = 1 − cost, 0 ≤ t ≤ 2π
1.4.2 Line intergral type 2 -Tích phân đường loại 2 1. Definition: - _ _
Cho hai hàm số P (x, y), Q(x, y) xác định trên cung AB. Chia cung AB thành n cung
nhỏ bởi các điểm A0 = A, A1, . . . , An = B.
- Gọi hình chiếu của vector −−−−−→ An ∆y
−1An lên hai trục Ox và Oy là ∆xi và i. - _
Lấy bất kì 1 điểm M(ξi, ηi) trên cung Ai−1Ai.
- Nếu khi n → ∞ sao cho max∆yi → 0 thì n
X [P (ξi, ηi)∆xi + Q(ξi, ηi)∆yi] i=1 _
dần tới một giới hạn xác định, không phụ thuộc cách chia cung AB và cách chọn _
điểm Mi trên cung Ai−1Ai thì giới hạn đó được gọi là tích phân đường loại 2 của _
các hàm số P (x, y), Q(x, y) dọc theo cung AB. Ký hiệu: Z P (x, y)dx + Q(x, y)dy (1.28) _ AB 2. Tính chất: - _ _
Nếu cung AB trơn và các hàm số P (x, y), Q(x, y) liên tục trên AB thì tích phân trên tồn tại.
- Trong tích phân đường loại 2, chiều trên đường lấy tích phân đóng vai trò quan trọng. _
Nếu ta đổi chiều trên đường lấy tích phân thì hình chiếu của Ai−1Ai trên 2 trục Ox và Oy đổi dấu. Z Z _ P dx + Qdy = − _ P dx + Qdy (1.29) AB BA - _ _
Nếu cung C được chia làm 2 cung C1 và C2 không dẫm lên nhau thì Z Z Z P dx + Qdy = P dx + Qdy + P dx + Qdy (1.30) _ _ _ C C1 C2
3. Cách tính tích phân đường loại 2: Giả sử cần tính tích phân Z I = _ P (x, y)dx + Q(x, y)dy AB 10 Toán 2E1 ThS. Phạm Kim Thủy ( - _ y = y(x) Nếu cung AB: ⇒ dy = y0(x)dx thì x : xA → xB Z xB I =
P (x, y(x))dx + Q(x, y(x))y0(x)dx (1.31) xA ( - _ x = x(y) Nếu cung AB: ⇒ dx = x0(y)dx thì y : yA → yB Z yB I =
P (x(y), y)x0(y)dx + Q(x(y), y)dy (1.32) yA x = x(t) ( - _ dx = x0(t)dt Nếu cung AB: y = y(t) ⇒ thì dy = y0(t)dt t : tA → tB Z tB I =
P (x(t), y(t))x0(t)dt + Q(x(t), y(t))y0(t)dt (1.33) tA Example 1.4.3 Z (a) Evaluate I =
(x2 + 2y)dx + (x + y2)dy, from A(0, 1) toB(−1; 0) along the _ C curve C defined by y = x + 1. Z (b) Tính I =
ydx + x2dx, trong đó C là cung của Parabol y = x2 đi từ A(1, 1) _ C đến 0(0, 0) Z (c) Tính I =
3xdx + ydy, trong đó C là cung của Parabol x = y3 + y đi từ _ C A(−2, −1) đến B(2, 1) Z (d) Tính I =
(x2 + 3y)dx + 2ydy, trong đó C là biên của tam giác ABC với _ C
A(0, 0), B(1, 1), C(0, 2), ngược chiều kim đồng hồ. Z (e) Evaluate I =
xydx, from A(1, 0) to B(0, 1) along the curve C that is the _ C
portion of x2 + y2 = 1 in the first quadrant. Z (f) Tính I =
ydx + xdy, trong đó C là cung của đường tròn x2 + y2 = 2x đi từ _ C 0(0, 0) đến A(1, 1). Z (g) Tính I =
ydx+zdy +xdz, trong đó C là đường cong x = acost, y = asint, z = _ C
bt, 0 ≤ t ≤ 2π theo hướng tăng dần của t. 4. Một số chú ý:
- Cho 2 vector x = (x1, x2, x3) và y = (y1, y2, y3). Khi đó:
+ Tính vô hướng của 2 vector được xác định bởi: x · y = x1y2 + x2y2 + x3y3 (1.34)
+ Tích có hướng của 2 vector được xác định bởi: ! x2 x x x x × y = 3 3 x1 1 x2 ; ; (1.35) y 2 y y3 y y 3 1 1 y2
- If f1(x, y, z), f2(x, y, z), f3(x, y, z) are the scalar components of a vector field F (r) then Z Z h i
f(x, y, z)dx + f2(x, y, z)dy + f3(x, y, z)dz = F · dr (1.36) C C 11 Toán 2E1 ThS. Phạm Kim Thủy Example 1.4.4 Z (a) Evaluate the intergral
V · dr, where V = (2yz + 3x2, y2 + 4xz, 2z2 + 6xy), and C is C
the curve with parametric equations x = t3, y = t2, z = t joining the points 0(0, 0, 0) and A(1, 1, 1) Z
(b) If A = (2y + 3)i + xzj + (yz − x)k, evaluate
A · dr along the following paths C: C
i. x = 2t2, y = t, z = t3 from t = 0 to t = 1.
ii. The straight line from 0(0, 0, 0) to A(2, 1, 1)
- If F=(f1, f2, f3) and (C) is the part r = (r1, r2, r3) Z F × dr (1.37) C Example 1.4.5 Caculate Z (a) F · dr C Z (b) F × dr C
where C is the part of spiral R = (acosθ, asinθ, aθ) corresponding to 0 ≤ θ ≤ π and 2 F = r2i 5. Green’s theorem
- Nếu đường cong lấy tích phân là một đường kín L thì ta quy ước: Chọn chiều dương
trên L là chiều sao cho một người đi dọc L theo chiều đó sẽ thấy miền giới hạn bởi
L gần mình nhất ở về bên trái.
Ta ký hiệu tích phân đường loại 2 dọc đường cong kín L theo chiều dương là: I P dx + Qdy (1.38) _ L
- Consider a simple closed curve C, enclosing the region D (D là miền đóng, bị chặn
trong mặt phẳng Oxy, với biên C trơn từng khúc, có chiều dương). 12 Toán 2E1 ThS. Phạm Kim Thủy
- If P (x, y), Q(x, y) are contiunous function with continuous partial dervatives then ! I Z Z ∂Q ∂P P dx + Qdy = − dxdy (1.39) C D ∂x ∂y
Với D là miền bị bao bọc bởi C Example 1.4.6 I (a) Evauluate
2x(x + y)dx + (x2 + xy + y2)dy around the square with vertices at C
(0, 0), (1, 0), (1, 1), (0, 1). I (b) Tính
(x2+3y)dx+2ydy, trong đó C là biên của tam giác OAB, với 0(0, 0), A(1, 1), B(0, 2), C
ngược chiều kim đồng hồ. I (c) Tính
e−x2(−2xsinydx + cosydy), trong đó C là đường tròn x2 + y2 = 4, ngược C chiều kim đồng hồ. I (d) Tính (x − y)2dx + (x 2
y ) dy, trong đó C là nửa trên của đường tròn x2 + y2 = 2x, C
và chiều kim đồng hồ (HD: Có thể chuyển về đường cong kín để dùng Green).
6. Điều kiện để tích phân đường không phụ thuộc đường lấy tích phân:
Cho hàm số P (x, y), Q(x, y) liên tục cùng với các đạo hàm riêng cấp một của chúng trong
một miền đơn liên D nào đó. Khi đó, các mệnh đề sau là tương đương nhau: (a) ∂P = ∂Q ∂y ∂x I (b)
= 0 dọc theo mọi đường cong kín L nằm trong D. L Z _ (c) _
P dx + Qdy, trong đó cung AB là một cung nằm trong D, chỉ phụ thuộc hai AB
điểm đầu mút A và B mà không phụ thuộc vào đường di từ A đến B.
(d) Biểu thức P dx + Qdy là vi phân toàn phần của một hàm số u(x, y) nào đó trong miền D. Tức là: du(x, y) = P dx + Qdy (1.40)
Tìm hàm số u(x, y) : Chọn (x0, y0) thuộc miền xác định của P (x, y), Q(x, y). Khi
đó, hàm u(x, y) được xác định bởi: Z x Z y u(x, y) = P (x, y0)dx + Q(x, y)dy + C (1.41) x0 y0 Hoặc Z x Z y u(x, y) = P (x, y)dx + Q(x0, y)dy + C (1.42) x0 y0 Tức là, Z Z P dx + Qdy = du = u(x, y) |L (1.43) L L Example 1.4.7 Z (a) Tính
ydx+, với L là đường gấp khúc ABC, với A(−1, 2), B(2, 2), C(2, 3) (Yêu L
cầu: tính theo 2 cách: trong đó có 1 cách dùng vi phân toàn phần) 13 Toán 2E1 ThS. Phạm Kim Thủy Z (6,8) xdx + ydy (b) Tính √ (1,0) x2 + y2
7. Ứng dụng: Diện tích của miền phẳng D, có biên C theo chiều dương được xác định bởi: I I 1 I SD = −ydx = xdy = xdy − ydx (1.44) C C 2 C Example 1.4.8
Tính diện tích của đường elip (E) : x2 + y2 ≤ 1 a2 b2
1.5 Surface integrals − Tích phân mặt
Một hồ chứa nước chống hạn ở một địa phương, có một cửa xả. Khi xả nước, người ta phải
mở cửa xả với một diện tích S trong khoảng thời gian t nào đó. Để biết được phải mở cửa xả
với diện tích S là bao nhiêu và trong thời gian bao lâu, người ta cần phải tích được lưu lượng
nucosw chảy qua cửa xả trong một đơn vị thời gian. Tuy nhiên, dòng nước chảy qua đó có vận
tốt và hướng thay đổi. Do vậy, lượng nucosw chảy qua cửa xả đó trong một đơn vị thời gian
tại những thời điểm khác nhau là khác nhau. 1.5.1 Surface integrals Type 1 1. Định nghĩa:
- Cho một mặt cong S và một hàm số f(M) = f(x, y, z) xác định trên S. Chia S thành
n mảnh nhỏ. Gọi tên và cả diện tích của các mảnh ấy là ∆S1, ∆S2, . . . , ∆Sn. Trong
mỗi mảnh ∆Si, lấy một điểm tuỳ ý Mi(ξi, ηi, ζi). n - Nếu khi X
n → ∞ sao cho maxdi → 0 là đường kính của ∆Si, tổng f (Mi)∆Si dần tới i=n
một giới hạn xác định không phụ thuộc cách chia mặt S và cách lấy điểm Mi trên
∆Si thì giới hạn đó được gọi là tích phân mặt loại 1 của hàm số f (x, y, z) trên mặt S và ký hiệu Z Z f (x, y, z)dS 2. Tính chất:
- Nếu mặt S trơn (liên tục và có pháp tuyến biến thiên liên tục) và nếu hàm số f(x, y, z)
liên tục trên mặt S thì tích phân tồi tại. 14 Toán 2E1 ThS. Phạm Kim Thủy
- Mặt S có khối lượng riêng tại M(x, y, z) là ρ(x, y, z) thì khối lượng của mặt S được xác định bởi: Z Z ρ(x, y, z)dS S
- Tích phân mặt loại 1 không phụ thuộc phía của mặt S. - Nếu S = S1 ∪ S2 thì Z Z Z Z Z Z f (x, y, z)dS = f (x, y, z)dS + f (x, y, z)dS (1.45) S S1 S2
- Tích phân mặt loại 1 có tính chất giống tích phân kép.
3. Cách tính tích phân mặt loại 1: Giả sử cần tính tích phân Z Z I = f (x, y, z)dS S
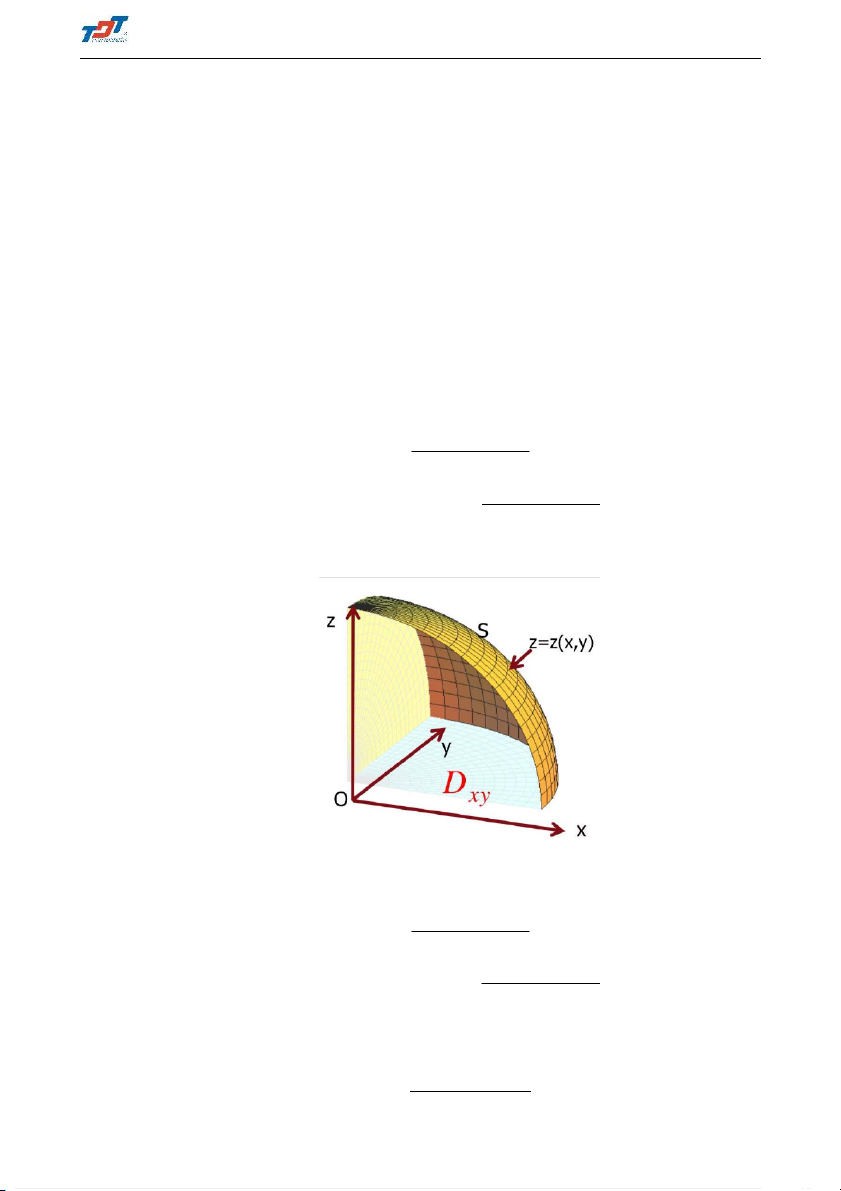
- Trường hợp 1: Nếu mặt S được cho bởi: z = z(x, y), trong đó z(x, y) là một hàm số
liên tục, có các đạo hàm riêng liên tục trong miền đóng, giới nội D là hình xy, Dxy
chiếu của S lên mặt phẳng Oxy. Khi đó, q dS = 1 + (z0 )2 + (z0 x )2dxdy (1.46) y và Z Z q I =
f (x, y, z(x, y)) 1 + (z0 )2 + (z0 )2dxdy (1.47) x y Dxy
(Chuyển về tích phân kép) ( - Trường hợp 2: y = y(z, x) Nếu mặt S :
(z, x) ∈ Dzx( Hình chiếu của S lên Ozx) Khi đó, q dS = 1 + (y0 )2 + (y0 z )2dzdx (1.48) z và Z Z q I =
f (x, y(z, x), z) 1 + (y0 )2 + (y0 )2dzdx (1.49) z x Dzx ( - Trường hợp 3: x = x(y, z) Nếu mặt S :
(y, z) ∈ Dyz( Hình chiếu của S lên Oyz) Khi đó, q dS = 1 + (x0 )2 + (x0 )2dydz (1.50) y z 15 Toán 2E1 ThS. Phạm Kim Thủy và Z Z q I =
f (x(y, z), y, z) 1 + (x0 )2 + (x0 )2dydz (1.51) y z Dyz Example 1.5.1 Z Z (a) Tính
ydS, với mặt S là phần của mặt z = x + y2, 0 ≤ x ≤ 1, 0 ≤ y ≤ 2 S Z Z (b) Tính
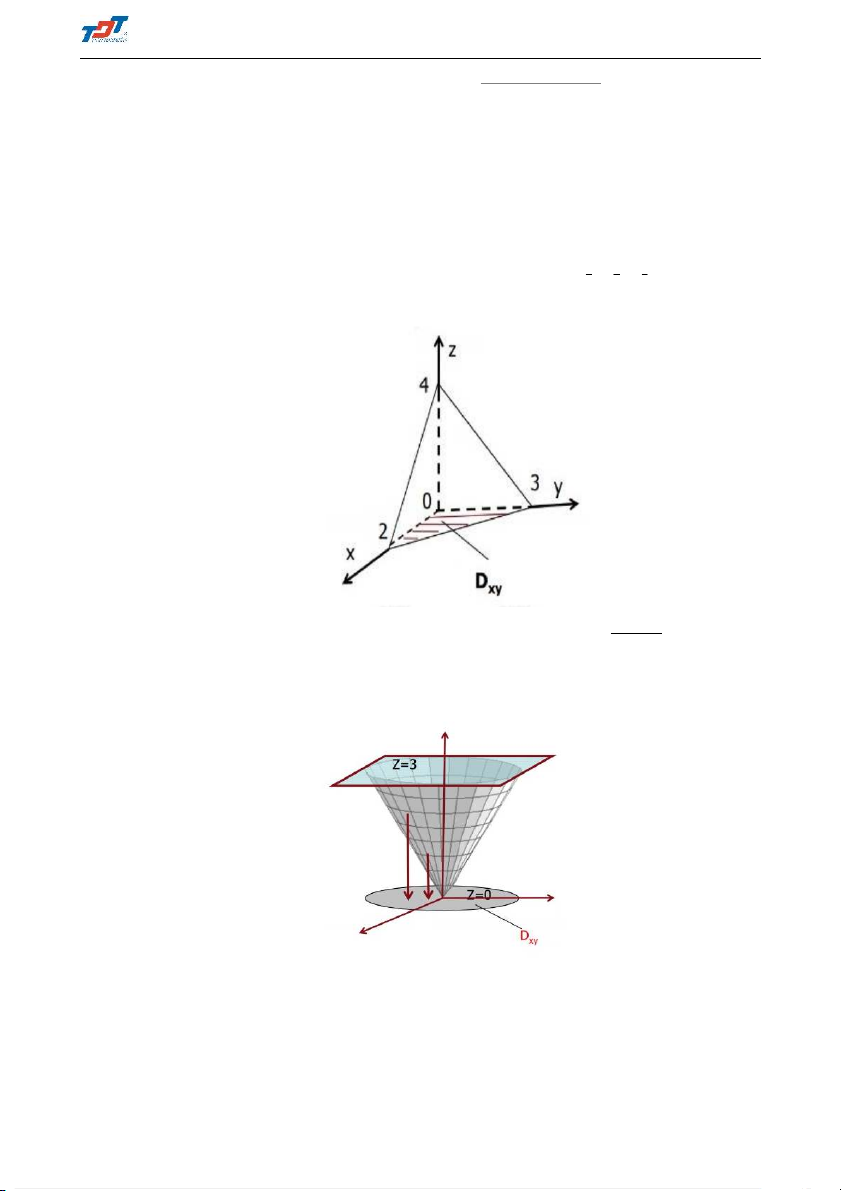
(6x + 4y + 3z)dS, trong đó S là phần mặt phẳng x + y + z = 1, x ≥ 0, y ≥ 2 3 4 S 0, z ≥ 0 Z Z √ (c) Tính
(x2 + y2 + z2)dS, trong đó S là phần mặt nón z = x2 + y2 nằm giữa hai S mặt phẳng z = 0, z = 3
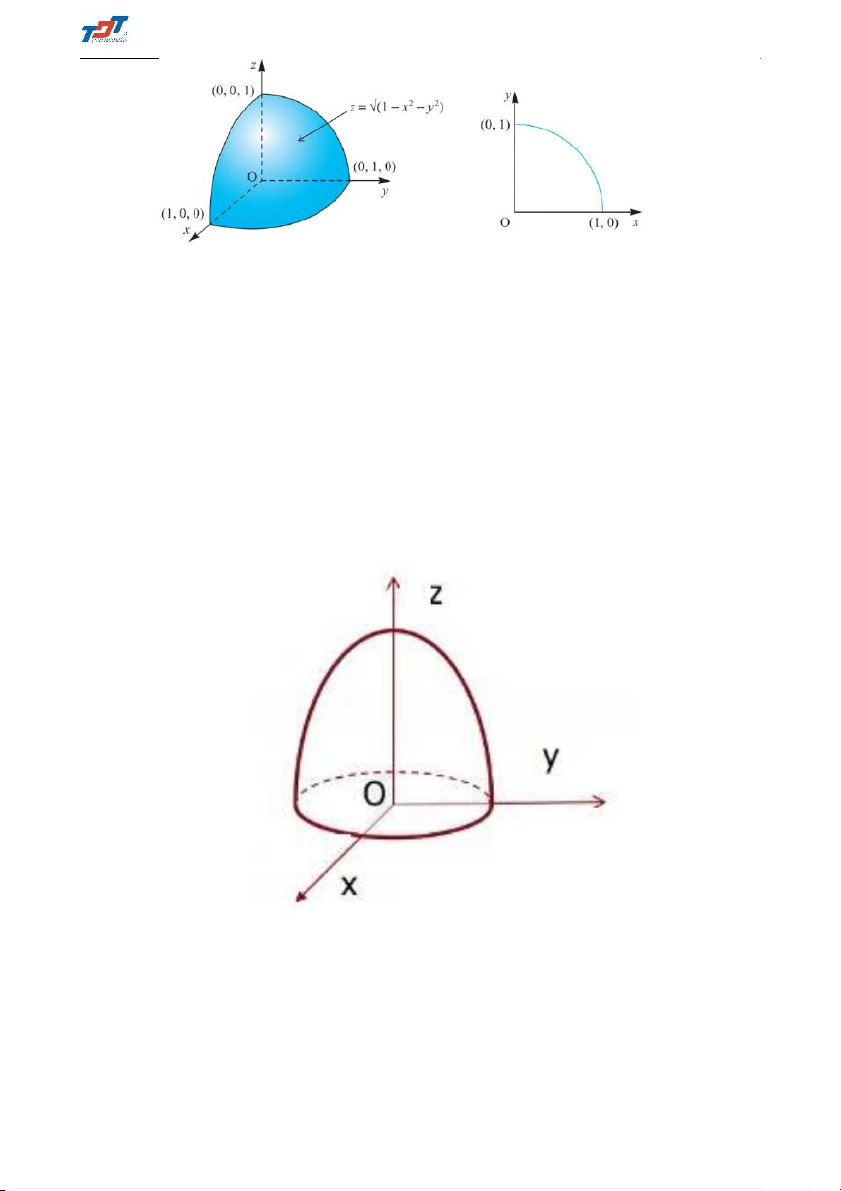
(d) Evaluate the surface integral Z Z (x + y + z)dS S
, where S is thf portion of the sphere x2 + y2 + z2 = 1 that lies in the first octant. 16 Toán 2E1 ThS. Phạm Kim Thủy
4. Ứng dụng: Diện tích của mặt α được xác định bởi: Z Z S(α) = dS (1.52) (α) Example 1.5.2
Tính diện tích mặt phẳng paraboloid (P ) : z = 1 − x2 − y2 nằm giữa hai mặt phẳng z = 0, z = 1 1.5.2 Surface integrals Type 2 1. Định nghĩa:
- Cho mặt cong S, tại một điểm chính quy M của S, có 2 vector pháp tuyến đơn vị ~n và ~n0 = −~n 17 Toán 2E1 ThS. Phạm Kim Thủy
- Nếu có thể chọn được điểm M của mặt S một vector pháp đơn vị ~n sao cho ~n biến
thiên liên tục trên S, ta nói mặt S định hướng được và hướng của mặt S được xác
định bởi hướng của ~n. Vector pháp tuyến của mặt định hướng thì vector pháp tuyến đi từ chân lên đâu.
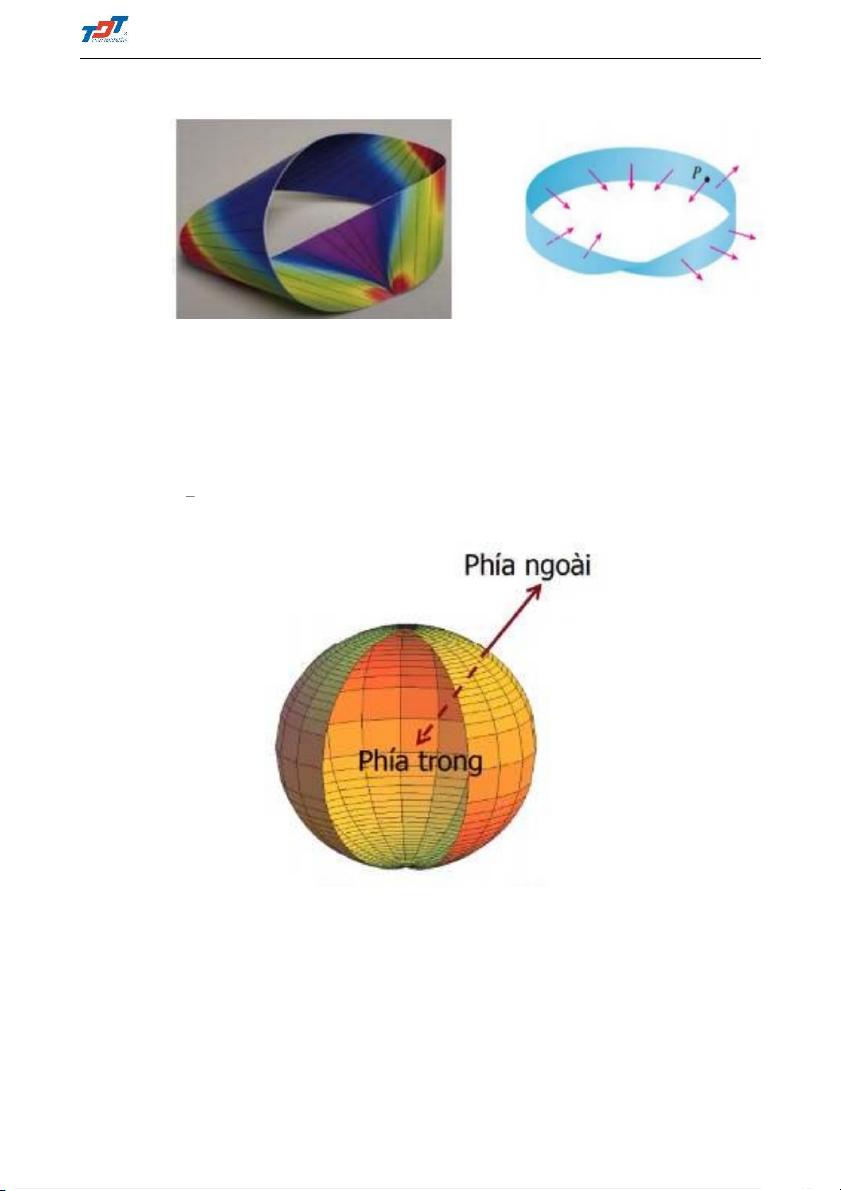
- Trong trường hợp ngược lại, vector pháp tuyến đổi chiều thì mặt cong S được gọi là
mặt không định hướng. Dải Mobius (Mobius band/ Mobius strip) là một ví dụ cho
mặt không định hướng. Lấy một băng giấy dài hình chữ nhật, xoắn băng giấy ấy 18 Toán 2E1 ThS. Phạm Kim Thủy
nữa vòng theo chiều dài, rồi gnasw 2 dầu lại. Khi điểm M chạy một vòng trên dải
Mobius, xuất phát từ vị trí M0 thì lúc gập lại M0, vector ~n đổi hướng. Do đó, ~n
không biến thiên liên tục trên dải Mobius.
2. Cách xác định vector pháp tuyến đơn vị của mặt S: Viết lại phương trình mặt S
dạng F (x, y, z) = 0. Khi đó, vector phát tuyến của mặt S được xác định bởi: ~n = F 0, F 0, F 0 (1.53) x y z
Vector pháp tuyến đơn vị của mặt S được xác định bởi: Lấy thành phần tương ứng của
~n chia cho độ dài của ~n.
Example 1.5.3 Tìm vector pháp tuyến đơn vị của mặt S : x2 + y2 + z2 = 4 tại điểm √ A(1, 0,
3), biết mặt S được định hướng phía ngoài.
3. Định nghĩa tích phân mặt loại 2:
- Nếu tại một điểm M(x, y, z) ở trong miền hữu hạn V của không gian Oxyz có một hàm vector ~ F (M ) = ~
F (x, y, z) xác định, ta nói rằng, trong miền V có một trường vector ~ F (M ) được xác định.
- Giả sử trong miền V có S là một mặt cong định hướng mà pháp tuyến đơn vị là ~n.
Nếu vecor ~F không đổi và S là mặt định hướng có diện tích cũng được ký hiệu là
S, người ta gọi thông lượng Φ của trường vector ~ F qua mặt S là tích: Φ = S · cos ~n, ~ F = S · ~ F , ~n (1.54) 19 Toán 2E1 ThS. Phạm Kim Thủy
- Nếu ~v là vận tốc của chất lỏng có mật đọ ρ chảy qua mặt S thì thông lượng Φ của trường vector ~
F = ρ~v biểu thị khối lượng của chất lỏng chảy qua S trong một đơn vị thời gian.
- Bây giờ, giả sử trường vector ~F (r) biến thiên liên tục trong V , nghĩa là các toạ độ
P (M ), Q(M ), R(M ) của nó là những hàm số biến thiên liên tục trong V . Hãy tính
thông lượng Φ của ~F (M) qua mặt định hướn S.
- Ta chia mặt S thàhnh n mảnh nhỏ. Gọi tên và diện tích của các mảnh ấy là ∆S1, ∆S2, . . . , ∆Sn.
Nếu mảnh ∆Si có đường kính khá bé, có thể coi như vector ~F (M) không đổi trên mảnh ấy và bằng ~ F (Mi),
Mi(ξi, ηi, ζi) là một điểm nào đó trong mảnh ∆Si và coi
mảnh ∆Si xấp xỉ như một mảnh phẳng ứng với phía đã chọn của mặt.
- Do đó, thông lượng ∆Φi của ~
F (M ) qua ∆Si xấp xỉ bằng: n
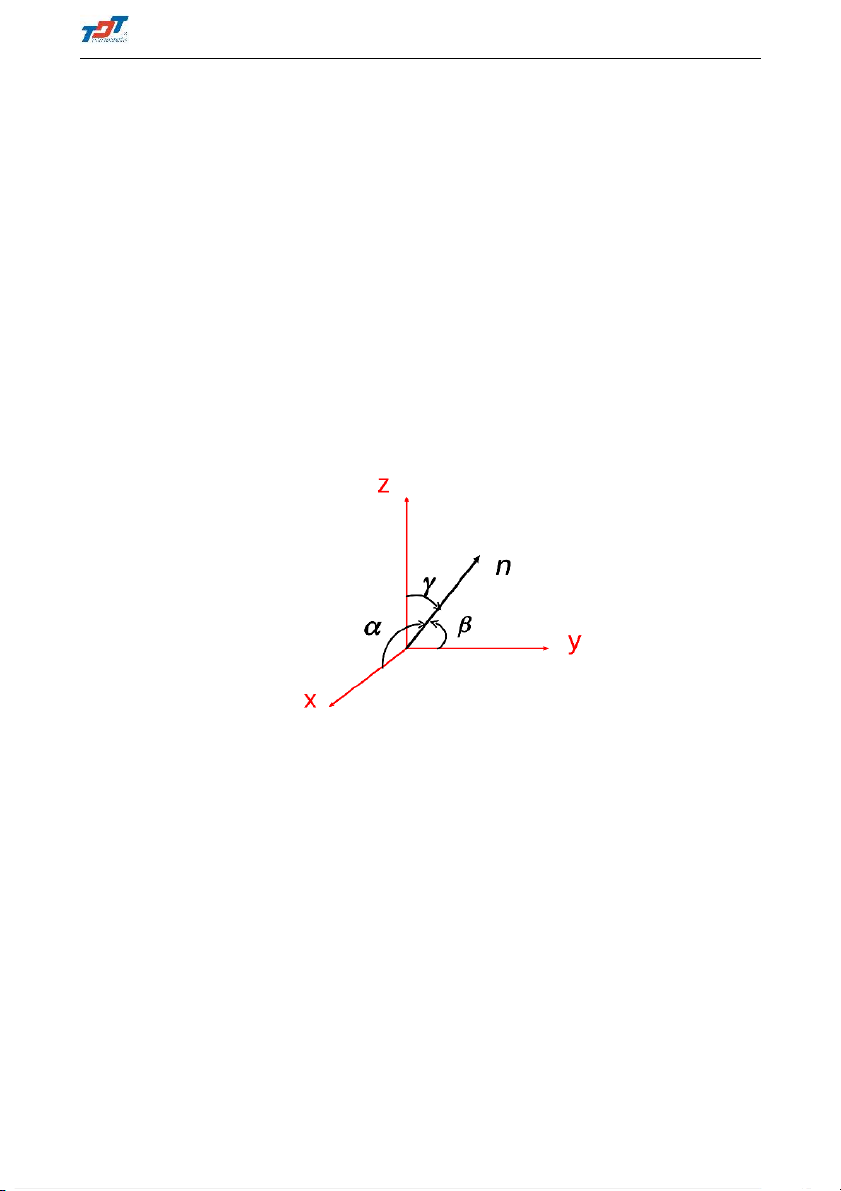
Φ ∼ X [P (Mi)cosαi + Q(Mi)cosβi + R(Mi)cosγi] ∆Si (1.55) i=1 Trong đó, αi = (~n(Mi), Ox); βi = (~n(Mi), Oy), γi = (~n(Mi), Oz) (1.56)
- Phép tính gần đúng này càng chính xác nếu n càng lớn và các mảnh ∆Si có đường kính
càng nhỏ. Nếu khi n → ∞ sao cho maxdi → 0, di là đường kính của Si, mà tổng ở vế
phải của (1.55) dần về giới hạn xác định I không phụ thuộc cách chia mặt S và cách
lấy điểm Mi trên ∆Si thì I được gọi là thông lượng của ~
F (M ) qua mặt S. Giới hạn
đó được gọi là tích phân mặt loại 2 của các hàm số P (x, y, z), Q(x, y, z), R(x, y, z) trên mặt S. Kí hiệu: Z Z
P (x, y, z)dydz + Q(x, y, z)dzdx + R(x, y, z)dxdy (1.57) S - Nếu ~
F (x, y, z) có các thành phần là P (x, y, z), Q(x, y, z), R(x, y, z) và vector pháp tuyến
đơn vị của S là ~n thì tích phân mặt loại 2 (1.57) có thể viết thành: Z Z Z Z F · ~ndS = F · dS (1.58) S S Tính chất:
- Nếu đổi hướng của vector pháp tuyến thì tích phân (1.57) đổi dấu.
- Tích phân mặt loại 2 có tính chất tương tự tích phân kép. 20




