Giáo trình thí nghiệm vật lý 1 – Khoa khoa học ứng dụng | Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh

Bài mở đầu
CƠ SỞ LÝ THUYẾT VỀ CÁC PHÉP TÍNH SAI SỐ
1. KHÁI NIỆM VỀ CÁC PHÉP ĐO
Những tính chất vật lý của vật thể, của trường đều được đặc
trưng bởi những đại lượng vật lý. Mục tiêu của các thí nghiệm vật lý
là xác định các đại lượng vật lý một cách định lượng, tức là phải đo
đạc, thu được các giá trị bằng số của các đại lượng vật lý đó.
1.1. Khái niệm về phép đo
Trong vật lý, phép đo (measurement) là so sánh giữa đại lượng
vật lý cần đo với đại lượng vật lý cùng thể loại, nhưng ở những điều
kiện tiêu chuẩn (thường là không thay đổi theo thời gian) gọi là đơn vị
đo. Việc đo này đem lại một con số thể hiện mối liên hệ về độ lớn giữa
đại lượng cần đo với đơn vị đo.
1.2. Phân loại phép đo
Về phương diện toán, người ta chia các phép đo thành hai
loại: trực tiếp và gián tiếp.
1.2.1. Phép đo trực tiếp
Phép đo trực tiếp là phép đo trong đó ta đọc kết quả trực tiếp trên dụng cụ đo.
1.2.2. Phép gián tiếp
Phép đo gián tiếp là phép đo mà kết quả đo được xác định
thông qua những biểu thức liên hệ giữa đại lượng cần đo với những
đại lượng được đo trực tiếp hoặc gián tiếp trước đó. Tuy nhiên một số
phép đo trực tiếp thực chất là phép đo gián tiếp.
2. KHÁI NIỆM VỀ SAI SỐ PHÉP ĐO
Khi đo nhiều lần cùng một đại lượng, dù cẩn thận đến mấy,
kết quả giữa các lần đo cũng có sự khác nhau. Điều đó chứng tỏ rằng
trong kết quả đo được luôn luôn có sai số và kết quả chúng ta nhận
được chỉ là giá trị gần đúng.
Xác định giá trị thực của một đại lượng vật lý với sự chính
xác tuyệt đối là không thể, mà ta chỉ có thể xác định được giá trị thực
của đại lượng đó nằm trong khoảng tin cậy là bao nhiêu. VD: phép đo
thời gian thu được kết quả t = (2,5 ± 0,1).100 (s) tức là thời gian t nằm
trong khoảng từ 2,4 s đến 2,6 s.
2.1. Định nghĩa sai số phép đo
Sai số phép đo là giá trị chênh lệch giữa giá trị đo được hoặc
tính được và giá trị thực hay giá trị chính xác của một đại lượng cần đo.
2.2. Nguyên nhân gây ra sai số phép đo
Các nguyên nhân chính gây ra sai số phép đo: -
Do phương pháp đo lường không chính xác. -
Do thiết bị đo không chính xác. -
Do sự vụng về hay khéo léo của người đo. -
Do các yếu tố bên ngoài tác động đến phép đo.
2.3. Phân loại sai số
Sai số của phép đo có thể được phân loại theo cách thể hiện bằng
số, theo nguyên nhân gây ra sai số hoặc quy luật xuất hiện sai số.
2.3.1. Phân loại sai số theo quy luật xuất hiện
Tùy theo quy luật xuất hiện, người ta chia sai số ra làm ba loại:
sai số thô, sai số hệ thống và sai số ngẫu nhiên. a. Sai số thô
Số liệu thu được bởi phép đo có sự chênh lệch một cách rõ rệt
và vô lý so với giá trị có thể có của đại lượng cần đo và chúng ta
không thể sử dụng số liệu đó. Ta nói số liệu đó có chứa sai số thô. Sai
số thô xuất hiện do các điều kiện cơ bản của phép đo bị vi phạm hoặc
do sự sơ suất của người làm thí nghiệm, hoặc do bị chấn động đột
ngột từ bên ngoài. Do thiếu ánh sáng có thể đọc nhầm 3 thành 8 hoặc 171,78 thành 1717,8 v.v….
Khi gặp kết quả có chứa sai số thô, chúng ta phải loại trừ nó ra
khỏi kết quả đo bằng cách lặp lại nhiều lần phép đo và mạnh dạn bỏ
nó ra khỏi bảng số liệu. Như vậy trong phần tính toán sai số ta luôn
xem rằng các kết quả đo không chứa sai số thô. b. Sai số hệ thống
Sai số hệ thống là sai số gây bởi những yếu tố tác động như
nhau lên kết quả đo, có giá trị không đổi trong các lần đo được tiến
hành bằng cùng một dụng cụ theo cùng một phương pháp. Các sai số
này có thể tính được, chúng luôn làm cho kết quả đo lớn hơn hoặc
nhỏ hơn một đại lượng nào đó, hoặc thay đổi theo một quy luật nhất
định. Người ta thường chia sai số hệ thống ra làm 2 loại: -
Sai số hệ thống biết được chính xác nguyên nhân và độ
lớn: sai số này xuất hiện khi dụng cụ đo đã bị sai lệch. Chẳng hạn, khi
chưa có dòng điện chạy qua mà kim của ampere kế đã chỉ 0,1A; khi
chưa kẹp vật cần đo chiều dài vào thước kẹp mà thước đã cho chiều
dài là 0,1 mm… Sai số loại này có thể loại khỏi kết quả đo bằng cách
hiệu chỉnh lại dụng cụ đo, hoặc hiệu chỉnh lại kết quả (cộng thêm
hoặc trừ bớt vào kết quả thu được sai lệch ban đầu). -
Sai số hệ thống biết được nguyên nhân nhưng không
biết chính xác độ lớn: Sai số này phụ thuộc vào độ chính xác của
dụng cụ đo. Mỗi dụng cụ đo đều có độ chính xác nhất định của nó. Ví
dụ: đối với các dụng cụ đo điện hiện kim thì sai số hệ thống có thể
gặp 2 loại như sau: sai số thứ nhất là sai số do nhà sản xuất quy định
(sai số dụng cụ), sai số thứ hai là sai số ở vạch chia nhỏ nhất của
thang đo (sai số làm tròn). c. Sai số ngẫu nhiên
Sai số ngẫu nhiên là sai số còn lại của phép đo sau khi đã loại
trừ hết sai số thô và sai số hệ thống. Sai số ngẫu nhiên gây nên bởi
một số rất lớn các nhân tố mà ta không thể tách riêng và tính riêng
biệt cho chúng được. Có thể xem sai số ngẫu nhiên là tác dụng tổng
hợp của các nhân tố đó. Chẳng hạn do giác quan của người làm thí
nghiệm không tinh, không nhạy dẫn đến không phân biệt được đúng
chỗ trùng nhau của hai vạch chia trên thước kẹp, do điều kiện thí
nghiệm thay đổi một cách ngẫu nhiên ta không thể biết được mà dẫn
đến kết quả đo mắc sai số…Ví dụ, đo cường độ dòng điện trong mạch
có điện áp luôn thăng giáng hoặc nhiệt độ, áp suất trong phòng luôn
luôn thay đổi mà ta không phát hiện được làm cho kết quả đo bị thăng
giáng… Sai số ngẫu nhiên có độ lớn và chiều thay đổi hỗn loạn.
Chúng ta không thể loại trừ chúng ra khỏi kết quả đo vì không biết
chắc chắn, mà chúng ta chỉ có thể sử dụng các phương pháp toán học,
như các lý thuyết xác suất để tính ảnh hưởng của chúng đến việc ước
lượng các giá trị chân thực của các đại lượng. Và thường sai số ngẫu
nhiên của các phép đo được phân bố theo phân bố chuẩn Gauss.
Có thể thấy rằng sai số ngẫu nhiên và sai số hệ thống luôn tồn
tại trong các phép đo vật lý. Chúng ta có thể làm giảm sai số ngẫu
nhiên bằng cách đo nhiều lần một phép đo, nhưng sai số hệ thống thì
không thể giảm bằng cách đo nhiều lần mà chỉ có thể giảm bằng cách
thay bằng các dụng cụ có độ chính xác hơn, dụng cụ có sai số nhỏ
hơn hoặc canh chỉnh các dụng cụ chính xác, lựa chọn thang đo hợp lý.
2.3.2. Phân loại theo cách thể hiện bằng số
Theo cách thể hiện bằng số, người ta chia sai số ra làm hai
loại: sai số tuyệt đối và sai số tương đối. a.
Sai số tuyệt đối
Sai số tuyệt đối là giá trị tuyệt đối (module) của hiệu số giữa
giá trị thực của x và giá trị đo được X của nó và được kí hiệu: ∆ = | − | (1) Khi đó khoảng [
 − ∆,  + ∆ ] sẽ bao quanh giá trị thực x, nghĩa là:
 − ∆ ≤  ≤  + ∆ (2)
Vậy sai số tuyệt đối cho biết độ lớn của sai số, nó chứa cả sai
số ngẫu nhiên và sai số hệ thống.
Ví dụ: Khi xác định khối lượng của một vật, người ta dùng
cân và được kết quả:  = (15,5 ± 0,3) g
điều này có nghĩa là khối lượng thực của vật được xác định trong khoảng giới hạn: 15,2 g ≤ m1≤15,8g b.
Sai số tương đối
Sai số tương đối là tỉ số phần trăm giữa sai số tuyệt đối ∆ và
giá trị đo được X, ký hiệu là ε:  = ∆ 100% (3) 
Sai số tương đối cho biết độ chính xác của một phép đo, nó
cũng chứa cả sai số ngẫu nhiên và sai số hệ thống. Muốn đánh giá đầy
đủ kết quả của phép đo một đại lượng vật lý, chúng ta cần phải xác
định được sai số tuyệt đối và sai số tương đối của phép đo đó.
3. CÁCH TÍNH SAI SỐ
Sai số ngẫu nhiên của phép đo vật lý sẽ được tính toán thông
qua giá trị độ lệch chuẩn (SD – standard deviation of mean).
3.1. Sai số của phép đo trực tiếp
3.1.1. Sai số hệ thống
Đối với các thiết bị đo, trong catalog hoặc trên dụng cụ có chỉ
ra giới hạn sai số của dụng cụ Δmax, số này có nghĩa là giá trị sai số
lớn nhất (giới hạn sai số) khi dụng cụ hoạt động ở điều kiện nhà sản
xuất đề ra. Và thông thường sai số dụng cụ cũng được phân bố theo
phân bố chuẩn, vì vậy nhà sản xuất xác định giá trị Δmax, được đặc
trưng bằng độ lệch bình phương trung bình (đối với phân bố chuẩn
theo quy tắc 3σ thì độ tin cậy đạt tới 0,997) :  =  (4) 
Ví dụ : Đối với thước kẹp, trên thước có ghi 0,05 thì đó là giới
hạn sai số của phép đo Δmax=0,05 mm, và độ lệch bình phương trung
bình của thước kẹp :  =  = .   
Ngoài ra, như đã trình bày ở trên, trong đo đạc chúng ta còn
gặp sai số làm tròn, sai số chủ quan, …. Sai số làm tròn được tính từ
vạch chia nhỏ nhất của thang đo ω, do đó độ lệch chuẩn của sai số làm tròn :  =  (5) 
Ví dụ : Trở lại với thước kẹp ở trên, vạch chia nhỏ nhất của
thước kẹp đó sẽ là 0,05 mm, do đó độ lệch chuẩn của sai số làm tròn
của thước sẽ là :  = .  
Sai số hệ thống được tính theo công thức, độ lệch chuẩn của sai
số hệ thống nhân với hệ số bất đẳng thức Chebyshev :
 =  +  + ⋯ (6)
∆ = .  = .  +  + ⋯ (7)
với γα là hệ số của bất đẳng thức Chebyshev (xem bảng 1), trong đó α là độ tin cậy.
Tiếp tục ví dụ trên, vậy thước kẹp sẽ có sai số hệ thống (nếu
lấy độ tin cậy là 0,7) :  0.05  ∆  0.05
 = .  +  = 1,8.  3  +  3  ≈ 0,0424 
3.1.2. Sai số ngẫu nhiên
Như đã nói ở trên sai số ngẫu nhiên của các phép đo thường
tuân theo các định luật thống kê. Giả sử chúng ta đo n lần một đại
lượng vật lý X và thu được các giá trị X1, X2, …Xn .
Bước 1: Sau khi đo đạc các giá trị của phép đo trực tiếp. Lập
bảng các kết quả đo được. Lần đo 1 2 3 … N Giá trị đo được X1 X2 X3 … Xn
Bước 2: Tính giá trị trung bình của các lần đo.
 = ⋯ =  ∑  (8)   
Khi n càng lớn,  càng gần với giá trị X.
Bước 3: Tính sai số tuyệt đối cho từng lần đo:
∆ = | − | (9)
Bước 4: Sai số ngẫu nhiên trung bình của phép đo được tính
bằng độ lệch chuẩn của các giá trị đo được:     ∆ 
∆∆⋯∆   = ∆ =   ∑ (   (10)    − )
3.1.3. Sai số của phép đo trực tiếp
Vậy sai số tuyệt đối trung bình của phép đo trực tiếp được tính theo công thức:  = ∆     +  (11)
Bảng 1 : Hệ số γα của bất đẳng thức Chebyshev α 0,5 0,6 0,7 0,8 0,9 … 0,95 γα 1,4 1,6 1,8 2,2 3,2 … 4,4
3.1.4. Sai số của phép đo gián tiếp
Giả sử, ta phải đo một đại lượng F liên hệ với các đại lượng x1,
x2, x3,... bởi hàm số: F = f (x1, x2, x3,...) trong đó đại lượng x1, x2, x3,..
được đo trực tiếp. Từ phép đo và cách tính sai số của phép đo trực tiếp
đã trình bày ở trên, chúng ta thu được giá trị trung bình của các đại
lượng , , , … và sai số tuyệt đối trung bình của các đại lượng đó
∆, ∆∆,…
Giá trị trung bình của đại lượng F được tính như sau:
 = (, , ,… ) (12)
Sai số tuyệt đối trung bình ∆ được tính theo công thức lan truyền sai số:  
∆ = 󰇡  󰇢 + 󰇡  󰇢 + ⋯ (13)     
Và sai số tương đối được tính theo công thức: ∆  
= 󰇡 󰇢 + 󰇡 󰇢 + ⋯ (14)      
Tuy nhiên, khi không cần độ chính xác cao người ta lấy giới
hạn trên (sai số cực đại) theo công thức tính gần đúng như sau:
∆ = 󰇻  󰇻 ∆ + 󰇻  󰇻 ∆+… (15)      ∆ 󰇻 ∆
 + 󰇻󰇻∆   +… (16)  = 󰇻     
Ví dụ 1: Cho  =    
Giá trị trung bình của đại lượng F:  =  
Sai số tuyệt đối trung bình ∆
 và sai số tương đối trung bình
 của đại lượng F được tính như sau:
Cách 1: Áp dụng công thức (15), ta được:
Bước 1: Tính các dạo hàm riêng theo 2 biến x, y:
󰇻󰇻 = 󰇻 2 󰇻, 󰇻󰇻 = 󰇻 −2 󰇻  (+)2  (+)2
Bước 2: Thế các đạo hàm riêng trên vào công thức (15), ta
được sai số tuyệt đối trung bình của đại lượng F: 2 −2 ∆
 = ( +)∆+ ( +)∆
Bước 3: Thế ∆ vào công thức (3), ta được sai số tương đối
trung bình của đại lượng F:  2  ∆ −2
 =  =  −  ∆ +  −  ∆
Cách 2: Áp dụng công thức (16), chúng ta có thể tính sai số
tương đối trước theo các bước như sau:
Bước 1: lnF = ln (x-y) – ln (x+y)
Bước 2: () =  =   − 󰇡  󰇢       Bước 3:  = ∆ 󰇻 ∆ + 󰇻   = 󰇻   󰇻 ∆ ∆
 =  ∗ =󰇻  󰇻∆
 + 󰇻  󰇻∆  () ()
* Chú ý: Hai cách trên cho cùng một kết quả. Như vậy, hai
cách trên tương đương nhau.
4. CÁCH LÀM TRÒN SỐ VÀ VIẾT KẾT QUẢ
4.1. Cách làm tròn số
Các bài thí nghiệm trong giáo trình thí nghiệm vật lý đại
cương có yêu cầu về độ chính xác trong các phép đo không cao lắm
vì số lần đo một đại lượng vào khoảng 10 lần. Do đó, thông thường
trong sai số chỉ giữ lại một đến hai chữ số có nghĩa khác 0.
Tuy nhiên, trong tính toán, sai số có thể gồm nhiều chữ số và
ta phải làm tròn theo qui tắc làm tròn sao cho độ tin cậy của phép đo
không bị giảm đi, tức là chữ số khác không được giữ lại sẽ tăng lên 1
đơn vị khi chữ số sau nó khác không. Thí dụ các sai số 0,164; 0,275;
0,285; 1,94 được làm tròn thành 0,2; 0,3; 0,3; 2.
Trong trường hợp làm tròn theo cách trên mà sai số đã làm
tròn tăng lên quá 25% so với sai số ban đầu thì có thể giữ lại hai chữ
số khác không. Thí dụ 0,127 thành 0,13.
4.2. Chữ số có nghĩa và chữ số vô nghĩa
Mọi số A bất kỳ đều có thể viết dưới dạng chuẩn hóa: A = a.10n
Trong đó 1< a < 10 và n được gọi là bậc của số A.
Ví dụ: 5,12 =5,12.100 (bậc 0); 0,0031 = 3,1.10-3(bậc -3)
Từ khái niệm bậc của một số chúng ta đi đến khái niệm về
chữ số tin cậy, chữ số nghi ngờ và chữ số không tin cậy của một giá trị đo nào đó như sau:
- Những chữ số của giá trị trung bình có bậc lớn hơn bậc của
sai số là chữ số tin cậy.
- Những chữ số có cùng bậc với sai số là chữ số nghi ngờ
- Những chữ số có bậc nhỏ hơn bậc của sai số là chữ số không tin cậy. Ví dụ: Giá trị Sai số Chữ số tin cậy Chữ số nghi Chữ số trung ngờ không tin bình cậy 216 3 2;1 6 - 0,365 0,01 3 6 5 1,34 0,03 1;3 4 - 13100 10 1;3;1 0 0
Từ cách phân biệt các loại chữ số, chúng ta có thể chia làm hai
loại chữ số là chữ số có nghĩa và chữ số vô nghĩa:
- Chữ số có nghĩa là các chữ số tin cậy và nghi ngờ.
- Chữ số vô nghĩa là chữ số không tin cậy, chữ số không đứng
đầu một số trước dấu phẩy và các chữ số không đứng ngay sau dấu phẩy. Ví dụ: Giá trị trung bình Sai số Chữ số có nghĩa Chữ số vô nghĩa 0,025 0,001 2;5 0;0 0,78 0,01 7;8 0 13100 10 1;3;1;0 0
4.3. Cách viết kết quả
Chúng ta viết kết quả theo qui tắc sau đây:
- Giá trị trung bình của đại lượng cần đo được viết dưới dạng chuẩn hóa.
- Làm tròn sai số (theo quy tắc làm tròn trình bày ở trên).
- Bậc của chữ số có nghĩa nhỏ nhất của giá trị trung bình bằng
bậc của sai số (nghĩa là cần làm tròn giá trị trung bình khi bậc của chữ
số khác không của nó nhỏ hơn bậc của sai số).
Ví dụ: Viết kết quả của phép đo một đại lượng vật lý khi đã biết giá
trị trung bình và sai số Giá trị trung bình Sai số Kết quả 279,16 0,27 (2,792  0,003).102 1000 1 (1,000  0,001).103 0,062 0,001 (6,2  0,1).102 12,54 0,26 (1,25  0,03)10 Lưu ý:
- Trong một tổng của nhiều sai số tương đối, nếu một số hạng
nào đó nhỏ hơn 1/10 số hạng khác thì có thể bỏ qua số hạng đó.
- Cách sử dụng các hằng số: khi tính kết quả trong công thức ta
thường gặp các hằng số như , g, … việc lấy đến mấy số lẻ trong các
hằng số này phụ thuộc vào các đại lượng trong bài thí nghiệm. Tốt nhất
là nên lấy đến số lẻ sao cho sai số tương đối của hằng số đó nhỏ hơn
1/10 sai số của các đại lượng khác.
5. CÁCH VẼ ĐƯỜNG BIỂU DIỄN THỰC NGHIỆM
Trong một bài thí nghiệm chúng ta cần biểu diễn kết quả trên đồ
thị. Để vẽ đồ thị bước đầu tiên là chọn tỉ lệ cho hệ trục tọa độ. Tỉ lệ của
các hệ trục phải được chọn sao cho góc nghiêng của các đường thẳng
(hoặc các đường tiếp tuyến với đường cong) trên đồ thị gần 45 độ. Các
đường biểu diễn phải chiếm gần hết phần mặt đồ thị.
Phía bên trái và phía trên các trục phải viết tên, kí hiệu, đơn vị
đo của các đơn vị được thể hiện trên 2 trục đó.
Chẳng hạn cần vẽ đồ thị của hàm số Y = f(X). Bằng thực
nghiệm, ta đã tìm được các giá trị của Yi theo Xi. Vì phép đo có sai số
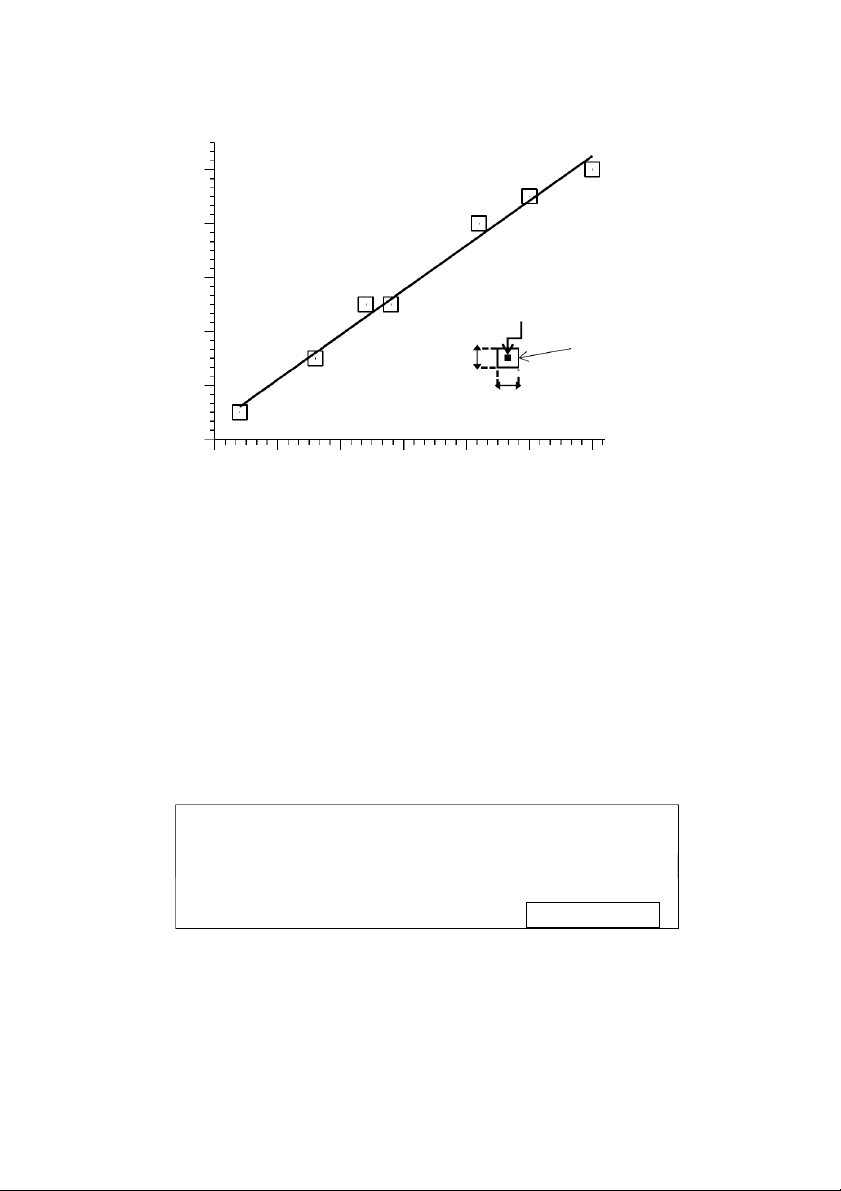
nên ứng với một cặp (Xi Xi) và (Yi Yi) nên điểm thực nghiệm
không phải là một điểm mà là một hình chữ nhật có hai cạnh là 2Xi
và 2Yi (hình 1). Lúc đó đường biểu diễn hàm số Y = f(X) phải được
vẽ sao cho đường biểu diễn đều đi qua các hình chữ nhật ấy.
Cần chú ý rằng đường cong thực nghiệm biểu diễn mối quan
hệ giữa hai đại lượng là một đường cong trơn tru, không thể là một
đường gãy khúc. Do đó, khi vẽ đường biểu diễn, chúng ta cần lưu ý
không nối các điểm thực nghiệm lại mà phải là đường đi qua ô sai số. lnI 3 2 1 Điểm biểu diễn 0 Ô sai số 2Δ Yi -1 2ΔX i -2 5.20 5.25 5.30 5.35 5.40 5.45 5.50 1/T, 10-4K-1
Hình 1: Ví dụ một đồ thị biểu diễn ln(I)=f(1/T)
6. TRÌNH TỰ TIẾN HÀNH MỘT BÀI THÍ NGHIỆM VÀ VIẾT
BÁO CÁO CÁC KẾT QUẢ
6.1. Trình tự làm bài thí nghiệm a.
Đọc kỹ tài liệu thí nghiệm tại nhà. b.
Làm quen với dụng cụ của bài thí nghiệm được giao.
Đối với các bài thí nghiệm về điện phải tuân theo sự chỉ dẫn của
người hướng dẫn trước khi đóng mạch. c.
Tiến hành thí nghiệm thận trọng, nghiêm túc và đều phải
làm nhiều lần. Ghi kết quả thu được vào bảng số liệu. d.
Tính toán kết quả và tính sai số. e. Làm báo cáo kết quả.
6.2. Mẫu báo cáo
Ngày…tháng…năm… Phòng thí nghiệm: …..
Bài thí nghiệm số…: TÊN BÀI THÍ NGHIỆM
Nhóm…: 1. Họ và tên sinh viên 1
Xác nhận của giáo viên:
2. Họ và tên sinh viên 2 …….
1. Mục đích thí nghiệm:
……………………………………………………………………………………….. 2. Bảng số liệu: Lần đo Đại lượng ΔXnn Đại lượng ΔYnn X Y 1 X1 Y1 2 X2 Y2 ….
3. Tính toán các giá trị trung bình và các sai số 4. Đồ thị (nếu có)
5. Viết kết quả tính toán
&&&&&&&
Bài thí nghiệm số 1
XÁC ĐỊNH MOMENT QUÁN TÍNH CỦA BÁNH
XE VÀ LỰC MA SÁT TRONG Ổ TRỤC QUAY ------ooo------
Mục tiêu: Sau khi học xong bài này các sinh viên có khả năng:
- Về kiến thức: Nêu được phương pháp đo và các bước tiến hành thí
nghiệm xác định moment quán tính của bánh xe và lực ma sát trong ổ trục quay.
- Về kỹ năng: Sử dụng thành thạo các dụng cụ đo, tiến hành đúng
trình tự thí nghiệm để thu được số liệu chính xác.
- Về thái độ: Cẩn thận, kiên trì, chính xác, trung thực, khách quan.
1. CƠ SỞ LÝ THUYẾT
1.1. Các khái niệm A
1.1.1. Moment quán tính
Moment quán tính (I) của một vật rắn
đối với một trục quay () là đại lượng đặc C
trưng cho mức quán tính của vật rắn đó khi quay xung quanh trục. h1
Công thức tính moment quán tính của một
vật rắn phân bố liên tục: h2 2 I  R dm  (1.1) m
(Với R: khoảng cách từ chất điểm dm đến B trục quay ()).
Hình 1.1: Sơ đồ phân
1.1.2. Lực ma sát tích lực
Khi hai vật tiếp xúc có chuyển động tương đối với nhau, ở chỗ tiếp
xúc xuất hiện một lực làm cản trở chuyển động của vật. Lực này gọi là
lực ma sát. Nếu hai vật tiếp xúc là những lớp chất lỏng hoặc một vật rắn
chuyển động trên chất lỏng, ta có ma sát nhớt, còn nếu hai vật tiếp xúc
đều là vật rắn thì ta có ma sát khô. Nếu vật rắn này lăn trên vật rắn kia ta
có lực ma sát lăn, nếu vật này trượt trên vật kia ta có lực ma sát trượt.
1.2. Cơ sở lý thuyết để xây dựng công thức tính moment quán tính và lực ma sát
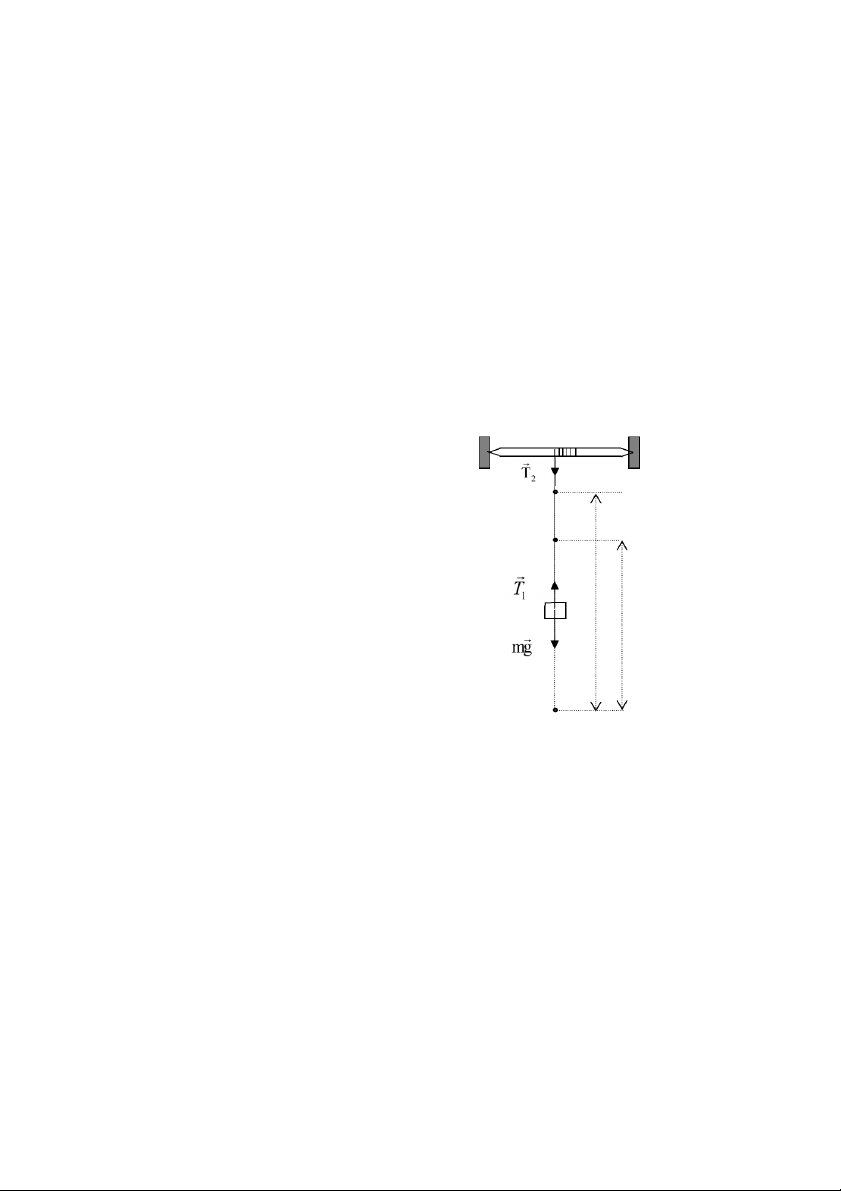
Xét một cơ hệ như hình 1.1 gồm có một bánh xe bán kính trục R có
moment quán tính I quay quanh một trục nằm ngang. Trên trục bánh xe
có quấn một dây nhẹ, không dãn, đầu còn lại có treo vật nặng khối lượng
m. Lúc đầu, bánh xe đứng yên và vật nặng ở vị trí A có độ cao h1 so với
vị trí thấp nhất của nó tại B. Sau đó thả cho hệ vật chuyển động dưới tác
dụng của trọng lực P  mg của quả nặng. Quả nặng chuyển động tịnh
tiến từ A đến B, đồng thời bánh xe quay quanh trục của nó.
Áp dụng định luật II Newton đối với chuyển động tịnh tiến của
quả nặng và phương trình moment đối với chuyển động quay của bánh xe ta được: mg  T  ma 1 (1.2) M  RT  I (1.3) ms 2
Ngoài ra, do dây nhẹ, không dãn và không trượt trên ròng rọc nên: a   R (1.4) T  T 1 2 (1.5)
Từ (1.2), (1.3), (1.4), (1.5), ta tính được gia tốc a của vật nặng: Mms mg  R a  const (1.6) I m  2 R
và gia tốc góc của bánh xe: mg f ms   (1.7)     const mR I R
Các hệ thức (1.6) và (1.7) chứng tỏ quả nặng chuyển động thẳng
biến đổi đều theo phương thẳng đứng với gia tốc a và bánh xe quay
quanh trục của nó với gia tốc góc  không đổi.
Gọi v vận tốc của vật nặng và  là vận tốc góc của bánh xe tại B, t
là thời gian vật nặng chuyển động trên quãng đường, ta có: