Group Assignment Presentation 8 on Monopoly Analysis | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

Group assignment presentation 8
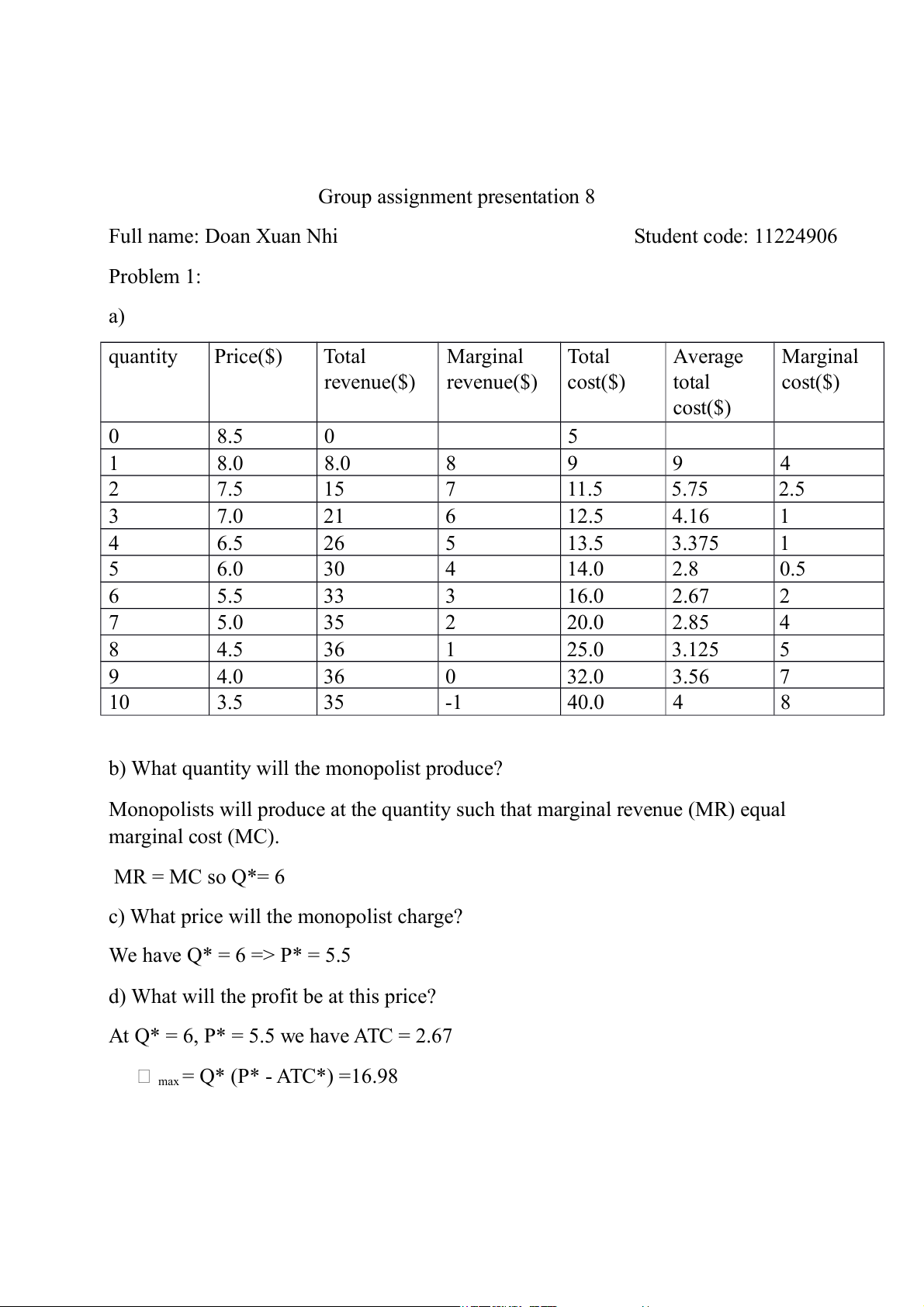
Full name: Doan Xuan Nhi Student code: 11224906 Problem 1: a) quantity Price($) Total Marginal Total Average Marginal revenue($) revenue($) cost($) total cost($) cost($) 0 8.5 0 5 1 8.0 8.0 8 9 9 4 2 7.5 15 7 11.5 5.75 2.5 3 7.0 21 6 12.5 4.16 1 4 6.5 26 5 13.5 3.375 1 5 6.0 30 4 14.0 2.8 0.5 6 5.5 33 3 16.0 2.67 2 7 5.0 35 2 20.0 2.85 4 8 4.5 36 1 25.0 3.125 5 9 4.0 36 0 32.0 3.56 7 10 3.5 35 -1 40.0 4 8
b) What quantity will the monopolist produce?
Monopolists will produce at the quantity such that marginal revenue (MR) equal marginal cost (MC). MR = MC so Q*= 6
c) What price will the monopolist charge? We have Q* = 6 => P* = 5.5
d) What will the profit be at this price?
At Q* = 6, P* = 5.5 we have ATC = 2.67 max = Q* (P* - ATC*) =16.98 Problem 2:
A firm has demand function of P = 100 – Q ($) and total cost function of TC = 500 + 4Q + Q2 ($)
a) Is this firm a perfect competitive firm? Why?
This firm is not a perfect competitive firm. Because if the firm is perfect
competition, D will be perfect elastic. But D in this situation is P = 100 – Q, D is slope down. This firm is a monopoly firm.
b) What is price and quantity to maximize total revenue? What is that maximum total revenue? TR = P.Q = 100Q – Q2 Total revenue max when: (TR)’ = 0 100 – 2Q =0 Q = 50 P = 100 – 50 =50 TRmax = P.Q = 2500
c) What is price and optimal quantity to maximize profit? What is that maximum total profit? MR = (TR)’ = 100 - 2Q MC = (TC)’ = 4 + 2Q To maximize profit: MR = MC 100 – 2Q = 4 + 2Q Q = 24 P = 76 ATC = = + 4 +Q Q = 24 => ATC = 48.83 max = Q* (P* - ATC*) = 652
d) Assume government imposes a tax of $8 per unit of good sold, what is price
and optimal quantity that gives the firm maximum profit? What is this maximum profit?
After government imposes a tax of $8 per unit of good sold, we have:
TC’ = 500 + 4Q + Q2 + 8Q = 500 + 12Q + Q2 MC’ = 12 + 2Q To maximize profit: MC’ = MR 12 + 2Q = 100 – 2Q Q = 22 P = 100 – 22 = 78 ATC = + 12 +Q = 56.72 max = Q* (P* - ATC*) = 468
e) Assume government imposes a fixed tax of $100, what is price and optimal
quantity that gives the firm maximum profit?
Government imposes a fixed tax of $100, we have:
TC’’ = 500 + 4Q + Q2 + 100 = 600 + 4Q + Q2 MC’’ = 4 + 2Q To maximize profit: MC’’ = MR 4 + 2Q = 100 – 2Q Q = 24 P = 100 – 24 = 76