GTLN – GTNN của hàm trị tuyệt đối có chứa tham số Toán 12

Tài liệu gồm 25 trang được biên soạn bởi tập thể quý thầy, cô giáo nhóm Nhóm Word Và Biên Soạn Tài Liệu Môn Toán THPT, hướng dẫn giải bài toán GTLN – GTNN (giá trị lớn nhất – giá trị nhỏ nhất / max – min) của hàm trị tuyệt đối có chứa tham số, được phát triển dựa trên câu 42 đề thi minh họa THPT Quốc gia môn Toán năm học 2019 – 2020 do Bộ Giáo dục và Đào tạo công bố. 

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

25 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 548
KIẾN THỨC CẦN NHỚ:
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất hàm số trên đoạn
;a b
- Tìm nghiệm ( 1,2,...)
i
x i của 0y
thuộc
;a b
- Tính các giá trị
; ;
i
f x f a f b
so sánh các giá trị, suy ra giá trị lớn nhất, giá trị nhỏ nhất.
BÀI TẬP MẪU:
Gọi S là tập tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
3
3f x x x m
trên đoạn
0;3 bằng
16
. Tổng tất cả các phần tử của
S
bằng
A. 16 . B. 16 . C. 12 . D. 2 .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán max, min của hàm trị tuyệt đối có chứa tham số.
2. KIẾN THỨC CẦN NHỚ:
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất hàm số trên đoạn
;a b
- Tìm nghiệm ( 1,2,...)
i
x i của
0y
thuộc
;a b
- Tính các giá trị
; ;
i
f x f a f b so sánh các giá trị, suy ra giá trị lớn nhất, giá trị nhỏ nhất.
3. HƯỚNG GIẢI: Tìm giá trị lớn nhất hàm số
y f x
, ta xét hàm số
y f x .
B1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số
y f x .
B2: Giá trị lớn nhất của hàm số
y f x
tại
max f x hoặc
min f x .
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn A
Đặt
3
3g x x x m
.
2
3 3g x x
;
1 0;3
0
1 0;3
x
g x
x
.
0 ; 1 2 ; 3 18g m g m g m .
Suy ra
0;3
max 18g x m
;
0;3
min 2g x m
.
GTLN - GTNN CỦA HÀM TRỊ TUYỆT ĐỐI CÓ CHỨA THAM SỐ
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 549
Để giá trị lớn nhất hàm số
y f x
là
16
18 16 2
2 16 14
2 16 14
18 16 2
m m
m m
m m
m m
.
Vậy
2; 14
S
nên tổng là
2 14 16
.
Bài tập tương tự và phát triển:
Câu 42.1: Gọi tập
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
3
3
y x x m
trên đoạn
0;2
bằng 3. Số phần tử của
S
là
A.
1
. B.
2
. C.
0
. D.
6
.
Lời giải
Chọn B
Xét
3
3
u x x m
. Ta có:
2
' 3 3
u x
;
0 1 0;2
u x
. Khi đó:
0;2
max max 0 , 1 , 2 max , 2, 2 2
A u u u u m m m m
.
0;2
min min 0 , 1 , 2 min , 2, 2 2
a u u u u m m m m
.
Ta có:
0;2
2 3
2 2
1
max max , max 2 , 2 3
1
2 3
2 2
m
m m
m
y A a m m
m
m
m m
.
Vậy
1
S
.
Câu 42.2: Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để hàm số
2
y x x m
thỏa mãn
2; 2
min 2
y
. Tổng tất cả các phần tử của
S
bằng
A.
31
4
. B.
8
. C.
23
4
. D.
9
4
.
Lời giải
Chọn C
Xét hàm số
2
u x x m
trên đoạn
2;2
, có:
1
0 2 1 0
2
u x x
.
2;2
1
max max 2 , , 2 6
2
u u u u m
;
3;2
1 1
min min 2 , , 2
2 4
u u u u m
.
Nếu
1
0
4
m
hay
1
4
m
thì
2; 2
1 9
min 2
4 4
y m m
(thỏa mãn).
Nếu
6 0
m
hay
6
m
thì
2; 2
min 6 2 8
y m m
(thỏa mãn).
Nếu
1
6
4
m
thì
2; 2
min 0
y
(không thỏa mãn).
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 550
Ta có:
9
8;
8
S
. Vậy tổng các phần tử của
S
bằng
23
4
.
Câu 42.3: Gọi
M
là giá trị lớn nhất của hàm số
4 3 2
3 4 12
f x x x x m
trên đoạn
1;3
. Có bao
nhiêu số thực
m
để
59
2
M
?
A.
2
. B.
6
. C.
1
. D.
4
.
Lời giải
Chọn C
Xét hàm số:
4 3 2
3 4 12
u x x x m
.
Có
3 2
12 12 24
u x x x
0
0 1
2
x
u x
x
.
Khi đó:
1;3
1;3
min min 1 , 0 , 2 , 3 2 32
max max 1 , 0 , 2 , 3 3 27
u u u u u u m
u u u u u u m
.
Do đó:
59
max 32 , 27
2
M m m
59
32
2
32 27
5
2
59
27
2
27 32
m
m m
m
m
m m
.
Vậy có
1
số thực
m
để
59
2
M
.
Câu 42.4: Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để hàm số
2
2
x m m
y
x
thỏa
1;2
max 1
y
.
Tích các phần tử của
S
bằng
A.
16
. B.
4
. C.
16
. D.
4
.
Lời giải
Chọn B
Xét
2
2
x m m
u
x
, ta có:
2
2
2
0 , 1;2 ,
2
m m
u x m
x
.
Do đó
2
1;2
2
max 2
4
m m
A u u
;
2
1;2
1
min 1
3
m m
a u u
.
2 2
1;2
2 1
max max , 1
4 3
m m m m
y
1 17
2
m
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 551
Ta có:
1 17
2
S
. Vậy tích các phần tử của
S
bằng
4
.
Câu 42.5: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1
x mx m
y
x
trên
1;2
bằng
2
. Số phần tử của
S
là
A.
1
. B.
2
. C.
4
. D.
3
.
Lời giải
Chọn A
Xét hàm số:
2
1
x mx m
u
x
.
2
2
2
1
x x
u
x
;
0
u
2
2
2
0
1
x x
x
2
2 0
x x
0 1;2
2 1;2
x
x
.
Ta có:
0 1;2
u x
nên
1;2
4 1
max ,
3 2
y m m
.
1;2
max 2
y
2
3
10
3
m
m
. Vậy
2 10
;
3 3
S
.
Câu 42.6: Xét hàm số
2
f x x ax b
, với
a
,
b
là tham số. Gọi
M
là giá trị lớn nhất của hàm số
trên
1;3
. Khi
M
nhận giá trị nhỏ nhất tính
2
T a b
.
A.
3
T
. B.
4
T
. C.
4
T
. D.
2
T
.
Lời giải
Chọn C
Ta có:
max , 1
2
A B
A B
. Dấu
xảy ra khi
A B
.
Ta có:
max , 2
2
A B
A B
. Dấu
xảy ra khi
A B
.
Xét hàm số
2
g x x ax b
, có
0
2
a
g x x
.
Trường hợp 1:
1;3
2
a
6;2
a
. Khi đó
M max 1 , 9 3
a b a b
.
Áp dụng bất đẳng thức
1
ta có
M 4 2 8
a
.
Trường hợp 2:
1;3
2
a
6;2
a . Khi đó
2
M max 1 , 9 3 ,
4
a
a b a b b
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 552
Áp dụng bất đẳng thức
1
và
2
ta có
2
M max 5 ,
4
a
a b b
2
1
M 20 4
8
a a
2
1
M 16 2
8
a
.
Suy ra
M 2
.
Ta có:
M
nhận giá trị nhỏ nhất có thể được là
2
M
khi
2
2
5
2
1 9 3
a
a
a b b
a b a b
2
1
a
b
.
Vậy
2 4
a b
.
Câu 42.7: Cho hàm số
3 2
3
y x x m
(với
m
là tham số thực). Hỏi
1;2
max
y
có giá trị nhỏ nhất bằng
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn C
Xét hàm số :
3 2
3
t x x
với
1;2
x
.
Ta có
2
0 1;2
3 6 0
2 1;2
x
t x x
x
;
1 2
t
,
2 4
t
. Nên
1;2
max 2
t
và
1;2
min 4
t
.
Do đó
1;2 1;2
max max max 4 ; 2
y m t m m
4 2
4 2
max 4 ; 2 1
2 2
m m
m m
m m
.
Dấu bằng đạt tại
4 2 3
m m m
.
Câu 42.8: Cho hàm số
4 2
8
f x x ax b
, trong đó
a
,
b
là tham số thực. Tìm mối liên hệ giữa
a
và
b
để giá trị lớn nhất của hàm số
f x
trên đoạn
1;1
bằng
1
.
A.
8 0
b a
. B.
4 0
b a
. C.
4 0
b a
. D.
8 0
b a
.
Lời giải
Chọn D
Đặt
2
t x
, vì
1;1
x
nên
0;1
t
.
Ta có:
2
8
g t t at b
, đây là parabol có bề lõm quay lên và có tọa độ đỉnh là
2
;
6 32
a a
I b
Trường hợp 1:
0;1
6
a
. Theo yêu cầu bài toán ta có:
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 553
2
1 0 1
1 1 1
1 1
32
g
g
a
b
2
1 1
1 8 1
32 32 32
b
a b
b a
2
1 1 1
1 8 1 2
32 32 32 3
b
a b
a b
Lấy
1 32 3
ta có :
2
64 64
a
do đó
8 8
a
.
Lấy
3 32 2
ta có :
2
64 32 256 64
a a
Suy ra :
2
32 192 0
a a
24 8
a
.
Khi đó ta có :
8
a
và
1
b
.
Thử lại:
2
8 8 1
g t t t
2
2 2 1 1
t
Vì
0 1
t
nên
1 2 1 1
t
2
0 2 1 1
t
2
1 2 2 1 1 1
g t t
.
Ta có:
max 1
g t
khi
1 1
t x
. Nên
8
a
và
1
b
(thỏa mãn).
Trường hợp 2 :
0;1
6
a
. Theo yêu cầu bài toán ta có:
1 0 1
1 1 1
g
g
1 1
1 8 1
b
a b
1 1
1 8 1
b
a b
2 8 2 10 6
a a
(loại).
Vậy
8
a
và
1
b
.
Câu 42.9: Cho hàm số
4 3 2
4 4
f x x x x a
. Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất
của hàm số đã cho trên đoạn
0;2
. Có bao nhiêu số nguyên
a
thuộc đoạn
3;3
sao cho
2
M m
?
A.
5
. B.
7
. C.
6
. D.
3
.
Lời giải
Chọn A
Xét hàm số
4 3 2
4 4
.
3 2
4 12 8
g x x x x
;
0
g x
3 2
4 12 8 0
x x x
0
1
2
x
x
x
.
Bảng biến thiên
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 554
`
TH1:
1 1 ;a m a M a
2 1 2 3; 2a a a a
.
TH2: 1 0 0; 0a m M 2M m (loại ).
TH3:
0 ; 1a m a M a
2 1 1 1;2;3a a a a .
Vậy có 5 giá trị của
a
thỏa mãn đề bài.
Câu 42.10: Cho hàm số
4
1
x ax a
y
x
. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số trên đoạn
1;2
. Có bao nhiêu số nguyên a sao cho 2M m ?
A. 15. B. 14. C. 16. D. 13.
Lời giải
Chọn C
Xét
4
1
x ax a
u
x
trên đoạn
1;2 , ta có
4 3
2
3 4
0
1
x x
u
x
,
1;2x .
Do đó,
1;2
16
max 2
3
u u a ,
1;2
1
min 1
2
u u a .
TH1:
1
0
2
a
16
3
1
2
M a
m a
1
0
2
16 1
2
3 2
a
a a
1 13
2 3
a .
TH2:
16
0
3
a
1
2
16
3
M a
m a
16
0
3
1 16
2
2 3
a
a a
61 16
6 3
a
.
TH3:
1 16
. 0
2 3
a a
0m ,
1 16
max ,
2 3
M a a
2M m ( thỏa mãn).
Ta có:
61 13
6 3
a
10;....;4a . Vậy có 15 số nguyên thỏa mãn.
Câu 42.11: Cho hàm số
4 2
8cos cosf x x a x b
, trong đó
a
,
b
là tham số thực. Gọi M là giá
trị lớn nhất của hàm số. Tính tổng a b khi M nhận giá trị nhỏ nhất.
A. 8a b . B. 9a b . C. 0a b . D. 7a b .
Lời giải
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 555
Chọn D
Đặt
2
cos
t x
,
0;1
t , ta có hàm số
2
8
g t t at b
. Khi đó
0;1
max
M g t
.
Do đó:
0
M g b
;
1 8
M g a b
;
1 1
2 2 4 2
2 2
M g a b M a b
;
Từ đó ta có
4 8 4 2 8 4 2 4
M b a b a b b a b a b
Hay
1
M
.
Dấu đẳng thức xảy ra khi và chỉ khi
4 2
8 1
2
a b
b a b
và
b
,
8
a b
,
4 2
a b
cùng dấu
8
1
a
b
.
Vậy
7
a b
.
Câu 42.12: Cho hàm số
2
2 1 3
y x x x x m
. Có tất cả bao nhiêu giá trị thực của tham số
m
để
max 3
y
?
A.
1.
B.
2.
C.
0.
D.
4.
Lời giải
Chọn B
Hàm số xác định khi:
1 3 0 1 3
x x x
.
Đặt
2
1 3 3 2 0;2
t x x x x t và
2 2
2 3
x x t
.
Khi đó ta cần tìm giái trị lớn nhất của hàm số
2
3
y t t m
trên đoạn
0;2
.
Với
2
3
u t t m
ta có:
0;2 0;2
13
max 1;min
4
u m u m
.
Do đó
13 1
max max 1 ; 3 4;
4 4
y m m m m
.
Câu 42.13: Cho hàm số
2
2 1 3
y x x x x m
. Khi giá trị lớn nhất của hàm số đạt giá trị
nhỏ nhất. Mệnh đề nào sau đây đúng?
A.
17
.
8
B.
9
.
8
C.
7
.
8
D.
15
.
8
Lời giải
Chọn B
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 556
Hàm số xác định khi:
1 3 0 1 3
x x x
.
Đặt
2
1 3 3 2 0;2
t x x x x t
và
2 2
2 3
x x t
.
Khi đó ta cần tìm giái trị lớn nhất của hàm số
2
3
y t t m
trên đoạn
0;2
.
Với
2
3
u t t m
ta có:
0;2 0;2
13
max 1;min
4
u m u m
.
Do đó
13 13
1 1
13 9
4 4
max max 1 ;
4 2 2 8
m m m m
y m m
.
Dấu bằng xảy ra
13 9 17
1
4 8 8
m m m
.
Câu 42.14: Gọi
S
là tập hợp tất cả các số nguyên
m
để hàm số
4 2
1 19
30
4 2
y x x x m
có giá trị
lớn nhất trên đoạn
0;2
không vượt quá
20
. Tổng các phần tử của
S
bằng
A.
195
. B.
210
. C.
195
. D.
210
.
Lời giải
Chọn A
Xét
4 2
1 19
30
4 2
u x x x m
trên đoạn
0;2
có
3
5
19 30; 0 3
2
x
u x x u x
x
.
Do đó:
0;2
0;2
max max (0); (2)} max{ ; 6} 6;min .
u u u m m m u m
Do đó:
0;2
6 20
13 6
max max{ ; 6} 20 20 6
20 13
6 20
m m
m
y m m m
m
m m
.
Mà m
nên
{ 20; 19;..., 6}
m
. Vậy
20
6
195
S k
.
Câu 42.15: Cho hàm số
3 2
2 3
y x x m
. Có bao nhiêu số nguyên
m
để
1;3
min 3
f x
?
A. 4. B. 8. C. 31. D. 39.
Lời giải
Chọn D
Xét
3 2
2 3
u x x m
, ta có:
2
' 6 6
u x x
;
0
0
1
x
u
x
.
Do đó:
1;3
1;3
min min 1 , 3 , 0 , 1 min 5, 27, , 1 5
max max 1 , 3 , 0 , 1 max 5, 27, , 1 27
u u u u u m m m m m
u u u u u m m m m m
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 557
TH1:
1;3
5 0 5 min 5 3 8 5;6;7;8
m m f x m m m
.
TH2:
1;3
27 0 27 min ( 27) 3 30 30; 29; 28; 27
m m f x m m m
.
TH3:
1;3
( 5) 27 0 27 5 min 0
m m m f x
(thỏa mãn).
Vậy
30; 29; 28;...;7;8
m .
Câu 42.16: Cho hàm số
2
( ) ,
f x ax bx c
( ) 1, [0;1]
f x x . Tìm giá trị lớn nhất của
(0).
f
A.
8
. B.
0
. C.
6
. D.
4
.
Lời giải.
Chọn A
( ) 2 (0)
f x ax b f b
.
Bài toán trở thành tìm giá trị lớn nhất của
b
với điều kiện
( ) 1, [0;1].
f x x
Ta có.
(1) (0)
(0)
1 1
1 2 4 4 (0) 4 (1) 3 (0).
2 2
1
(0)
2 4 2
a b f f
f c
f a b c a b f f b f f f
a b
c f
f c
1 (0) 1
1
( ) 1, [0;1] 1 1 1 4 (1) 3 (0) 4 1 3 8.
2
1
1 1
2
f
f x x f b f f f
f
Đẳng thức xảy ra
2
1
1
1, 8
2
(1) 1 1, 8 ( ) 8 8 1.
(0) 1 1
1
4 2
f
c a
f a b c b f x x x
f a b c
c
Vậy giá trị lớn nhất của
(0)
f
bằng 8.
Câu 42.17: Cho hàm số
4 3 2
2
y x x x a
. Có bao nhiêu số thực
a
để
1; 2
1; 2
min max 10
y y
?
A.
2
. B.
5
. C.
3
. D.
1
.
Lời giải
Chọn A
Xét
4 3 2
2
u x x x a
trên đoạn
1; 2
, ta có :
3 2
' 4 6 2
u x x x
;
0
' 0 1
1
2
x
u x
x
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 558
Suy ra:
1; 2
1; 2
1
max max 1 , 0 , , 1 1 2 4
2
1
min min 1 , 0 , , 1 0 1
2
M u u u u u u u a
m u u u u u u u a
.
TH1:
0 0
m a
. Khi đó:
1; 2
1; 2
min ; max
y m y M
Ta có điều kiện :
0
3
4 10
a
a
a a
.
TH2:
0 4
M a
. Khi đó :
1; 2
1; 2
min ; max
y M y m
.
Ta có điều kiện :
4
7
4 10
a
a
a a
.
TH3:
0 4 0
m M a
.
Khi đó:
1;2
1; 2
min 0; max max 4 , max 4, 10
y y a a a a
.
Suy ra
1; 2
1; 2
min max 0 10 10
y y
(loại).
Vậy
3; 7
a
.
Câu 42.18: Cho hai số thực
x
;
y
thỏa mãn
2 2 2 2
4 6 4 6 10 6 4
x y x y y y x x
. Gọi
M
,
m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức
2 2
T x y a
. Có bao
nhiêu giá trị nguyên thuộc đoạn
10;10
của tham số
a
để
2
M m
?
A.
17
. B.
16
. C.
15
. D.
18
.
Lời giải
Chọn B
Biến đổi giả thiết có:
2 2 2 2
4 6 4 6 10 6 4
x y x y y y x x
2 2 2 2
6 10 6 10 6 4 6 4
y y y y x x x x
(*).
Đặt
, 0;f t t t t

. Ta có
f t
đồng biến trên
0;

.
Do đó ta có: (*)
2 2 2 2
6 10 6 4 6 10 6 4
f y y f x x y y x x
2 2 2 2 2 2 2 2
4 6 4 0 4 4 6 4 6
x y x y x y x y x y
2 2 2 2
13 3 3 13 13 3 ;3 13
x y x y a a a
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 559
TH1:
13 3 0
a
13 3 0
13 3
13 9 9 13
3 13 2 13 3
3 13
a
m a
ycbt a
a a
M a
.
TH2:
13 3 0
a
13 3
3 13 0
3 13 9 13
13 3 2 13 3
3 13
m a
a
ycbt a
a a
M a
.
TH3:
0
13 3 3 13 0 13 3 13 3
0
m
a a a
M
(
2
M m
).
Vậy
13 9;9 13
a
. Đối chiếu với
10;10 5;...;10
a a .
Câu 42.19: Cho hàm số
3 2
( ) 2 9 12
f x x x x m
. Có bao nhiêu số nguyên
( 20; 20)
m
để với
mọi bộ ba số thực
, , 1;3
a b c thì
( ), ( ), ( )
f a f b f c
là độ dài ba cạnh một tam giác?
A.
10
. B.
8
. C.
25
. D.
23
.
Lời giải
Chọn D
Xét
3 2
2 9 12
u x x x m
trên
1;3
, ta có:
2
6 18 12
u x x
;
0
0
2
x
u
x
.
[1;3]
min min (0), (1), (2), (3) 4
u u u u u m
.
[1;3]
max ax (0), (1), (2), (3) 9
u m u u u u m
.
Để
( ), ( ), ( )
f a f b f c
là độ dài ba cạnh một tam giác thì ta phải có
( ) ( ) ( )
f a f b f c
.
Chọn
[ 2;1]
[ 2;1]
( ) ( ) min ( ), ( ) max ( )
f a f b f x f c f x
ta có điều kiện
[ 2;1]
[ 2;1]
2min ( ) max ( )
f x f x
.
Ngược lại: với
[ 2;1]
[ 2;1]
2min ( ) max ( )
f x f x
, ta có :
[ 2;1]
[ 2;1]
( ) ( ) ( ) 2min ( ) max ( ) 0
f a f b f c f x f x
.
Vậy điều kiện cần và đủ để
( ), ( ), ( )
f a f b f c
là độ dài ba cạnh một tam giác là
[ 2;1]
[ 2;1]
2min ( ) max ( )
f x f x
TH1:
[1;3]
[1;3]
4 0
4 0 min ( ) 4;m ( ) 9 1
2( 4) 9
m
m f x m ax f x m m
m m
TH2:
[1;3]
[1;3]
9 0
9 0 min ( ) 9;m ( ) 4 14
2( 9) 4
m
m f x m ax f x m m
m m
TH3:
[1;3]
[1;3]
( 4)( 9) 0 min ( ) 0 2.0 m ( ) 9
m m f x ax f x m
(loại)
Vậy
19; 15;2......;18;19
m . Có 23 số nguyên thỏa mãn.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 560
Câu 42.20: Cho hàm số
3
3
f x x x m
. Có bao nhiêu số nguyên
20;20
m để với mọi bộ ba
số thực
, , 2;1
a b c thì
, ,
f a f b f c
là độ dài ba cạnh của một tam giác nhọn.
A.
18
. B.
16
. C.
14
. D.
12
.
Lời giải
Chọn B
Xét
3
3
u x x m
trên đoạn , ta có:
2
0 3 3 0 1
u x x
.
Khi đó:
2;1
2;1
max u max 2 , 1 , 1 max m 2,m 2,m 2 2
min u min 2 , 1 , 1 min m 2,m 2,m 2 2
u u u m
u u u m
.
Để
, ,
f a f b f c
là độ dài ba cạnh của một tam giác nhọn ta phải có
2 2 2
f a f b f c
.
Chọn
2;1
2;1
min ; max
f a f b f x f c f x
ta có điều kiện
2
2
2;1
2;1
2 min max
f x f x
.
Ngược lại với
2
2
2;1
2;1
2 min max
f x f x
, ta có
2
2
2 2 2
2;1
2;1
2 min max 0
f a f b f c f x f x
.
Vậy điều kiện cần và đủ để
, ,
f a f b f c
là độ dài ba cạnh của một tam giác là
2
2
2;1
2;1
2 min max
f x f x
.
TH1:
2
2
2;1 2;1
2 2 0 2min 0 2.0 max
m m f x f x
(loại).
TH2:
2 0
m
.
2 2
2;1 2;1
2 0
min 2;max 2 6 4 2
2 2 2
m
f x m f x m m
m m
.
TH3:
2 0
m
.
2 2
2;1
2;1
2 0
min 2 ;max 2 6 4 2
2 2 2
m
f x m f x m m
m m
.
Suy ra
19, 18,..., 12,12,13,...,19
m . Vậy có 16 số nguyên
m
thỏa mãn.
Câu 42.21: Gọi tập
S
là tập hợp giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
3
3
y x x m
trên đoạn
0;2
bằng 3. Số phần tử của
S
là
A.
1
. B.
2
. C.
0
. D.
6
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 561
Lời giải
Chọn B
Xét
3
3
u x x m
có:
2
' 3 3 ; ' 0 1 0;2
u x u x
. Khi đó:
0;2
max max 0 , 1 , 2 max , 2, 2 2
A u u u u m m m m
.
0;2
min min 0 , 1 , 2 min , 2, 2 2
a u u u u m m m m
.
Vậy
0;2
2 3
2 2
1
max max , max 2 , 2 3
1
2 3
2 2
m
m m
m
y A a m m
m
m
m m
.
Câu 42.22: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
4 2
8
f x x x m
trên đoạn
1;1
bằng 5. Tổng tất cả các phần tử của S bằng
A.
7
. B. 7. C.
5
. D.
5
.
Lời giải
Chọn B
Xét hàm số
4 2
8 , 1;1
g x x x m x , ta có
3
0
4 16 ; 0
2
x
g x x x g x
x
.
1 1 7
g g m
,
0
g m
.
Do đó:
1;1
7 5
7
2
max max 7 , 5
5
5
7
m
m m
m
f x m m
m
m
m m
Vậy
2;5
S
. Vậy tổng các giá trị của
S
bằng 7.
Câu 42.23: Gọi S là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
4
3
x m
f x
x
trên đoạn
2;2
bằng 6. Tổng tất cả các phần tử của S bằng
A.
16
. B. 16. C. 2. D.
14
.
Lời giải
Chọn B
Xét hàm số
4
, 2;2
3
x m
g x x
x
, ta có
2
12
3
m
g x
x
.
8
2 , 2 8
5
m
g g m
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 562
Do đó :
2;2
8
6
5
8
8
2
8
5
max max , 8 6
14
5
8 6
8
8
5
m
m
m
m
m
f x m
m
m
m
m
.
Vậy
2;14
S
. Vậy tổng các giá trị của
S
bằng 16.
Câu 42.24: Có bao nhiêu giá trị thực của tham số
m
để giá trị lớn nhất của hàm số
2
2 4
y x x m
trên đoạn
2;1
bằng
4
?
A.
1
. B.
2
. C.
3
. D.
4
.
Lời giải
Chọn B
2
2 4
f x x x m
có
2 2
f x x
,
0 1
f x x
. Do đó
2
2;1
max 2 4 max 1 ; 4 ; 5
x x m m m m
.
Ta thấy
5 4 1
m m m
với mọi
m
, suy ra
2;1
max
y
chỉ có thể là
5
m
hoặc
1
m
.
Nếu
2;1
max 5
y m
thì
5 4
5 1
m
m m
1
m
.
Nếu
2;1
max 1
y m
thì
1 4
1 5
m
m m
5
m
.
Vậy
1; 5
m .
Câu 42.25: Cho hàm số
2
2
x m
y
x
với
m
là tham số,
4
m
. Biết
0;2 0;2
min max 8
x x
f x f x
. Giá trị
của tham số
m
bằng
A.
10
. B.
8
. C.
9
. D.
12
.
Lời giải
Chọn D
Xét hàm số xác định trên tập
0;2
D
Ta có
2
4
2
m
y
x
. Nhận xét
4
m
hàm số luôn đồng biến hoặc nghịch biến trên
0;2
nên
giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên
0;2
luôn đạt được tại
0
x
,
2
x
.
Theo bài ra ta có
4
0 2 8 8 12
2 4
m m
f f m
.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 563
Câu 42.26: Cho hàm số
3 2
( ) 2 3
f x x x m
. Có bao nhiêu số nguyên
m
để
1;3
min 3
f x
?
A. 4. B. 8. C.
31
. D.
39
.
Lời giải
Chọn D
Xét
3 2
2 3
u x x m
có
2
0
6 6 ; 0
1
x
u x x u
x
.
Do đó
1;3
1;3
min min 1 , 3 , 0 , 1 min 5, 27, , 1 5
max max 1 , 3 , 0 , 1 max 5, 27, , 1 27
u u u u u m m m m m
u u u u u m m m m m
.
+ Nếu
5 0 5
m m
thì
1;3
min 5 3 8 5;6;7;8
f x m m m
.
+ Nếu
27 0 27
m m
thì
1;3
min ( 27) 3 30
f x m m
.
30; 29; 28; 27
m
.
Nếu
( 5) 27 0 27 5
m m m
thì
1;3
min 0
f x
(thỏa mãn).
Vậy
30;...;8
m có tất cả 39 số nguyên thỏa mãn.
Câu 42.27: Cho hàm số
3 2
3
y x x m
. Có bao nhiêu số nguyên
m
để
1;3
min 3
f x
?
A. 4. B. 10. C. 6. D. 11.
Lời giải
Chọn D
Với
3 2
3
u x x m
có
2
0
3 6 ; 0
2
x
u x x u
x
.
Do đó
1;3
1;3
min min 1 , 3 , 0 , 2 min 2, , 4 4
max max 1 , 3 , 0 , 2 max 2, , 4
u u u u u m m m m
u u u u u m m m m
.
+ Nếu
4 0 4
m m
thì
1;3
min 4 3 7 4;5;6;7
f x m m m .
+ Nếu
0
m
thì
1;3
min 3 3 3; 2;1;0
f x m m m .
+ Nếu
0 4
m
thì
1;3 1;3
1;3
min 0;max 0 min 0
u u f x
(thỏa mãn).
Vậy
3;...;7
m có tất cả 11 số nguyên thỏa mãn.
Câu 42.28: Cho hàm số
2
y x x m
. Tổng tất cả giá trị thực của tham số
m
để
2; 2
min 2
y
bằng
A.
31
4
. B.
8
. C.
23
4
. D.
9
4
.
Lời giải
Chọn C
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 564
Xét hàm số
2
u x x m
trên đoạn
2;2
, có:
1
0 2 1 0
2
u x x
.
Khi đó:
2;2
2;2
1
max 2 , , 2 6
2
1 1
min min 2 , , 2
2 4
u max u u u m
u u u u m
.
+ Nếu
1
0
4
m
hay
1
4
m
thì
2; 2
1 9
min 2
4 4
y m m
(thỏa mãn).
+ Nếu
6 0
m
hay
6
m
thì
2; 2
min 6 2 8
y m m
(thỏa mãn).
+ Nếu
1
6
4
m
thì
2; 2
min 0
y
(không thỏa mãn).
Vậy có hai số thực
9
4
m
và
8
m
thỏa mãn yêu cầu bài toán.
Tổng các giá trị đó bằng
23
4
.
Câu 42.29: Gọi
,
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
4 3 2
3 4 12
y f x x x x m
trên đoạn
3;2
. Có bao nhiêu giá trị nguyên
2019;2019
m để 2
.
A.
3209
. B.
3215
. C.
3211
. D.
3213
.
Lời giải
Chọn D
Xét hàm số
4 3 2 3 2
3 4 12 12 12 24
y g x x x x m y g x x x x
.
3 2
0
0 12 12 24 0 1
2
x
g x x x x x
x
.
0 ; 1 5; 2 32; 3 243
g m g m g m g m
.
3;2
3;2
max 243; min 32
g m g m
.
+Nếu
32 0 32
m m
thì
243
m
,
32
m
. Khi đó:
2 307
m
.
+Nếu
243 0 243
m m
thì
32 ; 243
m m
.
Khi đó:
2 518
m
.
+Nếu
243 32 32 243 0
m m m
thì
max 243 , 32 max 243,32 0; 0
m m m m
.
Khi đó, không thỏa điều kiện 2
.
Do đó:
2019 518
m
hoặc
307 2019
m
.
Vậy
3213
số.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 565
Câu 42.30: Cho hàm số
4 3 2
4 4f x x x x a . Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ
nhất của hàm số đã cho trên đoạn
0;2 . Có bao nhiêu số nguyên a thuộc đoạn
3;3 sao cho
2M m
?
A.
3
. B.
7
. C.
6
. D.
5
.
Lời giải
Chọn D
Xét hàm số
4 3 2
4 4g x x x x a .
3 2
4 12 8g x x x x
;
0g x
3 2
4 12 8 0x x x
0
1
2
x
x
x
.
Bảng biến thiên
Do
2 0m M
nên
0m
suy ra
0 0;2g x x .
Suy ra
1 0 1
0 0
a a
a a
.
Nếu
1a
thì
M a
,
1m a
2 1a a
2a
.
Nếu 0a thì 1M a , m a 2 1a a 1a .
Do đó
2a
hoặc
1a
, do a nguyên và thuộc đoạn
3;3 nên
3; 2;1;2;3a .
Vậy có
5
giá trị của a thỏa mãn đề bài.
Câu 42.31: Xét hàm số
2
f x x ax b
, với a,
b
là tham số. Gọi M là giá trị lớn nhất của hàm số
trên
1;3
. Khi
M
nhận giá trị nhỏ nhất có thể được, tính 2a b .
A.
3
. B. 4. C. 4 . D. 2.
Lời giải
Chọn C
Ta có
max , 1
2
A B
A B
. Dấu xảy ra khi A B .
Ta có
max , 2
2
A B
A B
. Dấu xảy ra khi A B .
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 566
Xét hàm số
2
g x x ax b
, có
0
2
a
g x x
.
Trường hợp 1:
1;3
2
a
6;2
a . Khi đó
M max 1 , 9 3
a b a b
.
Áp dụng bất đẳng thức
1
ta có
M 4 2 8
a
.
Trường hợp 2:
1;3
2
a
6;2
a . Khi đó
2
M max 1 , 9 3 ,
4
a
a b a b b
.
Áp dụng bất đẳng thức
1
và
2
ta có
2
M max 5 ,
4
a
a b b
2
1
M 20 4
8
a a
2
1
M 16 2
8
a
.
Suy ra
M 2
.
Vậy
M
nhận giá trị nhỏ nhất có thể được là
M 2
khi
2
2
5
2
1 9 3
a
a
a b b
a b a b
2
1
a
b
.
Do đó
2 4
a b
.
Câu 42.32: Có bao nhiêu số thực m để hàm số
4 3 2
3 4 12
y x x x m
có giá trị lớn nhất trên đoạn
3;2
bằng
275
2
?
A. 4. B. 0. C. 2. D. 1.
Lời giải
Chọn D
4 3 2
4 3 2
4 3 2
275
3 4 12 ; 3;2
275
2
3 4 12 ; 3; 2
2752
3 4 12 ; 3;2
2
x x x m x
y x x x m x
x x x m x
4 3 2
4 3 2
275 275
3 4 12 ; 3; 2 min ; 3;2
2 2
275 275
3 4 12 ; 3;2 max ; 3;2
2 2
m x x x x m g x x
m x x x x m g x x
Xét
4 3 2
3 4 12 ; 3;2
g x x x x x
Khảo sát hàm số trên đoạn
3;2
ta được
min 243
;
max 32
.
275 211
243
211
2 2
275 211
2
32
2 2
m m
m
m m
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 567
Như vậy
4 3 2
211 275
3 4 12 ; 3;2
2 2
m y x x x m x
Dấu = xẩy ra khi và chỉ khi
211
2
m
nên có 1 giá trị cần tìm.
Câu 42.33: Cho hàm số
2
2 4
y x x m
(với
m
là tham số thực). Hỏi
2;1
max
y
có giá trị nhỏ nhất là
A.
3
. B.
2
. C.
1
. D.
5
.
Lời giải
Chọn B
Đặt
2
2 4
t x x
, ta có
2 2
t x
.
2 2 0 1 2;1
t x x
.
2 4
t
,
1 5
t
,
1 1
t
.
Suy ra:
2;1
2;1
max 1, min 5
t m m t m m
, do đó
2;1 2;1
5 1
max max max 5 , 1 max 5 , 1 m
2
m m
y t m m m m
5 1
2
2
m m
dấu bằng đặt tại
5 1 3
m m m
.
Câu 42.34: Cho hàm số
3 2
3
y x x m
(với
m
là tham số thực). Hỏi
1;2
max
y
có giá trị nhỏ nhất là bao
nhiêu?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn C
Xét hàm số:
3 2
3
t x x
với
1; 2
x
.
Ta có
2
0 1;2
3 6 0
2 1;2
x
t x x
x
;
1 2
t
,
2 4
t
. Nên
1;2
max 2
t
và
1;2
min 4
t
.
Do đó
1;2 1;2
max max max 4 ; 2
y m t m m
4 2
4 2
max 4 ; 2 1
2 2
m m
m m
m m
.
Dấu bằng đạt tại
4 2 3
m m m
.
Câu 42.35: Cho hàm số
2
1 2 2
2
x m x m
y
x
(với
m
là tham số thực). Hỏi
1;1
max
y
có giá trị nhỏ
nhất là bao nhiêu?
A.
3
2
. B.
1
2
. C.
2
. D.
3
.
Lời giải
Chọn B
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 568
Ta có
2
2
2
x x
y m t m
x
, trong đó
2
2
2; 1 , 1;1
2
x x
t x
x
.
2
2
0 1;1
4
0
4 1;1
2
x
x x
t t
x
x
.
4
1 , 0 1, 1 2
3
t t t
Do đó
1;1 1;1
max max max 2 , 1 max 2 , 1
y t m m m m m
2 1
2 1
1
2 2 2
m m
m m
.
Dấu bằng đạt tại
3
2 1
2
m m m
.
Câu 42.36: Gọi
S
là tập hợp tất cả các giá trị thực của tham số
m
sao cho giá trị lớn nhất của hàm số
2
1
x mx m
y
x
trên
1;2
bằng
2
. Số phần tử của
S
là
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Chọn C
Tập xác định:
\ 1
D
.
Xét hàm số:
2
1
x mx m
f x
x
.
2
2
2
1
x x
f x
x
;
0
f x
2
2
2
0
1
x x
x
2
2 0
x x
0 1;2
2 1;2
x
x
.
0, 1;2
f x x
nên
1;2
4 1
max max ,
3 2
y m m
1;2
Max 2
y
4
2
3
4 1
2
3 2
3
5
1
2
2
2
1 4
2 3
m
m m
m
m
m
m m
.
Vậy có hai giá trị của
m
thỏa mãn.
Câu 42.37: Cho hàm số
3 2 2
1 27
y x x m x
. Giá trị lớn nhất của hàm số trên đoạn
3; 1
có
giá trị nhỏ nhất bằng
A.
26
. B.
18
. C.
28
. D.
16
.
Lời giải
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 569
Chọn B
Xét
3 2 2
1 27
u x x m x
trên đoạn
3; 1
ta có:
2 2
3 2 1 0,
u x x m x
.
Do đó
2
3; 1
max 1 26
A u u m
;
2
3; 1
min 3 6 3
a u u m
.
Do
2 2
3; 1
M max max 26 , 6 3
y m m
và
2 2
4 3 26 6 3 72
M m m
.
Vậy
18
M
.
Dấu bằng xảy ra khi
2 2
26 6 3 18 2 2
m m m .
Câu 42.38: Xét các số thực dương
,
x y
thoả mãn
2
2 1
2
2
2018
1
x y
x y
x
. Giá trị nhỏ nhất
min
P
của biểu
thức
2 3
P y x
bằng
A.
min
3
4
P
. B.
min
5
6
P
. C.
min
7
8
P
. D.
min
1
2
P
.
Lời giải
Chọn C
Ta có:
2
2 1
2
2 2
2018 2018
2 2
2018 2018
2
2018
1
2( 1) log 2 log 2 1
log 2 1 2 2 1 log 2 2 2 *
x y
x y
x
x y x y x x
x x x x x y x y
.
Xét hàm:
2018
log 2 , 0
f t t t t
.
Suy ra:
1
2 0 , 0.
ln 2018
f t t
t
Do đó hàm
f t
đồng biến trên khoảng
0;

.
Mà
2 2 2
* 2 1 2 2 1 2 1
f x x f x y x x x y y x
.
Khi đó:
2
2
3 7 7
2 3 2 3 2 2
4 8 8
P y x x x x
.
Kết luận:
min
7
8
P
khi
3
4
x
.
Câu 42.39: Cho hàm số
4 2
8
f x x ax b
, trong đó
a
,
b
là tham số thực. Biết rằng giá trị lớn nhất
của hàm số
f x
trên đoạn
1;1
bằng
1
. Hãy chọn khẳng định đúng?
A.
0
a
,
0
b
B.
0
a
,
0
b
C.
0
a
,
0
b
D.
0
a
,
0
b
Lời giải
Chọn C
Cách 1.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 570
Xét
4 2
8g x x ax b ,
3
32 2 0g x x ax
2
0
16
x
a
x
.
Ta có
1;1
max 1f x
0g
1;1b
.
TH1. 0a . Ta có
1g
1g
8 1a b . Suy ra
1;1
max 1f x
không thỏa YCBT.
TH2.
0a
.
Nếu
1 16
16
a
a
. Ta có
1 1 8 1g g a b . Suy ra
1;1
max 1f x
không thỏa
YCBT.
Nếu
1 16
16
a
a
.
Ta có BBT
▪
1;1
max 1f x b
. Khi đó YCBT
2
1 1
32
8 1
a
a b
2
64
8
a
a
8a
(thỏa
16a
)
▪
1;1
max 8 1f x a b
. Khi đó, YCBT
2
1
1
32
b
a
b
2
8
6 0
32
a
a
a
8
24 8
a
a
8a 1b
.
▪
2
1;1
max 1
32
a
f x b
. Khi đó, YCBT
2
1
32
8 1
1
a
b
a b
b
2
2
1
32
6 0
32
8
a
b
a
a
a
8
1
a
b
.
Vậy
8a
,
1b
thỏa YCBT.
Cách 2.
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 571
Đặt
2
t x
khi đó ta có
2
8
g t t at b
.
Vì
1;1
x
nên
0;1
t
.
Theo yêu cầu bài toán thì ta có:
0 1
g t
với mọi
0;1
t và có dấu bằng xảy ra.
Đồ thị hàm số
g t
là một parabol có bề lõm quay lên trên do đó điều kiện trên dẫn đến hệ
điều kiện sau xảy ra :
1 0 1
1 1 1
1 1
32
g
g
2
1 1
1 8 1
32 32 32
b
a b
b a
2
1 1 1
1 8 1 2
32 32 32 3
b
a b
a b
Lấy
1 32 3
ta có :
2
64 64
a
do đó
8 8
a
.
Lấy
3 32 2
ta có :
2
64 32 256 64
a a
Suy ra :
2
32 192 0
a a
24 8
a
.
Khi đó ta có
8
a
và
1
b
.
Kiểm tra :
2
8 8 1
g t t t
2
2 2 1 1
t
Vì
0 1
t
nên
1 2 1 1
t
2
0 2 1 1
t
2
1 2 2 1 1 1
g t t
.
Vậy
max 1
g t
khi
1 1
t x
(t/m).
Câu 42.40: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số
2
sin 2sin
y x x m
bằng
1
. Số phần tử của S là
A. 0 B. 1 B. 4 D. 3
Lời giải
Chọn A
Đặt
2
sin 1;1 2
x t t y t t m
Xét hàm số
2
2
f t t t m
có
' 2 2 0 1 1;1
f t t t
Có
1 3, 1 1
f m f m
. Khi đó
1;1
1;1
max max 3; 1 3
min min 3; 1 1
f x m m m
f x m m m
TH1:
3 1 1
m m m
NHÓM WORD – BIÊN SOẠN TÀI LIỆU 50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Trang 572
2
max 3 1
4
m l
f x m
m l
TH1:
3 1 1
m m m
2
max 1 1
0
m l
f x m
m l
Không tồn tại m thỏa mãn
| 1/25
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
GTLN - GTNN CỦA HÀM TRỊ TUYỆT ĐỐI CÓ CHỨA THAM SỐ
KIẾN THỨC CẦN NHỚ:
 Cách tìm giá trị lớn nhất, giá trị nhỏ nhất hàm số trên đoạn a;b
- Tìm nghiệm x (i  1, 2,...) của y  0 thuộc a;bi
- Tính các giá trị f x ; f a; f b so sánh các giá trị, suy ra giá trị lớn nhất, giá trị nhỏ nhất. i   BÀI TẬP MẪU:
Gọi S là tập tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số f x 3
x  3x m trên đoạn 0; 
3 bằng 16 . Tổng tất cả các phần tử của S bằng A. 1  6 . B. 16 . C. 12 . D. 2 .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán max, min của hàm trị tuyệt đối có chứa tham số.
2. KIẾN THỨC CẦN NHỚ:
Cách tìm giá trị lớn nhất, giá trị nhỏ nhất hàm số trên đoạn a;b
- Tìm nghiệm x (i  1, 2,...) của y  0 thuộc a;bi
- Tính các giá trị f x ; f a; f b so sánh các giá trị, suy ra giá trị lớn nhất, giá trị nhỏ nhất. i  
3. HƯỚNG GIẢI: Tìm giá trị lớn nhất hàm số y f x , ta xét hàm số y f x .
B1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y f x .
B2: Giá trị lớn nhất của hàm số y f x tại max f x hoặc min f x .
Từ đó, ta có thể giải bài toán cụ thể như sau: Lời giải Chọn A
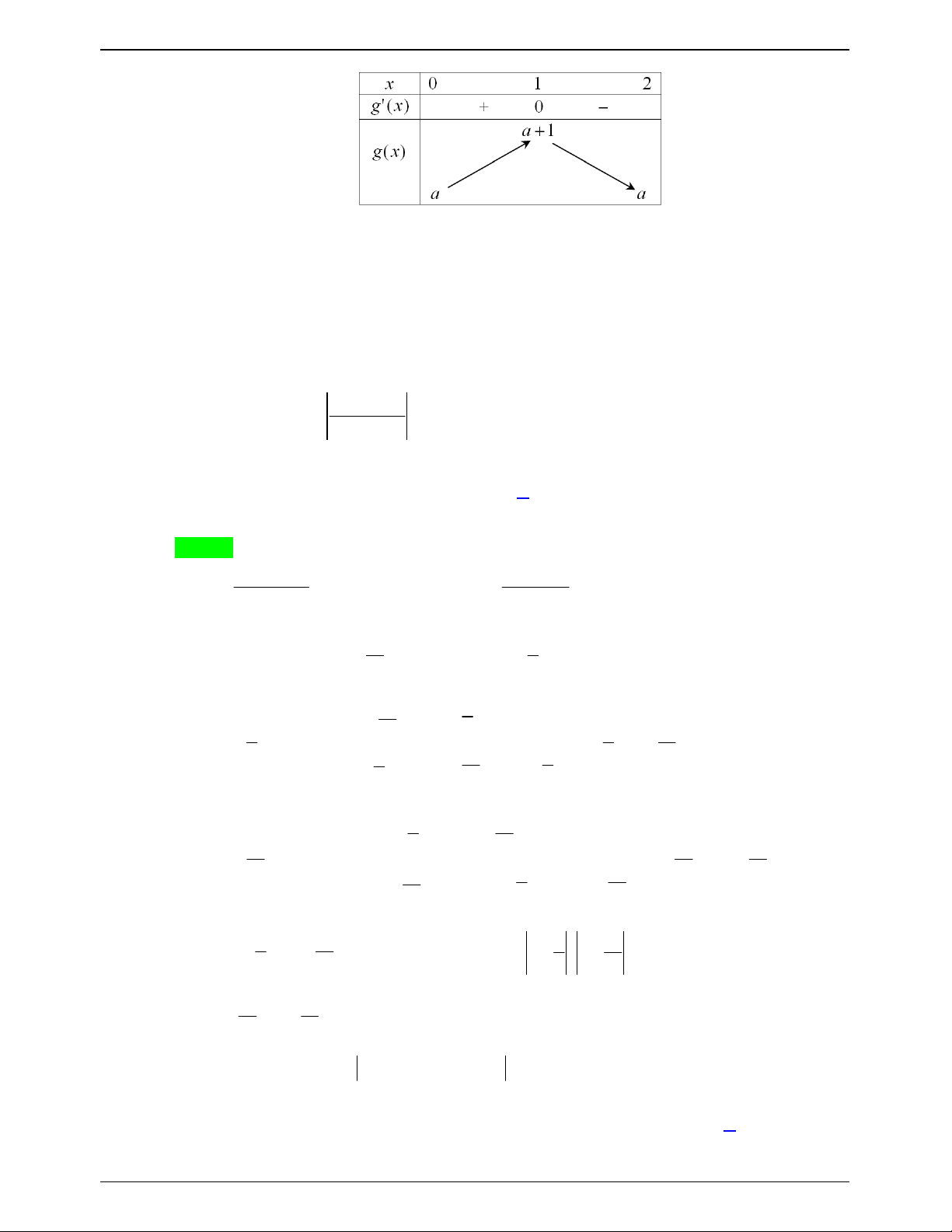
Đặt g x 3
x  3x m .
x  10;  3 g x 2
 3x  3 ; g x  0   . x  10;  3  g 0  ; m g   1  2   ;
m g 3  18  m .
Suy ra max g x  18  m ; min g x  2   m . 0;3 0;  3 Trang 548
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  1  8  m  16 m  2   2  m  16 m  14  
Để giá trị lớn nhất hàm số y f x là 16   .  2 m 16      m  14      18  m  16   m  2   Vậy S  2; 1  
4 nên tổng là 2 14  16 .
Bài tập tương tự và phát triển:
Câu 42.1: Gọi tập S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 3
y x  3x m trên đoạn 0;2 bằng 3. Số phần tử của S là A. 1. B. 2 . C. 0 . D. 6 . Lời giải Chọn B Xét 3
u x  3x m . Ta có: 2
u '  3x  3 ; u  0  x  10;2 . Khi đó:
A  max u  max u 0,u  
1 , u 2  max ,
m m  2, m   2  m  2 . 0;2
a  min u  min u 0,u  
1 , u 2  minm, m  2, m   2  m  2 . 0;2  m  2  3
 m  2  m  2    m  1
Ta có: max y  max  A , a   max m  2 , m  2   3     . 0;2   m  2  3 m  1  
m  2  m  2   Vậy S    1 .
Câu 42.2: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số 2
y x x m thỏa mãn
min y  2 . Tổng tất cả các phần tử của S bằng 2; 2 31 23 9 A.  . B. 8  . C.  . D. . 4 4 4 Lời giải Chọn C 1 Xét hàm số 2
u x x m trên đoạn  2
 ; 2 , có: u  0  2x 1  0  x   . 2   1     1   1 max u  max u  2 ,u  ,u  
2  m  6 ; min u  min u   2 ,u  ,u   2  m  . 2;2   2   3;2   2  4  1 1 1 9 Nếu m   0 hay m
thì min y m   2  m  (thỏa mãn). 4 4 2; 2 4 4
Nếu m  6  0 hay m   6 thì min y  m  6  2  m  8 (thỏa mãn). 2; 2 1 Nếu 6  m
thì min y  0 (không thỏa mãn). 4 2; 2 Trang 549
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  9  23 Ta có: S   8
 ;  . Vậy tổng các phần tử của S bằng  .  8  4
Câu 42.3: Gọi M là giá trị lớn nhất của hàm số f x 4 3 2
 3x  4x 12x m trên đoạn  1  ;  3 . Có bao 59
nhiêu số thực m để M  ? 2 A. 2 . B. 6 . C. 1. D. 4 . Lời giải Chọn C Xét hàm số: 4 3 2
u  3x  4x 12 x m .  x  0  Có 3 2
u  12x 12 x  24 x u  0  x  1   .  x  2 
min u  minu  
1 ,u 0,u 2,u 3  u 2  m  32   1  ;  3 Khi đó:  . max u  max  u 
1 ,u 0,u 2,u 3  u 3  m  27  1  ;  3   59 m  32   2  
m  32  m  27  5 Do đó: M   m m   59 max 32 , 27     m  . 2  59 2  m  27    2
 m  27  m  32  59
Vậy có 1 số thực m để M  . 2 2
x m m
Câu 42.4: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số y  thỏa max y  1 . x  2 1;2
Tích các phần tử của S bằng A. 1  6 . B. 4 . C. 16 . D. 4 . Lời giải Chọn B 2
x m m 2 2  m m Xét u  , ta có: u 
 0 , x  1; 2 , m    . 2   x  2 x  2 2 m m  2 2 m m 1
Do đó A  max u u 2  
; a  min u u   1   . 1;2 4 1;2 3 2 2 
m m  2 m m 1   1   17 max y  max  ,   1  m  . 1;2  4 3    2 Trang 550
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020   1   17   Ta có: S  
 . Vậy tích các phần tử của S bằng 4 .  2   
Câu 42.5: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m y
trên 1;2 bằng 2 . Số phần tử của S là x 1 A. 1 . B. 2 . C. 4 . D. 3 . Lời giải Chọn A 2
x mx m Xét hàm số: u  . x 1 2 x  2x 2 x  2xx  0 1;2 u  ; u  0   0 2
x  2x  0   .  2 x  2 1 x   1
x  2 1; 2   4 1 
Ta có: u  0 x
 1;2 nên max y   m  , m  . 1;2 3 2    2 m   3 2 10  max y  2   . Vậy S   ;   . 1;2 10  3 3  m    3
Câu 42.6: Xét hàm số   2
f x x ax b , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên 1; 
3 . Khi M nhận giá trị nhỏ nhất tính T a  2b . A. T  3. B. T  4 . C. T  4 . D. T  2 . Lời giải Chọn C A B
Ta có: max  A , B    
1 . Dấu  xảy ra khi A B . 2 A B
Ta có: max  A , B  
2 . Dấu  xảy ra khi A  B . 2 a Xét hàm số   2
g x x ax b , có g  x  0  x   . 2 a Trường hợp 1:    1
 ;3  a  6
 ; 2 . Khi đó M  max1 a b , 9  3a b  . 2
Áp dụng bất đẳng thức  
1 ta có M  4  2a  8 . a 2   a   Trường hợp 2:   1  ;  3  a  6
 ; 2 . Khi đó M  max 1 a b , 9  3a b , b    . 2  4    Trang 551
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2   a   1
Áp dụng bất đẳng thức   1 và 2 ta có M  max 2
 5  a b , b    M  20  4a a  4    8 1  M 
16  a  22 . 8 Suy ra M  2 . a  2  2  aa  2
Ta có: M nhận giá trị nhỏ nhất có thể được là M  2 khi 5
  a b   b   . 2  b  1   1
  a b  9  3a b
Vậy a  2b  4  .
Câu 42.7: Cho hàm số 3 2
y x  3x m (với m là tham số thực). Hỏi max y có giá trị nhỏ nhất bằng 1;2 A. 2 . B. 4 . C. 1. D. 3 . Lời giải Chọn C Xét hàm số : 3 2
t x  3x với x 1; 2 .
x  0  1;2 Ta có 2
t  3x  6x  0   ; t   1  2  , t 2  4  . Nên max t  2
 và min t  4 .
x  2  1; 2 1;2 1;2 
Do đó max y  max m t  max m  4 ; m  2 1;2 1;2
m  4  2  m
m  4  2  m
 max m  4 ; 2  m     1. 2 2
Dấu bằng đạt tại m  4  2  m m  3 .
Câu 42.8: Cho hàm số f x 4 2
 8x ax b , trong đó a , b là tham số thực. Tìm mối liên hệ giữa a và
b để giá trị lớn nhất của hàm số f x trên đoạn  1  ;  1 bằng 1.
A. b  8a  0 .
B. b  4a  0 .
C. b  4a  0 .
D. b  8a  0 . Lời giải Chọn D Đặt 2
t x , vì x  1  ;  1 nên t 0;  1 .
Ta có: g t  2
 8t at b , đây là parabol có bề lõm quay lên và có tọa độ đỉnh là 2  a aI  ;   b   6 32   a Trường hợp 1:   0; 
1 . Theo yêu cầu bài toán ta có: 6 Trang 552
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
1  g 0 1  1   b  1  1   b  1   1     1  g   1  1   1
  8  a b  1   1
  8  a b  1 2   2  a 2 3
 2  32b a  32 2   3
 2  a  32b  32 3 1    b  1    32 Lấy   1  323 ta có : 2
64  a  64 do đó 8   a  8 .
Lấy 3  322 ta có : 2
64  a  32a  256  64 Suy ra : 2
a  32a 192  0  24   a  8  .
Khi đó ta có : a  8  và b  1.
Thử lại: g t  2
 8t  8t 1   t  2 2 2 1 1
Vì 0  t  1 nên 1
  2t 1  1    t  2 0 2 1
 1    g t    t  2 1 2 2 1 1  1.
Ta có: max g t   1 khi t  1 x  1  . Nên a  8
 và b 1 (thỏa mãn). a Trường hợp 2 :   0; 
1 . Theo yêu cầu bài toán ta có: 6  1   g  0  1 1  b  1 1  b  1      1   g    1  1 
1  8  a b  1 
1  8  a b  1   2
  a  8  2  1  0  a  6  (loại). Vậy a  8  và b 1.
Câu 42.9: Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất
của hàm số đã cho trên đoạn 0;2 . Có bao nhiêu số nguyên a thuộc đoạn  3  ;  3 sao cho M  2m ? A. 5 . B. 7 . C. 6 . D. 3 . Lời giải Chọn A
Xét hàm số g x 4 3 2
x  4x  4x a . x  0 g x 3 2 
 4x 12x  8x ; g x  0 3 2
 4x 12x  8x  0  x  1 .  x  2  Bảng biến thiên Trang 553
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 ` TH1: a  1
  m   a  
1 ; M  a   2a  
1  a a  2   a  3  ;   2 . TH2: 1
  a  0  m  0; M  0  M  2m (loại ).
TH3: a  0  m a ; M a 1  2a a 1  a  1 a 1;2;  3 .
Vậy có 5 giá trị của a thỏa mãn đề bài. 4
x ax a Câu 42.10: Cho hàm số y
. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của x  1
hàm số trên đoạn 1;2. Có bao nhiêu số nguyên a sao cho M  2m ? A. 15. B. 14. C. 16. D. 13. Lời giải Chọn C 4
x ax a 4 3 3x  4x Xét u
trên đoạn 1;2, ta có u   0 , x  1;2 . x 1 x  2 1 16 1
Do đó, max u u 2  a
, min u u 1  a  . 1;2 3 1;2 2  16  1 M a a   0 1    3  2 1 13 TH1: a   0        a  . 2 1  16  1  2 3 m a  a   2 a      2  3   2    1   16 M   a     a   0  16   2   3 61 16 TH2: a   0        a   . 3  16    1   16  6 3 m   a      a   2  a         3     2   3   1   16   1 16  TH3: a  . a   0    
m  0 , M  max  a  , a
  M  2m ( thỏa mãn).  2   3  2 3   61 13 Ta có:   a a  1  0;....; 
4 . Vậy có 15 số nguyên thỏa mãn. 6 3 Câu 42.11:
Cho hàm số f x 4 2
 8 cos x a cos x b , trong đó a , b là tham số thực. Gọi M là giá
trị lớn nhất của hàm số. Tính tổng a b khi M nhận giá trị nhỏ nhất.
A. a b  8  .
B. a b  9  .
C. a b  0 .
D. a b  7  . Lời giải Trang 554
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn D Đặt 2
t  cos x , t 0; 
1 , ta có hàm số g t  2
 8t at b . Khi đó M  max g t  . 0;  1 Do đó:
M g 0  b ; M g  
1  8  a b ;  1  1 M g  2 
a b  2M  4  a  2b   ;  2  2 Từ đó ta có
4M b  8  a b  4  a  2b b  8  a b  4  a  2b  4 Hay M  1.
4  a  2b
Dấu đẳng thức xảy ra khi và chỉ khi b  8  a b
 1 và b , 8  a b , 2 a  8  4
  a  2b cùng dấu   . b  1 
Vậy a b  7  . Câu 42.12: Cho hàm số 2
y  2x x   x  
1 3  x  m . Có tất cả bao nhiêu giá trị thực của tham số
m để max y  3 ? A. 1. B. 2. C. 0. D. 4. Lời giải Chọn B
Hàm số xác định khi:  x  
1 3  x  0  1   x  3 .
Đặt t   x    x 2 1 3
 3  2x x t 0;2 và 2 2
2x x t  3.
Khi đó ta cần tìm giái trị lớn nhất của hàm số 2
y t t  3  m trên đoạn 0;2 . 13 Với 2
u t t  3  m ta có: max u m 1; min u m  . 0;2 0;2 4  13  1
Do đó max y  max  m 1 ; m
  3  m  4; m  . 4 4   Câu 42.13: Cho hàm số 2
y  2x x   x  
1 3  x  m . Khi giá trị lớn nhất của hàm số đạt giá trị
nhỏ nhất. Mệnh đề nào sau đây đúng? 17 9 7 15 A. . B. . C. . D. . 8 8 8 8 Lời giải Chọn B Trang 555
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Hàm số xác định khi:  x  
1 3 x  0  1   x  3 .
Đặt t   x    x 2 1 3
 3  2x x t 0;2 và 2 2
2x x t  3.
Khi đó ta cần tìm giái trị lớn nhất của hàm số 2
y t t  3  m trên đoạn 0;2 . 13 Với 2
u t t  3  m ta có: max u m 1; min u m  . 0;2 0;2 4 13 13 m 1   m m 1   m  13  4 4 9
Do đó max y  max  m 1 ; m      . 4 2 2 8   13 9 17
Dấu bằng xảy ra m 1   m   m  . 4 8 8 1 19 Câu 42.14:
Gọi S là tập hợp tất cả các số nguyên m để hàm số 4 2 y x
x  30x m có giá trị 4 2
lớn nhất trên đoạn 0;2 không vượt quá 20 . Tổng các phần tử của S bằng A. 1  95. B. 210 . C. 195 . D. 2  10 . Lời giải Chọn A x  5 1 19  Xét 4 2 u x
x  30x m trên đoạn 0;2 có 3
u  x 19x  30; u  0  x  3 . 4 2  x  2 
Do đó: max u  maxu(0);u(2)}  max{ ;
m m  6}  m  6 ; min u  . m 0;2 0;2
m m  6  20 13  m  6
Do đó: max y  max{ m ; m  6 }  20     20  m  6   0;2
m  6  m  20 20  m  13   . 20
Mà m   nên m {  20; 19;..., 6  } . Vậy S   k  1  95  . 6 Câu 42.15: Cho hàm số 3 2
y  2x  3x m . Có bao nhiêu số nguyên m để min f x  3 ? 1;  3 A. 4. B. 8. C. 31. D. 39. Lời giải Chọn D x  0 Xét 3 2
u  2x  3x m , ta có: 2
u '  6x  6x ; u  0   . x  1 
min u  minu  
1 ,u 3,u 0,u  
1   minm  5,m  27, , m m   1  m  5  1;  3 Do đó:  . max u  max  u  
1 , u 3,u 0,u  
1   maxm  5,m  27, , m m   1  m  27 1;3  Trang 556
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
TH1: m  5  0  m  5  min f x  m  5  3  m  8  m 5; 6; 7;  8 . 1;  3 TH2:
m  27  0  m  27  min f x  (m  27)  3  m  3  0  m  3  0; 29; 28; 2   7 .  1  ;  3
TH3: (m  5) m  27  0  27  m  5  min
f x  0 (thỏa mãn). 1  ;3     Vậy m  30  ; 29  ;  28;...; 7;  8 . Câu 42.16: Cho hàm số 2
f (x)  ax bx c, f (x)  1, x
 [0;1] . Tìm giá trị lớn nhất của f (  0). A. 8 . B. 0 . C. 6 . D. 4 . Lời giải. Chọn A f (
x)  2ax b f (  0)  b .
Bài toán trở thành tìm giá trị lớn nhất của b với điều kiện f (x)  1, x  [0;1].  
a b f (1)  f (0) f (0)  c      1   1  Ta có.  f  
1  a b c
 a  2b  4 f
 4 f (0)  b  4 f
f (1)  3 f (0).      2   2     1  a bf    c c   f (0)       2  4 2   1   f (0)  1    1 
f (x)  1, x  [0;1]   1   f  
1  1  b  4 f
    f (1)  3  f (0)  4 1 3  8.  2    1   1   f  1      2    1  f 1       2  c   1  , a  8      Đẳng thức xảy ra 2   f (1)  1
  a b c  1,   b  8  f (x)  8x  8x 1.  f (0) 1  a b    c  1 c 1         4 2 
Vậy giá trị lớn nhất của f (0) bằng 8. Câu 42.17: Cho hàm số 4 3 2
y x  2x x a . Có bao nhiêu số thực a để min y  max y  10 ? 1; 2 1; 2 A. 2 . B. 5 . C. 3 . D. 1. Lời giải Chọn A   x  0  Xét 4 3 2
u x  2x x a trên đoạn  1  ; 2, ta có : 3 2
u '  4x  6x  2x ; u '  0  x  1  .  1  x   2 Trang 557
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020    1  
M  max u  max u      1 , u 0, u , u     1   u  
1  u 2  a  4 1; 2    2   Suy ra:  .    1  
m  min u  min u    1 , u 0, u , u    
1   u 0  u   1  a  1; 2    2  
TH1: m  0  a  0 . Khi đó: min y  ;
m max y M  1  ; 2  1  ; 2  a  0 Ta có điều kiện :   a  3 .
a a  4  10 
TH2: M  0  a  4
 . Khi đó : min y  M ; max y  m .  1  ; 2 1; 2  a  4 Ta có điều kiện :   a  7  .
 a  4  a  10 
TH3: m  0  M  4   a  0 .
Khi đó: min y  0; max y  max  a  4 , a   maxa  4,   a  10 .  1  ; 2  1  ; 2
Suy ra min y  max y  0 10  10 (loại). 1; 2 1; 2 Vậy a 3;  7 . Câu 42.18:
Cho hai số thực x ; y thỏa mãn 2 2 2 2
x y  4x  6 y  4 
y  6 y 10 
6  4x x . Gọi
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2 T
x y a . Có bao
nhiêu giá trị nguyên thuộc đoạn  1  0;1 
0 của tham số a để M  2m ? A. 17 . B. 16 . C. 15 . D. 18 . Lời giải Chọn B
Biến đổi giả thiết có: 2 2 2 2
x y  4x  6 y  4 
y  6 y 10  6  4 x x 2 2 2 2
y  6 y 10 
y  6 y 10  6  4x x  6  4x x (*).
Đặt f t   t t , t 0;  . Ta có f t đồng biến trên 0; .
Do đó ta có: (*)  f  2 y y    f  2  x x  2 2 6 10 6 4
y  6 y 10  6  4x x 2 2 2 2
x y x y    x y   x y   2 2   2 2 4 6 4 0 4 4 6 4 6 x y  2 2 2 2  13  3 
x y  3  13 
x y a   13  3  a;3  13  a .   Trang 558
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
TH1: 13  3  a  0   13  3  a  0
m  13  3  a     ycbt  
 13  9  a  9  13 .
M  3  13  a 3  13  a  2    13 3a  TH2: 13  3  a  0 m     13 3 a 3  13  a  0     ycbt  
 3  13  a  9  13        
  13  3  a  2   13  3 3 13  a M a    . m TH3:    a   a 0 13 3 3 13
 0  13  3  a  13  3   ( M  2m ). M  0 
Vậy a   13  9;9  13 . Đối chiếu với a  1  0;  10  a  5  ;...;  10 .   Câu 42.19: Cho hàm số 3 2
f (x)  2 x  9x  12 x m . Có bao nhiêu số nguyên m  (20; 20) để với
mọi bộ ba số thực a,b, c 1; 
3 thì f (a), f (b), f (c) là độ dài ba cạnh một tam giác? A. 10 . B. 8 . C. 25 . D. 23. Lời giải Chọn D x  0 Xét 3 2
u  2 x  9x 12x m trên 1;  3 , ta có: 2
u  6x 18x 12 ; u  0   . x  2 
min u  min u(0), u(1),u(2),u(3  )  m  4 . [1;3]
max u max u(0),u(1),u(2),u(3  )  m  9 . [1;3]
Để f (a), f (b), f (c) là độ dài ba cạnh một tam giác thì ta phải có f (a)  f (b)  f (c) .
Chọn f (a)  f (b)  min f (x), f (c)  max f (x) ta có điều kiện 2 min f (x)  max f (x) . [2;1] [2;1] [2;1] [2;1]
Ngược lại: với 2 min f (x)  max f (x) , ta có : f (a)  f (b)  f (c)  2 min f (x)  max f (x)  0 . [2;1] [2;1] [2;1] [2;1]
Vậy điều kiện cần và đủ để f (a), f (b), f (c) là độ dài ba cạnh một tam giác là
2 min f (x)  max f (x) [2;1] [2;1] m  4  0
TH1: m  4  0  min f (x)  m  4; m ax f (x)  m  9    m  1 [1;3] [1;3]
2(m  4)  m  9  m  9  0
TH2: m  9  0  min f (x)  m  9; m ax f (x)  m  4    m  14 [1;3] [1;3]
2(m  9)  m  4 
TH3: (m  4)(m  9)  0  min f (x)  0  2.0  m ax f (x)  m  9 (loại) [1;3] [1;3] Vậy m  19  ; 15  ; 2......;18; 
19 . Có 23 số nguyên thỏa mãn. Trang 559
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Câu 42.20:
Cho hàm số f x 3
x  3x m . Có bao nhiêu số nguyên m   20 
; 20 để với mọi bộ ba số thực a, , b c  2  ; 
1 thì f a, f b, f c là độ dài ba cạnh của một tam giác nhọn. A. 18 . B. 16 . C. 14 . D. 12 . Lời giải Chọn B Xét 3
u x  3x m trên đoạn , ta có: 2
u  0  3x  3  0  x  1.
max u  maxu 2,u   1 ,u  
1   maxm 2, m 2,m  2  m  2  2; 1 Khi đó:  . min u  min  u  2  ,u   1 ,u  
1   minm 2, m 2,m  2  m  2 2;  1 
Để f a, f b, f c là độ dài ba cạnh của một tam giác nhọn ta phải có 2   2    2 f a f
b f c .
Chọn f a  f b  min f x; f c  max f x ta có điều kiện 2;  1 2;  1 2 2
2 min f x 
   max f x  .  2  ;  1    2  ;  1   2 2    
Ngược lại với 2 min f x   max f x , ta có  2  ;  1    2  ;  1   2 2 2 f a 2  f b 2
f c  2 min f x 
   max f x   0 .  2  ;  1    2  ;  1  
Vậy điều kiện cần và đủ để f a, f b, f c là độ dài ba cạnh của một tam giác là 2 2
2 min f x 
   max f x  .  2  ;  1    2  ;  1   2  
TH1:m  2m  2  0  2 min f x 2
 0  2.0   max f x (loại).  2  ;  1  2  ;  1  
TH2: m  2  0 . m  2  0 
 min f x  m  2; m ax f x  m  2    m  6  4 2 .   2 2 2;1 2;  1 2
 m  2  m  2 
TH3: m  2  0 . m  2  0 
 min f x   m  2; m ax f x   m  2  
m  6  4 2 .   2 2 2;1 2;  1 2
  m  2   m  2  Suy ra m  1  9, 18  ,..., 12  ,12,13,...,1 
9 . Vậy có 16 số nguyên m thỏa mãn.
Câu 42.21: Gọi tập S là tập hợp giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 3
y x  3x m trên đoạn 0; 2 bằng 3. Số phần tử của S là A. 1. B. 2 . C. 0 . D. 6 . Trang 560
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
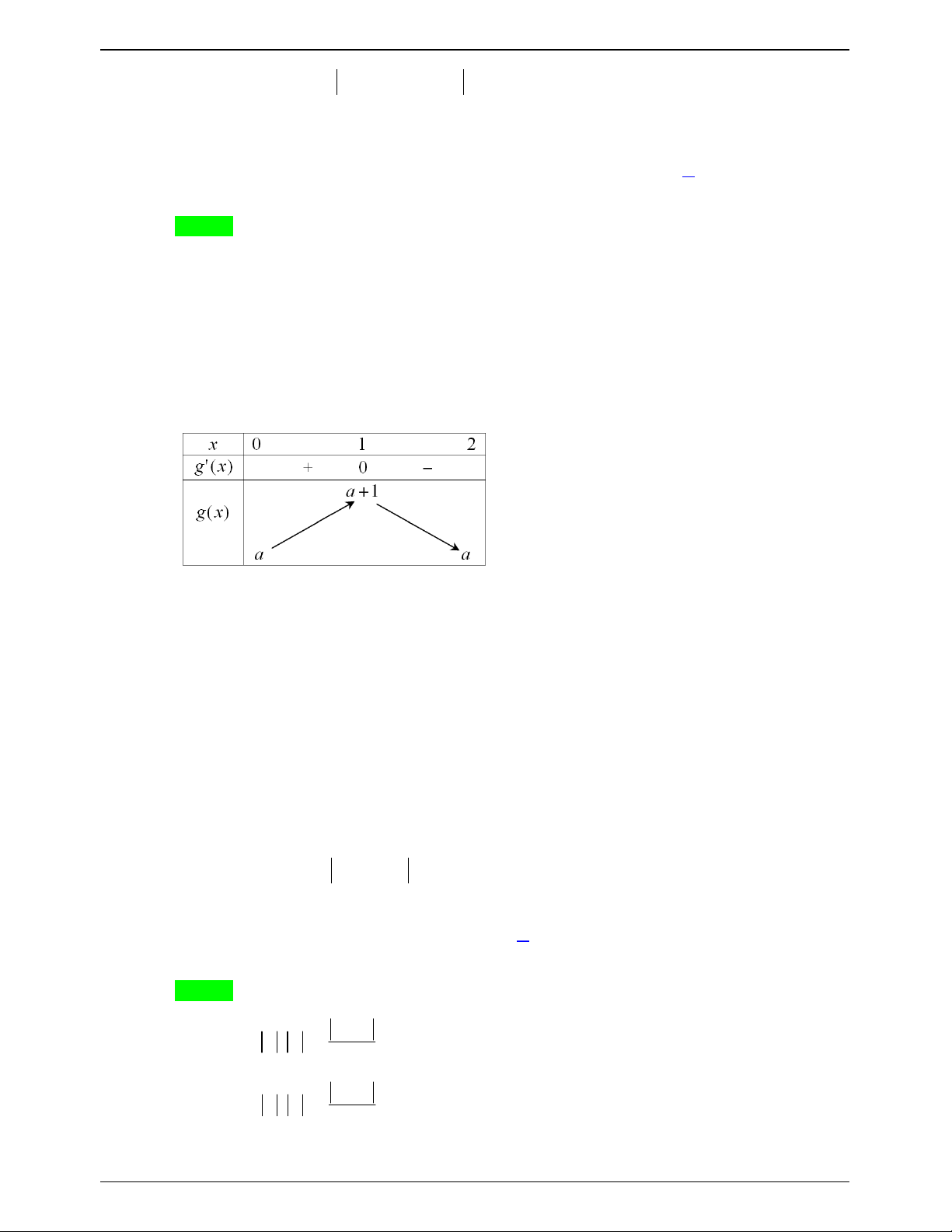
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Lời giải Chọn B Xét 3
u x  3x m có: 2
u '  3x  3 ; u '  0  x  10; 2 . Khi đó:
A  max u  max u 0,u  
1 , u 2  max  ,
m m  2, m   2  m  2 . 0;2
a  min u  min u 0,u  
1 , u 2  minm, m  2, m   2  m  2 . 0;2  m  2  3
 m  2  m  2    m  1
Vậy max y  max  A , a   max m  2 , m  2   3     . 0;2   m  2  3 m  1  
m  2  m  2  
Câu 42.22: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số f x 4 2
x  8x m trên đoạn  1  ; 
1 bằng 5. Tổng tất cả các phần tử của S bằng A. 7 . B. 7. C. 5 . D. 5 . Lời giải Chọn B x  0
Xét hàm số g x 4 2
x  8x  , m x  1  ; 
1 , ta có g x 3  4x 16 ;
x g x  0   . x  2   g   1  g  
1  7  m , g 0  m .  7   m  5    7   m m   m  2
Do đó: max f x  max 7  m , m   5     1;  1  m  5 m  5    m  7   m   Vậy S  2; 
5 . Vậy tổng các giá trị của S bằng 7.
Câu 42.23: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 4  x m f x  trên đoạn  2
 ; 2 bằng 6. Tổng tất cả các phần tử của S bằng x  3 A. 16 . B. 16. C. 2. D. 14. Lời giải Chọn B 4x m 12  m
Xét hàm số g x 
, x  2; 2, ta có g x  . x  3  x  32 8  m g 2  
, g 2  8  m . 5 Trang 561
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020  8  m   6  5   8  m        8 8  m mm  2
Do đó : max f x max  , 8 m  6       5    . 2;2 5 m  14      8  m  6   8  m 8  m    5  Vậy S  2;1 
4 . Vậy tổng các giá trị của S bằng 16.
Câu 42.24: Có bao nhiêu giá trị thực của tham số m để giá trị lớn nhất của hàm số 2
y x  2x m  4 trên đoạn  2  ;  1 bằng 4? A. 1. B. 2 . C. 3 . D. 4. Lời giải Chọn B f x 2
x  2x m  4 có f  x  2x  2 , f  x  0  x  1  . Do đó 2
max x  2x m  4  max m 1 ; m  4 ; m  5 .  2;   1
Ta thấy m  5  m  4  m 1 với mọi m   , suy ra max y chỉ có thể là m  5 hoặc m 1 . 2;  1  m  5  4 
Nếu max y m  5 thì   m  1 . 2;  1
m  5  m 1    m 1  4 
Nếu max y m 1 thì   m  5 . 2;  1
m 1  m  5   Vậy m 1;  5 . 2x m
Câu 42.25: Cho hàm số y
với m là tham số, m  4
 . Biết min f x  max f x  8  . Giá trị x  2 x   0;2 x   0;2
của tham số m bằng A. 10 . B. 8 . C. 9 . D. 12 . Lời giải Chọn D
Xét hàm số xác định trên tập D  0;2 4  m Ta có y 
. Nhận xét  m  4 hàm số luôn đồng biến hoặc nghịch biến trên 0;2 nên  x  22
giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên 0;2 luôn đạt được tại x  0 , x  2 . m 4  m
Theo bài ra ta có f 0  f 2  8    8  m  12 . 2 4 Trang 562
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Câu 42.26: Cho hàm số 3 2
f (x)  2x  3x m . Có bao nhiêu số nguyên m để min f x  3 ? 1;  3 A. 4. B. 8. C. 31. D. 39 . Lời giải Chọn D x  0 Xét 3 2
u  2x  3x m có 2
u  6x  6 ;
x u  0   . x  1 
min u  minu  
1 ,u 3,u 0,u  
1   minm  5,m  27, , m m   1  m  5  1  ;  3 Do đó  . max u  max  u 
1 , u 3,u 0,u  
1   maxm  5,m  27, , m m   1  m  27  1  ;3 
+ Nếu m  5  0  m  5thì min f x  m  5  3  m  8  m 5;6;7;  8 .  1  ;3
+ Nếu m  27  0  m  27 
thì min f x  (m  27)  3  m  3  0 .  1  ;3
m 30; 29; 28; 2  7 .
Nếu (m  5) m  27  0  27 
m  5 thì min f x  0 (thỏa mãn). 1;  3 Vậy m  3  0;...; 
8 có tất cả 39 số nguyên thỏa mãn.
Câu 42.27: Cho hàm số 3 2
y x  3x m . Có bao nhiêu số nguyên m để min f x  3 ? 1;  3 A. 4. B. 10. C. 6. D. 11. Lời giải Chọn D x  0 Với 3 2
u x  3x m có 2
u  3x  6 ;
x u  0   . x  2 
min u  min u  
1 , u 3,u 0,u 2  minm  2, m, m   4  m  4  1;  3 Do đó  . max u  max  u  
1 , u 3,u 0,u 2  maxm  2, m, m   4  m 1;  3 
+ Nếu m  4  0  m  4 thì min f x  m  4  3  m  7  m 4;5;6;  7 . 1;  3
+ Nếu m  0 thì min f x  m  3  m  3  m  3  ; 2;1;  0 . 1;3
+ Nếu 0  m  4 thì min u  0; max u  0  min f x  0 (thỏa mãn). 1;  3 1;  3 1;  3 Vậy m  3  ;...; 
7 có tất cả 11 số nguyên thỏa mãn.
Câu 42.28: Cho hàm số 2
y x x m . Tổng tất cả giá trị thực của tham số m để min y  2 bằng  2  ;  2 31 23 9 A.  . B.  8 . C.  . D. . 4 4 4 Lời giải Chọn C Trang 563
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 1 Xét hàm số 2
u x x m trên đoạn 2; 2 , có: u  0  2x 1  0  x   . 2    1   max u max
u 2 , u  , u   2  m  6  2;2   2   Khi đó:  .    1   1
min u  min u 2,u  , u   2  m   2;2    2  4  1 1 1 9 + Nếu m   0 hay m
thì min y m   2  m  (thỏa mãn). 4 4  2  ; 2 4 4
+ Nếu m  6  0 hay m  6 thì min y m
  6  2  m  8  (thỏa mãn).  2  ;  2 1 + Nếu 6  m
thì min y  0 (không thỏa mãn). 4  2  ; 2 9
Vậy có hai số thực m  và m  8 thỏa mãn yêu cầu bài toán. 4 23
Tổng các giá trị đó bằng  . 4
Câu 42.29: Gọi , lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y f x 4 3 2
 3x  4x 12x m trên đoạn  3
 ; 2 . Có bao nhiêu giá trị nguyên m  20 
19; 2019 để 2. A. 3209 . B. 3215 . C. 3211. D. 3213 . Lời giải Chọn D
Xét hàm số y g x 4 3 2  x x
x m y  g x 3 2 3 4 12
 12x 12x  24x . x  0  g x 3 2
 0 12x 12x  24x  0  x  1.  x  2  g 0  ; m g  
1  m  5; g 2  m  32; g  3
   243  m .
max g m  243; min g m  32 .  3  ;  2  3  ;  2
+Nếu m  32  0  m  32 thì m  243 , m  32 . Khi đó: 2m  307 .
+Nếu m  243  0  m  2
 43 thì   m  32;  m  243 .
Khi đó: 2m  5  18. 2
 43  m  32  m  32m  243  0 +Nếu thì
max m  243 , m  32  maxm  243,32  
m  0;  0 .
Khi đó, không thỏa điều kiện 2. Do đó: 2019   m  518 
hoặc 307  m  2019 . Vậy 3213 số. Trang 564
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020
Câu 42.30: Cho hàm số f x 4 3 2
x  4x  4x a . Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ
nhất của hàm số đã cho trên đoạn 0; 2 . Có bao nhiêu số nguyên a thuộc đoạn  3  ;  3 sao cho
M  2m ? A. 3 . B. 7 . C. 6 . D. 5 . Lời giải Chọn D
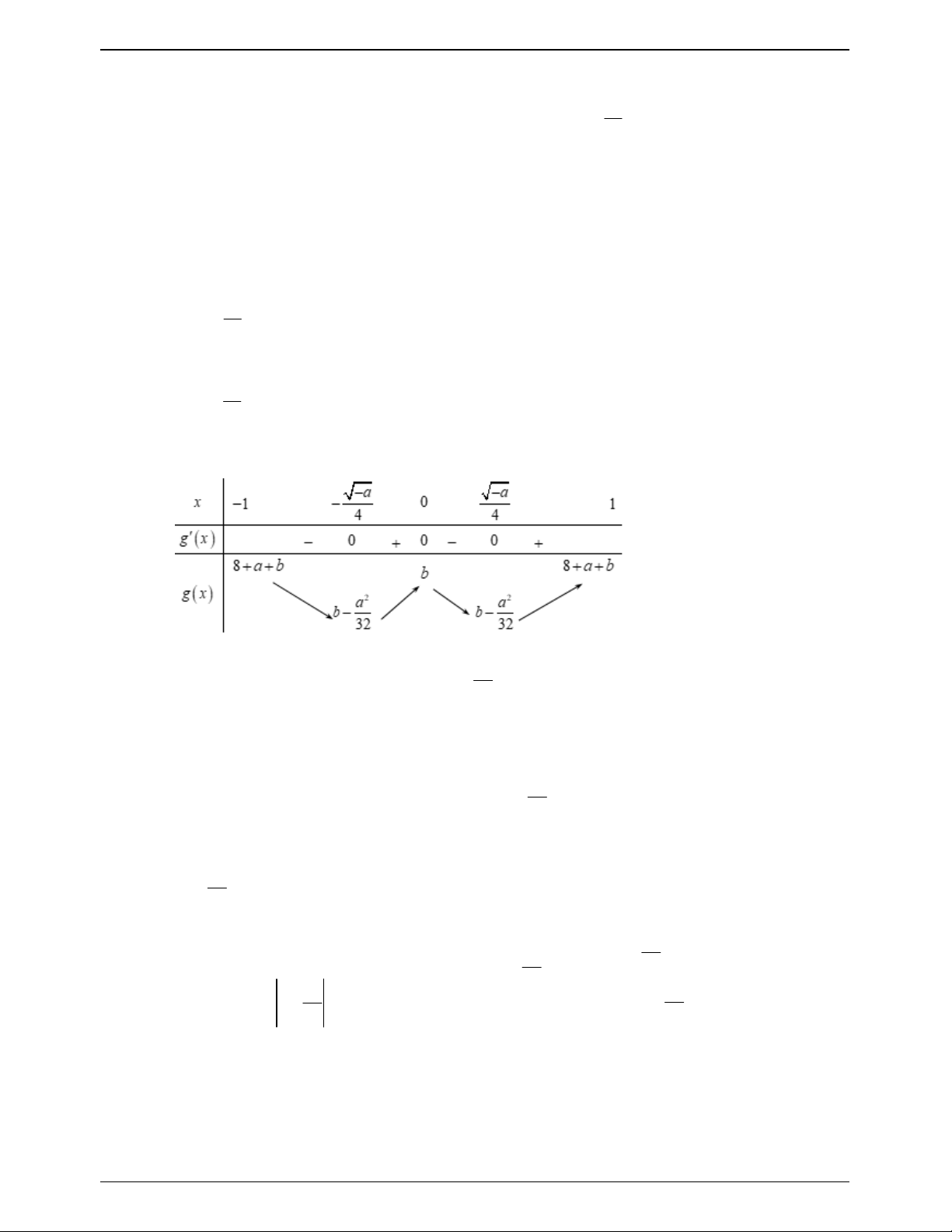
Xét hàm số g x 4 3 2
x  4x  4x a .  x  0 g x 3 2
 4x 12x  8x ; g x  0 3 2 
 4x 12x  8x  0  x  1 .   x  2  Bảng biến thiên
Do 2m M  0 nên m  0 suy ra g x  0 x  0; 2 . a 1  0 a  1 Suy ra    . a  0 a  0   Nếu a  1
 thì M  a , m  a 1  2a  
1  a a  2  .
Nếu a  0 thì M a  1 , m a  2a a 1  a  1.
Do đó a  2 hoặc a  1 , do a nguyên và thuộc đoạn  3  ;  3 nên a  3  ; 2  ;1; 2;  3 .
Vậy có 5 giá trị của a thỏa mãn đề bài.
Câu 42.31: Xét hàm số   2
f x x ax b , với a , b là tham số. Gọi M là giá trị lớn nhất của hàm số trên  1  ; 
3 . Khi M nhận giá trị nhỏ nhất có thể được, tính a  2b . A. 3 . B. 4 . C. 4  . D. 2 . Lời giải Chọn C A B
Ta có max  A , B    
1 . Dấu  xảy ra khi A B . 2 A B
Ta có max  A , B  
2 . Dấu  xảy ra khi A  B . 2 Trang 565
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 a Xét hàm số   2
g x x ax b , có g x  0  x  . 2 a Trường hợp 1:   1  ;  3  a  6
 ; 2 . Khi đó M  max1 a b , 9  3a b  . 2
Áp dụng bất đẳng thức  
1 ta có M  4  2a  8 . a 2   a   Trường hợp 2:   1  ;  3  a  6
 ; 2 . Khi đó M  max 1 a b , 9  3a b , b   . 2  4    2   a   1
Áp dụng bất đẳng thức   1 và 2 ta có M  max 2
 5  a b , b    M  20  4a a  4    8 1  M 
16  a  22 . 8 Suy ra M  2 . a  2   2  aa  2
Vậy M nhận giá trị nhỏ nhất có thể được là M  2 khi 5
  a b   b   . 2  b  1  1
  a b  9  3a b
Do đó a  2b  4  .
Câu 42.32: Có bao nhiêu số thực m để hàm số 4 3 2
y  3x  4 x  12 x m có giá trị lớn nhất trên đoạn 275  3  ; 2 bằng ? 2 A. 4. B. 0. C. 2. D. 1. Lời giải Chọn D  275 4 3 2
3x  4x 12x m  ; x   3  ; 2 275  4 3 2 
y x x x m x    2 3 4 12 ; 3; 2   2 275 4 3 2 3
x  4x 12x m   ; x  3; 2   2  275  275 4 3 2 m
 3x  4x 12x ; x  3; 2 m
 min g x; x  3; 2  2    2     275 275 4 3 2 m 3x 4x 12x ; x  3;2          m
 max g x; x  3;2   2   2 Xét g x 4 3 2  3
x  4x 12x ; x   3  ; 2
Khảo sát hàm số trên đoạn  3
 ; 2 ta được min  2  43 ; max  32 .  275  211 m   243 m    2    2 211      m   275 211 2 m 32    m     2   2 Trang 566
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 211 275 Như vậy 4 3 2 m  
y  3x  4x 12x m  ; x   3  ; 2 2 2 211
Dấu = xẩy ra khi và chỉ khi m  
nên có 1 giá trị cần tìm. 2
Câu 42.33: Cho hàm số 2
y x  2 x m  4 (với m là tham số thực). Hỏi max y có giá trị nhỏ nhất là 2;  1 A. 3 . B. 2. C. 1. D. 5 . Lời giải Chọn B 2
Đặt t x  2x  4 , ta có t  2x  2 .
t  2x  2  0  x  1   2  ;  1 . t  2    4  , t   1  5  , t   1  1  .
Suy ra: max t m  m 1, min t m  m  5 , do đó 2;  1 2;  1
m  5  1  m
max y  max t m  max  m  5 , m 1  max m  5 , 1 m   2;  1 2;  1 2
m 5  1 m 
 2 dấu bằng đặt tại m  5  1 m m  3 . 2
Câu 42.34: Cho hàm số 3 2
y x  3x m (với m là tham số thực). Hỏi max y có giá trị nhỏ nhất là bao 1;2 nhiêu? A. 2. B. 4. C. 1. D. 3 . Lời giải Chọn C Xét hàm số: 3 2
t x  3x với x 1; 2 .
x  0 1;2 Ta có 2
t  3x  6x  0   ; t  
1  2 , t 2  4 . Nên max t  2 và min t  4 .
x  2 1; 2 1;2 1;2 
Do đó max y  max m t  max  m  4 ; m  2  1;2 1;2
m  4  2  m
m  4  2  m
 max  m  4 ; 2  m     1 . 2 2
Dấu bằng đạt tại m  4  2  m m  3 . 2
x  m   1 x  2m  2
Câu 42.35: Cho hàm số y
(với m là tham số thực). Hỏi max y có giá trị nhỏ x  2 1;  1 nhất là bao nhiêu? 3 1 A. . B. . C. 2. D. 3 . 2 2 Lời giải Chọn B Trang 567
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 2 x x  2 2 x x  2 Ta có y
m t m , trong đó t   2  ;   1 , x  1  ;1 . x  2 x  2 2  x  0 x x   1  ;  1 4 t   t  0   .  x  22  x  4 1  ;  1  4 t   1   ,t 0  1,  t   1  2  3
Do đó max y  max t m  max  m  2 , m 1  max m  2 , m 1 1;  1 1;  1
m  2  m 1
m  2  m   1 1    . 2 2 2 3
Dấu bằng đạt tại m  2  m 1  m   . 2
Câu 42.36: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
x mx m y  trên 1; 
2 bằng 2. Số phần tử của S là x 1 A. 3 . B. 1. C. 2. D. 4. Lời giải Chọn C
Tập xác định: D   \   1 . 2
x mx m
Xét hàm số: f x  . x 1 2 x  2x 2 x  2xx  01; 2
f   x 
; f  x  0   0 2
x  2x  0   .  2 x  2 1  x   1 x  2    1;2  4 1 
f  x  0, x
 1;2 nên max y  max m  , m    1;2 3 2    4 m   2  3   4 1   2 m   m   m   3 2   Max y  2 3    . 1;2  1 5   m   2 m     2  2   1 4   m   m    2 3 
Vậy có hai giá trị của m thỏa mãn.
Câu 42.37: Cho hàm số 3 2
y x x   2 m  
1 x  27 . Giá trị lớn nhất của hàm số trên đoạn 3;   1 có
giá trị nhỏ nhất bằng A. 26 . B. 18 . C. 28 . D. 16 . Lời giải Trang 568
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Chọn B Xét 3 2
u x x   2 m  
1 x  27 trên đoạn 3;   1 ta có: 2 2
u  3x  2x m 1  0, x  .
Do đó A  max u u   2
1  26  m ; a  min u u 3 2  6  3m . 3;  1 3;  1
Do M  max y  max 2 2
26  m , 6  3m  và 2 2
4M  3 26  m  6  3m  72 .  3  ;  1 Vậy M  18 . Dấu bằng xảy ra khi 2 2
26  m  6  3m  18  m  2 2 .  2 2 x y  1 2x y
Câu 42.38: Xét các số thực dương x, y thoả mãn 2018 
. Giá trị nhỏ nhất P của biểu  min x  2 1
thức P  2 y  3x bằng 3 5 7 1 A. P  . B. P  . C. P  . D. P  . min 4 min 6 min 8 min 2 Lời giải Chọn C Ta có:  2 2 x y  1 2x y 2018  x 2 1 2
 2(x y 1)  log
2x y  log  2 x  2x  1 . 2018 2018   log  2 x  2x   1  2  2
x  2x 1  log
2x y  2 2x y * 2018  2018      
Xét hàm: f t   log
t  2t ,t  0 . 2018 1
Suy ra: f t  
 2  0 , t  0. t ln 2018
Do đó hàm f t  đồng biến trên khoảng 0;. Mà    f  2
x x    f x y 2 2 * 2 1 2
x  2x 1  2x y y x 1 . 2  3  7 7 Khi đó: 2
P  2 y  3x  2x  3x  2  2 x      .  4  8 8 7 3 Kết luận: P  khi x  . min 8 4
Câu 42.39: Cho hàm số f x 4 2
 8x ax b , trong đó a , b là tham số thực. Biết rằng giá trị lớn nhất
của hàm số f x trên đoạn  1  ; 
1 bằng 1. Hãy chọn khẳng định đúng?
A. a  0 , b  0
B. a  0 , b  0
C. a  0 , b  0
D. a  0 , b  0 Lời giải Chọn C Cách 1. Trang 569
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 x  0 Xét g x 4 2
 8x ax b , g x 3
 32x  2ax  0   a . 2 x    16
Ta có max f x  1  g 0  b  1  ;  1 . 1;  1
TH1. a  0 . Ta có g   1  g  
1  8  a b  1 . Suy ra max f x  1 không thỏa YCBT. 1;  1 TH2. a  0 . a Nếu 
 1  a  16 . Ta có g   1  g  
1  8  a b  1
 . Suy ra max f x  1 không thỏa 16 1;  1 YCBT. a Nếu   1  a  16 . 16 Ta có BBT 2  a 1    1  2 a  64
▪ max f x  b  1. Khi đó YCBT   32  
a  8 (thỏa a  16 ) 1;  1 a  8  8
  a b  1   b   1 
▪ max f x  8  a b  1. Khi đó, YCBT 2   a 1;  1 b   1   32 a  8  a  8 2  a  
a  8  b  1 .  a  6  0  24  a  8  32 2  a 2  a b  1  b   1   32 32  2 a  2   aa  8
▪ max f x  b   1 . Khi đó, YCBT  8
  a b  1  6  a   0   .  1  ;  1 32 32 b  1  b   1   a  8    
Vậy a  8 , b  1 thỏa YCBT. Cách 2. Trang 570
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 Đặt 2
t x khi đó ta có g t 2
 8t at b . Vì x 1;  1 nên t 0;  1 .
Theo yêu cầu bài toán thì ta có: 0  g t  1 với mọi t 0; 
1 và có dấu bằng xảy ra.
Đồ thị hàm số g t  là một parabol có bề lõm quay lên trên do đó điều kiện trên dẫn đến hệ điều kiện sau xảy ra : 
1  g 0  1 1  b  1  1   b  1   1    1  g  
1  1  1  8  a b  1   1
  8  a b  1 2     2
32  32b a  32 2  3
 2  a  32b  323 1   1    32 Lấy   1  323 ta có : 2
64  a  64 do đó 8  a  8 .
Lấy 3  322 ta có : 2
64  a  32a  256  64 Suy ra : 2
a  32a  192  0  24  a  8 .
Khi đó ta có a  8 và b  1.
Kiểm tra : g t  2
 8t  8t 1   t  2 2 2 1 1
Vì 0  t  1 nên 1  2t 1  1    t  2 0 2 1
 1    g t    t  2 1 2 2 1 1  1.
Vậy max g t   1 khi t  1  x  1  (t/m).
Câu 42.40: Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất của hàm số 2
y  sin x  2sin x m bằng 1. Số phần tử của S là A. 0 B. 1 B. 4 D. 3 Lời giải Chọn A Đặt
x t t   2 sin
1;1  y t  2t m
Xét hàm số f t  2
t  2t m có f 't  2t  2  0  t 1 1  ;  1
max f x  maxm  3; m   1  m  3  1;  1 Có f  
1  m  3, f  
1  m 1. Khi đó min f
x  minm  3; m   1  m 1  1  ;  1 
TH1: m  3  m 1  m  1  Trang 571
NHÓM WORD – BIÊN SOẠN TÀI LIỆU
50 BÀI TOÁN ÔN THI THPTQG: 2019-2020 m  2  l
 max f x  m  3  1   m  4  l  
TH1: m  3  m 1  m  1 
m  2 l
 max f x  m 1  1  m  0 l 
 Không tồn tại m thỏa mãn Trang 572