Hàm số và ứng dụng đạo hàm trong đề thi THPT môn Toán (2017 – 2020)

Hàm số và ứng dụng đạo hàm trong đề thi THPT môn Toán (2017 – 2020) được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

14 7 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

122 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THCS-THPT HOA SEN
NĂM HỌC 2020-2021
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC ĐỀ THI TỐT NGHIỆP TRUNG PHỔ THÔNG QUỐC GIA
VÀ CÁC ĐỀ THI THỬ
TỪ NĂM 2017 ĐẾN 2020
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
PHẦN I
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC KỲ THI TỐT NGHIỆP TRUNG
HỌC PHỔ THÔNG QUỐC GIA 2017-2020
Câu 1.
Đường cong trong hình bên là đồ thị của một hàm số trong bốn
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi
hàm số đó là hàm số nào?
A y = −x
2
+ x − 1. B y = −x
3
+ 3x + 1.
C y = x
3
− 3x + 1. D y = x
4
− x
2
+ 1.
x
y
Câu 2. Cho hàm số y = f(x) có lim
x→+∞
= 1 và lim
x→−∞
= −1. Khẳng định nào sau đây là
khẳng định đúng?
A Đồ thị hàm số đã cho không có tiệm cận ngang.
B Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = −1.
D Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1 và x = −1.
Câu 3. Hỏi hàm số y = 2x
4
+ 1 đồng biến trên khoảng nào?
A
Å
−∞; −
1
2
ã
. B (0; +∞). C
Å
−
1
2
; +∞
ã
. D (−∞; 0).
Câu 4. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên:
x
y
0
y
−∞
0 1
+∞
+ −
0
+
−∞−∞
00
−1−1
+∞+∞
Khẳng định nào sau đây là khẳng định đúng?
A Hàm số có đúng một cực trị.
B Hàm số có giá trị cực tiểu bằng 1.
C Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng −1.
D Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.
Câu 5. Tìm giá trị cực đại y
CĐ
của hàm số y = x
3
− 3x + 2.
A y
CĐ
= 4. B
y
CĐ
= 1. C y
CĐ
= 0. D y
CĐ
= −1.
Câu 6. Tìm giá trị nhỏ nhất của hàm số y =
x
2
+ 3
x − 1
trên đoạn [2; 4].
A min
[2;4]
y = 6. B min
[2;4]
y = −2. C min
[2;4]
y = −3. D min
[2;4]
y =
19
3
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 2
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 7. Biết rằng đường thẳng y = −2x + 2 cắt đồ thị hàm số y = x
3
+ x + 2 tại điểm duy
nhất; kí hiệu (x
◦
; y
◦
) là tọa độ của điểm đó. Tìm y
◦
.
A y
◦
= 4. B y
◦
= 0. C y
◦
= 2. D y
◦
= −1.
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x
4
+2mx
2
+1
có ba điểm cực trị tạo thành một tam giác vuông cân.
A m = −
1
3
√
9
. B m = −1. C m =
1
3
√
9
. D m = 1.
Câu 9. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y =
x + 1
√
mx
2
+ 1
có hai đường tiệm cận ngang.
A Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài.
B m < 0.
C m = 0.
D m > 0.
Câu 10. Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm
đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm, rồi gập tấm nhôm lại
như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích
lớn nhất.
A x = 6. B x = 3. C x = 2. D x = 4.
Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y =
tan x − 2
tan x − m
đồng
biến trên khoảng
0;
π
4
.
A m ≤ 0 hoặc 1 ≤ m < 2. B m ≤ 0.
C 1 ≤ m < 2. D m ≥ 2.
Câu 12. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số y =
2x + 1
x + 1
?
A x = 1. B y = −1. C y = 2. D x = −1.
Câu 13. Đồ thị của hàm số y = x
4
− 2x
2
+ 2 và đồ thị của hàm số y = −x
2
+ 4 có tất cả
bao nhiêu điểm chung?
A 0. B 4. C 1. D 2.
Câu 14.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 3
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số y = f(x) xác định, liên tục trên đoạn [−2; 2] và có đồ thị
là đường cong trong hình vẽ bên. Hàm số f(x) đạt cực đại tại điểm
nào dưới đây?
A x = 2. B x = −1. C x = 1. D x = 2.
−2 −1 1 2
−4
−2
2
4
x
y
O
Câu 15. Cho hàm số y = x
3
− 2x
2
+ x + 1. Mệnh đề nào dưới đây đúng?
A Hàm số nghịch biến trên khoảng
Å
1
3
; 1
ã
.
B Hàm số nghịch biến trên khoảng
Å
−∞;
1
3
ã
.
C Hàm số đồng biến trên khoảng
Å
1
3
; 1
ã
.
D Hàm số nghịch biến trên khoảng (1; +∞).
Câu 16. Cho hàm số y = f(x) xác định trên R \{0}, liên tục trên mỗi khoảng xác định và
có bảng biến thiên như sau.
x
y
0
y
−∞
0 1
+∞
− +
0
−
+∞+∞
−1 −∞
22
−∞−∞
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f(x) = m có ba
nghiệm thực phân biệt.
A [−1; 2]. B (−1; 2). C (−1; 2]. D (−∞; 2].
Câu 17. Cho hàm số y =
x
2
+ 3
x + 1
. Mệnh đề nào dưới đây đúng ?
A Cực tiểu của hàm số bằng −3. B Cực tiểu của hàm số bằng 1.
C Cực tiểu của hàm số bằng −6. D Cực tiểu của hàm số bằng 2.
Câu 18. Một vật chuyển động theo quy luật s = −
1
2
t
3
+9t
2
, với t (giây) là khoảng thời gian
tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng
thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn
nhất của vật đạt được bằng bao nhiêu ?
A 216(m/s). B 30(m/s). C 400(m/s). D 54(m/s).
Câu 19. Tìm tất cả các tiệm cận đứng của đồ thị hàm số y =
2x − 1 −
√
x
2
+ x + 3
x
2
− 5x + 6
A x = −3 và x = −2. B x = −3.
C x = 3 và x = 2. D x = 3.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 4
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 20. Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = ln(x
2
+1)−mx+1
đồng biến trên khoảng (−∞; +∞)
A (−∞; −1]. B (−∞; −1). C [−1; 1]. D [1; +∞).
Câu 21. Biết M(0; 2), N(2; −2) là các điểm cực trị của đồ thị hàm số y = ax
3
+bx
2
+cx+d.
Tính giá trị của hàm số tại x = −2.
A y(−2) = 2. B y(−2) = 22. C y(−2) = 6. D y(−2) = −18.
Câu 22.
Cho hàm số y = ax
3
+ bx
2
+ cx + d có đồ thị như hình vẽ
bên. Mệnh đề nào dưới đây đúng ?
A a < 0, b > 0, c > 0, d < 0.
B a < 0, b < 0, c > 0, d < 0.
C a < 0, b < 0, c < 0, d > 0.
D a < 0, b > 0, c < 0, d < 0.
x
y
O
Câu 23. Cho hàm số y = x
3
−3x có đồ thị (C). Tìm số giao điểm của (C) và trục hoành.
A 2. B 3. C 1. D 0.
Câu 24. Cho hàm số y =
x − 2
x + 1
. Mệnh đề nào dưới đây đúng?
A Hàm số nghịch biến trên khoảng (−∞; −1).
B Hàm số đồng biến trên khoảng (−∞; −1).
C Hàm số đồng biến trên khoảng (−∞; +∞).
D Hàm số nghịch biến trên khoảng (−1; +∞).
Câu 25.
Cho hàm số y = f(x) có bảng biến
thiên như hình vẽ bên. Mệnh đề nào
dưới đây đúng?
A y
CĐ
= 5. B y
CT
= 0.
C min
R
y = 4. D max
R
y = 5.
x
y
0
y
−∞
0 1
+∞
−
0
+
0
−
+∞+∞
44
55
−∞−∞
Câu 26.
Cho hàm số y = f(x) có
bảng biến thiên như hình
dưới đây. Hỏi đồ thị của
hàm số đã cho có bao nhiêu
tiệm cận?
A 1. B 3.
C 2. D 4.
x
−∞ +∞
−2
0
y
0
+ −
y
+∞
1
−∞
0
Câu 27. Hàm số nào dưới đây đồng biến trên khoảng (−∞; +∞)?
A y = 3x
3
+ 3x − 2. B y = 2x
3
− 5x + 1.
C y = x
4
+ 3x
2
. D y =
x − 2
x + 1
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 5
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 28. Cho hàm số f(x) = x ln x. Một trong bốn đồ thị cho trong bốn phương án A, B,
C, D dưới đây là đồ thị của hàm số y = f
0
(x). Tìm đồ thị đó.
A
x
O
1
y
1
. B
x
O
1
y
.
C
x
O
1
y
. D
x
O
y
1
.
Câu 29. Tính giá trị nhỏ nhất của hàm số y = 3x +
4
x
2
trên khoảng (0; +∞).
A min
(0;+∞)
y = 3
3
√
9. B min
(0;+∞)
y = 7. C min
(0;+∞)
y =
33
5
. D min
(0;+∞)
y = 2
3
√
9.
Từ bảng biến thiên suy ra: min
(0;+∞)
y = 3
3
√
9.
Câu 30.
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong
4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi
đó là hàm số nào?
A y =
2x + 3
x + 1
. B y =
2x − 1
x + 1
.
C y =
2x − 2
x − 1
. D y =
2x + 1
x − 1
.
x
y
−1
2
O
Câu 31. Tìm tất cả các giá trị thực của tham số m để hàm số y = (m−1)x
4
−2(m−3)x
2
+1
không có cực đại.
A 1 ≤ m ≤ 3. B m ≤ 1. C m ≥ 1. D 1 < m ≤ 3.
Câu 32.
Hàm số y = (x − 2)(x
2
− 1) có đồ thị như hình vẽ bên. Hình nào dưới
đây là đồ thị của hàm số y = |x − 2|(x
2
− 1)?
A
x
y
O
. B
x
y
O
.
C
x
y
O
. D
x
y
O
.
x
y
O
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 6
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 33. Hỏi có bao nhiêu số nguyên m để hàm số y = (m
2
− 1)x
3
+ (m − 1)x
2
− x + 4
nghịch biến trên khoảng (−∞; +∞).
A 2. B 1. C 0. D 3.
Câu 34. Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số
y =
1
3
x
3
− mx
2
+ (m
2
− 1)x có hai điểm cực trị là A và B sao cho A, B nằm khác phía và
cách đều đường thẳng d : y = 5x − 9. Tính tổng tất cả các phần tử của S.
A 0. B 6. C −6. D 3.
Câu 35. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
00
33
00
+∞+∞
Mệnh đề nào dưới đây sai?
A Hàm số có ba điểm cực trị. B Hàm số có giá trị cực đại bằng 3.
C Hàm số có giá trị cực đại bằng 0. D Hàm số có hai điểm cực tiểu.
Câu 36.
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới
đây. Hàm số đó là hàm số nào?
A y = −x
3
+ x
2
− 1. B y = x
4
− x
2
− 1.
C y = x
3
− x
2
− 1. D y = −x
4
+ x
2
− 1.
x
y
O
Câu 37. Cho hàm số y = x
3
+ 3x + 2. Mệnh đề nào dưới đây đúng?
A Hàm số đồng biến trên khoảng (−∞; 0) và nghịch biến trên khoảng (0; +∞).
B Hàm số nghịch biến trên khoảng (−∞; +∞).
C Hàm số đồng biến trên khoảng (−∞; +∞).
D Hàm số nghịch biến trên khoảng (−∞; 0) và đồng biến trên khoảng (0; +∞).
Câu 38. Tìm số tiệm cận đứng của đồ thị hàm số y =
x
2
− 3x − 4
x
2
− 16
.
A 2. B 3. C 1. D 0.
Câu 39. Hàm số y =
2
x
2
+ 1
nghịch biến trên khoảng nào dưới đây?
A (0; +∞). B (−1; 1). C (−∞; +∞). D (−∞; 0).
Câu 40. Cho hình phẳng D giới hạn bởi đường cong y =
√
2 + cos x, trục hoành và các
đường thẳng x = 0, x =
π
2
. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể
tích V bằng bao nhiêu?
A V = π − 1. B V = (π − 1)π. C V = (π + 1)π. D V = π + 1.
Câu 41. Tìm giá trị nhỏ nhất m của hàm số y = x
3
−7x
2
+ 11x −2 trên đoạn [0; 2].
A m = 11. B m = 0. C m = −2. D m = 3.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 7
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 42.
Đường cong ở hình bên là đồ thị của hàm số y =
ax + b
cx + d
với a, b, c, d
là các số thực. Mệnh đề nào dưới đây đúng?
A y
0
> 0, ∀x ∈ R.
B y
0
< 0, ∀x ∈ R.
C y
0
> 0, ∀x 6= 1.
D y
0
< 0, ∀x 6= 1.
x
y
O
1
Câu 43. Cho hàm số y =
x + m
x − 1
(m là tham số thực) thỏa mãn min
[2;4]
y = 3. Mệnh đề nào
dưới đây đúng?
A m < −1. B 3 < m ≤ 4. C m > 4. D 1 ≤ m < 3.
Câu 44. Cho hàm số y = −x
3
− mx
2
+ (4m + 9)x + 5 với m là tham số. Có bao nhiêu giá
trị nguyên của m để hàm số nghịch biến trên khoảng (−∞; +∞)?
A 7. B 4. C 6. D 5.
Câu 45. Tìm giá trị thực của tham số m để phương trình log
2
3
x − m log
3
x + 2m − 7 = 0
có hai nghiệm thực x
1
,x
2
thỏa mãn x
1
x
2
= 81.
A m = −4. B m = 4. C m = 81. D m = 44.
Câu 46. Đồ thị hàm số y = x
3
− 3x
2
− 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới
đây thuộc đường thẳng AB?
A P (1; 0). B M(0; −1). C N(1; −10). D Q(−1; 10).
Câu 47. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = mx −m + 1 cắt đồ
thị của hàm số y = x
3
−3x
2
+ x + 2 tại ba điểm A, B, C phân biệt sao cho AB = BC.
A m ∈ (−∞; 0] ∪ [4; +∞). B m ∈ R.
C m ∈
−
5
4
; +∞
. D m ∈ (−2; +∞).
Câu 48. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−2
2
+∞
+
0
−
0
+
−∞−∞
33
00
+∞+∞
Tìm giá trị cực đại y
CĐ
và giá trị cực tiểu y
CT
của hàm số đã cho.
A y
CĐ
= 3 và y
CT
= −2. B y
CĐ
= 2 và y
CT
= 0.
C
y
CĐ
= −2 và y
CT
= 2. D y
CĐ
= 3 và y
CT
= 0.
Câu 49. Hàm số nào dưới đây đồng biến trên khoảng (−∞; +∞)?
A y =
x + 1
x + 3
. B y = x
3
+ 3x. C y =
x − 1
x − 2
. D y = −x
3
− 3x.
Câu 50.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 8
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới
đây. Hàm số đó là hàm số nào?
A y = x
4
− 2x
2
+ 1. B y = −x
4
+ 2x
2
+ 1.
C y = −x
3
+ 3x
2
+ 1. D y = x
3
− 3x
2
+ 3.
x
y
O
Câu 51. Cho hàm số y = x
3
− 3x
2
. Mệnh đề nào dưới đây đúng?
A Hàm số nghịch biến trên (0; 2).
B Hàm số nghịch biến trên khoảng (2; +∞).
C Hàm số đồng biến trên khoảng (0; 2).
D Hàm số nghịch biến trên khoảng (−∞; 0).
Câu 52. Đường
cong ở hình bên là đồ thị của hàm số y = ax
4
+ bx
2
+ c
với a, b, c là các số thực. Mệnh đề nào dưới đây đúng?
A Phương trình y
0
= 0 có đúng ba nghiệm thực phân
biệt.
B Phương trình y
0
= 0 có đúng hai nghiệm thực phân
biệt.
x
y
O
C Phương trình y
0
= 0 vô nghiệm trên tập số thực.
D Phương trình y
0
= 0 có đúng một nghiệm thực.
Câu 53. Tìm số tiệm cận của đồ thị hàm số y =
x
2
− 5x + 4
x
2
− 1
.
A 3. B 1. C 0. D 2.
Câu 54. Tìm giá trị thực của tham số m để hàm số y =
1
3
x
3
− mx
2
+ (m
2
− 4) x + 3 đạt
cực đại tại x = 3.
A m = 1. B m = −1. C m = 5. D m = −7.
Câu 55. Cho hàm số y =
x + m
x + 1
(m là tham số thực) thỏa mãn min
[1;2]
y + max
[1;2]
y =
16
3
. Mệnh
đề nào dưới đây đúng?
A m ≤ 0. B m > 4. C 0 < m ≤ 2. D 2 < m ≤ 4.
Câu 56. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
55
11
+∞+∞
Đồ thị của hàm số y = |f (x)| có bao nhiêu điểm cực trị?
A 4. B 2. C 3. D 5.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 9
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 57. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = −mx cắt đồ thị
hàm số y = x
3
− 3x
2
− m + 2 tại ba điểm phân biệt A, B, C sao cho AB = BC.
A m ∈ (−∞; 3). B m ∈ (−∞; −1). C m ∈ (−∞; +∞). D m ∈ (1; +∞).
Câu 58. Cho hàm số y = (x − 2)(x
2
+ 1) có đồ thị (C). Mệnh đề nào sau đây đúng?
A (C) cắt trục hoành tại hai điểm. B (C) cắt trục hoành tại một điểm.
C (C) không cắt trục hoành. D (C) cắt trục hoành tại ba điểm.
Câu 59. Cho hàm số y = f(x) có đạo hàm f
0
(x) = x
2
+ 1, ∀x ∈ R. Mệnh đề nào dưới đây
đúng?
A Hàm số nghịch biến trên khoảng (−∞; 0).
B Hàm số nghịch biến trên khoảng (1; +∞).
C Hàm số nghịch biến trên khoảng (−1; 1).
D Hàm số đồng biến trên khoảng (−∞; +∞).
Câu 60. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
2
+∞
+
0
−
0
+
22
44
55
22
Mệnh đề nào dưới đây đúng?
A Hàm số có bốn điểm cực trị. B Hàm số đạt cực tiểu tại x = 2.
C Hàm số không có cực đại. D Hàm số đạt cực tiểu tại x = −5.
Câu 61. Tìm giá trị nhỏ nhất m của hàm số y = x
4
− x
2
+ 13 trên đoạn [−2; 3].
A m =
51
4
. B m =
49
4
. C m = 13. D m =
51
2
.
Câu 62. Đường cong ở hình bên
là đồ thị của hàm số y =
ax + b
cx + d
với a, b, c, d là các số thực.
Mệnh đề nào dưới đây đúng?
A y
0
< 0, ∀x 6= 2. B y
0
< 0, ∀x 6= 1.
C y
0
> 0, ∀x 6= 2. D y
0
> 0, ∀x 6= 1.
x
y
O
2
1
Câu 63. Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng?
A y =
1
√
x
. B y =
1
x
2
+ x + 1
. C y =
1
x
4
+ 1
. D y =
1
x
2
+ 1
.
Câu 64. Cho hàm số y = x
4
− 2x
2
. Mệnh đề nào dưới đây đúng?
A Hàm số đồng biến trên khoảng (−∞; −2).
B Hàm số nghịch biến trên khoảng (−∞; −2).
C Hàm số đồng biến trên khoảng (−1; 1).
D Hàm số nghịch biến trên khoảng (−1; 1).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 10
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 65. Cho hàm số y =
mx − 2m − 3
x − m
với m là tham số. Gọi S là tập hợp tất cả các giá
trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S.
A 5. B 4. C Vô số. D 3.
Câu 66. Đồ thị của hàm số y = −x
3
+ 3x
2
+ 5 có hai điểm cực trị A và B. Tính diện tích
S của tam giác OAB với O là gốc tọa độ.
A S = 9. B S =
10
3
. C S = 5. D S = 10.
Câu 67. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x
4
− 2mx
2
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.
A m > 0. B m < 1. C 0 < m <
3
√
4. D 0 < m < 1.
Câu 68. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau
x
y
0
−∞
−2
0 2
+∞
+
0
− −
0
+
Mệnh đề nào dưới đây đúng?
A Hàm số đồng biến trên khoảng (−2; 0).
B Hàm số đồng biến trên khoảng (−∞; 0).
C Hàm số nghịch biến trên khoảng (0; 2).
D Hàm số nghịch biến trên khoảng (−∞; −2).
Câu 69. Hàm số y =
2x + 3
x + 1
có bao nhiêu điểm cực trị?
A 3. B 0. C 2. D 1.
Câu 70. Đồ thị của hàm số y =
x − 2
x
2
− 4
có bao nhiêu tiệm cận?
A 0. B 3. C 1. D 2.
Câu 71. Tìm giá trị nhỏ nhất m của hàm số y = x
2
+
2
x
trên đoạn
ï
1
2
; 2
ò
.
A m =
17
4
. B m = 10. C m = 5. D m = 3.
Câu 72. Cho hàm số y =
√
2x
2
+ 1. Mệnh đề nào dưới đây đúng?
A Hàm số nghịch biến trên khoảng (−1; 1).
B Hàm số đồng biến trên khoảng (0; +∞).
C Hàm số đồng biến trên khoảng (−∞; 0).
D Hàm số nghịch biến trên khoảng (0; +∞).
Câu 73. Cho hàm số y = −x
4
+ 2x
2
có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham
số m để phương trình −x
4
+ 2x
2
= m có bốn nghiệm thực phân
biệt.
A m > 0. B 0 ≤ m ≤ 1.
C 0 < m < 1. D m < 1.
x
y
O
−1 1
1
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 11
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 74. Một vật chuyển động theo quy luật s = −
1
3
t
3
+ 6t
2
với t (giây) là khoảng thời gian
tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận
tốc lớn nhất của vật đạt được bằng bao nhiêu?
A 144 m/s. B 36 m/s. C 243 m/s. D 27 m/s.
Câu 75. Tìm giá trị thực của tham số m để đường thẳng d : y = (2m −1)x + 3 + m vuông
góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x
3
− 3x
2
+ 1.
A m =
3
2
. B m =
3
4
. C m = −
1
2
. D m =
1
4
.
Câu 76. Cho hàm số y =
mx + 4m
x + m
với m là tham số. Gọi S là tập hợp tất cả các giá trị
nguyêncủa m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S.
A 5. B 4. C Vô số. D 3.
Câu 77. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x
3
−3mx
2
+4m
3
có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa
độ.
A
m = −
1
4
√
2
; m =
1
4
√
2
. B m = −1; m = 1.
C m = 1. D m 6= 0.
Câu 78. Cho hàm số y = f(x).
Đồ thị của hàm số y = f
0
(x) như hình bên.
Đặt g(x) = 2f(x) + (x + 1)
2
.
Mệnh đề nào dưới đây đúng?
A
g(1) < g(3) < g(−3). B
g(1) < g(−3) < g(3).
C g(3) = g(−3) < g(1). D g(3) = g(−3) > g(1).
x
y
1 3
−4
2
O
−3
−2
Câu 79. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−2
0
−2
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
∞∞
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?
A (−2; 0). B (−∞; −2). C (0; 2) . D (0; +∞) .
Câu 80. Cho hàm số y = f(x) có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 12
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
x
y
0
y
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
11
55
−∞−∞
Hàm số đạt cực đại tại điểm
A x = 1. B x = 0. C x = 5. D x = 2.
Câu 81.
Đường cong hình bên là đồ thị của hàm số nào dưới
đây?
A y = −x
4
+ 2x
2
+ 2. B y = x
4
− 2x
2
+ 2.
C y = x
3
− 3x
2
+ 2. D y = −x
3
+ 3x
2
+ 2.
O
x
y
Câu 82. Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A y =
x
2
− 3x + 2
x − 1
. B y =
x
2
x
2
+ 1
. C y =
√
x
2
− 1. D y =
x
x + 1
.
Câu 83.
Cho hàm số y = f(x) có bảng biến thiên như
hình vẽ. Số nghiệm của phương trình f(x) −
2 = 0 là
A 0. B 3. C 1. D 2.
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
44
−2−2
+∞+∞
Câu 84. Có bao nhiêu giá trị nguyên âm của m để hàm số y = x
3
+ mx −
1
5x
5
đồng biến
trên (0; +∞).
A 5. B 3. C 0. D 4.
Câu 85. Có bao nhiêu giá trị nguyên của tham số m để phương trình
3
p
m + 3
3
√
m + 3 sin x =
sin x có nghiệm thực.
A 5. B 7. C 3. D 2.
Câu 86.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 13
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số y = f(x). Hàm số y = f
0
(x) có đồ
thị như hình bên. Hàm số y = f(2 − x) đồng
biến trên khoảng
A (1; 3). B (2; +∞).
C (−2; 1). D (−∞; −2).
x
y
0
−1
1 4
Câu 87. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = |3x
4
− 4x
3
− 12x
2
+ m|
có 7 điểm cực trị
A 3. B 5. C 6. D 4.
Câu 88.
Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có đồ thị như hình vẽ
bên. Số điểm cực trị của hàm số đã cho là
A 2. B 0. C 3. D 1.
x
y
O
Câu 89. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
33
−2−2
+∞+∞
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A (0; 1). B (−∞; 0). C (1; +∞). D (−1; 0).
Câu 90.
Đường cong trong hình vẽ bên là của hàm số nào dưới đây?
A y = x
4
− 3x
2
− 1. B y = x
3
− 3x
2
− 1.
C y = −x
3
+ 3x
2
− 1. D y = −x
4
+ 3x
2
− 1.
x
y
O
Câu 91.
Cho hàm số f(x) = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R). Đồ thị của
hàm số y = f(x) như hình vẽ bên. Số nghiệm thực của phương trình
3f(x) + 4 = 0 là
A 3. B 0. C 1. D 2.
x
y
O
2
−2
2
Câu 92. Số tiệm cận đứng của đồ thị hàm số y =
√
x + 9 − 3
x
2
+ x
là
A 3. B 2. C 0. D 1.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 14
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 93. Giá trị lớn nhất của hàm số y = x
4
− 4x
2
+ 9 trên đoạn [−2; 3] bằng
A 201. B 2. C 9. D 54.
Câu 94. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
x + 2
x + 5m
đồng biến trên
khoảng (−∞; −10)?
A 2. B Vô số. C 1. D 3.
Câu 95. Có tất cả bao nhiêu giá trị nguyên của m để hàm số y = x
8
+ (m − 2)x
5
−(m
2
−
4)x
4
+ 1 đạt cực tiểu tại x = 0?
A 3. B 5. C 4. D Vô số.
Câu 96. Cho hàm số y =
1
4
x
4
−
7
2
x
2
có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho
tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M(x
1
; y
1
), N(x
2
; y
2
) (M, N khác A)
thỏa mãn y
1
− y
2
= 6(x
1
− x
2
)?
A 1. B 2. C 0. D 3.
Câu 97. Cho hàm số y =
x − 1
x + 2
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C).
Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng
A
√
6. B 2
√
3. C 2. D 2
√
2.
Câu 98. Cho hai hàm số y = f(x), y = g(x). Hai hàm số y = f
0
(x) và y = g
0
(x) có đồ thị
như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y = g
0
(x).
x
y
O
3 8 10
11
4
5
8
10
y = f
0
(x)
y = g
0
(x)
Hàm số h(x) = f(x + 4) − g
Å
2x −
3
2
ã
đồng biến trên khoảng nào dưới đây?
A
Å
5;
31
5
ã
. B
Å
9
4
; 3
ã
. C
Å
31
5
; +∞
ã
. D
Å
6;
25
4
ã
.
Câu 99.
Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có đồ thị như
hình vẽ bên. Số điểm cực trị của hàm số đã cho là
A 0. B 1. C 3. D 2.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 15
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 100.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới
đây?
A y = x
4
− 2x
2
− 1. B y = −x
4
+ 2x
2
− 1.
C y = x
3
− x
2
− 1. D y = −x
3
+ x
2
− 1.
x
y
O
Câu 101. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
1
+∞
+
0
−
0
+
−∞−∞
33
−2−2
+∞+∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A (−1; +∞). B (1; +∞). C (−1; 1). D (−∞; 1).
Câu 102.
Cho hàm số f(x) = ax
4
+bx
2
+c (a, b, c ∈ R). Đồ thị của hàm số y = f(x)
như hình vẽ bên. Số nghiệm thực của phương trình 4f(x)−3 = 0 là
A
4. B 3. C 2. D 0.
x
y
O
−1
1
1
Câu 103. Giá trị nhỏ nhất của hàm số y = x
3
+ 2x
2
− 7x trên đoạn [0; 4] bằng
A −259. B 68. C 0. D −4.
Câu 104. Số tiệm cận đứng của đồ thị hàm số y =
√
x + 4 − 2
x
2
+ x
là
A 3. B 0. C 2. D 1.
Câu 105. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
x + 6
x + 5m
nghịch biến
trên khoảng (10; +∞)?
A 3. B Vô số. C 4. D 5.
Câu 106. Có bao nhiêu giá trị nguyên của tham số m để hàm số
y = x
8
+ (m − 1)x
5
− (m
2
− 1)x
4
+ 1
đạt cực tiểu tại x = 0?
A 3. B 2. C Vô số. D 1.
Câu 107.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 16
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Cho hai hàm số y = f(x) và y = g(x). Hai
hàm số y = f
0
(x) và y = g
0
(x) có đồ thị
như hình vẽ bên, trong đó đường cong đậm
hơn là đồ thị hàm số y = g
0
(x). Hàm số
h (x) = f (x + 7) − g
Å
2x +
9
2
ã
đồng biến
trên khoảng nào dưới đây?
A
Å
2;
16
5
ã
. B
Å
−
3
4
; 0
ã
.
C
Å
16
5
; +∞
ã
. D
Å
3;
13
4
ã
.
x
y
O
3 8 10
4
5
8
10
y = f
0
(x)
y = g
0
(x)
11
Câu 108. Cho hàm số y =
x − 1
x + 1
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của
(C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn AB có độ dài bằng
A 3. B 2. C 2
√
2. D 2
√
3.
Câu 109. Cho hàm số y =
1
8
x
4
−
7
4
x
2
có đồ thị là (C). Có bao nhiêu điểm A thuộc (C)
sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M(x
1
; y
1
); N(x
2
; y
2
) (M, N
khác A) thỏa mãn y
1
− y
2
= 3(x
1
− x
2
)?
A 0. B 2. C 3. D 1.
Câu 110.
Cho hàm số y = ax
4
+ bx
2
+ c (a, b, c ∈ R) có đồ thị như hình
vẽ bên. Số điểm cực trị của hàm số đã cho là
A 2. B 3. C 0. D 1.
x
y
O
Câu 111.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A y = −x
4
+ x
2
− 1. B y = x
4
− 3x
2
− 1.
C y = −x
3
− 3x − 1. D y = x
3
− 3x − 1.
x
y
O
Câu 112. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
−1−1
−2−2
−1−1
−∞−∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 17
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A (−1; 0). B (1; +∞). C (−∞; 1). D (0; 1).
Câu 113. Số tiệm cận đứng của đồ thị hàm số y =
√
x + 25 − 5
x
2
+ x
là
A 2. B 0. C 1. D 3.
Câu 114. Giá trị nhỏ nhất của hàm số y = x
3
+ 3x
2
trên đoạn [−4; −1] bằng
A −4. B −16. C 0. D 4.
Câu 115.
Cho hàm số y = f(x) liên tục trên [−2; 2] và có đồ thị như hình
vẽ bên. Số nghiệm thực của phương trình 3f(x) −4 = 0 trên đoạn
[−2; 2] là
A 3. B 1. C 2. D 4.
x
y
O
−2
1
−1 2
−1
3
Câu 116. Ông A dự định sử dụng hết 5 m
2
kính để làm một bể cá bằng kính có dạng hình
hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không
đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần
trăm)?
A 1,01 m
3
. B 0,96 m
3
. C 1,33 m
3
. D 1,51 m
3
.
Câu 117. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
x + 1
x + 3m
nghịch biến
trên khoảng (6; +∞)?
A 3. B Vô số. C 0. D 6.
Câu 118. Cho hàm số y =
x − 2
x + 2
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của
(C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng
A 2
√
2. B 4. C 2. D 2
√
3.
Câu 119. Cho hai hàm số y = f(x), y = g(x). Hai hàm số y = f
0
(x) và y = g
0
(x) có đồ thị
như hình vẽ bên dưới
x
y
O
3 8 10
11
4
5
8
10
y = f
0
(x)
y = g
0
(x)
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 18
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
trong đó đường cong đậm hơn là đồ thị của hàm số y = g
0
(x). Hàm số h(x) = f (x + 3) −
g
Å
2x −
7
2
ã
đồng biến trên khoảng nào dưới đây?
A
Å
13
4
; 4
ã
. B
Å
7;
29
4
ã
. C
Å
6;
36
5
ã
. D
Å
36
5
; +∞
ã
.
Câu 120. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x
8
+ (m − 4)x
5
−
(m
2
− 16)x
4
+ 1 đạt cực tiểu tại x = 0.
A 8. B Vô số. C 7. D 9.
Câu 121. Cho hàm số y =
1
3
x
4
−
14
3
x
2
có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao
cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M(x
1
; y
1
), N(x
2
; y
2
) (M, N
khác A) thỏa mãn y
1
− y
2
= 8(x
1
− x
2
)?
A 1. B 2. C 0. D 3.
Câu 122.
Cho hàm số y = ax
4
+ bx
2
+ c (a, b, c ∈ R) có đồ thị như hình vẽ bên.
Số điểm cực trị của hàm số đã cho là
A 0. B 1. C 2. D 3.
x
y
O
Câu 123.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?
A y = x
3
− 3x
2
− 2. B y = x
4
− x
2
− 2.
C y = −x
4
+ x
2
− 2. D y = −x
3
+ 3x
2
− 2.
x
y
O
Câu 124. Cho hàm số y = f (x) có bảng biến thiên như sau
x
y
0
y
−∞
−2
3
+∞
−
0
+
0
−
+∞+∞
00
44
−∞−∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A (−2; +∞). B (−2; 3). C (3; +∞). D (−∞; −2).
Câu 125. Số tiệm cận đứng của đồ thị hàm số y =
√
x + 16 − 4
x
2
+ x
là
A 0. B 3. C 2. D 1.
Câu 126. Giá trị lớn nhất của hàm số y = x
4
− x
2
+ 13 trên đoạn [−1; 2] bằng
A
25. B
51
4
. C 13. D 85.
Câu 127.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 19
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số y = f (x) liên tục trên đoạn [−2; 4] và có đồ thị như
hình vẽ bên. Số nghiệm thực của phương trình 3f (x) − 5 = 0 trên
đoạn [−2; 4] là
A 0. B 3. C 2. D 1.
x
y
−2
−3
2
1
6
4
2
O
Câu 128. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
x + 2
x + 3m
đồng biến
trên khoảng (−∞; −6) ?
A 2. B 6. C Vô số. D 1.
Câu 129. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x
8
+ (m − 3) x
5
−
(m
2
− 9) x
4
+ 1 đạt cực tiểu tại x = 0
A 4. B 7. C 6. D Vô số.
Câu 130. Cho hàm số y =
x − 2
x + 1
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của
(C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng
A 2
√
3. B 2
√
2. C
√
3. D
√
6.
Câu 131. Cho hàm số y =
1
6
x
4
−
7
3
x
2
có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao
cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M (x
1
; y
1
), N (x
2
; y
2
) thỏa mãn
y
1
− y
2
= 4 (x
1
− x
2
)?
A 3. B 0. C 1. D 2.
Câu 132.
Cho hai hàm số y = f (x), y = g (x). Hai hàm số y =
f
0
(x) và y = g
0
(x) có đồ thị như hình vẽ bên, trong đó
đường cong đậm hơn là đồ thị của hàm số y = g
0
(x).
Hàm số h (x) = f (x + 6) − g
Å
2x +
5
2
ã
đồng biến trên
khoảng nào dưới đây?
A
Å
21
5
; +∞
ã
. B
Å
1
4
; 1
ã
.
C
Å
3;
21
5
ã
. D
Å
4;
17
4
ã
.
x
y
O
3 8 1011
4
5
8
10
y = g
0
(x)
y = f
0
(x)
Câu 133. Hàm số y = f (x) có bảng biến thiên như sau
x
y
0
y
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
11
55
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 20
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Giá trị cực đại của hàm số đã cho bằng
A 1. B 2. C 0. D 5.
Câu 134.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số
đồng biến trên khoảng nào dưới đây?
A (0; 1). B (−∞; −1).
C (−1; 1). D (−1; 0).
x
y
O
−1
1
−1
−2
Câu 135.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào
dưới đây?
A y =
2x − 1
x − 1
. B y =
x + 1
x − 1
.
C y = x
4
+ x
2
+ 1. D y = x
3
− 3x − 1.
x
y
O
1
1
Câu 136.
Cho hàm số y = f(x) liên tục tên đoạn [−1; 3] có đồ thị như
hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất, giá trị
nhỏ nhất của hàm số đã cho trên đoạn [−1; 3]. Giá trị của
M − m bằng
A 0. B 1. C 4. D 5.
x
y
−1
2
3
3
2
1
−2
O
Câu 137. Cho hàm số f(x) có đạo hàm f
0
(x) = x(x −1)(x + 2)
3
. Số điểm cực trị của hàm
số đã cho là
A 3. B 2. C 5. D 1.
Câu 138. Cho hàm số y = f(x) có bảng biến thiên như sau.
x
y
0
y
−∞
1
+∞
+ +
22
+∞
3
55
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A 4. B 1. C 3. D 2.
Câu 139. Cho hàm số y = f(x) có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 21
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
11
−2−2
+∞+∞
Số nghiệm của phương trình 2f (x) + 3 = 0 là
A 4. B 3. C 2. D 1.
Câu 140. Tập hợp các giá trị thực của tham số m để hàm số y = −x
3
−6x
2
+(4m − 9) x+4
nghịch biến trên khoảng (−∞; −1) là
A (−∞; 0]. B
ï
−
3
4
; +∞
ã
. C
Å
−∞; −
3
4
ò
. D [0; +∞).
Câu 141.
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình
vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để
phương trình f(sin x) = m có nghiệm thuộc khoảng (0; π)
là
A [−1; 3). B (−1; 3). C (−1; 3). D [−1; 1).
O
x
y
−1
1
−1
3
1
Câu 142. Cho hàm số f(x) có bảng xét dấu của đạo hàm như sau
x
f
0
(x)
−∞
1 2 3 4
+∞
−
0
+
0
+
0
−
0
+
Hàm số y = 3f(x + 2) − x
3
+ 3x đồng biến trên khoảng nào dưới đây ?
A (1; +∞). B (−∞; −1). C (−1; 0). D (0; 2).
Câu 143. Cho hàm số f (x) = mx
4
+ nx
3
+ px
2
+ qx + r (m, n, p, q, r ∈ R).
Hàm số y = f
0
(x) có đồ thị như hình vẽ bên. Tập nghiệm của
phương trình f (x) = r có số phần tử là
A 4. B 3. C 1. D 2.
x
y
y = f
0
(x)
O
3
5
4
−1
Câu 144. Cho hàm số có bảng biến thiên như sau:
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞+∞
11
33
11
+∞+∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 22
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A (−2; 0). B (2; +∞). C (0; 2). D (0; +∞).
Câu 145.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình vẽ bên?
A y = x
3
− 3x
2
+ 3. B y = −x
3
+ 3x
2
+ 3.
C y = x
4
− 2x
2
+ 3. D y = −x
4
+ 2x
2
+ 3.
x
y
O
Câu 146. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
2
+∞
−
0
+
0
−
+∞+∞
−3−3
11
−∞−∞
Hàm số đã cho đạt cực tiểu tại
A x = 2. B x = 1. C x = −1. D x = −3.
Câu 147. Cho hàm số f(x) có bảng biến thiên như sau:
x
−∞
−2
0 2
+∞
f
0
(x)
+
0
−
0
+
0
−
3 3
f(x)
−∞
−1
−∞
Số nghiệm thực của phương trình 2f(x) − 3 = 0 là
A 2. B 1. C 4. D 3.
Câu 148. Giá trị lớn nhất của hàm số f(x) = x
3
− 3x + 2 trên đoạn [−3; 3] là
A −16. B 20. C 0. D 4.
Câu 149. Cho hàm số f(x) có đạo hàm f
0
(x) = x(x + 2)
2
, ∀x ∈ R. Số điểm cực trị của
hàm số đã cho là
A 0. B 3. C 2. D 1.
Câu 150. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
−∞
0 1
+∞
y
0
− −
0
+
y
2
−4
+∞
−2
+∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 23
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A 4. B 1. C 3. D 2.
Câu 151. Cho hàm số f(x), bảng xét dấu của f
0
(x) như sau
x
f
0
−∞
−3 −1
1
+∞
−
0
+
0
−
0
+
Hàm số y = f(3 − 2x) nghịch biến trên khoảng nào dưới đây?
A (4; +∞). B (−2; 1). C (2; 4). D (1; 2).
Câu 152.
Cho hàm số y = f(x), hàm số y = f
0
(x) liên tục trên R và có đồ thị
như hình vẽ bên. Bất phương trình f(x) < x + m (m là tham số thực)
nghiệm đúng với mọi x ∈ (0; 2) khi và chỉ khi
A m ≥ f(2) − 2. B m ≥ f(0).
C m > f(2) − 2. D m > f(0).
O
x
y
1
2
y = f
0
(x)
Câu 153.
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên.
Số nghiệm thực của phương trình |f(x
3
−3x)| =
4
3
là
A 3. B 8. C 7. D 4.
x
y
O
−2
2
2
−1
Câu 154. Cho hàm số y = f(x), bảng biến thiên của hàm số f
0
(x) như sau:
x
f
0
(x)
−∞
−1
0 1
+∞
+∞
−3
2
−1
+∞
Số điểm cực trị của hàm số y = f(x
2
− 2x) là
A 9. B 3. C 7. D 5.
Câu 155. Cho hai hàm số y =
x − 3
x − 2
+
x − 2
x − 1
+
x − 1
x
+
x
x + 1
và y = |x + 2|−x + m (m là
tham số thực) có đồ thị lần lượt là (C
1
) và (C
2
). Tập hợp tất cả các giá trị của m để (C
1
)
và (C
2
) cắt nhau tại đúng bốn điểm phân biệt là
A (−∞; 2]. B [2; +∞). C (−∞; 2). D (2; +∞).
Câu 156.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 24
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Đồ thị của hàm số nào dưới đây có dạng như đường cong
trong hình vẽ bên
A y = −x
4
+ 2x
2
+ 1. B y = −x
3
+ 3x + 1.
C y = x
3
− 3x + 1. D y = x
4
− 2x
2
+ 1.
x
y
O
Câu 157. Cho hàm số f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞+∞
11
33
11
+∞+∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A (0; +∞). B (0; 2). C
(−2; 0). D (−∞; −2).
Câu 158. Cho hàm số f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
1 3
+∞
−
0
+
0
−
+∞+∞
−2−2
22
−∞−∞
Hàm số đạt cực đại tại
A x = 2. B x = −2. C x = 3. D x = 1.
Câu 159. Giá trị nhỏ nhất của hàm số f(x) = x
3
− 3x + 2 trên đoạn [−3; 3] bằng
A 20. B 4. C 0. D −16.
Câu 160. Cho hàm số y = f(x) có đạo hàm f
0
(x) = x(x −2)
2
, ∀x ∈ R. Số điểm cực trị của
hàm số đã cho là
A 2. B 1. C 0. D 3.
Câu 161. Cho hàm số f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
22
−1−1
+∞+∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 25
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Số nghiệm thực của phương trình 3f(x) − 5 = 0 là
A 2. B 3. C 4. D 0.
Câu 162. Cho hàm số f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
0 1
+∞
− −
0
+
00
−∞
2
−2−2
+∞+∞
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A 3. B 1. C 2. D 4.
Câu 163. Cho hàm số f(x) có bảng dấu f
0
(x) như sau
x
f
0
(x)
−∞
−3 −1
1
+∞
−
0
+
0
−
0
+
Hàm số y = f(5 − 2x) nghịch biến trên khoảng nào dưới đây?
A (2; 3). B (0; 2). C (3; 5). D (5; +∞).
Câu 164.
Cho hàm số f(x), hàm số y = f
0
(x) liên tục trên R và có đồ thị
như hình vẽ. Bất phương trình f(x) > x + m (m là tham số thực)
nghiệm đúng với mọi x ∈ (0; 2) khi và chỉ khi
A m ≤ f(2) − 2. B m < f(2) − 2.
C m ≤ f(0). D m < f(0).
x
y
O
2
1
Câu 165.
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. Số
nghiệm thực của phương trình |f (x
3
− 3x)| =
1
2
là
A 6. B 10. C 12. D 3.
x
y
O
2
−2
−1
2
Câu 166. Cho hàm số f(x), bảng biến thiên của hàm số f
0
(x) như hình vẽ bên dưới
x
f
0
(x)
−∞
−1
0 1
+∞
+∞+∞
−3−3
22
−1−1
+∞
+∞
Số điểm cực trị của hàm số y = f(x
2
+ 2x) là
A 3. B 9. C 5. D 7.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 26
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 167. Cho hai hàm số y =
x
x + 1
+
x + 1
x + 2
+
x + 2
x + 3
+
x + 3
x + 4
và y = |x + 1|−x + m (m là
tham số thực) có đồ thị lần lượt là (C
1
) và (C
2
). Tập hợp tất cả các giá trị của m để (C
1
)
và (C
2
) cắt nhau tại đúng 4 điểm phân biệt là
A (3; +∞). B (−∞; 3]. C (−∞; 3). D [3; +∞).
Câu 168.
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình
vẽ bên?
A y = x
3
− 3x
2
− 2. B y = x
4
− 2x
2
− 2.
C y = −x
3
+ 3x
2
− 2. D y = −x
4
+ 2x
2
− 2.
x
y
O
Câu 169. Cho hàm số f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
1 2
+∞
+
0
−
0
+
−∞−∞
33
−2−2
+∞+∞
Hàm số đạt cực đại tại
A x = 2. B x = −2. C x = 3. D x = 1.
Câu 170. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
00
33
00
+∞+∞
Hàm số đã cho đồng biến trên khoảng nào sau đây ?
A (−1; 0). B (−1; +∞). C (−∞; −1). D (0; 1).
Câu 171. Cho hàm số f(x) bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
2
+∞
−
0
+
0
−
+∞+∞
−1−1
22
−∞−∞
Số nghiệm thực của phương trình 2f(x) − 3 = 0 là
A 1. B 2. C 3. D 0.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 27
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 172. Giá trị lớn nhất của hàm số f(x) = x
3
− 3x trên đoạn [−3; 3] bằng
A 18. B 2. C −18. D −2.
Câu 173. Cho hàm số f (x) có đạo hàm f
0
(x) = x(x − 1)
2
, ∀x ∈ R. Số điểm cực trị của
hàm số đã cho là
A 2. B 0. C 1. D 3.
Câu 174. Cho hàm số y = f(x) có báng biến thiên như sau:
x
y
0
y
−∞
0 3
+∞
− +
0
−
11
−∞
2
−3−3
33
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A 1. B 2. C 3. D 4.
Câu 175. Cho hàm số f(x), bảng xét dấu của f
0
(x) như sau:
x
f
0
(x)
−∞
−3 −1
1
+∞
−
0
+
0
−
0
+
Hàm số y = f(3 − 2x) đồng biến trên khoảng nào dưới đây?
A (3; 4). B (2; 3). C (−∞; −3). D (0; 2).
Câu 176.
Cho hàm số y = f(x), hàm số y = f
0
(x) liên tục trên R và có
đồ thị như hình vẽ bên. Bất phương trình f(x) < 2x + m (m
là tham số thực) nghiệm đúng với mọi x ∈ (0; 2) khi và chỉ khi
x
y
O
y = f (x)
−1 1 2
2
A m > f(0). B m > f(2) − 4. C m ≥ f(0). D m ≥ f(2) − 4.
Câu 177.
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ
dưới đây. Số nghiệm thực của phương trình |f(x
3
−
3x)| =
3
2
là
A 8. B 4. C 7. D 3.
x
y
O
2
2
−2
−1
Câu 178. Cho hàm số f(x), bảng biến thiên của hàm số f
0
(x) như sau:
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 28
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
x
f
0
(x)
−∞
−1
0 1
+∞
+∞+∞
−3−3
22
−1−1
+∞+∞
Số cực trị của hàm số y = f(4x
2
− 4x) là
A 9. B 5. C 7. D 3.
Câu 179. Cho hai hàm số y =
x − 1
x
+
x
x + 1
+
x + 1
x + 2
+
x + 2
x + 3
và y = |x + 2| − x − m (m
là tham số thực) có đồ thị lần lượt là (C
1
), (C
2
). Tập hợp tất cả các giá trị của m để (C
1
)
và (C
2
) cắt nhau tại đúng bốn điểm phân biệt là
A [−2; +∞). B (−∞; −2). C (−2; +∞). D (−∞; −2].
Câu 180.
Đồ thị hàm số nào dưới đây có dạng như đường cong trong
hình vẽ bên?
A y = 2x
3
− 3x + 1. B y = −2x
4
+ 4x
2
+ 1.
C y = 2x
4
− 4x
2
+ 1. D y = −2x
3
+ 3x + 1.
x
y
O
Câu 181. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
00
33
00
+∞+∞
Hỏi hàm số nghịch biến trên khoảng nào dưới đây?
A (0; 1). B (1; +∞). C (−1; 0). D (0; +∞).
Câu 182. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
1 3
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
Hàm số đã cho đạt cực tiểu tại
A x = −2. B x = 1. C x = 3. D x = 2.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 29
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 183. Giá trị nhỏ nhất của hàm số f(x) = x
3
− 3x trên đoạn [−3; 3] bằng
A 18. B −18. C −2. D 2.
Câu 184. Cho hàm số y = f (x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
0 3
+∞
− −
0
+
00
−4
+∞
−3−3
33
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A 2. B 1. C 3. D 4.
Câu 185. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
2
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
Số nghiệm thực của phương trình 2f(x) + 3 = 0 là
A 3. B 1. C 2. D 0.
Câu 186. Cho hàm số f(x) có đạo hàm f
0
(x) = x(x + 1)
2
, ∀x ∈ R. Số điểm cực trị của
hàm số đã cho là
A
0. B 1. C 2. D 3.
Câu 187. Cho hàm số f(x), bảng xét dấu của f
0
(x) như sau:
x
f
0
(x)
−∞
−3 −1
1
+∞
−
0
+
0
−
0
+
Hàm số y = f(5 − 2x) đồng biến trên khoảng nào dưới đây?
A (−∞; −3). B (4; 5). C (3; 4). D (1; 3).
Câu 188.
Cho hàm số f(x), hàm số y = f
0
(x) liên tục trên
R và có đồ thị như hình vẽ bên. Bất phương trình
f(x) > 2x + m (m là tham số thực) nghiệm đúng với
mọi x ∈ (0; 2) khi và chỉ khi
x
y
O
y = f
0
(x)
2
2
A m ≤ f(2) − 4. B m ≤ f(0). C m < f(0). D m < f(2) − 4.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 30
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 189.
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ bên. Số nghiệm
thực của phương trình |f(x
3
− 3x)| =
2
3
là
A 6. B 10. C 3. D 9.
O
x
y
2
2
−2
−1
Câu 190. Cho hai hàm số y =
x − 2
x − 1
+
x − 1
x
+
x
x + 1
+
x + 1
x + 2
và y = |x + 1|−x −m (m là
tham số thực) có đồ thị lần lượt là (C
1
) và (C
2
). Tập hợp tất cả các giá trị của m để (C
1
)
và (C
2
) cắt nhau tại đúng bốn điểm phân biệt là
A (−3; +∞). B (−∞; −3). C [−3; +∞). D (−∞; −3].
Câu 191. Cho hàm số f(x), bảng biến thiên của hàm số f
0
(x) như sau:
x
f
0
(x)
−∞
−1
0 1
+∞
+∞+∞
−3−3
22
−1−1
+∞+∞
Số điểm cực trị của hàm số y = f(4x
2
+ 4x) là
A 5. B 9. C 7. D 3.
Câu 192. Cho hàm số f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
22
11
22
−∞−∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây ?
A (1; +∞). B (−1; 0). C (−1 ; 1). D (0 ; 1).
Câu 193. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
0 3
+∞
+
0
−
0
+
−∞−∞
22
−4−4
+∞+∞
Giá trị cực tiểu của hàm số đã cho bằng
A 2. B 3. C 0. D −4.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 31
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 194. Đồ thị của hàm số nào sau đây có dạng như hình cong
trong hình bên?
A y = −x
4
+ 2x
2
. B y = x
4
− 2x
2
.
C y = x
3
− 3x
2
. D y = −x
3
+ 3x
2
.
x
y
O
Câu 195. Cho hàm số f(x), bảng xét dấu của f
0
(x) như sau
x
f
0
(x)
−∞
−1
0 1
+∞
+
0
−
0
−
0
+
Số điểm cực trị của hàm số đã cho là
A 0. B 2. C 1. D 3.
Câu 196. Giá trị lớn nhất của hàm số f(x) = −x
4
+ 12x
2
+ 1 trên đoạn [−1 ; 2] bằng
A 1. B 37. C 33. D 12.
Câu 197. Cho hàm số f(x) có bảng biến thiên như sau
x
y
0
y
−∞
2 3
+∞
+
0
−
0
+
−∞−∞
11
00
+∞+∞
Số nghiệm thực của phương trình 3f(x) − 2 = 0là
A 2. B 0. C 3. D 1.
Câu 198. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =
5x
2
− 4x − 1
x
2
− 1
là
A
1. B 0. C 2. D 3.
Câu 199. Cho hàm số f(x) =
mx − 4
x − m
( m là tham số thực). Có bao nhiêu giá trị nguyên
của m để hàm số đồng biến trên khoảng (0; +∞)?
A 5. B 4. C 3. D 2.
Câu 200. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất
của hàm số f(x) = |x
3
− 3x + m| trên đoạn [0; 3] bằng 16. Tổng tất cả các phần tử của S
bằng
A −16. B 16. C −12. D −2.
Câu 201. Cho hàm số f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
−1−1
−2−2
+∞+∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 32
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Số nghiệm thuộc đoạn [−π ; 2π] của phương trình 2f (sin x) + 3 = 0 là
A 4. B 6. C 3. D 8.
Câu 202. Cho hàm số bậc bốn y = f(x) có đồ thị như hình
bên . Số điểm cực trị của hàm số g(x) = f (x
3
+ 3x
2
) là
A 5.
B 3.
C 7.
D 11.
x
y
O
4
Câu 203. Cho hàm số f(x). Hàm số y = f
0
(x) có đồ thị
như hình bên. Hàm số g(x) = f (1 − 2x) + x
2
−x nghịch
biến trên khoảng nào dưới đây?
A
Å
1;
3
2
ã
. B
Å
0;
1
2
ã
.
C (−2; −1). D (2; 3).
x
y
O
4
−2
1
−2
Câu 204. Cho hàm số f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
22
−1−1
22
−∞−∞
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A (−∞; −1). B (0; 1). C (−1; 0). D (−∞; 0).
Câu 205. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
2
+∞
+
0
−
0
+
−∞−∞
11
−2−2
+∞+∞
Hàm số đã cho đạt cực đại tại
A x = −2. B x = 2. C x = 1. D x = −1.
Câu 206.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 33
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A y = x
3
− 3x. B y = −x
3
+ 3x.
C y = x
4
− 2x
2
. D y = −x
4
+ 2x
2
.
x
y
O
Câu 207. Tiệm cận ngang của đồ thị hàm số y =
x − 1
x + 1
là
A y = −2. B y = 1. C x = −1. D x = 2.
Câu 208.
Cho hàm số bậc bốn y = f(x) có đồ thị trong hình bên. Số
nghiệm của phương trình f(x) = −1 là
A 3. B 1. C 1. D 4.
x
y
O
−2
2
−3
1
Câu 209. Cho hàm số f(x) có bảng xét dấu của f
0
(x) như sau
x
f
0
(x)
−∞
−2
0 2
+∞
+
0
−
0
+
0
+
Số điểm cực trị của hàm số đã cho là
A 3. B 0. C 2. D 1.
Câu 210. Giá trị nhỏ nhất của hàm số f(x) = x
4
− 10x
2
+ 2 trên đoạn [−1; 2] bằng
A 2. B −23. C −22. D −7.
Câu 211. Số giao điểm của đồ thị hàm số y = x
3
− 3x + 1 và trục hoành là
A 3. B 0. C 2. D
1.
Câu 212. Có bao nhiêu giá trị nguyên của m để hàm số f(x) =
1
3
x
3
+ mx
2
+ 4x + 3 đồng
biến trên R?
A 5. B 4. C 3. D 2.
Câu 213. Cho hàm số f(x) =
ax + 1
bx + c
(a, b, c ∈ R) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
2
+∞
+ +
11
+∞
−∞
11
Trong các số a, b và c có bao nhiêu số dương?
A 2. B 3. C 1. D 0.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 34
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 214. Cho hàm số y = f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
22
00
22
−∞−∞
Số nghiệm thuộc đoạn
ï
0;
5π
2
ò
của phương trình f(sin x) = 1 là
A 7. B 4. C 5. D 6.
Câu 215. Cho hàm số y =
x + m
x + 1
(m là tham số thực). Gọi S là tập hợp tất cả các giá trị
của m sao cho max
[0;1]
|f(x)| + min
[0;1]
|f(x)| = 2. Số phần tử của S là
A 6. B 2. C 1. D 4.
Câu 216. Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ?
x
y
O
A y = x
3
− 3x
2
+ 1. B y = −x
3
+ 3x
2
+ 1.
C y = −x
4
+ 2x
2
+ 1. D y = x
4
− 2x
2
+ 1.
Câu 217. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
0 3
+∞
+
0
−
0
+
−∞−∞
22
−5−5
+∞+∞
Giá trị cực tiểu của hàm số đã cho bằng
A 3. B −5. C 0. D 2.
Câu 218. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
44
−1−1
+∞+∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 35
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A (−∞; −1). B (0; 1). C (−1; 1). D (−1; 0).
Câu 219. Tiệm cận ngang của đồ thị hàm số y =
4x + 1
x − 1
là
A y =
1
4
. B y = 4. C y = 1. D y = −1.
Câu 220.
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong như hình
vẽ bên. Số nghiệm thực của phương trình f(x) = −1 là
A 3. B 1. C 0. D 2.
x
y
0
−1
2
1
−2
Câu 221. Số giao điểm của đồ thị hàm số y = x
3
+ 3x
2
và đồ thị hàm số y = 3x
2
+ 3x
là
A 3. B 1. C 2. D 0.
Câu 222. Cho hàm số f(x) liên tục trên R và có bảng xét dấu của f
0
(x) như sau:
x
f
0
(x)
−∞
−1
0 1 2
+∞
+
0
−
0
+ −
0
−
Số điểm cực đại của hàm số đã cho là
A 4. B 1. C 2. D 3.
Câu 223. Giá trị nhỏ nhất của của hàm số f(x) = x
3
− 24x trên đoạn [2; 19] bằng
A 32
√
2. B −40. C −32
√
2. D −45.
Câu 224. Tập hợp tất cả các giá trị thực của tham số m để hàm số y =
x + 4
x + m
đồng biến
trên khoảng (−∞; −7) là
A [4; 7). B (4; 7]. C (4; 7). D (4; +∞).
Câu 225. Cho hàm số bậc bốn f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
33
−2−2
+∞+∞
Số điểm cực trị của hàm số g(x) = x
4
[f(x + 1)]
2
là
A 11. B 9. C 7. D 5.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 36
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 226.
Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có đồ thị là
đường cong trong hình bên. Có bao nhiêu số dương trong các số a,
b, c, d?
A 4. B 1. C 2. D 3.
x
y
O
Câu 227. Xét các số thực không âm x và y thỏa mãn 2x + y ·4
x+y−1
≥ 3. Giá trị nhỏ nhất
của biểu thức P = x
2
+ y
2
+ 4x + 6y bằng
A
33
4
. B
65
8
. C
49
8
. D
57
8
.
Câu 228.
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong
trong hình bên. Số nghiệm thực phân biệt của phương trình
f (x
3
f(x)) + 1 = 0 là
A 8. B 5. C 6. D 4.
x
y
O
−1
Câu 229. Tiệm cận ngang của đồ thị hàm số y =
5x + 1
x − 1
là
A y = 1. B y =
1
5
. C y = −1. D y = 5.
Câu 230.
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong
hình bên. Số nghiệm thực của phương trình f(x) = 1 là
A 0. B 3. C 1. D 2.
O
x
y
−1
−1
1
3
Câu 231. Cho hàm số f (x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
44
11
44
−∞−∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A (1; +∞). B (−1; 1). C (0; 1). D (−1; 0).
Câu 232. Cho hàm số f (x) có bảng biến thiên sau
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 37
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
x
f
0
(x)
f(x)
−∞
−2
3
+∞
−
0
+
0
−
+∞+∞
−3−3
22
−∞−∞
Giá trị cực đại của hàm số đã cho bằng
A 3. B 2. C −2. D −3.
Câu 233.
Đồ thị hàm số nào có dạng như đường cong trong hình bên?
A y = −x
4
+ 2x
2
. B y = −x
3
+ 3x.
C y = x
4
− 2x
2
. D y = x
3
− 3x.
O
x
y
Câu 234. Giá trị nhỏ nhất của hàm số f (x) = x
3
− 21x trên đoạn [2; 19] bằng
A −36. B −14
√
7. C 14
√
7. D −34.
Câu 235. Cho hàm số f (x) liên tục trên và có bảng xét dấu của f
0
(x) như sau
x
f
0
(x)
−∞
−1
0 1 2
+∞
−
0
+
0
− +
0
+
Số điểm cực tiểu của hàm số đã cho là
A 1. B 2. C 3. D 4.
Câu 236. Số giao điểm của đồ thị hàm số y = x
3
− x
2
và đồ thị hàm số y = −x
2
+ 5x
là
A 2. B 3. C 1. D 0.
Câu 237. Tập hợp tất cả các giá trị thực của tham số m để hàm số y =
x + 5
x + m
đồng biến
trên khoảng (−∞; −8) là
A (5; +∞). B (5; 8]. C [5; 8). D (5; 8).
Câu 238. Cho hàm số bậc bốn f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
33
−1−1
33
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 38
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Số điểm cực trị của hàm số g(x) = x
2
[f(x − 1)]
4
là
A 7. B 8. C 5. D 9.
Câu 239.
Cho hàm số y = ax
3
+ bx
2
+ cx + d, (a, b, c, d ∈ R) có đồ thị là
đường cong trong hình vẽ. Có bao nhiêu số dương trong các
số a, b, c, d?
A 4. B 3. C 1. D 2.
x
y
O
Câu 240.
Cho hàm số bậc ba y = f(x) có đồ thị là đường
cong trong hình bên. Số nghiệm thực phân biệt của
phương trình f (x
3
f(x)) + 1 = 0 là
A 6. B 4. C 5. D 8.
x
y
O
−1
Câu 241. Cho hàm số f(x) có bảng biến thiên như sau.
x
y
0
y
−∞
−2
2
+∞
−
0
+
0
−
+∞+∞
−1−1
33
−∞−∞
Giá trị cực tiểu của hàm số bằng
A 2. B −2. C 3. D −1.
Câu 242.
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình
bên. Số nghiệm thực của phương trình f (x) = 1 là
A 1. B 0. C 2. D 3.
x
y
−1
−2
2
1
Câu 243. Cho hàm số f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
−2
0 2
+∞
+
0
−
0
+
0
−
−∞−∞
33
22
33
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 39
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A (−2; 2). B (0; 2). C (−2; 0). D (2; +∞).
Câu 244. Tiệm cận ngang của đồ thị hàm số y =
2x + 1
x − 1
là:
A y =
1
2
. B y = −1. C y = 1. D y = 2.
Câu 245.
Đồ thị của hàm số nào dưới đây có dạng như đường cong như hình
bên
A y = −x
4
+ 2x
2
. B y = x
3
− 3x
2
.
C y = x
4
− 2x
2
. D y = −x
3
+ 3x
2
.
x
y
Câu 246. Giá trị nhỏ nhất của hàm số f(x) = x
3
− 30x trên đoạn [2; 19] bằng
A 20
√
10. B −63. C −20
√
10. D −52.
Câu 247. Cho hàm số f(x) liên tục trên và có bảng xét dấu của f
0
(x) như sau:
x
f
0
(x
−∞
−2
1 2 3
+∞
−
0
+
0
−
0
+
0
+
Số điểm cực trị của hàm số đã cho là
A 2. B 4. C 3. D 1.
Câu 248. Số giao điêm của đồ thị hàm số y = x
3
+ x
2
và đồ thị hàm số y = x
2
+ 5x.
A 3. B 0. C 1. D 2.
Câu 249. Tập hợp tất cả các giá trị thực của tham số m để hàm số y =
x + 2
x + m
đồng biến
trên khoảng(−∞; −5) là
A (2; 5]. B [2; 5). C (2; +∞). D (2; 5).
Câu 250. Cho hàm số bậc bốn f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
33
−1−1
+∞+∞
Số điểm cực trị của hàm số g(x) = x
4
[f(x − 1)]
2
là
A 7. B 5. C 9. D 11.
Ta có : f(x) = 4x
4
− 8x
2
+ 3 ⇒ f
0
(x) = 16x(x
2
− 1)
Ta có g
0
(x) = 2x
3
.f(x − 1).[2f(x − 1) + x.f
0
(x − 1)]
g
0
(x) = 0 ⇔
x
3
= 0
f(x − 1) = 0
2f(x − 1) + x.f
0
(x − 1) = 0
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 40
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Phương trình x
3
= 0 có x = 0 (nghiệm bội ba).
Phương trình f(x−1) = 0 có cùng số nghiệm với phương trình f(x) = 0 nên (2) có 4 nghiệm
đơn.
Phương trình 2f (x − 1) + x · f
0
(x − 1) = 0 có cùng số nghiệm với phương trình :
2f(x) + (x + 1) · f
0
(x) = 0 ⇔ 2(4x
4
− 8x
2
+ 3) + 16x(x + 1)(x
2
− 1) = 0
⇔ 24x
4
+ 16x
3
− 32x
2
− 16x + 6 = 0
có 4 nghiệm phân biệt.
Dễ thấy 9 nghiệm trên phân biệt nên hàm số g(x) = 0 có tất cả 9 điểm cực trị.
Câu 251. Xét các số thực không âm x và y thoản mãn 2x + y.4
x+y−1
≥ 3 Giá trị nhỏ nhất
của biểu thức P = x
2
+ y
2
+ 2x + 4y bằng
A
33
8
. B
9
8
. C
21
4
. D
41
8
.
Câu 252.
Cho hàm số y = ax
3
+ bx
2
+ cx + d có đồ thị là đường cong
trong hình bên. Có bao nhiêu số dương trong các a, b, c,
d?
A 4. B 2. C 1. D 3.
x
y
O
Câu 253.
Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong
trong hình bên. Số nghiệm thực phân biệt của phương
trình f (x
2
f (x)) + 2 = 0 là
A 8. B 12. C 6. D 9.
x
y
O
−2
Câu 254.
Cho đồ thị hàm số bậc ba y = f(x) có đồ thị là đường cong trong
hình bên. Số nghiệm thực của phương trình f(x) = 2 là
A 0. B 3. C 1. D 2.
x
y
O
−1
1
−1
3
Câu 255. Tiệm cận ngang của đồ thị hàm số y =
3x + 1
x − 1
là
A y =
1
3
. B y = 3. C y = −1. D y = 1.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 41
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 256.
Đồ thị của hàm số nào dưới đây có dạng như đường cong
trong hình bên?
x
y
O
A y = x
4
− 2x
2
+ 1. B y = −x
3
+ 3x
2
+ 1.
C y = x
3
− 3x
2
+ 1. D y = −x
4
+ 2x
2
+ 1.
Câu 257. Cho hàm số y = f (x) có bảng biến thiên như sau
x
y
0
y
−∞
−3
0 3
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
11
−1−1
+∞+∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A (−3; 0). B (−3; 3). C (0; 3). D (−∞; −3).
Câu 258. Cho hàm số f (x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
3
+∞
+
0
−
0
+
−∞−∞
22
−3−3
+∞+∞
Giá trị cực đại của hàm số đã cho bằng
A 3. B −3. C −1. D 2.
Câu 259. Giá trị nhỏ nhất của hàm số f (x) = x
3
− 33x trên đoạn [2; 19] bằng
A −72. B −22
√
11. C −58. D 22
√
11.
Câu 260. Cho hàm số f (x) liên tục trên R và có bảng xét dấu f
0
(x) như sau
x
f
0
(x)
−∞
−2
1 2 3
+∞
+
0
−
0
+ −
0
−
Số điểm cực đại của hàm số đã cho là
A 3. B 1. C 2. D 4.
Câu 261. Số giao điểm của đồ thị hàm số y = x
3
− x
2
và đồ thị hàm số y = −x
2
+ 3x
là
A 1. B 0. C 2. D 3.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 42
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 262. Tập hợp tất cả các giá trị thực của tham số m để hàm số y =
x + 3
x + m
đồng biến
trên khoảng (−∞, −6) là
A (3; 6]. B (3; 6). C (3; +∞). D [3; 6).
Câu 263. Cho hàm số bậc bốn f (x) có bảng biến thiên sau:
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
33
−2−2
33
−∞−∞
Số điểm cực trị của hàm số g (x) = x
2
[f (x + 1)]
4
là
A 7. B 8. C 5. . D 9.
Câu 264.
Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c,) có đồ thị là đường
cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c,
d?
A 4. B 2. C 1. D 3.
x
y
O
Câu 265.
Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong
hình bên. Số nghiệm thực của phương trình f (x
2
f(x))−2 =
0 là
A 6. B 12. C 8. D 9.
x
y
O
2
Câu 266. Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong
hình bên. Số nghiệm thực của phương trình f(x) = −
1
2
là
A 3. B 4. C 2. D 1.
x
y
O
−1
1
−1
−2
Câu 267. Cho hàm số y = f(x) có đồ thị là đường cong
trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới
đây?
A (1; +∞). B (−1; 0). C (0; 1). D (−∞; 0).
x
y
O
1−1
1
2
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 43
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 268. Cho hàm số f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
3
+∞
−
0
+
0
−
+∞+∞
−3−3
22
−∞−∞
Điểm cực đại của hàm số đã cho là
A x = 3. B x = −1. C x = 2. D x = −3.
Câu 269. Tiệm cận đứng của đồ thị hàm số y =
2x + 2
x − 1
là
A x = 2. B x = −2. C x = 1. D x = −1.
Câu 270.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A y = x
4
− 2x
2
− 2. B y = −x
3
+ 3x
2
− 2.
C y = x
3
− 3x
2
− 2. D y = −x
4
+ 2x
2
− 2.
x
y
O
Câu 271. Số giao điểm của đồ thị hàm số y = −x
3
+ 6x với trục hoành là
A 2. B 3. C 1. D 0.
Câu 272. Giá trị nhỏ nhất của hàm số f(x) = x
4
− 10x
2
− 4 trên đoạn [0; 9] bằng
A −28. B −4. C −13. D −29.
Câu 273. Cho hàm số f (x) có đạo hàm f
0
(x) = x(x − 1)(x + 4)
3
, ∀x ∈ R. Số điểm cực đại
của hàm số đã cho là
A 3. B 4. C 2. D 1.
Câu 274. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x
3
−3x
2
+ (4 −m)x
đồng biến trên khoảng (2; +∞) là
A (−∞; 1]. B (−∞; 4]. C (−∞; 1). D (−∞; 4).
Câu 275. Cho hàm số f(x) = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có bảng biến thiên như
sau
x
f
0
(x)
f(x)
−∞
0 4
+∞
+
0
−
0
+
−∞−∞
33
−5−5
+∞+∞
Có bao nhiêu số dương trong các số a, b, c, d?
A 2. B 3. C 1. D 4.
Câu 276. Cho hàm số f(x) có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 44
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
x
−∞
−4 −2
0
+∞
f
0
(x)
−
0
+
0
−
0
+
f(x)
+∞
−2
−3
2
+∞
Có bao nhiêu giá trị nguyên của m để phương trình 5f (x
2
− 4x) = m có ít nhất 3 nghiệm
thực phân biệt thuộc khoảng (0; +∞)?
A 24. B 21. C 25. D 20.
Câu 277.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình
bên?
A y = −x
4
+ 2x
2
− 1. B y = x
4
− 2x
2
− 1.
C y = x
3
− 3x
2
− 1. D y = −x
3
+ 3x
2
− 1.
x
y
O
Câu 278. Tiệm cận đứng của đồ thị hàm số y =
x − 1
x − 3
là
A x = −3. B x = −1. C x = 1. D x = 3.
Câu 279.
Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình
bên. Số nghiệm thực của phương trình f(x) = −
3
2
là
A 4. B 1. C 3. D 2.
x
y
O
−1
1
−1
−2
Câu 280. Cho hàm số f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−2
1
+∞
−
0
+
0
−
+∞+∞
−1−1
33
−∞−∞
Điểm cực đại của hàm số đã cho là
A x = 3. B x = −1. C x = 1. D x = −2.
Câu 281.
Cho hàm số y = f(x) có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A (−1; 0). B (−∞; −1). C (0; 1). D (0; +∞).
x
y
−1
1
1
O
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 45
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 282. Cho hàm số f(x) có đạo hàm f
0
(x) = x(x −1)(x + 4)
3
, ∀x ∈ R. Số điểm cực tiểu
của hàm số đã cho là
A 2. B 3. C 4. D 1.
Câu 283. Giá trị nhỏ nhất của hàm số f(x) = x
4
− 12x
2
− 4 trên đoạn [0; 9] bằng
A −39. B −40. C −36. D −4.
Câu 284. Số giao điểm của đồ thị hàm số y = −x
3
+ 7x với trục hoành là
A 0. B 3. C 2. D 1.
Câu 285. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x
3
−3x
2
+ (5 −m)x
đồng biến trên khoảng (2; +∞) là
A (−∞; 2). B (−∞; 5). C (−∞; 5]. D (−∞; 2].
Câu 286. Cho hàm số f(x) = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có bảng biến thiên như sau
x
y
0
y
−∞
−2
0
+∞
+
0
−
0
+
−∞−∞
22
11
+∞+∞
Có bao nhiêu số dương trong các số a, b, c, d?
A 2. B 4. C 1. D 3.
Câu 287.
Cho hàm số f (x) có f (0) = 0. Biết y = f
0
(x) là hàm số
bậc bốn và có đồ thị là đường cong trong hình bên. Số
điểm cực trị của hàm số g(x) = |f(x
3
) + x| là
A 4. B 5. C 3. D 6.
x
y
O
y = f
0
(x)
Câu 288. Cho hàm số f(x) có bảng biến thiên như sau
x
−∞
−4 −2
0
+∞
f
0
(x)
−
0
+
0
−
0
+
f(x)
+∞
−2
−3
2
+∞
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6f (x
2
− 4x) = m có ít nhất 3
nghiệm thực phân biệt thuộc khoảng (0; +∞)?
A 25. B 30. C 29. D 24.
Câu 289. Tiệm cận đứng của đồ thị hàm số y =
2x − 2
x + 1
là
A x = −2. B x = 1. C x = −1. D x = 2.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 46
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 290. Cho hàm số f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−1
2
+∞
+
0
−
0
+
−∞−∞
33
−2−2
+∞+∞
Điểm cực đại của hàm số đã cho là
A x = 3. B x = 2. C x = −2. D x = −1.
Câu 291. Cho hàm số y = f(x) có đồ thị là đường cong như hình bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A (−1; 0). B (−∞; −1). C (0; +∞). D (0; 1).
x
y
O
−1
1
−1
Câu 292. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
A y = x
3
− 3x + 1. B y = x
4
− 2x
2
+ 1.
C y = −x
4
+ 2x
2
+ 1. D y = −x
3
+ 3x + 1.
x
y
O
Câu 293.
Cho hàm số bậc bốn có đồ thị là đường cong trong hình
bên. Số nghiệm thực của phương trình f(x) =
1
2
là
A 2. B 4. C 1. D 3.
x
y
O
1
2
−1 1
Câu 294. Số giao điểm của y = −x
3
+ 3x với trục hoành là
A 2. B 0. C 3. D 1.
Câu 295. Giá trị nhỏ nhất của hàm số f(x) = x
4
− 10x
2
− 2 trên đoạn [0; 9] bằng
A −2. B −11. C −26. D −27.
Câu 296. Cho hàm số f (x) có đạo hàm f
0
(x) = x(x + 1)(x −4)
3
, ∀x ∈ R. Số điểm cực đại
của hàm số đã cho là
A 2. B 3. C 4. D 1.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 47
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 297. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x
3
−3x
2
+ (2 −m)x
đồng biến trên khoảng (2; +∞) là
A (−∞; −1]. B (−∞; 2). C (−∞; −1). D (−∞; 2].
Câu 298. Cho hàm số f(x) = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có bảng biến thiên như
sau
x
f
0
(x)
f(x)
−∞
−2
0
+∞
+
0
−
0
+
−∞−∞
11
−1−1
+∞+∞
Có bao nhiêu số dương trong các số a, b, c, d?
A 3. B 4. C 2. D
1.
Câu 299.
Cho hàm số f(x) có f(0) = 0. Biết y = f
0
(x) là hàm số
bậc bốn và có đồ thị là đường cong trong hình bên. Số
điểm cực trị của hàm số g(x) = |f(x
4
) − x
2
| là
A 4. B 3. C 6. D 5.
x
y
O
y = f
0
(x)
Câu 300. Xét các số thực x, y thỏa mãn 2
x
2
+y
2
+1
≤ (x
2
+ y
2
−2x + 2)4
x
. Giá trị nhỏ nhất
của biểu thức P =
8x + 4
2x − y + 1
gần nhất với số nào dưới đây?
A
1. B 2. C 3. D 4.
Câu 301. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−4 −2
0
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
22
−3−3
+∞+∞
Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f (x
2
− 4x) = m có ít nhất 3
nghiệm thực phân biệt thuộc khoảng (0; +∞)?
A 15. B 12. C 14. D 13.
Câu 302. Tiệm cận đứng của đồ thị hàm số y =
x + 1
x + 3
là
A x = −1. B x = 1. C x = −3. D x = 3.
Câu 303.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 48
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Cho hàm số y = f(x) có đồ thị là đường cong trong hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A (1; +∞). B (0; 1). C (−1; 0). D (−∞; 0).
x
y
O
−1
1
−2
−1
Câu 304. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−2
3
+∞
+
0
−
0
+
−∞−∞
11
−3−3
+∞+∞
Điểm cực đại của hàm số đã cho là
A x = −2. B x = −3. C x = 1. D x = 3.
Câu 305.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong
hình bên?
A
y = x
4
+ 2x
2
. B y = −x
3
− 3x.
C y = x
3
− 3x. D y = −x
4
+ 2x
2
.
x
y
O
Câu 306.
Cho hàm số bậc bốn y = f(x) có đồ thị là đường cong trong hình bên. Số
nghiệm thực của phương trình f(x) =
1
2
là
A 4. B 2. C 3. D 1.
x
y
O
1−1
1
Câu 307. Số giao điểm của đồ thị hàm số y = −x
3
+ 5x với trục hoành là
A 3. B 2. C 0. D 1.
Câu 308. Giá trị nhỏ nhất của hàm số f(x) = x
4
− 12x
2
− 1 trên đoạn [0; 9] bằng
A −28. B −1. C −36. D −37.
Câu 309. Cho hàm số f(x) có đạo hàm f
0
(x) = x(x + 1)(x −4)
3
, ∀x ∈ R. Số điểm cực tiểu
của hàm số đã cho là
A 4. B 3. C 1. D 2.
Câu 310. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x
3
−3x
2
+ (1 −m)x
đồng biến trên khoảng (2; +∞) là
A (−∞; −2). B (−∞; 1). C (−∞; −2]. D (−∞; 1].
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 49
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 311.
Cho hàm số f(x) có f(0) = 0. Biết y = f
0
(x) là hàm số bậc bốn và
có đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số
g(x) = |f(x
4
) + x
2
| là
A 3. B 6. C 5. D 4.
x
y
O
Câu 312. Cho hàm số y = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R) có bảng biến thiên như sau:
x
y
0
y
−∞
0 4
+∞
+
0
−
0
+
−∞−∞
−1−1
−5−5
+∞+∞
Có bao nhiêu số dương trong các số a, b, c, d?
A 4. B 2. C 3. D 1.
Câu 313. Cho hàm số f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
+∞
−4
0
−2
−2
0
2
0
0
−3
+∞
+∞
− + − +
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4f (x
2
− 4x) = m có ít nhất 3
nghiệm thực phân biệt thuộc khoảng (0; +∞)?
A 16. B 19. C 20. D 17.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 50
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
PHẦN II
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC ĐỀ THI THỬ 2017-2020
Câu 1. Hàm số y = 2x
4
+ 1 đồng biến trên khoảng nào trong các khoảng dưới đây?
A (0; +∞). B
Å
−
1
2
; +∞
ã
. C
Å
−∞; −
1
2
ã
. D (−∞; 0).
Câu 2. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x
4
+2mx
2
+1
có ba điểm cực trị tạo thành tam giác vuông cân.
A m = −
3
√
3. B m = −1.
C m = −1; m =
3
√
3. D m = −
3
√
3; m = 1.
Câu 3. Cho hàm số y =
x − 2
x + 2
có đồ thị (C). Tìm tọa độ giao điểm I của hai đường tiệm
cận của đồ thị (C).
A I (−2; 2). B I (−2; −2). C I (2; 1). D I (−2; 1).
Câu 4. Xét hàm số y =
√
4 − 3x trên đoạn [−1; 1]. Mệnh đề nào sau đây đúng?
A Hàm số có cực trị trên khoảng (−1; 1).
B Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [−1; 1].
C Hàm số đồng biến trên đoạn [−1; 1].
D Hàm số đạt giá trị nhỏ nhất tại x = 1 và đạt giá trị lớn nhất tại x = −1.
Câu 5. Đồ thị của hàm số y = x
3
−3x
2
−9x + 1 có hai điểm cực trị A và B. Điểm nào dưới
đây thuộc đường thẳng AB ?
A M (1; −10). B N (−10; 1). C P (1; 0). D Q(0; −1).
Câu 6. Phát biểu nào sau đây là đúng?
A Hàm số y = f(x) đạt cực trị tại x
0
khi và chỉ khi x
0
là nghiệm của đạo hàm.
B Nếu f
0
(x
0
) = 0 và f
00
(x
0
) > 0 thì hàm số đạt cực đại tại x
0
.
C Nếu f
0
(x
0
) = 0 và f
00
(x
0
) = 0 thì x
0
không phải là cực trị của hàm số y = f(x) đã
cho.
D Nếu f
0
(x) đổi dấu khi x qua điểm x
0
và f(x) liên tục tại x
0
thì hàm số y = f(x) đạt
cực trị tại điểm x
0
.
Câu 7. Tìm tập giá trị T của hàm số y =
√
x − 3 +
√
5 − x
A T =
î
0;
√
2
ó
. B T = [3; 5]. C T =
î
√
2; 2
ó
. D T = (3; 5).
Câu 8. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau.
x
y
0
y
−∞
0 1
+∞
+ −
0
+
−∞−∞
00
−1−1
+∞+∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 51
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Tìm tất cả các giá trị thực của tham số m để phương trình f (|x|) = 2m + 1 có bốn nghiệm
phân biệt?
A −
1
2
≤ m ≤ 0. B −
1
2
< m < 0. C −1 < m < −
1
2
. D −1 ≤ m ≤ −
1
2
.
Câu 9.
Đường cong trong hình bên là đồ thị của một hàm số trong
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới
đây. Hỏi hàm số đó là hàm số nào ?
y
x
2
1
−2
−1
−1
3
1
O
A y = x
4
− x
2
+ 1. B y = −x
3
+ 3x + 1.
C y = x
3
− 3x + 1. D y = −x
2
+ x − 1.
Câu 10. Tìm giá trị lớn nhất của hàm số y = 1 − 2 cos x − cos
2
x .
A 2. B 3. C 0. D 5.
Câu 11. Tìm tất cả các giá trị thực của m đế đường thẳng d : y = −2x + m cắt đồ thị hàm
số (H) : y =
2x+3
x+2
tại hai điểm A, B phân biệt sao cho P = k
2018
1
+ k
2018
2
đạt giá trị nhỏ nhất
(với k
1
, k
2
là hệ số góc của tiếp tuyến tại A, B)
A m = −3. B m = −2. C m = 2. D m = 3.
Câu 12. Trong bốn hàm số sau:(1)y = sin 2x; (2)y = cos 4x; (3)y = tan 2x; (4)y = cot 3x có
mấy hàm số tuần hoàn với chu kỳ
π
2
?
A 0. B 2. C 3. D 1.
Câu 13.
Đường cong trong hình bên là đồ thị của một hàm số nào sau đây?
A y =
x + 2
x − 1
. B y =
x + 2
x − 2
.
C y =
x − 2
x − 1
. D y =
x − 2
x + 1
.
x
y
O
1 2
1
2
Câu 14. Đường cong y = x
3
−5x cắt đường thẳng y = −2x −2 lần lượt tại hai điểm phân
biệt A, B có hoành độ tăng dần. Tọa độ của
# »
AB là
A (3; −6). B (−3; 6). C (−3; −6). D (3; 6).
Câu 15. Cho hàm số y = f(x) có bảng biến thiên như bên dưới. Phát biểu nào đúng?
x
y
0
y
−∞
−2
0 2
+∞
+
0
−
0
+
0
−
−∞−∞
22
11
44
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 52
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
A Hàm số đạt cực đại tại x = 2. B Hàm số đạt cực đại tại x = 4.
C Hàm số có ba cực tiểu. D Hàm số có giá trị cực tiểu là 0.
Câu 16. Cho hàm số y = f(x) có đạo hàm f
0
(x) = x(x − 1)(x + 2)
3
, ∀x ∈ R. Số điểm cực
trị của hàm số đã cho là
A 3. B 5. C
1. D 2.
Câu 17. Số đường tiệm cận của đồ thị hàm số y =
1 − x
2x − 1
là
A 2. B 1. C 4. D 3.
Câu 18. Hàm số y = x
3
− 3x
2
+ 2 nghịch biến trên khoảng nào trong các khoảng sau
đây?
A (2; +∞). B (−∞; 0). C (−∞; +∞). D (0; 2).
Câu 19. Điểm nào trong các điểm sau đây không thuộc đồ thị hàm số y =
√
x + 3
x
2
+ 1
?
A N
Å
−2;
1
5
ã
. B Q(1; 1). C M(1; 2). D P
Ä
0;
√
3
ä
.
Câu 20. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau.
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
00
−1−1
+∞+∞
Tìm tất cả các giá trị của tham số m để phương trình f(x)−1 = m có đúng hai nghiệm.
A −2 < m < −1. B m > 0; m = −1.
C m = −2; m > −1. D m = −2; m ≥ −1.
Câu 21. Tập hợp tất cả các giá trị của tham số m để hàm số: y = −x
3
−6x
2
+(4m−9)x+4
nghịch biến trên khoảng (−∞; −1) là
A
ï
−
3
4
; +∞
ã
. B
Å
−∞; −
3
4
ò
. C (−∞; 0]. D [0; +∞).
Câu 22. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y =
|x
3
− 3x
2
+ 3m
2
− m
3
| có 5 điểm cực trị. Tìm số phần tử của S.
A 0. B 3. C 1. D 2.
Câu 23. Cho phương trình x
4
−3x
3
−(2m −1)x
2
−3x + 1 = 0. Điều kiện của m để phương
trình có bốn nghiệm phân biệt là m ∈
a
b
; +∞
. Trong đó a, b là các số nguyên dương và
a, b nguyên tố cùng nhau. Giá trị của biểu thức a + b là
A 12. B 9. C 10. D 11.
Câu 24.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 53
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số f (x) có đạo hàm liên tục trên R và có f(1) = 1,
f(−1) = −
1
3
. Đặt g(x) = f
2
(x) − 4f(x). Cho biết đồ thị của
y = f
0
(x) có dạng như hình vẽ dưới đây.
A Hàm số g(x) có giá trị lớn nhất và không có giá trị nhỏ
nhất trên R.
B Hàm số g(x) có giá trị nhỏ nhất và không có giá trị lớn
nhất trên R.
C Hàm số g(x) có giá trị lớn nhất và giá trị nhỏ nhất trên
R.
D Hàm số g(x) không có giá trị lớn nhất và không có giá
trị nhỏ nhất trên R.
x
y
O
-1 1
1
Câu 25. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
0 2
+∞
+
0
−
0
+
−∞−∞
33
11
+∞+∞
Hàm số đã cho đạt cực đại tại giá trị nào của x?
A 2. B 1. C 0. D 3.
Câu 26. Hàm số y = x
3
− 3x + 1 nghịch biến trên khoảng nào dưới đây?
A (0; 2). B (1; +∞). C (∞; −1). D (−1; 1).
Câu 27. Tìm giá trị lớn nhất của hàm số y = x
3
− 2x
2
− 4x + 5 trên đoạn [1; 3].
A −3. B 0. C 2. D 3.
Câu 28. Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = x
3
−mx
2
−(m−6)x+1
đồng biến trên khoảng (0; 4).
A (−∞; 6]. B (−∞; 3). C (−∞; 3]. D [3; 6].
Câu 29. Đồ thị hàm số y =
x +
√
x − 1
√
x
2
+ 1
có bao nhiêu tiệm cận ngang?
A 2. B 1. C 3. D 0.
Câu 30. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
0 2
+∞
− +
0
−
+∞+∞
−1 −∞
22
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 54
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Tìm tập hợp tất cả giá trị của tham số m để phương trình f(x) + m = 0 có ba nghiệm phân
biệt.
A (−2; 1). B [−1; 2). C (−1; 2). D (−2; 1].
Câu 31.
Một bức tường cao 2 m nằm song song với tòa nhà
và cách tòa nhà 2 m. Người ta muốn chế tạo một
cái thang bắc từ mặt đất bên ngoài bức tường, gác
qua bức tường và chạm vào tòa nhà (hình vẽ). Hỏi
chiều dài tối thiểu của thang là bao nhiêu mét?
A
5
√
13
3
m. B 4
√
2 m.
C 6 m. D 3
√
5 m.
2m
2m
Tòa nhà
Câu 32. Cho hàm số f (x) = x
3
−3x
2
+ m. Hỏi có bao nhiêu giá trị nguyên của m (m < 10)
để với mọi bộ ba số thực phân biệt a, b, c ∈ [1; 3] thì f(a), f(b), f(c) là ba cạnh của một tam
giác?
A 4. B 3. C 1. D 2.
Câu 33. Với tham số m, đồ thị của hàm số y =
x
2
− mx
x + 1
có hai điểm cực trị A, B và
AB = 5. Mệnh đề nào dưới đây đúng?
A m > 2. B 0 < m < 1. C 1 < m < 2. D m < 0.
Câu 34. Có bao nhiêu số nguyên dương m sao cho đường thẳng y = x + m cắt đồ thị hàm
số y =
2x − 1
x + 1
tại hai điểm phân biệt A, B và AB ≤ 4?
A 7. B 6. C 1. D 2.
Câu 35 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1Y1-2]
Cho hàm số y = f(x) có đồ thị như hình vẽ. Hàm số đã cho đồng biến
trong khoảng nào dưới đây?
A (1; +∞). B (0; 1). C (−3; 1). D (−2; 0).
x
y
O
−1
1
1
−3
Câu 36 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-7]
Cho hàm số f(x) liên tục trên đoạn [−3; 2] và có đồ thị như hình
vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của
hàm số đã cho trên đoạn [−3; 2]. Giá trị của M −m là
A 4. B 3. C 5. D 0.
x
y
O
−3
2
1
−2
1
3
−1
Câu 37 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-4] Số giao điểm của đồ thị hàm số
y = x
3
− 3x + 3 và đường thẳng y = x.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 55
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A 2. B 3. C 1. D 0.
Câu 38 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B4-1] Cho hàm số y = f(x) có bảng biến
thiên như sau
x
y
0
y
−∞
−2
0
+∞
+ −
−∞
+∞
1
00
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A 4. B 2. C 1. D 3.
Câu 39 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B2-1] Biết đồ thị hàm số y = x
3
−3x + 1
có hai điểm cực trị A, B. Khi đó phương trình đường thẳng AB là
A y = 2x − 1. B y = x − 2. C y = −x + 2. D y = −2x + 1.
Câu 40 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1K1-1] Cho hàm số y = f(x) có đạo hàm
f
0
(x) = x
2
(x
2
− 1), ∀x ∈ R. Hàm số y = 2f(−x) đồng biến trên khoảng nào.
A (−∞; −1). B (−1; 1). C (0; 2). D (2; +∞).
Câu 41 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-1]
Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới
đây?
A y = x
3
− 3x
2
− 1. B y = −x
3
+ 3x + 1.
C y =
x + 1
x − 1
. D y =
x − 1
x + 1
.
x
y
O
1
1
Câu 42 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1K1-3] Cho hàm số y =
mx + 2
2x + m
, m là
tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số nghịch
biến trên khoảng (0; 1). Số phần tử của S bằng
A 1. B 5. C 2. D 3.
Câu 43 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1K1-3] Tất cả các giá trị thực của tham
số m để hàm số y = 2x
3
+ x
2
− mx + 2m − 1 nghịch biến trên đoạn [−1; 1] là
A m ≥ −
1
6
. B m ≤ 8. C m ≥ 8. D m ≤ −
1
6
.
Câu 44 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-4] Cho hàm số y = f(x) liên tục trên
R và có bảng biến thiên như hình sau:
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 56
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
x
y
0
y
−∞
−2
0 2
+∞
−
0
+
0
−
0
+
+∞+∞
−2−2
11
−2−2
+∞+∞
Số nghiệm thực của phương trình 4f
2
(x) − 9 = 0 là:
A 4. B 6. C 3. D 2.
Câu 45. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y =
x − 3
3x − 2
.
A x =
1
3
. B x =
2
3
. C y =
2
3
. D y =
1
3
.
Câu 46.
Cho hàm số y = f(x) có đồ thị trên một khoảng K như
hình vẽ bên. Trên K, hàm số có bao nhiêu cực trị?
A 3. B 2. C 0. D 1.
x
y
O
Câu 47. Cho hàm số f(x) có đạo hàm trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề
nào sai?
A Nếu f
0
(x) < 0 với mọi x thuộc (a; b) thì hàm số f(x) nghịch biến trên (a; b).
B Nếu hàm số f(x) đồng biến trên (a; b) thì f
0
(x) > 0 với mọi x thuộc (a; b).
C Nếu hàm số f(x) đồng biến trên (a; b) thì f
0
(x) ≥ 0 với mọi x thuộc (a; b).
D Nếu f
0
(x) > 0 với mọi x thuộc (a; b) thì hàm số f(x) đồng biến trên (a; b).
Câu 48. Hàm số f(x) = x
3
+ ax
2
+ bx + c đạt cực tiểu tại điểm x = 1, f(1) = −3 và đồ thị
hàm số cắt trục tung tại điểm có tung độ bằng 2. Tính T = a + b + c.
A T = 9. B T = 1. C T = −2. D T = −4.
Câu 49. Đồ thị hàm số y =
x
2
+ 1
x
2
− 4
có tất cả bao nhiêu đường tiệm cận?
A 0. B 1. C 2. D 3.
Câu 50.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 57
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây.
Tìm tất cả các giá trị của tham số thực m để phương trình
f(x) + m = 0 có đúng 3 nghiệm thực phân biệt.
A m < 3. B m = −3.
C −4 < m < −3. D m = 3.
x
y
O
−3
−1 1
−4
Câu 51. Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?
A y = x − sin
2
x. B y = cot x. C y = sin x. D y = −x
3
.
Câu 52. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = 3x +
m
2
+ 3m
x + 1
đồng biến trên từng khoảng xác định của nó?
A 4. B 2. C 1. D 3.
Câu 53.
Cho hàm số y = f(x). Hàm số y = f
0
(x) có đồ thị trên một
khoảng K như hình vẽ bên. Trong các khẳng định sau, có
tất cả bao nhiêu khẳng định đúng?
(I). Trên K, hàm số y = f(x) có hai điểm cực trị.
(II). Hàm số y = f(x) đạt cực đại tại x
3
.
(III). Hàm số y = f(x) đạt cực tiểu tại x
1
.
x
y
O
f
0
(x)
x
1
x
2
x
3
A 3. B 0. C 1. D 2.
Câu 54. Tìm giá trị nhỏ nhất của hàm số f(x) = cos
2
2x − sin x cos x + 4 trên R.
A min
x∈R
f(x) =
7
2
. B min
x∈R
f(x) = 3. C min
x∈R
f(x) =
10
3
. D min
x∈R
f(x) =
16
5
.
Câu 55. Tập hợp tất cả các giá trị của tham số thực m để phương trình
m
√
1 + x +
√
1 − x + 3
+ 2
√
1 − x
2
− 5 = 0 có đúng hai nghiệm thực phân biệt là một
nửa khoảng (a; b]. Tính b −
5
7
a,
A
6 − 5
√
2
35
. B
6 − 5
√
2
7
. C
12 − 5
√
2
35
. D
12 − 5
√
2
7
.
Câu 56.
Cho hàm số y = f(x) xác định và liên tục
trên R có bảng biến thiên như hình bên. Hàm
số y = f(x) đồng biến trên khoảng nào sau
đây?
A (−∞; 0). B (0; 2).
C (0; 4). D (2; +∞).
x
y
0
y
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
00
44
−∞−∞
Câu 57. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y =
2x + 1
x − 1
?
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 58
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
A y = 2. B y = −1. C x = 1. D x = −
1
2
.
Câu 58. Cho hàm số có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−4−4
−3−3
−4−4
+∞+∞
Hàm số đạt cực đại tại điểm
A x = 1. B x = −3. C x = −1. D x = 0.
Câu 59. Gọi m là giá trị nhỏ nhất của hàm số y =
3x + 1
x − 2
trên [−1; 1]. Khi đó, giá trị của
m là
A m = −4. B m =
2
3
. C m = 4. D m = −
2
3
.
Câu 60. Tọa độ điểm cực đại của đồ thị hàm số y =
1
2
x
4
− 3x
2
+ 2 là
A
Å
√
3; −
5
2
ã
. B
Å
−
√
3; −
5
2
ã
. C (0; 2). D (2; 0).
Câu 61.
Đồ thị sau đây là của hàm số nào?
A y =
x + 1
x − 1
. B y =
2x + 1
x − 1
.
C y =
x + 2
1 − x
. D y =
2x − 1
x − 1
.
−3 −2 2 3
−2
2
3
4
5
O
x
y
1
−1
−1
1
Câu 62. Có bao nhiêu giá trị nguyên âm a để đồ thị hàm số y = x
3
+ (a + 10)x
2
− x + 1
cắt trục hoành tại đúng một điểm?
A 10. B 8. C 9. D 11.
Câu 63.
Cho hàm số y = f(x) có bảng biến thiên như
hình bên. Khi đó tất cả các giá trị của m để
phương trình f(x) = m − 1 có ba nghiệm
thực phân biệt là
A m ∈ [4; 6].
B m ∈ (3; 5).
C m ∈ (−∞; 3) ∪ (5; +∞).
D m ∈ (4; 6).
x
y
0
y
−∞
−2
0
+∞
+
0
−
0
+
−∞−∞
55
33
+∞+∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 59
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 64. Cho hàm số y =
2x − 2
x − 2
có đồ thị (C), M là điểm thuộc (C) sao cho tiếp tuyến
của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn AB = 2
√
5. Gọi
S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Giá trị của S bằng
A 8. B 5. C 7. D 6.
Câu 65. Cho hàm số y = x
3
−3x
2
+ mx + 1 có đồ thị là (C
m
). Tìm m sao cho (C
m
) có hai
điểm cực trị có hoành độ x
1
, x
2
thỏa mãn x
3
1
+ x
3
2
= 5.
A m =
3
√
2. B m = −
3
2
. C m =
3
2
. D m = −
4
3
.
Câu 66. Đường tiệm cận đứng của đồ thị hàm số y =
x + 1
x − 2
là
A y = 2. B x = 2. C y = 1. D x = 1.
Câu 67. Số điểm cực trị của hàm số f(x) = −x
4
+ 2x
2
− 3 là
A 0. B 2. C 3. D 1.
Câu 68.
Đường cong trong hình sau là đồ thị của hàm số nào?
A y = −x
4
+ 2x
2
+ 3. B y = x
4
+ 2x
2
− 3.
C y = x
4
− 2x
2
− 3. D y = −x
4
− 2x
2
+ 3.
x
y
O
-1 1
-3
Câu 69. Số đường tiệm cận của đồ thị hàm số y =
√
x
2
+ 3
2x − 1
là
A 3. B 0. C 2. D 1.
Câu 70. Cho hàm số y = −2x
3
+ 6x
2
− 5 có đồ thị (C). Phương trình tiếp tuyến của (C)
tại điểm M thuộc (C) và có hoành độ bằng 3 là
A y = 18x + 49. B y = −18x − 49. C y = −18x + 49. D y = 18x − 49.
Câu 71. Giá trị lớn nhất của hàm số y =
√
−x
2
+ 2x là
A 0. B 1. C 2. D
√
3.
Câu 72. Hàm số nào sau đây đồng biến trên R?
A y = −x
3
− x − 2. B
y =
x − 1
x + 3
.
C y = x
4
+ 2x
2
+ 3. D y = x
3
+ x
2
+ 2x + 1.
Câu 73. Cho hàm số y =
2x + 1
x + 1
có đồ thị (C). Tìm các giá trị của tham số m để đường
thẳng d: y = x + m −1 cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho AB = 2
√
3.
A m = 4 ±
√
3. B m = 2 ±
√
3. C m = 4 ±
√
10. D m = 2 ±
√
10.
Câu 74. Cho hàm số y =
2x + 1
x + 2
có đồ thị (C). Viết phương trình tiếp tuyến của (C), biết
tiếp tuyến song song với đường thẳng ∆ : 3x − y + 2 = 0.
A y = 3x − 8. B y = 3x + 14.
C y = 3x + 5, y = 3x − 8. D y = 3x + 14, y = 3x + 2.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 60
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 75.
Từ kho hàng hóa A dọc theo đường sắt AB cần phải xây một
kho trung chuyển tại điểm C và xây dựng một con đường từ C
đến D. Biết rằng vận tốc trên đường sắt là v
1
và trên đường bộ
là v
2
(v
1
> v
2
). Tìm điều kiện của cos α để điểm C được chọn là
địa điểm sao cho thời gian chuyển hàng hóa từ A đến D qua C
là nhanh nhất (góc α như hình vẽ).
A BC
D
α
A cos α =
v
1
v
2
. B cos α =
v
1
+ v
2
2
. C cos α =
√
2
2
. D cos α =
v
2
v
1
.
Câu 76. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị của
hàm số y = x
4
− 2x
2
− 3 tại bốn điểm phân biệt.
A m > −1. B −1 < m < 1. C m < −4. D −4 < m < −3.
Câu 77. Khoảng nghịch biến của hàm số y = x
3
+ 3x
2
+ 4 là
A (−∞; 0). B (−∞; −2) và (0; +∞).
C (2; +∞). D (−2; 0).
Câu 78. Cho bảng biến thiên của hàm số y = f(x) như hình vẽ bên dưới. Đồ thị hàm số
đã cho có tổng số bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
x
y
−∞
√
2
+∞
66
2
+∞
33
A 1. B 2. C 0. D 3.
Câu 79. Cho đồ thị của hàm số y =
x − 2
x + 1
là một trong bốn đường cong được liệt kê trong
bốn phương án dưới đây. Hỏi đồ thị đó là hình nào?
A
1
1 2
x
y
O
. B
2
2
−2
x
y
O
.
C
1
−1
−2
2
x
y
O
. D
1
1 2
x
y
O
.
Câu 80. Phương trình tiếp tuyến của đồ thị hàm số y = x
4
−2x
2
−3 tại giao điểm của đồ
thị hàm số với trục tung là
A y = 2x + 3. B y = 3. C y = 2x − 3. D y = −3.
Câu 81. Bảng biến thiên trong hình dưới là bảng biến thiên của hàm số nào dưới đây?
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 61
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
x
y
0
y
−∞
−1
+∞
+
0
+
−∞−∞
+∞+∞
A y = x
4
− 2x
2
+ 2. B y = −
1
3
x
3
+ x
2
− x − 1.
C y =
1
3
x
3
+ x
2
+ x − 1. D y =
1
3
x
3
+ x
2
− x − 1.
Câu 82. Hàm số nào trong các hàm số sau đồng biến trên tập xác định?
A y =
2 − 3x
1 + 5x
. B y = x
4
+ 3x
2
+ 18.
C y = x
3
+ 2x
2
− 7x + 1. D y = x
3
+ 3x
2
+ 9x − 20.
Câu 83. Cho các đường cong (C
1
): y = x
3
−3x
2
+ 4, (C
2
): y = −x
4
+ x
2
−3 và (C
3
): y =
5x + 2
x − 1
. Hỏi các đường cong nào có tâm đối xứng?
A (C
1
), (C
2
) và (C
3
). B (C
1
) và (C
3
).
C (C
2
) và (C
3
). D (C
1
) và (C
2
).
Câu 84. Cho hàm số y = f(x) = sin x + cos
2
x . Tính giá trị S =
√
7(1 + min y)
2
+
16 max
2
y.
A S =
25
16
. B S = 25. C S = 4
√
7 + 25. D 25 − 4
√
7.
Câu 85. Tìm tất cả các giá trị thực của m để hàm số y =
x − m
(m − 1)x − 2
nghịch biến trên
(−∞; 1).
A m ∈ (−1; 2). B m ∈ (−1; 3]. C m ∈ [1; 2). D m ∈ (1; 2].
Câu 86.
Cho đường cong trong hình bên là đồ thị của hàm số y =
f(x). Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu
diễn nghiệm của phương trình f(f(cos 2x)) = 0?
A 3 điểm. B 4 điểm. C 2 điểm. D 1 điểm.
x
y
−1 1
1
O
Câu 87. Gọi M là tập tất cả các giá trị nguyên của m để hàm số y = x
4
+2(m
2
−16)x
2
+m
2
có ba cực trị. Lấy ngẫu nhiên một giá trị m thuộc tập M. Tính xác suất P với m lấy được
để hàm số có 3 cực trị lập thành một tam giác có diện tích lớn hơn hoặc bằng 3.
A P =
3
7
. B P =
5
7
. C P =
5
9
. D P = 1.
Câu 88.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 62
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Cho hàm số y = f(x) liên tục trên R, có f(−2) < 0 và đồ
thị hàm số f
0
(x) như hình vẽ bên. Khẳng định nào sau đây
là khẳng định sai?
A Hàm số y = |f(1 − x
2018
)| nghịch biến trên khoảng
(−∞; −2).
B Hàm số y = |f(1 − x
2018
)| có hai cực tiểu.
C Hàm số y = |f(1 − x
2018
)| có hai cực đại và một cực
tiểu.
D Hàm số y = |f(1 − x
2018
)| đồng biến trên khoảng
(2; +∞).
x
y
O
−2 2
Câu 89. Cho hàm số y = x
3
−6x
2
+9x−2 có đồ thị (C). Đường thẳng đi qua điểm A(−1; 1)
và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) là
A y = x + 3 . B y =
1
2
x +
3
2
. C y =
−1
2
x +
3
2
. D x − 2y − 3 = 0 .
Câu 90. Bác Tôm có một cái ao có diện tích 50 m
2
để nuôi cá. Vụ vừa qua bác nuôi với
mật độ 20 con/m
2
và thu được tất cả 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá thu
được, bác thấy cứ thả giảm đi 8 con/m
2
thì tương ứng sẽ có mỗi con cá thành phẩm thu
được tăng thêm 0,5 kg. Hỏi vụ tới bác phải mua bao nhiêu con cá giống để đạt được tổng
khối lượng cá thành phẩm cao nhất? (Giả sử không có hao hụt trong quá trình nuôi).
A 1100 con. B 1000 con. C 500 con. D 512 con.
Câu 91.
Cho hàm số f(x) có bảng biến thiên như hình
vẽ bên. Khẳng định nào dưới đây đúng?
A min
x∈[−2;2]
f(x) = −2; max
x∈[−2;2]
f(x) = −1 .
B min
x∈[−2;2]
f(x) = 3; max
x∈[−2;2]
f(x) = 4 .
C min
x∈[−2;2]
f(x) = −2; max
x∈[−2;2]
f(x) = 2 .
D min
x∈[−2;2]
f(x) = 3; max
x∈[−2;2]
f(x) = 11 .
x
f
0
(x)
f(x)
−2 −1
0 2
+
0
− +
33
44
33
1111
Câu 92.
Hàm số y = f(x) có đồ thị y = f
0
(x) như
hình vẽ (đồ thị f
0
(x) cắt Ox ở các điểm
có hoành độ lần lượt là 1, 2, 5, 6). Chọn
khẳng định đúng:
A f(x) nghịch biến trên khoảng (1; 2).
B f(x) đồng biến trên khoảng (5; 6).
C f(x) nghịch biến trên khoảng (1; 5).
D f(x) đồng biến trên khoảng (4; 5).
x
y
O
1 2 5 6
Câu 93.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 63
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số y = f(x) có đồ thị y = f
0
(x) trên R như
hình vẽ (trên R thì đồ thị y = f
0
(x) là một nét liền
và chỉ có 4 điểm chung với Ox tại các điểm có hoành
độ lần lượt là −1, 1, 2, 4). Đặt g(x) = f(1 − x). Chọn
khẳng định đúng:
A g(x) đồng biến trên (−3; 0).
B g(x) đồng biến trên (−4; −3).
C g(x) nghịch biến trên (−1; 0).
D g(x) đồng biến trên (−4; −3) và (0; 2).
x
y
O
−1
1 2 4
Câu 94.
Cho hàm số y =
ax + b
cx + d
có đồ thị như hình vẽ.
Chọn khẳng định đúng.
A Hàm số nghịch biến trên từng khoảng
xác định.
B Hàm số đồng biến trên từng khoảng xác
định.
C Hàm số đồng biến trên tập xác định.
D Hàm số đồng biến trên R.
−1
1
x
y
O
Câu 95.
Cho hàm số f(x) liên tục trên
[−2; 2] và có bảng biến thiên như
hình vẽ. Chọn khẳng định đúng về
tổng số các tiệm cận đứng và tiệm
cận ngang của đồ thị f(x).
A
Đồ thị hàm số có đúng 4 tiệm
cận.
B
Đồ thị hàm số có đúng 2 tiệm
cận.
C
Đồ thị hàm số có đúng 1 tiệm
cận.
D
Đồ thị hàm số có đúng 3 tiệm
cận.
x
y
0
y
−∞
−2
2
+∞
− − −
00
−∞
+∞
−∞
+∞
−∞−∞
Câu 96. Tìm tất cả các giá trị m để hàm số y =
1
3
x
3
−
mx
2
2
+ 2x + 2017 đồng biến trên
R.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 64
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
A −2
√
2 6 m 6 2
√
2 . B −2
√
2 6 m .
C m 6 2
√
2 . D −2
√
2 < m < 2
√
2 .
Câu 97. Tìm tất cả các giá trị của tham số m để phương trình −x
4
+ 2x
2
+ 3 + 2m = 0 có
4 nghiệm phân biệt.
A −2 6 m 6
−3
2
. B
−3
2
< m < 2. C −2 < m <
−3
2
. D 3 < m < 4.
Câu 98. Đồ thị hàm số nào sau đây không có tiệm cận ngang?
A y =
√
x
2
− 1. B y =
2x − 1
x + 1
.
C y =
x
2
− 3x + 2
x
2
− x − 2
. D y = x −
√
x
2
+ 1.
Câu 99. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức f (x) = 0,025x
2
(30−
x), trong đó x (miligam) là liều lượng thuốc được tiêm cho bệnh nhân. Khi đó liều lượng
thuốc được tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là
A 20 miligam. B 10 miligam. C 15 miligam. D 30 miligam.
Câu 100. Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =
2x − 3
x + 1
tương
ứng có phương trình là
A x = 2 và y = 1. B x = −1 và y = 2.
C x = 1 và y = −3. D x = 1 và y = 2.
Câu 101. Tổng hoành độ các giao điểm của đồ thị hàm số y = x
3
−3x
2
+ 3 và đường thẳng
y = x là
A 3. B 2. C 4. D 0.
Câu 102.
Đường cong bên là hình biểu diễn của đồ thị hàm số nào sau
đây?
A y = −x
4
+ 4x
2
+ 3. B y = x
4
− 2x
2
+ 3.
C y = −x
3
+ 3x + 3. D y = −x
4
+ 2x
2
+ 3.
x
y
O
−1 1
4
Câu 103.
Cho hàm số y = f(x) xác định, liên tục trên R
và có bảng biến thiên như hình vẽ. Hàm số đã
cho nghịch biến trên khoảng nào sau đây?
A (−3; 2).
B (−∞; 0) và (1; +∞).
C (−∞; −3).
D (0; 1).
x
y
0
y
−∞
0 1
+∞
+ −
0
+
−∞−∞
22
−3−3
+∞+∞
Câu 104. Có bao nhiêu số nguyên m để hàm số y = x
3
−3x
2
−mx + 4 có hai điểm cực trị
thuộc khoảng (−3; 3).
A 12. B 11. C 13. D 10.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 65
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 105.
Cho hàm số y = f(x) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị
nguyên của tham số m để phương trình f (x) = m có 3 nghiệm phân
biệt.
A 0. B 3. C 1. D 2.
x
y
1
1
−2
1
O
Câu 106.
Cho hàm số y = f(x) có đạo hàm trên R
và có bảng xét dấu f
0
(x) như hình bên.
Hỏi hàm số y = f(x
2
−2x) có bao nhiêu
điểm cực tiểu?
A 1. B 2. C 3. D
4.
x
f
0
(x)
−∞
−2
1 3
+∞
−
0
+
0
+
0
−
Câu 107. Tìm giá trị của tham số m để đồ thị hàm số y = x
4
− 2(m + 1)x
2
+ 2m + 3 có
ba điểm cực trị A, B, C sao cho trục hoành chia tam giác ABC thành một tam giác và một
hình thang, biết rằng tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC
bằng
4
9
.
A m =
1 +
√
15
2
. B m =
−1 +
√
3
2
. C m =
5 +
√
3
2
. D m =
−1 +
√
15
2
.
Câu 108. Cho hàm số y =
2x
x + 1
có đồ thị (C) và điểm A(0; a). Gọi S là tập hợp tất cả
các giá trị thực của a để từ A kẻ được hai tiếp tuyến AM, AN đến (C) với M, N là các tiếp
điểm và MN = 4. Tổng các phần tử của S bằng bao nhiêu?
A 4. B 3. C 6. D 1.
Câu 109. Hàm số nào sau đây không có GTLN, GTNN trên [−2; 2]?
A y =
x − 1
x + 1
. B y = x
2
. C y = −x + 1. D y = x
3
+ 2.
Câu 110.
Cho hàm số y = f(x) có bảng biến
thiên như hình vẽ bên. Hàm số y =
f(x) đồng biến trên khoảng nào dưới
đây?
A (1; +∞). B (0; 1).
C (−∞; 3). D (−4; +∞).
x
y
0
y
−∞
0 1
+∞
+
0
−
0
+
−∞−∞
33
−4−4
+∞+∞
Câu 111. Cho hàm số y =
ax + 1
bx − 2
. Tìm a và b để đồ thị hàm số nhận đường thẳng x = 1
là tiệm cận đứng và đường thẳng y =
1
2
là tiệm cận ngang.
A a = 1, b = 2. B a = 2, b = 2. C a = 2, b = −2. D a = −1, b = −2.
Câu 112.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 66
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới
đây. Hàm số đó là hàm số nào?
A y = −x
3
− 3x + 1. B y = −x
3
+ 3x + 1.
C y = x
3
+ 3x + 1. D y = x
3
− 3x + 1.
x
y
0
−1
1
−1
1
3
Câu 113. Tìm tất cả các giá trị thực của tham số m để hàm số f(x) = −x
3
+2(2m−1)x
2
−
(m
2
− 8)x + 2 đạt giá trị cực tiểu tại điểm x = −1.
A m = −2. B m = 3. C m = 1. D m = −9.
Câu 114. Cho hàm số y =
2x − 1
x + 1
có đồ thị (C) và đường thẳng d : y = 2x − 3. Đường
thẳng d cắt đồ thị (C) tại hai điểm A và B. Tính khoảng cách giữa hai điểm A và B.
A AB =
2
√
5
5
. B AB =
5
√
5
2
. C AB =
2
5
. D AB =
5
2
.
Câu 115. Tìm số giá trị nguyên của tham số m ∈ [0; 30] để phương trình x
4
−6x
3
+ mx
2
−
12x + 4 = 0 có nghiệm.
A 17. B 16. C 15. D 14.
Câu 116.
Cho hàm số y = f(x). Biết hàm số y = f
0
(x)
có đồ thị như hình vẽ bên. Hàm số y = f(3 −
x
2
) + 2018 đồng biến trong khoảng nào dưới
đây?
A (2; 3). B (−2; −1).
C (0; 1). D (−1; 0).
x
y
0
−1 2−6
Câu 117. Cho đường cong (C): y = x
4
− 4x
2
+ 2 và điểm A(0; a). Nếu qua A kẻ được 4
tiếp tuyến với (C) thì a phải thỏa mãn điều kiện
A a ∈
Å
2;
10
3
ã
. B a ∈ (2; +∞).
C a ∈ (−∞; 2) ∪
Å
10
3
; +∞
ã
. D a ∈
Å
−∞;
10
3
ã
.
Câu 118. Tìm tất cả các giá trị của tham số m để hàm số y = |x
3
+ 3x
2
− 3 + m| có ba
điểm cực trị.
A m = 3 hoặc m = −1. B m ≤ −3 hoặc m ≥ 1.
C m ≤ −1 hoặc m ≥ 3. D 1 ≤ m ≤ 3.
Câu 119. Hàm số nào sau đây đồng biến trên R?
A y = x
4
+ x. B y = x
4
− x. C y = (x − 1)
2018
. D y = (x − 1)
2019
.
Câu 120. Cho hàm số y =
x + 1
x
(C). Hỏi trên đồ thị (C) về phía bên phải trục tung có
bao nhiêu điểm mà tại đó ta dựng được tiếp tuyến cắt hai trục tọa độ tạo thành tam giác
cân.
A Vô số. B 2. C 1. D 0.
Câu 121. Cho hàm số y = x
3
− 3x + 2. Tọa độ điểm cực tiểu của đồ thị hàm số là
A B(−1; 4). B D(2; 4). C C(0; 2). D A(1; 0).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 67
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 122. Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x
3
−3x
2
trên đoạn [−2; 1]. Tính giá trị của T = M + m.
A T = −20. B T = −22. C T = −4. D T = 2.
Câu 123.
Đường cong trong hình bên là đồ thị của một trong bốn hàm
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi
hàm số đó là hàm số nào?
A y = −x
4
+ 1. B y = −|x|
3
+ 3|x| + 1.
C y = −x
4
− 2x
2
+ 1. D y = −x
4
+ 2x
2
+ 1.
O
x
y
1
2
−1
Câu 124. Biết rằng hàm số y =
x + m
x − 2
đồng biến trên các khoảng (−∞; 2) và (2; +∞) và
tiếp tuyến của đồ thị tại điểm x
0
= 1 cắt hai trục tọa độ tạo thành một tam giác vuông cân.
Tìm giá trị của tham số m.
A
m = −3. B m = −4. C m = −5. D m = 0.
Câu 125. Phương trình m +
2
3
√
x − x
2
=
√
x +
√
1 − x. Gọi S là tập hợp tất cả các giá trị
nguyên của tham số m để phương trình có nghiệm duy nhất. Tìm số phần tử của S.
A 3. B 2. C 1. D 0.
Câu 126. Đồ thị hàm số y =
x + 1
x − 2
có tâm đối xứng I là
A I(−2; 1). B I(2; 1). C I(2; −1). D I(−2; −1).
Câu 127. Biết rằng đồ thị hàm số y = x
3
− 3x
2
+ m có điểm uốn nằm trên đường thẳng
y = x. Tìm giá trị của tham số m.
A m = 1. B m = −1. C m = 3. D m = 2.
Câu 128. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x
3
− 3mx
2
+
3 (m
2
− 1) x + 1 − m
2
có hai điểm phân biệt đối xứng nhau qua gốc tọa độ O.
A 0 < m < 1. B 0 ≤ m < 1 hoặc m ≤ −1.
C m < −1. D 0 < m < 1 hoặc m < −1.
Câu 129. Đồ thị hàm số y = (x − 1) (x
2
− 1) (x
3
− 1) cắt trục hoành tại mấy điểm phân
biệt?
A 3. B 1. C 2. D 4.
Câu 130. Hàm số y = f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
0 2
+∞
−
0
+
0
−
+∞+∞
11
55
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 68
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A (1; 5). B (0; 2). C (2; +∞). D (−∞; 0).
Câu 131. Giá trị nhỏ nhất của hàm số y = x
3
− 3x + 1 trên đoạn [−2; 0] bằng
A 1. B −2. C −1. D 3.
Câu 132. Đồ thị hàm số y =
x + 2
x − 1
có đường tiệm cận ngang là
A y = 2. B y = −2. C x = 1. D y = 1.
Câu 133. Hàm số y = f(x) có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
−
√
2
0
√
2
+∞
+
0
−
0
+
0
−
−∞−∞
11
−3−3
11
−∞−∞
Hàm số đạt cực tiểu tại điểm
A x = 1. B x = −3. C x = 0. D x = ±
√
2.
Câu 134.
Đường cong như hình bên là đồ thị của hàm số nào dưới đây?
A y = −x
4
+ 3x
2
− 2.
B y = x
4
− 2x
2
− 2.
C y = −x
3
+ 3x
2
− 2.
D y = x
3
+ 3x
2
+ 1.
x
y
O
Câu 135. Cho hàm số y =
1
3
(m
2
− 1)x
3
+ (m + 1)x
2
+ 3x + 5 với m là tham số thực. Có
bao nhiêu giá trị nguyên của m để hàm số có hai điểm cực trị?
A 3. B 0. C 2. D 1.
Câu 136.
Cho hàm số y = f(x), biết hàm số y = f
0
(x) có đồ thị như hình
vẽ dưới đây. Hàm số y = f(x) đạt giá trị nhỏ nhất trên đoạn
ï
1
2
;
3
2
ò
tại điểm nào sau đây?
A x =
3
2
. B x =
1
2
.
C x = 1. D x = 0.
x
y
O
3
2
1
Câu 137. Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau
x
y
0
−∞
1
+∞
−
0
+
Hàm số g = f(x
2
) nghịch biến trên khoảng
A (0; 1). B (1; +∞). C (−1; 0). D (−∞; 0).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 69
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 138.
Cho hàm số y = f(x) liên tục trên R có đồ thị như hình bên.
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?
A (−∞; −1). B (−1; 1).
C (−∞; 0). D (0; +∞).
O
x
y
−2
−1
1
−1
Câu 139.
Cho hàm số y = f (x) liên tục
trên R có bảng biến thiên dưới
đây. Mệnh đề nào sau đây là
đúng?
A
Hàm số đạt cực đại tại
x = 2.
B
Hàm số đạt cực tiểu tại
x = −4.
C
Hàm số đạt cực đại tại
x = 1.
D
Hàm số đạt cực đại tại
x = 0.
x
y
0
y
−∞
1 3
+∞
+
0
−
0
+
−∞−∞
22
−4−4
+∞+∞
Câu 140. Đồ thị hàm số y =
x − 1
2x − 1
có bao nhiêu đường tiệm cận?
A 0. B 1. C 2. D 3.
Câu 141.
Cho hàm số y = f(x) có đồ thị như hình bên. Khi đó y = f(x)
là hàm số nào sau đây?
A y = x
3
− 3x. B y = −x
3
+ 3x.
C y = x
3
+ x
2
− 4. D y = x
3
− 3x + 1.
O
x
y
−2
−2
−1
−1
1
1
2
2
Câu 142. Cho hàm số y = f(x) xác định trên tập D = R \{−1}, liên tục trên mỗi khoảng
xác định và có bảng biến thiên như sau:
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 70
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
x
y
0
y
−∞
−4 −1
2
+∞
+
0
− −
0
+
−∞−∞
00
−∞
+∞
44
+∞+∞
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f (x) = m − 1 có hai
nghiệm thực phân biệt.
A
m < 1
m > 5.
B 1 < m < 5. C m < 1. D m > 5.
Câu 143. Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số f(x) = 2x
3
+3x
2
−1
trên đoạn
ï
−2; −
1
2
ò
. Khi đó giá trị của M − m bằng
A −5. B 1. C 4. D 5.
Câu 144. Cho hàm số y = −x
2
+5 có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm
M có tung độ y
0
= −1, với hoành độ x
0
< 0 là kết quả nào sau đây?
A y = 2
√
6
Ä
x +
√
6
ä
− 1. B y = −2
√
6
Ä
x +
√
6
ä
− 1.
C y = 2
√
6
Ä
x −
√
6
ä
+ 1. D y = 2
√
6
Ä
x −
√
6
ä
− 1.
Câu 145. Cho hàm số y = ax
3
+ bx
2
+ cx + d đồng biến trên R khi
A
a = b; c > 0
b
2
− 3ac ≤ 0
. B
a = b = c = 0
a > 0; b
2
− 3ac < 0
.
C
a = b = 0; c > 0
a > 0; b
2
− 3ac ≤ 0
. D
a = b = 0; c > 0
a > 0; b
2
− 3ac ≥ 0
.
Câu 146. Đồ thị hàm số y = ax
3
+ bx
2
+ cx + d có hai điểm cực trị A(1; −7), B(2; −8).
Tính y(−1).
A y(−1) = 7. B y(−1) = 11. C y(−1) = −11. D y(−1) = −35.
Câu 147.
Cho hàm số y = f(x) có đạo hàm và liên tục trên R, có đồ thị
y = f
0
(x) như hình vẽ bên. Tìm số điểm cực trị của hàm số
y = f(x − 2009) + 2017x − 2018.
A 1. B 2. C 3. D 4.
−2 −1 1
2
4
O
x
y
Câu 148. Cho hàm số y =
x + 5
x + 2
. Mệnh đề nào sau đây là đúng?
A Hàm số nghịch biến trên mỗi khoảng (−∞; −2) và (−2; +∞).
B Hàm số đồng biến trên mỗi khoảng (−∞; −2) và (−2; +∞).
C Hàm số nghịch biến trên khoảng (−∞; 5).
D Hàm số nghịch biến trên R \ {−2}.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 71
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 149. Cho hàm số y = x
3
− 3x có giá trị cực đại và cực tiểu lần lượt là y
1
, y
2
. Khi
đó:
A y
1
− y
2
= −4. B 2y
1
− y
2
= 6. C 2y
1
− y
2
= −6. D y
1
+ y
2
= 4.
Câu 150.
Đồ thị như hình vẽ là đồ thị của hàm số nào sau đây?
A y = −x
3
−
3
2
x
2
+ 1. B y = −2x
3
− 3x
2
+ 1.
C y = 2x
3
+ 3x
2
+ 1. D y = x
3
+
3
2
x
2
+ 1.
y
x
−1
2
Câu 151. Đồ thị hàm số y =
x + 4
√
x
2
− 4
có tất cả bao nhiêu đường tiệm cận đứng và tiệm
cận ngang?
A 3. B 1. C 2. D 4.
Câu 152.
Tìm a, b để hàm số y =
ax + b
x + 1
có đồ thị như hình vẽ
bên.
A
a = −1, b = −2.
B
a = 1, b = −2.
C
a = −2, b = 1.
D
a = 2, b = 1.
x
y
O
−1
1
1
−2
Câu 153. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
33
55
33
+∞+∞
Tìm m để phương trình f(x) = 2 − 3m có bốn nghiệm phân biệt.
A m < −1 hoặc m > −
1
3
. B −1 < m < −
1
3
.
C m = −
1
3
. D m 6 −1.
Câu 154. Tìm m để hàm số y = x
4
− 2mx
2
+ 2m + m
4
− 5 đạt cực tiểu tại x = −1.
A m = −1. B m 6= 1. C m = 1. D m 6= −1.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 72
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 155.
Đồ thị hàm số y = ax
3
+ bx
2
+ cx + d có đồ
thị như hình vẽ bên. Mệnh đề nào sau đây đúng.
A a < 0; b > 0; c > 0; d > 0.
B a < 0; b < 0; c < 0; d > 0.
C a < 0; b < 0; c > 0; d > 0.
D a < 0; b > 0; c < 0; d > 0.
y
x
−1
2
O
2 3
Câu 156. Cho các số thực dương x, y thỏa mãn x
2
− xy + 3 = 0 và 2x + 3y 6 14. Gọi M,
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 3x
2
y −xy
2
−2x(x
2
−1).
Tính giá trị của T = 2M − m.
A 4. B 0. C 12. D 3.
Câu 157.
Cho hàm số y = ax
3
+ bx
2
+ cx + d có đồ thị cắt trục tung tại điểm
có tung độ −3; hoành độ điểm cực đại là 2 và đi qua điểm (1; −1)
như hình vẽ. Tỷ số
a
b
bằng
x
y
2
1
1
-1
-3
O
A −1. B 1. C −3. D 3.
Câu 158. Biết hai đường tiệm cận của đồ thị hàm số y =
2x + 1
x − m
(m là tham số thực)
tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Giá trị của m bằng bao
nhiêu?
A m = ±1. B m = ±2. C m = 2. D m = 1.
Câu 159. Cho hàm số y =
2
3
x
3
+ (m + 1)x
2
+ (m
2
+ 4m + 3)x − 3, (m là tham số thực).
Tìm điều kiện của m để hàm số có cực đại cực tiểu và các điểm cực trị của đồ thị hàm số
nằm bên phải của trục tung.
A −5 < m < −1. B −5 < m < −3. C −3 < m < −1. D
m > −1
m < −5
.
Câu 160. Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =
√
x
2
− 4
2x
2
− 5x + 2
là
A 2. B 1. C 3. D 4.
Câu 161. Cho các hàm số y =
x + 1
x − 1
, y = x
4
+ 2x
2
+ 2, y = −x
3
+ x
2
− 3x + 1. Trong các
hàm số trên, có bao nhiêu hàm số đơn điệu trên R
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 73
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A 3. B 1. C 2. D 0.
Câu 162. Cho hàm số y = −x
3
− 3x
2
+ 4. Biết rằng có hai giá trị m
1
, m
2
của tham số
m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tiếp xúc với đường tròn
(C) : (x − m)
2
+ (y − m − 1)
2
= 5. Tính tổng m
1
+ m
2
.
A m
1
+ m
2
= 0. B m
1
+ m
2
= 6. C m
1
+ m
2
= 10. D m
1
+ m
2
= −6.
Câu 163. Gọi (C) là parabol đi qua ba điểm cực trị của đồ thị hàm số y =
1
4
x
4
−mx
2
+m
2
,
tìm m để (C) đi qua điểm A(2; 24).
A m = −4. B m = 6. C m = 4. D m = 3.
Câu 164. Cho hàm số y = f(x) liên tục trên R \{1} và có bảng biến thiên như hình dưới.
x
f
0
(x)
f(x)
−∞
0 2
+∞
− −
0
+
22
−∞
+∞
22
+∞+∞
Hỏi phương trình |f(x)| = 3 có bao nhiêu nghiệm?
A 1 nghiệm. B 2 nghiệm. C 3 nghiệm. D 4 nghiệm.
Câu 165. Chi phí xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, giấy
in,...) được cho bởi C(x) = 0.0001x
2
−0.2x + 10000, C(x) được tính theo đơn vị là vạn đồng.
Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số M(x) =
T (x)
x
với T (x) là tổng chi
phí (xuất bản và phát hành) cho x cuốn tạp chí, được gọi là chi phí trung bình cho một
cuốn tạp chí khi xuất bản x cuốn. Khi chi phí trung bình cho mỗi cuốn tạp chí M(x) là thấp
nhất, tính chi phí cho mỗi cuốn tạp chí đó.
A 20.000 đ. B 15.000 đ. C 10.000 đ. D 22.000 đ.
Câu 166. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = x
2
− 2 ln x trên
[e
−1
; e]
A M = e
2
− 2, m = e
−2
+ 2. B M = e
−2
+ 2, m = 1.
C M = e
−2
+ 1, m = 1. D M = e
2
− 2, m = 1.
Câu 167.
Cho hàm số f(x) có đạo hàm f
0
(x) xác định, liên tục trên
R và f
0
(x) có đồ thị như hình vẽ bên, biết f(c) < 0. Hỏi
đồ thị hàm số f (x) cắt trục hoành tại nhiều nhất bao nhiêu
điểm?
A 3. B 1. C 0. D 2.
O
x
y
a
b
c
Câu 168.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 74
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Cho hàm số f(x) có đồ thị của hàm số y = f
0
(x) như hình
vẽ. Biết f (0) + f(1) − 2f(2) = f(4) − f(3). Giá trị nhỏ
nhất m, giá trị lớn nhất M của hàm số f(x) trên đoạn
[0; 4] là
A m = f(4), M = f(1). B m = f(4), M = f(2).
C m = f(1), M = f (2). D m = f(0), M = f(2).
O
x
y
2
4
y = f
0
(x)
Câu 169.
Cho hàm số y = ax
4
+ bx
2
+ c có đồ thị như hình bên. Mệnh
đề nào sau đây đúng?
A a > 0, b < 0, c < 0. B a > 0, b > 0, c < 0.
C a < 0, b > 0, c < 0. D a > 0, b < 0, c > 0.
O
x
y
Câu 170. Cho hàm số y = (m + 1)x
4
− (m − 1)x
2
+ 1. Có bao nhiêu giá trị nguyên của m
để hàm số có một điểm cực đại mà không có điểm cực tiểu?
A 1. B 2. C 3. D 0.
Câu 171. Số đường tiệm cận của đồ thị hàm số y =
√
x
2
+ 2x
x − 1
là
A 1. B 3. C 0. D 2.
Câu 172. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số y = x
3
−3x
2
−9x+35
trên đoạn [−4; 4]. Khi đó M −m nhận kết quả nào sau đây?
A M − m = 1. B M −m = 86. C M −m = 76. D M − m = 81.
Câu 173. Biết m
0
là giá trị của tham số m để hàm số y = x
3
− 3x
2
+ mx − 1 có hai điểm
cực trị x
1
, x
2
sao cho x
2
1
+ x
2
2
− x
1
x
2
= 13. Mệnh đề nào dưới đây đúng?
A m
0
∈ (−15; −7). B
m
0
∈ (−1; 7). C m
0
∈ (7; 10). D m
0
∈ (−7; −1).
Câu 174. Cho hàm số y =
2mx − 8
x − 1
. Tìm tất cả giá trị của m để đường tiệm cận đứng,
tiệm cận ngang của đồ thị hàm số đã cho cùng hai trục tọa độ tạo thành một hình chữ nhật
có diện tích bằng 8. Mệnh đề nào sau đây đúng?
A Có một giá trị của m thuộc đoạn [3; 5].
B Không tìm được m thỏa mãn yêu cầu bài toán.
C Có một giá trị của m thuộc đoạn [−5; −3].
D Tổng các giá trị tìm được của m bằng 0.
Câu 175. Trong các hàm số sau hàm số nào đồng biến trên R?
A y =
√
x
2
− 3x + 2. B y = x
4
+ x
2
+ 1.
C y =
x − 1
x + 1
. D y = x
3
+ 5x + 13.
Câu 176. Tìm đường tiệm cận ngang của đồ thị hàm số y =
2x + 1
3 − x
.
A y = −2. B y =
2
3
. C y = −1. D y = 3.
Câu 177. Hàm số f(x) = −x
3
+ 3x
2
+ 9x + 1 đồng biến trong khoảng nào sau đây?
A (3; +∞). B (−1; +∞). C (−1; 3). D (−∞; 3).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 75
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 178. Cho hàm số f(x) có đạo hàm cấp 2 trên khoảng K và x
0
∈ K . Tìm mệnh đề
sai trong các mệnh đề sau:
A Nếu hàm số đạt cực đại tại x
0
thì f
00
(x
0
) < 0.
B Nếu hàm số đạt cực đại tại x
0
thì tồn tại a < x
0
để f
0
(a) > 0.
C Nếu hàm số đạt cực trị tại x
0
thì f
0
(x
0
) = 0.
D Nếu f
0
(x
0
) = 0 và f
00
(x
0
) 6= 0 thì hàm số đạt cực trị tại x
0
.
Câu 179. Hàm số nào sau đây đồng biến trên R?
A y =
x
x + 1
. B y =
x
√
x
2
+ 1
.
C y = (x
2
− 1)
2
− 3x + 2. D
y = tan x.
Câu 180.
Cho hàm số y = f(x) liên tục, có đạo hàm trên đoạn
[a; b] và đồ thị của hàm số f
0
(x) là đường cong như
hình vẽ bên. Khi đó, mệnh đề nào sau đây đúng?
A min
x∈[a;b]
f(x) = f(b). B min
x∈[a;b]
f(x) = f(x
1
).
C min
x∈[a;b]
f(x) = f(a). D min
x∈[a;b]
f(x) = f(x
2
).
O
x
y
a
x
1
b
x
2
Câu 181. Cho hàm số y = f(x) có đồ thị trên đoạn [−2; 4] như hình vẽ dưới đây.
O
x
y
−2 −1 2 4
−3
−2
−1
1
Phương trình |f (x)| = 2 có tất cả bao nhiêu nghiệm thực thuộc đoạn [−2; 4]?
A 4. B 2. C 1. D 3.
Câu 182. Cho phương trình 2x
2
−2(m + 1)x + 4 −m = 0 với m là tham số thực. Biết rằng
đoạn [a; b] là tập hợp tất cả các giá trị của m để phương trình đã cho có nghiệm thực thuộc
đoạn
ï
0;
3
2
ò
. Tính a + b.
A 3 +
√
11. B 2 +
√
11. C 2 + 3
√
11. D 2 −
√
11.
Câu 183. Cho hàm số f(x) = mx
4
+2x
2
−1 với m là tham số thực. Có tất cả bao nhiêu giá
trị nguyên của m thuộc khoảng (−2018; 2018) sao cho hàm số đã cho đồng biến trên khoảng
Å
0;
1
2
ã
?
A 2022. B 4032. C 4. D 2014.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 76
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 184. Cho biểu thức P = 3x
p
a − y
2
− 3y
√
a − x
2
+ 4xy + 4
p
a
2
− ax
2
− ay
2
+ x
2
y
2
trong đó a là số thực dương cho trước. Biết rằng giá trị lớn nhất của P bằng 2018. Khi đó,
mệnh đề nào dưới đây đúng?
A a =
√
2018. B a ∈ (500; 525]. C a ∈ (400; 500]. D a ∈ (340; 400].
Câu 185. Cho hàm số f(x) = x
3
−
3
2
(m −1)x
2
−3mx −
3m
2
với m là tham số thực. Có tất
cả bao nhiêu giá trị nguyên của m thuộc khoảng (−20; 18) sao cho đồ thị của hàm số đã cho
có hai điểm cực trị nằm cùng một phía đối với trục hoành?
A 1. B 19. C 20. D 18.
Câu 186. Cho hàm số y = x
2
+ m
√
2018 − x
2
+ 1
− 2021 với m là tham số thực. Gọi S
là tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số đã cho cắt trục hoành tại
đúng hai điểm phân biệt. Tính S.
A 860. B 986. C 984. D 990.
Câu 187. Tập hợp nào dưới đây chứa được tất cả các giá trị thực của tham số m để giá trị
lớn nhất của hàm số y = |x
4
− 8x
2
− m| trên đoạn [0; 3] bằng 14?
A (−∞; −5) ∪ (−3; +∞). B (−5; −2).
C (−7; 1). D (−4; 2).
Câu 188. Giá trị lớn nhất của hàm số f(x) = x
4
−4x
2
+ 9 trên đoạn
î
−
√
3; 2
ó
bằng
A 5. B 9. C 6. D 8.
Câu 189. Cho hàm số y = f(x) có đạo hàm f
0
(x) = (x + 2)
2
(x − 2)
3
(3 − x). Hàm số f(x)
đồng biến trên khoảng nào dưới đây?
A (2; 3). B (−2; 2). C (3; +∞). D (−∞; −2).
Câu 190. Cho hàm số y = x
3
−3x
2
+ 1. Tích các giá trị cực đại và giá trị cực tiểu của hàm
số bằng
A 0. B 6. C −6. D −3.
Câu 191. Có bao nhiêu số nguyên m để phương trình m(x + 3) = (x
2
− 2)(x
2
− 4) có 4
nghiệm thực phân biệt?
A 4. B 2. C 3. D 5.
Câu 192. Tìm m để đồ thị hàm số y =
1
3
mx
3
+ (2m
2
−1)x
2
+ (m − 1)x − m
3
có các điểm
cực trị nằm về hai phía của trục tung.
A
m < 0
m > 1
. B 0 < m < 1. C m ≥ 1. D m < 0.
Câu 193. Cho hàm số y = f(x) có bảng xét dấu y
0
như hình vẽ.
x
y
0
−∞
−1
3 4
+∞
+
0
− −
0
+
Mệnh đề nào sau đây là sai?
A Hàm số đồng biến trên khoảng (−∞; −2).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 77
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
B Hàm số đồng biến trên khoảng (5; +∞).
C Hàm số nghịch biến trên khoảng (−1; 0).
D Hàm số nghịch biến trên khoảng (1; 4).
Câu 194. Cho hàm số y = −
x
3
3
+ 3x
2
− 5x + 1. Mệnh đề nào dưới đây sai?
A Hàm số đồng biến trên khoảng (1; 5).
B Hàm số nghịch biến trên khoảng (−∞; 1).
C Hàm số nghịch biến trên khoảng (1; 5).
D Hàm số nghịch biến trên khoảng (5; +∞).
Câu 195. Trong các hàm số sau, đồ thị hàm số nào có đường tiệm cận đứng x = 3?
A y =
x + 3
x − 3
. B y =
−x + 3
x + 3
. C y =
x − 3
x
2
− 9
. D y =
3x + 1
x + 3
.
Câu 196. Cho hàm số f(x) có đạo hàm f
0
(x) = (x + 1)
2
(x − 1)
3
(x − 2). Số điểm cực trị
của hàm số f (|x|) là
A 1. B 6. C 5. D 3.
Câu 197.
Đường cong trong hình bên là đồ thị của hàm số nào dưới
đây?
A y = x
3
− 3x − 2. B y = −x
3
+ 3x
2
+ 1.
C y = −x
3
+ 3x
2
− 2. D y = −2x
3
+ 6x
2
− 2.
x
y
O
−2
1 2
2
Câu 198. Cho hàm số y =
√
1 − 4x
x + 1
. Hỏi đồ thị hàm số trên có tất cả bao nhiêu đường
tiệm cận đứng và ngang?
A 0. B 3. C 1. D 2.
Câu 199. Có bao nhiêu giá trị nguyên của tham số m để phương trình 4x
√
4x − m − 2
=
x
3
+ (m − 8)
√
4x − m có hai nghiệm thực phân biệt?
A 4. B 5. C 8. D 6.
Câu 200. Cho hàm số y = f(x) có bảng biến thiên sau đây
x
y
0
y
−∞
−2
0 1
+∞
− +
0
− −
+∞+∞
55
77
−1
+∞
−∞−∞
Trong các mệnh đề sau, mệnh đề nào sai?
A Hàm số có hai điểm cực trị.
B Đồ thị hàm số có một tiệm cận đứng.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 78
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
C Hàm số nghịch biến trên khoảng (0; +∞).
D Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt.
Câu 201. Cho hàm số y =
x + 2
x
2
− mx + 4
có đồ thị (C). Tìm m để (C) có 3 đường tiệm
cận.
A m ∈ (−∞; −4) ∪ (4; +∞). B m ∈ (−∞; −4) ∪ [4; +∞).
C m ∈ (4; +∞). D Không tồn tại m.
Câu 202. Đồ thị hàm số y =
2x
2
+ x
x + 1
có hai điểm cực trị A, B. Tìm tọa độ trung điểm của
đoạn AB.
A (1; 2). B (1; 3). C (−1; −3). D (−1; −2).
Câu 203. Cho hàm số y = x
3
− 9x
2
+ 17x + 2 có đồ thị (C). Qua điểm M(−2; 5) kẻ được
tất cả bao nhiêu tiếp tuyến đến (C)?
A 0. B 1. C 2. D 3.
Câu 204. Tìm m để hàm số y = mx
3
− 2mx
2
+ 3x − 1 có cực đại và cực tiểu.
A m > 2. B m < 2. C m < 0 ∨ m >
9
4
. D 0 < m <
9
4
.
Câu 205. S là tập tất cả các số nguyên m để phương trình cos
2
x = m + sin x có nghiệm.
Tìm tổng các phần tử của S.
A 0. B 1. C 2. D 3.
Câu 206. Biết rằng tồn tại hai giá trị của m sao cho hàm số y =
x
3
−3x
2
+ m
đạt giá trị
nhỏ nhất bằng 2 trên đoạn [−2; 3]. Tính tổng hai giá trị đó.
A 18. B 24. C 20. D 22.
Câu 207. Với mỗi số thực m ∈ (−1; 1), kí hiệu S
m
là diện tích hình phẳng giới hạn bởi
đồ thị hàm số y = |x| và đường thẳng d: y = mx + 1. Khi đó giá trị nhỏ nhất S của S
m
thỏa
A 0 < S ≤
2
3
. B
2
3
< S ≤
4
3
. C
4
3
< S ≤ 2. D S > 2.
Câu 208. Cho hàm số y = x
3
+ ax
2
− 3x + b có đồ thị (C). Hỏi có bao nhiêu cặp (a, b)
nguyên dương để (C) cắt trục hoành tại 3 điểm phân biệt?
A 0. B 4. C 1. D vô số.
Câu 209. Cho hàm số y =
x
3
3
− 2x
2
+ 3x +
2
3
. Toạ độ điểm cực đại của đồ thị hàm số
là
A (1; 2). B (−1; 2). C
Å
3;
2
3
ã
. D (1; −2).
Câu 210. Số điểm cực trị của hàm số f(x) = 21x
4
+ 5x
2
+ 2018 là
A 1. B 3. C 2. D 0.
Câu 211. Cho hàm số f(x) = x
3
− x
2
+ ax + b có đồ thị là (C). Biết (C) có điểm cực tiểu
là A (1; 2). Giá trị 2a − b bằng
A −1. B 1. C −5. D 5.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 79
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 212.
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Đồ thị hàm
f(x) như hình vẽ. Số đường tiệm cận đứng của đồ thị hàm số y =
x
2
− 1
f
2
(x) − 4f(x)
bằng
A 3. B 1. C 2. D 4.
O
x
y
−1 1
2
4
Câu 213. Cho hàm số y = −x
3
+ 3x
2
+ 2 có đồ thị (C). Phương trình tiếp tuyến của (C)
mà có hệ số góc lớn nhất là
A y = 3x + 1. B y = −3x + 1. C y = 3x − 1. D y = −3x − 1.
Câu 214. Cho hàm số y = −x
3
+ 3x
2
+ 9x − 5. Mệnh đề nào sau đây đúng?
A Hàm số đồng biến trên (−1; 3); nghịch biến trên mỗi khoảng (−∞; −1) , (3; +∞).
B Hàm số đồng biến trên mỗi khoảng (−∞; −3) , (1; +∞); nghịch biến trên (−3; 1).
C Hàm số đồng biến trên mỗi khoảng (−∞; −1) , (3; +∞); nghịch biến trên (−1; 3).
D Hàm số đồng biến trên (−1; 3); nghịch biến trên (−∞; −1) ∪ (3; +∞).
Câu 215. Cho hàm số y = x
3
− 3x
2
− 9x + 11. Tổng giá trị lớn nhất và giá trị nhỏ nhất
của hàm số trên đoạn [−2; 2] bằng
A 25. B 5. C −5. D 0.
Câu 216. Trong các hàm số sau hàm số nào có cực đại, cực tiểu và x
CT
< x
CĐ
?
A y = −x
3
+ 9x
2
+ 3x + 2. B y = −x
3
− 3x − 2.
C y = x
3
− 9x
2
− 3x + 5. D y = x
3
+ 2x
2
+ 8x + 2.
Câu 217. Cho hàm số y =
2
√
x + m
√
x + 1
. Giá trị nguyên lớn hơn 1 của tham số m sao cho
max
x∈[0;4]
y ≤ 3 thỏa mãn
A m > 8. B 4 < m ≤ 6 . C Không có m. D 1 < m < 5.
Câu 218. Cho hàm số f(x) = (1 − m
3
)x
3
+ 3x
2
+ (4 − m)x + 2 với m là tham số. Có bao
nhiêu số nguyên m ∈ [−2018; 2018] sao cho f(x) ≥ 0 với mọi giá trị x ∈ [2; 4]?
A 2020. B 2019. C 4037. D 2021.
Câu 219.
Đồ thị hình bên là của hàm số nào?
A y = −x
3
− 3x. B y = x
3
+ 3x.
C y = x
3
− 3x. D y = −x
3
+ 3x.
O
x
y
2
−1
1
−2
Câu 220. Đường tiệm cận ngang của đồ thị hàm số y =
3x + 1
2 − x
là
A y = 2. B y =
3
2
. C y = −3. D y =
1
2
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 80
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 221. Hàm số nào sau đây là hàm số đồng biến trên R?
A y =
x
√
x
2
+ 1
. B y = (x
2
− 1)
2
− 3x + 2.
C y =
x
x + 1
. D y = tan x.
Câu 222.
Cho hàm số y = f (x). Hàm số y = f
0
(x) có đồ thị
như hình vẽ sau. Hàm số y = f(x
2
) đồng biến trên
khoảng
A (−2; +∞). B (−1; 1).
C (1; 2). D (−2; −1).
O
x
y
y = f
0
(x)
−1
1
4
Câu 223. Gọi A, B là giao điểm của đồ thị hàm số y =
2x − 1
x + 2
với đường thẳng y = x −2.
Độ dài AB bằng
A 2
√
2. B 1. C 4
√
2. D
√
2.
Câu 224. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu
điểm cực trị?
x
f
0
(x)
f(x)
−∞
−1
0 1
+∞
+
0
− +
0
−
−∞−∞
22
−1 −1
33
−∞−∞
A Có ba điểm. B Có bốn điểm. C Có một điểm. D Có hai điểm.
Câu 225. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
x
3
− 3x
2
− 9x + 35 trên đoạn [−4; 4]. Tính M · m.
A −1640. B −984. C 1640. D 320.
Câu 226. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y =
x + 1
√
mx
2
+ 1
có hai đường tiệm cận ngang.
A m < 0.
B m = 0.
C Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài.
D m > 0.
Câu 227. Cho hàm số y = ax
3
+ bx
2
+ cx + d, biết đồ thị hàm số đi qua các điểm A(2; 4),
B(3; 9) và C(4; 16). Các đường thẳng AB, AC, BC cắt đồ thị lần lượt tại các điểm D, E,
F . Biết x
D
+ x
E
+ x
F
= −18. Tính f(0).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 81
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A −
8
3
. B −
1
3
. C 0. D −
1
8
.
Câu 228. Tổng số giữa giá trị cực đại và giá trị cực tiểu của hàm số y = x
3
−3x
2
+1 là
A 6. B 2. C 4. D −2.
Câu 229.
Cho hàm số y = f(x) có bảng biến
thiên như hình bên. Hàm số y =
f(x) đồng biến trên khoảng nào dưới
đây?
A (−∞; 2). B (−∞; 0).
C (1; 2). D (0; +∞).
x
y
0
y
-∞
0 2
+∞
−
0
+
0
−
+∞+∞
11
55
−∞−∞
Câu 230.
Cho hàm số y = f(x) có bảng biến
thiên như hình bên. Cực đại của hàm
số là
A −1. B
3. C 4. D
−2.
x
y
0
y
-∞
−1
3
+∞
+
0
−
0
+
−∞−∞
44
−2−2
+∞+∞
Câu 231.
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây?
A y = −x
4
+ 2x
2
− 3. B y = x
4
− 2x
2
+ 3.
C y = x
3
− 3x
2
+ 1. D y = −x
3
+ 3x
2
+ 1.
O
x
y
2
1
Câu 232. Đồ thị của hàm số nào dưới đây có tiệm cận ngang?
A y =
x
2
− 3x + 2
x − 1
. B y =
x
3
+ 3
x
2
+ 1
. C y =
√
1 − x
2
. D y =
3x − 2
x
2
+ 1
.
Câu 233.
Cho hàm số y = f(x) có bảng biến thiên
như hình bên. Số nghiệm của phương trình
f(x) + 2 = 0 là
A 0. B 3. C 4. D 2.
x
y
0
y
−∞
−2
0 2
+∞
+
0
−
0
+ −
−∞−∞
33
−1−1
33
−∞−∞
Câu 234. Giá trị nhỏ nhất của hàm số f(x) = x
4
− 4x
2
+ 15 trên đoạn [−2; 3] bằng
A 60. B 15. C 11. D 132.
Câu 235. Tìm tất cả các giá trị thực của tham số m để hàm số y = −(m − 1)x
4
+ 2(m −
3)x
2
+ 5 không có cực tiểu.
A 1 ≤ m ≤ 3. B m ≤ 1. C m ≥ 1. D 1 < m ≤ 3.
Câu 236. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất
của hàm số y = −|x
3
− 3x + m| trên đoạn [0; 2] bằng −3. Tổng tất cả các phần tử của S
là
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 82
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
A 1. B 2. C 0. D 6.
Câu 237. Hỏi có bao nhiêu số nguyên dương m để hàm số y = −(m
2
−1)x
3
−(m−1)x
2
+x−7
đồng biến trên khoảng (−∞; +∞)?
A 1. B 2. C 0. D 3.
Câu 238. Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = x
4
−2mx
2
+2m+m
4
có ba điểm cực trị tạo thành một tam giác đều.
A m =
3
√
3. B m = 1. C m =
3
√
6
2
. D m =
3
√
3
2
.
Câu 239. Cho hàm số y = x
3
− 2x
2
+ (m − 1)x + 2m có đồ thị là (C
m
). Gọi S là tập hợp
tất cả các giá trị của m để từ M(1; 2) kẻ được đúng hai tiếp tuyến với (C
m
). Tính tổng các
phần tử của S.
A
4
3
. B
81
109
. C
3
4
. D
217
81
.
Câu 240. Kí hiệu M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
x
2
+ x + 4
x + 1
trên đoạn [0; 3]. Tính
M
m
.
A 2. B
2
3
. C
4
3
. D
5
3
.
Câu 241.
Đường cong như hình bên là đồ thị của hàm số nào sau đây?
A y =
1
3
x
3
− x
2
− 2. B y = 2x
3
+ 3x
2
+ 2.
C y = −3x
3
+ 2x
2
+ 2. D y = x
3
− 3x
2
+ 3.
O
x
y
Câu 242. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
y
0
y
−∞
1
+∞
+ +
−1−1
+∞
−∞
−1−1
Số nghiệm của phương trình f(x) − x
2
+ 2x − 1 = 0 là
A vô số. B 0. C 2. D 1.
Câu 243. Cho hàm số y = x
3
+ mx
2
− x − m (C
m
). Hỏi có tất cả bao nhiêu giá trị của
tham số m để đồ thị hàm số (C
m
) cắt trục Ox tại ba điểm phân biệt có hoành độ lập thành
một cấp số cộng ?
A 2. B 3. C 1. D 0.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 83
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 244. Cho hàm số y = f(x) xác định, liên tục trên [−1; 1] và có bảng biến thiên như
sau:
x
y
0
y
−∞
0
+∞
+
0
−
00
11
00
Trong các khẳng định sau, khẳng định nào đúng?
A Hàm số có giá trị lớn nhất bằng 0. B Hàm số có đúng một cực trị.
C Hàm số đạt cực đại tại x = 1. D Hàm số có giá trị cực tiểu bằng 1.
Câu 245. Đồ thị hàm số nào sau đây không có tiệm cận ngang?
A y =
x + 2
x − 1
. B y =
x + 2
x
2
− 1
.
C y =
x
2
x − 1
. D y = x +
√
x
2
− 1.
Câu 246. Cho hàm số y = |x
3
− 3x
2
+ m| với m là tham số. Gọi S là tập hợp tất cả các
giá trị nguyên của tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử
của tập S là
A 3. B 10. C 6. D 5.
Câu 247.
Cho hàm số y = f (x). Hàm số y = f
0
(x) có đồ thị như hình vẽ.
Hàm số y = f(x
2
) đồng biến trên khoảng nào sau đây?
A (1; 2). B (−1; 1). C (1; +∞). D (−2; −1).
O
x
−1
1 4
y
Câu 248. Hàm số y = f(x) có đạo hàm trên R \ {−2; 2}, có bảng biến thiên như sau
x
y
0
y
−∞
−2
0 2
+∞
− −
0
+ +
+∞+∞
−∞
+∞
00
+∞
−∞
−1−1
Gọi k, l là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =
1
f(x) − 2018
.
Tính k + l.
A k + l = 2. B k + l = 3. C k + l = 4. D k + l = 5.
Câu 249. Hàm số y = x
4
− 2x
2
đồng biến trên khoảng nào trong các khoảng sau?
A (−1; 0). B (0; 1). C (0; +∞). D (−∞; −1).
Câu 250. Tìm số đường tiệm cận ngang và đứng của đồ thị hàm số y =
x − 2
x + 1
.
A 3. B 2. C 4. D 1.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 84
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 251. Tìm giá trị cực đại của hàm số y = x
3
−3x
2
+ m (với m là tham số thực).
A 0. B m. C 2. D −4 + m.
Câu 252.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào
sau đây?
A y = x
3
− 3x + 1. B y = −x
3
+ 3x + 1.
C y = −x
3
− 3x + 1. D y = −x
3
+ 1.
−2 −1
2
1
−1
−2
x
y
O
1
2
3
Câu 253. Cho hàm số y = f(x) xác định trên R và có bảng biến thiên như sau
x
f
0
(x)
f(x)
−∞
0 1
+∞
−
0 −
|| +
0
−
+∞+∞
−1−1
33
−∞−∞
−1
f(−1)
Hỏi mệnh đề nào sau đây là mệnh đề sai?
A Hàm số nghịch biến trên khoảng (−∞; 0).
B Hàm số có 3 điểm cực trị.
C Đồ thị hàm số y = f(x) không có tiệm cận ngang.
D Điểm cực tiểu của hàm số là x = 0.
Câu 254.
Cho hàm số y = f(x). Biết rằng hàm số y = f
0
(x) liên tục trên
R và có đồ thị như hình vẽ bên. Hỏi hàm số y = f(5 − x
2
) có
bao nhiêu điểm cực trị?
A 7. B 9. C 4. D 3.
x
y
O
−4 1 4
Câu 255. Tìm giá trị nhỏ nhất của hàm số f(x) = 4x
2
+
1
x
−4 trên khoảng (0; +∞).
A min
x∈(0;+∞)
f(x) = −1. B min
x∈(0;+∞)
f(x) = −4.
C min
x∈(0;+∞)
f(x) = 7. D min
x∈(0;+∞)
f(x) = −3.
Câu 256. Cho hàm số y =
2x + 1
x − 1
có đồ thị là (C). Tiếp tuyến của đồ thị (C) tại điểm
thuộc đồ thị (C) với hoành độ x
0
= 0 cắt hai đường tiệm cận của đồ thị (C) tại hai điểm
A, B. Tính diện tích tam giác IAB, với I là giao điểm hai đường tiệm cận của đồ thị (C).
A S
4IAB
= 6. B S
4IAB
= 3. C S
4IAB
= 12. D S
4IAB
= 6
3
√
2.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 85
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 257. Cho hàm số y =
x + 1
x − m
, với m là tham số thực. Có bao nhiêu giá trị nguyên của
tham số m nhỏ hơn 2 để hàm số đã cho nghịch biến trên khoảng (2; 3)?
A 3. B 4. C 1. D 2.
Câu 258. Có bao nhiêu giá trị nguyên của m lớn hơn −2019 để đồ thị hàm số y = x
3
−
3mx
2
+ 3(m
2
− 1)x + 1 − m
2
có hai điểm phân biệt đối xứng nhau qua gốc tọa độ?
A 2017. B Vô số. C 2019. D 2018.
Câu 259. Cho phương trình
√
x +
√
x − 1
Å
m
√
x +
1
√
x − 1
+ 16
4
√
x
2
− x
ã
= 1, với m
là tham số thực. Tìm số các giá trị nguyên của tham số m để phương trình đã cho có hai
nghiệm thực phân biệt.
A 11. B 9. C 20. D 4.
Câu 260. Hàm số nào dưới đây nghịch biến trên R?
A y =
x + 2
x − 1
. B y = −x
4
− x
2
− 1.
C y = −x
3
+ x
2
− 3x + 11. D y = cot x.
Câu 261. Hàm số nào dưới đây chỉ có cực tiểu và không có cực đại?
A y = −x
4
+ x
2
. B y =
x + 1
x − 1
.
C y = x
4
+ 1. D y = x
3
+ x
2
+ 2x − 1.
Câu 262.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới
đây?
A y =
2x − 1
x + 1
. B y =
x + 1
2x − 1
.
C y =
2x + 1
x − 1
. D y =
x − 1
2x + 1
.
x
y
O
−1−2−3 1 2 3
−1
−2
1
2
3
Câu 263. Cho hàm số y =
mx + n
x − 1
có đồ thị (C). Biết tiệm cận ngang của (C) đi qua
A(−1; 2) và điểm B(2; 1) thuộc (C). Tính m + n.
A −3. B 3. C 1. D −1.
Câu 264. Đồ thị hàm số y = x
4
−2x
2
có bao nhiêu tiếp tuyến song song với trục Ox.
A 3. B 2. C 1. D 0.
Câu 265. Cho hàm số y = x +
√
18 − x
2
. Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ
nhất của hàm số. Khi đó M + m bằng
A 6 − 3
√
2. B 0. C 6. D 6 + 3
√
2.
Câu 266. Tìm tất cả các giá trị thực của tham số m để hàm số y =
1
3
x
3
+ mx + 2 ln x đồng
biến trên (0; +∞).
A m ≤ −3. B m ≥ −3. C m ≥ 3. D m ≤ 3.
Câu 267.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 86
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Cho hàm số y = f(x) có bảng biến
thiên như hình vẽ bên. Hỏi hàm số y =
f (x
2
+ 8x + 2018) có bao nhiêu điểm cực
trị?
A 0. B 2. C 3. D 1.
x
y
0
y
−∞
−2
1
+∞
−
0
+
0
+
+∞+∞
−2−2
+∞+∞
Câu 268. Cho hàm số y = x
3
−3x
2
có đồ thị (C) và điểm A(0; a). Gọi S là tập hợp tất cả
các giá trị thực của a để có đúng hai tiếp tuyến của (C) đi qua A. Tích các giá trị các phần
tử của S là
A 1. B −1. C 0. D 3.
Câu 269. Có bao nhiêu giá trị nguyên của tham số m để phương trình sin
3
2x−
Ä
m +
√
3 cos 2x
ä
3
−
m = 2 sin
Å
2x +
8π
3
ã
có nghiệm?
A 6. B 4. C Vô số. D 5.
Câu 270. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho trị lớn nhất của
hàm số y = |3x
2
− 6x + 2m − 1| trên đoạn [−2; 3] đạt giá trị nhỏ nhất. Số phần tử của tập
S là
A 0. B 3. C 2. D 1.
Câu 271. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
1
3
|x
3
|− (3 −m)x
2
+
(3m + 7) |x| − 1 có 5 điểm cực trị?
A 3. B 5. C 2. D 4.
Câu 272. Cho hàm số y = x
3
− 3x. Mệnh đề nào dưới đây đúng?
A Hàm số đồng biến trên khoảng (−∞; −1) và nghịch biến trên khoảng (1; +∞).
B Hàm số đồng biến trên khoảng (−∞; +∞).
C Hàm số nghịch biến trên khoảng (−∞; −1) và đồng biến trên khoảng (1; +∞).
D Hàm số nghịch biến trên khoảng (−1; 1).
Câu 273. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
2 3
+∞
−
0
+
0
−
+∞+∞
−5−5
11
−∞−∞
Hàm số đạt cực tiểu tại điểm
A x = −5. B x = 2. C x = 3. D x = 1.
Câu 274. Đồ thị hàm số y = (x
2
− 1)(x
2
+ 1) cắt trục hoành tại bao nhiêu điểm phân
biệt?
A 0. B 1. C 2. D 4.
Câu 275. Tính tổng giá trị lớn nhất và nhỏ nhất của hàm số f(x) = x
2
+
2
x
trên đoạn
ï
1
2
; 2
ò
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 87
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A 8. B 5. C 4. D 6.
Câu 276. Cho hàm số y = f(x) xác định trên R và liên tục trên từng khoảng xác định và
có bảng biến thiên
x
y
0
y
−∞
0 1
+∞
− +
0
−
+∞+∞
−1 −∞
22
−∞−∞
Chọn mệnh đề đúng về đồ thị hàm số.
A Đồ thị có đúng một tiệm cận ngang.
B Đồ thị có đúng 2 tiệm cận ngang.
C Đồ thị có đúng một tiệm cận đứng.
D Đồ thị không có tiệm cận ngang và tiệm cận đứng.
Câu 277. Cho hàm số y = x
3
− 3x + 2 có đồ thị (C). Hình vẽ nào sao đây có thể là đồ thị
(C)
A
x
y
O
. B
x
y
1−2
2
O
.
C
x
y
1−2
2
−2
O
. D
x
y
1−2
2
O
.
Câu 278. Cho hàm số y = f(x) xác định trên R \ {0} có bảng biến thiên như hình vẽ sau
x
y
0
y
−∞
0 1
+∞
− +
0
−
+∞+∞
−1 −∞
22
−∞−∞
Số nghiệm của phương trình f(x) + 2 = 0 là
A 0. B 1. C 2. D 3.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 88
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 279. Cho hàm số y =
mx + 2
2x + m
, m là tham số thực. Gọi S là tập hợp tất cả các giá trị
nguyên của tham số m để hàm số nghịch biến trên khoảng (0; 1). Số phần tử của S bằng
A 1. B 5. C 2. D 3.
Câu 280. Cho hàm số y = f(x) có đạo hàm liên tục trên R. Hàm số y = f
0
(x) có đồ thị
như hình vẽ dưới đây
x
y
O
4
1
−1
Cho bốn mệnh đề sau 1) Hàm số y = f(x) có hai điểm cực trị.
2) Hàm số y = f(x) đồng biến trên khoảng (1; +∞).
3) f(1) > f(2) > f(4).
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f(x) là f(1).
Số mệnh đề đúng trong bốn mệnh đề trên là
A 1. B 4. C 2. D 3.
Câu 281. Cho điểm A có hoành độ bằng −1 nằm trên đồ thị hàm số (C): y = 2x
3
−3x
2
+m,
(m ∈ R). Biết tiếp tuyến của (C) tại A cắt đồ thị (C) tại điểm thứ hai là B. Có bao nhiêu
giá trị thực của tham số m để 4ABO vuông tại O?
A 2. B 1. C 3. D 0.
Câu 282. Đồ thị hàm số y =
4x + 4
x − 1
và y = x
2
− 1 cắt nhau tại bao nhiêu điểm?
A 0. B 1. C 2. D 3.
Câu 283. Tìm giá trị nhỏ nhất của hàm số y =
1
x
3
−
1
x
khi x > 0.
A
2
√
3
9
. B −
1
4
. C 0. D −
2
√
3
9
.
Câu 284. Tìm số đường tiệm cận của đồ thị hàm số y =
√
x + 1
|x| − 1
.
A 0. B 1. C 2. D 3.
Câu 285. Một trong các đồ thị hàm số dưới đây là đồ thị của hàm số g(x) liên tục trên R
thỏa mãn g
0
(0) = 0, g
00
(x) < 0, ∀x ∈ (−1; 2). Hỏi đó là đồ thị nào?
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 89
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A
x
y
O
−1
2
1
. B
x
y
O
−1
2
1
.
C
x
y
O
−1
2
1
. D
x
y
O
−1
2
1
.
Câu 286. Tìm tất cả các giá trị của tham số m để hàm số y = x
3
− 3mx
2
− 9m
2
x nghịch
biến trên (0; 1).
A m >
1
3
. B m < −1.
C m ≥
1
3
hoặc m ≤ −1. D −1 < m <
1
3
.
Câu 287. Phương trình |x
2
−2x|(|x| − 1) = m (với m là tham số thực) có tối đa bao nhiêu
nghiệm thực?
A 3. B 4. C 5. D 6.
Câu 288. Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số y = x(x
2
− 3) sao cho tiếp
tuyến tại M của (C) cắt (C) và trục hoành lần lượt tại hai điểm phân biệt A (khác M) và
B sao cho M là trung điểm của AB.
A 0. B 1. C 2. D 3.
Câu 289. Cho hàm số f(x) có đạo hàm liên tục và có đúng 3 điểm cực trị là −2, −1 và 0.
Hỏi hàm số y = f(x
2
− 2x) có bao nhiêu điểm cực trị.
A 3. B 4. C 5. D 6.
Câu 290. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
+ −
0
+
0
−
−∞−∞
22
11
22
−∞−∞
Hàm số y = f(x) nghịch biến trên khoảng nào dưới đây?
A (−∞; −1). B (0; 1). C (−1; 1). D (−1; 0).
Câu 291.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 90
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Cho hàm số y = f(x) có đồ thị như hình bên.
Hàm số đạt cực đại tại điểm
A x = 1. B x = 2.
C x = −1. D x = −3.
x
y
−2
−3
1
−1
1
2
Câu 292. Đồ thị hàm số nào dưới đây không có tiệm cận đứng?
A y =
x
2
+ 1
x + 1
. B y =
x
2
+ 3x + 2
x + 1
. C y =
x − 1
x + 1
. D y =
2
x + 1
.
Câu 293.
Đường cong trong hình bên là đồ thị của hàm số nào dưới
đây?
A y =
x − 1
x + 1
.
B y = −x
4
+ 2x
2
− 1.
C y = x
3
− 3x + 2.
D y =
x + 1
x − 1
.
x
y
0 1
1
Câu 294. Giá trị lớn nhất của hàm số f(x) =
1
3
x
3
−3x
2
+ 5x −
2
3
trên đoạn [0; 5] bằng
A
2
3
. B
5
3
. C −
2
3
. D 5.
Câu 295.
Cho hàm số y = f(x) = ax
4
+ bx
2
+ c có đồ thị như hình bên.
Số nghiệm của phương trình f(x) − 1 = 0 là
A 3. B 2.
C 4. D 1.
x
y
−3
1
Câu 296. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y =
mx + 10
2x + m
nghịch
biến trên khoảng (0; 2)?
A 6. B 5. C 9. D 4.
Câu 297.
Cho hàm số y = f (x). Hàm số y = f
0
(x) có đồ thị như hình
bên. Biết rằng phương trình f
0
(x) = 0 có bốn nghiệm phân
biệt a, 0, b, c với a < 0 < b < c.
Mệnh đề nào dưới đây đúng?
A f(a) > f(b) > f(c). B f (a) > f(c) > f(b).
C f(c) > f(a) > f(b). D f (b) > f(a) > f(c).
x
y
a
0
b c
Câu 298. Cho hàm số y =
1
3
mx
3
− (m − 1)x
2
+ 3(m − 2)x + 2018 với m là tham số. Tổng
bình phương của tất cả các giá trị của m để hàm số có hai điểm cực trị x
1
, x
2
thỏa mãn
2x
1
+ x
2
= 2 bằng
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 91
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A
52
9
. B
10
9
. C
73
16
. D
34
9
.
Câu 299. Biết A(x
1
; y
1
), B(x
2
; y
2
) là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm
số y =
x + 4
x + 1
sao cho độ dài đoạn thẳng AB nhỏ nhất. Tính P = y
2
1
+ y
2
2
− x
1
x
2
.
A P = 6. B P = 6 − 2
√
3. C P = 10 −
√
3. D P = 10.
Câu 300. Cho hàm số f(x) = x
3
− 6x
2
+ 9x. Đặt f
k
(x) = f
f
k−1
(x)
với k là số nguyên
dương lớn hơn 1. Hỏi phương trình f
5
(x) = 0 có tất cả bao nhiêu nghiệm phân biệt?
A 120. B 365. C 122. D 363.
Câu 301. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
mx + 25
x + m
nghịch biến
trên khoảng (−∞; 1)?
A 11. B 4. C 5. D 9.
Câu 302. Đồ thị hàm số nào sau đây có tiệm cận ngang?
A y =
x
x
2
+ 1
. B y =
x
2
x + 1
. C y =
x
2
− 3x + 2
x − 1
. D y =
√
4 − x
2
1 + x
.
Câu 303.
Cho hàm số y = f(x) xác định và liên tục trên R, có
đồ thị ở hình bên. Hàm số y = f(x) nghịch biến trên
khoảng nào dưới đây?
A (0; 1). B (−∞; 0).
C (1; 2). D (2; +∞).
x
y
−1
O
1 2
Câu 304. Tìm giá trị lớn nhất của hàm số y =
x
2
− 3x + 3
x − 1
trên đoạn
ï
−2;
1
2
ò
.
A −
13
3
. B 1. C −3. D −
7
2
.
Câu 305. Cho hàm số y = f(x) xác định và liên tục trên R, có bảng biến thiên như sau
x
y
0
y
−∞
−2
0
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
Tìm tập hợp tất cả các giá trị của tham số m để phương trình f(x) = m có đúng một
nghiệm.
A (−∞; −2) ∪ (2; +∞). B (−∞; −2] ∪ [2; +∞).
C (−2; 2). D [−2; 2].
Câu 306. Điểm cực đại của hàm số y = x
3
− 3x + 1 là
A x = 3. B x = 1. C x = 0. D x = −1.
Câu 307. Cho hàm số y =
x + 2
x + 1
có đồ thị là (C) và I là giao điểm hai đường tiệm cận của
(C). Điểm M di chuyển trên (C). Xác định giá trị nhỏ nhất độ dài đoạn thẳng MI.
A 1. B
√
2. C 2
√
2. D
√
6.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 92
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 308.
Cho hàm số y = f(x) liên tục trên
R và có đồ thị như hình vẽ bên. Đặt
M = max
R
f
2
sin
4
x + cos
4
x

, m =
min
R
f
2
sin
4
x + cos
4
x

. Tính S = M +
m.
A S = 6. B S = 4.
C S = 5. D S = 3.
x
1 2 4
y
1
3
5
O
Câu 309. Cho hàm số f(x) = |x
4
− 4x
3
+ 4x
2
+ a|. Gọi M và m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số đã cho trên [0; 2]. Có bao nhiêu số nguyên a ∈ [−4; 4] sao
cho M ≤ 2m?
A 7. B 5. C 6. D 4.
Câu 310. Cho hàm số y = f(x) có bảng biến thiên như sau:
x
f
0
(x)
f(x)
−∞
−1
3
+∞
−
0
+
0
−
+∞+∞
−1−1
44
−∞−∞
Mệnh đề nào sau đây đúng?
A Hàm số y = f(x) nghịch biến trên (−∞; 3).
B Hàm số y = f(x) đồng biến trên (−1; 3).
C Hàm số y = f(x) đồng biến trên (−1; 4).
D Hàm số y = f(x) nghịch biến trên (−1; +∞).
Câu 311. Giá trị nhỏ nhất của hàm số y =
2x + 1
1 − x
trên đoạn [2; 3] bằng
A
3
4
. B −5. C −
7
2
. D −3.
Câu 312. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = x
3
+ (m +
2)x
2
+ 3x − 3 đồng biến trên khoảng (−∞; +∞)?
A 6. B 7. C 8. D 5.
Câu 313.
Cho hàm số y = f(x) liên tục trên R, đồ thị của hàm số y = f
0
(x)
có dạng như hình vẽ bên. Số nào bé nhất trong các số sau: f(0),
f(1), f(2), f(3)?
A f(1). B f(2). C f(3). D f(0).
1 2 3
x
y
O
y = f
0
(x)
Câu 314. Tìm tất cả các giá trị thực của a để đồ thị hàm số y = ax +
√
9x
2
+ 4 có tiệm
cận ngang.
A a = ±3. B a = −3. C a = ±
1
3
. D a = −
1
3
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 93
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 315. Tìm m để đồ thị hàm số y = x
3
− 3x
2
+ 3(m + 1)x − m − 1 có hai điểm cực trị
nằm cùng phía đối với trục hoành.
A m ∈ (−∞; 0). B m ∈ (−1; +∞).
C m ∈ (−1; 0). D m ∈ (−∞; −1) ∪ (0; +∞).
Câu 316. Cho đường thẳng d : y = mx + m + 2 (m là tham số) và đường cong (C) : y =
2x − 1
x + 1
. Biết rằng khi m = m
0
thì (C) cắt d tại hai điểm A, B thỏa mãn độ dài AB ngắn
nhất. Khẳng định nào sau đây đúng?
A m
0
∈ (−4; −3). B m
0
∈ (−5; −4). C m
0
∈ (−2; 0). D m
0
∈ (−3; −1).
Câu 317. Đồ thị hàm số y = x
4
− x
3
− 3 cắt trục tung tại mấy điểm?
A 1 điểm. B 2 điểm. C 4 điểm. D 3 điểm.
Câu 318. Số đường tiệm cận của đồ thị hàm số y =
2x − 1
x + 3
là
A 2. B 3. C 1. D 0.
Câu 319. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
11
22
11
+∞+∞
Xác định số điểm cực tiểu của hàm số y = f(x).
A 3. B 6. C 2. D 1.
Câu 320. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
00
−1−1
+∞+∞
Tìm tất cả các giá trị của m để phương trình f(x) = m có đúng hai nghiệm.
A m > 0. B m ≥ −1.
C m > 0 hoặc m = −1. D m ≥ 0 hoặc m = −1.
Câu 321. Giá trị nhỏ nhất của hàm số y = 4x
3
− 3x
4
trên đoạn [−1; 2] là
A −7. B −24. C 0. D −16.
Câu 322. Hàm số y =
√
x
2
− 2x nghịch biến trên khoảng nào?
A (1; +∞). B (−∞; 0). C (2; +∞). D (−∞; 1).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 94
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 323. Cho hàm số y = f (x) có đạo hàm f
0
(x) = 2018(x − 1)
2017
(x − 2)
2018
(x − 3)
2019
.
Tìm số điểm cực trị của f(x).
A 2. B 1. C 3. D 0.
Câu 324. Cho hàm số f(x) = |x
3
− 3x
2
+ m| với m ∈ [−5; 7] là tham số. Có bao nhiêu giá
trị nguyên của m để hàm số có đúng ba điểm cực trị?
A 13. B 12. C 10. D 8.
Câu 325. Hàm số y =
1
3
x
3
− (m − 3)x + 2018 luôn đồng biến trên R thì
A m ≤ 4. B m ≤ 3. C m ≤ 2018. D m ≤ 9.
Câu 326. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y =
x − 3
x
2
− 2mx + 1
có hai
đường tiệm cận đứng.
A m ∈ (−∞; −1) ∪ (1; +∞). B m ∈ (−∞; −1] ∪ [1; +∞).
C m 6=
5
3
. D m ∈ (−∞; −1) ∪ (1; +∞) \
ß
5
3
™
.
Câu 327. Cho hàm số f(x) = x
3
+ ax
2
+ bx − 2 thỏa mãn
a + b > 1
3 + 2a + b < 0
. Số điểm cực
trị của hàm số y = |f (|x|)| là
A 9. B 11. C 2. D 5.
Câu 328. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên dưới.
x
y
0
y
−∞
0 2
+∞
+
0
−
0
+
−∞−∞
11
−1−1
+∞+∞
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A (2; +∞). B (−∞; +∞). C (−∞; 1). D (0; +∞).
Câu 329. Cho hàm số y = f(x) có đồ thị như hình vẽ bên dưới.
Hàm số y = f(x) đạt cực đại tại điểm nào sau đây?
A x = 1. B x = −1. C y = −2. D y = 2.
x
y
O
−1 1
−2
2
Câu 330. Tìm tiệm cận ngang của đồ thị hàm số y =
2x + 1
x − 1
.
A x = −1. B
y = −1. C x = 1. D y = 2.
Câu 331. Tìm giá trị nhỏ nhất của hàm số y = x − 5 +
1
x
trên khoảng (0; +∞).
A min
(0;+∞)
y = 2. B min
(0;+∞)
y = −4. C min
(0;+∞)
y = −3. D min
(0;+∞)
y = −5.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 95
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 332. Cho hàm số có đồ thị như hình vẽ bên dưới.
Tìm tất cả các giá trị thực của tham số m để đường thẳng
y = 2m − 1 cắt đồ thị tại hai điểm phân biệt có hoành độ
lớn hơn 2.
A 1 < m < 2. B 1 6 m < 2.
C 1 6 m 6 2. D 1 < m < 3.
x
y
O
1 2 3
1
3
5
Câu 333. Có bao nhiêu giá trị nguyên của m để hàm số y =
x
3
3
−
mx
2
2
+ 2x + 2019 đồng
biến trên R?
A 3. B 4. C 5. D 6.
Câu 334. Khoảng cách từ điểm cực tiểu của đồ thị hàm số y = x
3
−3x
2
+ 2 đến trục tung
bằng
A 1. B 2. C 4. D 0.
Câu 335. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y =
3
4
x
4
− (m −
1)x
2
−
1
4x
4
đồng biến trên khoảng (0; +∞)?
A 1. B 2. C 3. D 4.
Câu 336. Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau:
x
f
0
(x)
−∞
−3
1 3
+∞
−
0
+
0
−
0
+
Bất phương trình f(x) < e
x
2
−2x
+ m đúng ∀x ∈ (0; 2) khi chỉ khi
A m > f(1) −
1
e
. B m > f(1) −
1
e
. C m > f(0) − 1. D m > f(0) − 1.
Câu 337. Tập hợp các giá trị của tham số m để hàm số y = |3x
4
−4x
3
−12x
2
+ m −1| có
7 điểm cực trị là
A (0; 6). B (6; 33). C (1; 33). D (1; 6).
Câu 338. Tâm đối xứng của đồ thị hàm số nào sau đây cách gốc tọa độ một khoảng lớn
nhất?
A y =
2x − 1
x + 3
. B y =
1 − x
1 + x
.
C y = 2x
3
− 3x
2
− 2. D y = −x
3
+ 3x − 2.
Câu 339. Một sợi dây kim loại dài a (cm). Người ta cắt đoạn dây đó thành hai đoạn, đoạn
có độ dài x (cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông
(a > x > 0). Tìm x để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
A x =
a
π + 4
(cm). B x =
2a
π + 4
(cm). C x =
πa
π + 4
(cm). D x =
4a
π + 4
(cm).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 96
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 340. Gieo một con súc sắc cân đối đồng chất một lần. Giả sử con súc sắc xuất hiện
mặt k chấm. Xét phương trình −x
3
+ 3x
2
−x = k. Tính xác suất để phương trình trên có 3
nghiệm thực phân biệt.
A
1
3
. B
1
2
. C
2
3
. D
1
6
.
Câu 341. Gọi S là tập hợp các giá trị của m sao cho đường thẳng d : y = mx − m − 3 cắt
đồ thị (C) : y = 2x
3
− 3x
2
− 2 tại ba điểm phân biệt A, B, I(1; −3) mà tiếp tuyến với (C)
tại A và B vuông góc với nhau. Tính tổng các phần tử của S.
A −1. B 1. C 2. D 5.
Câu 342. Tìm tất cả các giá trị của m sao cho đồ thị hàm số y = x
4
+ (m + 1)x
2
−2m −1
có ba điểm cực trị là ba đỉnh của một tam giác có một góc bằng 120
◦
.
A m = −1 −
2
3
√
3
. B m = −1 −
2
3
√
3
, m = −1.
C m = −
1
3
√
3
. D m < −1.
Câu 343. Đường thẳng y = m tiếp xúc với đồ thị (C) : y = −2x
4
+ 4x
2
− 1 tại hai điểm
phân biệt. Tìm tung độ tiếp điểm.
A −1. B 1. C 0. D 3.
Câu 344. Cho hàm số f(x) có f
0
(x) = x
2017
· (x − 1)
2018
· (x + 1), ∀x ∈ R.
Hàm số đã cho có bao nhiêu cực trị?
A 0. B 1. C 2. D 3.
Câu 345 (Thi thử L5, Toán học tuổi trẻ, 2018).
[Phan Quốc Trí, dự án 12-EX6][2D1B4-3] Đường tiệm cận đứng và đường tiệm cận ngang
của đồ thị hàm số y =
mx + 1
2m + 1 − x
cùng với hai trục tọa độ tạo thành một hình chữ nhật
có diện tích bằng 3. Tìm m.
A m = 1, m =
3
2
. B m = −1, m = −
3
2
.
C m = 1, m = −
3
2
. D m = −1, m = 3.
Câu 346 (Thi thử L5, Toán học tuổi trẻ, 2018).
[Phan Quốc Trí, dự án 12-EX6][2D1B3-1] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
f(x) =
8
1 + 2x
+ x trên đoạn [1; 2] lần lượt là
A
11
3
;
7
2
. B
11
3
;
18
5
. C
13
3
;
7
2
. D
18
5
;
3
2
.
Câu 347 (Thi thử L5, Toán học tuổi trẻ, 2018).
[Phan Quốc Trí, dự án 12-EX6][2D1B2-1] Viết phương trình đường thẳng đi qua hai điểm
cực trị của đồ thị hàm số y =
x
2
+ 2x + 3
2x + 1
.
A y = 2x + 2. B y = x + 1. C y = 2x + 1. D y = 1 − x.
Câu 348 (Thi thử L5, Toán học tuổi trẻ, 2018).
[Phan Quốc Trí, dự án 12-EX6][2D1B5-7] Trên đồ thị hàm số y =
2x − 1
3x + 4
có bao nhiêu điểm
có tọa độ nguyên?
A 1. B 2. C 0. D 4.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 97
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 349. Cho hàm số y =
x + 1
2 − x
. Mệnh đề nào dưới đây đúng?
A Hàm số nghịch biến trên từng khoảng xác định của nó.
B Hàm số đồng biến trên từng khoảng xác định của nó.
C Hàm số đồng biến trên (−∞; 2) ∪ (2; +∞).
D Hàm số nghịch biến trên khoảng (−∞; +∞).
Câu 350.
Cho hàm số y = f(x) có đồ thị như hình bên. Khi đó f(x) đồng
biến trên các khoảng
A (−∞; −1) , (1; +∞).
B (−∞; −1) , (−1; 0).
C (−1; 0) , (1; +∞).
D (−1; 0) , (0; 1).
−2
2
−1
1
2
O
x
y
Câu 351. Số đường tiệm cận của đồ thị hàm số y =
x
√
x
2
+ 1
là
A 1. B 2. C 4. D 3.
Câu 352. Hàm số y = x
3
− 3x
2
+ 3x − 4 có bao nhiêu cực trị?
A 1. B 2. C 0. D 3.
Câu 353. Giá trị của tham số m để phương trình x
3
− 3x = 2m + 1 có ba nghiệm phân
biệt là
A −
3
2
< m <
1
2
. B −2 < m < 2. C −
3
2
≤ m ≤
1
2
. D −2 ≤ m ≤ 2.
Câu 354. Cho đường cong (C ) : y =
2x + 3
x − 1
và M là điểm bất kỳ trên (C ). Giả sử d
1
, d
2
tương ứng là các khoảng cách từ M đến hai tiệm cận của (C ), khi đó d
1
· d
2
bằng
A 3. B 4. C 5. D 6.
Câu 355. Cho hàm số y =
x +
√
4x
2
− 3
2x + 3
có đồ thị (C ). Gọi m là số tiệm cận của (C ) và
n là giá trị của hàm số tại x = 1. Tính tích m × n.
A
6
5
. B
14
5
. C
3
5
. D
2
15
.
Câu 356. Giả sử A, B là hai điểm cực trị của đồ thị hàm số f(x) = x
3
+ ax
2
+ bx + c và
đường thẳng AB đi qua gốc tọa độ. Tính giá trị nhỏ nhất của biểu thức P = abc+ab+c.
A −
16
25
. B −9. C −
25
9
. D 1.
Câu 357. Hai điểm M, N thuộc hai nhánh khác nhau của đồ thị hàm số y =
3x − 1
x − 3
. Khi
đó độ đà đoạn thẳng MN ngắn nhất bằng
A 8
√
2. B 2017. C 8. D 4.
Câu 358. Cho hàm số y = f(x) có bảng biến thiên như sau.
x
f
0
(x)
f(x)
−∞
−1
1
+∞
−
0
+
0
−
+∞+∞
−2−2
22
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 98
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Hàm số đã cho đạt cực tiểu tại điểm x
0
bằng
A −1. B −2. C 1. D 2.
Câu 359. Đồ thị hàm số y =
x
2
− 3x + 2
x
2
− 1
có tất cả bao nhiêu đường tiệm cận?
A 3. B 1. C 0. D 2.
Câu 360.
Hàm số nào có đồ thị như hình bên?
A y = −x
3
+ 3x
2
− 1. B y = −x
3
+ 3x − 1.
C y = x
3
− 3x − 1. D y = −x
3
− 3x − 1.
x
y
O
1
−1
−2
2
−3
−2
−1
Câu 361. Cho hàm số y = f(x) có đạo hàm f
0
(x) = x
2
(4 − x
2
). Hàm số f(x) đồng biến
trên khoảng nào sau đây?
A (−2; 1). B (2; +∞). C (−∞; −2). D (−∞; +∞).
Câu 362. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
x
x
2
+ 1
trên đoạn [−1; 2]
bằng
A 0. B −
1
10
. C 1. D
9
10
.
Câu 363. Cho hàm số y = f(x) xác định trên R và có bảng biến thiên như hình vẽ.
x
f
0
(x)
f(x)
−∞
0 2
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
Hỏi phương trình 2f(x) + 3 = 0 có bao nhiêu nghiệm?
A 4. B 1. C 2. D 3.
Câu 364. Cho hàm số y = f(x) có đạo hàm f
0
(x) = x
3
−x
2
−m
2
x+m
2
, m là tham số thực.
Có bao nhiêu giá trị nguyên của m thuộc khoảng (−2019; 2019) để hàm số đã cho nghịch
biến trên khoảng (1; 10)?
A 4018. B 21. C 4016. D 18.
Câu 365. Biết đồ thị hàm số y = x
3
− 2ax
2
+ a
2
x + b có một điểm cực tiểu là
Å
−
1
2
;
1
4
ã
.
Khi đó giá trị cực đại của hàm số đã cho bằng
A
3
4
. B
79
108
. C
83
108
. D
5
4
.
Câu 366.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 99
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Đường cong ở hình bên là đồ thị hàm số nào?
A y = x
3
− 3x − 1.
B y = −x
3
+ 3x
2
+ 1.
C y = x
3
− 3x + 1.
D y = −x
3
− 3x
2
− 1.
1
−1
3
1
−1
O
x
y
Câu 367. Phương trình tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y =
1 − 2x
−x + 2
lần lượt là
A x = −2; y = −2. B x = 2; y = −2. C x = −2; y = 2. D x = 2; y = 2.
Câu 368. Cho hàm số y =
x + 1
2 − x
. Khẳng định nào sau đây đúng?
A Hàm số đã cho đồng biến trên từng khoảng xác định của nó.
B Hàm số đã cho nghịch biến trên R.
C Hàm số đã cho đồng biến trên khoảng (−∞; 2) ∪ (2; +∞).
D Hàm số đã cho nghịch biến trên từng khoảng xác định của nó.
Câu 369. Trong các hàm số sau, hàm số nào không đồng biến trên tập số thực?
A y = 4x − 3 sin x + cos x. B y = 3x
3
− x
2
+ 2x − 7.
C y = 4x −
3
x
. D y = x
3
+ x.
Câu 370. Có bao nhiêu tiếp tuyến của đồ thị hàm số y = x
4
− 2x
2
+ 1 song song với trục
hoành?
A 2. B 1. C 0. D 3.
Câu 371. Tìm giá trị cực tiểu y
CT
của hàm số y = x
3
− 3x
2
+ 2.
A y
CT
= 4. B y
CT
= 1. C y
CT
= 0. D y
CT
= −2.
Câu 372. Cho hàm số y =
1
3
x
3
+ x
2
− 2, có đồ thị (C). Phương trình tiếp tuyến của (C)
tại điểm có hoành độ là nghiệm của phương trình y
00
(x) = 0 là
A y = −x −
7
3
. B y = x −
7
3
. C y = −x +
7
3
. D y =
7
3
x.
Câu 373. Xét tính đúng sai của các mệnh đề sau (với a, b, c, d là các hằng số).
(I): Giá trị cực đại của hàm số y = f(x) luôn lớn hơn giá trị cực tiểu của nó.
(II): Hàm số y = ax
4
+ bx
2
+ c (a 6= 0) luôn có ít nhất 1 điểm cực trị.
(III): Giá trị cực đại của hàm số y = f(x) luôn lớn hơn mọi giá trị của hàm số đó trên tập
xác định.
(IV): Hàm số y = f(x) =
ax + b
cx + d
(c 6= 0; ad − bc 6= 0) không có cực trị.
Số mệnh đề đúng là:
A 1. B 4. C 3. D 2.
Câu 374. Biết đường thẳng d : y = x − 2 cắt đồ thị hàm số y =
2x + 1
x − 1
tại hai điểm phân
biệt A và B có hoành độ lần lượt là x
A
và x
B
. Giá trị của biểu thức x
A
+ x
B
bằng
A 2. B 5. C 1. D 3.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 100
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 375. Tìm tất cả giá trị của tham số thực m để đường thẳng d : y = x + m cắt đồ thị
hàm số y =
−x + 1
2x − 1
tại hai điểm phân biệt A, B.
A m < 0. B m ∈ R. C m > 1. D m = 5.
Câu 376. Cho hàm số y = x
4
− 2(m + 1)x
2
+ m có đồ thị (C), m là tham số. (C) có ba
điểm cực trị A, B , C sao cho OA = BC, trong đó O là gốc tọa độ, A là điểm cực trị thuộc
trục tung khi
A m = 0 hoặc m = 2. B m = 2 ± 2
√
2.
C m = 3 ± 3
√
3. D m = 5 ± 5
√
5.
Câu 377. Cho hàm số y =
x + 3
x + 1
có đồ thị (C) và đường thẳng d : y = 2x + m. Tìm tất cả
các giá trị thực của tham số m để d cắt (C) tại hai điểm phân biệt M, N sao cho MN nhỏ
nhất.
A m = −1. B m = 3. C m = 2. D m = 1.
Câu 378.
Cho hàm số y = f(x) có đạo hàm f
0
(x), biết rằng đồ thị của
hàm số f
0
(x) như hình vẽ. Biết f(a) > 0, hỏi đồ thị hàm số
y = f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
A 4.
B 2.
C 3.
D 1.
x
y
O
a
b
c
Câu 379. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y =
x
2
+ 2
√
mx
4
+ 3
có
một đường tiệm cận ngang.
A m < 0. B m > 3. C m = 0. D m > 0.
Câu 380. Thầy Tâm cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có
thể tích bằng
500
3
m
3
. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê
nhân công để xây hồ là 500.000 đồng/m
2
. Khi đó, kích thước của hồ nước như thế nào để
chi phí thuê nhân công mà thầy Tâm phải trả thấp nhất?
A Chiều dài 20 m, chiều rộng 15 m và chiều cao
20
3
m.
B Chiều dài 20 m, chiều rộng 10 m và chiều cao
5
6
m.
C Chiều dài 10 m, chiều rộng 5 m và chiều cao
10
3
m.
D Chiều dài 30 m, chiều rộng 15 m và chiều cao
10
27
m.
Câu 381. Cho một tấm tôn hình chữ nhật có kích thước 10 cm × 16 cm. Người ta cắt bỏ
4 góc của tấm tôn 4 miếng hình vuông bằng nhau rồi gò lại thành một hình hộp chữ nhật
không có nắp. Để thể tích của hình hộp đó lớn nhất thì độ dài cạnh hình vuông của các
miếng tôn bị cắt bỏ bằng
A 2 m. B 4 m. C 5 m. D 3 m.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 101
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 382. Cho hàm số y =
3x − 1
x − 2
. Tìm m để đường thẳng y = x + m cắt đồ thị tại 2 điểm
phân biệt A, B sao cho tam giác OAB vuông tại O với O là gốc tọa độ.
A
3
2
. B
5
2
. C −
3
2
. D −2.
Câu 383. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x −2
√
x trên đoạn [0; 9] lần
lượt là m và M. Giá trị của tổng m + M bằng
A 0. B 1. C 2. D 3.
Câu 384. Cho hàm số y =
x
3
+ x − 2
x
2
− 3x + 2
. Đồ thị hàm số có mấy tiệm cận?
A 1. B 2. C 0. D 3.
Câu 385. Cho hàm số y =
1 + x
2 − x
. Mệnh đề nào dưới đây đúng?
A Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).
B Hàm số đồng biến trên R.
C Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞).
D Hàm số đồng biến trên khoảng R\{2}.
Câu 386. Hàm số y = −x
4
+ 3x
2
− 1 có mấy cực đại?
A 2. B 0. C 1. D 3.
Câu 387. Cho hàm số y =
1
3
x
3
− (m − 1)x
2
+ x + m. Tìm m để hàm số đồng biến trên
R.
A 0 < m < 2. B m > 2 hoặc m < 0.
C m ≥ 2 hoặc m ≤ 0. D 0 ≤ m ≤ 2.
Câu 388. Cho hàm số y = x
4
+ 2m(m + 2)x
2
+ m + 2, với m là tham số. Tìm tất cả các
giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác có diện tích lớn
nhất.
A m =
−1
2
. B m =
−3
2
. C m = −1. D m =
−1
3
√
3
.
Câu 389. Cho hàm số y =
−x
2x + 1
có đồ thị là (C). Tìm tất cả các giá trị của m sao cho
đường thẳng y = x + m cắt (C) tại 2 điểm phân biệt A, B và tổng các hệ số góc của các tiếp
tuyến với (C) tại A, B là lớn nhất.
A m =
−1
2
. B m = 0. C m = 1. D m = −1.
Câu 390. Hàm số nào sau đây đồng biến trên R?
A y = x
2
+ 1. B y =
x
x + 1
. C y = x + 1. D y = x
4
+ 1.
Câu 391. Cho hàm số y = f(x) xác định trên khoảng K. Điều kiện đủ để hàm số y = f(x)
đồng biến trên K là
A f
0
(x) > 0 với mọi x ∈ K.
B f
0
(x) > 0 tại hữu hạn điểm thuộc khoảng K.
C f
0
(x) 6 0 với mọi x ∈ K.
D f
0
(x) > 0 với mọi x ∈ K.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 102
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 392. Điểm cực đại của đồ thị hàm số y = −x
3
+ 6x
2
− 9x + 4 là
A (1; 0). B (3; 4). C (−1; 0). D (2; 2).
Câu 393. Đồ thị hàm số y =
2x − 3
x − 1
có các đường tiệm cận đứng và tiệm cận ngang lần
lượt là
A x = 1 và y = −3. B x = 2 và y = 1.
C x = 1 và y = 2. D x = −1 và y = 2.
Câu 394.
Cho hàm số y = ax
3
+ bx
2
+ cx + d có đồ thị như hình vẽ bên.
Mệnh đề nào dưới đây đúng?
A a < 0, b > 0, c > 0, d > 0.
B a < 0, b < 0, c = 0, d > 0.
C a > 0, b < 0, c > 0, d > 0.
D a < 0, b > 0, c = 0, d > 0.
x
y
O
Câu 395.
Đồ thị sau là đồ thị của hàm số nào sau?
A y =
2x − 3
2x − 2
. B y =
x
x − 1
.
C
x − 1
x + 1
. D y =
x + 1
x − 1
.
x
y
O
−1 1
−1
1
Câu 396. Tìm giá trị nhỏ nhất của hàm số y = sin
2
x − 4 sin x − 5.
A −20. B −8. C −9. D 0.
Câu 397. Tìm tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = 3x + 1
cắt đồ thị hàm số y = x
3
+ 2x
2
− mx + 1 tại ba điểm phân biệt.
A (−4; +∞) \ {−3}. B (−7; +∞).
C (−4; +∞). D (−7; +∞) \ {−3}.
Câu 398. Cho hàm số y =
x + m
x − 1
(với m là tham số thực) thỏa mãn min
[2;4]
y = 3. Mệnh đề
nào dưới đây là đúng?
A 3 < m ≤ 4. B
1 ≤ m < 3. C m > 4. D m < −1.
Câu 399.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 103
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số y = f(x) có đồ thị như hình bên.
Số đường tiệm cận đứng của đồ thị hàm số y =
x
2
− x − 2
f
2
(x) − 5f(x)
là
A 3. B 4. C 1. D 2.
x
y
O
5
1−1 2−2
Câu 400. Có bao nhiêu giá trị nguyên m ∈ (−10; 10) để hàm số y = m
2
x
4
−2(4m−1)x
2
+1
đồng biến trên khoảng (1; +∞)?
A 7. B 16. C 15. D 6.
Câu 401. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như hình
vẽ bên dưới
x
y
0
y
−∞
0 1
+∞
+ −
0
+
−∞−∞
00
−1−1
+∞+∞
Khẳng định nào sau đây là khẳng định đúng?
A Hàm số có đúng một cực trị.
B Hàm số có giá trị cực tiểu bằng 1.
C Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
D Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1.
Câu 402.
Cho bảng biến thiên như hình vẽ bên. Mệnh
đề nào sau đây sai?
A Hàm số đã cho đồng biến trên khoảng
(−∞; 1).
B Hàm số đã cho nghịch biến trên khoảng
(0; 3).
C Hàm số đã cho đồng biến trên khoảng
(2; +∞).
D Hàm số đã cho đồng biến trên khoảng
(3; +∞).
x
y
0
y
−∞
1 2
+∞
+
0
−
0
+
−∞−∞
33
00
+∞+∞
Câu 403.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 104
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Đồ thị ở hình vẽ bên là của hàm số nào sau đây?
A y =
x + 3
1 − x
. B y =
x − 1
x + 1
.
C y =
x + 2
x + 1
. D y =
2x + 1
x + 1
.
x
y
O
−1
1
2
Câu 404. Đồ thị của hàm số nào dưới đây có tiệm cận đứng?
A y =
x
2
− 3x + 2
x − 1
. B y =
x
2
x
2
+ 1
. C y =
√
x
2
− 1. D y =
x
x + 1
.
Câu 405. Tìm giá trị lớn nhất của hàm số y = f (x) = x
3
− 2x
2
+ x − 2 trên đoạn [0; 2].
A max
[0;2]
y = 1. B max
[0;2]
y = 0. C max
[0;2]
y = −2. D max
[0;2]
y = −
50
27
.
Câu 406. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên sau
x
y
0
y
−∞
1 0 1
+∞
−
0
+
0
−
0
+
+∞+∞
−1−1
00
−1−1
+∞+∞
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) − 1 = m có đúng hai
nghiệm.
A m = −2, m ≥ −1. B m > 0, m = −1.
C m = −2, m > −1. D −2 < m < −1.
Câu 407. Có bao nhiêu giá trị nguyên của tham số m để hàm số y =
mx + 4
x + m
giảm trên
khoảng (−∞; 1)?
A 2. B Vô số. C 1. D 0.
Câu 408. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có
thể tích bằng
500
3
m
3
. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê
nhân công để xây hồ là 500.000 đồng/m
2
. Người ta xác định kích thước của hồ nước sao cho
chi phí thuê nhân công thấp nhất và chi phí đó là
A 74 triệu đồng. B 75 triệu đồng. C 76 triệu đồng. D 77 triệu đồng.
Câu 409. Cho hàm số y = x
3
+ 3x
2
có đồ thị (C) và điểm M (m; 0) sao cho từ M vẽ được
ba tiếp tuyến đến đồ thị (C), trong đó có hai tiếp tuyến vuông góc với nhau. Khi đó khẳng
định nào sau đây đúng?
A m ∈
Å
1
2
; 1
ã
. B m ∈
Å
−
1
2
; 0
ã
. C m ∈
Å
0;
1
2
ã
. D m ∈
Å
−1; −
1
2
ã
.
Câu 410.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 105
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Cho hàm số f (x) có đạo hàm trên R và có
đồ thị hàm y = f
0
(x) như hình vẽ. Xét hàm
số g(x) = f (x
2
− 2). Mệnh đề nào dưới đây
sai?
A Hàm số g(x) nghịch biến trên (−1; 0).
B Hàm số g(x) nghịch biến trên (−∞; −2).
C Hàm số g(x) nghịch biến trên (0; 2).
D Hàm số g(x) đồng biến trên (2; +∞).
O
x
y
−4
−4
−3
−3
−1
−1
−2
−2
1
1
2
2
3
3
4
4
Câu 411. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |3x
4
− 4x
3
− 12x
2
+ m|
có năm điểm cực trị?
A 44. B 27. C 26. D 16.
Câu 412. Số đường tiệm cận của đồ thị hàm số y =
2x − 3
x − 5
là
A 0. B 1. C 2. D 3.
Câu 413.
Đường cong bên dưới là đồ thị của hàm số nào sau đây?
A y = x
3
+ 3x. B y = x
3
− 3x − 1.
C y = x
3
− 3x. D y = x
3
− 3x + 1.
O
x
y
Câu 414. Tiếp tuyến với đồ thị hàm số y = x
3
−4x + 1 tại điểm có hoành độ bằng 2 thuộc
đồ thị hàm số có phương trình là
A y = −8x + 17. B y = 8x − 16. C y = 8x + 15. D y = 8x − 15.
Câu 415. Hàm số nào sau đây đồng biến trên R ?
A y = tan x. B y = x
4
+ 2. C y = x
3
− 2019. D y =
2x − 1
x + 2
.
Câu 416. Tập hợp tất cả giá trị thực của tham số m để hàm số y = x
3
−mx
2
+(m+6)x−m
có điểm cực trị là
A (−∞; −3) ∪ (6; +∞). B (−∞; −6) ∪ (3; +∞).
C (−∞; −3] ∪ [6; +∞). D (−∞; −6] ∪ [3; +∞).
Câu 417.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 106
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Hình vẽ cho ở hình bên là đồ thị của hàm số nào sau đây?
A y =
x − 1
x + 1
. B y =
3 − x
x − 1
.
C y =
x + 1
x − 1
. D y =
x − 2
x − 1
.
x
y
O
1
1
−1
Câu 418.
Cho hàm số y = ax
4
+ bx
2
+ c (a, b, c ∈ R) có đồ thị như hình
bên.Trong các mệnh đề sau, mệnh đề nào đúng?
A a > 0, b < 0, c > 0. B a > 0, b < 0, c < 0.
C a > 0, b > 0, c < 0. D a < 0, b > 0, c < 0.
O
x
y
Câu 419. Tìm tất cả những giá trị thực của tham số m để đồ thị hàm số y = x
4
−2mx
2
+
m
4
+ 2m có 3 điểm cực trị tạo thành một tam giác đều.
A m =
3
√
3. B m = 1. C m = −1. D m = −
3
√
3.
Câu 420. Gọi M là giá trị lớn nhất của hàm số y =
1
2
x
3
− 2x
2
+ 1
trên khoảng
Å
−
9
8
;
10
3
ã
.
Biết M =
a
b
với
a
b
là phân số tối giản và a ∈ Z, b ∈ N
∗
. Tính S = a + b
2
.
A S = 127. B S = 830. C S = 2. D S = 122.
Câu 421. Cho phương trình 4
√
1−x
2
− (m − 2) · 2
√
1−x
2
+ 2m + 1 = 0. Có bao nhiêu giá trị
nguyên thuộc đoạn [−10; 20] của tham số m để phương trình có nghiệm?
A 6. B 7. C 8. D 9.
Câu 422. Cho hàm số y = f(x) xác định trong khoảng (a, b) và có đồ thị như hình bên
dưới. Trong các khẳng định dưới đây, khẳng định nào sai?
x
y
O
a x
1
x
2
x
3
b
A Hàm số y = f(x) có đạo hàm trong khoảng (a; b).
B f
0
(x
1
) > 0.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 107
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
C f
0
(x
2
) > 0.
D f
0
(x
3
) = 0.
Câu 423. Cho hàm số y =
bx − c
x − a
(a 6= 0) và a, b, c ∈ R có đồ thị như trên dưới. Khẳng
định nào sau đây đúng?
x
y
O
A a > 0, b < 0, c − ab < 0. B a > 0, b > 0, c − ab < 0.
C a < 0, b > 0, c − ab < 0. D a < 0, b < 0, c − ab > 0.
Câu 424. Đồ thị hàm số nào dưới đây không có tiệm cận ngang?
A y = 3
x
. B g(x) = log
3
x. C h(x) =
1
x + 1
. D k(x) =
√
x
2
+ 1
2x + 3
.
Câu 425. Cho hàm số y = f(x) có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực
của tham số m để phương trình |f(x)| = m có 6 nghiệm phân biệt.
x
y
O
−4
−3
−1
1
A −4 < m < −3. B 0 < m < 3. C m > 4. D 3 < m < 4.
Câu 426. Xét f(x) là một hàm số tùy ý. Trong bốn mệnh đề dưới đây có bao nhiêu mệnh
đề đúng?
(I) Nếu f(x) là hàm số có đạo hàm tại x
0
và đạt cực trị tại x
0
thì f
0
(x
0
) = 0.
(II) Nếu f
0
(x
0
) = 0 thì hàm số đạt cực trị tại điểm x
0
.
(III) Nếu f
0
(x
0
) = 0 và f
00
(x) > 0 thì hàm số đạt cực đại tại điểm x
0
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 108
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
(IV) Nếu f(x) đạt cực tiểu tại điểm x
0
thì f
00
(x) < 0.
A 1. B 2. C 3. D 4.
Câu 427. Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f (x) = (x −6)
√
x
2
+ 4
trên đoạn [0; 3] có dạng a − b
√
c với a là số nguyên và b, c là các số nguyên dương. Tính
S = a + b + c.
A S = 4. B S = −2. C S = −22. D S = 5.
Câu 428. Số giờ có ánh sáng của một thành phố X ở vĩ độ 40
◦
bắc trong ngày thứ t của
một năm không nhuận được cho bởi số d(t) = 3 sin
π
182
(t − 80)
+12, t ∈ Z và 0 < t ≤ 365.
Vào ngày nào trong năm thì thành phố X có nhiều giờ có ánh sáng nhất?
A 262. B 353. C 80. D 171.
Câu 429. Tìm tất cả các giá trị thực của m để phương trình x + 1 = m
√
2x
2
+ 1 có hai
nghiệm phân biệt.
A −
√
2
2
< m <
√
6
6
. B m <
√
2
2
.
C m >
√
6
6
. D
√
2
2
< m <
√
6
2
.
Câu 430. Tìm giá trị nguyên của tham số m để hàm số y = x
4
− 2(m
2
+ 1)x
2
+ 2 có ba
điểm cực trị sao cho giá trị cực tiểu đạt giá trị lớn nhất.
A m = 2. B m = 0. C m = 1. D m = 2.
Câu 431. Hàm số nào sau đây đồng biến trên R?
A y =
x − 1
x + 2
. B y = x
3
+ 4x
2
+ 3x − 1.
C y = x
4
− 2x
2
− 1. D y =
1
3
x
3
−
1
2
x
2
+ 3x + 1.
Câu 432. Cho hàm số y = x
4
− 8x
2
− 4. Các khoảng đồng biến của hàm số là
A (−2; 0) và (2; +∞). B (−2; 0) và (0; 2).
C (−∞; −2) và (0; 2). D (−∞; −2) và (2; +∞).
Câu 433. Giá trị cực đại và cực tiểu của hàm số y = x
3
− 3x
2
− 9x + 30 lần lượt là
A 35 và 3. B 3 và 35. C −1 và 3. D 3 và −1.
Câu 434. Cho hàm số y = f(x) xác định trên khoảng (−2; −1) và có lim
x→(−2)
+
f(x) = 2,
lim
x→(−1)
−
f(x) = −∞. Hỏi khẳng định nào dưới đây là khẳng định đúng?
A Đồ thị hàm số y = f(x) có đúng hai tiệm cận đứng là các đường thẳng x = −2 và
x = −1.
B Đồ thị hàm số y = f(x) có đúng một tiệm cận ngang là đường thẳng y = 2.
C Đồ thị hàm số y = f(x) có đúng một tiệm cận đứng là đường thẳng x = −1.
D Đồ thị hàm số y = f(x) có đúng hai tiệm cận ngang là các đường thẳng y = 2 và
y = −1.
Câu 435. Tìm giá trị lớn nhất của hàm số y =
x
x
2
+ 4
trên đoạn [1; 5].
A max
[1;5]
y =
1
5
. B max
[1;5]
y =
1
4
. C max
[1;5]
y =
5
29
. D max
[1;5]
y =
√
2
6
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 109
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Câu 436. Tìm tất cả các giá trị thực của tham số m để hàm số y =
1
3
x
3
−mx
2
+(2m+3)x+2
đồng biến trên R.
A m > 3. B −1 6 m 6 3. C −1 < m < 3. D m < 3.
Câu 437.
Cho hàm số f(x). Đồ thị của hàm số y = f
0
(x) trên [−3; 3]
như hình vẽ (phần đường cong của đồ thị là một phần của
parabol y = ax
2
+ bx + c ). Biết f(3) = 0, giá trị của
f(−1) + f(1) bằng
x
y
O
−3 −2 −1 1 2 3
1
2
A
8
3
. B −
16
3
. C −
8
3
. D
16
3
.
Câu 438.
Cho hàm số y = f(x) liên tục trên R và có đồ thị hàm
số y = f
0
(x) như hình bên. Hỏi hàm số g(x) = f(3 − 2x)
nghịch biến trên khoảng nào sau đây?
x
y
O
y = f
0
(x)
−2
2
5
A (−1; +∞). B (−∞; −1). C (1; 3). D (0; 2).
Câu 439. Cho các số thực a, b, c thỏa mãn
− 1 + a − b + c > 0
8 + 4a + 2b + c < 0
. Số giao điểm của đồ thị
hàm số y = x
3
+ ax
2
+ bx + c và trục Ox là:
A 0. B 2. C 1. D 3.
Câu 440. Hàm số nào sau đây không có cực trị?
A y = x
3
− 2x
2
+ 2x + 1. B y = 2x
2
− 3x + 2.
C y =
1
2
x
4
− 3x
2
+ 2. D y =
x
3
3
− 2x
2
+ 3x +
2
3
.
Câu 441. Cho hàm số y = x
3
− (m + 3)x
2
+ (m
2
+ 1) x + m + 5 (1). Tổng các giá trị m
nguyên để hàm số (1) có cực trị là
A 6. B 5. C 10. D 7.
Câu 442. Cho hàm số y = f(x) có đồ thị như hình vẽ dưới. Mệnh đề nào dưới đây là mệnh
đề sai?
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 110
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
O
x
y
1 2
−1
1
2
3
4
−1
A Hàm số đồng biến trên các khoảng (−∞; 0) và (1; +∞).
B Hàm số nghịch biến trên khoảng (0; 1).
C Hàm số đồng biến trên các khoảng (−∞; 3) và (1; +∞).
D Hàm số đạt cực trị tại các điểm x = 0 và x = 1.
Câu 443. Cho hàm số y = (x
2
+ 3) (x
2
− 5) có đồ thị (C). Mệnh đề nào dưới đây là mệnh
đề đúng?
A (C) cắt trục hoành tại hai điểm phân biệt.
B (C) cắt trục hoành tại một điểm.
C (C) cắt trục hoành tại ba điểm phân biệt.
D (C) không cắt trục hoành.
Câu 444. Cho hàm số y = f(x) xác định trên R \ {1}, liên tục trên mỗi khoảng xác định
và có bảng biến thiên như sau
x
y
0
y
−∞
1 2
+∞
+ +
0
−
−∞−∞
2
−∞
44
−∞−∞
Mệnh đề nào dưới đây là mệnh đề đúng?
A Đồ thị hàm số có đúng một tiệm cận ngang.
B Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.
C Đồ thị hàm số có đúng một tiệm cận đứng.
D Đồ thị hàm số có hai tiệm cận ngang.
Câu 445. Giá trị lớn nhất của hàm số y = 2x +
1
x
khi x < 0 là
A 2
√
2. B −2
√
2. C Không tồn tại. D 4.
Câu 446. Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 111
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
x
y
0
y
−∞
−2
1
+∞
−
0
+
0
−
+∞+∞
−4−4
11
−∞−∞
Số nghiệm thực của phương trình |f(x)| = 3 là
A 3. B 1. C 4. D 2.
Câu 447. Giá trị m nguyên lớn nhất để hàm số y = x
3
+ (3 −2m)x
2
+
Å
m −
2
3
ã
x + 5 đồng
biến trên R thuộc tập hợp nào sau đây?
A [1; 2). B (−2; 1]. C
ï
1;
3
2
ò
. D (1; 3).
Câu 448. Số giá trị nguyên của tham số m để phương trình 3 sin
4
x + m cos
2
x + 2 = 0 có
nghiệm trên đoạn
h
0;
π
4
i
là
A 3. B 5. C 4. D 2.
Câu 449. Cho hàm số y =
3x − 2
x + 1
có đồ thị (C) và điểm A(−5; 5). Tìm tất cả giá trị thực
của tham số m để đường thẳng d : y = −x + m cắt (C) tại hai điểm phân biệt M, N sao
cho tứ giác OAMN là hình bình hành (O là gốc tọa độ).
A m = 3. B m = 2 +
√
5.
C m = 2 +
√
5, m = 2 −
√
5. D m = 2 −
√
5.
Câu 450. Ông A cần sản xuất một cái thang để trèo qua một bức tường nhà. Ông muốn
cái thang phải luôn đi qua vị trí điểm C, biết rằng điểm C cao 3m so với nền nhà và điểm C
cách tường nhà 2m. Giả sử kinh phí sản xuất thang là 500000 đồng/1m dài. Hỏi ông cần ít
nhất bao nhiêu tiền để sản xuất cái thang đó?(Kết quả làm tròn đến hàng nghìn đồng).
A 3512000 đồng. B 4755000 đồng. C 2750000 đồng. D 3115000 đồng.
Câu 451. Cho hàm số y = x
3
− 3x + 2. Tọa độ điểm cực tiểu của đồ thị hàm số là
A (−2; 0). B (−1; 4). C (0; 1). D (1; 0).
Câu 452. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y =
3x + 2
x + 1
.
A x = −1. B y = 3. C y = 2. D x = 3.
Câu 453.
Cho hàm số y = f(x) có đồ thị như hình bên. Mệnh đề nào dưới
đây đúng?
A Hàm số có giá trị cực tiểu bằng 2.
B Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng
−2.
C Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2.
D Hàm số có ba cực trị.
x
y
O
2
2
−2
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 112
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 454.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các
hàm số bên dưới?
A y = −x
4
+ 1. B y = −x
4
+ 2x
2
+ 1.
C y = −x
4
− 2x
2
+ 1. D y = −x
4
+ 2x
2
− 1.
x
−2 −1 1 2
y
−1
2
O
1
Câu 455. Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó?
A y = x
3
+ x − 5. B y = x
4
+ 3x
2
+ 4.
C y = x
2
+ 1. D y =
2x − 1
x + 1
.
Câu 456. Tìm tập giá trị T của hàm số y =
√
x − 3 +
√
5 − x.
A T = (3; 5). B T = [3; 5]. C T =
î
√
2; 2
ó
. D T =
î
0;
√
2
ó
.
Câu 457. Hàm số y = x
3
− 3x
2
nghịch biến trên khoảng nào dưới đây?
A (−1; 1). B (−∞; 1). C (2; +∞). D (0; 2).
Câu 458. Tìm số giao điểm n của đồ thị hàm số y = x
2
|x
2
−3| và đường thẳng y = 2.
A n = 8. B n = 2. C n = 6. D n = 4.
Câu 459. Tìm tất cả các giá trị của m để hàm số y =
mx + 4
x + m
nghịch biến trên (−∞; 1).
A −2 < m < −1. B −2 < m < 2. C −2 ≤ m ≤ 1. D −2 < m ≤ −1.
Câu 460. Tìm tất cả các giá trị của m để phương trình sin
4
x + cos
4
x + cos
2
4x = m có
bốn nghiệm phân biệt thuộc đoạn
h
−
π
4
;
π
4
i
.
A m ≤
47
64
hoặc m ≥
3
2
. B
47
64
< m <
3
2
.
C
47
64
< m ≤
3
2
. D
47
64
≤ m ≤
3
2
.
Câu 461.
Cho hàm số y = f(x) có đạo hàm trên R. Đường cong
trong hình vẽ bên là đồ thị của hàm số y = f
0
(x) (y =
f
0
(x) liên tục trên R). Xét hàm số g(x) = f(x
2
− 3).
Mệnh đề nào dưới đây sai?
A Hàm số g(x) đồng biến trên (−1; 0).
B Hàm số g(x) nghịch biến trên (−∞; −1).
C Hàm số g(x) nghịch biến trên (1; 2).
D Hàm số g(x) đồng biến trên (2; +∞).
x
y
O
1−2
2
Câu 462. Cho hàm số y = f(x) có bảng biến thiên như sau
x
y
0
y
−∞
−1
0 1
+∞
+
0
−
0
+
0
−
−∞−∞
22
11
22
−∞−∞
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 113
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
Giá trị cực đại của hàm số là
A y = −1. B y = 0. C y = 2. D y = 1.
Câu 463. Cho hàm số y = f(x) có đồ thị như sau
x
y
O
−2 2
2
−2
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
A (−1; 2). B (−2; 0). C (−1; 3). D (2; 5).
Câu 464. Tìm tọa độ các điểm cực trị của đồ thị hàm số y = x
3
− 3x
2
.
A (0; 0) và (−2; −4). B (0; 0) và (2; −4).
C (0; 0) và (2; 4). D (0; 0) và (1; −2).
Câu 465. Đồ thị của hàm số nào sau đây có tiệm cận ngang?
A y =
√
4 − x
2
x
. B y =
√
x − 1
x + 1
. C y =
x
2
+ 1
x
. D y =
√
x
2
− 1.
Câu 466. Tìm giá trị của tham số m biết giá trị lớn nhất của hàm số y =
2x + m
x − 1
trên
[2; 5] bằng 7.
A m = 3. B m = 8. C m = −3. D m = 18.
Câu 467. Cho hàm số y = f(x) có đạo hàm trên R và f
0
(x) > 0, ∀x ∈ (0; +∞). Biết
f(1) = 2. Khẳng định nào dưới đây có thể xảy ra?
A f(2) + f(3) = 4. B f(2) = 1.
C f(2017) > f(2018). D f(−1) = 2.
Câu 468. Đồ thị hàm số y = x
3
− 3x
2
+ 2ax + b có điểm cực tiểu A(2; −2). Khi đó a + b
bằng
A −2. B 4. C 2. D −4.
Câu 469.
Cho hàm số y = f(x). Hàm số y = f
0
(x) có đồ thị như hình bên.
Tìm m để hàm số y = f (x
2
+ m) có 3 điểm cực trị?
A m ∈ [0; 3]. B m ∈ [0; 3).
C m ∈ (3; +∞). D m ∈ (−∞; 0).
x
y
O
1 2 3
Câu 470. Biết rằng hàm số y = (m
2
− 1)x
3
+ (m − 1)x
2
− x + 4 nghịch biến trên khoảng
(−∞; +∞) với m ∈ [a; b]. Khi đó biếu thức T = 2a + b có giá trị bằng
A
3
2
. B 0. C −1. D 1.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 114
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 471. Cho hàm số y = f(x) xác định và có đạo hàm cấp một và cấp hai trên khoảng
(a; b) và x
0
∈ (a; b). Khẳng định nào sau đây là sai?
A Hàm số đạt cực đại tại x
0
thì y
0
(x
0
) = 0.
B y
0
(x
0
) = 0 và y
00
(x
0
) = 0 thì x
0
không là điểm cực trị của hàm số.
C y
0
(x
0
) = 0 và y
00
(x
0
) > 0 thì x
0
là điểm cực tiểu của hàm số.
D y
0
(x
0
) = 0 và y
00
(x
0
) 6= 0 thì x
0
là điểm cực trị của hàm số.
Câu 472. Tìm m để hàm số y = x
3
− 3x
2
+ mx + 2 tăng trên khoảng (1; +∞).
A m 6= 3. B m ≥ 3. C m ≤ 3. D m < 3.
Câu 473. Tìm tất cả các giá trị của m để đồ thị hàm số y =
2x + 4
x − m
có tiệm cận đứng.
A m > −2. B
m = −2. C m < −2. D m 6= −2.
Câu 474. Biết rằng giá trị lớn nhất của hàm số y = x +
√
4 − x
2
+ m là 3
√
2. Giá trị của
m là
A m =
√
2. B m = 2
√
2. C m = −
√
2. D m =
√
2
2
.
Câu 475.
Cho hàm số y = f(x) có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị
của hàm số nào?
A y = (x − 1)
3
. B y = x
3
− 1.
C y = x
3
+ 1. D y = (x + 3)
3
.
1
−1
x
y
O
Câu 476. Cho các hàm số (I) : y = x
2
+3; (II) : y = x
3
+3x
2
+3x−5; (III) : y = x−
1
x + 2
;
(IV ) : y = (2x + 1)
7
. Các hàm số không có cực trị là
A (I) , (II) , (III). B (II) , (III) , (IV ).
C (III) , (IV ) , (I). D (IV ) , (I) , (II).
Câu 477. Tiệm cận đứng của đồ thị hàm số y =
x
3
− 3x − 2
x
2
+ 3x + 2
là
A x = −1; x = −2. B x = −2.
C x = −1. D Không có tiệm cận đứng.
Câu 478. Tìm m để đường thẳng y = x + m (d) cắt đồ thị hàm số y =
2x + 1
x − 2
(C) tại hai
điểm phân biệt thuộc hai nhánh của đồ thị (C).
A m ∈ R. B m > −
1
2
. C m < −
1
2
. D m ∈ R \
ß
−
1
2
™
.
Câu 479. Cho hàm số y = x + sin 2x + 2017. Tìm tất cả các điểm cực tiểu của hàm số.
A x = −
π
3
+ k2π, k ∈ Z. B x = −
π
3
+ kπ, k ∈ Z.
C x =
π
3
+ k2π, k ∈ Z. D x =
π
3
+ kπ, k ∈ Z.
Câu 480. Số tiệm cận ngang của đồ thị hàm số y = 2x − 1 +
√
4x
2
− 4 là
A
0. B 1. C 2. D 3.
Câu 481. Cho hàm số y = f(x) = ax
3
+ bx
2
+ cx + d, (a 6= 0). Khẳng định nào sau đây
đúng?
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 115
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
A Đồ thị hàm số luôn cắt trục hoành. B Hàm số luôn có cực trị.
C lim
x→−∞
f(x) = +∞. D Hàm số luôn tăng trên R.
Câu 482.
Một công ty muốn làm đường ống dẫn dầu
từ một kho A ở trên bờ biển đến một vị trí B
trên một hòn đảo. Hòn đảo cách bờ biển 6 km.
Gọi C là điểm trên bờ sao cho BC vuông góc
với bờ biển. Khoảng cách từ A đến C là 9 km.
Người ta cần xác định một vị trí D trên AC
để lắp ống dẫn theo đường gấp khúc ADB.
Tính khoảng cách AD để số tiền chi phí thấp
nhất, biết rằng giá để lắp đặt mỗi km đường
ống trên bờ là 100.000.000 đồng và dưới nước
là 260.000.000 đồng.
A 6 km. B 6.5 km.
C 7 km. D 7.5 km.
B
C
D
A
6 km
9 km
Câu 483. Cho hàm số y = x
4
− 2mx
2
− 2m
2
+ m
4
có đồ thị (C). Biết đồ thị (C) có ba
điểm cực trị A, B, C và ABDC là hình thoi trong đó D(0; −3), A thuộc trục tung. Khi đó
m thuộc khoảng nào?
A m ∈
Å
−1;
1
2
ã
. B m ∈
Å
1
2
;
9
5
ã
. C m ∈
Å
9
5
; 2
ã
. D m ∈ (2; 3).
Câu 484. Cho hàm số y =
x
3
3
− ax
2
− 3ax + 4. Để hàm số đạt cực trị tại x
1
, x
2
thỏa mãn
x
2
1
+ 2ax
2
+ 9a
a
2
+
a
2
x
2
2
+ 2ax
1
+ 9a
= 2
thì a thuộc khoảng nào?
A a ∈
Å
−5; −
7
2
ã
. B a ∈
Å
−
7
2
; −3
ã
. C a ∈
Å
−3; −
5
2
ã
. D a ∈ (−2; −1).
Câu 485. Cho hàm số y =
x + m
x + 1
(m là tham số thực) thỏa mãn min
[1;2]
y + max
[1;2]
y =
16
3
.
Mệnh đề nào dưới đây là đúng?
A 2 < m ≤ 4. B 0 < m ≤ 2. C m ≤ 0. D m > 4.
Câu 486. Cho hàm số y = x
3
− 6x
2
+ 12x + 1. Khẳng định nào sau đây là đúng?
A Hàm số đồng biến trên R.
B Hàm số nghịch biến R.
C Hàm số đồng biến trên khoảng (−∞; 2) và nghịch biến trên khoảng (2; +∞).
D Hàm số nghịch biến trên khoảng (−∞; 2) và đồng biến trên khoảng (2; +∞).
Câu 487. Điểm cực đại của đồ thị hàm số y = −2x
3
− 3x
2
+ 12x là
A (−2; −20). B (−2; 7). C (1; 7). D (1; −20).
Câu 488. Giá trị lớn nhất của hàm số y =
x
4
2
−x
3
−
3x
2
2
+ 2x trên đoạn
ï
−
4
3
;
3
2
ò
là
A −2. B
17
32
. C
17
8
. D −
112
81
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 116
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
Câu 489. Cho hàm số y =
x + 2
x − 2
có đồ thị là (C). Khẳng định nào sau đây là đúng?
A Đồ thị (C) có một tiệm cận đứng là x = 2 và một tiệm cận ngang là y = 1.
B Đồ thị (C) có một tiệm cận đứng là x = −2 và một tiệm cận ngang là y = 1.
C Đồ thị (C) có một tiệm cận đứng là x = −2 và một tiệm cận ngang là y = 2.
D Đồ thị (C) có một tiệm cận đứng là x = −2 và một tiệm cận ngang là y = −2.
Câu 490. Hàm số y = x
3
+ 3(m −3)x
2
+ m(m −2)x + 1 đạt cực tiểu tại x = −2 khi và chỉ
khi
A m = 6. B m = 6 hay m = 8.
C m = 8. D 6 < m < 8.
Câu 491.
Hàm số y = f(x) có đồ thị như hình vẽ. Khẳng định nào sau
đây đúng?
A Đồ thị hàm số có điểm cực đại là (1; −1).
B Đồ thị hàm số có điểm cực tiểu là (1; −1).
C Hàm số có điểm cực tiểu là x = −1.
D Hàm số có điểm cực tiểu là (1; −1).
x
y
O
−1
1
−1
1
3
Câu 492. Cho hàm số y = f(x) xác định trên R \ {1}, liên tục trên mỗi khoảng xác định
và có bảng biến thiên như hình vẽ sau:
x
y
0
y
−∞
−1
1
+∞
−
0
+ +
11
−
√
2−
√
2
+∞
−∞
−1−1
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f(x) = m có ba
nghiệm thực phân biệt.
A
Ä
−
√
2; −1
ó
. B
Ä
−
√
2; −1
ä
. C (−1; 1]. D (−1; 1).
Câu 493. Tìm m để hàm số y = x
3
−3(m + 3)x
2
−6(m −1)x + 1 luôn luôn đồng biến trên
R.
A −7 6 m 6 −1. B −7 < m < −1.
C m 6 −7 hoặc m > −1. D m < −7 hoặc m > −1.
Câu 494. Hàm số y = x
3
+ 3(m + 1)x
2
−6(m −3)x + 1 đạt cực trị tại hai điểm x
1
, x
2
thỏa
x
2
1
+ x
2
2
< 64 khi và chỉ khi
A
− 6 < m 6 −5
1 6 m < 3
. B
− 6 < m < −5
1 < m < 3
.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 117
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
C
m < −6
m > 3
. D −6 < m < 3.
Câu 495. Cho hàm số y = f(x) có bảng biến thiên:
x
y
0
y
−∞
−1
1
+∞
−
0
+
0
−
+∞+∞
00
44
−∞−∞
Chọn khẳng định đúng?
A Hàm số nghịch biến trên (−1; +∞). B Hàm số nghịch biến trên (−1; 1).
C Hàm số đồng biến trên (−∞; −1). D Hàm số đồng biến trên (−1; 1).
Câu 496.
Cho hàm số f(x) = ax
3
+ bx
2
+ cx + d (a, b, c, d ∈ R). Đồ
thị của hàm số y = f(x) như hình vẽ bên. Số nghiệm
thực của phương trình 3f(x) − 1 = 0 là
A 3. B 2. C 1. D 4.
x
y
O
2
−2
2
Câu 497.
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. Tất cả
các giá trị của tham số m để hàm số y = |f (x) + m| có ba điểm
cực trị là
A m ≤ −1 hoặc m ≥ 3. B m = −1 hoặc m = 3.
C m ≤ −3 hoặc m ≥ 1. D 1 ≤ m ≤ 3.
x
y
O
x
y
1
−3
O
Câu 498. Cho x, y là hai số không âm thỏa mãn: x + y = 2. Giá trị nhỏ nhất của biểu thức
P =
1
3
x
3
+ x
2
+ y
2
− x + 1 là
A min P =
7
3
. B min P = 5. C min P =
17
3
. D min P =
115
3
.
Câu 499. Cho hàm số y = f(x) liên tục trên R và có bảng biến thiên dưới đây.
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 118
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
x
f
0
(x)
f(x)
+∞
0 2
+∞
+
0
−
0
+
−∞−∞
22
−2−2
+∞+∞
−1
−2
3
2
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = f(m) có ba nghiệm phân
biệt.
A m ∈ (−1; 3) \ {0; 2}. B m ∈ [−1; 3] \ {0; 2}.
C m ∈ (−1; 3). D m ∈ (−2; 2).
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 119
PHẦN I
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC KỲ THI TỐT NGHIỆP TRUNG
HỌC PHỔ THÔNG QUỐC GIA 2017-2020
BẢNG ĐÁP ÁN THAM KHẢO
1. C 2. C 3. B 4. D 5. A 6. A 7. C 8. B 9. D 10. C
11. A 12. D 13. D 14. B 15. A 16. B 17. D 18. D 19. D 20. A
21. D 22. A 23. B 24. B 25. A 26. B 27. A 28. C 29. A 30. B
31. A 32. A 33. A 34. A 35. C 36. B 37. C 38. C 39. A 40. C
41. C 42. D 43. C 44. A 45. B 46. C 47. D 48. D 49. B 50. D
51. A 52. A 53. D 54. C 55. B 56. C 57. A 58. B 59. D 60. B
61. A 62. A 63. A 64. B 65. D 66. C 67. D 68. C 69. B 70. D
71. D 72. B 73. C 74. B 75. B 76. D 77. B 78. A 80. D 81. A
82. D 83. B 84. D 85. A 86. C 87. D 88. A 89. A 90. D 91. A
92. D 93. D 94. A 95. C 96. B 97. B 98. B 99. D 100. A 101. B
102. A 103. D 104. D 105. C 106. B 107. B 108. C 109. B 110. B 111. D
112. D 113. C 114. B 115. A 116. A 117. A 118. B 119. A 120. A 121. B
122. D 123. D 124. B 125. D 126. A 127. B 128. A 129. C 130. A 131. D
132. B 133. D 134. D 135. B 136. D 137. A 138. C 139. A 140. C 141. D
142. C 143. B 144. C 145. A 146. C 147. C 148. B 149. D 150. D 151. B
152. B 153. B 154. C 155. B 156. B 157. C 158. C 159. D 160. B 161. C
162. C 163. B 164. A 165. B 166. D 167. D 168. B 169. D 170. A 171. C
172. A 173. C 174. C 175. A 176. C 177. A 178. C 179. D 180. B 181. A
182. C 183. B 184. C 185. A 186. B 187. B 188. A 189. B 190. C 191. C
192. D 193. D 194. A 195. B 196. C 197. C 198. C 199. D 200. A 201. B
202. C 203. A 204. C 205. D 206. A 207. B 208. D 209. C 210. C 211. A
212. A 213. C 214. C 215. B 216. C 217. B 218. D 219. B 220. A 221. A
222. C 223. C 224. B 225. B 226. C 227. B 228. C 229. D 230. B 231. C
232. B 233. A 234. B 235. B 236. B 237. B 238. D 239. C 240. A 241. D
242. D 243. B 244. D 245. C 246. C 247. C 248. A 249. A 250. C 251. D
252. C 253. D 254. B 255. B 256. A 257. A 258. D 259. B 260. C 261. D
262. A 263. D 264. C 265. D 266. C 267. C 268. A 269. C 270. B 271. B
272. D 273. D 274. B 275. A 276. C 277. D 278. D 279. A 280. C 281. A
282. A 283. B 284. B 285. C 286. D 287. B 288. B 289. C 290. D 291. A
292. A 293. A 294. C 295. D 296. D 297. D 298. C 299. D 300. C 301. A
302. C 303. B 304. A 305. C 306. A 307. A 308. D 309. D 310. D 311. C
312. D 313. C
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 1
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM TRONG CÁC KỲ THI TỐT NGHIỆP THPT QUỐC GIA VÀ CÁC ĐỀ THI THỦ
PHẦN II
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC ĐỀ THI THỬ 2017-2020
BẢNG ĐÁP ÁN THAM KHẢO
1. A 2. B 3. D 4. D 5. A 6. D 7. C 8. C 9. C 10. A
11. B 12. B 13. C 14. A 15. A 16. A 17. A 18. D 19. C 20. C
21. B 22. C 23. D 24. B 25. C 26. D 27. C 28. C 29. B 30. A
31. B 32. C 33. B 34. C 35. A 36. C 37. B 38. D 39. D 40. B
41. C 42. C 43. C 44. B 45. D 46. B 47. B 48. D 49. D 50. D
51. A 52. A 53. D 54. A 55. D 56. B 57. A 58. D 59. A 60. C
61. A 62. A 63. D 64. A 65. C 66. B 67. C 68. C 69. A 70. C
71. B 72. D 73. C 74. D 75. D 76. D 77. D 78. D 79. C 80. D
81. C 82. D 83. B 84. B 85. C 86. B 87. D 88. C 89. B 90. D
91. D 92. B 93. B 94. B 95. D 96. D 97. C 98. A 99. A 100. B
101. A 102. D 103. D 104. B 105. C 106. A 107. A 108. D 109. A 110. A
111. A 112. D 113. C 114. B 115. D 116. D 117. A 118. C 119. D 120. C
121. D 122. A 123. D 124. A 125. D 126. B 127. C 128. D 129. C 130. B
131. C 132. D 133. C 134. C 135. D 136. C 137. A 138. A 139. C 140. C
141. A 142. A 143. D 144. A 145. C 146. D 147. A 148. A 149. B 150. C
151. D 152. C 153. B 154. C 155. A 156. C 157. C 158. A 159. B 160. A
161. B 162. D 163. B 164. C 165. D 166. D 167. D 168. B 169. A 170. D
171. B 172. D 173. A 174. C 175. D 176. A 177. C 178. A 179. B 180. D
181. B 182. B 183. A 184. C 185. B 186. B 187. C 188. B 189. A 190. D
191. C 192. B 193. D 194. C 195. A 196. C 197. C 198. D 199. A 200. C
201. A 202. C 203. D 204. C 205. A 206. C 207. B 208. C 209. A 210. A
211. C 212. D 213. A 214. A 215. B 216. A 217. D 218. A 219. C 220. C
221. A 222. C 223. C 224. D 225. A 226. D 227. A 228. D 229. C 230. C
231. C 232. D 233. D 234. C 235. A 236. C 237. A 238. A 239. D 240. C
241. D 242. D 243. B 244. B 245. C 246. C 247. D 248. D 249. A 250. B
251. B 252. B 253. B 254. A 255. A 256. A 257. D 258. A 259. D 260. C
261. C 262. D 263. D 264. C 265. A 266. B 267. D 268. C 269. D 270. D
271. A 272. D 273. B 274. C 275. A 276. C 277. D 278. C 279. C 280. C
281. A 282. C 283. D 284. D 285. A 286. C 287. B 288. C 289. A 290. D
291. C 292. B 293. D 294. B 295. A 296. A 297. B 298. A 299. D 300. C
301. B 302. A 303. A 304. C 305. A 306. D 307. B 308. B 309. A 310. B
311. B 312. B 313. C 314. A 315. C 316. C 317. A 318. A 319. C 320. C
321. D 322. B 323. A 324. C 325. B 326. D 327. B 328. A 329. B 330. D
331. C 332. A 333. C 334. B 335. C 336. A 337. D 338. A 339. C 340. A
341. A 342. A 343. B 344. C 345. C 346. A 347. B 348. B 349. B 350. C
351. B 352. C 353. A 354. C 355. A 356. C 357. C 358. A 359. D 360. B
361. A 362. A 363. D 364. A 365. A 366. C 367. D 368. A 369. C 370. B
371. D 372. A 373. D 374. B 375. B 376. B 377. B 378. B 379. D 380. C
381. A 382. D 383. C 384. A 385. C 386. A 387. B 388. C 389. B 390. C
391. A 392. B 393. C 394. D 395. D 396. B 397. A 398. C 399. A 400. B
401. D 402. B 403. D 404. D 405. B 406. C 407. C 408. B 409. C 410. A
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 2
HƯỚNG TỚI KỲ THI TỐT NGHIỆP THPT QUỐC GIA 2021
411. B 412. C 413. C 414. D 415. C 416. A 417. C 418. A 419. A 420. B
421. B 422. C 423. B 424. B 425. D 426. A 427. A 428. D 429. D 430. B
431. D 432. A 433. A 434. C 435. B 436. B 437. B 438. B 439. D 440. A
441. A 442. C 443. A 444. C 445. B 446. C 447. D 448. C 449. C 450. A
451. D 452. B 453. C 454. B 455. A 456. C 457. D 458. C 459. D 460. C
461. C 462. C 463. D 464. B 465. B 466. A 467. D 468. C 469. B 470. B
471. B 472. B 473. D 474. A 475. A 476. B 477. B 478. A 479. B 480. B
481. A 482. B 483. B 484. A 485. D 486. A 487. C 488. B 489. A 490. B
491. B 492. B 493. A 494. B 495. D 496. A 497. A 498. A 499. A
Hàm số và ứng dụng đạo hàm Những nẻo đường phù sa
Trang 3
| 1/122
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ HỒ CHÍ MINH 1
TRƯỜNG THCS-THPT HOA SEN
HÀMSỐVÀỨNGDỤNGĐẠOHÀM
TRONG CÁC ĐỀ THI TỐT NGHIỆP TRUNG PHỔ THÔNG QUỐC GIA
VÀ CÁC ĐỀ THI THỬ
TỪ NĂM 2017 ĐẾN 2020 NĂM HỌC 2020-2021 PHẦN I
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC KỲ THI TỐT NGHIỆP TRUNG
HỌC PHỔ THÔNG QUỐC GIA 2017-2020 THỦ Câu 1. THI
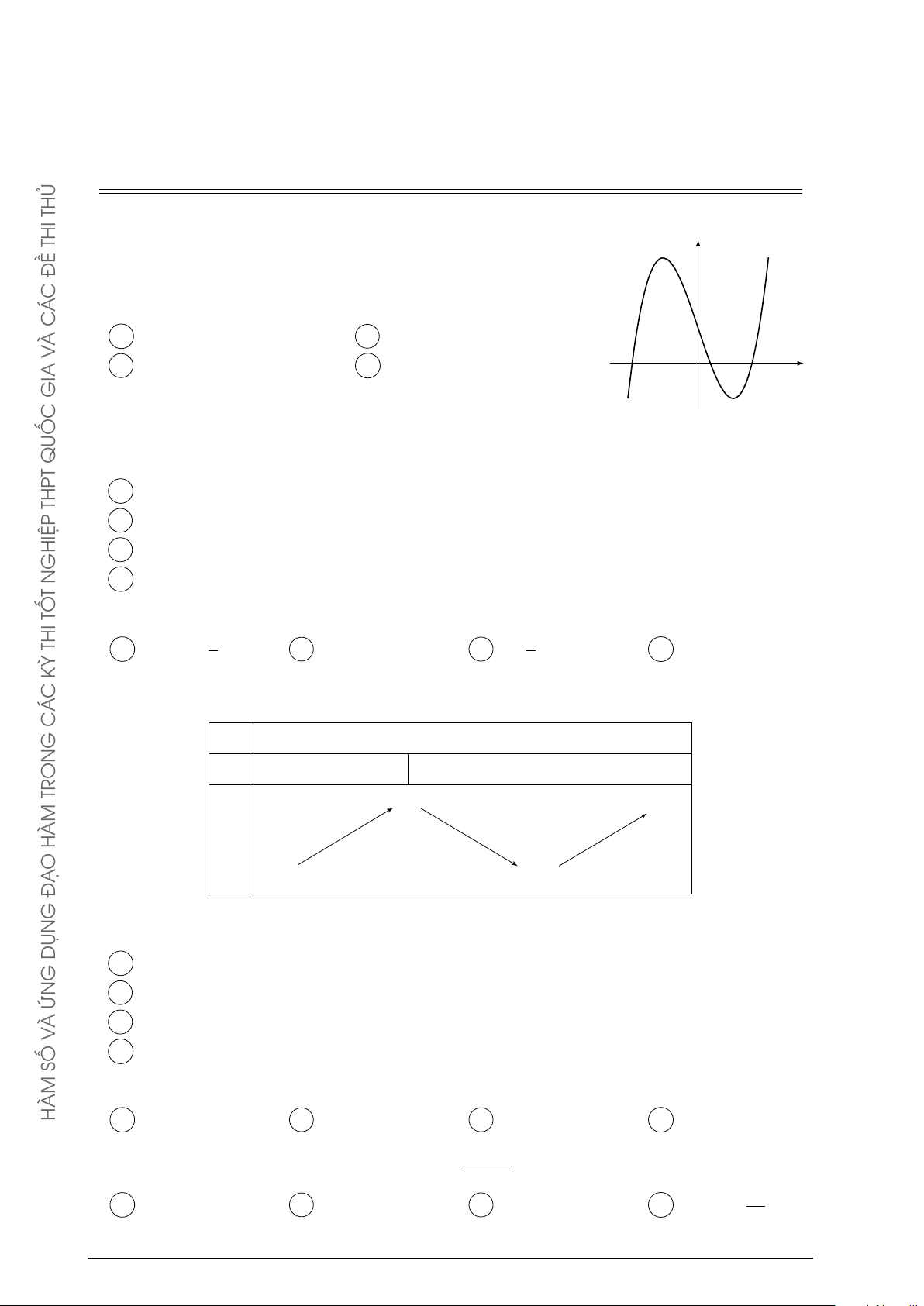
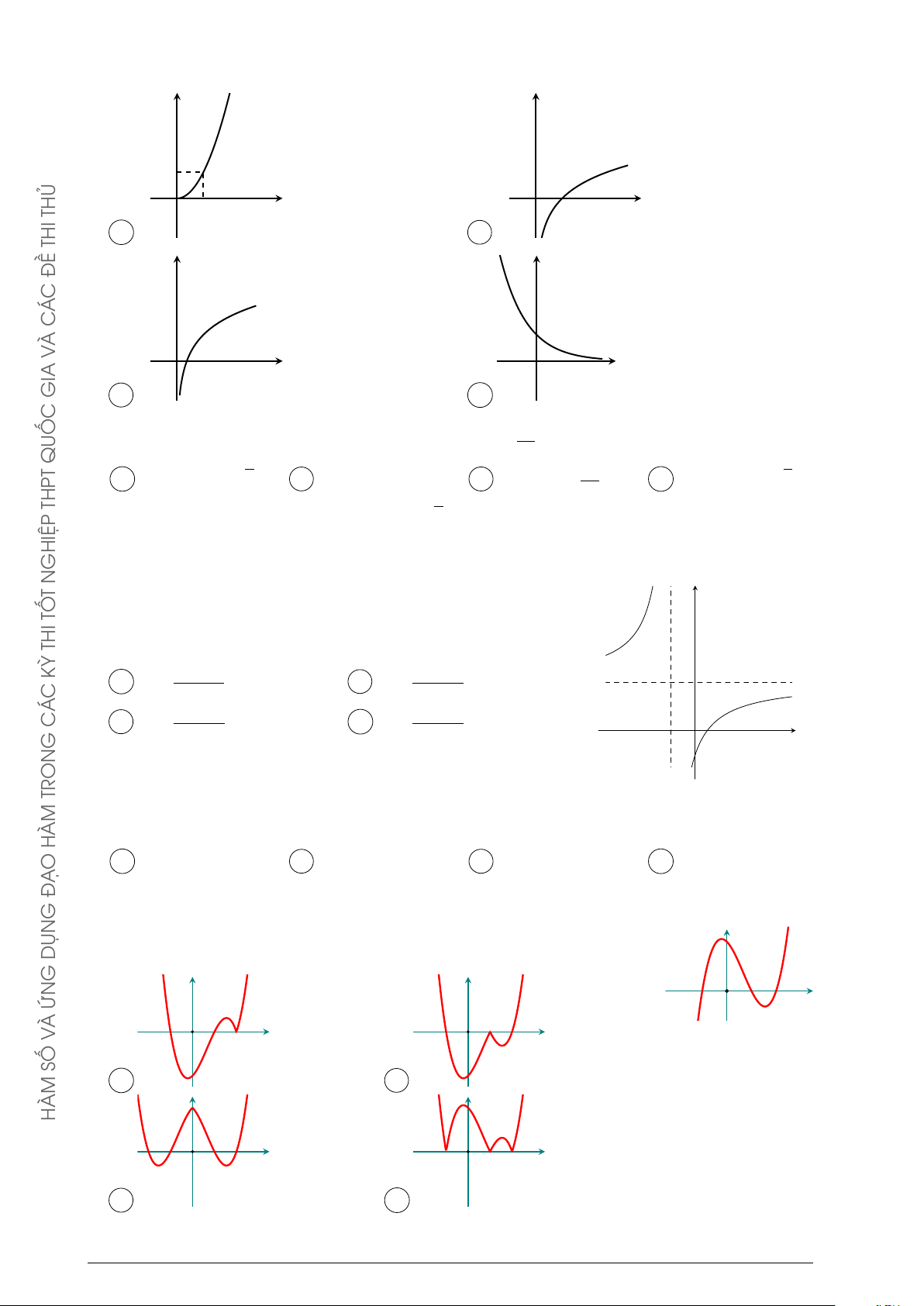
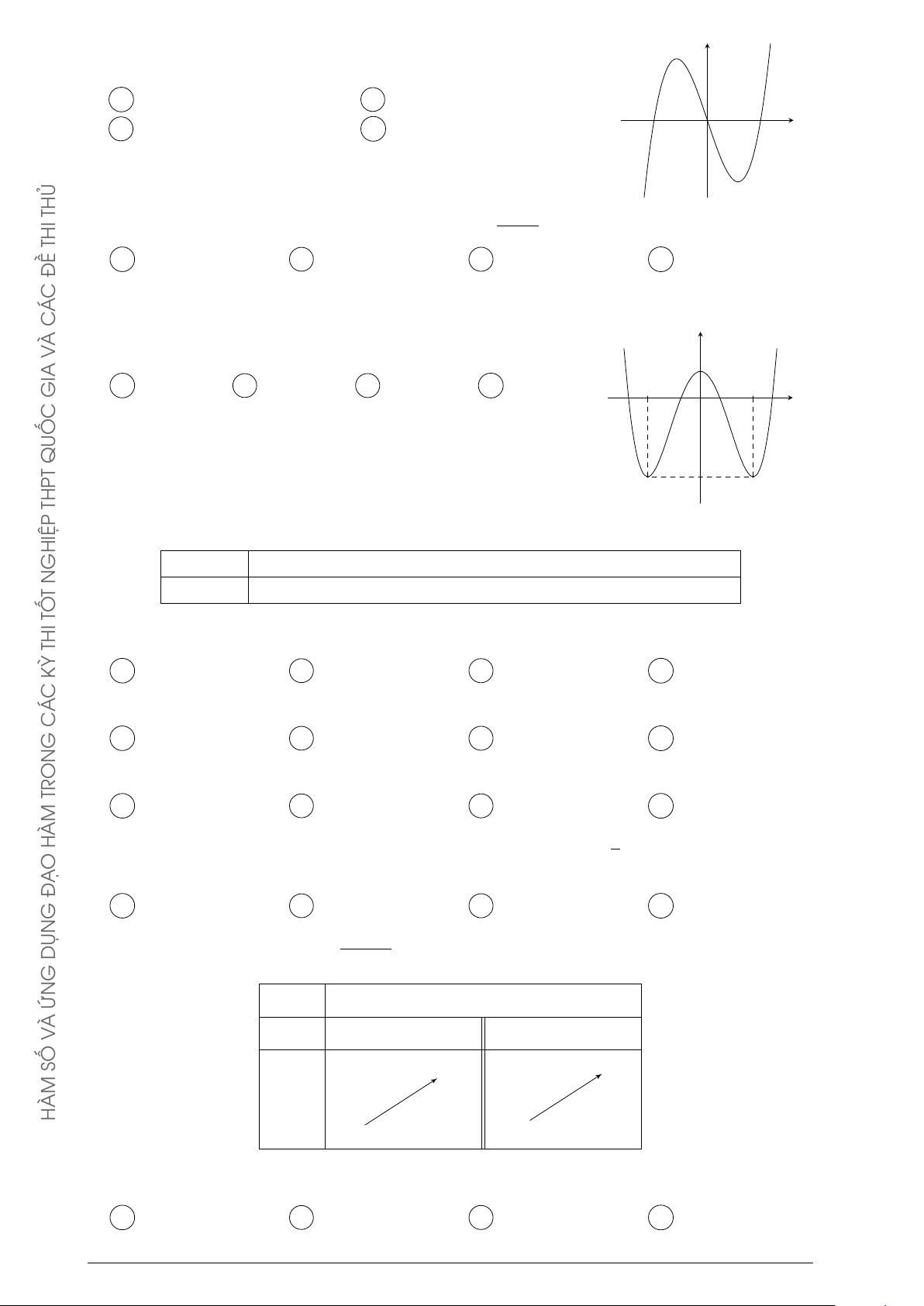
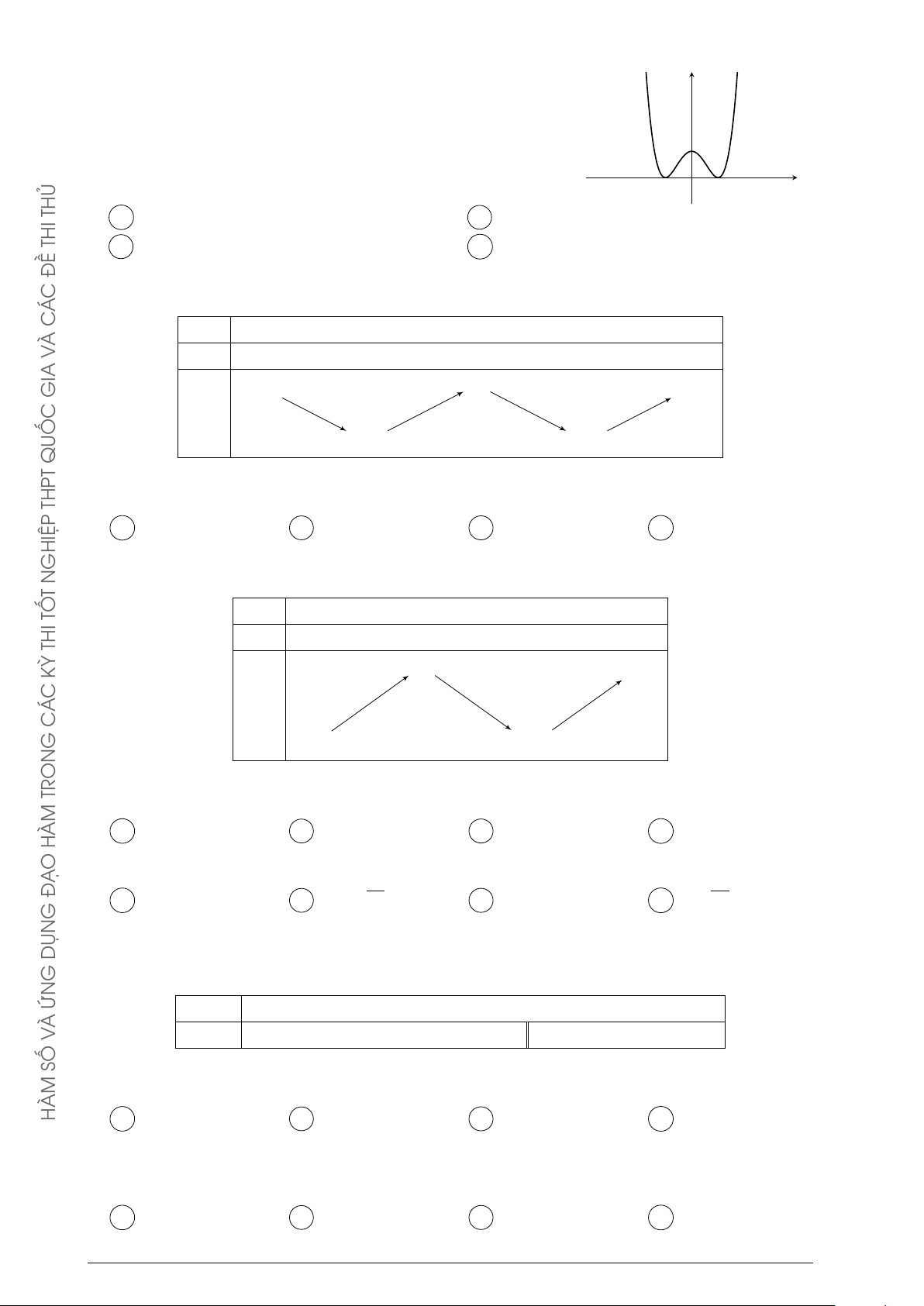
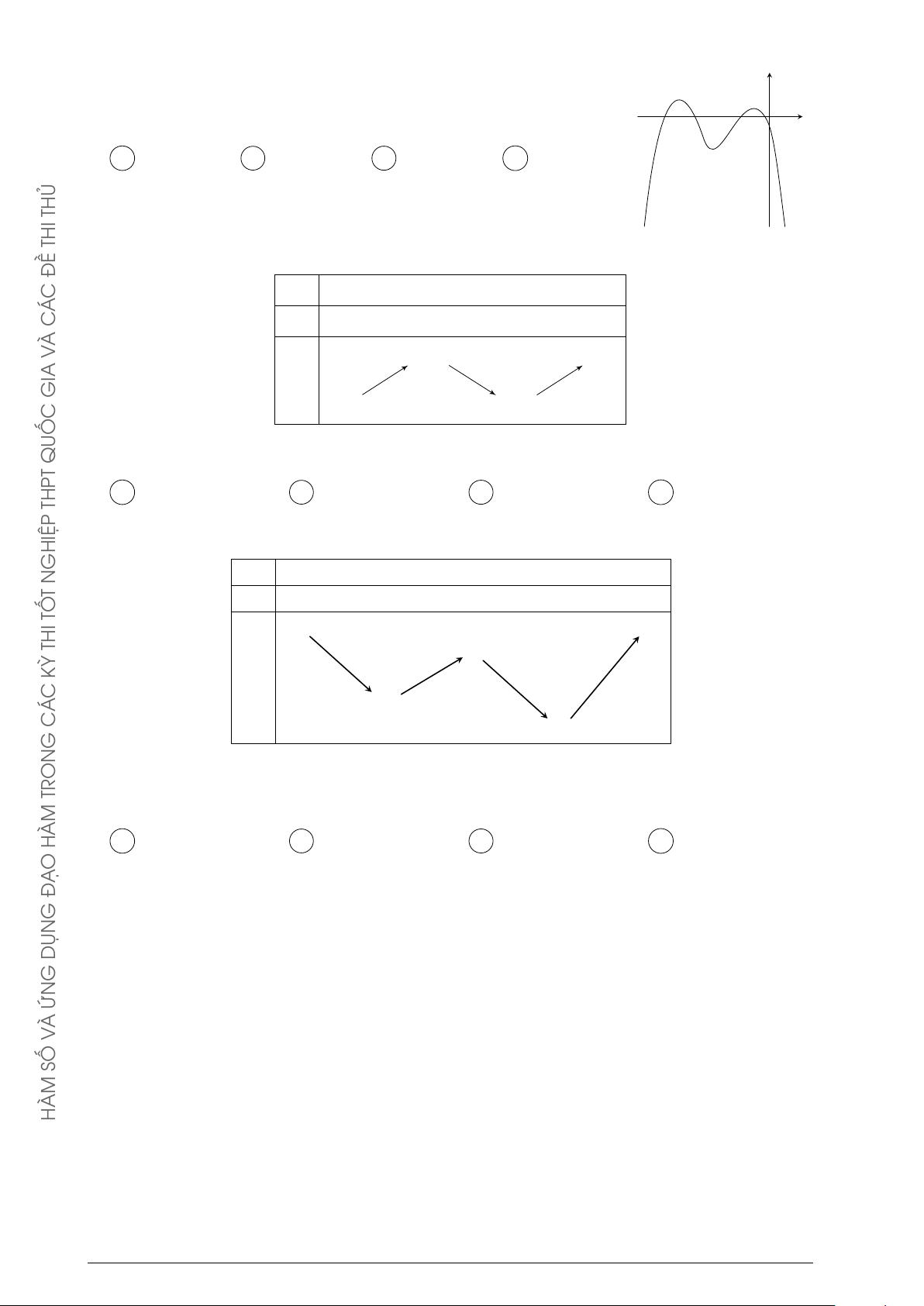
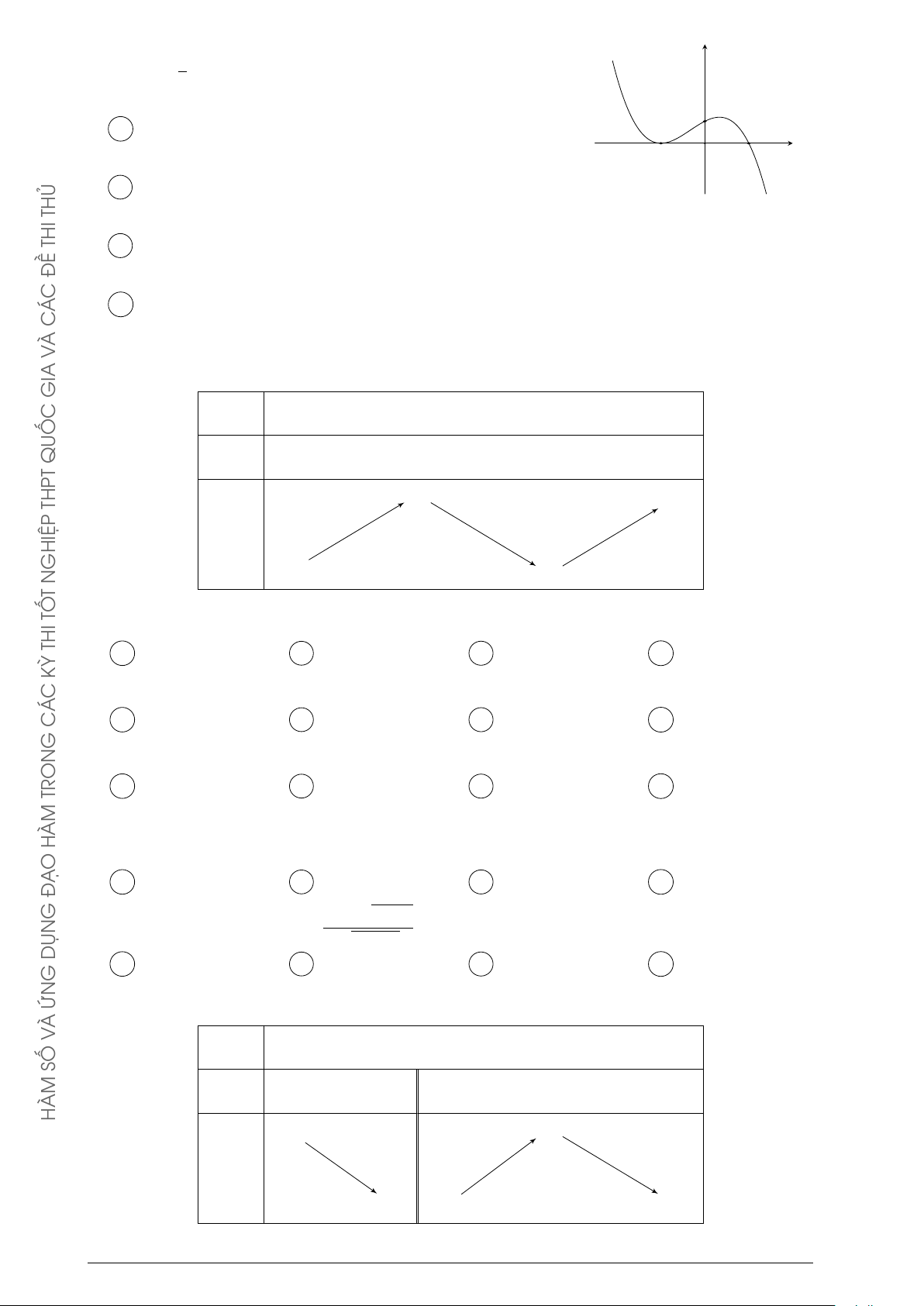
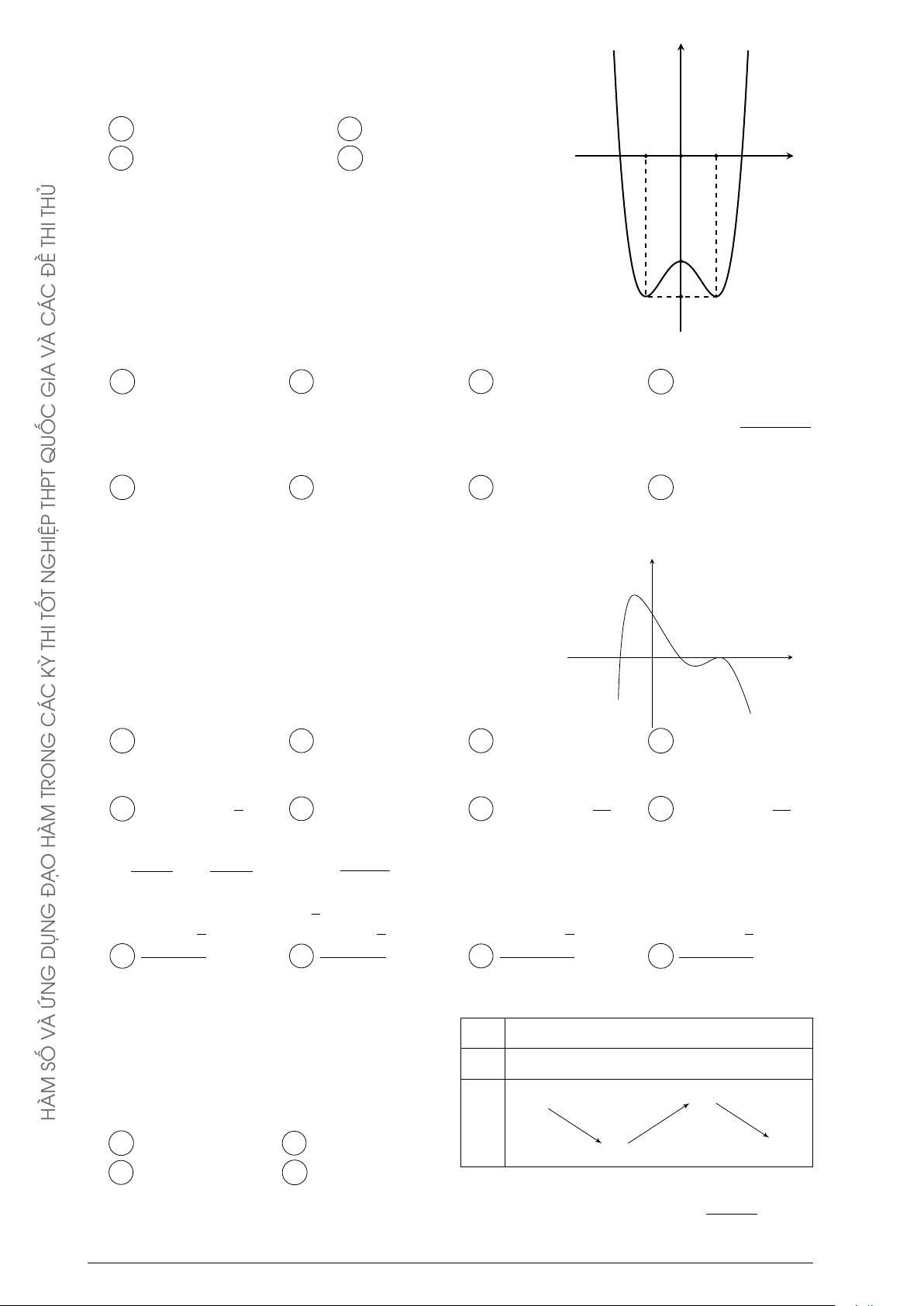
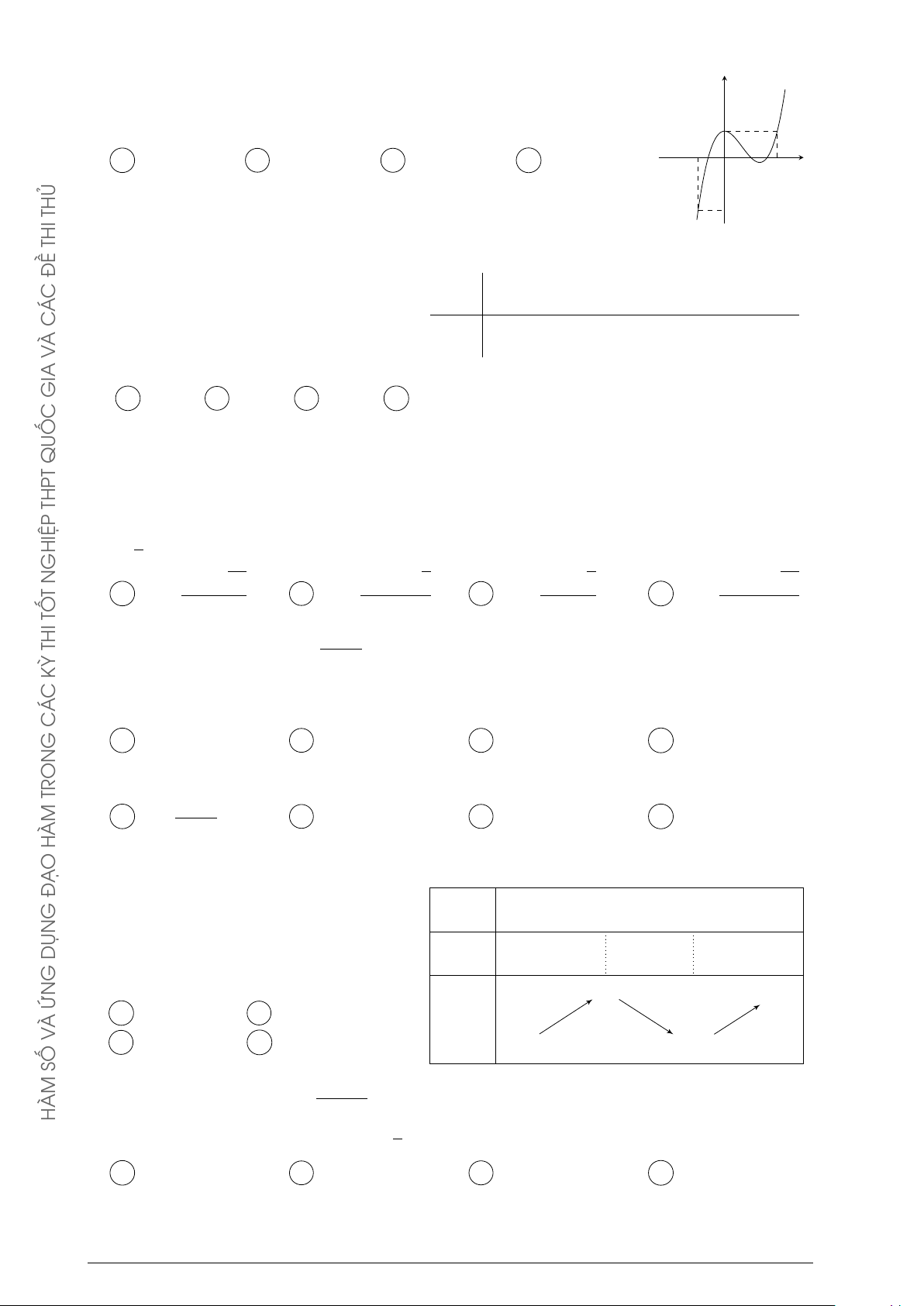
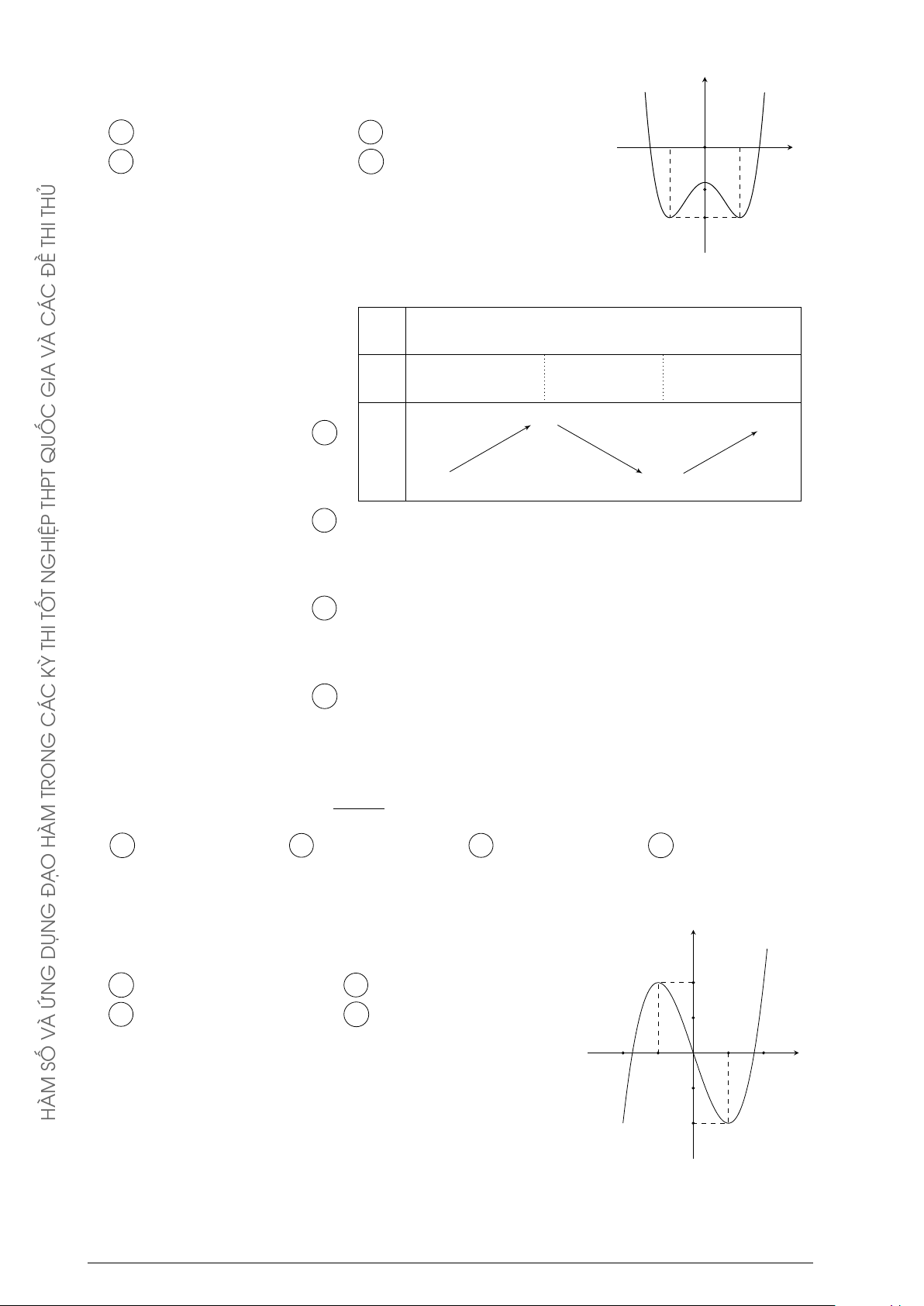
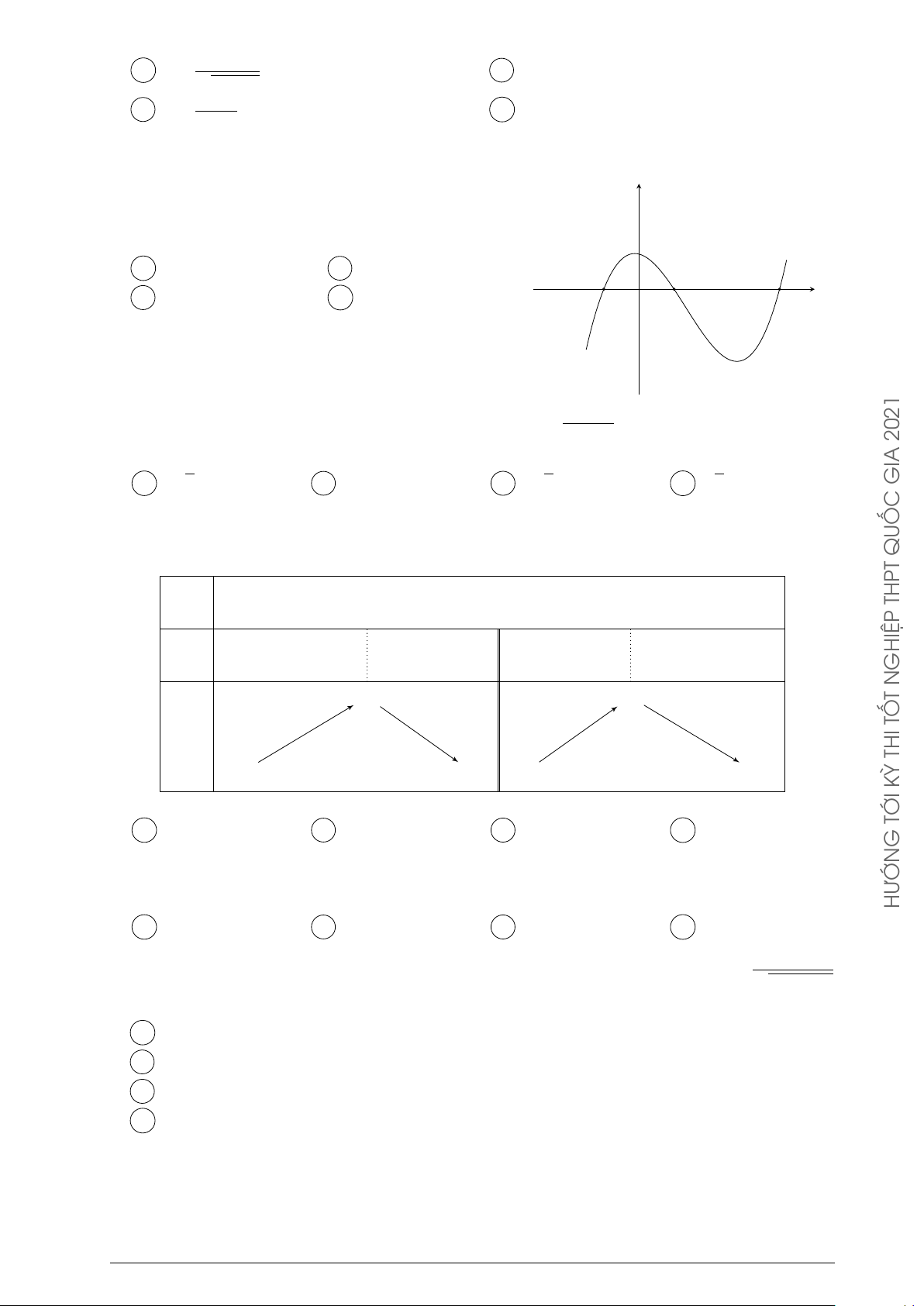
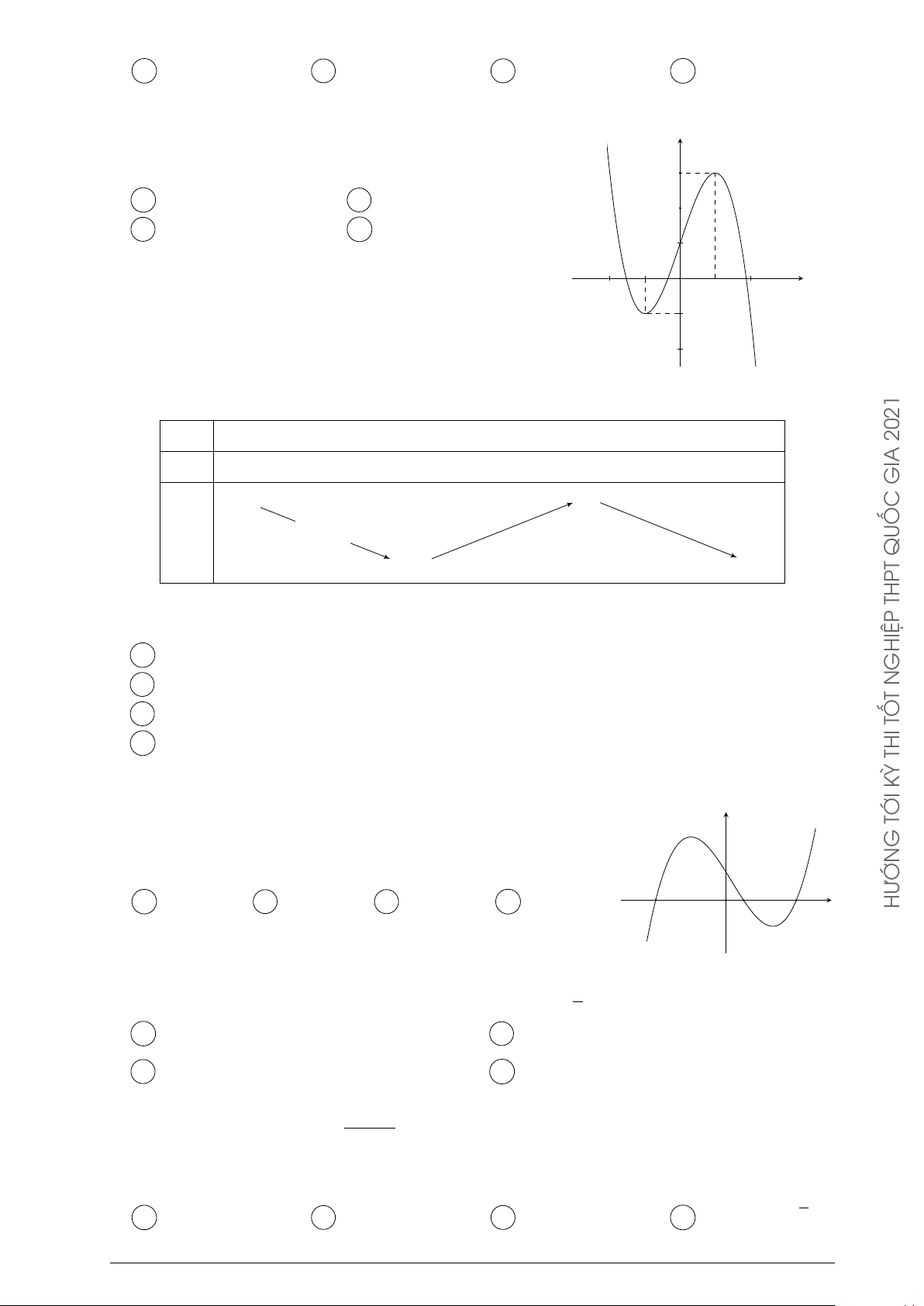
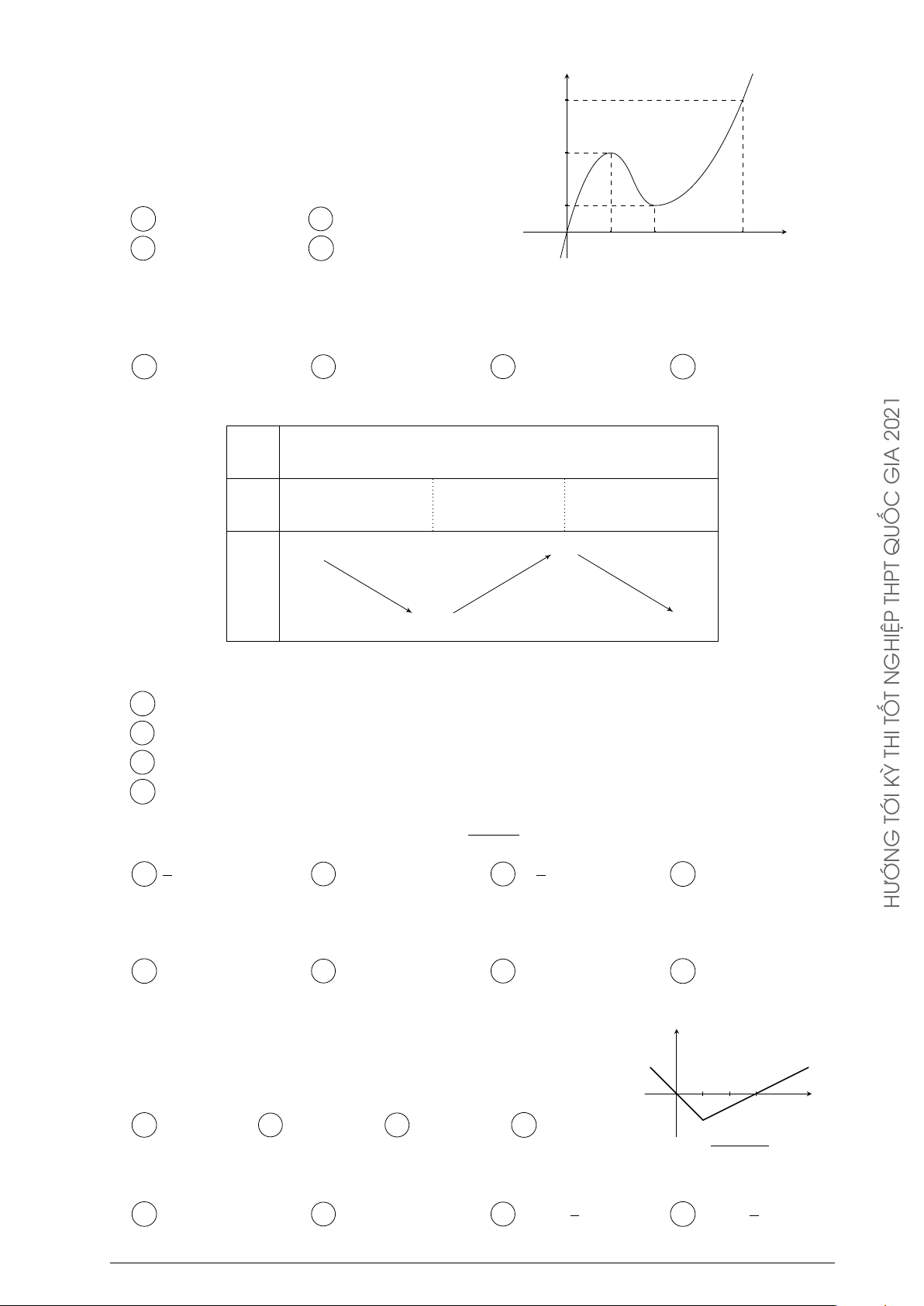
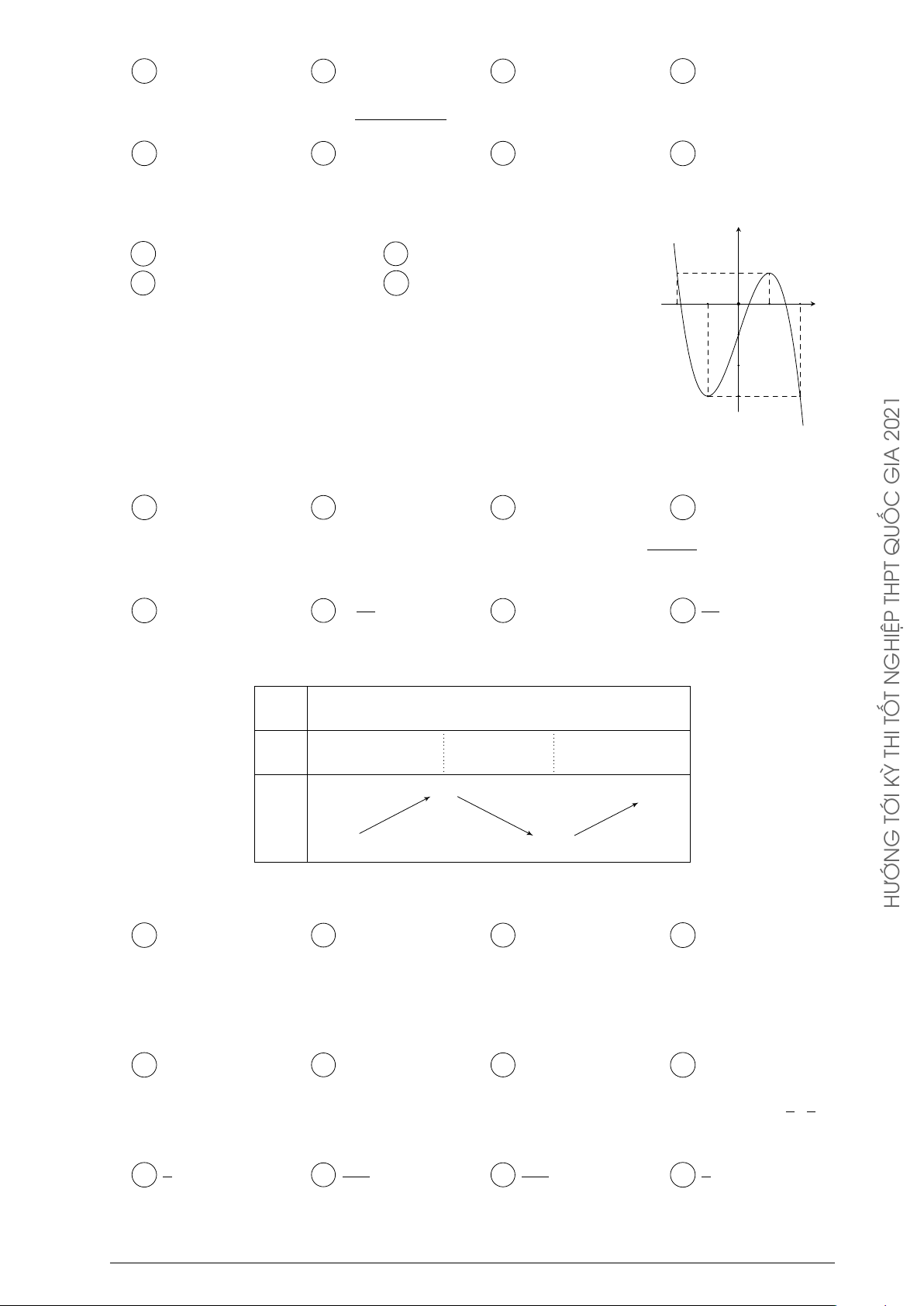
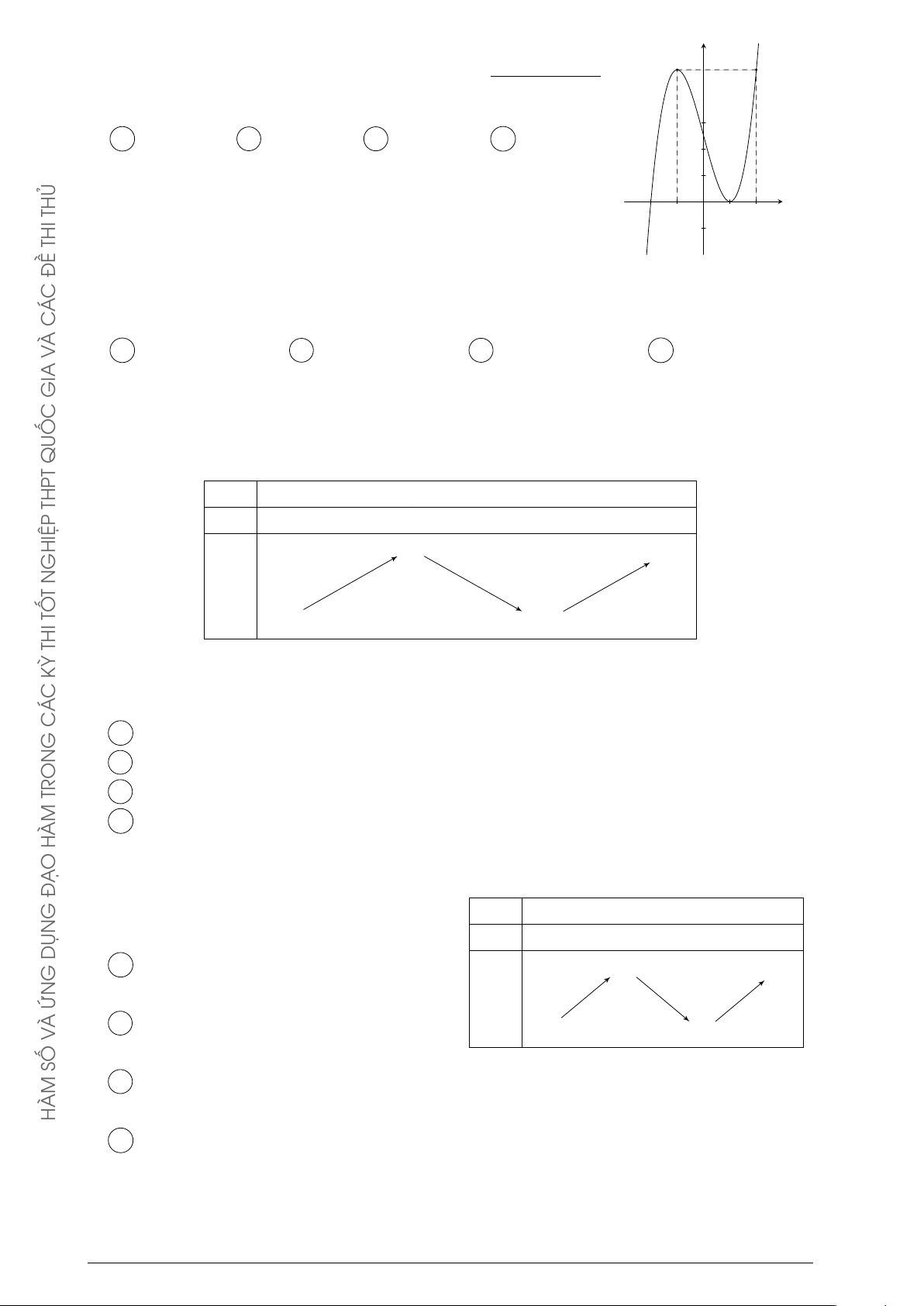
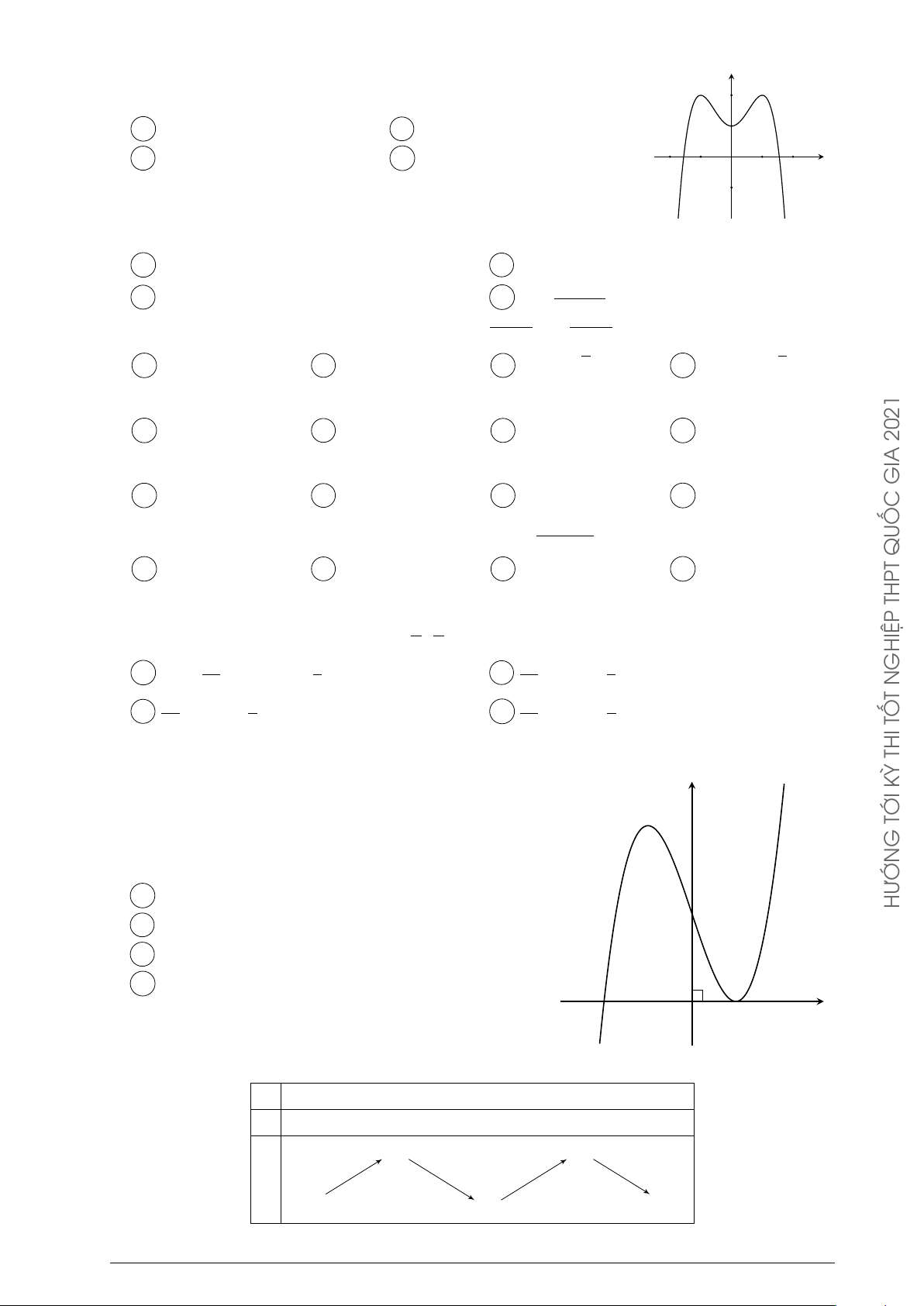
Đường cong trong hình bên là đồ thị của một hàm số trong bốn y ĐỀ
hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi C Á
hàm số đó là hàm số nào? C À A y = −x2 + x − 1. B y = −x3 + 3x + 1. V x C y = x3 − 3x + 1. D y = x4 − x2 + 1. GIA
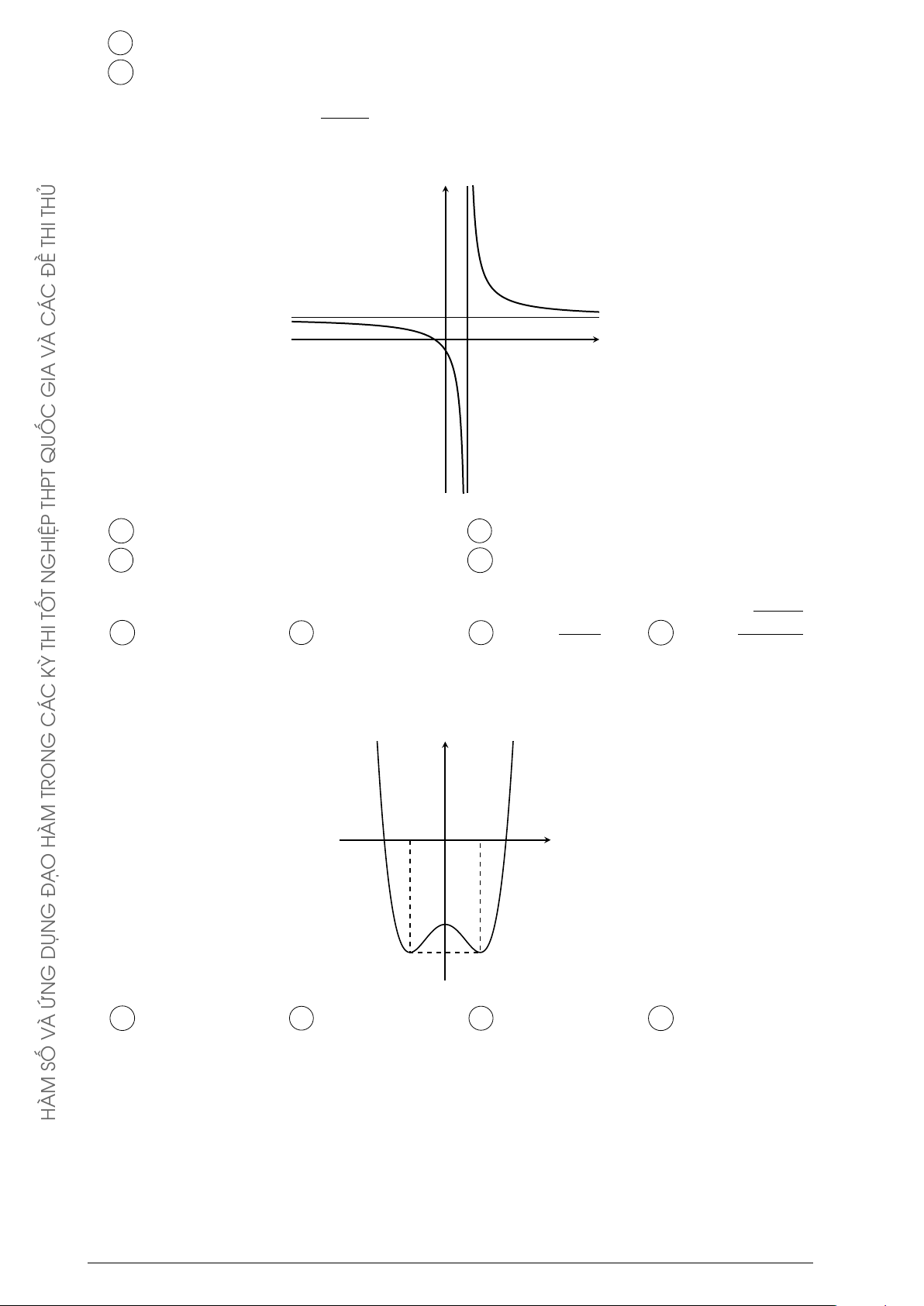
Câu 2. Cho hàm số y = f (x) có lim = 1 và lim
= −1. Khẳng định nào sau đây là x→+∞ x→−∞ QUỐC khẳng định đúng?
A Đồ thị hàm số đã cho không có tiệm cận ngang. THPT
B Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
C Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = −1. GHIỆP N
D Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1 và x = −1. T TỐ
Câu 3. Hỏi hàm số y = 2x4 + 1 đồng biến trên khoảng nào? Å ã Å ã THI 1 1 A −∞; − . B (0; +∞). C − ; +∞ . D (−∞; 0). 2 2 KỲ C
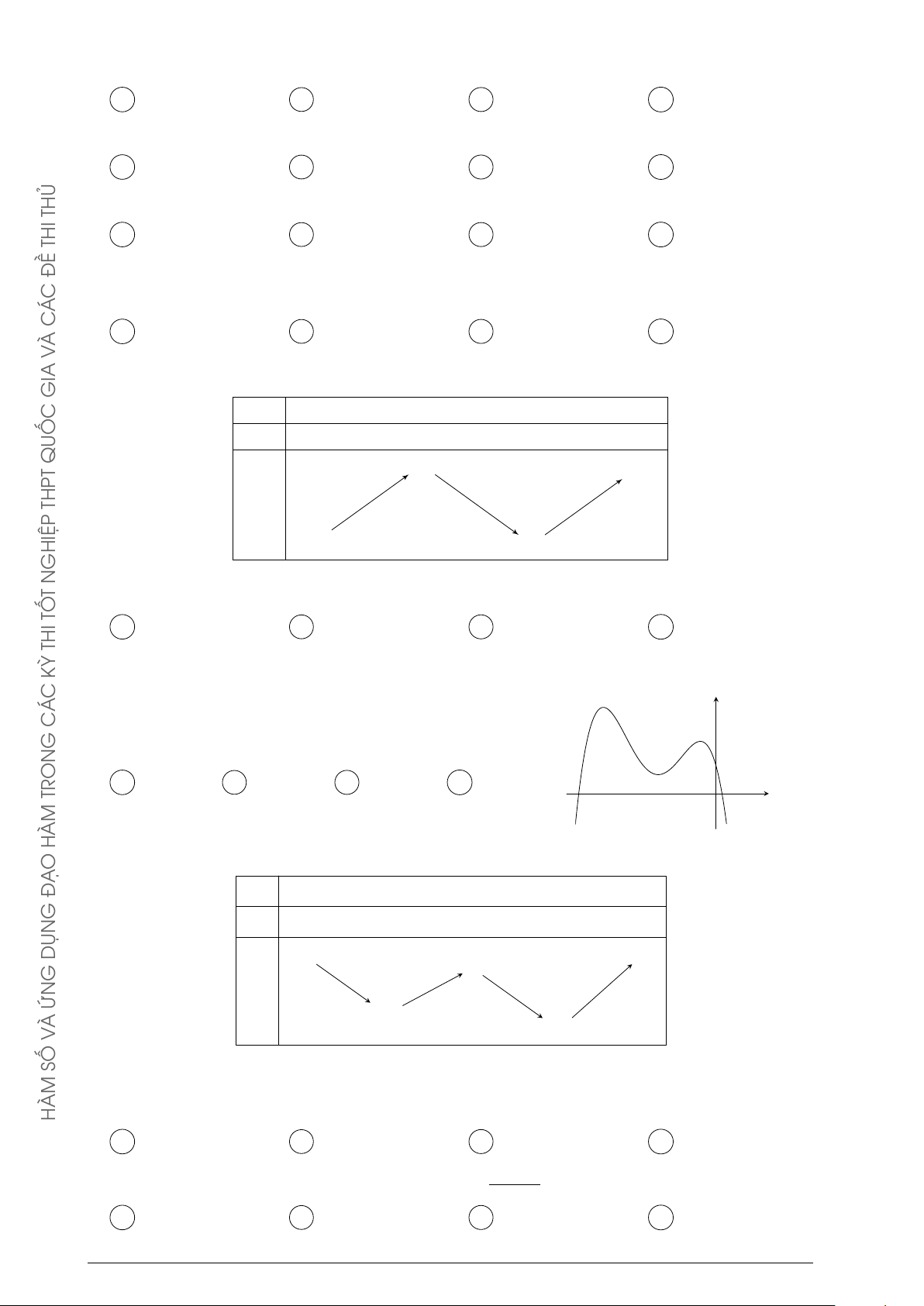
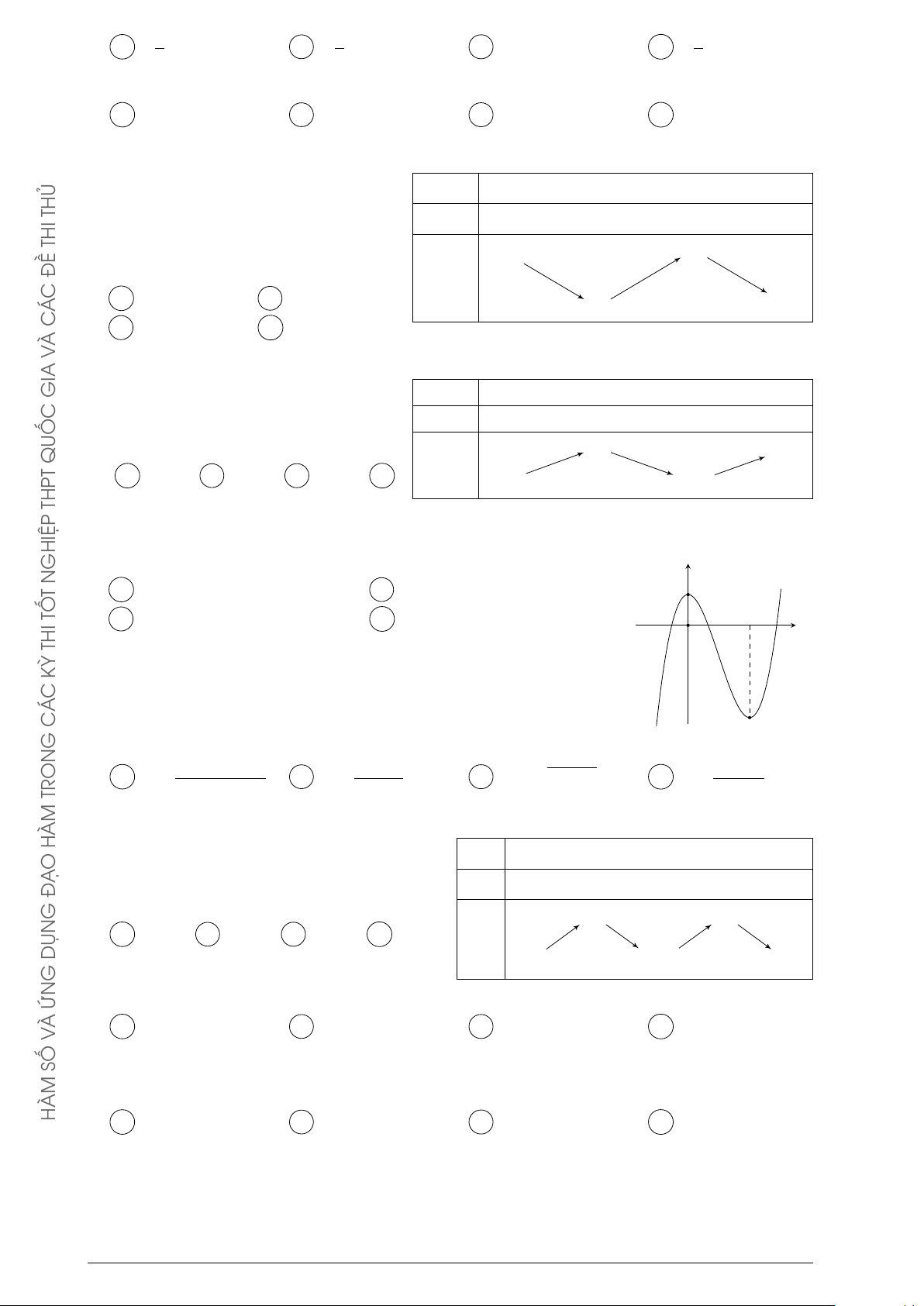
Câu 4. Cho hàm số y = f (x) xác định, liên tục trên Á
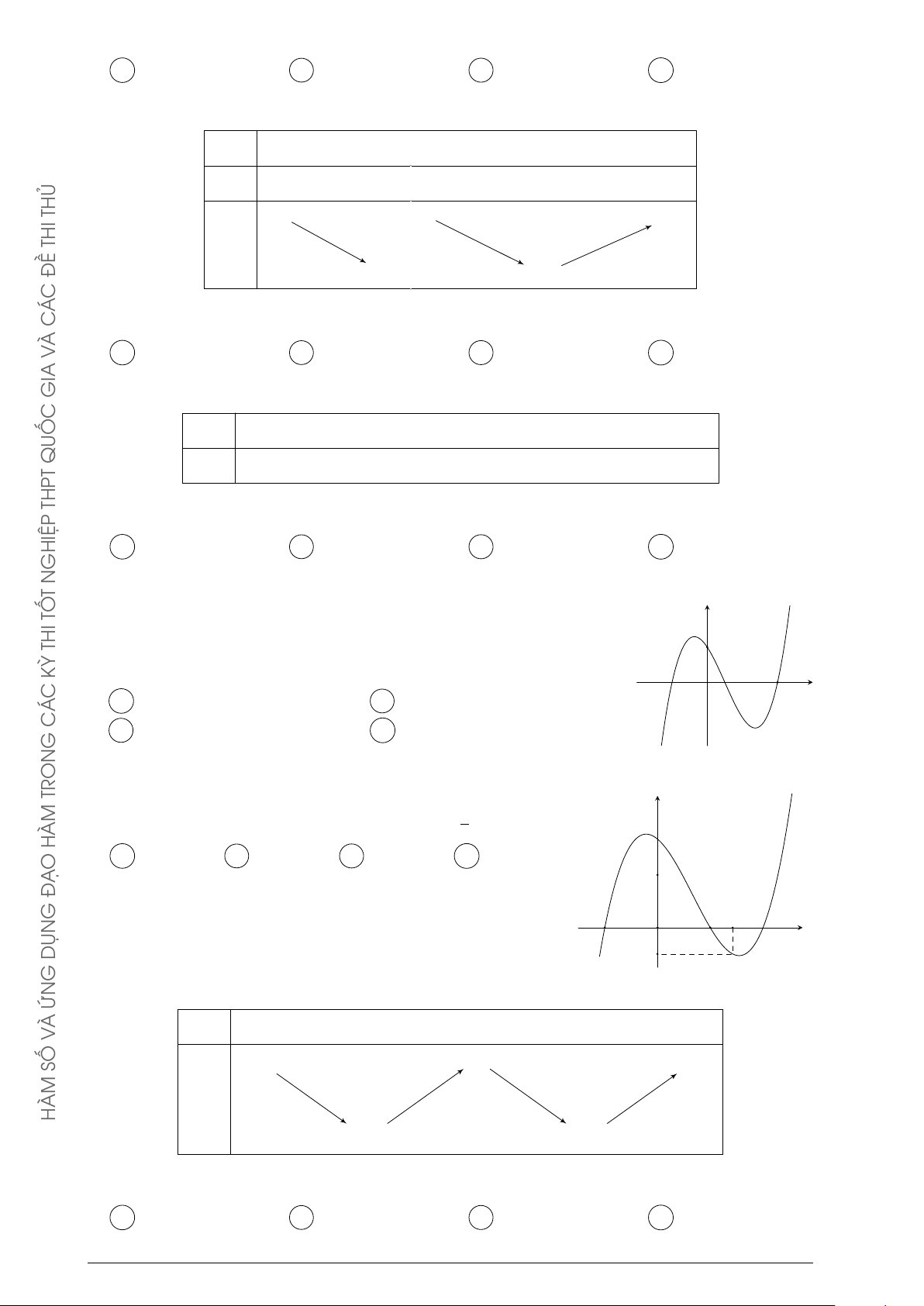
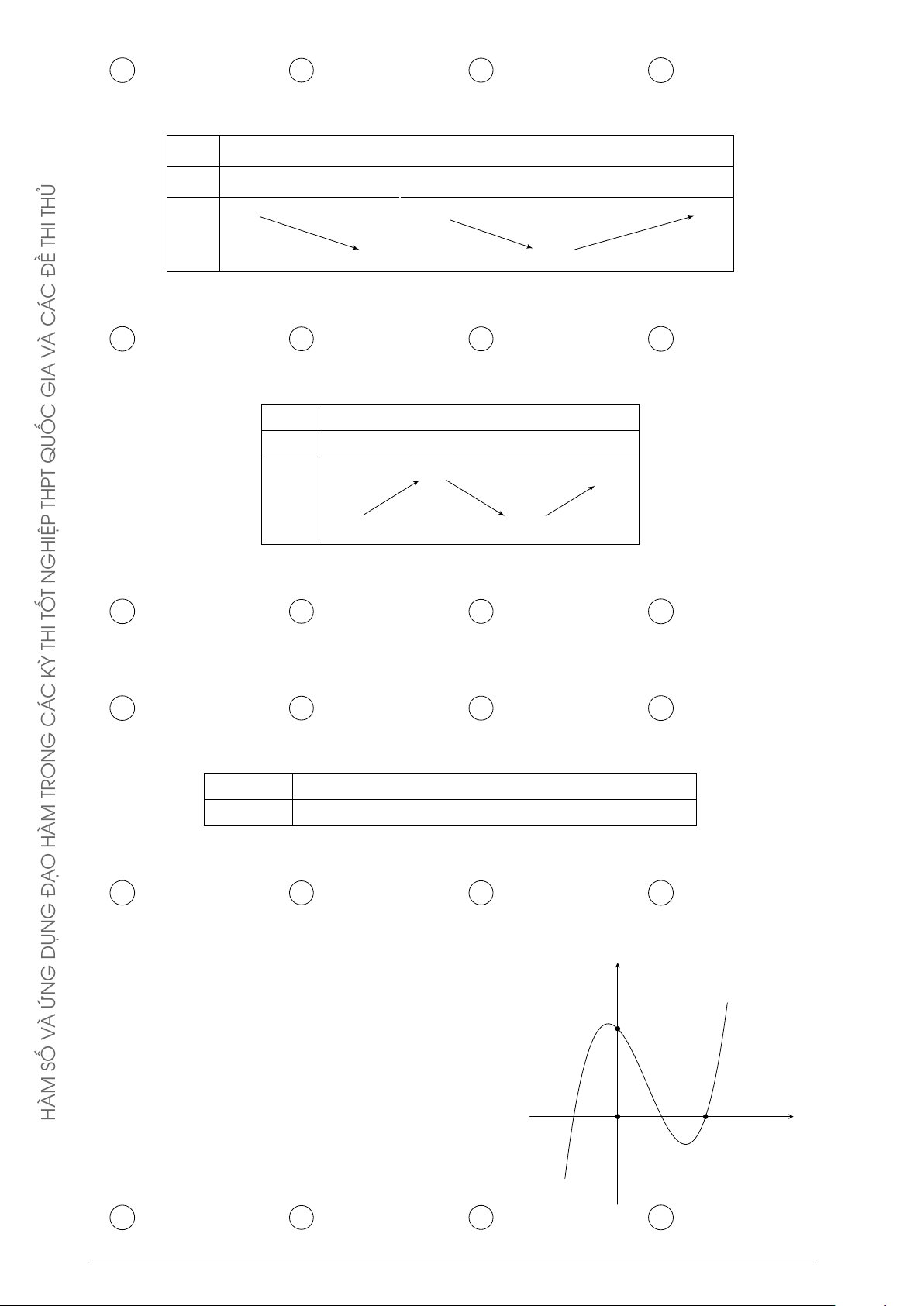
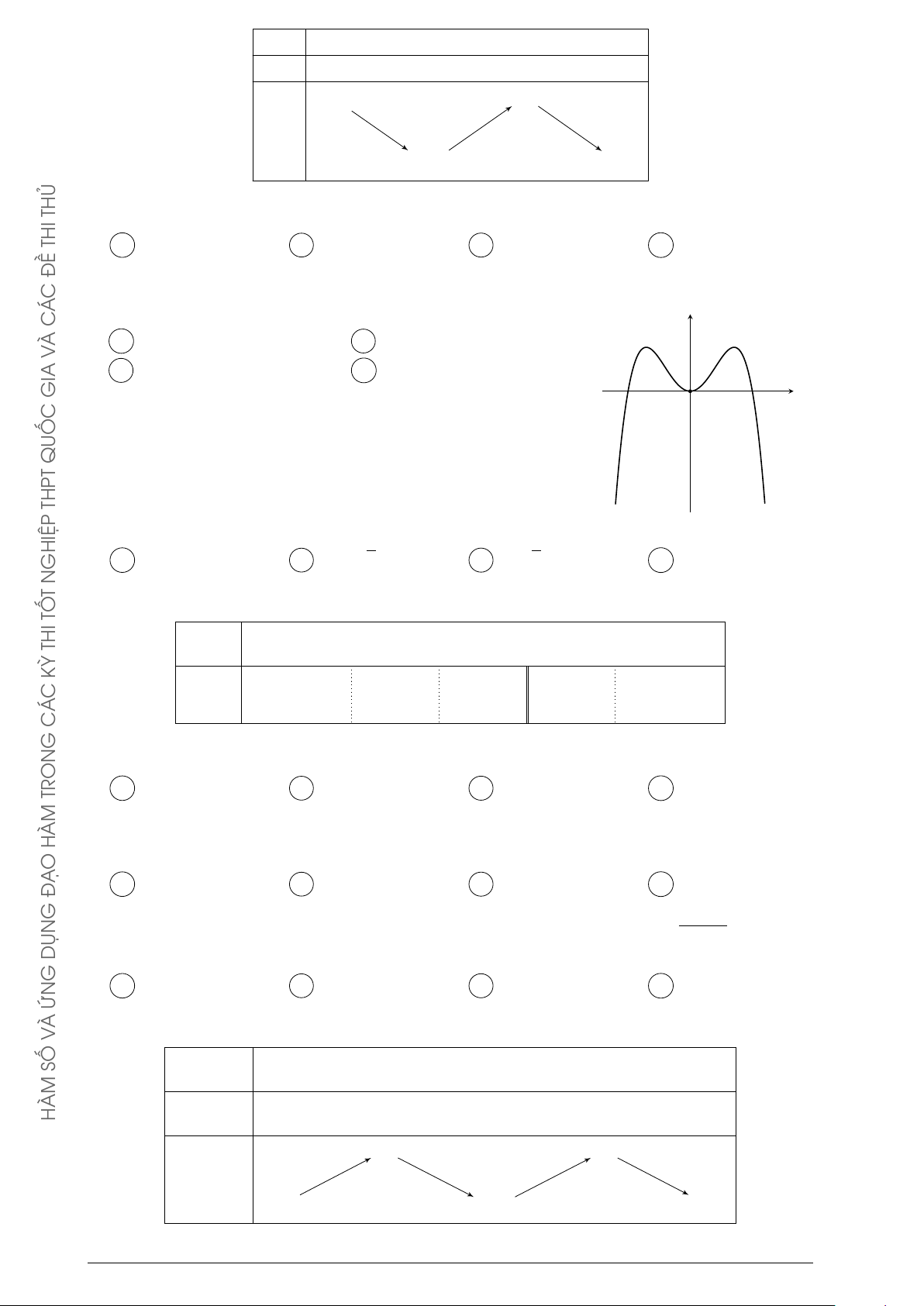
R và có bảng biến thiên: C G x −∞ 0 1 +∞ y0 + − 0 + TRON 0 +∞ + HÀM y O Ạ −∞ −1 Đ G
Khẳng định nào sau đây là khẳng định đúng? DỤN
A Hàm số có đúng một cực trị. G
B Hàm số có giá trị cực tiểu bằng 1. ỨN À
C Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng −1. V
D Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1. SỐ
Câu 5. Tìm giá trị cực đại yCĐ của hàm số y = x3 − 3x + 2. HÀM A yCĐ = 4. B yCĐ = 1. C yCĐ = 0. D yCĐ = −1. x2 + 3
Câu 6. Tìm giá trị nhỏ nhất của hàm số y = trên đoạn [2; 4]. x − 1 19 A min y = 6. B min y = −2. C min y = −3. D min y = . [2;4] [2;4] [2;4] [2;4] 3
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 2
Câu 7. Biết rằng đường thẳng y = −2x + 2 cắt đồ thị hàm số y = x3 + x + 2 tại điểm duy
nhất; kí hiệu (x◦; y◦) là tọa độ của điểm đó. Tìm y◦. A y◦ = 4. B y◦ = 0. C y◦ = 2. D y◦ = −1.
Câu 8. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x4+2mx2+1
có ba điểm cực trị tạo thành một tam giác vuông cân. 1 1 A m = − √ . B m = −1. C m = √ . D m = 1. 3 9 3 9 x + 1
Câu 9. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = √mx2 + 1
có hai đường tiệm cận ngang.
A Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. B m < 0. C m = 0. D m > 0. 2021
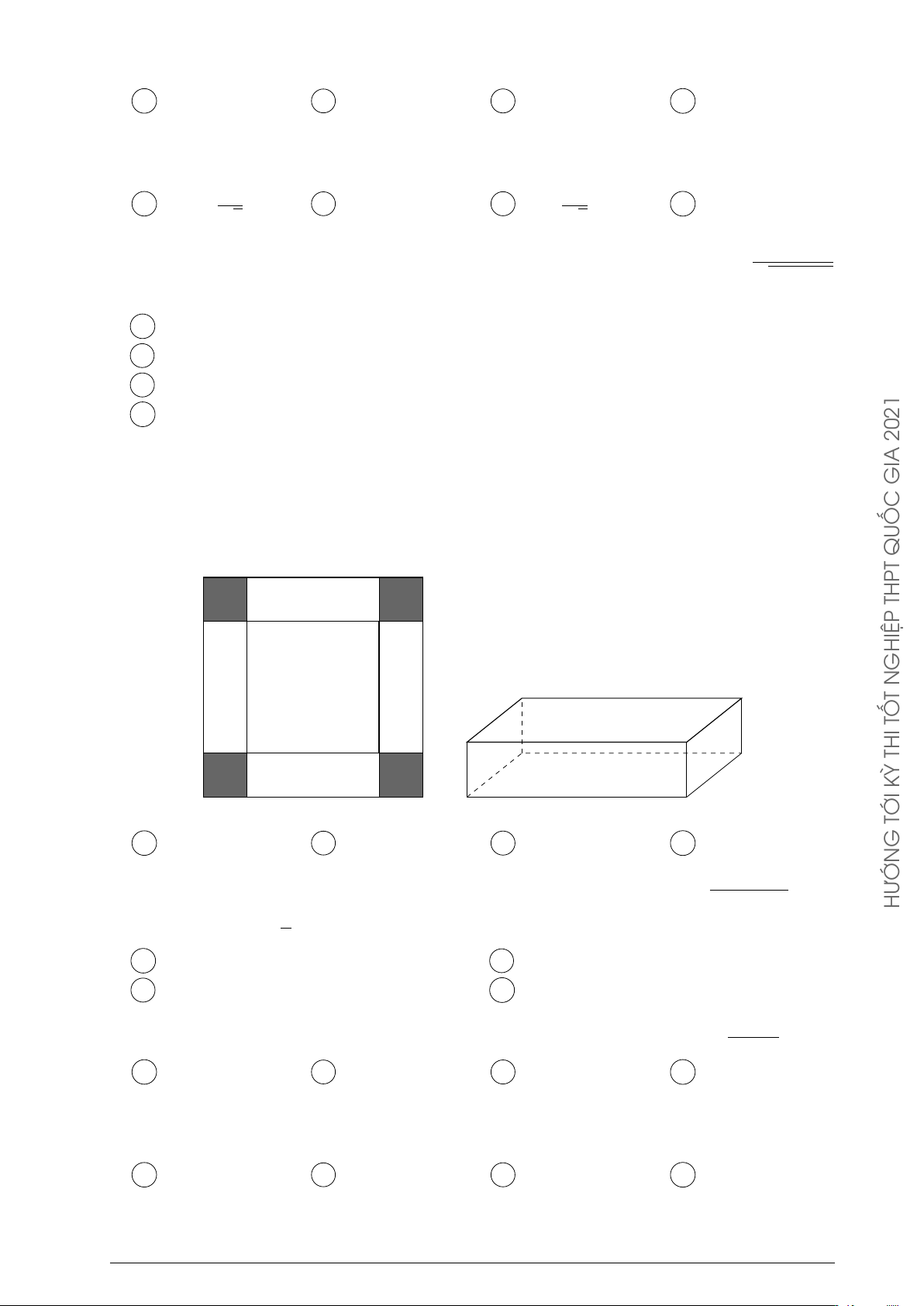
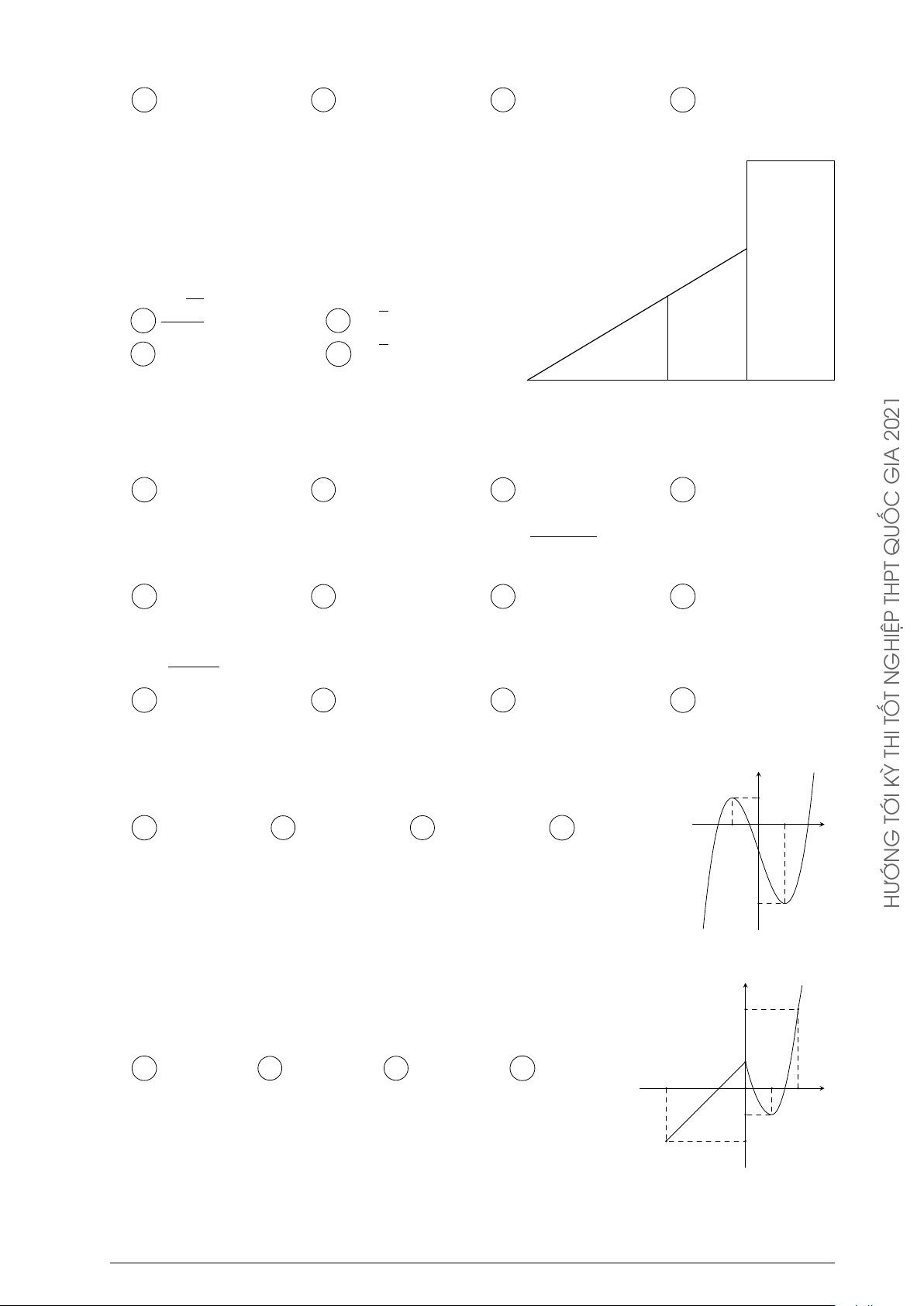
Câu 10. Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm GIA
đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm, rồi gập tấm nhôm lại
như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. QUỐC THPT GHIỆP N T TỐ THI KỲ TỚI A x = 6. B x = 3. C x = 2. D x = 4. G tan x − 2
Câu 11. Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = đồng tan x − m HƯỚN π biến trên khoảng 0; . 4
A m ≤ 0 hoặc 1 ≤ m < 2. B m ≤ 0. C 1 ≤ m < 2. D m ≥ 2. 2x + 1
Câu 12. Đường thẳng nào dưới đây là tiệm cận đứng của đồ thị hàm số y = ? x + 1 A x = 1. B y = −1. C y = 2. D x = −1.
Câu 13. Đồ thị của hàm số y = x4 − 2x2 + 2 và đồ thị của hàm số y = −x2 + 4 có tất cả bao nhiêu điểm chung? A 0. B 4. C 1. D 2. Câu 14.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 3
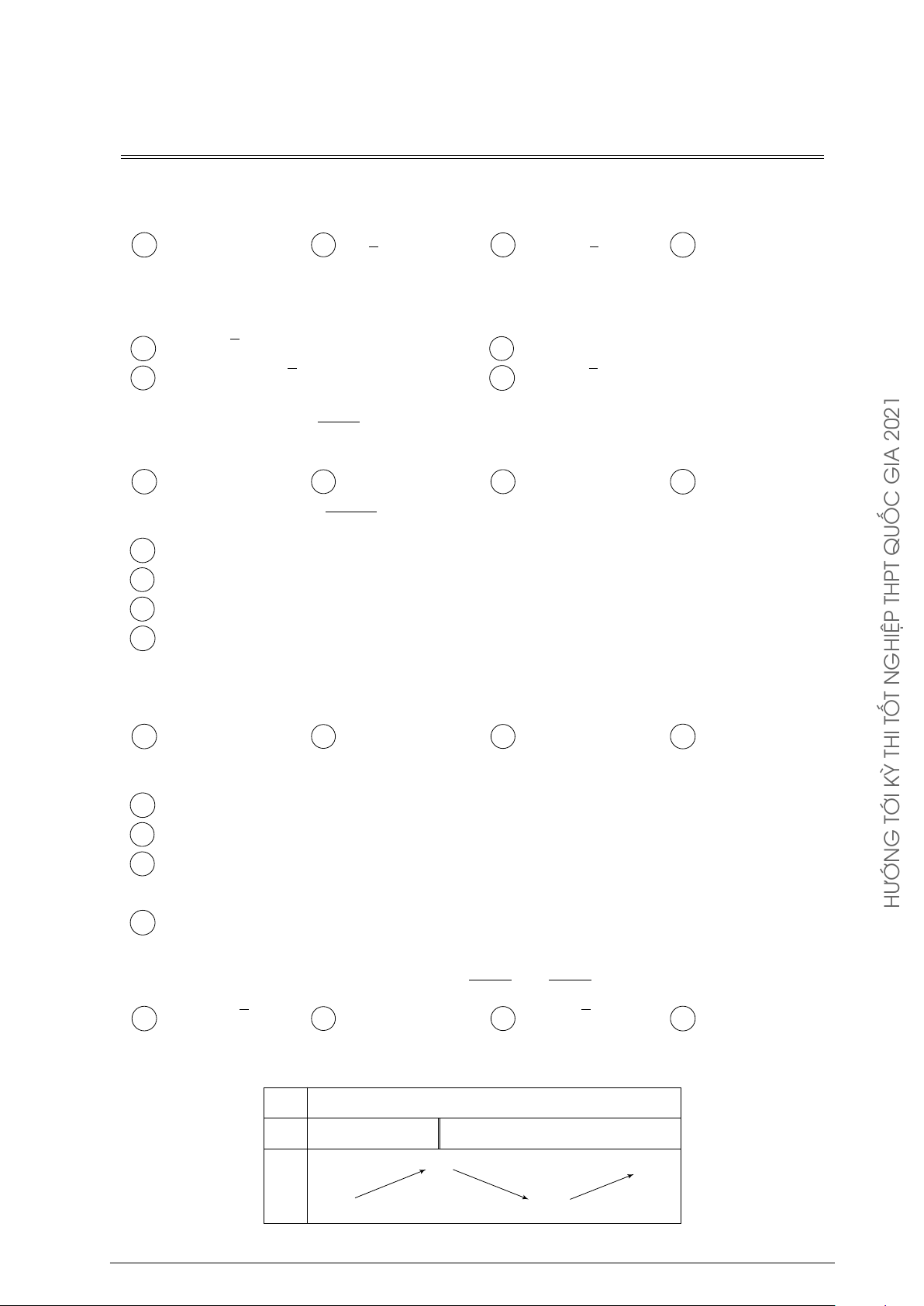
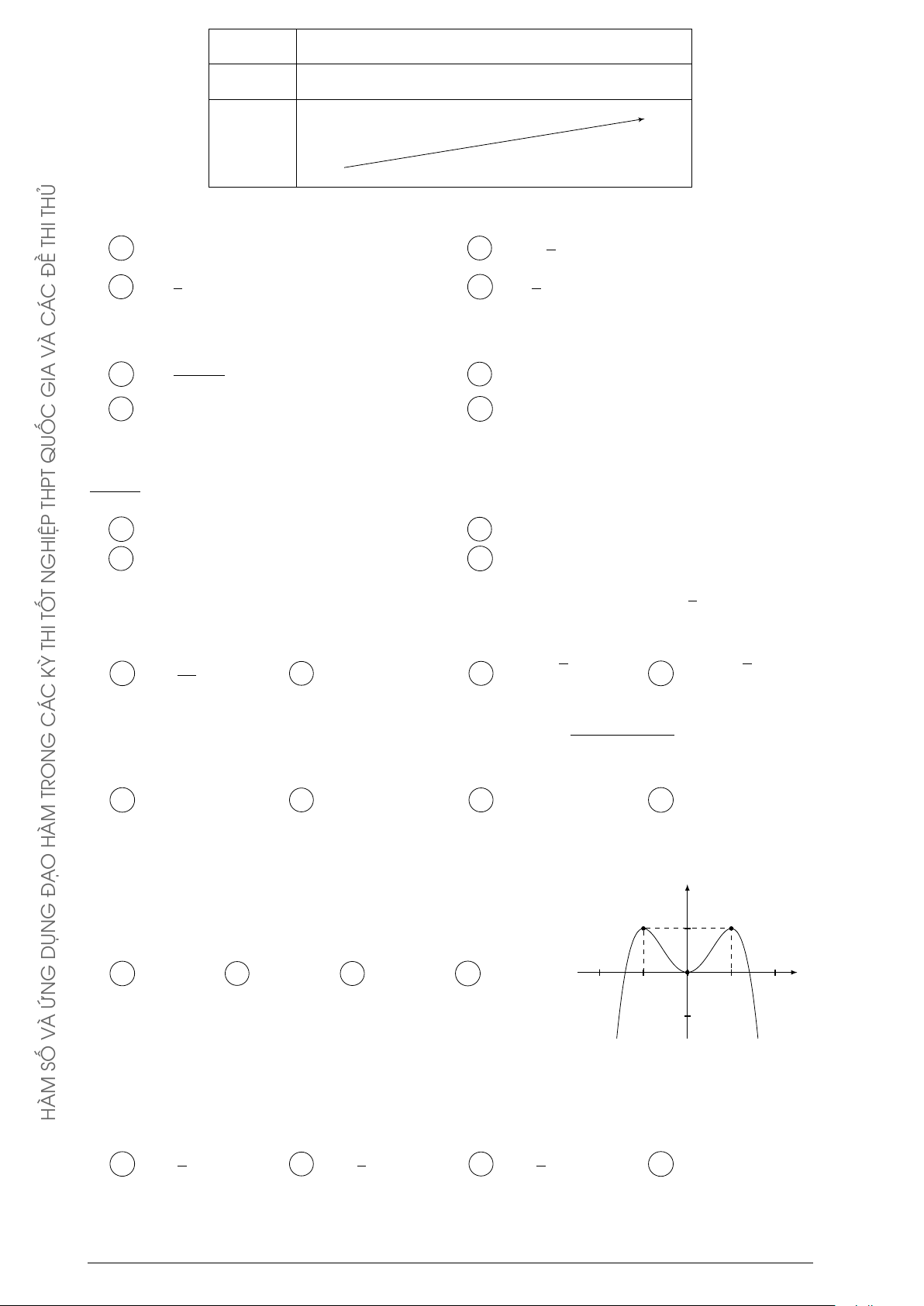
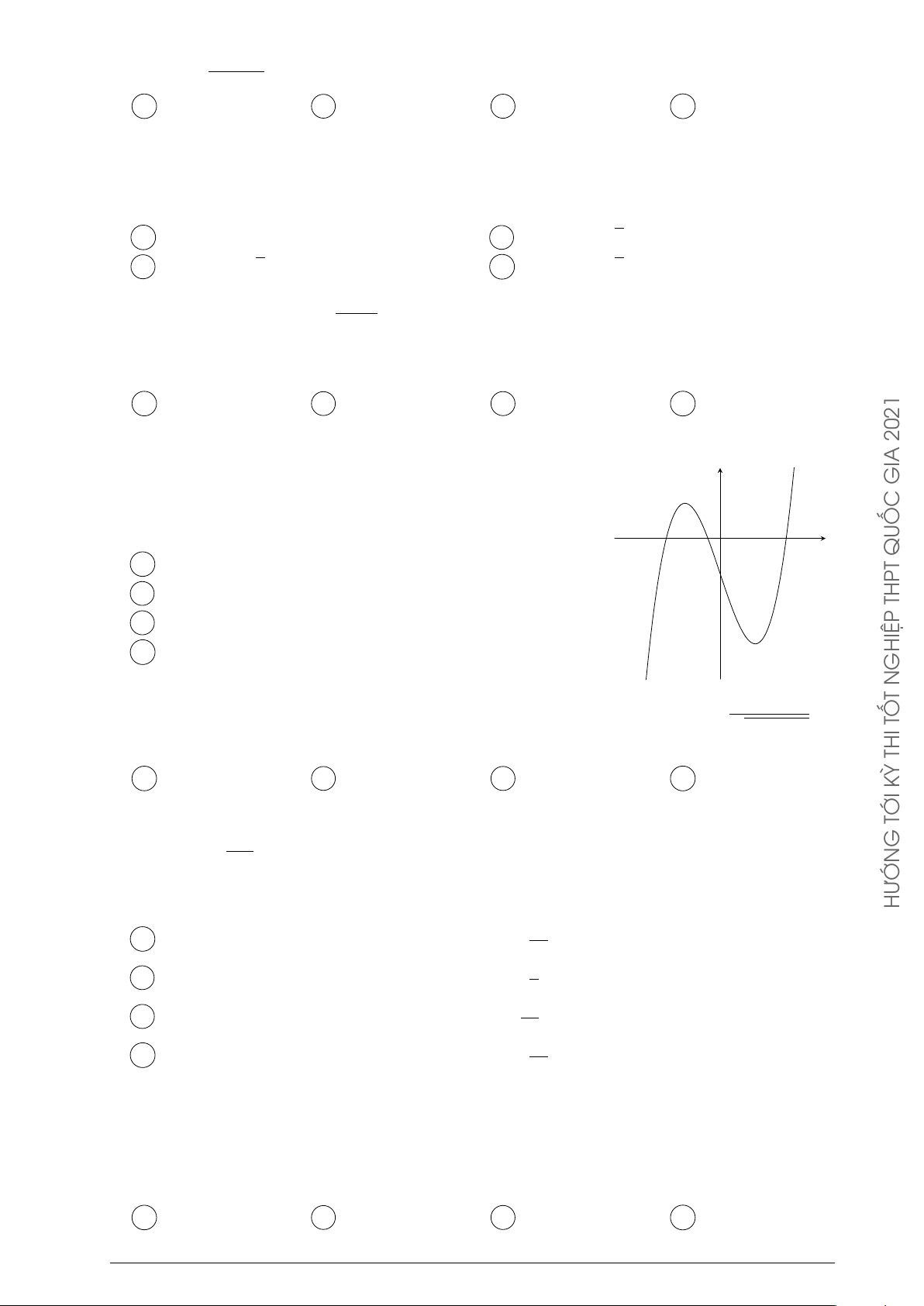
Cho hàm số y = f (x) xác định, liên tục trên đoạn [−2; 2] và có đồ thị y 4
là đường cong trong hình vẽ bên. Hàm số f (x) đạt cực đại tại điểm nào dưới đây? 2 A x = 2. B x = −1. C x = 1. D x = 2. O x −2 −1 1 2 THỦ −2 THI ĐỀ −4 C Á C
Câu 15. Cho hàm số y = x3 − 2x2 + x + 1. Mệnh đề nào dưới đây đúng? À Å 1 ã V
A Hàm số nghịch biến trên khoảng ; 1 . 3 Å 1 ã GIA
B Hàm số nghịch biến trên khoảng −∞; . 3 Å 1 ã
C Hàm số đồng biến trên khoảng ; 1 . QUỐC 3
D Hàm số nghịch biến trên khoảng (1; +∞). THPT
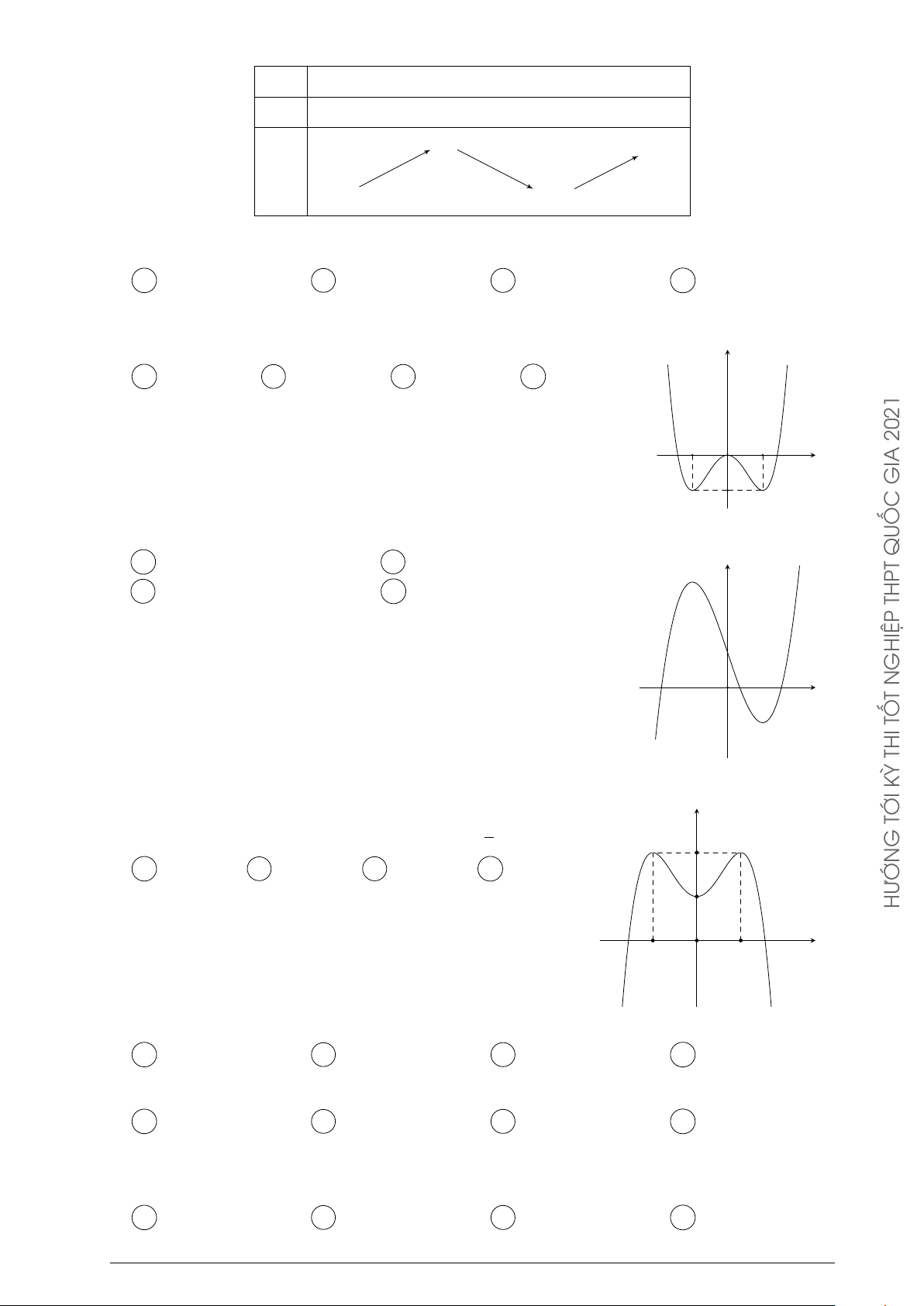
Câu 16. Cho hàm số y = f (x) xác định trên R \ {0}, liên tục trên mỗi khoảng xác định và
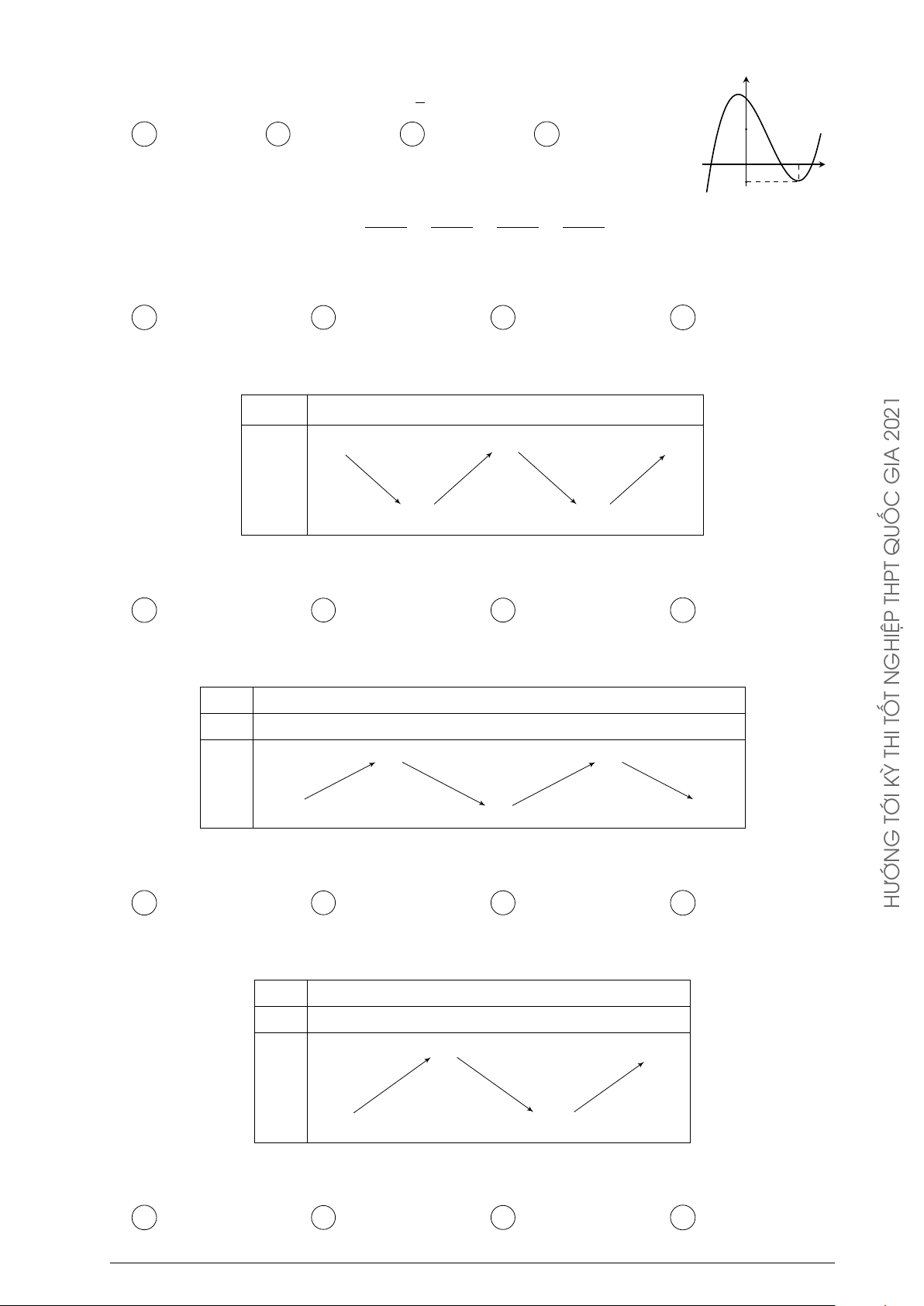
có bảng biến thiên như sau. GHIỆP N T x −∞ 0 1 +∞ TỐ y0 − + 0 − THI +∞ + 2 KỲ y C Á C −1 −∞ −∞ G
Tìm tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f (x) = m có ba TRON nghiệm thực phân biệt. HÀM A [−1; 2]. B (−1; 2). C (−1; 2]. D (−∞; 2]. O Ạ x2 + 3 Đ Câu 17. Cho hàm số y =
. Mệnh đề nào dưới đây đúng ? x + 1 G
A Cực tiểu của hàm số bằng −3.
B Cực tiểu của hàm số bằng 1. DỤN
C Cực tiểu của hàm số bằng −6.
D Cực tiểu của hàm số bằng 2. G 1
Câu 18. Một vật chuyển động theo quy luật s = − t3 + 9t2, với t (giây) là khoảng thời gian ỨN 2 À
tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng V
thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn SỐ
nhất của vật đạt được bằng bao nhiêu ? HÀM A 216(m/s). B 30(m/s). C 400(m/s). D 54(m/s). √ 2x − 1 − x2 + x + 3
Câu 19. Tìm tất cả các tiệm cận đứng của đồ thị hàm số y = x2 − 5x + 6 A x = −3 và x = −2. B x = −3. C x = 3 và x = 2. D x = 3.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 4
Câu 20. Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y = ln(x2 +1)−mx+1
đồng biến trên khoảng (−∞; +∞) A (−∞; −1]. B (−∞; −1). C [−1; 1]. D [1; +∞).
Câu 21. Biết M (0; 2), N (2; −2) là các điểm cực trị của đồ thị hàm số y = ax3 + bx2 + cx + d.
Tính giá trị của hàm số tại x = −2. A y(−2) = 2. B y(−2) = 22. C y(−2) = 6. D y(−2) = −18. Câu 22.
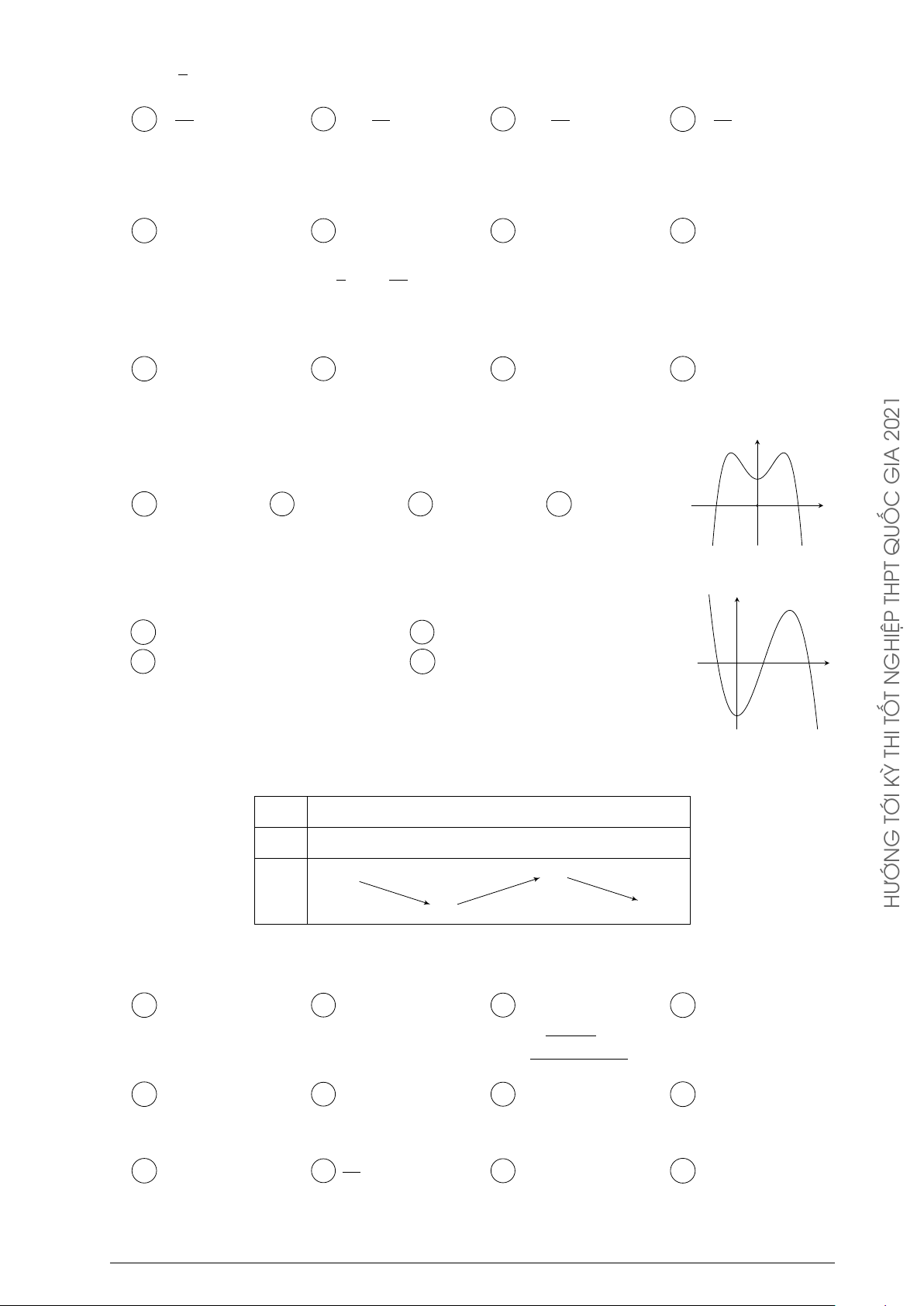
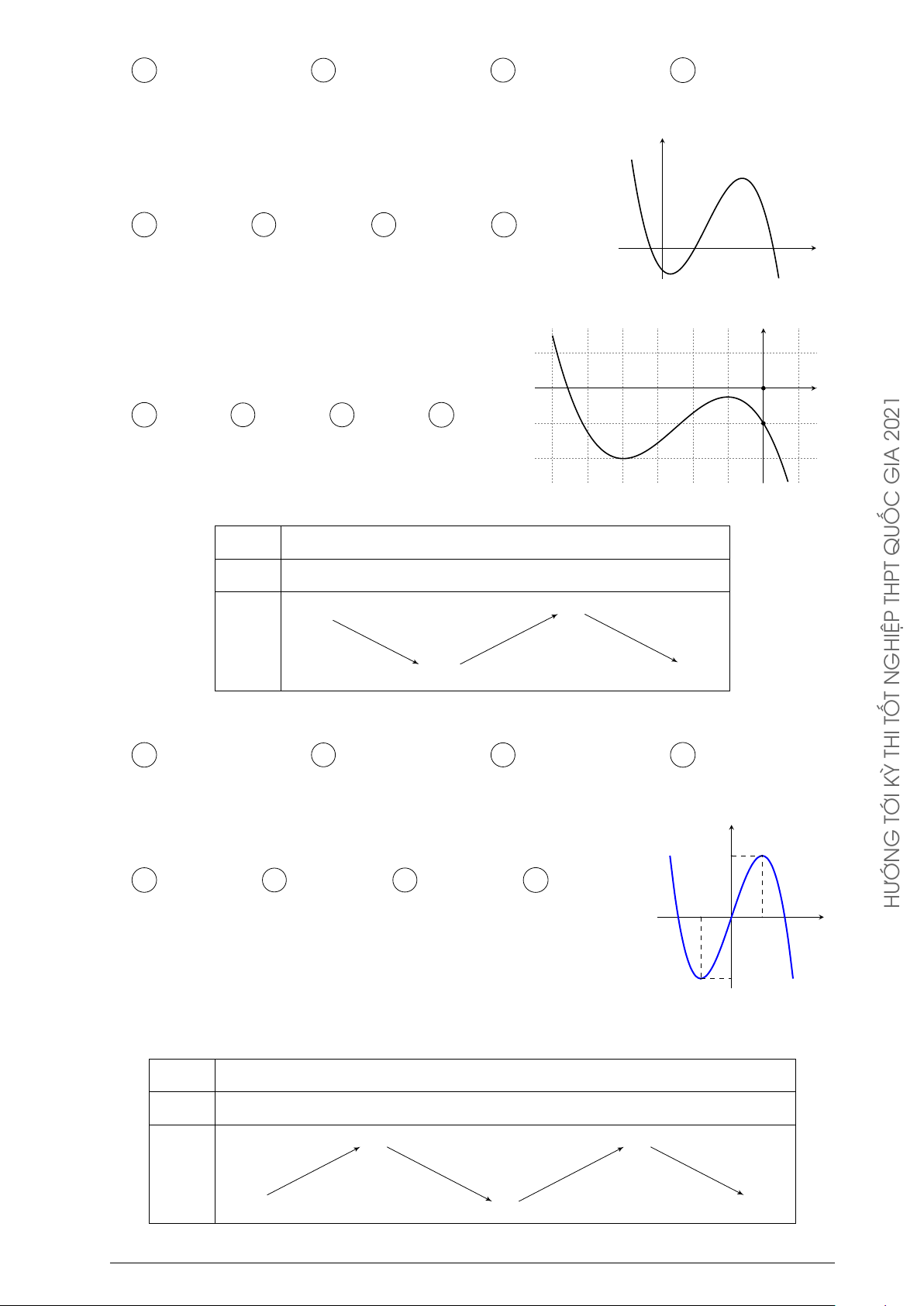
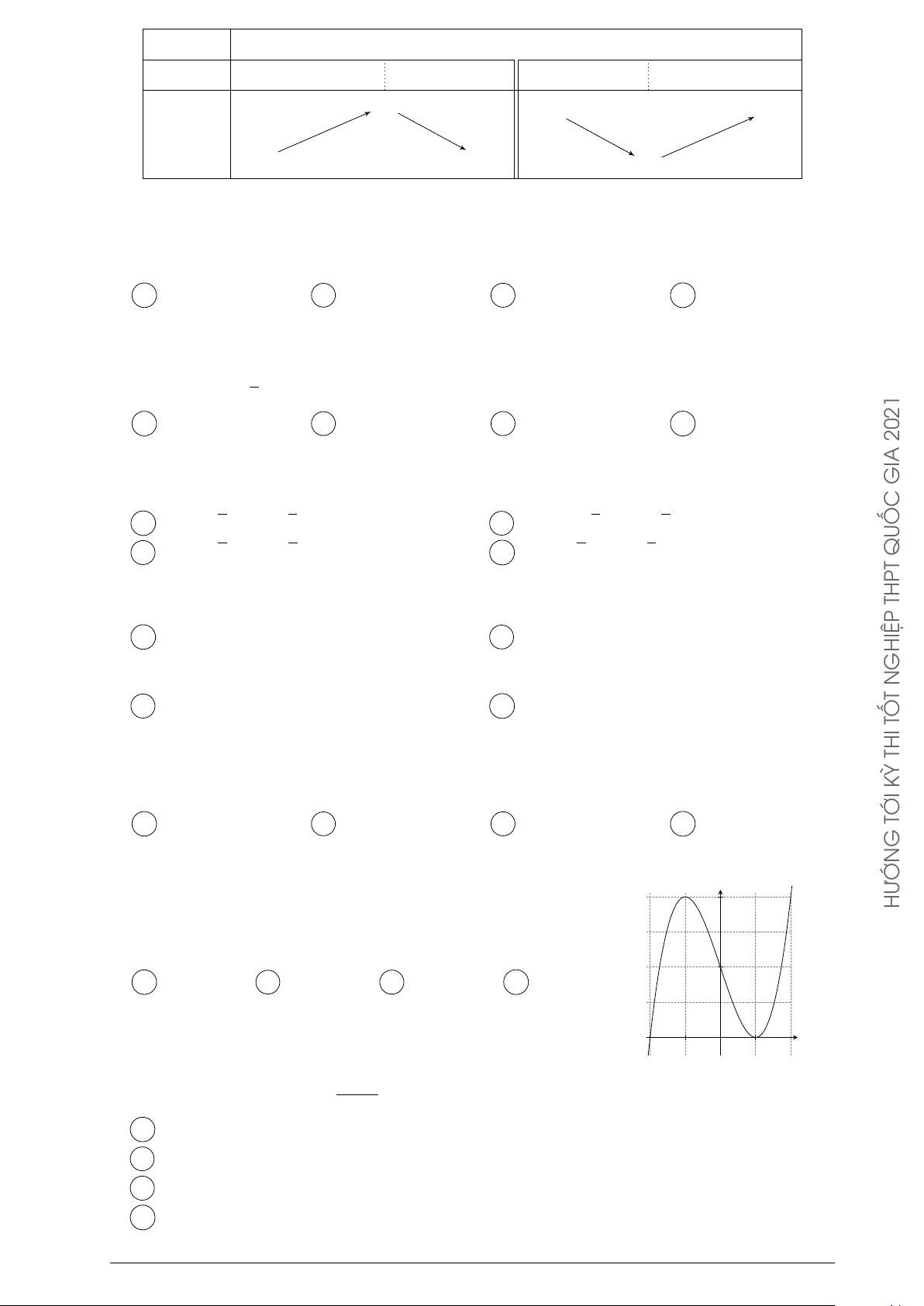
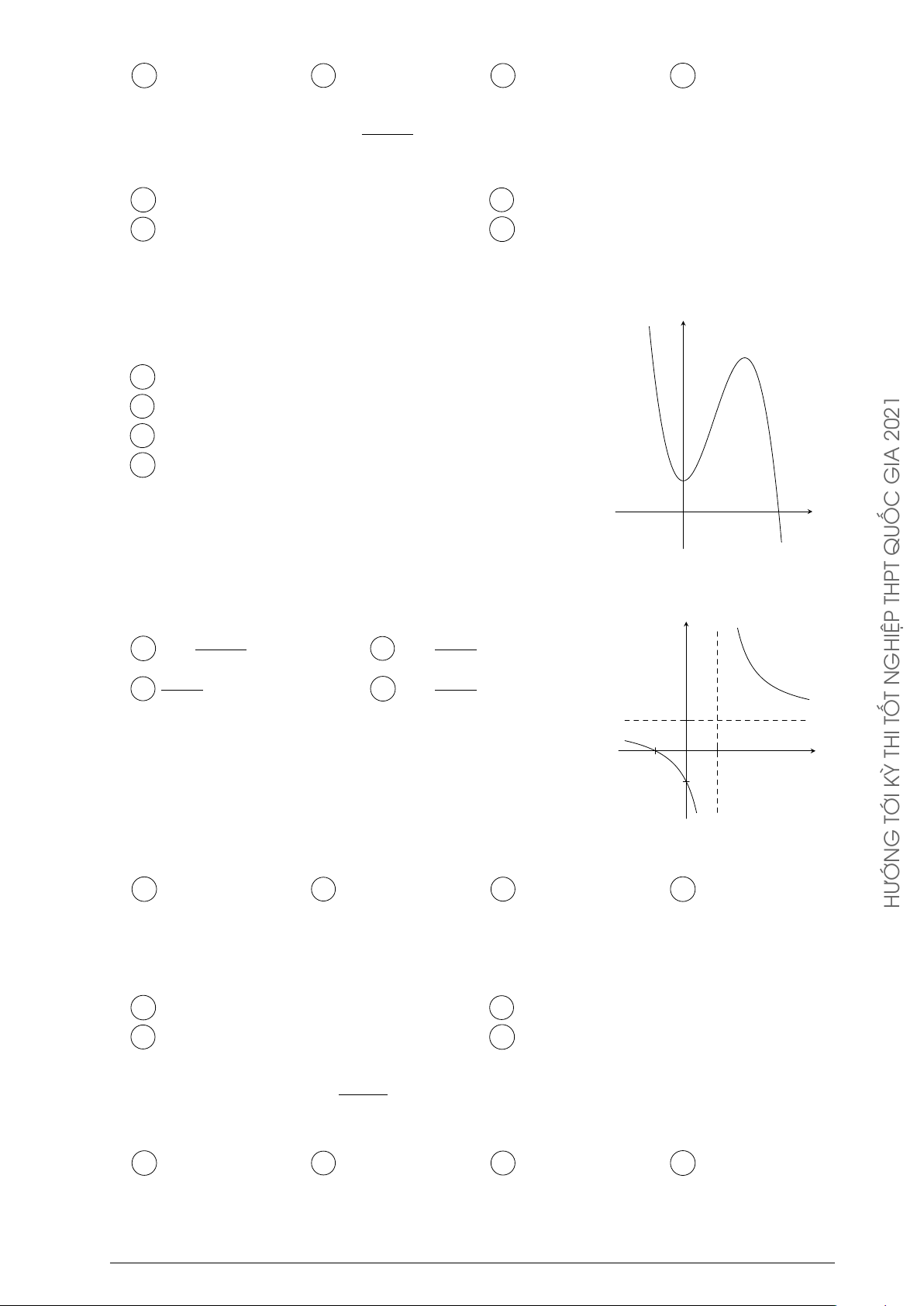
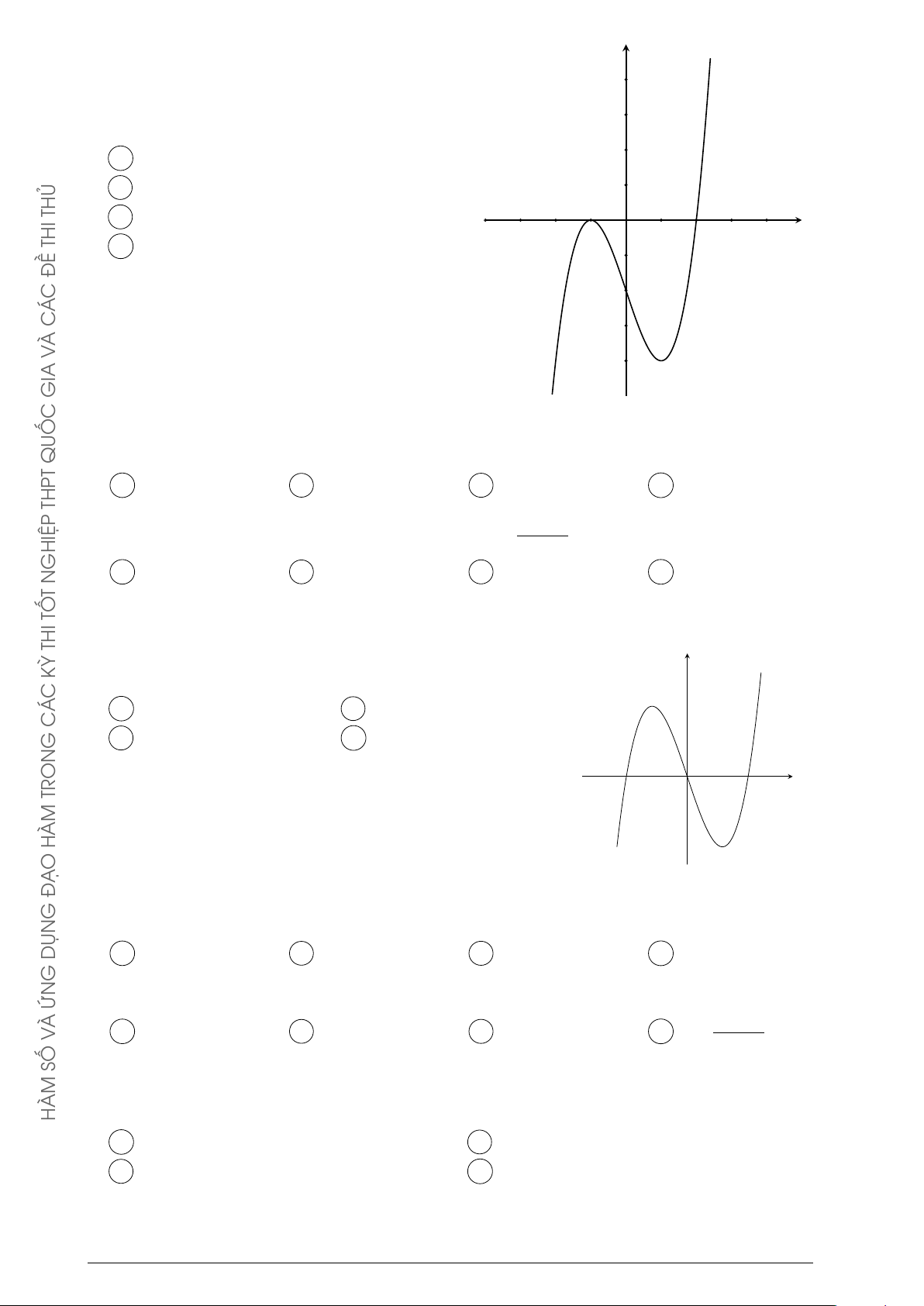
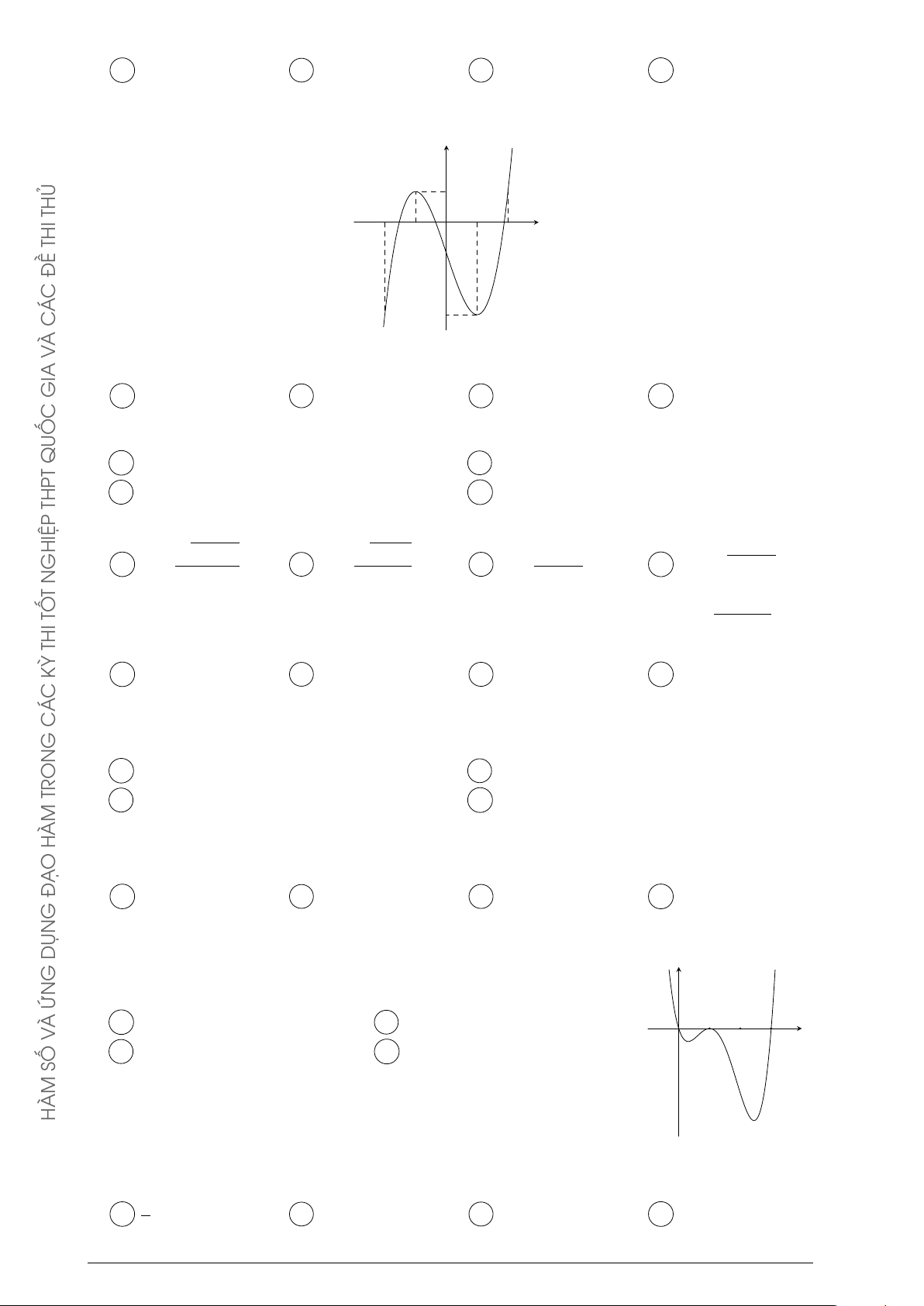
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ y
bên. Mệnh đề nào dưới đây đúng ?
A a < 0, b > 0, c > 0, d < 0.
B a < 0, b < 0, c > 0, d < 0.
C a < 0, b < 0, c < 0, d > 0. O x
D a < 0, b > 0, c < 0, d < 0. 2021 GIA
Câu 23. Cho hàm số y = x3−3x có đồ thị (C). Tìm số giao điểm của (C) và trục hoành. A 2. B 3. C 1. D 0. QUỐC x − 2 Câu 24. Cho hàm số y =
. Mệnh đề nào dưới đây đúng? x + 1
A Hàm số nghịch biến trên khoảng (−∞; −1). THPT
B Hàm số đồng biến trên khoảng (−∞; −1).
C Hàm số đồng biến trên khoảng (−∞; +∞). GHIỆP N
D Hàm số nghịch biến trên khoảng (−1; +∞). T TỐ Câu 25. THI
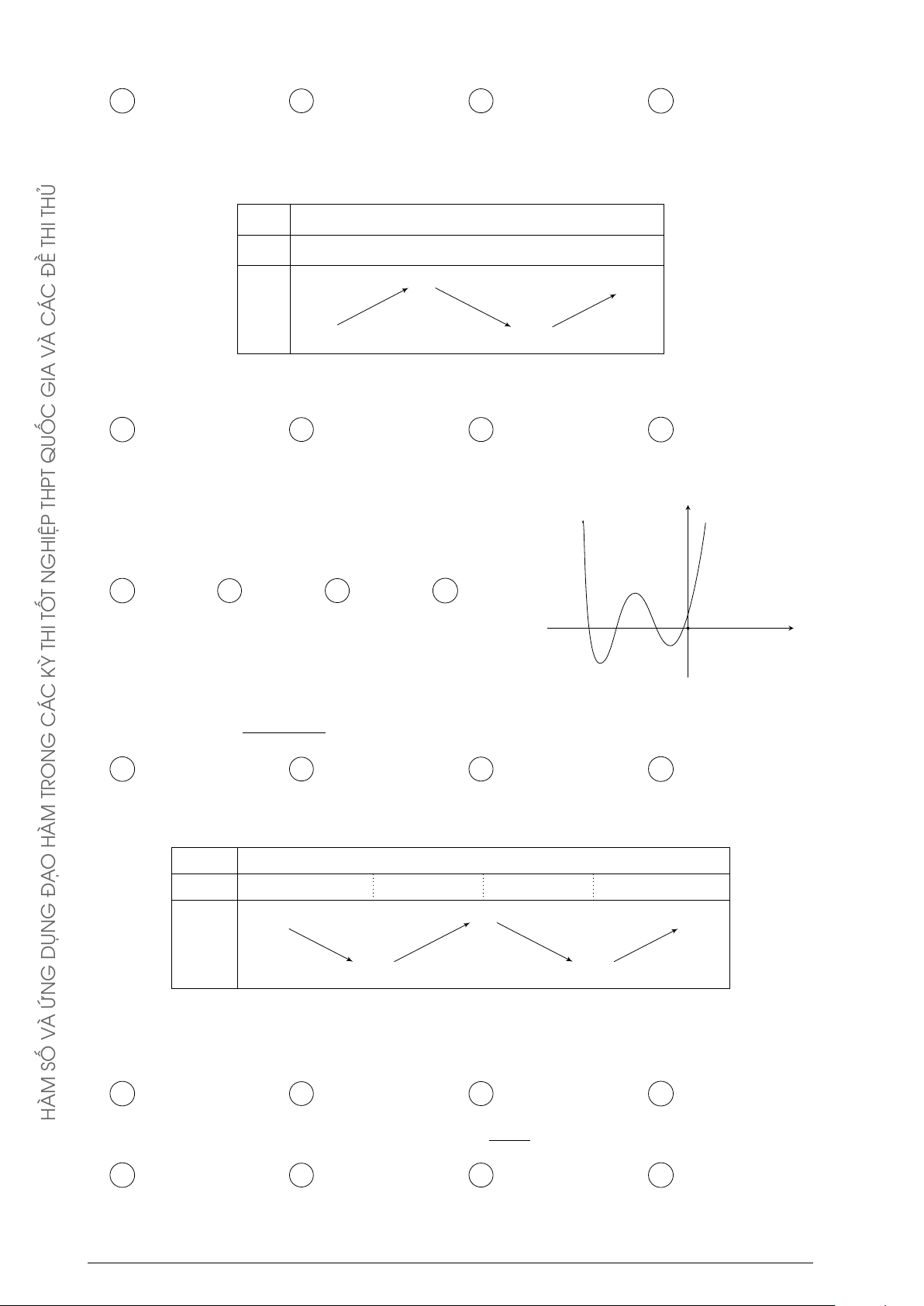
Cho hàm số y = f (x) có bảng biến x −∞ 0 1 +∞ KỲ
thiên như hình vẽ bên. Mệnh đề nào y0 − 0 + 0 − dưới đây đúng? TỚI +∞ + 5 A y G CĐ = 5. B yCT = 0. y C min y = 4. D max y = 5. 4 −∞ R R HƯỚN Câu 26. Cho hàm số y = f (x) có x −∞ −2 0 +∞
bảng biến thiên như hình y0 + −
dưới đây. Hỏi đồ thị của +∞ 1
hàm số đã cho có bao nhiêu y tiệm cận? −∞ 0 A 1. B 3. C 2. D 4.
Câu 27. Hàm số nào dưới đây đồng biến trên khoảng (−∞; +∞)? A y = 3x3 + 3x − 2. B y = 2x3 − 5x + 1. x − 2 C y = x4 + 3x2. D y = . x + 1
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 5
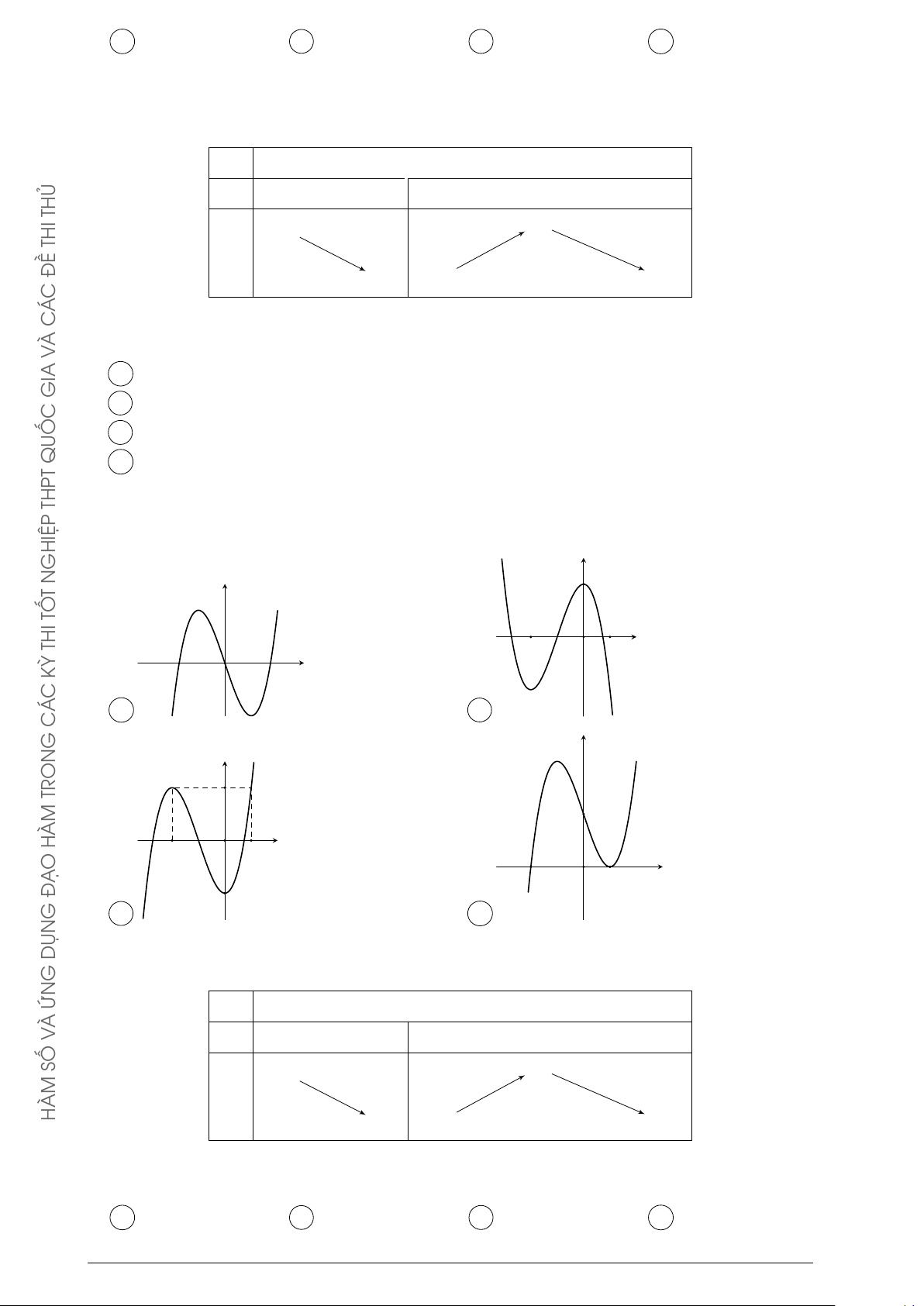
Câu 28. Cho hàm số f (x) = x ln x. Một trong bốn đồ thị cho trong bốn phương án A, B,
C, D dưới đây là đồ thị của hàm số y = f 0(x). Tìm đồ thị đó. y y 1 THỦ x O 1 x O 1 THI A . B . y y ĐỀ C Á C À 1 V x O 1 x O GIA C . D . 4
Câu 29. Tính giá trị nhỏ nhất của hàm số y = 3x + trên khoảng (0; +∞). QUỐC x2 √ 33 √ A min y = 3 3 9. B min y = 7. C min y = . D min y = 2 3 9. (0;+∞) (0;+∞) (0;+∞) 5 (0;+∞) THPT √
Từ bảng biến thiên suy ra: min y = 3 3 9. (0;+∞) GHIỆP Câu 30. N T
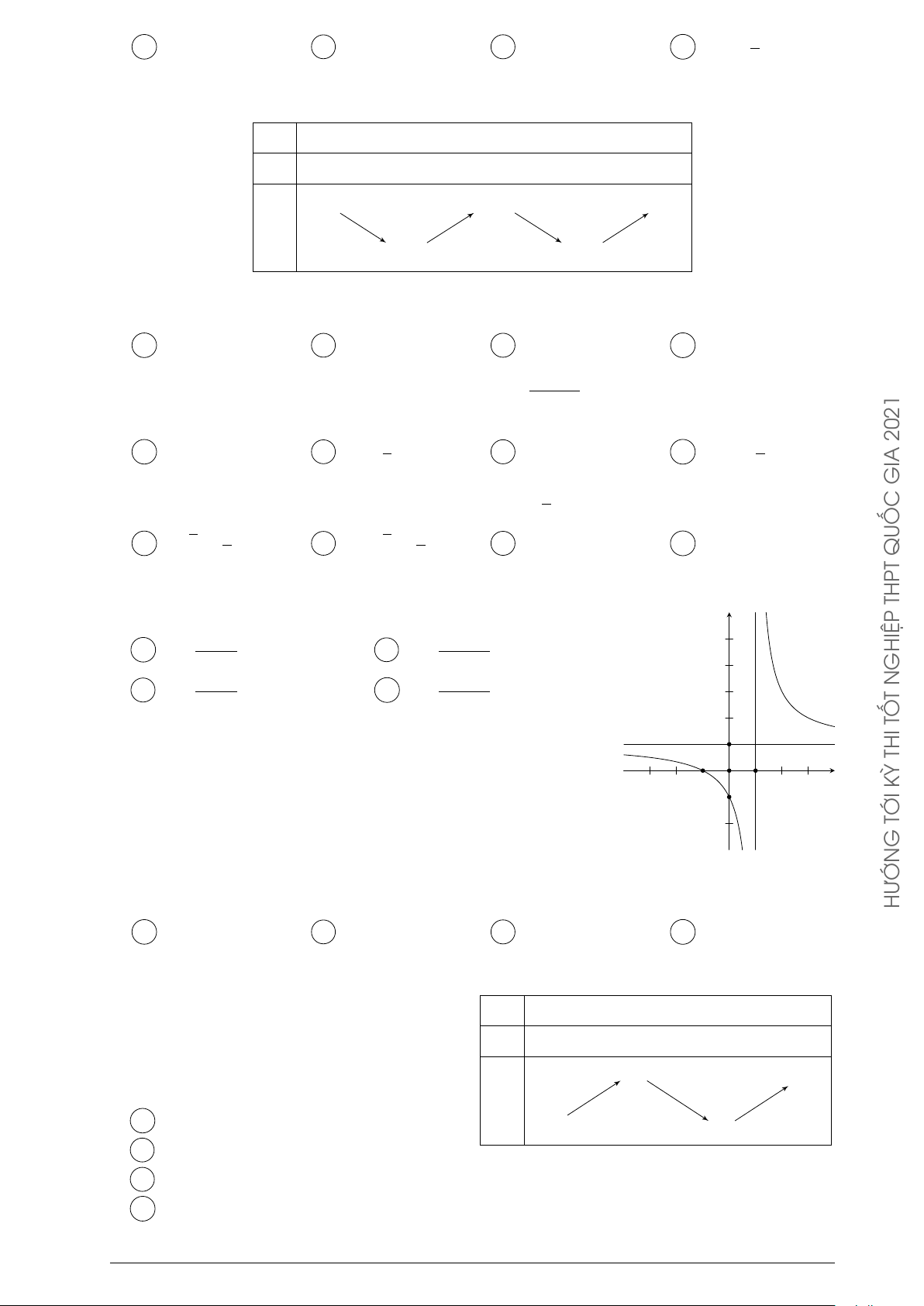
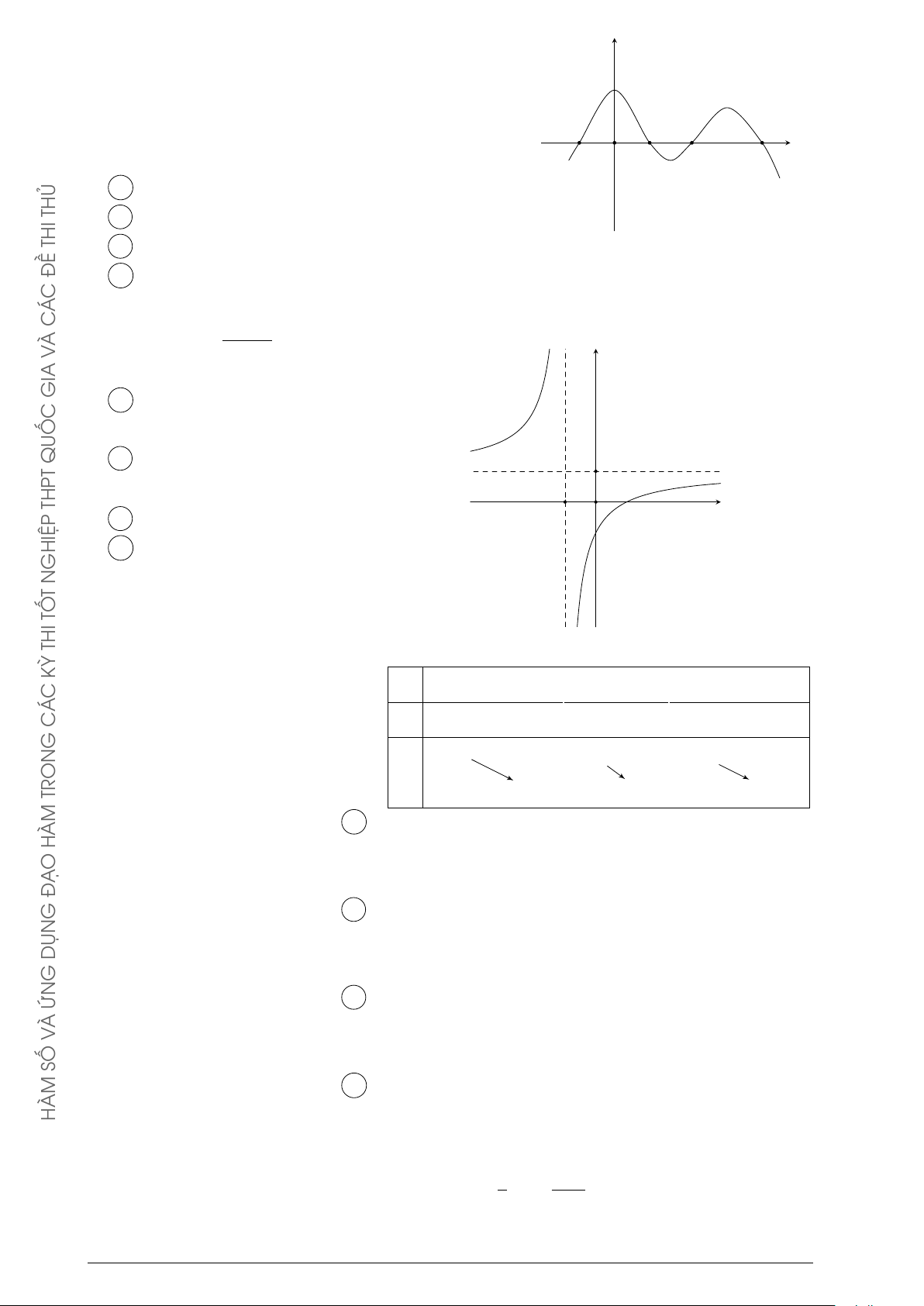
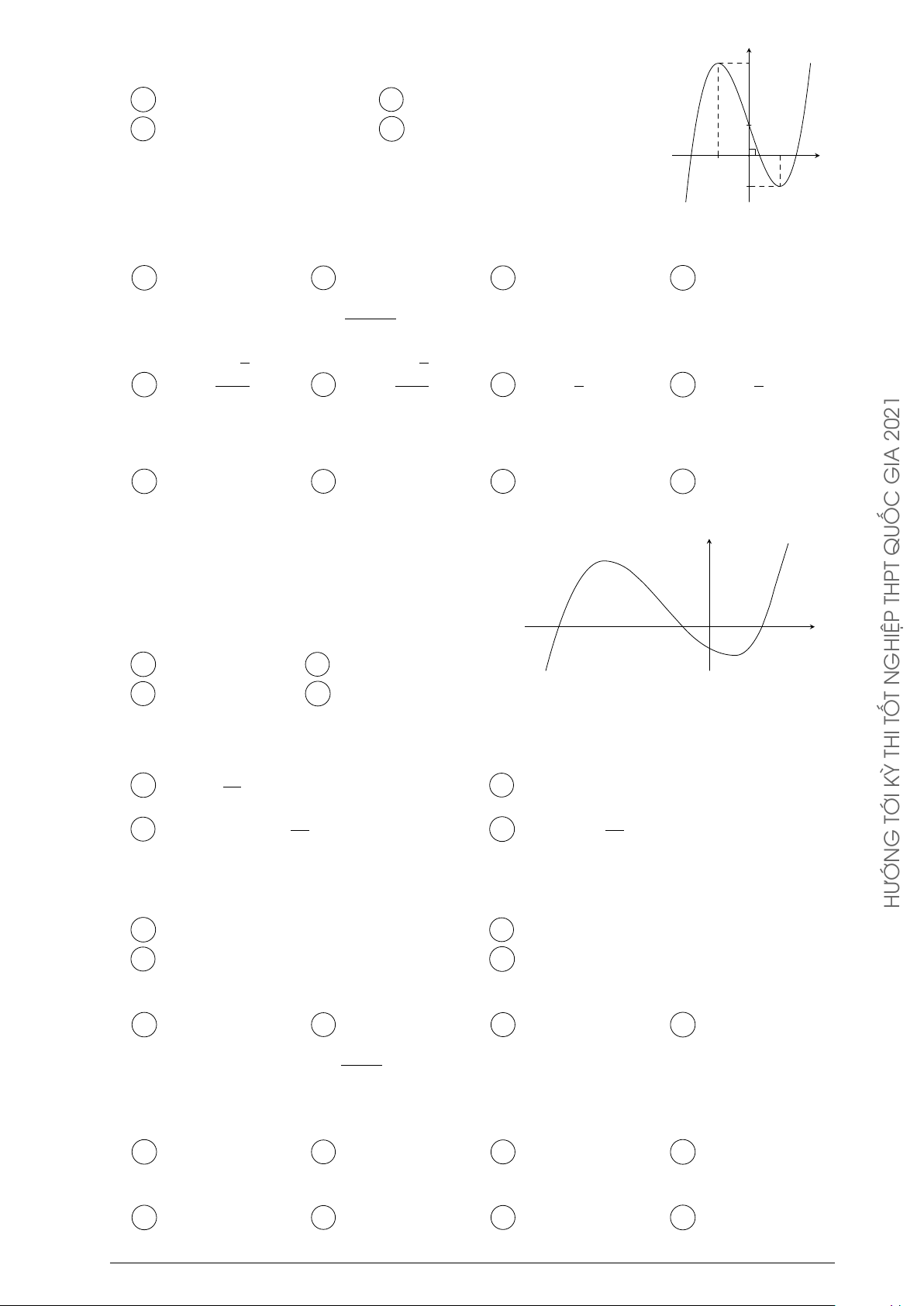
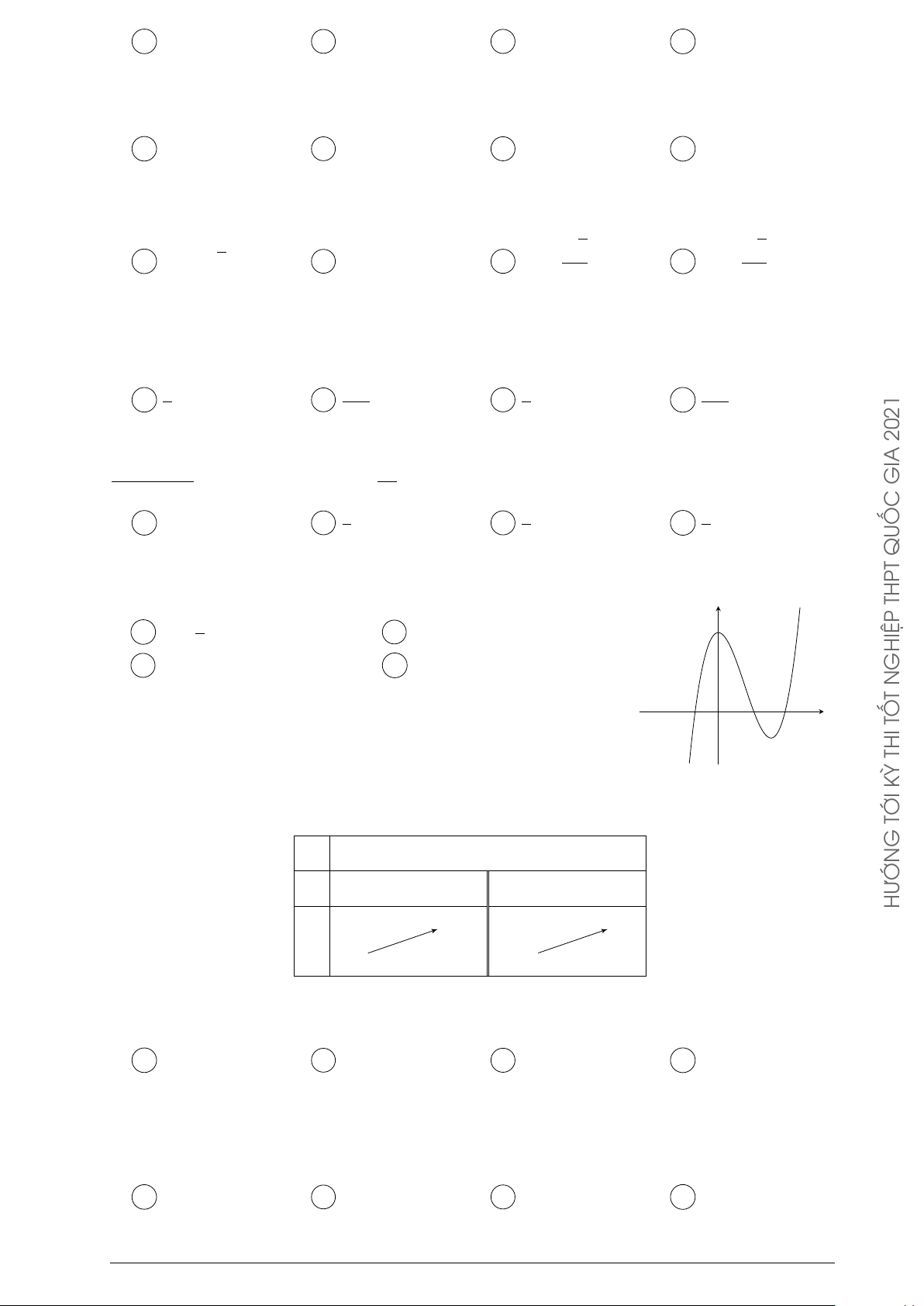
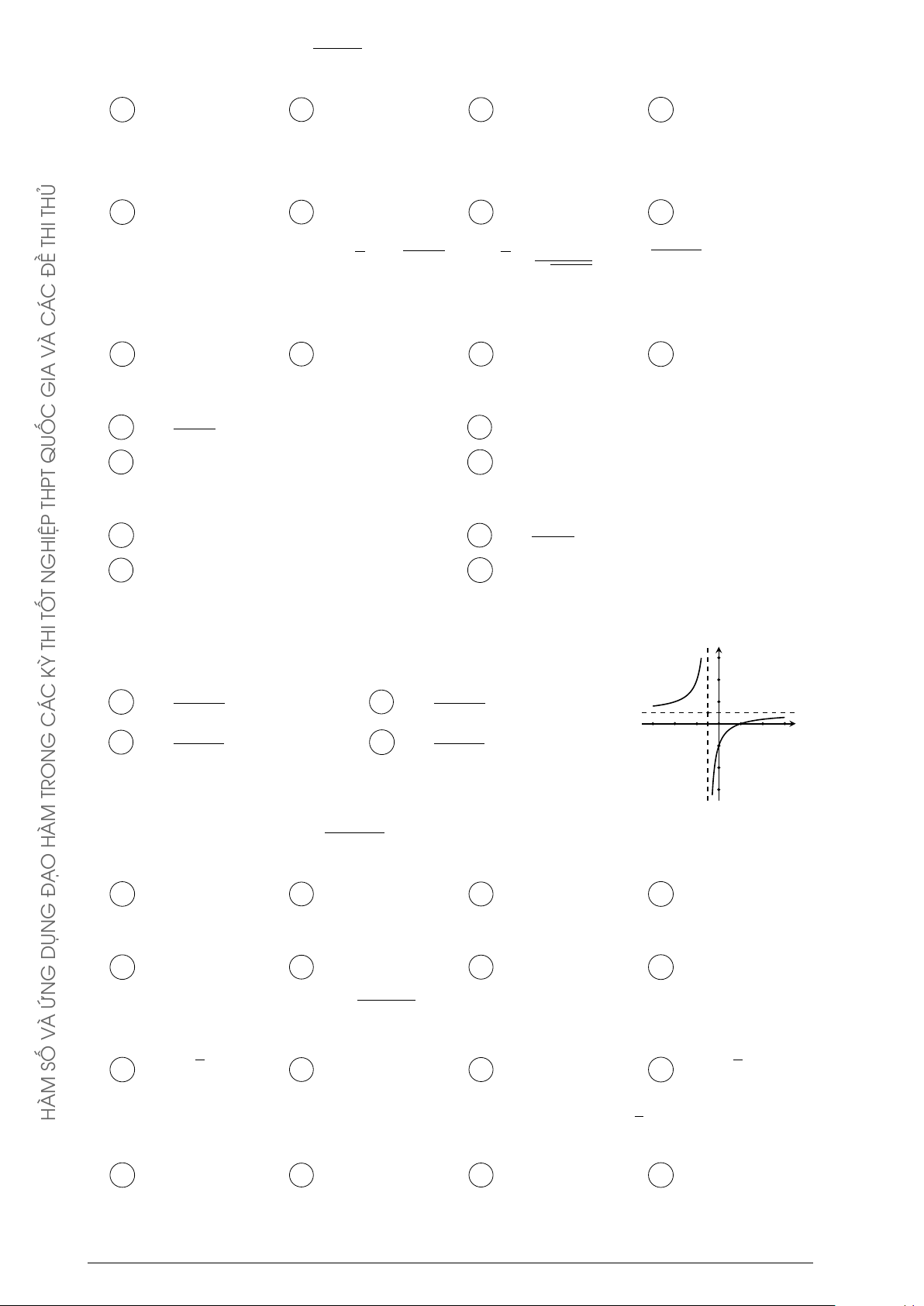
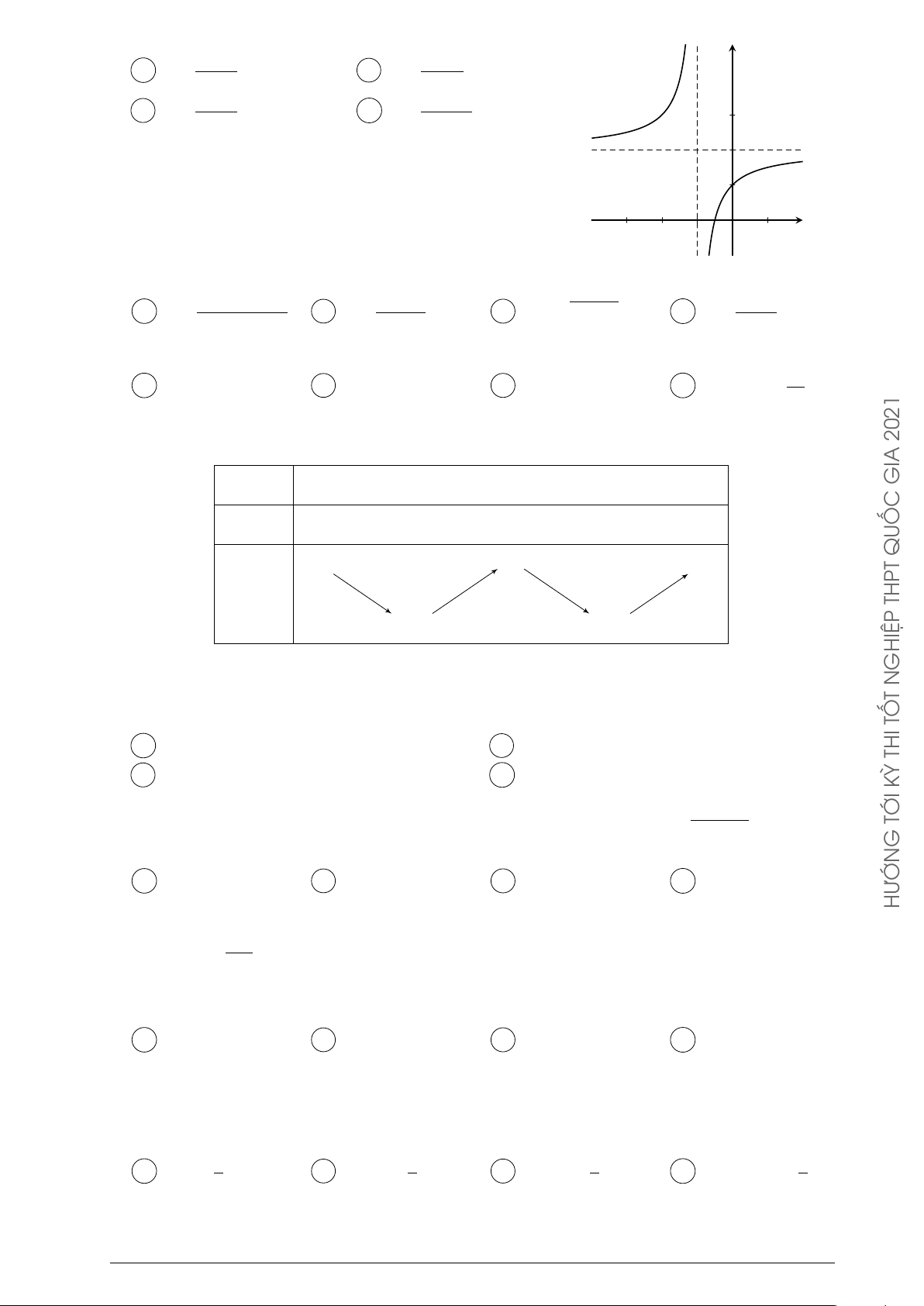
Đường cong trong hình vẽ bên là đồ thị của một hàm số trong y TỐ
4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi THI đó là hàm số nào? KỲ 2x + 3 2x − 1 2 A y = . B y = . C x + 1 x + 1 Á 2x − 2 2x + 1 C C y = . D y = . O G x − 1 x − 1 x −1 TRON
Câu 31. Tìm tất cả các giá trị thực của tham số m để hàm số y = (m−1)x4 −2(m−3)x2 +1 không có cực đại. HÀM O A 1 ≤ m ≤ 3. B m ≤ 1. C m ≥ 1. D 1 < m ≤ 3. Ạ Đ Câu 32. G
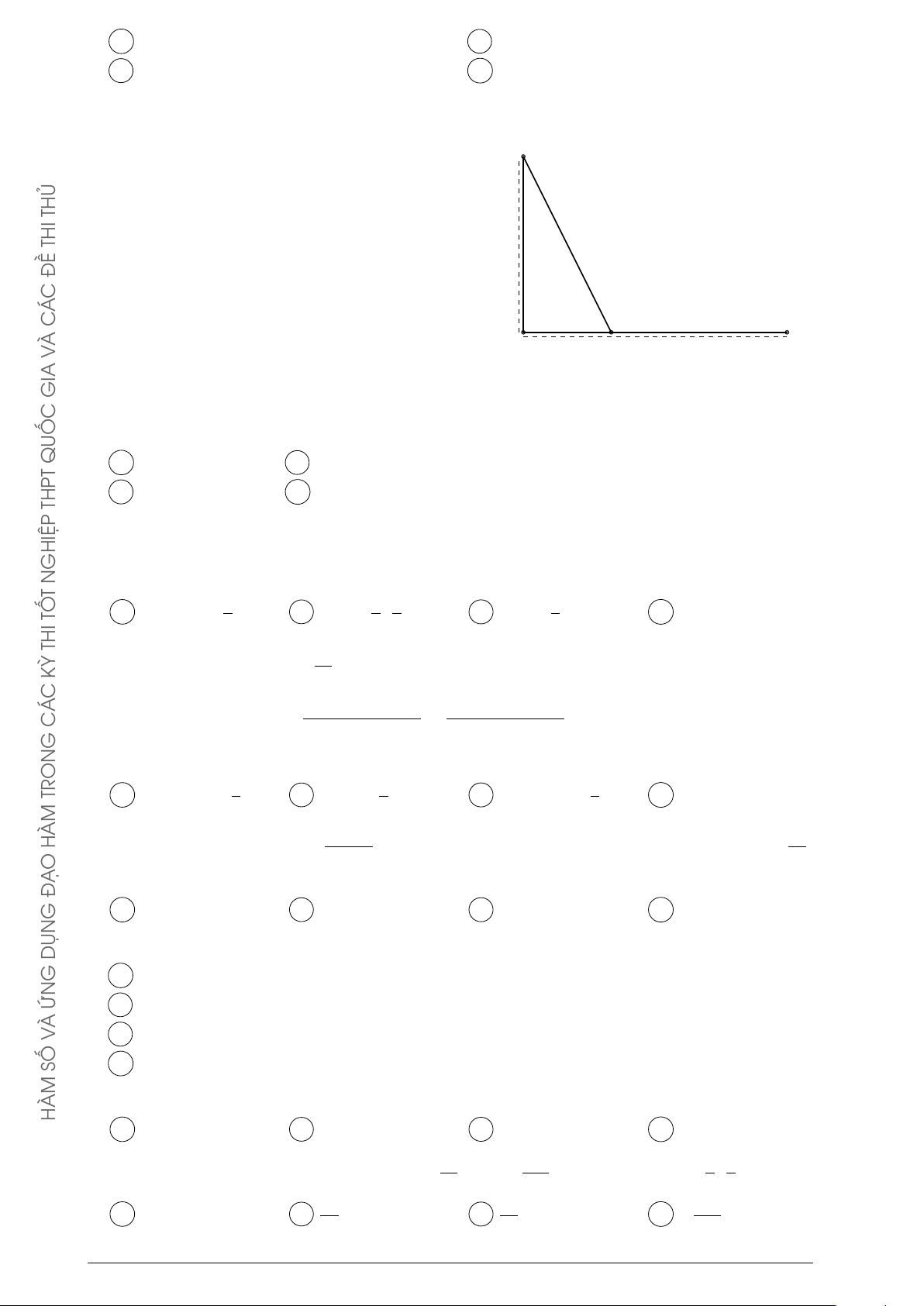
Hàm số y = (x − 2)(x2 − 1) có đồ thị như hình vẽ bên. Hình nào dưới y DỤN
đây là đồ thị của hàm số y = |x − 2|(x2 − 1)? G y y x ỨN O À x x V O O SỐ A . B . y y HÀM x x O O C . D .
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 6
Câu 33. Hỏi có bao nhiêu số nguyên m để hàm số y = (m2 − 1)x3 + (m − 1)x2 − x + 4
nghịch biến trên khoảng (−∞; +∞). A 2. B 1. C 0. D 3.
Câu 34. Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị của hàm số 1 y =
x3 − mx2 + (m2 − 1)x có hai điểm cực trị là A và B sao cho A, B nằm khác phía và 3
cách đều đường thẳng d : y = 5x − 9. Tính tổng tất cả các phần tử của S. A 0. B 6. C −6. D 3.
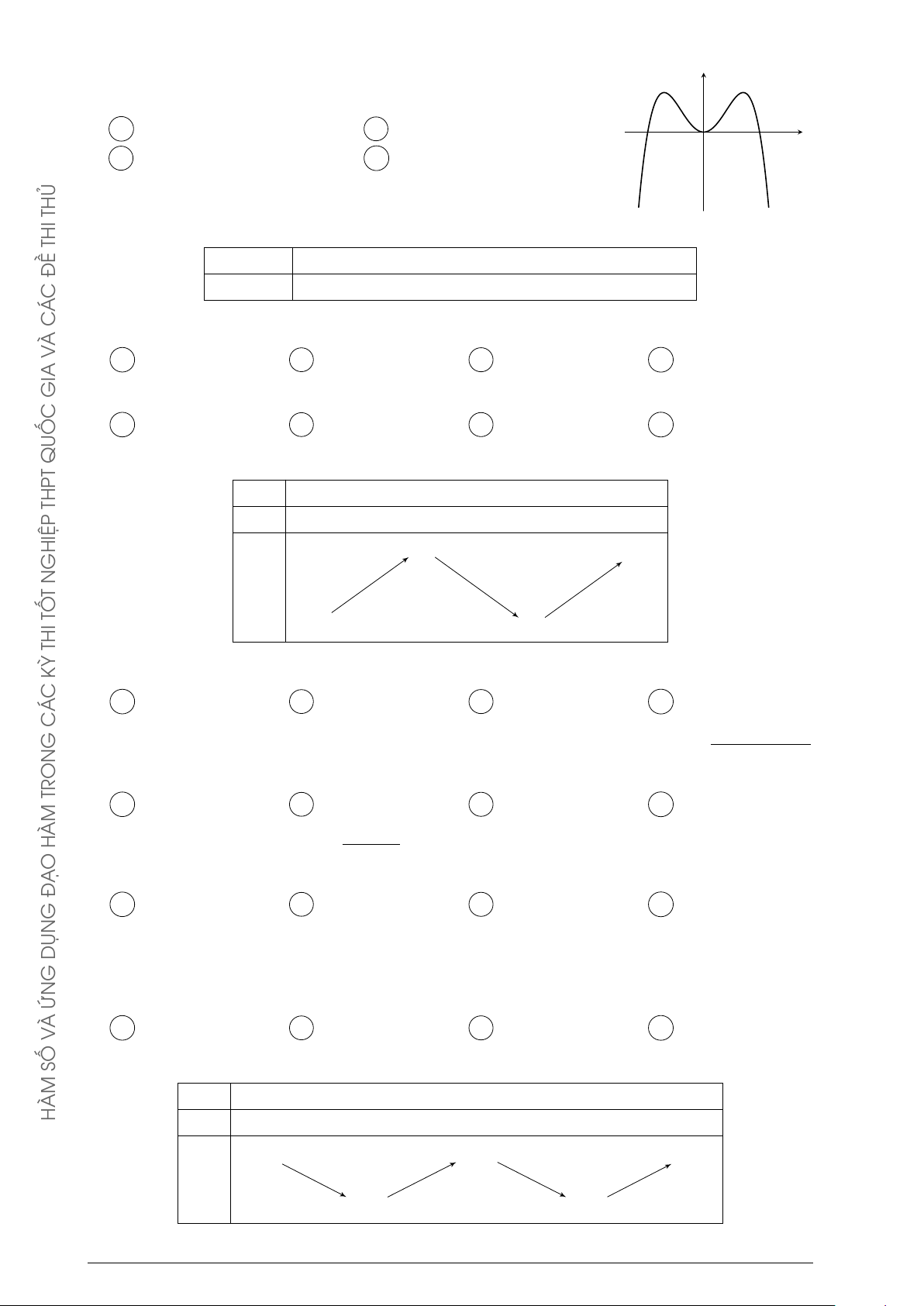
Câu 35. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + +∞ + 3 +∞ + y 0 0 2021 GIA
Mệnh đề nào dưới đây sai?
A Hàm số có ba điểm cực trị.
B Hàm số có giá trị cực đại bằng 3.
C Hàm số có giá trị cực đại bằng 0.
D Hàm số có hai điểm cực tiểu. QUỐC Câu 36. THPT
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới y
đây. Hàm số đó là hàm số nào? x A y = −x3 + x2 − 1. B y = x4 − x2 − 1. O GHIỆP N C y = x3 − x2 − 1. D y = −x4 + x2 − 1. T TỐ
Câu 37. Cho hàm số y = x3 + 3x + 2. Mệnh đề nào dưới đây đúng? THI
A Hàm số đồng biến trên khoảng (−∞; 0) và nghịch biến trên khoảng (0; +∞). KỲ
B Hàm số nghịch biến trên khoảng (−∞; +∞). TỚI
C Hàm số đồng biến trên khoảng (−∞; +∞). G
D Hàm số nghịch biến trên khoảng (−∞; 0) và đồng biến trên khoảng (0; +∞). x2 − 3x − 4 HƯỚN
Câu 38. Tìm số tiệm cận đứng của đồ thị hàm số y = . x2 − 16 A 2. B 3. C 1. D 0. 2 Câu 39. Hàm số y =
nghịch biến trên khoảng nào dưới đây? x2 + 1 A (0; +∞). B (−1; 1). C (−∞; +∞). D (−∞; 0). √
Câu 40. Cho hình phẳng D giới hạn bởi đường cong y =
2 + cos x, trục hoành và các π đường thẳng x = 0, x =
. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể 2 tích V bằng bao nhiêu? A V = π − 1. B V = (π − 1)π. C V = (π + 1)π. D V = π + 1.
Câu 41. Tìm giá trị nhỏ nhất m của hàm số y = x3 − 7x2 + 11x − 2 trên đoạn [0; 2]. A m = 11. B m = 0. C m = −2. D m = 3.
Hàm số và ứng dụng đạo hàm
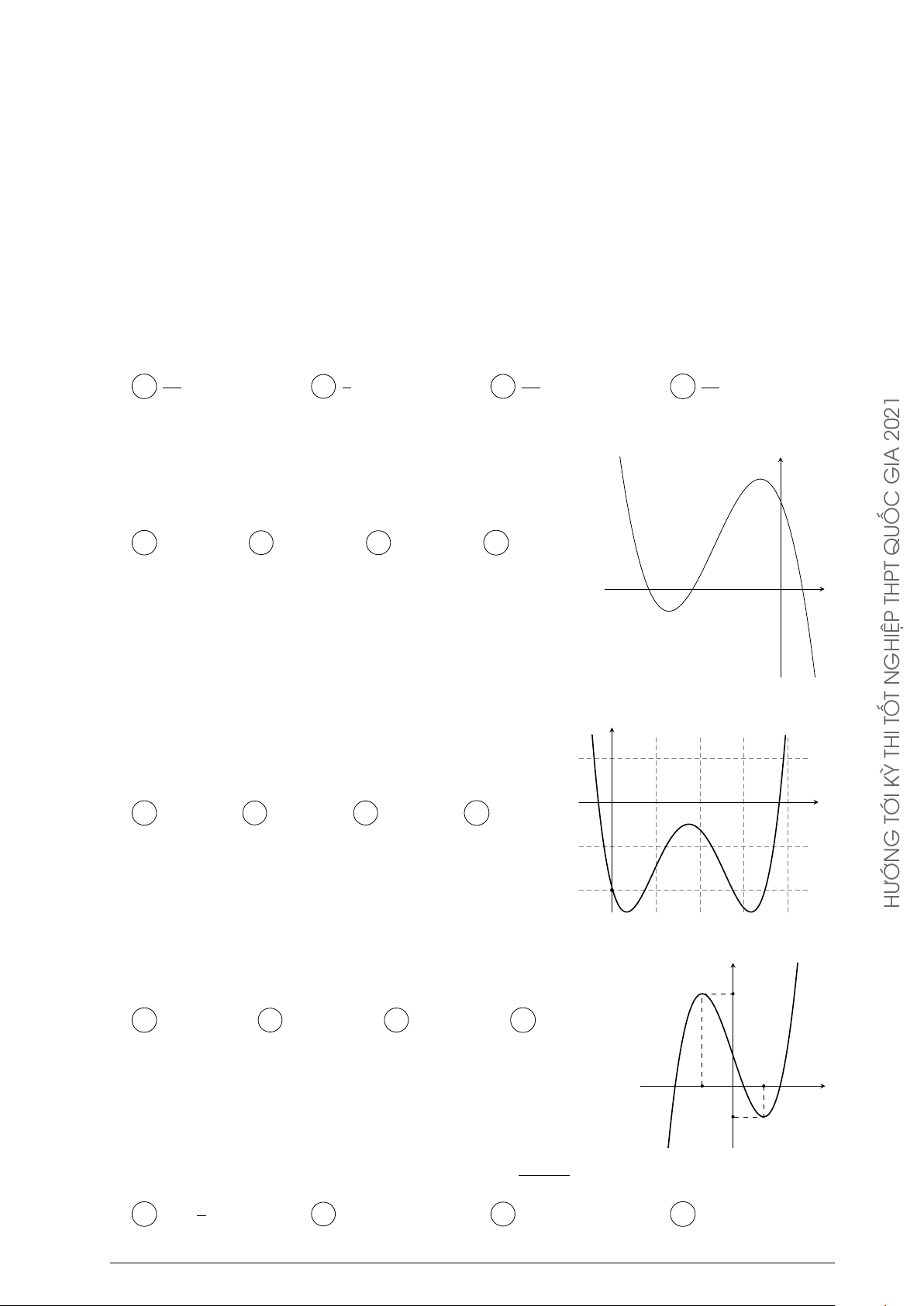
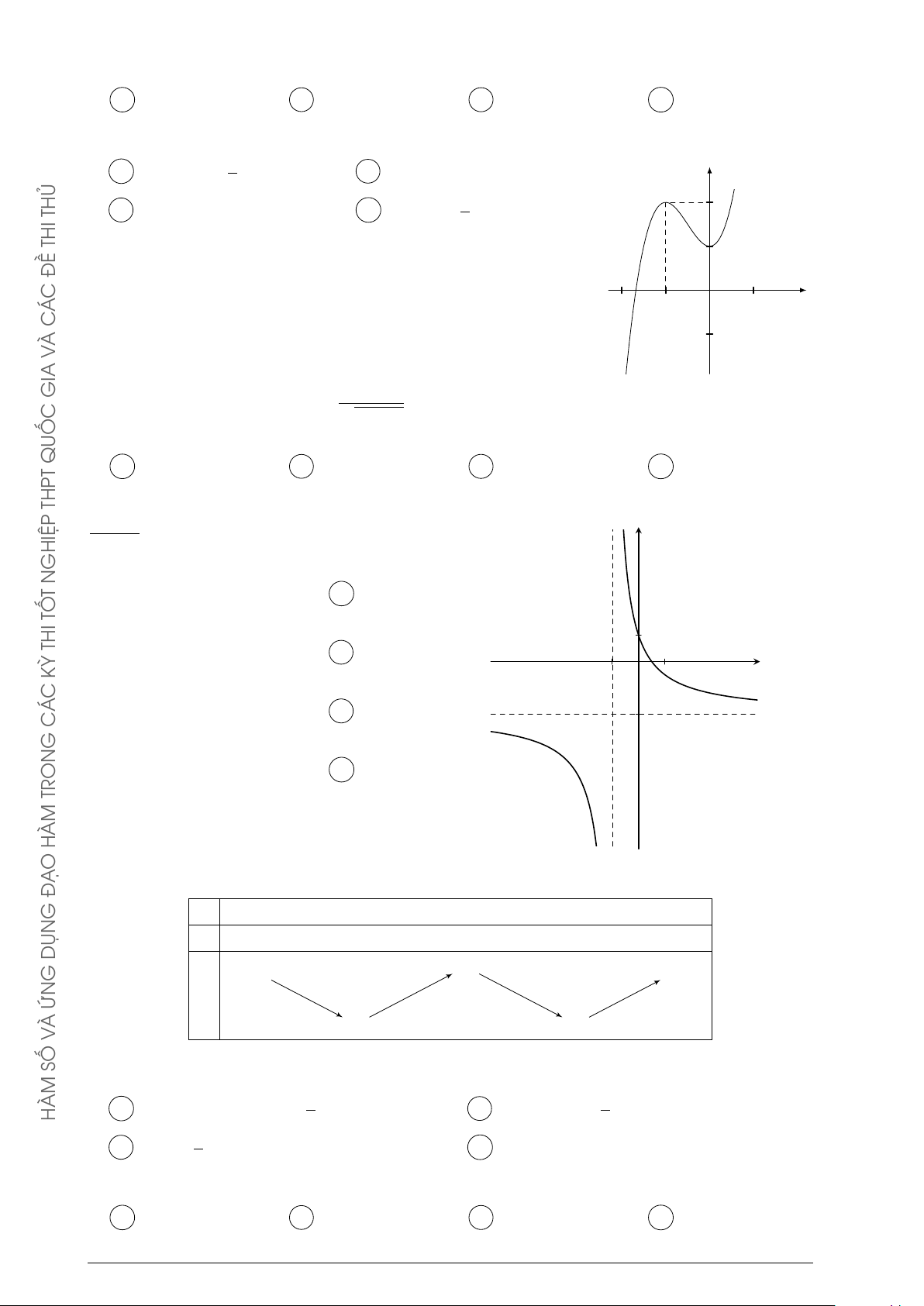
Những nẻo đường phù sa Trang 7 Câu 42. ax + b
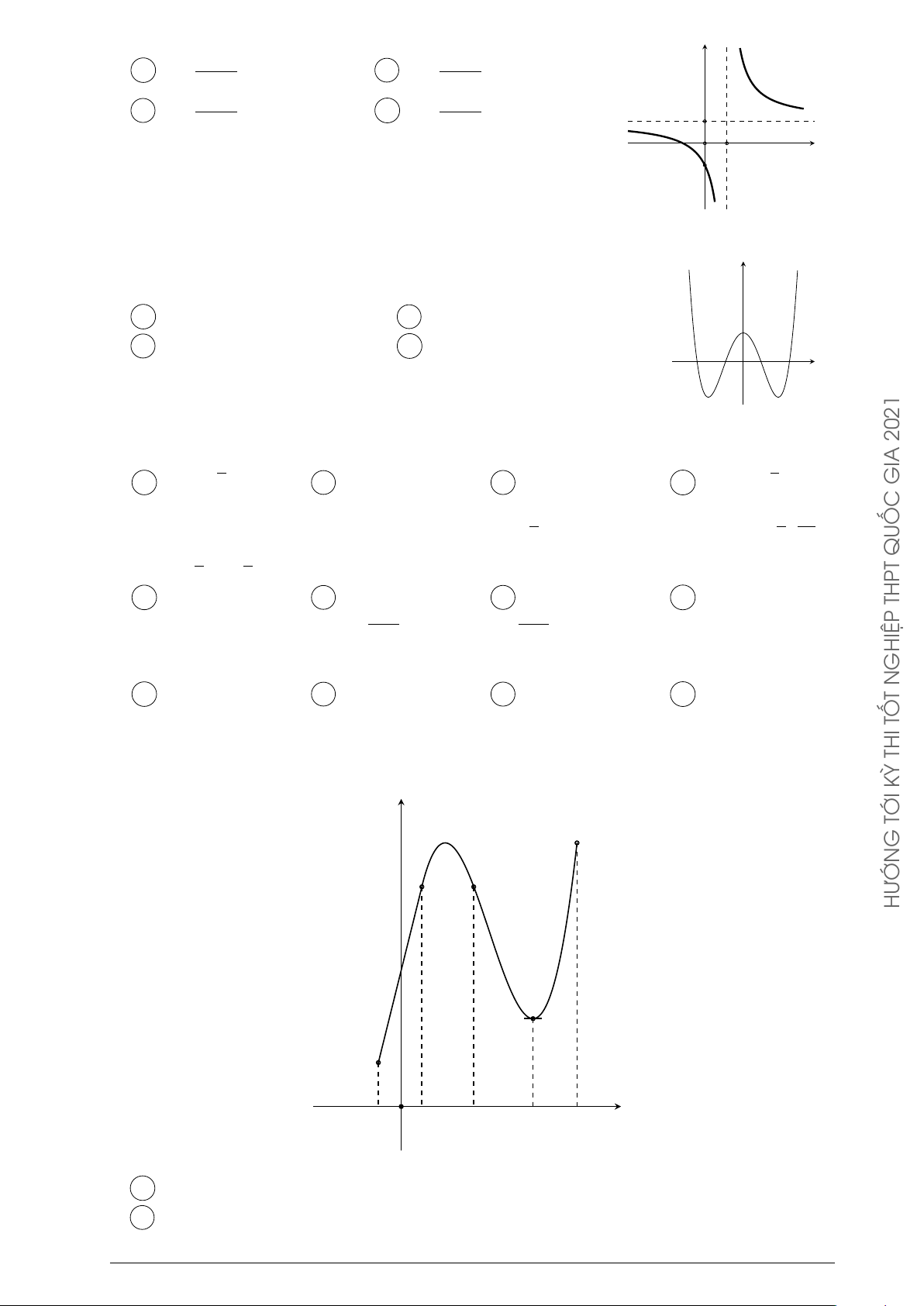
Đường cong ở hình bên là đồ thị của hàm số y = với a, b, c, d y cx + d
là các số thực. Mệnh đề nào dưới đây đúng? A y0 > 0, ∀x ∈ R. O B y0 < 0, ∀x ∈ R. 1 x C y0 > 0, ∀x 6= 1. THỦ D y0 < 0, ∀x 6= 1. THI x + m ĐỀ Câu 43. Cho hàm số y =
(m là tham số thực) thỏa mãn min y = 3. Mệnh đề nào x − 1 [2;4] C Á dưới đây đúng? C A m < −1. B 3 < m ≤ 4. C m > 4. D 1 ≤ m < 3. À V
Câu 44. Cho hàm số y = −x3 − mx2 + (4m + 9)x + 5 với m là tham số. Có bao nhiêu giá GIA
trị nguyên của m để hàm số nghịch biến trên khoảng (−∞; +∞)? A 7. B 4. C 6. D 5. QUỐC
Câu 45. Tìm giá trị thực của tham số m để phương trình log2 x − m log x + 2m − 7 = 0 3 3 THPT
có hai nghiệm thực x1,x2 thỏa mãn x1x2 = 81. A m = −4. B m = 4. C m = 81. D m = 44. GHIỆP N
Câu 46. Đồ thị hàm số y = x3 − 3x2 − 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới T TỐ
đây thuộc đường thẳng AB? A P (1; 0). B M (0; −1). C N (1; −10). D Q(−1; 10). THI KỲ
Câu 47. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = mx − m + 1 cắt đồ C Á
thị của hàm số y = x3 − 3x2 + x + 2 tại ba điểm A, B, C phân biệt sao cho AB = BC. C G
A m ∈ (−∞; 0] ∪ [4; +∞). B m ∈ R. 5 C m ∈ − ; +∞. D m ∈ (−2; +∞). 4 TRON
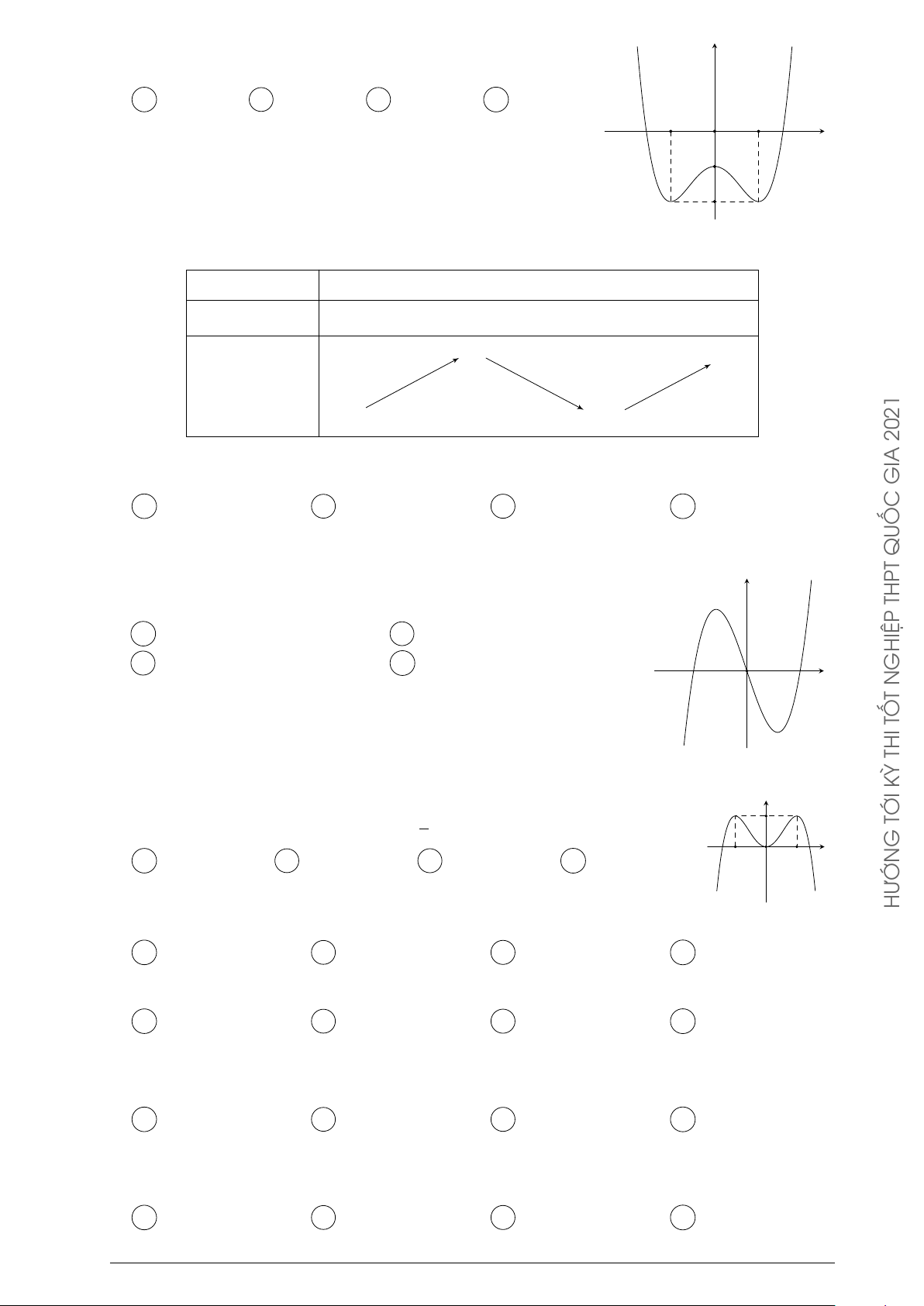
Câu 48. Cho hàm số y = f (x) có bảng biến thiên như sau HÀM O x −∞ −2 2 +∞ Ạ Đ y0 + 0 − 0 + G 3 +∞ + DỤN y G −∞ 0 ỨN À V
Tìm giá trị cực đại yCĐ và giá trị cực tiểu yCT của hàm số đã cho. SỐ A yCĐ = 3 và yCT = −2. B yCĐ = 2 và yCT = 0. C yCĐ = −2 và yCT = 2. D yCĐ = 3 và yCT = 0. HÀM
Câu 49. Hàm số nào dưới đây đồng biến trên khoảng (−∞; +∞)? x + 1 x − 1 A y = . B y = x3 + 3x. C y = . D y = −x3 − 3x. x + 3 x − 2 Câu 50.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 8
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới y
đây. Hàm số đó là hàm số nào? A y = x4 − 2x2 + 1. B y = −x4 + 2x2 + 1. C y = −x3 + 3x2 + 1. D y = x3 − 3x2 + 3. x O
Câu 51. Cho hàm số y = x3 − 3x2. Mệnh đề nào dưới đây đúng?
A Hàm số nghịch biến trên (0; 2).
B Hàm số nghịch biến trên khoảng (2; +∞).
C Hàm số đồng biến trên khoảng (0; 2).
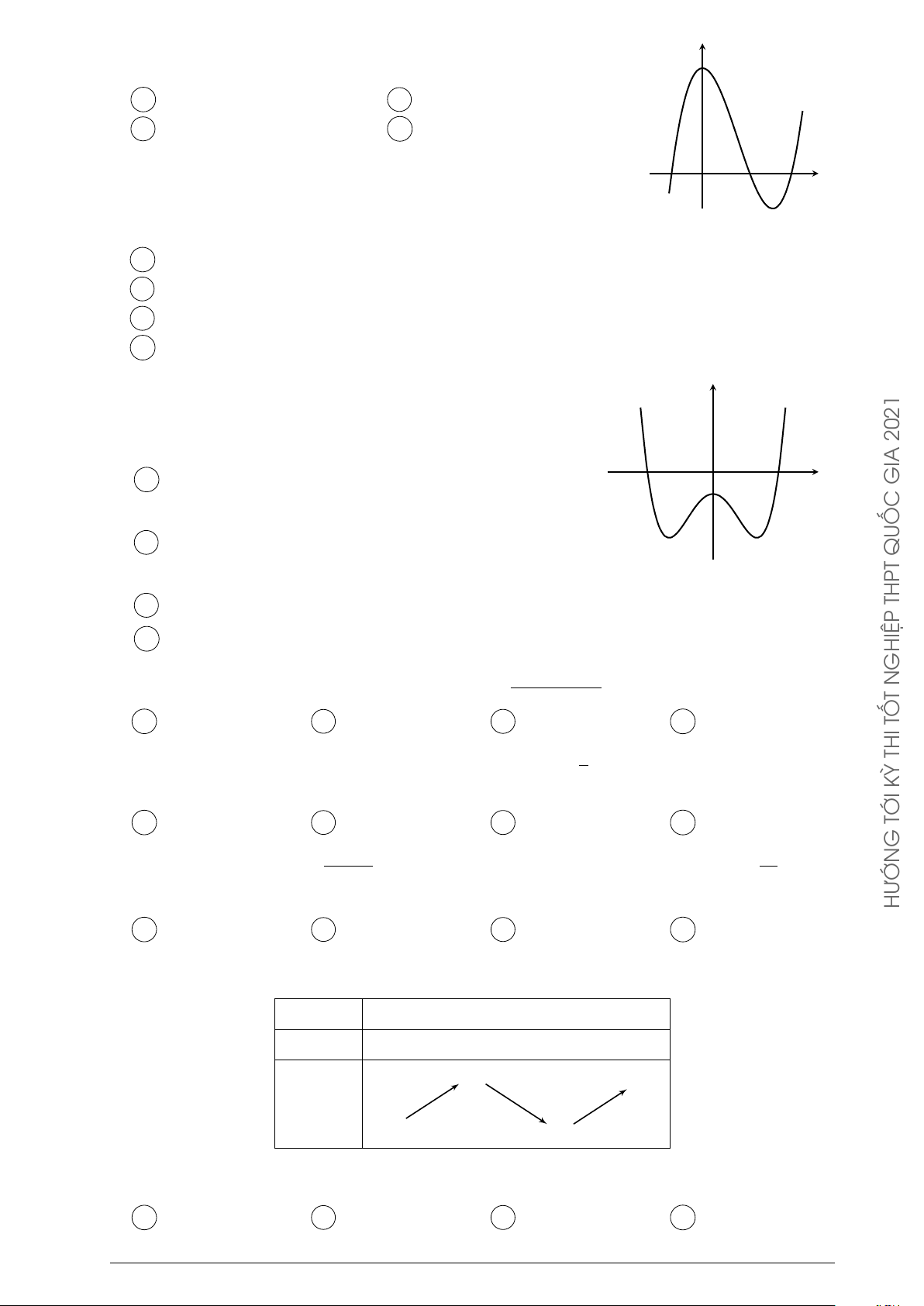
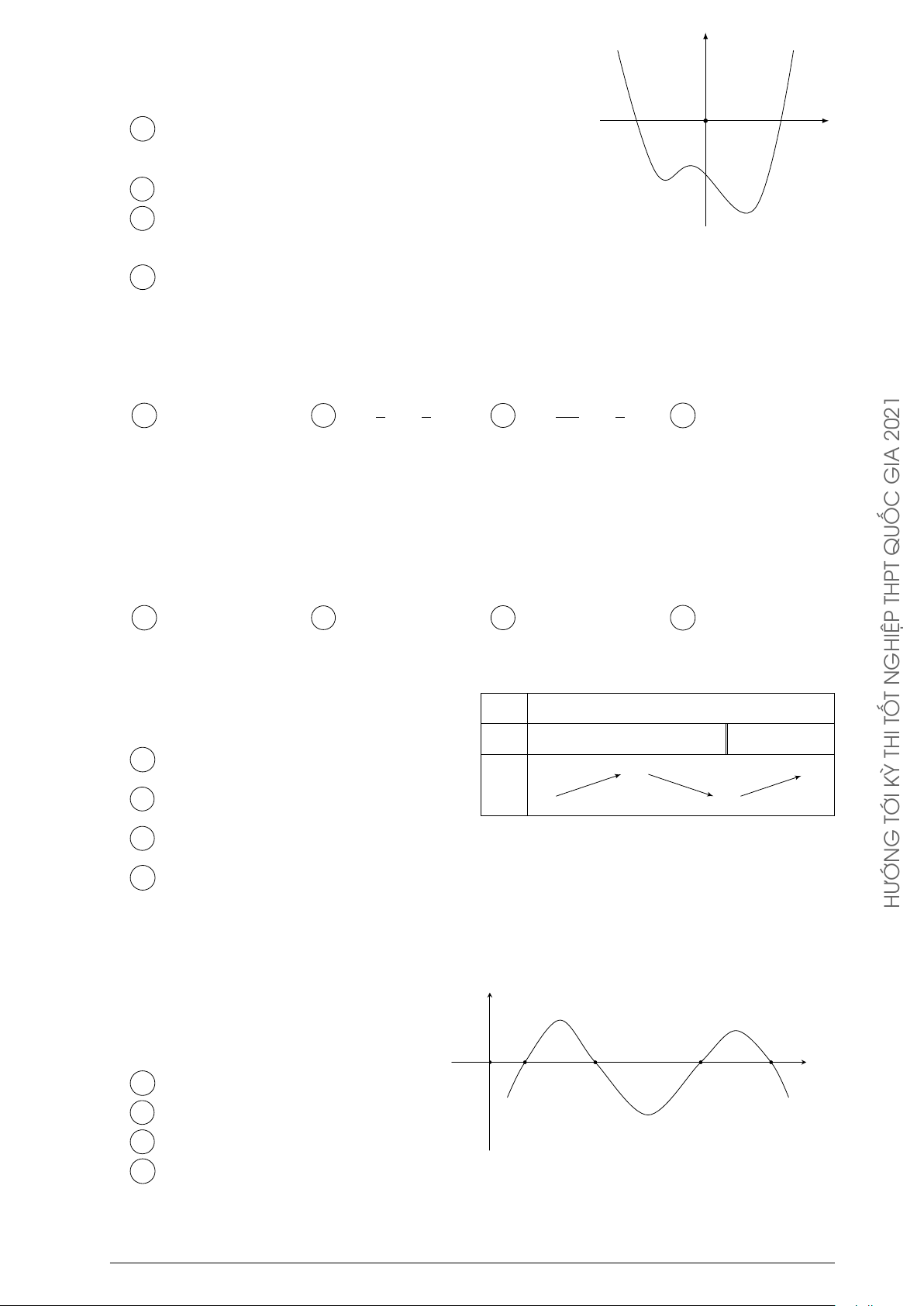
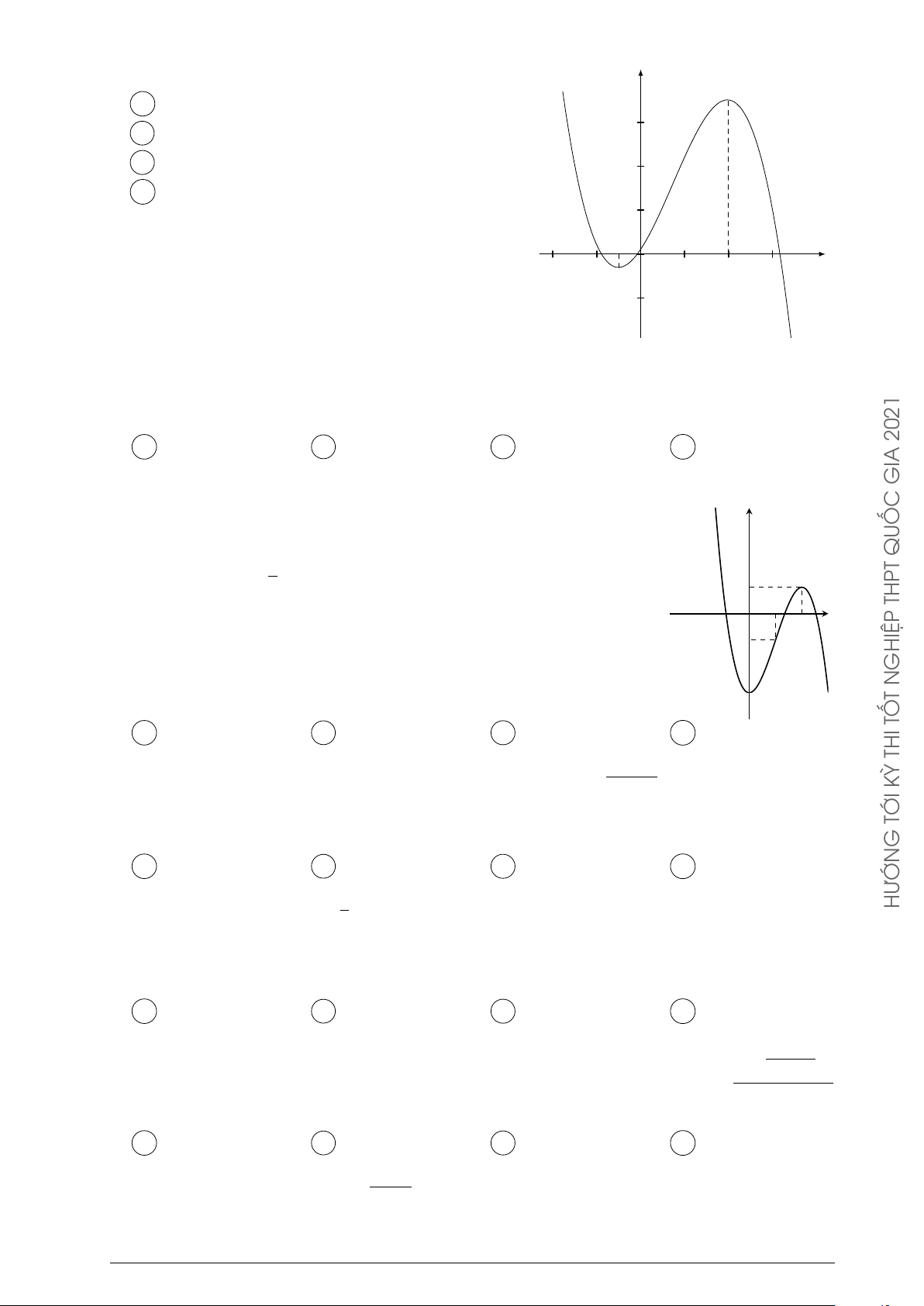
D Hàm số nghịch biến trên khoảng (−∞; 0). y Câu 52. Đường
cong ở hình bên là đồ thị của hàm số y = ax4 + bx2 + c 2021
với a, b, c là các số thực. Mệnh đề nào dưới đây đúng?
A Phương trình y0 = 0 có đúng ba nghiệm thực phân x GIA O biệt.
B Phương trình y0 = 0 có đúng hai nghiệm thực phân QUỐC biệt. THPT
C Phương trình y0 = 0 vô nghiệm trên tập số thực.
D Phương trình y0 = 0 có đúng một nghiệm thực. GHIỆP x2 − 5x + 4 N
Câu 53. Tìm số tiệm cận của đồ thị hàm số y = . T x2 − 1 A 3. B 1. C 0. D 2. TỐ 1 THI
Câu 54. Tìm giá trị thực của tham số m để hàm số y =
x3 − mx2 + (m2 − 4) x + 3 đạt 3 KỲ cực đại tại x = 3. TỚI A m = 1. B m = −1. C m = 5. D m = −7. G x + m 16 Câu 55. Cho hàm số y =
(m là tham số thực) thỏa mãn min y + max y = . Mệnh x + 1 [1;2] [1;2] 3
đề nào dưới đây đúng? HƯỚN A m ≤ 0. B m > 4. C 0 < m ≤ 2. D 2 < m ≤ 4.
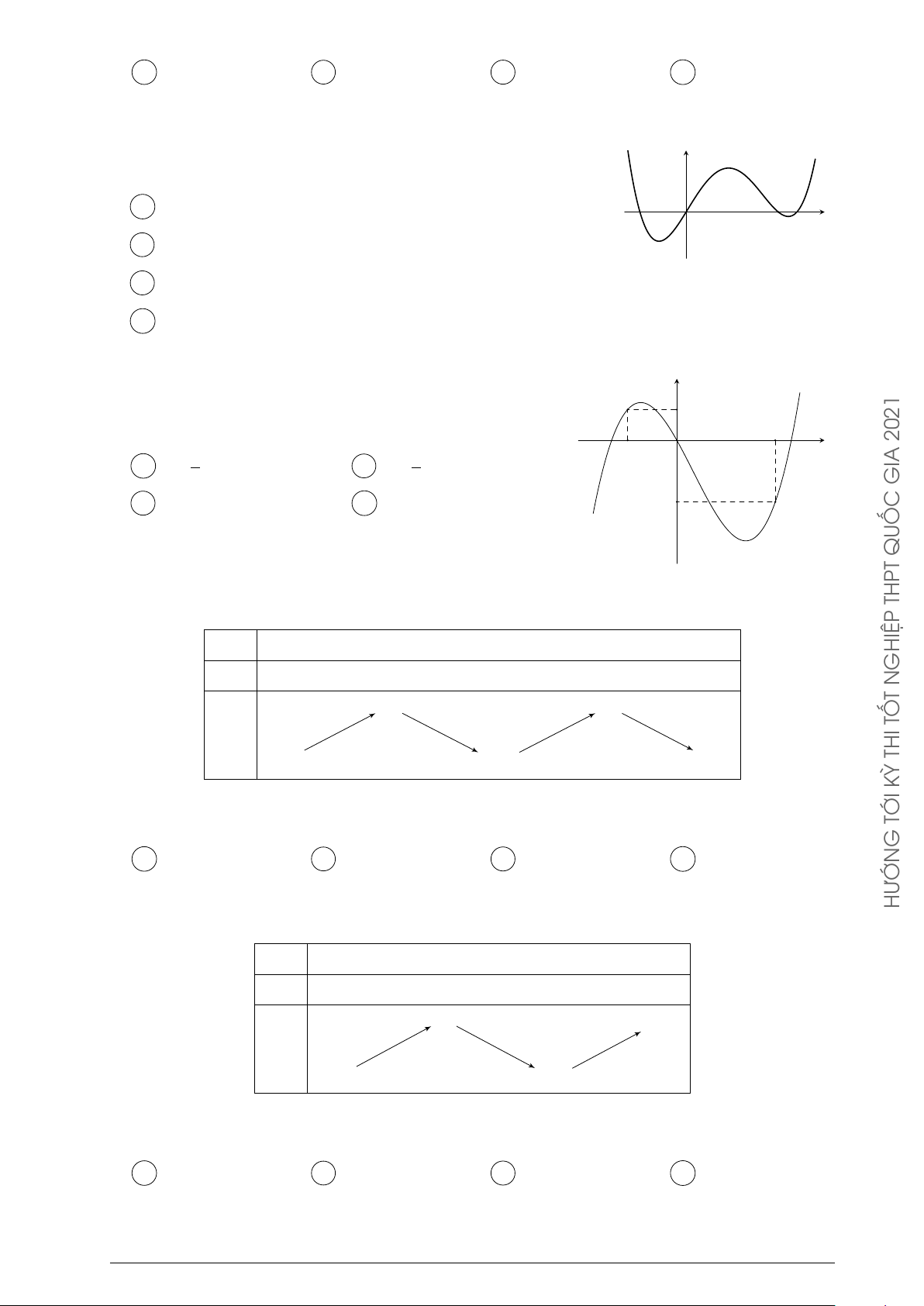
Câu 56. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ −1 3 +∞ y0 + 0 − 0 + 5 +∞ + y −∞ 1
Đồ thị của hàm số y = |f (x)| có bao nhiêu điểm cực trị? A 4. B 2. C 3. D 5.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 9
Câu 57. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = −mx cắt đồ thị
hàm số y = x3 − 3x2 − m + 2 tại ba điểm phân biệt A, B, C sao cho AB = BC. A m ∈ (−∞; 3). B m ∈ (−∞; −1). C m ∈ (−∞; +∞). D m ∈ (1; +∞).
Câu 58. Cho hàm số y = (x − 2)(x2 + 1) có đồ thị (C). Mệnh đề nào sau đây đúng?
A (C) cắt trục hoành tại hai điểm.
B (C) cắt trục hoành tại một điểm.
C (C) không cắt trục hoành.
D (C) cắt trục hoành tại ba điểm. THỦ THI
Câu 59. Cho hàm số y = f (x) có đạo hàm f 0(x) = x2 + 1, ∀x ∈ R. Mệnh đề nào dưới đây ĐỀ đúng? C Á
A Hàm số nghịch biến trên khoảng (−∞; 0). C
B Hàm số nghịch biến trên khoảng (1; +∞). À V
C Hàm số nghịch biến trên khoảng (−1; 1). GIA
D Hàm số đồng biến trên khoảng (−∞; +∞).
Câu 60. Cho hàm số y = f (x) có bảng biến thiên như sau QUỐC x −∞ −1 2 +∞ y0 + THPT 0 − 0 + 4 2 y 2 5 GHIỆP N T TỐ
Mệnh đề nào dưới đây đúng? THI
A Hàm số có bốn điểm cực trị.
B Hàm số đạt cực tiểu tại x = 2. KỲ
C Hàm số không có cực đại.
D Hàm số đạt cực tiểu tại x = −5. C Á
Câu 61. Tìm giá trị nhỏ nhất m của hàm số y = x4 − x2 + 13 trên đoạn [−2; 3]. C 51 49 51 G A m = . B m = . C m = 13. D m = . 4 4 2
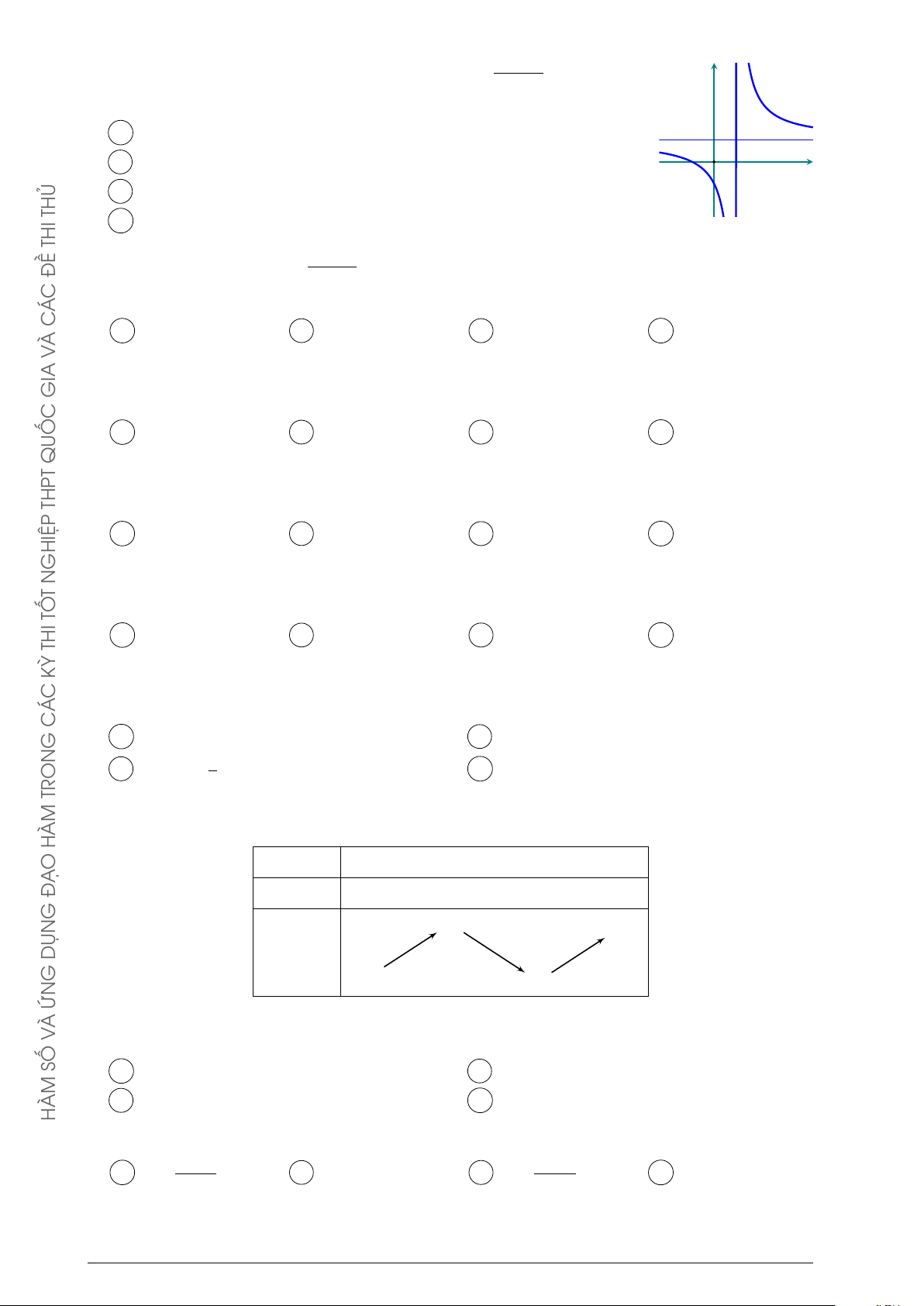
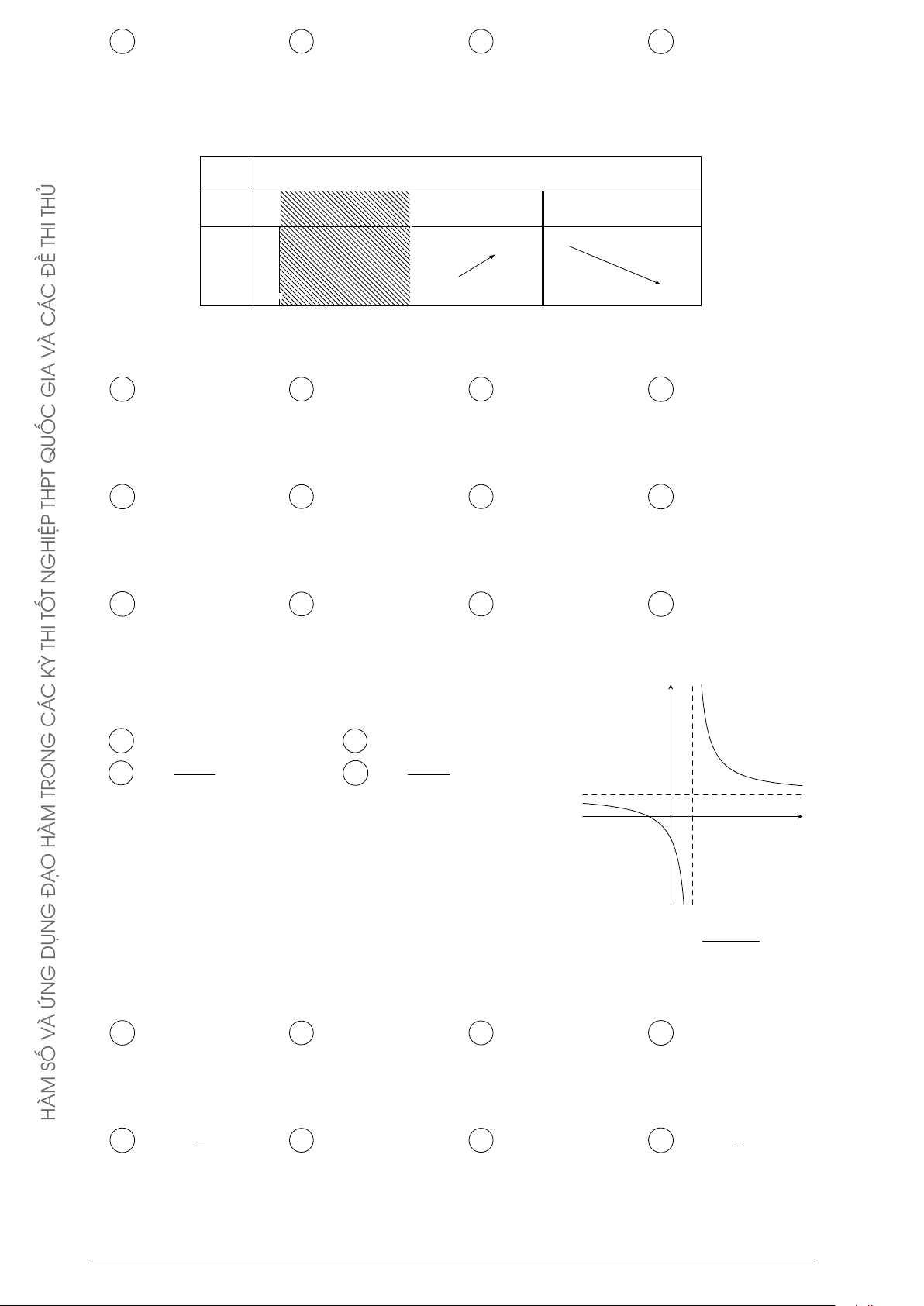
Câu 62. Đường cong ở hình bên TRON ax + b
là đồ thị của hàm số y = y cx + d HÀM
với a, b, c, d là các số thực. O Ạ
Mệnh đề nào dưới đây đúng? 1 Đ A y0 < 0, ∀x 6= 2. B y0 < 0, ∀x 6= 1. G x O 2 C y0 > 0, ∀x 6= 2. D y0 > 0, ∀x 6= 1. DỤN G ỨN À
Câu 63. Đồ thị của hàm số nào trong các hàm số dưới đây có tiệm cận đứng? V 1 1 1 1 A y = √ . B y = . C y = . D y = . SỐ x x2 + x + 1 x4 + 1 x2 + 1
Câu 64. Cho hàm số y = x4 − 2x2. Mệnh đề nào dưới đây đúng? HÀM
A Hàm số đồng biến trên khoảng (−∞; −2).
B Hàm số nghịch biến trên khoảng (−∞; −2).
C Hàm số đồng biến trên khoảng (−1; 1).
D Hàm số nghịch biến trên khoảng (−1; 1).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 10 mx − 2m − 3 Câu 65. Cho hàm số y =
với m là tham số. Gọi S là tập hợp tất cả các giá x − m
trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S. A 5. B 4. C Vô số. D 3.
Câu 66. Đồ thị của hàm số y = −x3 + 3x2 + 5 có hai điểm cực trị A và B. Tính diện tích
S của tam giác OAB với O là gốc tọa độ. 10 A S = 9. B S = . C S = 5. D S = 10. 3
Câu 67. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x4 − 2mx2
có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1. √ A m > 0. B m < 1. C 0 < m < 3 4. D 0 < m < 1.
Câu 68. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau x −∞ −2 0 2 +∞ y0 + 0 − − 0 + 2021 GIA
Mệnh đề nào dưới đây đúng?
A Hàm số đồng biến trên khoảng (−2; 0).
B Hàm số đồng biến trên khoảng (−∞; 0). QUỐC
C Hàm số nghịch biến trên khoảng (0; 2). THPT
D Hàm số nghịch biến trên khoảng (−∞; −2). 2x + 3 Câu 69. Hàm số y =
có bao nhiêu điểm cực trị? GHIỆP x + 1 N A 3. B 0. C 2. D 1. T TỐ x − 2
Câu 70. Đồ thị của hàm số y = có bao nhiêu tiệm cận? x2 − 4 THI A 0. B 3. C 1. D 2. KỲ 2 ï 1 ò
Câu 71. Tìm giá trị nhỏ nhất m của hàm số y = x2 + trên đoạn ; 2 . TỚI x 2 G 17 A m = . B m = 10. C m = 5. D m = 3. 4 √ Câu 72. Cho hàm số y =
2x2 + 1. Mệnh đề nào dưới đây đúng? HƯỚN
A Hàm số nghịch biến trên khoảng (−1; 1).
B Hàm số đồng biến trên khoảng (0; +∞).
C Hàm số đồng biến trên khoảng (−∞; 0).
D Hàm số nghịch biến trên khoảng (0; +∞).
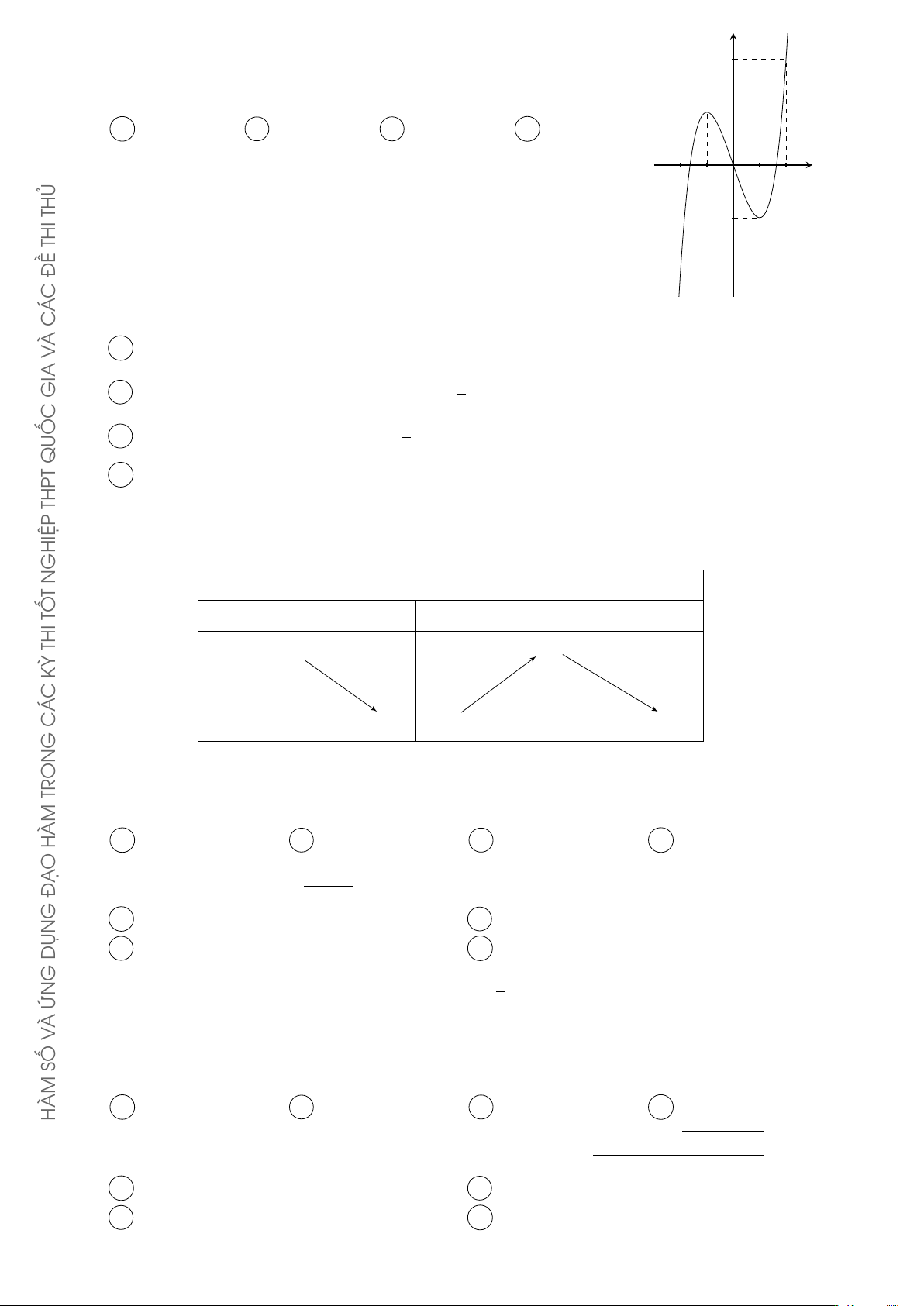
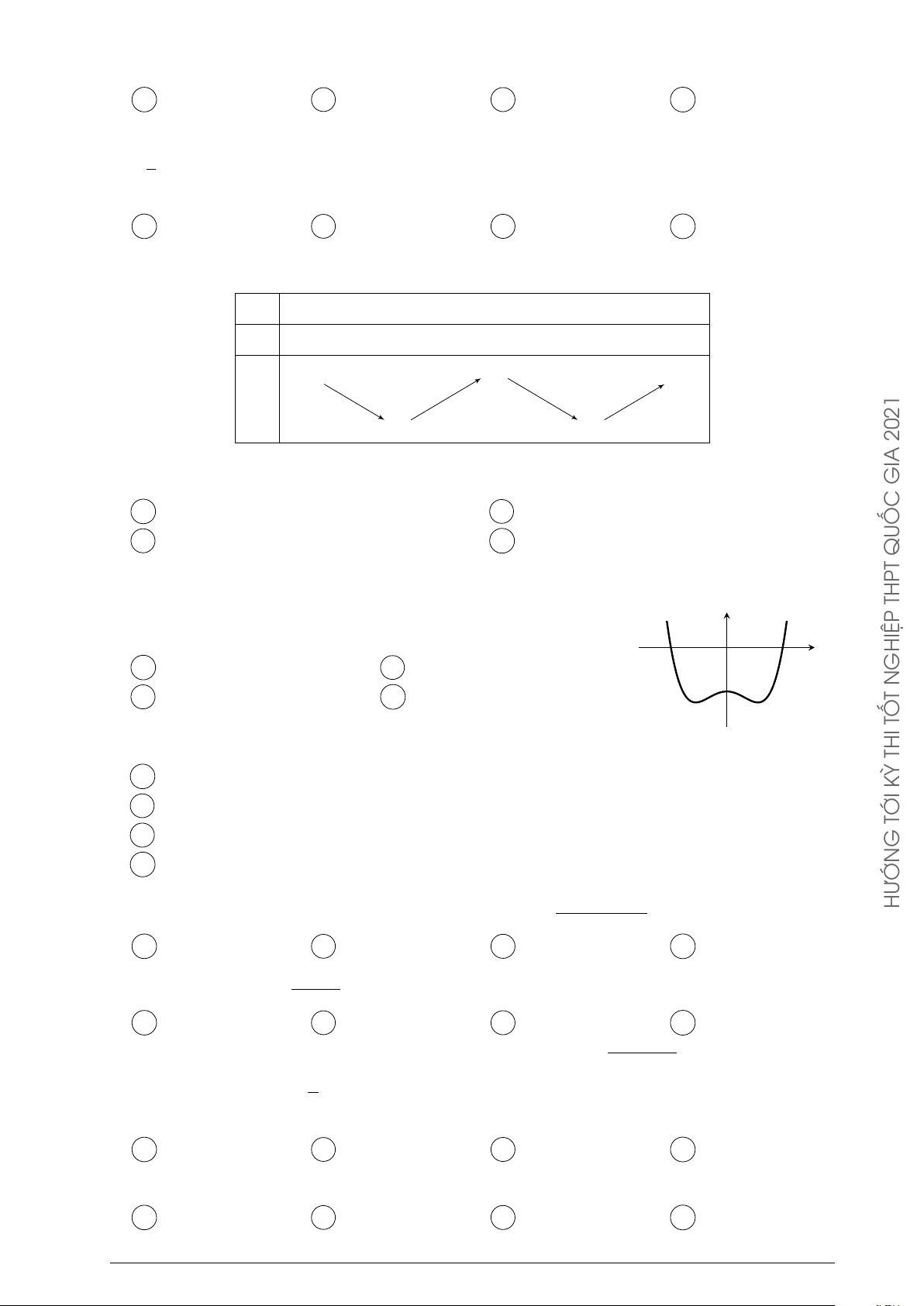
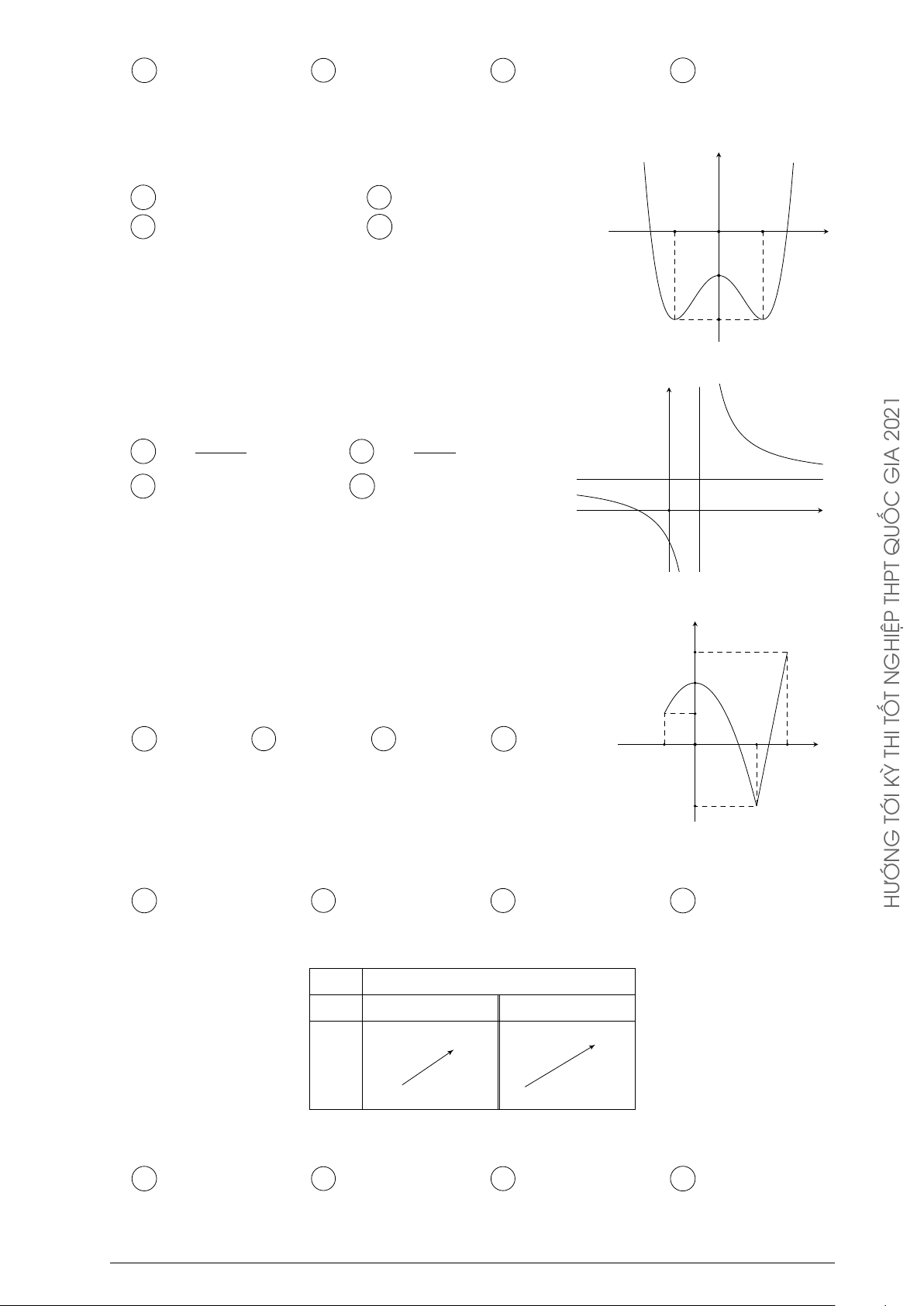
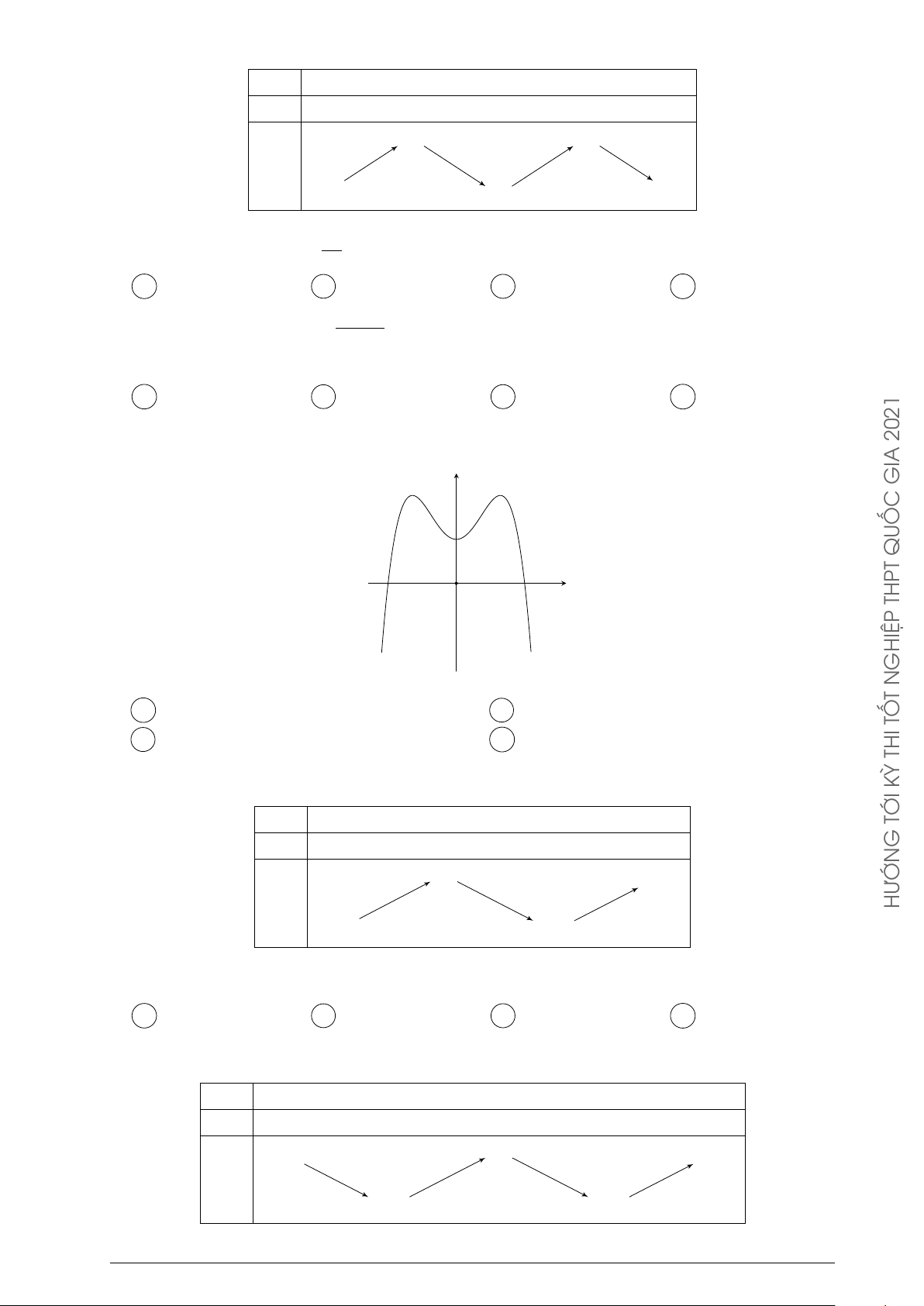
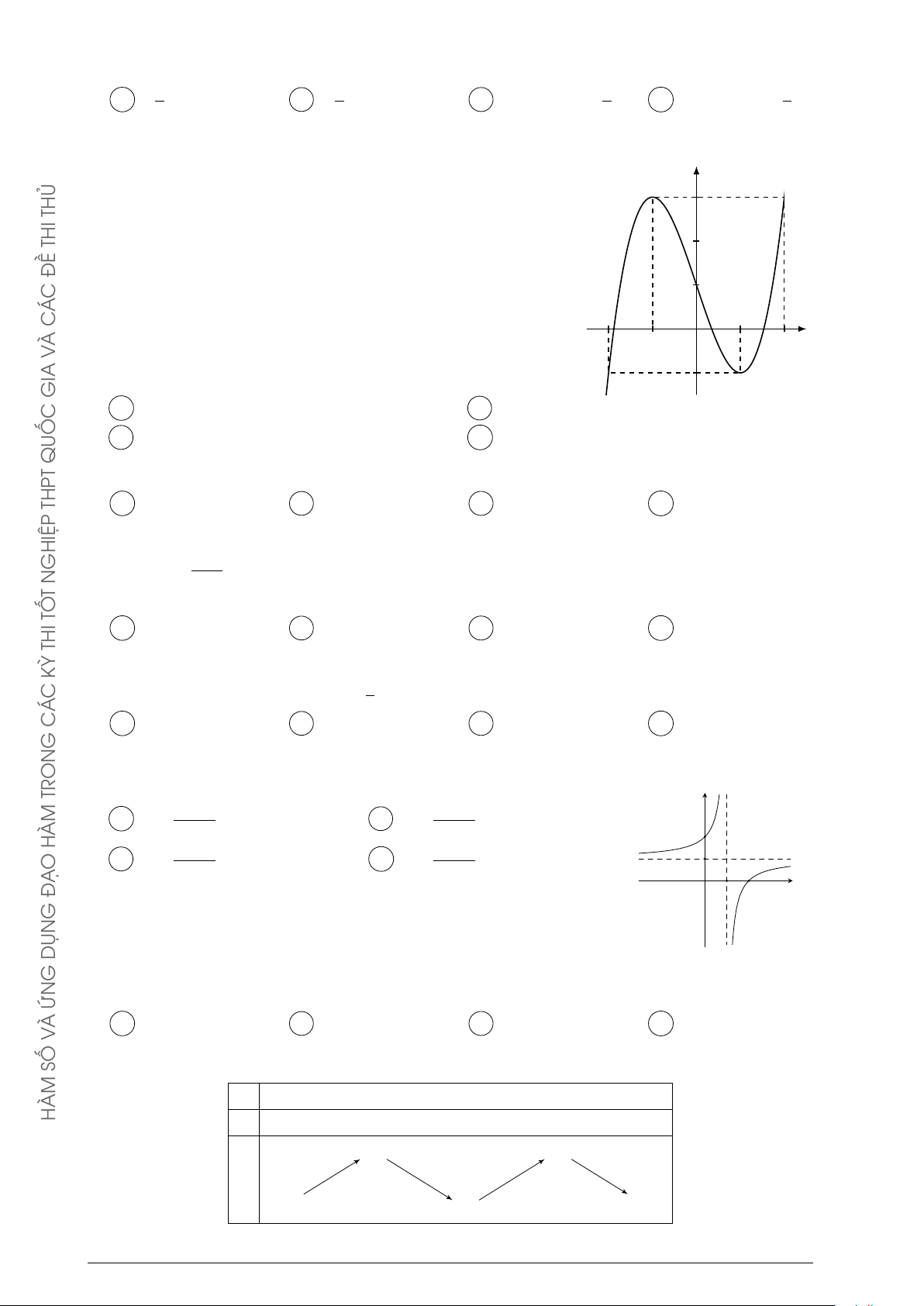
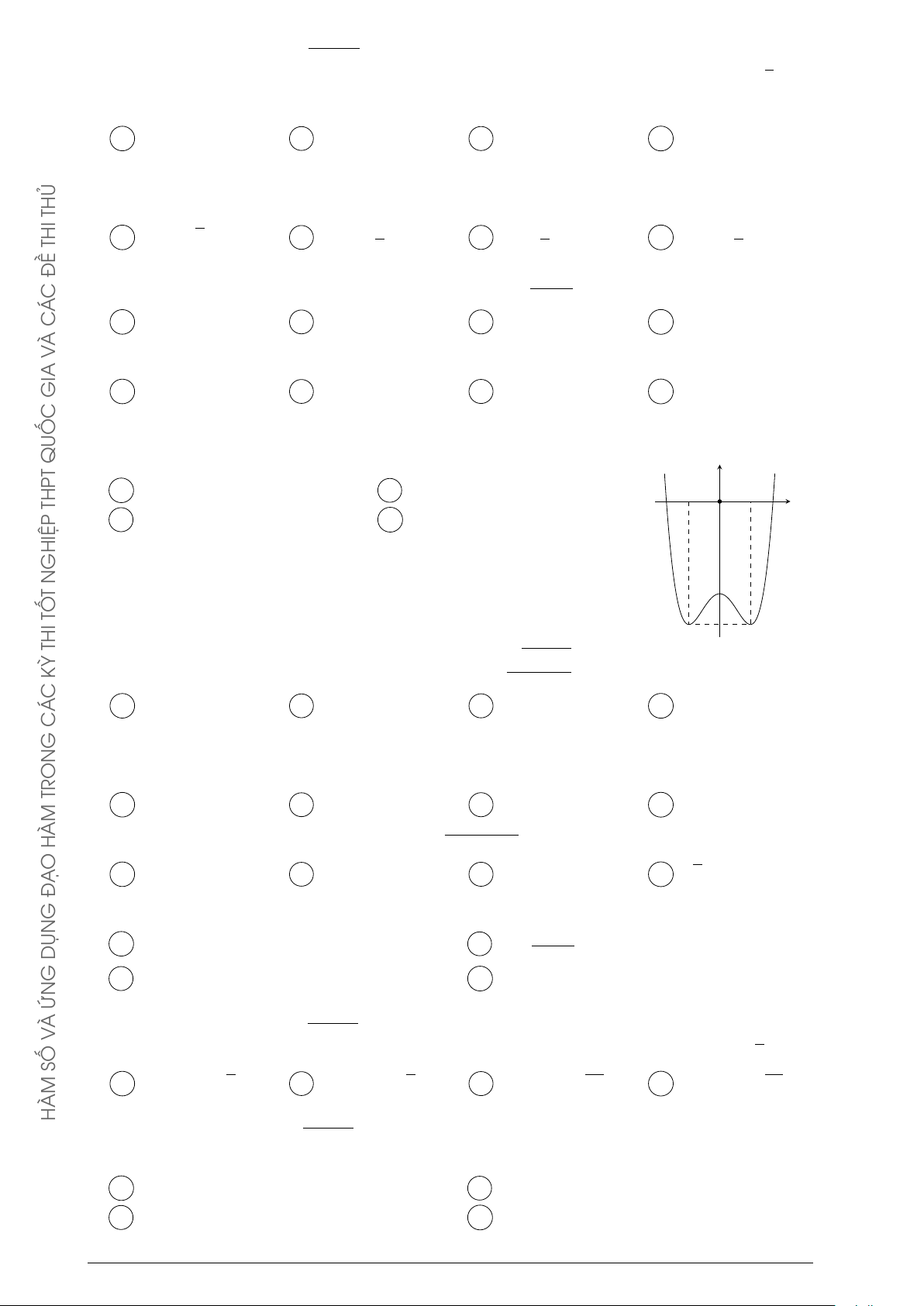
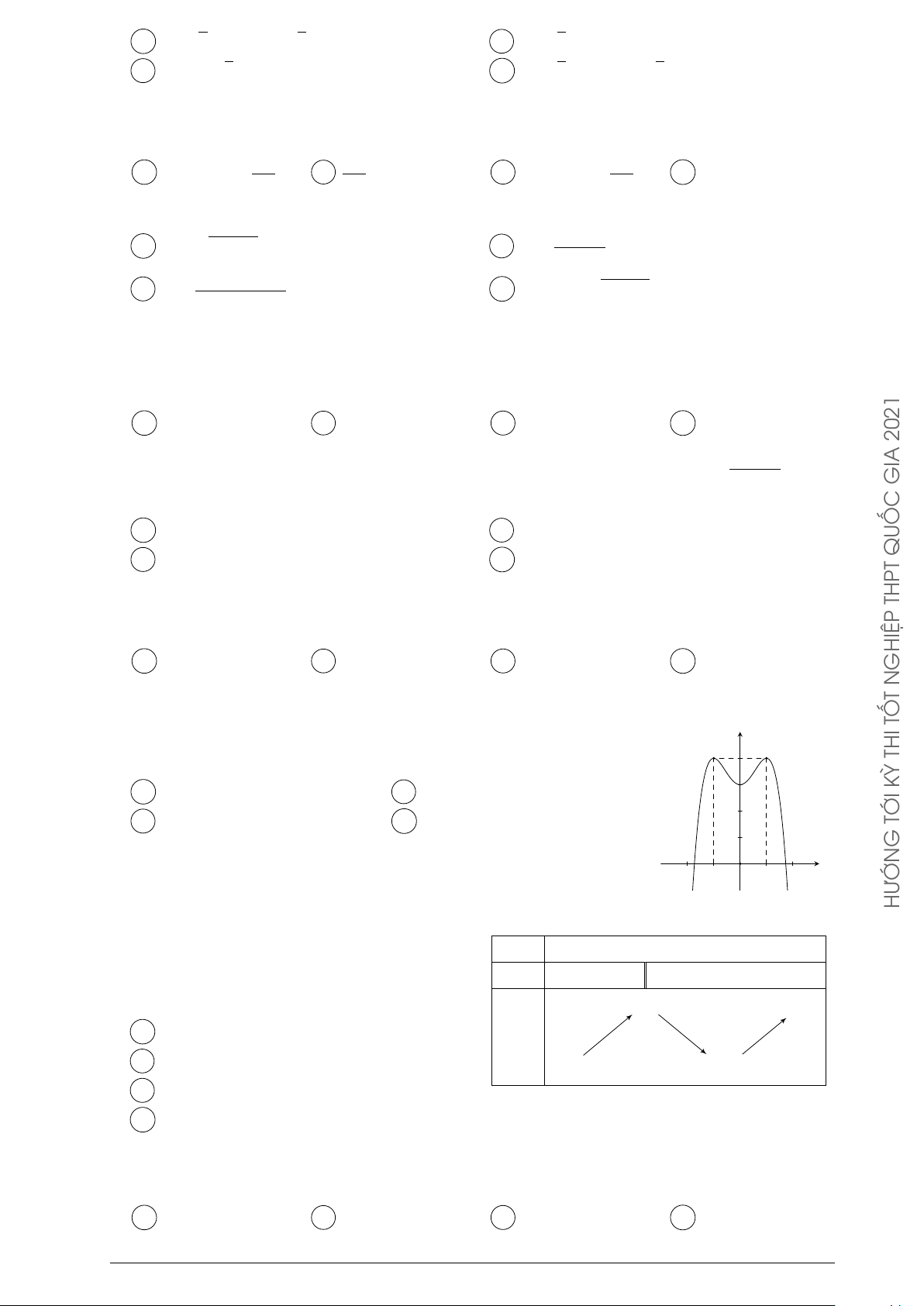
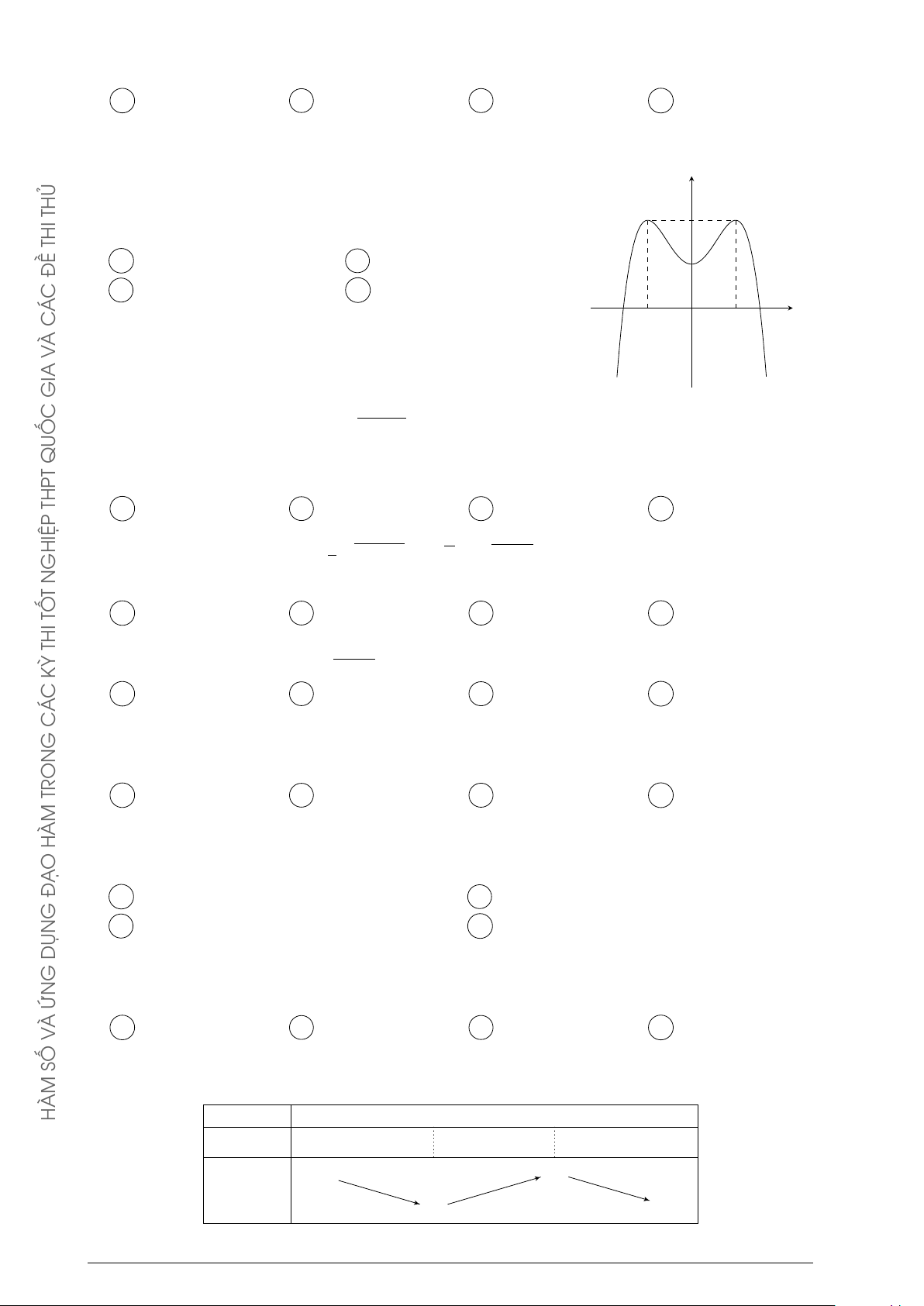
Câu 73. Cho hàm số y = −x4 + 2x2
có đồ thị như hình bên. Tìm tất cả các giá trị thực của tham y 1
số m để phương trình −x4 + 2x2 = m có bốn nghiệm thực phân biệt. −1 1 x O A m > 0. B 0 ≤ m ≤ 1. C 0 < m < 1. D m < 1.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 11 1
Câu 74. Một vật chuyển động theo quy luật s = − t3 + 6t2 với t (giây) là khoảng thời gian 3
tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong
khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây, kể từ khi bắt đầu chuyển động, vận
tốc lớn nhất của vật đạt được bằng bao nhiêu? A 144 m/s. B 36 m/s. C 243 m/s. D 27 m/s. THỦ
Câu 75. Tìm giá trị thực của tham số m để đường thẳng d : y = (2m − 1)x + 3 + m vuông THI
góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 1. ĐỀ 3 3 1 1 A m = . B m = . C m = − . D m = . C 2 4 2 4 Á C mx + 4m À Câu 76. Cho hàm số y =
với m là tham số. Gọi S là tập hợp tất cả các giá trị V x + m
nguyêncủa m để hàm số nghịch biến trên các khoảng xác định. Tìm số phần tử của S. GIA A 5. B 4. C Vô số. D 3. QUỐC
Câu 77. Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = x3−3mx2+4m3
có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 với O là gốc tọa THPT độ. 1 1 A m = − √ ; m = √ . B m = −1; m = 1. GHIỆP 4 2 4 2 N T C m = 1. D m 6= 0. TỐ THI
Câu 78. Cho hàm số y = f (x). KỲ
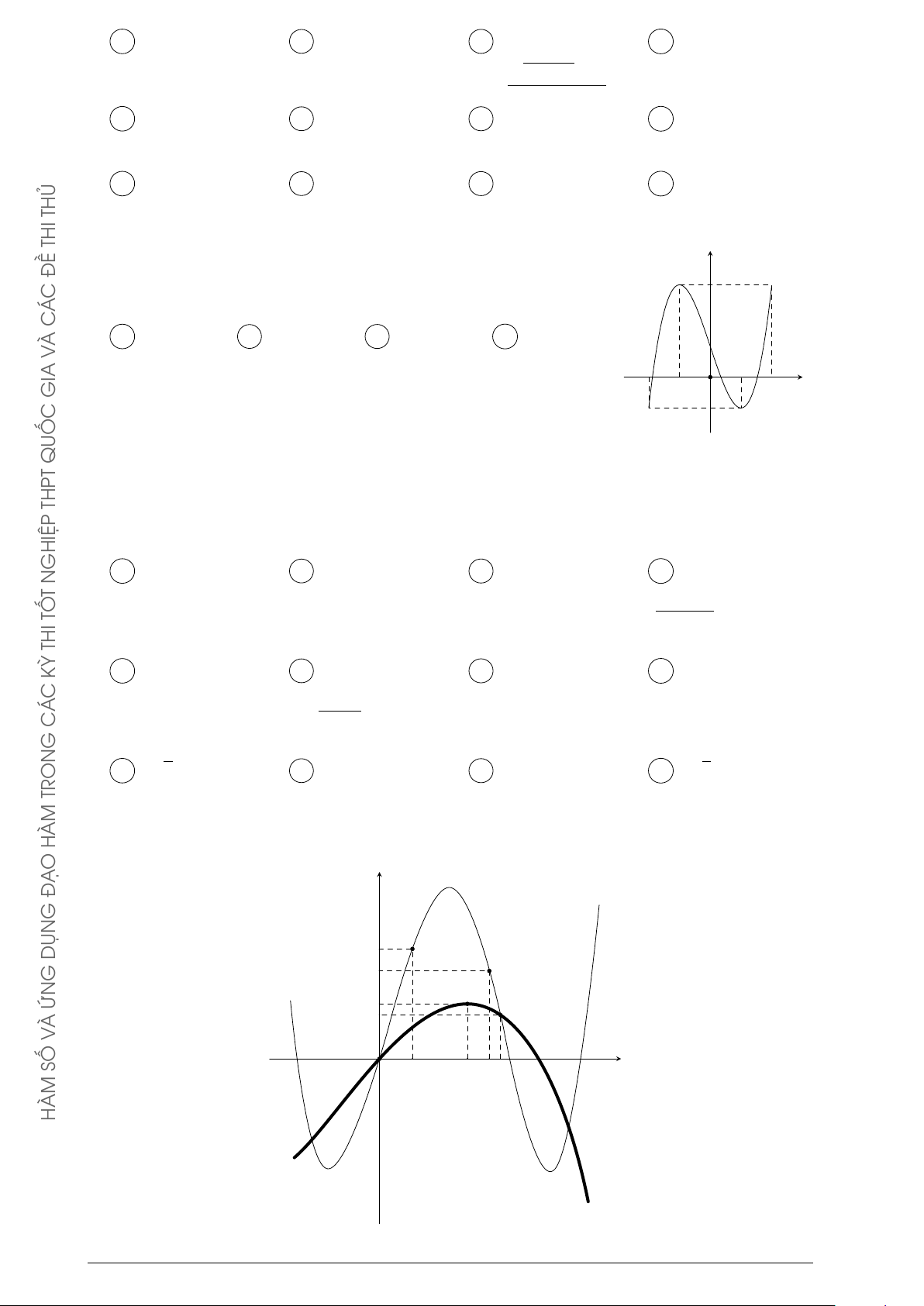
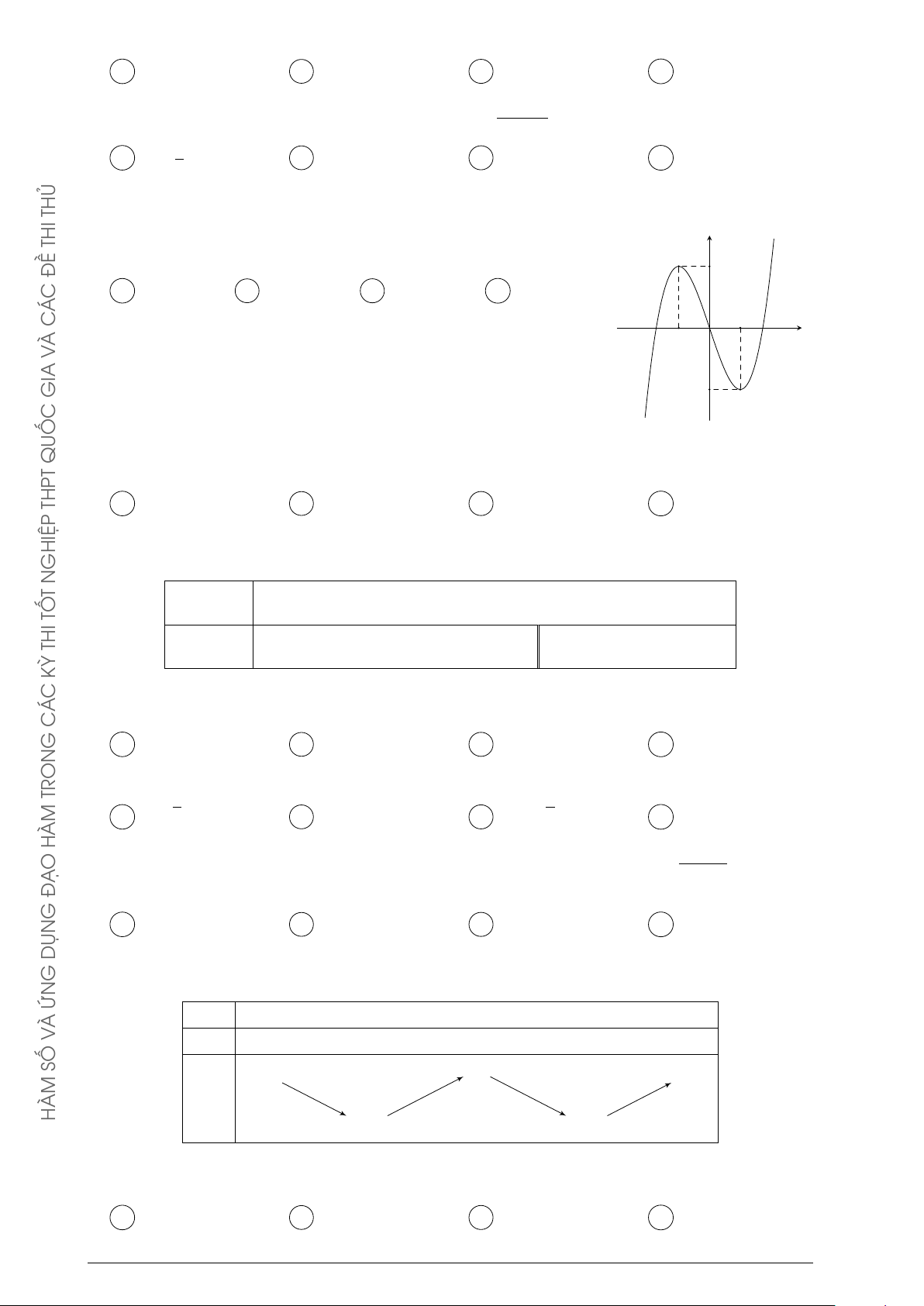
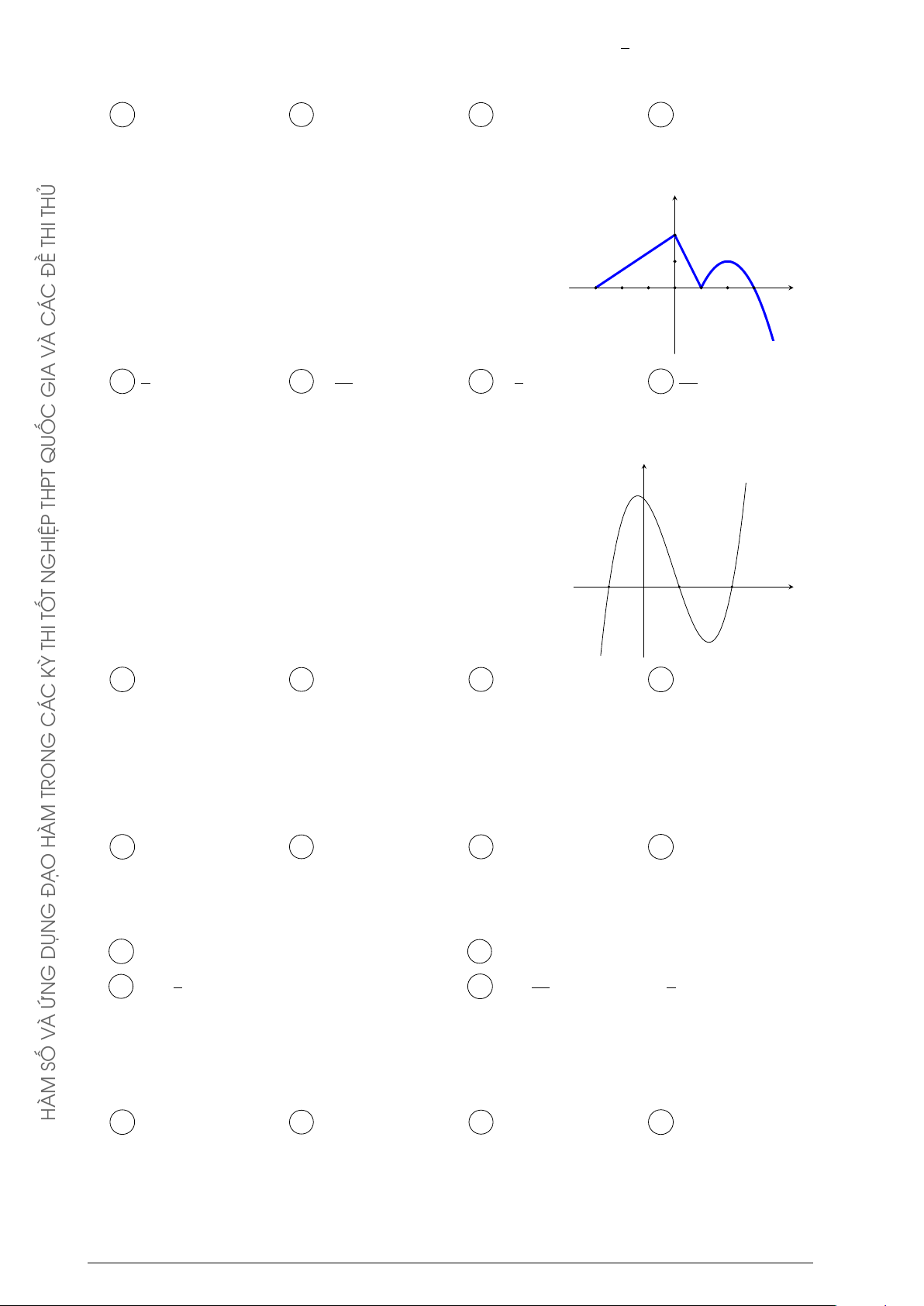
Đồ thị của hàm số y = f 0(x) như hình bên. y C Á
Đặt g(x) = 2f (x) + (x + 1)2. C 2 −
Mệnh đề nào dưới đây đúng? 3 1 3 G x O A g(1) < g(3) < g(−3). B g(1) < g(−3) < g(3). −2 TRON C g(3) = g(−3) < g(1). D g(3) = g(−3) > g(1). −4 HÀM O Ạ
Câu 79. Cho hàm số y = f (x) có bảng biến thiên như sau Đ G DỤN x −∞ −2 0 −2 +∞ G y0 + 0 − 0 + 0 − ỨN À 3 3 V y SỐ −∞ −1 − ∞ HÀM
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây? A (−2; 0). B (−∞; −2). C (0; 2) . D (0; +∞) .
Câu 80. Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 12 x −∞ 0 2 +∞ y0 − 0 + 0 − +∞ + 5 y 1 −∞
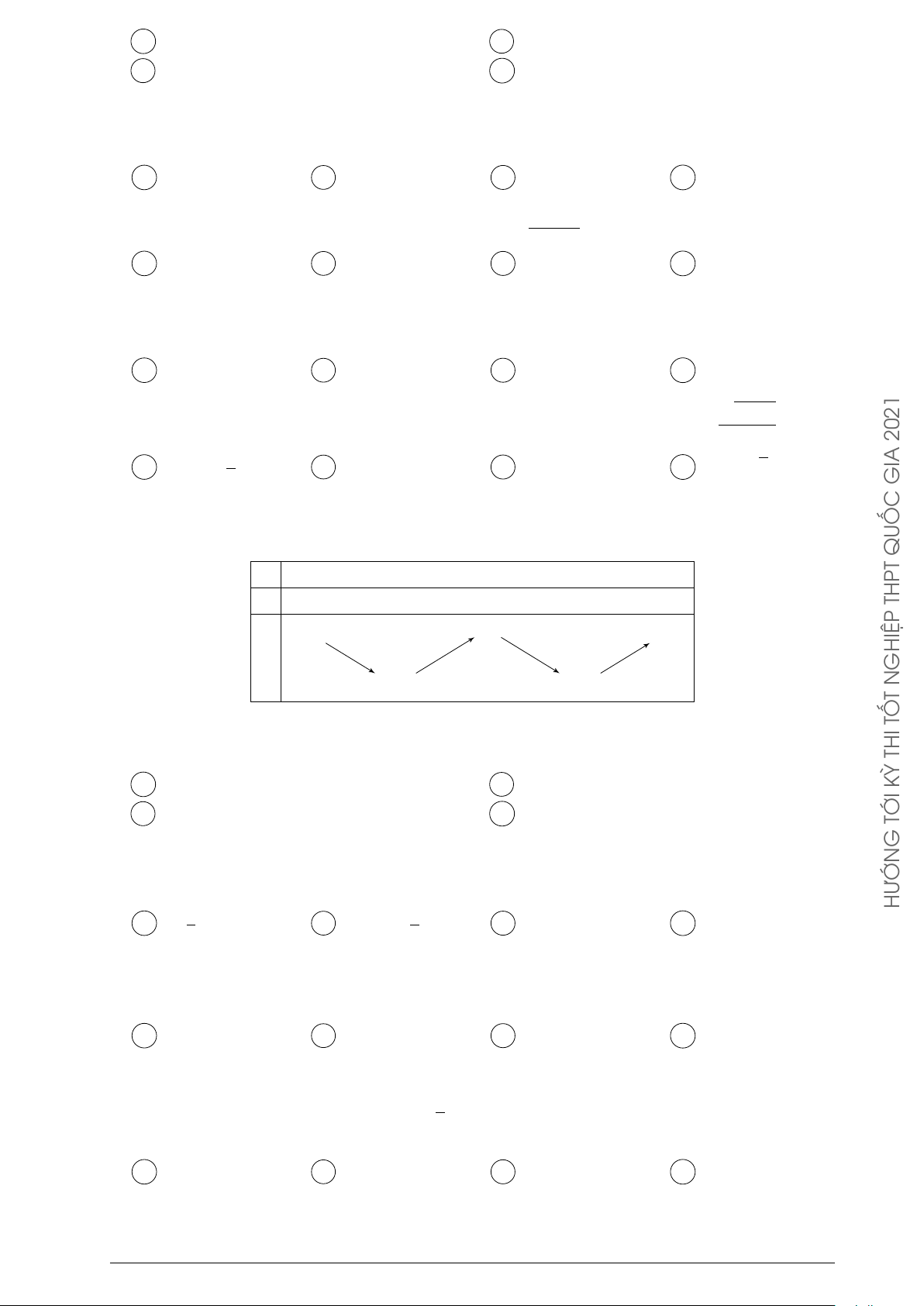
Hàm số đạt cực đại tại điểm A x = 1. B x = 0. C x = 5. D x = 2. Câu 81.
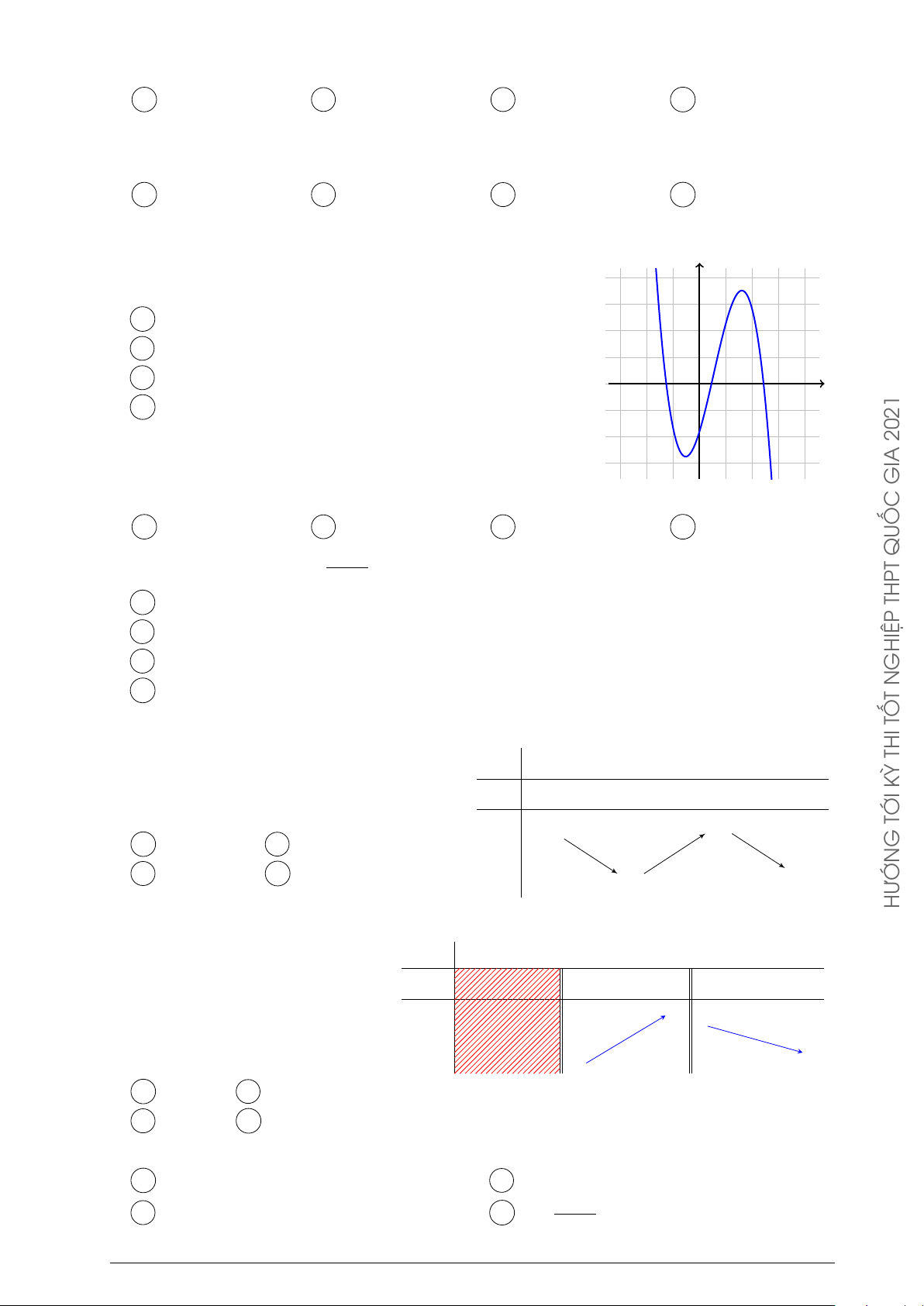
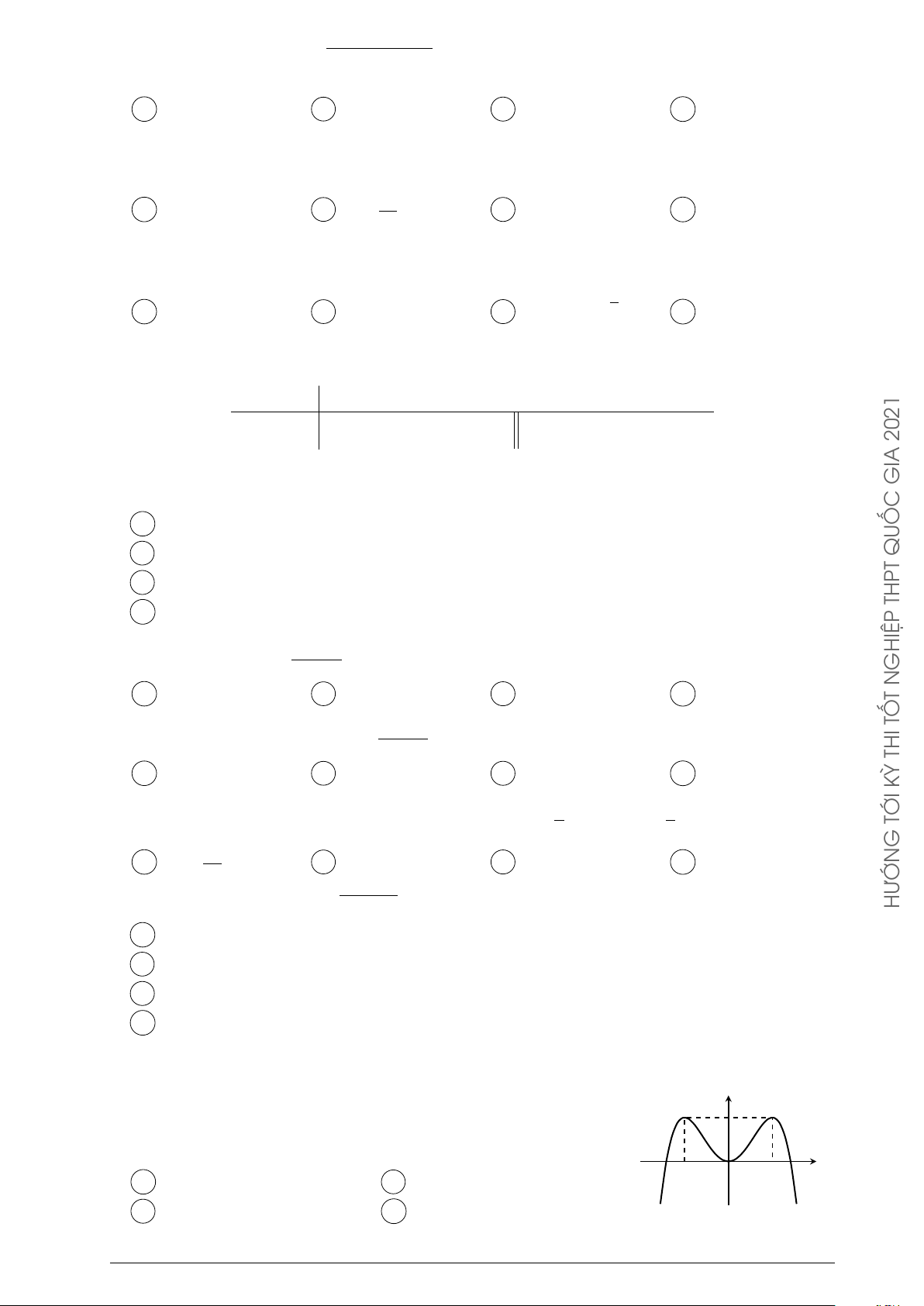
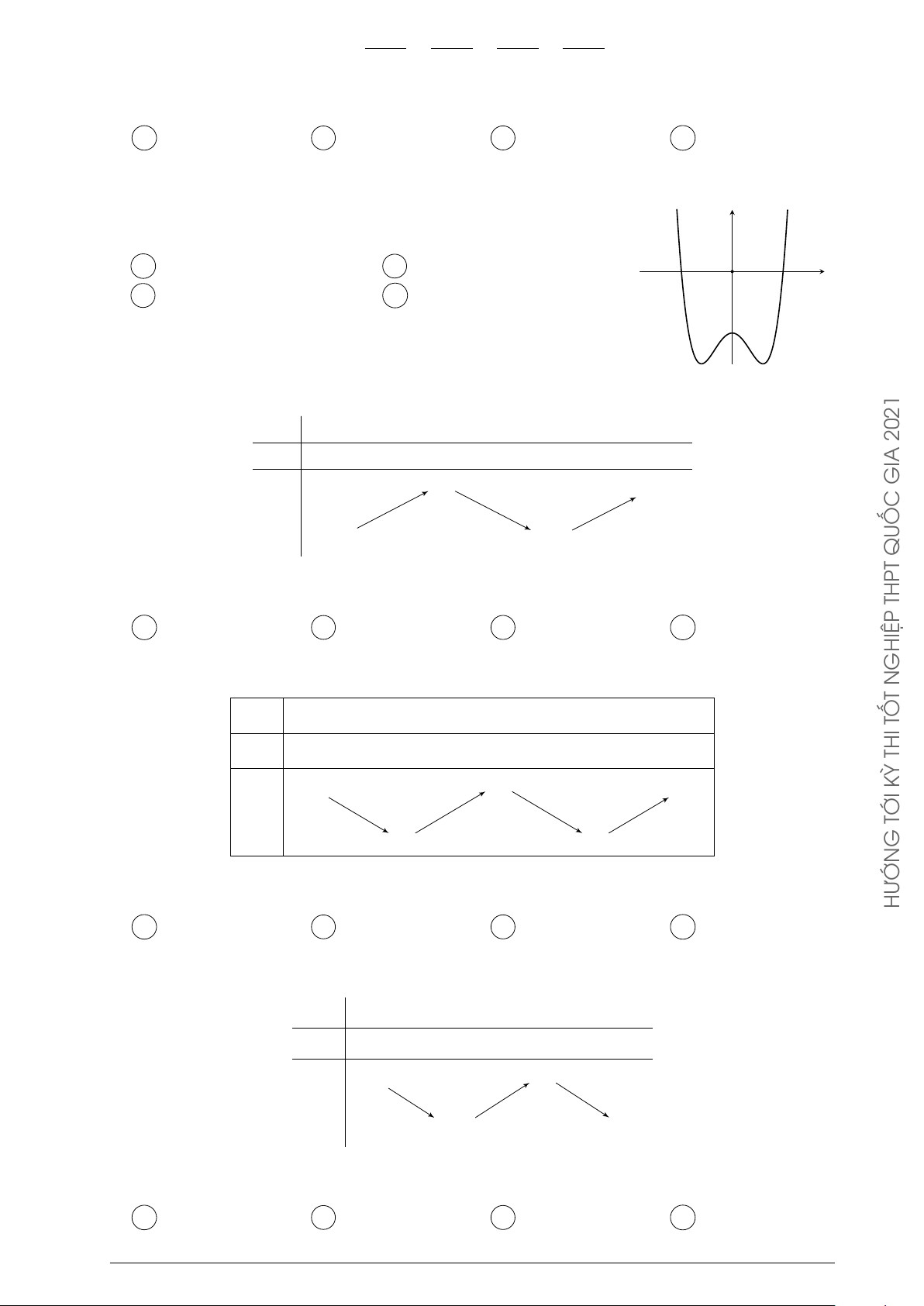
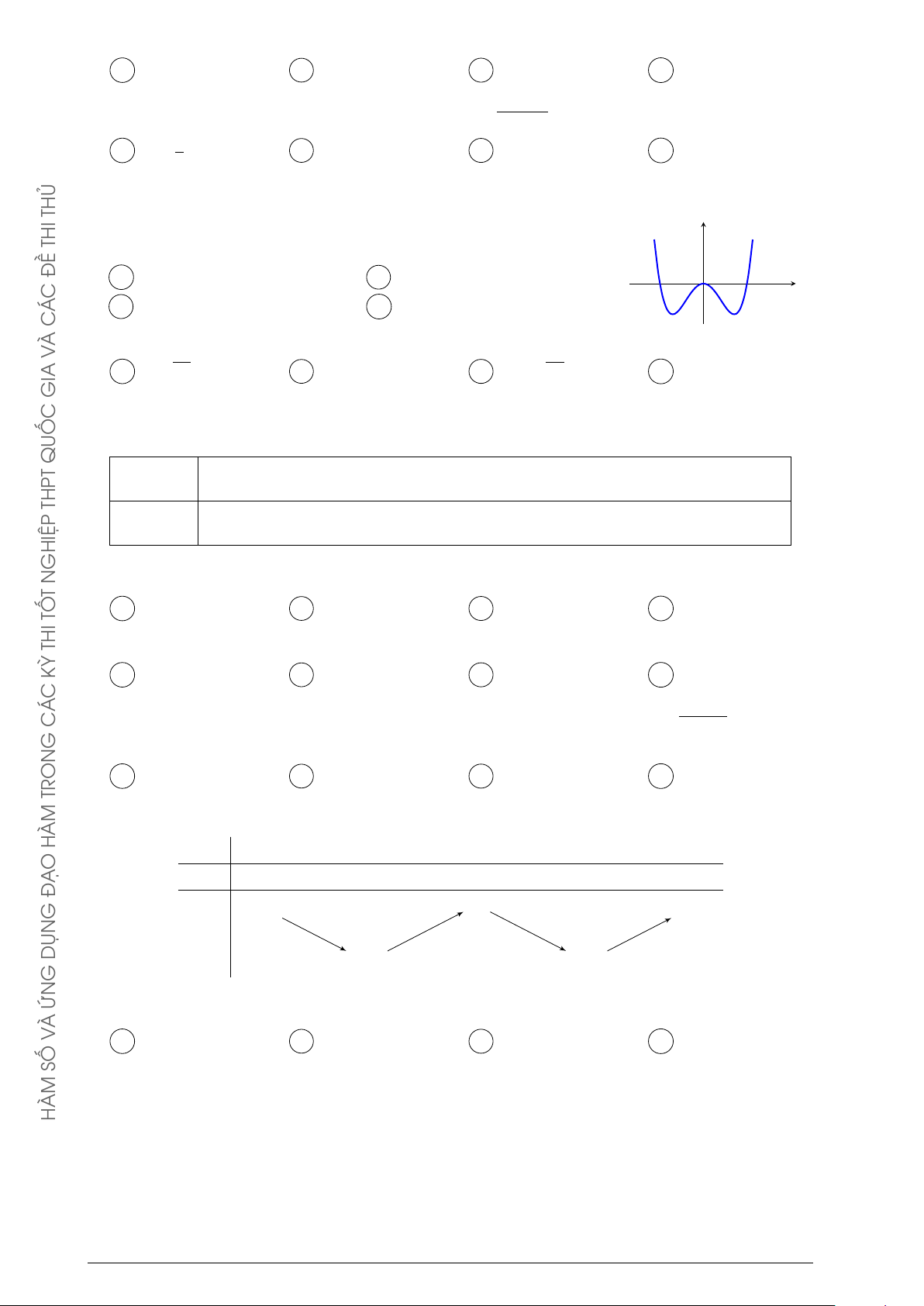
Đường cong hình bên là đồ thị của hàm số nào dưới y đây? 2021 A y = −x4 + 2x2 + 2. B y = x4 − 2x2 + 2. GIA C y = x3 − 3x2 + 2. D y = −x3 + 3x2 + 2. QUỐC O x THPT GHIỆP N
Câu 82. Đồ thị của hàm số nào dưới đây có tiệm cận đứng? T x2 − 3x + 2 x2 √ x TỐ A y = . B y = . C y = x2 − 1. D y = . x − 1 x2 + 1 x + 1 THI Câu 83. KỲ
Cho hàm số y = f (x) có bảng biến thiên như TỚI x −∞ −1 3 +∞
hình vẽ. Số nghiệm của phương trình f (x) − G y0 + 0 − 0 + 2 = 0 là 4 +∞ + A 0. B 3. C 1. D 2. HƯỚN y −∞ −2 − 1
Câu 84. Có bao nhiêu giá trị nguyên âm của m để hàm số y = x3 + mx − đồng biến 5x5 trên (0; +∞). A 5. B 3. C 0. D 4. √
Câu 85. Có bao nhiêu giá trị nguyên của tham số m để phương trình 3 pm + 3 3 m + 3 sin x = sin x có nghiệm thực. A 5. B 7. C 3. D 2. Câu 86.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 13
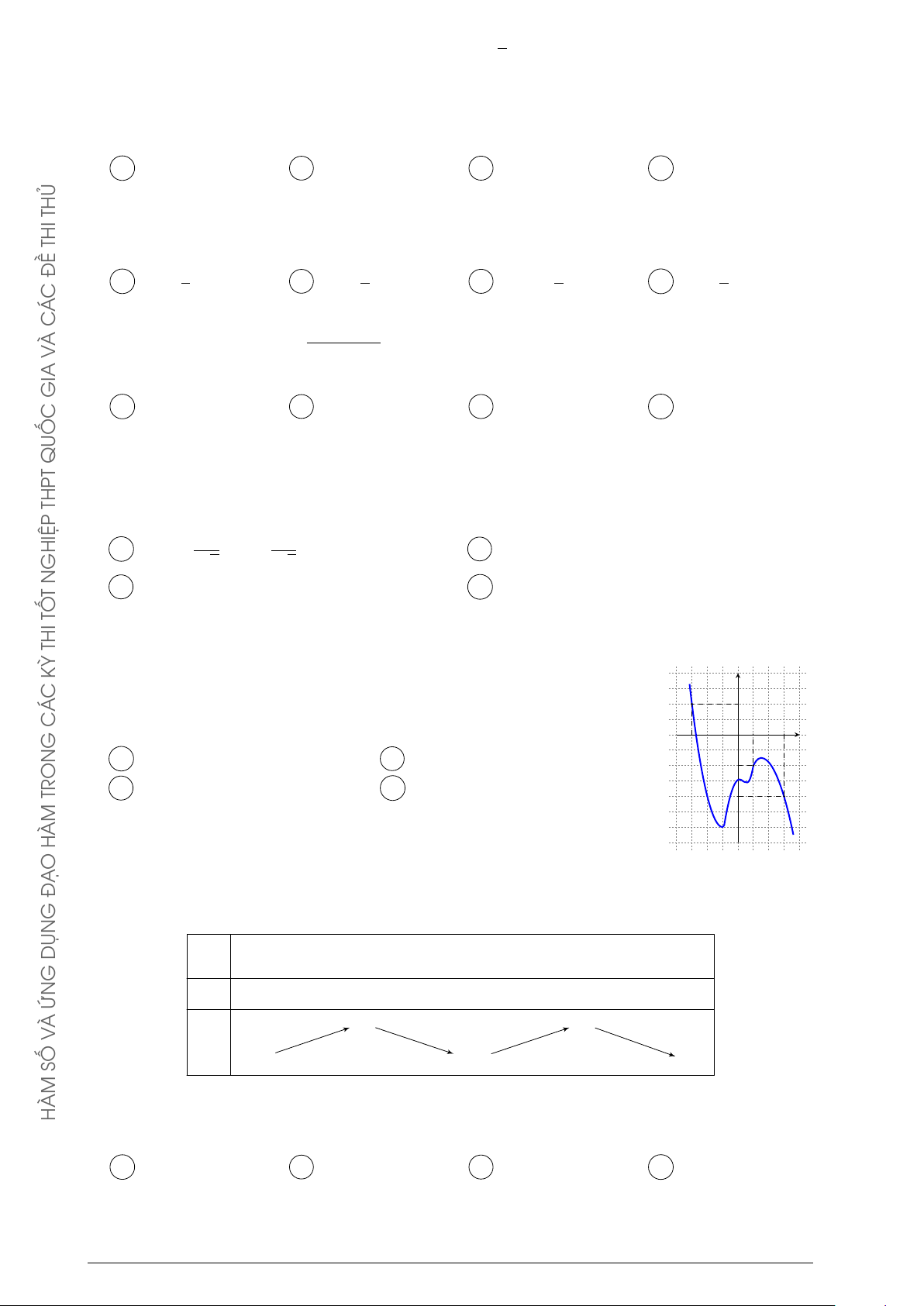
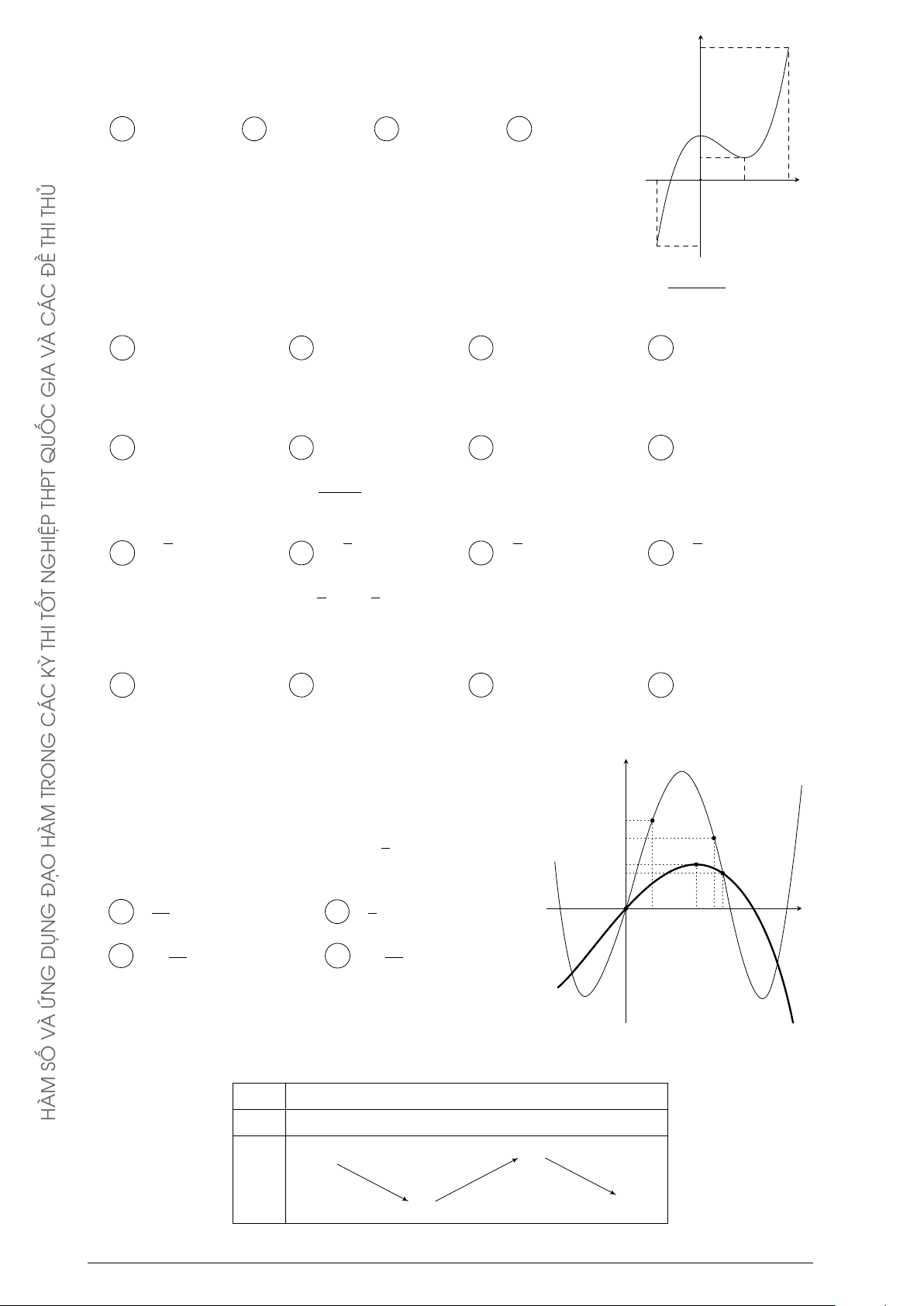
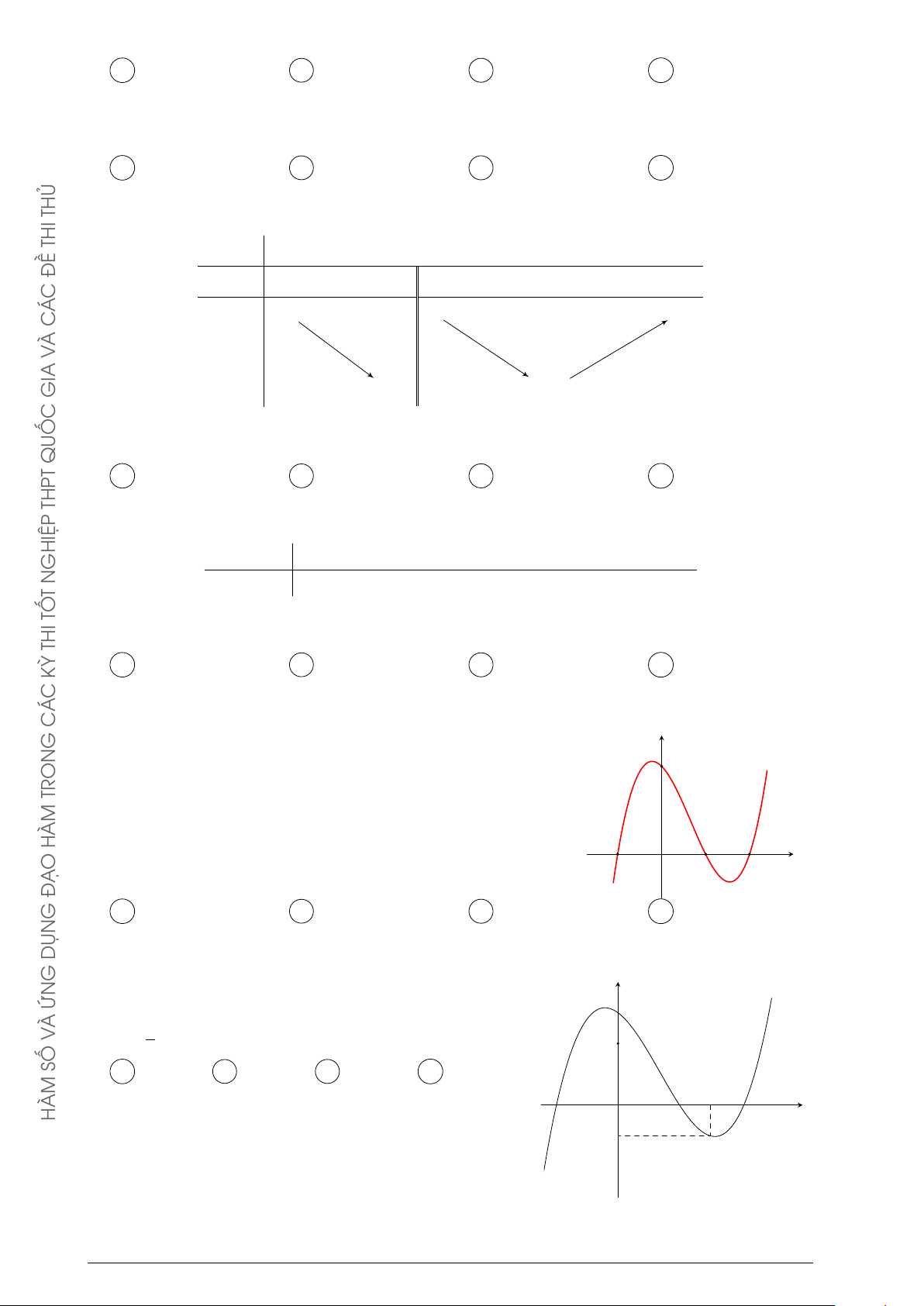
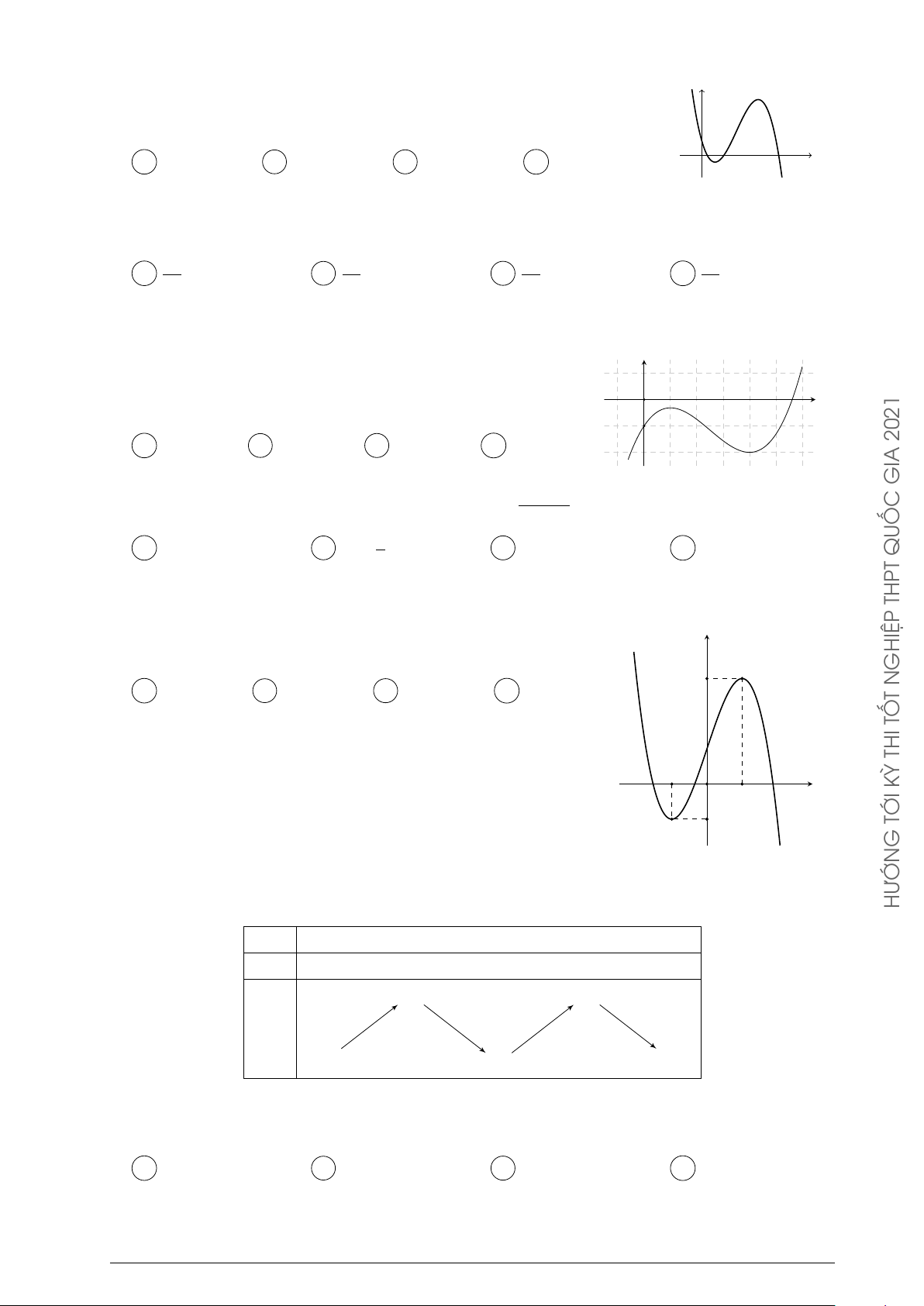
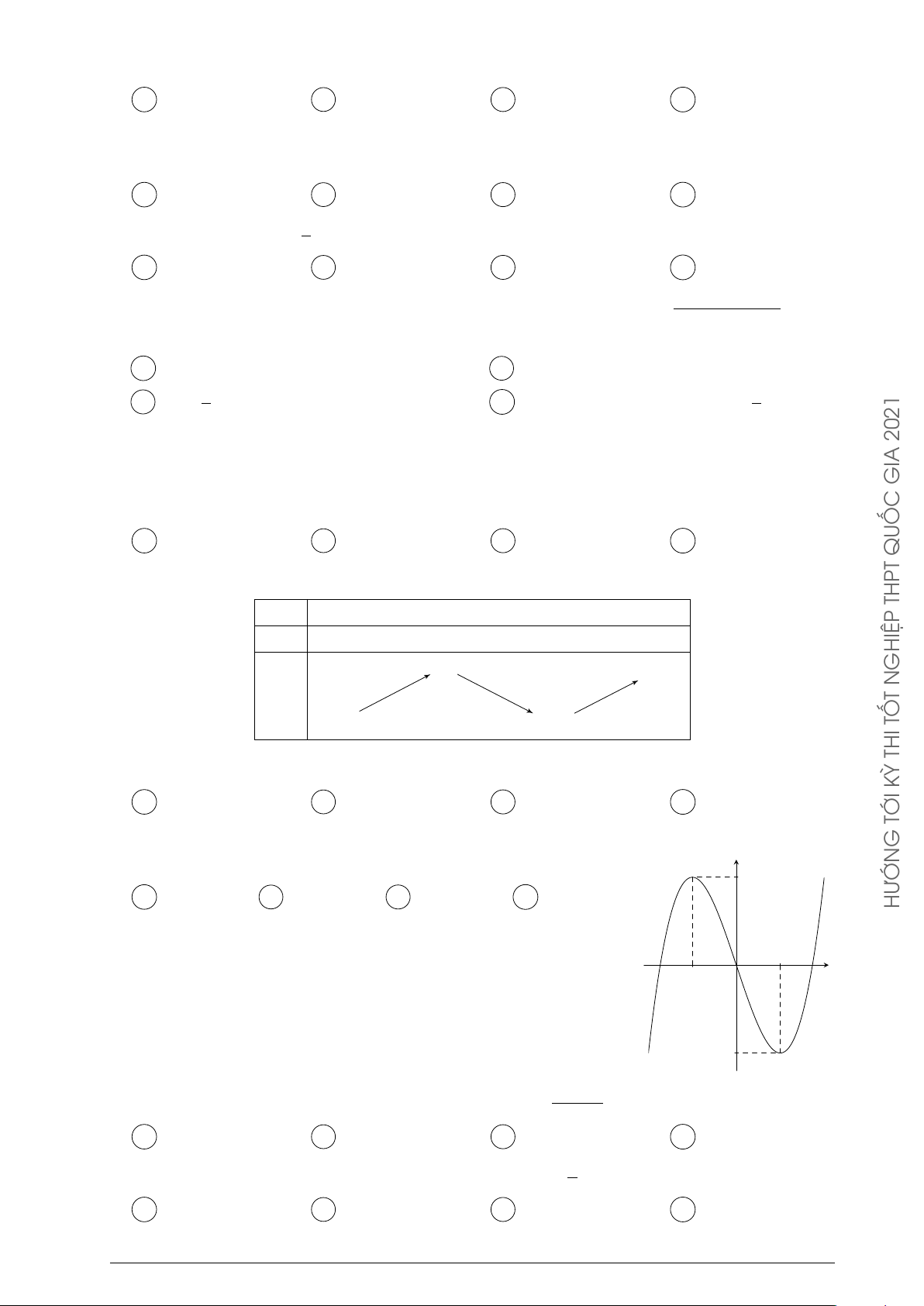
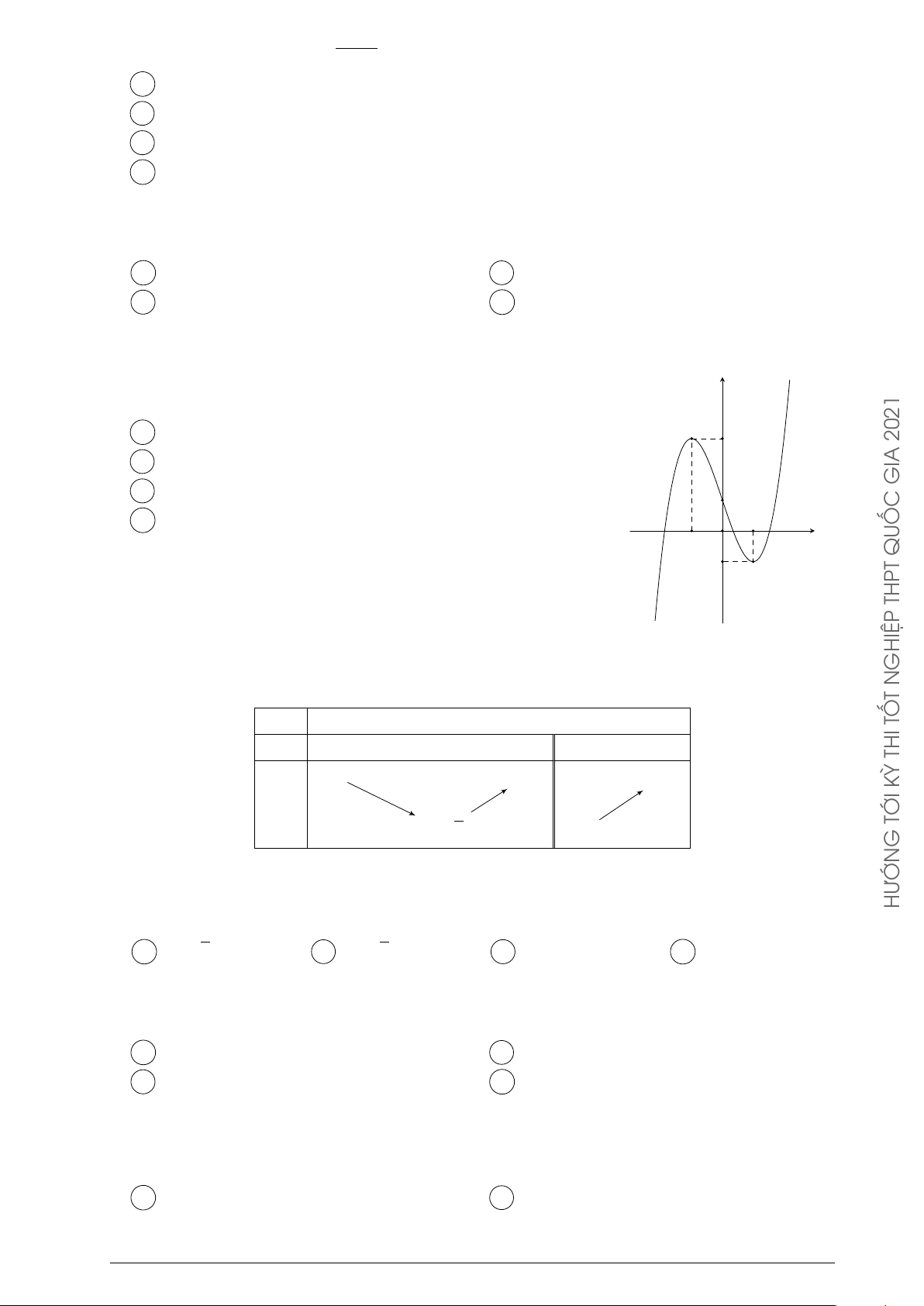
Cho hàm số y = f (x). Hàm số y = f 0(x) có đồ y
thị như hình bên. Hàm số y = f (2 − x) đồng biến trên khoảng A (1; 3). B (2; +∞). −1 x C (−2; 1). D (−∞; −2). 0 1 4 THỦ THI ĐỀ
Câu 87. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = |3x4 − 4x3 − 12x2 + m| C Á có 7 điểm cực trị C À A 3. B 5. C 6. D 4. V Câu 88. GIA
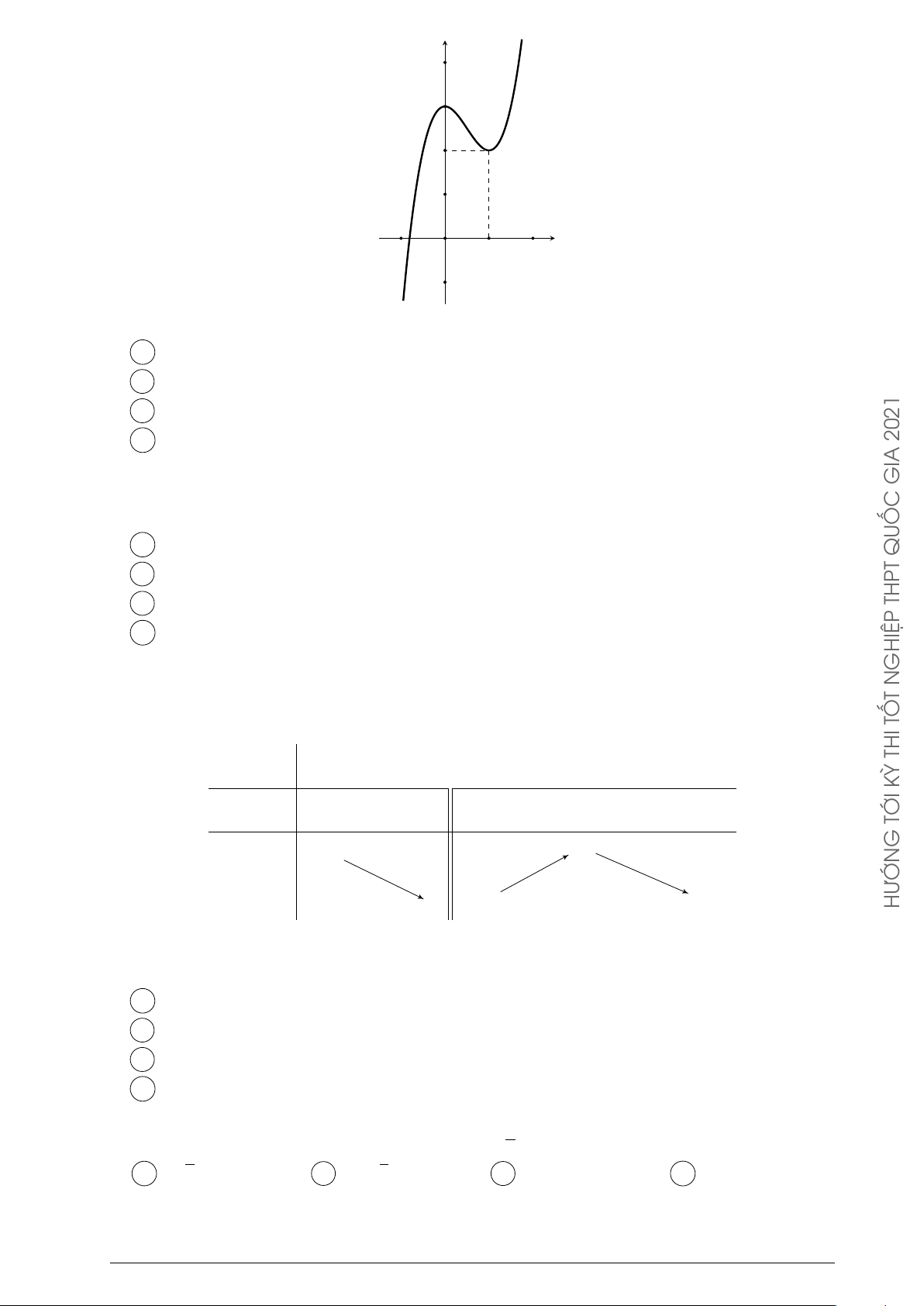
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ y
R) có đồ thị như hình vẽ
bên. Số điểm cực trị của hàm số đã cho là QUỐC A 2. B 0. C 3. D 1. O x THPT
Câu 89. Cho hàm số y = f (x) có bảng biến thiên như sau GHIỆP x −∞ −1 0 1 +∞ N T y0 − 0 + 0 − 0 + TỐ +∞ + 3 +∞ + THI y KỲ −2 − −2 − C Á C
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? G A (0; 1). B (−∞; 0). C (1; +∞). D (−1; 0). Câu 90. TRON
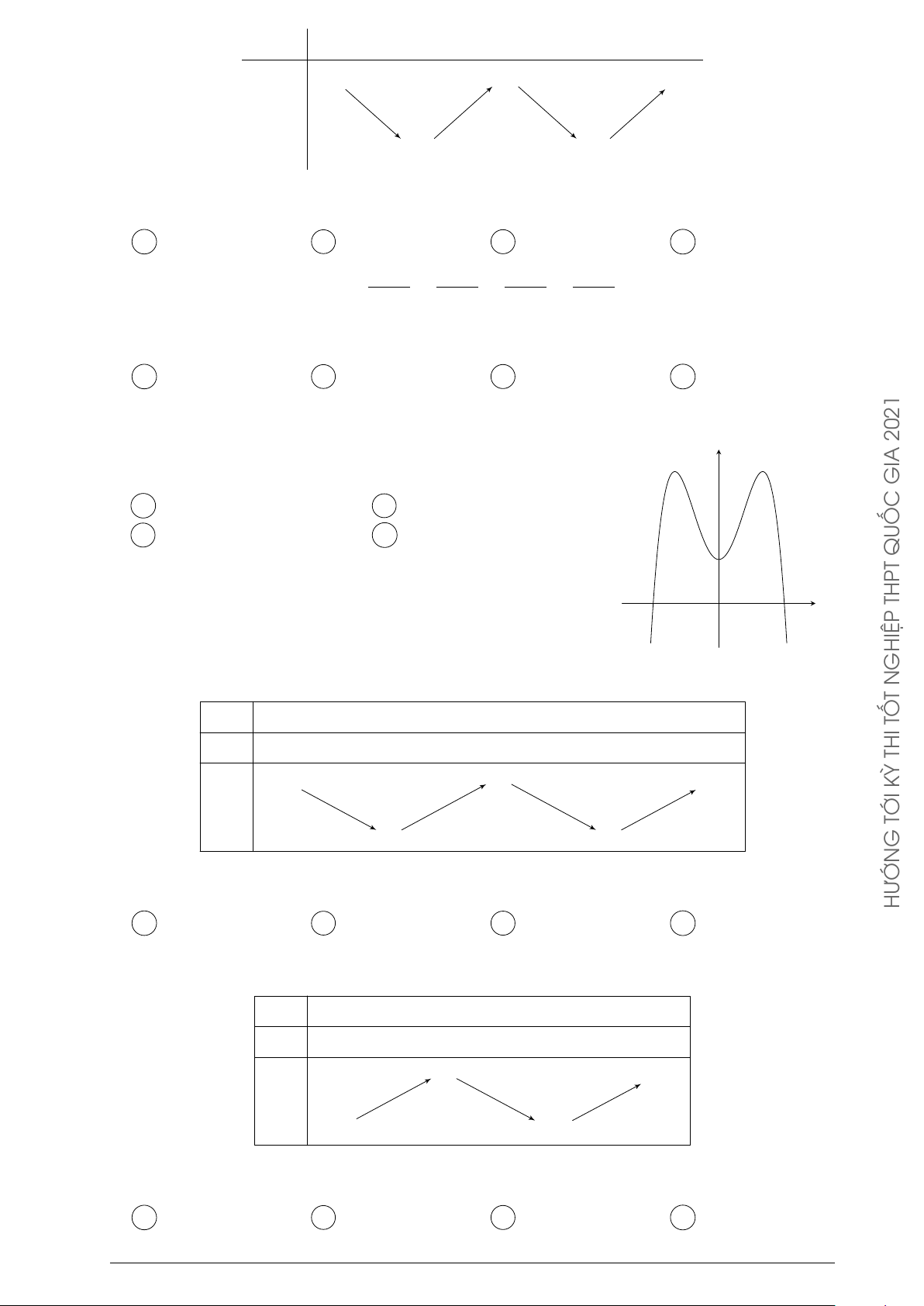
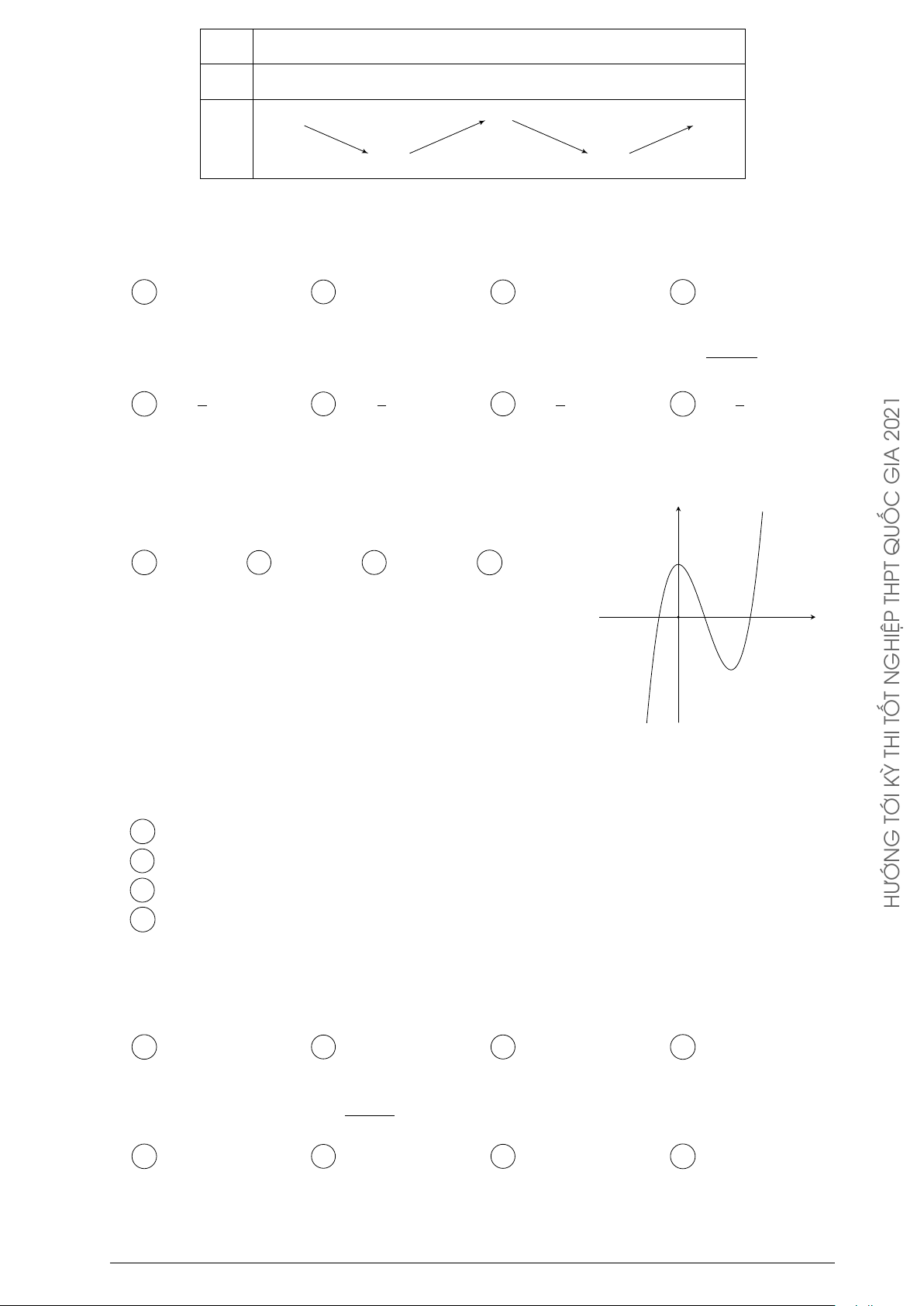
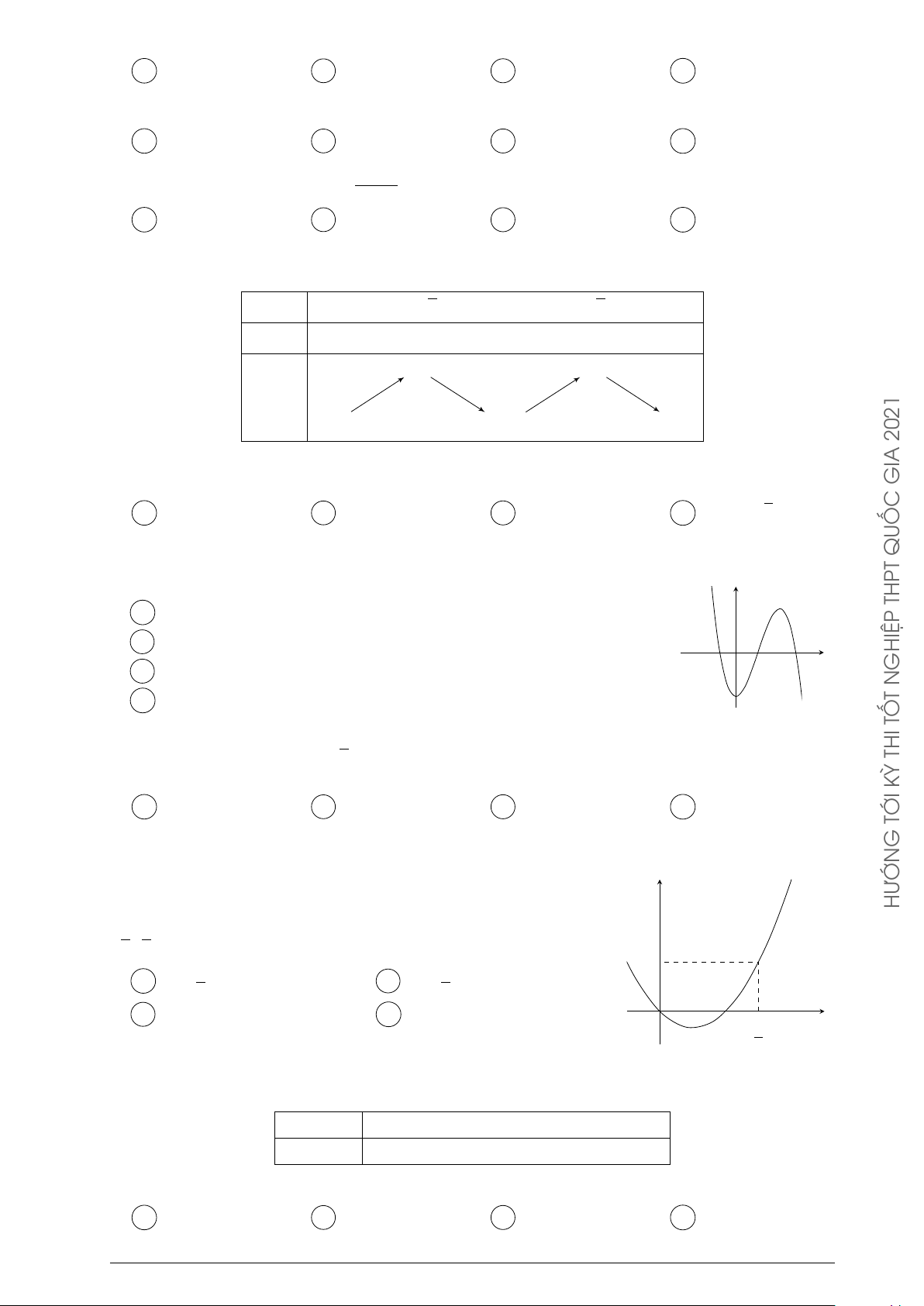
Đường cong trong hình vẽ bên là của hàm số nào dưới đây? y HÀM A y = x4 − 3x2 − 1. B y = x3 − 3x2 − 1. O x O Ạ C y = −x3 + 3x2 − 1. D y = −x4 + 3x2 − 1. Đ G Câu 91. DỤN G
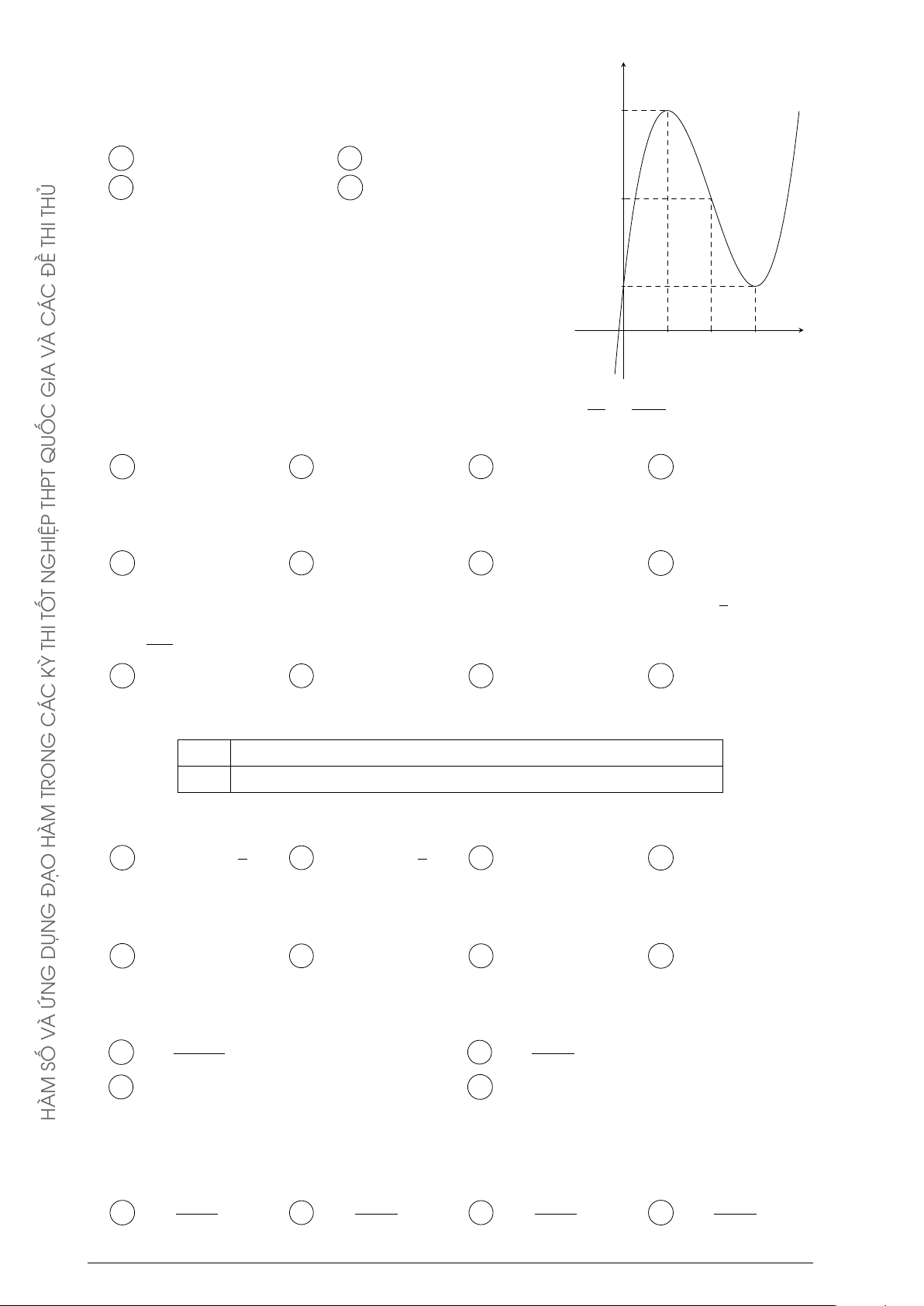
Cho hàm số f (x) = ax3 + bx2 + cx + d (a, b, c, d ∈ R). Đồ thị của y ỨN
hàm số y = f (x) như hình vẽ bên. Số nghiệm thực của phương trình 2 À V 3f (x) + 4 = 0 là 2 SỐ A 3. B 0. C 1. D 2. x O HÀM −2 √x + 9 − 3
Câu 92. Số tiệm cận đứng của đồ thị hàm số y = là x2 + x A 3. B 2. C 0. D 1.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 14
Câu 93. Giá trị lớn nhất của hàm số y = x4 − 4x2 + 9 trên đoạn [−2; 3] bằng A 201. B 2. C 9. D 54. x + 2
Câu 94. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = đồng biến trên x + 5m khoảng (−∞; −10)? A 2. B Vô số. C 1. D 3.
Câu 95. Có tất cả bao nhiêu giá trị nguyên của m để hàm số y = x8 + (m − 2)x5 − (m2 −
4)x4 + 1 đạt cực tiểu tại x = 0? A 3. B 5. C 4. D Vô số. 1 7 Câu 96. Cho hàm số y =
x4 − x2 có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao cho 4 2
tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M (x1; y1), N (x2; y2) (M, N khác A)
thỏa mãn y1 − y2 = 6(x1 − x2)? A 1. B 2. C 0. D 3. x − 1 Câu 97. Cho hàm số y =
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của (C). 2021 x + 2
Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng GIA √ √ √ A 6. B 2 3. C 2. D 2 2.
Câu 98. Cho hai hàm số y = f (x), y = g(x). Hai hàm số y = f 0(x) và y = g0(x) có đồ thị QUỐC
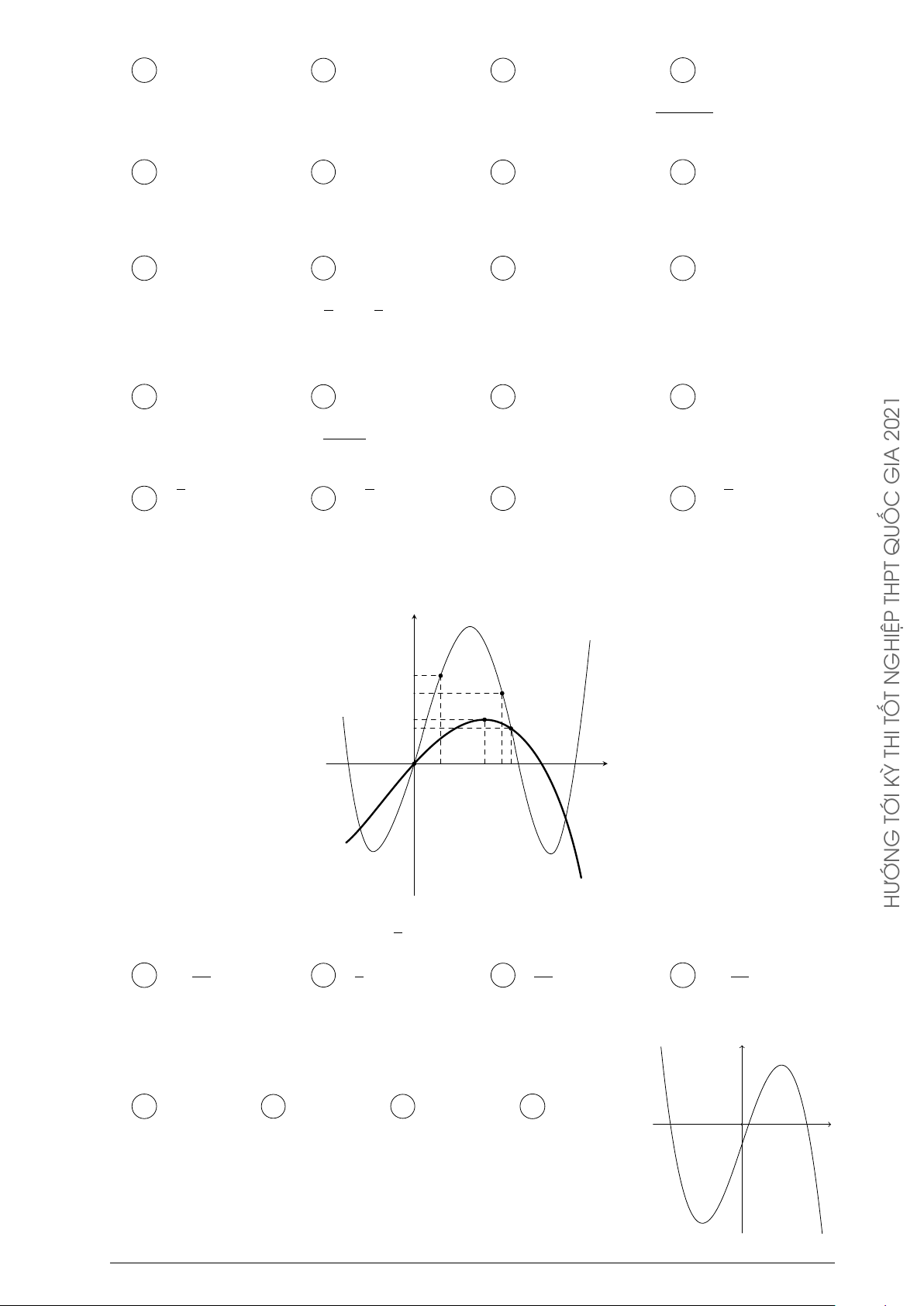
như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y = g0(x). y THPT y = f 0(x) GHIỆP 10 N 8 T 5 TỐ 4 O x THI 3 8 1011 KỲ TỚI G y = g0(x) HƯỚN Å 3 ã
Hàm số h(x) = f (x + 4) − g 2x −
đồng biến trên khoảng nào dưới đây? 2 Å 31 ã Å 9 ã Å 31 ã Å 25 ã A 5; . B ; 3 . C ; +∞ . D 6; . 5 4 5 4 Câu 99.
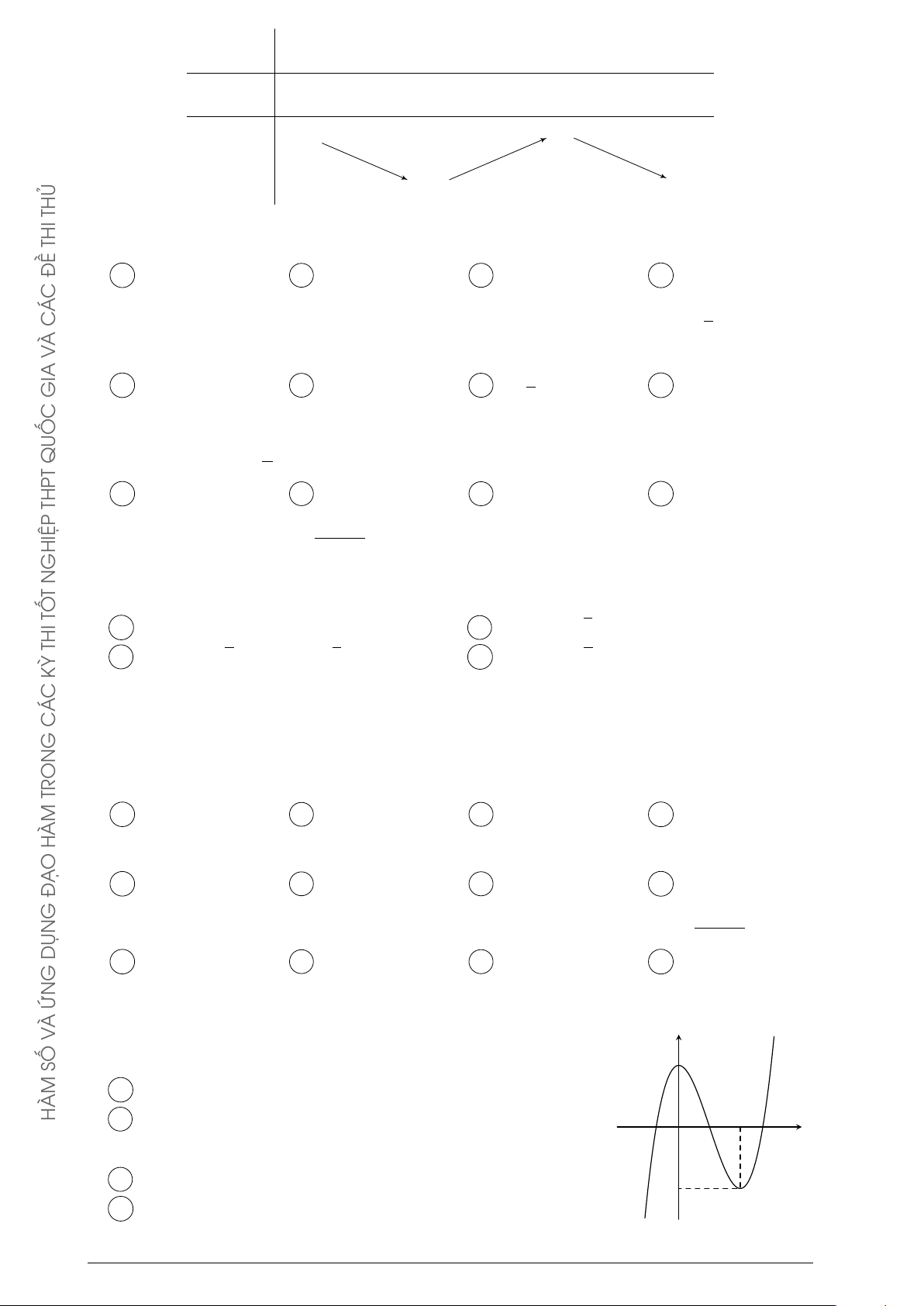
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ y R) có đồ thị như
hình vẽ bên. Số điểm cực trị của hàm số đã cho là A 0. B 1. C 3. D 2. x O
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 15 Câu 100. y
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? A y = x4 − 2x2 − 1. B y = −x4 + 2x2 − 1. x O C y = x3 − x2 − 1. D y = −x3 + x2 − 1. THỦ THI ĐỀ
Câu 101. Cho hàm số y = f (x) có bảng biến thiên như sau C x −∞ −1 1 +∞ Á y0 + 0 − 0 + C À 3 +∞ V y −∞ −2 − GIA
Hàm số đã cho đồng biến trên khoảng nào dưới đây? QUỐC A (−1; +∞). B (1; +∞). C (−1; 1). D (−∞; 1). THPT Câu 102. y
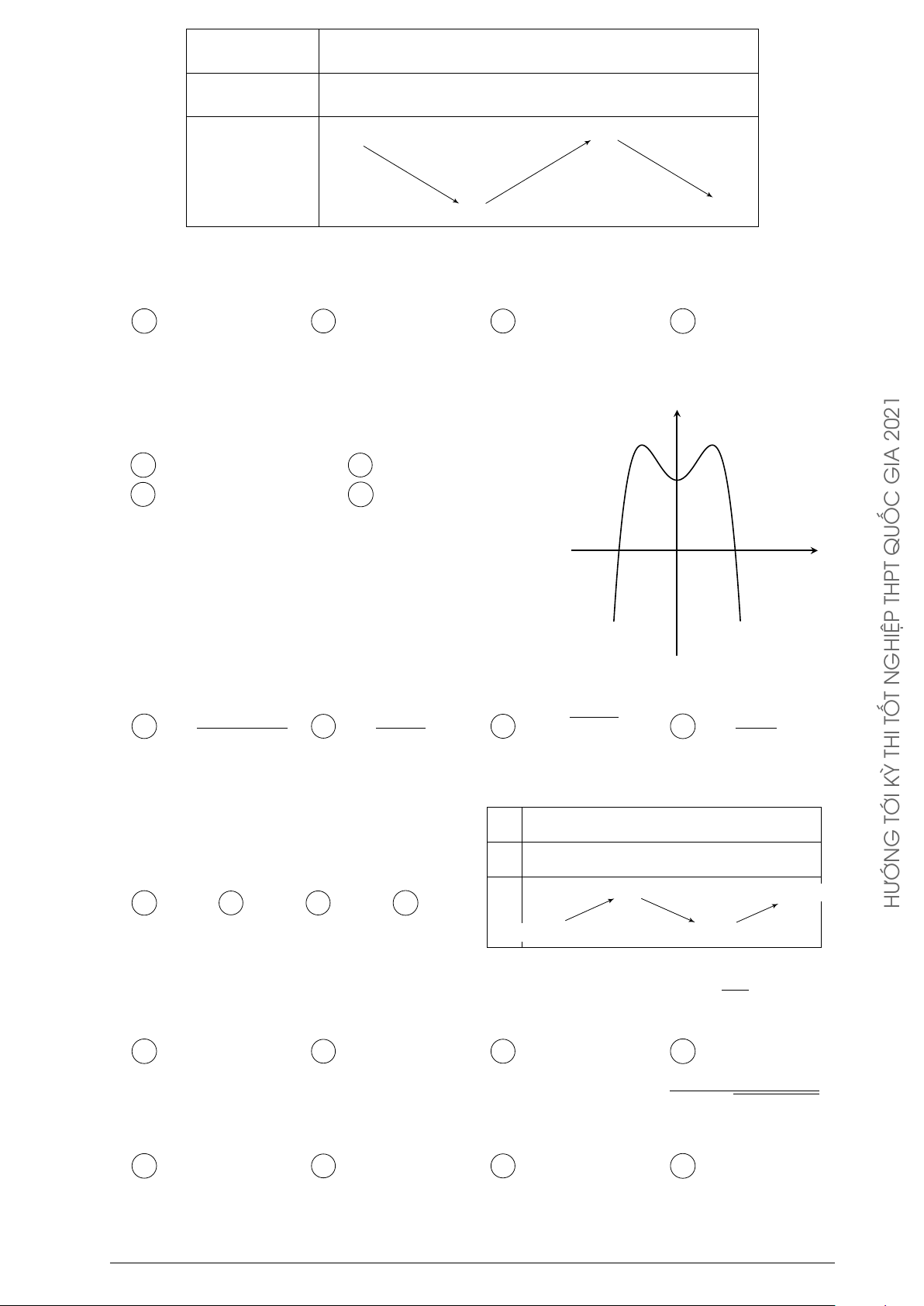
Cho hàm số f (x) = ax4+bx2+c (a, b, c ∈ R). Đồ thị của hàm số y = f (x) GHIỆP 1 N
như hình vẽ bên. Số nghiệm thực của phương trình 4f (x)−3 = 0 là T A 4. B 3. C 2. D 0. TỐ −1 1 x O THI KỲ
Câu 103. Giá trị nhỏ nhất của hàm số y = x3 + 2x2 − 7x trên đoạn [0; 4] bằng C Á C A −259. B 68. C 0. D −4. G √x + 4 − 2
Câu 104. Số tiệm cận đứng của đồ thị hàm số y = là TRON x2 + x A 3. B 0. C 2. D 1. HÀM O x + 6 Ạ
Câu 105. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = nghịch biến Đ x + 5m G trên khoảng (10; +∞)? A 3. B Vô số. C 4. D 5. DỤN G ỨN
Câu 106. Có bao nhiêu giá trị nguyên của tham số m để hàm số À V SỐ
y = x8 + (m − 1)x5 − (m2 − 1)x4 + 1 HÀM
đạt cực tiểu tại x = 0? A 3. B 2. C Vô số. D 1. Câu 107.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 16
Cho hai hàm số y = f (x) và y = g(x). Hai y
hàm số y = f 0(x) và y = g0(x) có đồ thị y = f 0(x)
như hình vẽ bên, trong đó đường cong đậm
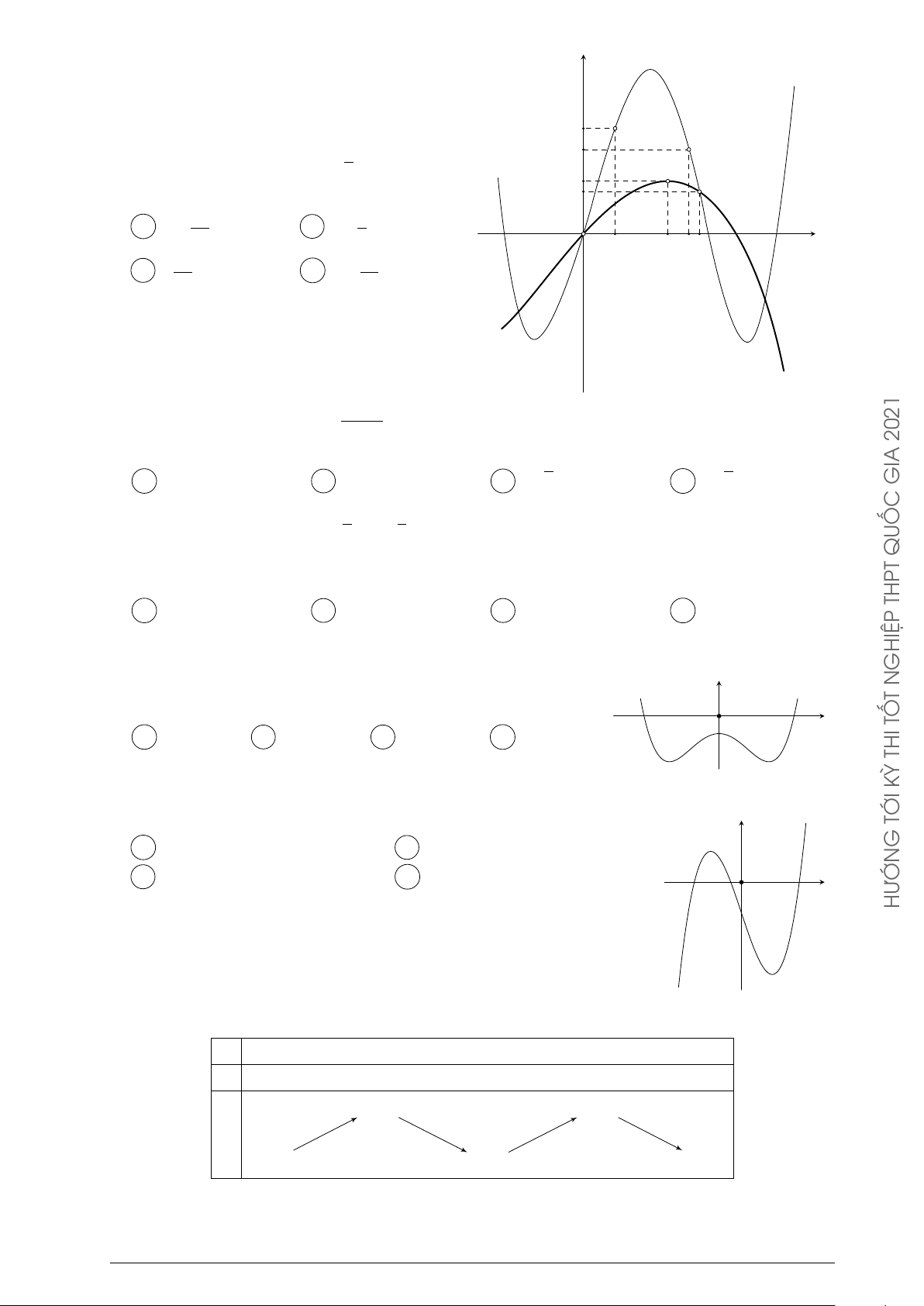
hơn là đồ thị hàm số y = g0(x). Hàm số 10 Å 9 ã 8 h (x) = f (x + 7) − g 2x + đồng biến 2 5
trên khoảng nào dưới đây? 4 Å 16 ã Å 3 ã A 2; . B − ; 0 . O x 5 4 3 8 1011 Å 16 ã Å 13 ã C ; +∞ . D 3; . 5 4 y = g0(x) x − 1 Câu 108. Cho hàm số y =
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của x + 1 2021
(C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn AB có độ dài bằng √ √ A 3. B 2. C 2 2. D 2 3. GIA 1 7 Câu 109. Cho hàm số y = x4 −
x2 có đồ thị là (C). Có bao nhiêu điểm A thuộc (C) 8 4
sao cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M (x QUỐC 1; y1); N (x2; y2) (M , N
khác A) thỏa mãn y1 − y2 = 3(x1 − x2)? THPT A 0. B 2. C 3. D 1. Câu 110. GHIỆP
Cho hàm số y = ax4 + bx2 + c (a, b, c ∈ R) có đồ thị như hình y N T
vẽ bên. Số điểm cực trị của hàm số đã cho là O x TỐ A 2. B 3. C 0. D 1. THI KỲ Câu 111.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y TỚI G A y = −x4 + x2 − 1. B y = x4 − 3x2 − 1. C y = −x3 − 3x − 1. D y = x3 − 3x − 1. x O HƯỚN
Câu 112. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ −1 0 1 +∞ y0 + 0 − 0 + 0 − −1 − −1 y −∞ −2 − −∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 17 A (−1; 0). B (1; +∞). C (−∞; 1). D (0; 1). √x + 25 − 5
Câu 113. Số tiệm cận đứng của đồ thị hàm số y = là x2 + x A 2. B 0. C 1. D 3.
Câu 114. Giá trị nhỏ nhất của hàm số y = x3 + 3x2 trên đoạn [−4; −1] bằng A −4. B −16. C 0. D 4. THỦ Câu 115. THI
Cho hàm số y = f (x) liên tục trên [−2; 2] và có đồ thị như hình y ĐỀ
vẽ bên. Số nghiệm thực của phương trình 3f (x) − 4 = 0 trên đoạn 3 C Á [−2; 2] là C À A 3. B 1. C 2. D 4. V −2 O 1 GIA x −1 2 −1 QUỐC
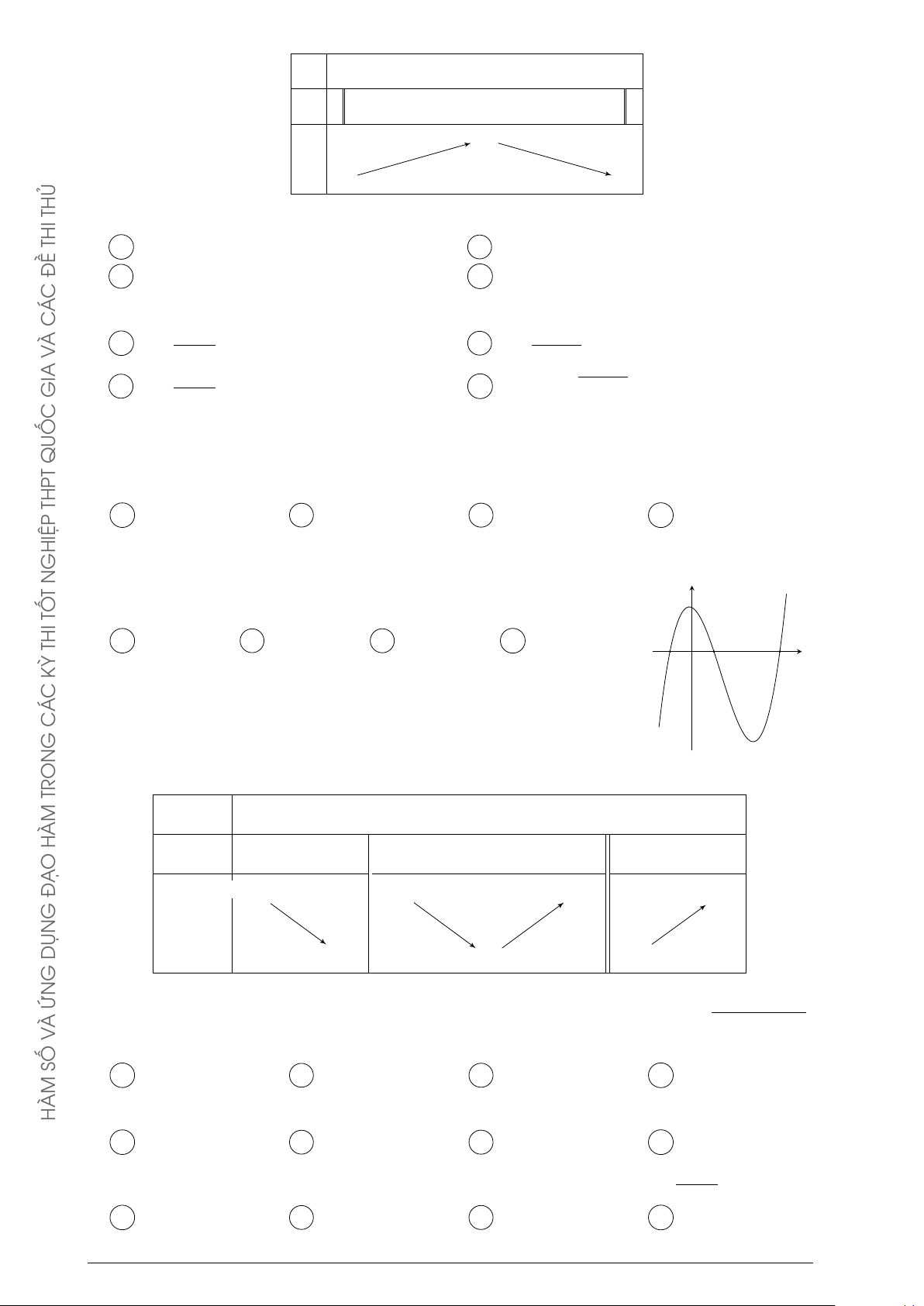
Câu 116. Ông A dự định sử dụng hết 5 m2 kính để làm một bể cá bằng kính có dạng hình
hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không THPT
đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? GHIỆP N A 1,01 m3. B 0,96 m3. C 1,33 m3. D 1,51 m3. T x + 1 TỐ
Câu 117. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = nghịch biến x + 3m THI trên khoảng (6; +∞)? KỲ A 3. B Vô số. C 0. D 6. C Á x − 2 Câu 118. Cho hàm số y =
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của C x + 2 G
(C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng √ √ A 2 2. B 4. C 2. D 2 3. TRON
Câu 119. Cho hai hàm số y = f (x), y = g(x). Hai hàm số y = f 0(x) và y = g0(x) có đồ thị HÀM như hình vẽ bên dưới O y Ạ Đ y = f 0(x) G DỤN 10 G 8 ỨN 5 À 4 V O x SỐ 3 8 1011 HÀM y = g0(x)
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 18
trong đó đường cong đậm hơn là đồ thị của hàm số y = g0(x). Hàm số h(x) = f (x + 3) − Å 7 ã g 2x −
đồng biến trên khoảng nào dưới đây? 2 Å 13 ã Å 29 ã Å 36 ã Å 36 ã A ; 4 . B 7; . C 6; . D ; +∞ . 4 4 5 5
Câu 120. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x8 + (m − 4)x5 −
(m2 − 16)x4 + 1 đạt cực tiểu tại x = 0. A 8. B Vô số. C 7. D 9. 1 14 Câu 121. Cho hàm số y = x4 −
x2 có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao 3 3
cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M (x1; y1), N (x2; y2) (M , N
khác A) thỏa mãn y1 − y2 = 8(x1 − x2)? A 1. B 2. C 0. D 3. Câu 122. 2021
Cho hàm số y = ax4 + bx2 + c (a, b, c ∈ R) có đồ thị như hình vẽ bên. y
Số điểm cực trị của hàm số đã cho là GIA A 0. B 1. C 2. D 3. O x QUỐC Câu 123. THPT
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây? y A y = x3 − 3x2 − 2. B y = x4 − x2 − 2. C y = −x4 + x2 − 2. D y = −x3 + 3x2 − 2. GHIỆP O x N T TỐ
Câu 124. Cho hàm số y = f (x) có bảng biến thiên như sau THI KỲ x −∞ −2 3 +∞ TỚI y0 − 0 + 0 − G +∞ + 4 y HƯỚN 0 −∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A (−2; +∞). B (−2; 3). C (3; +∞). D (−∞; −2). √x + 16 − 4
Câu 125. Số tiệm cận đứng của đồ thị hàm số y = là x2 + x A 0. B 3. C 2. D 1.
Câu 126. Giá trị lớn nhất của hàm số y = x4 − x2 + 13 trên đoạn [−1; 2] bằng 51 A 25. B . C 13. D 85. 4 Câu 127.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 19
Cho hàm số y = f (x) liên tục trên đoạn [−2; 4] và có đồ thị như y 6
hình vẽ bên. Số nghiệm thực của phương trình 3f (x) − 5 = 0 trên đoạn [−2; 4] là A 0. B 3. C 2. D 1. 2 1 −2 2 4 O x THỦ THI −3 ĐỀ x + 2 C
Câu 128. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = đồng biến Á x + 3m C
trên khoảng (−∞; −6) ? À V A 2. B 6. C Vô số. D 1. GIA
Câu 129. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x8 + (m − 3) x5 −
(m2 − 9) x4 + 1 đạt cực tiểu tại x = 0 A 4. B 7. C 6. D Vô số. QUỐC x − 2 Câu 130. Cho hàm số y =
có đồ thị (C). Gọi I là giao điểm của hai tiệm cận của THPT x + 1
(C). Xét tam giác đều ABI có hai đỉnh A, B thuộc (C), đoạn thẳng AB có độ dài bằng √ √ √ √ A 2 3. B 2 2. C 3. D 6. GHIỆP N T 1 7 Câu 131. Cho hàm số y = x4 −
x2 có đồ thị (C). Có bao nhiêu điểm A thuộc (C) sao TỐ 6 3
cho tiếp tuyến của (C) tại A cắt (C) tại hai điểm phân biệt M (x1; y1), N (x2; y2) thỏa mãn THI y1 − y2 = 4 (x1 − x2)? KỲ C A 3. B 0. C 1. D 2. Á C Câu 132. G
Cho hai hàm số y = f (x), y = g (x). Hai hàm số y = y TRON
f 0 (x) và y = g0 (x) có đồ thị như hình vẽ bên, trong đó
đường cong đậm hơn là đồ thị của hàm số y = g0 (x). y = f 0(x) 10 Å ã HÀM 5 8
Hàm số h (x) = f (x + 6) − g 2x + đồng biến trên O 2 5 Ạ 4 khoảng nào dưới đây? Đ Å 21 ã Å 1 ã G A ; +∞ . B ; 1 . 5 4 x O 3 8 1011 Å 21 ã Å 17 ã DỤN C 3; . D 4; . G 5 4 ỨN y = g0(x) À V
Câu 133. Hàm số y = f (x) có bảng biến thiên như sau SỐ x −∞ 0 2 +∞ HÀM y0 − 0 + 0 − +∞ + 5 y 1 −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 20
Giá trị cực đại của hàm số đã cho bằng A 1. B 2. C 0. D 5. Câu 134.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Hàm số y
đồng biến trên khoảng nào dưới đây? A (0; 1). B (−∞; −1). −1 C (−1; 1). D (−1; 0). 1 O x −1 −2 Câu 135.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào y dưới đây? 2021 2x − 1 x + 1 A y = . B y = . x − 1 x − 1 1 GIA C y = x4 + x2 + 1. D y = x3 − 3x − 1. x O 1 QUỐC Câu 136. THPT
Cho hàm số y = f (x) liên tục tên đoạn [−1; 3] có đồ thị như y
hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất, giá trị 3 GHIỆP 2
nhỏ nhất của hàm số đã cho trên đoạn [−1; 3]. Giá trị của N T M − m bằng 1 TỐ A 0. B 1. C 4. D 5. 2 −1 O 3 x THI KỲ −2 TỚI
Câu 137. Cho hàm số f (x) có đạo hàm f 0(x) = x(x − 1)(x + 2)3. Số điểm cực trị của hàm G số đã cho là A 3. B 2. C 5. D 1. HƯỚN
Câu 138. Cho hàm số y = f (x) có bảng biến thiên như sau. x −∞ 1 +∞ y0 + + +∞ 5 y 2 3
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là A 4. B 1. C 3. D 2.
Câu 139. Cho hàm số y = f (x) có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 21 x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + +∞ 1 +∞ y −2 −2 THỦ
Số nghiệm của phương trình 2f (x) + 3 = 0 là THI A 4. B 3. C 2. D 1. ĐỀ
Câu 140. Tập hợp các giá trị thực của tham số m để hàm số y = −x3 − 6x2 + (4m − 9) x + 4 C Á
nghịch biến trên khoảng (−∞; −1) là C ï 3 ã Å 3 ò À A (−∞; 0]. B − ; +∞ . C −∞; − . D [0; +∞). V 4 4 Câu 141. GIA
Cho hàm số y = f (x) liên tục trên R và có đồ thị như hình y
vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để 3 QUỐC
phương trình f (sin x) = m có nghiệm thuộc khoảng (0; π) là THPT 1 A [−1; 3). B (−1; 3). C (−1; 3). D [−1; 1). 1 GHIỆP −1 O x N T −1 TỐ THI
Câu 142. Cho hàm số f (x) có bảng xét dấu của đạo hàm như sau KỲ x −∞ 1 2 3 4 +∞ C Á f 0(x) − 0 + 0 + 0 − 0 + C G
Hàm số y = 3f (x + 2) − x3 + 3x đồng biến trên khoảng nào dưới đây ? A (1; +∞). B (−∞; −1). C (−1; 0). D (0; 2). TRON
Câu 143. Cho hàm số f (x) = mx4 + nx3 + px2 + qx + r (m, n, p, q, r ∈ R). HÀM
Hàm số y = f 0(x) có đồ thị như hình vẽ bên. Tập nghiệm của y O Ạ
phương trình f (x) = r có số phần tử là Đ G A 4. B 3. C 1. D 2. 5 4 x −1 O 3 DỤN G ỨN À y = f 0(x) V SỐ
Câu 144. Cho hàm số có bảng biến thiên như sau: x −∞ −2 0 2 +∞ HÀM y0 − 0 + 0 − 0 + +∞ + 3 +∞ + y 1 1
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 22
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A (−2; 0). B (2; +∞). C (0; 2). D (0; +∞). Câu 145.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong y hình vẽ bên? A y = x3 − 3x2 + 3. B y = −x3 + 3x2 + 3. C y = x4 − 2x2 + 3. D y = −x4 + 2x2 + 3. x O
Câu 146. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ −1 2 +∞ f 0(x) − 0 + 0 − +∞ + 1 2021 f (x) GIA −3 −∞
Hàm số đã cho đạt cực tiểu tại QUỐC A x = 2. B x = 1. C x = −1. D x = −3. THPT
Câu 147. Cho hàm số f (x) có bảng biến thiên như sau: x −∞ −2 0 2 +∞ GHIỆP f 0(x) + 0 − 0 + 0 − N T 3 3 TỐ f (x) −1 THI −∞ −∞ KỲ
Số nghiệm thực của phương trình 2f (x) − 3 = 0 là TỚI G A 2. B 1. C 4. D 3.
Câu 148. Giá trị lớn nhất của hàm số f (x) = x3 − 3x + 2 trên đoạn [−3; 3] là HƯỚN A −16. B 20. C 0. D 4.
Câu 149. Cho hàm số f (x) có đạo hàm f 0(x) = x(x + 2)2, ∀x ∈ R. Số điểm cực trị của hàm số đã cho là A 0. B 3. C 2. D 1.
Câu 150. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ 0 1 +∞ y0 − − 0 + +∞ +∞ 2 y −2 −4
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 23
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là A 4. B 1. C 3. D 2.
Câu 151. Cho hàm số f (x), bảng xét dấu của f 0(x) như sau x −∞ −3 −1 1 +∞ THỦ f 0 − 0 + 0 − 0 + y = f 0(x) THI ĐỀ C
Hàm số y = f (3 − 2x) nghịch biến trên khoảng nào dưới đây? Á C A (4; +∞). B (−2; 1). C (2; 4). D (1; 2). À V Câu 152. GIA
Cho hàm số y = f (x), hàm số y = f 0(x) liên tục trên R và có đồ thị y
như hình vẽ bên. Bất phương trình f (x) < x + m (m là tham số thực) 1 QUỐC
nghiệm đúng với mọi x ∈ (0; 2) khi và chỉ khi A m ≥ f (2) − 2. B m ≥ f (0). 2 THPT O x C m > f (2) − 2. D m > f (0). GHIỆP N Câu 153. T TỐ
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. y 4 THI
Số nghiệm thực của phương trình |f (x3 −3x)| = là 3 KỲ A 3. B 8. C 7. D 4. 2 C Á C −2 2 G x O −1 TRON
Câu 154. Cho hàm số y = f (x), bảng biến thiên của hàm số f 0(x) như sau: HÀM O x −∞ −1 0 1 +∞ Ạ +∞ +∞ Đ 2 G f 0(x) −1 −3 DỤN G ỨN
Số điểm cực trị của hàm số y = f (x2 − 2x) là À V A 9. B 3. C 7. D 5. SỐ x − 3 x − 2 x − 1 x
Câu 155. Cho hai hàm số y = + + +
và y = |x + 2| − x + m (m là x − 2 x − 1 x x + 1 HÀM
tham số thực) có đồ thị lần lượt là (C1) và (C2). Tập hợp tất cả các giá trị của m để (C1)
và (C2) cắt nhau tại đúng bốn điểm phân biệt là A (−∞; 2]. B [2; +∞). C (−∞; 2). D (2; +∞). Câu 156.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 24
Đồ thị của hàm số nào dưới đây có dạng như đường cong y trong hình vẽ bên A y = −x4 + 2x2 + 1. B y = −x3 + 3x + 1. C y = x3 − 3x + 1. D y = x4 − 2x2 + 1. x O
Câu 157. Cho hàm số f (x) có bảng biến thiên như sau: x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + +∞ + 3 +∞ + 2021 y 1 1 GIA
Hàm số đã cho đồng biến trên khoảng nào dưới đây QUỐC A (0; +∞). B (0; 2). C (−2; 0). D (−∞; −2).
Câu 158. Cho hàm số f (x) có bảng biến thiên như sau: THPT x −∞ 1 3 +∞ GHIỆP y0 − 0 + 0 − N T +∞ + 2 TỐ y THI −2 −∞ KỲ
Hàm số đạt cực đại tại TỚI G A x = 2. B x = −2. C x = 3. D x = 1.
Câu 159. Giá trị nhỏ nhất của hàm số f (x) = x3 − 3x + 2 trên đoạn [−3; 3] bằng HƯỚN A 20. B 4. C 0. D −16.
Câu 160. Cho hàm số y = f (x) có đạo hàm f 0(x) = x(x − 2)2, ∀x ∈ R. Số điểm cực trị của hàm số đã cho là A 2. B 1. C 0. D 3.
Câu 161. Cho hàm số f (x) có bảng biến thiên như sau x −∞ −2 0 2 +∞ f 0(x) − 0 + 0 − 0 + +∞ 2 +∞ + f (x) −1 −1
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 25
Số nghiệm thực của phương trình 3f (x) − 5 = 0 là A 2. B 3. C 4. D 0.
Câu 162. Cho hàm số f (x) có bảng biến thiên như sau x −∞ 0 1 +∞ f 0(x) − − 0 + THỦ 0 2 +∞ THI f (x) ĐỀ −∞ −2 − C Á C
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là À V A 3. B 1. C 2. D 4. GIA
Câu 163. Cho hàm số f (x) có bảng dấu f 0(x) như sau x −∞ −3 −1 1 +∞ QUỐC f 0(x) − 0 + 0 − 0 + THPT
Hàm số y = f (5 − 2x) nghịch biến trên khoảng nào dưới đây? A (2; 3). B (0; 2). C (3; 5). D (5; +∞). GHIỆP N T Câu 164. TỐ
Cho hàm số f (x), hàm số y = f 0(x) liên tục trên R và có đồ thị y THI
như hình vẽ. Bất phương trình f (x) > x + m (m là tham số thực) 1 KỲ
nghiệm đúng với mọi x ∈ (0; 2) khi và chỉ khi C x O 2 Á A m ≤ f (2) − 2. B m < f (2) − 2. C C m ≤ f (0). D m < f (0). G Câu 165. TRON
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. Số y 1
nghiệm thực của phương trình |f (x3 − 3x)| = là HÀM 2 O A 6. B 10. C 12. D 3. 2 Ạ Đ G −2 O 2 x −1 DỤN G
Câu 166. Cho hàm số f (x), bảng biến thiên của hàm số f 0(x) như hình vẽ bên dưới ỨN À x −∞ V −1 0 1 +∞ SỐ +∞ + 2 +∞ + f 0(x) HÀM −3 −1
Số điểm cực trị của hàm số y = f (x2 + 2x) là A 3. B 9. C 5. D 7.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 26 x x + 1 x + 2 x + 3
Câu 167. Cho hai hàm số y = + + +
và y = |x + 1| − x + m (m là x + 1 x + 2 x + 3 x + 4
tham số thực) có đồ thị lần lượt là (C1) và (C2). Tập hợp tất cả các giá trị của m để (C1)
và (C2) cắt nhau tại đúng 4 điểm phân biệt là A (3; +∞). B (−∞; 3]. C (−∞; 3). D [3; +∞). Câu 168.
Đồ thị hàm số nào dưới đây có dạng như đường cong trong hình y vẽ bên? A y = x3 − 3x2 − 2. B y = x4 − 2x2 − 2. O x C y = −x3 + 3x2 − 2. D y = −x4 + 2x2 − 2.
Câu 169. Cho hàm số f (x) có bảng biến thiên như sau x −∞ 1 2 +∞ 2021 f 0(x) + 0 − 0 + GIA 3 +∞ + f (x) −∞ −2 QUỐC
Hàm số đạt cực đại tại THPT A x = 2. B x = −2. C x = 3. D x = 1.
Câu 170. Cho hàm số f (x) có bảng biến thiên như sau: GHIỆP N T x −∞ −1 0 1 +∞ TỐ f 0(x) − 0 + 0 − 0 + THI +∞ + 3 +∞ + KỲ f (x) TỚI 0 0 G
Hàm số đã cho đồng biến trên khoảng nào sau đây ? HƯỚN A (−1; 0). B (−1; +∞). C (−∞; −1). D (0; 1).
Câu 171. Cho hàm số f (x) bảng biến thiên như sau: x −∞ −1 2 +∞ f 0(x) − 0 + 0 − +∞ + 2 f (x) −1 −∞
Số nghiệm thực của phương trình 2f (x) − 3 = 0 là A 1. B 2. C 3. D 0.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 27
Câu 172. Giá trị lớn nhất của hàm số f (x) = x3 − 3x trên đoạn [−3; 3] bằng A 18. B 2. C −18. D −2.
Câu 173. Cho hàm số f (x) có đạo hàm f 0(x) = x(x − 1)2, ∀x ∈ R. Số điểm cực trị của hàm số đã cho là A 2. B 0. C 1. D 3. THỦ
Câu 174. Cho hàm số y = f (x) có báng biến thiên như sau: THI x −∞ 0 3 +∞ ĐỀ y0 − + 0 − C Á 2 C 1 3 À V y GIA −∞ −3 −
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là QUỐC A 1. B 2. C 3. D 4. THPT
Câu 175. Cho hàm số f (x), bảng xét dấu của f 0(x) như sau: GHIỆP x −∞ −3 −1 1 +∞ N f 0(x) − T 0 + 0 − 0 + TỐ THI
Hàm số y = f (3 − 2x) đồng biến trên khoảng nào dưới đây? KỲ A (3; 4). B (2; 3). C (−∞; −3). D (0; 2). C Á Câu 176. C
Cho hàm số y = f (x), hàm số y = f 0(x) liên tục trên y G R và có
đồ thị như hình vẽ bên. Bất phương trình f (x) < 2x + m (m y = f (x) 2 TRON
là tham số thực) nghiệm đúng với mọi x ∈ (0; 2) khi và chỉ khi HÀM O −1 1 2 x O Ạ Đ G A m > f (0). B m > f (2) − 4. C m ≥ f (0). D m ≥ f (2) − 4. DỤN Câu 177. G
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ y ỨN
dưới đây. Số nghiệm thực của phương trình |f (x3 − À V 3 3x)| = là 2 2 SỐ A 8. B 4. C 7. D 3. 2 HÀM x −2 O −1
Câu 178. Cho hàm số f (x), bảng biến thiên của hàm số f 0(x) như sau:
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 28 x −∞ −1 0 1 +∞ +∞ + 2 +∞ + f 0(x) −3 −1
Số cực trị của hàm số y = f (4x2 − 4x) là A 9. B 5. C 7. D 3. x − 1 x x + 1 x + 2
Câu 179. Cho hai hàm số y = + + + và y = |x + 2| − x − m (m x x + 1 x + 2 x + 3
là tham số thực) có đồ thị lần lượt là (C1), (C2). Tập hợp tất cả các giá trị của m để (C1)
và (C2) cắt nhau tại đúng bốn điểm phân biệt là A [−2; +∞). B (−∞; −2). C (−2; +∞). D (−∞; −2]. Câu 180. 2021
Đồ thị hàm số nào dưới đây có dạng như đường cong trong y hình vẽ bên? GIA A y = 2x3 − 3x + 1. B y = −2x4 + 4x2 + 1. C y = 2x4 − 4x2 + 1. D y = −2x3 + 3x + 1. QUỐC THPT x O GHIỆP
Câu 181. Cho hàm số y = f (x) có bảng biến thiên như sau: N T x −∞ −1 0 1 +∞ TỐ f 0(x) − 0 + 0 − 0 + THI +∞ 3 +∞ KỲ f (x) TỚI 0 0 G
Hỏi hàm số nghịch biến trên khoảng nào dưới đây? HƯỚN A (0; 1). B (1; +∞). C (−1; 0). D (0; +∞).
Câu 182. Cho hàm số f (x) có bảng biến thiên như sau: x −∞ 1 3 +∞ f 0(x) + 0 − 0 + 2 +∞ f (x) −∞ −2
Hàm số đã cho đạt cực tiểu tại A x = −2. B x = 1. C x = 3. D x = 2.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 29
Câu 183. Giá trị nhỏ nhất của hàm số f (x) = x3 − 3x trên đoạn [−3; 3] bằng A 18. B −18. C −2. D 2.
Câu 184. Cho hàm số y = f (x) có bảng biến thiên như sau: x −∞ 0 3 +∞ f 0(x) − − 0 + THỦ 0 +∞ 3 THI f (x) −4 −3 − ĐỀ C Á
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là C À A 2. B 1. C 3. D 4. V
Câu 185. Cho hàm số f (x) có bảng biến thiên như sau: GIA x −∞ −1 2 +∞ f 0(x) + 0 − 0 + QUỐC 2 +∞ + THPT f (x) −∞ −2 − GHIỆP N T
Số nghiệm thực của phương trình 2f (x) + 3 = 0 là TỐ A 3. B 1. C 2. D 0. THI
Câu 186. Cho hàm số f (x) có đạo hàm f 0(x) = x(x + 1)2, ∀x ∈ R. Số điểm cực trị của KỲ hàm số đã cho là C Á A 0. B 1. C 2. D 3. C G
Câu 187. Cho hàm số f (x), bảng xét dấu của f 0(x) như sau: TRON x −∞ −3 −1 1 +∞ f 0 (x) − 0 + 0 − 0 + HÀM O
Hàm số y = f (5 − 2x) đồng biến trên khoảng nào dưới đây? Ạ Đ A (−∞; −3). B (4; 5). C (3; 4). D (1; 3). G Câu 188. DỤN
Cho hàm số f (x), hàm số y = f 0(x) liên tục trên y G
R và có đồ thị như hình vẽ bên. Bất phương trình y = f 0 (x) ỨN À
f (x) > 2x + m (m là tham số thực) nghiệm đúng với V 2
mọi x ∈ (0; 2) khi và chỉ khi SỐ HÀM x O 2 A m ≤ f (2) − 4. B m ≤ f (0). C m < f (0). D m < f (2) − 4.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 30 Câu 189.
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. Số nghiệm 2 y
thực của phương trình |f (x3 − 3x)| = là 3 A 6. B 10. C 3. D 9. 2 −2 O 2 x −1 x − 2 x − 1 x x + 1
Câu 190. Cho hai hàm số y = + + +
và y = |x + 1| − x − m (m là x − 1 x x + 1 x + 2
tham số thực) có đồ thị lần lượt là (C1) và (C2). Tập hợp tất cả các giá trị của m để (C1)
và (C2) cắt nhau tại đúng bốn điểm phân biệt là A (−3; +∞). B (−∞; −3). C [−3; +∞). D (−∞; −3].
Câu 191. Cho hàm số f (x), bảng biến thiên của hàm số f 0(x) như sau: x −∞ −1 0 1 +∞ 2021 +∞ + 2 +∞ + f 0(x) GIA −3 −1 QUỐC
Số điểm cực trị của hàm số y = f (4x2 + 4x) là THPT A 5. B 9. C 7. D 3.
Câu 192. Cho hàm số f (x) có bảng biến thiên như sau GHIỆP N T x −∞ −1 0 1 +∞ TỐ y0 + 0 − 0 + 0 − 2 2 THI y KỲ −∞ 1 −∞ TỚI G
Hàm số đã cho đồng biến trên khoảng nào dưới đây ? A (1; +∞). B (−1; 0). C (−1 ; 1). D (0 ; 1). HƯỚN
Câu 193. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ 0 3 +∞ y0 + 0 − 0 + 2 +∞ + y −∞ −4
Giá trị cực tiểu của hàm số đã cho bằng A 2. B 3. C 0. D −4.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 31
Câu 194. Đồ thị của hàm số nào sau đây có dạng như hình cong y trong hình bên? A y = −x4 + 2x2. B y = x4 − 2x2. x O C y = x3 − 3x2. D y = −x3 + 3x2. THỦ
Câu 195. Cho hàm số f (x), bảng xét dấu của f 0(x) như sau THI x −∞ −1 0 1 +∞ ĐỀ C f 0(x) + 0 − 0 − 0 + Á C
Số điểm cực trị của hàm số đã cho là À V A 0. B 2. C 1. D 3. GIA
Câu 196. Giá trị lớn nhất của hàm số f (x) = −x4 + 12x2 + 1 trên đoạn [− 1 ; 2] bằng A 1. B 37. C 33. D 12. QUỐC
Câu 197. Cho hàm số f (x) có bảng biến thiên như sau x −∞ 2 3 +∞ THPT y0 + 0 − 0 + 1 +∞ + GHIỆP N T y TỐ −∞ 0 THI KỲ
Số nghiệm thực của phương trình 3f (x) − 2 = 0là C Á A 2. B 0. C 3. D 1. C 5x2 − 4x − 1 G
Câu 198. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = x2 − 1 là TRON A 1. B 0. C 2. D 3. mx − 4 HÀM
Câu 199. Cho hàm số f (x) =
( m là tham số thực). Có bao nhiêu giá trị nguyên O x − m Ạ
của m để hàm số đồng biến trên khoảng (0; +∞)? Đ G A 5. B 4. C 3. D 2.
Câu 200. Gọi S là tập hợp tất cả các giá trị thực của tham số m sao cho giá trị lớn nhất DỤN G
của hàm số f (x) = |x3 − 3x + m| trên đoạn [0; 3] bằng 16. Tổng tất cả các phần tử của S ỨN bằng À V A −16. B 16. C −12. D −2. SỐ
Câu 201. Cho hàm số f (x) có bảng biến thiên như sau x −∞ −1 0 1 +∞ HÀM f 0(x) − 0 + 0 − 0 + +∞ + −1 +∞ + f (x) −2 −2
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 32
Số nghiệm thuộc đoạn [−π ; 2π] của phương trình 2f (sin x) + 3 = 0 là A 4. B 6. C 3. D 8.
Câu 202. Cho hàm số bậc bốn y = f (x) có đồ thị như hình y
bên . Số điểm cực trị của hàm số g(x) = f (x3 + 3x2) là A 5. x O 4 B 3. C 7. D 11.
Câu 203. Cho hàm số f (x). Hàm số y = f 0(x) có đồ thị y
như hình bên. Hàm số g(x) = f (1 − 2x) + x2 − x nghịch 1
biến trên khoảng nào dưới đây? 4 2021 Å 3 ã Å 1 ã x −2 O A 1; . B 0; . 2 2 GIA C (−2; −1). D (2; 3). −2 QUỐC
Câu 204. Cho hàm số f (x) có bảng biến thiên như sau: THPT x −∞ −1 0 1 +∞ GHIỆP y0 + 0 − 0 + 0 − N T 2 2 TỐ y THI −∞ −1 −∞ KỲ TỚI
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? G A (−∞; −1). B (0; 1). C (−1; 0). D (−∞; 0).
Câu 205. Cho hàm số f (x) có bảng biến thiên như sau: HƯỚN x −∞ −1 2 +∞ f 0(x) + 0 − 0 + 1 +∞ f (x) −∞ −2
Hàm số đã cho đạt cực đại tại A x = −2. B x = 2. C x = 1. D x = −1. Câu 206.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 33
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong y hình bên? A y = x3 − 3x. B y = −x3 + 3x. C y = x4 − 2x2. D y = −x4 + 2x2. x O THỦ x − 1
Câu 207. Tiệm cận ngang của đồ thị hàm số y = là THI x + 1 A y = −2. B y = 1. C x = −1. D x = 2. ĐỀ C Á Câu 208. C
Cho hàm số bậc bốn y = f (x) có đồ thị trong hình bên. Số y À V
nghiệm của phương trình f (x) = −1 là 1 GIA A 3. B 1. C 1. D 4. −2 2 x O QUỐC −3 THPT
Câu 209. Cho hàm số f (x) có bảng xét dấu của f 0(x) như sau GHIỆP x −∞ −2 0 2 +∞ N T f 0(x) + 0 − 0 + 0 + TỐ THI
Số điểm cực trị của hàm số đã cho là KỲ A 3. B 0. C 2. D 1. C Á
Câu 210. Giá trị nhỏ nhất của hàm số f (x) = x4 − 10x2 + 2 trên đoạn [−1; 2] bằng C G A 2. B −23. C −22. D −7.
Câu 211. Số giao điểm của đồ thị hàm số y = x3 − 3x + 1 và trục hoành là TRON A 3. B 0. C 2. D 1. HÀM 1
Câu 212. Có bao nhiêu giá trị nguyên của m để hàm số f (x) = x3 + mx2 + 4x + 3 đồng O 3 Ạ biến trên R? Đ G A 5. B 4. C 3. D 2. ax + 1 DỤN
Câu 213. Cho hàm số f (x) =
(a, b, c ∈ R) có bảng biến thiên như sau: bx + c G ỨN x −∞ 2 +∞ À V f 0(x) + + SỐ +∞ 1 f (x) HÀM 1 −∞
Trong các số a, b và c có bao nhiêu số dương? A 2. B 3. C 1. D 0.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 34
Câu 214. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 2 2 f (x) −∞ 0 −∞ ï 5π ò
Số nghiệm thuộc đoạn 0;
của phương trình f (sin x) = 1 là 2 A 7. B 4. C 5. D 6. x + m Câu 215. Cho hàm số y =
(m là tham số thực). Gọi S là tập hợp tất cả các giá trị x + 1
của m sao cho max |f (x)| + min |f (x)| = 2. Số phần tử của S là [0;1] [0;1] A 6. B 2. C 1. D 4.
Câu 216. Đồ thị của hàm số nào dưới đây có dạng đường cong trong hình vẽ? 2021 y GIA QUỐC x O THPT GHIỆP N T A y = x3 − 3x2 + 1. B y = −x3 + 3x2 + 1. TỐ C y = −x4 + 2x2 + 1. D y = x4 − 2x2 + 1. THI
Câu 217. Cho hàm số f (x) có bảng biến thiên như sau: KỲ x −∞ 0 3 +∞ TỚI f 0(x) + G 0 − 0 + 2 +∞ + f (x) HƯỚN −∞ −5 −
Giá trị cực tiểu của hàm số đã cho bằng A 3. B −5. C 0. D 2.
Câu 218. Cho hàm số f (x) có bảng biến thiên như sau: x −∞ −1 0 1 +∞ f 0(x) − 0 + 0 − 0 + +∞ + 4 +∞ + f (x) −1 −1 −
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 35
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A (−∞; −1). B (0; 1). C (−1; 1). D (−1; 0). 4x + 1
Câu 219. Tiệm cận ngang của đồ thị hàm số y = là x − 1 1 A y = . B y = 4. C y = 1. D y = −1. 4 Câu 220. THỦ
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong như hình y THI
vẽ bên. Số nghiệm thực của phương trình f (x) = −1 là ĐỀ 2 C A 3. B 1. C 0. D 2. Á C 1 À x −1 0 V GIA −2
Câu 221. Số giao điểm của đồ thị hàm số y = x3 + 3x2 và đồ thị hàm số y = 3x2 + 3x QUỐC là THPT A 3. B 1. C 2. D 0.
Câu 222. Cho hàm số f (x) liên tục trên R và có bảng xét dấu của f 0(x) như sau: GHIỆP N T x −∞ −1 0 1 2 +∞ TỐ THI f 0(x) + 0 − 0 + − 0 − KỲ C Á C
Số điểm cực đại của hàm số đã cho là G A 4. B 1. C 2. D 3. TRON
Câu 223. Giá trị nhỏ nhất của của hàm số f (x) = x3 − 24x trên đoạn [2; 19] bằng √ √ A 32 2. B −40. C −32 2. D −45. HÀM x + 4 O
Câu 224. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = đồng biến Ạ x + m Đ
trên khoảng (−∞; −7) là G A [4; 7). B (4; 7]. C (4; 7). D (4; +∞). DỤN G
Câu 225. Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: ỨN x −∞ À −1 0 1 +∞ V y0 − 0 + 0 − 0 + SỐ +∞ + 3 +∞ + y HÀM −2 −2
Số điểm cực trị của hàm số g(x) = x4 [f (x + 1)]2 là A 11. B 9. C 7. D 5.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 36 Câu 226.
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có đồ thị là y
đường cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d? A 4. B 1. C 2. D 3. x O
Câu 227. Xét các số thực không âm x và y thỏa mãn 2x + y · 4x+y−1 ≥ 3. Giá trị nhỏ nhất
của biểu thức P = x2 + y2 + 4x + 6y bằng 33 65 49 57 A . B . C . D . 4 8 8 8 Câu 228.
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong y
trong hình bên. Số nghiệm thực phân biệt của phương trình O x f (x3f (x)) + 1 = 0 là −1 2021 A 8. B 5. C 6. D 4. GIA 5x + 1
Câu 229. Tiệm cận ngang của đồ thị hàm số y = là x − 1 1 A y = 1. B y = . C y = −1. D y = 5. QUỐC 5 Câu 230. THPT
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong y
hình bên. Số nghiệm thực của phương trình f (x) = 1 là GHIỆP 3 N A 0. B 3. C 1. D 2. T TỐ THI −1 KỲ O x 1 −1 TỚI G
Câu 231. Cho hàm số f (x) có bảng biến thiên như sau HƯỚN x −∞ −1 0 1 +∞ f 0(x) + 0 − 0 + 0 − 4 4 f (x) −∞ 1 −∞
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A (1; +∞). B (−1; 1). C (0; 1). D (−1; 0).
Câu 232. Cho hàm số f (x) có bảng biến thiên sau
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 37 x −∞ −2 3 +∞ f 0(x) − 0 + 0 − +∞ + 2 f (x) −3 −∞ THỦ
Giá trị cực đại của hàm số đã cho bằng THI A 3. B 2. C −2. D −3. ĐỀ Câu 233. C Á y C
Đồ thị hàm số nào có dạng như đường cong trong hình bên? À A y = −x4 + 2x2. B y = −x3 + 3x. V C y = x4 − 2x2. D y = x3 − 3x. x GIA O QUỐC THPT
Câu 234. Giá trị nhỏ nhất của hàm số f (x) = x3 − 21x trên đoạn [2; 19] bằng √ √ GHIỆP A −36. B −14 7. C 14 7. D −34. N T
Câu 235. Cho hàm số f (x) liên tục trên và có bảng xét dấu của f 0 (x) như sau TỐ THI x −∞ −1 0 1 2 +∞ KỲ C f 0(x) − 0 + 0 − + 0 + Á C G
Số điểm cực tiểu của hàm số đã cho là TRON A 1. B 2. C 3. D 4.
Câu 236. Số giao điểm của đồ thị hàm số y = x3 − x2 và đồ thị hàm số y = −x2 + 5x HÀM O là Ạ Đ A 2. B 3. C 1. D 0. G x + 5
Câu 237. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = đồng biến x + m DỤN
trên khoảng (−∞; −8) là G A (5; +∞). B (5; 8]. C [5; 8). D (5; 8). ỨN À
Câu 238. Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: V SỐ x −∞ −1 0 1 +∞ HÀM f 0(x) + 0 − 0 + 0 − 3 3 f (x) −∞ −1 − −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 38
Số điểm cực trị của hàm số g(x) = x2 [f (x − 1)]4 là A 7. B 8. C 5. D 9. Câu 239.
Cho hàm số y = ax3 + bx2 + cx + d, (a, b, c, d ∈ R) có đồ thị là y
đường cong trong hình vẽ. Có bao nhiêu số dương trong các số a, b, c, d? A 4. B 3. C 1. D 2. O x Câu 240.
Cho hàm số bậc ba y = f (x) có đồ thị là đường y
cong trong hình bên. Số nghiệm thực phân biệt của
phương trình f (x3f (x)) + 1 = 0 là O x A 6. B 4. C 5. D 8. −1 2021 GIA
Câu 241. Cho hàm số f (x) có bảng biến thiên như sau. x −∞ −2 2 +∞ QUỐC y0 − 0 + 0 − THPT +∞ + 3 y GHIỆP −1 − −∞ N T TỐ
Giá trị cực tiểu của hàm số bằng A 2. B −2. C 3. D −1. THI KỲ Câu 242. y TỚI
Cho hàm số bậc ba y = f (x) có đồ thị là đường cong trong hình G
bên. Số nghiệm thực của phương trình f (x) = 1 là 2 A 1. B 0. C 2. D 3. −1 HƯỚN x 1 −2
Câu 243. Cho hàm số f (x) có bảng biến thiên như sau: x −∞ −2 0 2 +∞ y0 + 0 − 0 + 0 − 3 3 y −∞ 2 −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 39
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A (−2; 2). B (0; 2). C (−2; 0). D (2; +∞). 2x + 1
Câu 244. Tiệm cận ngang của đồ thị hàm số y = là: x − 1 1 A y = . B y = −1. C y = 1. D y = 2. 2 Câu 245. THỦ
Đồ thị của hàm số nào dưới đây có dạng như đường cong như hình y THI bên ĐỀ A y = −x4 + 2x2. B y = x3 − 3x2. C x Á C y = x4 − 2x2. D y = −x3 + 3x2. C À
Câu 246. Giá trị nhỏ nhất của hàm số f (x) = x3 − 30x trên đoạn [2; 19] bằng V √ √ A 20 10. B −63. C −20 10. D −52. GIA
Câu 247. Cho hàm số f (x) liên tục trên và có bảng xét dấu của f 0(x) như sau: QUỐC x −∞ −2 1 2 3 +∞ THPT f 0(x − 0 + 0 − 0 + 0 + GHIỆP N
Số điểm cực trị của hàm số đã cho là T TỐ A 2. B 4. C 3. D 1. THI
Câu 248. Số giao điêm của đồ thị hàm số y = x3 + x2 và đồ thị hàm số y = x2 + 5x. KỲ A 3. B 0. C 1. D 2. C Á x + 2 C
Câu 249. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = đồng biến x + m G
trên khoảng(−∞; −5) là A (2; 5]. B [2; 5). C (2; +∞). D (2; 5). TRON
Câu 250. Cho hàm số bậc bốn f (x) có bảng biến thiên như sau: HÀM x −∞ −1 0 1 +∞ O Ạ y0 − 0 + 0 − 0 + Đ +∞ + +∞ + G 3 y DỤN −1 −1 G ỨN
Số điểm cực trị của hàm số g(x) = x4[f (x − 1)]2 là À V A 7. B 5. C 9. D 11. SỐ
Ta có : f (x) = 4x4 − 8x2 + 3 ⇒ f 0(x) = 16x(x2 − 1) HÀM
Ta có g0(x) = 2x3.f (x − 1).[2f (x − 1) + x.f 0(x − 1)]  x3 = 0 
g0(x) = 0 ⇔ f (x − 1) = 0  
2f (x − 1) + x.f 0(x − 1) = 0
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 40
Phương trình x3 = 0 có x = 0 (nghiệm bội ba).
Phương trình f (x − 1) = 0 có cùng số nghiệm với phương trình f (x) = 0 nên (2) có 4 nghiệm đơn.
Phương trình 2f (x − 1) + x · f 0(x − 1) = 0 có cùng số nghiệm với phương trình :
2f (x) + (x + 1) · f 0(x) = 0 ⇔ 2(4x4 − 8x2 + 3) + 16x(x + 1)(x2 − 1) = 0
⇔ 24x4 + 16x3 − 32x2 − 16x + 6 = 0 có 4 nghiệm phân biệt.
Dễ thấy 9 nghiệm trên phân biệt nên hàm số g(x) = 0 có tất cả 9 điểm cực trị.
Câu 251. Xét các số thực không âm x và y thoản mãn 2x + y.4x+y−1 ≥ 3 Giá trị nhỏ nhất
của biểu thức P = x2 + y2 + 2x + 4y bằng 33 9 21 41 A . B . C . D . 8 8 4 8 Câu 252. 2021
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị là đường cong y GIA
trong hình bên. Có bao nhiêu số dương trong các a, b, c, d? A 4. B 2. C 1. D 3. QUỐC x O THPT GHIỆP N Câu 253. T TỐ
Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong y
trong hình bên. Số nghiệm thực phân biệt của phương THI trình f (x2f (x)) + 2 = 0 là KỲ A 8. B 12. C 6. D 9. x O TỚI G −2 HƯỚN Câu 254.
Cho đồ thị hàm số bậc ba y = f (x) có đồ thị là đường cong trong y
hình bên. Số nghiệm thực của phương trình f (x) = 2 là 3 A 0. B 3. C 1. D 2. 1 −1 O x −1 3x + 1
Câu 255. Tiệm cận ngang của đồ thị hàm số y = là x − 1 1 A y = . B y = 3. C y = −1. D y = 1. 3
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 41 Câu 256.
Đồ thị của hàm số nào dưới đây có dạng như đường cong y trong hình bên? x O THỦ A y = x4 − 2x2 + 1. B y = −x3 + 3x2 + 1. THI C y = x3 − 3x2 + 1. D y = −x4 + 2x2 + 1. ĐỀ C
Câu 257. Cho hàm số y = f (x) có bảng biến thiên như sau Á C x −∞ −3 0 3 +∞ À V y0 − 0 + 0 − 0 + GIA +∞ + 1 +∞ + y −1 −1 QUỐC THPT
Hàm số đã cho đồng biến trên khoảng nào dưới đây? A (−3; 0). B (−3; 3). C (0; 3). D (−∞; −3). GHIỆP
Câu 258. Cho hàm số f (x) có bảng biến thiên như sau N T TỐ x −∞ −1 3 +∞ THI y0 + 0 − 0 + KỲ 2 +∞ + C Á y C G −∞ −3 TRON
Giá trị cực đại của hàm số đã cho bằng A 3. B −3. C −1. D 2. HÀM O Ạ
Câu 259. Giá trị nhỏ nhất của hàm số f (x) = x3 − 33x trên đoạn [2; 19] bằng Đ √ √ A −72. B −22 11. C −58. D 22 11. G
Câu 260. Cho hàm số f (x) liên tục trên R và có bảng xét dấu f 0 (x) như sau DỤN G ỨN x −∞ −2 1 2 3 +∞ À V f 0(x) + 0 − 0 + − 0 − SỐ
Số điểm cực đại của hàm số đã cho là HÀM A 3. B 1. C 2. D 4.
Câu 261. Số giao điểm của đồ thị hàm số y = x3 − x2 và đồ thị hàm số y = −x2 + 3x là A 1. B 0. C 2. D 3.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 42 x + 3
Câu 262. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = đồng biến x + m
trên khoảng (−∞, −6) là A (3; 6]. B (3; 6). C (3; +∞). D [3; 6).
Câu 263. Cho hàm số bậc bốn f (x) có bảng biến thiên sau: x −∞ −1 0 1 +∞ y0 + 0 − 0 + 0 − 3 3 y −∞ −2 −∞
Số điểm cực trị của hàm số g (x) = x2 [f (x + 1)]4 là A 7. B 8. C 5. . D 9. Câu 264. 2021
Cho hàm số y = ax3 + bx2 + cx + d (a, b, c,) có đồ thị là đường y GIA
cong trong hình bên. Có bao nhiêu số dương trong các số a, b, c, d? A 4. B 2. C 1. D 3. QUỐC THPT x O GHIỆP Câu 265. N T
Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong y TỐ
hình bên. Số nghiệm thực của phương trình f (x2f (x))−2 = THI 0 là 2 KỲ A 6. B 12. C 8. D 9. TỚI x G O HƯỚN
Câu 266. Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong y 1
hình bên. Số nghiệm thực của phương trình f (x) = − là −1 O 1 2 x A 3. B 4. C 2. D 1. −1 −2 Câu 267.
Cho hàm số y = f (x) có đồ thị là đường cong y
trong hình bên. Hàm số đã cho đồng biến trên khoảng nào dưới 2 đây? 1 A (1; +∞). B (−1; 0). C (0; 1). D (−∞; 0). x −1 O 1
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 43
Câu 268. Cho hàm số f (x) có bảng biến thiên như sau x −∞ −1 3 +∞ f 0(x) − 0 + 0 − +∞ + 2 f (x) −3 − −∞ THỦ
Điểm cực đại của hàm số đã cho là THI A x = 3. B x = −1. C x = 2. D x = −3. ĐỀ C 2x + 2 Á
Câu 269. Tiệm cận đứng của đồ thị hàm số y = là C x − 1 À A x = 2. B x = −2. C x = 1. D x = −1. V Câu 270. GIA
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong y hình bên? QUỐC A y = x4 − 2x2 − 2. B y = −x3 + 3x2 − 2. x O THPT C y = x3 − 3x2 − 2. D y = −x4 + 2x2 − 2. GHIỆP N
Câu 271. Số giao điểm của đồ thị hàm số y = −x3 + 6x với trục hoành là T A 2. B 3. C 1. D 0. TỐ THI
Câu 272. Giá trị nhỏ nhất của hàm số f (x) = x4 − 10x2 − 4 trên đoạn [0; 9] bằng KỲ A −28. B −4. C −13. D −29. C Á C
Câu 273. Cho hàm số f (x) có đạo hàm f 0(x) = x(x − 1)(x + 4)3, ∀x ∈ R. Số điểm cực đại G của hàm số đã cho là A 3. B 4. C 2. D 1. TRON
Câu 274. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x3 − 3x2 + (4 − m)x HÀM
đồng biến trên khoảng (2; +∞) là O Ạ A (−∞; 1]. B (−∞; 4]. C (−∞; 1). D (−∞; 4). Đ G
Câu 275. Cho hàm số f (x) = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có bảng biến thiên như sau DỤN G x −∞ 0 4 +∞ ỨN f 0(x) + 0 − 0 + À V 3 +∞ + SỐ f (x) −∞ −5 HÀM
Có bao nhiêu số dương trong các số a, b, c, d? A 2. B 3. C 1. D 4.
Câu 276. Cho hàm số f (x) có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 44 x −∞ −4 −2 0 +∞ f 0(x) − 0 + 0 − 0 + +∞ +∞ 2 f (x) −2 −3
Có bao nhiêu giá trị nguyên của m để phương trình 5f (x2 − 4x) = m có ít nhất 3 nghiệm
thực phân biệt thuộc khoảng (0; +∞)? A 24. B 21. C 25. D 20. Câu 277.
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình y bên? A y = −x4 + 2x2 − 1. B y = x4 − 2x2 − 1. 2021 C y = x3 − 3x2 − 1. D y = −x3 + 3x2 − 1. O x GIA x − 1
Câu 278. Tiệm cận đứng của đồ thị hàm số y = là x − 3 A x = −3. B x = −1. C x = 1. D x = 3. QUỐC Câu 279. THPT
Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình y 3
bên. Số nghiệm thực của phương trình f (x) = − là 2 GHIỆP A 4. B 1. C 3. D 2. −1 1 N x O T −1 TỐ THI −2 KỲ
Câu 280. Cho hàm số f (x) có bảng biến thiên như sau TỚI x −∞ G −2 1 +∞ f 0(x) − 0 + 0 − +∞ + 3 HƯỚN f (x) −1 −∞
Điểm cực đại của hàm số đã cho là A x = 3. B x = −1. C x = 1. D x = −2. Câu 281.
Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên. y
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? 1 A (−1; 0). B (−∞; −1). C (0; 1). D (0; +∞). x −1 O 1
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 45
Câu 282. Cho hàm số f (x) có đạo hàm f 0(x) = x(x − 1)(x + 4)3, ∀x ∈ R. Số điểm cực tiểu của hàm số đã cho là A 2. B 3. C 4. D 1.
Câu 283. Giá trị nhỏ nhất của hàm số f (x) = x4 − 12x2 − 4 trên đoạn [0; 9] bằng A −39. B −40. C −36. D −4. THỦ
Câu 284. Số giao điểm của đồ thị hàm số y = −x3 + 7x với trục hoành là THI A 0. B 3. C 2. D 1. ĐỀ
Câu 285. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x3 − 3x2 + (5 − m)x C Á
đồng biến trên khoảng (2; +∞) là C À A (−∞; 2). B (−∞; 5). C (−∞; 5]. D (−∞; 2]. V
Câu 286. Cho hàm số f (x) = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có bảng biến thiên như sau GIA x −∞ −2 0 +∞ y0 + 0 − 0 + QUỐC 2 +∞ + THPT y −∞ 1 GHIỆP N T
Có bao nhiêu số dương trong các số a, b, c, d? TỐ A 2. B 4. C 1. D 3. THI KỲ Câu 287. C
Cho hàm số f (x) có f (0) = 0. Biết y = f 0(x) là hàm số y Á C
bậc bốn và có đồ thị là đường cong trong hình bên. Số G
điểm cực trị của hàm số g(x) = |f (x3) + x| là A 4. B 5. C 3. D 6. TRON x O y = f 0(x) HÀM
Câu 288. Cho hàm số f (x) có bảng biến thiên như sau O Ạ Đ x −∞ −4 −2 0 +∞ G f 0(x) − 0 + 0 − 0 + DỤN +∞ +∞ G 2 ỨN f (x) − À 2 V −3 SỐ
Có bao nhiêu giá trị nguyên của tham số m để phương trình 6f (x2 − 4x) = m có ít nhất 3 HÀM
nghiệm thực phân biệt thuộc khoảng (0; +∞)? A 25. B 30. C 29. D 24. 2x − 2
Câu 289. Tiệm cận đứng của đồ thị hàm số y = là x + 1 A x = −2. B x = 1. C x = −1. D x = 2.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 46
Câu 290. Cho hàm số f (x) có bảng biến thiên như sau x −∞ −1 2 +∞ f 0(x) + 0 − 0 + 3 +∞ + f (x) −∞ −2 −
Điểm cực đại của hàm số đã cho là A x = 3. B x = 2. C x = −2. D x = −1.
Câu 291. Cho hàm số y = f (x) có đồ thị là đường cong như hình bên.
Hàm số đã cho đồng biến trên khoảng nào dưới đây? y A (−1; 0). B (−∞; −1). C (0; +∞). D (0; 1). 2021 −1 O 1 x GIA −1
Câu 292. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? QUỐC A y = x3 − 3x + 1. B y = x4 − 2x2 + 1. y C y = −x4 + 2x2 + 1. D y = −x3 + 3x + 1. THPT GHIỆP x N T O TỐ THI Câu 293. KỲ
Cho hàm số bậc bốn có đồ thị là đường cong trong hình y TỚI 1
bên. Số nghiệm thực của phương trình f (x) = là 2 G 2 A 2. B 4. C 1. D 3. HƯỚN 1 x −1 O 1
Câu 294. Số giao điểm của y = −x3 + 3x với trục hoành là A 2. B 0. C 3. D 1.
Câu 295. Giá trị nhỏ nhất của hàm số f (x) = x4 − 10x2 − 2 trên đoạn [0; 9] bằng A −2. B −11. C −26. D −27.
Câu 296. Cho hàm số f (x) có đạo hàm f 0(x) = x(x + 1)(x − 4)3, ∀x ∈ R. Số điểm cực đại của hàm số đã cho là A 2. B 3. C 4. D 1.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 47
Câu 297. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x3 − 3x2 + (2 − m)x
đồng biến trên khoảng (2; +∞) là A (−∞; −1]. B (−∞; 2). C (−∞; −1). D (−∞; 2].
Câu 298. Cho hàm số f (x) = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có bảng biến thiên như sau THỦ x −∞ −2 0 +∞ THI f 0(x) + 0 − 0 + ĐỀ 1 +∞ + C Á f (x) C À −∞ −1 V GIA
Có bao nhiêu số dương trong các số a, b, c, d? A 3. B 4. C 2. D 1. QUỐC Câu 299. THPT
Cho hàm số f (x) có f (0) = 0. Biết y = f 0(x) là hàm số y y = f 0(x)
bậc bốn và có đồ thị là đường cong trong hình bên. Số GHIỆP
điểm cực trị của hàm số g(x) = |f (x4) − x2| là N T A 4. B 3. C 6. D 5. TỐ THI O x KỲ C Á
Câu 300. Xét các số thực x, y thỏa mãn 2x2+y2+1 ≤ (x2 + y2 − 2x + 2)4x. Giá trị nhỏ nhất C 8x + 4 của biểu thức P =
gần nhất với số nào dưới đây? G 2x − y + 1 A 1. B 2. C 3. D 4. TRON
Câu 301. Cho hàm số f (x) có bảng biến thiên như sau: HÀM O x −∞ −4 −2 0 +∞ Ạ Đ f 0(x) − 0 + 0 − 0 + G +∞ + 2 +∞ + f (x) DỤN G −2 −3 ỨN À V
Có bao nhiêu giá trị nguyên của tham số m để phương trình 3f (x2 − 4x) = m có ít nhất 3 SỐ
nghiệm thực phân biệt thuộc khoảng (0; +∞)? A 15. B 12. C 14. D 13. HÀM x + 1
Câu 302. Tiệm cận đứng của đồ thị hàm số y = là x + 3 A x = −1. B x = 1. C x = −3. D x = 3. Câu 303.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 48
Cho hàm số y = f (x) có đồ thị là đường cong trong hình bên. y
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A (1; +∞). B (0; 1). C (−1; 0). D (−∞; 0). −1 1 x O −1 −2
Câu 304. Cho hàm số f (x) có bảng biến thiên như sau: x −∞ −2 3 +∞ f 0(x) + 0 − 0 + 1 +∞ + f (x) −∞ −3 − 2021
Điểm cực đại của hàm số đã cho là GIA A x = −2. B x = −3. C x = 1. D x = 3. Câu 305. QUỐC
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong y THPT hình bên? A y = x4 + 2x2. B y = −x3 − 3x. C y = x3 − 3x. D y = −x4 + 2x2. GHIỆP x N O T TỐ THI Câu 306. KỲ
Cho hàm số bậc bốn y = f (x) có đồ thị là đường cong trong hình bên. Số y 1 1 TỚI
nghiệm thực của phương trình f (x) = là 2 G A 4. B 2. C 3. D 1. x −1 O 1 HƯỚN
Câu 307. Số giao điểm của đồ thị hàm số y = −x3 + 5x với trục hoành là A 3. B 2. C 0. D 1.
Câu 308. Giá trị nhỏ nhất của hàm số f (x) = x4 − 12x2 − 1 trên đoạn [0; 9] bằng A −28. B −1. C −36. D −37.
Câu 309. Cho hàm số f (x) có đạo hàm f 0(x) = x(x + 1)(x − 4)3, ∀x ∈ R. Số điểm cực tiểu của hàm số đã cho là A 4. B 3. C 1. D 2.
Câu 310. Tập hợp tất cả các giá trị thực của tham số m để hàm số y = x3 − 3x2 + (1 − m)x
đồng biến trên khoảng (2; +∞) là A (−∞; −2). B (−∞; 1). C (−∞; −2]. D (−∞; 1].
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 49 Câu 311.
Cho hàm số f (x) có f (0) = 0. Biết y = f 0(x) là hàm số bậc bốn và y
có đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số O x g(x) = |f (x4) + x2| là A 3. B 6. C 5. D 4. THỦ THI
Câu 312. Cho hàm số y = ax3 + bx2 + cx + d (a, b, c, d ∈ R) có bảng biến thiên như sau: ĐỀ C x −∞ 0 4 +∞ Á C y0 + 0 − 0 + À V −1 +∞ + y GIA −∞ −5 − QUỐC
Có bao nhiêu số dương trong các số a, b, c, d? A 4. B 2. C 3. D 1. THPT
Câu 313. Cho hàm số f (x) có bảng biến thiên như sau: GHIỆP N x −∞ −4 −2 0 +∞ T f 0(x) − 0 + 0 − 0 + TỐ +∞ +∞ THI 2 KỲ f (x) C Á −2 C −3 G
Có bao nhiêu giá trị nguyên của tham số m để phương trình 4f (x2 − 4x) = m có ít nhất 3 TRON
nghiệm thực phân biệt thuộc khoảng (0; +∞)? HÀM A 16. B 19. C 20. D 17. O Ạ Đ G DỤN G ỨN À V SỐ HÀM
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 50 PHẦN II
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC ĐỀ THI THỬ 2017-2020
Câu 1. Hàm số y = 2x4 + 1 đồng biến trên khoảng nào trong các khoảng dưới đây? Å 1 ã Å 1 ã A (0; +∞). B − ; +∞ . C −∞; − . D (−∞; 0). 2 2
Câu 2. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số y = x4+2mx2+1
có ba điểm cực trị tạo thành tam giác vuông cân. √ A m = − 3 3. B m = −1. √ √ C m = −1; m = 3 3. D m = − 3 3; m = 1. x − 2 Câu 3. Cho hàm số y =
có đồ thị (C). Tìm tọa độ giao điểm I của hai đường tiệm x + 2 2021 cận của đồ thị (C). A I (−2; 2). B I (−2; −2). C I (2; 1). D I (−2; 1). GIA √ Câu 4. Xét hàm số y =
4 − 3x trên đoạn [−1; 1]. Mệnh đề nào sau đây đúng?
A Hàm số có cực trị trên khoảng (−1; 1). QUỐC
B Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn [−1; 1]. THPT
C Hàm số đồng biến trên đoạn [−1; 1].
D Hàm số đạt giá trị nhỏ nhất tại x = 1 và đạt giá trị lớn nhất tại x = −1. GHIỆP
Câu 5. Đồ thị của hàm số y = x3 − 3x2 − 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới N T
đây thuộc đường thẳng AB ? TỐ A M (1; −10). B N (−10; 1). C P (1; 0). D Q(0; −1). THI
Câu 6. Phát biểu nào sau đây là đúng? KỲ
A Hàm số y = f (x) đạt cực trị tại x0 khi và chỉ khi x0 là nghiệm của đạo hàm. TỚI
B Nếu f 0 (x0) = 0 và f 00 (x0) > 0 thì hàm số đạt cực đại tại x0. G
C Nếu f 0 (x0) = 0 và f 00 (x0) = 0 thì x0 không phải là cực trị của hàm số y = f (x) đã cho. HƯỚN
D Nếu f 0(x) đổi dấu khi x qua điểm x0 và f (x) liên tục tại x0 thì hàm số y = f (x) đạt cực trị tại điểm x0 . √ √
Câu 7. Tìm tập giá trị T của hàm số y = x − 3 + 5 − x √ √ î ó î ó A T = 0; 2 . B T = [3; 5]. C T = 2; 2 . D T = (3; 5).
Câu 8. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau. x −∞ 0 1 +∞ y0 + − 0 + 0 +∞ + y −∞ −1 −
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 51
Tìm tất cả các giá trị thực của tham số m để phương trình f (|x|) = 2m + 1 có bốn nghiệm phân biệt? 1 1 1 1 A − ≤ m ≤ 0. B − < m < 0. C −1 < m < − . D −1 ≤ m ≤ − . 2 2 2 2 Câu 9.
Đường cong trong hình bên là đồ thị của một hàm số trong y
bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới 3 THỦ
đây. Hỏi hàm số đó là hàm số nào ? THI ĐỀ C 1 Á C −2 1 À x −1 O 2 V GIA −1 A y = x4 − x2 + 1. B y = −x3 + 3x + 1. C y = x3 − 3x + 1. D y = −x2 + x − 1. QUỐC
Câu 10. Tìm giá trị lớn nhất của hàm số y = 1 − 2 cos x − cos2 x . THPT A 2. B 3. C 0. D 5.
Câu 11. Tìm tất cả các giá trị thực của m đế đường thẳng d : y = −2x + m cắt đồ thị hàm GHIỆP N
số (H) : y = 2x+3 tại hai điểm A, B phân biệt sao cho P = k2018 + k2018 đạt giá trị nhỏ nhất x+2 1 2 T
(với k1, k2 là hệ số góc của tiếp tuyến tại A, B) TỐ A m = −3. B m = −2. C m = 2. D m = 3. THI KỲ
Câu 12. Trong bốn hàm số sau:(1)y = sin 2x; (2)y = cos 4x; (3)y = tan 2x; (4)y = cot 3x có C
mấy hàm số tuần hoàn với chu kỳ π ? Á 2 C A 0. B 2. C 3. D 1. G Câu 13. TRON
Đường cong trong hình bên là đồ thị của một hàm số nào sau đây? y x + 2 x + 2 A y = . B y = . x − 1 x − 2 HÀM 2 x − 2 x − 2 O C y = . D y = . 1 Ạ x − 1 x + 1 Đ x O 1 2 G DỤN
Câu 14. Đường cong y = x3 − 5x cắt đường thẳng y = −2x − 2 lần lượt tại hai điểm phân G # » ỨN
biệt A, B có hoành độ tăng dần. Tọa độ của AB là À A (3; −6). B (−3; 6). C (−3; −6). D (3; 6). V SỐ
Câu 15. Cho hàm số y = f (x) có bảng biến thiên như bên dưới. Phát biểu nào đúng? x −∞ −2 0 2 +∞ HÀM y0 + 0 − 0 + 0 − 2 4 y −∞ 1 −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 52
A Hàm số đạt cực đại tại x = 2.
B Hàm số đạt cực đại tại x = 4.
C Hàm số có ba cực tiểu.
D Hàm số có giá trị cực tiểu là 0.
Câu 16. Cho hàm số y = f (x) có đạo hàm f 0(x) = x(x − 1)(x + 2)3, ∀x ∈ R. Số điểm cực
trị của hàm số đã cho là A 3. B 5. C 1. D 2. 1 − x
Câu 17. Số đường tiệm cận của đồ thị hàm số y = là 2x − 1 A 2. B 1. C 4. D 3.
Câu 18. Hàm số y = x3 − 3x2 + 2 nghịch biến trên khoảng nào trong các khoảng sau đây? A (2; +∞). B (−∞; 0). C (−∞; +∞). D (0; 2). √x + 3
Câu 19. Điểm nào trong các điểm sau đây không thuộc đồ thị hàm số y = ? x2 + 1 2021 Å 1 ã √ Ä ä A N −2; . B Q(1; 1). C M (1; 2). D P 0; 3 . 5 GIA
Câu 20. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên sau. QUỐC x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + THPT +∞ + 0 +∞ + y GHIỆP N −1 −1 − T TỐ
Tìm tất cả các giá trị của tham số m để phương trình f (x) − 1 = m có đúng hai nghiệm. THI A −2 < m < −1. B m > 0; m = −1. KỲ C m = −2; m > −1. D m = −2; m ≥ −1. TỚI G
Câu 21. Tập hợp tất cả các giá trị của tham số m để hàm số: y = −x3 − 6x2 + (4m − 9)x + 4
nghịch biến trên khoảng (−∞; −1) là ï ã Å ò HƯỚN 3 3 A − ; +∞ . B −∞; − . C (−∞; 0]. D [0; +∞). 4 4
Câu 22. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số y =
|x3 − 3x2 + 3m2 − m3| có 5 điểm cực trị. Tìm số phần tử của S. A 0. B 3. C 1. D 2.
Câu 23. Cho phương trình x4 − 3x3 − (2m − 1)x2 − 3x + 1 = 0. Điều kiện của m để phương a
trình có bốn nghiệm phân biệt là m ∈
; +∞ . Trong đó a, b là các số nguyên dương và b
a, b nguyên tố cùng nhau. Giá trị của biểu thức a + b là A 12. B 9. C 10. D 11. Câu 24.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 53
Cho hàm số f (x) có đạo hàm liên tục trên R và có f (1) = 1, y 1
f (−1) = − . Đặt g(x) = f 2(x) − 4f (x). Cho biết đồ thị của 3
y = f 0(x) có dạng như hình vẽ dưới đây. 1
A Hàm số g(x) có giá trị lớn nhất và không có giá trị nhỏ nhất trên x R. -1 O 1
B Hàm số g(x) có giá trị nhỏ nhất và không có giá trị lớn THỦ nhất trên R. THI
C Hàm số g(x) có giá trị lớn nhất và giá trị nhỏ nhất trên ĐỀ R. C Á
D Hàm số g(x) không có giá trị lớn nhất và không có giá C À trị nhỏ nhất trên R. V
Câu 25. Cho hàm số y = f (x) có bảng biến thiên như sau: GIA x −∞ 0 2 +∞ QUỐC y0 + 0 − 0 + +∞ + THPT 3 y GHIỆP N −∞ 1 T TỐ
Hàm số đã cho đạt cực đại tại giá trị nào của x? THI A 2. B 1. C 0. D 3. KỲ C
Câu 26. Hàm số y = x3 − 3x + 1 nghịch biến trên khoảng nào dưới đây? Á C A (0; 2). B (1; +∞). C (∞; −1). D (−1; 1). G
Câu 27. Tìm giá trị lớn nhất của hàm số y = x3 − 2x2 − 4x + 5 trên đoạn [1; 3]. TRON A −3. B 0. C 2. D 3.
Câu 28. Tìm tập hợp tất cả các giá trị của tham số m để hàm số y = x3 −mx2 −(m−6)x+1 HÀM
đồng biến trên khoảng (0; 4). O Ạ A (−∞; 6]. B (−∞; 3). C (−∞; 3]. D [3; 6]. Đ √ G x + x − 1
Câu 29. Đồ thị hàm số y = √
có bao nhiêu tiệm cận ngang? x2 + 1 DỤN A 2. B 1. C 3. D 0. G ỨN
Câu 30. Cho hàm số y = f (x) có bảng biến thiên như sau: À V x −∞ 0 2 +∞ SỐ y0 − + 0 − HÀM +∞ + 2 y −1 −∞ −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 54
Tìm tập hợp tất cả giá trị của tham số m để phương trình f (x) + m = 0 có ba nghiệm phân biệt. A (−2; 1). B [−1; 2). C (−1; 2). D (−2; 1]. Câu 31.
Một bức tường cao 2 m nằm song song với tòa nhà
và cách tòa nhà 2 m. Người ta muốn chế tạo một
cái thang bắc từ mặt đất bên ngoài bức tường, gác
qua bức tường và chạm vào tòa nhà (hình vẽ). Hỏi Tòa nhà
chiều dài tối thiểu của thang là bao nhiêu mét? √ 5 13 √ A m. B 4 2 m. 3 √ 2m C 6 m. D 3 5 m. 2m
Câu 32. Cho hàm số f (x) = x3 − 3x2 + m. Hỏi có bao nhiêu giá trị nguyên của m (m < 10)
để với mọi bộ ba số thực phân biệt a, b, c ∈ [1; 3] thì f (a), f (b), f (c) là ba cạnh của một tam 2021 giác? GIA A 4. B 3. C 1. D 2. x2 − mx
Câu 33. Với tham số m, đồ thị của hàm số y =
có hai điểm cực trị A, B và x + 1 QUỐC
AB = 5. Mệnh đề nào dưới đây đúng? A m > 2. B 0 < m < 1. C 1 < m < 2. D m < 0. THPT
Câu 34. Có bao nhiêu số nguyên dương m sao cho đường thẳng y = x + m cắt đồ thị hàm 2x − 1 số y =
tại hai điểm phân biệt A, B và AB ≤ 4? GHIỆP x + 1 N T A 7. B 6. C 1. D 2. TỐ
Câu 35 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1Y1-2] THI
Cho hàm số y = f (x) có đồ thị như hình vẽ. Hàm số đã cho đồng biến y KỲ
trong khoảng nào dưới đây? 1 1 x TỚI A (1; +∞). B (0; 1). C (−3; 1). D (−2; 0). −1 O G −3 HƯỚN
Câu 36 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-7]
Cho hàm số f (x) liên tục trên đoạn [−3; 2] và có đồ thị như hình y
vẽ bên. Gọi M , m lần lượt là giá trị lớn nhất và nhỏ nhất của 3
hàm số đã cho trên đoạn [−3; 2]. Giá trị của M − m là 1 A 4. B 3. C 5. D 0. −3 1 x O 2 −1 −2
Câu 37 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-4] Số giao điểm của đồ thị hàm số
y = x3 − 3x + 3 và đường thẳng y = x.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 55 A 2. B 3. C 1. D 0.
Câu 38 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B4-1] Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ −2 0 +∞ THỦ y0 + − THI +∞ 1 y ĐỀ C −∞ 0 Á C À V
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận? GIA A 4. B 2. C 1. D 3.
Câu 39 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B2-1] Biết đồ thị hàm số y = x3 − 3x + 1 QUỐC
có hai điểm cực trị A, B. Khi đó phương trình đường thẳng AB là THPT A y = 2x − 1. B y = x − 2. C y = −x + 2. D y = −2x + 1.
Câu 40 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1K1-1] Cho hàm số y = f (x) có đạo hàm GHIỆP N
f 0(x) = x2(x2 − 1), ∀x ∈ R. Hàm số y = 2f (−x) đồng biến trên khoảng nào. T A (−∞; −1). B (−1; 1). C (0; 2). D (2; +∞). TỐ THI
Câu 41 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-1] KỲ
Đường cong ở hình vẽ bên là đồ thị của hàm số nào dưới y C Á đây? C G A y = x3 − 3x2 − 1. B y = −x3 + 3x + 1. x + 1 x − 1 C y = . D y = . 1 TRON x − 1 x + 1 O x 1 HÀM O Ạ Đ G mx + 2
Câu 42 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1K1-3] Cho hàm số y = , m là DỤN 2x + m G
tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số nghịch ỨN
biến trên khoảng (0; 1). Số phần tử của S bằng À V A 1. B 5. C 2. D 3. SỐ
Câu 43 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1K1-3] Tất cả các giá trị thực của tham HÀM
số m để hàm số y = 2x3 + x2 − mx + 2m − 1 nghịch biến trên đoạn [−1; 1] là 1 1 A m ≥ − . B m ≤ 8. C m ≥ 8. D m ≤ − . 6 6
Câu 44 (Đề ôn 10 - Mức 7-8). [Phan Anh][2D1B5-4] Cho hàm số y = f (x) liên tục trên
R và có bảng biến thiên như hình sau:
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 56 x −∞ −2 0 2 +∞ y0 − 0 + 0 − 0 + +∞ + 1 +∞ + y −2 −2 −
Số nghiệm thực của phương trình 4f 2(x) − 9 = 0 là: A 4. B 6. C 3. D 2. x − 3
Câu 45. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y = . 3x − 2 1 2 2 1 A x = . B x = . C y = . D y = . 3 3 3 3 2021 Câu 46. GIA
Cho hàm số y = f (x) có đồ thị trên một khoảng K như y
hình vẽ bên. Trên K, hàm số có bao nhiêu cực trị? QUỐC A 3. B 2. C 0. D 1. THPT O x GHIỆP N T TỐ THI
Câu 47. Cho hàm số f (x) có đạo hàm trên khoảng (a; b). Trong các mệnh đề sau, mệnh đề KỲ nào sai? TỚI
A Nếu f 0(x) < 0 với mọi x thuộc (a; b) thì hàm số f (x) nghịch biến trên (a; b). G
B Nếu hàm số f (x) đồng biến trên (a; b) thì f 0(x) > 0 với mọi x thuộc (a; b).
C Nếu hàm số f (x) đồng biến trên (a; b) thì f 0(x) ≥ 0 với mọi x thuộc (a; b). HƯỚN
D Nếu f 0(x) > 0 với mọi x thuộc (a; b) thì hàm số f (x) đồng biến trên (a; b).
Câu 48. Hàm số f (x) = x3 + ax2 + bx + c đạt cực tiểu tại điểm x = 1, f (1) = −3 và đồ thị
hàm số cắt trục tung tại điểm có tung độ bằng 2. Tính T = a + b + c. A T = 9. B T = 1. C T = −2. D T = −4. x2 + 1
Câu 49. Đồ thị hàm số y =
có tất cả bao nhiêu đường tiệm cận? x2 − 4 A 0. B 1. C 2. D 3. Câu 50.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 57
Cho hàm số y = f (x) có đồ thị như hình vẽ dưới đây. y
Tìm tất cả các giá trị của tham số thực m để phương trình
f (x) + m = 0 có đúng 3 nghiệm thực phân biệt. A m < 3. B m = −3. C −4 < m < −3. D m = 3. −1 O 1 x THỦ THI −3 ĐỀ C Á −4 C À V
Câu 51. Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó? A y = x − sin2 x. B y = cot x. C y = sin x. D y = −x3. GIA m2 + 3m
Câu 52. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = 3x + x + 1 QUỐC
đồng biến trên từng khoảng xác định của nó? A 4. B 2. C 1. D 3. THPT Câu 53. GHIỆP
Cho hàm số y = f (x). Hàm số y = f 0(x) có đồ thị trên một y N T
khoảng K như hình vẽ bên. Trong các khẳng định sau, có f 0(x) TỐ
tất cả bao nhiêu khẳng định đúng? THI
(I). Trên K, hàm số y = f (x) có hai điểm cực trị. x1 x2 x3 KỲ
(II). Hàm số y = f (x) đạt cực đại tại x x O 3. C Á
(III). Hàm số y = f (x) đạt cực tiểu tại x1. C G A 3. B 0. C 1. D 2.
Câu 54. Tìm giá trị nhỏ nhất của hàm số f (x) = cos2 2x − sin x cos x + 4 trên R. TRON 7 10 16 A min f (x) = . B min f (x) = 3. C min f (x) = . D min f (x) = . x∈R 2 x∈R x∈R 3 x∈R 5 HÀM
Câu 55. Tập hợp tất cả các giá trị của tham số thực m để phương trình O √ √ √ Ạ m 1 + x +
1 − x + 3 + 2 1 − x2 − 5 = 0 có đúng hai nghiệm thực phân biệt là một Đ 5 G
nửa khoảng (a; b]. Tính b − a, √ 7 √ √ √ 6 − 5 2 6 − 5 2 12 − 5 2 12 − 5 2 DỤN A . B . C . D . G 35 7 35 7 ỨN Câu 56. À V
Cho hàm số y = f (x) xác định và liên tục x −∞ 0 2 +∞ trên SỐ
R có bảng biến thiên như hình bên. Hàm y0 − 0 + 0 −
số y = f (x) đồng biến trên khoảng nào sau +∞ + 4 HÀM đây? y A (−∞; 0). B (0; 2). 0 −∞ C (0; 4). D (2; +∞). 2x + 1
Câu 57. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số y = ? x − 1
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 58 1 A y = 2. B y = −1. C x = 1. D x = − . 2
Câu 58. Cho hàm số có bảng biến thiên như sau x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + +∞ + −3 − +∞ + y −4 − −4 −
Hàm số đạt cực đại tại điểm A x = 1. B x = −3. C x = −1. D x = 0. 3x + 1
Câu 59. Gọi m là giá trị nhỏ nhất của hàm số y =
trên [−1; 1]. Khi đó, giá trị của x − 2 m là 2021 2 2 A m = −4. B m = . C m = 4. D m = − . 3 3 GIA 1
Câu 60. Tọa độ điểm cực đại của đồ thị hàm số y = x4 − 3x2 + 2 là 2 Å√ 5 ã Å √ 5 ã A 3; − . B − 3; − . C (0; 2). D (2; 0). QUỐC 2 2 Câu 61. THPT
Đồ thị sau đây là của hàm số nào? y x + 1 2x + 1 5 A y = . B y = . x − 1 x − 1 4 GHIỆP x + 2 2x − 1 N C y = . D y = . 3 T 1 − x x − 1 2 TỐ 1 THI −3 −2 O 2 3 x KỲ − −1 1 1 − TỚI 2 G
Câu 62. Có bao nhiêu giá trị nguyên âm a để đồ thị hàm số y = x3 + (a + 10)x2 − x + 1
cắt trục hoành tại đúng một điểm? HƯỚN A 10. B 8. C 9. D 11. Câu 63.
Cho hàm số y = f (x) có bảng biến thiên như x −∞ −2 0 +∞
hình bên. Khi đó tất cả các giá trị của m để y0 + 0 − 0 +
phương trình f (x) = m − 1 có ba nghiệm 5 +∞ + thực phân biệt là y A m ∈ [4; 6]. −∞ 3 B m ∈ (3; 5).
C m ∈ (−∞; 3) ∪ (5; +∞). D m ∈ (4; 6).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 59 2x − 2 Câu 64. Cho hàm số y =
có đồ thị (C), M là điểm thuộc (C) sao cho tiếp tuyến x − 2 √
của (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm A, B thỏa mãn AB = 2 5. Gọi
S là tổng các hoành độ của tất cả các điểm M thỏa mãn bài toán. Giá trị của S bằng A 8. B 5. C 7. D 6.
Câu 65. Cho hàm số y = x3 − 3x2 + mx + 1 có đồ thị là (Cm). Tìm m sao cho (Cm) có hai THỦ
điểm cực trị có hoành độ x1, x2 thỏa mãn x3 + x3 = 5. 1 2 √ 3 3 4 THI A m = 3 2. B m = − . C m = . D m = − . 2 2 3 ĐỀ x + 1 C
Câu 66. Đường tiệm cận đứng của đồ thị hàm số y = là Á x − 2 C A y = 2. B x = 2. C y = 1. D x = 1. À V
Câu 67. Số điểm cực trị của hàm số f (x) = −x4 + 2x2 − 3 là GIA A 0. B 2. C 3. D 1. Câu 68. QUỐC
Đường cong trong hình sau là đồ thị của hàm số nào? y A y = −x4 + 2x2 + 3. B y = x4 + 2x2 − 3. -1 1 x THPT O C y = x4 − 2x2 − 3. D y = −x4 − 2x2 + 3. GHIỆP N T -3 TỐ THI √x2 + 3 KỲ
Câu 69. Số đường tiệm cận của đồ thị hàm số y = là 2x − 1 C Á A 3. B 0. C 2. D 1. C G
Câu 70. Cho hàm số y = −2x3 + 6x2 − 5 có đồ thị (C). Phương trình tiếp tuyến của (C)
tại điểm M thuộc (C) và có hoành độ bằng 3 là TRON A y = 18x + 49. B y = −18x − 49. C y = −18x + 49. D y = 18x − 49. √ HÀM
Câu 71. Giá trị lớn nhất của hàm số y = −x2 + 2x là O √ Ạ A 0. B 1. C 2. D 3. Đ G
Câu 72. Hàm số nào sau đây đồng biến trên R? x − 1 A y = −x3 − x − 2. B y = . DỤN x + 3 G C y = x4 + 2x2 + 3. D y = x3 + x2 + 2x + 1. ỨN 2x + 1 À Câu 73. Cho hàm số y =
có đồ thị (C). Tìm các giá trị của tham số m để đường V x + 1 √
thẳng d : y = x + m − 1 cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho AB = 2 3. SỐ √ √ √ √ A m = 4 ± 3. B m = 2 ± 3. C m = 4 ± 10. D m = 2 ± 10. HÀM 2x + 1 Câu 74. Cho hàm số y =
có đồ thị (C). Viết phương trình tiếp tuyến của (C), biết x + 2
tiếp tuyến song song với đường thẳng ∆ : 3x − y + 2 = 0. A y = 3x − 8. B y = 3x + 14. C y = 3x + 5, y = 3x − 8. D y = 3x + 14, y = 3x + 2.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 60 Câu 75.
Từ kho hàng hóa A dọc theo đường sắt AB cần phải xây một D
kho trung chuyển tại điểm C và xây dựng một con đường từ C α
đến D. Biết rằng vận tốc trên đường sắt là v1 và trên đường bộ A C B
là v2 (v1 > v2). Tìm điều kiện của cos α để điểm C được chọn là
địa điểm sao cho thời gian chuyển hàng hóa từ A đến D qua C
là nhanh nhất (góc α như hình vẽ). √ v1 v1 + v2 2 v2 A cos α = . B cos α = . C cos α = . D cos α = . v2 2 2 v1
Câu 76. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m cắt đồ thị của
hàm số y = x4 − 2x2 − 3 tại bốn điểm phân biệt. A m > −1. B −1 < m < 1. C m < −4. D −4 < m < −3.
Câu 77. Khoảng nghịch biến của hàm số y = x3 + 3x2 + 4 là A (−∞; 0).
B (−∞; −2) và (0; +∞). 2021 C (2; +∞). D (−2; 0). GIA
Câu 78. Cho bảng biến thiên của hàm số y = f (x) như hình vẽ bên dưới. Đồ thị hàm số
đã cho có tổng số bao nhiêu đường tiệm cận đứng và tiệm cận ngang? √ QUỐC x −∞ 2 +∞ 6 +∞ THPT y 2 3 GHIỆP N T A 1. B 2. C 0. D 3. TỐ x − 2
Câu 79. Cho đồ thị của hàm số y =
là một trong bốn đường cong được liệt kê trong THI x + 1 KỲ
bốn phương án dưới đây. Hỏi đồ thị đó là hình nào? y y TỚI 2 G 1 O 1 2 x O 2 x HƯỚN −2 A . B . y y 1 1 O −1 O 2 x 1 2 x −2 C . D .
Câu 80. Phương trình tiếp tuyến của đồ thị hàm số y = x4 − 2x2 − 3 tại giao điểm của đồ
thị hàm số với trục tung là A y = 2x + 3. B y = 3. C y = 2x − 3. D y = −3.
Câu 81. Bảng biến thiên trong hình dưới là bảng biến thiên của hàm số nào dưới đây?
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 61 x −∞ −1 +∞ y0 + 0 + +∞ + y −∞ THỦ THI 1 A y = x4 − 2x2 + 2. B y = − x3 + x2 − x − 1. 3 ĐỀ 1 1 C C y = x3 + x2 + x − 1. D y = x3 + x2 − x − 1. Á 3 3 C À
Câu 82. Hàm số nào trong các hàm số sau đồng biến trên tập xác định? V 2 − 3x A y = . B y = x4 + 3x2 + 18. GIA 1 + 5x C y = x3 + 2x2 − 7x + 1. D y = x3 + 3x2 + 9x − 20. QUỐC
Câu 83. Cho các đường cong (C1) : y = x3 − 3x2 + 4, (C2) : y = −x4 + x2 − 3 và (C3) : y =
5x + 2 . Hỏi các đường cong nào có tâm đối xứng? THPT x − 1 A (C1), (C2) và (C3). B (C1) và (C3). GHIỆP C (C2) và (C3). D (C1) và (C2). N T √ TỐ
Câu 84. Cho hàm số y = f (x) = sin x + cos2 x . Tính giá trị S = 7(1 + min y)2 + THI 16 max2 y. 25 √ √ KỲ A S = . B S = 25. C S = 4 7 + 25. D 25 − 4 7. C 16 Á C x − m G
Câu 85. Tìm tất cả các giá trị thực của m để hàm số y = nghịch biến trên (m − 1)x − 2 (−∞; 1). TRON A m ∈ (−1; 2). B m ∈ (−1; 3]. C m ∈ [1; 2). D m ∈ (1; 2]. HÀM Câu 86. O Ạ y Đ
Cho đường cong trong hình bên là đồ thị của hàm số y = G
f (x). Hỏi có bao nhiêu điểm trên đường tròn lượng giác biểu 1
diễn nghiệm của phương trình f (f (cos 2x)) = 0? DỤN G A 3 điểm. B 4 điểm. C 2 điểm. D 1 điểm. x −1 O 1 ỨN À V SỐ
Câu 87. Gọi M là tập tất cả các giá trị nguyên của m để hàm số y = x4 +2(m2 −16)x2 +m2
có ba cực trị. Lấy ngẫu nhiên một giá trị m thuộc tập M . Tính xác suất P với m lấy được HÀM
để hàm số có 3 cực trị lập thành một tam giác có diện tích lớn hơn hoặc bằng 3. 3 5 5 A P = . B P = . C P = . D P = 1. 7 7 9 Câu 88.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 62
Cho hàm số y = f (x) liên tục trên R, có f (−2) < 0 và đồ y
thị hàm số f 0(x) như hình vẽ bên. Khẳng định nào sau đây là khẳng định sai? x
A Hàm số y = |f (1 − x2018)| nghịch biến trên khoảng −2 O 2 (−∞; −2).
B Hàm số y = |f (1 − x2018)| có hai cực tiểu.
C Hàm số y = |f (1 − x2018)| có hai cực đại và một cực tiểu.
D Hàm số y = |f (1 − x2018)| đồng biến trên khoảng (2; +∞).
Câu 89. Cho hàm số y = x3 − 6x2 + 9x − 2 có đồ thị (C). Đường thẳng đi qua điểm A(−1; 1)
và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) là 1 3 −1 3 A y = x + 3 . B y = x + . C y = x + . D x − 2y − 3 = 0 . 2 2 2 2 2021
Câu 90. Bác Tôm có một cái ao có diện tích 50 m2 để nuôi cá. Vụ vừa qua bác nuôi với GIA
mật độ 20 con/m2 và thu được tất cả 1,5 tấn cá thành phẩm. Theo kinh nghiệm nuôi cá thu
được, bác thấy cứ thả giảm đi 8 con/m2 thì tương ứng sẽ có mỗi con cá thành phẩm thu QUỐC
được tăng thêm 0,5 kg. Hỏi vụ tới bác phải mua bao nhiêu con cá giống để đạt được tổng
khối lượng cá thành phẩm cao nhất? (Giả sử không có hao hụt trong quá trình nuôi). THPT A 1100 con. B 1000 con. C 500 con. D 512 con. GHIỆP Câu 91. N T
Cho hàm số f (x) có bảng biến thiên như hình x −2 −1 0 2 TỐ
vẽ bên. Khẳng định nào dưới đây đúng? f 0(x) + 0 − + THI A
min f (x) = −2; max f (x) = −1 . x∈[−2;2] x∈[−2;2] 4 11 f (x) KỲ B min f (x) = 3; max f (x) = 4 . 3 3 x∈[−2;2] x∈[−2;2] TỚI C
min f (x) = −2; max f (x) = 2 . G x∈[−2;2] x∈[−2;2] D
min f (x) = 3; max f (x) = 11 . x∈[−2;2] x∈[−2;2] HƯỚN Câu 92.
Hàm số y = f (x) có đồ thị y = f 0(x) như
hình vẽ (đồ thị f 0(x) cắt Ox ở các điểm y
có hoành độ lần lượt là 1, 2, 5, 6). Chọn khẳng định đúng: 1 2 5 6 x O
A f (x) nghịch biến trên khoảng (1; 2).
B f (x) đồng biến trên khoảng (5; 6).
C f (x) nghịch biến trên khoảng (1; 5).
D f (x) đồng biến trên khoảng (4; 5). Câu 93.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 63
Cho hàm số y = f (x) có đồ thị y = f 0(x) trên R như y
hình vẽ (trên R thì đồ thị y = f 0(x) là một nét liền
và chỉ có 4 điểm chung với Ox tại các điểm có hoành
độ lần lượt là −1, 1, 2, 4). Đặt g(x) = f (1 − x). Chọn −1 1 2 4 x khẳng định đúng: O
A g(x) đồng biến trên (−3; 0). THỦ
B g(x) đồng biến trên (−4; −3). THI
C g(x) nghịch biến trên (−1; 0). ĐỀ
D g(x) đồng biến trên (−4; −3) và (0; 2). C Á Câu 94. C ax + b À Cho hàm số y =
có đồ thị như hình vẽ. y V cx + d Chọn khẳng định đúng. GIA
A Hàm số nghịch biến trên từng khoảng xác định. QUỐC
B Hàm số đồng biến trên từng khoảng xác 1 định. O x THPT
C Hàm số đồng biến trên tập xác định. −1
D Hàm số đồng biến trên R. GHIỆP N T TỐ THI Câu 95. KỲ
Cho hàm số f (x) liên tục trên x −∞ − C 2 2 +∞ Á
[−2; 2] và có bảng biến thiên như C y0 − − − G
hình vẽ. Chọn khẳng định đúng về 0 +∞ +∞
tổng số các tiệm cận đứng và tiệm y TRON
cận ngang của đồ thị f (x). −∞ −∞ −∞ A HÀM
Đồ thị hàm số có đúng 4 tiệm O Ạ cận. Đ G B
Đồ thị hàm số có đúng 2 tiệm DỤN G cận. ỨN C À V
Đồ thị hàm số có đúng 1 tiệm cận. SỐ D HÀM
Đồ thị hàm số có đúng 3 tiệm cận. 1 mx2
Câu 96. Tìm tất cả các giá trị m để hàm số y = x3 −
+ 2x + 2017 đồng biến trên 3 2 R.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 64 √ √ √ A −2 2 6 m 6 2 2 . B −2 2 6 m . √ √ √ C m 6 2 2 . D −2 2 < m < 2 2 .
Câu 97. Tìm tất cả các giá trị của tham số m để phương trình −x4 + 2x2 + 3 + 2m = 0 có 4 nghiệm phân biệt. −3 −3 −3 A −2 6 m 6 . B < m < 2. C −2 < m < . D 3 < m < 4. 2 2 2
Câu 98. Đồ thị hàm số nào sau đây không có tiệm cận ngang? √ 2x − 1 A y = x2 − 1. B y = . x + 1 x2 − 3x + 2 √ C y = . D y = x − x2 + 1. x2 − x − 2
Câu 99. Độ giảm huyết áp của một bệnh nhân được cho bởi công thức f (x) = 0,025x2(30 −
x), trong đó x (miligam) là liều lượng thuốc được tiêm cho bệnh nhân. Khi đó liều lượng
thuốc được tiêm cho bệnh nhân để huyết áp giảm nhiều nhất là A 20 miligam. B 10 miligam. C 15 miligam. D 30 miligam. 2021 2x − 3
Câu 100. Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = tương x + 1 GIA ứng có phương trình là A x = 2 và y = 1. B x = −1 và y = 2. QUỐC C x = 1 và y = −3. D x = 1 và y = 2.
Câu 101. Tổng hoành độ các giao điểm của đồ thị hàm số y = x3 − 3x2 + 3 và đường thẳng THPT y = x là A 3. B 2. C 4. D 0. GHIỆP N T Câu 102. TỐ
Đường cong bên là hình biểu diễn của đồ thị hàm số nào sau y 4 THI đây? KỲ A y = −x4 + 4x2 + 3. B y = x4 − 2x2 + 3. C y = −x3 + 3x + 3. D y = −x4 + 2x2 + 3. TỚI G −1 1 x O HƯỚN Câu 103.
Cho hàm số y = f (x) xác định, liên tục trên R x −∞ 0 1 +∞
và có bảng biến thiên như hình vẽ. Hàm số đã y0 + − 0 +
cho nghịch biến trên khoảng nào sau đây? 2 +∞ + A (−3; 2). y B (−∞; 0) và (1; +∞). −∞ −3 C (−∞; −3). D (0; 1).
Câu 104. Có bao nhiêu số nguyên m để hàm số y = x3 − 3x2 − mx + 4 có hai điểm cực trị thuộc khoảng (−3; 3). A 12. B 11. C 13. D 10.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 65 Câu 105.
Cho hàm số y = f (x) có đồ thị như hình vẽ bên. Có bao nhiêu giá trị y
nguyên của tham số m để phương trình f (x) = m có 3 nghiệm phân biệt. 1 x A 0. B 3. C 1. D 2. O 1 THỦ −2 THI Câu 106. ĐỀ
Cho hàm số y = f (x) có đạo hàm trên C R x −∞ −2 1 3 +∞ Á
và có bảng xét dấu f 0(x) như hình bên. C À
Hỏi hàm số y = f (x2 − 2x) có bao nhiêu f 0(x) − 0 + 0 + 0 − V điểm cực tiểu? GIA A 1. B 2. C 3. D 4. QUỐC
Câu 107. Tìm giá trị của tham số m để đồ thị hàm số y = x4 − 2(m + 1)x2 + 2m + 3 có
ba điểm cực trị A, B, C sao cho trục hoành chia tam giác ABC thành một tam giác và một THPT
hình thang, biết rằng tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC 4 bằng . GHIỆP 9 √ √ √ √ N 1 + 15 −1 + 3 5 + 3 −1 + 15 T A m = . B m = . C m = . D m = . TỐ 2 2 2 2 2x THI Câu 108. Cho hàm số y =
có đồ thị (C) và điểm A(0; a). Gọi S là tập hợp tất cả x + 1 KỲ
các giá trị thực của a để từ A kẻ được hai tiếp tuyến AM , AN đến (C) với M , N là các tiếp C Á
điểm và M N = 4. Tổng các phần tử của S bằng bao nhiêu? C G A 4. B 3. C 6. D 1. TRON
Câu 109. Hàm số nào sau đây không có GTLN, GTNN trên [−2; 2]? x − 1 A y = . B y = x2. C y = −x + 1. D y = x3 + 2. x + 1 HÀM O Câu 110. Ạ Đ
Cho hàm số y = f (x) có bảng biến G x −∞ 0 1 +∞
thiên như hình vẽ bên. Hàm số y = DỤN
f (x) đồng biến trên khoảng nào dưới y0 + 0 − 0 + G đây? 3 +∞ + ỨN À A (1; +∞). B (0; 1). y V C (−∞; 3). D (−4; +∞). −∞ −4 − SỐ ax + 1 Câu 111. Cho hàm số y =
. Tìm a và b để đồ thị hàm số nhận đường thẳng x = 1 HÀM bx − 2 1
là tiệm cận đứng và đường thẳng y = là tiệm cận ngang. 2 A a = 1, b = 2. B a = 2, b = 2. C a = 2, b = −2. D a = −1, b = −2. Câu 112.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 66
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới y
đây. Hàm số đó là hàm số nào? 3 A y = −x3 − 3x + 1. B y = −x3 + 3x + 1. C y = x3 + 3x + 1. D y = x3 − 3x + 1. 1 1 x 0 −1 −1
Câu 113. Tìm tất cả các giá trị thực của tham số m để hàm số f (x) = −x3 + 2(2m − 1)x2 −
(m2 − 8)x + 2 đạt giá trị cực tiểu tại điểm x = −1. A m = −2. B m = 3. C m = 1. D m = −9. 2x − 1 Câu 114. Cho hàm số y =
có đồ thị (C) và đường thẳng d : y = 2x − 3. Đường x + 1
thẳng d cắt đồ thị (C) tại hai điểm A và B. Tính khoảng cách giữa hai điểm A và B. √ √ 2 5 5 5 2 5 A AB = . B AB = . C AB = . D AB = . 5 2 5 2
Câu 115. Tìm số giá trị nguyên của tham số m ∈ [0; 30] để phương trình x4 − 6x3 + mx2 − 2021 12x + 4 = 0 có nghiệm. A 17. B 16. C 15. D 14. GIA Câu 116.
Cho hàm số y = f (x). Biết hàm số y = f 0(x) y QUỐC
có đồ thị như hình vẽ bên. Hàm số y = f (3 − THPT
x2) + 2018 đồng biến trong khoảng nào dưới x đây? −6 −1 0 2 A (2; 3). B (−2; −1). GHIỆP N C (0; 1). D (−1; 0). T TỐ
Câu 117. Cho đường cong (C) : y = x4 − 4x2 + 2 và điểm A(0; a). Nếu qua A kẻ được 4
tiếp tuyến với (C) thì a phải thỏa mãn điều kiện THI Å 10 ã A a ∈ 2; . B a ∈ (2; +∞). KỲ 3 Å 10 ã Å 10 ã TỚI C a ∈ (−∞; 2) ∪ ; +∞ . D a ∈ −∞; . 3 3 G
Câu 118. Tìm tất cả các giá trị của tham số m để hàm số y = |x3 + 3x2 − 3 + m| có ba điểm cực trị. HƯỚN A m = 3 hoặc m = −1. B m ≤ −3 hoặc m ≥ 1. C m ≤ −1 hoặc m ≥ 3. D 1 ≤ m ≤ 3.
Câu 119. Hàm số nào sau đây đồng biến trên R? A y = x4 + x. B y = x4 − x. C y = (x − 1)2018. D y = (x − 1)2019. x + 1 Câu 120. Cho hàm số y =
(C). Hỏi trên đồ thị (C) về phía bên phải trục tung có x
bao nhiêu điểm mà tại đó ta dựng được tiếp tuyến cắt hai trục tọa độ tạo thành tam giác cân. A Vô số. B 2. C 1. D 0.
Câu 121. Cho hàm số y = x3 − 3x + 2. Tọa độ điểm cực tiểu của đồ thị hàm số là A B(−1; 4). B D(2; 4). C C(0; 2). D A(1; 0).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 67
Câu 122. Gọi M, n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x3 − 3x2
trên đoạn [−2; 1]. Tính giá trị của T = M + m. A T = −20. B T = −22. C T = −4. D T = 2. Câu 123.
Đường cong trong hình bên là đồ thị của một trong bốn hàm y THỦ
số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi 2
hàm số đó là hàm số nào? THI A y = −x4 + 1. B y = −|x|3 + 3|x| + 1. ĐỀ C C y = −x4 − 2x2 + 1. D y = −x4 + 2x2 + 1. O Á C x −1 1 À V GIA x + m
Câu 124. Biết rằng hàm số y =
đồng biến trên các khoảng (−∞; 2) và (2; +∞) và x − 2 QUỐC
tiếp tuyến của đồ thị tại điểm x0 = 1 cắt hai trục tọa độ tạo thành một tam giác vuông cân.
Tìm giá trị của tham số m. THPT A m = −3. B m = −4. C m = −5. D m = 0. 2 √ √ √ Câu 125. Phương trình m + x − x2 = x +
1 − x. Gọi S là tập hợp tất cả các giá trị GHIỆP 3 N T
nguyên của tham số m để phương trình có nghiệm duy nhất. Tìm số phần tử của S. TỐ A 3. B 2. C 1. D 0. THI x + 1
Câu 126. Đồ thị hàm số y = có tâm đối xứng I là KỲ x − 2 C A I(−2; 1). B I(2; 1). C I(2; −1). D I(−2; −1). Á C G
Câu 127. Biết rằng đồ thị hàm số y = x3 − 3x2 + m có điểm uốn nằm trên đường thẳng
y = x. Tìm giá trị của tham số m. TRON A m = 1. B m = −1. C m = 3. D m = 2. HÀM
Câu 128. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3 − 3mx2 + O
3 (m2 − 1) x + 1 − m2 có hai điểm phân biệt đối xứng nhau qua gốc tọa độ O. Ạ Đ A 0 < m < 1.
B 0 ≤ m < 1 hoặc m ≤ −1. G C m < −1.
D 0 < m < 1 hoặc m < −1. DỤN G
Câu 129. Đồ thị hàm số y = (x − 1) (x2 − 1) (x3 − 1) cắt trục hoành tại mấy điểm phân ỨN biệt? À V A 3. B 1. C 2. D 4. SỐ
Câu 130. Hàm số y = f (x) có bảng biến thiên như sau HÀM x −∞ 0 2 +∞ f 0(x) − 0 + 0 − +∞ + 5 f (x) 1 −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 68
Hàm số y = f (x) đồng biến trên khoảng nào dưới đây? A (1; 5). B (0; 2). C (2; +∞). D (−∞; 0).
Câu 131. Giá trị nhỏ nhất của hàm số y = x3 − 3x + 1 trên đoạn [−2; 0] bằng A 1. B −2. C −1. D 3. x + 2
Câu 132. Đồ thị hàm số y =
có đường tiệm cận ngang là x − 1 A y = 2. B y = −2. C x = 1. D y = 1.
Câu 133. Hàm số y = f (x) có bảng biến thiên như sau √ √ x −∞ − 2 0 2 +∞ f 0(x) + 0 − 0 + 0 − 1 1 f (x) −∞ −3 −∞ 2021 GIA
Hàm số đạt cực tiểu tại điểm √ A x = 1. B x = −3. C x = 0. D x = ± 2. Câu 134. QUỐC
Đường cong như hình bên là đồ thị của hàm số nào dưới đây? y THPT A y = −x4 + 3x2 − 2. B y = x4 − 2x2 − 2. O x GHIỆP C y = −x3 + 3x2 − 2. N T D y = x3 + 3x2 + 1. TỐ 1 Câu 135. Cho hàm số y =
(m2 − 1)x3 + (m + 1)x2 + 3x + 5 với m là tham số thực. Có THI 3
bao nhiêu giá trị nguyên của m để hàm số có hai điểm cực trị? KỲ A 3. B 0. C 2. D 1. TỚI G Câu 136.
Cho hàm số y = f (x), biết hàm số y = f 0(x) có đồ thị như hình y
vẽ dưới đây. Hàm số y = f (x) đạt giá trị nhỏ nhất trên đoạn HƯỚN ï 1 3 ò ; tại điểm nào sau đây? 2 2 3 1 A x = . B x = . 2 2 C x = 1. D x = 0. x O 1 3 2
Câu 137. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau x −∞ 1 +∞ y0 − 0 +
Hàm số g = f (x2) nghịch biến trên khoảng A (0; 1). B (1; +∞). C (−1; 0). D (−∞; 0).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 69 Câu 138.
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình bên. y
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây? A (−∞; −1). B (−1; 1). −1 1 C (−∞; 0). D (0; +∞). O x −1 THỦ −2 THI ĐỀ Câu 139. C Á C
Cho hàm số y = f (x) liên tục x −∞ 1 3 +∞ À V
trên R có bảng biến thiên dưới
đây. Mệnh đề nào sau đây là y0 + 0 − 0 + GIA đúng? 2 +∞ + A y QUỐC
Hàm số đạt cực đại tại x = 2. −∞ −4 THPT B
Hàm số đạt cực tiểu tại GHIỆP N x = −4. T TỐ C THI
Hàm số đạt cực đại tại KỲ x = 1. C D Á C
Hàm số đạt cực đại tại G x = 0. TRON x − 1
Câu 140. Đồ thị hàm số y =
có bao nhiêu đường tiệm cận? 2x − 1 HÀM A 0. B 1. C 2. D 3. O Ạ Đ Câu 141. G
Cho hàm số y = f (x) có đồ thị như hình bên. Khi đó y = f (x) y DỤN là hàm số nào sau đây? G 2 A y = x3 − 3x. B y = −x3 + 3x. ỨN 1 À C y = x3 + x2 − 4. D y = x3 − 3x + 1. V SỐ −2 −1 O x − 1 2 1 HÀM −2
Câu 142. Cho hàm số y = f (x) xác định trên tập D = R \ {−1}, liên tục trên mỗi khoảng
xác định và có bảng biến thiên như sau:
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 70 x −∞ −4 −1 2 +∞ y0 + 0 − − 0 + 0 +∞ +∞ + y −∞ −∞ 4
Tìm tập hợp tất cả các giá trị của tham số m sao cho phương trình f (x) = m − 1 có hai nghiệm thực phân biệt.  m < 1 A  B 1 < m < 5. C m < 1. D m > 5. m > 5.
Câu 143. Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số f (x) = 2x3 +3x2 −1 ï 1 ò trên đoạn −2; −
. Khi đó giá trị của M − m bằng 2 A −5. B 1. C 4. D 5. 2021
Câu 144. Cho hàm số y = −x2 + 5 có đồ thị (C). Phương trình tiếp tuyến của (C) tại điểm GIA
M có tung độ y0 = −1, với hoành độ x0 < 0 là kết quả nào sau đây? √ √ √ √ Ä ä Ä ä A y = 2 6 x + 6 − 1. B y = −2 6 x + 6 − 1. √ √ √ √ Ä ä Ä ä C y = 2 6 x − 6 + 1. D y = 2 6 x − 6 − 1. QUỐC
Câu 145. Cho hàm số y = ax3 + bx2 + cx + d đồng biến trên R khi THPT   a = b; c > 0 a = b = c = 0 A  . B  . b2 − 3ac ≤ 0 a > 0; b2 − 3ac < 0 GHIỆP   N a = b = 0; c > 0 a = b = 0; c > 0 T C  . D  . TỐ a > 0; b2 − 3ac ≤ 0 a > 0; b2 − 3ac ≥ 0 THI
Câu 146. Đồ thị hàm số y = ax3 + bx2 + cx + d có hai điểm cực trị A(1; −7), B(2; −8). KỲ Tính y(−1). TỚI A y(−1) = 7. B y(−1) = 11. C y(−1) = −11. D y(−1) = −35. G Câu 147.
Cho hàm số y = f (x) có đạo hàm và liên tục trên y R, có đồ thị 4 HƯỚN
y = f 0(x) như hình vẽ bên. Tìm số điểm cực trị của hàm số
y = f (x − 2009) + 2017x − 2018. 2 A 1. B 2. C 3. D 4. x −2 −1 O 1 x + 5 Câu 148. Cho hàm số y =
. Mệnh đề nào sau đây là đúng? x + 2
A Hàm số nghịch biến trên mỗi khoảng (−∞; −2) và (−2; +∞).
B Hàm số đồng biến trên mỗi khoảng (−∞; −2) và (−2; +∞).
C Hàm số nghịch biến trên khoảng (−∞; 5).
D Hàm số nghịch biến trên R \ {−2}.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 71
Câu 149. Cho hàm số y = x3 − 3x có giá trị cực đại và cực tiểu lần lượt là y1, y2. Khi đó: A y1 − y2 = −4. B 2y1 − y2 = 6. C 2y1 − y2 = −6. D y1 + y2 = 4. Câu 150.
Đồ thị như hình vẽ là đồ thị của hàm số nào sau đây? 3 y A y = −x3 − x2 + 1. B y = −2x3 − 3x2 + 1. 2 3 THỦ C y = 2x3 + 3x2 + 1. D y = x3 + x2 + 1. 2 2 THI ĐỀ C Á x −1 C À V GIA x + 4
Câu 151. Đồ thị hàm số y = √
có tất cả bao nhiêu đường tiệm cận đứng và tiệm x2 − 4 cận ngang? QUỐC A 3. B 1. C 2. D 4. THPT Câu 152. Tìm a, b để hàm số y =
ax + b có đồ thị như hình vẽ y x + 1 GHIỆP bên. N T A TỐ a = −1, b = −2. THI B −1 1 1 KỲ x a = 1, b = −2. O C Á C C −2 G a = −2, b = 1. D TRON a = 2, b = 1. HÀM O Ạ
Câu 153. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ Đ G x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + DỤN +∞ + +∞ + G 5 y ỨN À 3 3 V SỐ
Tìm m để phương trình f (x) = 2 − 3m có bốn nghiệm phân biệt. 1 1 HÀM
A m < −1 hoặc m > − . B −1 < m < − . 3 3 1 C m = − . D m 6 −1. 3
Câu 154. Tìm m để hàm số y = x4 − 2mx2 + 2m + m4 − 5 đạt cực tiểu tại x = −1. A m = −1. B m 6= 1. C m = 1. D m 6= −1.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 72 Câu 155.
Đồ thị hàm số y = ax3 + bx2 + cx + d có đồ y
thị như hình vẽ bên. Mệnh đề nào sau đây đúng.
A a < 0; b > 0; c > 0; d > 0.
B a < 0; b < 0; c < 0; d > 0.
C a < 0; b < 0; c > 0; d > 0. 2
D a < 0; b > 0; c < 0; d > 0. x −1 O 2 3
Câu 156. Cho các số thực dương x, y thỏa mãn x2 − xy + 3 = 0 và 2x + 3y 6 14. Gọi M ,
m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 3x2y − xy2 − 2x(x2 − 1).
Tính giá trị của T = 2M − m. 2021 A 4. B 0. C 12. D 3. GIA Câu 157.
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị cắt trục tung tại điểm y
có tung độ −3; hoành độ điểm cực đại là 2 và đi qua điểm (1; −1) QUỐC a như hình vẽ. Tỷ số bằng b 1 1 x THPT O 2 -1 GHIỆP N T -3 TỐ A −1. B 1. C −3. D 3. THI 2x + 1
Câu 158. Biết hai đường tiệm cận của đồ thị hàm số y = (m là tham số thực) KỲ x − m
tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng 2. Giá trị của m bằng bao TỚI nhiêu? G A m = ±1. B m = ±2. C m = 2. D m = 1. 2 HƯỚN Câu 159. Cho hàm số y =
x3 + (m + 1)x2 + (m2 + 4m + 3)x − 3, (m là tham số thực). 3
Tìm điều kiện của m để hàm số có cực đại cực tiểu và các điểm cực trị của đồ thị hàm số
nằm bên phải của trục tung.  m > −1 A −5 < m < −1. B −5 < m < −3. C −3 < m < −1. D  . m < −5 √x2 − 4
Câu 160. Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2x2 − 5x + 2 là A 2. B 1. C 3. D 4. x + 1
Câu 161. Cho các hàm số y =
, y = x4 + 2x2 + 2, y = −x3 + x2 − 3x + 1. Trong các x − 1
hàm số trên, có bao nhiêu hàm số đơn điệu trên R
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 73 A 3. B 1. C 2. D 0.
Câu 162. Cho hàm số y = −x3 − 3x2 + 4. Biết rằng có hai giá trị m1, m2 của tham số
m để đường thẳng đi qua hai điểm cực trị của đồ thị hàm số tiếp xúc với đường tròn
(C) : (x − m)2 + (y − m − 1)2 = 5. Tính tổng m1 + m2. A m1 + m2 = 0. B m1 + m2 = 6. C m1 + m2 = 10. D m1 + m2 = −6. THỦ 1
Câu 163. Gọi (C) là parabol đi qua ba điểm cực trị của đồ thị hàm số y = x4 − mx2 + m2, THI 4
tìm m để (C) đi qua điểm A(2; 24). ĐỀ C A m = −4. B m = 6. C m = 4. D m = 3. Á C À
Câu 164. Cho hàm số y = f (x) liên tục trên R \ {1} và có bảng biến thiên như hình dưới. V GIA x −∞ 0 2 +∞ f 0(x) − − 0 + QUỐC 2 +∞ +∞ + f (x) THPT −∞ 2 GHIỆP N T
Hỏi phương trình |f (x)| = 3 có bao nhiêu nghiệm? TỐ A 1 nghiệm. B 2 nghiệm. C 3 nghiệm. D 4 nghiệm. THI
Câu 165. Chi phí xuất bản x cuốn tạp chí (bao gồm: lương cán bộ, công nhân viên, giấy KỲ C
in,...) được cho bởi C(x) = 0.0001x2 − 0.2x + 10000, C(x) được tính theo đơn vị là vạn đồng. Á T (x) C
Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số M (x) = với T (x) là tổng chi G x
phí (xuất bản và phát hành) cho x cuốn tạp chí, được gọi là chi phí trung bình cho một
cuốn tạp chí khi xuất bản x cuốn. Khi chi phí trung bình cho mỗi cuốn tạp chí M (x) là thấp TRON
nhất, tính chi phí cho mỗi cuốn tạp chí đó. HÀM A 20.000 đ. B 15.000 đ. C 10.000 đ. D 22.000 đ. O Ạ Đ
Câu 166. Giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y = x2 − 2 ln x trên G [e−1; e] DỤN A M = e2 − 2, m = e−2 + 2. B M = e−2 + 2, m = 1. G C M = e−2 + 1, m = 1. D M = e2 − 2, m = 1. ỨN À V Câu 167. y SỐ
Cho hàm số f (x) có đạo hàm f 0(x) xác định, liên tục trên
R và f 0(x) có đồ thị như hình vẽ bên, biết f (c) < 0. Hỏi HÀM
đồ thị hàm số f (x) cắt trục hoành tại nhiều nhất bao nhiêu O a b c x điểm? A 3. B 1. C 0. D 2. Câu 168.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 74
Cho hàm số f (x) có đồ thị của hàm số y = f 0(x) như hình y y = f 0(x)
vẽ. Biết f (0) + f (1) − 2f (2) = f (4) − f (3). Giá trị nhỏ 4 x
nhất m, giá trị lớn nhất M của hàm số f (x) trên đoạn O 2 [0; 4] là A m = f (4), M = f (1). B m = f (4), M = f (2). C m = f (1), M = f (2). D m = f (0), M = f (2). Câu 169. y
Cho hàm số y = ax4 + bx2 + c có đồ thị như hình bên. Mệnh đề nào sau đây đúng?
A a > 0, b < 0, c < 0.
B a > 0, b > 0, c < 0. O x
C a < 0, b > 0, c < 0.
D a > 0, b < 0, c > 0.
Câu 170. Cho hàm số y = (m + 1)x4 − (m − 1)x2 + 1. Có bao nhiêu giá trị nguyên của m
để hàm số có một điểm cực đại mà không có điểm cực tiểu? 2021 A 1. B 2. C 3. D 0. GIA √x2 + 2x
Câu 171. Số đường tiệm cận của đồ thị hàm số y = là x − 1 A 1. B 3. C 0. D 2. QUỐC
Câu 172. Gọi M , m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số y = x3 − 3x2 − 9x + 35 THPT
trên đoạn [−4; 4]. Khi đó M − m nhận kết quả nào sau đây? A M − m = 1. B M − m = 86. C M − m = 76. D M − m = 81. GHIỆP Câu 173. Biết m N
0 là giá trị của tham số m để hàm số y = x3 − 3x2 + mx − 1 có hai điểm T
cực trị x1, x2 sao cho x2 + x2 − x 1 2
1x2 = 13. Mệnh đề nào dưới đây đúng? TỐ A m0 ∈ (−15; −7). B m0 ∈ (−1; 7). C m0 ∈ (7; 10). D m0 ∈ (−7; −1). THI 2mx − 8 Câu 174. Cho hàm số y =
. Tìm tất cả giá trị của m để đường tiệm cận đứng, KỲ x − 1
tiệm cận ngang của đồ thị hàm số đã cho cùng hai trục tọa độ tạo thành một hình chữ nhật TỚI
có diện tích bằng 8. Mệnh đề nào sau đây đúng? G
A Có một giá trị của m thuộc đoạn [3; 5].
B Không tìm được m thỏa mãn yêu cầu bài toán. HƯỚN
C Có một giá trị của m thuộc đoạn [−5; −3].
D Tổng các giá trị tìm được của m bằng 0.
Câu 175. Trong các hàm số sau hàm số nào đồng biến trên R? √ A y = x2 − 3x + 2. B y = x4 + x2 + 1. x − 1 C y = . D y = x3 + 5x + 13. x + 1 2x + 1
Câu 176. Tìm đường tiệm cận ngang của đồ thị hàm số y = . 3 − x 2 A y = −2. B y = . C y = −1. D y = 3. 3
Câu 177. Hàm số f (x) = −x3 + 3x2 + 9x + 1 đồng biến trong khoảng nào sau đây? A (3; +∞). B (−1; +∞). C (−1; 3). D (−∞; 3).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 75
Câu 178. Cho hàm số f (x) có đạo hàm cấp 2 trên khoảng K và x0 ∈ K . Tìm mệnh đề
sai trong các mệnh đề sau:
A Nếu hàm số đạt cực đại tại x0 thì f 00(x0) < 0.
B Nếu hàm số đạt cực đại tại x0 thì tồn tại a < x0 để f 0(a) > 0.
C Nếu hàm số đạt cực trị tại x0 thì f 0(x0) = 0.
D Nếu f 0(x0) = 0 và f 00(x0) 6= 0 thì hàm số đạt cực trị tại x0. THỦ
Câu 179. Hàm số nào sau đây đồng biến trên R? THI x x A y = . B y = √ . ĐỀ x + 1 x2 + 1 C 2 C y = (x2 − 1) − 3x + 2. D y = tan x. Á C À Câu 180. V
Cho hàm số y = f (x) liên tục, có đạo hàm trên đoạn y GIA
[a; b] và đồ thị của hàm số f 0(x) là đường cong như
hình vẽ bên. Khi đó, mệnh đề nào sau đây đúng? QUỐC A min f (x) = f (b). B min f (x) = f (x1). a x1 x∈[a;b] x∈[a;b] O x2 x b C min f (x) = f (a). D min f (x) = f (x2). THPT x∈[a;b] x∈[a;b] GHIỆP N
Câu 181. Cho hàm số y = f (x) có đồ thị trên đoạn [−2; 4] như hình vẽ dưới đây. T TỐ y THI KỲ 1 C Á C G −2 −1 O x 2 4 −1 TRON −2 HÀM −3 O Ạ Đ G
Phương trình |f (x)| = 2 có tất cả bao nhiêu nghiệm thực thuộc đoạn [−2; 4]? A 4. B 2. C 1. D 3. DỤN G
Câu 182. Cho phương trình 2x2 − 2(m + 1)x + 4 − m = 0 với m là tham số thực. Biết rằng ỨN
đoạn [a; b] là tập hợp tất cả các giá trị của m để phương trình đã cho có nghiệm thực thuộc À V ï 3 ò đoạn 0; . Tính a + b. 2 SỐ √ √ √ √ A 3 + 11. B 2 + 11. C 2 + 3 11. D 2 − 11. HÀM
Câu 183. Cho hàm số f (x) = mx4 + 2x2 − 1 với m là tham số thực. Có tất cả bao nhiêu giá
trị nguyên của m thuộc khoảng (−2018; 2018) sao cho hàm số đã cho đồng biến trên khoảng Å 1 ã 0; ? 2 A 2022. B 4032. C 4. D 2014.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 76 √
Câu 184. Cho biểu thức P = 3xpa − y2 − 3y a − x2 + 4xy + 4pa2 − ax2 − ay2 + x2y2
trong đó a là số thực dương cho trước. Biết rằng giá trị lớn nhất của P bằng 2018. Khi đó,
mệnh đề nào dưới đây đúng? √ A a = 2018. B a ∈ (500; 525]. C a ∈ (400; 500]. D a ∈ (340; 400]. 3 3m
Câu 185. Cho hàm số f (x) = x3 − (m − 1)x2 − 3mx −
với m là tham số thực. Có tất 2 2
cả bao nhiêu giá trị nguyên của m thuộc khoảng (−20; 18) sao cho đồ thị của hàm số đã cho
có hai điểm cực trị nằm cùng một phía đối với trục hoành? A 1. B 19. C 20. D 18. √
Câu 186. Cho hàm số y = x2 + m
2018 − x2 + 1 − 2021 với m là tham số thực. Gọi S
là tổng tất cả các giá trị nguyên của tham số m để đồ thị hàm số đã cho cắt trục hoành tại
đúng hai điểm phân biệt. Tính S. A 860. B 986. C 984. D 990.
Câu 187. Tập hợp nào dưới đây chứa được tất cả các giá trị thực của tham số m để giá trị 2021
lớn nhất của hàm số y = |x4 − 8x2 − m| trên đoạn [0; 3] bằng 14? GIA
A (−∞; −5) ∪ (−3; +∞). B (−5; −2). C (−7; 1). D (−4; 2). √ î ó
Câu 188. Giá trị lớn nhất của hàm số f (x) = x4 − 4x2 + 9 trên đoạn − 3; 2 bằng QUỐC A 5. B 9. C 6. D 8. THPT
Câu 189. Cho hàm số y = f (x) có đạo hàm f 0(x) = (x + 2)2(x − 2)3(3 − x). Hàm số f (x)
đồng biến trên khoảng nào dưới đây? GHIỆP A (2; 3). B (−2; 2). C (3; +∞). D (−∞; −2). N T
Câu 190. Cho hàm số y = x3 − 3x2 + 1. Tích các giá trị cực đại và giá trị cực tiểu của hàm TỐ số bằng THI A 0. B 6. C −6. D −3. KỲ
Câu 191. Có bao nhiêu số nguyên m để phương trình m(x + 3) = (x2 − 2)(x2 − 4) có 4 TỚI nghiệm thực phân biệt? G A 4. B 2. C 3. D 5. 1 HƯỚN
Câu 192. Tìm m để đồ thị hàm số y =
mx3 + (2m2 − 1)x2 + (m − 1)x − m3 có các điểm 3
cực trị nằm về hai phía của trục tung.  m < 0 A  . B 0 < m < 1. C m ≥ 1. D m < 0. m > 1
Câu 193. Cho hàm số y = f (x) có bảng xét dấu y0 như hình vẽ. x −∞ −1 3 4 +∞ y0 + 0 − − 0 +
Mệnh đề nào sau đây là sai?
A Hàm số đồng biến trên khoảng (−∞; −2).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 77
B Hàm số đồng biến trên khoảng (5; +∞).
C Hàm số nghịch biến trên khoảng (−1; 0).
D Hàm số nghịch biến trên khoảng (1; 4). x3
Câu 194. Cho hàm số y = −
+ 3x2 − 5x + 1. Mệnh đề nào dưới đây sai? 3
A Hàm số đồng biến trên khoảng (1; 5). THỦ
B Hàm số nghịch biến trên khoảng (−∞; 1). THI
C Hàm số nghịch biến trên khoảng (1; 5). ĐỀ
D Hàm số nghịch biến trên khoảng (5; +∞). C Á
Câu 195. Trong các hàm số sau, đồ thị hàm số nào có đường tiệm cận đứng x = 3? C x + 3 −x + 3 x − 3 3x + 1 À A y = . B y = . C y = . D y = . V x − 3 x + 3 x2 − 9 x + 3
Câu 196. Cho hàm số f (x) có đạo hàm f 0(x) = (x + 1)2(x − 1)3(x − 2). Số điểm cực trị GIA của hàm số f (|x|) là A 1. B 6. C 5. D 3. QUỐC Câu 197. THPT
Đường cong trong hình bên là đồ thị của hàm số nào dưới y đây? 2 GHIỆP A y = x3 − 3x − 2. B y = −x3 + 3x2 + 1. N T C y = −x3 + 3x2 − 2. D y = −2x3 + 6x2 − 2. O TỐ x 1 2 THI KỲ −2 C √ Á 1 − 4x C Câu 198. Cho hàm số y =
. Hỏi đồ thị hàm số trên có tất cả bao nhiêu đường G x + 1
tiệm cận đứng và ngang? TRON A 0. B 3. C 1. D 2. √
Câu 199. Có bao nhiêu giá trị nguyên của tham số m để phương trình 4x 4x − m − 2 = HÀM √
x3 + (m − 8) 4x − m có hai nghiệm thực phân biệt? O Ạ A 4. B 5. C 8. D 6. Đ G
Câu 200. Cho hàm số y = f (x) có bảng biến thiên sau đây DỤN x −∞ − G 2 0 1 +∞ ỨN y0 − + 0 − − À V +∞ + 7 +∞ SỐ y −1 −∞ HÀM 5
Trong các mệnh đề sau, mệnh đề nào sai?
A Hàm số có hai điểm cực trị.
B Đồ thị hàm số có một tiệm cận đứng.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 78
C Hàm số nghịch biến trên khoảng (0; +∞).
D Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt. x + 2 Câu 201. Cho hàm số y =
có đồ thị (C). Tìm m để (C) có 3 đường tiệm x2 − mx + 4 cận.
A m ∈ (−∞; −4) ∪ (4; +∞).
B m ∈ (−∞; −4) ∪ [4; +∞). C m ∈ (4; +∞). D Không tồn tại m. 2x2 + x
Câu 202. Đồ thị hàm số y =
có hai điểm cực trị A, B. Tìm tọa độ trung điểm của x + 1 đoạn AB. A (1; 2). B (1; 3). C (−1; −3). D (−1; −2).
Câu 203. Cho hàm số y = x3 − 9x2 + 17x + 2 có đồ thị (C). Qua điểm M (−2; 5) kẻ được
tất cả bao nhiêu tiếp tuyến đến (C)? A 0. B 1. C 2. D 3. 2021
Câu 204. Tìm m để hàm số y = mx3 − 2mx2 + 3x − 1 có cực đại và cực tiểu. 9 9 GIA A m > 2. B m < 2. C m < 0 ∨ m > . D 0 < m < . 4 4
Câu 205. S là tập tất cả các số nguyên m để phương trình cos2 x = m + sin x có nghiệm. QUỐC
Tìm tổng các phần tử của S. A 0. B 1. C 2. D 3. THPT
Câu 206. Biết rằng tồn tại hai giá trị của m sao cho hàm số y = x3 − 3x2 + m đạt giá trị
nhỏ nhất bằng 2 trên đoạn [−2; 3]. Tính tổng hai giá trị đó. GHIỆP N A 18. B 24. C 20. D 22. T TỐ
Câu 207. Với mỗi số thực m ∈ (−1; 1), kí hiệu Sm là diện tích hình phẳng giới hạn bởi THI
đồ thị hàm số y = |x| và đường thẳng d : y = mx + 1. Khi đó giá trị nhỏ nhất S của Sm KỲ thỏa 2 2 4 4 TỚI A 0 < S ≤ . B < S ≤ . C < S ≤ 2. D S > 2. 3 3 3 3 G
Câu 208. Cho hàm số y = x3 + ax2 − 3x + b có đồ thị (C). Hỏi có bao nhiêu cặp (a, b)
nguyên dương để (C) cắt trục hoành tại 3 điểm phân biệt? HƯỚN A 0. B 4. C 1. D vô số. x3 2 Câu 209. Cho hàm số y = − 2x2 + 3x +
. Toạ độ điểm cực đại của đồ thị hàm số 3 3 là Å 2 ã A (1; 2). B (−1; 2). C 3; . D (1; −2). 3
Câu 210. Số điểm cực trị của hàm số f (x) = 21x4 + 5x2 + 2018 là A 1. B 3. C 2. D 0.
Câu 211. Cho hàm số f (x) = x3 − x2 + ax + b có đồ thị là (C). Biết (C) có điểm cực tiểu
là A (1; 2). Giá trị 2a − b bằng A −1. B 1. C −5. D 5.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 79 Câu 212.
Cho hàm số y = f (x) có đạo hàm liên tục trên R. Đồ thị hàm y
f (x) như hình vẽ. Số đường tiệm cận đứng của đồ thị hàm số y = 4 x2 − 1 bằng f 2(x) − 4f (x) 2 A 3. B 1. C 2. D 4. −1 O 1 x THỦ THI
Câu 213. Cho hàm số y = −x3 + 3x2 + 2 có đồ thị (C). Phương trình tiếp tuyến của (C) ĐỀ
mà có hệ số góc lớn nhất là C Á C A y = 3x + 1. B y = −3x + 1. C y = 3x − 1. D y = −3x − 1. À V
Câu 214. Cho hàm số y = −x3 + 3x2 + 9x − 5. Mệnh đề nào sau đây đúng?
A Hàm số đồng biến trên (−1; 3); nghịch biến trên mỗi khoảng (−∞; −1) , (3; +∞). GIA
B Hàm số đồng biến trên mỗi khoảng (−∞; −3) , (1; +∞); nghịch biến trên (−3; 1).
C Hàm số đồng biến trên mỗi khoảng (−∞; −1) , (3; +∞); nghịch biến trên (−1; 3). QUỐC
D Hàm số đồng biến trên (−1; 3); nghịch biến trên (−∞; −1) ∪ (3; +∞). THPT
Câu 215. Cho hàm số y = x3 − 3x2 − 9x + 11. Tổng giá trị lớn nhất và giá trị nhỏ nhất
của hàm số trên đoạn [−2; 2] bằng GHIỆP A 25. B 5. C −5. D 0. N T
Câu 216. Trong các hàm số sau hàm số nào có cực đại, cực tiểu và xCT < xCĐ? TỐ A y = −x3 + 9x2 + 3x + 2. B y = −x3 − 3x − 2. THI C y = x3 − 9x2 − 3x + 5. D y = x3 + 2x2 + 8x + 2. KỲ √ C 2 x + m Á Câu 217. Cho hàm số y = √
. Giá trị nguyên lớn hơn 1 của tham số m sao cho C x + 1 G max y ≤ 3 thỏa mãn x∈[0;4] A m > 8. B 4 < m ≤ 6 . C Không có m. D 1 < m < 5. TRON
Câu 218. Cho hàm số f (x) = (1 − m3)x3 + 3x2 + (4 − m)x + 2 với m là tham số. Có bao HÀM
nhiêu số nguyên m ∈ [−2018; 2018] sao cho f (x) ≥ 0 với mọi giá trị x ∈ [2; 4]? O A 2020. B 2019. C 4037. D 2021. Ạ Đ G Câu 219.
Đồ thị hình bên là của hàm số nào? y DỤN A y = −x3 − 3x. B y = x3 + 3x. G 2 C y = x3 − 3x. D y = −x3 + 3x. ỨN À V 1 −1 O x SỐ HÀM −2 3x + 1
Câu 220. Đường tiệm cận ngang của đồ thị hàm số y = là 2 − x 3 1 A y = 2. B y = . C y = −3. D y = . 2 2
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 80
Câu 221. Hàm số nào sau đây là hàm số đồng biến trên R? x A y = √ . B y = (x2 − 1)2 − 3x + 2. x2 + 1 x C y = . D y = tan x. x + 1 Câu 222.
Cho hàm số y = f (x). Hàm số y = f 0(x) có đồ thị y
như hình vẽ sau. Hàm số y = f (x2) đồng biến trên khoảng y = f 0(x) A (−2; +∞). B (−1; 1). −1 1 C (1; 2). D (−2; −1). O x 4 2x − 1
Câu 223. Gọi A, B là giao điểm của đồ thị hàm số y =
với đường thẳng y = x − 2. x + 2 2021 Độ dài AB bằng √ √ √ GIA A 2 2. B 1. C 4 2. D 2.
Câu 224. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị? QUỐC x −∞ −1 0 1 +∞ THPT f 0(x) + 0 − + 0 − GHIỆP N 2 3 T TỐ f (x) THI −∞ −1 −1 −∞ KỲ TỚI A Có ba điểm. B Có bốn điểm. C Có một điểm. D Có hai điểm. G
Câu 225. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y =
x3 − 3x2 − 9x + 35 trên đoạn [−4; 4]. Tính M · m. HƯỚN A −1640. B −984. C 1640. D 320. x + 1
Câu 226. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị hàm số y = √mx2 + 1
có hai đường tiệm cận ngang. A m < 0. B m = 0.
C Không có giá trị thực nào của m thỏa mãn yêu cầu đề bài. D m > 0.
Câu 227. Cho hàm số y = ax3 + bx2 + cx + d, biết đồ thị hàm số đi qua các điểm A(2; 4),
B(3; 9) và C(4; 16). Các đường thẳng AB, AC, BC cắt đồ thị lần lượt tại các điểm D, E,
F . Biết xD + xE + xF = −18. Tính f (0).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 81 8 1 1 A − . B − . C 0. D − . 3 3 8
Câu 228. Tổng số giữa giá trị cực đại và giá trị cực tiểu của hàm số y = x3 − 3x2 + 1 là A 6. B 2. C 4. D −2. Câu 229.
Cho hàm số y = f (x) có bảng biến x -∞ 0 2 +∞ THỦ
thiên như hình bên. Hàm số y = y0 − 0 + 0 − THI
f (x) đồng biến trên khoảng nào dưới +∞ + 5 ĐỀ đây? y C Á A (−∞; 2). B (−∞; 0). 1 −∞ C C (1; 2). D (0; +∞). À V Câu 230. GIA
Cho hàm số y = f (x) có bảng biến x -∞ −1 3 +∞
thiên như hình bên. Cực đại của hàm y0 + 0 − 0 + số là 4 +∞ + QUỐC y A −1. B 3. C 4. D −∞ −2 − THPT −2. Câu 231. GHIỆP
Đường cong trong hình bên là đồ thị của hàm số nào dưới đây? y N T A y = −x4 + 2x2 − 3. B y = x4 − 2x2 + 3. 1 TỐ C y = x3 − 3x2 + 1. D y = −x3 + 3x2 + 1. 2 THI O x KỲ C Á C G
Câu 232. Đồ thị của hàm số nào dưới đây có tiệm cận ngang? x2 − 3x + 2 x3 + 3 √ 3x − 2 A y = . B y = . C y = 1 − x2. D y = . TRON x − 1 x2 + 1 x2 + 1 Câu 233. HÀM
Cho hàm số y = f (x) có bảng biến thiên x −∞ −2 0 2 +∞ O Ạ
như hình bên. Số nghiệm của phương trình Đ y0 + 0 − 0 + − G f (x) + 2 = 0 là 3 3 A 0. B 3. C 4. D 2. y DỤN −∞ −1 − −∞ G ỨN
Câu 234. Giá trị nhỏ nhất của hàm số f (x) = x4 − 4x2 + 15 trên đoạn [−2; 3] bằng À V A 60. B 15. C 11. D 132. SỐ
Câu 235. Tìm tất cả các giá trị thực của tham số m để hàm số y = −(m − 1)x4 + 2(m −
3)x2 + 5 không có cực tiểu. HÀM A 1 ≤ m ≤ 3. B m ≤ 1. C m ≥ 1. D 1 < m ≤ 3.
Câu 236. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị nhỏ nhất
của hàm số y = − |x3 − 3x + m| trên đoạn [0; 2] bằng −3. Tổng tất cả các phần tử của S là
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 82 A 1. B 2. C 0. D 6.
Câu 237. Hỏi có bao nhiêu số nguyên dương m để hàm số y = −(m2−1)x3−(m−1)x2+x−7
đồng biến trên khoảng (−∞; +∞)? A 1. B 2. C 0. D 3.
Câu 238. Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số y = x4−2mx2+2m+m4
có ba điểm cực trị tạo thành một tam giác đều. √ √ √ 3 6 3 3 A m = 3 3. B m = 1. C m = . D m = . 2 2
Câu 239. Cho hàm số y = x3 − 2x2 + (m − 1)x + 2m có đồ thị là (Cm). Gọi S là tập hợp
tất cả các giá trị của m để từ M (1; 2) kẻ được đúng hai tiếp tuyến với (Cm). Tính tổng các phần tử của S. 4 81 3 217 A . B . C . D . 3 109 4 81 2021
Câu 240. Kí hiệu M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x2 + x + 4 M trên đoạn [0; 3]. Tính . GIA x + 1 m 2 4 5 A 2. B . C . D . 3 3 3 QUỐC Câu 241. y THPT
Đường cong như hình bên là đồ thị của hàm số nào sau đây? 1 A y = x3 − x2 − 2. B y = 2x3 + 3x2 + 2. 3 C y = −3x3 + 2x2 + 2. D y = x3 − 3x2 + 3. GHIỆP N T TỐ O x THI KỲ
Câu 242. Cho hàm số y = f (x) có bảng biến thiên như sau: TỚI G x −∞ 1 +∞ y0 + + HƯỚN +∞ −1 − y −1 −∞
Số nghiệm của phương trình f (x) − x2 + 2x − 1 = 0 là A vô số. B 0. C 2. D 1.
Câu 243. Cho hàm số y = x3 + mx2 − x − m
(Cm). Hỏi có tất cả bao nhiêu giá trị của
tham số m để đồ thị hàm số (Cm) cắt trục Ox tại ba điểm phân biệt có hoành độ lập thành một cấp số cộng ? A 2. B 3. C 1. D 0.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 83
Câu 244. Cho hàm số y = f (x) xác định, liên tục trên [−1; 1] và có bảng biến thiên như x −∞ 0 +∞ y0 + 0 − 1 y 0 0 sau: THỦ
Trong các khẳng định sau, khẳng định nào đúng? THI
A Hàm số có giá trị lớn nhất bằng 0.
B Hàm số có đúng một cực trị. ĐỀ
C Hàm số đạt cực đại tại x = 1.
D Hàm số có giá trị cực tiểu bằng 1. C Á C
Câu 245. Đồ thị hàm số nào sau đây không có tiệm cận ngang? x + 2 x + 2 À V A y = . B y = . x − 1 x2 − 1 x2 √ GIA C y = . D y = x + x2 − 1. x − 1
Câu 246. Cho hàm số y = |x3 − 3x2 + m| với m là tham số. Gọi S là tập hợp tất cả các QUỐC
giá trị nguyên của tham số m để đồ thị hàm số có 5 điểm cực trị. Tổng tất cả các phần tử của tập S là THPT A 3. B 10. C 6. D 5. Câu 247. GHIỆP N y T
Cho hàm số y = f (x). Hàm số y = f 0(x) có đồ thị như hình vẽ. TỐ
Hàm số y = f (x2) đồng biến trên khoảng nào sau đây? THI A (1; 2). B (−1; 1). C (1; +∞). D (−2; −1). −1 1 4 KỲ O x C Á C G
Câu 248. Hàm số y = f (x) có đạo hàm trên R \ {−2; 2}, có bảng biến thiên như sau TRON x −∞ −2 0 2 +∞ HÀM y0 − − 0 + + O Ạ Đ +∞ + +∞ +∞ −1 − G y DỤN −∞ 0 −∞ G ỨN 1
Gọi k, l là số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = . À f (x) − 2018 V Tính k + l. SỐ A k + l = 2. B k + l = 3. C k + l = 4. D k + l = 5. HÀM
Câu 249. Hàm số y = x4 − 2x2 đồng biến trên khoảng nào trong các khoảng sau? A (−1; 0). B (0; 1). C (0; +∞). D (−∞; −1). x − 2
Câu 250. Tìm số đường tiệm cận ngang và đứng của đồ thị hàm số y = . x + 1 A 3. B 2. C 4. D 1.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 84
Câu 251. Tìm giá trị cực đại của hàm số y = x3 − 3x2 + m (với m là tham số thực). A 0. B m. C 2. D −4 + m. Câu 252.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào y sau đây? 3 A y = x3 − 3x + 1. B y = −x3 + 3x + 1. 2 C y = −x3 − 3x + 1. D y = −x3 + 1. 1 −2 −1 2 x O 1 −1 −2
Câu 253. Cho hàm số y = f (x) xác định trên R và có bảng biến thiên như sau x −∞ −1 0 1 +∞ 2021 f 0(x) − 0 − || + 0 − GIA +∞ + 3 f (x) f (−1) QUỐC −1 − −∞ THPT
Hỏi mệnh đề nào sau đây là mệnh đề sai?
A Hàm số nghịch biến trên khoảng (−∞; 0). GHIỆP N
B Hàm số có 3 điểm cực trị. T
C Đồ thị hàm số y = f (x) không có tiệm cận ngang. TỐ
D Điểm cực tiểu của hàm số là x = 0. THI Câu 254. KỲ
Cho hàm số y = f (x). Biết rằng hàm số y = f 0(x) liên tục trên y TỚI G
R và có đồ thị như hình vẽ bên. Hỏi hàm số y = f (5 − x2) có
bao nhiêu điểm cực trị? A 7. B 9. C 4. D 3. HƯỚN x −4 O 1 4 1
Câu 255. Tìm giá trị nhỏ nhất của hàm số f (x) = 4x2 +
− 4 trên khoảng (0; +∞). x A min f (x) = −1. B min f (x) = −4. x∈(0;+∞) x∈(0;+∞) C min f (x) = 7. D min f (x) = −3. x∈(0;+∞) x∈(0;+∞) 2x + 1 Câu 256. Cho hàm số y =
có đồ thị là (C). Tiếp tuyến của đồ thị (C) tại điểm x − 1
thuộc đồ thị (C) với hoành độ x0 = 0 cắt hai đường tiệm cận của đồ thị (C) tại hai điểm
A, B. Tính diện tích tam giác IAB, với I là giao điểm hai đường tiệm cận của đồ thị (C). √ A S4IAB = 6. B S4IAB = 3. C S4IAB = 12. D S4IAB = 6 3 2.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 85 x + 1 Câu 257. Cho hàm số y =
, với m là tham số thực. Có bao nhiêu giá trị nguyên của x − m
tham số m nhỏ hơn 2 để hàm số đã cho nghịch biến trên khoảng (2; 3)? A 3. B 4. C 1. D 2.
Câu 258. Có bao nhiêu giá trị nguyên của m lớn hơn −2019 để đồ thị hàm số y = x3 −
3mx2 + 3(m2 − 1)x + 1 − m2 có hai điểm phân biệt đối xứng nhau qua gốc tọa độ? THỦ A 2017. B Vô số. C 2019. D 2018. THI √ √ Å √ 1 √ ã Câu 259. Cho phương trình x + x − 1 m x + √ + 16 4 x2 − x = 1, với m ĐỀ x − 1 C
là tham số thực. Tìm số các giá trị nguyên của tham số m để phương trình đã cho có hai Á C nghiệm thực phân biệt. À V A 11. B 9. C 20. D 4. GIA
Câu 260. Hàm số nào dưới đây nghịch biến trên R? x + 2 A y = . B y = −x4 − x2 − 1. x − 1 QUỐC C y = −x3 + x2 − 3x + 11. D y = cot x. THPT
Câu 261. Hàm số nào dưới đây chỉ có cực tiểu và không có cực đại? x + 1 A y = −x4 + x2. B y = . x − 1 GHIỆP N C y = x4 + 1. D y = x3 + x2 + 2x − 1. T TỐ Câu 262. THI
Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới y 3 KỲ đây? 2 C 2x − 1 x + 1 Á A y = . B y = . 1 x C x + 1 2x − 1 O 2x + 1 x − 1 G C y = . D y = . − − 3 − 2 1 1 2 3 −1 x − 1 2x + 1 −2 TRON mx + n Câu 263. Cho hàm số y =
có đồ thị (C). Biết tiệm cận ngang của (C) đi qua HÀM x − 1 O
A(−1; 2) và điểm B(2; 1) thuộc (C). Tính m + n. Ạ Đ A −3. B 3. C 1. D −1. G
Câu 264. Đồ thị hàm số y = x4 − 2x2 có bao nhiêu tiếp tuyến song song với trục Ox. DỤN G A 3. B 2. C 1. D 0. ỨN √
Câu 265. Cho hàm số y = x +
18 − x2 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ À V
nhất của hàm số. Khi đó M + m bằng √ √ SỐ A 6 − 3 2. B 0. C 6. D 6 + 3 2. 1 HÀM
Câu 266. Tìm tất cả các giá trị thực của tham số m để hàm số y = x3 + mx + 2 ln x đồng 3 biến trên (0; +∞). A m ≤ −3. B m ≥ −3. C m ≥ 3. D m ≤ 3. Câu 267.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 86 Cho hàm số y = f (x) có bảng biến x −∞ −2 1 +∞
thiên như hình vẽ bên. Hỏi hàm số y = y0 − 0 + 0 +
f (x2 + 8x + 2018) có bao nhiêu điểm cực +∞ + +∞ + trị? y −2 A 0. B 2. C 3. D 1.
Câu 268. Cho hàm số y = x3 − 3x2 có đồ thị (C) và điểm A(0; a). Gọi S là tập hợp tất cả
các giá trị thực của a để có đúng hai tiếp tuyến của (C) đi qua A. Tích các giá trị các phần tử của S là A 1. B −1. C 0. D 3. √ Ä ä3
Câu 269. Có bao nhiêu giá trị nguyên của tham số m để phương trình sin3 2x− m + 3 cos 2x − Å 8π ã m = 2 sin 2x + có nghiệm? 3 A 6. B 4. C Vô số. D 5.
Câu 270. Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho trị lớn nhất của 2021
hàm số y = |3x2 − 6x + 2m − 1| trên đoạn [−2; 3] đạt giá trị nhỏ nhất. Số phần tử của tập GIA S là A 0. B 3. C 2. D 1. 1 QUỐC
Câu 271. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = |x3| − (3 − m)x2 + 3
(3m + 7) |x| − 1 có 5 điểm cực trị? THPT A 3. B 5. C 2. D 4.
Câu 272. Cho hàm số y = x3 − 3x. Mệnh đề nào dưới đây đúng? GHIỆP
A Hàm số đồng biến trên khoảng (−∞; −1) và nghịch biến trên khoảng (1; +∞). N T
B Hàm số đồng biến trên khoảng (−∞; +∞). TỐ
C Hàm số nghịch biến trên khoảng (−∞; −1) và đồng biến trên khoảng (1; +∞). THI
D Hàm số nghịch biến trên khoảng (−1; 1). KỲ
Câu 273. Cho hàm số y = f (x) có bảng biến thiên như sau TỚI x −∞ 2 3 +∞ G y0 − 0 + 0 − +∞ + 1 HƯỚN y −5 −∞
Hàm số đạt cực tiểu tại điểm A x = −5. B x = 2. C x = 3. D x = 1.
Câu 274. Đồ thị hàm số y = (x2 − 1)(x2 + 1) cắt trục hoành tại bao nhiêu điểm phân biệt? A 0. B 1. C 2. D 4. 2
Câu 275. Tính tổng giá trị lớn nhất và nhỏ nhất của hàm số f (x) = x2 + trên đoạn x ï 1 ò ; 2 . 2
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 87 A 8. B 5. C 4. D 6.
Câu 276. Cho hàm số y = f (x) xác định trên R và liên tục trên từng khoảng xác định và có bảng biến thiên x −∞ 0 1 +∞ y0 − + 0 − THỦ +∞ + 2 THI y ĐỀ −1 −∞ −∞ C Á C À V
Chọn mệnh đề đúng về đồ thị hàm số.
A Đồ thị có đúng một tiệm cận ngang. GIA
B Đồ thị có đúng 2 tiệm cận ngang.
C Đồ thị có đúng một tiệm cận đứng. QUỐC
D Đồ thị không có tiệm cận ngang và tiệm cận đứng. THPT
Câu 277. Cho hàm số y = x3 − 3x + 2 có đồ thị (C). Hình vẽ nào sao đây có thể là đồ thị (C) y GHIỆP N 2 y T TỐ THI O x −2 O 1 KỲ x C Á A . B . C y G y 2 TRON 2 HÀM x −2 O 1 O O Ạ x −2 1 Đ −2 G C . D . DỤN
Câu 278. Cho hàm số y = f (x) xác định trên R \ {0} có bảng biến thiên như hình vẽ sau G ỨN x −∞ 0 1 +∞ À V y0 − + 0 − SỐ +∞ + 2 y HÀM −1 −∞ −∞
Số nghiệm của phương trình f (x) + 2 = 0 là A 0. B 1. C 2. D 3.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 88 mx + 2 Câu 279. Cho hàm số y =
, m là tham số thực. Gọi S là tập hợp tất cả các giá trị 2x + m
nguyên của tham số m để hàm số nghịch biến trên khoảng (0; 1). Số phần tử của S bằng A 1. B 5. C 2. D 3.
Câu 280. Cho hàm số y = f (x) có đạo hàm liên tục trên R. Hàm số y = f 0(x) có đồ thị như hình vẽ dưới đây y −1 O 1 x 4 2021 GIA QUỐC
Cho bốn mệnh đề sau 1) Hàm số y = f (x) có hai điểm cực trị.
2) Hàm số y = f (x) đồng biến trên khoảng (1; +∞). THPT
3) f (1) > f (2) > f (4).
4) Trên đoạn [−1; 4], giá trị lớn nhất của hàm số y = f (x) là f (1). GHIỆP
Số mệnh đề đúng trong bốn mệnh đề trên là N T A 1. B 4. C 2. D 3. TỐ THI
Câu 281. Cho điểm A có hoành độ bằng −1 nằm trên đồ thị hàm số (C) : y = 2x3 −3x2 +m, KỲ
(m ∈ R). Biết tiếp tuyến của (C) tại A cắt đồ thị (C) tại điểm thứ hai là B. Có bao nhiêu
giá trị thực của tham số m để 4ABO vuông tại O? TỚI G A 2. B 1. C 3. D 0. 4x + 4
Câu 282. Đồ thị hàm số y =
và y = x2 − 1 cắt nhau tại bao nhiêu điểm? HƯỚN x − 1 A 0. B 1. C 2. D 3. 1 1
Câu 283. Tìm giá trị nhỏ nhất của hàm số y = − khi x > 0. x3 x √ √ 2 3 1 2 3 A . B − . C 0. D − . 9 4 9 √x + 1
Câu 284. Tìm số đường tiệm cận của đồ thị hàm số y = . |x| − 1 A 0. B 1. C 2. D 3.
Câu 285. Một trong các đồ thị hàm số dưới đây là đồ thị của hàm số g(x) liên tục trên R
thỏa mãn g0(0) = 0, g00(x) < 0, ∀x ∈ (−1; 2). Hỏi đó là đồ thị nào?
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 89 y y 1 2 1 2 −1 x O −1 x O A . B . y y THỦ THI ĐỀ 1 1 2 2 C Á −1 x O x −1 O C C . D . À V
Câu 286. Tìm tất cả các giá trị của tham số m để hàm số y = x3 − 3mx2 − 9m2x nghịch GIA biến trên (0; 1). 1 A m > . B m < −1. 3 QUỐC 1 1 C m ≥ hoặc m ≤ −1. D −1 < m < . 3 3 THPT
Câu 287. Phương trình |x2 − 2x| (|x| − 1) = m (với m là tham số thực) có tối đa bao nhiêu nghiệm thực? GHIỆP N T A 3. B 4. C 5. D 6. TỐ
Câu 288. Có bao nhiêu điểm M thuộc đồ thị (C) của hàm số y = x(x2 − 3) sao cho tiếp THI
tuyến tại M của (C) cắt (C) và trục hoành lần lượt tại hai điểm phân biệt A (khác M ) và KỲ C
B sao cho M là trung điểm của AB. Á C A 0. B 1. C 2. D 3. G
Câu 289. Cho hàm số f (x) có đạo hàm liên tục và có đúng 3 điểm cực trị là −2, −1 và 0. TRON
Hỏi hàm số y = f (x2 − 2x) có bao nhiêu điểm cực trị. A 3. B 4. C 5. D 6. HÀM O Ạ
Câu 290. Cho hàm số y = f (x) có bảng biến thiên như sau Đ G x −∞ −1 0 1 +∞ DỤN G y0 + − 0 + 0 − ỨN 2 2 À V y SỐ −∞ 1 −∞ HÀM
Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây? A (−∞; −1). B (0; 1). C (−1; 1). D (−1; 0). Câu 291.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 90
Cho hàm số y = f (x) có đồ thị như hình bên. y
Hàm số đạt cực đại tại điểm 1 − A x = 1. B x = 2. 2 1 x −1 2 C x = −1. D x = −3. −3
Câu 292. Đồ thị hàm số nào dưới đây không có tiệm cận đứng? x2 + 1 x2 + 3x + 2 x − 1 2 A y = . B y = . C y = . D y = . x + 1 x + 1 x + 1 x + 1 Câu 293.
Đường cong trong hình bên là đồ thị của hàm số nào dưới y đây? x − 1 A y = . x + 1 1 B y = −x4 + 2x2 − 1. 2021 C y = x3 − 3x + 2. 0 1 x GIA x + 1 D y = . x − 1 1 2 QUỐC
Câu 294. Giá trị lớn nhất của hàm số f (x) = x3 − 3x2 + 5x − trên đoạn [0; 5] bằng 3 3 2 5 2 A . B . C − . D 5. THPT 3 3 3 Câu 295.
Cho hàm số y = f (x) = ax4 + bx2 + c có đồ thị như hình bên. y GHIỆP 1 N
Số nghiệm của phương trình f (x) − 1 = 0 là T x TỐ A 3. B 2. C 4. D 1. THI −3 KỲ mx + 10
Câu 296. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = nghịch TỚI 2x + m G biến trên khoảng (0; 2)? A 6. B 5. C 9. D 4. HƯỚN Câu 297.
Cho hàm số y = f (x). Hàm số y = f 0(x) có đồ thị như hình y
bên. Biết rằng phương trình f 0(x) = 0 có bốn nghiệm phân
biệt a, 0, b, c với a < 0 < b < c. a b c
Mệnh đề nào dưới đây đúng? x 0 A f (a) > f (b) > f (c). B f (a) > f (c) > f (b). C f (c) > f (a) > f (b). D f (b) > f (a) > f (c). 1 Câu 298. Cho hàm số y =
mx3 − (m − 1)x2 + 3(m − 2)x + 2018 với m là tham số. Tổng 3
bình phương của tất cả các giá trị của m để hàm số có hai điểm cực trị x1, x2 thỏa mãn 2x1 + x2 = 2 bằng
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 91 52 10 73 34 A . B . C . D . 9 9 16 9
Câu 299. Biết A(x1; y1), B(x2; y2) là hai điểm thuộc hai nhánh khác nhau của đồ thị hàm x + 4 số y =
sao cho độ dài đoạn thẳng AB nhỏ nhất. Tính P = y2 + y2 − x1x2. x + 1 1 2 √ √ A P = 6. B P = 6 − 2 3. C P = 10 − 3. D P = 10.
Câu 300. Cho hàm số f (x) = x3 − 6x2 + 9x. Đặt f k(x) = f f k−1(x) với k là số nguyên THỦ
dương lớn hơn 1. Hỏi phương trình f 5(x) = 0 có tất cả bao nhiêu nghiệm phân biệt? THI A 120. B 365. C 122. D 363. ĐỀ mx + 25
Câu 301. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = nghịch biến C x + m Á C trên khoảng (−∞; 1)? À V A 11. B 4. C 5. D 9.
Câu 302. Đồ thị hàm số nào sau đây có tiệm cận ngang? GIA √ x x2 x2 − 3x + 2 4 − x2 A y = . B y = . C y = . D y = . x2 + 1 x + 1 x − 1 1 + x QUỐC Câu 303.
Cho hàm số y = f (x) xác định và liên tục trên R, có y THPT
đồ thị ở hình bên. Hàm số y = f (x) nghịch biến trên khoảng nào dưới đây? GHIỆP N A (0; 1). B (−∞; 0). T C (1; 2). D (2; +∞). TỐ THI x −1 O 1 2 KỲ x2 − 3x + 3 ï 1 ò
Câu 304. Tìm giá trị lớn nhất của hàm số y = trên đoạn −2; . C x − 1 2 Á 13 7 C A − . B 1. C −3. D − . G 3 2
Câu 305. Cho hàm số y = f (x) xác định và liên tục trên R, có bảng biến thiên như sau TRON x −∞ −2 0 +∞ y0 + 0 − 0 + HÀM O 2 +∞ + Ạ Đ y G −∞ −2 DỤN
Tìm tập hợp tất cả các giá trị của tham số m để phương trình f (x) = m có đúng một G nghiệm. ỨN À
A (−∞; −2) ∪ (2; +∞).
B (−∞; −2] ∪ [2; +∞). V C (−2; 2). D [−2; 2]. SỐ
Câu 306. Điểm cực đại của hàm số y = x3 − 3x + 1 là HÀM A x = 3. B x = 1. C x = 0. D x = −1. x + 2 Câu 307. Cho hàm số y =
có đồ thị là (C) và I là giao điểm hai đường tiệm cận của x + 1
(C). Điểm M di chuyển trên (C). Xác định giá trị nhỏ nhất độ dài đoạn thẳng M I. √ √ √ A 1. B 2. C 2 2. D 6.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 92 Câu 308. Cho hàm số y = f (x) liên tục trên y
R và có đồ thị như hình vẽ bên. Đặt 5 M = max f 2 sin4 x + cos4 x, m = R
min f 2 sin4 x + cos4 x. Tính S = M + 3 R m. 1 A S = 6. B S = 4. x C S = 5. D S = 3. O 1 2 4
Câu 309. Cho hàm số f (x) = |x4 − 4x3 + 4x2 + a|. Gọi M và m lần lượt là giá trị lớn nhất
và giá trị nhỏ nhất của hàm số đã cho trên [0; 2]. Có bao nhiêu số nguyên a ∈ [−4; 4] sao cho M ≤ 2m? A 7. B 5. C 6. D 4.
Câu 310. Cho hàm số y = f (x) có bảng biến thiên như sau: 2021 x −∞ −1 3 +∞ GIA f 0(x) − 0 + 0 − +∞ + 4 QUỐC f (x) THPT −1 − −∞ GHIỆP
Mệnh đề nào sau đây đúng? N T
A Hàm số y = f (x) nghịch biến trên (−∞; 3). TỐ
B Hàm số y = f (x) đồng biến trên (−1; 3). THI
C Hàm số y = f (x) đồng biến trên (−1; 4). KỲ
D Hàm số y = f (x) nghịch biến trên (−1; +∞). 2x + 1 TỚI
Câu 311. Giá trị nhỏ nhất của hàm số y = trên đoạn [2; 3] bằng G 1 − x 3 7 A . B −5. C − . D −3. 4 2 HƯỚN
Câu 312. Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y = x3 + (m +
2)x2 + 3x − 3 đồng biến trên khoảng (−∞; +∞)? A 6. B 7. C 8. D 5. Câu 313.
Cho hàm số y = f (x) liên tục trên R, đồ thị của hàm số y = f 0(x) y y = f 0(x)
có dạng như hình vẽ bên. Số nào bé nhất trong các số sau: f (0), x f (1), f (2), f (3)? O 1 2 3 A f (1). B f (2). C f (3). D f (0). √
Câu 314. Tìm tất cả các giá trị thực của a để đồ thị hàm số y = ax + 9x2 + 4 có tiệm cận ngang. 1 1 A a = ±3. B a = −3. C a = ± . D a = − . 3 3
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 93
Câu 315. Tìm m để đồ thị hàm số y = x3 − 3x2 + 3(m + 1)x − m − 1 có hai điểm cực trị
nằm cùng phía đối với trục hoành. A m ∈ (−∞; 0). B m ∈ (−1; +∞). C m ∈ (−1; 0).
D m ∈ (−∞; −1) ∪ (0; +∞).
Câu 316. Cho đường thẳng d : y = mx + m + 2 (m là tham số) và đường cong (C) : y =
2x − 1 . Biết rằng khi m = m THỦ
0 thì (C ) cắt d tại hai điểm A, B thỏa mãn độ dài AB ngắn x + 1
nhất. Khẳng định nào sau đây đúng? THI A m ĐỀ 0 ∈ (−4; −3). B m0 ∈ (−5; −4). C m0 ∈ (−2; 0). D m0 ∈ (−3; −1). C Á
Câu 317. Đồ thị hàm số y = x4 − x3 − 3 cắt trục tung tại mấy điểm? C À A 1 điểm. B 2 điểm. C 4 điểm. D 3 điểm. V 2x − 1
Câu 318. Số đường tiệm cận của đồ thị hàm số y = là GIA x + 3 A 2. B 3. C 1. D 0. QUỐC
Câu 319. Cho hàm số y = f (x) có bảng biến thiên như sau THPT x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + GHIỆP N T +∞ + 2 +∞ + TỐ y THI 1 1 KỲ C Á
Xác định số điểm cực tiểu của hàm số y = f (x). C A 3. B 6. C 2. D 1. G
Câu 320. Cho hàm số y = f (x) có bảng biến thiên như sau TRON x −∞ −1 0 1 +∞ HÀM O y0 − 0 + 0 − 0 + Ạ Đ +∞ + 0 +∞ + G y DỤN −1 −1 G ỨN À
Tìm tất cả các giá trị của m để phương trình f (x) = m có đúng hai nghiệm. V A m > 0. B m ≥ −1. SỐ C m > 0 hoặc m = −1. D m ≥ 0 hoặc m = −1. HÀM
Câu 321. Giá trị nhỏ nhất của hàm số y = 4x3 − 3x4 trên đoạn [−1; 2] là A −7. B −24. C 0. D −16. √ Câu 322. Hàm số y =
x2 − 2x nghịch biến trên khoảng nào? A (1; +∞). B (−∞; 0). C (2; +∞). D (−∞; 1).
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 94
Câu 323. Cho hàm số y = f (x) có đạo hàm f 0(x) = 2018(x − 1)2017(x − 2)2018(x − 3)2019.
Tìm số điểm cực trị của f (x). A 2. B 1. C 3. D 0.
Câu 324. Cho hàm số f (x) = |x3 − 3x2 + m| với m ∈ [−5; 7] là tham số. Có bao nhiêu giá
trị nguyên của m để hàm số có đúng ba điểm cực trị? A 13. B 12. C 10. D 8. 1 Câu 325. Hàm số y =
x3 − (m − 3)x + 2018 luôn đồng biến trên R thì 3 A m ≤ 4. B m ≤ 3. C m ≤ 2018. D m ≤ 9. x − 3
Câu 326. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = có hai x2 − 2mx + 1
đường tiệm cận đứng.
A m ∈ (−∞; −1) ∪ (1; +∞).
B m ∈ (−∞; −1] ∪ [1; +∞). 5 ß 5 ™ C m 6= .
D m ∈ (−∞; −1) ∪ (1; +∞) \ . 3 3  2021 a + b > 1
Câu 327. Cho hàm số f (x) = x3 + ax2 + bx − 2 thỏa mãn . Số điểm cực GIA 3 + 2a + b < 0
trị của hàm số y = |f (|x|)| là A 9. B 11. C 2. D 5. QUỐC
Câu 328. Cho hàm số y = f (x) có bảng biến thiên như hình vẽ bên dưới. THPT x −∞ 0 2 +∞ y0 + 0 − 0 + 1 +∞ + GHIỆP N y T TỐ −∞ −1 THI
Hàm số y = f (x) đồng biến trên khoảng nào dưới đây? KỲ A (2; +∞). B (−∞; +∞). C (−∞; 1). D (0; +∞). TỚI
Câu 329. Cho hàm số y = f (x) có đồ thị như hình vẽ bên dưới. G
Hàm số y = f (x) đạt cực đại tại điểm nào sau đây? y 2 A x = 1. B x = −1. C y = −2. D y = 2. HƯỚN x −1 O 1 −2 2x + 1
Câu 330. Tìm tiệm cận ngang của đồ thị hàm số y = . x − 1 A x = −1. B y = −1. C x = 1. D y = 2. 1
Câu 331. Tìm giá trị nhỏ nhất của hàm số y = x − 5 + trên khoảng (0; +∞). x A min y = 2. B min y = −4. C min y = −3. D min y = −5. (0;+∞) (0;+∞) (0;+∞) (0;+∞)
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 95
Câu 332. Cho hàm số có đồ thị như hình vẽ bên dưới.
Tìm tất cả các giá trị thực của tham số m để đường thẳng y
y = 2m − 1 cắt đồ thị tại hai điểm phân biệt có hoành độ 5 lớn hơn 2. A 1 < m < 2. B 1 6 m < 2. C 1 6 m 6 2. D 1 < m < 3. 3 THỦ THI ĐỀ C 1 Á C À x O 1 2 3 V GIA x3 mx2
Câu 333. Có bao nhiêu giá trị nguyên của m để hàm số y = − + 2x + 2019 đồng 3 2 biến trên R? QUỐC A 3. B 4. C 5. D 6. THPT
Câu 334. Khoảng cách từ điểm cực tiểu của đồ thị hàm số y = x3 − 3x2 + 2 đến trục tung bằng GHIỆP A 1. B 2. C 4. D 0. N T 3
Câu 335. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = x4 − (m − TỐ 4 1 THI 1)x2 −
đồng biến trên khoảng (0; +∞)? 4x4 KỲ A 1. B 2. C 3. D 4. C Á C
Câu 336. Cho hàm số y = f (x) có bảng xét dấu đạo hàm như sau: G x −∞ −3 1 3 +∞ f 0(x) − 0 + 0 − 0 + TRON
Bất phương trình f (x) < ex2−2x + m đúng ∀x ∈ (0; 2) khi chỉ khi HÀM 1 1 O A m > f (1) − . B m > f (1) − . C m > f (0) − 1. D m > f (0) − 1. Ạ e e Đ
Câu 337. Tập hợp các giá trị của tham số m để hàm số y = |3x4 − 4x3 − 12x2 + m − 1| có G 7 điểm cực trị là DỤN A (0; 6). B (6; 33). C (1; 33). D (1; 6). G
Câu 338. Tâm đối xứng của đồ thị hàm số nào sau đây cách gốc tọa độ một khoảng lớn ỨN À nhất? V 2x − 1 1 − x A y = . B y = . SỐ x + 3 1 + x C y = 2x3 − 3x2 − 2. D y = −x3 + 3x − 2. HÀM
Câu 339. Một sợi dây kim loại dài a (cm). Người ta cắt đoạn dây đó thành hai đoạn, đoạn
có độ dài x (cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông
(a > x > 0). Tìm x để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất. a 2a πa 4a A x = (cm). B x = (cm). C x = (cm). D x = (cm). π + 4 π + 4 π + 4 π + 4
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 96
Câu 340. Gieo một con súc sắc cân đối đồng chất một lần. Giả sử con súc sắc xuất hiện
mặt k chấm. Xét phương trình −x3 + 3x2 − x = k. Tính xác suất để phương trình trên có 3 nghiệm thực phân biệt. 1 1 2 1 A . B . C . D . 3 2 3 6
Câu 341. Gọi S là tập hợp các giá trị của m sao cho đường thẳng d : y = mx − m − 3 cắt
đồ thị (C) : y = 2x3 − 3x2 − 2 tại ba điểm phân biệt A, B, I(1; −3) mà tiếp tuyến với (C)
tại A và B vuông góc với nhau. Tính tổng các phần tử của S. A −1. B 1. C 2. D 5.
Câu 342. Tìm tất cả các giá trị của m sao cho đồ thị hàm số y = x4 + (m + 1)x2 − 2m − 1
có ba điểm cực trị là ba đỉnh của một tam giác có một góc bằng 120◦. 2 2 A m = −1 − √ . B m = −1 − √ , m = −1. 3 3 3 3 1 C m = − √ . D m < −1. 3 3 2021
Câu 343. Đường thẳng y = m tiếp xúc với đồ thị (C) : y = −2x4 + 4x2 − 1 tại hai điểm
phân biệt. Tìm tung độ tiếp điểm. GIA A −1. B 1. C 0. D 3.
Câu 344. Cho hàm số f (x) có f 0(x) = x2017 · (x − 1)2018 · (x + 1), ∀x ∈ R. QUỐC
Hàm số đã cho có bao nhiêu cực trị? THPT A 0. B 1. C 2. D 3.
Câu 345 (Thi thử L5, Toán học tuổi trẻ, 2018). GHIỆP
[Phan Quốc Trí, dự án 12-EX6][2D1B4-3] Đường tiệm cận đứng và đường tiệm cận ngang N mx + 1 T
của đồ thị hàm số y =
cùng với hai trục tọa độ tạo thành một hình chữ nhật 2m + 1 − x TỐ
có diện tích bằng 3. Tìm m. 3 3 THI A m = 1, m = . B m = −1, m = − . 2 2 KỲ 3 C m = 1, m = − . D m = −1, m = 3. 2 TỚI G
Câu 346 (Thi thử L5, Toán học tuổi trẻ, 2018).
[Phan Quốc Trí, dự án 12-EX6][2D1B3-1] Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 8 f (x) =
+ x trên đoạn [1; 2] lần lượt là HƯỚN 1 + 2x 11 7 11 18 13 7 18 3 A ; . B ; . C ; . D ; . 3 2 3 5 3 2 5 2
Câu 347 (Thi thử L5, Toán học tuổi trẻ, 2018).
[Phan Quốc Trí, dự án 12-EX6][2D1B2-1] Viết phương trình đường thẳng đi qua hai điểm x2 + 2x + 3
cực trị của đồ thị hàm số y = . 2x + 1 A y = 2x + 2. B y = x + 1. C y = 2x + 1. D y = 1 − x.
Câu 348 (Thi thử L5, Toán học tuổi trẻ, 2018). 2x − 1
[Phan Quốc Trí, dự án 12-EX6][2D1B5-7] Trên đồ thị hàm số y = có bao nhiêu điểm 3x + 4 có tọa độ nguyên? A 1. B 2. C 0. D 4.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 97 x + 1 Câu 349. Cho hàm số y =
. Mệnh đề nào dưới đây đúng? 2 − x
A Hàm số nghịch biến trên từng khoảng xác định của nó.
B Hàm số đồng biến trên từng khoảng xác định của nó.
C Hàm số đồng biến trên (−∞; 2) ∪ (2; +∞).
D Hàm số nghịch biến trên khoảng (−∞; +∞). THỦ Câu 350. THI
Cho hàm số y = f (x) có đồ thị như hình bên. Khi đó f (x) đồng y ĐỀ biến trên các khoảng C A (−∞; −1) , (1; +∞). Á C 2 B (−∞; −1) , (−1; 0). À V C (−1; 0) , (1; +∞). −2 −1 1 2 O x GIA D (−1; 0) , (0; 1). x
Câu 351. Số đường tiệm cận của đồ thị hàm số y = √ là x2 + 1 QUỐC A 1. B 2. C 4. D 3.
Câu 352. Hàm số y = x3 − 3x2 + 3x − 4 có bao nhiêu cực trị? THPT A 1. B 2. C 0. D 3. GHIỆP
Câu 353. Giá trị của tham số m để phương trình x3 − 3x = 2m + 1 có ba nghiệm phân N T biệt là 3 1 3 1 TỐ A − < m < . B −2 < m < 2. C − ≤ m ≤ . D −2 ≤ m ≤ 2. 2 2 2 2 THI 2x + 3
Câu 354. Cho đường cong (C ) : y =
và M là điểm bất kỳ trên (C ). Giả sử d KỲ 1, d2 x − 1 C
tương ứng là các khoảng cách từ M đến hai tiệm cận của (C ), khi đó d1 · d2 bằng Á C A 3. B 4. C 5. D 6. G √ x + 4x2 − 3 Câu 355. Cho hàm số y =
có đồ thị (C ). Gọi m là số tiệm cận của (C ) và 2x + 3 TRON
n là giá trị của hàm số tại x = 1. Tính tích m × n. 6 14 3 2 A . B . C . D . HÀM 5 5 5 15 O
Câu 356. Giả sử A, B là hai điểm cực trị của đồ thị hàm số f (x) = x3 + ax2 + bx + c và Ạ Đ
đường thẳng AB đi qua gốc tọa độ. Tính giá trị nhỏ nhất của biểu thức P = abc+ab+c. G 16 25 A − . B −9. C − . D 1. 25 9 DỤN 3x − 1 G
Câu 357. Hai điểm M, N thuộc hai nhánh khác nhau của đồ thị hàm số y = . Khi x − 3 ỨN
đó độ đà đoạn thẳng M N ngắn nhất bằng √ À V A 8 2. B 2017. C 8. D 4. SỐ
Câu 358. Cho hàm số y = f (x) có bảng biến thiên như sau. x −∞ −1 1 +∞ HÀM f 0(x) − 0 + 0 − +∞ + 2 f (x) −2 −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 98
Hàm số đã cho đạt cực tiểu tại điểm x0 bằng A −1. B −2. C 1. D 2. x2 − 3x + 2
Câu 359. Đồ thị hàm số y =
có tất cả bao nhiêu đường tiệm cận? x2 − 1 A 3. B 1. C 0. D 2. Câu 360.
Hàm số nào có đồ thị như hình bên? y A y = −x3 + 3x2 − 1. B y = −x3 + 3x − 1. C y = x3 − 3x − 1. D y = −x3 − 3x − 1. −1 2 x −2 O 1 −1 −2 −3 2021
Câu 361. Cho hàm số y = f (x) có đạo hàm f 0(x) = x2(4 − x2). Hàm số f (x) đồng biến trên khoảng nào sau đây? GIA A (−2; 1). B (2; +∞). C (−∞; −2). D (−∞; +∞). x
Câu 362. Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = trên đoạn [−1; 2] QUỐC x2 + 1 bằng 1 9 THPT A 0. B − . C 1. D . 10 10
Câu 363. Cho hàm số y = f (x) xác định trên R và có bảng biến thiên như hình vẽ. GHIỆP N T x −∞ 0 2 +∞ TỐ f 0(x) + 0 − 0 + THI KỲ 2 +∞ + f (x) TỚI G −∞ −2
Hỏi phương trình 2f (x) + 3 = 0 có bao nhiêu nghiệm? HƯỚN A 4. B 1. C 2. D 3.
Câu 364. Cho hàm số y = f (x) có đạo hàm f 0(x) = x3 − x2 − m2x + m2, m là tham số thực.
Có bao nhiêu giá trị nguyên của m thuộc khoảng (−2019; 2019) để hàm số đã cho nghịch biến trên khoảng (1; 10)? A 4018. B 21. C 4016. D 18. Å 1 1 ã
Câu 365. Biết đồ thị hàm số y = x3 − 2ax2 + a2x + b có một điểm cực tiểu là − ; . 2 4
Khi đó giá trị cực đại của hàm số đã cho bằng 3 79 83 5 A . B . C . D . 4 108 108 4 Câu 366.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 99
Đường cong ở hình bên là đồ thị hàm số nào? y A y = x3 − 3x − 1. 3 B y = −x3 + 3x2 + 1. C y = x3 − 3x + 1. 1 O 1 D y = −x3 − 3x2 − 1. −1 x −1 THỦ 1 − 2x THI
Câu 367. Phương trình tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = −x + 2 ĐỀ lần lượt là C Á A x = −2; y = −2. B x = 2; y = −2. C x = −2; y = 2. D x = 2; y = 2. C x + 1 À Câu 368. Cho hàm số y =
. Khẳng định nào sau đây đúng? V 2 − x
A Hàm số đã cho đồng biến trên từng khoảng xác định của nó. GIA
B Hàm số đã cho nghịch biến trên R.
C Hàm số đã cho đồng biến trên khoảng (−∞; 2) ∪ (2; +∞). QUỐC
D Hàm số đã cho nghịch biến trên từng khoảng xác định của nó. THPT
Câu 369. Trong các hàm số sau, hàm số nào không đồng biến trên tập số thực? A y = 4x − 3 sin x + cos x. B y = 3x3 − x2 + 2x − 7. GHIỆP 3 N C y = 4x − . D y = x3 + x. T x TỐ
Câu 370. Có bao nhiêu tiếp tuyến của đồ thị hàm số y = x4 − 2x2 + 1 song song với trục THI hoành? KỲ A 2. B 1. C 0. D 3. C Á C
Câu 371. Tìm giá trị cực tiểu yCT của hàm số y = x3 − 3x2 + 2. G A yCT = 4. B yCT = 1. C yCT = 0. D yCT = −2. 1 TRON Câu 372. Cho hàm số y =
x3 + x2 − 2, có đồ thị (C). Phương trình tiếp tuyến của (C) 3
tại điểm có hoành độ là nghiệm của phương trình y00(x) = 0 là HÀM 7 7 7 7 O A y = −x − . B y = x − . C y = −x + . D y = x. Ạ 3 3 3 3 Đ
Câu 373. Xét tính đúng sai của các mệnh đề sau (với a, b, c, d là các hằng số). G
(I): Giá trị cực đại của hàm số y = f (x) luôn lớn hơn giá trị cực tiểu của nó. DỤN
(II): Hàm số y = ax4 + bx2 + c (a 6= 0) luôn có ít nhất 1 điểm cực trị. G
(III): Giá trị cực đại của hàm số y = f (x) luôn lớn hơn mọi giá trị của hàm số đó trên tập ỨN À xác định. V ax + b (IV): Hàm số y = f (x) =
(c 6= 0; ad − bc 6= 0) không có cực trị. SỐ cx + d Số mệnh đề đúng là: HÀM A 1. B 4. C 3. D 2. 2x + 1
Câu 374. Biết đường thẳng d : y = x − 2 cắt đồ thị hàm số y = tại hai điểm phân x − 1
biệt A và B có hoành độ lần lượt là xA và xB. Giá trị của biểu thức xA + xB bằng A 2. B 5. C 1. D 3.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 100
Câu 375. Tìm tất cả giá trị của tham số thực m để đường thẳng d : y = x + m cắt đồ thị −x + 1 hàm số y =
tại hai điểm phân biệt A, B. 2x − 1 A m < 0. B m ∈ R. C m > 1. D m = 5.
Câu 376. Cho hàm số y = x4 − 2(m + 1)x2 + m có đồ thị (C), m là tham số. (C) có ba
điểm cực trị A, B , C sao cho OA = BC, trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung khi √ A m = 0 hoặc m = 2. B m = 2 ± 2 2. √ √ C m = 3 ± 3 3. D m = 5 ± 5 5. x + 3 Câu 377. Cho hàm số y =
có đồ thị (C) và đường thẳng d : y = 2x + m. Tìm tất cả x + 1
các giá trị thực của tham số m để d cắt (C) tại hai điểm phân biệt M , N sao cho M N nhỏ nhất. A m = −1. B m = 3. C m = 2. D m = 1. 2021 Câu 378.
Cho hàm số y = f (x) có đạo hàm f 0(x), biết rằng đồ thị của y GIA
hàm số f 0(x) như hình vẽ. Biết f (a) > 0, hỏi đồ thị hàm số a c x
y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm? b O QUỐC A 4. B 2. THPT C 3. D 1. GHIỆP N T x2 + 2
Câu 379. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = √ có TỐ mx4 + 3
một đường tiệm cận ngang. THI A m < 0. B m > 3. C m = 0. D m > 0. KỲ
Câu 380. Thầy Tâm cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có TỚI 500 G thể tích bằng
m3. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê 3
nhân công để xây hồ là 500.000 đồng/m2. Khi đó, kích thước của hồ nước như thế nào để HƯỚN
chi phí thuê nhân công mà thầy Tâm phải trả thấp nhất? 20
A Chiều dài 20 m, chiều rộng 15 m và chiều cao m. 3 5
B Chiều dài 20 m, chiều rộng 10 m và chiều cao m. 6 10
C Chiều dài 10 m, chiều rộng 5 m và chiều cao m. 310
D Chiều dài 30 m, chiều rộng 15 m và chiều cao m. 27
Câu 381. Cho một tấm tôn hình chữ nhật có kích thước 10 cm × 16 cm. Người ta cắt bỏ
4 góc của tấm tôn 4 miếng hình vuông bằng nhau rồi gò lại thành một hình hộp chữ nhật
không có nắp. Để thể tích của hình hộp đó lớn nhất thì độ dài cạnh hình vuông của các
miếng tôn bị cắt bỏ bằng A 2 m. B 4 m. C 5 m. D 3 m.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 101 3x − 1 Câu 382. Cho hàm số y =
. Tìm m để đường thẳng y = x + m cắt đồ thị tại 2 điểm x − 2
phân biệt A, B sao cho tam giác OAB vuông tại O với O là gốc tọa độ. 3 5 3 A . B . C − . D −2. 2 2 2 √
Câu 383. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = x − 2 x trên đoạn [0; 9] lần
lượt là m và M . Giá trị của tổng m + M bằng THỦ A 0. B 1. C 2. D 3. THI x3 + x − 2 Câu 384. Cho hàm số y =
. Đồ thị hàm số có mấy tiệm cận? ĐỀ x2 − 3x + 2 C A 1. B 2. C 0. D 3. Á C 1 + x À Câu 385. Cho hàm số y =
. Mệnh đề nào dưới đây đúng? V 2 − x
A Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞). GIA
B Hàm số đồng biến trên R.
C Hàm số đồng biến trên các khoảng (−∞; 2) và (2; +∞). QUỐC
D Hàm số đồng biến trên khoảng R\{2}. THPT
Câu 386. Hàm số y = −x4 + 3x2 − 1 có mấy cực đại? A 2. B 0. C 1. D 3. GHIỆP N 1 T Câu 387. Cho hàm số y =
x3 − (m − 1)x2 + x + m. Tìm m để hàm số đồng biến trên 3 TỐ R. THI A 0 < m < 2. B m > 2 hoặc m < 0. KỲ C m ≥ 2 hoặc m ≤ 0. D 0 ≤ m ≤ 2. C Á C
Câu 388. Cho hàm số y = x4 + 2m(m + 2)x2 + m + 2, với m là tham số. Tìm tất cả các G
giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác có diện tích lớn nhất. TRON −1 −3 −1 A m = . B m = . C m = −1. D m = √ . 2 2 3 3 HÀM −x O Câu 389. Cho hàm số y =
có đồ thị là (C). Tìm tất cả các giá trị của m sao cho Ạ 2x + 1 Đ
đường thẳng y = x + m cắt (C) tại 2 điểm phân biệt A, B và tổng các hệ số góc của các tiếp G
tuyến với (C) tại A, B là lớn nhất. −1 DỤN A m = . B m = 0. C m = 1. D m = −1. 2 G ỨN
Câu 390. Hàm số nào sau đây đồng biến trên R? x À A y = x2 + 1. B y = . C y = x + 1. D y = x4 + 1. V x + 1 SỐ
Câu 391. Cho hàm số y = f (x) xác định trên khoảng K. Điều kiện đủ để hàm số y = f (x) đồng biến trên K là HÀM
A f 0(x) > 0 với mọi x ∈ K.
B f 0(x) > 0 tại hữu hạn điểm thuộc khoảng K.
C f 0(x) 6 0 với mọi x ∈ K.
D f 0(x) > 0 với mọi x ∈ K.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 102
Câu 392. Điểm cực đại của đồ thị hàm số y = −x3 + 6x2 − 9x + 4 là A (1; 0). B (3; 4). C (−1; 0). D (2; 2). 2x − 3
Câu 393. Đồ thị hàm số y =
có các đường tiệm cận đứng và tiệm cận ngang lần x − 1 lượt là A x = 1 và y = −3. B x = 2 và y = 1. C x = 1 và y = 2. D x = −1 và y = 2. Câu 394.
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên. y
Mệnh đề nào dưới đây đúng?
A a < 0, b > 0, c > 0, d > 0.
B a < 0, b < 0, c = 0, d > 0.
C a > 0, b < 0, c > 0, d > 0. 2021
D a < 0, b > 0, c = 0, d > 0. GIA x O QUỐC Câu 395. THPT
Đồ thị sau là đồ thị của hàm số nào sau? y 2x − 3 x A y = . B y = . 2x − 2 x − 1 GHIỆP x − 1 x + 1 N C . D y = . T x + 1 x − 1 1 TỐ THI x −1 O 1 −1 KỲ TỚI G
Câu 396. Tìm giá trị nhỏ nhất của hàm số y = sin2 x − 4 sin x − 5. A −20. B −8. C −9. D 0. HƯỚN
Câu 397. Tìm tập hợp tất cả các giá trị thực của tham số m để đường thẳng y = 3x + 1
cắt đồ thị hàm số y = x3 + 2x2 − mx + 1 tại ba điểm phân biệt. A (−4; +∞) \ {−3}. B (−7; +∞). C (−4; +∞). D (−7; +∞) \ {−3}. x + m Câu 398. Cho hàm số y =
(với m là tham số thực) thỏa mãn min y = 3. Mệnh đề x − 1 [2;4] nào dưới đây là đúng? A 3 < m ≤ 4. B 1 ≤ m < 3. C m > 4. D m < −1. Câu 399.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 103
Cho hàm số y = f (x) có đồ thị như hình bên. y x2 − x − 2 5
Số đường tiệm cận đứng của đồ thị hàm số y = f2(x) − 5f(x) là A 3. B 4. C 1. D 2. x THỦ −2 − O 1 1 2 THI ĐỀ C
Câu 400. Có bao nhiêu giá trị nguyên m ∈ (−10; 10) để hàm số y = m2x4 − 2(4m − 1)x2 + 1 Á C
đồng biến trên khoảng (1; +∞)? À V A 7. B 16. C 15. D 6. GIA
Câu 401. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như hình vẽ bên dưới QUỐC x −∞ 0 1 +∞ THPT y0 + − 0 + 0 +∞ + GHIỆP N T y TỐ −∞ −1 − THI KỲ C Á
Khẳng định nào sau đây là khẳng định đúng? C
A Hàm số có đúng một cực trị. G
B Hàm số có giá trị cực tiểu bằng 1. TRON
C Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1.
D Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1. HÀM O Ạ Câu 402. Đ G
Cho bảng biến thiên như hình vẽ bên. Mệnh x −∞ 1 2 +∞ đề nào sau đây sai? y0 + 0 − 0 + DỤN
A Hàm số đã cho đồng biến trên khoảng 3 +∞ + G ỨN (−∞; 1). y À
B Hàm số đã cho nghịch biến trên khoảng V −∞ 0 (0; 3). SỐ
C Hàm số đã cho đồng biến trên khoảng HÀM (2; +∞).
D Hàm số đã cho đồng biến trên khoảng (3; +∞). Câu 403.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 104
Đồ thị ở hình vẽ bên là của hàm số nào sau đây? y x + 3 x − 1 A y = . B y = . 1 − x x + 1 x + 2 2x + 1 C y = . D y = . x + 1 x + 1 2 1 −1 x O
Câu 404. Đồ thị của hàm số nào dưới đây có tiệm cận đứng? x2 − 3x + 2 x2 √ x A y = . B y = . C y = x2 − 1. D y = . x − 1 x2 + 1 x + 1
Câu 405. Tìm giá trị lớn nhất của hàm số y = f (x) = x3 − 2x2 + x − 2 trên đoạn [0; 2]. 50 A max y = 1. B max y = 0. C max y = −2. D max y = − . [0;2] [0;2] [0;2] [0;2] 27
Câu 406. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên sau 2021 GIA x −∞ 1 0 1 +∞ y0 − 0 + 0 − 0 + QUỐC +∞ + 0 +∞ + y THPT −1 − −1 − GHIỆP N
Tìm tất cả các giá trị thực của tham số m để phương trình f (x) − 1 = m có đúng hai T nghiệm. TỐ A m = −2, m ≥ −1. B m > 0, m = −1. THI C m = −2, m > −1. D −2 < m < −1. KỲ mx + 4
Câu 407. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = giảm trên TỚI x + m G khoảng (−∞; 1)? A 2. B Vô số. C 1. D 0. HƯỚN
Câu 408. Người ta cần xây một hồ chứa nước với dạng khối hộp chữ nhật không nắp có 500 thể tích bằng
m3. Đáy hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê 3
nhân công để xây hồ là 500.000 đồng/m2. Người ta xác định kích thước của hồ nước sao cho
chi phí thuê nhân công thấp nhất và chi phí đó là A 74 triệu đồng. B 75 triệu đồng. C 76 triệu đồng. D 77 triệu đồng.
Câu 409. Cho hàm số y = x3 + 3x2 có đồ thị (C) và điểm M (m; 0) sao cho từ M vẽ được
ba tiếp tuyến đến đồ thị (C), trong đó có hai tiếp tuyến vuông góc với nhau. Khi đó khẳng định nào sau đây đúng? Å 1 ã Å 1 ã Å 1 ã Å 1 ã A m ∈ ; 1 . B m ∈ − ; 0 . C m ∈ 0; . D m ∈ −1; − . 2 2 2 2 Câu 410.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 105
Cho hàm số f (x) có đạo hàm trên R và có y
đồ thị hàm y = f 0(x) như hình vẽ. Xét hàm 4
số g(x) = f (x2 − 2). Mệnh đề nào dưới đây 3 sai? 2
A Hàm số g(x) nghịch biến trên (−1; 0).
B Hàm số g(x) nghịch biến trên (−∞; −2). 1 THỦ −4 −3 −2 −1 1 2 3 4
C Hàm số g(x) nghịch biến trên (0; 2). THI O x
D Hàm số g(x) đồng biến trên (2; +∞). −1 ĐỀ C −2 Á C −3 À V −4 GIA
Câu 411. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = |3x4 − 4x3 − 12x2 + m| QUỐC có năm điểm cực trị? A 44. B 27. C 26. D 16. THPT 2x − 3
Câu 412. Số đường tiệm cận của đồ thị hàm số y = là x − 5 GHIỆP N A 0. B 1. C 2. D 3. T TỐ Câu 413. THI
Đường cong bên dưới là đồ thị của hàm số nào sau đây? y KỲ C Á A y = x3 + 3x. B y = x3 − 3x − 1. C G C y = x3 − 3x. D y = x3 − 3x + 1. TRON O x HÀM O Ạ Đ
Câu 414. Tiếp tuyến với đồ thị hàm số y = x3 − 4x + 1 tại điểm có hoành độ bằng 2 thuộc G
đồ thị hàm số có phương trình là DỤN A y = −8x + 17. B y = 8x − 16. C y = 8x + 15. D y = 8x − 15. G ỨN
Câu 415. Hàm số nào sau đây đồng biến trên R ? À 2x − 1 V A y = tan x. B y = x4 + 2. C y = x3 − 2019. D y = . x + 2 SỐ
Câu 416. Tập hợp tất cả giá trị thực của tham số m để hàm số y = x3 −mx2 +(m+6)x−m HÀM có điểm cực trị là
A (−∞; −3) ∪ (6; +∞).
B (−∞; −6) ∪ (3; +∞).
C (−∞; −3] ∪ [6; +∞).
D (−∞; −6] ∪ [3; +∞). Câu 417.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 106
Hình vẽ cho ở hình bên là đồ thị của hàm số nào sau đây? y x − 1 3 − x A y = . B y = . x + 1 x − 1 x + 1 x − 2 C y = . D y = . 1 x − 1 x − 1 O 1 x −1 Câu 418.
Cho hàm số y = ax4 + bx2 + c (a, b, c ∈ R) có đồ thị như hình y
bên.Trong các mệnh đề sau, mệnh đề nào đúng?
A a > 0, b < 0, c > 0.
B a > 0, b < 0, c < 0.
C a > 0, b > 0, c < 0.
D a < 0, b > 0, c < 0. O x
Câu 419. Tìm tất cả những giá trị thực của tham số m để đồ thị hàm số y = x4 − 2mx2 + 2021
m4 + 2m có 3 điểm cực trị tạo thành một tam giác đều. √ √ GIA A m = 3 3. B m = 1. C m = −1. D m = − 3 3. 1 Å 9 10 ã
Câu 420. Gọi M là giá trị lớn nhất của hàm số y = x3 − 2x2 + 1 trên khoảng − ; . 2 8 3 a a QUỐC Biết M = với
là phân số tối giản và a ∈ ∗ Z, b ∈ N . Tính S = a + b2. b b A S = 127. B S = 830. C S = 2. D S = 122. THPT √ √
Câu 421. Cho phương trình 4 1−x2 − (m − 2) · 2 1−x2 + 2m + 1 = 0. Có bao nhiêu giá trị
nguyên thuộc đoạn [−10; 20] của tham số m để phương trình có nghiệm? GHIỆP N A 6. B 7. C 8. D 9. T TỐ
Câu 422. Cho hàm số y = f (x) xác định trong khoảng (a, b) và có đồ thị như hình bên THI
dưới. Trong các khẳng định dưới đây, khẳng định nào sai? KỲ y TỚI G HƯỚN O a x1 x2 x3 x b
A Hàm số y = f (x) có đạo hàm trong khoảng (a; b). B f 0(x1) > 0.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 107 C f 0(x2) > 0. D f 0(x3) = 0. bx − c Câu 423. Cho hàm số y =
(a 6= 0) và a, b, c ∈ R có đồ thị như trên dưới. Khẳng x − a định nào sau đây đúng? y THỦ THI ĐỀ C Á C À V x O GIA QUỐC THPT
A a > 0, b < 0, c − ab < 0.
B a > 0, b > 0, c − ab < 0. GHIỆP
C a < 0, b > 0, c − ab < 0.
D a < 0, b < 0, c − ab > 0. N T
Câu 424. Đồ thị hàm số nào dưới đây không có tiệm cận ngang? √ TỐ 1 x2 + 1 A y = 3x. B g(x) = log x. C h(x) = . D k(x) = . THI 3 x + 1 2x + 3 KỲ
Câu 425. Cho hàm số y = f (x) có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực C Á
của tham số m để phương trình |f (x)| = m có 6 nghiệm phân biệt. C G y TRON −1 1 HÀM x O O Ạ Đ G −3 DỤN −4 G ỨN À A −4 < m < −3. B 0 < m < 3. C m > 4. D 3 < m < 4. V SỐ
Câu 426. Xét f (x) là một hàm số tùy ý. Trong bốn mệnh đề dưới đây có bao nhiêu mệnh đề đúng? HÀM
(I) Nếu f (x) là hàm số có đạo hàm tại x0 và đạt cực trị tại x0 thì f 0(x0) = 0.
(II) Nếu f 0(x0) = 0 thì hàm số đạt cực trị tại điểm x0.
(III) Nếu f 0(x0) = 0 và f 00(x) > 0 thì hàm số đạt cực đại tại điểm x0.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 108
(IV) Nếu f (x) đạt cực tiểu tại điểm x0 thì f 00(x) < 0. A 1. B 2. C 3. D 4. √
Câu 427. Tổng giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số f (x) = (x − 6) x2 + 4 √
trên đoạn [0; 3] có dạng a − b c với a là số nguyên và b, c là các số nguyên dương. Tính S = a + b + c. A S = 4. B S = −2. C S = −22. D S = 5.
Câu 428. Số giờ có ánh sáng của một thành phố X ở vĩ độ 40◦ bắc trong ngày thứ t của π
một năm không nhuận được cho bởi số d(t) = 3 sin
(t − 80) + 12, t ∈ Z và 0 < t ≤ 365. 182
Vào ngày nào trong năm thì thành phố X có nhiều giờ có ánh sáng nhất? A 262. B 353. C 80. D 171. √
Câu 429. Tìm tất cả các giá trị thực của m để phương trình x + 1 = m 2x2 + 1 có hai nghiệm phân biệt. √ √ √ 2 6 2 2021 A − < m < . B m < . 2 √ 6 √ 2 √ 6 2 6 GIA C m > . D < m < . 6 2 2
Câu 430. Tìm giá trị nguyên của tham số m để hàm số y = x4 − 2(m2 + 1)x2 + 2 có ba QUỐC
điểm cực trị sao cho giá trị cực tiểu đạt giá trị lớn nhất. A m = 2. B m = 0. C m = 1. D m = 2. THPT
Câu 431. Hàm số nào sau đây đồng biến trên R? x − 1 A y = . B y = x3 + 4x2 + 3x − 1. x + 2 GHIỆP 1 1 N C y = x4 − 2x2 − 1. D y = x3 − x2 + 3x + 1. T 3 2 TỐ
Câu 432. Cho hàm số y = x4 − 8x2 − 4. Các khoảng đồng biến của hàm số là THI A (−2; 0) và (2; +∞). B (−2; 0) và (0; 2). KỲ C (−∞; −2) và (0; 2).
D (−∞; −2) và (2; +∞). TỚI
Câu 433. Giá trị cực đại và cực tiểu của hàm số y = x3 − 3x2 − 9x + 30 lần lượt là G A 35 và 3. B 3 và 35. C −1 và 3. D 3 và −1.
Câu 434. Cho hàm số y = f (x) xác định trên khoảng (−2; −1) và có lim f (x) = 2, HƯỚN x→(−2)+ lim
f (x) = −∞. Hỏi khẳng định nào dưới đây là khẳng định đúng? x→(−1)−
A Đồ thị hàm số y = f (x) có đúng hai tiệm cận đứng là các đường thẳng x = −2 và x = −1.
B Đồ thị hàm số y = f (x) có đúng một tiệm cận ngang là đường thẳng y = 2.
C Đồ thị hàm số y = f (x) có đúng một tiệm cận đứng là đường thẳng x = −1.
D Đồ thị hàm số y = f (x) có đúng hai tiệm cận ngang là các đường thẳng y = 2 và y = −1. x
Câu 435. Tìm giá trị lớn nhất của hàm số y = trên đoạn [1; 5]. x2 + 4 √ 1 1 5 2 A max y = . B max y = . C max y = . D max y = . [1;5] 5 [1;5] 4 [1;5] 29 [1;5] 6
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 109 1
Câu 436. Tìm tất cả các giá trị thực của tham số m để hàm số y = x3−mx2+(2m+3)x+2 3 đồng biến trên R. A m > 3. B −1 6 m 6 3. C −1 < m < 3. D m < 3. Câu 437. y THỦ
Cho hàm số f (x). Đồ thị của hàm số y = f 0(x) trên [−3; 3] 2 THI
như hình vẽ (phần đường cong của đồ thị là một phần của 1 ĐỀ
parabol y = ax2 + bx + c ). Biết f (3) = 0, giá trị của C x Á −3 −2 − O 1 1 2 3 f (−1) + f (1) bằng C À V 8 16 8 16 A . B − . C − . D . GIA 3 3 3 3 QUỐC Câu 438. y
Cho hàm số y = f (x) liên tục trên y = f 0(x) R và có đồ thị hàm THPT
số y = f 0(x) như hình bên. Hỏi hàm số g(x) = f (3 − 2x)
nghịch biến trên khoảng nào sau đây? GHIỆP N −2 2 T x O 5 TỐ THI KỲ A (−1; +∞). B (−∞; −1). C (1; 3). D (0; 2). C Á C  G  − 1 + a − b + c > 0
Câu 439. Cho các số thực a, b, c thỏa mãn
. Số giao điểm của đồ thị 8 + 4a + 2b + c < 0 TRON
hàm số y = x3 + ax2 + bx + c và trục Ox là: HÀM A 0. B 2. C 1. D 3. O Ạ Đ G
Câu 440. Hàm số nào sau đây không có cực trị? DỤN A y = x3 − 2x2 + 2x + 1. B y = 2x2 − 3x + 2. G 1 x3 2 C y = x4 − 3x2 + 2. D y = − 2x2 + 3x + . ỨN 2 3 3 À V
Câu 441. Cho hàm số y = x3 − (m + 3)x2 + (m2 + 1) x + m + 5 (1). Tổng các giá trị m SỐ
nguyên để hàm số (1) có cực trị là HÀM A 6. B 5. C 10. D 7.
Câu 442. Cho hàm số y = f (x) có đồ thị như hình vẽ dưới. Mệnh đề nào dưới đây là mệnh đề sai?
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 110 y 4 3 2 1 −1 O x 1 2 −1
A Hàm số đồng biến trên các khoảng (−∞; 0) và (1; +∞).
B Hàm số nghịch biến trên khoảng (0; 1).
C Hàm số đồng biến trên các khoảng (−∞; 3) và (1; +∞). 2021
D Hàm số đạt cực trị tại các điểm x = 0 và x = 1. GIA
Câu 443. Cho hàm số y = (x2 + 3) (x2 − 5) có đồ thị (C). Mệnh đề nào dưới đây là mệnh đề đúng?
A (C) cắt trục hoành tại hai điểm phân biệt. QUỐC
B (C) cắt trục hoành tại một điểm. THPT
C (C) cắt trục hoành tại ba điểm phân biệt.
D (C) không cắt trục hoành. GHIỆP
Câu 444. Cho hàm số y = f (x) xác định trên R \ {1}, liên tục trên mỗi khoảng xác định N T
và có bảng biến thiên như sau TỐ THI x −∞ 1 2 +∞ KỲ y0 + + 0 − TỚI G −∞ 4 y 2 −∞ −∞ HƯỚN
Mệnh đề nào dưới đây là mệnh đề đúng?
A Đồ thị hàm số có đúng một tiệm cận ngang.
B Đồ thị hàm số không có tiệm cận đứng, không có tiệm cận ngang.
C Đồ thị hàm số có đúng một tiệm cận đứng.
D Đồ thị hàm số có hai tiệm cận ngang. 1
Câu 445. Giá trị lớn nhất của hàm số y = 2x + khi x < 0 là x √ √ A 2 2. B −2 2. C Không tồn tại. D 4.
Câu 446. Cho hàm số y = f (x) xác định, liên tục trên R và có bảng biến thiên như sau
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 111 x −∞ −2 1 +∞ y0 − 0 + 0 − +∞ + 1 y −4 −∞ THỦ THI
Số nghiệm thực của phương trình |f (x)| = 3 là ĐỀ A 3. B 1. C 4. D 2. C Á Å 2 ã C
Câu 447. Giá trị m nguyên lớn nhất để hàm số y = x3 + (3 − 2m)x2 + m − x + 5 đồng À 3 V
biến trên R thuộc tập hợp nào sau đây? ï 3 ò GIA A [1; 2). B (−2; 1]. C 1; . D (1; 3). 2
Câu 448. Số giá trị nguyên của tham số m để phương trình 3 sin4 x + m cos2 x + 2 = 0 có h π i QUỐC nghiệm trên đoạn 0; là 4 A 3. B 5. C 4. D 2. THPT 3x − 2 Câu 449. Cho hàm số y =
có đồ thị (C) và điểm A(−5; 5). Tìm tất cả giá trị thực x + 1 GHIỆP N
của tham số m để đường thẳng d : y = −x + m cắt (C) tại hai điểm phân biệt M , N sao T
cho tứ giác OAM N là hình bình hành (O là gốc tọa độ). TỐ √ A m = 3. B m = 2 + 5. THI √ √ √ C m = 2 + 5, m = 2 − 5. D m = 2 − 5. KỲ C
Câu 450. Ông A cần sản xuất một cái thang để trèo qua một bức tường nhà. Ông muốn Á C
cái thang phải luôn đi qua vị trí điểm C, biết rằng điểm C cao 3m so với nền nhà và điểm C G
cách tường nhà 2m. Giả sử kinh phí sản xuất thang là 500000 đồng/1m dài. Hỏi ông cần ít TRON
nhất bao nhiêu tiền để sản xuất cái thang đó?(Kết quả làm tròn đến hàng nghìn đồng). A 3512000 đồng. B 4755000 đồng. C 2750000 đồng. D 3115000 đồng. HÀM
Câu 451. Cho hàm số y = x3 − 3x + 2. Tọa độ điểm cực tiểu của đồ thị hàm số là O Ạ Đ A (−2; 0). B (−1; 4). C (0; 1). D (1; 0). G 3x + 2
Câu 452. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y = . x + 1 DỤN A x = −1. B y = 3. C y = 2. D x = 3. G ỨN Câu 453. À V
Cho hàm số y = f (x) có đồ thị như hình bên. Mệnh đề nào dưới y 2 SỐ đây đúng?
A Hàm số có giá trị cực tiểu bằng 2. HÀM
B Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng 2 x − O 2.
C Hàm số đạt cực đại tại x = 0 và đạt cực tiểu tại x = 2. −2
D Hàm số có ba cực trị.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 112 Câu 454.
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các y hàm số bên dưới? 2 A y = −x4 + 1. B y = −x4 + 2x2 + 1. 1 C y = −x4 − 2x2 + 1. D y = −x4 + 2x2 − 1. −2 −1 1 2 x O −1
Câu 455. Trong các hàm số sau, hàm số nào đồng biến trên tập xác định của nó? A y = x3 + x − 5. B y = x4 + 3x2 + 4. 2x − 1 C y = x2 + 1. D y = . x + 1 √ √
Câu 456. Tìm tập giá trị T của hàm số y = x − 3 + 5 − x. √ √ î ó î ó A T = (3; 5). B T = [3; 5]. C T = 2; 2 . D T = 0; 2 .
Câu 457. Hàm số y = x3 − 3x2 nghịch biến trên khoảng nào dưới đây? A (−1; 1). B (−∞; 1). C (2; +∞). D (0; 2). 2021
Câu 458. Tìm số giao điểm n của đồ thị hàm số y = x2|x2 − 3| và đường thẳng y = 2. GIA A n = 8. B n = 2. C n = 6. D n = 4. mx + 4
Câu 459. Tìm tất cả các giá trị của m để hàm số y =
nghịch biến trên (−∞; 1). x + m QUỐC A −2 < m < −1. B −2 < m < 2. C −2 ≤ m ≤ 1. D −2 < m ≤ −1. THPT
Câu 460. Tìm tất cả các giá trị của m để phương trình sin4 x + cos4 x + cos2 4x = m có h π π i
bốn nghiệm phân biệt thuộc đoạn − ; . 4 4 47 3 47 3 GHIỆP A m ≤ hoặc m ≥ . B < m < . N 64 2 64 2 T 47 3 47 3 C < m ≤ . D ≤ m ≤ . TỐ 64 2 64 2 Câu 461. THI
Cho hàm số y = f (x) có đạo hàm trên R. Đường cong y KỲ
trong hình vẽ bên là đồ thị của hàm số y = f 0(x) (y = TỚI
f 0(x) liên tục trên R). Xét hàm số g(x) = f (x2 − 3). G
Mệnh đề nào dưới đây sai?
A Hàm số g(x) đồng biến trên (−1; 0). HƯỚN 2
B Hàm số g(x) nghịch biến trên (−∞; −1).
C Hàm số g(x) nghịch biến trên (1; 2).
D Hàm số g(x) đồng biến trên (2; +∞). − x 2 O 1
Câu 462. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ −1 0 1 +∞ y0 + 0 − 0 + 0 − 2 2 y −∞ 1 −∞
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 113
Giá trị cực đại của hàm số là A y = −1. B y = 0. C y = 2. D y = 1.
Câu 463. Cho hàm số y = f (x) có đồ thị như sau y 2 THỦ x THI −2 O 2 ĐỀ −2 C Á C À V
Hàm số y = f (x) đồng biến trên khoảng nào dưới đây? GIA A (−1; 2). B (−2; 0). C (−1; 3). D (2; 5).
Câu 464. Tìm tọa độ các điểm cực trị của đồ thị hàm số y = x3 − 3x2. QUỐC A (0; 0) và (−2; −4). B (0; 0) và (2; −4). C (0; 0) và (2; 4). D (0; 0) và (1; −2). THPT
Câu 465. Đồ thị của hàm số nào sau đây có tiệm cận ngang? √ √ 4 − x2 x − 1 x2 + 1 √ GHIỆP A y = . B y = . C y = . D y = x2 − 1. N x x + 1 x T 2x + m TỐ
Câu 466. Tìm giá trị của tham số m biết giá trị lớn nhất của hàm số y = trên x − 1 THI [2; 5] bằng 7. KỲ A m = 3. B m = 8. C m = −3. D m = 18. C Á C
Câu 467. Cho hàm số y = f (x) có đạo hàm trên R và f 0(x) > 0, ∀x ∈ (0; +∞). Biết G
f (1) = 2. Khẳng định nào dưới đây có thể xảy ra? A f (2) + f (3) = 4. B f (2) = 1. TRON C f (2017) > f (2018). D f (−1) = 2. HÀM
Câu 468. Đồ thị hàm số y = x3 − 3x2 + 2ax + b có điểm cực tiểu A(2; −2). Khi đó a + b O bằng Ạ Đ A −2. B 4. C 2. D −4. G Câu 469. DỤN
Cho hàm số y = f (x). Hàm số y = f 0(x) có đồ thị như hình bên. y G
Tìm m để hàm số y = f (x2 + m) có 3 điểm cực trị? ỨN À A m ∈ [0; 3]. B m ∈ [0; 3). 1 2 3 V x O C m ∈ (3; +∞). D m ∈ (−∞; 0). SỐ HÀM
Câu 470. Biết rằng hàm số y = (m2 − 1)x3 + (m − 1)x2 − x + 4 nghịch biến trên khoảng
(−∞; +∞) với m ∈ [a; b]. Khi đó biếu thức T = 2a + b có giá trị bằng 3 A . B 0. C −1. D 1. 2
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 114
Câu 471. Cho hàm số y = f (x) xác định và có đạo hàm cấp một và cấp hai trên khoảng
(a; b) và x0 ∈ (a; b). Khẳng định nào sau đây là sai?
A Hàm số đạt cực đại tại x0 thì y0(x0) = 0.
B y0(x0) = 0 và y00(x0) = 0 thì x0 không là điểm cực trị của hàm số.
C y0(x0) = 0 và y00(x0) > 0 thì x0 là điểm cực tiểu của hàm số.
D y0(x0) = 0 và y00(x0) 6= 0 thì x0 là điểm cực trị của hàm số.
Câu 472. Tìm m để hàm số y = x3 − 3x2 + mx + 2 tăng trên khoảng (1; +∞). A m 6= 3. B m ≥ 3. C m ≤ 3. D m < 3. 2x + 4
Câu 473. Tìm tất cả các giá trị của m để đồ thị hàm số y = có tiệm cận đứng. x − m A m > −2. B m = −2. C m < −2. D m 6= −2. √ √
Câu 474. Biết rằng giá trị lớn nhất của hàm số y = x +
4 − x2 + m là 3 2. Giá trị của m là √ √ √ √ 2 A m = 2. B m = 2 2. C m = − 2. D m = . 2021 2 Câu 475. GIA
Cho hàm số y = f (x) có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị y của hàm số nào? QUỐC A y = (x − 1)3. B y = x3 − 1. x C y = x3 + 1. D y = (x + 3)3. O 1 −1 THPT 1 GHIỆP
Câu 476. Cho các hàm số (I) : y = x2 +3; (II) : y = x3 +3x2 +3x−5; (III) : y = x− ; N x + 2 T
(IV ) : y = (2x + 1)7. Các hàm số không có cực trị là TỐ A (I) , (II) , (III). B (II) , (III) , (IV ). THI C (III) , (IV ) , (I). D (IV ) , (I) , (II). KỲ x3 − 3x − 2
Câu 477. Tiệm cận đứng của đồ thị hàm số y = là x2 + 3x + 2 TỚI A x = −1; x = −2. B x = −2. G C x = −1.
D Không có tiệm cận đứng. 2x + 1 HƯỚN
Câu 478. Tìm m để đường thẳng y = x + m (d) cắt đồ thị hàm số y = (C) tại hai x − 2
điểm phân biệt thuộc hai nhánh của đồ thị (C). 1 1 ß 1 ™ A m ∈ R. B m > − . C m < − . D m ∈ R \ − . 2 2 2
Câu 479. Cho hàm số y = x + sin 2x + 2017. Tìm tất cả các điểm cực tiểu của hàm số. π π A x = − + k2π, k ∈ Z. B x = − + kπ, k ∈ Z. 3 3 π π C x = + k2π, k ∈ Z. D x = + kπ, k ∈ Z. 3 3 √
Câu 480. Số tiệm cận ngang của đồ thị hàm số y = 2x − 1 + 4x2 − 4 là A 0. B 1. C 2. D 3.
Câu 481. Cho hàm số y = f (x) = ax3 + bx2 + cx + d, (a 6= 0). Khẳng định nào sau đây đúng?
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 115
A Đồ thị hàm số luôn cắt trục hoành.
B Hàm số luôn có cực trị. C lim f (x) = +∞.
D Hàm số luôn tăng trên R. x→−∞ Câu 482.
Một công ty muốn làm đường ống dẫn dầu B
từ một kho A ở trên bờ biển đến một vị trí B
trên một hòn đảo. Hòn đảo cách bờ biển 6 km. THỦ
Gọi C là điểm trên bờ sao cho BC vuông góc THI 6 km
với bờ biển. Khoảng cách từ A đến C là 9 km. ĐỀ C
Người ta cần xác định một vị trí D trên AC Á C
để lắp ống dẫn theo đường gấp khúc ADB. À C A V
Tính khoảng cách AD để số tiền chi phí thấp D 9 km
nhất, biết rằng giá để lắp đặt mỗi km đường GIA
ống trên bờ là 100.000.000 đồng và dưới nước là 260.000.000 đồng. QUỐC A 6 km. B 6.5 km. C 7 km. D 7.5 km. THPT
Câu 483. Cho hàm số y = x4 − 2mx2 − 2m2 + m4 có đồ thị (C). Biết đồ thị (C) có ba
điểm cực trị A, B, C và ABDC là hình thoi trong đó D(0; −3), A thuộc trục tung. Khi đó GHIỆP N m thuộc khoảng nào? T Å 1 ã Å 1 9 ã Å 9 ã TỐ A m ∈ −1; . B m ∈ ; . C m ∈ ; 2 . D m ∈ (2; 3). 2 2 5 5 THI x3 KỲ Câu 484. Cho hàm số y =
− ax2 − 3ax + 4. Để hàm số đạt cực trị tại x1, x2 thỏa mãn 3 C Á x2 + 2ax a2 1 2 + 9a C + = 2 a2 x2 + 2ax G 2 1 + 9a thì a thuộc khoảng nào? Å 7 ã Å 7 ã Å 5 ã TRON A a ∈ −5; − . B a ∈ − ; −3 . C a ∈ −3; − . D a ∈ (−2; −1). 2 2 2 x + m 16 HÀM Câu 485. Cho hàm số y =
(m là tham số thực) thỏa mãn min y + max y = . O x + 1 [1;2] [1;2] 3 Ạ
Mệnh đề nào dưới đây là đúng? Đ G A 2 < m ≤ 4. B 0 < m ≤ 2. C m ≤ 0. D m > 4. DỤN
Câu 486. Cho hàm số y = x3 − 6x2 + 12x + 1. Khẳng định nào sau đây là đúng? G
A Hàm số đồng biến trên R. ỨN B Hàm số nghịch biến R. À V
C Hàm số đồng biến trên khoảng (−∞; 2) và nghịch biến trên khoảng (2; +∞). SỐ
D Hàm số nghịch biến trên khoảng (−∞; 2) và đồng biến trên khoảng (2; +∞).
Câu 487. Điểm cực đại của đồ thị hàm số y = −2x3 − 3x2 + 12x là HÀM A (−2; −20). B (−2; 7). C (1; 7). D (1; −20). x4 3x2 ï 4 3 ò
Câu 488. Giá trị lớn nhất của hàm số y = − x3 − + 2x trên đoạn − ; là 2 2 3 2 17 17 112 A −2. B . C . D − . 32 8 81
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 116 x + 2 Câu 489. Cho hàm số y =
có đồ thị là (C). Khẳng định nào sau đây là đúng? x − 2
A Đồ thị (C) có một tiệm cận đứng là x = 2 và một tiệm cận ngang là y = 1.
B Đồ thị (C) có một tiệm cận đứng là x = −2 và một tiệm cận ngang là y = 1.
C Đồ thị (C) có một tiệm cận đứng là x = −2 và một tiệm cận ngang là y = 2.
D Đồ thị (C) có một tiệm cận đứng là x = −2 và một tiệm cận ngang là y = −2.
Câu 490. Hàm số y = x3 + 3(m − 3)x2 + m(m − 2)x + 1 đạt cực tiểu tại x = −2 khi và chỉ khi A m = 6. B m = 6 hay m = 8. C m = 8. D 6 < m < 8. Câu 491.
Hàm số y = f (x) có đồ thị như hình vẽ. Khẳng định nào sau y đây đúng?
A Đồ thị hàm số có điểm cực đại là (1; −1). 3 2021
B Đồ thị hàm số có điểm cực tiểu là (1; −1). GIA
C Hàm số có điểm cực tiểu là x = −1. 1
D Hàm số có điểm cực tiểu là (1; −1). O 1 x −1 QUỐC −1 THPT
Câu 492. Cho hàm số y = f (x) xác định trên R \ {1}, liên tục trên mỗi khoảng xác định GHIỆP
và có bảng biến thiên như hình vẽ sau: N T x −∞ −1 1 +∞ TỐ y0 − 0 + + THI 1 +∞ −1 − KỲ y √ TỚI − 2 −∞ G
Tìm tập hợp tất cả các giá trị thực của tham số m sao cho phương trình f (x) = m có ba HƯỚN nghiệm thực phân biệt. √ √ Ä ó Ä ä A − 2; −1 . B − 2; −1 . C (−1; 1]. D (−1; 1).
Câu 493. Tìm m để hàm số y = x3 − 3(m + 3)x2 − 6(m − 1)x + 1 luôn luôn đồng biến trên R. A −7 6 m 6 −1. B −7 < m < −1. C m 6 −7 hoặc m > −1.
D m < −7 hoặc m > −1.
Câu 494. Hàm số y = x3 + 3(m + 1)x2 − 6(m − 3)x + 1 đạt cực trị tại hai điểm x1, x2 thỏa
x2 + x2 < 64 khi và chỉ khi 1 2   − 6 < m 6 −5 − 6 < m < −5 A  . B  . 1 6 m < 3 1 < m < 3
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 117  m < −6 C  . D −6 < m < 3. m > 3
Câu 495. Cho hàm số y = f (x) có bảng biến thiên: x −∞ −1 1 +∞ THỦ y0 − 0 + 0 − THI +∞ + 4 ĐỀ C y Á C −∞ À 0 V GIA Chọn khẳng định đúng?
A Hàm số nghịch biến trên (−1; +∞).
B Hàm số nghịch biến trên (−1; 1). QUỐC
C Hàm số đồng biến trên (−∞; −1).
D Hàm số đồng biến trên (−1; 1). THPT Câu 496. GHIỆP
Cho hàm số f (x) = ax3 + bx2 + cx + d (a, b, c, d ∈ R). Đồ y N T
thị của hàm số y = f (x) như hình vẽ bên. Số nghiệm TỐ
thực của phương trình 3f (x) − 1 = 0 là 2 THI KỲ A 3. B 2. C 1. D 4. 2 C x O Á C G −2 TRON HÀM Câu 497. y O Ạ
Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ bên. Tất cả y Đ
các giá trị của tham số m để hàm số y = |f (x) + m| có ba điểm G cực trị là 1 DỤN x O x O G A m ≤ −1 hoặc m ≥ 3. B m = −1 hoặc m = 3. ỨN À C m ≤ −3 hoặc m ≥ 1. D 1 ≤ m ≤ 3. V −3 SỐ
Câu 498. Cho x, y là hai số không âm thỏa mãn: x + y = 2. Giá trị nhỏ nhất của biểu thức HÀM 1 P = x3 + x2 + y2 − x + 1 là 3 7 17 115 A min P = . B min P = 5. C min P = . D min P = . 3 3 3
Câu 499. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên dưới đây.
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 118 x +∞ −1 0 2 3 +∞ f 0(x) + 0 − 0 + 2 +∞ + f (x) −2 2 −∞ −2 −
Tìm tất cả các giá trị thực của tham số m để phương trình f (x) = f (m) có ba nghiệm phân biệt. A m ∈ (−1; 3) \ {0; 2}. B m ∈ [−1; 3] \ {0; 2}. C m ∈ (−1; 3). D m ∈ (−2; 2). 2021 GIA QUỐC THPT GHIỆP N T TỐ THI KỲ TỚI G HƯỚN
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 119 PHẦN I
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC KỲ THI TỐT NGHIỆP TRUNG
HỌC PHỔ THÔNG QUỐC GIA 2017-2020 BẢNG ĐÁP ÁN THAM KHẢO 1. C 2. C 3. B 4. D 5. A 6. A 7. C 8. B 9. D 10. C 11. A 12. D 13. D 14. B 15. A 16. B 17. D 18. D 19. D 20. A 21. D 22. A 23. B 24. B 25. A 26. B 27. A 28. C 29. A 30. B 31. A 32. A 33. A 34. A 35. C 36. B 37. C 38. C 39. A 40. C 41. C 42. D 43. C 44. A 45. B 46. C 47. D 48. D 49. B 50. D 51. A 52. A 53. D 54. C 55. B 56. C 57. A 58. B 59. D 60. B 61. A 62. A 63. A 64. B 65. D 66. C 67. D 68. C 69. B 70. D 71. D 72. B 73. C 74. B 75. B 76. D 77. B 78. A 80. D 81. A 82. D 83. B 84. D 85. A 86. C 87. D 88. A 89. A 90. D 91. A 92. D 93. D 94. A 95. C 96. B 97. B 98. B 99. D 100. A 101. B 102. A 103. D 104. D 105. C 106. B 107. B 108. C 109. B 110. B 111. D 112. D 113. C 114. B 115. A 116. A 117. A 118. B 119. A 120. A 121. B 122. D 123. D 124. B 125. D 126. A 127. B 128. A 129. C 130. A 131. D 132. B 133. D 134. D 135. B 136. D 137. A 138. C 139. A 140. C 141. D 142. C 143. B 144. C 145. A 146. C 147. C 148. B 149. D 150. D 151. B 152. B 153. B 154. C 155. B 156. B 157. C 158. C 159. D 160. B 161. C 162. C 163. B 164. A 165. B 166. D 167. D 168. B 169. D 170. A 171. C 172. A 173. C 174. C 175. A 176. C 177. A 178. C 179. D 180. B 181. A 182. C 183. B 184. C 185. A 186. B 187. B 188. A 189. B 190. C 191. C 192. D 193. D 194. A 195. B 196. C 197. C 198. C 199. D 200. A 201. B 202. C 203. A 204. C 205. D 206. A 207. B 208. D 209. C 210. C 211. A 212. A 213. C 214. C 215. B 216. C 217. B 218. D 219. B 220. A 221. A 222. C 223. C 224. B 225. B 226. C 227. B 228. C 229. D 230. B 231. C 232. B 233. A 234. B 235. B 236. B 237. B 238. D 239. C 240. A 241. D 242. D 243. B 244. D 245. C 246. C 247. C 248. A 249. A 250. C 251. D 252. C 253. D 254. B 255. B 256. A 257. A 258. D 259. B 260. C 261. D 262. A 263. D 264. C 265. D 266. C 267. C 268. A 269. C 270. B 271. B 272. D 273. D 274. B 275. A 276. C 277. D 278. D 279. A 280. C 281. A 282. A 283. B 284. B 285. C 286. D 287. B 288. B 289. C 290. D 291. A 292. A 293. A 294. C 295. D 296. D 297. D 298. C 299. D 300. C 301. A 302. C 303. B 304. A 305. C 306. A 307. A 308. D 309. D 310. D 311. C 312. D 313. C
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 1 PHẦN II
HÀM SỐ VÀ ỨNG DỤNG ĐẠO HÀM
TRONG CÁC ĐỀ THI THỬ 2017-2020 BẢNG ĐÁP ÁN THAM KHẢO THỦ 1. A 2. B 3. D 4. D 5. A 6. D 7. C 8. C 9. C 10. A THI 11. B 12. B 13. C 14. A 15. A 16. A 17. A 18. D 19. C 20. C ĐỀ 21. B 22. C 23. D 24. B 25. C 26. D 27. C 28. C 29. B 30. A C 31. B 32. C 33. B 34. C 35. A 36. C 37. B 38. D 39. D 40. B Á C 41. C 42. C 43. C 44. B 45. D 46. B 47. B 48. D 49. D 50. D À 51. A 52. A 53. D 54. A 55. D 56. B 57. A 58. D 59. A 60. C V 61. A 62. A 63. D 64. A 65. C 66. B 67. C 68. C 69. A 70. C GIA 71. B 72. D 73. C 74. D 75. D 76. D 77. D 78. D 79. C 80. D 81. C 82. D 83. B 84. B 85. C 86. B 87. D 88. C 89. B 90. D 91. D 92. B 93. B 94. B 95. D 96. D 97. C 98. A 99. A 100. B QUỐC 101. A 102. D 103. D 104. B 105. C 106. A 107. A 108. D 109. A 110. A 111. A 112. D 113. C 114. B 115. D 116. D 117. A 118. C 119. D 120. C THPT 121. D 122. A 123. D 124. A 125. D 126. B 127. C 128. D 129. C 130. B 131. C 132. D 133. C 134. C 135. D 136. C 137. A 138. A 139. C 140. C GHIỆP 141. A 142. A 143. D 144. A 145. C 146. D 147. A 148. A 149. B 150. C N T 151. D 152. C 153. B 154. C 155. A 156. C 157. C 158. A 159. B 160. A TỐ 161. B 162. D 163. B 164. C 165. D 166. D 167. D 168. B 169. A 170. D THI 171. B 172. D 173. A 174. C 175. D 176. A 177. C 178. A 179. B 180. D KỲ 181. B 182. B 183. A 184. C 185. B 186. B 187. C 188. B 189. A 190. D C 191. C 192. B 193. D 194. C 195. A 196. C 197. C 198. D 199. A 200. C Á C 201. A 202. C 203. D 204. C 205. A 206. C 207. B 208. C 209. A 210. A G 211. C 212. D 213. A 214. A 215. B 216. A 217. D 218. A 219. C 220. C 221. A 222. C 223. C 224. D 225. A 226. D 227. A 228. D 229. C 230. C TRON 231. C 232. D 233. D 234. C 235. A 236. C 237. A 238. A 239. D 240. C 241. D 242. D 243. B 244. B 245. C 246. C 247. D 248. D 249. A 250. B HÀM 251. B 252. B 253. B 254. A 255. A 256. A 257. D 258. A 259. D 260. C O 261. C 262. D 263. D 264. C 265. A 266. B 267. D 268. C 269. D 270. D Ạ Đ 271. A 272. D 273. B 274. C 275. A 276. C 277. D 278. C 279. C 280. C G 281. A 282. C 283. D 284. D 285. A 286. C 287. B 288. C 289. A 290. D 291. C 292. B 293. D 294. B 295. A 296. A 297. B 298. A 299. D 300. C DỤN 301. B 302. A 303. A 304. C 305. A 306. D 307. B 308. B 309. A 310. B G 311. B 312. B 313. C 314. A 315. C 316. C 317. A 318. A 319. C 320. C ỨN 321. D 322. B 323. A 324. C 325. B 326. D 327. B 328. A 329. B 330. D À V 331. C 332. A 333. C 334. B 335. C 336. A 337. D 338. A 339. C 340. A SỐ 341. A 342. A 343. B 344. C 345. C 346. A 347. B 348. B 349. B 350. C 351. B 352. C 353. A 354. C 355. A 356. C 357. C 358. A 359. D 360. B HÀM 361. A 362. A 363. D 364. A 365. A 366. C 367. D 368. A 369. C 370. B 371. D 372. A 373. D 374. B 375. B 376. B 377. B 378. B 379. D 380. C 381. A 382. D 383. C 384. A 385. C 386. A 387. B 388. C 389. B 390. C 391. A 392. B 393. C 394. D 395. D 396. B 397. A 398. C 399. A 400. B 401. D 402. B 403. D 404. D 405. B 406. C 407. C 408. B 409. C 410. A
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 2 411. B 412. C 413. C 414. D 415. C 416. A 417. C 418. A 419. A 420. B 421. B 422. C 423. B 424. B 425. D 426. A 427. A 428. D 429. D 430. B 431. D 432. A 433. A 434. C 435. B 436. B 437. B 438. B 439. D 440. A 441. A 442. C 443. A 444. C 445. B 446. C 447. D 448. C 449. C 450. A 451. D 452. B 453. C 454. B 455. A 456. C 457. D 458. C 459. D 460. C 461. C 462. C 463. D 464. B 465. B 466. A 467. D 468. C 469. B 470. B 471. B 472. B 473. D 474. A 475. A 476. B 477. B 478. A 479. B 480. B 481. A 482. B 483. B 484. A 485. D 486. A 487. C 488. B 489. A 490. B 491. B 492. B 493. A 494. B 495. D 496. A 497. A 498. A 499. A 2021 GIA QUỐC THPT GHIỆP N T TỐ THI KỲ TỚI G HƯỚN
Hàm số và ứng dụng đạo hàm
Những nẻo đường phù sa Trang 3
Document Outline

  • HAM SO VA UNG DUNG DAO HAM TRONG DE TNTHPT QG VA CAC DE THI THU
  • TRA DAP AN