Hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị – bảng biến thiên (phần 1 – 10) Toán 12

Tài liệu gồm 21 trang được biên soạn bởi thầy Lương Tuấn Đức (Giang Sơn), tuyển tập hệ thống bài tập trắc nghiệm vận dụng cao, phân loại đồ thị – bảng biến thiên (phần 1 – 10) thuộc chương trình Giải tích 12, giúp học sinh ôn tập chuẩn bị cho kỳ thi THPT Quốc gia môn Toán.

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

21 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
1
THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VẬN DỤNG CAO, PHÂN LOẠI
ĐỒ THỊ – BẢNG BIẾN THIÊN LỚP 12 THPT
PHẦN 1 – 10
CREATED BY GIANG SƠN
TP.THÁI BÌNH; THÁNG 4/2020
_____________________________________________________________________________________________________________
2 2
1
9
2
3 sin
y L
x
x y O
y x V
x y E
2
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 1)
___________________________________________________
Câu 1. Phương trình
2
2 2
4 5 4 4 0
x x x x
có bao nhiêu nghiệm thực ?
A. 3 B. 4 C. 5 D. 6
Câu 1. Tìm điều kiện tham số m để phương trình
2 2
2
có 6 nghiệm thực phân biệt.
A.
0 2
m
B.
0 1
m
C.
4
m
D.
1 2
m
Câu 2. Cho hàm số
3
3 2
f x x x
. Phương trình
0
f f x
có bao nhiêu nghiệm thực ?
A. 3 B. 4 C. 5 D. 6
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
C
C
ó
ó
t
t
ấ
ấ
t
t
c
c
ả
ả
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
:
:
2
( 4 )
f x m
.
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
5
5
Câu 4. Cho hàm số
3
3 2
f x x x
. Phương trình
3
0
f x f x
có bao nhiêu nghiệm thực dương ?
A. 3 B. 4 C. 5 D. 6
C
C
â
â
u
u
5
5
.
.
Hàm số
y f x
có bảng biến thiên
như hình vẽ bên. Có bao nhiêu số nguyên m để
phương trình
(sin ) 1
f x m
có nghiệm thực ?
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
4
4
D
D
.
.
5
5
Câu 6. Cho hàm số
3 2
7 14 8
f x x x x
. Phương trình
2
( 9 ) 0
f x
có bao nhiêu nghiệm thực ?
A. 4 B. 3 C. 2 D. 1
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
( 2 3) 3
f x x
.
.
A
A
.
.
5
5
B
B
.
.
3
3
C
C
.
.
4
4
D
D
.
.
2
2
Câu 8. Cho hàm số
3 2
5 7 3
f x x x x
. Phương trình
2
( 3 2) 0
f x x
có bao nhiêu nghiệm ?
A. 4 B. 3 C. 2 D. 1
3
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
4 3 2
f x x
.
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
Câu 10. Cho hàm số
3 2
6 9 3
f x x x x
. Phương trình
3
4 0
f x f x
có bao nhiêu nghiệm ?
A. 7 B. 8 C. 5 D. 6
Câu 11. Cho
3
( ) 3 2
f x x x
. Có bao nhiêu số nguyên m để phương trình
(3sin 4cos ) 1
f x x m
có
nghiệm thực ?
A. 220 B. 1999 C. 221 D. 2019
Câu 12. Hàm số y = f (x) có đồ thị như hình vẽ. Có bao nhiêu số nguyên k để
phương trình sau có nghiệm:
( os3 1)
f c x k
.
A. 3 B. 4
C. 5 D. 6
C
C
â
â
u
u
1
1
3
3
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
3 2 0
f x f x
.
.
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
C
C
â
â
u
u
1
1
4
4
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
4 0
f x x
.
.
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
_________________________________
4
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 2)
___________________________________________________
C
C
â
â
u
u
1
1
.
.
Hàm số
3 2
f x ax bx cx d
có đồ thị
như hình dưới đây. Hỏi phương trình sau có bao nhiêu
nghiệm thực ?
4 3 2
6 11 6 2 1
f x x x x
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
Câu 2. Cho
3 2
6 9 4
f x x x x
. Phương trình
3
3 2 0
f x f x
có bao nhiêu nghiệm thực ?
A. 2 B. 8 C. 4 D. 6
C
C
â
â
u
u
3
3
.
.
Hàm số
3 2
f x ax bx cx d
có đồ thị
như hình dưới đây. Tồn tại bao nhiêu giá trị nguyên
của m để phương trình sau có 4 nghiệm thực ?
5
f x m
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
1
1
Câu 4. Cho hàm số
3 2
6 11 6
f x x x x
. Phương trình
2
(4 4 ) 0
f x x
có bao nhiêu nghiệm thực ?
A. 3 B. 4 C. 5 D. 6
C
C
â
â
u
u
5
5
.
.
Hàm số
3 2
f x ax bx cx d
có đồ thị
như hình dưới đây. Với
m
là tham số thực thuộc đoạn
[2;3], hỏi phương trình sau có tối đa bao nhiêu nghiệm
thực ?
2 3
f x m m
.
A
A
.
.
6
6
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
4
4
Câu 6. Cho hàm số
3
( ) 3 4
f x x x
. Có bao nhiêu số nguyên m để phương trình sau có nghiệm thực ?
3
8cos 6cos 2
f x x m
A. 59 B. 55 C. 50 D. 90
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
H
H
ỏ
ỏ
i
i
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
3 2
2 14 17 17
f x x x
.
.
A
A
.
.
4
4
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
3
3
5
C
C
â
â
u
u
8
8
.
.
Hàm số y = f (x) có đồ thị như hình vẽ. Tính tổng tất cả các giá trị
nguyên của tham số m để phương trình ( os2 cos 1)
f c x x m
có nghiệm.
A. 168 B. 150 C. 60 D. 45
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 3 2
f x x
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
C
C
â
â
u
u
1
1
0
0
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
3
( ) 40 64
f x x
.
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
C
C
â
â
u
u
1
1
1
1
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
h
h
a
a
i
i
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
t
t
h
h
u
u
ộ
ộ
c
c
2
0;
3
?
?
(4sin 2) 1999 89
f x m
.
.
A
A
.
.
1
1
B
B
.
.
2
2
C
C
.
.
5
5
D
D
.
.
3
3
C
C
â
â
u
u
1
1
2
2
.
.
Hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
bên. Phương trình sau có bao nhiêu nghiệm thực ?
4 5
4 3
x
f x
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
4
4
_________________________________
6
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 3)
___________________________________________________
Câu 1. Cho hàm số
4 2
( ) 2 2
f x x x
. Tìm điều kiện tham số m để phương trình 3 ( 2019)
f x m
có
6 nghiệm phân biệt.
A. 1 < m < 2 B. 2 < m < 3 C. 1 < m < 3 D. 0 < m < 2
C
C
â
â
u
u
2
2
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
5 3
4 5
f x x x
.
.
A
A
.
.
5
5
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
Câu 3. Cho hàm
3
( ) 3 1
f x x x
. Khi đó phương trình
3
( ) 3 ( ) 1 0
f x f x
có bao nhiêu nghiệm ?
A. 6 B. 7 C. 5 D. 8
Câu 4. hàm số
3
( ) 3
f x x x
. Có bao nhiêu số nguyên m để phương trình
(sin 1)
f x m
có nghiệm.
A. 2 B. 3 C. 4 D. 5
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ì
ì
m
m
s
s
ố
ố
n
n
g
g
h
h
i
i
ệ
ệ
m
m
d
d
ư
ư
ơ
ơ
n
n
g
g
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
( 4) 2 1999
f x x
.
.
A
A
.
.
5
5
B
B
.
.
3
3
C
C
.
.
2
2
D
D
.
.
4
4
Câu 6. Cho hàm số
3 2
3 2
f x x x
. Phương trình
3 2
3 2 3 2
3 2 3 3 2 2 0
x x x x
có bao
nhiêu nghiệm thực ?
A. 9 B. 7 C. 6 D. 5
Câu 7. Cho hàm số
3 2
3 2
f x x x
. Hỏi phương trình
3
2
( 3 )
3
f x x
có bao nhiêu nghiệm thực ?
A. 14 B. 15 C. 9 D. 12
C
C
â
â
u
u
8
8
.
.
Hàm số
y f x
có bảng biến thiên
như hình bên. Phương trình
2
f x có bao
nhiêu nghiệm thực ?
A
A
.
.
2
2
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
4
4
Câu 9. Cho hàm số
3
( ) 3 1
f x x x
. Có bao nhiêu số nguyên m < 1999 để phương trình sau có ít nhất ba
nghiệm dương phân biệt ?
7
2
( ) (sin ) ( ) sin 0
f x x m f x m x
A. 2000 B. 2001 C. 1999 D. 2019
Câu 10. Cho hàm số
3
( ) 3 3
f x x x
. Tìm số nghiệm tối thiểu của phương trình
( 2) 3 4 1
f x m m
.
A. 4 B. 2 C. 5 D. 3
Câu 11. Cho hàm số
3 2
( ) 3 2
f x x x
. Tìm tập hợp tất cả các giá trị m để phương trình (cos )
f x m
có
hai nghiệm phân biệt thuộc
3
0;
2
.
A. [– 2;2] B. (0;2) C. (– 2;2) D. [0;2)
C
C
â
â
u
u
1
1
2
2
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
H
H
ỏ
ỏ
i
i
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2 3 3
f x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
h
h
ự
ự
c
c
?
?
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
Câu 13. Cho hàm số
5 2
( ) 2 5 10 2019
f x x x x
. Tồn tại bao nhiêu số nguyên n để phương trình sau có
nghiệm:
2
(4sin 2 cos 1999) (14 6 2019)
f x x f n n
.
A. 1 B. 4 C. 2 D. 3
Câu 14. Cho hàm số
3
( ) 3 1
f x x x
. Tìm tập hợp tất cả các giá trị m để phương trình sau có đúng ba
nghiệm phân biệt thuộc
;
.
A.
3;1
B. (– 3;1) C. [– 3;1) D. (– 3;1]
C
C
â
â
u
u
1
1
5
5
.
.
Hàm số y = f (x) có đồ thị như hình vẽ. Có tất cả bao nhiêu
giá trị nguyên của tham số m để phương trình
( (cos ))
f f x m
có
nghiệm.
A. 5 B. 10 C. 4 D. 8
Câu 16. Cho hàm số
3 2
( ) 3 1
f x x x
. Có bao nhiêu số nguyên m để phương trình sau có nghiệm
( (sin 2)) 2019
f f x m
.
A. 6 B. 5 C. 4 D. 7
C
C
â
â
u
u
1
1
7
7
.
.
Hàm số
3 2
f x ax bx cx d
có đồ thị như hình vẽ
bên. Với
m
là tham số thực, hỏi phương trình
2
2
1
m
f x
m
có tối
thiểu bao nhiêu nghiệm thực ?
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
1
1
D
D
.
.
2
2
_________________________________
8
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 4)
___________________________________________________
C
C
â
â
u
u
1
1
.
.
Hàm số
3 2
f x ax bx cx d
có đồ thị như hình
dưới đây. Hỏi phương trình
(3 2) 1
f x b
có bao nhiêu
nghiệm thực ?
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
Câu 2. Hàm số y = f (x) có đồ thị như hình vẽ. Tìm điều kiện tham số
k để phương trình sau có hai nghiệm phân biệt :
2
( )
x
f e k
.
A. 0 < k < 4 B. k > 1
C. 0 < k < 2 D. k > 0
Câu 3. Cho hàm số
y f x
có đồ thị như hình vẽ. Có bao nhiêu
giá trị nguyên của
m
để phương trình
2
2
1 0
3 5
m
f x
x x
có
nghiệm trên khoảng
1;1
A. 13 B.
11
C. 5 D. 10
Câu 4. Cho hàm số
y f x
có bảng biến thiên như
hình vẽ. Có bao nhiêu giá trị nguyên của
m
để đồ thị
hàm số
x
y
f x
có đúng hai đường tiệm cận đứng
A.
4
B. Vô số. C.
1
. D.
5.
Câu 5. Cho hàm số
y f x
trên
2;4
như hình vẽ. Gọi
S
là tập
chứa các giá trị của
m
để hàm số
2
2
y f x m
có giá trị lớn
nhất trên đoạn
2;4
bằng
49
. Tổng các phần tử tập
S
bằng
A. - 9 B. - 23
C. - 2 D. - 12
9
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
đ
đ
ể
ể
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
s
s
a
a
u
u
c
c
ó
ó
n
n
g
g
h
h
i
i
ệ
ệ
m
m
t
t
r
r
ê
ê
n
n
đ
đ
o
o
ạ
ạ
n
n
[
[
0
0
;
;
3
3
]
]
:
:
2 3 .
x x m f x
.
.
A
A
.
.
4
4
B
B
.
.
3
3
C
C
.
.
5
5
D
D
.
.
2
2
Câu 7. Cho hàm số
y f x
liên tục và có đạo hàm trên
, đồ thị
y f x
như hình vẽ bên. Ký hiệu
3
1
g x f x x m
. Tồn tại
bao nhiêu số nguyên dương m sao cho
0;1
max 2
g x m
.
A. 4 B. 3 C. 5 D. 2
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
l
l
i
i
ê
ê
n
n
t
t
ụ
ụ
c
c
v
v
à
à
c
c
ó
ó
đ
đ
ạ
ạ
o
o
h
h
à
à
m
m
t
t
r
r
ê
ê
n
n
,
,
đ
đ
ồ
ồ
t
t
h
h
ị
ị
y f x
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
ý
ý
h
h
i
i
ệ
ệ
u
u
2 2 1
T x f x x m
.
.
T
T
ì
ì
m
m
đ
đ
i
i
ề
ề
u
u
k
k
i
i
ệ
ệ
n
n
c
c
ủ
ủ
a
a
t
t
h
h
a
a
m
m
s
s
ố
ố
m
m
s
s
a
a
o
o
c
c
h
h
o
o
0;1 0;1
max 2min
g x g x
.
.
A
A
.
.
4
m
B
B
.
.
3
m
C
C
.
.
0 5
m
D
D
.
.
2
m
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
có
có
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Gọ
Gọ
i
i
S
S
là
là
t
t
ậ
ậ
p
p
h
h
ợ
ợ
p
p
t
t
ấ
ấ
t
t
cả cá
cả cá
c
c
giá trị
giá trị
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
để
để
h
h
à
à
m
m
s
s
ố
ố
2
1
2019
3
y f x m
có 5 cực trị. Tổng
tất cả các giá trị của tập hợp S bằng
A
A
.
.
7
7
B
B
.
.
0
0
C. 4 D. 5
C
C
â
â
u
u
1
1
0
0
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
có
có
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
Có
Có
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
m
m
t
t
h
h
u
u
ộ
ộ
c
c
[
[
–
–
2
2
0
0
1
1
9
9
;
;
2
2
0
0
2
2
0
0
]
]
để
để
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
trì
trì
n
n
h
h
s
s
a
a
u
u
có
có
8
8
n
n
g
g
h
h
i
i
ệ
ệ
m
m
p
p
h
h
â
â
n
n
b
b
i
i
ệ
ệ
t
t
2 2 2
2 ( ) (4 2 1) ( ) 2 0
f x m m f x m m
.
.
A
A
.
.
2
2
B
B
.
.
2
2
0
0
1
1
9
9
C. 1 D. 2020
_________________________________
O
x
y
1
1
3
3
1
2
10
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 5)
___________________________________________________
C
C
â
â
u
u
1
1
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
l
l
i
i
ê
ê
n
n
t
t
ụ
ụ
c
c
v
v
à
à
c
c
ó
ó
đ
đ
ạ
ạ
o
o
h
h
à
à
m
m
t
t
r
r
ê
ê
n
n
,
,
đ
đ
ồ
ồ
t
t
h
h
ị
ị
y f x
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
ý
ý
h
h
i
i
ệ
ệ
u
u
3 2
2 3
g x f x x x m
,
,
v
v
ớ
ớ
i
i
m
m
l
l
à
à
t
t
h
h
a
a
m
m
s
s
ố
ố
t
t
h
h
ự
ự
c
c
.
.
H
H
ã
ã
y
y
t
t
ì
ì
m
m
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
h
h
ỏ
ỏ
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
b
b
i
i
ể
ể
u
u
t
t
h
h
ứ
ứ
c
c
2
0;1 0;1
3max 4 min
S m g x g x m
.
.
A. 4 B. – 50 C. – 150 D. – 102
C
C
â
â
u
u
2
2
.
.
H
H
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
b
b
a
a
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
ý
ý
h
h
i
i
ệ
ệ
u
u
M
M
v
v
à
à
m
m
t
t
ư
ư
ơ
ơ
n
n
g
g
ứ
ứ
n
n
g
g
l
l
à
à
g
g
i
i
á
á
t
t
r
r
ị
ị
l
l
ớ
ớ
n
n
n
n
h
h
ấ
ấ
t
t
,
,
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
h
h
ỏ
ỏ
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
h
h
à
à
m
m
s
s
ố
ố
4 4
sin cos
g x f x x
.
.
T
T
í
í
n
n
h
h
8
M m
.
.
A
A
.
.
3
3
5
5
B
B
.
.
3
3
8
8
C
C
.
.
3
3
6
6
D
D
.
.
4
4
3
3
C
C
â
â
u
u
3
3
.
.
H
H
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
b
b
a
a
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
B
B
i
i
ế
ế
t
t
r
r
ằ
ằ
n
n
g
g
t
t
ổ
ổ
n
n
g
g
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
l
l
ớ
ớ
n
n
n
n
h
h
ấ
ấ
t
t
v
v
à
à
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
h
h
ỏ
ỏ
n
n
h
h
ấ
ấ
t
t
c
c
ủ
ủ
a
a
h
h
à
à
m
m
s
s
ố
ố
2 2
g x f x x
c
c
ó
ó
d
d
ạ
ạ
n
n
g
g
, ,a b c a b c
.
.
T
T
í
í
n
n
h
h
2 3
a b c
.
.
A
A
.
.
–
–
2
2
1
1
B
B
.
.
6
6
C
C
.
.
–
–
4
4
D
D
.
.
5
5
Câu 4. Hàm số
3 2
y f x ax bx cx d
có đồ thị như hình vẽ bên. Có
bao nhiêu số nguyên m để phương trình
2
( 3) 4 0
f x m f x m
có 7
nghiệm phân biệt ?
A. 1 B. 2 C. 3 D. 4
11
Câu 5. Hàm số
2
2
x
y e
có đồ thị như hình vẽ bên. ABCD là
hình chữ nhật thay đổi sao cho A và B luôn thuộc đồ thị
hàm số đã cho. CD luôn nằm trên trục hoành. Giá trị lớn
nhất của diện tích hình chữ nhật ABCD là
A.
1
e
B.
e
C.
2
e
D.
2
1
e
Câu 6. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Biết
0 0
;
u v
là một
nghiệm của hệ
(1 4 ) (5 8 )
2 3 2
f v f u
u v u v
và
*
0 0
; ,
a
u v a b
b
,
a
b
tối
giản. Giá trị biểu thức P = a + b là
A. 1 B. 2 C. 3 D. 4
Câu 7. Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Xác định số nghiệm thực của phương trình
11
( ( )) 2 ( ) ( ) 2
2
f f x f x f x
.
A. 5 B. 2 C. 3 D. 4
Câu 8. Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Số điểm cực trị của đồ thị hàm số
(1 )
y f x
là
A. 9 B. 8 C. 7 D. 6
Câu 9. Cho hàm số
y g x
xác định trên
(0; )

và có
bảng biến thiên như hình bên. Tìm số giao điểm của đồ thị
hàm số
2
1
( )
3
y f x x x
và
y g x
.
A. 1 B. 2 C. 3 D. 0
Câu 10. Cho hàm số
y f x
có đồ thị như hình vẽ bên.
Tìm số điểm cực trị của hàm số
( ( ))
y f f x
.
A. 5 B. 6 C. 3 D. 4
_________________________________
12
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 6)
___________________________________________________
Câu 1. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Đặt hàm số
3
( ) (2 1)
y g x f x x m
. Tìm m để
[0;1]
max ( ) 10
g x
.
A. m = - 13 B. m = - 12 C. m = - 1 D. m = 3
Câu 2. Cho hàm số
y f x
xác định và liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của m để phương trình sau có nghiệm
2
30
2. 3 3 9 20
21
19
xf x m
.
A. 15 B. 14 C. 10 D. 13
Câu 3. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao nhiêu
giá trị nguyên m để phương trình
(6sin 8cos ) ( ( 1))
f x x f m m
có
nghiệm thực.
A. 6 B. 2 C. 5 D. 4
Câu 4. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Bất phương
trình
( ) (3 2019)
x x
f e m e có nghiệm
(0;1)
x
khi và chỉ khi
A.
4
1011
m
B.
4
3 2019
m
e
C.
2
1011
m
D.
( )
3 2019
f e
m
e
Câu 5. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tồn tại bao
nhiêu số nguyên m để phương trình sau có nghiệm:
2
3sin cos 1
( 4 4)
2cos sin 4
x x
f f m m
x x
A. Vô số B. 5 C. 3 D. 4
13
Câu 6. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Hỏi có bao
nhiêu điểm trên đường tròn lượng giác biểu diễn nghiệm của phương trình
(cos 2 ) 0
f f x
.
A. 1 B. Vô số C. 3 D. 4
Câu 7. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tập hợp tất cả
các giá trị thực của tham số m để phương trình f (cosx) = m có 3 nghiệm
phân biệt thuộc
3
0;
2
là
A. [-2;2] B. (0;2) C. (-2;2) D. [0;2)
Câu 8. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tập hợp tất cả
các giá trị thực của m để phương trình f (1 – cos2x) = m có nghiệm thuộc
khoảng
(0; )
là
A. [- 1;3] B. (- 1;1) C. (- 1;3) D. (-1;1]
Câu 9. Cho hàm số
y f x
liên tục trên R và có đồ thị như hình vẽ
bên. Đặt
( ) ( ( ))
g x f f x
. Hỏi phương trình
( )
g x
có mấy nghiệm thực ?
A. 14 B. 12 C. 10 D. 8
Câu 10. Cho hàm số
y f x
liên tục trên R và có đồ thị như hình vẽ
bên. Tập hợp tất cả các giá trị m để phương trình
2
(sin ) log
f x m
có
nghiệm thuộc khoảng
(0; )
là
A.
1
;2
2
B. (0;2) C.
1
;2
2
D.
1
;2
2
Câu 11. Hàm số
y f x
thỏa mãn
7
(0)
6
f
có
bảng biến thiên như hình vẽ bên. Tìm giá trị lớn
nhất của m để phương trình sau có nghiệm trên
[0;2] :
3 2
13 3
2 ( ) ( ) 7 ( ) ln
2 2
f x f x f x m
.
A. 2 B.
15
13
C. 3 D. 4
____________________________
14
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 7)
___________________________________________________
Câu 1. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Để đồ thị hàm
số
2
( ) ( ) ( )
h x f x f x m
có số điểm cực trị ít nhất thì giá trị nhỏ nhất
của tham số
0
m m
. Tìm mệnh đề đúng trong các mệnh đề sau
A.
0
(0;1)
m
B.
0
( 1;0)
m
C.
0
( ; 1)
m

D.
0
(1; )
m

Câu 2. Cho hàm số
y f x
có bảng biến
thiên hình vẽ bên. Tìm giá trị nhỏ nhất của m để
bất phương trình
( 1 1)
f x m
có nghiệm
A. – 2 B. 2
C. 3 D. 4
Câu 3. Hàm số
y f x
có đồ thị như hình vẽ bên. Tìm điều kiện
tham số m để bất phương trình sau nghiệm đúng với mọi
( 1;3)
x
:
2
2 ( ) 4
f x x x m
.
A. m < - 3 B. m < - 10
C. m < - 2 D. m < 5
Câu 4. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tập hợp S =
[a;b] bao gồm tất cả các giá trị m để phương trình sau có nghiệm
2 2
( 1) ( 1) 3 ( 1) 2 ( ( 1) 2 ( 1) 1)
f x f x f x m f x f x
.
Tính a + 2b.
A. 5 B. 2 C. 3 D. 4
Câu 5. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Đặt
( ) ( ( ) 1)
f x f f x
. Tìm số nghiệm của phương trình
( ) 0
g x
.
A. 10 B. 8 C. 6 D. 9
15
Câu 6. Cho
2
( ) 1
f x mx
với
0
m
. Tìm tổng tất cả các giá trị nguyên của tham số m thuộc [– 2019;2019] để
phương trình
( ( ))
f f x x
có 4 nghiệm thực phân biệt.
A. – 2037171 B. – 2035153 C. – 2039190 D. – 2041210
Câu 7. Cho hàm số
y f x
có bảng biến thiên như hình vẽ bên.
Khi đó hàm số
3
( 1) 12 2019
y f x x x nghịch biến trên khoảng nào dưới đây ?
A. (1;2) B. (3;4) C.
(1; )

D.
( ;1)

Câu 8. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Số các
giá trị nguyên của tham số m không vượt quá 5 để phương trình
2
1
0
8
x
m
f
có hai nghiệm phân biệt là
A. 5 B. 6 C. 7 D. 4
Câu 9. Cho hàm số
y f x
có bảng biến thiên
như hình vẽ bên. Gọi S là tập hợp các số nguyên
dương m để bất phương trình
3 2
( ) ( 3 5)
f x m x x
có nghiệm thuộc đoạn [-1;3].
Số phần tử của S là
A. 1 B. 2 C. 3 D. 0
Câu 10. Hàm số
y f x
có bảng biến
thiên như hình vẽ bên. Hàm số
3 2
( ) 3 ( )
y f x f x
nghịch biến trên khoảng
nào dưới đây
A. (1;2) B. (2;3)
C. (3;4) D.
( ;1)

Câu 11. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tồn tại bao
nhiêu số nguyên m nhỏ hơn 10 để phương trình
2
( )
x
f e m
có đúng
hai nghiệm thực
A. 6 B. 5 C. 7 D. 4
Câu 12. Cho hàm số
3
( ) 3 3
f x x x
. Có bao nhiêu số nguyên m để bất phương trình sau nghiệm đúng mọi
giá trị x:
2
( 3sin 4 cos 6) 1993 2019
f x x m m
.
A. 1990 B. 1991 C. 1992 D. 1993
_________________________________
16
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 8)
___________________________________________________
C
C
â
â
u
u
1
1
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
5
5
C
C
.
.
3
3
B
B
.
.
4
4
D
D
.
.
2
2
C
C
â
â
u
u
2
2
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
8
8
C
C
.
.
5
5
B
B
.
.
7
7
D
D
.
.
6
6
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
9
9
C
C
.
.
1
1
0
0
B
B
.
.
8
8
D
D
.
.
6
6
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
5
5
C
C
.
.
6
6
B
B
.
.
8
8
D
D
.
.
4
4
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
5 2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
7
7
C
C
.
.
9
9
B
B
.
.
8
8
D
D
.
.
1
1
1
1
17
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
7
g f x m
c
c
ó
ó
t
t
ố
ố
i
i
đ
đ
a
a
s
s
ố
ố
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
.
.
A
A
.
.
3
3
B
B
.
.
1
1
5
5
C
C
.
.
1
1
0
0
D
D
.
.
6
6
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
3
3
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
1
1
B
B
.
.
2
2
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
b
b
ậ
ậ
c
c
n
n
ă
ă
m
m
y f x
.
.
G
G
i
i
ả
ả
s
s
ử
ử
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
3
7
9
3
g f x x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
.
.
A
A
.
.
1
1
B
B
.
.
3
3
C
C
.
.
0
0
D
D
.
.
2
2
C
C
â
â
u
u
9
9
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
4
3
2 3
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
7
7
B
B
.
.
1
1
0
0
C
C
.
.
9
9
D
D
.
.
5
5
C
C
â
â
u
u
1
1
0
0
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
l
l
i
i
ê
ê
n
n
t
t
ụ
ụ
c
c
t
t
r
r
ê
ê
n
n
[
[
0
0
;
;
5
5
,
,
5
5
]
]
,
,
đ
đ
ồ
ồ
t
t
h
h
ị
ị
c
c
ủ
ủ
a
a
h
h
à
à
m
m
s
s
ố
ố
t
t
r
r
ê
ê
n
n
[
[
0
0
;
;
5
5
,
,
5
5
]
]
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
.
.
H
H
ỏ
ỏ
i
i
h
h
à
à
m
m
s
s
ố
ố
2
g f x
c
c
ó
ó
t
t
ố
ố
i
i
đ
đ
a
a
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
3
3
C
C
.
.
6
6
B
B
.
.
7
7
D
D
.
.
4
4
_________________________________
18
ÔN TẬP ĐỒ THỊ – BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 9)
___________________________________________________
C
C
â
â
u
u
1
1
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
3
3
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
1
1
B
B
.
.
2
2
C
C
.
.
3
3
D
D
.
.
4
4
C
C
â
â
u
u
2
2
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
C
C
.
.
8
8
B
B
.
.
5
5
C
C
.
.
7
7
D
D
.
.
6
6
C
C
â
â
u
u
3
3
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
C
C
.
.
9
9
B
B
.
.
1
1
0
0
C
C
.
.
8
8
D
D
.
.
6
6
C
C
â
â
u
u
4
4
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
.
.
G
G
i
i
ả
ả
s
s
ử
ử
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
K
K
h
h
i
i
đ
đ
ó
ó
h
h
à
à
m
m
s
s
ố
ố
2
36 7 108 5
g x f x x x
đ
đ
ồ
ồ
n
n
g
g
b
b
i
i
ế
ế
n
n
t
t
r
r
ê
ê
n
n
k
k
h
h
o
o
ả
ả
n
n
g
g
n
n
à
à
o
o
s
s
a
a
u
u
đ
đ
â
â
y
y
?
?
A
A
.
.
(
(
0
0
;
;
4
4
)
)
v
v
à
à
(
(
9
9
;
;
1
1
3
3
,
,
5
5
)
)
B
B
.
.
(
(
0
0
;
;
4
4
)
)
v
v
à
à
9;

C
C
.
.
(
(
4
4
;
;
9
9
)
)
v
v
à
à
13,5;

D
D
.
.
(
(
0
0
;
;
9
9
)
)
19
C
C
â
â
u
u
5
5
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
A
A
.
.
5
5
B
B
.
.
3
3
C
C
.
.
4
4
D
D
.
.
2
2
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
5 2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
C
C
.
.
7
7
D
D
.
.
9
9
E
E
.
.
8
8
F
F
.
.
1
1
1
1
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
T
T
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
t
t
ấ
ấ
t
t
c
c
ả
ả
c
c
á
á
c
c
g
g
i
i
á
á
t
t
r
r
ị
ị
n
n
g
g
u
u
y
y
ê
ê
n
n
c
c
ủ
ủ
a
a
m
m
đ
đ
ể
ể
h
h
à
à
m
m
s
s
ố
ố
2
7
g f x m
c
c
ó
ó
t
t
ố
ố
i
i
đ
đ
a
a
s
s
ố
ố
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
.
.
B
B
.
.
3
3
B
B
.
.
1
1
5
5
C
C
.
.
1
1
0
0
D
D
.
.
6
6
C
C
â
â
u
u
8
8
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
y f x
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
v
v
ẽ
ẽ
b
b
ê
ê
n
n
.
.
H
H
à
à
m
m
s
s
ố
ố
2
2
g f x
c
c
ó
ó
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
đ
đ
i
i
ể
ể
m
m
c
c
ự
ự
c
c
t
t
r
r
ị
ị
?
?
C
C
.
.
5
5
B
B
.
.
6
6
C
C
.
.
8
8
D
D
.
.
4
4
_________________________________
20
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 10)
___________________________________________________
Câu 1. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tính tổng
các giá trị nguyên của tham số m để bất phương trình sau nghiệm
đúng với mọi x.
( ) 2 ( ) 2 ( )
9.6 4 ( ) .9 ( 5 ).4
f x f x f x
f x m m
A. 10 B. 5 C. 9 D. 4
Câu 2. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao nhiêu số
nguyên m để phương trình
3
( 3 )
f x x m
có 6 nghiệm phân biệt thuộc [– 1;2]
A. 6 B. 2 C. 3 D. 7
Câu 3. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Phương
trình
(2 2 )
x x
f m
có nhiều nhất bao nhiêu nghiệm phân biệt
thuộc đoạn [– 1;2] ?
A. 5 B. 2 C. 3 D. 4
Câu 4. Cho hàm số
y f x
có bảng xét dấu đạo hàm như hình vẽ bên.
Hàm số
2
log ( (2 ))
y f x
đồng biến trên khoảng nào sau đây
A. (1;2) B. (– 1;0) C. (– 1;1) D.
( ; 1)

Câu 5. Cho hàm số
3
( ) ( 1) 3 3
f x x x
. Đồ thị hình bên là của
hàm số nào
A.
( 1) 1
y f x
B.
( 1) 1
y f x
C.
( 1) 1
y f x
D.
( 1) 1
y f x
21
Câu 6. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Xác định
số nghiệm của phương trình:
1993 ( ) 1993 1999
f x x
A. 4 B. 1 C. 2 D. 0
Câu 7. Cho hàm số
2019 2017 3
( ) 2019 2017 ... 3 1999 1993 1 1992
f x x x x x x
. Có bao nhiêu giá trị
nguyên không âm của m để phương trình
2 2
(3sin 2 8cos 4) ( )
f x x f m m
có nghiệm thực ?
A. 2 B. 3 C. 4 D. 6
Câu 8. Xét hàm số
3 2
4 2
5
( )
2 1 4
x x x
g x f
x x
.
Đặt
min ( ); max ( )
m g x M g x
. Trong các khẳng định sau, khẳng
định nào đúng ?
A. M + m = 6 B. 2M + m = 2
C. 2M – m = 5 D. M – m = 4
Câu 9. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao
nhiêu số nguyên m để phương trình
1
( 1)
3 2
x
f x m
có nghiệm
thuộc đoạn [– 2;2] ?
A. 11 B. 9 C. 8 D. 10
Câu 10. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Có bao
nhiêu số nguyên m để bất phương trình sau nghiệm đúng với mọi
2; 2
x ?:
2 2
( 5 2 1). ( ) 0
mx m x m f x
.
A. 1 B. 2 C. 3 D. 0
Câu 11. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Tìm số
giá trị nguyên của m để phương trình
2
( 2 )
f x x m
có đúng 4
nghiệm thực phân biệt thuộc đoạn
3 7
;
2 2
.
A. 1 B. 2 C. 3 D. 4
_________________________________
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

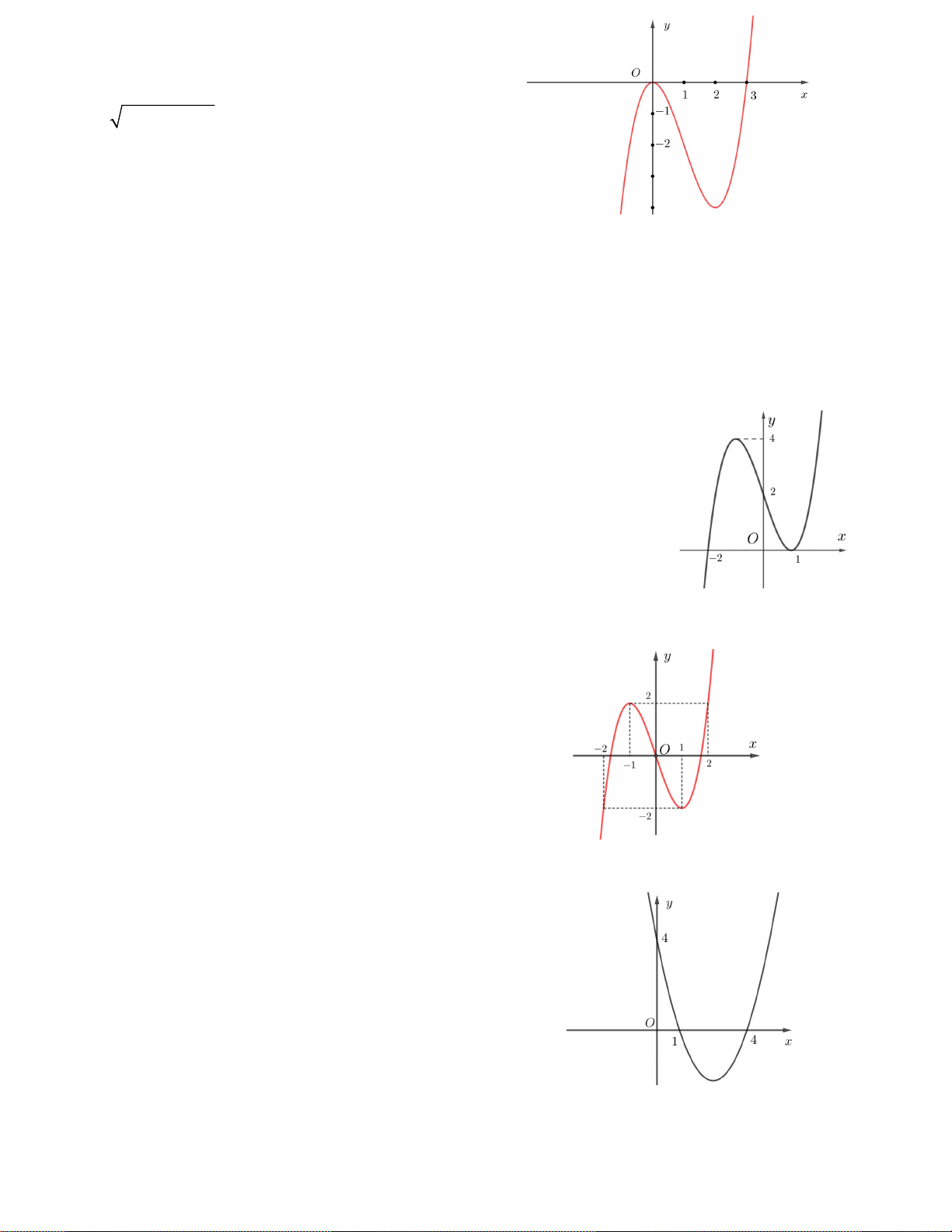
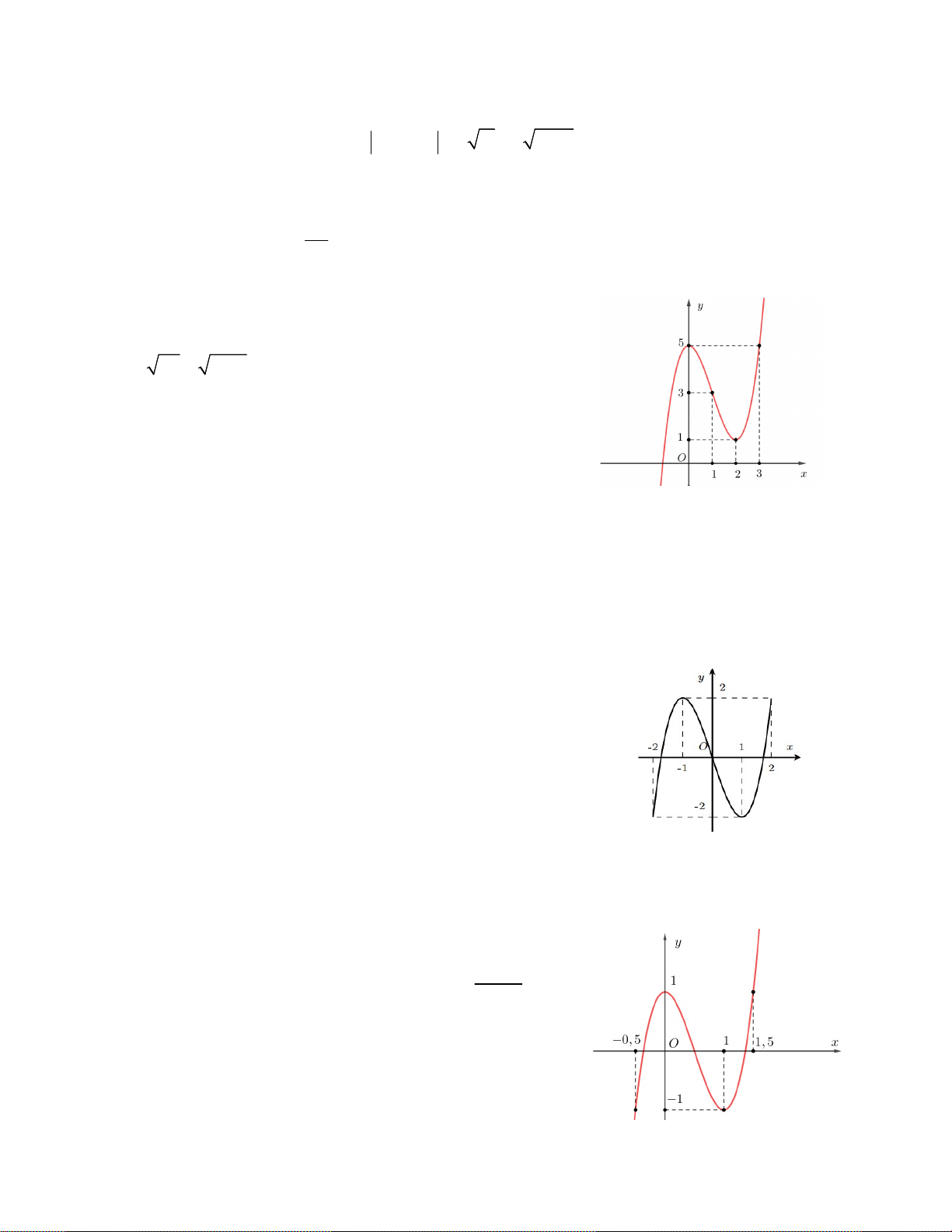
Preview text:

THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VẬN DỤNG CAO, PHÂN LOẠI
ĐỒ THỊ – BẢNG BIẾN THIÊN LỚP 12 THPT PHẦN 1 – 10 CREATED BY GIANG SƠN TP.THÁI BÌNH; THÁNG 4/2020
_____________________________________________________________________________________________________________ 1 y  L x 2 2 x  y  9 O y   2 x V x   3 sin y E 1
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 1)
___________________________________________________ 2 Câu 1. Phương trình  2 x  x   2 4
5 x  4x  4  0có bao nhiêu nghiệm thực ? A. 3 B. 4 C. 5 D. 6
Câu 1. Tìm điều kiện tham số m để phương trình 2 2
x x  2  m có 6 nghiệm thực phân biệt. A. 0  m  2 B. 0  m  1 C. m  4 D. 1  m  2
Câu 2. Cho hàm số f  x 3
 x  3x  2. Phương trình f  f x  0 có bao nhiêu nghiệm thực ? A. 3 B. 4 C. 5 D. 6
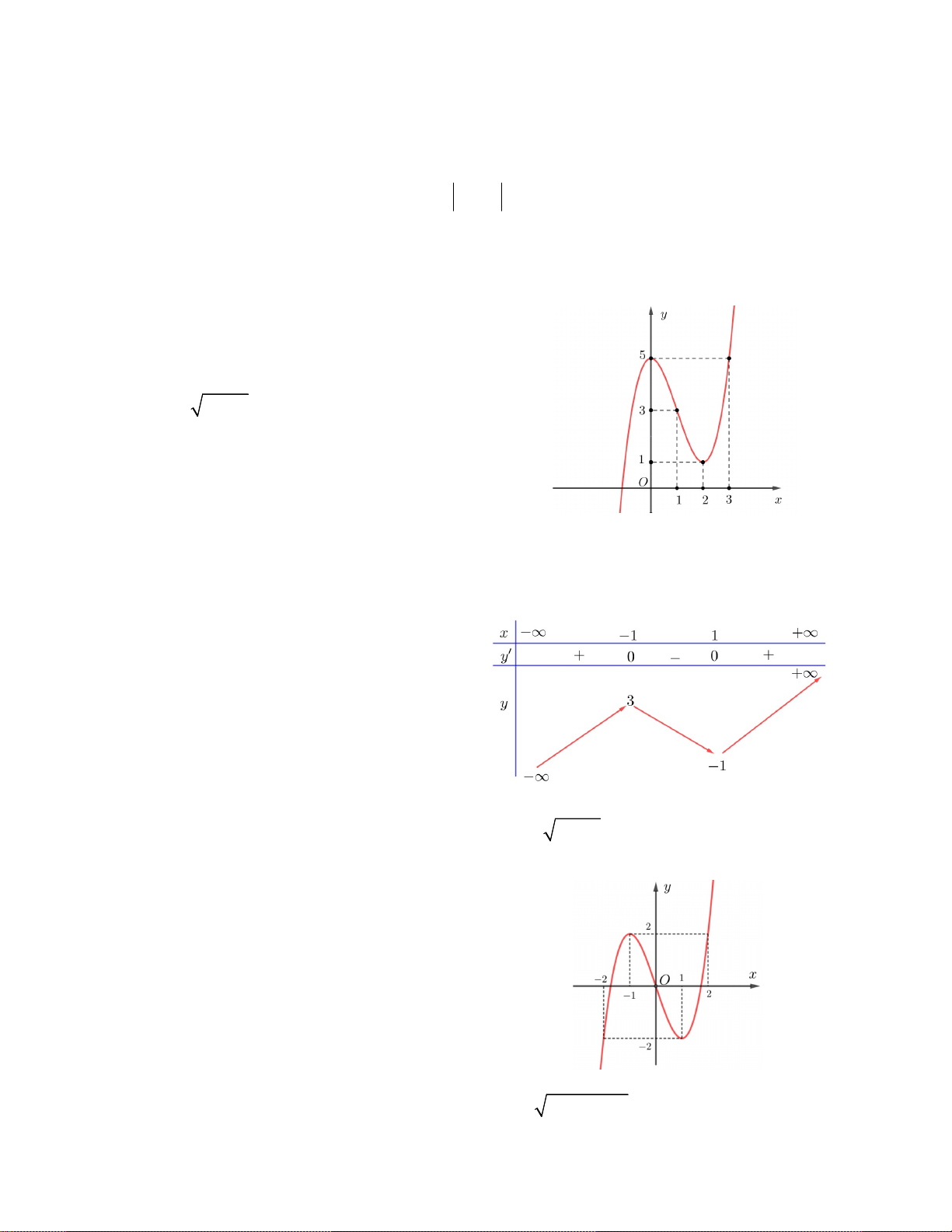
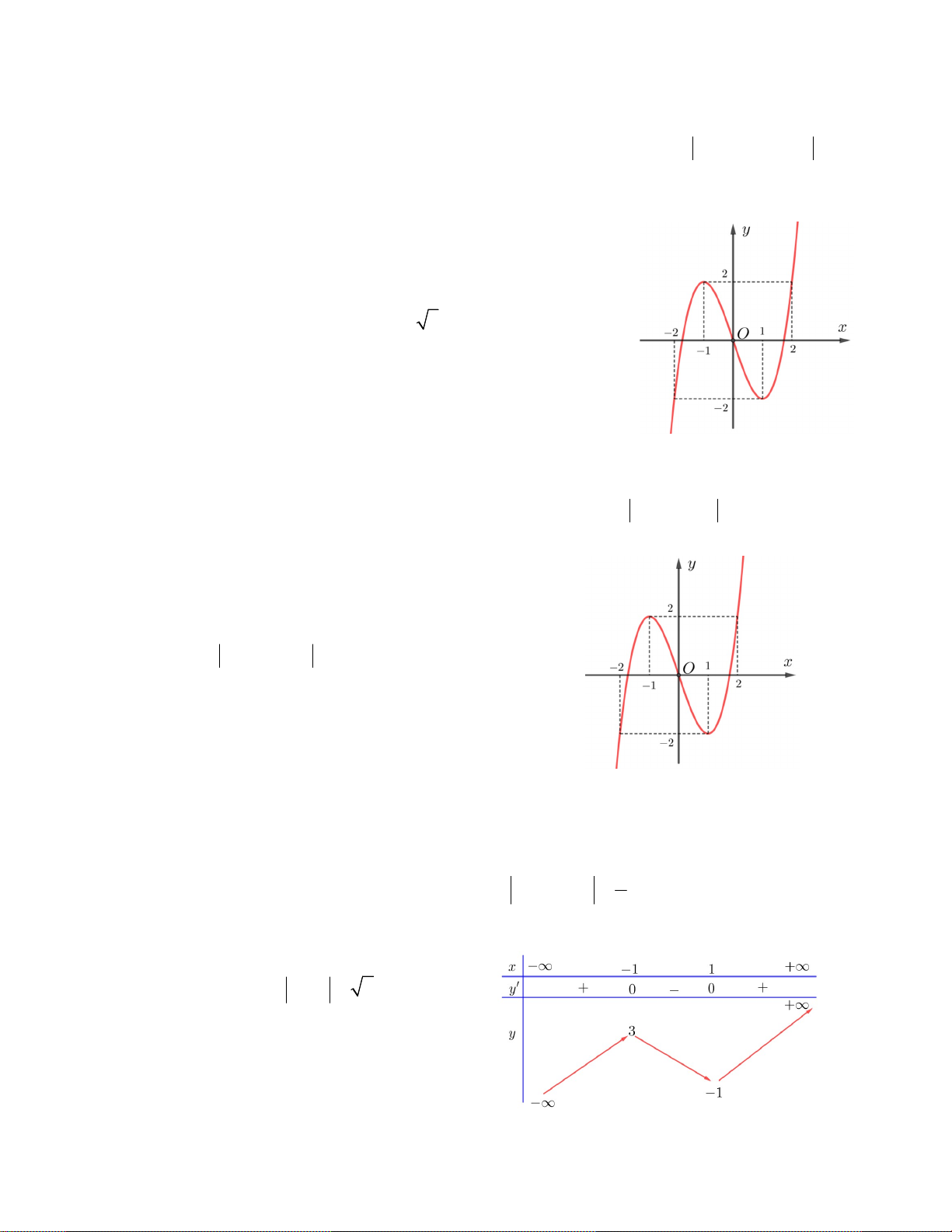
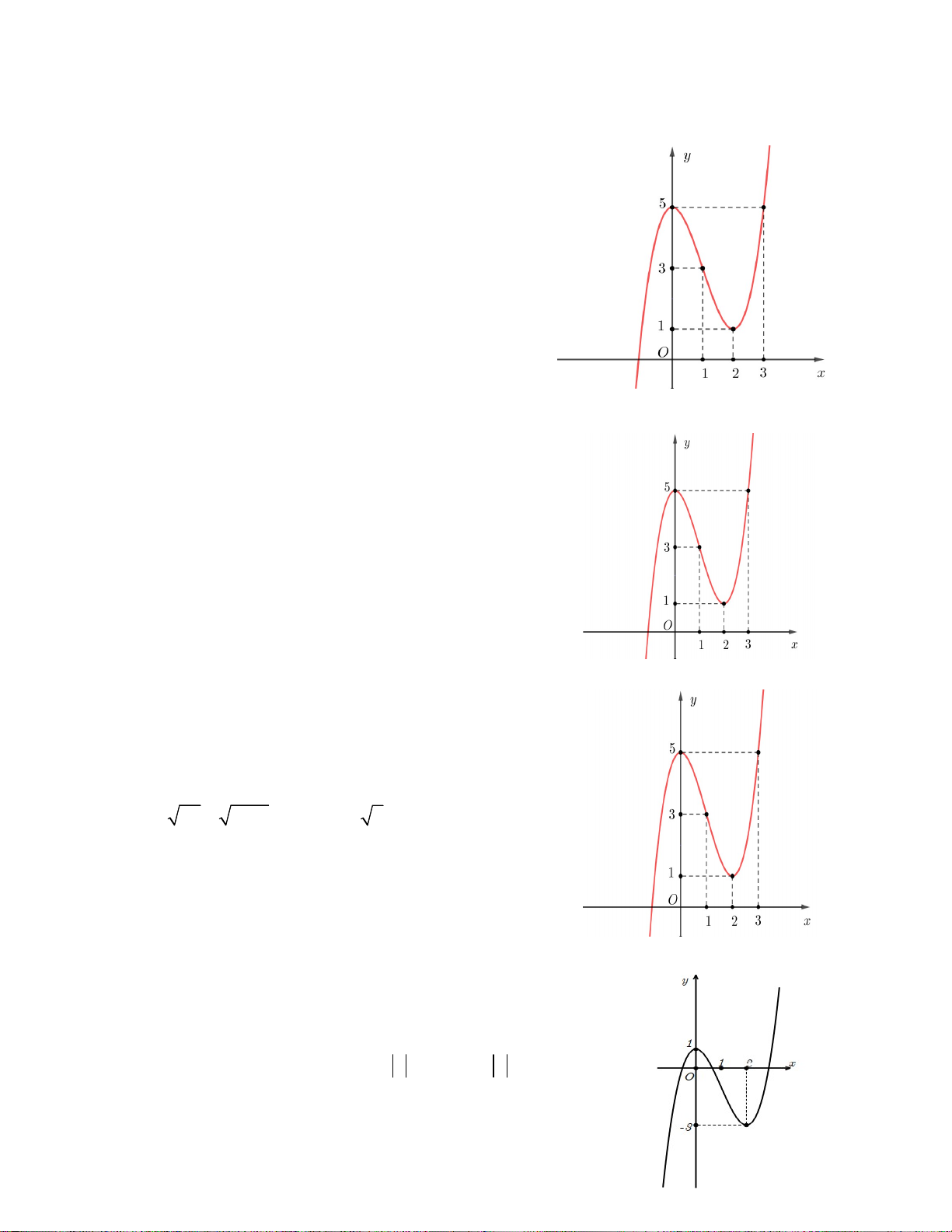
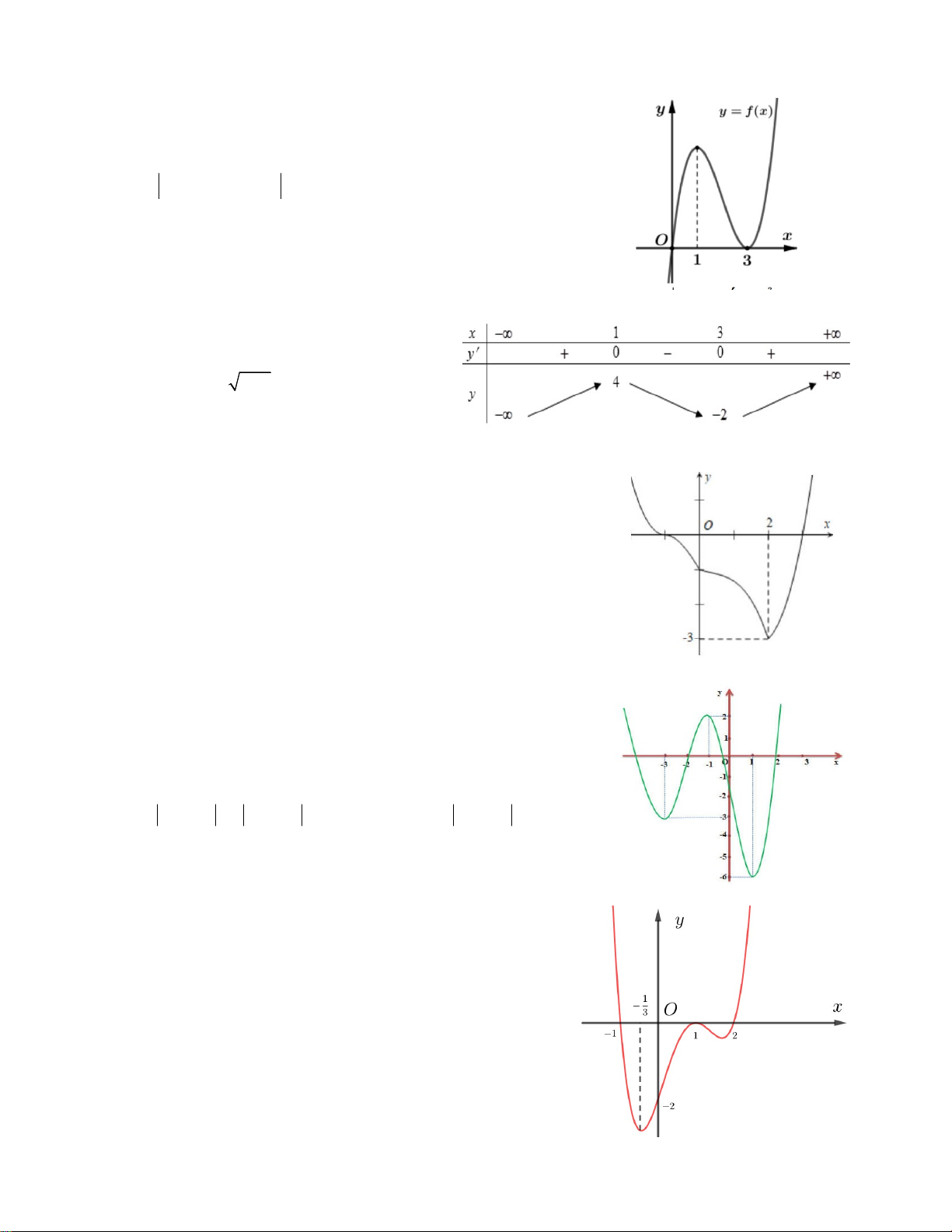
Câu 3. Cho hàm số y  f  x có đồ thị như hình vẽ.
Có tất cả bao nhiêu số nguyên m để phương trình sau có nghiệm: 2 f ( 4  x )  m . A. 4 B. 3 C. 2 D. 5
Câu 4. Cho hàm số f  x 3
 x  3x  2. Phương trình 3
f x  f  x  0 có bao nhiêu nghiệm thực dương ? A. 3 B. 4 C. 5 D. 6
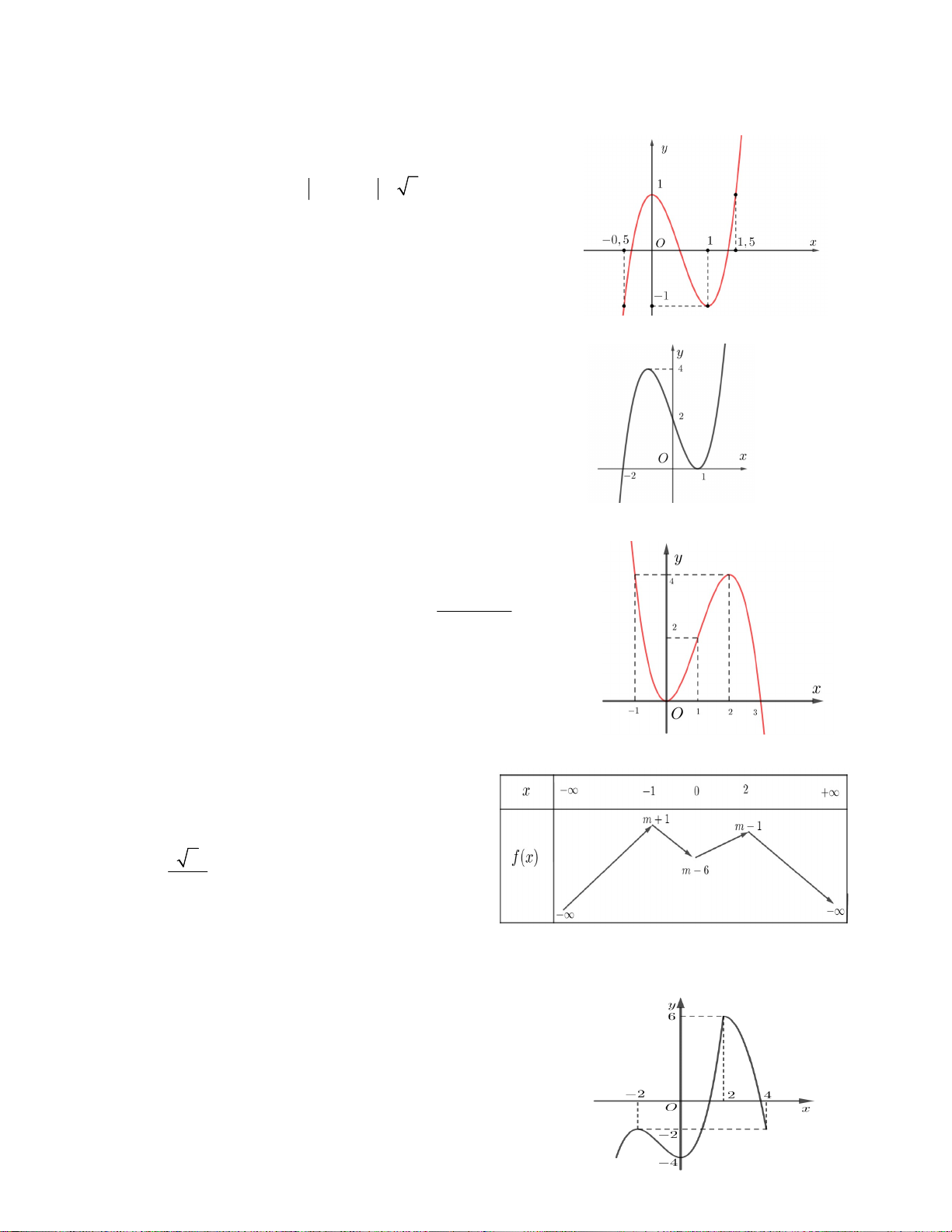
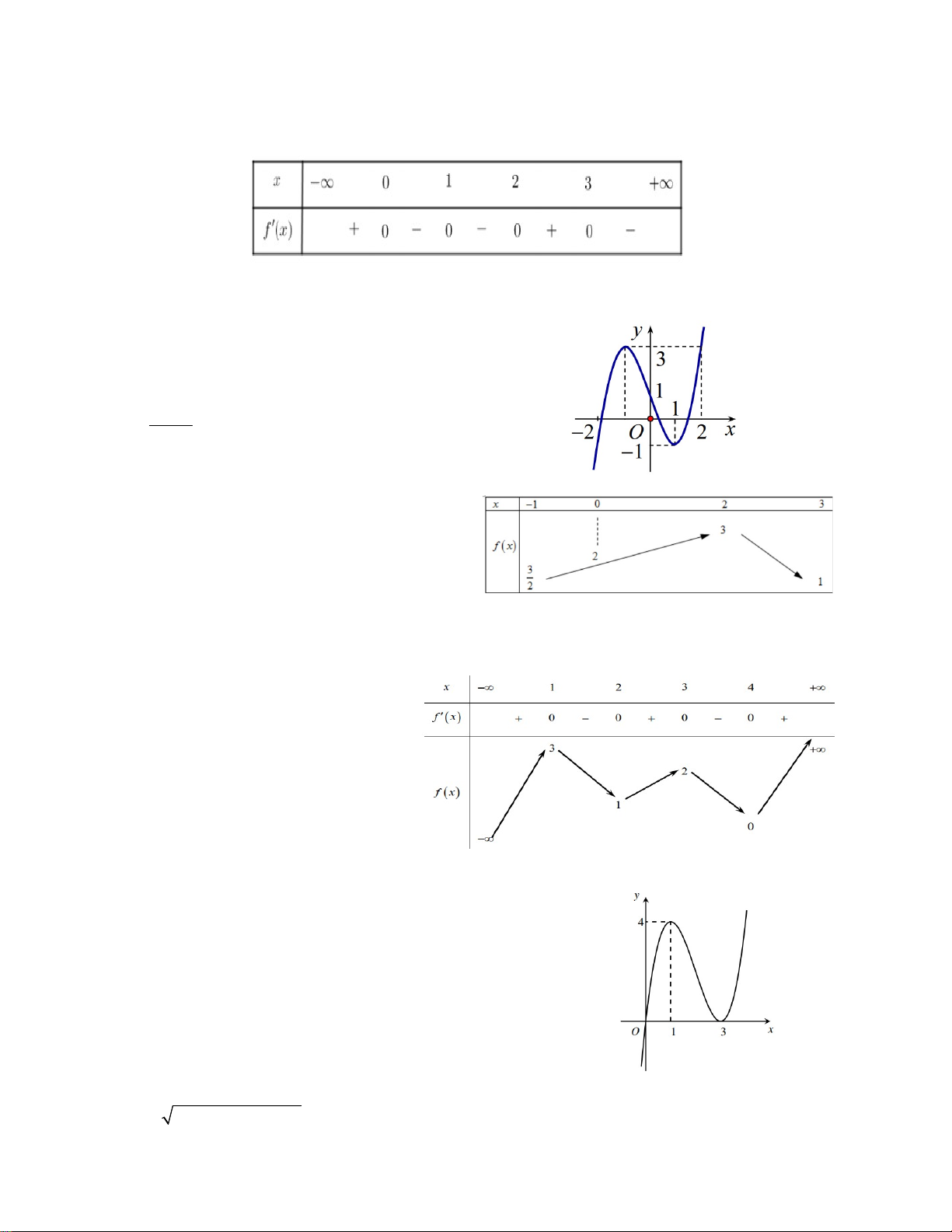
Câu 5. Hàm số y  f  x có bảng biến thiên
như hình vẽ bên. Có bao nhiêu số nguyên m để
phương trình f (sin x)  m 1 có nghiệm thực ? A. 2 B. 3 C. 4 D. 5
Câu 6. Cho hàm số f x 3 2
 x  7x 14x  8 . Phương trình 2
f ( 9  x )  0 có bao nhiêu nghiệm thực ? A. 4 B. 3 C. 2 D. 1
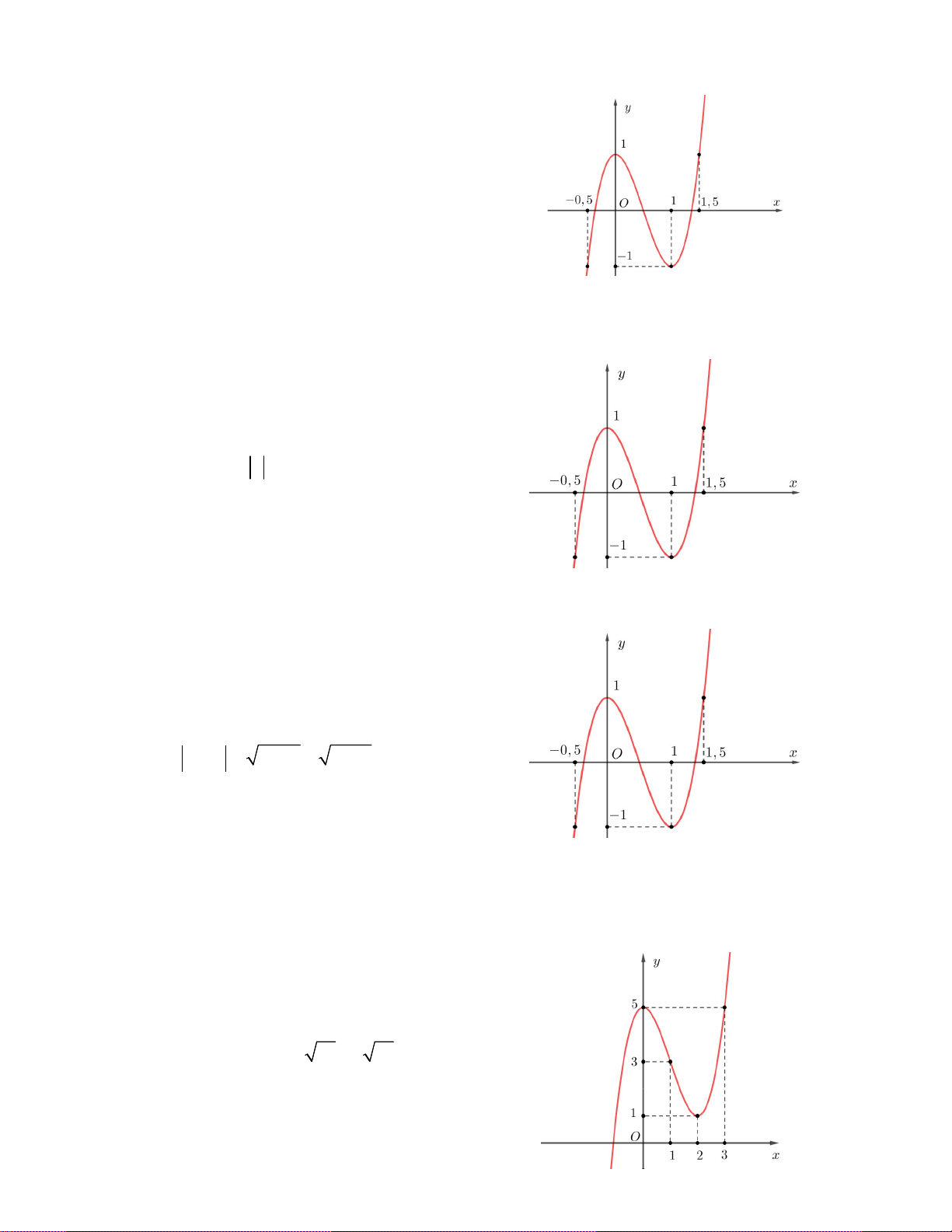
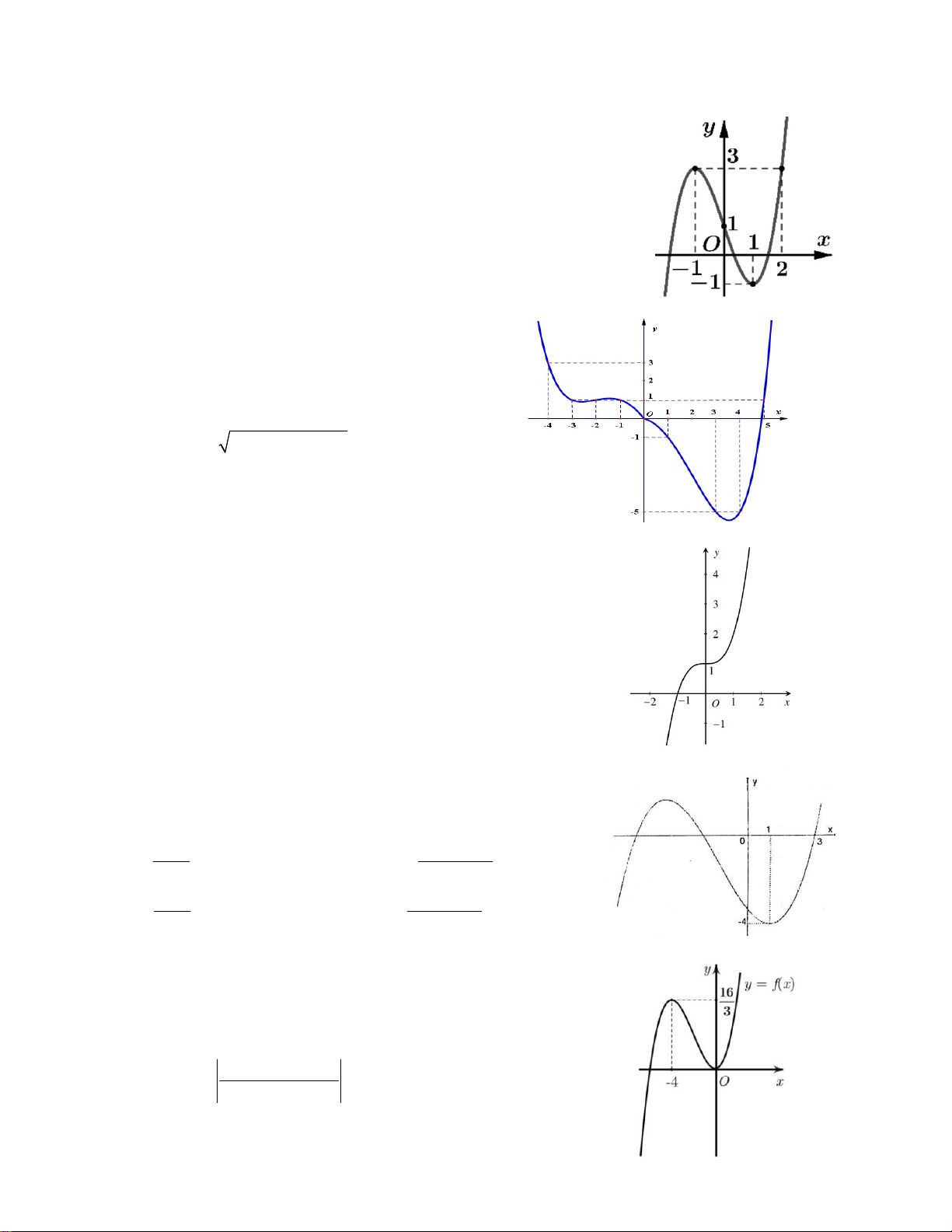
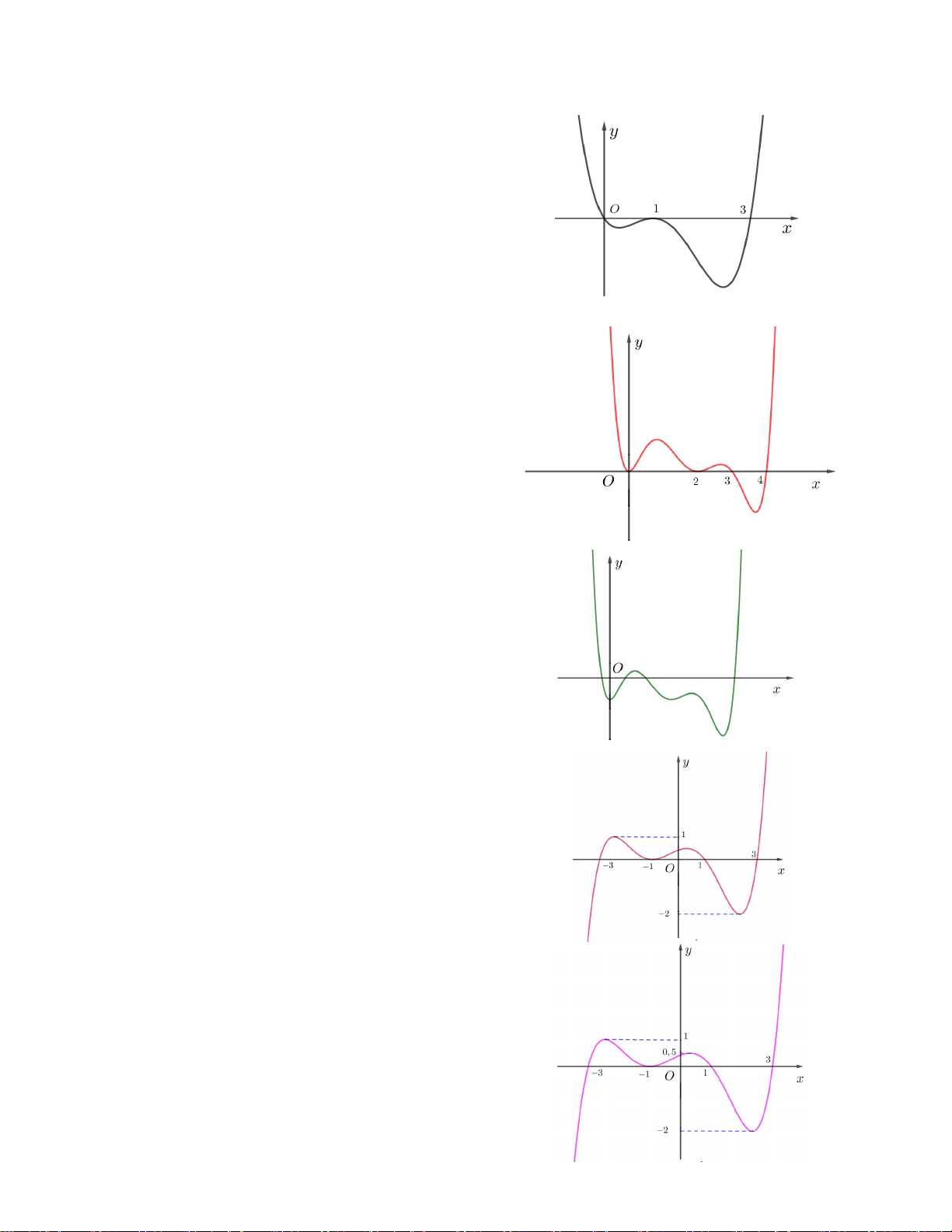
Câu 7. Cho hàm số y  f  x có đồ thị như hình
vẽ bên. Tìm số nghiệm thực của phương trình 2 f (x  2x  3)  3 . A. 5 B. 3 C. 4 D. 2
Câu 8. Cho hàm số f  x 3 2
 x  5x  7x  3. Phương trình 2
f ( x  3x  2)  0 có bao nhiêu nghiệm ? A. 4 B. 3 C. 2 D. 1 2
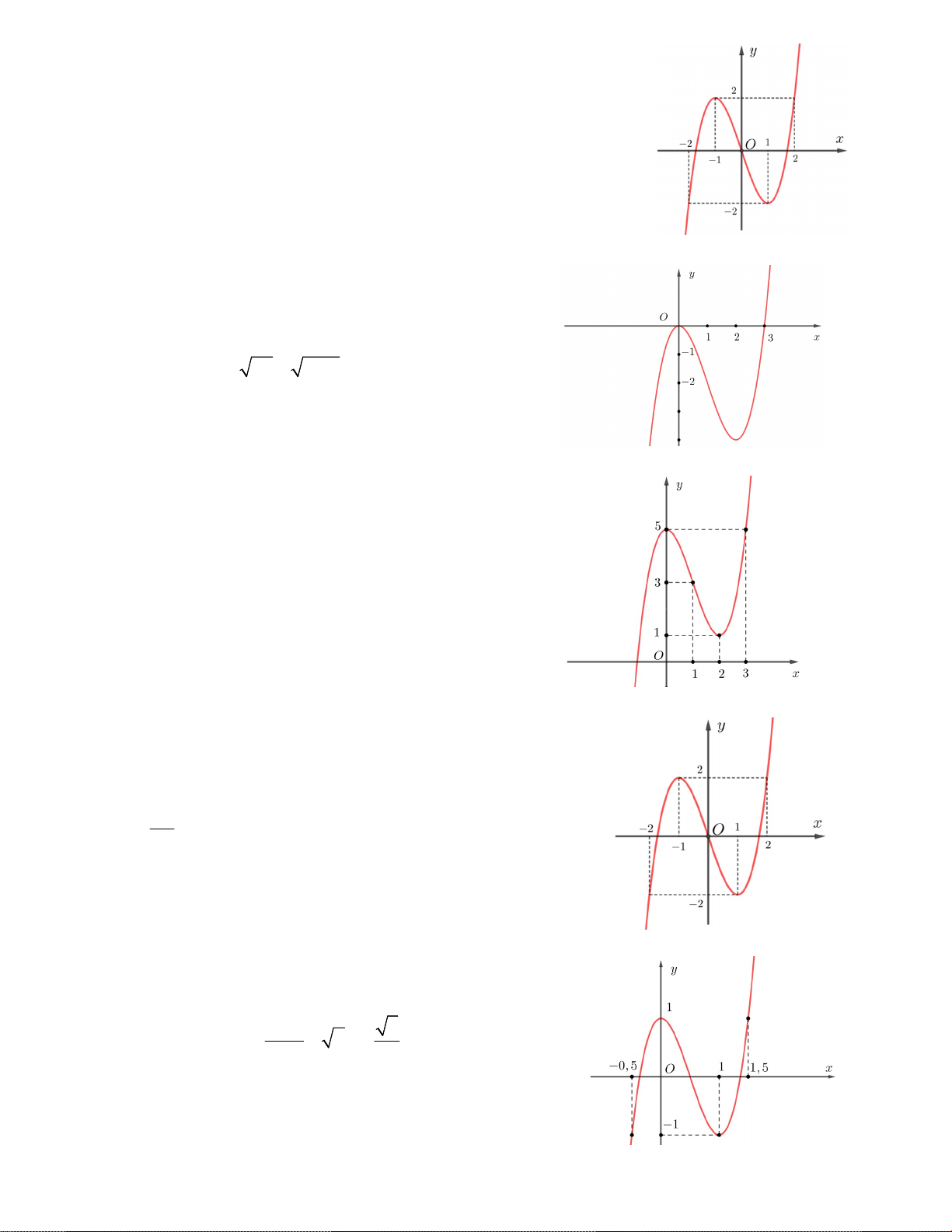
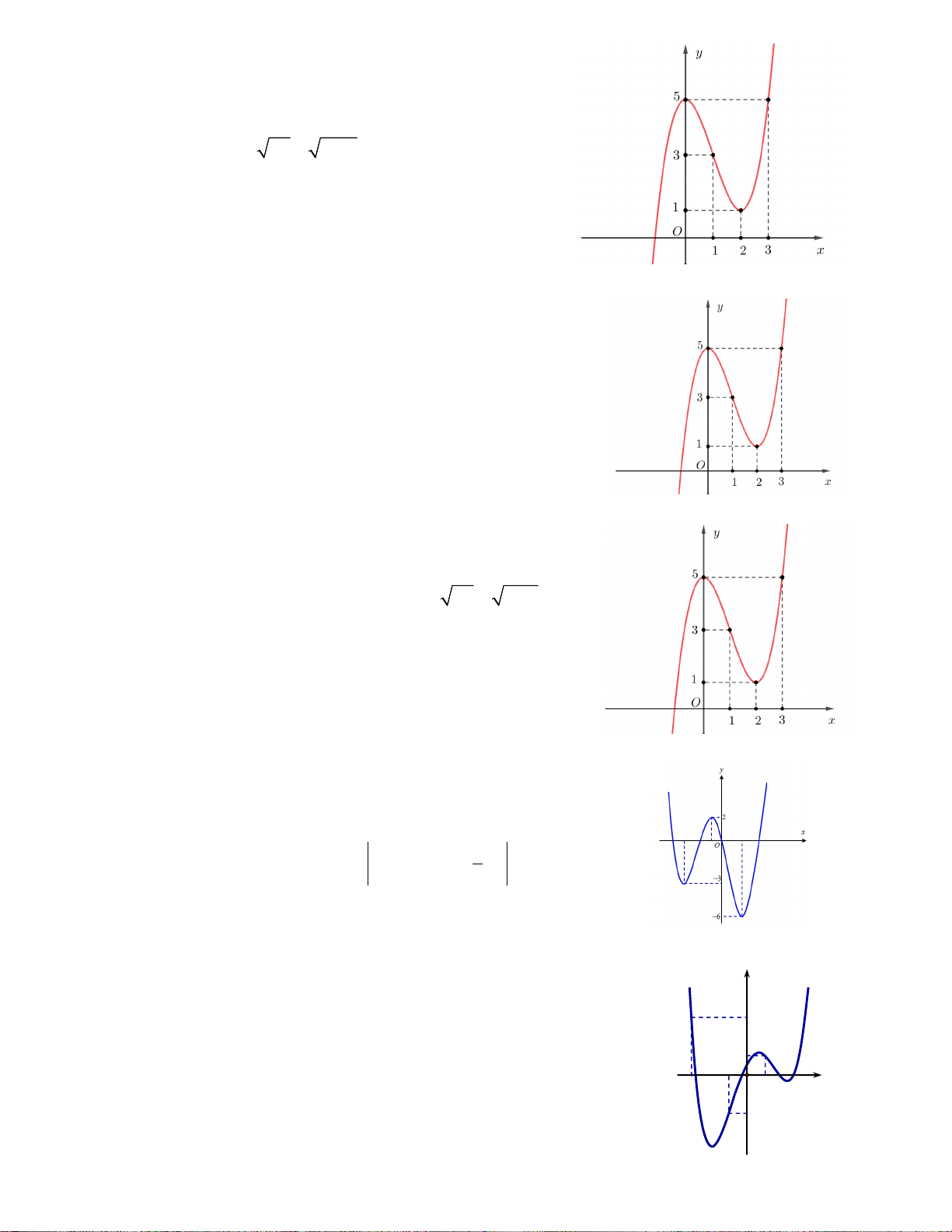
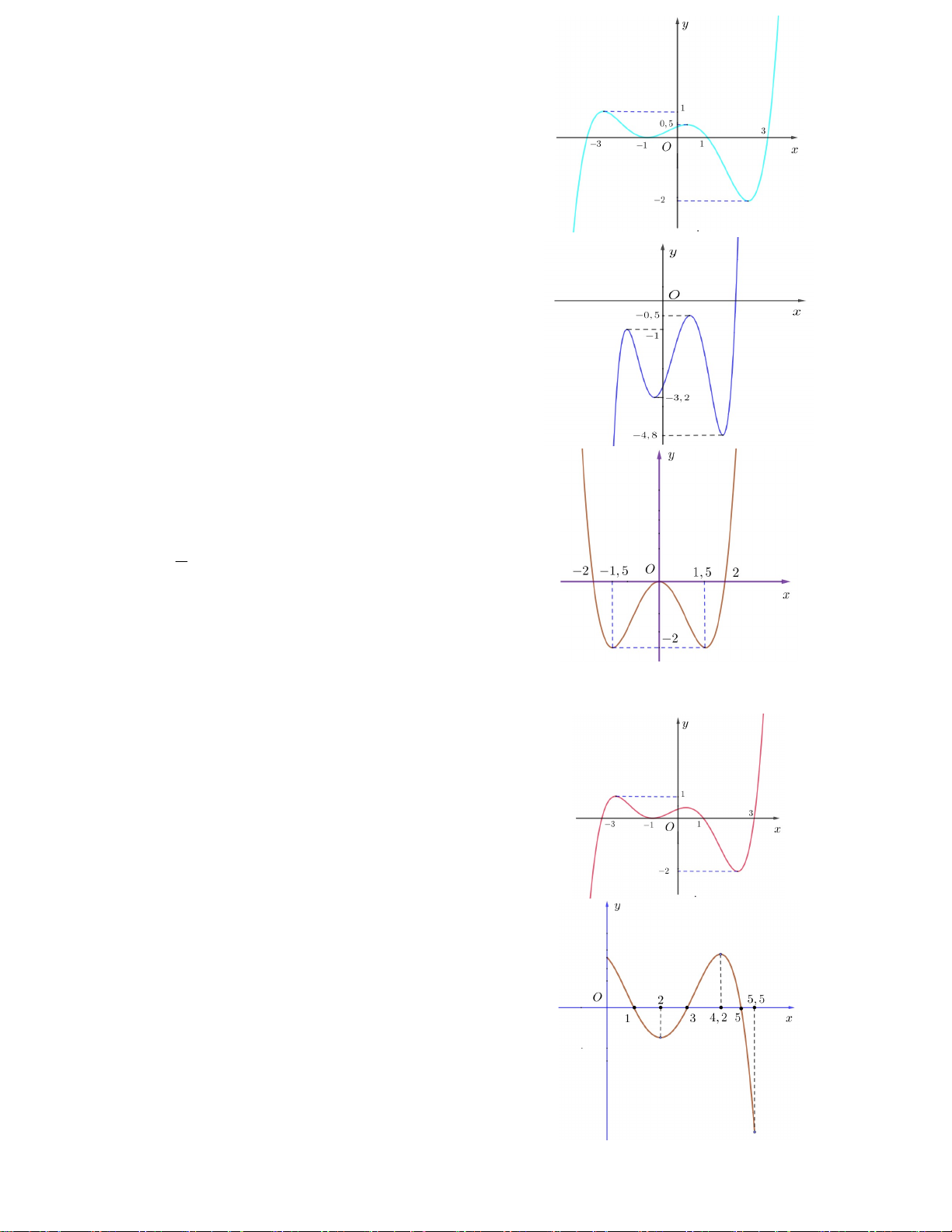
Câu 9. Cho hàm số y  f  x có đồ thị như hình
vẽ bên. Tìm số nghiệm thực của phương trình f  2 x  4x  3  2  . A. 4 B. 3 C. 1 D. 2
Câu 10. Cho hàm số f  x 3 2
 x  6x  9x  3. Phương trình 3
f  x  4 f  x  0 có bao nhiêu nghiệm ? A. 7 B. 8 C. 5 D. 6 Câu 11. Cho 3
f (x)  x  3x  2 . Có bao nhiêu số nguyên m để phương trình f (3sin x  4cos x)  m 1có nghiệm thực ? A. 220 B. 1999 C. 221 D. 2019
Câu 12. Hàm số y = f (x) có đồ thị như hình vẽ. Có bao nhiêu số nguyên k để
phương trình sau có nghiệm: f ( o c s3x 1)  k . A. 3 B. 4 C. 5 D. 6
Câu 13. Cho hàm số y  f  x có đồ thị như hình
vẽ bên. Tìm số nghiệm thực của phương trình 2
f  x  3 f  x  2  0 . A. 1 B. 3 C. 5 D. 2
Câu 14. Cho hàm số y  f  x có đồ thị như hình vẽ
bên. Tìm số nghiệm của phương trình f  2 x  4x  0 . A. 1 B. 3 C. 5 D. 2
_________________________________ 3
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 2)
___________________________________________________ Câu 1. Hàm số   3 2
f x  ax  bx  cx  d có đồ thị
như hình dưới đây. Hỏi phương trình sau có bao nhiêu nghiệm thực ? f  4 3 2
x  6x 11x  6x  2  1. A. 4 B. 3 C. 5 D. 2 Câu 2. Cho f x 3 2
 x  6x  9x  4 . Phương trình 3
f x  3 f  x  2  0có bao nhiêu nghiệm thực ? A. 2 B. 8 C. 4 D. 6 Câu 3. Hàm số   3 2
f x  ax  bx  cx  d có đồ thị
như hình dưới đây. Tồn tại bao nhiêu giá trị nguyên
của m để phương trình sau có 4 nghiệm thực ? f  x   m  5 A. 4 B. 3 C. 2 D. 1
Câu 4. Cho hàm số f  x 3 2
 x  6x 11x  6. Phương trình 2
f (4x  4x)  0 có bao nhiêu nghiệm thực ? A. 3 B. 4 C. 5 D. 6 Câu 5. Hàm số   3 2
f x  ax  bx  cx  d có đồ thị
như hình dưới đây. Với m là tham số thực thuộc đoạn
[2;3], hỏi phương trình sau có tối đa bao nhiêu nghiệm thực ?
f  x  m  2  3  m . A. 6 B. 3 C. 5 D. 4 Câu 6. Cho hàm số 3
f (x)  x  3x  4 . Có bao nhiêu số nguyên m để phương trình sau có nghiệm thực ? f  3
8cos x  6cos x  2  m A. 59 B. 55 C. 50 D. 90
Câu 7. Cho hàm số y  f  x có đồ thị như hình vẽ.
Hỏi phương trình sau có bao nhiêu nghiệm thực ? f  3 2
x  2x 14x  17   17 . A. 4 B. 2 C. 5 D. 3 4
Câu 8. Hàm số y = f (x) có đồ thị như hình vẽ. Tính tổng tất cả các giá trị
nguyên của tham số m để phương trình f ( o
c s2x  cos x 1)  m có nghiệm. A. 168 B. 150 C. 60 D. 45
Câu 9. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Tìm số nghiệm thực của phương trình f  2x  3 x   2  A. 4 B. 3 C. 1 D. 2
Câu 10. Cho hàm số y  f  x có đồ thị như hình vẽ. Tìm
số nghiệm dương của phương trình sau 3 f (x)  40x  64 . A. 4 B. 3 C. 5 D. 2
Câu 11. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Tồn tại
bao nhiêu số nguyên m để phương trình sau có hai nghiệm phân biệt  2  thuộc 0;  ? 3   
f (4sin x  2)  1999  89m . A. 1 B. 2 C. 5 D. 3 Câu 12. Hàm số   3 2
f x  ax  bx  cx  d có đồ thị như hình vẽ
bên. Phương trình sau có bao nhiêu nghiệm thực ?  x  4  5 f  x    .  4  3 A. 4 B. 3 C. 5 D. 4
_________________________________ 5
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 3)
___________________________________________________ Câu 1. Cho hàm số 4 2
f (x)  x  2x  2 . Tìm điều kiện tham số m để phương trình 3  f (x  2019)  m có 6 nghiệm phân biệt. A. 1 < m < 2 B. 2 < m < 3 C. 1 < m < 3 D. 0 < m < 2
Câu 2. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Tìm số nghiệm thực của phương trình f  5 3
x  x  x  4  5 . A. 5 B. 3 C. 1 D. 2 Câu 3. Cho hàm 3
f (x)  x  3x 1. Khi đó phương trình 3
f (x)  3 f (x) 1  0 có bao nhiêu nghiệm ? A. 6 B. 7 C. 5 D. 8 Câu 4. hàm số 3
f (x)  x  3x . Có bao nhiêu số nguyên m để phương trình f (sin x 1)  m có nghiệm. A. 2 B. 3 C. 4 D. 5
Câu 5. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Tìm số nghiệm dương của phương trình f (x  4)  2  1999x . A. 5 B. 3 C. 2 D. 4 3 2
Câu 6. Cho hàm số f x 3 2
 x  3x  2 . Phương trình  3 2 x  x     3 2 3 2
3 x  3x  2  2  0có bao nhiêu nghiệm thực ? A. 9 B. 7 C. 6 D. 5
Câu 7. Cho hàm số f  x 3 2
 x  3x  2 . Hỏi phương trình 3 2
f (x  3x)  có bao nhiêu nghiệm thực ? 3 A. 14 B. 15 C. 9 D. 12
Câu 8. Hàm số y  f  x có bảng biến thiên
như hình bên. Phương trình f  x  2 có bao nhiêu nghiệm thực ? A. 2 B. 3 C. 5 D. 4 Câu 9. Cho hàm số 3
f (x)  x  3x 1. Có bao nhiêu số nguyên m < 1999 để phương trình sau có ít nhất ba
nghiệm dương phân biệt ? 6 2
f (x)  (sin x  m) f (x)  msin x  0 A. 2000 B. 2001 C. 1999 D. 2019 Câu 10. Cho hàm số 3
f (x)  x  3x  3. Tìm số nghiệm tối thiểu của phương trình
f (x  2)  3 m  4 1 m . A. 4 B. 2 C. 5 D. 3 Câu 11. Cho hàm số 3 2
f (x)  x  3x  2 . Tìm tập hợp tất cả các giá trị m để phương trình f (cos x)  m có  3 
hai nghiệm phân biệt thuộc 0;  . 2    A. [– 2;2] B. (0;2) C. (– 2;2) D. [0;2)
Câu 12. Cho hàm số y  f  x có đồ thị như hình vẽ. Hỏi phương
trình f  2x  3 x   3 có bao nhiêu nghiệm thực ? A. 4 B. 3 C. 5 D. 2 Câu 13. Cho hàm số 5 2
f (x)  2x  5x 10x  2019 . Tồn tại bao nhiêu số nguyên n để phương trình sau có nghiệm: 2
f (4sin x  2cos x 1999)  f (14n  6n  2019) . A. 1 B. 4 C. 2 D. 3 Câu 14. Cho hàm số 3
f (x)  x  3x 1. Tìm tập hợp tất cả các giá trị m để phương trình sau có đúng ba
nghiệm phân biệt thuộc    ; . A.  3  ;  1 B. (– 3;1) C. [– 3;1) D. (– 3;1]
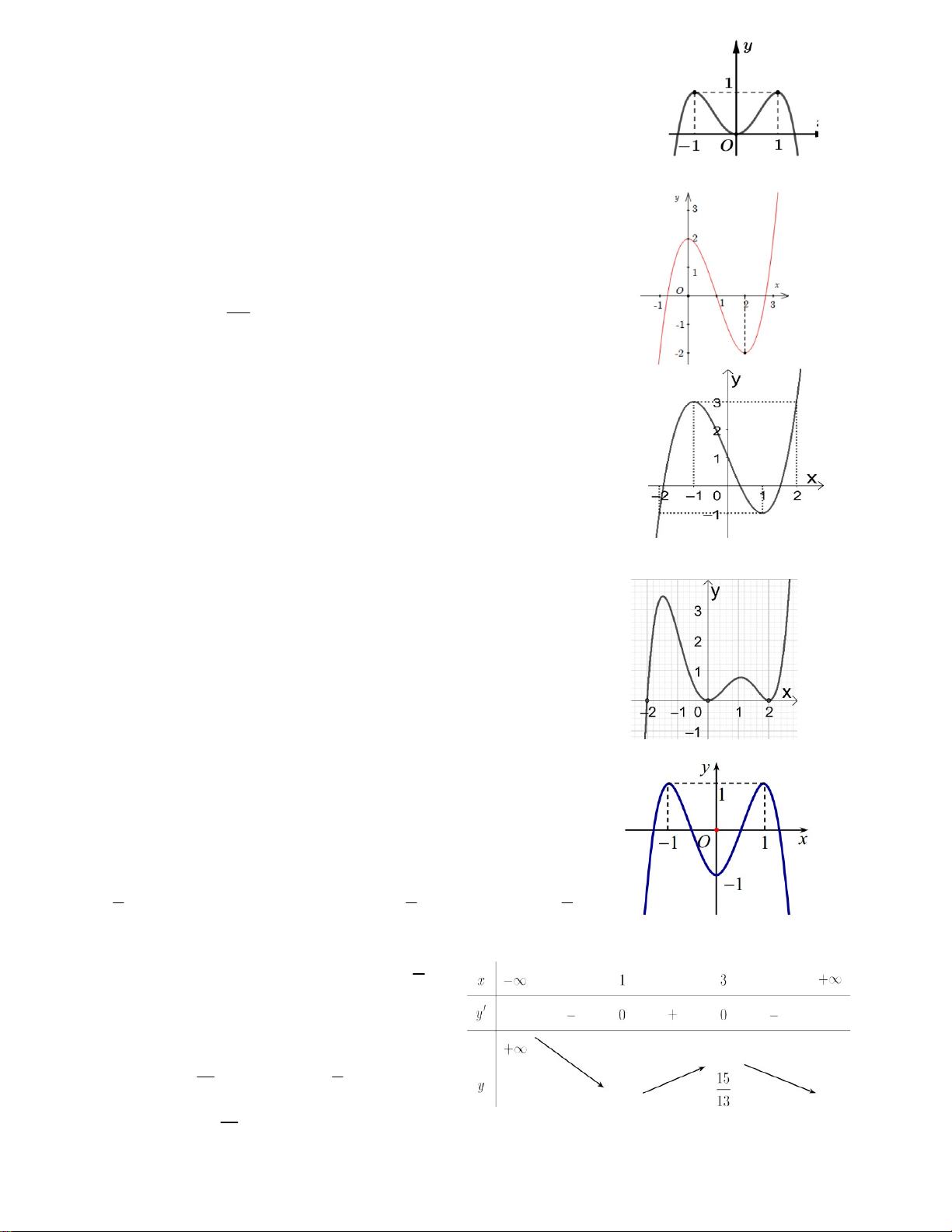
Câu 15. Hàm số y = f (x) có đồ thị như hình vẽ. Có tất cả bao nhiêu
giá trị nguyên của tham số m để phương trình f ( f (cos x))  m có nghiệm. A. 5 B. 10 C. 4 D. 8 Câu 16. Cho hàm số 3 2
f (x)  x  3x 1. Có bao nhiêu số nguyên m để phương trình sau có nghiệm
f ( f (sin x  2))  m  2019. A. 6 B. 5 C. 4 D. 7 Câu 17. Hàm số   3 2
f x  ax  bx  cx  d có đồ thị như hình vẽ 2m
bên. Với m là tham số thực, hỏi phương trình f  x  có tối 2 m 1
thiểu bao nhiêu nghiệm thực ? A. 4 B. 3 C. 1 D. 2
_________________________________ 7
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 4)
___________________________________________________ Câu 1. Hàm số   3 2
f x  ax  bx  cx  d có đồ thị như hình
dưới đây. Hỏi phương trình f (3x  2)  b 1có bao nhiêu nghiệm thực ? A. 4 B. 3 C. 5 D. 2
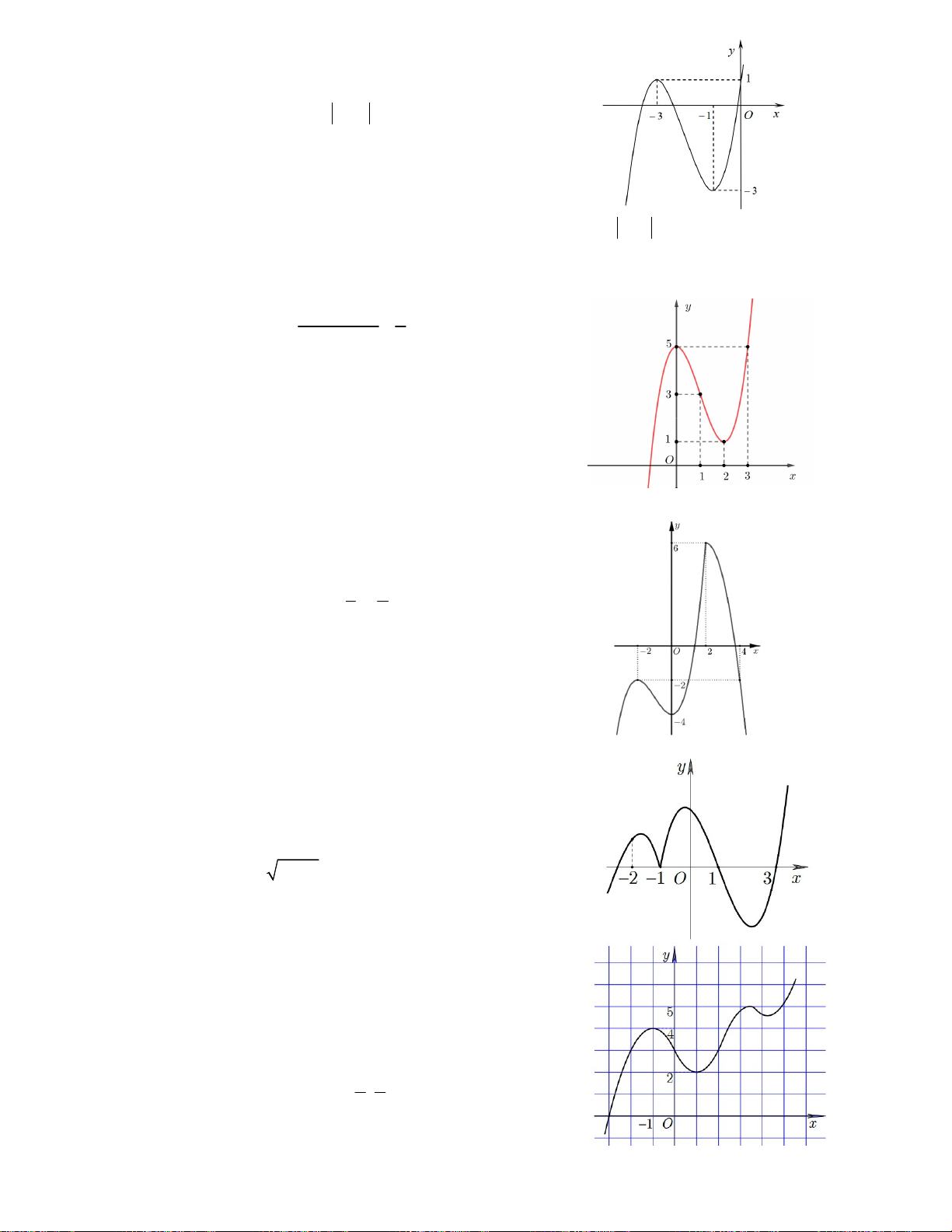
Câu 2. Hàm số y = f (x) có đồ thị như hình vẽ. Tìm điều kiện tham số
k để phương trình sau có hai nghiệm phân biệt : 2 ( x f e )  k .
A. 0 < k < 4 B. k > 1
C. 0 < k < 2 D. k > 0
Câu 3. Cho hàm số y  f x có đồ thị như hình vẽ. Có bao nhiêu 2 m
giá trị nguyên của m để phương trình f  x   1   0 có 2 x  3x  5
nghiệm trên khoảng 1;  1 A. 13 B. 11 C. 5 D. 10
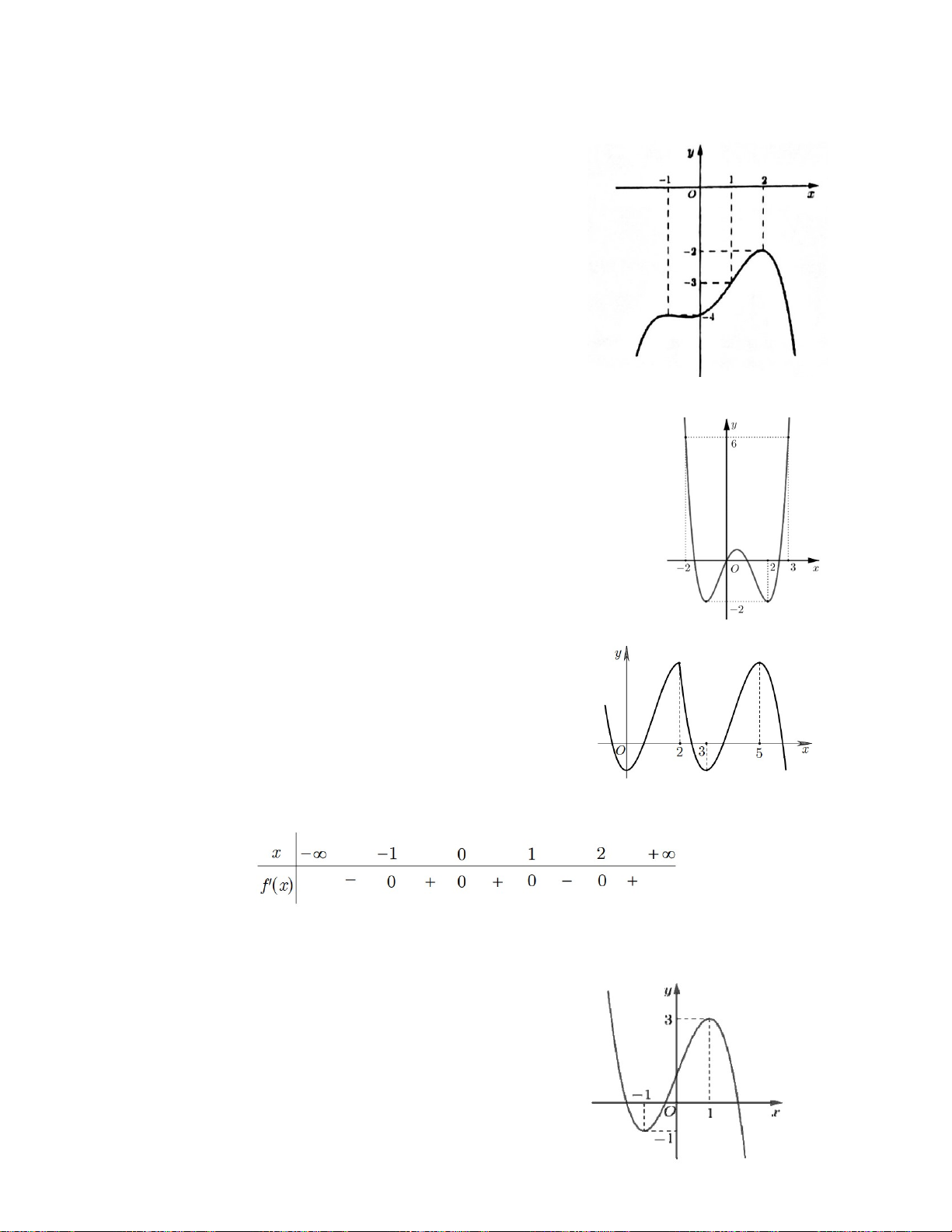
Câu 4. Cho hàm số y  f x có bảng biến thiên như
hình vẽ. Có bao nhiêu giá trị nguyên của m để đồ thị x hàm số y 
có đúng hai đường tiệm cận đứng f  x A. 4 B. Vô số. C. 1. D. 5.
Câu 5. Cho hàm số y  f  x trên  2
 ;4như hình vẽ. Gọi S là tập
chứa các giá trị của m để hàm số y   f   x  m2 2 có giá trị lớn nhất trên đoạn  2
 ;4 bằng 49. Tổng các phần tử tập S bằng A. - 9 B. - 23 C. - 2 D. - 12 8
Câu 6. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Tồn tại
bao nhiêu giá trị nguyên của tham số m để phương trình sau có
nghiệm trên đoạn [0;3]: 2x  3  x  . m f  x . A. 4 B. 3 C. 5 D. 2
Câu 7. Cho hàm số y  f x liên tục và có đạo hàm trên  , đồ thị
y  f x như hình vẽ bên. Ký hiệu g  x  f  3 x  x   1  m . Tồn tại
bao nhiêu số nguyên dương m sao cho max g  x  2m . 0; 1 A. 4 B. 3 C. 5 D. 2
Câu 8. Cho hàm số y  f  x liên tục và có đạo hàm trên  , đồ thị
y  f x như hình vẽ bên. Ký hiệu T  x  f 2 2x  1 x   m .
Tìm điều kiện của tham số m sao cho max g  x  2min g  x . 0; 1 0; 1
A. m  4 B. m  3 C. 0  m  5 D. m  2
Câu 9. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Gọi S là tập hợp tất 1
cả các giá trị nguyên m để hàm số y  f x  2019 2
 m có 5 cực trị. Tổng 3
tất cả các giá trị của tập hợp S bằng A. 7 B. 0 C. 4 D. 5 y 3
Câu 10. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Có bao nhiêu số
nguyên m thuộc [– 2019;2020] để phương trình sau có 8 nghiệm phân biệt 1 1  2 2 2
2 f (x)  (4m  2m 1) f (x)  2m  m  0 . 3  O x 1 A. 2 B. 2019 C. 1 D. 2020 2 
_________________________________ 9
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 5)
___________________________________________________
Câu 1. Cho hàm số y  f  x liên tục và có đạo hàm trên  , đồ thị
y  f x như hình vẽ bên. Ký hiệu g  x  f  3 2
x  x  x  2  3m , với m là tham số thực. Hãy
tìm giá trị nhỏ nhất của biểu thức 2
S  m  3max g  x 4min g x m . 0; 1 0; 1
A. 4 B. – 50 C. – 150 D. – 102
Câu 2. Hàm số bậc ba y  f  x có đồ thị như hình vẽ bên. Ký
hiệu M và m tương ứng là giá trị lớn nhất, giá trị nhỏ nhất của
hàm số g  x  f  4 4
sin x  cos x . Tính 8M  m . A. 35 B. 38 C. 36 D. 43
Câu 3. Hàm số bậc ba y  f  x có đồ thị như hình vẽ bên. Biết
rằng tổng các giá trị lớn nhất và giá trị nhỏ nhất của hàm số
g  x  f  2x  2  x có dạng a b  ca,b,c. Tính a  2b  3c . A. – 21 B. 6 C. – 4 D. 5 Câu 4. Hàm số    3 2 y
f x  ax  bx  cx  d có đồ thị như hình vẽ bên. Có
bao nhiêu số nguyên m để phương trình 2
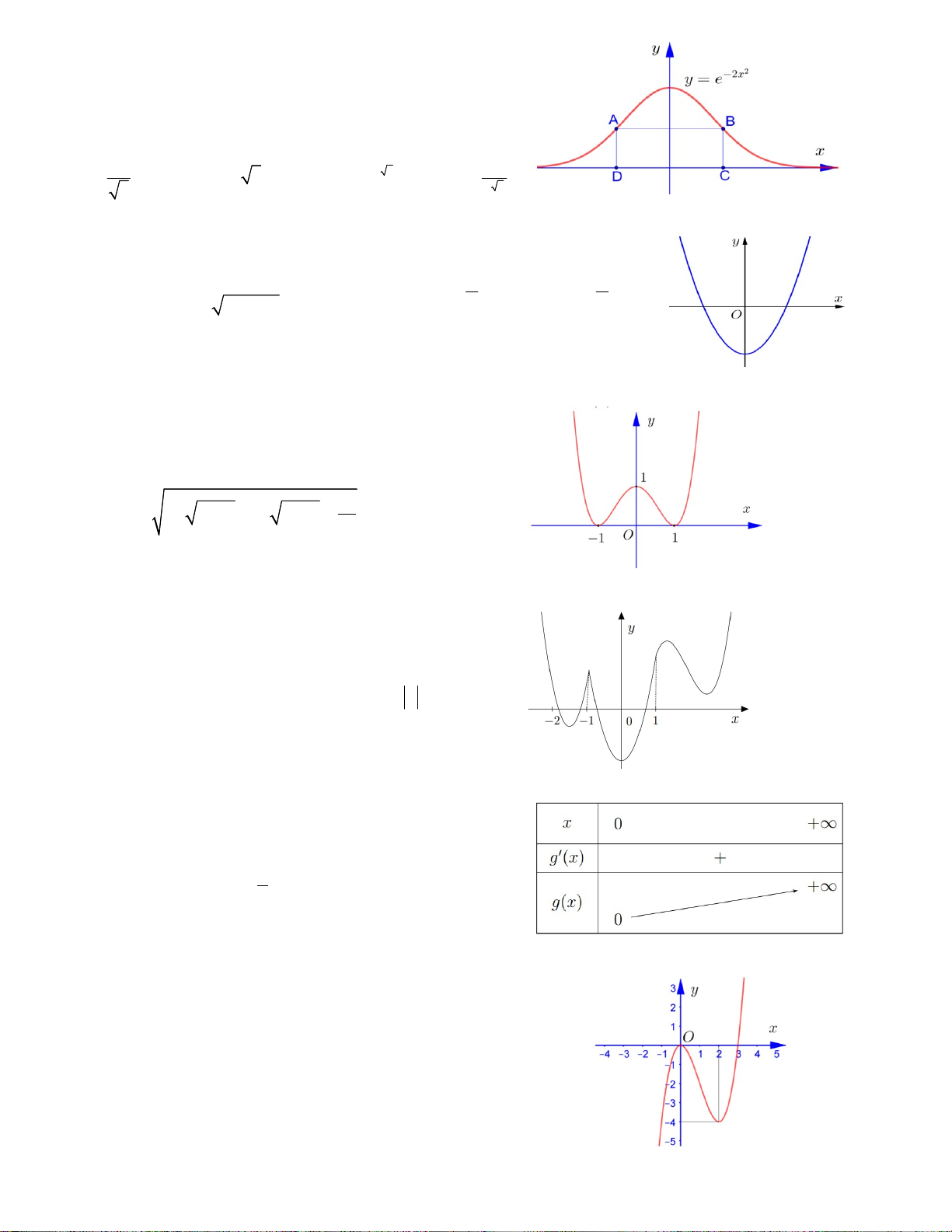
f x  (m  3) f x  m  4  0 có 7 nghiệm phân biệt ? A. 1 B. 2 C. 3 D. 4 10 Câu 5. Hàm số 2 2x y e 
có đồ thị như hình vẽ bên. ABCD là
hình chữ nhật thay đổi sao cho A và B luôn thuộc đồ thị
hàm số đã cho. CD luôn nằm trên trục hoành. Giá trị lớn
nhất của diện tích hình chữ nhật ABCD là 1 1 A. B. e C. 2 e D. e 2 e
Câu 6. Cho hàm số y  f x có đồ thị như hình vẽ bên. Biết u ;v là một 0 0 
 f (1 4v)  f (5  8u)  a a nghiệm của hệ  và *
u  v  ;a  ,b   , tối  0 0  2u  3v  2u  v b b
giản. Giá trị biểu thức P = a + b là A. 1 B. 2 C. 3 D. 4
Câu 7. Cho hàm số y  f x có đồ thị như hình vẽ bên.
Xác định số nghiệm thực của phương trình 11 f ( f (x))  2 f (x)   f (x)  2 . 2 A. 5 B. 2 C. 3 D. 4
Câu 8. Cho hàm số y  f x có đồ thị như hình vẽ bên.
Số điểm cực trị của đồ thị hàm số y  f (1 x ) là A. 9 B. 8 C. 7 D. 6
Câu 9. Cho hàm số y  g  x xác định trên (0;) và có
bảng biến thiên như hình bên. Tìm số giao điểm của đồ thị 1 hàm số 2
y  f (x)  x   x và y  g x . 3 A. 1 B. 2 C. 3 D. 0
Câu 10. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Tìm số điểm cực trị của hàm số y  f ( f (x)) . A. 5 B. 6 C. 3 D. 4
_________________________________ 11
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 6)
___________________________________________________
Câu 1. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Đặt hàm số 3
y  g(x)  f (2x  x 1)  m . Tìm m để max g(x)  1  0 . [0;1]
A. m = - 13 B. m = - 12 C. m = - 1 D. m = 3
Câu 2. Cho hàm số y  f  x xác định và liên tục trên
và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên
của m để phương trình sau có nghiệm 2. f  2
33 9x 30x2 1 m2019. A. 15 B. 14 C. 10 D. 13
Câu 3. Cho hàm số y  f x có đồ thị như hình vẽ bên. Có bao nhiêu
giá trị nguyên m để phương trình f (6sin x  8cos x)  f (m(m 1)) có nghiệm thực. A. 6 B. 2 C. 5 D. 4
Câu 4. Cho hàm số y  f x có đồ thị như hình vẽ bên. Bất phương trình ( x )  (3 x f e
m e  2019) có nghiệm x  (0;1) khi và chỉ khi 4 4 A. m   B. m   1011 3e  2019 2 f (e) C. m   D. m  1011 3e  2019
Câu 5. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Tồn tại bao
nhiêu số nguyên m để phương trình sau có nghiệm:  3sin x  cos x 1  2 f  f (m  4m  4)    2cos x  sin x  4  A. Vô số B. 5 C. 3 D. 4 12
Câu 6. Cho hàm số y  f x có đồ thị như hình vẽ bên. Hỏi có bao
nhiêu điểm trên đường tròn lượng giác biểu diễn nghiệm của phương trình f  f (cos 2x)  0 . A. 1 B. Vô số C. 3 D. 4
Câu 7. Cho hàm số y  f x có đồ thị như hình vẽ bên. Tập hợp tất cả
các giá trị thực của tham số m để phương trình f (cosx) = m có 3 nghiệm  3  phân biệt thuộc 0;  là 2   
A. [-2;2] B. (0;2) C. (-2;2) D. [0;2)
Câu 8. Cho hàm số y  f x có đồ thị như hình vẽ bên. Tập hợp tất cả
các giá trị thực của m để phương trình f (1 – cos2x) = m có nghiệm thuộc khoảng (0; ) là
A. [- 1;3] B. (- 1;1) C. (- 1;3) D. (-1;1]
Câu 9. Cho hàm số y  f  x liên tục trên R và có đồ thị như hình vẽ
bên. Đặt g(x)  f ( f (x)) . Hỏi phương trình g (x) có mấy nghiệm thực ? A. 14 B. 12 C. 10 D. 8
Câu 10. Cho hàm số y  f  x liên tục trên R và có đồ thị như hình vẽ
bên. Tập hợp tất cả các giá trị m để phương trình f (sin x)  log m có 2
nghiệm thuộc khoảng (0; ) là A.  1      ; 2  B. (0;2) C. 1 ;2 D. 1 ;2   2    2     2  7
Câu 11. Hàm số y  f  x thỏa mãn f (0)  có 6
bảng biến thiên như hình vẽ bên. Tìm giá trị lớn
nhất của m để phương trình sau có nghiệm trên [0;2] : 13 3 3 2 2 f (x) 
f (x)  7 f (x)   ln m . 2 2 15 A. 2 B. C. 3 D. 4 13 ____________________________ 13
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 7)
___________________________________________________
Câu 1. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Để đồ thị hàm số 2
h(x)  f (x)  f (x)  m có số điểm cực trị ít nhất thì giá trị nhỏ nhất
của tham số m  m . Tìm mệnh đề đúng trong các mệnh đề sau 0
A. m (0;1) B. m (1;0) 0 0 C. m ( ;  1  ) D. m (1;) 0 0
Câu 2. Cho hàm số y  f x có bảng biến
thiên hình vẽ bên. Tìm giá trị nhỏ nhất của m để
bất phương trình f ( x 1 1)  m có nghiệm A. – 2 B. 2 C. 3 D. 4
Câu 3. Hàm số y  f  x có đồ thị như hình vẽ bên. Tìm điều kiện
tham số m để bất phương trình sau nghiệm đúng với mọi x (1;3) : 2 2 f (x)  x  4x  m . A. m < - 3 B. m < - 10 C. m < - 2 D. m < 5
Câu 4. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Tập hợp S =
[a;b] bao gồm tất cả các giá trị m để phương trình sau có nghiệm 2 2
 f (x 1) f (x 1)  3 f (x 1)  2  m( f (x 1)  2 f (x 1) 1) . Tính a + 2b. A. 5 B. 2 C. 3 D. 4
Câu 5. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Đặt
f (x)  f ( f (x) 1) . Tìm số nghiệm của phương trình g (  x)  0 . A. 10 B. 8 C. 6 D. 9 14 Câu 6. Cho 2
f (x)  1 mx với m  0 . Tìm tổng tất cả các giá trị nguyên của tham số m thuộc [– 2019;2019] để
phương trình f ( f (x))  x có 4 nghiệm thực phân biệt.
A. – 2037171 B. – 2035153 C. – 2039190 D. – 2041210
Câu 7. Cho hàm số y  f  x có bảng biến thiên như hình vẽ bên. Khi đó hàm số 3
y  f (x 1)  x 12x  2019 nghịch biến trên khoảng nào dưới đây ? A. (1;2) B. (3;4) C. (1;) D. ( ;  1)
Câu 8. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Số các
giá trị nguyên của tham số m không vượt quá 5 để phương trình  f  m x   2 1 
 0 có hai nghiệm phân biệt là 8 A. 5 B. 6 C. 7 D. 4
Câu 9. Cho hàm số y  f x có bảng biến thiên
như hình vẽ bên. Gọi S là tập hợp các số nguyên dương m để bất phương trình 3 2
f (x)  m(x  3x  5) có nghiệm thuộc đoạn [-1;3]. Số phần tử của S là A. 1 B. 2 C. 3 D. 0
Câu 10. Hàm số y  f x có bảng biến
thiên như hình vẽ bên. Hàm số 3 2
y  f (x)  3 f (x) nghịch biến trên khoảng nào dưới đây A. (1;2) B. (2;3) C. (3;4) D. ( ;  1)
Câu 11. Cho hàm số y  f x có đồ thị như hình vẽ bên. Tồn tại bao
nhiêu số nguyên m nhỏ hơn 10 để phương trình 2 ( x f e )  m có đúng hai nghiệm thực A. 6 B. 5 C. 7 D. 4 Câu 12. Cho hàm số 3
f (x)  x  3x  3 . Có bao nhiêu số nguyên m để bất phương trình sau nghiệm đúng mọi giá trị x: 2
f ( 3sin x  4 cos x  6)  m 1993m  2019 .
A. 1990 B. 1991 C. 1992 D. 1993
_________________________________ 15
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 8)
___________________________________________________
Câu 1. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số    2 g f x
có bao nhiêu điểm cực trị ? A. 5 C. 3 B. 4 D. 2
Câu 2. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số    2 g f x
có bao nhiêu điểm cực trị ? A. 8 C. 5 B. 7 D. 6
Câu 3. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số    2 g f x
có bao nhiêu điểm cực trị ? A. 9 C. 10 B. 8 D. 6
Câu 4. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Hàm số g   f  x  2
2 có bao nhiêu điểm cực trị ? A. 5 C. 6 B. 8 D. 4
Câu 5. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Hàm số g   f  x  2 5
2 có bao nhiêu điểm cực trị ? A. 7 C. 9 B. 8 D. 11 16
Câu 6. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Tính tổng tất cả các giá trị nguyên của m để hàm số g   f  x  m2 7
có tối đa số điểm cực trị. A. 3 B. 15 C. 10 D. 6
Câu 7. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Hàm số g   f  x  3 3
2 có bao nhiêu điểm cực trị ? A. 1 B. 2 C. 3 D. 4
Câu 8. Cho hàm số bậc năm y  f  x . Giả sử hàm số
y  f  x có đồ thị như hình vẽ bên. Hàm số g  f  x 7 3
 x  9 có bao nhiêu điểm cực trị. 3 A. 1 B. 3 C. 0 D. 2
Câu 9. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số g   f  x 4 3 2  3 
 có bao nhiêu điểm cực trị ? A. 7 B. 10 C. 9 D. 5
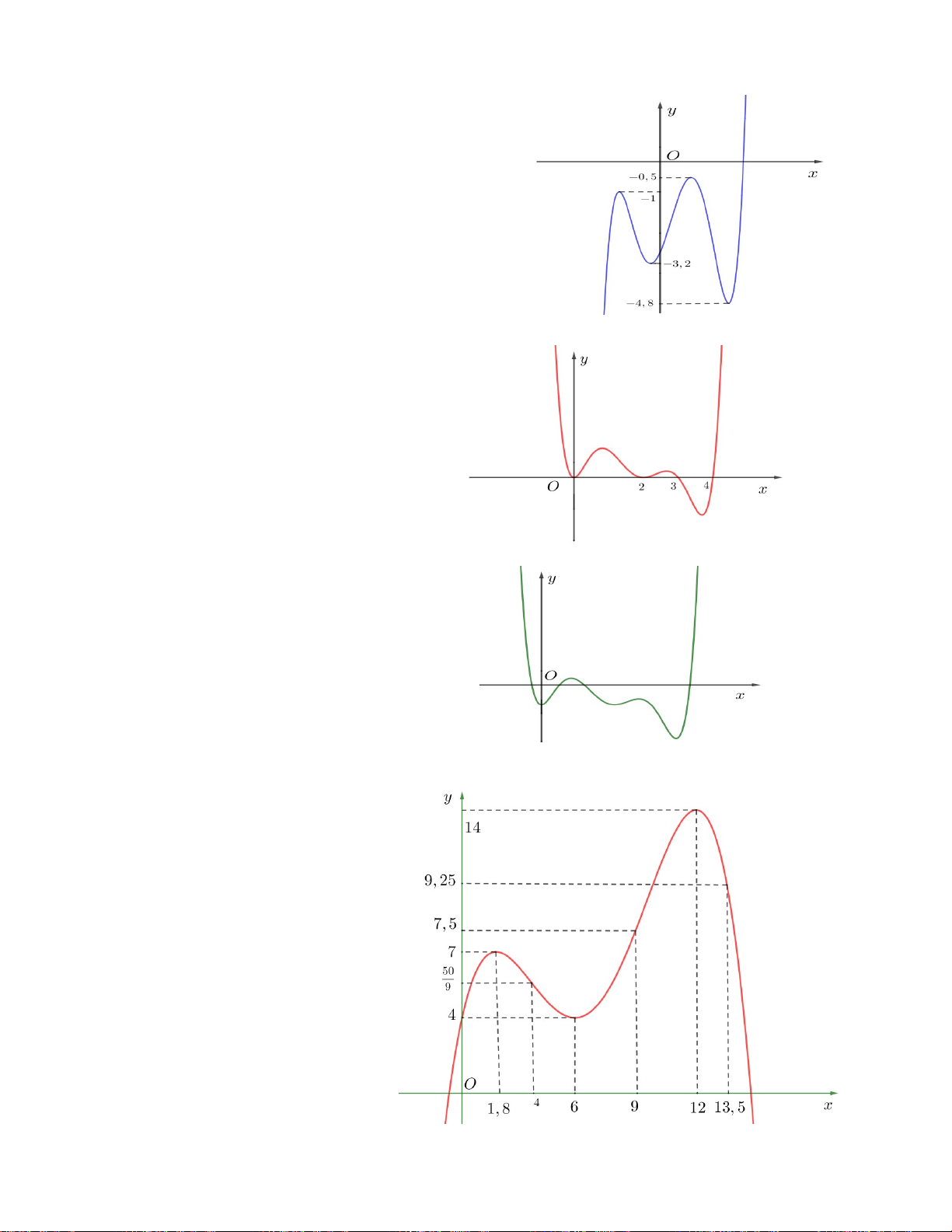
Câu 10. Cho hàm số y  f  x liên tục trên [0;5,5], đồ
thị của hàm số trên [0;5,5] như hình vẽ. Hỏi hàm số     2 g f x  
 có tối đa bao nhiêu điểm cực trị ? A. 3 C. 6 B. 7 D. 4
_________________________________ 17
ÔN TẬP ĐỒ THỊ – BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 9)
___________________________________________________
Câu 1. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Hàm số g   f  x  3 3
2 có bao nhiêu điểm cực trị ? A. 1 B. 2 C. 3 D. 4
Câu 2. Cho hàm số y  f  x có đồ thị
như hình vẽ bên. Hàm số    2 g f x
có bao nhiêu điểm cực trị ? C. 8 B. 5 C. 7 D. 6
Câu 3. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Hàm số    2 g f x
có bao nhiêu điểm cực trị ? C. 9 B. 10 C. 8 D. 6
Câu 4. Cho hàm số y  f  x . Giả sử
hàm số y  f  x có đồ thị như hình vẽ bên. Khi đó hàm số g  x  f x 2 36  7x 108x  5 đồng
biến trên khoảng nào sau đây ? A. (0;4) và (9;13,5) B. (0;4) và 9;
C. (4;9) và 13,5; D. (0;9) 18
Câu 5. Cho hàm số y  f  x có đồ
thị như hình vẽ bên. Hàm số    2 g f x có bao nhiêu điểm cực trị ? A. 5 B. 3 C. 4 D. 2
Câu 6. Cho hàm số y  f  x có đồ thị như hình vẽ
bên. Hàm số g   f  x  2 5 2 có bao nhiêu điểm cực trị ? C. 7 D. 9 E. 8 F. 11
Câu 7. Cho hàm số y  f  x có đồ thị như hình vẽ bên.
Tính tổng tất cả các giá trị nguyên của m để hàm số g   f  x  m2 7
có tối đa số điểm cực trị. B. 3 B. 15 C. 10 D. 6
Câu 8. Cho hàm số y  f  x có đồ thị như hình
vẽ bên. Hàm số g   f  x  2 2 có bao nhiêu điểm cực trị ? C. 5 B. 6 C. 8 D. 4
_________________________________ 19
ÔN TẬP ĐỒ THỊ HÀM SỐ - BẢNG BIẾN THIÊN LỚP 12 THPT
(LỚP BÀI TOÁN VẬN DỤNG CAO, PHÂN LOẠI – PHẦN 10)
___________________________________________________
Câu 1. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Tính tổng
các giá trị nguyên của tham số m để bất phương trình sau nghiệm đúng với mọi x. f ( x) 2 f ( x) 2 f ( x) 9.6  4  f (x).9  (m  5m).4   A. 10 B. 5 C. 9 D. 4
Câu 2. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Có bao nhiêu số
nguyên m để phương trình 3
f (x  3x)  m có 6 nghiệm phân biệt thuộc [– 1;2] A. 6 B. 2 C. 3 D. 7
Câu 3. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Phương trình (2x  2x f
)  m có nhiều nhất bao nhiêu nghiệm phân biệt thuộc đoạn [– 1;2] ? A. 5 B. 2 C. 3 D. 4
Câu 4. Cho hàm số y  f  x có bảng xét dấu đạo hàm như hình vẽ bên.
Hàm số y  log ( f (2x)) đồng biến trên khoảng nào sau đây 2
A. (1;2) B. (– 1;0) C. (– 1;1) D. ( ;  1  ) Câu 5. Cho hàm số 3
f (x)  (x 1)  3x  3 . Đồ thị hình bên là của hàm số nào
A. y   f (x 1) 1 B. y   f (x 1) 1
C. y   f (x 1) 1 D. y   f (x 1) 1 20
Câu 6. Cho hàm số y  f x có đồ thị như hình vẽ bên. Xác định
số nghiệm của phương trình: 1993 f (x)  1993x 1999 A. 4 B. 1 C. 2 D. 0 Câu 7. Cho hàm số 2019 2017 3 f (x)  2019x  2017x
... 3x 1999x 1993 x 1 1992 . Có bao nhiêu giá trị
nguyên không âm của m để phương trình 2 2
f (3sin 2x  8cos x  4)  f (m  m) có nghiệm thực ? A. 2 B. 3 C. 4 D. 6 3 2  x  x  x 5 
Câu 8. Xét hàm số g(x)  f   . 4 2   x  2x 1 4 
Đặt m  min g(x); M  max g(x) . Trong các khẳng định sau, khẳng định nào đúng ? A. M + m = 6 B. 2M + m = 2
C. 2M – m = 5 D. M – m = 4
Câu 9. Cho hàm số y  f x có đồ thị như hình vẽ bên. Có bao
nhiêu số nguyên m để phương trình 1 x
f ( 1)  x  m có nghiệm 3 2 thuộc đoạn [– 2;2] ? A. 11 B. 9 C. 8 D. 10
Câu 10. Cho hàm số y  f x có đồ thị như hình vẽ bên. Có bao
nhiêu số nguyên m để bất phương trình sau nghiệm đúng với mọi x 2;2 ?: 2 2 (mx  m
5  x  2m 1). f (x)  0 . A. 1 B. 2 C. 3 D. 0
Câu 11. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Tìm số
giá trị nguyên của m để phương trình 2
f (x  2x)  m có đúng 4
nghiệm thực phân biệt thuộc đoạn  3 7   ;  . 2 2    A. 1 B. 2 C. 3 D. 4
_________________________________ 21