Hệ thống bài tập trắc nghiệm vận dụng cao, phân loại nguyên hàm, tích phân Toán 12

Hệ thống bài tập trắc nghiệm vận dụng cao, phân loại nguyên hàm, tích phân Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

12 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 3: Nguyên hàm - Tích phân và ứng dụng

Môn: Toán 12

Thông tin:

21 trang 6 tháng trước

Tác giả:

Profile Mai Nguyệt
1
THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VẬN DỤNG CAO, PHÂN LOẠI
NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(KHÔNG BAO GỒM ỨNG DỤNG)
PHẦN 1 – 10
9
4
(1993 )
f x dx
CREATED BY GIANG SƠN
TP.THÁI BÌNH; THÁNG 4/2020
_____________________________________________________________________________________________________________
2
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 1)
__________________________________________________
Câu 1. Cho tích phân
2
0
cos sin 8
xf x dx
. Tính
2
0
sin . cos
x f x dx
.
A. – 8 B. 4 C. 8 D. 16
Câu 2. Cho hàm số
liên tục, có đạo hàm trên R thỏa mãn
3 2
2
f x dx x x
. Giá trị của
2
2
1
1
I xf x dx
gần nhất với giá trị nào ?
A. 83 B. 38 C. 120 D. 70
Câu 3. Hàm số
y f x
liên tục trên
thỏa mãn
5
1 2
f x x x
. Tính
33 37
1 5
4
f x dx f x dx
.
A. 696 B. 200 C. 236 D. 120
Câu 4. Giả sử hàm số
y f x
liên tục, nhận giá trị dương trên
0;

đồng thời thỏa mãn điều kiện
2 1; 4 1
f f x f x x
. Mệnh đề nào sau đây đúng ?
A. 1 < f (5) < 2 B. 2 < f (5) < 3 C. 3 < f (5) < 4 D. 4 < f (5) < 5
Câu 5. Hàm số f (x) xác định trên
\ 1;5
thỏa mãn
2
1
4 5
f x
x x
; f (1) = 1;
ln 2
7
3
f .
Giá trị biểu thức f (0) + f (– 3) gần nhất số nào sau đây ?
A. 1,38 B. 0,38 C. 3,31 D. 32,22
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
f x
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
2
2
. 24 12 3,f x f x f x x x x
;
;
0 0 1
f f
.
.
G
G
i
i
á
á
t
t
r
r
ị
ị
c
c
ủ
ủ
a
a
t
t
í
í
c
c
h
h
p
p
h
h
â
â
n
n
2
1
1
f x dx
l
l
à
à
A
A
.
.
–
–
2
2
B
B
.
.
1
3
C
C
.
.
5
6
D
D
.
.
2
3
Câu 7. Cho hàm số
f x
liên tục và có đạo hàm trên đoạn [1;3] thỏa mãn điều kiện
3 5, 1;3
f x x
.
Giả sử tồn tại hai số thực a và b sao cho
3 1 , 1;3
a f f b x . Tính giá trị của tổng
S a b
.
A. 16 B. 15 C. 17 D. 8
Câu 8. Hàm số
f x
thỏa mãn
(3) 3; ( ) , 0
1 1
x
f f x x
x x
. Tính
8
3
( )
f x dx
.
A.
197
6
B.
181
6
C. 7 D. 14,5
Câu 9. Tính K =
3
4
0
;
max x x dx
.
A. K = 15,5 B. K = 2,6 C. K = 48,9 D. K = 11,2
Câu 10. Hàm số
f x
là hàm số chẵn, liên tục trên R thỏa mãn
1
0
( ) 2018
f x dx
, hàm số
( )
g x
là hàm số liên
tục trên R thỏa mãn
( ) ( ) 1
g x g x
. Tính tích phân
1
1
( ) ( )
f x g x dx
.
A. 2018 B. 504,5 C. 4036 D. 1008
3
Câu 11. Cho hàm số
( )
f x
liên tục trên [0;1] thỏa mãn
1 1
2 2
0 0
1
( ) ( )
3
f x dx f x dx
. Tính
1
0
( )
f x dx
.
A. 1 B.
2
3
C.
5
3
D. 3
Câu 12. Biết
cos 2
x
là một nguyên hàm của hàm số
( ).
x
f x e
. Khi đó
( )
F x
là một nguyên hàm của hàm số
( ).
x
f x e
. Biết rằng
( )
F x
có hệ số tự do bằng 0, giá trị nhỏ nhất của
( )
F x
gần nhất giá trị nào
A. – 2,23 B. – 1,56 C. – 1,41 D. 1
Câu 13. Biết rằng
4
2
2 1
3. 4 3 31. 1
m
x x dx mx dx
. Khi đó
2
1
(2 )
m
x x dx
gần nhât với số nào
A. 14 B. 13 C. 17 D. 18
Câu 14. Cho hàm số
( )
f x
thỏa mãn
( )
( 1) ( ) ; (0) 2
2
f x
x f x f
x
. Tính
(2)
f .
A. 1 B. 3 C. 2 D. 4
Câu 15. Cho
f x
liên tục trên R sao cho
2
0
1 14;3 2 0 10
x f x dx f f
. Tính
4
0
2
x
f dx
.
A. – 4 B. 3 C. – 8 D. – 2
Câu 16. Hai hàm số f (x), g (x) có đạo hàm trên [1;4] thỏa mãn đồng thời
;
g x xf x f x xg x
,
ngoài ra f (1) + g (1) = 4. Tính
4
1
( )
f x g x dx
.
A. 3ln2 B. 6ln2 C. 4ln2 D. 8ln2
Câu 17. Hàm f (x) liên tục trên R thỏa mãn
1
2
4
2
0 0
( )
(tan ) 4; 2
1
x f x
f x dx dx
x
. Khi đó
1
0
( )
f x dx
thuộc khoảng
A. (5;9) B. (3;6) C. (1;4) D.
( 2;5)
Câu 18. Hàm số
( )
f x
liên tục trên
thỏa mãn
2 3 2
( 1) (7 7) 3
x f x f x x x
. Tính
7
0
( )
f x dx
.
A. – 4,55 B. – 2,68 C. – 8,25 D. – 5
Câu 19. Cho hàm số
y f x
liên tục trên [0;9] và
8 9
0 0
5; 4
f x dx f x dx
. Tính
2
2
4 1
f x dx
A. 6 B. 21 C. 4 D. 2
Câu 20. Hàm số
( )
y f x
xác định trên
\ 0
thỏa mãn
2
( ) 1; ( ) 1 ( ) ( ) 0
xf x xf x xf x f x
.
Tính tích phân
1
( )
e
f x dx
.
A.
1
2
e
B.
1
2
e
C. –
1
e
D.
1
e
– 1
Câu 21. Hàm số
( )
f x
liên tục trên R sao cho
2
2
4
2
0
(ln )
tan . (cos ) 2; 2
ln
e
e
f x
x f x dx dx
x x
. Tính
2
1
4
(2 )
f x
dx
x
.
A. 0 B. 1 C. 4 D. 8
_________________________________
4
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 2)
__________________________________________________
Câu 1. Hàm số
y f x
liên tục trên
0;
4
thỏa mãn
4 4
0 0
( )
3; 1; sin .tan . ( ) 2
4 cos
f x
f dx x x f x dx
x
.
Tính
4
0
sin ( )
xf x dx
.
A. 4 B. 6 C.
3 2
1
2
D.
1 3 2
2
Câu 2. Cho
f x
liên tục trên R;
2
2
1
( 1) 3; (2) 4
x f x dx f e
. Khi đó
2
3
1
( 1) ( )
x f x dx
thuộc khoảng
A. (0;1) B. (1;2) C. (3;5) D. (6;10)
Câu 3. Cho hàm số
( )
f x
thỏa mãn (ln 3) 4; ( ) ,
1
x
x
e
f f x x
e
. Tính tích phân
ln 8
ln 3
( )
x
e f x dx
.
A.
76
3
B.
38
3
C.
136
3
D. 2
Câu 4. Cho hàm số
y f x
liên tục và nhận giá trị không âm trên
1;

thỏa mãn
2
2
2
1 0; 4 4 1
f x
f e f x x x
với mọi x thuộc
1;

.
Mệnh đề nào sau đây đúng ?
A.
1 4 0
f
B.
0 4 1
f
C.
1 4 2
f
D.
2 4 3
f
Câu 5. Cho hàm số
f x
liên tục trên đoạn [0;1] thỏa mãn
2
2 3 1 1
f x f x x
. Tính
1
0
f x dx
.
A.
4
B.
6
C.
20
D.
16
C
C
â
â
u
u
6
6
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
f x
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
2
. 1,f x f x f x x
;
;
0 0 4
f f
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
x
x
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
5
f x
.
.
A
A
.
.
2
2
0
0
B
B
.
.
1
1
3
3
C
C
.
.
2
2
6
6
D
D
.
.
1
1
6
6
Câu 7. Hàm số
( )
f x
liên tục trên R sao cho
2 5
2
2
2 1
( )
( 5 ) 1; 3
f x
f x x dx dx
x
. Tính
5
1
( )
f x dx
.
A. – 15 B. – 2 C. – 13 D. 0
Câu 8. Cho hàm số
y f x
liên tục trên
thỏa mãn
2 2
( 3) ( 1). (4 )
f x x x f x
.
Tính tích phân
1
0
( 2) ( ) ( )
x f x f x dx

.
A. 1 B.
77
6
C.
7
6
D.
17
3
Câu 9. Với tham số m thuộc [0;3], tính a + b khi a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của tích phân
2
3 2 2 3
4 5 2
m
m
S x mx m x m dx
.
A. 1 B. 2 C. 5,25 D.
41
6
5
Câu 10. Hàm số
( )
f x
liên tục trên [1;2] sao cho
( ) (3 )
f x f x
và
ln 2
2
0
( ) 1
x x
e f e dx
. Tính
4
1
( )
2
f x
dx
x
.
A. 2 B. 1 C.
2
3
D.
3
2
Câu 11. Hàm số bậc hai
f x
trên R có
( 2) ( ) 4 10; (0) 1
f x f x x f
. Tính
1
0
( ) ( ) 1
f x f x dx
.
A. 7,5 B. 2 C. – 1 D.
2
3
Câu 12. Hàm số
( )
y f x
thỏa mãn
2
2
( ) 3 2 1 4 ( )
f x x x xf x
và
3
1
( ) 12
f x dx
. Tính
2
0
( )
f x dx
.
A. 6 B. 7 C. 8 D. 5
Câu 13. Tính giá trị gần đúng của
3
0
( )
f x dx
biết hàm số
( )
y f x
liên tục trên [1;3] thỏa mãn
2
2 2
( ). 1 ( ) ( ).( 1) ; (1) 1; ( ) 0, 0;3
f x f x f x x f f x x
.
A. – 1,09 B. – 2,56 C. – 6,25 D. 4,16
Câu 14. Hàm số
( )
y f x
có đạo hàm trên [0;2] thỏa mãn
2
1
( ) ; (2) 1
3 ( ) 1
f x f
f x
. Tính
2
2
0
( )
f x dx
.
A. 1 B.
1
3
C.
14
15
D.
11
12
Câu 15. Đa thức bậc bốn
( )
y f x
đạt cực trị tại
1; 2
x x
và
0
6 (2 )
lim 3
6
x
x f x
x
. Tính
1
0
( )
f x dx
.
A. 2 B. 2,5 C. 0,75 D. 4
Câu 16. Tính
1
0
( 3)
xf x dx
khi
( )
y f x
là hàm số đa thức thỏa mãn điều kiện
3
( ) 2 ( 1) ( 2) ( 2) 17 3
f x f x f x x x
.
A. 29 B. 4 C. 2020 D. 11
Câu 17. Hàm số
( )
y f x
có đạo hàm xác định trên
và nhận giá trị dương trên
0;

, đồng thời thỏa mãn
điều kiện
( ) ln ( ) 1
f x f x x
. Giá trị tích phân
0
( )
e
f x dx
nằm trong khoảng
A. (4;5) B. (0;2) C. (2;4) D. (5;6)
Câu 18. Tính
0
1
( )
f x dx
khi hàm số
( )
y f x
là hàm số đa thức thỏa mãn
2 2 4 6 2
( ) 2 (1 ) 2 5 2
f x x f x x x
.
A. 1,5 B. 1 C. 2 D. 2,5
Câu 19. Cho số thực m thỏa mãn
1
2 1 1
m
mx dx
. Tham số m thu được thuộc khoảng nào sau đây
A. (4;6) B. (2;4) C. (3;5) D. (1;3)
Câu 20. Cho hàm số
( )
y f x
thỏa mãn
1
( ) , 0; (1) 1
f x x x f
x
. Giá trị nhỏ nhất của f (2) là
A. 2,5 + ln2 B. 2 + 2ln2 C. 3 – ln2 D. 3ln2 – 1
_________________________________
6
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 3)
__________________________________________________
Câu 1. Cho hàm
f x
liên tục và có đạo hàm trên R thỏa mãn
5
2
6
f x dx a
. Tính
1
2
0
3 2
xf x dx
.
A. a B. 0,5a C. 2a D. 4a
Câu 2. Cho
f x
thỏa mãn
3
1
( )
4; (1) 1; (3) 3
3 1
f x
dx f f
x
. Tính
3
1
ln(3 1) ( )
x f x dx
.
A. 8ln2 – 12 B. 8ln2 C. 6ln2 – 12 D. 2ln8 + 4
Câu 3. Hàm số
( )
f x
có đạo hàm liên tục trên R. Biết
( )
g x
là một nguyên hàm của hàm số
2
( )
x
y
x g x
sao
cho
2
1
( ) 1; 2 (2) (1) 2
g x dx g g
. Tính tích phân
2
2
2
1
( )
x
dx
x g x
.
A. 1,5 B. 1 C. 3 D. 2
Câu 4. Cho hàm số
( )
f x
có đạo hàm liên tục trên [0;1] thỏa mãn
1
2
0
1
(1) 0; ( )
3
f x f x dx
. Tính
1
3
0
( )
x f x dx
.
A. 1 B. – 1 C. 3 D. – 3
Câu 5. Hàm số f (x) liên tục trên R thỏa mãn
2 2
14 5
( ) 2; (ln 3) ; ( ln 2)
3 2
x x
f x e e f f
.
Tính giá trị biểu thức
(ln 5) ( ln 4)
f f
.
A. 11,55 B. 12,25 C. 10 D. 14,25
Câu 6. Hàm số
y f x
liên tục trên R thỏa mãn
0 1
1 0
1; 6
f x dx f x dx
. Tính
ln 3
0
( 2 )
x x
e f e dx
.
A. 5 B. 4 C. 2,5 D. 2
Câu 7. Hàm số
f x
là hàm số lẻ, liên tục trên [– 4;4] và
0 2
2 1
2; 2 4
f x dx f x dx
. Tính
4
0
f x dx
.
A. – 10 B. – 6 C. 6 D. 10
Câu 8. Tính tích phân
2
0
f x dx
khi
f x
là hàm số chẵn trên R thỏa mãn
1
1
(2 )
8
1 5
x
f x
dx
.
A. 8 B. 2 C. 1 D. 16
Câu 9. Cho
f x
liên tục trên R sao cho
3 2
2 ( ) 3 ( ) 6 ( )
f x f x f x x
. Tính
5
0
( )
f x dx
.
A. 1,25 B. 2,5 C.
5
3
D.
5
12
Câu 10. Tính tích phân
6
6
f x dx
khi
f x
là hàm số chẵn trên R thỏa mãn
1
1
4 . (6 )
7
4 5
x
x x
f x
dx
.
A. 84 B. 28 C. 42 D. 14
Câu 11. Hàm số
( )
y f x
xác định trên R thỏa mãn
2 3 4 2
2 ( 1) 3 ( 2) 3 2 9 4
f x xf x x x x
.
Tìm giá trị nhỏ nhất của biểu thức
1
2
0
( 2) ( ) ( 1)
x f x dx f x
.
A. 2,5 B. 3 C. 4 D. 4,5
7
Câu 12. Hai hàm số
( ), ( )
y f x y g x
xác định và có đạo hàm trên [1;2] thỏa mãn
( ) ( ) 0; 4 ( ) ( ) 0
(1) 2 (1) 3
f x xg x g x xf x
f g
Tính tích phân
2
1
[ ( ) 2 ( )]
f x g x dx
.
A. 3 B. 1,5 C. 2,5 D. 2
Câu 13. Hàm số f (x) liên tục trên
2
;1
3
thỏa mãn
2
2 ( ) 3 5
3
f x f x
x
. Hỏi giá trị
1
2
3
ln . ( )
x f x dx
gần nhất
giá trị nào sau đây ?
A. 0,34 B. 0,24 C. 0,26 D. 0,52
Câu 14. Hàm số f (x) liên tục trên [0;1] thỏa mãn
2 ( ) 3 (1 ) 1
f x f x x x
. Tính
2
0
2
x
xf dx
.
A.
4
75
B.
4
25
C.
16
75
D.
16
25
Câu 15. Cho hàm số
( )
y f x
có đạo hàm liên tục trên
, nhận giá trị dương trên [0;2018] và thỏa mãn điều
kiện
( ). (2018 ) 1
f x f x
. Tính tích phân
2018
0
1
1 ( )
dx
f x
.
A. 2018 B. 4016 C. 0 D. 1009
Câu 16. Cho hàm số
( )
y f x
xác định và có đạo hàm liên tục trên
, nhận giá trị dương trên [a;b] và thỏa
mãn điều kiện
( ). ( ) 9
f x f a b x
. Tìm giá trị nhỏ nhất của
2
1
( ) 36 2019
3 ( )
b
a
T b a dx
f x
.
A. 2019 B. 2010 C. 2016 D. 2015
Câu 17. Cho hàm số
( )
y f x
xác định và có đạo hàm liên tục trên
, nhận giá trị dương trên [2;7] và thỏa
mãn điều kiện
( 1). (7 ) 9
f x f x
. Tính
7
3
1
3 ( )
dx
f x
.
A. 1 B.
2
3
C.
1
6
D.
5
6
Câu 18. Tính
(2)
f
nếu hàm số f (x) liên tục trên [0;1] thỏa mãn
1 1
5
0 0
11 4
(1) 1; ( ) ; ( )
78 13
f x f x dx f x dx
.
A.
261
7
B.
13
7
C. 2 D.
100
7
Câu 19. Tính
1
0
( )
f x dx
khi hàm số f (x) có đạo hàm liên tục trên [0;1] thỏa mãn
1 1
2
0 0
9 3
(0) 0; ( ) ; ( ) cos
2 2 4
x
f f x dx f x dx
.
A. 6 B. 2 C. 4 D. 1
Câu 20. Cho hàm số
y f x
thỏa mãn
3
6 1 5 1
f x x x
. Tính tích phân
8
1
4
xf x dx
.
A. 30 B. 85 C. – 20 D. – 17
_________________________________
8
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 4)
__________________________________________________
Câu 1. Biết
2
( ) ( ) 2 3
F x ax bx c x
là một nguyên hàm của
2
20 30 7
( )
2 3
x x
f x
x
trên
3
;
2

. Tính
giá trị biểu thức abc.
A. 0 B. 3 C. 4 D. – 8
Câu 2. Cho hàm số thỏa mãn
2
1
' .sin .cos 2 sin .cos 3 0; , .
4 3
f x x f x x x x x f
Tìm họ các
nguyên hàm
f x dx
?
A.
1
2 sin 2 sin 4
12
x x C
. B.
1
sin 4 2sin 2
12
x x C
.
C.
1
sin 2 sin 4
12
x x C
. D.
1
2sin 2 sin 4
12
x x C
.
Câu 3. Hàm số
( )
f x
thỏa mãn
2
1
(0) ; ( ) sin 3 .cos 2
21
f f x x x
. Tính
2
0
( )
f x dx
.
A.
137
441
B.
137
441
C.
247
441
D.
167
882
Câu 4. Hàm số
( )
f x
thỏa mãn
2
2 ( ) ( ) 2 1
f x f x x
và
2
(1) 2
f e
. Khi đó
(2)
f
gần nhất giá trị nào
A. 166 B. 120 C. 90 D. 52
Câu 5. Hàm số
( )
f x
có đạo hàm liên tục trên [0;5] và thỏa mãn
( ) ( ) 3 1
x
f x f x e x
.
Tính
(5)
f
khi
(0) 0
f
.
A.
5
14
e
B.
5
13
e
C.
5
9
e
D.
5
11
e
Câu 6. Hàm số
( )
f x
liên tục trên
thỏa mãn
( ) (2020 )
f x f x
và
2017
3
( ) 4
f x dx
. Tính
2017
3
( )
xf x dx
.
A. 16160 B. 4040 C. 2020 D. 8080
Câu 7. Hàm số
( )
f x
có đạo hàm dương với mọi
0
x
thỏa mãn
2
(1) 2; ( ) ln ( )
f f x dx f x C
.
Tính
(3)
f
.
A. 1 B. 4 C.
6
D.
2 2
Câu 8. Hàm số
( )
f x
có đạo hàm liên tục trên [0;1] và
1
0
1
(1 ) ( )
2
xf x f x dx
. Tính
(0)
f
.
A. 1 B. 0,5 C. – 1 D. – 0,5
Câu 9. Hàm số
( )
f x
có
4
(0) 0; ( ) sin
f f x x
. Tính
2
0
( )
f x dx
.
A.
2
6
18
B.
2
3
32
C.
2
3 16
64
D.
2
3 6
112
Câu 10. ho hàm số
f x
xác định và có đạo hàm trên khoảng
0; ;

2
1 1
' 0, 0; ; 1 1 2 2 1 ' , 0.
2 3
f x x f f x x x f x f x x
9
Tính tích phân
2
1
.
'
f x
I dx
f x
A.
23
.
6
I
B.
3
.
2
I
C.
1 ln 3.
I
D.
2
1 ln .
3
I
Câu 11. Hàm số
( )
f x
liên tục thỏa mãn
1
( ) 1 ( ) , 0
f x x f x x
x
và
4
(4)
3
f
.
Khi đó
4
2
1
( 1) ( )
x f x dx
gần nhất giá trị nào sau đây
A. 30,5 B. 31,5 C. 32,5 D. 33,8
Câu 12. Cho hàm số
f x
liên tục trên
và thỏa mãn
16
2
2
1
4
cot . sin d d 1
f x
x f x x x
x
.
Tích phân
1
1
8
4
d
f x
I x
x
bằng
A.
3
2
I
. B.
3
I
. C.
5
2
I
. D.
2
I
.
Câu 13. Hàm số
f x
liên tục trên khoảng
0;

và thỏa mãn
2
2 1
1 .ln 1
2
4
f x
x
f x x
x
x x
.
Biết
17
1
d ln 5 2ln
f x x a b c
với , ,a b c
. Giá trị của
2
a b c
bằng
A.
29
2
. B.
5
. C.
7
. D.
37
.
Câu 14. Hàm số
f x
có đạo hàm xác định trên
. Biết
1 2
f
và
1 4
2
0 1
1 3
d 2 d 4
2
x
x f x x f x x
x
.
Giá trị của
1
0
d
f x x
bằng
A.
1
. B.
5
7
. C.
3
7
. D.
1
7
.
Câu 15. Cho hàm số
y f x
có đạo hàm
f x
liên tục trên thỏa mãn điều kiện
3 3 3 2
0
3 d 2020
x
f x f t f t f t f t t
.
Mệnh đề nào dưới đây đúng?
A.
3
1 2020
f e
. B.
1 2020
f e
. C.
3
1 2020
f e
. D.
2020
e
.
Câu 16. Hàm số
( )
y f x
có
(0) 0
f
và
8 8 6
( ) sin cos 4sin ,f x x x x x
. Tính
0
16 ( )d
I f x x
.
A.
I 160
. B.
2
I 10
. C.
2
I 16
. D.
2
I 10
Câu 17. Hàm số
0
f x
và có đạo hàm liên tục trên
, thỏa mãn
1
2
f x
x f x
x
và
2
ln 2
0
2
f
.
Giá trị
3
f
bằng
A.
2
1
4ln 2 ln 5
2
. B.
2
4 4ln 2 ln 5
. C.
2
1
4ln 2 ln 5
4
. D.
2
2 4ln 2 ln 5
.
_________________________________
10
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 5)
__________________________________________________
Câu 1. Biết rằng F (x) là nguyên hàm của hàm số
2
2 2
5 8 4
( 1)
x x
x x
trên (0;1) thỏa mãn
1
26
2
F
. Giá trị nhỏ
nhất của hàm số F (x) bằng
A. 24 B. 20 C. 25 D. 26
Câu 2. Cho hàm số
2
3 4 6 khi 1
7 2 khi 1
x x x
f x
x x
. Khi đó
3
2
0
ln
cos . sin d 4 d
e
e
f x
x f x x x
x
bằng
A.
29
. B.
28
. C.
94
. D.
49
.
Câu 3. Cho hàm số
f x
có đạo hàm liên tục trên
và
0 2
f
,
2
1
2
2
x
F x f x e x
là một nguyên
hàm của
f x
. Họ các nguyên hàm của
f x
là
A.
2
1
8 3
2
x
x e x C
. B.
2
1
8 1
2
x
x e x C
.
C.
2
1
8 3 .
2
x
x e x C
. D.
2
8 1 .
x
x e x C
.
Câu 4. Hàm số
( )
f x
liên tục trên
thỏa mãn
2 3
3
4 ( ) 6 (2 ) 4
5
xf x f x x
. Tính
4
0
( )
f x dx
.
A. 2,08 B. 52 C. 48 D. 1,92
Câu 5. Cho
1
x
F x x e
là một nguyên hàm của hàm số
2
x
f x e
. Tìm họ nguyên hàm của hàm
2
x
f x e
A.
2
2
x x
f x e dx x e C
. B.
2
2
.
2
x x
x
f x e dx e C
C.
2
4 2 .
x x
f x e dx x e C
D.
2
2 .
x x
f x e dx x e C
Câu 6. Cho hàm số
y f x
có đạo hàm liên tục trên
. Biết
1 e
f
và
3
2 . .
x f x x f x x
với
x
. Giá trị của
1
0
d
f x x
bằng
A.
2 4
e
e 3
. B.
1 2
. C.
1
e
e
. D.
2
e
3
.
Câu 7. Cho hàm số
f x
có
7 15
f
và
1
, 0
2 2
x
f x x
x x
. Khi đó
7
2
d
f x x
bằng
A.
347
6
. B.
271
6
. C. 7. D.
287
6
Câu 8. Giả sử
2
( )
F x x
là một nguyên hàm của
2
( ) sin
f x x
và
( )
G x
là một nguyên hàm của
2
( ) cos
f x x
trên
khoảng
0;
. Biết rằng
0
2
G
và
2
ln 2
4
G a b c
, với
, ,
a b c
là các số hữu tỉ. Tổng
a b c
bằng
A.
11
16
. B.
5
16
. C.
21
16
. D.
27
16
.
Câu 9. Hàm số
y f x
liên tục trên
thỏa mãn
1 5
0 0
x 9
f x d f x dx
. Tính tích phân
1
1
3 2
I f x dx
11
A.
9
I
. B.
3
I
. C.
4
I
. D.
2
I
.
Câu 10. Cho hàm số
f x
có
2
1 e
f
và
2
2
2 1
e
x
x
f x
x
,
0
x
. Khi đó
ln3
1
d
xf x x
bằng
A.
2
6 e
. B.
2
6 e
2
. C.
2
9 e
. D.
2
9 e
2
.
Câu 11. Hàm số
f x
có đạo hàm liên tục trên
thỏa mãn
3
0
(3) ( ) 3
f xf x dx
. Tính
6
2
0
( )
2
x
x f dx
.
A. 21 B. 42 C. 84 D. 168
Câu 12. Giả sử hàm
f
có đạo hàm cấp 2 trên
thoả mãn
' 1 1
f
và
2
' 1 '' 2
f x x f x x
với mọi
x . Giá trị tích phân
1
0
'
xf x dx
bằng
A.
2
3
. B.
1
. C.
0
. D.
2
.
Câu 13. Cho
( )
f x
là hàm số liên tục trên
R
thỏa mãn
( ) '( ) cos ,
f x f x x x
và
(0) 1.
f
Tính
( )
e f
bằng
A.
3
2
e
. B.
1
2
e
. C.
1
2
e
. D.
3
2
e
.
Câu 14. Hàm số
2
cos
x
f x
x
, với
;
2 2
x . Gọi
F x
là một nguyên hàm của
'
xf x
thoả mãn điều
kiện
0 0
F
. Biết
tan 7
a với
;
2 2
a . Biểu thức
2
50 7
F a a a
có giá trị là
A.
ln 50
. B.
1
ln 50
4
. C.
1
ln 50
2
. D.
1
ln 50
2
.
Câu 15. Cho
4
( ) sin 2 5sin cos ,f x x x x x
,
0
2
f
và
2
0
( )d
f x x a b
với
, .
a b
Đặt
1
.
T b
a
Mệnh đề nào sau đây đúng?
A.
1;2 .
T
B.
0;1 .
T
C.
2;3 .
T
D.
2;0 .
T
Câu 16. Cho hàm số
f x
liên tục trên
và
2 1 3 0 0
f f
,
1
0
d 7
f x x
. Tính
2
0
6 d
2
x
I x f x
A.
40
I
. B.
28
I
. C.
18
I
. D.
42
I
.
Câu 17. Cho hàm số
3
2 1
3 4 1
x x khi x
y f x
x khi x
. Biết tích phân
2
1
3
2 2
0
4
. ln 1
tan
d d
cos 1
e
x f x
f x
I x x
x x
bằng
a
b
với
, , 0
a b b
và
a
b
là phân số tối giản. Tính giá trị biểu thức
P a b
.
A.
77
P
. B.
45
P
. C.
29
P
. D.
54
P
.
Câu 18. Hàm số
y f x
xác định và dương trên khoảng
0;

, thỏa mãn
2
2
12
f x x f x f x

với
mọi
0;x

và
1 1; 1 4
f f
. Giá trị của
2
f
bằng
A.
46
. B.
7
. C.
3 5
. D.
2 10
.
_________________________________
12
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 6)
__________________________________________________
Câu 1. Cho hàm số
f x
liên tục thỏa mãn
3
( ) 4 2
f x dx x x C
. Tính
2
( )
xf x dx
.
A.
6 2
2
x x C
B.
10 6
10 6
x x
C
C.
6 2
4 2
x x C
D.
6 2
6 2
x x C
Câu 2. Hàm số
f x
liên tục trên R thỏa mãn
6
1
4
f x dx
. Tính tích phân
1,5
1
3 4
0 0,5
1 4
I x f x dx f x dx
.
A. 4 B. 0,5 C. 2 D. 1
Câu 3. Cho hàm số
f x
liên tục, có đạo hàm trên đoạn [2;4] thỏa mãn điều kiện
2 4 , 2; 4
x f x x x
.
Giả sử tồn tại hai số thực a và b sao cho
4 2 , 2;4
a f f b x . Tính giá trị của tổng
S a b
.
A. 36 B. 40 C. 50 D. 15
Câu 4. Cho các hàm
,
f x g x
liên tục trên R và có đạo hàm trên đoạn [1;3] thỏa mãn đồng thời các điều kiện
3 3
1 1
1 . 1 1; 3 . 3 3; 4
f g f g g x f x dx g x f x dx
. Tính
3 3
1 1
3 4
S g x f x dx g x f x dx
.
A. 5 B. 11 C. 12 D. 13
Câu 5. Cho
f x
liên tục trên R;
3
0
3 1 2; 10 3 0 11
x f x dx f f
. Tính
1 9
0 0
3
3
x
K f x dx f
.
A. 10 B. 3 C. – 2 D. 12
Câu 6. Hàm số
y f x
liên tục trên
thỏa mãn
5
1 2
f x x x
. Tính
33 37
1 5
4
f x dx f x dx
.
A. 696 B. 200 C. 236 D. 120
C
C
â
â
u
u
7
7
.
.
C
C
h
h
o
o
h
h
à
à
m
m
s
s
ố
ố
f x
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
2
. 1,f x f x f x x
;
;
0 0 4
f f
.
.
T
T
ồ
ồ
n
n
t
t
ạ
ạ
i
i
b
b
a
a
o
o
n
n
h
h
i
i
ê
ê
u
u
s
s
ố
ố
n
n
g
g
u
u
y
y
ê
ê
n
n
x
x
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
5
f x
.
.
A
A
.
.
2
2
0
0
B
B
.
.
1
1
3
3
C
C
.
.
2
2
6
6
D
D
.
.
1
1
6
6
Câu 8. Cho hàm số
y f x
liên tục và có đạo hàm trên
, đồ thị
y f x
như hình vẽ bên. Tính tích phân
2 4
1 1
1
1
f x
I f x dx dx
x
.
A. 12 B. 16 C. 18 D. 7
Câu 9. Hàm số
( )
f x
liên tục trên R sao cho
3
1
(6 ) ( 2); ( 2) 4
f x f x f x dx
. Tính
3
1
( 2)
xf x dx
.
A. 6 B. 8 C. 2 D. 10
Câu 10. Hàm số
( )
f x
liên tục trên
và
2 3 4 2
2 ( 1) 3 ( 1) 3 2 6 4
f x xf x x x x
. Tính
2
1
( )
f x dx
.
A. 1,5 B. 1 C. 2 D. 2,5
Câu 11. Biết rằng
2
( ) ( ) 2 1
F x ax bx c x
là một nguyên hàm của
2
10 7 2
( )
2 1
x x
f x
x
trên
1
;
2

.
Tính giá trị biểu thức a + b + c.
13
A. 3 B. 0 C. – 6 D. – 2
Câu 12. Tính giá trị f (2) khi hàm số
( )
y f x
luôn nhận giá trị khác 0 trên
(0; )

và thỏa mãn các điều kiện
2
2 2 2
( 1) ( ) ( ) ( 1); (1) 2
x f x f x x f
.
A. 0,4 B. – 0 ,4 C. – 2,5 D. 2,5
Câu 13. Hàm số
( )
y f x
thỏa mãn
2 2 2
(1) 2; ( ) 0; ( 1) ( ) ( ).( 1)
f f x x f x f x x
với
0
x
. Tính giá trị
biểu thức
(2)
f
.
A. 0,4 B. – 0,4 C. – 2,5 D. 2,5
Câu 14. Cho hàm số
y f x
liên tục trên R thỏa mãn
2
0
(3cos 4sin ) ( 3sin 4cos 5 ) 1
x x f x x dx
.
Tính tích phân
2
2
1
( 1) ( 2 1)
x f x x dx
.
A. – 2 B. – 4 C. 1 D. – 0,5
Câu 15. Hai hàm số
( ), ( )
f x g x
xác định trên R thỏa mãn
2 2
(0) (0) 1
f g
và
( ) ( ); ( ) ( )
f x g x g x f x
.
Tính tích phân
1
2 2
( ) ( )
f x g x dx
.
A. 1 B. 2 C. 0 D. – 1
Câu 16. Hàm số
( )
y f x
có đạo hàm trên [0;2] thỏa mãn
2
1
( ) ; (2) 1
3 ( ) 1
f x f
f x
. Tính
2
2
0
( )
f x dx
.
A. 1 B.
1
3
C.
14
15
D.
11
12
Câu 17. Đa thức bậc bốn
( )
y f x
đạt cực trị tại
2; 3
x x
và
0
2 ( )
lim 4
5
x
x f x
x
. Tính
1
0
( )
f x dx
.
A. 2,25 B. 2,75 C. 4,75 D. 5,5
Câu 18. Tính tích phân
2
0
f x dx
khi
f x
là hàm số chẵn trên R thỏa mãn
1
1
(2 )
8
1 5
x
f x
dx
.
A. 8 B. 2 C. 1 D. 16
Câu 19. Hàm số
( )
f x
liên tục trên
0;

và
6
2
2
0 1
(ln )
(cos ) sin 2 2; 6
e
f x
f x xdx dx
x
.
Tính tích phân
3
1
( ( ) 2)
f x dx
.
A. 16 B. 9 C. 5 D. 10
Câu 20. Hàm số
( )
y f x
có đạo hàm trên R thỏa mãn
4
2
2
( ) 2
f x x x
x
với
0
x
và
(1) 1
f
. Mệnh đề
nào sau đây đúng ?
A. Phương trình
( ) 0
f x
có một nghiệm trên (0;1).
B. Phương trình
( ) 0
f x
có đúng ba nghiệm trên
(0; )

.
C. Phương trình
( ) 0
f x
có một nghiệm trên (1;2)
D. Phương trình
( ) 0
f x
có một nghiệm trên (2;5).
_________________________________
14
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 7)
__________________________________________________
Câu 1. Cho
2
(4 ) 3
f x dx x x C
. Tính a + b biết rằng
2
( 2)
f x dx ax bx C
.
A. 5,5 B. 4,25 C. 4,5 D. 2
Câu 2. Hàm số
( )
f x
có đạo hàm liên tục trên [0;1] thỏa mãn
2
2
2 ( ) 3 ( ) 11 22 14; (1) 5
f x f x x x f
.
Khi đó tích phân
1
0
4 ( ) 9 ( ) 1993
f x f x dx
gần nhất số nào
A. 2030 B. 2020 C. 2033 D. 2026
Câu 3. Hàm số
( )
f x
liên tục trên [0;1] thỏa mãn
2 2 3 2
( ) 2 ( ) 3 ( ) 1
f x xf x x f x x
. Tính
1
0
( )
f x dx
.
A.
4
B.
24
C.
36
D.
12
Câu 4. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Biết rằng
diện tích hình phẳng tô đậm bằng 3.
Tính tích phân
2
0
cos (3sin 1)
xf x dx
.
A. 1 B. – 1 C. 9 D. – 9
Câu 5. Hàm số
( )
f x
liên tục trên R sao cho
3 8
2
2
0 4
( )
( 16 ) 2019; 1
f x
f x x dx dx
x
. Tính
8
4
( )
f x dx
.
A. 2019 B. 4022 C. 2020 D. 4038
Câu 6. Cho hàm số
y f x
thỏa mãn
3
6 1 5 1
f x x x
. Tính tích phân
8
1
4
xf x dx
.
A. 30 B. 85 C. – 20 D. – 17
C
C
â
â
u
u
7
7
.
.
T
T
í
í
n
n
h
h
2 2
1 2
f f
k
k
h
h
i
i
hàm số
f x
x
x
á
á
c
c
đ
đ
ị
ị
n
n
h
h
,
,
l
l
i
i
ê
ê
n
n
t
t
ụ
ụ
c
c
v
v
à
à
l
l
u
u
ô
ô
n
n
n
n
h
h
ậ
ậ
n
n
g
g
i
i
á
á
t
t
r
r
ị
ị
d
d
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ê
ê
n
n
[
[
0
0
;
;
2
2
]
]
,
,
đ
đ
ồ
ồ
n
n
g
g
t
t
h
h
ờ
ờ
i
i
0 1; 0 2
f f
;
;
2
2
.
2
f x
f x f x f x
x
.
.
A
A
.
.
2
2
0
0
B
B
.
.
1
1
0
0
C
C
.
.
1
1
5
5
D
D
.
.
2
2
5
5
Câu 8. Hàm số
( )
f x
có đạo hàm liên tục trên
thỏa mãn
3
2
0
1
(3) ; ( ) 5
3
f x f x dx
. Tính
3
3
0
( )
x f x dx
.
A. 5 B. 6 C. – 5 D. – 6
Câu 9. Hàm số
f x
là hàm số chẵn, liên tục trên [– a;a]. Tính
a
a
f x dx
theo tích phân
0
( )
1
a
x
f x
M dx
b
.
A. M B. M C. M – 1 D. – M
Câu 11. Hàm số y = f (x) liên tục trên R thỏa mãn
(2 ) 3 ( )
f x f x
. Tính
2
1
( )
f x dx
nếu
1
0
( ) 1
f x dx
.
A. 5 B. 3 C. 8 D. 2
15
Câu 12. Hàm
( )
f x
có đạo hàm liên tục trên
và
2
2
( 2) 5; (4) 1
xf x dx f
. Tính
4
2
0
( ) 4 ( )
x f x f x dx
.
A. – 6 B. 4 C. – 10 D. 6
Câu 13. Cho hàm số
y f x
liên tục trên [0;41] và
41 37
0 0
13; 26
f x dx f x dx
. Tính
3
3
13 2
f x dx
.
A.
2
7
B. 3 C.
10
7
D. 2
Câu 14. Biết rằng
4
2
0 2
72. max 2 1; 1 83. 2 3
m
x x x dx mx dx
, giá trị tham số m thu được thuộc khoảng
nào sau đây
A. (2;4) B. (4;7) C. (7;12) D. (12;15)
Câu 15. Hàm số
( )
f x
liên tục trên [0;2] thỏa mãn
2 2
2
2
0 0
1
(1) 4; ( ) ; ( ) 36
5
f x f x dx f x dx
.
Tính tích phân
2
0
( )
f x dx
.
A.
5
6
B.
3
2
C. 4 D.
2
3
Câu 16. Hàm số
( )
f x
liên tục trên R thỏa mãn
2
2
(1) 1; ( ) 4 ( ) 8 16 4
f f x f x x x
.
Tìm số nghiệm của phương trình
1
0
( ( )) ( ) 2020
f f x f x dx
.
A. 3 B. 4 C. 2 D. 1
Câu 17. Đa thức bậc bốn
( )
y f x
đạt cực trị tại
1; 2
x x
và
0
6 (2 )
lim 3
6
x
x f x
x
. Tính
1
0
( )
f x dx
.
A. 2 B. 2,5 C. 0,75 D. 4
Câu 18. Cho hàm số
y f x
, hàm số
y f x
có đồ thị như
hình vẽ bên. Biết rằng diện tích hình phẳng giới hạn bởi trục Ox và đồ
thị hàm số
y f x
trên đoạn [- 2;1] và [1;4] lần lượt bằng 9 và 12.
Cho f (1) = 3, giá trị biểu thức f (-2) + f (4) bằng
A. 21 B. 9 C. 3 D. 2
Câu 19. Hàm số
f x
là hàm số lẻ, liên tục trên [– 6;6] và
0 2
3 1
6; 3 3
f x dx f x dx
. Tính
6
0
f x dx
.
A. – 6 B. 2 C. 3 D. – 3
Câu 20. Tính
2
2
( )
1 3
x
f x
dx
khi hàm số
f x
là hàm chẵn liên tục trên R thỏa mãn
1 2
0 1
1
1
2
f x dx f x dx
.
A. 1 B. 6 C. 4 D. 3
Câu 21. Cho
f x
liên tục trên R;
1
3
0
4 5 8; 2 1 0 8
x x f x dx f f
. Tính
1
2
0
(3 4)
Q x f x dx
.
A. 14 B. 32 C. 69 D. 21
_________________________________
16
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 8)
__________________________________________________
Câu 1. Hàm số
( )
y f x
xác định trên R thỏa mãn
2
( ) ( 2) 2 1
f x f x x x
. Tính
5
1
( )
f x dx
.
A. 12 B.
37
3
C.
43
3
D.
44
3
Câu 2. Hàm số
( )
y f x
xác định trên R thỏa mãn
( ) 2 ( ) 3sin
f x f x x
. Tính
0
( )
f x dx
.
A. 18 B. 6 C. 2 D. 3
Câu 3. Tìm điều kiện tham số m để
1
I
với
1
0
; 0
2
dx
I m
x m
.
A.
1
0
4
m
B. m > 0,25 C.
1 1
8 4
m
D. m > 0
Câu 4. Hàm số
( )
f x
có đạo hàm liên tục trên
(0; )

thỏa mãn
( )
( ) ln 2
f x
f x x x
x
. Tính f (e).
A. e + 1 B. 2e – 3 C. e
2
– 1 D. 2e
2
– 7
Câu 5. Hàm số
( )
f x
liên tục trên R sao cho
8
3
3
2
0 1
( )
tan . (cos ) 6
f x
x f x dx dx
x
. Tính
2
2
1
2
( )
f x
dx
x
.
A. 4 B. 6 C. 7 D. 10
Câu 6. Hàm số
( )
f x
liên tục trên
0;

thỏa mãn
16
2
1 0
( )
6; (sin ) cos 3
f x
dx f x xdx
x
. Tính
4
0
( )
f x dx
.
A. – 2 B. 6 C. 9 D. 2
Câu 7. Hàm số
( )
f x
liên tục trên [1;2] sao cho
( ) (3 )
f x f x
và
ln 2
2
0
( ) 1
x x
e f e dx
. Tính
4
1
( )
2
f x
dx
x
.
A. 2 B. 1 C.
2
3
D.
3
2
Câu 8. Hàm số y = f (x) liên tục trên R thỏa mãn
2
( ) (2 ) 6 3
f x f x x x
. Tính
2
0
( )
f x dx
.
A. 2 B. 1 C. 2,5 D. 4
Câu 9. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Biết
rằng diện tích phần tô màu là
37
12
và
0
2
14
( )
3
f x dx
.
Tính tích phân
1
(ln )
e
f x
dx
x
.
A.
25
12
B.
12
25
C.
8
3
D.
3
8
Câu 10. Hàm số bậc hai
( )
y f x
xác định trên R thỏa mãn
( 2) ( 1) 2 4
f x f x x
.
17
Tính tổng các hệ số của đa thức
0
( ) [ ( ) ( )]
m
Q m f x f x dx
với m là tham số dương.
A. 2 B.
17
3
C.
35
6
D.
11
3
Câu 11. Hai hàm số
( ), ( )
y f x y g x
xác định và có đạo hàm trên [1;2] thỏa mãn
( ) ( ) 0; 4 ( ) ( ) 0
(1) 2 (1) 3
f x xg x g x xf x
f g
Tính tích phân
2
1
[ ( ) 2 ( )]
f x g x dx
.
A. 3 B. 1,5 C. 2,5 D. 2
Câu 12. Cho hàm số
y f x
liên tục, có đạo hàm trên R và có đồ thị
như hình vẽ bên. Tính
1
0
(5 3)
f x dx
.
A. 2 B. 3 C. 9 D. 1,8
C
C
â
â
u
u
1
1
3
3
.
.
H
H
à
à
m
m
s
s
ố
ố
f x
x
x
á
á
c
c
đ
đ
ị
ị
n
n
h
h
v
v
à
à
l
l
i
i
ê
ê
n
n
t
t
ụ
ụ
c
c
t
t
r
r
ê
ê
n
n
R
R
,
,
đ
đ
ồ
ồ
n
n
g
g
t
t
h
h
ờ
ờ
i
i
t
t
h
h
ỏ
ỏ
a
a
m
m
ã
ã
n
n
min
0 1
f x f
;
;
4 ln
f x xf x ef x
v
v
ớ
ớ
i
i
m
m
ọ
ọ
i
i
x
x
t
t
h
h
u
u
ộ
ộ
c
c
R
R
.
.
T
T
í
í
n
n
h
h
t
t
ổ
ổ
n
n
g
g
c
c
á
á
c
c
n
n
g
g
h
h
i
i
ệ
ệ
m
m
c
c
ủ
ủ
a
a
p
p
h
h
ư
ư
ơ
ơ
n
n
g
g
t
t
r
r
ì
ì
n
n
h
h
2
ln
f x m
.
.
A
A
.
.
–
–
m
m
B
B
.
.
–
–
2
2
C
C
.
.
m
m
D
D
.
.
0
0
Câu 14. Hàm số
( )
y f x
xác định trên R thỏa mãn
2 4 11 9 4 3
( ) (1 ) 2 3 5 2 3
f x x f x x x x x x
.
Tính tích phân
0
1
( )
f x dx
.
A.
11
3
B.
41
12
C.
41
15
D. 4
Câu 15. Hàm số y = f (x) liên tục trên
1
;3
3
thỏa mãn
3
1
( )
f x xf x x
x
. Tính
3
2
1
3
( )
f x
dx
x x
.
A.
8
9
B.
2
3
C.
3
4
D.
16
9
Câu 16. Hàm số
( )
y f x
có đạo hàm trên [0;1] thỏa mãn
2
4 1
( )
3 ( ) 2
x
f x
f x
. Khi đó
1
3
0
( )
xf x dx
gần nhất với
A. 0,52 B. 0,19 C. 0,12 D. 1,25
Câu 17. Cho số thực m thỏa mãn
1
2 1 1
m
mx dx
. Tham số m thu được thuộc khoảng nào sau đây
A. (4;6) B. (2;4) C. (3;5) D. (1;3)
Câu 18. Hàm số
( )
f x
liên tục trên [0;2] thỏa mãn
2 2
2
0 0
2
(2) 1; ( ) ( )
3
f f x dx f x dx
. Tính
2
2
1
( )
f x
dx
x
.
A. 1 B. 2 C. 0,25 D.
1
3
_________________________________
18
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 9)
__________________________________________________
Câu 1. Hàm số
( )
f x
liên tục trên [0;2] thỏa mãn
2 2
2
1 1
1 1
(2) 0; ( 1) ( ) ; ( )
30 45
f x f x dx f x dx
.
Tính tích phân
2
1
( )
f x dx
.
A.
1
36
B.
1
15
C.
1
12
D.
1
12
Câu 2. Hàm số f (x) liên trục trên [0;1] thỏa mãn
2 2
4 3 1 1
xf x f x x
. Tính
1
0
f x dx
.
A.
20
B.
6
C.
16
D.
4
Câu 3. Tồn tại hai hàm số
y f x
liên tục trên
1;

và
2 13 2
2
2
1 1
. ( )
( 3 1 ) 4; 2
3 2
x f x
f x x dx dx
x
.
Tích phân
13 2
1
( )
f x dx
có thể nhận hai giá trị A, B với A > B. Tính 2A + B.
A. 14 B. 6 C. 18 D. 7
C
C
â
â
u
u
4
4
.
.
H
H
à
à
m
m
s
s
ố
ố
y f x
có
có
đ
đ
ạ
ạ
o
o
hà
hà
m
m
l
l
i
i
ê
ê
n
n
tụ
tụ
c
c
t
t
r
r
ê
ê
n
n
R
R
.
.
H
H
à
à
m
m
s
s
ố
ố
y f x
t
t
r
r
ê
ê
n
n
đ
đ
oạ
oạ
n
n
[
[
–
–
2
2
;
;
6
6
]
]
c
c
ó
ó
đ
đ
ồ
ồ
t
t
h
h
ị
ị
n
n
h
h
ư
ư
h
h
ì
ì
n
n
h
h
b
b
ê
ê
n
n
.
.
Tì
Tì
m
m
giá trị
giá trị
l
l
ớ
ớ
n
n
n
n
h
h
ấ
ấ
t
t
củ
củ
a
a
hà
hà
m
m
s
s
ố
ố
y f x
t
t
r
r
ê
ê
n
n
đ
đ
oạ
oạ
n
n
[
[
–
–
2
2
;
;
6
6
]
]
.
.
A
A
.
.
( 2)
f
B.
( 1)
f
C.
(6)
f
D.
(2)
f
Câu 5. Tính
1
0
( )
f x dx
nếu hàm số
( )
f x
liên tục trên R thỏa mãn
(1) 1
f
và
2
2 6 4 2
( ) 4(6 1) ( ) 40 44 32 4
f x x f x x x x
.
.
A.
23
15
B.
13
15
C.
17
15
D.
7
15
Câu 6. Tính
1
0
( )
f x dx
khi hàm số f (x) có đạo hàm liên tục trên [0;1] thỏa mãn
1 1
2
0 0
9 3
(0) 0; ( ) ; ( ) cos
2 2 4
x
f f x dx f x dx
.
A. 6 B. 2 C. 4 D. 1
Câu 7. Biết
3
2
2
3 1 ln 3 2 1 ln 34 ln17 ; ,
a
x x x dx a c a b
b
. Tính
2 4
S a b c
.
A.
55
S
B.
42
S
C.
72
S
D.
30
S
Câu 8. Tính tích phân
4
4
f x dx
khi
f x
là hàm số chẵn trên R thỏa mãn
1
1
2 . (4 )
5
2 3
x
x x
f x
dx
.
A. 40 B. 20 C. 10 D. 5
19
Câu 9. Cho hàm số
f x
liên tục trên R sao cho
3
( ) 2 ( ) 1
x f x f x
. Tính
1
2
( )
f x dx
.
A. 1,75 B. 1,25 C. – 1,75 D. 3,5
Câu 10. Cho hàm số
y f x
liên tục trên
thỏa mãn
2 2
( 3) ( 1). (4 )
f x x x f x
.
Tính tích phân
1
0
( 2) ( ) ( )
x f x f x dx

.
A. 1 B.
77
6
C.
7
6
D.
17
3
Câu 11. Hàm số y = f (x) liên tục thỏa mãn
1 1
2 3 , ;2
2
f x f x x
x
. Tính
2
1
2
f x
dx
x
.
A. 1,5 B. 4,5 C. – 4,5 D. 3
Câu 12. Tính giá trị gần đúng của
3
0
( )
f x dx
biết hàm số
( )
y f x
liên tục trên [1;3] thỏa mãn
2
2 2
( ). 1 ( ) ( ).( 1) ; (1) 1; ( ) 0, 0;3
f x f x f x x f f x x
.
A. – 1,09 B. – 2,56 C. – 6,25 D. 4,16
Câu 13. Hàm số
( )
y f x
liên tục trên
thỏa mãn
2 2
2 ( ). ( ) 108 (8 9) ( ) (4 9 ) ( )
f x f x x x f x x x f x
.
Tính
1
0
4 ( ) 9 ( )
f x f x dx
biết rằng đồ thị hàm số
( )
y f x
đi qua gốc tọa độ và tiếp tuyến của đồ thị luôn cắt
trục hoành.
A. 99 B. 100 C. 49 D. 1993
Câu 14. Tính
2
3;4
2
( ) min ( )
f x dx f x
khi hàm số
( )
y f x
thỏa mãn
3
2 2
0
( ) 2(2 1) ( ) 3 2 ; ( ) 3
f x x f x x x f x dx
.
A. 2 B. 8 C. 4 D. 6
Câu 15. Hàm số
( )
y f x
liên tục trên R thỏa mãn
2
2
4
0
( ) 1
x
x
f t dt e x
. Tính
(4)
f
.
A.
4
e
+ 4 B. 4
4
e
C.
4
e
+ 8 D. 1
Câu 16. Hàm số
( )
y f x
thỏa mãn
2 2
1
( ).ln ( ) ln ( ) 0; ( )x f x x xf x x f e
e
. Tính
2
( )
e
e
f x dx
.
A. 2 B. 1,5 C. 3 D. 2,5
Câu 17. Hàm số
( )
y f x
liên tục và có đạo hàm trên [1;e] thỏa mãn
2
1 1
(1) ; ( ) ( ) 3 ( )
2
f xf x xf x f x
x
.
Tính giá trị biểu thức f (e).
A.
3
2
e
B.
4
3
e
C.
3
4
e
D.
2
3
e
Câu 18. Hàm số
( )
y f x
thỏa mãn
2
2
( ) 3 2 1 4 ( )
f x x x xf x
và
3
1
( ) 12
f x dx
. Tính
2
0
( )
f x dx
.
A. 6 B. 7 C. 8 D. 5
_________________________________
20
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 10)
__________________________________________________
Câu 1. Cho hàm số
y f x
có đồ thị như hình vẽ bên. Biết rằng diện
tích các phần (A), (B) lần lượt bằng 3 và 7.
Tính tích phân
2
0
cos . (5sin 1)
x f x dx
.
A. 2 B. 0,8 C. – 0,8 D. – 2
Câu 2. Trên [0;1], hàm số
( )
y f x
thỏa mãn
3 5
1. 4 (1 ) ( )
x xf x f x x
. Khi đó
1
0
( )
f x dx
có giá trị gần
nhất số nào sau đây ?
A. 0,0434 B. 0,0548 C. 0,5482 D. 0,1873
Câu 3. Hàm số
( )
y f x
thỏa mãn
4 2
3 ( )
3 ( ). ( ). (2 1) ; (0) 1
f x x x
f x f x e x e f
.
Giá trị nhỏ nhất của biểu thức
1
5
0
( ) ( )
f x dx f x
gần nhất giá trị nào sau đây
A. 0,94 B. 1,72 C. 3,65 D. 2,34
Câu 4. Trên [1;2] , hàm số
( )
y f x
có
( ) 5
f x x
thỏa mãn
2
2 ( ) 5 5 ( ); (1) 6
x f x x f x f
.
Tính giá trị biểu thức
(2) (1)
f f
.
A. 5 B. 8 C. 7 D. 6
Câu 5. Hàm số
f x
là hàm số chẵn, liên tục trên R thỏa mãn
1
0
( ) 2018
f x dx
, hàm số
( )
g x
là hàm số liên
tục trên R thỏa mãn
( ) ( ) 1
g x g x
. Tính tích phân
1
1
( ) ( )
f x g x dx
.
A. 2018 B. 504,5 C. 4036 D. 1008
Câu 6. Biết giá trị nhỏ nhất của
2
2 2
2 2 3
2
2( 1) 4
m
m
S x m m x m m dx
là phân số tối giản
a
b
. Tính a + b.
A. 7 B. 337 C. 25 D. 91
Câu 7. Với m là tham số thực thuộc [1;3]. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
2
2 2
( 2 ) ( )
m
m
P x m x m dx
.
A. 31 B. 36 C.
122
15
D.
121
4
Câu 8. Có bao nhiêu số nguyên m < 100 để phương trình
2
0
(2 1) 3 4
m
x dx x x
có hai nghiệm phân biệt ?
A. 98 B. 96 C. 97 D. 95
Câu 9. Hàm số
( )
y f x
có đạo hàm trên [0;1] thỏa mãn
1
4
4
4
0
10 1
( ) ; 15. ( ) (1) 1
5 ( ) 2
x
f x f x dx f
f x
.
Tính
1
4 4
0
( )
x f x dx
.
21
A.
14
15
B.
14
45
C.
4
45
D.
13
15
Câu 10. Tính tích phân
1
0
( )
f x dx
khi hàm số
( )
y f x
có đạo hàm trên [0;1] thỏa mãn
(1) 1; (0) 0
f f
và
2
( ) 2 ( ) 4 1 ( ) 2 ( ) 1 2 ( ) 1
f x f x x f x f x x f x
.
A. 1 B. 2 C. 1,5 D.
1
3
Câu 11. Cho hàm số
y f x
xác định và liên tục trên [– 2;1]. Biết
rằng diện tích hình phẳng
1 2
,
S S
giới hạn bởi đồ thị và đường thẳng
y ax b
lần lượt là m, n. Tính tích phân
1
2
( )
f x dx
.
A. m – n + 4,5 B. m + n + 2
C. n – m + 4,5 D. m + n + 1
Câu 12. Cho
f x
liên tục trên R sao cho
5 5
( ) 2 2 ( )
f x x x f x
. Tính
1
4 2
0
(10 1) ( )
x f x dx
.
A.
29
21
B. 1 C.
22
3
D.
11
3
Câu 13. Cho hàm số
f x
nhận giá trị không âm và liên tục trên
0;

sao cho
( ) ( ) 2
f x f x x
.
Tính tích phân
1
0
( )
f x dx
.
A. 1 B.
5
24
C.
5
12
D.
5
6
Câu 14. Giá trị
2
0
min 3 1;2
I x x dx
gần nhất với giá trị nào sau đây ?
A. 4,5 B. 3,3 C. 2,7 D. 7,1
Câu 15. Tính giá trị biểu thức
(2)
f
khi hàm số
( )
y f x
có đạo hàm liên tục trên R và thỏa mãn
3 4
6
( ) 27 ( ) 1 0
x f x f x
;
(1) 0
f
.
A. 1 B. – 1 C. 7 D. – 7
Câu 16. Cho hàm số
( )
f x
thỏa mãn
0 0
sin . ( ) 20; sin . ( ) 5;
x f x dx x x f x dx
Tính
2
0
cos( ). ( )
x f x dx
.
A. 25 B. 15 C. – 50 D. – 30
Câu 17. Tính
1
0
( )
f x dx
khi hàm số
( )
f x
liên tục trên
và thỏa mãn điều kiện
3
1
sin . (cos ) cos . (sin ) sin 2 sin 2
2
x f x x f x x x
.
A. 1 B.
1
6
C.
2
3
D.
1
3
Câu 18. Cho hàm số
( )
f x
thỏa mãn
3
(0) 4; ( ) ( )
f f x f x x
. Tính
(1)
f
.
A. – 10 B. – 2 C.
10
2
e
D.
10 4
e
_________________________________
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


THÂN TẶNG QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TOÀN QUỐC
HỆ THỐNG BÀI TẬP TRẮC NGHIỆM VẬN DỤNG CAO, PHÂN LOẠI
NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(KHÔNG BAO GỒM ỨNG DỤNG) PHẦN 1 – 10 9 f (  1993x) dx 4 CREATED BY GIANG SƠN TP.THÁI BÌNH; THÁNG 4/2020
_____________________________________________________________________________________________________________ 1
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 1)
__________________________________________________   2 2 Câu 1. Cho tích phân cos xf 
sin xdx  8. Tính sin .xf  cos xdx . 0 0 A. – 8 B. 4 C. 8 D. 16
Câu 2. Cho hàm số f x liên tục, có đạo hàm trên R thỏa mãn f  x 3 2
dx  x  x  2 . Giá trị của 2 I  xf  2 x  
1dxgần nhất với giá trị nào ? 1 A. 83 B. 38 C. 120 D. 70 33 37
Câu 3. Hàm số y  f x liên tục trên  thỏa mãn f  5 x  x   1  x  2 . Tính f  xdx  f  x 4dx. 1 5 A. 696 B. 200 C. 236 D. 120
Câu 4. Giả sử hàm số y  f x liên tục, nhận giá trị dương trên 0; đồng thời thỏa mãn điều kiện
f 2  1; f x  f x 4x 1. Mệnh đề nào sau đây đúng ? A. 1 < f (5) < 2 B. 2 < f (5) < 3 C. 3 < f (5) < 4 D. 4 < f (5) < 5 1
Câu 5. Hàm số f (x) xác định trên  \ 1  ; 
5 thỏa mãn f  x  ; f (1) = 1; f   ln 2 7   . 2 x  4x  5 3
Giá trị biểu thức f (0) + f (– 3) gần nhất số nào sau đây ? A. 1,38 B. 0,38 C. 3,31 D. 32,22 2
Câu 6. Cho hàm số f  x thỏa mãn f  x  f x f   x 2 .  24x 12x  3, x    
 ; f 0  f 0  1. 2
Giá trị của tích phân f  x   1dx là 1 1 5 2 A. – 2 B.  C.  D. 3 6 3
Câu 7. Cho hàm số f x liên tục và có đạo hàm trên đoạn [1;3] thỏa mãn điều kiện 3  f  x  5, x  1;  3 .
Giả sử tồn tại hai số thực a và b sao cho a  f 3  f   1  b, x  1; 
3 . Tính giá trị của tổng S  a  b . A. 16 B. 15 C. 17 D. 8 x 8
Câu 8. Hàm số f  x thỏa mãn f (3)  3; f (x)  , x   0 . Tính f (x)dx  . x 1 x 1 3 197 181 A. B. C. 7 D. 14,5 6 6 3 Câu 9. Tính K = max 4 x ;  x dx  . 0 A. K = 15,5 B. K = 2,6 C. K = 48,9 D. K = 11,2 1
Câu 10. Hàm số f  x là hàm số chẵn, liên tục trên R thỏa mãn f (x)dx  2018 
, hàm số g(x) là hàm số liên 0 1
tục trên R thỏa mãn g(x)  g(x)  1. Tính tích phân f (x)g(x)dx  . 1  A. 2018 B. 504,5 C. 4036 D. 1008 2 1 1 1 1
Câu 11. Cho hàm số f (x) liên tục trên [0;1] thỏa mãn 2 2 f (x)dx  f (x )dx    . Tính f (x)dx  . 3 0 0 0 2 5 A. 1 B. C. D. 3 3 3
Câu 12. Biết cos 2x là một nguyên hàm của hàm số ( ). x
f x e . Khi đó F(x) là một nguyên hàm của hàm số (  ). x
f x e . Biết rằng F(x) có hệ số tự do bằng 0, giá trị nhỏ nhất của F(x) gần nhất giá trị nào A. – 2,23 B. – 1,56 C. – 1,41 D. 1 4 m m Câu 13. Biết rằng 2
3. x  4x  3 dx  31. mx 1 dx   . Khi đó 2 (2x  x)dx  gần nhât với số nào 2  1 1 A. 14 B. 13 C. 17 D. 18 f (x)
Câu 14. Cho hàm số f (x) thỏa mãn (x 1) f (  x)  ; f (0)  2 . Tính f (2) . x  2 A. 1 B. 3 C. 2 D. 4 2 4 Câu 15. Cho  x 
f  x liên tục trên R sao cho x  
1 f  xdx  14;3 f 2  f 0  10 . Tính f dx    .  2  0 0 A. – 4 B. 3 C. – 8 D. – 2
Câu 16. Hai hàm số f (x), g (x) có đạo hàm trên [1;4] thỏa mãn đồng thời g  x  xf  x; f  x  xg x , 4
ngoài ra f (1) + g (1) = 4. Tính ( f  x gx)dx. 1 A. 3ln2 B. 6ln2 C. 4ln2 D. 8ln2  4 1 2 x f (x) 1
Câu 17. Hàm f (x) liên tục trên R thỏa mãn f (tan x)dx  4; dx  2   . Khi đó f (x)dx  thuộc khoảng 2 x 1 0 0 0 A. (5;9) B. (3;6) C. (1;4) D. ( 2;5) 7
Câu 18. Hàm số f (x) liên tục trên  thỏa mãn 2 3 2
x f (x 1)  f (7x  7)  x  3x . Tính f (x)dx  . 0 A. – 4,55 B. – 2,68 C. – 8,25 D. – 5 8 9 2
Câu 19. Cho hàm số y  f  x liên tục trên [0;9] và f  xdx  5; f  xdx  4. Tính f   4x 1dx 0 0 2  A. 6 B. 21 C. 4 D. 2
Câu 20. Hàm số y  f (x) xác định trên  \  0 thỏa mãn xf x   xf x  2 ( ) 1; ( ) 1  xf (  x)  f (x)  0 . e Tính tích phân f (x)dx  . 1 1 1 1 1 A.  2 B. 2  C. – D. – 1 e e e e  2 4 e 2 f (ln x) 2 f (2x)
Câu 21. Hàm số f (x) liên tục trên R sao cho 2 tan . x f (cos x)dx  2; dx  2   . Tính dx  . x ln x x 0 e 1 4 A. 0 B. 1 C. 4 D. 8
_________________________________ 3
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 2)
__________________________________________________      4 4    f (x)
Câu 1. Hàm số y  f  x liên tục trên 0;  thỏa mãn f  3; dx  1; sin . x tan . x f (x)dx  2     . 4     4  cos x 0 0  4 Tính sin xf (  x)dx  . 0 3 2 1 3 2 A. 4 B. 6 C. 1 D. 2 2 2 2
Câu 2. Cho f  x liên tục trên R; 2 (x 1) f 
xdx  3; f (2)  4e. Khi đó 3 (x 1) f (  x)dx  thuộc khoảng 1 1 A. (0;1) B. (1;2) C. (3;5) D. (6;10) x e ln 8
Câu 3. Cho hàm số f (x) thỏa mãn f (ln 3)  4; f (  x)  , x
   . Tính tích phân x e f (x)dx  . x e 1 ln 3 76 38 136 A. B. C. D. 2 3 3 3
Câu 4. Cho hàm số y  f x liên tục và nhận giá trị không âm trên 1; thỏa mãn f   f x  e  f    x 2 2 2 1 0;   4x  4x 1 
với mọi x thuộc 1; .
Mệnh đề nào sau đây đúng ?
A. 1  f 4  0 B. 0  f 4 1 C. 1  f 4  2 D. 2  f 4  3 1
Câu 5. Cho hàm số f  x liên tục trên đoạn [0;1] thỏa mãn f  x  f   x 2 2 3 1  1 x . Tính f xdx  . 0     A. B. C. D. 4 6 20 16 2
Câu 6. Cho hàm số f  x thỏa mãn  f  x  f  x. f   x  1,x   
 ; f 0  f 0  4 . Tồn tại bao
nhiêu số nguyên x thỏa mãn f  x  5 . A. 20 B. 13 C. 26 D. 16 2 5 f (x) 5
Câu 7. Hàm số f (x) liên tục trên R sao cho 2 f ( x  5  x)dx  1; dx  3   . Tính f (x)dx  . 2 x 2  1 1 A. – 15 B. – 2 C. – 13 D. 0
Câu 8. Cho hàm số y  f  x liên tục trên  thỏa mãn 2 2
f (x  3)  (x  x 1). f (4  x) . 1
Tính tích phân (x  2) f (x)  f  (x)dx . 0 77 7 17 A. 1 B.  C.  D.  6 6 3
Câu 9. Với tham số m thuộc [0;3], tính a + b khi a, b lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của tích phân 2m 3 2 2 3 S  x  4mx  5m x  2m dx  . m 41 A. 1 B. 2 C. 5,25 D. 6 4 ln 2 4 f ( x)
Câu 10. Hàm số f (x) liên tục trên [1;2] sao cho f (x)  f (3  x) và 2 x ( x e f e )dx  1  . Tính dx  . 2 x 0 1 2 3 A. 2 B. 1 C. D. 3 2 1
Câu 11. Hàm số bậc hai f  x trên R có f (x  2)  f (x)  4x 10; f (0)  1. Tính f (x) f (x)   1dx. 0 2 A. 7,5 B. 2 C. – 1 D.  3 3 2
Câu 12. Hàm số y  f (x) thỏa mãn  f x 2 2
( )  3x  2x 1  4xf (x) và f (x)dx  12  . Tính f (x)dx  . 1  0 A. 6 B. 7 C. 8 D. 5 3
Câu 13. Tính giá trị gần đúng của f (x)dx 
biết hàm số y  f (x) liên tục trên [1;3] thỏa mãn 0 f  x   f x 2 2 2 ( ). 1
( )  f (x).(x 1) ; f (1)  1  ; f (x)  0, x  0;  3 .
A. – 1,09 B. – 2,56 C. – 6,25 D. 4,16 1 2
Câu 14. Hàm số y  f (x) có đạo hàm trên [0;2] thỏa mãn f (  x)  ; f (2)  1. Tính 2 f (x)dx  . 2 3 f (x) 1 0 1 14 11 A. 1 B. C. D. 3 15 12 6x  f (  2x) 1
Câu 15. Đa thức bậc bốn y  f (x) đạt cực trị tại x  1; x  2và lim  3 . Tính f (x)dx  . x0 6x 0 A. 2 B. 2,5 C. 0,75 D. 4 1 Câu 16. Tính xf  (  x  3)dx 
khi y  f (x) là hàm số đa thức thỏa mãn điều kiện 0 3 f (x)  2 f (
 x 1)  f  (x  2)  (x  2) 17x  3. A. 29 B. 4 C. 2020 D. 11
Câu 17. Hàm số y  f (x) có đạo hàm xác định trên  và nhận giá trị dương trên 0; , đồng thời thỏa mãn e
điều kiện f (x)  ln f (x)  x 1. Giá trị tích phân f (x)dx  nằm trong khoảng 0 A. (4;5) B. (0;2) C. (2;4) D. (5;6) 0 Câu 18. Tính f (x)dx 
khi hàm số y  f (x) là hàm số đa thức thỏa mãn 1  2 2 4 6 2
f (x )  2x f (1 x )  2x  5x  2 . A. 1,5 B. 1 C. 2 D. 2,5 m
Câu 19. Cho số thực m thỏa mãn 2mx 1 dx  1 
. Tham số m thu được thuộc khoảng nào sau đây 1 A. (4;6) B. (2;4) C. (3;5) D. (1;3) 1
Câu 20. Cho hàm số y  f (x) thỏa mãn f (  x)  x  , x
  0; f (1)  1. Giá trị nhỏ nhất của f (2) là x A. 2,5 + ln2 B. 2 + 2ln2 C. 3 – ln2 D. 3ln2 – 1
_________________________________ 5
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 3)
__________________________________________________ 5 1
Câu 1. Cho hàm f x liên tục và có đạo hàm trên R thỏa mãn f
 xdx  6a . Tính xf   2 3x  2dx . 2 0 A. a B. 0,5a C. 2a D. 4a 3 f (x) 3
Câu 2. Cho f  x thỏa mãn
dx  4; f (1)  1; f (3)  3  . Tính ln(3x 1) f (x)dx  . 3x 1 1 1 A. 8ln2 – 12 B. 8ln2 C. 6ln2 – 12 D. 2ln8 + 4 x
Câu 3. Hàm số f (x) có đạo hàm liên tục trên R. Biết g(x) là một nguyên hàm của hàm số y  sao 2 x  g (x) 2 2 2 x
cho g(x)dx  1; 2g(2)  g(1)  2  . Tính tích phân dx  . 2 x  g (x) 1 1 A. 1,5 B. 1 C. 3 D. 2 1 1 1
Câu 4. Cho hàm số f (x) có đạo hàm liên tục trên [0;1] thỏa mãn 2 f (1)  0; x f (x)dx   . Tính 3 x f (  x)dx  . 3 0 0 A. 1 B. – 1 C. 3 D. – 3 x  x 14 5
Câu 5. Hàm số f (x) liên tục trên R thỏa mãn 2 2 f (
 x)  e  e  2; f (ln 3)  ; f ( ln 2)  . 3 2
Tính giá trị biểu thức f (ln 5)  f (ln 4) . A. 11,55 B. 12,25 C. 10 D. 14,25 0 1 ln 3
Câu 6. Hàm số y  f x liên tục trên R thỏa mãn f  xdx 1; f
 xdx  6. Tính x ( x e f e  2 )dx  . 1  0 0 A. 5 B. 4 C. 2,5 D. 2 0 2 4
Câu 7. Hàm số f  x là hàm số lẻ, liên tục trên [– 4;4] và f  xdx  2; f   2
 xdx  4. Tính f xdx  . 2  1 0 A. – 10 B. – 6 C. 6 D. 10 2 1 f (2x)
Câu 8. Tính tích phân f xdx 
khi f  x là hàm số chẵn trên R thỏa mãn dx  8  . 1 5x 0 1  A. 8 B. 2 C. 1 D. 16 5
Câu 9. Cho f  x liên tục trên R sao cho 3 2
2 f (x)  3 f (x)  6 f (x)  x . Tính f (x)dx  . 0 5 5 A. 1,25 B. 2,5 C. D. 3 12 6 1 4x. f (6x) Câu 10. Tính tích phân f
 xdx khi f x là hàm số chẵn trên R thỏa mãn dx  7  . 4x  5x 6  1  A. 84 B. 28 C. 42 D. 14
Câu 11. Hàm số y  f (x) xác định trên R thỏa mãn 2 3 4 2
2 f (x 1)  3xf (x  2)  3x  2x  9x  4 . 1
Tìm giá trị nhỏ nhất của biểu thức 2 (x  2) f (  x)dx  f (x 1)  . 0 A. 2,5 B. 3 C. 4 D. 4,5 6
Câu 12. Hai hàm số y  f (x), y  g(x) xác định và có đạo hàm trên [1;2] thỏa mãn
 f (x)  xg (x)  0; 4g(x)  xf (x)  0   f (1)  2g(1)  3 2
Tính tích phân [ f (x)  2g(x)]dx  . 1 A. 3 B. 1,5 C. 2,5 D. 2 2   2  1
Câu 13. Hàm số f (x) liên tục trên ;1  thỏa mãn 2 f (x)  3 f  5x   . Hỏi giá trị ln . x f (  x)dx  gần nhất 3     3x  2 3 giá trị nào sau đây ? A. 0,34 B. 0,24 C. 0,26 D. 0,52 2  x 
Câu 14. Hàm số f (x) liên tục trên [0;1] thỏa mãn 2 f (x)  3 f (1 x)  x 1 x . Tính xf  dx    .  2  0 4 4 16 16 A.  B.  C.  D.  75 25 75 25
Câu 15. Cho hàm số y  f (x) có đạo hàm liên tục trên  , nhận giá trị dương trên [0;2018] và thỏa mãn điều 2018 1
kiện f (x). f (2018  x)  1. Tính tích phân dx  . 1 f (x) 0 A. 2018 B. 4016 C. 0 D. 1009
Câu 16. Cho hàm số y  f (x) xác định và có đạo hàm liên tục trên  , nhận giá trị dương trên [a;b] và thỏa b
mãn điều kiện f (x). f (a  b  x)  9 . Tìm giá trị nhỏ nhất của 2 1 T  (b  a)  36 dx  2019  . 3  f (x) a A. 2019 B. 2010 C. 2016 D. 2015
Câu 17. Cho hàm số y  f (x) xác định và có đạo hàm liên tục trên  , nhận giá trị dương trên [2;7] và thỏa 7 1
mãn điều kiện f (x 1). f (7  x)  9 . Tính dx  . 3  f (x) 3 2 1 5 A. 1 B. C. D. 3 6 6 1 1 11 4
Câu 18. Tính f (2) nếu hàm số f (x) liên tục trên [0;1] thỏa mãn 5 f (1)  1; x f (x)dx  ; f (  x)dx    . 78 13 0 0 261 13 100 A. B. C. 2 D. 7 7 7 1 Câu 19. Tính f (x)dx 
khi hàm số f (x) có đạo hàm liên tục trên [0;1] thỏa mãn 0 1 1   2 9 x 3 f (0)  0; f (x)dx  ; f (  x)cos dx    . 2 2 4 0 0 A. 6 B. 2 C. 4 D. 1 8
Câu 20. Cho hàm số y  f  x thỏa mãn f  3 x  6x  
1  5x 1. Tính tích phân 4 xf   xdx . 1 A. 30 B. 85 C. – 20 D. – 17
_________________________________ 7
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 4)
__________________________________________________ 2 20x  30x  7  3  Câu 1. Biết 2
F(x)  (ax  bx  c) 2x  3 là một nguyên hàm của f (x)  trên ;   . Tính 2x  3  2  giá trị biểu thức abc. A. 0 B. 3 C. 4 D. – 8  
Câu 2. Cho hàm số thỏa mãn 
f ' x.sin x  f  x 1 2 .cos x  2 sin .
x cos 3x x  0; , f  .   Tìm họ các  4  3 nguyên hàm f xdx  ? A. 1  1
2 sin 2x  sin 4x  C . B.
sin 4x  2sin 2x  C . 12 12 C. 1  1 sin 2x  sin 4x  C . D.
2sin 2x sin 4x  C . 12 12  1 2
Câu 3. Hàm số f (x) thỏa mãn 2 f (0)  ; f (  x)  sin 3 . x cos 2x . Tính f (x)dx  . 21 0 137 137 247 167 A. B.  C. D. 441 441 441 882
Câu 4. Hàm số f (x) thỏa mãn 2 2 f (x)  f (  x)  2x 1và 2
f (1)  e  2 . Khi đó f (2) gần nhất giá trị nào A. 166 B. 120 C. 90 D. 52
Câu 5. Hàm số f (x) có đạo hàm liên tục trên [0;5] và thỏa mãn ( )  (  )  x f x f x  e 3x 1 . Tính f (5) khi f (0)  0 . 14 13 9 11 A. B. C. D. 5 e 5 e 5 e 5 e 2017 2017
Câu 6. Hàm số f (x) liên tục trên  thỏa mãn f (x)  f (2020  x)và f (x)dx  4  . Tính xf (x)dx  . 3 3 A. 16160 B. 4040 C. 2020 D. 8080
Câu 7. Hàm số f (x) có đạo hàm dương với mọi x  0 thỏa mãn f   f x 2 (1) 2; ( ) dx  ln f (x)  C . Tính f (3) . A. 1 B. 4 C. 6 D. 2 2 1 1
Câu 8. Hàm số f (x) có đạo hàm liên tục trên [0;1] và xf (1 x)  f (x)dx   . Tính f (0) . 2 0 A. 1 B. 0,5 C. – 1 D. – 0,5  2 Câu 9. Hàm số f (x) có 4 f (0)  0; f (
 x)  sin x . Tính f (x)dx  . 0 2   6 2   3 2 3 16 2 3  6 A. B. C. D. 18 32 64 112
Câu 10. ho hàm số f x xác định và có đạo hàm trên khoảng 0;;   f  x 1 1 '  0, x   0; f  ; 1   f    x 2  1   2x  2   x   1  f   x f ' x, x   0.  2  3 8 2 f  x Tính tích phân I  d . x  f ' x 1   A. 23 I  . B. 3 I  . C. I  1 ln 3. D. 2 I  1 ln . 6 2 3  1  4
Câu 11. Hàm số f (x) liên tục thỏa mãn f (x)  x 1  f (x) , x   0  và f (4)  . x    3 4 Khi đó 2 (x 1) f (  x)dx 
gần nhất giá trị nào sau đây 1 A. 30,5 B. 31,5 C. 32,5 D. 33,8  2 16 f x 2  
Câu 12. Cho hàm số f  x liên tục trên  và thỏa mãn cot .x f  sin xdx  dx  1  .  x 1 4 1 f 4x Tích phân I  dx  bằng x 1 8 3 5 A. I  . B. I  3 . C. I  . D. I  2 . 2 2 f x 2x 1 2  
Câu 13. Hàm số f  x liên tục trên khoảng 0; và thỏa mãn f x   1   .ln  x   1 . 4x x 2x 17 Biết f
 xdx  aln52lnbc với a, ,bc. Giá trị của ab2c bằng 1 A. 29 . B. 5. C. 7 . D. 37 . 2 1 4 1 3 x
Câu 14. Hàm số f  x có đạo hàm xác định trên  . Biết f   1  2 và 2 x f   xdx  f  2 xdx 4. 2 x 0 1 1 Giá trị của f xdx  bằng 0 5 3 A. 1. B. . C. . D. 1 . 7 7 7
Câu 15. Cho hàm số y  f  x có đạo hàm f x liên tục trên thỏa mãn điều kiện  x f  x3 
   f t3  f t3 3 f t f t2dt  2020   . 0
Mệnh đề nào dưới đây đúng? A. f   3 1  2020e . B. f   1  2  020e . C. f   3 1   2020e . D. 2020e . 
Câu 16. Hàm số y  f (x) có f (0)  0 và 8 8 6 f (
 x)  sin x  cos x  4sin x,x   . Tính I  16 f (x)d  x . 0 A. I  160 . B. 2 I  10 . C. 2 I  16 . D. 2 I  10 f x 2  ln 2 
Câu 17. Hàm số f  x  0 và có đạo hàm liên tục trên  , thỏa mãn  x   f x   1  và f 0    . x  2  2  Giá trị f 3 bằng A. 1  1 4ln 2  ln 52 . B.   2 4 4ln 2 ln 5 . C. 4ln 2  ln 52 . D.   2 2 4ln 2 ln 5 . 2 4
_________________________________ 9
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 5)
__________________________________________________ 2 5x  8x  4  1 
Câu 1. Biết rằng F (x) là nguyên hàm của hàm số trên (0;1) thỏa mãn F  26 . Giá trị nhỏ 2 2   x (x 1)  2 
nhất của hàm số F (x) bằng A. 24 B. 20 C. 25 D. 26  2 3  x  4x  6 khi x 1 3 2 e f ln x
Câu 2. Cho hàm số f x   . Khi đó cos . x f  sin x   dx  4 dx  bằng 7  2x khi x 1 x 0 e A. 29 . B. 28 . C. 94. D. 49 . 1
Câu 3. Cho hàm số f x có đạo hàm liên tục trên  và f 0  2 ,      2  2 x F x f x e  x là một nguyên 2
hàm của f x . Họ các nguyên hàm của f x là A. 1  1 8  3 2x x e  x  C . B. 8   2 1 x x e  x  C . 2 2 1 C. 8 3 2 . x x e  x  C . D.    2 8 1 . x x e  x  C . 2 3 4
Câu 4. Hàm số f (x) liên tục trên  thỏa mãn 2 3
4xf (x )  6 f (2x)  x  4. Tính f (x)dx  . 5 0 A. 2,08 B. 52 C. 48 D. 1,92
Câu 5. Cho       1 x F x x
e là một nguyên hàm của hàm số   2x
f x e . Tìm họ nguyên hàm của hàm   2x f x e  A. 
   2x  2 x f x e dx x e  C . B. f   x x x 2 2 x e dx  e  C. 2 C. 
   2x  42  x f x e dx x e  C. D. 
   2x  2  x f x e dx x e  C.
Câu 6. Cho hàm số y  f  x có đạo hàm liên tục trên  . Biết f  
1  e và  x   f  x  x f  x 3 2 . .  x với 1
x   . Giá trị của f xdx  bằng 0 2 4 1 2 1 2 A. e   . B.   . C. e  . D. e  . e 3 e 3 e 3 x 7
Câu 7. Cho hàm số f x có f 7 15 và f   1 x 
,x  0 . Khi đó f xdx  bằng x  2 x 2 2 347 271 287 A. . B. . C. 7. D. 6 6 6 Câu 8. Giả sử 2
F(x)  x là một nguyên hàm của 2
f (x)s in x và G(x) là một nguyên hàm của 2 f (x) cos x trên     khoảng   0;  . Biết rằng G  0   và 2 G  a  b  c ln 2  
, với a,b,c là các số hữu tỉ. Tổng a  b  c bằng  2   4  11 5  21 27 A. . B. . C. . D. . 16 16 16 16 1 5 1
Câu 9. Hàm số y  f  x liên tục trên  thỏa mãn f  xdx  f
 xdx  9. Tính tích phân I  f   3x 2 dx 0 0 1 10 A. I  9 . B. I  3 . C. I  4 . D. I  2 .  ln 3 Câu 10. Cho hàm số 2x 1 f x có f   2 1  e và f x 2  e x , x  0 . Khi đó xf  xdx  bằng 2 x 1 2  2  A. 2 6 e 9 e 6  e . B. . C. 2 9  e . D. . 2 2 3 6 x
Câu 11. Hàm số f x có đạo hàm liên tục trên  thỏa mãn f (3)  xf (x)dx  3  . Tính 2 x f ( )dx  . 2 0 0 A. 21 B. 42 C. 84 D. 168
Câu 12. Giả sử hàm f có đạo hàm cấp 2 trên  thoả mãn f '  1  1 và f   x 2 ' 1
 x f ' x  2x với mọi 1
x   . Giá trị tích phân '  xf xdx bằng 0 A. 2 . B. 1. C. 0 . D. 2 . 3
Câu 13. Cho f (x) là hàm số liên tục trên R thỏa mãn f (x)  f '(x)  cos , x x
 và f (0) 1. Tính e f ( ) bằng A. e  3 . B. e  1 . C. e 1 . D. e  3 . 2 2 2 2     Câu 14. Hàm số    x  f x , với x  ;
. Gọi F x là một nguyên hàm của xf 'x thoả mãn điều 2   cos x  2 2     kiện 
F 0  0 . Biết tan a  7 với a   ;   . Biểu thức F a 2
 50a  7a có giá trị là  2 2  1 1 1 A. ln 50. B.  ln 50 . C. ln 50 . D.  ln 50 . 4 2 2    2 1 Câu 15. Cho  4 f (
 x)  sin 2x  5sin x cos x,x   , f  0   và f (x)dx  a  b  với a,b  .  Đặt T   .b  2  a 0
Mệnh đề nào sau đây đúng? A. T 1;2. B. T 0;  1 . C. T 2;3. D. T  2  ;0. 1 2  x 
Câu 16. Cho hàm số f  x liên tục trên  và 2 f 1  3 f 0  0 , f
 xdx  7. Tính I  6 x f  dx    2  0 0 A. I  40 . B. I  28. C. I 18. D. I  42 .  3  2 2x  x khi x  1 3 f tan x e 1  . x f lnx   1
Câu 17. Cho hàm số y  f x   . Biết tích phân I  dx  dx    3  x  4 khi x  1 2 2   cos x x 1 0 4 a a bằng với a,b  ,
 b  0 và là phân số tối giản. Tính giá trị biểu thức P  a  b . b b A. P  77 . B. P  45 . C. P  29 . D. P  54 .
Câu 18. Hàm số y  f  x xác định và dương trên khoảng 0;, thỏa mãn  f    x 2 2   12x  f  x f  x với
mọi x 0; và f   1  1; f  
1  4 . Giá trị của f 2 bằng A. 46 . B. 7 . C. 3 5 . D. 2 10 .
_________________________________ 11
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 6)
__________________________________________________
Câu 1. Cho hàm số f  x liên tục thỏa mãn 3 f (x)dx  4x  2x  C  . Tính 2 xf (x )dx  . 10 6 x x A. 6 2 2x  x  C B.   C C. 6 2 4x  2x  C D. 6 2 6x  2x  C 10 6 6 1 1,5
Câu 2. Hàm số f  x liên tục trên R thỏa mãn f
 xdx  4. Tính tích phân 3 I  x f   4x  1dx f  4xdx . 1 0 0,5 A. 4 B. 0,5 C. 2 D. 1
Câu 3. Cho hàm số f  x liên tục, có đạo hàm trên đoạn [2;4] thỏa mãn điều kiện 2x  f x  4x, x  2;4.
Giả sử tồn tại hai số thực a và b sao cho a  f 4  f 2  b, x
 2;4 . Tính giá trị của tổng S  a  b . A. 36 B. 40 C. 50 D. 15
Câu 4. Cho các hàm f  x, g x liên tục trên R và có đạo hàm trên đoạn [1;3] thỏa mãn đồng thời các điều kiện 3 3 3 3 f   1 .g  
1  1; f 3.g 3  3; g
 xf xdx  g
 xf xdx  4 . Tính S  3 g
 xf xdx  4 g  xf xdx . 1 1 1 1 A. 5 B. 11 C. 12 D. 13 3 1 9  x Câu 5. Cho 
f  x liên tục trên R; 3x  
1 f  xdx  2; 10 f 3  f 0  11. Tính K  f  3xdx  f    .  3  0 0 0 A. 10 B. 3 C. – 2 D. 12 33 37
Câu 6. Hàm số y  f x liên tục trên  thỏa mãn f  5 x  x   1  x  2 . Tính f  xdx  f  x 4dx. 1 5 A. 696 B. 200 C. 236 D. 120 2
Câu 7. Cho hàm số f  x thỏa mãn  f  x  f  x. f   x  1, x    
 ; f 0  f 0  4 . Tồn tại bao
nhiêu số nguyên x thỏa mãn f  x  5 . A. 20 B. 13 C. 26 D. 16
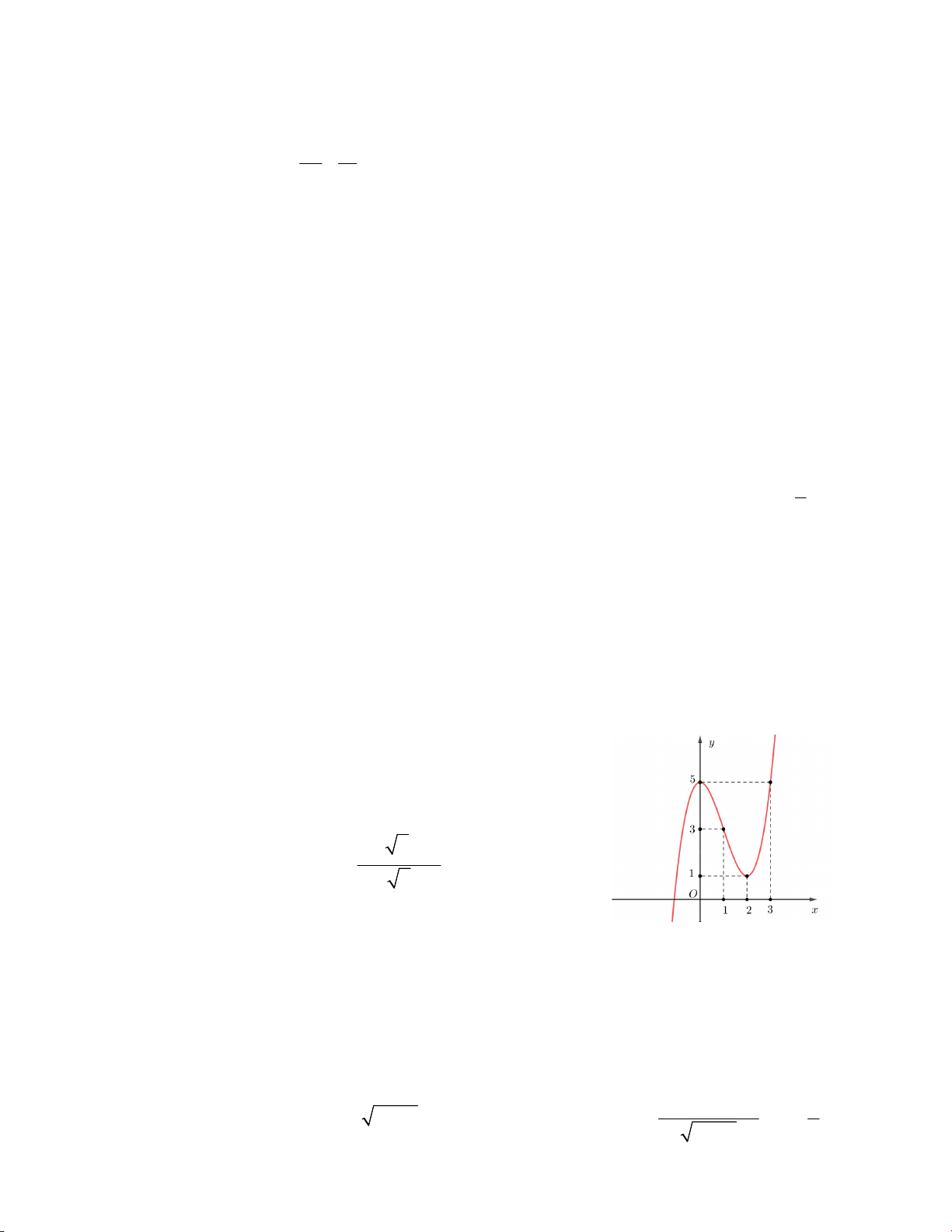
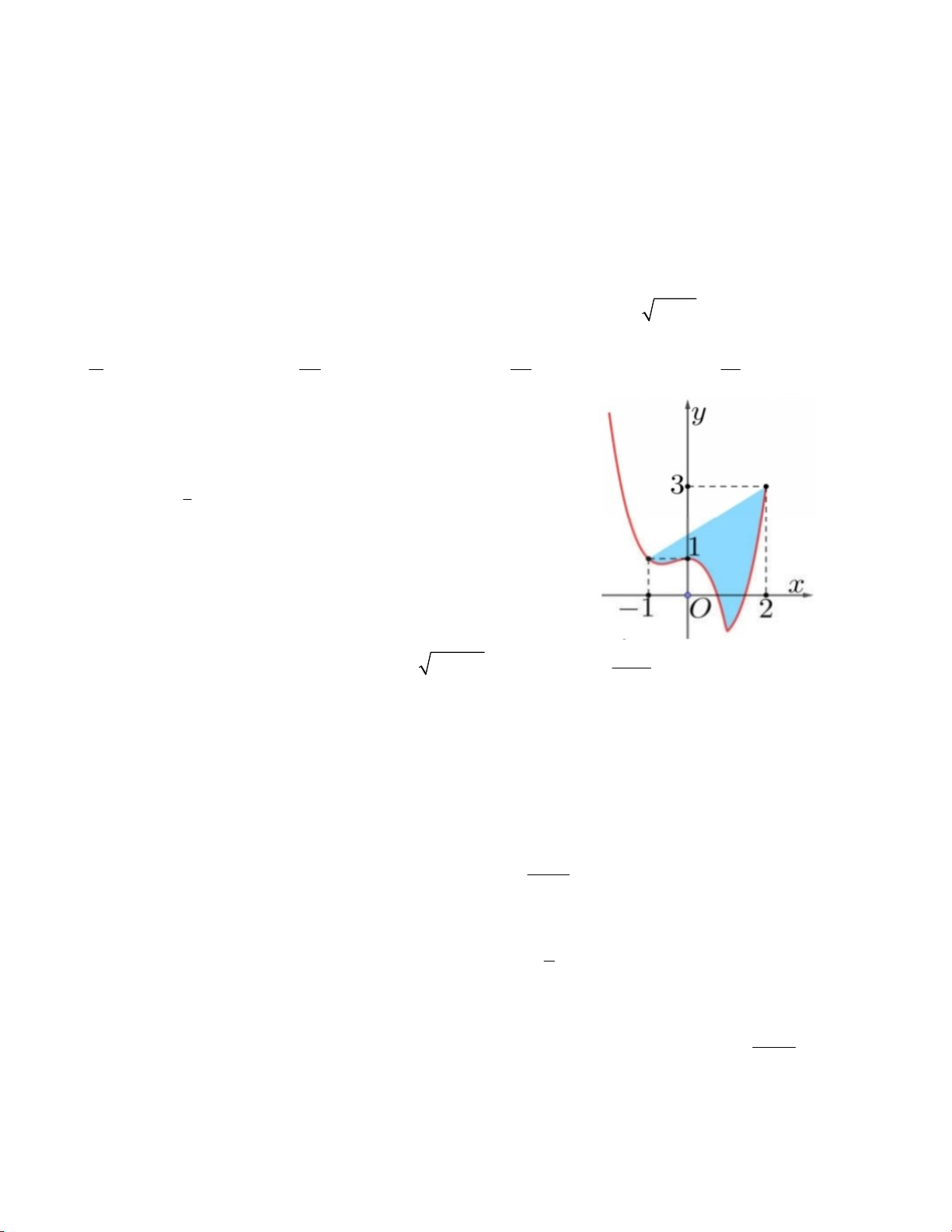
Câu 8. Cho hàm số y  f  x liên tục và có đạo hàm trên  , đồ thị
y  f x như hình vẽ bên. Tính tích phân 2 4 f  x   1 I  f   x  1dx  dx  . x 1 1 A. 12 B. 16 C. 18 D. 7 3 3
Câu 9. Hàm số f (x) liên tục trên R sao cho f (6  x)  f (x  2); f (x  2)dx  4  . Tính xf (x  2)dx  . 1 1 A. 6 B. 8 C. 2 D. 10 2
Câu 10. Hàm số f (x) liên tục trên  và 2 3 4 2
2 f (x 1)  3xf (x 1)  3x  2x  6x  4 . Tính f (x)dx  . 1 A. 1,5 B. 1 C. 2 D. 2,5 2 10x  7x  2  1  Câu 11. Biết rằng 2
F(x)  (ax  bx  c) 2x 1 là một nguyên hàm của f (x)  trên ;   . 2x 1  2 
Tính giá trị biểu thức a + b + c. 12 A. 3 B. 0 C. – 6 D. – 2
Câu 12. Tính giá trị f (2) khi hàm số y  f (x) luôn nhận giá trị khác 0 trên (0;) và thỏa mãn các điều kiện x  f  x   f x 2 2 2 2 ( 1) ( ) ( ) (x 1); f (1)  2 . A. 0,4 B. – 0 ,4 C. – 2,5 D. 2,5
Câu 13. Hàm số y  f (x) thỏa mãn 2 2 2
f (1)  2; f (x)  0; (x 1) f (
 x)  f (x).(x 1) với x  0 . Tính giá trị biểu thức f (2) . A. 0,4 B. – 0,4 C. – 2,5 D. 2,5  2
Câu 14. Cho hàm số y  f x liên tục trên R thỏa mãn (3cos x  4sin x) f ( 3sin x  4cos x  5 )dx  1  . 0 2 Tính tích phân 2 (x 1) f (x  2x 1)dx  . 1 A. – 2 B. – 4 C. 1 D. – 0,5
Câu 15. Hai hàm số f (x), g(x) xác định trên R thỏa mãn 2 2 f (0)  g (0)  1và f (
 x)  g(x); g (x)  f (x) . 1 Tính tích phân 2 2  f (x)  g (x) dx   .  A. 1 B. 2 C. 0 D. – 1 1 2
Câu 16. Hàm số y  f (x) có đạo hàm trên [0;2] thỏa mãn f (  x)  ; f (2)  1. Tính 2 f (x)dx  . 2 3 f (x) 1 0 1 14 11 A. 1 B. C. D. 3 15 12 2x  f (  x) 1
Câu 17. Đa thức bậc bốn y  f (x) đạt cực trị tại x  2; x  3và lim  4 . Tính f (x)dx  . x0 5x 0 A. 2,25 B. 2,75 C. 4,75 D. 5,5 2 1 f (2x)
Câu 18. Tính tích phân f xdx 
khi f  x là hàm số chẵn trên R thỏa mãn dx  8  . 1 5x 0 1  A. 8 B. 2 C. 1 D. 16  6 2 e f (ln x )
Câu 19. Hàm số f (x) liên tục trên 0; và 2 f (cos x)sin 2xdx  2; dx  6   . x 0 1 3
Tính tích phân ( f (x)  2)dx  . 1 A. 16 B. 9 C. 5 D. 10 2
Câu 20. Hàm số y  f (x) có đạo hàm trên R thỏa mãn 4 f (  x)  x 
 2x với x  0 và f (1)  1  . Mệnh đề 2 x nào sau đây đúng ?
A. Phương trình f (x)  0 có một nghiệm trên (0;1).
B. Phương trình f (x)  0 có đúng ba nghiệm trên (0;) .
C. Phương trình f (x)  0 có một nghiệm trên (1;2)
D. Phương trình f (x)  0 có một nghiệm trên (2;5).
_________________________________ 13
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 7)
__________________________________________________ Câu 1. Cho 2 f (4x)dx  x  3x  C  . Tính a + b biết rằng 2
f (x  2)dx  ax  bx  C  . A. 5,5 B. 4,25 C. 4,5 D. 2
Câu 2. Hàm số f (x) có đạo hàm liên tục trên [0;1] thỏa mãn  f  x 2 2 2
( )  3 f (x)  11x  22x 14; f (1)  5 . 1
Khi đó tích phân 4 f (x)  9 f (x)dx 1993gần nhất số nào 0 A. 2030 B. 2020 C. 2033 D. 2026 1
Câu 3. Hàm số f (x) liên tục trên [0;1] thỏa mãn 2 2 3 2
f (x)  2xf (x )  3x f (x )  1 x . Tính f (x)dx  . 0     A. B. C. D. 4 24 36 12
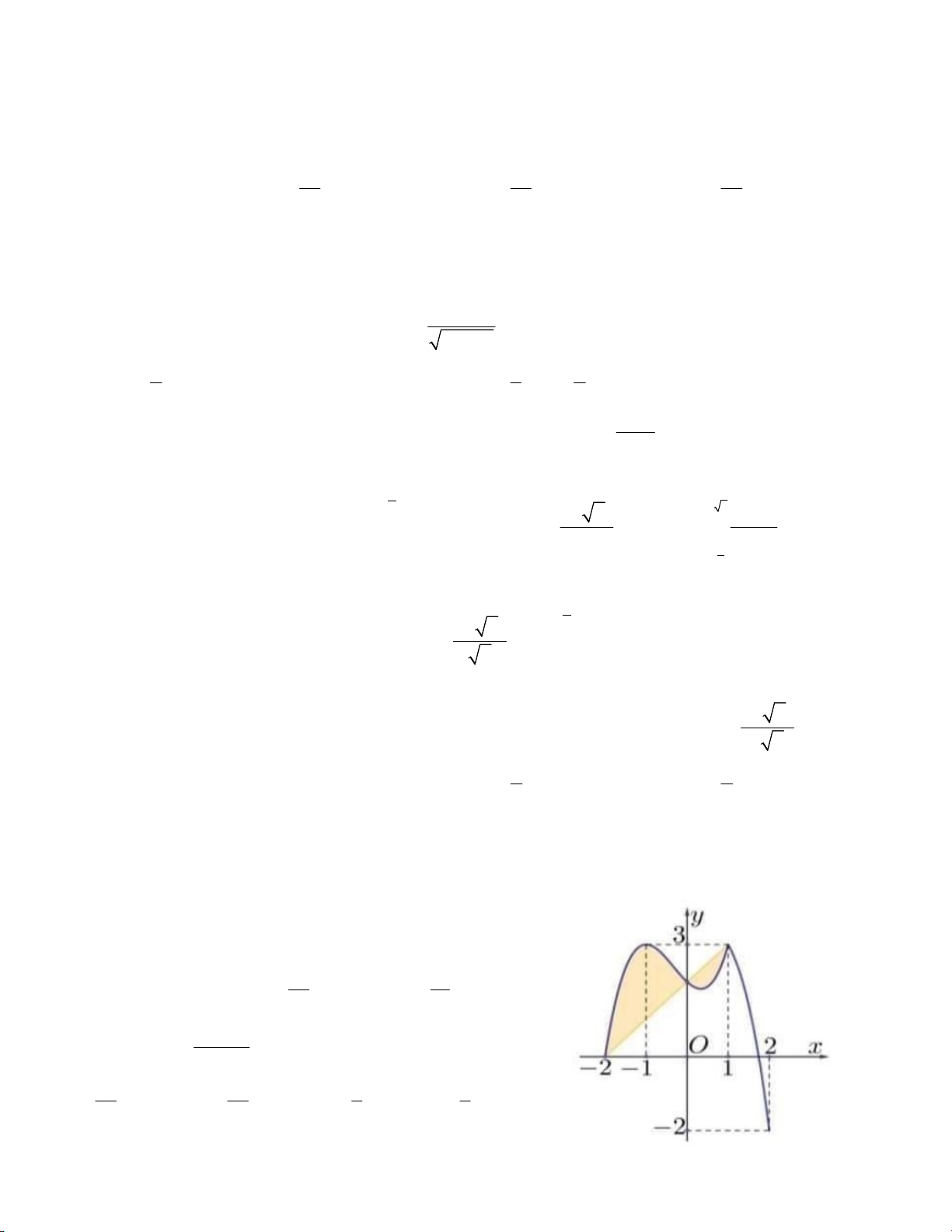
Câu 4. Cho hàm số y  f x có đồ thị như hình vẽ bên. Biết rằng
diện tích hình phẳng tô đậm bằng 3.  2
Tính tích phân cos xf (3sin x 1)dx  . 0 A. 1 B. – 1 C. 9 D. – 9 3 8 f (x) 8
Câu 5. Hàm số f (x) liên tục trên R sao cho 2 f ( x 16  x)dx  2019; dx  1   . Tính f (x)dx  . 2 x 0 4 4 A. 2019 B. 4022 C. 2020 D. 4038 8
Câu 6. Cho hàm số y  f  x thỏa mãn f  3 x  6x  
1  5x 1. Tính tích phân 4 xf   xdx . 1 A. 30 B. 85 C. – 20 D. – 17 Câu 7. Tính 2 f   2
1  f 2 khi hàm số f  x xác định, liên tục và luôn nhận giá trị dương trên [0;2], đồng thời 2  f x 
f 0  1; f 0  2 2 ; f  x. f   x      f    x   . x 2     A. 20 B. 10 C. 15 D. 25 3 1 3
Câu 8. Hàm số f (x) có đạo hàm liên tục trên  thỏa mãn 2 f (3)  ; x f (x)dx  5  . Tính 3 x f (  x)dx  . 3 0 0 A. 5 B. 6 C. – 5 D. – 6 a a f (x)
Câu 9. Hàm số f  x là hàm số chẵn, liên tục trên [– a;a]. Tính f
 xdxtheo tích phân M  dx  . x b 1 a 0 A. M B. M C. M – 1 D. – M 2 1
Câu 11. Hàm số y = f (x) liên tục trên R thỏa mãn f (2x)  3 f (x). Tính f (x)dx  nếu f (x)dx  1  . 1 0 A. 5 B. 3 C. 8 D. 2 14 2 4
Câu 12. Hàm f (x) có đạo hàm liên tục trên  và xf (x  2)dx  5; f (4)  1  . Tính 2
x f (x)  4 f (x) dx   . 2  0 A. – 6 B. 4 C. – 10 D. 6 41 37 3
Câu 13. Cho hàm số y  f x liên tục trên [0;41] và f  xdx 13; f  xdx  26. Tính f  13x 2 dx. 0 0 3  2 10 A. B. 3 C. D. 2 7 7 4 m Câu 14. Biết rằng 72. max 
 2x 2x 1;x  1dx  83. 2mx3dx 
, giá trị tham số m thu được thuộc khoảng 0 2 nào sau đây A. (2;4) B. (4;7) C. (7;12) D. (12;15) 2 2 1
Câu 15. Hàm số f (x) liên tục trên [0;2] thỏa mãn f (1)  4; x f (x)dx  ;   f (x)2 2 dx  36 . 5 0 0 2 Tính tích phân f (x)dx  . 0 5 3 2 A. B. C. 4 D. 6 2 3
Câu 16. Hàm số f (x) liên tục trên R thỏa mãn f    f  x 2 2 (1) 1;
( )  4 f (x)  8x 16x  4 . 1
Tìm số nghiệm của phương trình f ( f (x))  f (x)dx  2020  . 0 A. 3 B. 4 C. 2 D. 1 6x  f (  2x) 1
Câu 17. Đa thức bậc bốn y  f (x) đạt cực trị tại x  1; x  2và lim  3 . Tính f (x)dx  . x0 6x 0 A. 2 B. 2,5 C. 0,75 D. 4
Câu 18. Cho hàm số y  f x , hàm số y  f  xcó đồ thị như
hình vẽ bên. Biết rằng diện tích hình phẳng giới hạn bởi trục Ox và đồ
thị hàm số y  f  x trên đoạn [- 2;1] và [1;4] lần lượt bằng 9 và 12.
Cho f (1) = 3, giá trị biểu thức f (-2) + f (4) bằng A. 21 B. 9 C. 3 D. 2 0 2 6
Câu 19. Hàm số f  x là hàm số lẻ, liên tục trên [– 6;6] và f  xdx  6; f   3
 xdx  3 . Tính f xdx  . 3  1 0 A. – 6 B. 2 C. 3 D. – 3 2 f (x) 1 2 1 Câu 20. Tính dx 
khi hàm số f  x là hàm chẵn liên tục trên R thỏa mãn f  xdx  f  xdx 1. 1 3x 2 2  0 1 A. 1 B. 6 C. 4 D. 3 1 1
Câu 21. Cho f x liên tục trên R;  3x  4x 5 f xdx  8; 2 f  1 f 0  8 . Tính 2 Q  (3x  4) f  xdx. 0 0 A. 14 B. 32 C. 69 D. 21
_________________________________ 15
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 8)
__________________________________________________ 5
Câu 1. Hàm số y  f (x) xác định trên R thỏa mãn 2
f (x)  f (x  2)  x  2x 1. Tính f (x)dx  . 1 37 43 44 A. 12 B. C. D. 3 3 3 
Câu 2. Hàm số y  f (x) xác định trên R thỏa mãn f (  x)  2 f (x)  3sin x . Tính f (x)dx  . 0 A. 18 B. 6 C. 2 D. 3 1 dx
Câu 3. Tìm điều kiện tham số m để I  1với I  ;m  0  . 2x  m 0 1 1 1 A. 0  m  B. m > 0,25 C.  m  D. m > 0 4 8 4 f (x)
Câu 4. Hàm số f (x) có đạo hàm liên tục trên (0;) thỏa mãn f (  x)ln x   2x . Tính f (e). x A. e + 1 B. 2e – 3 C. e2 – 1 D. 2e2 – 7  3 8 3 f ( x) 2 2 f (x )
Câu 5. Hàm số f (x) liên tục trên R sao cho 2 tan . x f (cos x)dx  dx  6   . Tính dx  . x x 0 1 1 2 A. 4 B. 6 C. 7 D. 10  16 2 f ( x) 4
Câu 6. Hàm số f (x) liên tục trên 0;thỏa mãn
dx  6; f (sin x)cos xdx  3   . Tính f (x)dx  . x 1 0 0 A. – 2 B. 6 C. 9 D. 2 ln 2 4 f ( x)
Câu 7. Hàm số f (x) liên tục trên [1;2] sao cho f (x)  f (3  x) và 2 x ( x e f e )dx  1  . Tính dx  . 2 x 0 1 2 3 A. 2 B. 1 C. D. 3 2 2
Câu 8. Hàm số y = f (x) liên tục trên R thỏa mãn 2
f (x)  f (2  x)  6x  3x . Tính f (x)dx  . 0 A. 2 B. 1 C. 2,5 D. 4
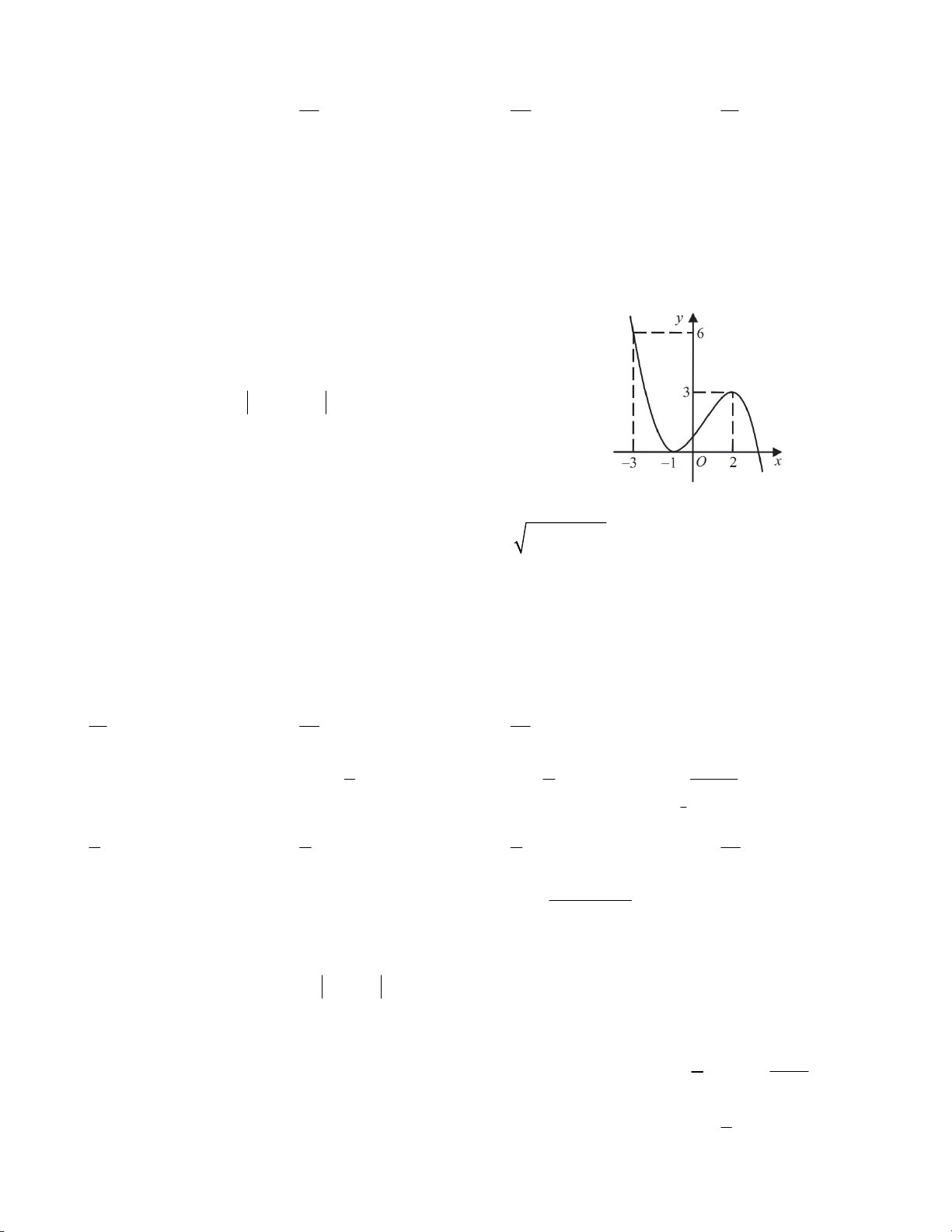
Câu 9. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Biết 37 0 14
rằng diện tích phần tô màu là và f (x)dx   . 12 3 2  e f (ln x) Tính tích phân dx  . x 1 25 12 8 3 A. B. C. D. 12 25 3 8
Câu 10. Hàm số bậc hai y  f (x) xác định trên R thỏa mãn f (x  2)  f (x 1)  2x  4 . 16 m
Tính tổng các hệ số của đa thức Q(m)  [ f  (  x)  f (x)]dx 
với m là tham số dương. 0 17 35 11 A. 2 B. C. D. 3 6 3
Câu 11. Hai hàm số y  f (x), y  g(x) xác định và có đạo hàm trên [1;2] thỏa mãn
 f (x)  xg (x)  0; 4g(x)  xf (x)  0   f (1)  2g(1)  3 2
Tính tích phân [ f (x)  2g(x)]dx  . 1 A. 3 B. 1,5 C. 2,5 D. 2
Câu 12. Cho hàm số y  f  x liên tục, có đạo hàm trên R và có đồ thị 1
như hình vẽ bên. Tính f (  5x  3) dx  . 0 A. 2 B. 3 C. 9 D. 1,8
Câu 13. Hàm số f  x xác định và liên tục trên R, đồng thời thỏa mãn f  x
 f 0 1; f x  4xf x ln ef   x min  với mọi x thuộc R.
Tính tổng các nghiệm của phương trình   2 ln f x  m . A. – m B. – 2 C. m D. 0
Câu 14. Hàm số y  f (x) xác định trên R thỏa mãn 2 4 11 9 4 3
f (x)  x f (1 x )  2x  3x  x  5x  2x  3 . 0 Tính tích phân f (x)dx  . 1  11 41 41 A. B. C. D. 4 3 12 15 1   1  3 f (x)
Câu 15. Hàm số y = f (x) liên tục trên ;3  thỏa mãn 3 f (x)  xf  x  x   . Tính dx  . 3     x  2 x  x 1 3 8 2 3 16 A. B. C. D. 9 3 4 9 4x 1 1
Câu 16. Hàm số y  f (x) có đạo hàm trên [0;1] thỏa mãn f (  x)  . Khi đó 3 xf (x)dx  gần nhất với 2 3 f (x)  2 0 A. 0,52 B. 0,19 C. 0,12 D. 1,25 m
Câu 17. Cho số thực m thỏa mãn 2mx 1 dx  1 
. Tham số m thu được thuộc khoảng nào sau đây 1 A. (4;6) B. (2;4) C. (3;5) D. (1;3) 2 2 2 2 f (x)
Câu 18. Hàm số f (x) liên tục trên [0;2] thỏa mãn f (2)  1; f (x)dx   f (x)2 dx    . Tính dx  . 3 2 x 0 0 1 1 A. 1 B. 2 C. 0,25 D. 3
_________________________________ 17
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 9)
__________________________________________________ 2 2 1 1
Câu 1. Hàm số f (x) liên tục trên [0;2] thỏa mãn f (2)  0; (x 1) f (x)dx   ;  f (x)2 dx    . 30 45 1 1 2 Tính tích phân f (x)dx  . 1 1 1 1 1 A.  B.  C.  D. 36 15 12 12 1
Câu 2. Hàm số f (x) liên trục trên [0;1] thỏa mãn xf  2 x   f   x 2 4 3 1  1 x . Tính f xdx  . 0     A. B. C. D. 20 6 16 4 2 132 . x f (x)
Câu 3. Tồn tại hai hàm số y  f  x liên tục trên 1; và 2 f ( 3x 1  x)dx  4; dx 2   . 2 1 1 3x  2 132 Tích phân f (x)dx 
có thể nhận hai giá trị A, B với A > B. Tính 2A + B. 1 A. 14 B. 6 C. 18 D. 7
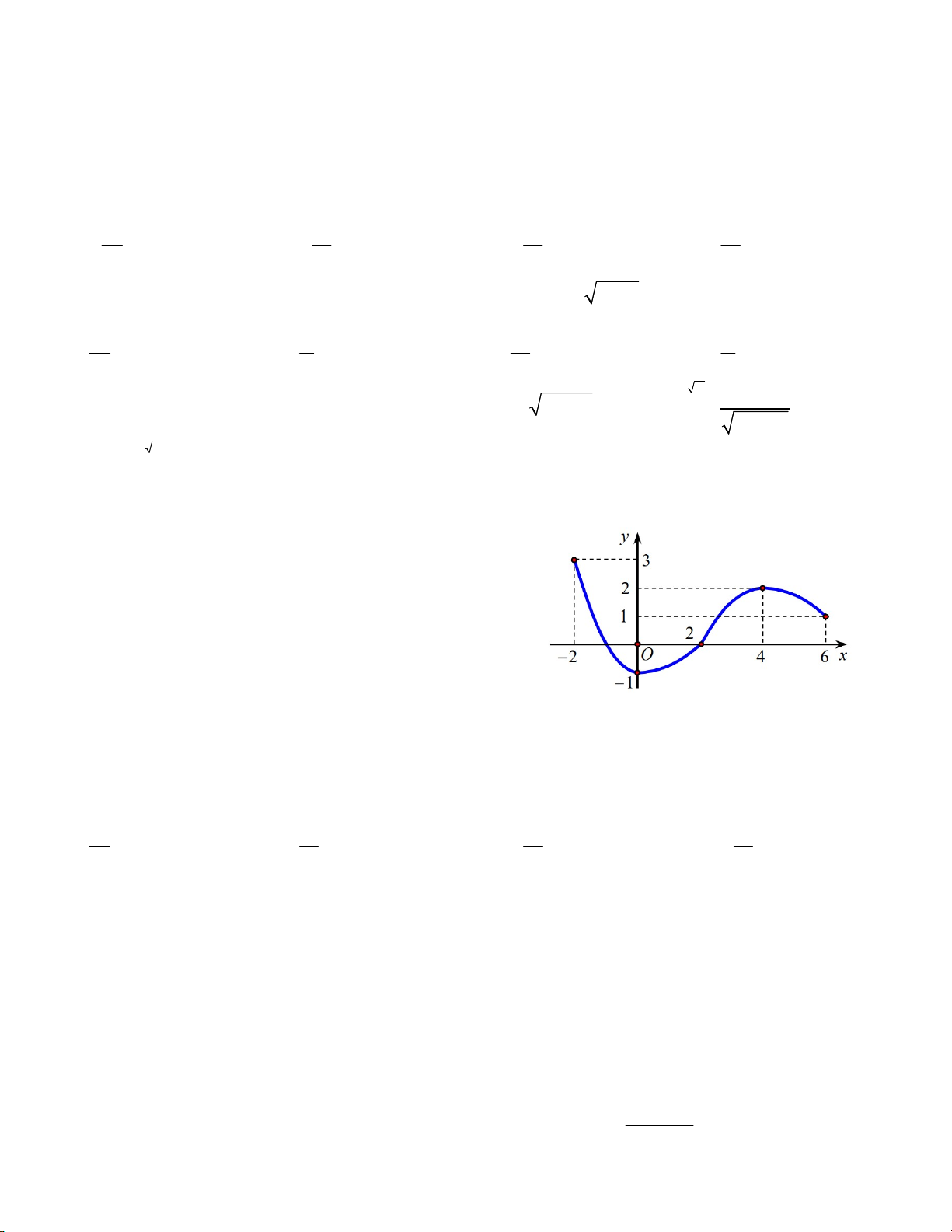
Câu 4. Hàm số y  f  x có đạo hàm liên tục trên R. Hàm số
y  f  x trên đoạn [– 2;6] có đồ thị như hình bên. Tìm giá trị
lớn nhất của hàm số y  f  x trên đoạn [– 2;6].
A. f (2) B. f (1) C. f (6) D. f (2) 1 Câu 5. Tính f (x)dx 
nếu hàm số f (x) liên tục trên R thỏa mãn f (1)  1 và 0  f  x 2 2 6 4 2
( )  4(6x 1) f (x)  40x  44x  32x  4 . . 23 13 17 7 A. B. C.  D.  15 15 15 15 1 Câu 6. Tính f (x)dx 
khi hàm số f (x) có đạo hàm liên tục trên [0;1] thỏa mãn 0 1 1   2 9 x 3 f (0)  0; f (x)dx  ; f (  x)cos dx    . 2 2 4 0 0 A. 6 B. 2 C. 4 D. 1 3 a Câu 7. Biết 3x   1 ln  2 3x  2x  
1 dx  a ln 34  ln17  ; c a,b  
 . Tính S  a  2b  4c . b 2 A. S  55 B. S  42 C. S  72 D. S  30 4 1 2x. f (4x) Câu 8. Tính tích phân f
 xdx khi f x là hàm số chẵn trên R thỏa mãn dx  5  . 2x  3x 4  1  A. 40 B. 20 C. 10 D. 5 18 1
Câu 9. Cho hàm số f  x liên tục trên R sao cho 3
x  f (x)  2 f (x)  1. Tính f (x)dx  . 2  A. 1,75 B. 1,25 C. – 1,75 D. 3,5
Câu 10. Cho hàm số y  f x liên tục trên  thỏa mãn 2 2
f (x  3)  (x  x 1). f (4  x) . 1
Tính tích phân (x  2) f (x)  f  (x)dx . 0 77 7 17 A. 1 B.  C.  D.  6 6 3     2 f x
Câu 11. Hàm số y = f (x) liên tục thỏa mãn f  x 1 1 2  f  3x, x   ;2   . Tính dx  . x 2      x 1 2 A. 1,5 B. 4,5 C. – 4,5 D. 3 3
Câu 12. Tính giá trị gần đúng của f (x)dx 
biết hàm số y  f (x) liên tục trên [1;3] thỏa mãn 0 f  x   f x 2 2 2 ( ). 1
( )  f (x).(x 1) ; f (1)  1  ; f (x)  0, x  0;  3 .
A. – 1,09 B. – 2,56 C. – 6,25 D. 4,16
Câu 13. Hàm số y  f (x) liên tục trên  thỏa mãn 2 2 2 f (x). f (
 x) 108x  (8x  9) f (x)  (4x  9x) f (x) . 1
Tính 4 f (x)  9 f (x)dx biết rằng đồ thị hàm số y  f (x)đi qua gốc tọa độ và tiếp tuyến của đồ thị luôn cắt 0 trục hoành. A. 99 B. 100 C. 49 D. 1993 2
Câu 14. Tính f (x)dx  min f (x) 
khi hàm số y  f (x) thỏa mãn 3;4 2  3 2 2
f (x)  2(2x 1) f (x)  3x  2 ; x f (x)dx  3  . 0 A. 2 B. 8 C. 4 D. 6 2 x
Câu 15. Hàm số y  f (x) liên tục trên R thỏa mãn 2 x 4 f (t)dt  e  x 1  . Tính f (4) . 0 A. 4 e + 4 B. 4 4 e C. 4 e + 8 D. 1 2 e
Câu 16. Hàm số y  f (x) thỏa mãn 2 2 1 x f (
 x).ln x  xf (x)  ln (x)  0; f (e)  . Tính f (x)dx  . e e A. 2 B. 1,5 C. 3 D. 2,5 1 1
Câu 17. Hàm số y  f (x) liên tục và có đạo hàm trên [1;e] thỏa mãn 2 f (1)  ; xf (
 x)  xf (x)  3 f (x)  . 2 x
Tính giá trị biểu thức f (e). 3 4 3 2 A. B. C. D. 2e 3e 4e 3e 3 2
Câu 18. Hàm số y  f (x) thỏa mãn  f x 2 2
( )  3x  2x 1  4xf (x) và f (x)dx  12  . Tính f (x)dx  . 1  0 A. 6 B. 7 C. 8 D. 5
_________________________________ 19
VẬN DỤNG CAO, PHÂN LOẠI NGUYÊN HÀM, TÍCH PHÂN LỚP 12 THPT
(LỚP BÀI TOÁN TỔNG HỢP – PHẦN 10)
__________________________________________________
Câu 1. Cho hàm số y  f  x có đồ thị như hình vẽ bên. Biết rằng diện
tích các phần (A), (B) lần lượt bằng 3 và 7.  2 Tính tích phân cos . x f (5sin x 1)dx  . 0
A. 2 B. 0,8 C. – 0,8 D. – 2 1
Câu 2. Trên [0;1], hàm số y  f (x) thỏa mãn 3
x   xf   x  f x  5 1. 4 (1 ) ( )  x . Khi đó f (x)dx  có giá trị gần 0 nhất số nào sau đây ? A. 0,0434 B. 0,0548 C. 0,5482 D. 0,1873
Câu 3. Hàm số y  f (x) thỏa mãn 4 2 3 f ( x) 3 ( ). (  ). x x f x f x e  (2x 1) ; e f (0)  1. 1
Giá trị nhỏ nhất của biểu thức 5 f (x)dx  f (x) 
gần nhất giá trị nào sau đây 0 A. 0,94 B. 1,72 C. 3,65 D. 2,34
Câu 4. Trên [1;2] , hàm số y  f (x) có f (
 x)  5x thỏa mãn x f  x  x2 2 ( ) 5
 5  f  (x); f (1)  6 .
Tính giá trị biểu thức f (2)  f (1). A. 5 B. 8 C. 7 D. 6 1
Câu 5. Hàm số f  x là hàm số chẵn, liên tục trên R thỏa mãn f (x)dx  2018 
, hàm số g(x) là hàm số liên 0 1
tục trên R thỏa mãn g(x)  g(x)  1. Tính tích phân f (x)g(x)dx  . 1  A. 2018 B. 504,5 C. 4036 D. 1008 2 2m 2 a
Câu 6. Biết giá trị nhỏ nhất của 2 2 3 S 
x  2(m  m 1)x  4m  m dx 
là phân số tối giản . Tính a + b. b 2m A. 7 B. 337 C. 25 D. 91
Câu 7. Với m là tham số thực thuộc [1;3]. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2m 2 2 P  (x  2 ) m (x  m) dx  . m 122 121 A. 31 B. 36 C. D. 15 4 m
Câu 8. Có bao nhiêu số nguyên m < 100 để phương trình 2 (2x 1)dx  x  3x  4 
có hai nghiệm phân biệt ? 0 A. 98 B. 96 C. 97 D. 95 4 1 10x 1
Câu 9. Hàm số y  f (x) có đạo hàm trên [0;1] thỏa mãn 4 f (  x)  ; 15. f (x)dx  f (1)  1  . 4 5 f (x)  2 0 1 Tính 4 4 x f (x)dx  . 0 20 14 14 4 13 A. B. C. D. 15 45 45 15 1
Câu 10. Tính tích phân f (x)dx 
khi hàm số y  f (x) có đạo hàm trên [0;1] thỏa mãn f (1)  1; f (  0)  0 và 0
f  x  f  x  x   2 ( ) 2 ( ) 4 1  f  (
 x) 2 f (x)  x 1  2 f (x)    1. 1 A. 1 B. 2 C. 1,5 D. 3
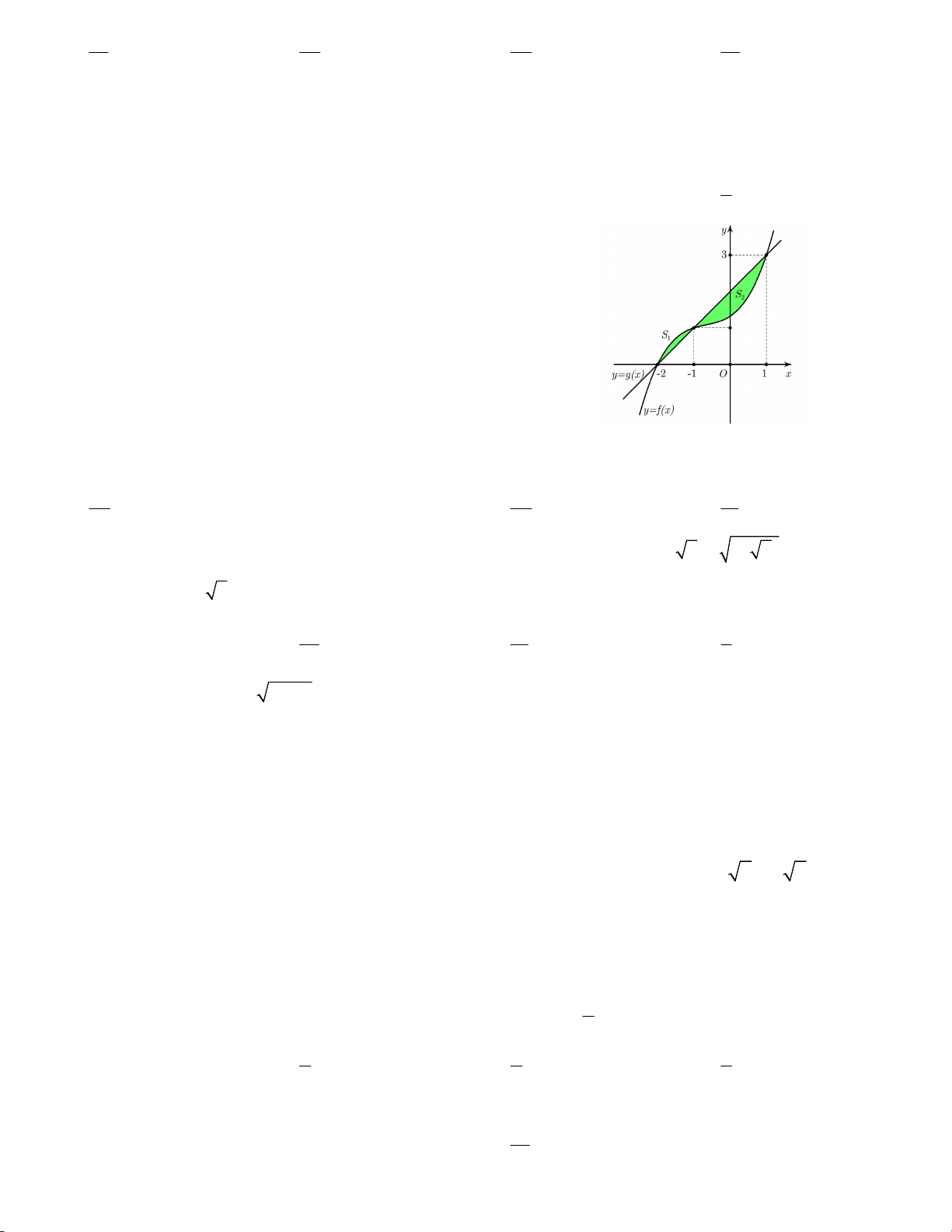
Câu 11. Cho hàm số y  f  x xác định và liên tục trên [– 2;1]. Biết
rằng diện tích hình phẳng S , S giới hạn bởi đồ thị và đường thẳng 1 2 1
y  ax  b lần lượt là m, n. Tính tích phân f (x)dx  . 2  A. m – n + 4,5 B. m + n + 2 C. n – m + 4,5 D. m + n + 1 1
Câu 12. Cho f x liên tục trên R sao cho 5 5
f (x)  2x  x  2 f (x) . Tính 4 2 (10x 1) f (x)dx  . 0 29 22 11 A. B. 1 C. D. 21 3 3
Câu 13. Cho hàm số f  x nhận giá trị không âm và liên tục trên 0; sao cho f ( x)  f ( x)  2x . 1 Tính tích phân f ( x)dx  . 0 A. 1 B. 5 C. 5 D. 5 24 12 6 2 Câu 14. Giá trị I  min
  3x 1;2 xdxgần nhất với giá trị nào sau đây ? 0 A. 4,5 B. 3,3 C. 2,7 D. 7,1
Câu 15. Tính giá trị biểu thức f (2) khi hàm số y  f (x) có đạo hàm liên tục trên R và thỏa mãn
x  f  x 3   f x  4 6 ( ) 27 ( ) 1  0 ; f (1)  0. A. 1 B. – 1 C. 7 D. – 7   2 
Câu 16. Cho hàm số f (x) thỏa mãn sin . x f (x)dx  20; xsin . x f (  x)dx  5;   Tính cos( x). f ( x)dx  . 0 0 0 A. 25 B. 15 C. – 50 D. – 30 1 Câu 17. Tính f (x)dx 
khi hàm số f (x) liên tục trên  và thỏa mãn điều kiện 0 1 3 sin . x f (cos x)  cos .
x f (sin x)  sin 2x  sin 2x . 2 1 2 1 A. 1 B. C. D. 6 3 3
Câu 18. Cho hàm số f (x) thỏa mãn 3 f (0)  4; f (x)  f (  x)  x . Tính f (1) . 10 A. – 10 B. – 2 C.  2 D. 10e  4 e
_________________________________ 21