Hệ thức lượng trong tam giác vuông – Lương Anh Nhật

Tài liệu gồm 31 trang, được biên soạn bởi thầy giáo Lương Anh Nhật, trình bày lý thuyết, các ví dụ minh họa và bài tập chuyên đề hệ thức lượng trong tam giác vuông (Toán 9 phần Hình học). Mời bạn đọc đón xem.

40 20 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hệ thức lượng trong tam giác vuông

Môn: Toán 9

Thông tin:

31 trang 3 tháng trước

Tác giả:

Profile Hà Việt Anh
GV. LƯƠNG ANH NHẬT
1
GV. LƯƠNG ANH NHẬT
CHƯƠNG
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
I
H
C
B
K
VỮNG KIẾN THỨC – NHẠY TƯ DUY
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 1
CHƯƠNG I HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
BÀI 1: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
I. Đặt vấn đề
Cho tam giác ABC vuông ở A có AH là đường cao. Chứng minh
a)
2
.AB BH BC=
,
2
.AC CH CB=
.
b)
..AB AC AH BC=
.
c)
2
.AH BH CH=
.
d)
222
1 1 1
AH AB AC
=+
.
Giải
a) Xét hai tam giác vuông ABH và CBA có
ABH
chung nên
ABH CBA∽
(g.g)
Suy ra
2
.
AB BH
AB BH BC
BC AB
= =
Tương tự, cũng có
2
.AC CH CB=
b) Vì
HBA ABC∽
(cmt)
nên
..
AH AB
AB AC AH BC
AC BC
= =
c) Xét hai tam giác vuông ABH và CHA có
HAB ACH=
(cùng phụ
ABC
)
Nên
AHB CHA∽
(g.g)
Suy ra
2
.
AH BH
AH BH CH
CH AH
= =
d) Ta có
2 2 2
2 2 2 2 2
11
..
.
..
BC BC AB AC
AH BC AB AC
AH AB AC
AH AB AC AB AC
+
= = = =
Vậy
222
1 1 1
AH AB AC
=+
.
H
C
B
A
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
2 – EDUCATION _ Vững kiến thức – Nhạy tư duy
II. Một số hệ thức về cạnh và đường cao trong tam giác
Từ kết quả của phần trên, ta suy ra
• Định lý 1: Trong một tam giác vuông, bình phương của cạnh góc vuông bằng tích của
cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
• Định lý 2: Trong một tam giác vuông, tích hai cạnh góc vuông bằng cạnh huyền nhân với
đường cao tương ứng của cạnh huyền đó.
• Định lý 3: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng
tích hình chiếu của hai cạnh góc vuông trên cạnh huyền.
• Định lý 4: Trong một tam giác vuông, nghịch đảo bình phương đường cao bằng tổng
nghịch đảo bình phương của hai cạnh góc vuông.
Ta dùng các kết quả nêu trên như là một công thức và được phép sử dụng.
Ví dụ 1: Cho tam giác ABC vuông ở A có đường cao AH. Biết
12,5BH =
cm, và
72CH =
cm. Tính
AH, AB và AC.
Giải
Ta có
12,5 72 84,5BC BH CH= + = + =
Lại có
2
. 12,5.72 900 30 cmAH BH CH AH= = = =
2
. 12,5.84,5 1056,25 32,5 cmAB BH BC AB= = = =
2
. 72.84,5 6084 78 cmAC CH CB AC= = = =
Ví dụ 2: Cho tam giác ABC vuông tại A có AH là đường cao. Biết
40 cmAC =
,
24 cmAH =
. Tính
AB, BC, BH và CH.
Giải
Ta có
2 2 2 2
40 24 32 cmCH AC AH= − = − =
22
2
40
. 50 cm
32
AC
AC CH CB CB
CH
= = = =
2 2 2 2
50 40 30 cmAB BC AC= − = − =
22
2
30
. 18 cm
50
AB
AB BH BC BH
BC
= = = =
Ví dụ 3: Cho hình chữ nhật ABCD, qua A kẻ đường thẳng vuông góc với BD tại H. Biết
20 cmAB =
,
12 cmAH =
. Tính các cạnh còn lại và đường chéo của hình chữ nhật ABCD.
Giải
D
H
C
B
A
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 3
Ta có
2 2 2 2
20 12 14 cmHB AB AH= − = − =
Áp dụng
22
2
20 200
. cm
14 7
AB
AB BH BD BD
BH
= = = =
..AD AB AH BD=
200
12.
. 120
7
cm
20 7
AH BD
AD
AB
= = =
Ví dụ 4: Cho tam giác ABC vuông tại A, có đường cao AH. Biết
15 cmAB =
,
9 cmBH =
. Tính
diện tích tam giác ABC.
Giải
Ta có
22
2
15
. 25 cm 25 9 16 cm
9
AB
AB BH BC BC CH BC BH
BH
= = = = = − = − =
Khi đó
2
. 9.16 9.16 12 cmAH BH CH AH= = = =
Diện tích tam giác ABC là
2
11
. 12.25 150 cm
22
ABC
S AH BC= = =
Ví dụ 5: Cho tam giác ABC vuông ở A có AH là đường cao, phân giác AD. Biết
15 cmBD =
,
20 cmDC =
. Tính độ dài AD.
Giải
Ta có AD là đường phân giác của tam giác ABC
Suy ra
15 3
20 4
AB BD
AC CD
= = =
Đặt
3
4
AB x AC x= =
với
0x
Lại có
35 cmBC BD CD= + =
Áp dụng định lý Pytago, ta có
2
2 2 2 2 2 2 2 2
3 25
35 35 784 28
4 16
AB AC BC x x x x x

+ = + = = = =


D
H
C
B
A
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
4 – EDUCATION _ Vững kiến thức – Nhạy tư duy
28 cmAB=
và
21 cmAC =
Áp dụng
22
2
28 112
. cm
35 5
AB
AB BH BC BH
BC
= = = =
112 37
15 cm
55
HD BH BD = − = − =
Ta lại có
. 28.21 84
. . cm
35 5
AB AC
AH BC AB AC AH
BC
= = = =
Khi đó
22
2 2 2
84 37
337 cm
55
AD AH HD
= + = + =
.
Ví dụ 6: Cho tam giác ABC nhọn, hai đường cao BD và CE cắt nhau tại H. Trên đoạn HB lấy điểm
M sao cho
0
90AMC =
và trên đoạn HC lấy N sao cho
0
90ANB =
. Chứng minh
a)
..AD AC AE AB=
b)
AM AN=
Giải
a) Xét hai tam giác vuông ABD và ACE có
BAC
chung nên
ABD ACE∽
Suy ra
..
AB AD
AD AC AE AB
AC AE
= =
b) Xét tam giác vuông AMC có MD là đường cao nên
2
.MA AD AC=
xét tam giác vuông ANB có NE là đường cao nên
2
.NA AE AB=
Mà
..AD AC AE AB=
Do đó
22
MA NA AM AN= =
.
Ví dụ 7: Cho tam giác ABC cân tại A, hai đường cao AH và BK. Chứng minh
a)
2 2 2
1 1 1
4BK BC AH
=+
b)
2
2.BC CK CA=
N
M
E
D
H
C
B
A
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 5
Giải
a) Vẽ HI vuông góc AC tại I
Suy ra HI là đường trung bình của tam giác BCK
Nên
1
2
HI BK=
Xét tam giác AHC vuông tại H có HI là đường cao
2 2 2 2 2 2
1 1 1 1 1 1
22
HI HC AH AH
BK BC
= + = +
Suy ra
2 2 2 2 2 2
4 4 1 1 1 1
4BK BC AH BK BC AH
= + = +
b) Xét tam giác AHC có
2
2
22
. . . 2 .
2 2 4 2
BC CK BC CK
CH CI CA CA CA BC CK CA

= = = =


Bài tập
1.1 Cho tam giác ABC vuông ở A có AH là đường cao. Biết
13,6 cmAB =
,
25,5 cmAC =
. Tính
AH, BH và CH.
1.2 Cho tam giác ABC vuông ở A có AH là đường cao. Biết
15 cmAB =
,
16 cmCH =
. Tính độ dài
AC, BC và AH.
1.3 Cho tam giác ABC vuông ở A có AH là đường cao. Biết
28,9 cmBC =
,
12 cmAH =
. Tính độ
dài AB và AC.
I
K
H
C
B
A
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
6 – EDUCATION _ Vững kiến thức – Nhạy tư duy
1.4 Cho tam giác ABC có đường cao AH, trung tuyến AM và
5 cmAB =
,
12 cmAC =
và
13 cmBC =
. Tính độ dài AM và AH.
1.5 Cho tam giác ABC vuông tại A có AH là đường cao. Biết rằng
9
16
HB
HC
=
và
48 cmAH =
. Tính
AB, AB và BC.
1.6 Cho tam giác ABC vuông ở A có AH là đường cao. Biết rằng
3
4
AB
AC
=
và
125 cmBC =
. Tính
độ dài AH.
1.7 Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Biết tam giác ABM là tam giác
đều và có cạnh bằng
3
cm.
a) Tính độ dài AC và AH. b) Tính diện tích tam giác ABC.
1.8 Cho tam giác ABC cân tại A có
5 cmAB =
, đường cao
3 cmAH =
. Gọi M và N là trung
điểm của HC và AC. Tính độ dài AM và BN.
1.9* Cho tam giác ABC cân có
5 cmAB AC==
,
6 cmBC =
, các đường cao AH và BK. Vẽ tia Bx
vuông góc AB tại B. Gọi M là giao điểm của tia Bx và tia AC. Tính diện tích tam giác ABM (làm
tròn đến chữ số thập phân thứ nhất).
1.10 Cho hình vuông ABCD. Một điểm bất kỳ trên cạnh BC. Đường thẳng AI cắt DC tại K. Chứng
minh
22
11
AI AK
+
không phụ thuộc vào vị trí của điểm I trên cạnh BC (I không tùng với B và C).
1.11 Cho tam giác ABC vuông ở A có I là trung điểm AB. Kẻ IH vuông góc với BC tại H. Chứng
minh
222
1 1 1
4IH AB AC
=+
.
1.12 Cho hình thang ABCD vuông tại A và D, đường chéo AC và BD vuông góc nhau. Chứng
minh
2 2 2
1 1 1
AD AC BD
=+
.
1.13 Hình vuông ABCD có I thuộc cạnh BC (I khác B và C). Gọi K là giao điểm của hai đường
thẳng AI và DC. Chứng minh
2 2 2
1 1 1
AB AI AK
=+
.
1.14* Cho hình chữ nhật ABCD có AB = a, AD = b. Gọi H là hình chiếu của A trên BD và K, I lần
lượt là hình chiếu của H trên BC và CD. Chứng minh
a)
2
2
HB a
HD
b
=
b)
3
22
a
HK
ab
=
+
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 7
1.15 Cho tam giác ABC vuông tại A và
AB a=
. Các đường trung tuyến AM và BN vuông góc
nhau. Tính AC và BC theo a.
1.16 Cho tam giác ABC vuông ở A có AH là đường cao. Vẽ
HE AB⊥
,
HF AC⊥
. Chứng minh
a) AEHF là hình chữ nhật. d)
3
..AH EB BC CF=
b)
..AE AB AD AC=
e)
3
3
AB BE
CF
AC
=
c)
. . .EA EB FA FC HB HC+=
f)
32
32
BH BE
CH CF
=
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
8 – EDUCATION _ Vững kiến thức – Nhạy tư duy
BÀI 2: TỶ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
I. Khái niệm tỷ số lượng giác của một góc nhọn
_ Cho góc
xOy
=
. Từ điểm A trên Ox (A khác O) vẽ
AB Oy⊥
tại B.
Bên cạnh đó, ta lấy thêm các điểm C và E trên Ox rồi lần lượt vẽ
CD Oy⊥
tại D và
EF Oy⊥
tại F.
Ta thấy các tỷ số
AB CD EF
OA OC OE
==
,
OB OD OF
OA OC OE
==
,
AB CD EF
OB OD OF
==
và
OB OD OF
AB CD EF
==
Việc ta lấy thêm các điểm C và E cũng giống như việc tịnh tiến hay còn gọi là thay đổi vị trí của
A trên Ox
Như vậy, các tỷ sô ban đầu là
AB
OA
,
OB
OA
,
AB
OB
và
OB
AB
không phụ thuộc vào vị trí của A trên Ox
mà chỉ phụ thuộc vào độ lớn của
xOy
.
Ta gọi
_ Tỷ số
AB
OA
là sin của góc
và ký hiệu là
sin
.
_ Tỷ số
OB
OA
là côsin của góc
và ký hiệu là
cos
.
_ Tỷ số
AB
OB
là tang của góc
và ký hiệu là
tan
.
_ Tỷ số
OB
AB
là côtang của góc
và ký hiệu là
cot
.
Các tỷ số trên gọi chung là tỷ số lượng giác của góc
và các tỷ số này luôn dương. Hơn nữa, ta
cũng có
sin 1
và
cos 1
α
O
E
y
F
D
x
C
B
A
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 9
II. Tỷ số lượng giác của hai góc phụ nhau
_ Định lý: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia và tang góc này bằng côtang
góc kia.
Ví dụ 1: Cho
0
60
=
và
0
30
=
. Khi đó
sin cos

=
và
tan cot

=
.
III. Một số hệ thức cơ bản
Cho
là góc nhọn, ta có các hệ thức sau
a)
22
sin cos 1

+=
b)
sin
tan
cos
=
và
cos
cot
sin
=
c)
tan .cot 1

=
Ví dụ 2: Cho
là góc nhọn và
1
sin
3
=
. Tính các giá trị lượng giác còn lại của
.
Giải
2
2 2 2
1 2 2
sin cos 1 cos 1 sin 1
33

+ = = − = − =


1
sin 1 1
3
tan cot 2 2
cos tan
2 2 2 2
3


= = = =
IV. Bảng giá trị lượng giác của một số góc đặc biệt
Tỷ số lượng giác
0
30
0
45
0
60
sin
1
2
2
2
3
2
cos
3
2
2
2
1
2
tan
1
3
1
3
cot
3
1
1
3
Bài toán so sánh các giá trị lượng giác
Cho hai góc nhọn a và b, ta có
•
sin sina b a b
và
tan tanab
•
cos cosa b a b
và
cot cotab
Ví dụ 3: Sắp xếp các tỷ số dưới đây theo tỷ lệ tăng dần.
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
10 – EDUCATION _ Vững kiến thức – Nhạy tư duy
a)
0
sin40
,
0
cos28
,
0
sin68
,
0
cos88
.
b)
0
tan65
,
0
cot42
,
0
tan76
,
0
cot27
.
Giải
a) Ta có
0 0 0 0
sin 40 cos50 ,sin68 cos22==
khi đó
0000
cos88 cos50 cos28 cos22
Hay
0 0 0 0
cos88 sin40 cos28 sin68
.
b) Ta có
0 0 0 0
tan65 cot 25 ,tan76 cot14==
khi đó
0 0 0 0
cot42 cot27 cot25 cot14
Hay
0 0 0 0
cot42 cot27 tan65 tan76
.
Ví dụ 4: Hãy so sánh
sin
và
tan
;
cos
và
cot
với
là góc nhọn.
Giải
•
sin
và
tan
Ta có
sin
tan sin sin sin sin .cos 1 cos
cos
(đúng)
•
cos
và
cot
Ta có
cos
cos cot cos sin .cos cos sin 1
sin
(đúng)
Ví dụ 5: Tính giá trị các biểu thức sau
a)
2 0 2 0 2 0 2 0
sin 10 sin 20 ... sin 70 sin 80A = + + + +
.
b)
0
2 0 2 0 0 0
0
3sin54
sin 14 sin 76 tan 2 .tan88
cos36
B = + + −
.
Giải
a) Ta có
2 0 2 0 2 0 2 0
sin 10 sin 20 ... sin 70 sin 80A = + + + +
( ) ( ) ( ) ( )
2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
sin 10 sin 80 sin 20 sin 70 sin 30 sin 60 sin 40 sin 50= + + + + + + +
( ) ( ) ( ) ( )
2 0 2 0 2 0 2 0 2 0 2 0 2 0 2 0
sin 10 cos 10 sin 20 cos 20 sin 30 cos 30 sin 40 cos 40= + + + + + + +
1 1 1 1 4= + + + =
b) Ta có
0
2 0 2 0 0 0
0
3sin54
sin 14 sin 76 tan 2 .tan88
cos36
B = + + −
0
2 0 2 0 0 0
0
3sin54
sin 14 cos 14 tan2 .cot2 1 1 3 1
sin54
= + + − = + − = −
Ví dụ 6: Cho
tan 3a =
. Tính
cos sin
cos sin
aa
P
aa
+
=
−
.
Giải
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 11
cos sin
cos sin 1 tan 1 3
cos cos
2
cos sin
cos sin 1 tan 1 3
cos cos
aa
a a a
aa
P
aa
a a a
aa
+
+ + +
= = = = = −
− − −
−
.
Bài tập
Không dùng bảng giá trị lượng giác của một số góc đặc biệt cho các câu từ 2.1 đến 2.9
2.1 Cho
là góc nhọn và
2
sin
5
=
. Tính các giá trị lượng giác còn lại của
.
2.2 Cho
là góc nhọn và
3
cos
2
=
. Tính các giá trị lượng giác còn lại của
.
2.3 Cho
là góc nhọn và
tan 3
=
. Tính các giá trị lượng giác còn lại của
.
2.4 Cho
là góc nhọn và
cot 1
=
. Tính các giá trị lượng giác còn lại của
.
2.5 Cho
là góc nhọn và
cos x
=
. Tính các giá trị lượng giác còn lại của
.
2.6 Không dùng máy tính hãy sắp xếp các giá trị lượng giác sau theo thứ tự tăng dần
a)
0 0 0 0
sin 25 ,cos15 ,sin50 ,cos66
. b)
0 0 0 0 0
cot 35 ,tan 48 ,cot 44 ,tan 53 ,cot 39
.
2.7 Không dùng máy tính hãy so sánh các giá trị lượng giác sau
a)
0
sin32
và
0
tan32
b)
0
cos35
và
0
cot35
c)
0
sin25
và
0
cot55
d)
0
cos54
và
0
tan42
2.8 Không dùng máy tính hãy sắp xếp các tỷ số lượng giác sau theo thứ tự giảm dần
0 0 0 0
cot 36 ,tan72 ,cot21 ,sin54
2.9 Cho
tan 3a =
. Tính
22
sin cos
sin .cos
aa
P
aa
−
=
và
33
33
sin cos
sin cos
aa
Q
aa
−
=
+
.
2.10 Cho góc a nhọn. Biết
22
1
cos 2sin
4
aa−=
. Tìm giá trị góc a.
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
12 – EDUCATION _ Vững kiến thức – Nhạy tư duy
BÀI 3: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
I. Các hệ thức
_ Cho tam giác ABC vuông ở C, ta có các hệ thức lượng giác của góc A như sau
sin
BC
A
AB
=
cos
AC
A
AB
=
tan
BC
A
AC
=
cot
AC
A
BC
=
Định lý
• Trong một tam giác vuông mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối
hoặc côsin góc kề.
• Trong một tam giác vuông thì cạnh góc vuông này bằng cạnh góc vuông kia nhân với tan
góc đối hoặc côtang góc kề.
Cho tam giác ABC vuông ở C với
BC a=
,
CA b=
và
AB c=
khi đó
II. Giải tam giác vuông
_ Giải tam giác vuông là tìm tất cả các cạnh và các góc của tam giác vuông đó khi biết trước hai
cạnh hoặc một cạnh và một góc nhọn của nó.
Ví dụ 1: Giải tam giác ABC vuông ở C biết
4 cmAC =
và
3 cmBC =
.
Giải
Ta có
2 2 2 2 2
4 3 25 5 cmAB AC BC AB= + = + = =
00
3
sin 37 53
4
BC
A BAC ABC
AC
= = =
.
.sin .cosa c A c B==
.sin .cosb c B c A==
.tan .cota b A b A==
.tan .cotb a B a B==
B
A
C
c
b
a
B
A
C
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 13
Ví dụ 2: Cho tam giác ABC vuông ở C biết
13 cmAB =
và
0
23A =
.
Giải
Ta có
0 0 0
23 90 67A B A= = − =
0 2 2 2 2
.cos 13.cos23 12 13 12 5 cmAC AB A cm BC AB AC= = = − = − =
.
Ví dụ 3: Giải tam giác ABC vuông ở C biết
20 cmBC =
và
0
43A =
.
Giải
Ta có
0 0 0
43 90 47A B A= = − =
0
0
20
.cot 20.cot43 21 cm, 29 cm
sin
sin43
BC
AC BC A AB
A
= = = =
.
Ví dụ 4: Cho tam giác ABC có
0
75A =
,
0
45B =
và
6 cmAB =
. Tính diện tích tam giác ABC.
Giải
Ta có
0 0 0 0 0 0
180 180 180 75 45 60A B C C A B+ + = = − − = − − =
Vẽ
AD BC⊥
Xét tam giác vuông ABD ta có
0
2
sin 6.sin 45 6. 3 2 cm
2
AD AB B= = = = =
0
2
cos 6.cos45 6. 3 2 cm
2
BC AB B= = = =
Xét tam giác vuông ACD ta có
0
3
.cot .cot60 3 2. 6 cm
3
CD AD C AD= = = =
Do đó
3 2 6 cmBC BD CD= + = +
Vậy diện tích tam giác ABC là
( ) ( )
2
11
. .3 2. 3 2 6 3 3 3 1 cm
22
ABC
S AD BC= = + = +
.
Ví dụ 5: Cho tam giác ABC cân tại A, đường cao
BK h=
và
ABC
=
. Tính các cạnh của của tam giác theo h và
.
Giải
Tam giác ABC cân nên
ACB ABC
==
Ta có
.sin
sin sin
BK h
BK BC BC

= = =
Vẽ đường cao AH của tam giác ABC suy ra H là trung điểm
BC nên
2 2sin
BC h
BH CH
= = =
K
H
C
B
A
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
14 – EDUCATION _ Vững kiến thức – Nhạy tư duy
Trong tam giác AHC ta có
.cos
cos 2sin cos
CH h
CH AC AC
= = =
Do đó
2sin cos
h
AB AC

==
.
Ví dụ 6: Cho hình thang cân ABCD có AB//CD, biết
5 cmAB =
,
13 cmCD =
và BD vuông góc với
BC.
a) Tính độ dài đường cao BH của hình thang.
b) Tính diện tích hình thang.
c) Tính các góc của hình thang.
Giải
a) Kẻ AK vuông CD tại K, ta có
AKD BHC =
suy ra
DK CH=
Lại có ABHK là hình bình hành có một góc vuông nên ABHK là hình chữ nhật
Suy ra
5 cmHK AB==
13 5
4 cm
22
DC HK
DK CH
−−
= = = =
Như vậy
4 5 9 cmDH DK HK= + = + =
Xét tam giác DBC có
2
. 9.4 36 6 cmBH DH CH BH= = = =
.
b) Ta có
( ) ( )
2
11
. 5 13 .6 54 cm
22
ABCD
S AB CD BH= + = + =
.
c) Xét tam giác BHC có
0
63
tan 56 19'
42
BH
CC
CH
= = =
Suy ra
0
56 19'D =
và
0 0 0
180 56 19' 123 41'DAB CBA= = − =
.
Bài tập
3.1 Với góc a nhọn. Chứng minh
22
sin cos 1aa+=
,
sin
tan
cos
a
a
a
=
,
cos
cot
sin
a
a
a
=
và
tan .cot 1aa=
.
3.2
a) Giải tam giác ABC vuông tại A biết
5 cmAB =
và
8 cmAC =
.
b) Giải tam giác DEF vuông tại D biết
100 cmDE =
và
0
51E =
.
c) Cho tam giác ABC vuông tại A có
3BC AB=
. Tính giá trị
C
.
d) Cho tam giác ABC cân tại A có
3AB BC=
. Tính giá trị
B
.
3.3 Tính góc nhọn
biết rằng
sin cos

=
.
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 15
3.4 Một chiếc đò ở điểm A muốn băng ngang qua sông theo đường AH nhưng bị nước cuốn đến
điểm B cách H một đoạn bằng 50m. Tìm độ rộng của con sông và quãng đường đò đã đi với dữ
kiện được thêm ở hình dưới đây.
3.5 Một chiếc máy bay đang bay ở độ cao 900 m. Một người quan sát nhìn chiếc máy bay đó dưới
góc
0
40
=
(như hình bên dưới). Tính khoảng cách từ người quan sát đến máy bay.
3.6 Cho tam giác ABC có
0
60B =
,
15 cmAB =
,
20 cmBC =
. Tính độ dài các góc và các cạnh còn
lại của tam giác ABC.
3.7 Cho tam giác ABC có AH là đường cao. Biết
25 cmAB =
,
0
70B =
và
0
50C =
. Tính độ dài AH
và BC.
3.8 Cho tam giác ABC có
0
75A =
,
0
60B =
và
6 cmAB =
. Tính diện tích tam giác ABC.
3.9 Cho tam giác ABC có
0
60A =
,
0
45B =
và
12 cmAB =
. Tính diện tích tam giác ABC.
3.10 Cho hình thang ABCD (AB//CD). Biết
4 cmAB =
,
4 cmAH =
và
0
70D =
. Vẽ hai đường cao
AH và BK. Biết rằng
0
50KBC =
. Tính BC và DC.
3.11 Cho hình bình hành ABCD có BD vuông góc với BC. Biết
AB a=
và
A
=
. Tính diện tích
ABCD theo a và
.
30
0
H
B
A
40
0
H
B
A
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
16 – EDUCATION _ Vững kiến thức – Nhạy tư duy
3.12 Cho tam giác nhọn ABC có
0
75A =
,
0
60B =
,
AB c=
. Tính độ dài AC, BC theo c.
3.13* Cho tam giác ABC vuông ở C. Chứng minh
tan
2
A BC
AB AC
=
+
.
Áp dụng kết quả trên tính giá trị lượng giác của góc
0
15
.
3.14* Cho tam giác ABC nhọn. Chứng minh
sin sin sin
AB BC CA
C A B
==
.
Áp dụng kết quả trên tính giá trị lượng giác của góc
0
75
.
3.15 Cho tam giác nhọn ABC có hai đường cao BE và CD. Chứng minh
.cosDE BC A=
.
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 17
HƯỚNG DẪN MỘT SỐ BÀI TẬP CHƯƠNG I
BÀI 1: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TỎNG TAM GIÁC VUÔNG
1.1
Dùng Pytago tìm được
28,9 cmBC =
Áp dụng
..AB AC AH BC=
12 cmAH =
Áp dụng
2
.AB BH BC=
6,4 cmBH =
và
22,5 cmCH =
.
1.2 Đặt
22
16 . 16 64 289 9BH x BC x BH BC AB x x x= = + = + + = =
và tính được
12 cmAH =
,
25 cmBC =
và
20 cmCA =
.
1.3
Cách 1:
Đặt
28,9BH x CH BC x x= = − = −
( )
2
2
.
14,45 64,8025 22,5 hay 6,4BH CH AH x x x = − = = =
Như vậy có hai trường hợp và kết quả là
25,5 cmAB =
,
13,6 cmAC =
và ngược lại.
Cách 2:
Xét
222
BC AB AC=+
và
..AB AC AH BC=
Ta dùng
( )
( )
2
22
2
22
2.
39,1
11,9
2.
AB AC AB AC AB AC
AB AC
AB AC
AB AC AB AC AB AC
+ + = +
+ =

−=
+ − = −
hoặc
39,1
11,9
AB AC
AC AB
+ =
−=
Kết quả thu được như Cách 1.
1.4
Kiểm tra được
222
BC AB AC ABC= +
vuông tại A
Suy ra
1 13
cm
22
AM BC==
Áp dụng
60
. . cm
13
AH BC AB AC AH= =
1.5
Đặt
9
16
HB x HC x= =
, với
0x
Áp dụng
22
9
. 48 . 64 64 cm
16
AH HB HC x x x BH= = = =
và
36 cmCH =
.
Suy ra
100 cmBC BH CH= + =
Áp dụng
22
. 64.100 6400 80 cmAB BH BC AB AB= = = =
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
18 – EDUCATION _ Vững kiến thức – Nhạy tư duy
Áp dụng định lý Pytago suy ra
60 cmAC =
.
1.6
Đặt
3
4
AB x AC x= =
, với
0x
Áp dụng định lý Pytago có
2
2 2 2 2 2 2
3
125 10000 100
4
BC AB AC x x x x

= + = + = =


Suy ra
100 cmAB =
và
75 cmAC =
Áp dụng
.
. . 60 cm
AB AC
AH BC AB AC AH AH
BC
= = =
.
1.7
a) Ta có
2 3 cm
2
BC
AM BC= =
Áp dụng định lý Pytago
222
3 cmBC AB AC AC= + =
Áp dụng
.3
. . cm
2
AB AC
AH BC AB AC AH
BC
= = =
b)
2
1 3 3
. cm
22
ABC
S AH BC==
.
1.8
Áp dụng định lý Pytago
2 2 2
2 cmBH AH AC BH+ = =
2
2 cm cm
2
CH HM = =
Áp dụng định lý Pytago
2 2 2
14
cm
2
AM AH HM AM= + =
Gọi G là giao điểm AH và BN
G là trọng tâm tam giác ABC
M
H
C
B
A
G
N
M
H
C
B
A
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 19
Nên
13
cm
33
GH AH==
Áp dụng định lý Pytago
2 2 2
21 3 21
cm cm
3 2 2
BN GH BH BN BN BG= + = = =
1.9*
Tam giác ABC cân tại A có AH là đường cao nên AH cũng là đường trung tuyến
3 cm
2
BC
HB HC = = =
Xét tam giác ABH
Áp dụng định lý Pytago
2 2 2
4 cmAB AH BH AH= + =
Dùng diện tích tam giác ABC có
11
. . 4,8 cm
22
AH BC BK AC BK= =
Xét tam giác ABK
Áp dụng định lý Pytago
2 2 2
1,4 cmAB AK BK AK= + =
Xét tam giác ABM
Áp dụng
2
. 17,9 cmAB AK AM AM= =
Diện tích tam giác ABM là
2
1
. 42,9 cm
2
ABM
S BK AM=
.
x
K
M
H
C
B
A
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
20 – EDUCATION _ Vững kiến thức – Nhạy tư duy
1.10
Vẽ
AJ AI⊥
với J thuộc CD
Xét hai tam giác vuông ABI và ADJ có
AB AD=
và
AIB AJD=
nên
ABI ADJ =
Suy ra
2 2 2 2 2
1 1 1 1 1
AI AK AJ AK AD
+ = + =
Vì AD không đổi nên
22
11
AI AK
+
không đổi hay nó không
phụ thuộc vào vị trí của điểm I.
1.11 Tương tự Ví dụ 7 a)
Bạn đọc tự giải bằng cách vẽ thêm đường cao AK của tam
giác ABC.
1.12
Vẽ tia Ax vuông góc với AC và cắt CD
tại E
Xét tam giác vuông ACE
Áp dụng
222
1 1 1
AD AE AC
=+
Xét tứ giác ABDE, dễ thấy ABDE là
hình bình hành nên AE = BD.
Vậy
2 2 2
1 1 1
AD BD AE
=+
.
1.13
Qua A vẽ Ax vuông góc với AK
cắt đường thẳng CD tại M
Ta có
MAD BAI=
(cùng phụ
DAI
) do đó
ADM ABI AM AI = =
Xét tam giác MAK vuông tại A
K
J
D
C
B
A
I
x
E
D
C
B
A
I
x
M
D
C
B
A
K
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 21
Áp dụng
2 2 2
1 1 1
AD AM AK
=+
mà AB = AD và AM = AI (cmt)
Vậy
2 2 2
1 1 1
AB AI AK
=+
.
1.14
a) Xét tam giác ABD
Áp dụng
22
..AB BH BD a BH BD= =
Tương tự, cũng có
2
.b HD BD=
Chia hai vế, ta có
2
2
HB a
HD
b
=
b) Vì HK // DC (cùng vuông góc với BC)
Hệ quả định lý Ta-lét cho ta
..HK HB DC HB a HB
HK
DC HD BC BD
= = =
Mà
2 2 2 2 2
2 2 2
HB a HB HD a b BD a b
HD HB HB
b a a
+ + +
= = =
(dùng tính chất dãy tỷ số bằng nhau)
Suy ra
2
22
.BD a
HB
ab
=
+
Khi đó
2
3
22
22
.BD a
a
a
ab
HK
BD
ab
+
==
+
.
1.15
Gọi G là trọng tâm tam giác ABC
Khi đó
2
3
BG BN=
Tam giác ABC vuông tại A
G
N
M
C
B
A
I
H
D
C
B
A
K
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
22 – EDUCATION _ Vững kiến thức – Nhạy tư duy
Áp dụng
2 2 2
26
.
32
a
AB BN BG a BN BN= = =
Áp dụng định lý Pytago, ta có
22
2 2 2 2 2
32
2 2 2
a a a
AN AB BN AN a AN+ = = − = =
Áp dụng định lý Pytago, ta có
222
3BC AB AC BC a= + =
1.16
a) Tứ giác AEHF có ba góc vuông nên nó là hình chữ nhật.
b) Xét tam giác AHB có
2
.HA AE AB=
Xét tam giác AHC có
2
.HA AF AC=
Vậy
..AE AB AF AC=
c) Xét tam giác AHB vuông tại H có HE là đường cao nên
2
.HE EA EB=
Xét tam giác AHC vuông tại H có HF là đường cao nên
2
.HF FA FC=
Xét tam giác ABC vuông tại A có AH là đường cao nên
2
.AH HB HC=
Ta có
2 2 2 2
..EF HE HF EF EA EB FA FC= + = +
Tứ giác AEHF là hình chữ nhật nên
22
AH EF AH EF= =
Vậy
. . .EA EB FA FC HB HC+=
.
d) Xét tam giác ABC vuông tại A có AH là đường cao
Ta có
2 4 2 2
..AH BH CH AH BH CH= =
Xét các tam giác ABH và ACH vuông tại H lần lượt có HE và HF là đường cao
Ta có
2
.BH BE BA=
và
2
.CH CF CA=
Suy ra
4
. . . . . .AH BE BA CACF EB AB AC CF==
Mà
..AB AC AH BC=
do đó
43
. . . . .AH EB AH BC CF AH EB BC CF= =
.
H
F
E
C
B
A
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 23
e) Xét tam giác ABC vuông ở A có AH là đường cao
Ta có
2
.AB BH BC=
và
2
.AC CH BC=
Suy ra
2 4 2
2 4 2
AB BH AB BH
CH
AC AC CH
= =
Mà
2
.BH EB AB=
và
2
.CH CF AC=
Do đó
43
43
.
.
AB EB AB AB EB
CF AC CF
AC AC
= =
.
f) Ta có
2
.BH EB AB=
và
2
.CH CF AC=
nên
4 2 2
.BH EB AB=
và
4 2 2
.CH CF AC=
Suy ra
4 2 2 2 2
4 2 2 2 2
. . . .
. . . .
BH EB AB EB BH BC EB BH
CH CF AC CF CH BC CF CF
= = =
Vậy
32
32
BH EB
CH CF
=
.
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
24 – EDUCATION _ Vững kiến thức – Nhạy tư duy
BÀI 2: TỶ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
2.1
Áp dụng
22
21 sin 2 21
sin cos 1 cos tan ,cot
5 cos 2
21
+ = = = = =
.
2.2
Áp dụng
22
1 sin 1
sin cos 1 sin tan ,cot 3
2 cos
3
+ = = = = =
.
2.3
Dùng
sin
tan 3
cos
==
và
22
1 3 1
sin cos 1 cos ,sin cot
22
3
+ = = = =
.
2.4
Dùng
cos
cot 1
sin
==
và
22
2
sin cos 1 cos sin tan 1
2
+ = = = =
.
2.5
Dùng
2
2 2 2
2
1
sin cos 1 sin 1 tan ,cot
1
xx
x
x
x
−
+ = = − = =
−
.
2.6
a)
0 0 0 0
sin 25 ,cos15 ,sin 50 ,cos66
.
Ta có
00
cos15 sin75=
và
00
cos66 sin24=
Mà
0 0 0 0
sin24 sin25 sin50 sin75
Vậy thứ tự cần sắp là
0 0 0 0
cos66 sin25 sin50 cos15
.
b)
0 0 0 0 0
cot 35 ,tan 48 ,cot 44 ,tan53 ,cot39
.
Ta có
00
tan48 cot42=
và
00
tan53 cot37=
Mà
0 0 0 0 0
cot 44 cot42 cot39 cot37 cot 35
Vậy
0 0 0 0 0
cot44 tan48 cot39 tan53 cot35
.
2.7
a)
0
sin32
và
0
tan32
Dùng cách làm của Ví dụ 4 có
00
tan32 sin32
b)
0
cos35
và
0
cot35
Dùng cách làm của Ví dụ 4 có
00
cot 35 cos35
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 25
c)
0
sin25
và
0
cot55
Ta có
00
cot 55 tan35=
dùng Ví dụ 4 ta có
000
tan35 sin35 sin25
Vậy
00
cot55 sin25
.
d)
0
cos54
và
0
tan42
Ta có
00
tan42 cot48=
dùng Ví dụ 4 ta có
000
cot48 cos48 cos54
Vậy
00
tan42 cos54
.
2.8
Ta có
00
tan72 cot18=
và
00
sin54 cos36=
Dùng Ví dụ 4 ta có
00
cot 36 cos36
Mà
0 0 0
cot36 cot 21 cot18
Vậy
0 0 0 0
sin54 cot36 cot21 tan72
.
2.9
2
2 2 2 2
2
2
sin
1
sin cos tan 1 3 1 8
cos
sin .cos
sin .cos tan 3 3
cos
a
a a a
a
P
aa
a a a
a
−
− − −
= = = = =
.
3
3 3 3
3
3 3 3 3
3
sin
1
sin cos 3 1 13
cos
14
sin cos sin 3 1
1
cos
a
aa
a
Q
a a a
a
−
−−
= = = =
++
+
.
2.10 Ta có
2 2 2 2 2 0
1 1 3 1
cos 2sin 1 sin 2sin 3sin sin 30
4 4 4 2
a a a a a a a− = − − = = = =
.
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
26 – EDUCATION _ Vững kiến thức – Nhạy tư duy
BÀI 3: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
3.1
Xét tam giác ABC vuông tại C, giả sử
Aa=
.
Ta có
sin
BC
a
AB
=
,
cos
AC
a
AB
=
Nên
22
22
22
sin cos
BC AC
aa
AB AB
+ = +
Suy ra
22
22
2
sin cos 1
BC AC
aa
AB
+
+ = =
sin
tan
cos
BC
BC a
AB
a
AC
AC a
AB
= = =
Tương tự
cos
cot
sin
a
a
a
=
và
tan .cot 1aa=
.
3.2
a) Áp dụng định lý Pytago
222
89 cmBC AB AC BC= + =
00
8
sin 58 32
89
AC
B B C
BC
= =
.
b)
0
39F =
,
.cos 158,9 cmDE EF E EF=
,
123,5 cmDF
.
c)
0
1
sin 19 28'
3
AB
CC
BC
= =
.
d) Vẽ đường cao AH suy ra
0
1 1 1
cos 80,4
2 6 6
BH
BH BC AB B B
AB
= = = =
.
3.3
Áp dụng
2 2 0
2
sin cos 1 sin 45
2
+ = = =
.
3.4 Độ rộng con sông
Ta có
0
0
tan30 50 3 m
tan30
HB HB
HA
HA
= = =
Quãng đường đã đi
22
100 mAB AH BH= + =
.
3.5 Ta có
0
00
900
sin40 1400,15 m
sin40 sin40
HB HB
AB
AB
= = =
.
a
C
B
A
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 27
3.6 Vẽ đường cao AH của tam giác ABC
Xét tam giác AHB có
15 25
cos .cos cm cm
22
BH
ABH BH AB ABH CH BC BH
AB
= = = = − =
Lại có
0
15 3
sin .sin 60 cm
2
AH
ABH AH AB
AB
= = =
Như vậy
2 2 0 0
5 13 cm sin 56,1 73,9
AH
AC AH CH ACB ACB BAC
AC
= + = =
.
3.7
Vẽ đường cao AH củ tam giác ABC.
Ta có
0
.cos 25.cos70 8,6 cmBH AB B= =
và
00
.sin .sin70 25.sin70 23,5 cmAH AB B AB= = =
Lại có
0
23,5
.sin 30,7 cm
sin50
sin
AH
AH AC C AC
C
= = =
0
.cos 30,7.cos50 19,7 cmCH AC C = =
Do đó
28,3 cmBC BH CH= +
.
3.8
Vẽ đường cao AD cyra tm giác ABC
Áp dụng
.sin 3 3 cmAD AB B AD= =
và
.cos 3 cmBD AB B BD= =
Xét tam giác ACD có
.cot 3 3 cmCD AD C CD= =
Suy ra
( )
3 1 3 cmBC BD CD= + = +
Vậy
( )
2
19
. 3 3 cm
22
ABC
S AD BC= = +
.
3.9
Vẽ đường cao CD của tam giác ABC
Đặt
CD x=
với
0x
Xét tam giác ACD có
3
.cot cm
3
x
AD CD A AD= =
.
Xét tam giác BCD có
.cot cmBD CD B BD x= =
( )
3
12 6 3 3 cm
3
AB AD BD x x x = + = + = = −
Vậy
( )
2
1
. 36 3 3 cm
2
ABC
S ABCD= = −
.
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
28 – EDUCATION _ Vững kiến thức – Nhạy tư duy
3.10
Dễ thấy ABHK là hình chữ nhật có hai cạnh kề bằng nhau nên nó là hình vuông.
Suy ra
4 cmBK AH==
Xét tam giác BKC
Áp dụng
.cos 6,22 cmBK BC KBC BC=
và
.tan 4,77 cmKC BK KBC=
Tương tự, xét tam giác AHD tính được
cot 1,46 cmDH AH ADH= =
Do đó
10,23 cmDC DH HK KC= + +
.
3.11
ABCD là hình bình hành
CA
= =
và
DC AB a==
Xét tam giác vuông BCD có
.cos cosBC CD C a
==
Vẽ BH vuông góc CD
Áp dụng
.sin cos .sinBH BC C a

==
Do đó
2
. sin .cos
ABCD
S DC BH a

==
.
K
H
D
C
B
A
α
H
D
C
B
A
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 29
3.12
Vẽ AD vuông góc BC
Xét tam giác ABD có
.sinAD AB B=
Xét tam giác ACD có
.sinAD AC C=
Do đó
.sin .sin
sin sin
AB AC
AB B AC C
CB
= =
Tương tự ta có
sin sin sin
AB BC CA
C A B
==
.
Như vậy
00
6
2
sin 45 sin 60
AB AC
AC c= =
.
Xét tam giác ABD có
cos
2
c
BD AB B==
Xét tam giác ACD có
3
.cos
2
c
CD AC C==
Như vậy
( )
31
2
c
BC BD CD
+
= + =
.
3.13*
Vẽ đường phân giác AD của góc A
Nên
BD BD
AC AB
=
CD BD CD BC
AC AB AC AB AC
+
= =
++
(tính chất
dãy tỷ số bằng nhau)
Mà
tan tan
2
A CD
ACD
AC
==
Vậy
tan
2
A BC
AB AC
=
+
Xét tam giác ABC vuông ở C với
0
30A =
Đặt BC = a
Ta có
.cot 3AC BC A a==
,
2
sin
BC
AB a
A
==
D
C
B
A
B
C
D
A
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
30 – EDUCATION _ Vững kiến thức – Nhạy tư duy
Dùng kết quả trên, ta có
00
tan15 tan 2 3 cot15 2 3
2
A BC
AB AC
= = = − = +
+
Laị có
( )
0
0 0 0
0
sin15
tan15 sin15 2 3 cos15
cos15
= = −
Áp dụng
2 0 2 0 0 0 0 0
6 2 6 2
sin 15 cos 15 1 cos15 sin15 tan15 .cos15
44
+−
+ = = = =
3.14*
Vẽ AD vuông góc BC
Xét tam giác ABD có
.sinAD AB B=
Xét tam giác ACD có
.sinAD AC C=
Do đó
.sin .sin
sin sin
AB AC
AB B AC C
CB
= =
. Tương tự ta có
sin sin sin
AB BC CA
C A B
==
.
Dùng giả thiết bài 3.12 (bạn đọc có thể dùng giả thiết khác)
Ta có
( )
0
31
2 6 2 6 2
2
sin sin . sin75
2 4 4
c
BC
AC
AB c
+
++
= = = =
Dùng
2 0 2 0 0
62
sin 75 cos 75 1 cos75
4
−
+ = =
Suy ra
00
tan75 2 3,cot75 2 3= + = −
.
3.15 Xét tam giác AED và ABC có
A
chung và
( )
cos
AE AD
A
AB AC
==
nên chúng đồng dạng
Suy ra
cos .cos
ED AE
A DE BC A
BC AB
= = =
D
C
B
A
| 1/31
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

GV. LƯƠNG ANH NHẬT CHƯƠNG
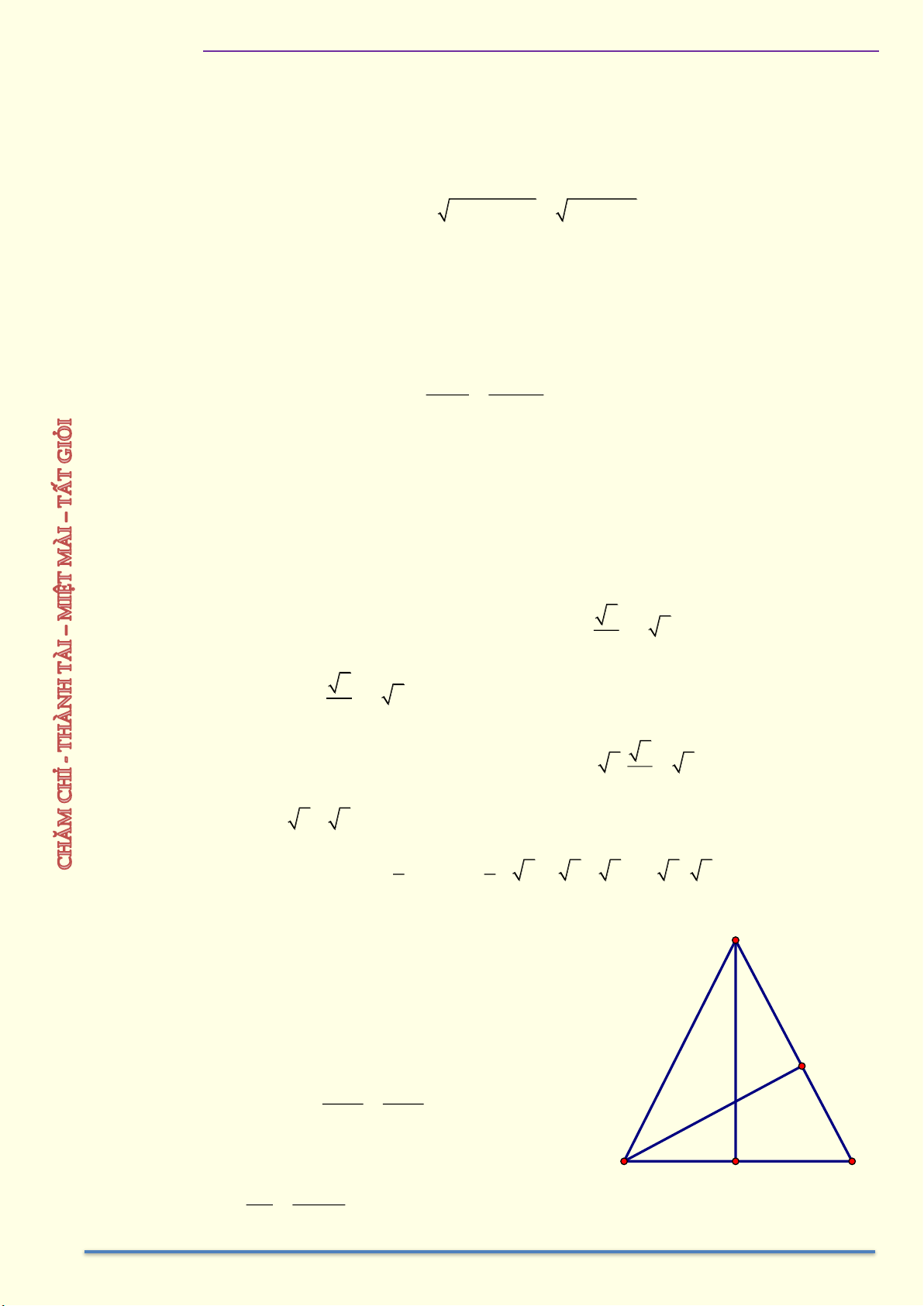
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG A B H K D I C
VỮNG KIẾN THỨC – NHẠY TƯ DUY 1 GV. LƯƠNG ANH NHẬT
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
CHƯƠNG I HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
BÀI 1: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG I. Đặt vấn đề
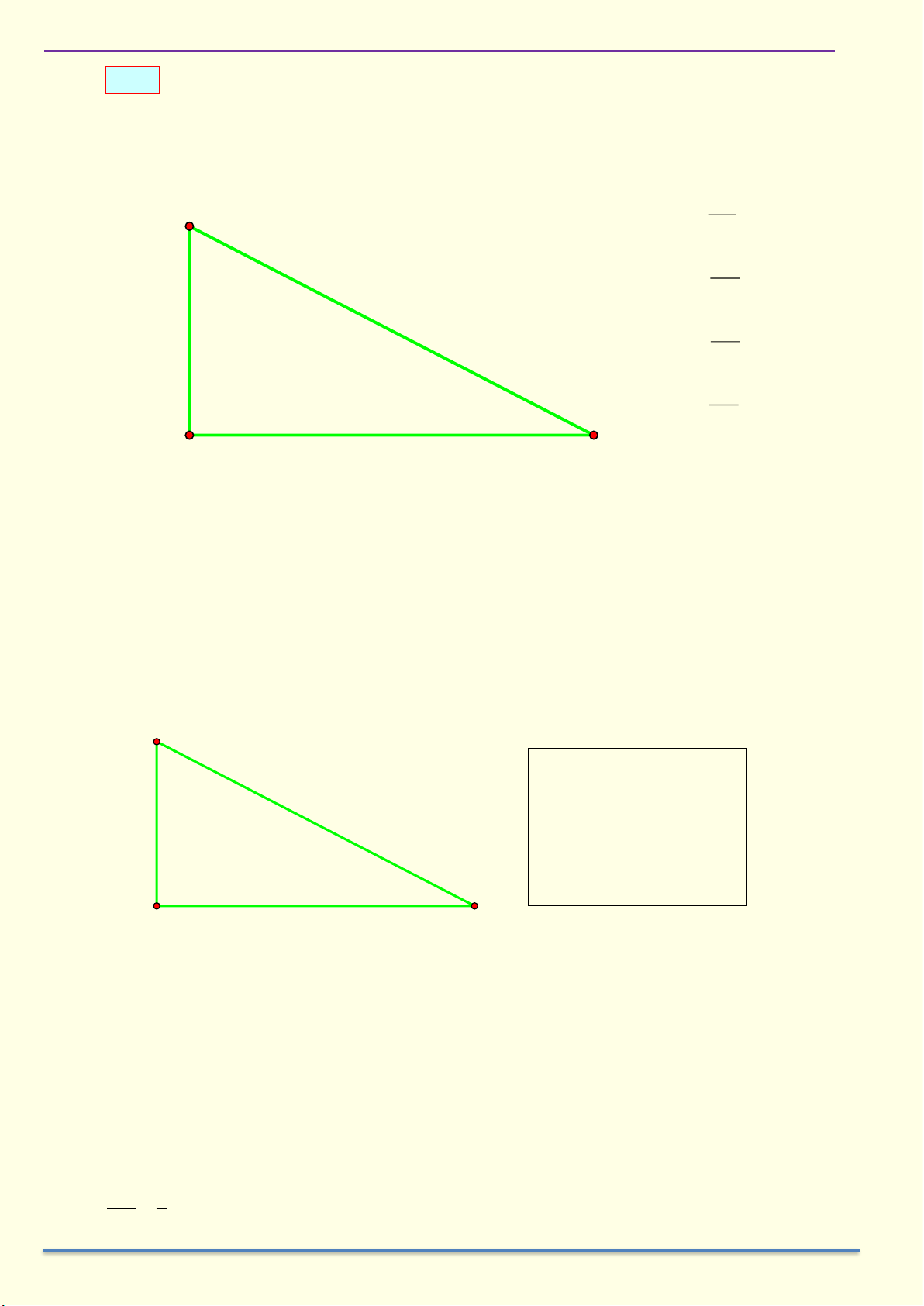
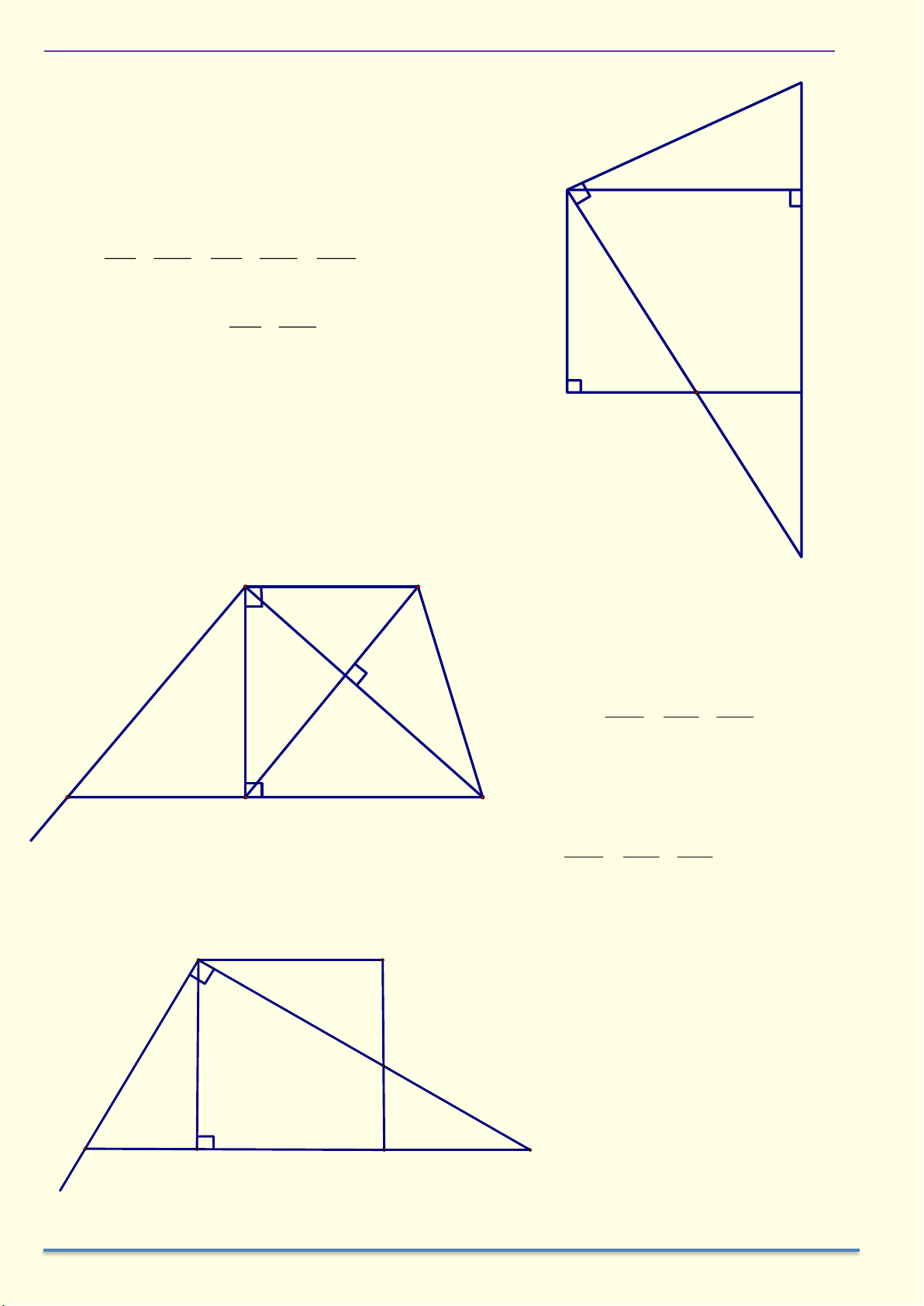
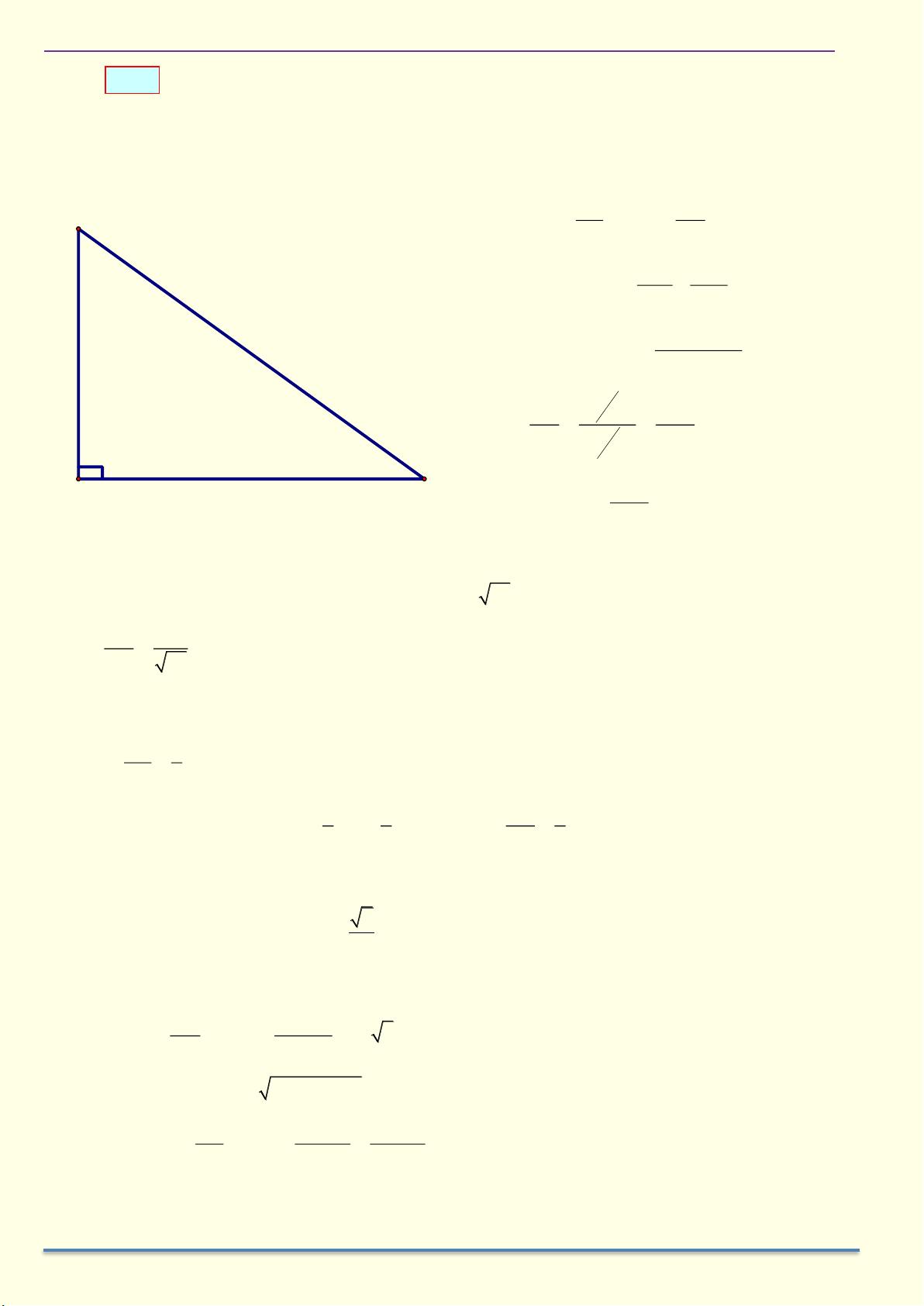
Cho tam giác ABC vuông ở A có AH là đường cao. Chứng minh a) 2
AB = BH.BC , 2
AC = CH.CB . b) A .
B AC = AH.BC . c) 2
AH = BH.CH . 1 1 1 d) = + . 2 2 2 AH AB AC Giải A C B H
a) Xét hai tam giác vuông ABH và CBA có ABH chung nên ABH ∽ CBA (g.g) AB BH Suy ra 2 =
AB = BH.BC BC AB Tương tự, cũng có 2
AC = CH.CB b) Vì HBA∽ ABC (cmt) AH AB nên =  A .
B AC = AH.BC AC BC
c) Xét hai tam giác vuông ABH và CHA có HAB = ACH (cùng phụ ABC ) Nên AHB∽ CHA (g.g) AH BH Suy ra 2 =
AH = BH.CH CH AH 2 2 2 1 BC 1 BC AB + AC
d) Ta có AH.BC = A . B AC  =  = = 2 2 2 2 2 AH A . B AC AH AB .AC AB .AC 1 1 1 Vậy = + . 2 2 2 AH AB AC
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 1
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
II. Một số hệ thức về cạnh và đường cao trong tam giác
Từ kết quả của phần trên, ta suy ra
• Định lý 1: Trong một tam giác vuông, bình phương của cạnh góc vuông bằng tích của
cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
• Định lý 2: Trong một tam giác vuông, tích hai cạnh góc vuông bằng cạnh huyền nhân với
đường cao tương ứng của cạnh huyền đó.
• Định lý 3: Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng
tích hình chiếu của hai cạnh góc vuông trên cạnh huyền.
• Định lý 4: Trong một tam giác vuông, nghịch đảo bình phương đường cao bằng tổng
nghịch đảo bình phương của hai cạnh góc vuông.
Ta dùng các kết quả nêu trên như là một công thức và được phép sử dụng.
Ví dụ 1: Cho tam giác ABC vuông ở A có đường cao AH. Biết BH = 12, 5 cm, và CH = 72 cm. Tính AH, AB và AC. Giải
Ta có BC = BH + CH = 12, 5 + 72 = 84, 5 Lại có 2
AH = BH.CH = 12, 5.72 = 900  AH = 30 cm 2
AB = BH.BC = 12, 5.84, 5 = 1056, 25  AB = 32, 5 cm 2
AC = CH.CB = 72.84, 5 = 6084  AC = 78 cm
Ví dụ 2: Cho tam giác ABC vuông tại A có AH là đường cao. Biết AC = 40 cm , AH = 24 cm . Tính
AB, BC, BH và CH. Giải A B Ta có 2 2 2 2
CH = AC − AH = 40 − 24 = 32 cm 2 2 2 AC 40
AC = CH.CB CB = = = 50 cm CH 32 2 2 2 2
AB = BC − AC = 50 − 40 = 30 cm 2 2 H 2 AB 30
AB = BH.BC BH = = = 18 cm BC 50 D C
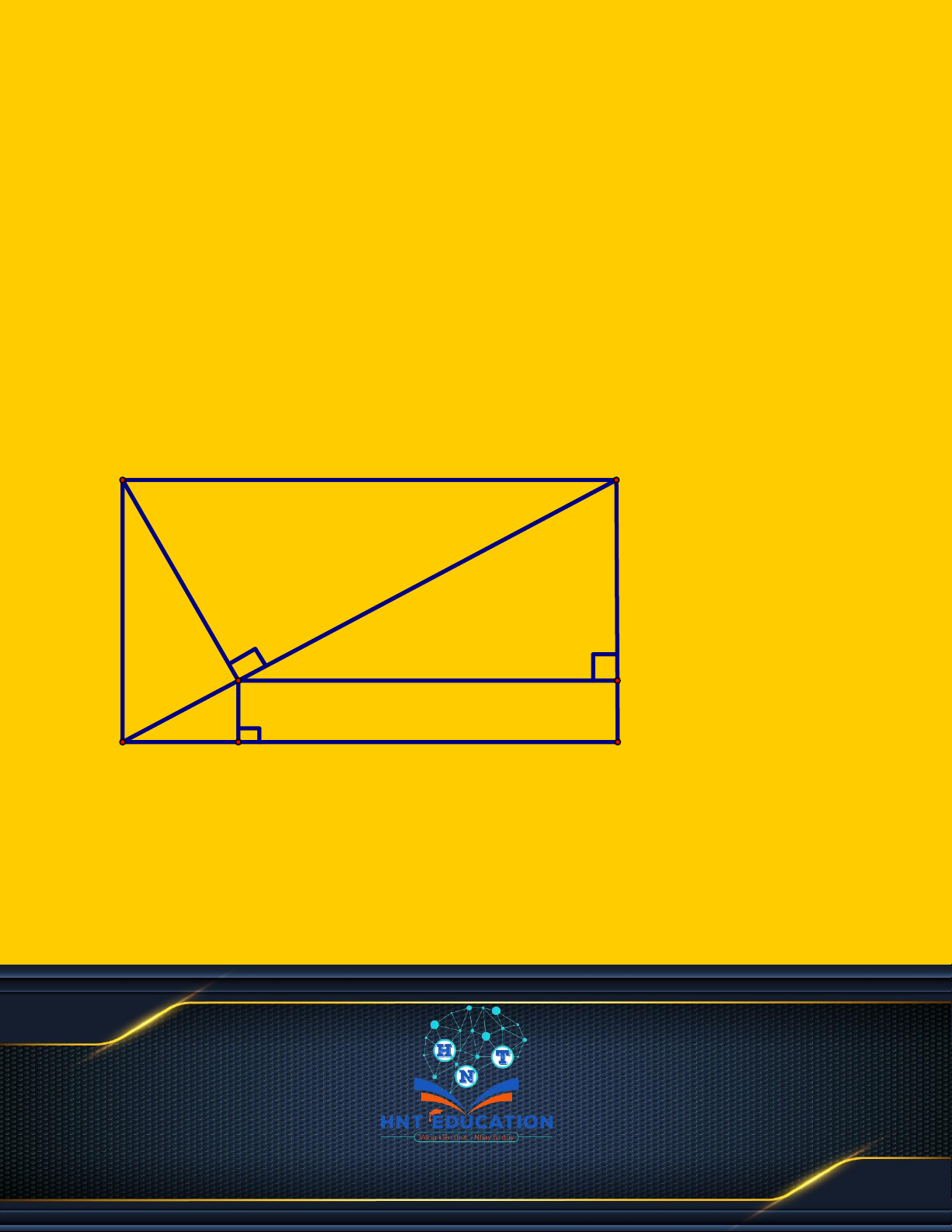
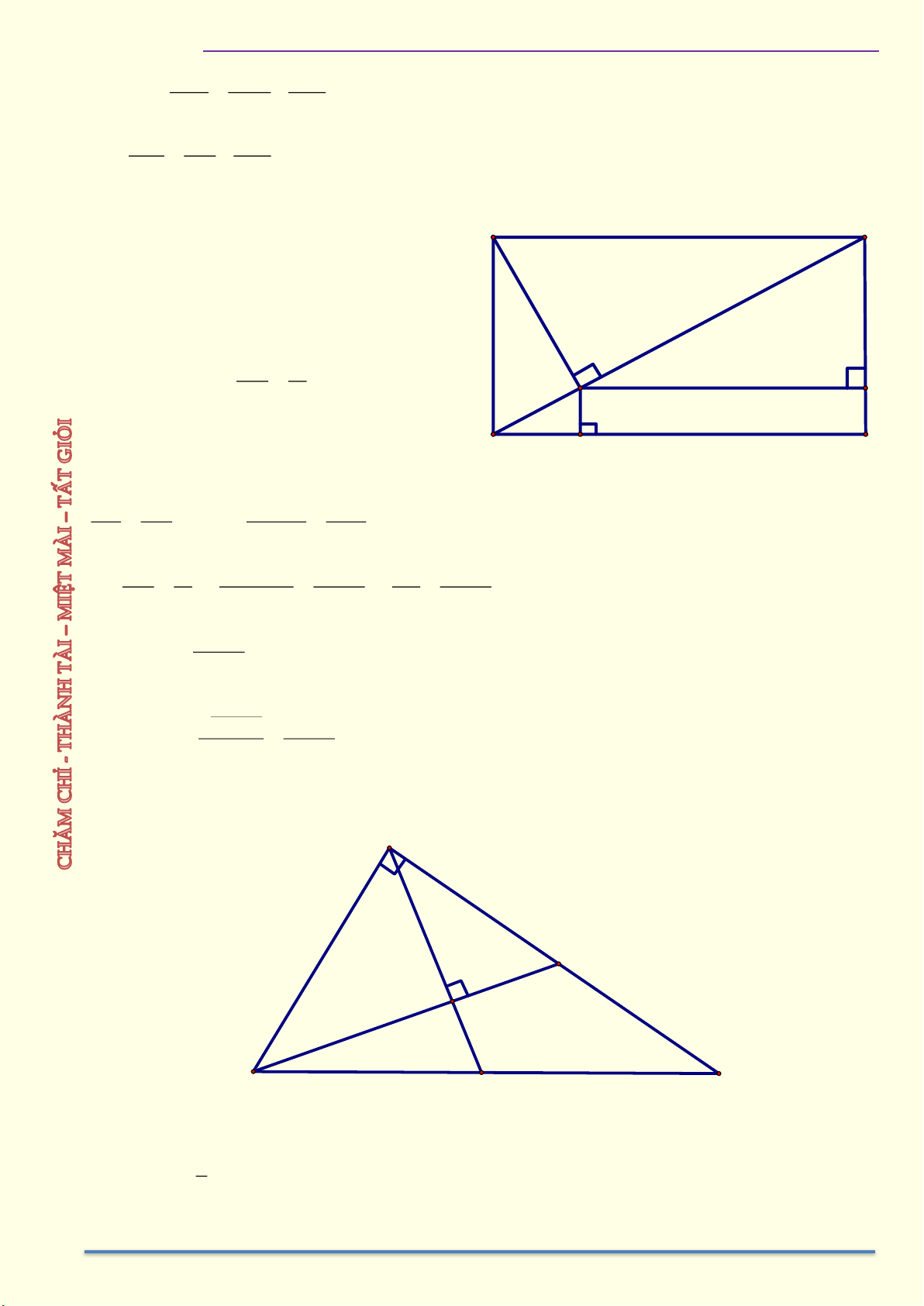
Ví dụ 3: Cho hình chữ nhật ABCD, qua A kẻ đường thẳng vuông góc với BD tại H. Biết
AB = 20 cm , AH = 12 cm . Tính các cạnh còn lại và đường chéo của hình chữ nhật ABCD. Giải
2 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Ta có 2 2 2 2
HB = AB − AH = 20 − 12 = 14 cm 2 2 AB Áp dụng 2 20 200
AB = BH.BD BD = = = cm BH 14 7 200 12. AH.BD 120 A .
D AB = AH.BD 7  AD = = = cm AB 20 7
Ví dụ 4: Cho tam giác ABC vuông tại A, có đường cao AH. Biết AB = 15 cm , BH = 9 cm . Tính
diện tích tam giác ABC. Giải 2 2 AB Ta có 2 15
AB = BH.BC BC = =
= 25 cm  CH = BC − BH = 25 − 9 = 16 cm BH 9 Khi đó 2 AH = B .
H CH = 9.16  AH = 9.16 = 12 cm 1 1
Diện tích tam giác ABC là 2 S
= AH.BC = 12.25 = 150 cm ABC 2 2
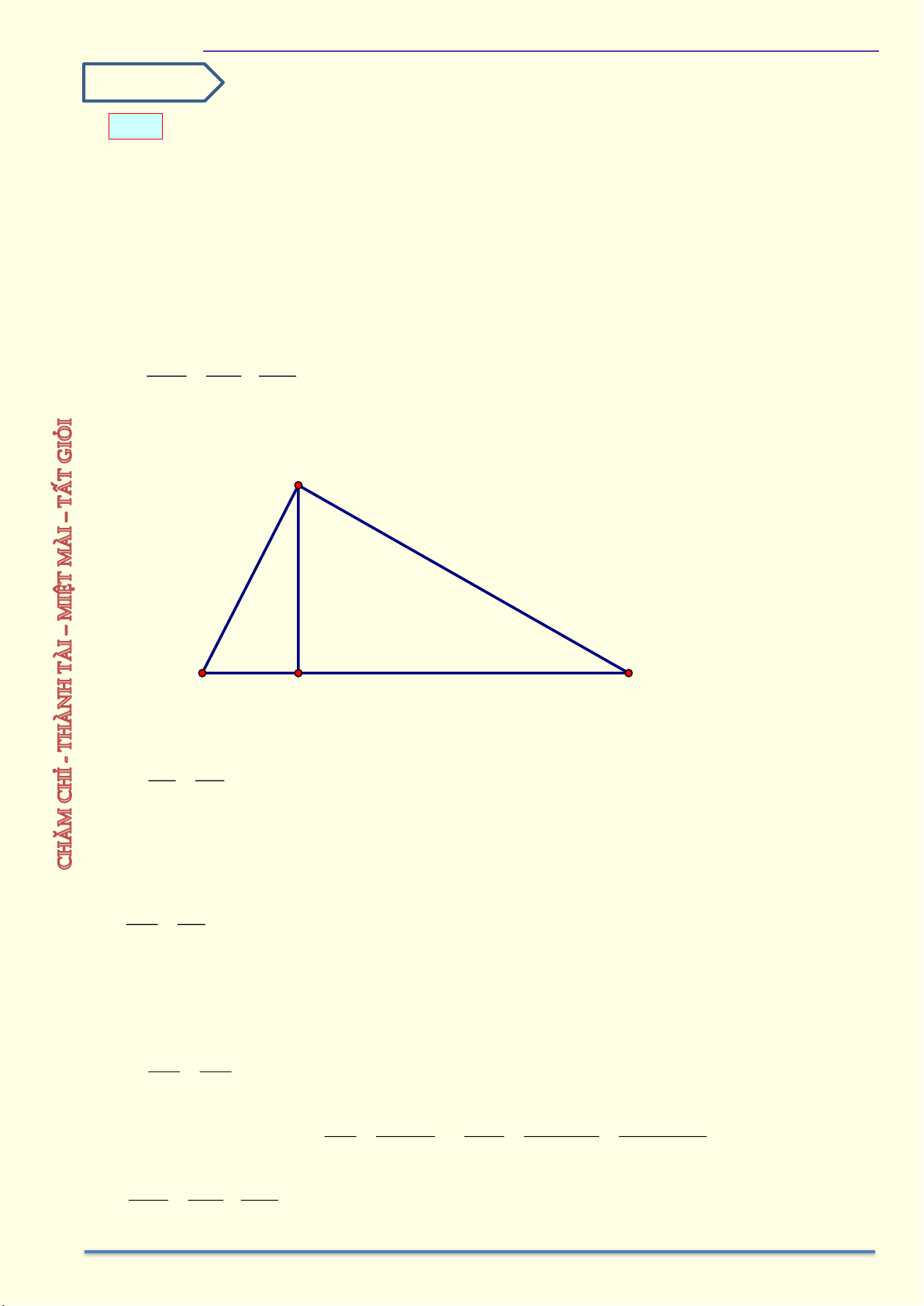
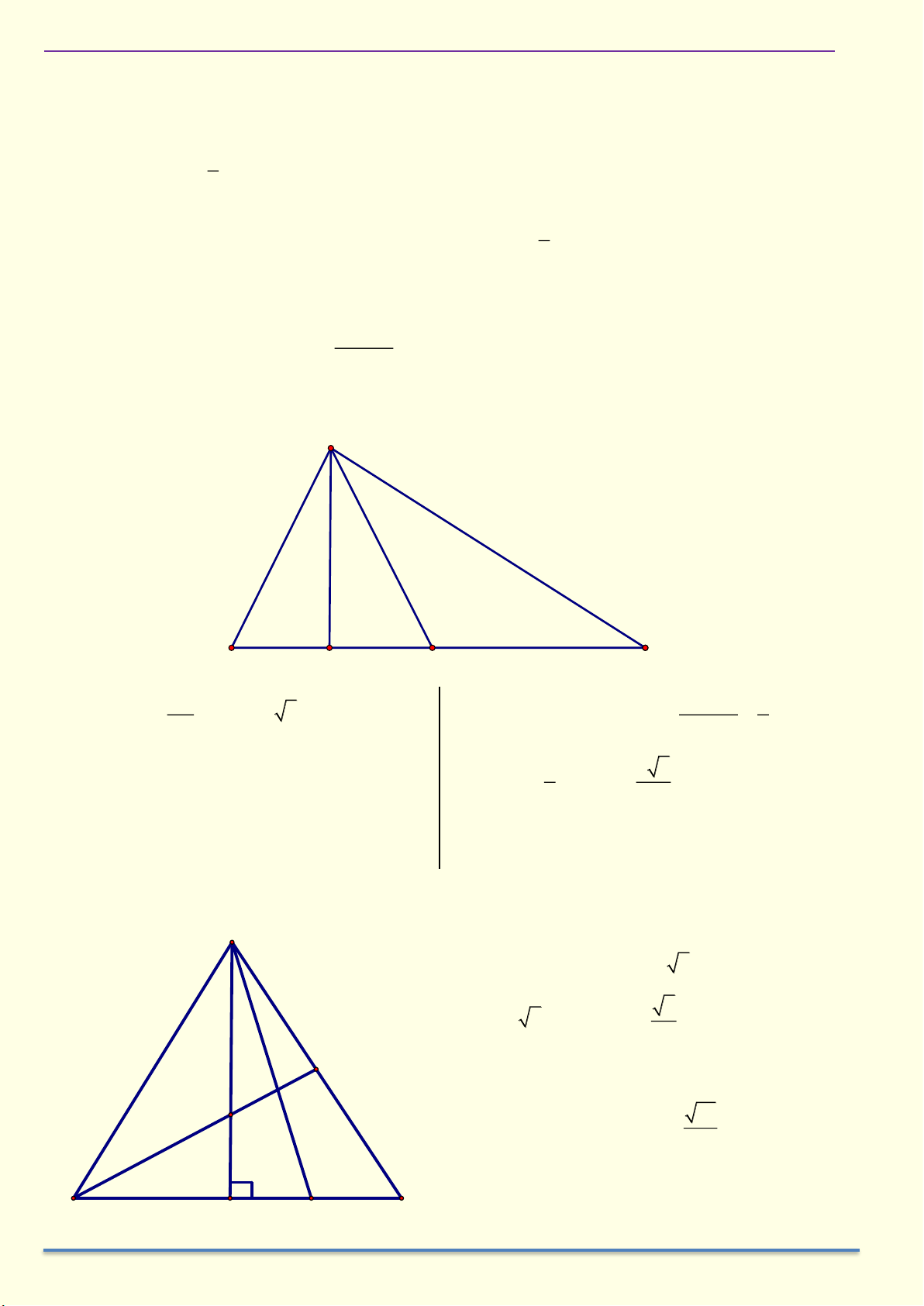
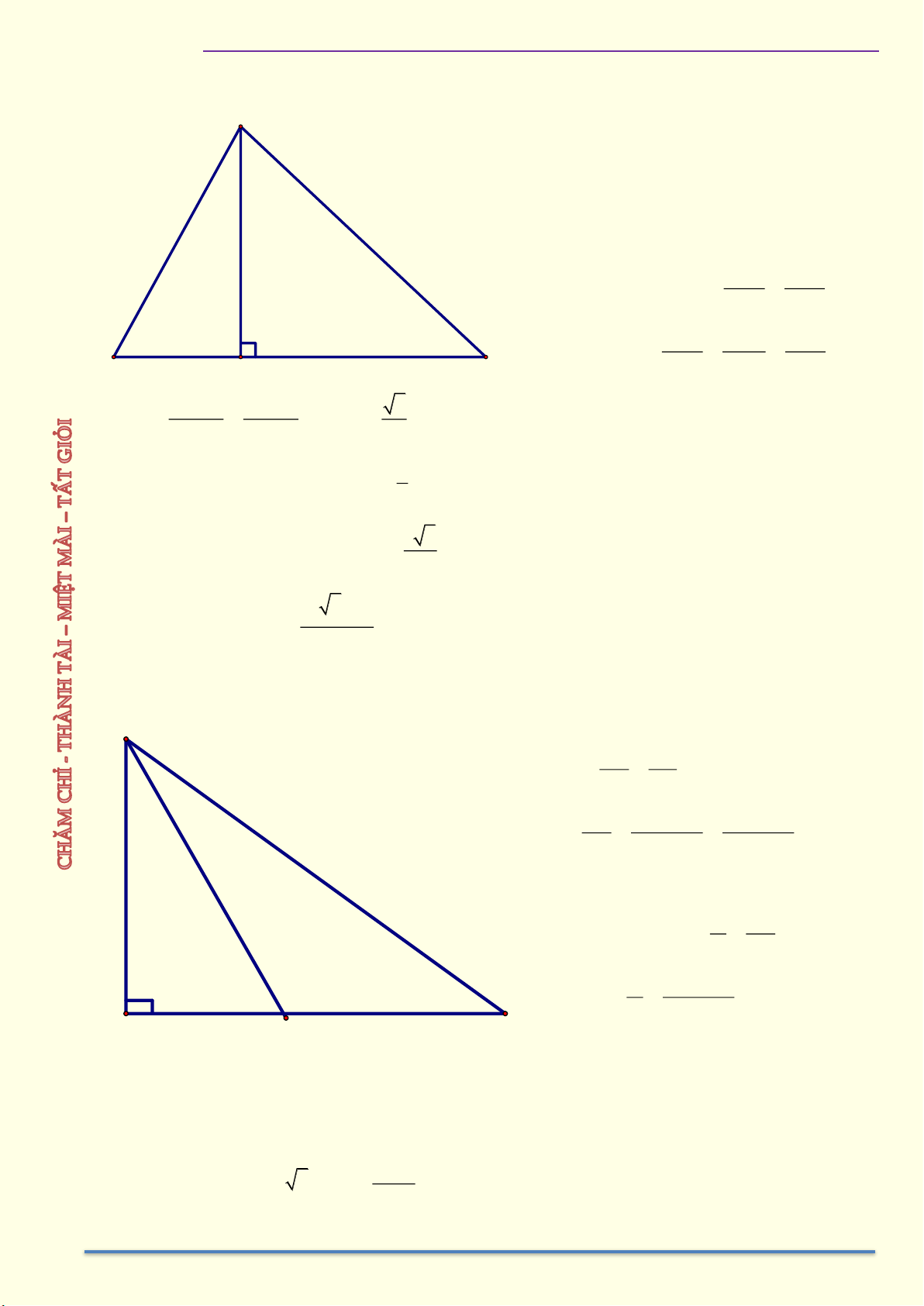
Ví dụ 5: Cho tam giác ABC vuông ở A có AH là đường cao, phân giác AD. Biết BD = 15 cm ,
DC = 20 cm . Tính độ dài AD. Giải A C B H D
Ta có AD là đường phân giác của tam giác ABC AB BD 15 3 Suy ra = = = AC CD 20 4 3
Đặt AB = x AC = x với x  0 4
Lại có BC = BD + CD = 35 cm
Áp dụng định lý Pytago, ta có 2   2 2 2 2 3 2 25 2 2 2
AB + AC = BC x + x = 35 
x = 35  x = 784  x =   28  4  16
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 3
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
AB = 28 cm và AC = 21 cm 2 2 AB Áp dụng 2 28 112
AB = BH.BC BH = = = cm BC 35 5 112 37
HD = BH − BD = −15 = cm 5 5 A . B AC 28.21 84 Ta lại có A . H BC = A . B AC AH = = = cm BC 35 5 2 2     Khi đó 2 2 2 84 37
AD = AH + HD = + =     337 cm .  5   5 
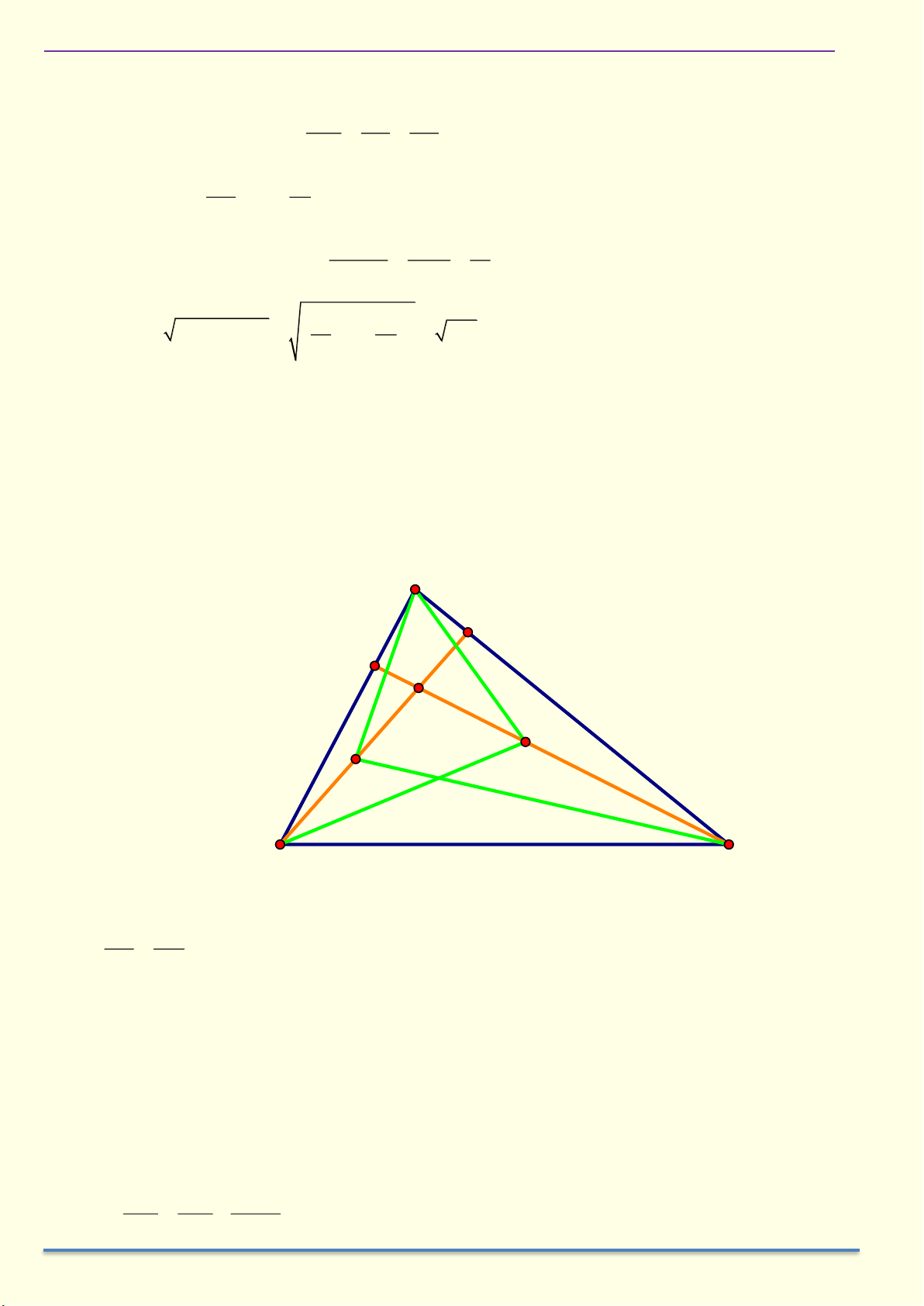
Ví dụ 6: Cho tam giác ABC nhọn, hai đường cao BD và CE cắt nhau tại H. Trên đoạn HB lấy điểm M sao cho 0
AMC = 90 và trên đoạn HC lấy N sao cho 0
ANB = 90 . Chứng minh a) A . D AC = A . E AB b) AM = AN Giải A D E H N M C B
a) Xét hai tam giác vuông ABD và ACE có BAC chung nên ABD ∽ ACE AB AD Suy ra =  A . D AC = A . E AB AC AE
b) Xét tam giác vuông AMC có MD là đường cao nên 2 MA = A . D AC
xét tam giác vuông ANB có NE là đường cao nên 2 NA = A . E AB Mà A . D AC = A . E AB Do đó 2 2
MA = NA AM = AN .
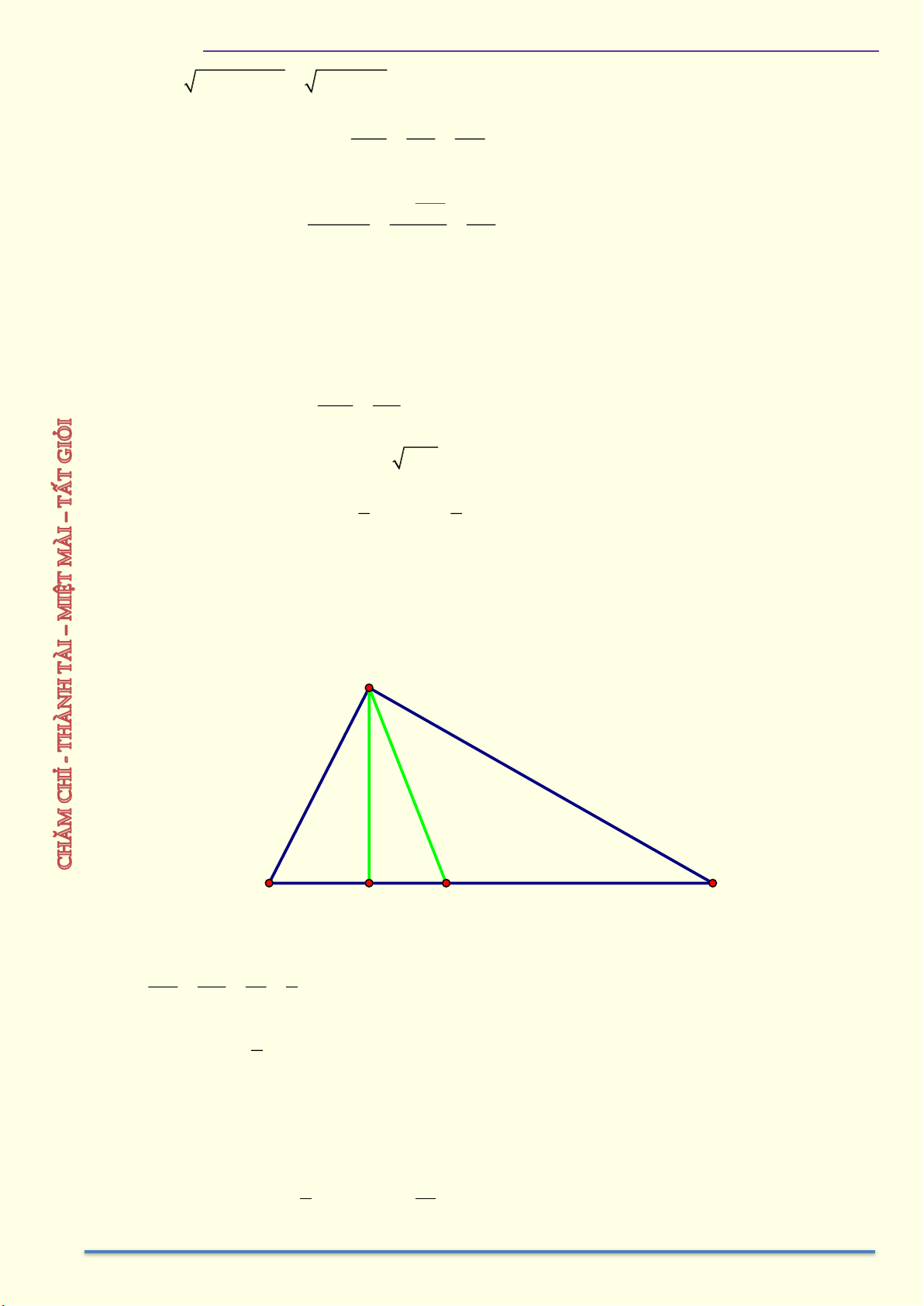
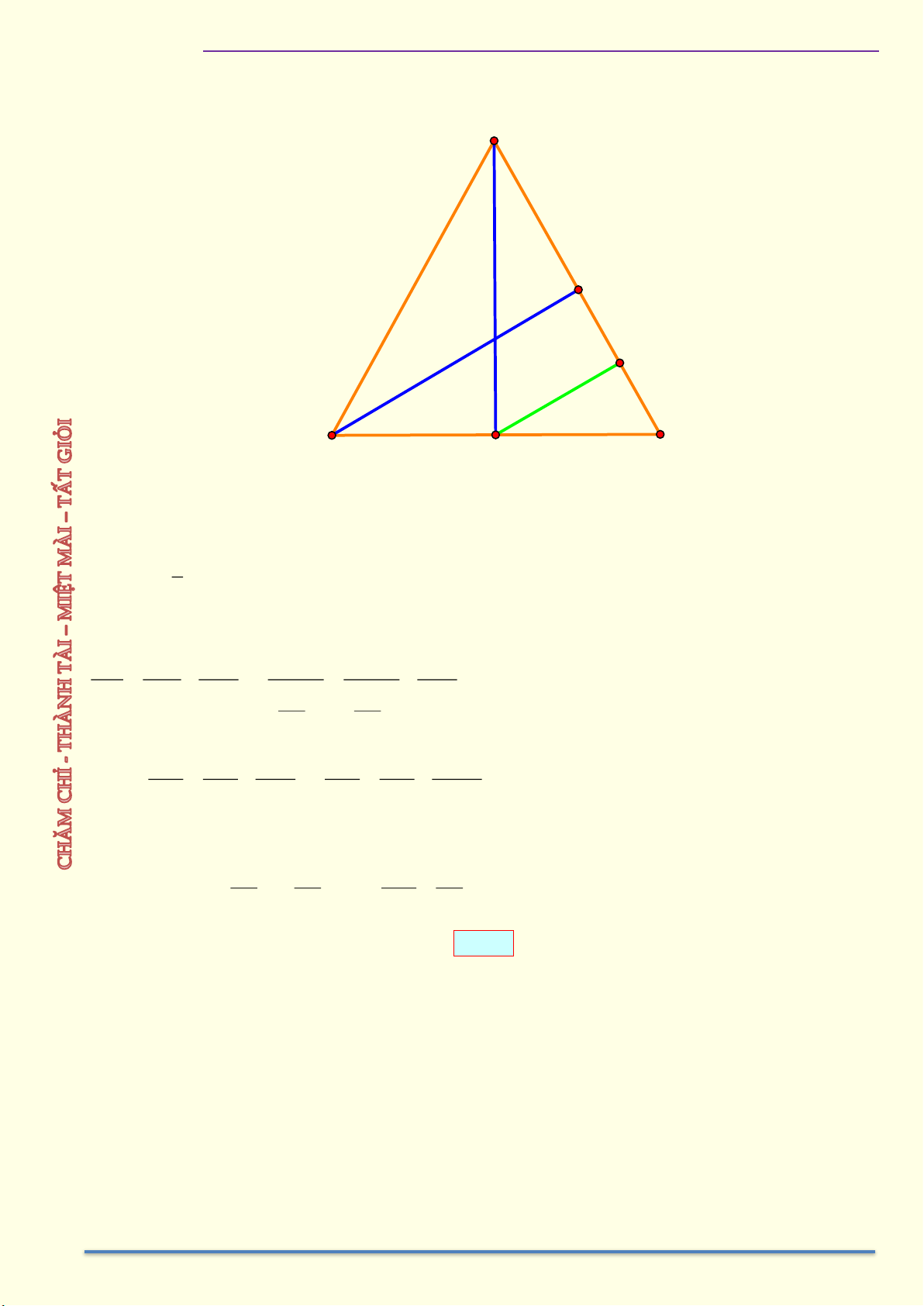
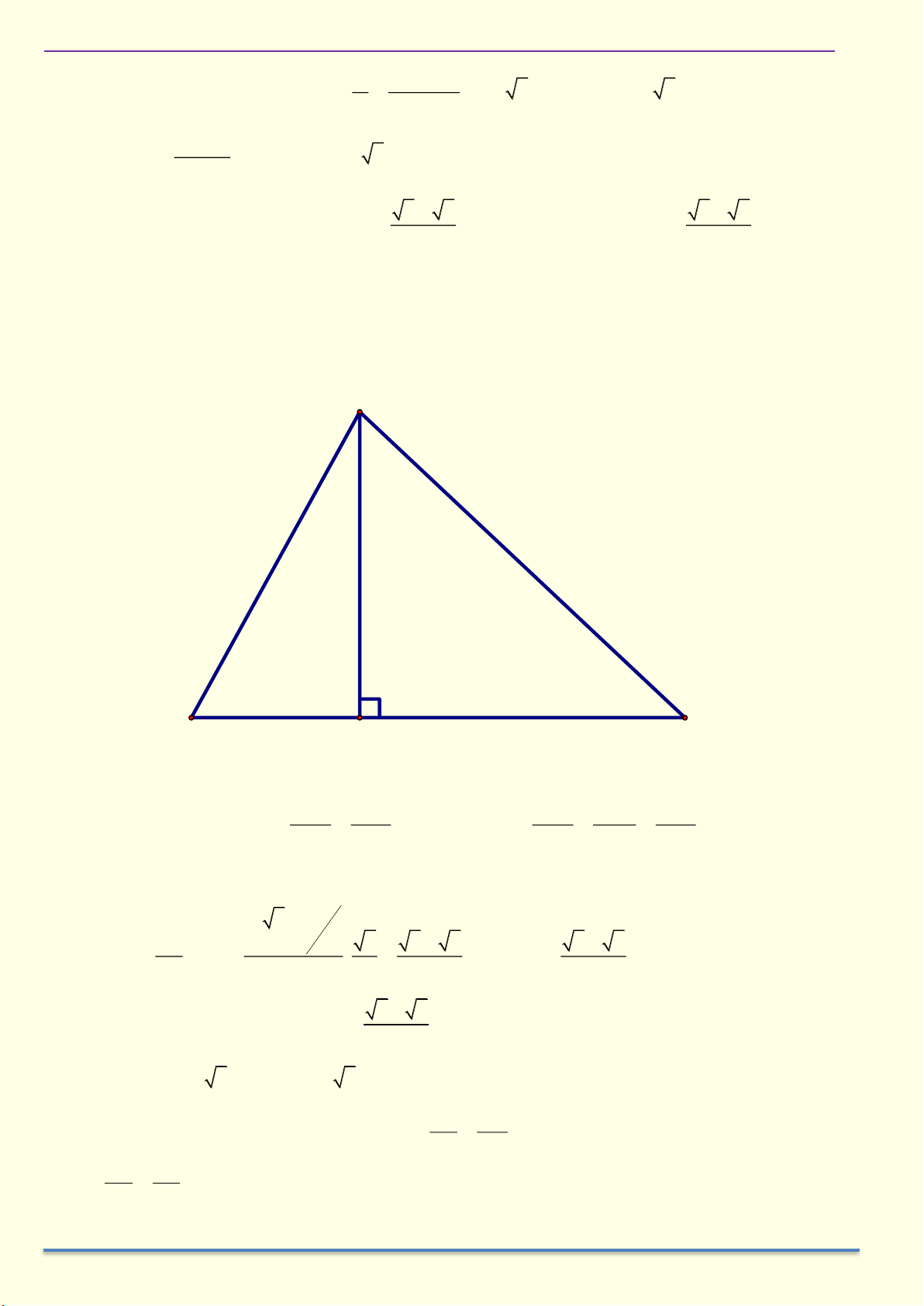
Ví dụ 7: Cho tam giác ABC cân tại A, hai đường cao AH và BK. Chứng minh 1 1 1 a) = + b) 2 BC = 2C . K CA 2 2 2 BK BC 4AH
4 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG Giải A K I C B H
a) Vẽ HI vuông góc AC tại I
Suy ra HI là đường trung bình của tam giác BCK 1 Nên HI = BK 2
Xét tam giác AHC vuông tại H có HI là đường cao 1 1 1 1 1 1 = +  = + 2 2 2 2 2 2 HI HC AH     AH BK BC      2   2  4 4 1 1 1 1 Suy ra = +  = + 2 2 2 2 2 2 BK BC AH BK BC 4AH
b) Xét tam giác AHC có 2 2   2 BC CK BC CK 2
CH = CI.CA  = .CA  = .CA BC =   2CK.CA  2  2 4 2 Bài tập
1.1 Cho tam giác ABC vuông ở A có AH là đường cao. Biết AB = 13,6 cm , AC = 25, 5 cm . Tính AH, BH và CH.
1.2 Cho tam giác ABC vuông ở A có AH là đường cao. Biết AB = 15 cm , CH = 16 cm . Tính độ dài AC, BC và AH.
1.3 Cho tam giác ABC vuông ở A có AH là đường cao. Biết BC = 28,9 cm , AH = 12 cm . Tính độ dài AB và AC.
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 5
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
1.4 Cho tam giác ABC có đường cao AH, trung tuyến AM và AB = 5 cm , AC = 12 cm và
BC = 13 cm . Tính độ dài AM và AH. HB 9
1.5 Cho tam giác ABC vuông tại A có AH là đường cao. Biết rằng =
và AH = 48 cm . Tính HC 16
AB, AB và BC. AB 3
1.6 Cho tam giác ABC vuông ở A có AH là đường cao. Biết rằng =
và BC = 125 cm . Tính AC 4 độ dài AH.
1.7 Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC. Biết tam giác ABM là tam giác
đều và có cạnh bằng 3 cm.
a) Tính độ dài AC và AH.
b) Tính diện tích tam giác ABC.
1.8 Cho tam giác ABC cân tại A có AB = 5 cm , đường cao AH = 3 cm . Gọi M và N là trung
điểm của HC và AC. Tính độ dài AM và BN.
1.9* Cho tam giác ABC cân có AB = AC = 5 cm , BC = 6 cm , các đường cao AH và BK. Vẽ tia Bx
vuông góc AB tại B. Gọi M là giao điểm của tia Bx và tia AC. Tính diện tích tam giác ABM (làm
tròn đến chữ số thập phân thứ nhất).
1.10 Cho hình vuông ABCD. Một điểm bất kỳ trên cạnh BC. Đường thẳng AI cắt DC tại K. Chứng 1 1 minh +
không phụ thuộc vào vị trí của điểm I trên cạnh BC (I không tùng với B và C). 2 2 AI AK
1.11 Cho tam giác ABC vuông ở A có I là trung điểm AB. Kẻ IH vuông góc với BC tại H. Chứng 1 1 1 minh = + . 2 2 2 4IH AB AC
1.12 Cho hình thang ABCD vuông tại A và D, đường chéo AC và BD vuông góc nhau. Chứng 1 1 1 minh = + . 2 2 2 AD AC BD
1.13 Hình vuông ABCD có I thuộc cạnh BC (I khác B và C). Gọi K là giao điểm của hai đường 1 1 1
thẳng AI và DC. Chứng minh = + . 2 2 2 AB AI AK
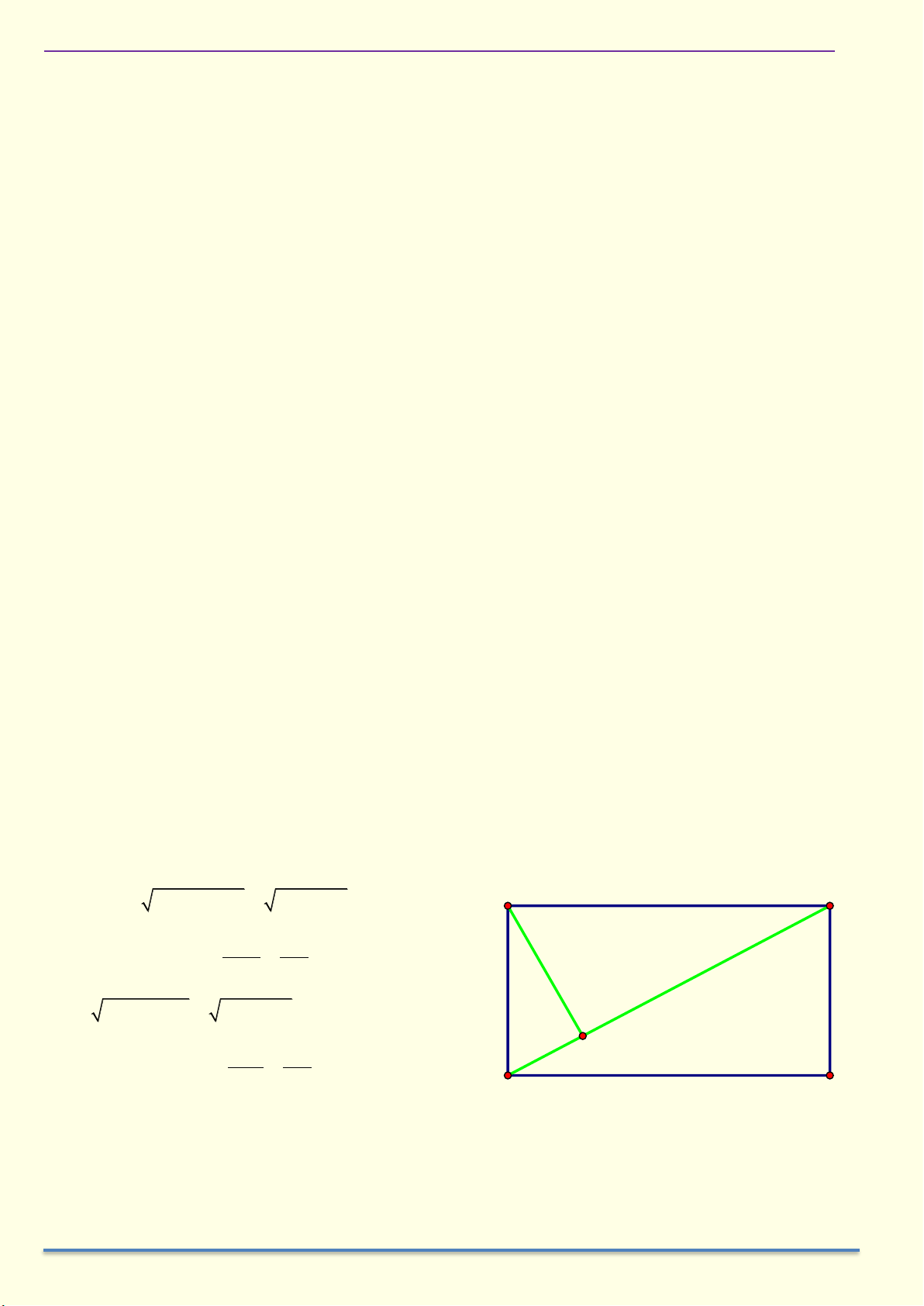
1.14* Cho hình chữ nhật ABCD có AB = a, AD = b. Gọi H là hình chiếu của A trên BD và K, I lần
lượt là hình chiếu của H trên BC và CD. Chứng minh 2 HB a 3 a a) = b) HK = 2 HD b 2 2 a + b
6 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
1.15 Cho tam giác ABC vuông tại A và AB = a . Các đường trung tuyến AM và BN vuông góc
nhau. Tính AC và BC theo a.
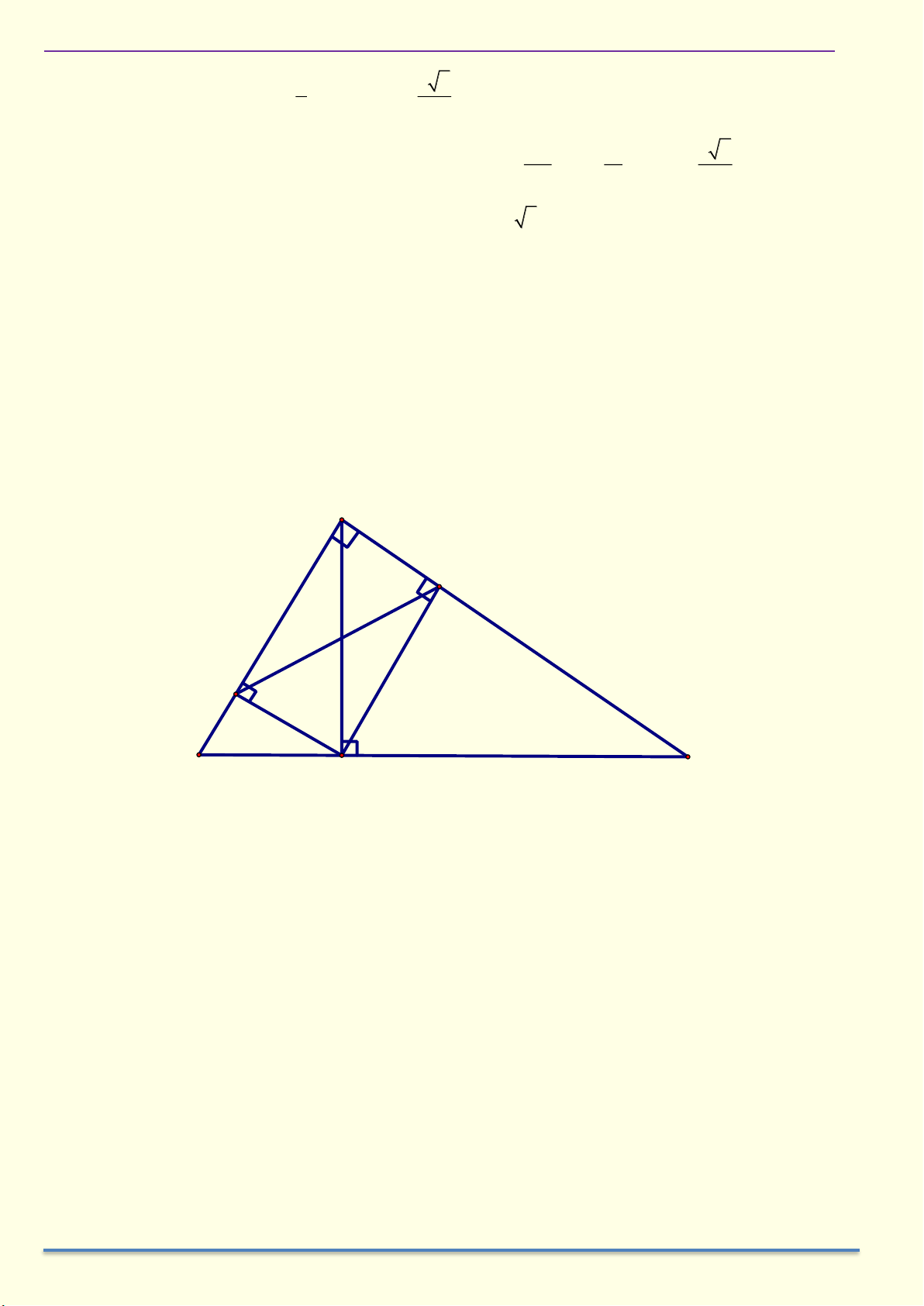
1.16 Cho tam giác ABC vuông ở A có AH là đường cao. Vẽ HE ⊥ AB, HF ⊥ AC . Chứng minh
a) AEHF là hình chữ nhật. d) 3 AH = E . B B . C CF 3 AB BE b) A . E AB = A . D AC e) = 3 AC CF 3 2 BH BE c) E . A EB + F . A FC = H . B HC f) = 3 2 CH CF
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 7
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
BÀI 2: TỶ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN
I. Khái niệm tỷ số lượng giác của một góc nhọn
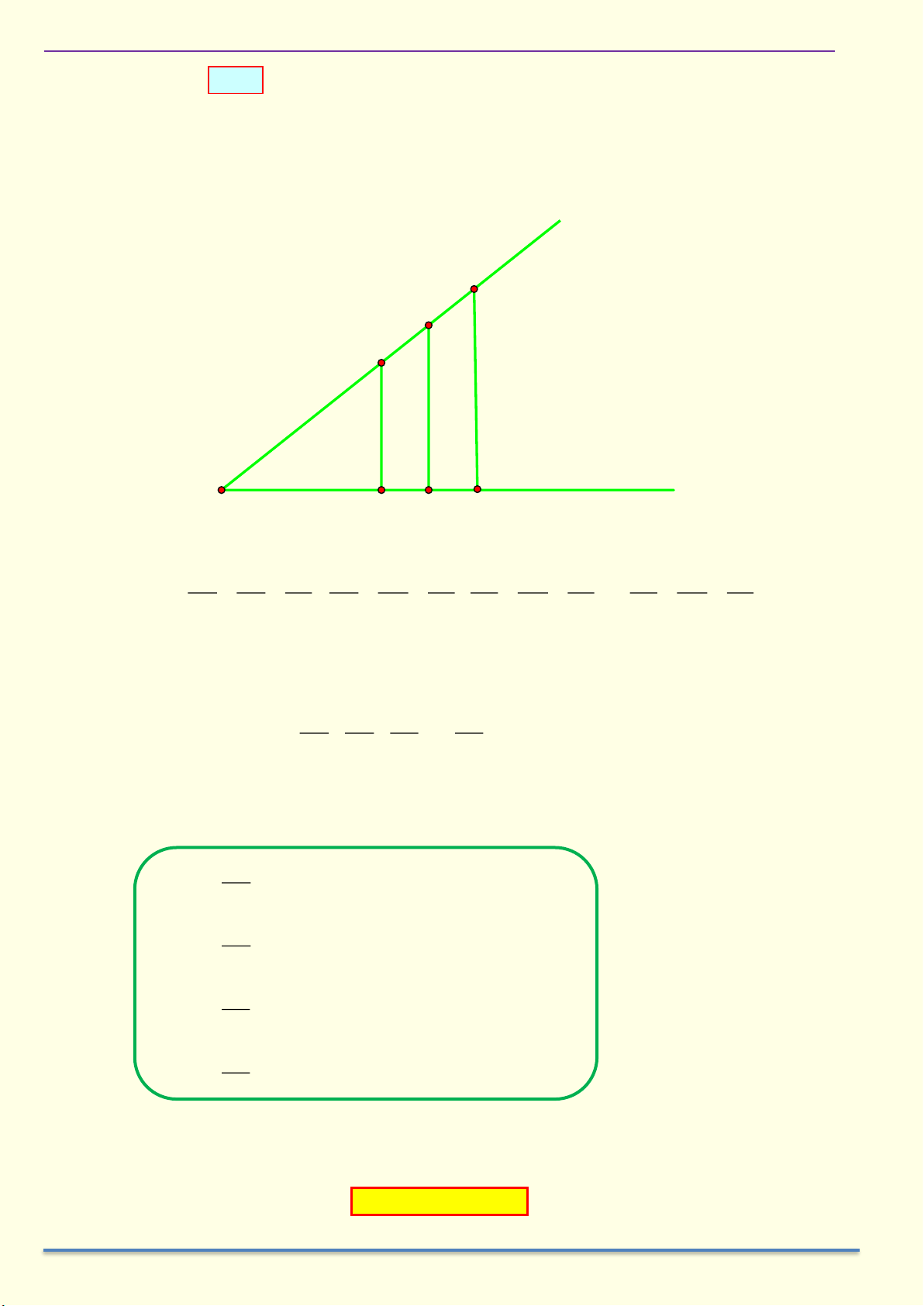
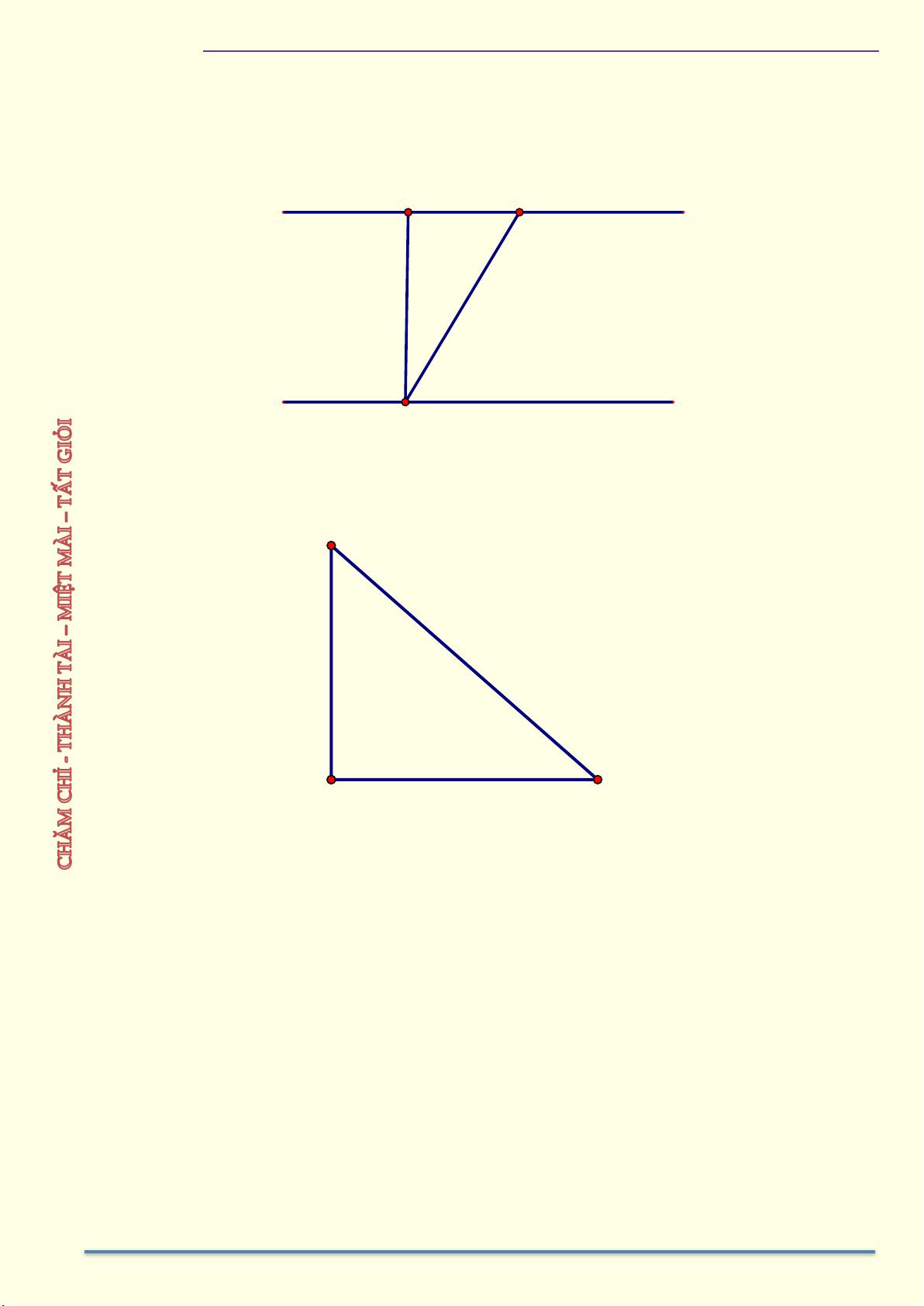
_ Cho góc xOy =  . Từ điểm A trên Ox (A khác O) vẽ AB ⊥ Oy tại B. x E C A α y O B D F
Bên cạnh đó, ta lấy thêm các điểm C và E trên Ox rồi lần lượt vẽ CD ⊥ Oy tại D và EF ⊥ Oy tại F. AB CD EF OB OD OF AB CD EF OB OD OF Ta thấy các tỷ số = = , = = , = = và = = OA OC OE OA OC OE OB OD OF AB CD EF
Việc ta lấy thêm các điểm C và E cũng giống như việc tịnh tiến hay còn gọi là thay đổi vị trí của A trên Ox AB OB AB OB
Như vậy, các tỷ sô ban đầu là , , và
không phụ thuộc vào vị trí của A trên Ox OA OA OB AB
mà chỉ phụ thuộc vào độ lớn của xOy . Ta gọi AB _ Tỷ số
là sin của góc  và ký hiệu là sin . OA OB _ Tỷ số
là côsin của góc  và ký hiệu là cos . OA AB _ Tỷ số
là tang của góc  và ký hiệu là tan . OB OB _ Tỷ số
là côtang của góc  và ký hiệu là cot . AB
Các tỷ số trên gọi chung là tỷ số lượng giác của góc  và các tỷ số này luôn dương. Hơn nữa, ta cũng có sin  1 và cos  1
8 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
II. Tỷ số lượng giác của hai góc phụ nhau
_ Định lý: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia và tang góc này bằng côtang góc kia. Ví dụ 1: Cho 0  = 60 và 0
 = 30 . Khi đó sin = cos và tan = cot  .
III. Một số hệ thức cơ bản
Cho  là góc nhọn, ta có các hệ thức sau sin cos a) 2 2 sin  + cos  = 1 b) tan = và cot = c) tan.cot = 1 cos sin 1
Ví dụ 2: Cho  là góc nhọn và sin = . Tính các giá trị lượng giác còn lại của  . 3 Giải 2 2 2 2 1 2 2 sin  cos  1 cos 1 sin    + =  = − = 1− =    3  3 1 sin 1 1 3  tan = =  cot = = 2 2 cos 2 2 2 2 tan 3
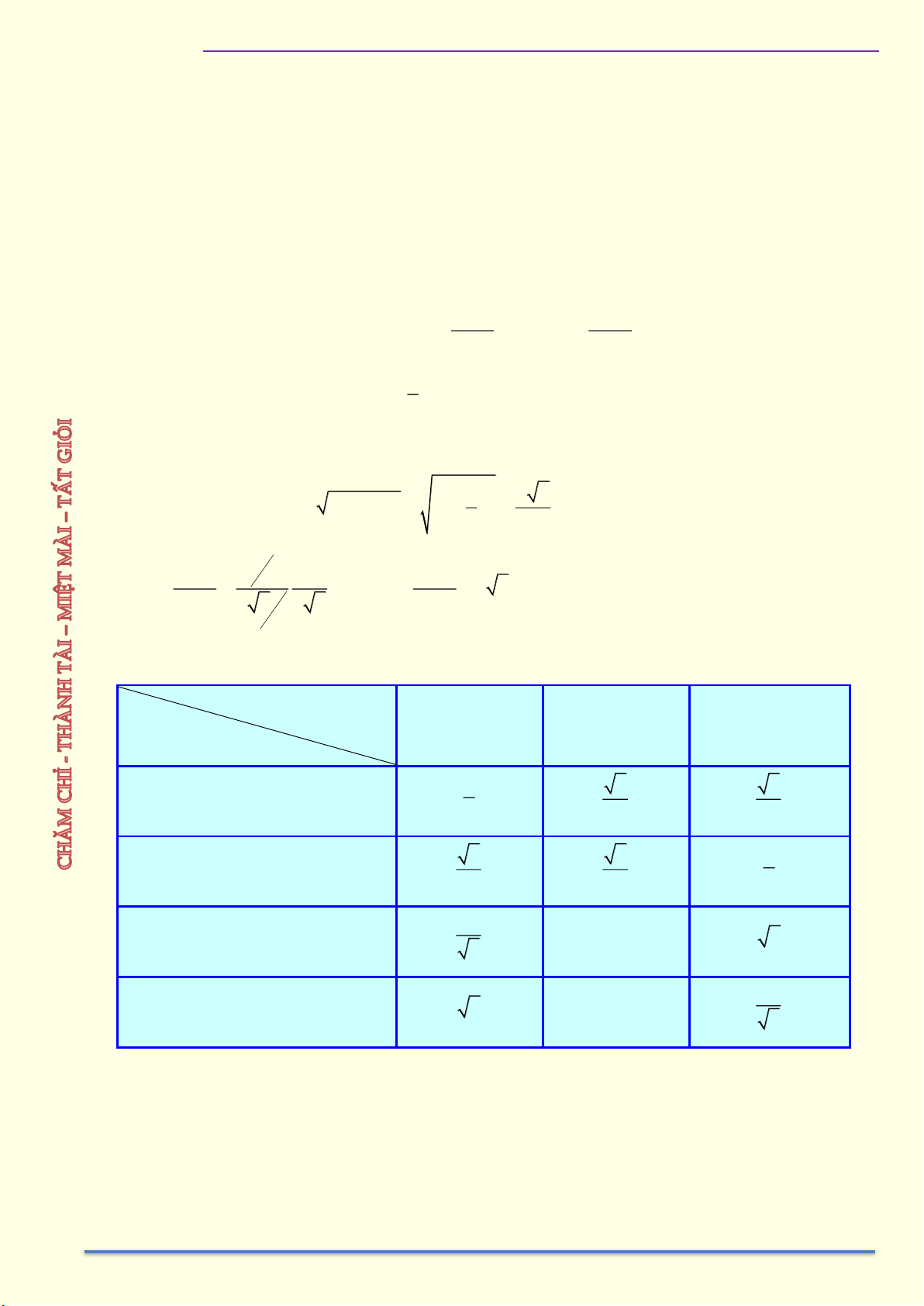
IV. Bảng giá trị lượng giác của một số góc đặc biệt  0 30 0 45 0 60 Tỷ số lượng giác 2 3 sin 1 2 2 2 2 1 cos 3 2 2 2 tan 1 1 3 3 1 cot 3 1 3
Bài toán so sánh các giá trị lượng giác
Cho hai góc nhọn a và b, ta có
• a b  sin a  sinb và tan a  tanb
• a b  cos a  cosb và cot a  cot b
Ví dụ 3: Sắp xếp các tỷ số dưới đây theo tỷ lệ tăng dần.
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 9
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9 a) 0 sin 40 , 0 cos 28 , 0 sin 68 , 0 cos 88 . b) 0 tan 65 , 0 cot 42 , 0 tan76 , 0 cot 27 . Giải a) Ta có 0 0 0 0
sin 40 = cos 50 ,sin 68 = cos 22 khi đó 0 0 0 0
cos 88  cos 50  cos 28  cos 22 Hay 0 0 0 0
cos 88  sin 40  cos 28  sin 68 . b) Ta có 0 0 0 0
tan 65 = cot 25 , tan 76 = cot 14 khi đó 0 0 0 0
cot 42  cot 27  cot 25  cot14 Hay 0 0 0 0
cot 42  cot 27  tan 65  tan76 .
Ví dụ 4: Hãy so sánh sin và tan ; cos và cot với  là góc nhọn. Giải • sin và tan sin Ta có tan  sin 
 sin  sin  sin.cos  1  cos (đúng) cos • cos và cot cos
Ta có cos  cot  cos 
 sin.cos  cos  sin  1 (đúng) sin
Ví dụ 5: Tính giá trị các biểu thức sau a) 2 0 2 0 2 0 2 0
A = sin 10 + sin 20 + ... + sin 70 + sin 80 . 0 3sin 54 b) 2 0 2 0 0 0
B = sin 14 + sin 76 + tan 2 .tan 88 − . 0 cos 36 Giải a) Ta có 2 0 2 0 2 0 2 0
A = sin 10 + sin 20 + ... + sin 70 + sin 80 = ( 2 0 2 0 + )+( 2 0 2 0 + )+( 2 0 2 0 + )+( 2 0 2 0 sin 10 sin 80 sin 20 sin 70 sin 30 sin 60 sin 40 + sin 50 ) = ( 2 0 2 0 + )+( 2 0 2 0 + )+( 2 0 2 0 + )+( 2 0 2 0 sin 10 cos 10 sin 20 cos 20 sin 30 cos 30 sin 40 + cos 40 ) = 1+1+1+1 = 4 0 3sin 54 b) Ta có 2 0 2 0 0 0
B = sin 14 + sin 76 + tan 2 .tan 88 − 0 cos 36 0 2 0 2 0 0 0 3sin 54
= sin 14 + cos 14 + tan 2 .cot 2 − = 1+1− 3 = 1 − 0 sin 54 cos a + sin a
Ví dụ 6: Cho tan a = 3 . Tính P = . cos a − sin a Giải
10 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG cos a sin a + cos a + sin a 1+ tan a 1 + 3 cos a cos a P = = = = = 2 − . cos a − sin a cos a sin a 1− tan a 1 − 3 − cos a cos a Bài tập
Không dùng bảng giá trị lượng giác của một số góc đặc biệt cho các câu từ 2.1 đến 2.9 2
2.1 Cho  là góc nhọn và sin = . Tính các giá trị lượng giác còn lại của  . 5 3
2.2 Cho  là góc nhọn và cos =
. Tính các giá trị lượng giác còn lại của  . 2
2.3 Cho  là góc nhọn và tan = 3 . Tính các giá trị lượng giác còn lại của  .
2.4 Cho  là góc nhọn và cot = 1. Tính các giá trị lượng giác còn lại của  .
2.5 Cho  là góc nhọn và cos = x . Tính các giá trị lượng giác còn lại của  .
2.6 Không dùng máy tính hãy sắp xếp các giá trị lượng giác sau theo thứ tự tăng dần a) 0 0 0 0
sin 25 ,cos15 ,sin 50 ,cos 66 . b) 0 0 0 0 0
cot 35 , tan 48 ,cot 44 , tan 53 ,cot 39 .
2.7 Không dùng máy tính hãy so sánh các giá trị lượng giác sau a) 0 sin 32 và 0 tan 32 b) 0 cos 35 và 0 cot 35 c) 0 sin 25 và 0 cot 55 d) 0 cos 54 và 0 tan 42
2.8 Không dùng máy tính hãy sắp xếp các tỷ số lượng giác sau theo thứ tự giảm dần 0 0 0 0
cot 36 , tan 72 ,cot 21 ,sin 54 2 2 sin a − cos a 3 3 sin a − cos a
2.9 Cho tan a = 3 . Tính P = và Q = . sin . a cos a 3 3 sin a + cos a
2.10 Cho góc a nhọn. Biết 2 2 1
cos a − 2 sin a = . Tìm giá trị góc a. 4
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 11
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
BÀI 3: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG I. Các hệ thức
_ Cho tam giác ABC vuông ở C, ta có các hệ thức lượng giác của góc A như sau BC B sin A = AB AC cos A = AB BC tan A = AC AC cot A = BC C A Định lý
• Trong một tam giác vuông mỗi cạnh góc vuông bằng cạnh huyền nhân với sin góc đối hoặc côsin góc kề.
• Trong một tam giác vuông thì cạnh góc vuông này bằng cạnh góc vuông kia nhân với tan
góc đối hoặc côtang góc kề.
Cho tam giác ABC vuông ở C với BC = a , CA = b và AB = c khi đó B a = . c sin A = . c cos B c b = . c sin B = . c cos A a a = . b tan A = . b cot A b = . a tan B = . a cot B C A b
II. Giải tam giác vuông
_ Giải tam giác vuông là tìm tất cả các cạnh và các góc của tam giác vuông đó khi biết trước hai
cạnh hoặc một cạnh và một góc nhọn của nó.
Ví dụ 1: Giải tam giác ABC vuông ở C biết AC = 4 cm và BC = 3 cm . Giải Ta có 2 2 2 2 2
AB = AC + BC = 4 + 3 = 25  AB = 5 cm BC 3 0 0 sin A =
=  BAC  37  ABC = 53 . AC 4
12 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Ví dụ 2: Cho tam giác ABC vuông ở C biết AB = 13 cm và 0 A = 23 . Giải Ta có 0 0 0
A = 23  B = 90 − A = 67 0 2 2 2 2 AC = A .
B cos A = 13.cos 23  12cm BC = AB − AC = 13 − 12 = 5 cm .
Ví dụ 3: Giải tam giác ABC vuông ở C biết BC = 20 cm và 0 A = 43 . Giải Ta có 0 0 0
A = 43  B = 90 − A = 47 0 BC 20 AC = B .
C cot A = 20.cot 43  21 cm, AB = =  29 cm . 0 sin A sin 43
Ví dụ 4: Cho tam giác ABC có 0 A = 75 , 0
B = 45 và AB = 6 cm . Tính diện tích tam giác ABC. Giải Ta có 0 0 0 0 0 0
A + B +C = 180  C = 180 − A − B = 180 −75 − 45 = 60 Vẽ AD ⊥ BC
Xét tam giác vuông ABD ta có 0 2
AD = AB = sin B = 6.sin 45 = 6. = 3 2 cm 2 0 2
BC = AB cos B = 6.cos 45 = 6. = 3 2 cm 2
Xét tam giác vuông ACD ta có 0 3 CD = . AD cot C = . AD cot 60 = 3 2. = 6 cm 3
Do đó BC = BD + CD = 3 2 + 6 cm 1 1
Vậy diện tích tam giác ABC là S = A . D BC = .3 2. + = + . ABC (3 2 6) 3 3( 3 ) 2 1 cm 2 2
Ví dụ 5: Cho tam giác ABC cân tại A, đường cao BK = h và A
ABC =  . Tính các cạnh của của tam giác theo h và  . Giải
Tam giác ABC cân nên ACB = ABC =  K BK h Ta có BK = B .
C sin  BC = = sin sin
Vẽ đường cao AH của tam giác ABC suy ra H là trung điểm C B H BC h
BC nên BH = CH = = 2 2 sin
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 13
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9 CH h
Trong tam giác AHC ta có CH = A .
C cos  AC = = cos 2 sin cos h
Do đó AB = AC = . 2sin cos
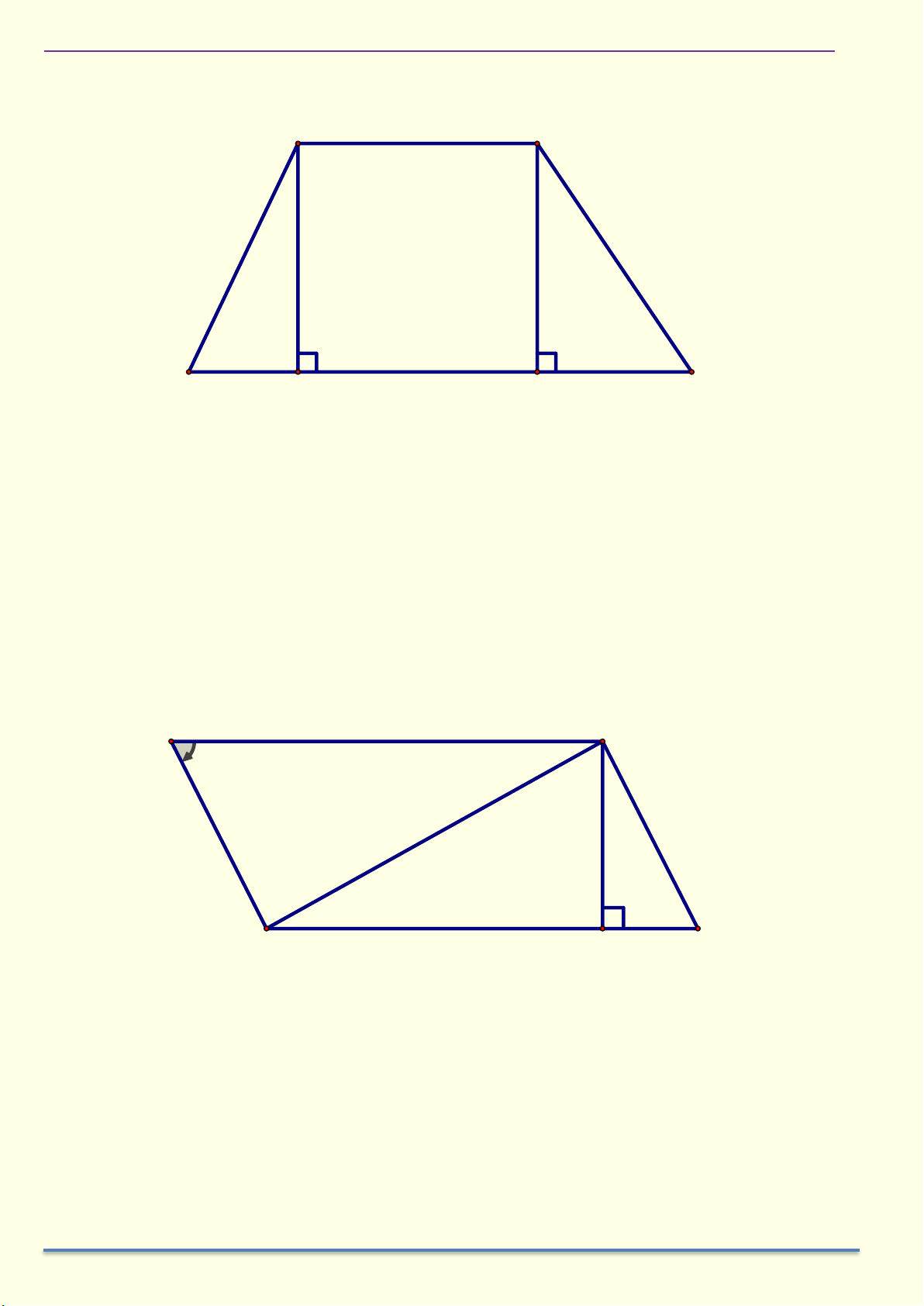
Ví dụ 6: Cho hình thang cân ABCD có AB//CD, biết AB = 5 cm , CD = 13 cm và BD vuông góc với BC.
a) Tính độ dài đường cao BH của hình thang.
b) Tính diện tích hình thang.
c) Tính các góc của hình thang. Giải
a) Kẻ AK vuông CD tại K, ta có AKD = B
HC suy ra DK = CH
Lại có ABHK là hình bình hành có một góc vuông nên ABHK là hình chữ nhật DC − HK − Suy ra HK = AB = 13 5
5 cm  DK = CH = = = 4 cm 2 2
Như vậy DH = DK + HK = 4 + 5 = 9 cm Xét tam giác DBC có 2
BH = DH.CH = 9.4 = 36  BH = 6 cm . 1 1 b) Ta có S = AB + CD BH = + = . ABCD ( ). (5 13) 2 .6 54 cm 2 2 BH 6 3
c) Xét tam giác BHC có 0 tanC = = =  C  56 19' CH 4 2 Suy ra 0 D = 56 19' và 0 0 0
DAB = CBA = 180 − 56 19' = 123 41' . Bài tập sin a cos a
3.1 Với góc a nhọn. Chứng minh 2 2
sin a + cos a = 1, tan a = , cot a = và tan . a cot a = 1 . cos a sin a 3.2
a) Giải tam giác ABC vuông tại A biết AB = 5 cm và AC = 8 cm .
b) Giải tam giác DEF vuông tại D biết DE = 100 cm và 0 E = 51 .
c) Cho tam giác ABC vuông tại A có BC = 3AB . Tính giá trị C .
d) Cho tam giác ABC cân tại A có AB = 3BC . Tính giá trị B .
3.3 Tính góc nhọn  biết rằng sin = cos .
14 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
3.4 Một chiếc đò ở điểm A muốn băng ngang qua sông theo đường AH nhưng bị nước cuốn đến
điểm B cách H một đoạn bằng 50m. Tìm độ rộng của con sông và quãng đường đò đã đi với dữ
kiện được thêm ở hình dưới đây. H B 300 A
3.5 Một chiếc máy bay đang bay ở độ cao 900 m. Một người quan sát nhìn chiếc máy bay đó dưới góc 0
 = 40 (như hình bên dưới). Tính khoảng cách từ người quan sát đến máy bay. B 400 H A
3.6 Cho tam giác ABC có 0
B = 60 , AB = 15 cm , BC = 20 cm . Tính độ dài các góc và các cạnh còn
lại của tam giác ABC.
3.7 Cho tam giác ABC có AH là đường cao. Biết AB = 25 cm , 0 B = 70 và 0
C = 50 . Tính độ dài AH và BC.
3.8 Cho tam giác ABC có 0 A = 75 , 0
B = 60 và AB = 6 cm . Tính diện tích tam giác ABC.
3.9 Cho tam giác ABC có 0 A = 60 , 0
B = 45 và AB = 12 cm . Tính diện tích tam giác ABC.
3.10 Cho hình thang ABCD (AB//CD). Biết AB = 4 cm , AH = 4 cm và 0
D = 70 . Vẽ hai đường cao
AH và BK. Biết rằng 0
KBC = 50 . Tính BC và DC.
3.11 Cho hình bình hành ABCD có BD vuông góc với BC. Biết AB = a và A =  . Tính diện tích
ABCD theo a và  .
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 15
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
3.12 Cho tam giác nhọn ABC có 0 A = 75 , 0
B = 60 , AB = c . Tính độ dài AC, BC theo c. A BC
3.13* Cho tam giác ABC vuông ở C. Chứng minh tan = . 2 AB + AC
Áp dụng kết quả trên tính giá trị lượng giác của góc 0 15 . AB BC CA
3.14* Cho tam giác ABC nhọn. Chứng minh = = . sinC sin A sin B
Áp dụng kết quả trên tính giá trị lượng giác của góc 0 75 .
3.15 Cho tam giác nhọn ABC có hai đường cao BE và CD. Chứng minh DE = BC.cos A .
16 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
HƯỚNG DẪN MỘT SỐ BÀI TẬP CHƯƠNG I
BÀI 1: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TỎNG TAM GIÁC VUÔNG 1.1
Dùng Pytago tìm được BC = 28,9 cm Áp dụng A .
B AC = AH.BC AH = 12 cm Áp dụng 2
AB = BH.BC BH = 6, 4 cm và CH = 22, 5 cm . 1.2 Đặt 2 2
BH = x BC = x + 16  BH.BC = AB x + 16x + 64 = 289  x = 9 và tính được
AH = 12 cm , BC = 25 cm và CA = 20 cm . 1.3 Cách 1:
Đặt BH = x CH = BC − x = 28,9 − x
BH CH = AH  (x − )2 2 . 14, 45
= 64,8025  x = 22,5 hay x = 6,4
Như vậy có hai trường hợp và kết quả là AB = 25, 5 cm , AC = 13,6 cm và ngược lại. Cách 2: Xét 2 2 2
BC = AB + AC và A .
B AC = AH.BC
AB + AC + 2A .BAC = (AB+ AC)2 2 2
AB + AC = 39,1
AB + AC = 39,1 Ta dùng    hoặc 
AB + AC − AB AC = − =  (AB− AC)2 2 2 AB − AC =  11,9 2 . AC AB 11,9
Kết quả thu được như Cách 1. 1.4 Kiểm tra được 2 2 2
BC = AB + AC A
BC vuông tại A 1 13 Suy ra AM = BC = cm 2 2 60
Áp dụng AH.BC = A . B AC AH = cm 13 1.5 9
Đặt HB = x HC =
x , với x  0 16 Áp dụng 2 2 9 AH = H . B HC  48 = . x
x x = 64  BH = 64 cm và CH = 36 cm . 16
Suy ra BC = BH + CH = 100 cm Áp dụng 2 2
AB = BH.BC AB = 64.100 = 6400  AB = 80 cm
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 17
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
Áp dụng định lý Pytago suy ra AC = 60 cm . 1.6 3
Đặt AB = x AC = x , với x  0 4 2  3 
Áp dụng định lý Pytago có 2 2 2 2 2 2
BC = AB + AC  125 = x + x
x = 10000  x =   100  4 
Suy ra AB = 100 cm và AC = 75 cm A . B AC
Áp dụng AH.BC = A . B AC AH =  AH = 60 cm . BC 1.7 A C B H M BC A . B AC 3 a) Ta có AM =  BC = 2 3 cm
AH.BC = A . B AC AH = = cm 2 BC 2 Áp dụng định lý Pytago 1 3 3 b) 2 S = AH.BC = cm . ABC 2 2 2 2 2
BC = AB + AC AC = 3 cm Áp dụng 1.8 Áp dụng định lý Pytago A 2 2 2
BH + AH = AC BH = 2 cm 2
CH = 2 cm  HM = cm 2 N Áp dụng định lý Pytago G 2 2 2 14
AM = AH + HM AM = cm 2
Gọi G là giao điểm AH và BN C B H M
G là trọng tâm tam giác ABC
18 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG 1 3 Nên GH = AH = cm 3 3 Áp dụng định lý Pytago 2 2 2 21 3 21
BN = GH + BH BN = cm  BN = BG = cm 3 2 2 1.9* A K B C H M x
Tam giác ABC cân tại A có AH là đường cao nên AH cũng là đường trung tuyến BCHB = HC = = 3 cm 2 Xét tam giác ABH Áp dụng định lý Pytago 2 2 2
AB = AH + BH AH = 4 cm
Dùng diện tích tam giác ABC có 1 1
AH.BC = B .
K AC BK = 4,8 cm 2 2 Xét tam giác ABK Áp dụng định lý Pytago 2 2 2
AB = AK + BK AK = 1, 4 cm Xét tam giác ABM Áp dụng 2
AB = AK.AM AM = 17,9 cm 1
Diện tích tam giác ABM là 2 S = B . K AM  42,9 cm . ABM 2
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 19
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9 1.10 J
Vẽ AJ ⊥ AI với J thuộc CD
Xét hai tam giác vuông ABI và ADJ có A D
AB = AD và AIB = AJD nên ABI = ADJ 1 1 1 1 1 Suy ra + = + = 2 2 2 2 2 AI AK AJ AK AD 1 1
Vì AD không đổi nên + không đổi hay nó không 2 2 AI AK
phụ thuộc vào vị trí của điểm I. B C
1.11 Tương tự Ví dụ 7 a) I
Bạn đọc tự giải bằng cách vẽ thêm đường cao AK của tam giác ABC. 1.12 K A B
Vẽ tia Ax vuông góc với AC và cắt CD tại E
Xét tam giác vuông ACE 1 1 1 Áp dụng = + 2 2 2 AD AE AC
Xét tứ giác ABDE, dễ thấy ABDE là E C D
hình bình hành nên AE = BD. x 1 1 1 Vậy = + . 2 2 2 AD BD AE 1.13 A B
Qua A vẽ Ax vuông góc với AK
cắt đường thẳng CD tại M
Ta có MAD = BAI (cùng phụ I DAI ) do đó ADM = A
BI AM = AI M K
Xét tam giác MAK vuông tại A D C x
20 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG 1 1 1 Áp dụng = +
mà AB = AD và AM = AI (cmt) 2 2 2 AD AM AK 1 1 1 Vậy = + . 2 2 2 AB AI AK 1.14 A B a) Xét tam giác ABD Áp dụng 2 2
AB = BH.BD a = BH.BD Tương tự, cũng có 2 b = H . D BD 2 HB a Chia hai vế, ta có = H 2 HD b K
b) Vì HK // DC (cùng vuông góc với BC) D I C Hệ quả định lý Ta-lét cho ta HK HB D . C HB . a HB =  HK = = DC HD BC BD 2 2 2 2 2 HB a HB + HD a + b BD a + b Mà =  =  =
(dùng tính chất dãy tỷ số bằng nhau) 2 2 2 HD b HB a HB a 2 B . D a Suy ra HB = 2 2 a + b 2 . BD a a 3 2 2 + a Khi đó a b HK = = . 2 2 BD a + b 1.15 A N G C B M
Gọi G là trọng tâm tam giác ABC 2 Khi đó BG = BN 3
Tam giác ABC vuông tại A
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 21
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9 2 a 6 Áp dụng 2 2 2
AB = BN.BG a = BN BN = 3 2 2 2 3a a a 2
Áp dụng định lý Pytago, ta có 2 2 2 2 2
AN + AB = BN AN = − a =  AN = 2 2 2
Áp dụng định lý Pytago, ta có 2 2 2
BC = AB + AC BC = a 3 1.16
a) Tứ giác AEHF có ba góc vuông nên nó là hình chữ nhật.
b) Xét tam giác AHB có 2 HA = A . E AB Xét tam giác AHC có 2
HA = AF.AC Vậy A .
E AB = AF.AC
c) Xét tam giác AHB vuông tại H có HE là đường cao nên 2 HE = E . A EB A F E C B H
Xét tam giác AHC vuông tại H có HF là đường cao nên 2 HF = . FA FC
Xét tam giác ABC vuông tại A có AH là đường cao nên 2 AH = H . B HC Ta có 2 2 2 2
EF = HE + HF EF = E . A EB + F . A FC
Tứ giác AEHF là hình chữ nhật nên 2 2
AH = EF AH = EF Vậy E . A EB + F . A FC = H . B HC .
d) Xét tam giác ABC vuông tại A có AH là đường cao Ta có 2 4 2 2
AH = BH.CH AH = BH .CH
Xét các tam giác ABH và ACH vuông tại H lần lượt có HE và HF là đường cao Ta có 2 BH = B . E BA và 2
CH = CF.CA Suy ra 4 AH = B . E B . A C . A CF = E . B A . B A . C CF Mà A .
B AC = AH.BC do đó 4 3 AH = E . B AH.B .
C CF AH = E . B B . C CF .
22 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
e) Xét tam giác ABC vuông ở A có AH là đường cao Ta có 2
AB = BH.BC và 2
AC = CH.BC 2 4 2 AB BH AB BH Suy ra =  = 2 4 2 AC CH AC CH Mà 2 BH = E . B AB và 2
CH = CF.AC 4 3 AB E . B AB AB EB Do đó =  = . 4 3 AC CF.AC AC CF f) Ta có 2 BH = E . B AB và 2
CH = CF.AC nên 4 2 2
BH = EB .AB và 4 2 2
CH = CF .AC 4 2 2 2 2 BH EB .AB EB .BH.BC EB .BH Suy ra = = = 4 2 2 2 2 CH CF .AC CF .CH.BC CF .CF 3 2 BH EB Vậy = . 3 2 CH CF
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 23
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
BÀI 2: TỶ SỐ LƯỢNG GIÁC CỦA MỘT GÓC NHỌN 2.1  Áp dụng 2 2 21 sin 2 21
sin  + cos  = 1  cos =  tan = = ,cot = . 5 cos 21 2 2.2  Áp dụng 2 2 1 sin 1
sin  + cos  = 1  sin =  tan = = ,cot = 3 . 2 cos 3 2.3 sin Dùng tan = = 3 và 2 2 1 3 1
sin  + cos  = 1  cos = ,sin =  cot = . cos 2 2 3 2.4 cos Dùng cot = = 1 và 2 2 2
sin  + cos  = 1  cos = sin =  tan = 1. sin 2 2.5 2 1− x x Dùng 2 2 2
sin  + cos  = 1  sin = 1− x  tan = ,cot = . 2 x 1− x 2.6 a) 0 0 0 0
sin 25 ,cos15 ,sin 50 ,cos 66 . Ta có 0 0 cos15 = sin 75 và 0 0 cos 66 = sin 24 Mà 0 0 0 0
sin 24  sin 25  sin 50  sin75
Vậy thứ tự cần sắp là 0 0 0 0
cos 66  sin 25  sin 50  cos15 . b) 0 0 0 0 0
cot 35 , tan 48 ,cot 44 , tan 53 ,cot 39 . Ta có 0 0 tan 48 = cot 42 và 0 0 tan 53 = cot 37 Mà 0 0 0 0 0
cot 44  cot 42  cot 39  cot 37  cot 35 Vậy 0 0 0 0 0
cot 44  tan 48  cot 39  tan 53  cot 35 . 2.7 a) 0 sin 32 và 0 tan 32
Dùng cách làm của Ví dụ 4 có 0 0 tan 32  sin 32 b) 0 cos 35 và 0 cot 35
Dùng cách làm của Ví dụ 4 có 0 0 cot 35  cos 35
24 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG c) 0 sin 25 và 0 cot 55 Ta có 0 0
cot 55 = tan 35 dùng Ví dụ 4 ta có 0 0 0 tan 35  sin 35  sin 25 Vậy 0 0 cot 55  sin 25 . d) 0 cos 54 và 0 tan 42 Ta có 0 0
tan 42 = cot 48 dùng Ví dụ 4 ta có 0 0 0 cot 48  cos 48  cos 54 Vậy 0 0 tan 42  cos 54 . 2.8 Ta có 0 0 tan72 = cot18 và 0 0 sin 54 = cos 36
Dùng Ví dụ 4 ta có 0 0 cot 36  cos 36 Mà 0 0 0 cot 36  cot 21  cot 18 Vậy 0 0 0 0
sin 54  cot 36  cot 21  tan72 . 2.9 2 sin a − 2 2 1 2 2 2 sin a − cos a tan a − 1 3 − 1 8 cos a P = = = = = . sin . a cos a sin . a cos a tan a 3 3 2 cos a 3 sin a − 3 3 1 3 3 sin a − cos a 3 − 1 13 cos a Q = = = = . 3 3 3 3 sin a + cos a sin a 3 + 1 14 + 1 3 cos a 1 1 3 1 2.10 Ta có 2 2 2 2 2 0
cos a − 2sin a =
 1−sin a − 2sin a =  3sin a =  sin a =  a = 30 . 4 4 4 2
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 25
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9
BÀI 3: MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG 3.1
Xét tam giác ABC vuông tại C, giả sử A = a . BC AC B Ta có sin a = , cos a = AB AB 2 2 BC AC Nên 2 2 sin a + cos a = + 2 2 AB AB 2 2 BC + AC Suy ra 2 2 sin a + cos a = = 1 2 AB BC BC sin a tan AB a = = = AC AC cos a AB a C A cos a Tương tự cot a = và tan . a cot a = 1 . sin a 3.2
a) Áp dụng định lý Pytago 2 2 2
BC = AB + AC BC = 89 cm AC 8 0 0 sin B = =
B  58  C  32 . BC 89 b) 0
F = 39 , DE = EF.cos E EF  158,9 cm , DF  123, 5 cm . AB 1 c) 0 sinC = =  C  19 28' . BC 3 1 1 BH 1
d) Vẽ đường cao AH suy ra 0 BH = BC = AB  cos B = =  B  80,4 . 2 6 AB 6 3.3 2 Áp dụng 2 2 0
sin  + cos  = 1  sin =   = 45 . 2
3.4 Độ rộng con sông HB HB Ta có 0 tan 30 =  HA = = 50 3 m 0 HA tan 30 Quãng đường đã đi 2 2
AB = AH + BH = 100 m . HB HB 900 3.5 Ta có 0 sin 40 =  AB = =  1400,15 m . 0 0 AB sin 40 sin 40
26 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
3.6 Vẽ đường cao AH của tam giác ABC BH 15 25
Xét tam giác AHB có cos ABH =  BH = A . B cos ABH =
cm  CH = BC − BH = cm AB 2 2 AH Lại có 0 15 3 sin ABH =  AH = . AB sin 60 = cm AB 2 AH Như vậy 2 2 0 0
AC = AH + CH = 5 13 cm  sinACB =
ACB  56,1  BAC  73,9 . AC 3.7
Vẽ đường cao AH củ tam giác ABC. Ta có 0 BH = A .
B cos B = 25.cos70  8,6 cm và 0 0 AH = A .
B sin B = A .
B sin70 = 25.sin70  23,5 cm AH 23, 5
Lại có AH = AC.sin C AC = =  30,7 cm 0 sin C sin 50 0  CH = A .
C cosC = 30,7.cos 50  19,7 cm
Do đó BC = BH + CH  28, 3 cm . 3.8
Vẽ đường cao AD cyra tm giác ABC
Áp dụng AD = A .
B sin B AD = 3 3 cm và BD = A .
B cos B BD = 3 cm
Xét tam giác ACD có CD = A .
D cotC CD = 3 3 cm
Suy ra BC = BD + CD = 3(1+ 3) cm 1 9 Vậy S = A . D BC = + . ABC ( 3 3) 2 cm 2 2 3.9
Vẽ đường cao CD của tam giác ABC
Đặt CD = x với x  0 x 3
Xét tam giác ACD có AD = C .
D cot A AD = cm . 3
Xét tam giác BCD có BD = C .
D cot B BD = x cm 3
AB = AD + BD = x + x
= 12  x = 6(3− 3) cm 3 1 Vậy S = A . B CD = 36 − . ABC (3 3) 2 cm 2
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 27
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9 3.10 A B D C H K
Dễ thấy ABHK là hình chữ nhật có hai cạnh kề bằng nhau nên nó là hình vuông.
Suy ra BK = AH = 4 cm Xét tam giác BKC
Áp dụng BK = BC.cos KBC BC  6,22 cm và KC = BK.tan KBC  4,77 cm
Tương tự, xét tam giác AHD tính được DH = AH = cot ADH  1,46 cm
Do đó DC = DH + HK + KC  10, 23 cm . 3.11 A B α D C H
ABCD là hình bình hành  C = A =  và DC = AB = a
Xét tam giác vuông BCD có BC = C .
D cosC = acos
Vẽ BH vuông góc CD
Áp dụng BH = BC.sinC = a cos.sin Do đó 2 S = D .
C BH = a sin.cos . ABCD
28 – EDUCATION _ Vững kiến thức – Nhạy tư duy
HÌNH HỌC 9 – CHƯƠNG I. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG 3.12 A
Vẽ AD vuông góc BC
Xét tam giác ABD có AD = A . B sin B
Xét tam giác ACD có AD = AC.sinC Do đó AB AC A .
B sin B = A . C sinC  = sinC sin B AB BC CA Tương tự ta có = = . B C D sinC sin A sin B AB AC 6 Như vậy =  AC = c . 0 0 sin 45 sin 60 2 c
Xét tam giác ABD có BD = ABcos B = 2 c 3
Xét tam giác ACD có CD = AC.cosC = 2 c ( 3 + ) 1
Như vậy BC = BD + CD = . 2 3.13*
Vẽ đường phân giác AD của góc A A BD BD Nên = AC AB CD BD + CD BC  = = (tính chất AC AB + AC AB + AC dãy tỷ số bằng nhau) A CD Mà tan ACD = tan = 2 AC A BC Vậy tan = C B 2 AB + AC D
Xét tam giác ABC vuông ở C với 0 A = 30 Đặt BC = a BC Ta có AC = B .
C cot A = a 3 , AB = = 2a sin A
HNT EDUCATION _ Vững kiến thức – Nhạy tư duy – 29
Gv. Lương Anh Nhật – ĐT: 0968.373.054 HÌNH HỌC 9 A BC
Dùng kết quả trên, ta có 0 0 tan15 = tan = = 2 − 3  cot15 = 2 + 3 2 AB + AC 0 sin15 Laị có 0 0 tan15 =  sin15 = (2− 3) 0 cos15 0 cos15 6 + 2 6 − 2 Áp dụng 2 0 2 0 0 0 0 0
sin 15 + cos 15 = 1  cos15 =  sin15 = tan15 .cos15 = 4 4 3.14*
Vẽ AD vuông góc BC
Xét tam giác ABD có AD = A . B sin B A B C D
Xét tam giác ACD có AD = AC.sinC AB AC AB BC CA Do đó A .
B sin B = A . C sinC  = . Tương tự ta có = = . sinC sin B sinC sin A sin B
Dùng giả thiết bài 3.12 (bạn đọc có thể dùng giả thiết khác) c ( 3 +1) BC 2 6 + 2 6 + 2 Ta có 2 0 sin A = sin C = . =  sin75 = AB c 2 4 4 − Dùng 2 0 2 0 0 6 2
sin 75 + cos 75 = 1  cos 75 = 4 Suy ra 0 0
tan75 = 2 + 3,cot 75 = 2 − 3 . AE AD
3.15 Xét tam giác AED và ABC có A chung và =
(= cosA) nên chúng đồng dạng AB AC ED AE Suy ra =
= cos A DE = B . C cos A BC AB
30 – EDUCATION _ Vững kiến thức – Nhạy tư duy