




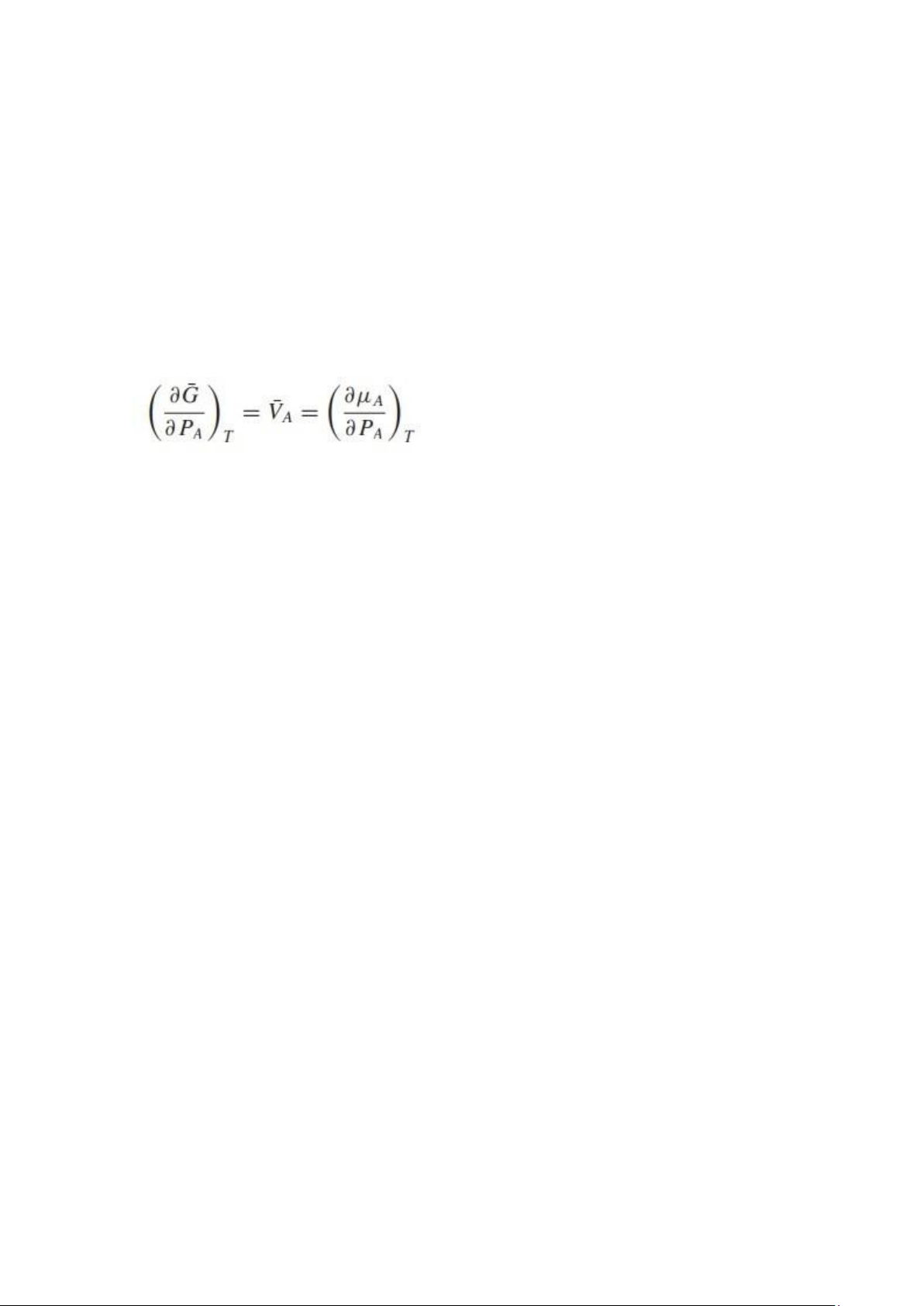


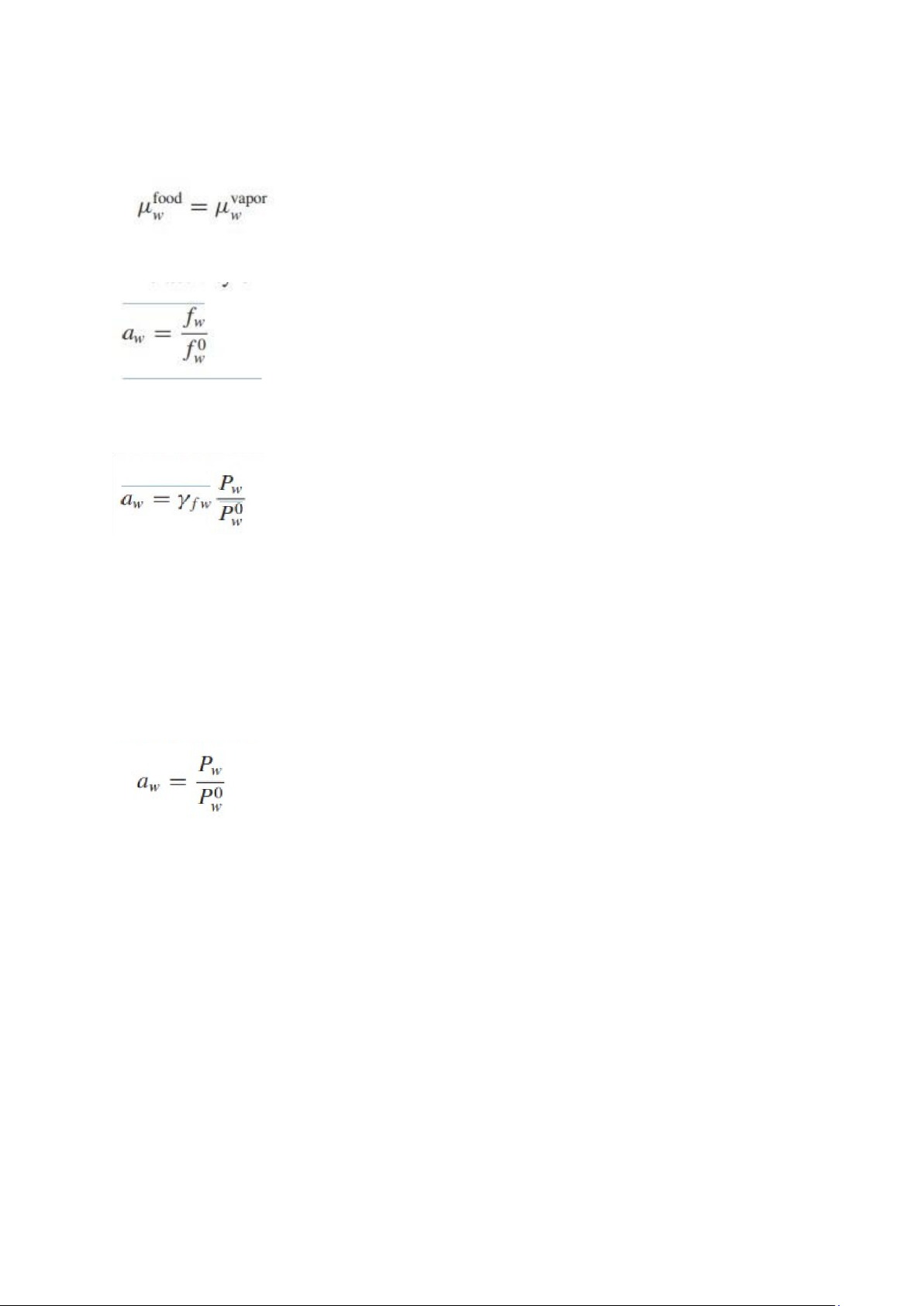



Preview text:
Chương 5 Hoạt động nước và tính chất hấp thụ của thực phẩm TÓM LƯỢC
Hoạt tính nước và đặc tính hấp thụ của thực phẩm được coi là những yếu tố vật
lý quan trọng trong công thức và quy trình thực phẩm. Hầu hết các phản ứng
sinh hóa và vi sinh được kiểm soát bởi hoạt động nước của hệ thống, do đó đây
là một thông số hữu ích để dự đoán độ ổn định và thời hạn sử dụng của thực
phẩm. Tốc độ truyền hơi ẩm trong quá trình làm khô và qua màng bao gói hoặc
lớp phủ thực phẩm ăn được trong quá trình bảo quản có thể được ước tính và do
đó điều kiện làm khô, sự lão hóa của bao bì hoặc vật liệu phủ có thể được lựa
chọn bằng cách sử dụng hoạt tính nước và tính chất hấp thụ của thực phẩm.
Ngoài ra, những đặc tính này phải được xem xét trong quá trình phát triển sản phẩm.
Có nhiều phương pháp để đo hoạt độ nước của thực phẩm. Chương này cung
cấp thông tin về lý thuyết hoạt động của nước, các phương pháp dự đoán và đo
lường của nó cũng như việc chuẩn bị các đường đẳng nhiệt hấp phụ. Các
nguyên tắc về tính chất đối chiếu như độ cao điểm sôi, độ giảm điểm đông đặc
và áp suất thẩm thấu cũng được thảo luận. Ngoài ra, các mô hình hấp phụ được
sử dụng phổ biến nhất cũng được đưa ra.
Hoạt độ nước của thực phẩm có thể được đo bằng các phương pháp dựa trên đặc
tính keo tụ, chuyển đồng đẳng, và độ hút ẩm của muối và sử dụng ẩm kế.
Đường đẳng nhiệt hấp thụ ẩm mô tả mối quan hệ giữa hoạt độ nước và độ ẩm
cân bằng của sản phẩm thực phẩm ở mức không đổi
Phương pháp đơn giản nhất để chuẩn bị đường đẳng nhiệt hấp phụ của thực
phẩm là bảo quản mẫu đã cân trong một vật chứa kín được duy trì ở một độ ẩm
tương đối nhất định ở nhiệt độ không đổi và cân lại sau khi đạt được trạng thái
cân bằng. , axit sunfuric và glixerol.
5.1 TIÊU CHÍ CỦA EQUILIBRIUM
Tiêu chí cho cân bằng nhiệt là bằng nhau về nhiệt độ trong khi tiêu chí cho cân
bằng cơ học là bằng nhau về áp suất. Cân bằng hóa lý được đặc trưng bởi sự
bằng nhau về thế hóa học (µ) của mỗi thành phần. Điện thế hóa học xác định
liệu một chất sẽ trải qua phản ứng hóa học hay khuếch tán từ phần này sang
phần khác của hệ thống.
Thế năng hóa học của một thành phần trong pha lỏng (L) bằng thế trong pha hơi
(V) nếu hơi và lỏng ở trạng thái cân bằng: µL i = µV i (5,1)
Thế năng hóa học là năng lượng riêng phần mol tự do và có thể được biểu thị bằng: µi = ∂G ∂ni
T, P, nj (5,2) trong đó G là năng lượng tự do Gibbs và ni là số mol của thành
phần i. Định nghĩa cho thấy rằng thế hóa học của một thành phần của một hỗn
hợp đồng nhất bằng tỷ lệ của sự gia tăng trong
Năng lượng tự do Gibbs khi bổ sung một lượng nhỏ chất này.
Năng lượng tự do Gibbs được định nghĩa là sự kết hợp của entanpi (H), nhiệt độ (T) và entropi (S): G = H - TS (5,3)
Entanpi có thể được biểu thị bằng nội năng (U), áp suất (P) và thể tích (V): H = U + PV (5,4)
Chèn Eq. (5.4) thành phương trình (5,3): G = U + PV - TS (5.5) Phân biệt Eq. (5.5):
dG = dU + PdV + VdP - TdS - SdT (5.6)
Đối với một quá trình thuận nghịch trong một hệ thống khép kín có thành phần
không đổi, định luật thứ nhất và thứ hai của nhiệt động lực học có thể được kết hợp để tạo ra: dU = TdS - PdV (5,7)
Giới thiệu Eq. (5,7) thành (5,6): dG = VdP - SdT (5,8)
Nếu hệ thống ở thành phần không đổi, Eqs. (5.9) và (5.10) có thể nhận được từ phương trình. (5,8): ∂G ∂T P, ni = −S (5,9)
Vì entropy của hệ luôn dương nên năng lượng tự do Gibbs giảm khi nhiệt độ
tăng ở áp suất không đổi.
Vì entropy của hệ luôn dương nên năng lượng tự do Gibbs giảm khi nhiệt độ
tăng ở áp suất không đổi. ∂G ∂ P T, ni = V (5,10)
Vì thể tích của hệ luôn dương, năng lượng tự do Gibbs tăng khi áp suất tăng ở nhiệt độ không đổi.
Đối với một hệ thống mở, trong đó có sự trao đổi vật chất với môi trường xung
quanh, tổng năng lượng tự do Gibbs có thể được biểu thị dưới dạng hàm số mol
của từng loại hóa chất có trong hệ ngoài nhiệt độ và áp suất. G = f (T, P, n1, n2, ..., ni)
5.1 Tiêu chí cân bằng 195
Tổng chênh lệch của năng lượng tự do Gibbs là: dG = ∂G ∂T P, ni dT + ∂G ∂P T, ni dP + k i = 1 ∂G ∂ni
T, P, nj dni (5,11) trong đó ni có nghĩa là lượng của tất cả các chất được giữ
không đổi và nj có nghĩa là lượng của tất cả các chất được giữ không đổi ngoại trừ chất bị thay đổi (j = i).
Thay thế các đạo hàm riêng thứ nhất và thứ hai của Eq. (5.11) theo Eqs. (5.9) và
(5.10), tương ứng: dG = VdP - SdT + k i = 1 ∂G ∂ni T, P, nj dni (5,12) Ghi nhớ Eq. (5.2): µi = ∂G ∂ni T, P, nj (5,2)
Ở nhiệt độ và áp suất không đổi, phương trình (5.12) được đơn giản hóa thành: dG = k i = 1 µidni (5,13)
Phương trình này chỉ ra rằng năng lượng tự do Gibbs của một hệ thống là tổng
đóng góp của các thành phần khác nhau.
Tiêu chí chung để một hệ thống ở trạng thái cân bằng là: (dG) T, P = 0 (5,14) (dG) T, P = k i = 1 (µL tôi dnL i) + k i = 1 (µV tôi dnV i) = 0 (5,15) Nếu hệ thống đóng: dnV i = −dnL tôi (5,16)
Sau đó, phương trình (5.15) trở thành:
Cách duy nhất mà Eq. (5.18) có thể hài lòng là: µL i = µV i (5,1)
Ở cùng nhiệt độ và áp suất, điều kiện cân bằng được thoả mãn khi thế hoá học
của mỗi loài trong pha lỏng và pha hơi như nhau:
5.2 GIẢI PHÁP LÝ TƯỞNG — LUẬT CỦA RAOULT
Một giải pháp có thể được định nghĩa là lý tưởng nếu các lực kết dính bên trong
một dung dịch là đồng nhất. Điều này có nghĩa là khi có hai thành phần A và B,
các lực giữa A và B, A và A, và B và B đều như nhau.
Phương trình (5.10) có thể được viết lại dưới dạng số mol từng phần và vì năng
lượng từng phần mol tự do là thế hóa học, đối với hợp chất A trong dung dịch: …
Áp suất hơi riêng phần của một thành phần, là thước đo xu hướng của thành
phần nhất định thoát ra khỏi dung dịch vào pha hơi, là một đặc tính quan trọng
đối với các dung dịch. Đối với một dung dịch ở trạng thái cân bằng với hơi của nó: µso ln A = µvapor A = µ0 A + RT ln PA (5,23)
Như vậy, thế hóa học của thành phần A trong dung dịch liên quan đến áp suất
hơi riêng phần của A ở trên dung dịch. Phương trình (5.23) chỉ đúng khi hơi
đóng vai trò là khí lý tưởng.
Một dung dịch là lý tưởng nếu xu hướng thoát ra của mỗi thành phần tỷ lệ với
phần mol của thành phần đó trong dung dịch. Xu hướng thoát ra của thành phần
A khỏi một dung dịch lý tưởng, được đo bằng áp suất hơi riêng phần của nó, tỷ
lệ với áp suất hơi của chất lỏng A nguyên chất và phần mol của các phân tử A
trong dung dịch. Điều này có thể được thể hiện bằng luật của Raoult như sau:
trong đó PA là áp suất hơi riêng phần của A, XA là phần mol của nó và P0A là
áp suất hơi của chất lỏng nguyên chất A ở cùng nhiệt độ. Nếu thêm thành phần
B vào A nguyên chất thì áp suất hơi giảm là:
Phương trình (5.25) (giảm áp suất tương đối) hữu ích cho các dung dịch của một
chất tan tương đối không bay hơi trong một dung môi dễ bay hơi.
Chèn Eq. (5.24) thành phương trình (5,23), phương trình (5.27) có thể nhận được: 5.3 LUẬT HENRY'S
Xét dung dịch chứa chất tan B trong dung môi A. Nếu dung dịch rất loãng, thì
điều kiện là mỗi phân tử B được bao bọc hoàn toàn bởi thành phần A. Chất tan
B ở trong một môi trường đồng nhất không phân biệt A và B có thể tạo thành
các dung dịch không lý tưởng ở nồng độ cao hơn. Trong trường hợp như vậy, xu
hướng thoát ra của B khỏi môi trường tỷ lệ với phần mol của nó, có thể được
biểu thị theo định luật Henry như sau: PB = k XB (5,28) trong đó k là hằng số định luật Henry.
Định luật của Henry không bị giới hạn đối với các hệ thống khí - lỏng. Nó có
giá trị đối với các dung dịch khá loãng và cực kỳ loãng.
5.4 CÁC TÍNH CHẤT THUỘC TÍNH
Tính chất keo tụ phụ thuộc vào số lượng phân tử chất tan hoặc ion được thêm
vào dung môi. Giảm áp suất hóa hơi, nâng cao điểm sôi, giảm điểm đóng băng
và áp suất thẩm thấu là các đặc tính liên kết. Những đặc tính này được sử dụng
để xác định trọng lượng phân tử và đo hoạt độ nước. 5.4.1 Độ cao điểm sôi
Nếu một lượng nhỏ chất tan không bay hơi được hòa tan trong dung môi dễ bay
hơi và dung dịch rất loãng để hoạt động lý tưởng, thì áp suất hơi giảm có thể
được tính từ phương trình. (5,25). Do áp suất hơi giảm, nhiệt độ sôi của dung
dịch cao hơn nhiệt độ của dung môi nguyên chất. Như đã thảo luận trước đây,
thế hóa học của A dễ bay hơi đối với pha lỏng và pha hơi bằng nhau ở trạng thái
cân bằng như trong phương trình. (5.1):
5.4.2 Suy giảm điểm đóng băng
Khi cân bằng giữa chất rắn A và dung dịch của nó, thế hóa học của A phải giống
nhau trong cả hai giai đoạn:
5.4.3 Áp suất thẩm thấu
Áp suất thẩm thấu là một tính chất đối chiếu có liên quan chặt chẽ đến áp suất
hơi, điểm đông đặc và điểm sôi. Hoạt tính của dung môi ảnh hưởng chủ yếu đến
áp suất thẩm thấu. Áp suất thẩm thấu phát sinh khi hai dung dịch có nồng độ
khác nhau được ngăn cách bởi một màng bán thấm. Hình 5.1 cho thấy máy đo
độ thẩm thấu hiển thị các điều kiện ở trạng thái cân bằng. Dung dịch và dung
môi được ngăn cách bởi một màng bán thấm chỉ cho phép dung môi đi qua.
Dòng thẩm thấu tiếp tục cho đến khi thế hóa học của thành phần khuếch tán là
như nhau ở cả hai phía của rào cản. Sự cân bằng xảy ra trong một máy đo độ
thẩm thấu trong đó áp suất tăng thêm π cần thiết cho trạng thái cân bằng được
tạo ra bởi áp suất thủy tĩnh của cột nước trên mặt dung dịch. Ở trạng thái cân
bằng sẽ không có dòng dung môi thực qua màng nên thế hóa học của dung môi
nguyên chất ở áp suất P phải bằng thế hóa học của dung môi trong dung dịch ở áp suất P + π.
5.5 EQUILIBRIA TRONG CÁC HỆ THỐNG KHÔNG BÊN NGOÀI — SỰ
TIỆN NGHI VÀ HOẠT ĐỘNG
Như đã thảo luận trước đó, đối với các hệ thống lý tưởng, sự thay đổi điện thế
hóa học được biểu thị bằng phương trình. (5,21): µA µ0 MỘT dµA = PA 1 RT dPA PA (5,21)
Thế hóa học của thành phần A ở áp suất PA được biểu thị bằng phương trình. (5,22): µA = µ0 A + RT ln PA (5,22)
Các phương trình này không hợp lệ đối với khí thực trừ khi P → 0. Lewis đề
xuất một hàm mới gọi là fugacity (f) để làm cho các phương trình này có thể áp
dụng cho các hệ thực. Fugacity được định nghĩa là xu hướng thoát ra của một
thành phần trong dung dịch. Nó có thể được coi là áp suất riêng phần đã hiệu
chỉnh. Một tham số không thứ nguyên được gọi là hệ số độ mờ, γ f, được xác
định để tính toán mối quan hệ giữa độ mờ và áp suất:
5.6 HOẠT ĐỘNG CỦA NƯỚC
Hãy xem xét một hệ thống thực phẩm được bao bọc trong một hộp đựng. Tất cả
các thành phần trong thực phẩm ở trạng thái cân bằng nhiệt động với nhau trong
cả pha hấp phụ và pha hơi ở nhiệt độ không đổi. Xem xét độ ẩm trong hệ thống
thực phẩm và hơi trong không gian vũ trụ, thế hóa học của chúng bằng nhau: (5,73)
Hoạt độ của nước trong thực phẩm có thể được biểu thị bằng Eq. (5,71):
Nếu hoạt độ của nước được biểu thị dưới dạng áp suất, thì phương trình sau thu được:
Hệ số độ mờ của hơi nước ở trạng thái cân bằng với chất lỏng bão hòa là trên
0,90 ở nhiệt độ từ 0,01◦C đến 210◦C và các giá trị áp suất trong khoảng từ 611
Pa đến 19,1 × 105 Pa (Rizvi, 2005).
Do đó, nó có thể được tính gần đúng với 1, có nghĩa là độ lệch không đáng kể
so với lý tưởng. Do đó, hoạt độ nước trong thực phẩm có thể được biểu thị bằng: (5,75)
Do đó, hoạt độ nước có thể được định nghĩa là tỷ số giữa áp suất hơi của nước
trong hệ thống với áp suất hơi của nước tinh khiết ở cùng nhiệt độ. Nó cũng có
thể được biểu thị bằng độ ẩm tương đối cân bằng (ERH) của không khí xung
quanh thực phẩm ở cùng nhiệt độ. Hoạt động của nước là một đặc tính quan
trọng trong hệ thống thực phẩm. Hầu hết các phản ứng hóa học và vi sinh hoạt
động được kiểm soát trực tiếp bởi hoạt động của nước. Trong khoa học thực
phẩm, nó rất hữu ích như một phép đo khả năng phản ứng tiềm tàng của các
phân tử nước với các chất hòa tan. Hoạt động của nước lệch khỏi định luật
Raoult ở nồng độ chất tan cao hơn. Có nhiều lý do cho sự sai lệch này. Sự thay
đổi của chất tan và kích thước phân tử dung môi dẫn đến sự thay đổi lực ular
liên động giữa các phân tử, dẫn đến chúng hoạt động như không phân tử. Lực
liên phân tử giữa các phân tử dung môi, tương tác giữa chất tan - chất tan và
chất tan - dung môi và hiệu ứng solvat hóa làm cho dung dịch hoạt động không
khác biệt. Nếu chất tan hoàn toàn phân ly thành ion khi phân tán trong dung môi
thì nó sẽ gây ra tính không phản ứng. Sự hiện diện của chất rắn không hòa tan
hoặc môi trường xốp gây ra hoạt động mao dẫn làm giảm áp suất hơi và cho
thấy sự sai lệch so với hành vi lý tưởng. Các lý do cho hành vi không giết người
(lệch khỏi luật Raoult) được giải thích chi tiết trong Rahman (1995).
5.7 DỰ KIẾN HOẠT ĐỘNG CỦA NƯỚC
Định luật Raoult là phương trình cơ bản để xác định hoạt độ nước của các dung
dịch lý tưởng. Theo định luật Raoult, hoạt độ của nước bằng phần mol của nước trong dung dịch:
Phương trình Gibbs-Duhem được sử dụng để tạo ra một loạt các mô hình dự báo
về hoạt động của nước. Phương trình Gibbs-Duhem có thể được sử dụng để mô
tả hoạt động của các dung dịch bao gồm N thành phần (Cazier & Gekas, 2001)
5.8 CÁC PHƯƠNG PHÁP ĐO HOẠT ĐỘNG CỦA NƯỚC
Nhiều phương pháp đo hoạt độ nước đã được sử dụng và báo cáo trong tài liệu
(Bell và Labuza, 2000; Nunes, Urbicain & Rotstein, 1985; Troller, 1983). Nói
chung, để đo hoạt độ nước của thực phẩm, các phương pháp dựa trên tính chất
keo tụ, có thể sử dụng phương pháp chuyển đồng đẳng, độ hút ẩm của muối và ẩm kế.
5.8.1 Các phép đo dựa trên các thuộc tính đối chiếu
Hoạt độ nước của thực phẩm có thể được xác định bằng cách đo trực tiếp áp
suất hơi của nước trong thực phẩm hoặc bằng cách sử dụng áp suất điểm đóng
băng. Cho đến nay các đặc tính tương đồng như áp suất thẩm thấu và độ cao
điểm sôi vẫn chưa được sử dụng cho các hệ thống thực phẩm (Rizvi, 2005).
5.8.1.1 Xác định hoạt độ nước bằng phép đo áp suất hơi
Phương pháp này cho phép đo trực tiếp áp suất hơi do mẫu tạo ra. Hoạt độ nước
được tính bằng tỷ số giữa áp suất hơi của mẫu so với áp suất hơi của nước tinh
khiết ở cùng nhiệt độ.
Hình 5.2 cho thấy một sơ đồ cho phương pháp này. Theo phương pháp này, một
mẫu có trọng lượng từ 10 g đến 50 g được cho vào bình chứa mẫu và gắn vào
thiết bị. Không gian không khí trong thiết bị được hút chân không. Sau khi
nguồn chân không được cách ly và cân bằng trong 30 đến 50 min, áp suất do
mẫu tạo ra được ghi lại là h1. Mức dầu trong áp kế sẽ thay đổi theo áp suất hơi
do mẫu tạo ra. Bình mẫu được loại trừ khỏi hệ thống và bình hút ẩm được mở.
Hơi nước được loại bỏ bằng cách hấp thụ vào CaSO4 và áp suất tạo ra bởi các
chất bay hơi và khí được biểu thị bằng h2 sau khi cân bằng. Sau đó, hoạt độ
nước có thể được tính toán bằng cách sử dụng
5.8.1.2 Xác định hoạt độ nước bằng cách suy giảm điểm đóng băng
Việc xác định hoạt độ nước bằng điểm trầm cảm là rất chính xác ở các hoạt độ
nước trên 0,85 (Rizvi, 2005). Tuy nhiên, phương pháp này chỉ có thể áp dụng
cho thực phẩm lỏng và cho giá trị hoạt độ nước ở điểm đóng băng hơn là ở nhiệt
độ phòng. Phương pháp này thích hợp cho các vật liệu có số lượng lớn các chất
dễ bay hơi có thể gây ra sai số trong phép đo áp suất hơi và trong ẩm kế điện.
Trong hệ thống hai pha (nước đá và dung dịch) ở trạng thái cân bằng, áp suất
hơi của nước dưới dạng tinh thể nước đá và dung dịch đậm đặc xen kẽ là như
nhau và hoạt độ của nước chỉ phụ thuộc vào nhiệt độ. Do đó, hoạt độ nước của
dung dịch ở một nhiệt độ nhất định dưới mức đóng băng có thể được biểu thị bằng:
aw = Áp suất hơi của nước đá
Áp suất hơi của nước lỏng
5.8.2 Các phép đo dựa trên chuyển giao Isopiestic
Phép đo hoạt độ nước trong phương pháp này đạt được bằng cách cân bằng các
hoạt động nước của hai vật liệu trong một hệ thống khép kín. Chủ yếu, cellulose
vi tinh thể được sử dụng làm chất nền hấp phụ chuẩn. Mẫu và xenluloza vi tinh
thể đã được làm khô trước được đặt trong bình hút ẩm loại chân không. Các
bình hút ẩm được đóng lại và hút chân không trong khoảng 1 phút và sau đó
được giữ ở nhiệt độ không đổi trong 24 giờ. Sau 24 giờ, chân không trên bình
hút ẩm được giải phóng từ từ. Xenlulozơ được cân lại và ghi lại sự thay đổi
trọng lượng. Độ ẩm được tính toán và hoạt độ nước được xác định từ đường
đẳng nhiệt xenluloza tiêu chuẩn đã được chuẩn bị trước đó với hỗn hợp axit
sulfuric-nước làm môi trường. Phương pháp này không được khuyến nghị cho
các mẫu dễ bị tạo bọt như dung dịch protein trong quá trình sơ tán bình hút ẩm.
Những loại mẫu như vậy có thể được khử khí trước khi sơ tán. Sự phát triển của
vi sinh vật phải được ngăn chặn bằng cách bổ sung K-sorbate và bằng cách sử
dụng các kỹ thuật vô trùng. Có thể tóm tắt lý do chọn cellulose vi tinh thể làm
tài liệu tham khảo như sau (Spiess & Wolf, 1987):
1. Nó ổn định trong sự thay đổi nhiệt độ từ -18 đến 80 ° C với ít thay đổi về
tínhchất hấp thụ istics.
2. Nó ổn định về tính chất hấp phụ sau hai đến ba chu kỳ hấp phụ và giải hấp phụ lặp lại.
3. Đường đẳng nhiệt hấp phụ của nó có dạng sigmoid và mô hình hấp thụ của
nó đã được biết đến.
4. Nó có sẵn như một chất phân tích sinh hóa tiêu chuẩn.




