Hướng dẫn giải các dạng toán giá trị lớn nhất và giá trị nhỏ nhất của hàm số – Đặng Việt Đông Toán 12

Hướng dẫn giải các dạng toán giá trị lớn nhất và giá trị nhỏ nhất của hàm số – Đặng Việt Đông Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

49 25 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

59 trang 7 tháng trước

Tác giả:

Profile Mai Nguyệt
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
A – LÝ THUYẾT TÓM TẮT
I. Định nghĩa.
Giả sử hàm số xác định trên tập K . Khi đó:
a) Nếu tồn tại một điểm sao cho thì số được gọi là giá trị
lớn nhất của hàm số trên K. Kí hiệu: .
b) Nếu tồn tại một điểm sao cho thì số được gọi là giá trị
nhỏ nhất của hàm số trên K. Kí hiệu: .
II. Nhận xét.
1.Như vậy để có được M (hoặc m) là giá trị lớn nhất (giá trị nhỏ nhất) của hàm số trên K ta phải chỉ
ra được :
a) ( hoặc ) với mọi .
b) Tồn tại ít nhất một điểm sao cho ( hoặc ).
2. Chú ý khi nói đến giá trị lớn nhất hay giá trị nhỏ nhất của hàm số (mà không nói rõ “trên tập K’’)
thì ta hiểu đó là giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
3. Mỗi hàm số liên tục trên đoạn thì đạt được giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Hơn nữa
a) Nếu hàm số đồng biến trên đoạn thì và .
b) Nếu hàm số nghịch biến trên đoạn thì và .
4. Cho phương trình
f x m
với
y f x
là hàm số liên tục trên D thì phương trình có nghiệm khi
D D
min f x m max f x
5. Một hàm số có thể đồng thời đạt được giá trị lớn nhất và giá trị nhỏ nhất trên một tập K hoặc chỉ đạt
được giá trị nhỏ nhất hoặc chỉ đạt được giá trị lớn nhất hoặc không tồn tại cả hai giá trị này. Chẳng
hạn:
a) Xét hàm số bậc hai trên tập xác định .
+ Khi thì hàm số có đạt được giá trị nhỏ nhất tại đồng thời bằng giá trị cực tiểu của hàm
số tại .
+ Khi thì hàm số có đạt được giá trị lớn nhất tại đồng thời bằng giá trị cực đại của hàm
số tại .
b) Xét trên tập hàm số bậc ba không tồn tại giá trị lớn nhất và giá trị
nhỏ nhất.
f
K
0
x K
0
,
f x f x x K
0
M f x
f
max
x D
M f x
0
x K
0
,
f x f x x K
0
m f x
f
min
x D
m f x
f
f x M
f x m
x K
0
x K
0
f x M
0
f x m
f
;
a b
f
;
a b
max
x D
f x f b
min
x D
f x f a
f
;
a b
max
x D
f x f a
min
x D
f x f b
2
y ax bx c
K
0
a
2
b
x
a
2
b
x
a
0
a
2
b
x
a
2
b
x
a
K
3 2
y ax bx cx d
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
c) Xét trên hàm số không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.
d) Xét hàm số trùng phương trên tập xác định .
+ Khi thì hàm số đạt được giá trị nhỏ nhất đồng thời bằng giá trị cực tiểu của hàm số.
+ Khi thì hàm số đạt được giá trị lớn nhất đồng thời bằng giá trị cực đại của hàm số.
B – BÀI TẬP
DẠNG 1: GTLN, GTNN CỦA HÀM SỐ TRÊN MỘT ĐOẠN
Phương pháp: Cho hàm số
y f x
xác định và liên tục trên
a;b
.
- Tính
f ' x
, giải phương trình
f ' x 0
tìm nghiệm trên
a,b
.
- Giả sử phương trình có 2 nghiệm
1 2
x ,x a,b
.
- Tính các giá trị
1 2
f a ,f b ,f x ,f x
. So sánh chúng và kết luận.
Câu 1. Cho hàm số
y f x
liên tục và luôn nghịch biến trên
;
a b
. Hỏi hàm số
f x
đạt giá trị lớn
nhất tại điểm nào sau đây ?
A.
x a
. B.
x b
. C.
2
a b
x
. D.
2
b a
x
.
Hướng dẫn giải:
Chọn đáp án A.
Ta có:
( )
y f x
liên tục và luôn nghịch biến trên
;
a b
;
x a b
thì
( ) ( ) ( )
f b f x f a
.
Suy ra hàm số
( )
y f x
đạt giá trị lớn nhất tại điểm
x a
.
Câu 2. Giá trị nhỏ nhất của hàm số
3
12 2
y x x
trên đoạn
1;4
là
A. 13. B. 2. C. -14. D. 18.
Hướng dẫn giải:
Chọn đáp án C.
Ta có
2
3 12
y x
. Cho
2
2
0 3 12 0
2
x
y x
x
. Do
4
1;
x nên
2
x
.
,
1 13 2 18, 4 14
y y y . Vậy
[1;4]
min 4 14
y y .
Câu 3. Giá trị lớn nhất của hàm số
3
3 3
f x x x
trên
3
1
2
;
bằng:
A.
5.
B.
3
. C.
4
. D.
6
.
Hướng dẫn giải:
Chọn đáp án A.
Ta có
2
3 3
y x
,
1
0
1
x
y
x
1 1
y
;
1 5
y
;
3 15
2 8
y
. Vậy
3
1;
2
5.
Max f x
\
c
K
d
ax b
y
cx d
4 2
y ax bx c
K
0
a
0
a
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
Câu 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3
2
3
3
x
y x x
trên đoạn
.
A.
0;2
0;2
2 5
max ; min .
3 3
y y
B.
0;2
0;2
2
max ; min 0.
3
y y
C.
0;2
0;2
5
max 9; min .
3
y y
D.
0;2
0;2
max 9; min 0.
y y
Hướng dẫn giải:
Chọn đáp án A.
Hàm số liên tục và xác định trên
.
2
2 3
y x x
,
1
0
3
x
y
x
1
x
(do
x ).
0 0
y
,
5
1
3
y
,
2
2
3
y
.
Vậy
0;2
2
max
3
y
,
0;2
5
min
3
y
.
Câu 5.Giá trị lớn nhất của hàm số
3 2
1 1
2 1
3 2
y x x x
trên đoạn
1
;2
2
là
A.
5
3
. B.
1
6
. C.
1
6
. D.
13
3
Hướng dẫn giải:
Chọn đáp án B.
Ta có:
2
2
y x x
;
0 1 2
y x x
(loại).
1 1 1 5
; 1 ; 2
2 6 6 3
y y y
;
Vậy
1
;2
2
1
max 1
6
y y
.
Câu 6. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 2
3 4
y x x
trên đoạn
1
;3
2
.
A.
1
1
;3
;3
2
2
37
max ;min 8
8
y y
. B.
1
1
;3
;3
2
2
37
max 4;min
8
y y
.
C.
1
1
;3
;3
2
2
37
max ;min 4
8
y y
. D.
1
1
;3;3
2
2
max 4;min 8
y y
.
Hướng dẫn giải:
Chọn đáp án D.
Hàm số
3 2
3 4
y x x
liên tục trên đoạn
1
;3
2
.
Ta có
2
3 6
y x x
1
2 ;3
2
0
1
0 ;3
2
x
y
x
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
Do
2 8
y
;
1 38
2 7
y
;
3 4
y
nên
1
1
;3;3
2
2
max 4;min 8
y y
.
Câu 7.Tìm giá trị nhỏ nhất của hàm số
3 2
2 3
5 1
3 2
y x x x
trên đoạn
2;2
.
A.
2;2 .
29
min
3
y
. B.
2;2 .
min 3
y
. C.
2;2 .
251
min
24
y
. D.
2;2 .
1
min
3
y
.
Hướng dẫn giải:
Chọn đáp án A.
Hàm số
3 2
2 3
5 1
3 2
y x x x
liên tục trên đoạn
2;2
.
Ta có
2
2 3 5
y x x
1 2;2
0
5
2;2
2
x
y
x
.
Do
26
1
3
y ;
29
2
3
y
;
1
2
3
y
nên
2;2 .
29
min
3
y
.
Câu 8. Tìm
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 2
3 9 35
y x x x
trên đoạn
là:
A.
40; 41
M m
. B.
40; 8
M m
. C.
41; 40
M m
. D.
15; 8
M m
.
Hướng dẫn giải:
Chọn đáp án A.
Hàm số liên tục trên đoạn
2
3 6 9
y x x
.
0
y
2
2 3 0
x x
3
1
x
x
Ta có
4 41
y
;
4 15
y
;
1 40
y
;
3 8
y
Vậy
[ 4;4]
max 40
M y
và
[ 4;4]
min 41
m y
.
A.
338
B. . C. -10. D.
14
27
.
3 2
2 7 5
y x x x
Hàm số xác định và liên tục trên đoạn [1;3].
2
' 3 4 7
y x x
' 0
y
1( )
7
( )
3
x l
x n
(1) 3
y
,
(3) 7
y
,
7 257
( )
3 27
y
257
27
m
;
3
M
338
27
m M .
Câu 9.Hàm số
y x
3
2x
2
7x 5
có giá trị nhỏ nhất là m và giá trị lớn nhất là M trên đoạn [1;3].
Khi đó tổng m + M bằng
446
.
27 27
Hướng dẫn giải:
Chọn đáp án A.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
Câu 10.Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số
3 2
2 3 1
y x x
trên đoạn
1
2;
2
. Tính giá trị của
M m
A. – 5. B. 1. C. 4. D. 5.
Hướng dẫn giải:
Chọn đáp án D.
Ta có :
2
0
' 6 6 ; ' 0
1
1 2;
2
x
y x x y
x
1 1
2 5 ; 1 0 ;
2 2
y y y
Khi do : 0, 5 5.
M m M m
Câu 11. Giá trị lớn nhất của hàm số
3 2
2 – 7 1
f x x x x
trên đoạn
là:
A.
1
. B.
1
. C.
3
. D.
4
.
Hướng dẫn giải:
Chọn đáp án C.
Xét hàm số
3 2
2 – 7 1
f x x x x
Ta có:
2
'( ) 3 4 -7
f x x x
.
2
1( )
'( ) 0 3 4 -7 0
7
( )
3
x n
f x x x
x l
(0) 1, (2) 3, (1) 3.
f f f
Vậy:
[0;2]
max ( ) 3.
f x
Câu 12. Tìm giá trị lớn nhất của hàm
3 2
( ) 2 3 12 2
y f x x x x
trên đoạn
1;2
.
A.
- ;
max
1 2
y 6
. B.
1;2
max 10
y
. C.
-1;2
max 15
y
. D.
1;2
max 11.
y
Hướng dẫn giải:
Chọn đáp án C.
Hàm số xác định và liên tục trên đoạn
1;2
.
2
( ) 6 6 12
f x x x .
2
( ) 0 6 6 12 0
f x x x
1 1;2
x hoặc
2 1;2
x .
1 15
f ;
2 6
f ;
1 5
f .
Vậy
1;2
max 1 15
y f
.
Câu 13. Gọi
m
là giá trị nhỏ nhất của hàm số
3
3
y x x
trên đoạn
0;38
. Tìm giá trị
m
A.
0.
m
B.
1.
m
C.
2.
m
D.
1.
m
Hướng dẫn giải:
Chọn đáp án C.
2
' 3 3
y x
1 0;38
' 0
1 0;38
x
y
x
.
0 0;
y
1 2
y
;
38 54758
y .
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
Vậy
2
m
Câu 14. Tìm giá trị lớn nhất của hàm số
3 2
8
y x x x
trên đoạn
[1;3]
.
A.
[1;3]
max 4
y
. B.
[1;3]
max 8
y . C.
[1;3]
max 6
y
. D.
[1;3]
176
max
27
y
.
Hướng dẫn giải:
Chọn đáp án C.
Hàm số xác định và liên tục trên
[1;3]
.
Ta có
2
3 2 8
y x x
. Cho
2
2
0 3 2 8 0
4
3
x
y x x
x
. Do
[1;3]
x
nên
2
x
.
1 8 2 12 3 6
, ,
y y y . Vậy
[1;3]
max 3 6
y y .
Câu 15. Cho hàm số
3 2
3 3
y x x
.Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số trên đoạn
1;3
.Tính giá trị
T M m
A.
2.
B.
4.
C.
3.
D.
0.
Hướng dẫn giải:
Chọn đáp án A.
Ta có :
2
3 6
y x x
. Khi đó
0
0
2
x
y
x
Xét
1;3
x : ta có
0
x
(loại );
2
x
( nhận).
Ta có :
1 1
y
;
2 1
y
;
3 3
y
.
Suy ra
3; 1
M m
. Do đó :
2
T
.
Câu 16. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3
3 1
y x x
trên đoạn
[0 ; 2]
A.
0 ; 2
max 3
y
và
0 ; 2
min 1
y
. B.
0 ; 2
max 1
y
và
0 ; 2
min 1
y
.
C.
0 ; 2
max 3
y
và
0 ; 2
min 1
y
. D.
0 ; 2
max 9
y
và
0 ; 2
min 3
y
.
Hướng dẫn giải:
Chọn đáp án C.
TXĐ:
D
.
Ta có
2
3 3
y x
,
0
y
2
3 3 0
x
1
1
x
x
.
Xét trên đoạn
[0 ; 2]
ta chỉ nhận
1
x
.
Khi đó ta có
0 1
y
,
2 3
y
,
1 1
y
.
Vậy ta có
0;2
max 3
y
và
0;2
min 1
y
.
Câu 17. Trên đoạn
1;1
, hàm số
3 2
4
2 3
3
y x x x
A. Có giá trị nhỏ nhất tại
1
x
và giá trị lớn nhất tại
1
x
.
B. Có giá trị nhỏ nhất tại
1
x
và giá trị lớn nhất tại
1
x
.
C. Có giá trị nhỏ nhất tại
1
x
và không có giá trị lớn nhất.
D. Không có giá trị nhỏ nhất và có giá trị lớn nhất tại
1
x
.
Hướng dẫn giải:
Chọn đáp án B.
Hàm số liên tục trên
1;1 .
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
Ta có
2
4 4 1.
y x x
2
1
0 4 4 1 0 .
2
y x x x
Vậy
22
1
3
y
,
8
1
3
y
,
1 17
.
2 6
y
Câu 18. Gọi
,
M m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3 2
2 3 12 2
y x x x
trên
đoạn
1;2 .
Tìm tổng bình phương của
M
và
m
A.
250
. B.
100
. C.
509
. D.
289
.
Hướng dẫn giải:
Chọn đáp án A.
Hàm số xác định và liên tục trên đoạn
1;2
.
2
' 6 6 12
y x x
.
2
1(N)
' 0 6 6 12
2(L)
x
y x x
x
.
(1) 5; ( 1) 15; (2) 6
y y y
.
Vậy:
2 2 2 2
( 5) 15 250
m M
.
Câu 19. Tìm các giá trị của
a
để trên đoạn
1;1
hàm số
3 2
3
y x x a
có giá trị nhỏ nhất bằng
2
A.
6
a
. B.
8
a
. C.
2
a
. D.
4
a
.
Hướng dẫn giải:
Chọn đáp án A.
Hàm số xác định và liên tục trên đoạn
1;1
.
Ta có:
2
' 3 6
y x x
.
2
0(N)
' 0 3 6
2(L)
x
y x x
x
.
(1) 4
y a
, ( 1) 2
y a
,
(0) a
y
.
Trên đoạn
1;1
thì giá trị nhỏ nhất của hàm số bằng
2
.
Suy ra
min (1) 4 2 6
y y a a
.
Câu 20. Hàm số
3 2
1 1
y x m x m
đạt GTNN bằng
5
trên
0;1
. Khi đó giá trị của
m
là
A.
5.
B.
3.
C.
1.
D.
4.
Hướng dẫn giải:
Chọn đáp án D.
Ta có
2 2
3 1 0
y x m
với mọi
0;1
x nên hàm số luôn đồng biến trên
0;1 .
Vì hàm số đã cho là hàm đa thức, liên tục trên
0;1
nên
0;1
min 0 1.
x
y y m
Ta cho
1 5 4.
m m
Vậy
4
m
thỏa mãn.
Câu 21. Cho hàm số
3
3 1
y x x
. Tìm tìm tập hợp tất cả giá trị
0
m
, để giá trị nhỏ nhất của hàm
số trên
1; 2
D m m
luôn bé hơn 3 là
A.
0;1 .
B.
1
;1 .
2
C.
;1 \ 2 .
D.
0;2 .
Hướng dẫn giải:
Chọn đáp án A.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
Ta có :
2
1
' 3 3. ' 0
1
x
y x y
x
.
Hàm số đồng biến trên khoảng
1;
.
Trên
1; 2D m m
, với
0m
, ta có :
3
1; 2
1 3 1 1
m m
Min y m m
Ycbt
2
3 2
1; 2
1
3 3 4 0 1 2 0
2
m m
m
Min y m m m m
m
Kết hợp điều kiện . Suy ra
0;1m .
Câu 22. Cho hàm số
4 2
2 1y x x . Tìm giá trị nhỏ nhất của hàm số trên
1;2
A.
1;2
min 2y
. B.
1;2
min 2y
. C.
1;2
min 1y
. D.
1;2
min 1y
.
Hướng dẫn giải:
Chọn đáp án D.
Ta có : +)
3
' 4 4y x x ,
3
' 0 4 4 0 0y x x x
+)
0 1y ,
1 2y ,
2 23y
Vậy
1;2
min 1y
Câu 23. Cho hàm số
y f x có đồ thị như hình bên. Tìm giá trị lớn nhất của hàm số
y f x trên
đoạn
1;2 .
A. 1. B. 2. C. 5. D. 0.
Hướng dẫn giải:
Chọn đáp án C.
Trên đoạn
1;2 , giá trị lớn nhất của hàm số bằng 5tại 2x .
Câu 24. Cho hàm số
y f x liên tục trên đoạn 2;2
và có đồ thị trên đoạn 2;2
như sau:.
.
Khẳng định nào sau đây là sai?
A.
2;2
max 2f x f
.
B.
2;2
max 2f x f
.
C.
2;2
min 1f x f
.
D.
2;2
min 0f x f
.
Hướng dẫn giải:
Chọn đáp án D.
O
1
1
2
2
x
y
2
2
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay
2;2
min 1
f x f
Câu 25. Giá trị nhỏ nhất của hàm số
4 2
4 5
y x x
trên đoạn
1; 2
bằng?
A.
1
. B.
2
. C.
3
. D.
5
.
Hướng dẫn giải:
Chọn đáp án A.
4 2
4 5
y x x
suy ra
/ 3
4 8
y x x
. Ta có
/
0
0
2
x
y
x
.
1 2
y
,
0 5
y
,
2 1
y
,
2 5
y
. Vậy GTNN là
1
.
Câu 26. Tìm giá trị lớn nhất của hàm số
3 1
3
x
y
x
trên đoạn
A.
1
3
. B. -5. C. 5. D.
1
3
.
Hướng dẫn giải:
Chọn đáp án D.
2
8
0, 3.
3
y x
x
0; 2
1
0
3
Max y y
.
Câu 27. Xét hàm số
4 1
x
y
x
trên đoạn
[ 2 ; 1]
. Hãy chọn khẳng định đúng
A.
2; 1
9
max
2
y
. B. Hàm số không có giá trị nhỏ nhất.
C. Hàm số không có giá trị lớn nhất. D.
2; 1
9
min
2
y
.
Hướng dẫn giải:
Chọn đáp án D.
TXĐ:
\ 0
D
.
Ta có
2
1
0
y
x
,
0
x
.
Hàm số đồng biến trên
2; 1
và
9
2
2
y
,
1 5
y
.
Vậy
2; 1
9
min
2
y
.
Câu 28.Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
1
2 1
x
y
x
trên đoạn
1;3
là:
A. GTNN bằng 1; GTLN bằng 3. B. GTNN bằng 0; GTLN bằng
2
7
.
C. GTNN bằng 0; GTLN bằng 1. D. GTNN bằng
2
7
; GTLN bằng 0.
Hướng dẫn giải:
Chọn đáp án B.
2
3 1
0,
2
2 1
y x
x
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay
2
1 0, 3
7
y y
.
Vậy GTNN bằng 0; GTLN bằng
2
7
.
Câu 29. Cho hàm số
1
2 1
x
y
x
. Chọn phương án đúng trong các phương án sau:
A.
1;2
min 1
x
y
. B.
0;1
max 2
x
y
. C.
1;0
max 0
x
y
. D.
3;5
2
max
3
x
y
.
Hướng dẫn giải:
Chọn đáp án C.
Hàm số không liên tục trên đoạn
1;2
Loại đáp án A.
Hàm số không liên tục trên đoạn
0;1
Loại đáp án B.
Ta có
2
3
0
2 1
y
x
,
1
2
x
và
[ 1;0]
max 1 0
y y
.
Câu 30. Giá trị nhỏ nhất của hàm số
2 1
1
x
y
x
trên đoạn
bằng:
A.
7
2
. B.
5
C.
3
D.
3
4
Hướng dẫn giải:
Chọn đáp án B.
+ TXĐ:
\ 1 .
D R
+
2
3
' 0
1
y x D
x
hàm số đồng biến trên các khoảng xác định
hàm số cũng đồng biến trên
2;3
2;3 2 5.
Min y y
Câu 31. Tìm giá trị lớn nhất của hàm số
3 1
3
x
y
x
trên đoạn
0;2
A.
1
3
. B.
5
.
C.
5
. D.
1
3
.
Hướng dẫn giải:
Chọn đáp án D.
2
8
3
y
x
1
0
3
y
,
2 5
y
Suy ra
0;2
max 5
y
.
0 2
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay
Câu 32. Kí hiệu
,
m M
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số
3
2 1
x
y
x
trên đoạn
[1;4].
Tính giá trị biểu thức
.
d M m
A.
3.
d
B.
4.
d
C.
5.
d
D.
2.
d
Hướng dẫn giải:
Chọn đáp án A.
2
7 1
0
2
2 1
y x
x
. Suy ra hàm nghịch biến trên từng khoảng xác định, do đó hàm số
nghịch biến trên đoạn
[1;4].
Vậy
4 1; 1 4 4 1 3.
m y M y d M m
Câu 33. Gọi
,
M n
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
( )
1
x
y f x
x
trên
đoạn
. Hãy tính tích
.
M n
.
A.
2
. B.
0
. C.
1
. D.
1
.
Hướng dẫn giải:
Chọn đáp án B.
Hàm số
f x
xác định và liên tục trên
.
2
3
0 0;2
1
f x x
x
.
f x
đồng biến trên
0;2
max 2 0
M f x f
,
0;2
min 0 2
m f x f
.
Vậy
. 0
M n
Câu 34.Gọi
Q
là giá trị lớn nhất và
K
là giá trị nhỏ nhất của hàm số
2
1
1
x
y
x
trên đoạn
1;2
. Khi
đó giá trị của biểu thức
24 27
1997
2
Q K
là:
A.
3923
2
.
B.
3925
2
.
C.
3927
2
.
D.
3929
2
.
Hướng dẫn giải:
Chọn đáp án C.
2
2
1 2
2 1
' 0 .
( 1)
1 2
x
x x
y
x
x
'
y
đồng biến trên
[1;2]
nên
(1) 1
.
5
(2)
3
K y
Q y
Suy ra
24 27 3927
1997 .
2 2
Q K
Câu 35. Tìm tất cả các giá trị của tham số
m
để hàm số
3 2
1 1
y x m x m
đạt GTNN bằng
5
trên
0;1
.
A.
5
. B.
3
. C.
1; 2
. D.
4
.
Hướng dẫn giải:
Chọn đáp án C.
2 2
3 1 0,y x m x
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay
Hàm số đồng biến trên
0;1
.
0;1
max 5
y
khi
1
x
.
Thay
1, 5
x y
và hàm số ta được
1; 2
m m
.
Câu 36. Giá trị của tham số thực
m
để giá trị lớn nhất của hàm số
1
mx
y
x m
trên đoạn
[1;2]
bằng
2
.
là:
A.
3
m
. B.
3
m
. C.
1
m
. D. Không tồn tại.
Hướng dẫn giải:
Chọn đáp án B.
Ta có:
\
D m
và
2
2
1
0,
m
y x D
x m
.
Do đó giá trị lớn nhất của hàm số
1
mx
y
x m
trên đoạn
[1;2]
bằng
2
khi và chỉ khi
1
1 2
2
3
1
1;2
1 2
m
y
m
m
m
m m
Câu 37.Trên đoạn [2;4] hàm số
1
mx
y
x m
đạt giá trị lớn nhất bằng 2. Khi đó :
A.
7
6
m
.
B.
1
m
.
C.
2
m
.
D.
3
4
m
.
Hướng dẫn giải:
Chọn đáp án D.
Ta có:
2
2 2
1
1
' 0
m x m mx
m
y
x m x m
với mọi
x m
.
Vậy hàm số nghịch biến trên mỗi khoảng xác định của nó.
Do đó trên đoạn
2;4
hàm số nghịch biến. Suy ra
2 4
f f
.
Giá trị lớn nhất của hàm số trên đoạn
2;4
là
2 1
2
2
m
f
m
.
2 1 3
2 2 1 4 2
2 4
m
m m m
m
.
Lưu ý. Nếu
2;4
m
thì hàm số không có giá trị lớn nhất.
Câu 38. Tìm tất cả giá trị của
m
để giá trị nhỏ nhất của hàm số
2 1
1
x m
f x
x
trên đoạn
1;2
bằng
1
A.
1
m
. B.
2
m
. C.
3
m
. D.
0
m
.
Hướng dẫn giải:
Chọn đáp án A.
2
3
'
( 1)
m
f x
x
Nếu
3 0 3
m m
thì hàm số đồng biến trên các khoảng xác định của nó, do đó GTNN
của hàm số trên đoạn
1;2
là
1
(1) 1 1 3
2
m
f m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay
Nếu
3 0 3
m m
thì hàm số nghịch biến trên các khoảng xác định của nó, do đó GTNN
của hàm số trên đoạn
1;2
là
3
(2) 1 0 3
3
m
f m
Vậy
1
m
Câu 39. Giá trị tham số m để giá trị nhỏ nhất của hàm số
2
1
x m m
y
x
trên đoạn
0;1
bằng
2 là:
A.
1, 2
m m
. B.
1 21 1 21
,
2 2
m m
.
C. Không có giá trị m D.
1, 2
m m
Hướng dẫn giải:
Chọn đáp án D.
+
\ 1 .
D R
+
2
2
2
2 2 2
1 3
1 1 3
2.
1
2 4
2 4 4
' 0
1 1 1
m
m m
m m
y x D
x x x
hàm số đồng biến trên các
khoảng xác định
hàm số đồng biến trên
0;1
2
0;1
0 .
Min y y m m
+ Theo yêu cầu đề bài ta có:
2 2
0;1
1
2 2 2 0 .
2
m
Min y m m m m
m
Câu 40. Tìm
m
để hàm số
5
mx
f x
x m
đạt giá trị nhỏ nhất trên đoạn
0;1
bằng
7.
A.
2
m
.
B.
0
m
.
C.
1
m
.
D.
5
m
.
Hướng dẫn giải:
Chọn đáp án A.
2
'
2 2
5 ( ) 5 5
( ) 0 .
mx m x m mx m
f x f x x m
x m
x m x m
Nên giá trị nhỏ nhất của hàm số trên đoạn
0;1
là
5
(1) 7 2.
1
m
f m
m
Câu 41. Giá trị nhỏ nhất của hàm số
2
1
x m
y
x
trên
1;0
bằng:
A.
2
1
2
m
. B.
2
m
. C.
2
1
2
m
. D.
2
m
Hướng dẫn giải:
Chọn đáp án B.
Hàm số
2
1
x m
y
x
có
2
2
1
' 0 1
1
m
y x
x
nên hàm số nghịch biến trên
1;0
.
Vậy:
2
[ 1;0]
min ( ) (0) .
f x f m
Câu 42. Giá trị lớn nhất của hàm số
2 1
mx
y
m x
trên đoạn
2;3
là
1
3
khi
m
nhận giá trị
A.
0.
B.
1.
C.
5.
D.
2.
Hướng dẫn giải:
Chọn đáp án A.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay
Ta có:
2
2
0,
12m
y m
m x
hàm số đồng biến trên
2;3
2;3
6 1
max 3
3
m
y y
m
6 1 1
0
3 3
m
m
m
.
Câu 43. Cho hàm số
1
2
y x
x
, giá trị nhỏ nhất
m
của hàm số trên
1,2
là
A.
9
4
m
. B.
1
2
m
. C.
2
m
. D.
0
m
.
Hướng dẫn giải:
Chọn đáp án D.
Xét hàm số
1
2
y x
x
trên
1,2
, ta có
2
2 2
2 1
1
1
2 2
x
y
x x
.
2
3 1,2
0 2 1 0
1 1,2
x
y x
x
Mà
1 0
y
và
9
2
4
y
. Do đó
1,2
min 0
y
. Vậy
0
m
.
Câu 44. Tính giá trị nhỏ nhất của hàm số
4
1
y x
x
trên đoạn
0;4
.
A.
0;4
min 4
y . B.
0;4
24
min
5
y
. C.
0;4
min 5
y
.
D.
0;4
min 3
y .
Hướng dẫn giải:
Chọn đáp án D.
4
1
y x
x
2 2
1 3
4
1
1 1
x x
y
x x
.
3 0;4
0
1 0;4
x
y
x
.
0 4
y ,
1 3
y ,
24
4
5
y .
Vậy
0;4
min 3
y .
Câu 45. Giá trị nhỏ nhất của hàm số
1
2 1
2 1
y x
x
trên đoạn
1;2
bằng
A.
26
5
. B.
10
3
. C.
14
3
. D.
24
5
.
Hướng dẫn giải:
Chọn đáp án B.
Hàm số
1
2 1
2 1
y x
x
liên tục trên đoạn
1;2
.
Ta có
2
2
0 1;2
2
2 0 2 1 1
1 1;2
2 1
x
y y x
x
x
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay
Do
10
1
3
y ;
26
2
5
y nên
1;2
10
min
3
y
.
Câu 46. Tìm giá trị nhỏ nhất của hàm số
2
5
3
x
y
x
trên đoạn
0;2
A.
x 0;2
1
min y
3
. B.
x 0;2
5
min y
3
. C.
x 0;2
min y 2
. D.
x 0;2
min y 10
.
Hướng dẫn giải:
Chọn đáp án D.
Ta có:
2
2
2 2
2 3 5
6 5
3 3
x x x
x x
y
x x
Suy ra :
0
y
2
6 5 0
x x
1
5
x
x
Do đó ta có:
1 2
f
,
5
0
3
f
,
5 10
f
,
1
2
5
f
Vậy
x 0;2
min y 10
.
Câu 47. Tìm giá trị nhỏ nhất của hàm số
2
3
1
x
y
x
trên đoạn
2; 4
.
A.
[2;4]
19
min
3
y
. B.
[2;4]
min 3
y
. C.
[2;4]
min 2
y
. D.
[2;4]
min 6
y
.
Hướng dẫn giải:
Chọn đáp án D.
Ta có :
2
2
2 2
2 1 3
2 3
1 1
x x x
x x
y
x x
.
1 2;4
0
3 2;4
x
y
x
.
19
2 7; 4 ; 3 6
3
y y y
.
[2;4]
min 6
y
.
Câu 48. Giá trị lớn nhất của hàm số
2
3 3
1
x x
y
x
trên đoạn
1
;1
2
là:
A.
13
2
. B. 3. C.
7
2
. D. – 1.
Hướng dẫn giải:
Chọn đáp án C.
Ta có
2
2
2
1
x x
y
x
. Cho
2
2
0
2
0 0
2
1
x
x x
y
x
x
. Do
1
;1
2
x nên
0
x
.
1 7 7
0 3, 1
2 2
,
2
y y y . Vậy
1
;1
2
7
max
2
y
.
Câu 49. Tìm giá trị nhỏ nhất của hàm số
2
4
2 1
x x
y
x
trên đoạn
0;3 .
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay
A.
0;3
min 0
y
.
B.
0;3
3
min
7
y
.
C.
0;3
min 4
y
.
D.
0;3
min 1
y
.
Hướng dẫn giải:
Chọn đáp án D.
2
2
2 2 4
2 1
x x
y
x
;
2
2
1
2 2 4
0 0
2
2 1
x
x x
y
x L
x
0 0
y
;
1 1
y
;
3
3
7
y
Câu 50. Hàm số
2
3
1
x x
y
x
giá trị lớn nhất trên đoạn
là:
A.
1
. B.
3
. C.
2
. D.
0
.
Hướng dẫn giải:
Chọn đáp án D.
Xét hàm số
2
3
1
x x
y
x
Ta có:
2 2
2 2
1( )
2 3 2 3
' . ' 0 0
3( )
1 1
x n
x x x x
y y
x l
x x
(0) 0, (3) 0, (1) 1.
y y y
Vậy:
[0;3]
max 0
y
.
Câu 51.Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
2 3
1
x x
y
x
trên đoạn
2;4
là:
A.
2;4
2;4
11
min ( ) 2;max ( )
3
f x f x
.
B.
2;4
2;4
min ( ) 2 2;max ( ) 3
f x f x
.
C.
2;4
2;4
min ( ) 2;max ( ) 3
f x f x
.
D.
2;4
2;4
11
min ( ) 2 2;max ( )
3
f x f x
.
Hướng dẫn giải:
Chọn đáp án D.
2 2
2
1 2
2 3 2 1
0 .
1
1
1 2
x
x x x x
y y
x
x
x
11
2 3; 4 ; 1 2 2 2.
3
f f f
2;4
2;4
11
min ( ) 2 2;max ( ) .
3
f x f x
Câu 51.Giá trị lớn nhất của hàm số
2
3 1
2
x x
f x
x
trên đoạn
2;0
là:
A. 2. B. 1. C.
1
2
. D.
3
.
4
Hướng dẫn giải:
Chọn đáp án B.
2
2
2 2
2 3 2 3 1
4 5
2 2
x x x x
x x
y
x x
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay
1
0
5
x
y
x loai
3 1
2 , 0 , 1 1
4 2
y y y
.
Vậy
2;0
Maxy=1
x
.
Câu 52. Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
y x x
?
A. Có giá trị lớn nhất và có giá trị nhỏ nhất.
B. Có giá trị nhỏ nhất và không có giá trị lớn nhất.
C. Có giá trị lớn nhất và không có giá trị nhỏ nhất.
D. Không có giá trị lớn nhất và giá trị nhỏ nhất.
Hướng dẫn giải:
Chọn đáp án A.
Tập xác định
0;1
D .
Hàm số đã cho liên tục trên
0;1
nên luôn có giá trị lớn nhất và giá trị nhỏ nhất trên
0;1
.
Vậy
4; 2
min 7
y
.
Câu 53. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
2
3 4
y x
lần lượt là
A.
–3
và
0
.
B.
–3
và
1
.
C.
0
và
2
.
D.
–2
và
2
.
Hướng dẫn giải:
Chọn đáp án B.
Điều kiện
2 2.
x
2 '
2
3 4 0 0.
4
(0) 1
x
y x y x
x
f
6 4
x x
đạt tại
0
x
, tìm
0
x
?
A.
0
10
x . B.
0
4
x
. C.
0
6
x
. D.
0
10
x .
Hướng dẫn giải:
Chọn đáp án B.
TXD:
4 6
x
.
Ta có
1 1
0, x 4;6
2 6 2 4
y
x x
, do đó hàm số đạt giá trị nhỏ nhất tại
0
6
x
.
Câu 55. Giá trị lớn nhất của hàm số
2
4
y x x
là:
A.
4.
B.
0.
C.
2.
D.
2.
Hướng dẫn giải:
Chọn đáp án D.
+ TXD:
0;4 .
D
+
2
2
' ,
4
x
y
x x
' 0 2 0 2.
y x x
ff (2) (2) 3.
Câu 54. Giá trị nhỏ nhất của hàm số y
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay
+ Ta có:
max
0 0
4 0 2.
2 2
y
y y
y
Câu 56. Tìm giá trị nhỏ nhất của hàm số
2
5 4
y x
trên đoạn
3;1
A.
3;1
min 3
y
. B.
3;1
min 7
y
. C.
3;1
min 2
y
. D.
3;1
min 0
y
.
Hướng dẫn giải:
Chọn đáp án C.
Cách 1:
2
5 4
y x
Hàm số xác định và liên tục trên đoạn
3;1
.
2
5
5 4
x
y
x
,
0 0 3;1
y x
.
Ta có:
3 7
0 2
1 3
y
y
y
. Vậy
3;1
min 2
y
.
Cách 2: Sử dụng tabe MTCT
Câu 57. Gọi
M
và
m
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2 4 6
f x x x
trên đoạn
3; 6
. Tổng
M m
có giá trị là:
A.
18
. B.
6
. C.
12
. D.
4
.
Hướng dẫn giải:
Chọn đáp án B.
Xét:
2 4 6
f x x x
Ta có:
1 6 1
' 2 2 2. .
6 6
x
f x
x x
'
f x
vô nghiệm trên
3; 6
.
( 3) 18, (6) 12.
f f
Vậy:
6.
M m
Câu 58. Tìm giá trị lớn nhất của hàm số
1 3
y x x
trên đoạn
[1;3]
A.
[1;3]
max 2
y
. B.
[1;3]
max 2
y .
C.
[1;3]
max 2
y
. D.
[1;3]
max 2
y
.
Hướng dẫn giải:
Chọn đáp án A.
Ta có hàm số đã cho xác đinh trên đoạn
1;3
.
3 1
1 1
2 1 2 3 2 1. 3
x x
y
x x x x
0 3 1 0 3 1 2 1;3
y x x x x x
Khi đó.
1 3 2
y y ;
2 2
y
. Vậy
1;3
max 2
x
y
.
Câu 59.Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
6 5
y x x
trên đoạn
1;5
lần lượt là:
A.
2
và
0
. B.
4
và
0
. C.
3
và
0
. D.
0
và
2
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn đáp án A.
Ta có
2
3
6 5
x
y
x x
nên
0 3 1;5
y x
.
Vì
1 5 0
y y
và
3 2
y
nên giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn
1;5
lần
lượt là
2
và
0
.
Câu 60. Cho hàm số 5 3
y x
. Tìm giá trị nhỏ nhất của hàm số
A. 3. B.
2
C. 0. D.
5
.
Hướng dẫn giải:
Chọn đáp án C.
TXD:
3.
x
Xét hàm số liên tục 5 3
y x
trên
;3

ta có :
5
0, ;3
2 3
y x
x

từ đó suy ra giá trị nhỏ nhất của hàm số là
3 0
Min y f
.
Câu 61. Hàm số
2 2
4 2 3 2
y x x x x
đạt giá trị lớn nhất tại hai giá trị
1 2
,
x x
. Tính
1 2
x x
.
A.
2
. B.
1
. C.
0
. D.
1
.
Hướng dẫn giải:
Chọn đáp án D.
Tập xác định
D
.
Ta có
2
2 2
2 1 2 2 3
4 2 2
2 2
2 2 3 2 3
x x x
x
y x
x x x x
2
2
1, 1 4 2
1
0 1 2 2 3 0 1 2, 7
2 3 2
1 2, 7
x y
x
y x x x x y
x x
x y
.
Bảng biến thiên
x

1 2
1
1 2
y
0
0
0
y

7
1 4 2
7

Suy ra hàm số đạt giá trị lớn nhất tại
1 2
1 2, 1 2
x x . Do đó,
1 2
1
x x
.
Câu 62. Giá trị nhỏ nhất của hàm số
5sin cos 2
y x x
là:
A.
6
. B.
7
. C.
4
. D.
3
.
Hướng dẫn giải:
Chọn đáp án C.
Tập xác định
D
.
Ta có:
2
5sin cos2 5sin 1 2sin
y x x x x
.
Đặt
sin
t x
,
1 1
t
.
Khi đó bài toán trở thành tìm giá trị nhỏ nhất của hàm số :
2
2 5 1
g t t t
trên
1;1
.
'( ) 4 5
g t t
;
5
'( ) 0 4 5 0
4
g t t t L
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay
1 4
g
;
1 6
g
;.
Vậy giá trị nhỏ nhất của hàm số là
4
.
Câu 63. Tìm giá trị nhỏ nhất của hàm số .
2
2cos 4cos
y x x
A.
min 5
y
. B.
min 2
y
. C.
min 7
y
. D.
min 8
y
.
Hướng dẫn giải:
Chọn đáp án B.
Ta có :
2
2cos 4cos
y x x
2
2 cos 1 2
x
.
Vì
1 cos 1
x
0 cos 1 2
x
2
0 cos 1 4
x
. Do đó :
2 6
y
.
Suy ra giá trị nhỏ nhất của hàm số là
2
y
khi
cos 1
x
.
Câu 64. Tìm giá trị lớn nhất của hàm số cos cos
2 4 1
y x x
.
A.
min 5
y
.
B.
max 6
y
.
C.
min 7
y
.
D.
min 8
y
.
Hướng dẫn giải:
Chọn đáp án B.
2
cos2x 4cos 1 2cos 4cos .
y x x x
Đặt
cos 1 1 .
t x t
.
Khi đó
[-1;1]
2
[-1;1]
( 1) 2 min ( ) min ( )
2 4 '( ) 4 4 0 1 .
(1) 6 max ( ) max ( )
f f t f x
y f t t t f t t t
f f t f x
Câu 65. Giá trị nhỏ nhất của hàm số
3 2
9 1
2cos cos 3cos
2 2
y x x x
là:
A. 1. B.
24
. C.
12
. D.
9
.
Hướng dẫn giải:
Chọn đáp án D.
Tập xác định
.
D
Đặt
cos ,
t x
1;1 .
t Hàm số trở thành
3 2
9 1
2 3 .
2 2
y t t t
Ta có
2
6 9 3,
y t t
1
0 .
1
2
t
y
t
1 1
y
,
1 9
y
,
1 9
2 8
y
Vậy giá trị nhỏ nhất là
9.
Câu 66. Cho hàm số
3cos 4sin 8
y x x
với
0;2
x
. Gọi
,
M m
lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của hàm số. Khi đó tổng
M m
bằng bao nhiêu?
A.
8 2
. B.
7 3
. C.
8 3
. D. 16.
Hướng dẫn giải:
Chọn đáp án D.
Ta có
3cos 4sin 8 5sin 8 5sin 8, 0;2
y x x x x x
Do
3 5sin 8 13 3 13, 0;2
x y x
Vậy
16
M m
Câu 67. Tìm giá trị lớn nhất
2
cos
f x x x
trên đoạn
0;
2
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay
A.
. B.
0
. C.
2
. D.
4
.
Hướng dẫn giải:
Chọn đáp án C.
Hàm số
f x
trên
0;
2
.
2
2 2
1 2sin cos sin cos 2sin cos sin cos 0 0;
2
f x x x x x x x x x x
f x
đồng biến trên
0;
2
. Vậy
0;
2
max
2 2
f x f
.
Câu 68. Tìm M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số
2 cos
y x x
trên đoạn
0;
2
A.
1; 2
4
M m
. B.
; 2
2
M m
. C.
1; 0
M m
. D.
2; 1
M m
.
Hướng dẫn giải:
Chọn đáp án A.
Xét hàm số
2 cos
y f x x x
trên
0;
2
,
' 1 2sin
f x x
Cho
2
1
4
' 0 1 2 sin 0 sin
3
2
2
4
x k
f x x x k
x k
Vì 0;
2 4
x x
Ta có:
0 2, 1,
4 4 2 2
f f f
Vậy hàm số đạt giá trị lớn nhất
0;
2
max 1
4
M
, đạt giá trị nhỏ nhất
0;
2
min 2
.
Câu 69. Tìm giá trị lớn nhất của hàm số
3
3sin 4sin
y x x
trên đoạn
;
2 2
bằng:
A.
1
. B. 1. C. 3. D. 7.
Hướng dẫn giải:
Chọn đáp án C.
Đặt
sin , 1 1
t x t
;
Ta có:
3
3 4
y t t
;
3
0
3
0 3 4 0
2
3
2
t
y t t t
t
(nhận cả 3 nghiệm)
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay
3 3
1 1; 1 1; 0 0; 0; 0
2 2
y y y y y
;
Vậy
;
2 2
max 1y
.
Câu 70.Tìm GTLN và GTNN của các hàm số sau: là:
A. B. C. D.
Hướng dẫn giải:
Chọn đáp án A.
- TXĐ:
- Đặt: Khi đó: .
- Ta có:
- Ta có bảng biến thiên hàm số trên [1; 1]:
- Từ bảng biến thiên ta suy ra:
Câu 71.Tìm GTLN và GTNN của các hàm số sau: là:
A. B. C. D.
Hướng dẫn giải:
Chọn đáp án D.
- TXĐ:
- Khi đó:
- Để (*) có nghiệm thì:
2sin 1
sin 2
x
y
x
1
3
max .
y
1
3
max .
y
3
min .
y
1
2
min .
y
.
11
sin ; .
t x t
2 1
2
t
y f t
t
2
5
0 1 1
2
' , ; .
f t t
t
f t
11
1
1
3
;
max max .
y f t f
11
1 3
;
min min .
y f t f
2sin cos 1
sin 2cos 3
x x
y
x x
2
1
2
max
.
min
y
y
2
1
max
.
min
y
y
1
1
2
max
.
min
y
y
2
1
2
max
.
min
y
y
2 3 0
sin cos .
x x x
2 3 2 1 2 2 1 1 3
sin cos sin cos sin cos (*)
y x x x x y x y x y
2
2 2
1
1 3 2 2 1 2
2
.
y y y y
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay
Từ đây suy ra:
Câu 72. Giá trị lớn nhất của hàm số
ln
x
f x
x
trên đoạn
1;3
là:
A.
1
e
.
B.
e
.
C.
ln3
3
.
D.
24,2
.
Hướng dẫn giải:
Chọn đáp án A.
Ta có:
2 2
1
. ln
1 ln
' ' 0 1 ln 0 .
x x
x
x
f x f x x x e
x x
.
Với
1;
x e
thì
' 0
f x
hàm số đồng biến trên nửa khoảng
1;
e
.
Với
;3
x e
thì
' 0
f x
hàm số nghịch biến trên nửa khoảng
;3
e
.
Vậy giá trị lớn nhất của hàm số trên đoạn
1;3
là
1
f e
e
.
Câu 73.Giá trị nhỏ nhất của hàm số
2 ln
f x x x
trên
2;3
là
A.
1
. B.
4 2ln2
. C.
e
. D.
2 2ln2
.
Hướng dẫn giải:
Chọn đáp án B.
Xét hàm số liên tục và xác định trên
2;3
.
Ta có
1 ln
f x x
,
0 2;3
f x x e
.
2 2 2 ln2
y ,
3 3 2 ln3
y ,
y e e
.
Vậy
2;3
min 2 2 2 ln 2
y y
.
Câu 74. Tìm giá trị nhỏ nhất của hàm số
2 ln 1 2
y x x
trên
1;0
A.
1;0
min 2 ln3
x
. B.
1;0
min 0
x
. C.
1;0
min 1
x
. D.
1;0
min 2 ln3
x
.
Hướng dẫn giải:
Chọn đáp án A.
Xét
2 ln 1 2
f x y x x
TXĐ:
1
,
2
D

2
' 2
1 2
f x
x
Cho
2 1 2 2
' 0 0 4 0 0 1;0
1 2
x
f x x x
x
Ta có:
1 2 ln3
0 0
f
f
Vậy
1;0
min 2 ln3
.
Câu 75. Tính giá trị lớn nhất của hàm số
ln
y x x
trên
1
;
2
e
.
2
1
2
max
.
min
y
y
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay
A.
1
;
2
max 1
x e
y e
. B.
1
;
2
max 1
x e
y
. C.
1
;
2
max
x e
y e
. D.
1
;
2
1
max ln 2
2
x e
y
.
Hướng dẫn giải:
Chọn đáp án A.
Hàm số
ln
y x x
liên tục trên đoạn
1
;
2
e
.
Ta có
1
1y
x
1
0 1 ;
2
y x e
.
Do
1 1
ln 2
2 2
y
;
1
y e e
;
1 1
y
nên
1
;
2
max 1
x e
y e
.
Câu 76. Tìm GTLN và GTNN của hàm số trên đoạn là:
A. và 1 B. và
C. và
D. và
Hướng dẫn giải:
Chọn đáp án C.
Xét hàm số trên ;
Vậy: tại x = 1, tại x = 3.
Câu 77. Tìm GTLN và GTNN của hàm số trên đoạn [–1; 2] là:
A. và
B. và C. và D. và
Hướng dẫn giải:
Chọn đáp án A.
Hàm số f(x) liên tục trên đoạn [–1; 2],
.
Câu 78. Biết rằng giá trị lớn nhất của hàm số
2
ln
x
y
x
trên đoạn
3
1;
e
là
,
n
m
M
e
trong đó
,
m n
là
các số tự nhiên. Tính
2 3
2 .
S m n
A.
.135
S
.
B.
.24
S
.
C.
.22
S
.
D.
.32
S
.
Hướng dẫn giải:
Chọn đáp án C.
2
2
2
1
ln 0
2ln ln
, 0 .
ln 2
x
x
x x
y y
xx
x e
2
4ln
f x x x
1;
e
2
4
e
2
4
e
2 2ln2
2
4
e
1
2
4
e
2 2ln2
1;4
2
9
'( ) 1f x
x
1;4 '( ) 0 3
x f x x

25
(1) 10; (3) 6; (4)
4
f f f
1;4
10
max f x
1;4
( ) 6
min f x
2 2x
f(x) (x 2).e
4
2
e
2
e
4
2
e
2
1
e
4
4
e
2
e
4
4
e
2
1
e
2 2x
f '(x) 2(x x 2)e
2
f '(x) 0
x x 2 0
x 1
x ( 1;2)
x ( 1;2)
2 4
2
1
f(1) e , f( 1) , f(2) 2e
e
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay
1 0
y
,
2
2
4
y e
e
,
3
3
9
.
y e
e
Suy ra
2 3
2
4
4, 2 4 2.2 32.
M m n S
e
Câu 79. Tìm tập hợp tất cả các giá trị của tham số
m
sao cho bất phương trình sau có nghiệm:
5 4
x x m
.
A.
;3

. B.
;3 2

. C.
3 2;

. D.
;3 2

.
Hướng dẫn giải:
Chọn đáp án B.
Đặt
5 4 , 5;4
f x x x x .
1 1
2 5 2 4
f x
x x
;
1
0 5 4
2
f x x x x
.
Bảng biến thiên:
x
5
1
2
4
( )
f x
+
( )
f x
3
3 2
3
2
4
x m
có nghiệm
2 2 2
m . D.
2 2
m
.
Chọn đáp án C.
Tập xác định
2
2;
D
Phương trình
2
4
x x m
có nghiệm khi đường thẳng
y m
cắt đồ thị của hàm số
2
4
y x x
C
Xét hàm số
2
4
y x x
trên
2
2;
D
Ta có
2
1
4
x
y
x
Cho
2
2 2
2
0
0 1 0 4 2
4
4
x
x
y x x x
x x
x
Bảng biến thiên:
x
2
2
2
y
y
2
Từ bảng biến thiên ta thấy đường thẳng
y m
cắt đồ thị hàm số
C
khi
2 2 2
m .
2 2
0
Yêu cầu bài toán m 3 2 .
Câu 80. Với giá trị nào của tham số m thì phương trình x
A. 2 m 2 . B. 2 m 2 2 . C.
Hướng dẫn giải:
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay
Câu 81. Cho
x
,
y
là các số thực thỏa mãn
1 2 2
x y x y
. Gọi
M
,
m
lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của
2 2
2 1 1 8 4
P x y x y x y
. Khi đó, giá trị của
M m
bằng
A.
44
. B.
41
. C.
43
. D.
42
.
Hướng dẫn giải:
Chọn đáp án C.
Ta có :
2
2
1 2. 1
x y x y
1 2 . 1 1
x y
3.
x y
Do đó :
0 3
x y
.
Theo bài ra :
2
2 2 8. 4
P x y x y x y
Đặt
t x y
. Đk :
0 3
t
.
Xét :
2
2 2 8 4
P f t t t t
trên
.
Có
4
2 2
4
f t t
t
.
Đặt
4
2 2
4
g t f t t
t
3
2
' 2 0
4
g t f t
t
với
0;3
t .
Do đó : hàm số
g t
đồng biến trên
.
Khi đó :
0 0 0
g t g f t f
. Suy ra hàm số
f t
đồng biến trên
.
3 25
0 18
M f
m f
. Vì vậy :
43
M m
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay
DẠNG 2: GTLN, GTNN TRÊN MỘT KHOẢNG, NỬA KHOẢNG
Phương pháp: Xét khoảng hoặc nửa khoảng D
- Tính
'
f x
, giải phương trình
' 0
f x tìm nghiệm trên D.
- Lập BBT cho hàm số trên D.
- Dựa vào BBT và định nghĩa từ đó suy ra GTLN, GTNN.
Câu 1.Trên khoảng (0; +) thì hàm số
3
3 1
y x x
A. Có giá trị nhỏ nhất là
min 3
y . B. Có giá trị lớn nhất là
max 1
y .
C. Có giá trị nhỏ nhất là
min 1
y . D. Có giá trị lớn nhất là
max 3
y .
Hướng dẫn giải:
Chọn đáp án D.
Xét hàm số đã cho trên
0,

D .
Ta có
2
3 3
y x ,
2
1 0,
0 3 3 0
1 0,

x
y x
x
.
Bảng biến thiên
x
0
1
y
0
y
1
3

Do đó,
max 3
y và không tồn tại
min
y
.
Câu 2. Tìm giá trị nhỏ nhất của hàm số
4
y x
x
trên khoảng
0;
.
A.
4
. B.
2
. C.
2
. D.
4
.
Hướng dẫn giải:
Chọn đáp án A.
Cách 1:
Vì hàm số xác định trên khoảng
0;
nên ta có
0
x và
4
0
x
.
Áp dụng bất đẳng thức Cô-si cho hai số
x
và
4
x
ta có
4 4
2 . 4
x x
x x
.
Vậy hàm số đạt giá trị nhỏ nhất bằng
4
, dấu bằng xảy ra khi
2
x .
Cách 2:
TXĐ:
0;

D .
Ta có
2
4
1
y
x
,
0
y
2
4
1 0
x
2
2
4
0
x
x
2
2
x
x
.
Bảng biến thiên.
.
4
x
y
y
0
3
0
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay
Dựa vào bảng biên thiên ta có giá trị nhỏ nhất của hàm số là 4 .
Câu 3. Hàm số
2
1
1
y
x
có bảng biến thiên như hình vẽ. Xét trên tập xác định của hàm số. Hãy
chọn khẳng định đúng ?
A. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
B. Hàm số có giá trị lớn nhất bằng 0.
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
D. Hàm số có giá trị lớn nhất bằng 1.
Hướng dẫn giải:
Chọn đáp án D.
Hàm số đạt giá trị lớn nhất bằng
1
khi
0x
nhưng hàm số không đạt giá trị nhỏ nhất tại
0
vì không tồn tại
giá trị nào của
x
thỏa mãn.
Câu 4. Hàm số
2
4
1
y
x
có bảng biến thiên như hình vẽ.
x

0
y
0
y
0
4
0
Xét trên tập xác định của hàm số. Hãy chọn khẳng định đúng?
A. Hàm số có giá trị lớn nhất bằng 4 và giá trị nhỏ nhất bằng 0 .
B. Hàm số có giá trị lớn nhất bằng 0 .
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
D. Hàm số có giá trị lớn nhất bằng 4 .
Hướng dẫn giải:
Chọn đáp án D.
Câu 5.Tìm giá trị lớn nhất của hàm số
2
3
2
x
y
x
trên khoảng
;2 .
A.
;2
max 4

y B.
;2
max 3

y C.
;2
max 1

y D.
;2
max 2

y .
Hướng dẫn giải:
Chọn đáp án D.
Ta có
2
2
4 3
2
x x
y
x
nên
1 ;2
0
3 ;2


x
y
x
.
Ta có bảng biến thiên
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay
Nên
;2
max 2

y .
Câu 6.Tìm giá trị nhỏ nhất của hàm số
1
3
2
y x
x
trên nửa khoảng
4; 2
.
A.
4; 2
min 5
y
. B.
4; 2
min 6
y
. C.
4; 2
min 4
y
. D.
4; 2
min 7
y
.
Hướng dẫn giải:
Chọn đáp án D.
Xét hàm số
1
3
2
y x
x
trên nửa khoảng
4; 2
2
2 2
1 4 3
1
2 2
x x
y
x x
2
1 4; 2
0 4 3 0
3 4; 2
x
y x x
x
Bảng biến thiên
Câu 7. Tìm giá trị nhỏ nhất
min
y
của hàm số
2 3 .
y x
A.
min
0
y . B.
min
6
y . C.
min
3
y . D.
min
2
y .
Hướng dẫn giải:
Chọn đáp án A.
Tập xác định:
( ;3].

D
Ta có:
1
0, ;3 .
3

y x
x
Hàm số nghịch biến trên khoảng
;3 .

x

3
y
–
y
0
Vậy
( ;3]
min 3 0.

y y
Câu 8. Giá trị nhỏ nhất của hàm số
3
sin cos2 sin 2
y x x x trên khoảng
;
2 2
bằng:
A.
1
. B. 6. C.
23
27
. D. 1.
Hướng dẫn giải:
Chọn đáp án C.
Ta có
3 2
sin 2sin sin 1
y x x x
.
Đặt
sin 1;1
t x thì hàm số trở thành
3 2
2 1, 1;1
y t t t t .
Ta có
2
3 4 1
y t t
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay
1( )
0
1
( )
3
t l
y
t n
1 23
3 27
Miny y .
Câu 9. Giá trị lớn nhất của hàm số
3
2
1
3
x
y x trên khoảng
;
2 2
bằng:
A. 3. B. 7. C. 1. D. -1.
Hướng dẫn giải:
Chọn đáp án C.
2
3cos 12sin cos
y x x x
.
2
2
cos 0
2
6
0 3cos 12sin cos 0 .
1
5
sin
2
2
6
7
2
6
x k
x
x k
y x x x k
x
x k
x k
.
Do
;
2 2 6
x x
.
Ta có
1
6
f
,
1
6
f
nên GTLN của hàm số trên khoảng
;
2 2
bằng
1
.
Câu 10. Tìm m để phương trình
5 3
1 0
x x x m có nghiệm trên
;1

.
A.
2
m . B.
2
m . C.
2
m . D.
2
m .
Hướng dẫn giải:
Chọn đáp án C.
5 3 5 3
1 0 1
x x x m x x x m
.
Xét hàm số
5 3
1
y x x x
trên
;1

.
4 2
1
5 3 0, ;1
2 1
y x x x
x
.
Bảng biến thiên
Ycbt
2 2.
m m
Câu 11. Cho hàm số
9
( )
f x x
x
. Tính giá trị lớn nhất của hàm số
f x
trên (
0
)
;

A.
3.
B.
6.
C.
9
D.
3.
Hướng dẫn giải:
Chọn đáp án B.
Ta có :
2
9
1
f x
x
.
x
y
y

1

2
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay
Khi đó
3
0
3
x
f x
x
.
Vì
;0
x nên ta lấy
3
x , loại
3
x .
Ta có bảng biến thiên như sau
Từ bảng biến thiên ta có giá trị lớn nhất của hàm số trên
;0
 là
6
.
Câu 12. Tìm tất cả giá trị của m để phương trình
24
1
x x m
có nghiệm
A.
0;1
. B.
;0
 . C.
1;
. D.
0;1
.
Hướng dẫn giải:
Chọn đáp án D.
ĐK:
0
x
Xét hàm số
24
1
f x x x
3
2
4
3
2
4
1
'
2 1 .
x x x
f x
x x
,
3
2 4 2
4
' 0 1 3 3 1 0( )
f x x x x x x VN
' 0
f x hàm số nghịch biến trên
0;

,
(0) 1, lim 0

x
f f x
Vậy
0;1
m .
Câu 13. Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
2 tan tan
m x m x
có ít nhất một
nghiệm thực.
A.
2 2
m . B.
1 1
m . C.
2 2
m . D.
1 1
m .
Hướng dẫn giải:
Chọn đáp án C.
2
tan
2 tan 1
x
pt m
x
Đặt
2
tan
2 1
t
x t m
t
Xét hàm số
2
2
2
2 2
2 2
' 0 2
2 1
2 . 2 1
t t
f t f t t
t
t t
Lập BBT với
lim 1, lim 1, 2 2, 2 2 2; 2 .
 
t t
f t f t f f m
Câu 14. Cho
,
x y
là hai số không âm thỏa mãn
2
x y . Tìm giá trị nhỏ nhất của biểu thức
3 2 2
1
1
3
P x x y x
A.
min 5
P . B.
7
min
3
P . C.
17
min
3
P . D.
115
min
3
P .
x

3
0
'
y
0
y
6


ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn đáp án B.
Ta có
2
x y 2
y x
3 2 2
1
1
3
P x x y x
2
3 2
1
2 1
3
P x x x x
3 2
1
2 5 5
3
P x x x
Xét hàm số
3 2
1
2 5 5
3
y x x x
trên
0;

2
4 5
y x x
. Cho
2
1
0 4 5 0
5
x
y x x
x
Bảng biến thiên:
x

5
1
y
0
0
y

115
3
7
3
Từ bảng biến thiên ta thấy
7
min
3
P .
Câu 15.Giá trị của
m
để phương trình
2
12
x x m
có nghiệm là:
A.
2
.
2
m B.
2
.
2
m C.
2
.
2
m D.
2
.
2
m
Hướng dẫn giải:
Chọn đáp án A.
Đặt
2
( 2
1
)
f x x x
2
2
1
1
2
x
f x
x
Ta có:
2
0
0 2 2
2
2
1
x
f x x x
x
2
2
x
Bảng biến thiên
Vậy,
2
2
m .
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay
DẠNG 3: ỨNG DỤNG GTLN, GTNN VÀO GIẢI TOÁN THỰC TẾ
Câu 1: Hình chữ nhật có chu vi không đổi là 8 m. Diện tích lớn nhất của hình chữ nhật đó là:
A.
4m
2
.
B.
8m
2
C.
16m
2
.
D.
2m
2
.
Hướng dẫn giải:
Chọn đáp án A.
Gọi 2 kích thước của hình chữ nhật là
, 4.a b a b
2
. 4
2
a b
S a b
. Vậy diện tích lớn nhất của hình chữ nhật bằng
2
4m
.
Câu 2: Cho một tấm nhôm hình vuông cạnh 18 cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn
hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm , rồi gấp tấm nhôm lại như hình vẽ dưới
đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A. 2x . B. 4x . C. 6x . D. 3x .
Hướng dẫn giải:
Chọn đáp án C.
Khối hộp có đáy là hình vuông với độ dài cạnh là 18 2x và độ dài chiều cao là x nên có thể tích
là
3
2
1 1 4 18 2 18 2
18 2 .4 . 18 2 . 18 2 432
4 4 3
x x x
V x x x x x
.
Đẳng thức xảy ra khi và chỉ khi 18 2 6x x x .
Vậy max 432 6V x .
Câu 3: Cho một tấm nhôm hình vuông cạnh 24cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông cạnh bằng nhau, mỗi hình vuông có cạnh bằng x (cm) rồi gập tấm nhôm lại như hình vẽ dưới
đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A. 6x . B. 4x . C. 2x . D. 8x
.
Hướng dẫn giải:
Chọn đáp án B.
Cạnh đáy của hộp là 24 2 x .
Khi đó thể tích của hộp :
2
24 2
V x x f x
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay
Có
3
3
24 2 24 2 4
4 24 2 24 2 4 16
3
x x x
V x x x
Dấu xảy ra khi và chỉ khi 24 2 4 4 x x x .
Câu 4: Cho hình vẽ.
A.
24 3(m)
. B.
3 3(m)
. C.
3 3(m)
. D.
24 3(m)
.
Hướng dẫn giải:
Ta có
2
12 72 72V x x x
,
0V x
2
12 72 72 0x x
3 3
3 3
x
x
.
Bảng biến thiên.
.
Dựa vào bảng biên thiên ta có
V x
lớn nhất khi
3 3x
.
Câu 5: Cho một tấm nhôm hình vuông cạnh
18
cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để
được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.
A.
6x
. B.
3x
. C.
2x
. D.
4x
.
x
0
3 3
3 3
6
V x
V x
0
0
0
0
41,57
41,57
.
Bạn An có một tấm nhôm hình chữ nhật có chiều dài
12
m
, chiều rộng
6
m
. Bạn nhờ bác thợ hàn cắt ở
bốn góc bốn hình vuông bằng nhau và gập tấm nhôm lại (như hình trên) để được một cái hộp không nắp
dùng để đựng nước. Hỏi bác thợ hàn phải cắt cạnh hình vuông bằng bao nhiêu sao cho khối hộp chứa được
nhiều nước nhất ?
Chọn đáp án B.
Gọi
x
là độ dài cạnh hình vuông bị cắt, khi đó ta có 0 x 6.
Thể tích của khối hộp là
V
x
x
122x
6 2x
4x
3
36x
2
72x
.
Ta cần tìm
x
sao cho
V
x
lớn nhất với 0 x 6.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn đáp án B.
Theo đề bài ta có
2
3 2
. . 18 2 4 72 324 .
V h S x x x x x
Xét
3 2
4 72 324
f x x x x
liên tục trên
0;9 .
Ta có
2
12 144 324.
f x x x
3
0 .
9
x
f x
x
Bảng biến thiên
x
0 3 9
f x
+ 0
0
f x
432
0 0
Vậy thể tích lớn nhất khi
3.
x
Câu 6: Một trang chữ của một quyển sách tham khảo Văn học cần diện tích
2
384
cm
. Biết rằng trang giấy được canh lề trái là
2
cm
, lề phải là
2
cm
, lề trên
3
cm
và lề dưới là
3
cm
. Tìm chiều dài và chiều rộng của trang sách để trang sách
có diện tích nhỏ nhất
A. Chiều dài:
32
cm
và chiều rộng:
12
cm
.
B. Chiều dài:
24
cm
và chiều rộng:
16
cm
.
C. Chiều dài:
40
cm
và chiều rộng:
20
cm
.
D. Chiều dài:
30
cm
và chiều rộng:
20
cm
.
Hướng dẫn giải:
Chọn đáp án B.
Gọi
x
,
y
là chiều dài và chiều rộng của trang chữ.
Theo đề bài ta có:
384
xy
. Ta cần tìm
x
,
y
sao cho
4 6
x y
đạt giá trị nhỏ nhất.
Ta có hàm
384
6 4 24 408 6 4.f x xy x y x
x
1536
6 408 2 6.1536 408 192
x
x
Dấu “=” xảy ra khi
1536
6 16
x x
x
và
24
y
Trên không, vài con cò về tổ trễ đập nhanh
đôi cánh trắng phau rồi khuất trong lùm cây rậm
lá. Những đám mây trắng đá ngả màu ngà, bầu
trời xanh cũng đã ngả sang màu sậm đưa đến
màu đen. Đâu đó có tiếng chim lẻ bạn, tiếng dơi
muỗi lào xào lẫn trong tiếng gió nhẹ lay cành.
Dưới bến sông, con nước ròng lên đầy mé đã
đứng lại không lùa được những đợt lục bình lờ
lững giữa dòng ra sông cái. Dòng nước xanh chìm
đi trong màu xám sậm và những bóng cây bên bờ
kia ngả xuống dòng càng lúc càng hiện rõ lù lù
thành hàng trong bóng nước.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay
Câu 7: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày
xuất hiện bệnh nhân đầu tiên đến ngày thứ t là
2 3
45f t t t
(kết quả khảo sát được trong tháng 8
vừa qua). Nếu xem
f t
là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Hỏi tốc độ truyền bệnh sẽ
lớn nhất vào ngày thứ mấy?
A. 12. B. 15. C. 20. D. 30.
Hướng dẫn giải:
Chọn đáp án B.
Ta có :
2
' 90 3f t t t
.Cần tính giá trị lớn nhất của hàm số
'g t f t
3
3
m . Tìm chiều rộng của đáy hình chữ nhật để chi phí xây dựng là
thấp nhất
A.
1,5 .x m B.
2 .x m C.
1 .x m D.
2,5 .x m
Hướng dẫn giải:
Chọn đáp án C.
Ta có
2
2
4 4 2
2
3 3 3
V x h h
x
Diện tích xung quang của bồn nước ( không nắp).
2 2 2
4
2 2 2 6 2 2S xh xh x xh x x
x
2
4
4 ; 0 1S x S x
x
BBT
Để chi phí xây dựng là thấp nhất thì S phải nhỏ nhất. Ta có 6 1.MinS khi x
–
Khi đó : g '
t
f ''
t
90 6t. g '
t
0 t 15 .
Câu 8: [2D1-3]Khi xây nhà, chủ nhà cần làm một bồn nước bằng gạch và xi măng có dạng hình hộp
đứng đáy là hình chữ nhật có chiều rộng là x
m
, chiều dài gấp
2
lần chiều rộng và không nắp, có
chiều cao là h
m
, có thể tích là
4
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay
Câu 9: Một chất điểm chuyển động theo phương trình
3 2
2 18 2 1,S t t t
trong đó t tính bằng
giây
s và
S
tính bằng mét
m . Thời gian vận tốc chất điểm đạt giá trị lớn nhất là
A.
5t s
. B.
6t s
. C.
3t s
. D.
1t s
.
Hướng dẫn giải:
Chọn đáp án C.
Ta có
2
2
' 6 36 2 6 3 56 56, .
v t S t t t t t
Suy ra
v t lớn nhất bằng
56 /m s
khi
3t s
.
Câu 10: Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức
2
0,024 30
G x x x
,
trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp ( x được tính bằng mg). Tìm lượng
thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất
A. 20 mg. B. 0,5mg. C. 2,8mg. D. 15mg.
Hướng dẫn giải:
Chọn đáp án A.
20
0
0360024,0'30024,0
22
x
Lx
xxxGxxxG
A. 6,5km B. 6km C. 0km D. 9km
Hướng dẫn giải::
Chọn đáp án A.
Theo hình vẽ, số tiền để xây dựng đường ống từ A đến
B
là:
2
50000. 9 130000 36f x x x ,
0 9x .
2
' 50000 130000.
36
x
f x
x
,
2
5
0 50000 36 130000
2
f x x x x
.
0 1230000f ,
5
1170000
2
f
,
9 1170000 17f .
0;9
5
min
2
f x f
.
Vậy C cách A 6,5km .
Lập BBT x 20mg là giá trị cần tìm.
Câu 11: Một công ty muốn làm đường ống dẫn từ một điểm A trên bờ đến một điểm
B
trên một hòn
đảo. Hòn đảo cách bờ biển 6km. Giá để xây đường ống trên bờ là 50000USD mỗi km, và
130000USD mỗi km để xây dưới nước. B
là điểm trên bờ biển sao cho BB
vuông góc với bờ biển.
Khoảng cách từ A đến B
là 9km . Vị trí C trên đoạn AB
sao cho khi nối ống theo ACB thì số tiền
ít nhất. Khi đó C cách A một đoạn bằng bao nhiêu ?
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay
Câu 12: Cho một tờ giấy hình chữ nhật với chiều dài 12 cm và chiều rộng 8 cm. Gấp góc bên phải
của tờ giấy sao cho góc ở đỉnh của nó chạm với đáy như hình vẽ. Khi độ dài nếp gấp là nhỏ nhất thì giá
trị nhỏ nhất đó là bao nhiêu.
A.
6 15 6 3
. B. 6 15 6 3 . C. 8 2 . D. 6 3.
Hướng dẫn giải:
Chọn đáp án D.
Đặt DG FG x , ED HC EF y . Khi đó
2
2
8 16 64FC x x x
,
16 64HF y x
.
Ta có:
2
2 2 2
8 16 64
8 16 64 64 2 16 64 16 64
x
EF y x y y y x x y y
x
Độ dài nếp gấp là
8 16 64x
f x x y x
x
với 0 8x .
Thay lần lượt các đáp án ta thấy với 6 3x thì ( )f x nhỏ nhất.
Câu 13: Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C khoảng cách
ngắn nhất từ C đến B là 1 km . Khoảng cách từ B đến A là 4 . Mỗi km dây điện đặt dưới nước là
mất 5000 USD, còn đặt dưới đất mất 3000 USD. Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc
dây điện từ A qua S rồi đến C là ít tốn kém nhất?
A.
15
km
4
. B.
13
km
4
. C.
10
km
4
. D.
19
km
4
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn đáp án B.
Gọi x là khoảng cách từ A đến S (0 4x ), ta có 4BS x ,
2
2
4 1 8 17CS x x x
.
Chi phí cho đường dây diện là
2
3000 5000 8 17y x x x .
Muốn ít tốn kém chi phí nhất ta cần tìm x để
min
y
.
Xét hàm số
2
3000 5000 8 17y x x x với
0,4x .
Ta có
2
2 2
1000 3 8 17 5 20
5000 2 8
3000
2 8 17 8 17
x x x
x
y
x x x x
.
2
2 2 2
0 3 8 17 20 5
4
19
4 4
loai
4
9 72 153 400 200 25 16 128 247 0
13
nhan
4
y x x x
x
x x
x
x x x x x x
x
Mà
0 5000 17y ,
4 17000y ,
13
16000
4
y
.
Suy ra
0,4
min 16000y khi
13
km
4
x .
Lập bảng xét dấu ta có 2 2x thì khối chóp đạt giá trị lớn nhất.
A. 72km kể từ P B. 42km kể từ Q C. 48km kể từ P D. tại P
Hướng dẫn giải:
Chọn đáp án A.
Vẽ lại hình vẽ thì ta có hình vẽ đơn giản hóa như sau:
Câu 14: Đường cao tốc mới xây nối hai thành phố A và B, hai thành phố này muốn xây một trạm thu
phí và trạm xăng ở trên đường cao tốc như hình vẽ. Để tiết kiệm chi phí đi lại, hai thành phố này quyết
định toán xem xây trạm thu phí ở vị trí nào để tổng khoảng cách từ hai trung tâm thành phố đến trạm là
ngắn nhất, biết khoảng cách từ trung tâm thành phố A, B đến đường cao tốc lần lượt là 60km và 40km
và khoảng cách giữa hai trung tâm thành phố là 120km (được tính theo khoảng cách của hình chiếu
vuông góc của hai trung tâm thành phố lên đường cao tốc, tức là PQ kí hiệu như hình vẽ). Tìm vị trí
của trạm thu phí và trạm xăng? (Giả sử chiều rộng của trạm thu phí không đáng kể).
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay
Thực chất bài toàn trở thành tìm x để AC+BC nhỏ nhất.
Theo định lý Pytago ta có
2 2
AC 60 x ;
2 2 2
BC (120 x ) 40 x 240x 16000
Khi đó
2 2
f(x) AC BC x 3600 x 240x 16000 . Ta cần tìm
(0;12)
Min f (x) .
Ta có
2 2
x x 120
f '(x)
x 3600 x 240x 16000
; khi bấm máy tính nhẩm bằng cách nhập vào màn
hình biểu thức f’(x) và ấn SHIFT SLOVE và chọn một số nằm trong khoảng (0;120) để dò nghiệm,
như tôi nhập 2 máy nhanh chóng hiện nghiệm là 72.
Bấm máy tính sử dụng nút TABLE ta nhận thấy phương trình có duy nhất một nghiệm này do f’(x) chỉ
đổi dấu qua 72. Khi đó ta có BBT sau:
x 0 72 120
f’(x) - 0 +
f(x)
Min
Vậy từ đó ta có thể kết luận CP=72.
Câu 15: Người ta cần xây dựng mương nước có dạng như hình vẽ, với diện tích tiết diện ngang của
mương là
2
8m
. Gọi l là độ dài đường biên giới hạn của tiết diện này. Để l đạt giá trị nhỏ nhất thì các
kích thước của mương là
A. 4m và 1m. B. 2m và 1m. C. 4m và 2m. D. 3m và 2m.
Hướng dẫn giải:
Chọn đáp án C.
Gọi
,x y
lần lượt là chiều rộng và chiều cao của mương.
Theo bài ra ta có 8 .x y ,
16
2l y x x
x
.
Xét hàm số
16
l x x
x
2
2 2
16 16
' 1
x
l x
x x
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay
Cho
4
' 0
4
x n
l x
x l
Lập bảng biến thiên
Ta được l đạt giá trị nhỏ nhất thì các kích thước của mương là 4 , 2x m y m
Câu 16: Một người thợ xây cần xây một bể chứa
3
108 m
nước có dạng hình hộp chữ nhật với đáy là
hình vuông và không có nắp. Hỏi chiều dài cạnh đáy và chiều cao của lòng bể bằng bao nhiêu để số
viên gạch dùng xây bể là ít nhất? Biết thành bể và đáy bể đều được xây bằng gạch, độ dày của thành bể
và đáy là như nhau, các viên gạch có kích thước như nhau và số viên gạch trên một đơn vị diện tích là
bằng nhau
A.
3 3
108 ; 108m m
. B. 6 ;3m m . C. 3 ;12m m . D. 2 ;27m m .
Hướng dẫn giải:
Chọn đáp án B.
Gọi x ,h tương ứng là độ dài cạnh đáy và đường cao của hình hộp chữ nhật.
Ta có:
2
2
108
. 108V h x h
x
.
2 2 2
432 216 216
4 4
xq d
S S S xh x x x
x x x
.
Áp dụng bất đẳng thức AM – GM ta được
3 2
3 216S .
Dấu đẳng thức xảy ra khi
2
216
6 x x
x
2
108
3
6
h .
A. 40x cm . B. 50x cm . C. 30x cm . D. 20x cm .
Hướng dẫn giải:
Chọn đáp án A.
Ta có độ dài cạnh
2
2 2 2
120 14400 240AC BC AB x x x
.
Diện tích tam giác ABC là:
1 1
. 14400 240
2 2
S AB AC x x .
Xét hàm số
14400 240
f x x x
với 0 60x .
Ta có:
120 14400 360
14400 240
14400 240 14400 240
x x
f x x
x x
;.
0 40 0;60f x x
.
Câu 17: Cho một tấm gỗ hình vuông cạnh 200cm . Người ta cắt một tấm gỗ có hình một tam giác
vuông ABC từ tấm gỗ hình vuông đã cho như hình vẽ sau. Biết AB x
0 x 60cm
là một cạnh
góc vuông của tam giác ABC và tổng độ dài cạnh góc vuông
AB
với cạnh huyền BC bằng 120cm.
Tìm x để tam giác ABC có diện tích lớn nhất.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay
I
M
BA
x
Bảng biến thiên:
.
Vậy
max
max
40
S f x x
.
Câu 18: Cho một tấm bìa hình vuông cạnh
5 dm
. Để làm một mô hình kim tự tháp Ai Cập, người ta
cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp lên, ghép lại
thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình là:
A.
3 2
2
. B.
5
2
. C.
5 2
2
. D.
2 2
.
Hướng dẫn giải:
Chọn đáp án D.
Gọi
x
là chiêu dài cạnh đáy (
0 5 2
x ), ta có
2 2
2
5 2 25 25 10 2 2 25 5 2
,
2 4 4 2
x x x x x
MI AM
Đường cao hình chóp là
2 2
25 5 2 25 5 2
2 2 2
x x x x
h
Thể tích của khối chóp là
2 2 4 5
1 25 5 2 1
25 5 2
3 2 18
x
V x V x x
Xét hàm số
4 5
25 5 2
y x x
trên khoảng
0;5 2
3 4 3
25.4 25 2 25 4 2
y x x x x
0
0
2 2
x
y
x
x
0
2 2
5 2
y
0
y
320
Suy ra
0;5 2
max 320
y tại
2 2
x . Suy ra
max
2 2
V x .
Câu 19: Một màn ảnh chữ nhật cao 1,4 mét được đặt ở độ cao 1,8 mét so với tầm mắt (tính từ đầu mép
dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng
O
sao cho góc nhìn lớn nhất. Hãy xác
định vị trí điểm
O
(
BOC
gọi là góc nhìn).
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay
A. 2,4AO m . B. 2AO m . C. 2,6AO m . D. 3AO m .
Hướng dẫn giải:
Chọn đáp án A.
Đặt .OA x Ta có:
3,2 1,8
tan ,tan .AOC AOB
x x
2
tan tan 1,4
tan tan
5,76
1 tan .tan
AOC AOB x
BOC AOC AOB
x
AOC AOB
.
Đặt
2
1,4
5,76
x
f x
x
2
2
2
1,4 8,064
5,76
x
f x
x
.
2
0 5,76 2,4.f x x x
x
0 2,4
y
0
0
y
0
7
24
0
Dựa vào BBT trên:
0;
7
max
24
f x

khi
2,4x m
.
Câu 20: Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy, để ít tốn vật liệu nhất thì chiều cao
dmh của bồn phải gần nhất với giá trị nào sau đây?
A. 10,84. B. 10,83. C. 10,85. D. 10,86.
Hướng dẫn giải:
Chọn đáp án A.
Để ít tốn vật liệu nhất thì diện tích toàn phần bồn nước phải nhỏ nhất.
Tức là:
2
2 2
tp
S R Rh
nhỏ nhất. (với
R
là bán kính đường tròn đáy.
Thể tích bồn nước
2
1000
1000V R h R
h
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay
1000 1000 2000
2 . 2 . 4000
tp
S h h
h h h
.
2
2000 2000
4000
tp
S
h
h
,
2
3
4000
0 4000 10,84
tp
S h h h
.
Sử dụng bảng biến thiên, ta tìm được
tp
S
nhỏ nhất khi
10,84
h
.
Câu 21:
Khi nuôi cá trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của
mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng:
480 20
P n n
(gam). Hỏi
phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được
nhiều cá nhất.
A.
8.
n
B.
12.
n
C.
20.
n
D.
24.
n
Hướng dẫn giải:
Chọn đáp án B.
Cân nặng của n con cá là:
2
( ) . ( ) 480 20
f n n P n n n
Ta có:
2 2
( ) 480 20 2880 20(12 ) 2880
f n n n n
Vậy nhiều cá nhất khi n = 12
A.
115 250 000
. B.
101 250 000
. C.
100 000 000
. D.
100 250 000
.
Hướng dẫn giải:
[0;50)
max 5 101 250 000
f x f
.
A.
6
. B.
5
. C.
4
. D.
7
.
Hướng dẫn giải:
Chọn đáp án A.
Ta có
10 10 (1)
x y y x
Và
0 6 4 10
y x
.
Số tiền lãi
2
3 2 3
2 326 27 2 326 10 27 10
f x x x y y x x x x
(thay
(1)
vào).
3 2
27 216 560
f x x x x với
4;10
x .
Câu 22: Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá
2000000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn
hộ thêm 50000 đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho
thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao
nhiêu?
Chọn đáp án B.
Gọi n là số lần tăng giá ( n là số tự nhiên). Khi đó số căn hộ bị bỏ trống cũng là n . Do đó số tiền
thu được khi cho thuê 50n căn hộ là A
2.10
6
5.10
4
.n
50 n
5.10
4
n
2
5.10
5
n 10
8
, điều
kiện n 50.
Xét hàm số f
x
5.10
4
x
2
5.10
5
x 10
8
, với 0 x 50 .
Ta có f
x
10
5
x 5.10
5
; f
x
0 x 5.
Lập bảng biến thiên, suy ra
Vậy thu nhập cao nhất công ty có thể đạt được trong một tháng là 101 250 000 .
Câu 23: Doanh nghiệp Alibaba cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai
máy A và B. Máy A làm việc trong x ngày và cho số tiền lãi là x
3
2x (triệu đồng), máy B làm việc
trong
y
ngày và cho số tiền lãi là 326y 27y
2
(triệu đồng). Hỏi doanh nghiệp Alibaba cần sử dụng
máy A làm việc trong bao nhiêu ngày sao cho số tiền lãi là nhiều nhất? (Biết rằng hai máy A và B
không đồng thời làm việc, máy B làm việc không quá 6 ngày)
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay
Ta có
2
3 54 216f x x x
.
2
0 3 54 216 0 6 12f x x x x x
.
Chỉ có
6 4;10x . Vậy máy A làm việc trong 6 ngày.
Câu 24: Một người thợ xây cần xây một bể chứa 108
3
m
nước có dạng hình hộp chữ nhật với đáy là
hình vuông và không có nắp. Hỏi chiều cao của lòng bể bằng bao nhiêu để số viên gạch dùng xây bể là
ít nhất. Biết thành bể và đáy bể đều được xây bằng gạch, độ dày thành bể và đáy bể là như nhau, các
viên gạch có kích thước như nhau và số viên gạch trên một đơn vị diện tích là bằng nhau.
A.
9 m
.
B.
3 m
. C. 2 m . D.
6 m
.
Hướng dẫn giải:
Chọn đáp án B.
Gọi độ dài cạnh đáy bằng
x
m , chiều cao bằng h
m
0; 0x h .
Khi đó
2
. 108h x
2
108
h
x
.
Tổng diện tích xung quanh và diện tích phần đáy bể là
2
4. .S x h x
2
108
4. x
x
Để số gạch dùng xây bể là ít nhất thì S nhỏ nhất.
Xét hàm số
2
432
f x x
x
trên khoảng
0;
Ta có
2
432
' 2f x x
x
;
' 0 6f x x
Lập bảng biến thiên và suy ra S nhỏ nhất khi 6x . Khi đó 3h .
A.
3
k
. B.
3
2
k
. C.
3
2
k
. D.
3
2
k
.
Hướng dẫn giải:
Chọn đáp án C.
Gọi lần lượt là bán kính đáy và chiều cao của hình trụ.
+ Thể tích khối trụ
2
2
.
k
V r h k h
r
+ Diện tích đáy và nắp là
2
nđ
S S r
; diện tích xung quanh là
2 .
xq
S rh
+ Khi đó chi phí làm bể là
2 2 2
2
600 200 400.2 800 800 800
k k
C r rh r r r
r
r
+ Đặt
3
2
2 2
2
( ) , 0 ( ) 2
k k r k
f r r r f r r
r
r r
;
3
( ) 0
2
k
f r r
, ( 0)k .
+ Bảng biến thiên:
,
r h
0, 0
r h
Câu 25: Ông An dự định làm một cái bể chứa nước hình trụ bằng inốc có nắp đậy với thể tích là
k m
3
(
k 0
). Chi phí mỗi
m
2
đáy là
600
nghìn đồng, mỗi
m
2
nắp là
200
nghìn đồng và mỗi
m
2
mặt bên
là
400
nghìn đồng. Hỏi ông An cần chọn bán kính đáy của bể là bao nhiêu để chi phí làm bể là ít
nhất? (Biết bề dày vỏ inốc không đáng kể)
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay
r
0
3
2
k
( )
f r
0
( )
f r
(0; )
min ( )
f r

Vậy: Chi phí làm bể ít nhất
( )
f r
đạt giá trị
nhỏ nhất
3
2
k
r
.
A.
6
. B.
5
. C.
4
. D.
7
.
Hướng dẫn giải:
Chọn đáp án A.
Ta có
10 10 (1)
x y y x
Và
0 6 4 10
y x
.
A.
12 (km/h)
. B.
15 (km/h)
. C.
18 (km/h)
. D.
20 (km/h)
.
Hướng dẫn giải:
Chọn đáp án B.
Ta có vận tốc cá bơi ngược dòng là
10 km/h
v
, thời gian cá bơi hết
400 km
là
400
10
t
v
.
Năng lượng tiêu hao của cá trong
400
10
t
v
(giờ) được cho bởi công thức
3
400
( ) .
10
E v cv
v
với
10
v
.
Ta có
2
2
15
800 .
10
v
E v c v
v
,
2
0 800 . 15 0
E v cv v
0
15
v
v
.
Bảng biến thiên.
Câu 26: Doanh nghiệp Alibaba cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai
máy A và B. Máy A làm việc trong x ngày và cho số tiền lãi là x
3
2x (triệu đồng), máy B làm việc
trong
y
ngày và cho số tiền lãi là 326y 27y
2
(triệu đồng). Hỏi doanh nghiệp Alibaba cần sử dụng
máy A làm việc trong bao nhiêu ngày sao cho số tiền lãi là nhiều nhất? (Biết rằng hai máy A và B
không đồng thời làm việc, máy B làm việc không quá 6 ngày)
Số tiền lãi f
x
x
3
2x 326y 27y
2
x
3
2x 326
10 x
27
10 x
2
(thay (1) vào).
f
x
x
3
27x
2
216x 560 với x
4;10
.
Ta có f
x
3x
2
54x 216. f
x
0 3x
2
54x 216 0 x 6 x 12 .
Chỉ có x 6
4;10
. Vậy máy A làm việc trong 6 ngày.
Câu 27: Một con cá hồi bơi ngược dòng để vượt một khoảng cách là
400
km
. Vận tốc dòng nước là
10
km/h
. Nếu vận tốc bơi của cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong
t giờ được cho bởi công thức
E(v) cv
3
t
, trong đó
c
là hằng số,
E
được tính bằng jun. Tìm vận tốc
của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay
.
Dựa vào bảng biến thiên vận tốc của cá khi nước đứng yên để năng lượng tiêu hao ít nhất là 15
km/h.
Câu 28: Từ một khúc gỗ tròn hình trụ có đường kính bằng 40cm , cần xả thành một chiếc xà có tiết
diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ
dưới đây. Tìm chiều rộng x của miếng phụ để diện tích sử dụng theo tiết
diện ngang là lớn nhất.
A.
3 34 17 2
2
x cm
. B.
3 34 19 2
2
x cm
.
C.
5 34 15 2
2
x cm
. D.
5 34 13 2
2
x cm
.
Hướng dẫn giải:
Chọn đáp án C.
Gọi
,x y
lần lượt là chiều rộng và dài của miếng phụ.
Diện tích sử dụng theo tiết diện ngang là
4
MNPQ
S S xy
.
Cạnh hình vuông
40
20 2
2 2
MP
MN cm
.
2
20 2 4 800 4S xy xy (1).
Ta có
2 20 2 20 2 40 20 2
x AB MN AB BD
.
0 20 10 2x
.
Lại có
2
2 2 2 2 2
40 2 20 2 1600AB AD BD x y .
2 2 2
800 80 2 4 800 80 2 4
y x x y x x
.
Thế vào
2 2 3 4
1 800 4 800 80 2 4 800 4 800 80 2 4S x x x x x x
.
Xét hàm số
2 3 4
800 80 2 4f x x x x , với
0;20 10 2x
có.
2 3 2
1600 240 2 16 16 100 15 2f x x x x x x x
.
Ta có
2
0;20 10 2
0;20 10 2
5 34 15 2
2
0 16 100 15 2 0
x
x
x
f x x x x
.
Khi đó
5 34 15 2
2
x
chính là giá trị thỏa mãn bài toán.
Câu 29: Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường
s mét đi được của
đoàn tàu là một hàm số của thời gian
t phút , hàm số đó là
2 3
6 –s t t
. Thời điểm
t giây mà tại
đó vận tốc
/v m s của chuyển động đạt giá trị lớn nhất là:
v
E v
E v
1 0
1 5
1 5
E
0
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay
A. 4t s . B. 2t s . C. 6t s . D. 8t s .
Hướng dẫn giải:
Chọn đáp án B.
Ta có:
2 3 2
( ) 12 3– .6 v ts t t t t
'( ) 12 6 '( ) 0 2.
v t t v t t
Bảng biến thiên của ( )v t là:
t
0 2

'( )
v t
+ 0 -
( )
v t
12
Vậy: Thời điểm
2 giây thì vận tốc
/v m s của chuyển động đạt giá trị lớn nhất.
A. 6250
2
m
B. 1250
2
m
C. 3125
2
m
. D. 50
2
m
Hướng dẫn giải:
Chọn đáp án A.
Phân tích ta đặt các kích thước của hàng rào như hình vẽ
Từ đề bài ban đầu ta có được mối quan hệ sau:
Do bác nông dân trả 15 000 000 đồng để chi trả cho nguyên vật liệu và đã biết giá thành từng mặt
nên ta có mối quan hệ:
3 .50000 2 .60000 15000000x y
15 12 1500x y
150 15 500 5
12 4
x x
y
Diện tích của khu vườn sau khi đã rào được tính bằng công thức:
2
500 5 1
2. . 2 . 5 500
4 2
x
f x x y x x x
Đến đây ta có hai cách để tìm giá trị lớn nhất của diện tích:
Cách 1: Xét hàm số trên một khoảng, vẽ BBT và kết luận GTLN:
Xét hàm số
2
1
5 500
2
f x x x trên
0;100
Câu 30: Một người nông dân có 15 000 000 đồng để làm một cái hàng rào hình chữ E dọc theo một
con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào
song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng là một mét, còn đối với ba mặt hàng
rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng một mét. Tìm diện tích lớn nhất của đất
rào thu được.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay
1
' 10 500 , ' 0 50
2
f x x f x x
Ta có BBT
Cách 2: Nhẩm nhanh như sau: Ta biết rằng
2
A g x A với mọi x, nên ta có thể nhẩm nhanh được:
2 2
5 5
100 2.50. 2500 2500
2 2
f x x x x x
2
5
. 2500 5 6250
2
x
A. 112687500 VN đồng.
C. 115687500 VN đồng.
Hướng dẫn giải:
2
2
25 625 625
25 25x 2x 2 78,125
8 8
2 2
S x y x x x x x
Dấu "=" xả ra
25 25 25 175
2 0 25
8 8 8
2 2
x x y
Như vậy, diện tích đất nước được bán ra lớn nhất 78,125 m
2
.
Khi đó số tiền lớn nhất mà gia đình Nam nhận được khi bán đất là 78,125.1500000 117187500
Câu 32: Chiều dài bé nhất của cái thang AB để nó có thể tựa vào tường AC và mặt đất BC, ngang qua
cột đỡ DH cao 4m, song song và cách tường CH=0,5m là:
Hoặc bấm máy tính phần giải phương trình bậc hai và ấn bằng nhiều lần máy sẽ hiện như sau:
Câu 31: Kỳ thi THPT Quốc gia năm 2016 vừa kết thúc, Nam đỗ vào trường Đại học Bách Khoa Hà
Nội. Kỳ I của năm nhất gần qua, kỳ II sắp đến. Hoàn cảnh không được tốt nên gia đình rất lo lắng về
việc đóng học phí cho Nam, kỳ I đã khó khăn, kỳ II càng khó khăn hơn. Gia đình đã quyết định bán
một phần mảnh đất hình chữ nhật có chu vi 50 m, lấy tiền lo cho việc học của Nam cũng như tương lai
của em. Mảnh đất còn lại sau khi bán là một hình vuông cạnh bằng chiều rộng của mảnh đất hình chữ
nhật ban đầu. Tìm số tiền lớn nhất mà gia đình Nam nhận được khi bán đất, biết giá tiền
1m
2
đất khi
bán là 1500000 VN đồng.
B. 114187500 VN đồng.
D. 117187500 VN đồng.
Chọn đáp án D.
Diện tích đất bán ra càng lớn thì số tiền bán được càng cao
Gọi chiều rộng và chiều dài của mảnh đất hình chữ nhật ban đầu lần lượt là x, y
m
,
x, y 0
Chu vi mảnh đất hình chữ nhật ban đầu bằng 50m 2
x y
50 y 25 x
Bài ra, ta có ngay mảnh đất được bán là một hình chữ nhật có diện tích là
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay
A. Xấp xỉ 5,602 B. Xấp xỉ 6,5902 C. Xấp xỉ 5,4902 D. Xấp xỉ 5,5902
Hướng dẫn giải:
Chọn đáp án D.
Đặt
0BH x x . Ta có
2 2 2
16BD DH BH x
Vì / / ACDH nên
2
. 16
2
DA HC DB HC x
DA
DB HB HB x
2
2
16
16
2
x
AB x
x
Xét hàm số
2
2
16
16
2
x
f x x
x
trên
0; . Ta có f(x)
liên tục trên
0; và
2
3
2
2
2 2 2 2 2 2
.2 2 16
8 8
16
'
4
16 16 16 16
x
x x
x x x
x
f x
x
x x x x x x
' 0 2; ' 0 2; ' 0 0 2f x x f x x f x x
Suy ra
0;
5 5
min min 2 5,5902
2
x
AB f x f m

A. 596,5m B. 671,4m C. 779,8m D. 741,2m
Hướng dẫn giải:
Chọn đáp án C.
Câu 33: Cho hai vị trí A , B cách nhau 615m , cùng nằm về một phía bờ sông như hình vẽ. Khoảng
cách từ A và từ B đến bờ sông lần lượt là 118m và
487m
Một người đi từ A đến bờ sông để lấy
nước mang về B . Đoạn đường ngắn nhất mà người đó có thể đi là:
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B.
dễ dàng tính được 369, 492.BD EF Ta đặt ,EM x khi đó ta được:
2
2 2 2
492 , 118 , 492 487 . MF x AM x BM x
Như vậy ta có hàm số
f x được xác định bằng tổng quãng đường AM và MB:
2
2 2 2
118 492 487 f x x x
với
0;492x
Ta cần tìm giá trị nhỏ nhất của
f x để có được quãng đường ngắn nhất và từ đó xác định được vị
trí điểm M.
2 2 2
2
492
' .
118
492 487
x x
f x
x
x
2 2 2
2
492
' 0 0
118
492 487
x x
f x
x
x
2 2 2
2
492
118
492 487
x x
x
x
2
2 2 2
492 487 492 118 x x x x
2 2
2 2 2 2
492 487 492 118
0 492
x x x x
x
2 2
487 58056 118
0 492
x x
x
58056 58056
58056
605 369
605
0 492
x hay x
x
x
Hàm số
f x liên tục trên đoạn
0;492 . So sánh các giá trị của (0)f ,
58056
605
f
,
492f ta có
giá trị nhỏ nhất là
58056
779,8
605
f m
Khi đó quãng đường đi ngắn nhất là xấp xỉ 779,8m.
Câu 34: Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá
2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ
100.000 đồng một tháng thì sẽ có 2 căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất thì công ty đó
phải cho thuê mỗi căn hộ với giá bao nhiêu một tháng.
A. 2.225.000. B. 2.100.000 C. 2.200.000 D. 2.250.000
Hướng dẫn giải:
Chọn đáp án D.
Gọi (đồng/tháng) là số tiền tăng thêm của giá cho thuê mỗi căn hộ. ( )
x
0
x
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 53
Facebook: https://www.facebook.com/dongpay
Khi đó số căn hộ bị bỏ trống là: (căn hộ).
Khi đó, số tiền công ti thu được là:
(đồng/tháng).
Khảo sát hàm số trên .
.
.
Bảng biến thiên
x
0 250 000
T’
0
T 2 250 000
Do đó
=
2.250.000
.
Câu 35: Một cửa hàng bán lẻ bán 2500 cái ti vi mỗi năm. Chi phí gửi trong kho là 10$ một cái mỗi
năm. Để đặt hàng chi phí cố định cho mỗi lần đặt là 20$ cộng thêm 9$ mỗi cái. Cửa hàng nên đặt hàng
bao nhiêu lần trong mỗi năm và mỗi lần bao nhiêu cái để chi phí hàng tồn kho là nhỏ nhất ?
A. Đặt hàng 25 lần, mỗi lần 100 cái ti vi. B. Đặt hàng 20 lần, mỗi lần 100 cái ti vi.
C. Đặt hàng 25 lần, mỗi lần 90 cái ti vi. D. Đặt hàng 20 lần, mỗi lần 90 cái ti vi.
Hướng dẫn giải:
Chọn đáp án A.
Gọi x là số ti vi mà cừa hàng đặt mỗi lần (
x 1;2500
, đơn vị cái)
nên chi phí lưu kho tương ứng là
x
10. 5x
2
Số lần đặt hàng mỗi năm là
2500
x
và chi phí đặt hàng là:
2500
20 9x
x
Khi đó chi phí mà cửa hàng phải trả là:
2500 50000
C x 20 9x 5x 5x 22500
x x
Lập bảng biến thiên ta được:
min
C C 100 23500
Kết luận: đặt hàng 25 lần, mỗi lần 100 cái tivi.
Câu 36: Có một tấm gỗ hình vuông cạnh 200 cm. Cắt một tấm gỗ có hình tam giác vuông, có tổng của
một cạnh góc vuông và cạnh huyền bằng hằng số từ tấm gỗ trên sao cho tấm gỗ hình tam giác
vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu?
A. . B. . C. . D. .
Hướng dẫn giải:
Chọn đáp án C.
Kí hiệu cạnh góc vuông
Khi đó cạnh huyền , cạnh góc vuông kia là
2
100000
x
2
2000000 50
100000
x
T x x
2
2
100000000 10
100000
x
x
T x
0;

'T x
4
10
100000
x
' 0 1000000 4 0 250000
T x x x
0
max 250000
x
T x T
120cm
40
cm
40 3
cm
80
cm
40 2
cm
,0 60
AB x x
120
BC x
2 2 2
120 240
AC BC AB x
Số lượng ti vi trung bình gửi trong kho là
x
2
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 54
Facebook: https://www.facebook.com/dongpay
Diện tích tam giác ABC là: . Ta tìm giá trị lớn nhất của hàm số này trên
khoảng
Ta có
Lập bảng biến thiên:
Lập bảng biến thiên ta có:
Tam giác ABC có diện tích lớn nhất khi
Câu 37: Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính , biết
một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn.
A. B. C. D.
Hướng dẫn giải:
Chọn đáp án B.
Gọi là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn .
Khi đó độ dài cạnh hình chữ nhật nằm dọc trên đường tròn là:
Diện tích hình chữ nhật:
Ta có
. Suy ra là điểm cực đại của hàm .
Vậy diện tích lớn nhất của hình chữ nhật là:
Câu 38: Trong bài thực hành của môn huấn luyện quân sự có tình huống chiến sĩ phải bơi qua một con
sông để tấn công một mục tiêu ở phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi
của chiến sĩ bằng một nửa vận tốc chạy trên bộ. Bạn hãy cho biết chiến sĩ phải bơi bao nhiêu mét để
đến được mục tiêu nhanh nhất, nếu như dòng sông là thẳng, mục tiêu ở cách chiến sĩ 1km theo đường
chim bay.
A.
400
3
B.
40
33
C.
100
3
D.
200
3
2
1
. 120 240
2
S x x x
0;60
2
2 2
1 1 240 14400 360
, 120 240 . ' 0 40
2 2
2 120 240 2 120 240
x
S x x x S x x
x x
x
0
40
60
S'
x
0
S x
40
S
80
BC
10
cm
2
80
cm
2
100
cm
2
160
cm
2
200
cm
( )
x cm
0 10
x
2 2
2 10 .
x cm
2 2
2 10
S x x
2
2 2 2 2
2 2
2
2 10 2.10 4
10
x
S x x
x
10 2
thoûa
2
0
10 2
khoâng thoûa
2
x
S
x
10 2
8 40 2 0
2
S x S
10 2
2
x
S x
2
2 2
10
S 10 2. 10 100
2
cm
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 55
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn đáp án A.
Vấn đề là chọn thời gian bơi và thời gian đi bộ sao cho “tối ưu”. Giả sử độ dài đoạn bơi là l và tốc
độ bơi của chiến sĩ là v. Ký hiệu m là độ dài đoạn sông kể từ người chiến sĩ đến đồn địch, khi ấy
tổng thời gian bơi và chạy bộ của người chiến sĩ là
2 2
100
2
l m l
t
v v
.
Do
,m v
là cố định nên thời gian đạt cực tiểu khi hàm số
2 2 2 2
100 2 100
( )
2 2
l l l l
f l
v v v
đạt cực tiểu, và cũng tức là khi hàm
2 2
( ) 2 100 g l l l đạt cực tiểu. Điều này xảy ra khi
2 2
2 0
100
l
l
, hay
2
2 100 l l , tức là 400 / 3 133,333333 l (met).
Câu 39: Cần phải đặt một ngọn điện ở phía trên và chính giữa một cái bàn hình tròn có bán kính a. Hỏi
phải treo ở độ cao bao nhiêu để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được
biểu thị bởi công thức
2
sin
C k
r
( là góc nghiêng giữa tia sáng và mép bàn, k là hằng số tỷ lệ chỉ
phụ thuộc vào nguồn sáng).
A.
3a
h
2
B.
a 2
h
2
C.
a
h
2
D.
a 3
h
2
Hướng dẫn giải:
Chọn đáp án B.
Ta có:
2 2
r a h
(Định lý Py- ta- go)
2 2
h h
sin
R
a h
2
2 2 2 2
sin h
C k. k
R
a h a h
Xét hàm
3
2 2
h
f h h 0
a h
, ta có:
m
l
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 56
Facebook: https://www.facebook.com/dongpay
3
2 2 2 2 2
3
2 2
3
a h 2h . a h
2
f ' h
a h
3
2 2 2 2 2
f ' h 0 h a 3.h . a h
2 2 2
a 2
h a 3h h
2
Bảng biến thiên:
h
0
a 2
2
f '(h) + -
f(h)
Từ bảng biến thiên suy ra:
max max
a 2 a 2
f h h C k.f h h
2 2
Câu 40: Nhà Nam có một chiếc bàn tròn có bán kính bằng m. Nam muốn mắc một bóng điện ở
phía trên và chính giữa chiếc bàn sao cho mép bàn nhận được nhiều ánh sáng nhất. Biết rằng cường độ
sáng C của bóng điện được biểu thị bởi công thức ( là góc tạo bởi tia sáng tới mép bàn
và mặt bàn, c - hằng số tỷ lệ chỉ phụ thuộc vào nguồn sáng, l khoảng cách từ mép bàn tới bóng điện).
Khoảng cách nam cần treo bóng điện tính từ mặt bàn là
A. 1m B. 1,2m C. 1.5 m D. 2m
Hướng dẫn giải:
Chọn đáp án D.
Gọi h là độ cao của bóng điện so với mặt bàn (h > 0); Đ là bóng điện; I là hình chiếu của Đ lên
mặt bàn. MN là đường kính của mặt bàn. ( như hình vẽ)
Ta có và , suy ra cường độ sáng là: .
2
2
sin
C c
l
sin
h
l
2 2
2
h l
2
3
2
( ) ( 2)
l
C l c l
l
2
4 2
6
' . 0 2
. 2
l
C l c l
l l
' 0 6 2
C l l l
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 57
Facebook: https://www.facebook.com/dongpay
Lập bảng biến thiên ta thu được kết quả C lớn nhất khi , khi đó
Câu 41: Nhà của 3 bạn A, B, C nằm ở 3 vị trí tạo thành một tam giác vuông tại B ( như hình vẽ), AB =
10 km; BC = 25 km và 3 bạn tổ chức họp mặt ở nhà bạn C. Bạn B hẹn chở bạn A tại vị trí M trên đoạn
đường BC. Từ nhà, bạn A đi xe buýt đến điểm hẹn M với tốc độ 30km/h và từ M hai bạn A, B di
chuyển đến nhà bạn C bằng xe máy với tốc độ 50km/h. Hỏi điểm hẹn M cách nhà bạn B bao nhiêu km
để bạn A đến nhà bạn C nhanh nhất ?
A. 5 km B. 7,5 km C. 10 km D. 12,5 km
Hướng dẫn giải:
Chọn đáp án B.
Đặt BM = x (km),
Thời gian để bạn A di chuyển từ A đến M rồi đến nhà C là:
(h)
Lập bảng biến thiên, ta tìm được giá trị nhỏ nhất của là khi
Câu 42: Một sợi dây có chiều dài là 6 m, được chia thành 2 phần. Phần thứ nhất được uốn thành hình
tam giác đều, phầm thứ hai uốn thành hình vuông. Hỏi độ dài của cạnh hình tam giác đều bằng bao
nhiêu để diện tích 2 hình thu được là nhỏ nhất?
A.
18
9 4 3
(m) B.
36 3
4 3
(m) C.
12
4 3
(m) D.
18 3
4 3
(m)
Hướng dẫn giải:
Chọn đáp án A.
Gọi độ dài cạnh hình tam giác đều là x (m) khi đó độ dài cạnh hình vuông là
6 3
4
x
Tổng diện tích khi đó là:
2
2 2
3 6 3 1
9 4 3 36 36
4 4 16
x
S x x x
Diện tích nhỏ nhất khi
18
2
9 4 3
b
x
a
Vậy diện tích Min khi
18
9 4 3
x
Hoặc đến đây ta có thể bấm máy tính giải phương trình
2
9 4 3 36 36x x
ấn bằng và hiện giá
trị.
6
l
2
h
0
x
2
100 25
30 50
( )
x x
t x
( )
t x
23
30
15
2
x
C
M
B
A
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 58
Facebook: https://www.facebook.com/dongpay
Câu 43: Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì
toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì có thêm 2 phòng
trống. Giám đốc phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn
nhất.
A. 480 ngàn. B. 50 ngàn. C. 450 ngàn. D. 80 ngàn.
Hướng dẫn giải:
Chọn đáp án C.
Gọi x (ngàn đồng) là giá phòng khách sạn cần đặt ra, 400x (đơn vị: ngàn đồng).
Giá chênh lệch sau khi tăng 400x .
Số phòng cho thuê giảm nếu giá là x:
400 2
400
20 10
x
x
.
Số phòng cho thuê với giá x là
400
50 90
10 10
x x
.
Tổng doanh thu trong ngày là:
2
( ) 90 90
10 10
x x
f x x x
.
( ) 90
5
x
f x
. ( ) 0 450
f x x .
Bảng biến thiên:
A. 10 B. 12 C. 16 D. 24
Hướng dẫn giải:
Chọn đáp án B.
Gọi n là số con cá trên một đơn vị diện tích hồ n 0 . Khi đó:
Cân nặng của một con cá là:
P n 480 20n gam
Cân nặng của n con cá là:
2
n.P n 480n 20n gam
Xét hàm số:
2
f n 480n 20n ,n 0; .
Ta có:
f ' n 480 40n , cho
f ' n 0 n 12
Lập bảng biến thiên ta thấy số cá phải thả trên một đơn vị diện tích hồ để có thu hoạch nhiều nhất là
12 con.
Dựa vào bảng biến thiên ta thấy f (x) đạt giá trị lớn nhất khi x 450.
Vậy nếu cho thuê với giá 450 ngàn đồng thì sẽ có doanh thu cao nhất trong ngày là 2.025.000 đồng.
Câu 44: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện
tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng P
n
480 20n (gam).
Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được
nhiều cá nhất ?
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 59
Facebook: https://www.facebook.com/dongpay
Câu 45: Hai con chuồn chuồn bay trên hai quỹ đạo khác nhau tại cùng một thời điểm. Một con bay
trên quỹ đạo đường thẳng từ điểm
0;0A đến điểm
0;100B với vận tốc 5 /m s . Con còn lại bay trên
quỹ đạo đường thẳng từ
60;80C về
A
với vận tốc10 /m s . Hỏi trong quá trình bay, thì khoảng cách
ngắn nhất mà hai con đạt được là bao nhiêu?
A. 20( )m B. 50( )m C. 20 10( )m D. 20 5( )m
Hướng dẫn giải:
Chọn đáp án D.
4
tan
3
k
nên tọa độ của
3
60 10 .cos 60 10 . 60 6
5
80 10sin 80 8
x t t t
y t
Ta có:
20
( ) 90 600 0
3
f t t t
20
min ( ) 2000
3
f t f
khoảng cách ngắn nhất giữa 2 con chuồn chuồn trong quá trình bay là 2000 20 5( )m
Nhận xét: Đây là một bài toán cần khả năng tư duy thật nhanh khi làm bài thi trắc nghiệm. Và bài toán
này cũng cần khả năng tính toán rất cẩn thận vì số liệu khá lớn. Ở bước xử lí đạo hàm của hàm số ( )f t
nếu tính toán sai rất có thể các bạn sẽ chọn min ở 2 đầu của đoạn
0;10 nên sẽ chọn đáp án B hoặc C.
Xét ở thời điểm t
Tọa độ của con chuồn chuồn bay từ B về A là
0;100 5t
.
Do con chuồn chuồn bay từ C về A trên đường thẳng AC có hệ số góc
con chuồn chuồn này là:
Như vậy ở thời điểm t khoảng cách giữa 2 con chuồn chuồn sẽ là: d (60 6t)
2
(20 3t)
2
Khoảng cách giữa 2 con chuồn chuồn nhỏ nhất khi và chỉ khi
(60 6t)
2
(203t)
2
đạt giá trị nhỏ
nhất với t
0;10
Xét
f (t) (606t)
2
(20 3t)
2
trên
0;10
| 1/59
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ
A – LÝ THUYẾT TÓM TẮT I. Định nghĩa.
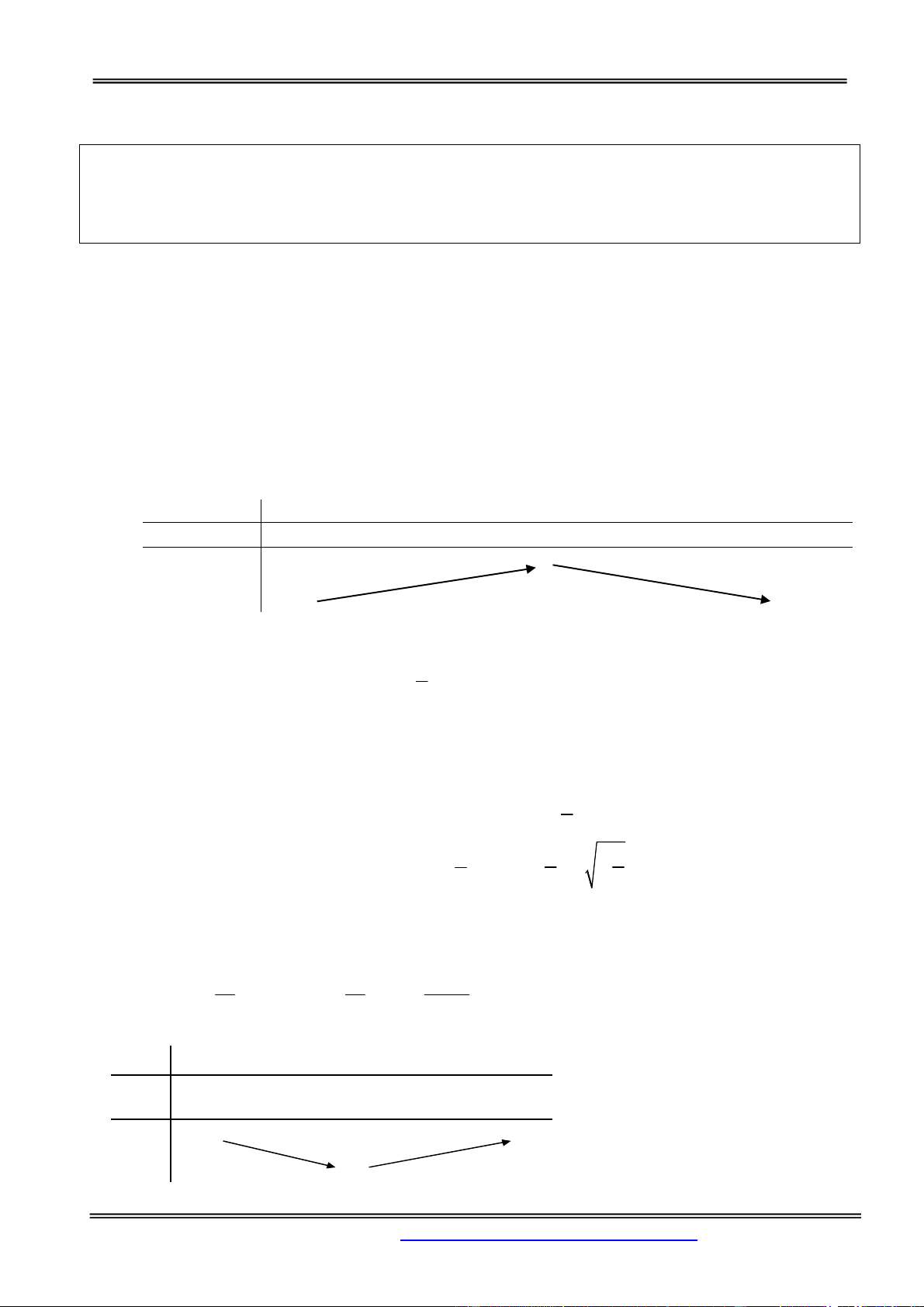
Giả sử hàm số f xác định trên tập K K  . Khi đó:
a) Nếu tồn tại một điểm x K sao cho f x  f x , x K M f x 0    thì số 
 0 được gọi là giá trị 0
lớn nhất của hàm số f trên K. Kí hiệu: M  max f x .  x D
b) Nếu tồn tại một điểm x K sao cho f x  f x , x K m f x 0    thì số 
 0 được gọi là giá trị 0
nhỏ nhất của hàm số f trên K. Kí hiệu: m  min f x  .  x D II. Nhận xét.
1.Như vậy để có được M (hoặc m) là giá trị lớn nhất (giá trị nhỏ nhất) của hàm số f trên K ta phải chỉ ra được :
a) f x  M ( hoặc f x  m) với mọi x K .
b) Tồn tại ít nhất một điểm x K sao cho f x M f x m 0   ( hoặc  0   ). 0
2. Chú ý khi nói đến giá trị lớn nhất hay giá trị nhỏ nhất của hàm số f (mà không nói rõ “trên tập K’’)
thì ta hiểu đó là giá trị lớn nhất và giá trị nhỏ nhất trên tập xác định của nó.
3. Mỗi hàm số liên tục trên đoạn  ;
a b thì đạt được giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.   Hơn nữa
a) Nếu hàm số f đồng biến trên đoạn  ;
a b thì max f x  f b và min f x  f a .    x Dx D
b) Nếu hàm số f nghịch biến trên đoạn  ;
a b thì max f x  f a và min f x  f b .    x Dx D
4. Cho phương trình f x  m với y  f  x là hàm số liên tục trên D thì phương trình có nghiệm khi
min f  x   m  max f  x  D D
5. Một hàm số có thể đồng thời đạt được giá trị lớn nhất và giá trị nhỏ nhất trên một tập K hoặc chỉ đạt
được giá trị nhỏ nhất hoặc chỉ đạt được giá trị lớn nhất hoặc không tồn tại cả hai giá trị này. Chẳng hạn: a) Xét hàm số bậc hai  2 y
ax bx c trên tập xác định K . b
+ Khi a  0 thì hàm số có đạt được giá trị nhỏ nhất tại x
đồng thời bằng giá trị cực tiểu của hàm 2ab số tại x  . 2ab
+ Khi a  0 thì hàm số có đạt được giá trị lớn nhất tại x
đồng thời bằng giá trị cực đại của hàm 2ab số tại x  . 2a
b) Xét trên tập K hàm số bậc ba  3  2 y ax
bx cx d không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 c ax b
c) Xét trên K
\   hàm số y
không tồn tại giá trị lớn nhất và giá trị nhỏ nhất.  d cx d
d) Xét hàm số trùng phương  4  2 y ax
bx c trên tập xác định K .
+ Khi a  0 thì hàm số đạt được giá trị nhỏ nhất đồng thời bằng giá trị cực tiểu của hàm số.
+ Khi a  0 thì hàm số đạt được giá trị lớn nhất đồng thời bằng giá trị cực đại của hàm số. B – BÀI TẬP
DẠNG 1: GTLN, GTNN CỦA HÀM SỐ TRÊN MỘT ĐOẠN
Phương pháp: Cho hàm số y  f  x xác định và liên tục trên a;b .
- Tính f 'x , giải phương trình f 'x  0 tìm nghiệm trên a, b .
- Giả sử phương trình có 2 nghiệm x , x  a, b . 1 2  
- Tính các giá trị f a, f b , f x , f x . So sánh chúng và kết luận. 1   2 
Câu 1. Cho hàm số y f x liên tục và luôn nghịch biến trên  ;
a b . Hỏi hàm số f x đạt giá trị lớn
nhất tại điểm nào sau đây ? a b b a
A. x a .
B. x b . C. x  . D. x  . 2 2 Hướng dẫn giải: Chọn đáp án A.
Ta có: y f (x) liên tục và luôn nghịch biến trên  ; a b  x   ;
a b thì f (b)  f (x)  f (a) .
Suy ra hàm số y f (x) đạt giá trị lớn nhất tại điểm x a .
Câu 2. Giá trị nhỏ nhất của hàm số 3
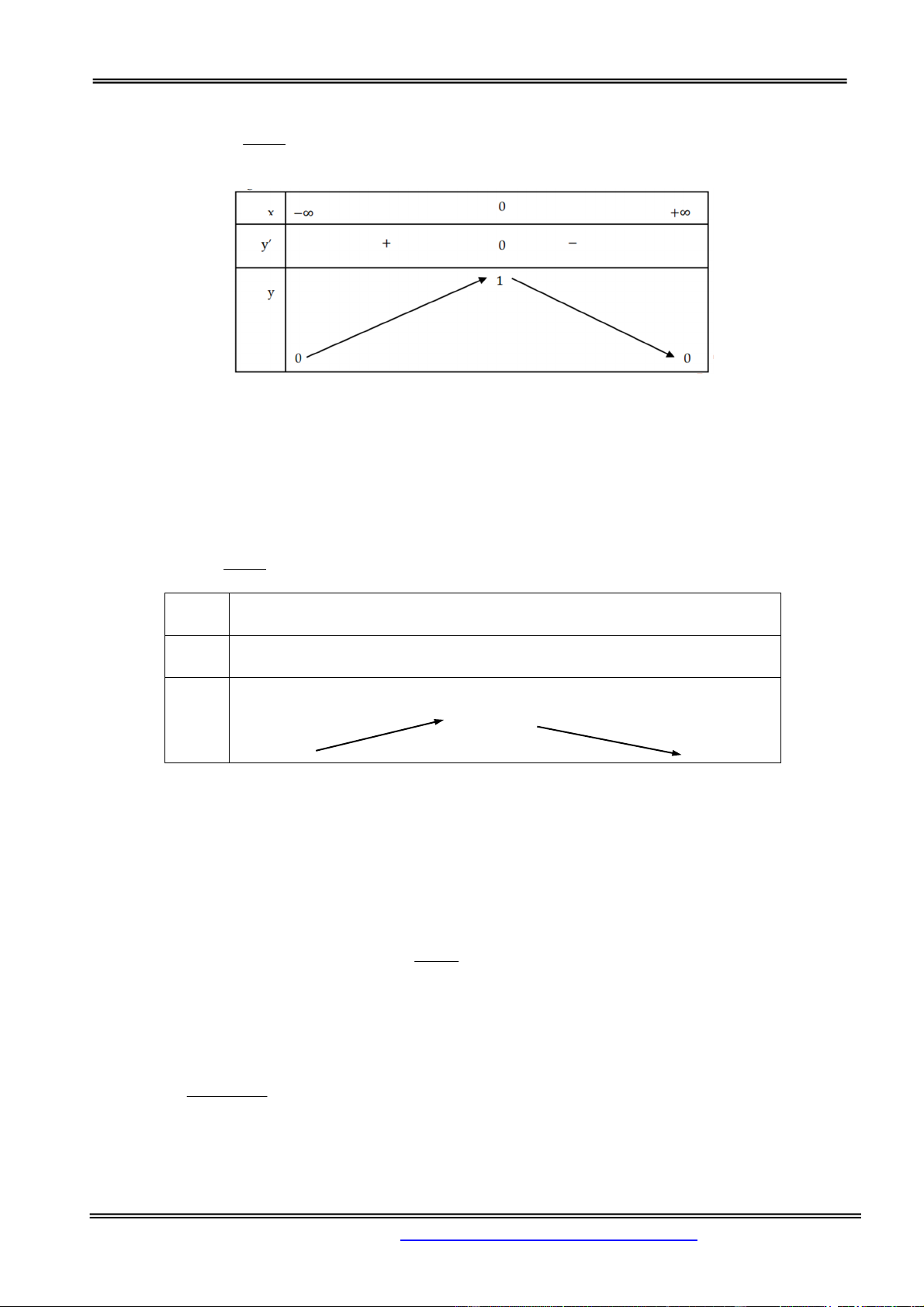
y  x 12x  2 trên đoạn 1;4 là A. 13. B. 2. C. -14. D. 18. Hướng dẫn giải: Chọn đáp án C. x  2 Ta có 2 y  3  x 12 . Cho 2
y  0  3x  12  0   . Do x 1; 4  nên x  2 . x  2  y   1  1 ,
3 y 2  18, y 4  1
 4 . Vậy min y y 4  14 . [1;4]  3 
Câu 3. Giá trị lớn nhất của hàm số f x 3
x  3x  3 trên 1   ;  bằng: 2   A. 5. B. 3 . C. 4 . D. 6 . Hướng dẫn giải: Chọn đáp án A. x  1 Ta có 2
y  3x  3 , y  0  x  1   3  15 y   1  1 ; y   1  5 ; y   
. Vậy Max f x  5.  2  8  3  1  ;  2   
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3 x
Câu 4. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y
x  3x trên đoạn 0;2 . 3 2 5 2 A. max y  ; min y   . B. max y  ; min y  0. 0;2 0;2 3 3 0;2 0;2 3 5
C. max y  9; min y   .
D. max y  9; min y  0. 0;2 0;2 3 0;2 0;2 Hướng dẫn giải: Chọn đáp án A.
Hàm số liên tục và xác định trên 0;2 .  x  1 2
y  x  2x  3 , y  0  
x  1 (do x 0;2 ). x  3  5 2
y 0  0 , y  
1   , y 2  . 3 3 2 5 Vậy max y  , min y   . 0;2 3 0;2 3 1 1  1 
Câu 5.Giá trị lớn nhất của hàm số 3 2 y   x
x  2x  1 trên đoạn ;2 là 3 2  2    5 1 1 13 A.  . B. . C.  . D.  3 6 6 3 Hướng dẫn giải: Chọn đáp án B. Ta có: 2
y  x x  2 ;
y  0  x  1 x  2  (loại).  1  1 1 5 y   ; y   1  ; y 2     ;  2  6 6 3 1
Vậy max y y   1  .  1  ;2 6  2     1 
Câu 6. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y x  3x  4 trên đoạn ; 3  . 2    37 37 A. max y   ; min y  8 .
B. max y  4; min y   .  1   1   1   1  ;3 8 ;3 8  ;3 ;3      2     2   2   2  37 C. max y   ; min y  4 .
D. max y  4; min y  8 .  1   1   1   1  ;3 8 ;3  ;3 ;3      2     2   2   2  Hướng dẫn giải: Chọn đáp án D.  1  Hàm số 3 2
y x  3x  4 liên tục trên đoạn ; 3  . 2      1  x  2  ;3   2    Ta có 2
y  3x  6x y  0   .   1  x  0  ;3   2    
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  1  38 Do y 2  8  ; y    
; y 3  4 nên max y  4; min y  8 .  2  7  1   1  ;3 ;3   2     2  2 3
Câu 7.Tìm giá trị nhỏ nhất của hàm số 3 2 y x
x  5x 1 trên đoạn   2;2 . 3 2 29 251 1 A. min y   .
B. min y  3 . C. min y   . D. min y   . 2;2. 3 2;2. 2;2. 24 2;2. 3 Hướng dẫn giải: Chọn đáp án A. 2 3 Hàm số 3 2 y x
x  5x 1 liên tục trên đoạn   2;2 . 3 2 x  1    2;2 Ta có 2
y  2x  3x  5  y  0    5 .
x    2;2  2 26 29 1 29 Do y   1  ; y 2   ; y  2
    nên min y   . 3 3 3 2;2. 3
Câu 8. Tìm M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y x  3x  9x  35
trên đoạn 4;4 là:
A. M  40; m  4  1 .
B. M  40; m  8  . C. M  4  1; m  40 .
D. M  15; m  8  . Hướng dẫn giải: Chọn đáp án A.
Hàm số liên tục trên đoạn 4;4  x  3 2
y  3x  6x  9 . y  0 2
x  2x  3  0  x  1  
Ta có y 4  41 ; y 4  15 ; y  
1  40 ; y 3  8
Vậy M  max y  40 và m  min y  4  1 . [ 4  ;4] [ 4  ;4]
Câu 9.Hàm số y x3  2x2  7x  5 có giá trị nhỏ nhất là m và giá trị lớn nhất là M trên đoạn [1;3].
Khi đó tổng m + M bằng 338 446 14 A.  . B.  . C. -10. D.  . 27 27 27 Hướng dẫn giải: Chọn đáp án A. 3 2
y x  2x  7x  5
Hàm số xác định và liên tục trên đoạn [1;3]. 2
y '  3x  4x  7  x  1  (l) y '  0   7  x  (n)  3 7 25  7 257 338 y(1)  3  , y(3)  7  , y( )   m  ; M  3
  m M   . 3 27 27 27
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 10.Gọi m là giá trị nhỏ nhất và M là giá trị lớn nhất của hàm số 3 2
y  2x  3x 1 trên đoạn  1  2  ; 
. Tính giá trị của M m 2    A. – 5. B. 1. C. 4. D. 5. Hướng dẫn giải: Chọn đáp án D.x  0 2 
Ta có : y '  6x  6x ; y '  0   1
x  1  2;     2  1  1 y  2
   5 ; y   1  0 ; y       2  2
Khi do : M  0, m  5
  M m  5.
Câu 11. Giá trị lớn nhất của hàm số f x 3 2
x  2x – 7 x  1 trên đoạn 0; 2 là: A. 1. B. 1. C. 3 . D. 4 . Hướng dẫn giải: Chọn đáp án C.
Xét hàm số f x 3 2
x  2x – 7 x  1  x  1(n) Ta có: 2
f '(x)  3x  4x - 7 . 2 f '(x) 0 3x 4x - 7 0       7  x  (l)  3
f (0)  1, f (2)  3, f (1)  3.
Vậy: max f (x)  3. [0;2]
Câu 12. Tìm giá trị lớn nhất của hàm 3 2
y f (x)  2x  3x 12x  2 trên đoạn  1  ; 2 . A. max y  6 .
B. max y  10 .
C. max y  15 .
D. max y  11. - ; 1 2 1;2 -1;2 1;2   Hướng dẫn giải: Chọn đáp án C.
Hàm số xác định và liên tục trên đoạn  1  ; 2 . 2 f (
x)  6x  6x 12 . 2 f (
x)  0  6x  6x 12  0  x  1 1
 ; 2 hoặc x  2   1  ; 2 . f  
1  15 ; f 2  6 ; f   1  5 .
Vậy max y f   1  15 . 1;2
Câu 13. Gọi m là giá trị nhỏ nhất của hàm số 3
y x  3x trên đoạn 0;38   . Tìm giá trị m A. m  0. B. m  1  . C. m  2  . D. m  1. Hướng dẫn giải: Chọn đáp án C. 2
y '  3x  3 x  10;  38 y '  0   . x  1  0;38 
y 0  0; y  
1  2 ; y 38  54758 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Vậy m  2 
Câu 14. Tìm giá trị lớn nhất của hàm số 3 2
y x x  8x trên đoạn [1;3] . 176 A. max y  4  .
B. max y  8 . C. max y  6  . D. max y  . [1;3] [1;3] [1;3] [1;3] 27 Hướng dẫn giải: Chọn đáp án C.
Hàm số xác định và liên tục trên [1;3] .  x  2 Ta có 2
y  3x  2x  8 . Cho 2 y 0 3x 2x 8 0        
4 . Do x [1;3] nên x  2 .  x    3 y   1  8
 , y 2  12, y 3  6
 . Vậy max y y 3  6  . [1;3] Câu 15. Cho hàm số 3 2
y x  3x  3 .Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
hàm số trên đoạn 1; 
3 .Tính giá trị T M m A. 2. B. 4. C. 3. D. 0. Hướng dẫn giải: Chọn đáp án A. x  0 Ta có : 2
y  3x  6x . Khi đó y  0  x  2  Xét x 1; 
3 : ta có x  0 (loại ); x  2 ( nhận). Ta có : y  
1  1 ; y 2  1; y 3  3 .
Suy ra M  3; m  1 . Do đó : T  2 .
Câu 16. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y x  3x  1 trên đoạn [0 ; 2]
A. max y  3 và min y  1 .
B. max y  1 và min y  1 . 0 ; 2 0 ; 2 0 ; 2 0 ; 2
C. max y  3 và min y  1 .
D. max y  9 và min y  3 . 0 ; 2 0 ; 2 0 ; 2 0 ; 2 Hướng dẫn giải: Chọn đáp án C. TXĐ: D   . x  1  Ta có 2
y  3x  3 , y  0 2
 3x  3  0   . x  1 
Xét trên đoạn [0 ; 2] ta chỉ nhận x 1.
Khi đó ta có y 0 1, y 2  3 , y   1  1  .
Vậy ta có max y  3 và min y  1  . 0;2 0;2 4
Câu 17. Trên đoạn  1   ;1 , hàm số 3 2 y  
x  2x x  3 3
A. Có giá trị nhỏ nhất tại x  1
 và giá trị lớn nhất tại x 1.
B. Có giá trị nhỏ nhất tại x 1 và giá trị lớn nhất tại x  1  .
C. Có giá trị nhỏ nhất tại x  1
 và không có giá trị lớn nhất.
D. Không có giá trị nhỏ nhất và có giá trị lớn nhất tại x 1. Hướng dẫn giải: Chọn đáp án B.
Hàm số liên tục trên 1  ;1 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Ta có 2 y  4
x  4x 1. 1 2 y  0  4
x  4x 1  0  x   . 2 22 8  1  17 Vậy y   1   , y   1   , y    .   3 3  2  6
Câu 18. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 3 2
y  2x  3x 12x  2 trên đoạn  1  ; 
2 . Tìm tổng bình phương của M và m A. 250 . B. 100 . C. 509 . D. 289 . Hướng dẫn giải: Chọn đáp án A.
Hàm số xác định và liên tục trên đoạn  1  ;  2 . 2
y '  6x  6x  12 . x  1(N) 2
y '  0  6x  6x 12   . x  2  (L)  y(1)  5  ; y( 1
 )  15; y(2)  6 . Vậy: 2 2 2 2
m M  (5)  15  250 .
Câu 19. Tìm các giá trị của a để trên đoạn  1  ;  1 hàm số 3 2
y   x  3x a có giá trị nhỏ nhất bằng 2 A. a  6 . B. a  8 . C. a  2 . D. a  4 . Hướng dẫn giải: Chọn đáp án A.
Hàm số xác định và liên tục trên đoạn  1  ;  1 . Ta có: 2
y '  3x  6x . x  0(N) 2 y '  0  3
x  6x  x  2  (L) .  y(1)  4
  a , y(1)  2
  a , y(0)  a . Trên đoạn  1  ; 
1 thì giá trị nhỏ nhất của hàm số bằng 2 .
Suy ra min y y(1)  4
  a  2  a  6 . Câu 20. Hàm số 3
y x   2 m  
1 x m  1 đạt GTNN bằng 5 trên 0; 
1 . Khi đó giá trị của m là A. 5. B. 3. C. 1. D. 4. Hướng dẫn giải: Chọn đáp án D. Ta có 2 2
y  3x m 1  0 với mọi x 0; 
1 nên hàm số luôn đồng biến trên 0;  1 .
Vì hàm số đã cho là hàm đa thức, liên tục trên 0; 
1 nên min y y 0  m 1. x   0;  1
Ta cho m  1  5  m  4.
Vậy m  4 thỏa mãn. Câu 21. Cho hàm số 3
y x  3x 1. Tìm tìm tập hợp tất cả giá trị m  0 , để giá trị nhỏ nhất của hàm
số trên D  m 1; m  2 luôn bé hơn 3 là  1  A. 0;  1 . B. ;1 .   C.  ;   1 \   2 . D. 0;2.  2  Hướng dẫn giải: Chọn đáp án A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  1 Ta có : 2
y '  3x  3. y '  0   1; . x  1  .
Hàm số đồng biến trên khoảng    3
Trên D  m 1;m  
2 , với m  0 , ta có : Min y  m   1  3m   1 1 m 1  ;m2 2 m  1 Ycbt 3 2
Min y  3  m  3m  4  0  m  
1 m  2  0  m 1  ;m2    m  2 
Kết hợp điều kiện . Suy ra m  0  ;1 . Câu 22. Cho hàm số 4 2
y x  2x 1. Tìm giá trị nhỏ nhất của hàm số trên  1  ; 2 A. min y  2  .
B. min y  2 . C. min y  1. D. min y  1  .  1  ;2 1;2 1;2 1;2 Hướng dẫn giải: Chọn đáp án D. Ta có : +) 3
y '  4x  4x , 3
y '  0  4x  4x  0  x  0 +) y 0  1  , y  
1  2 , y 2  23 Vậy min y  1  1;2
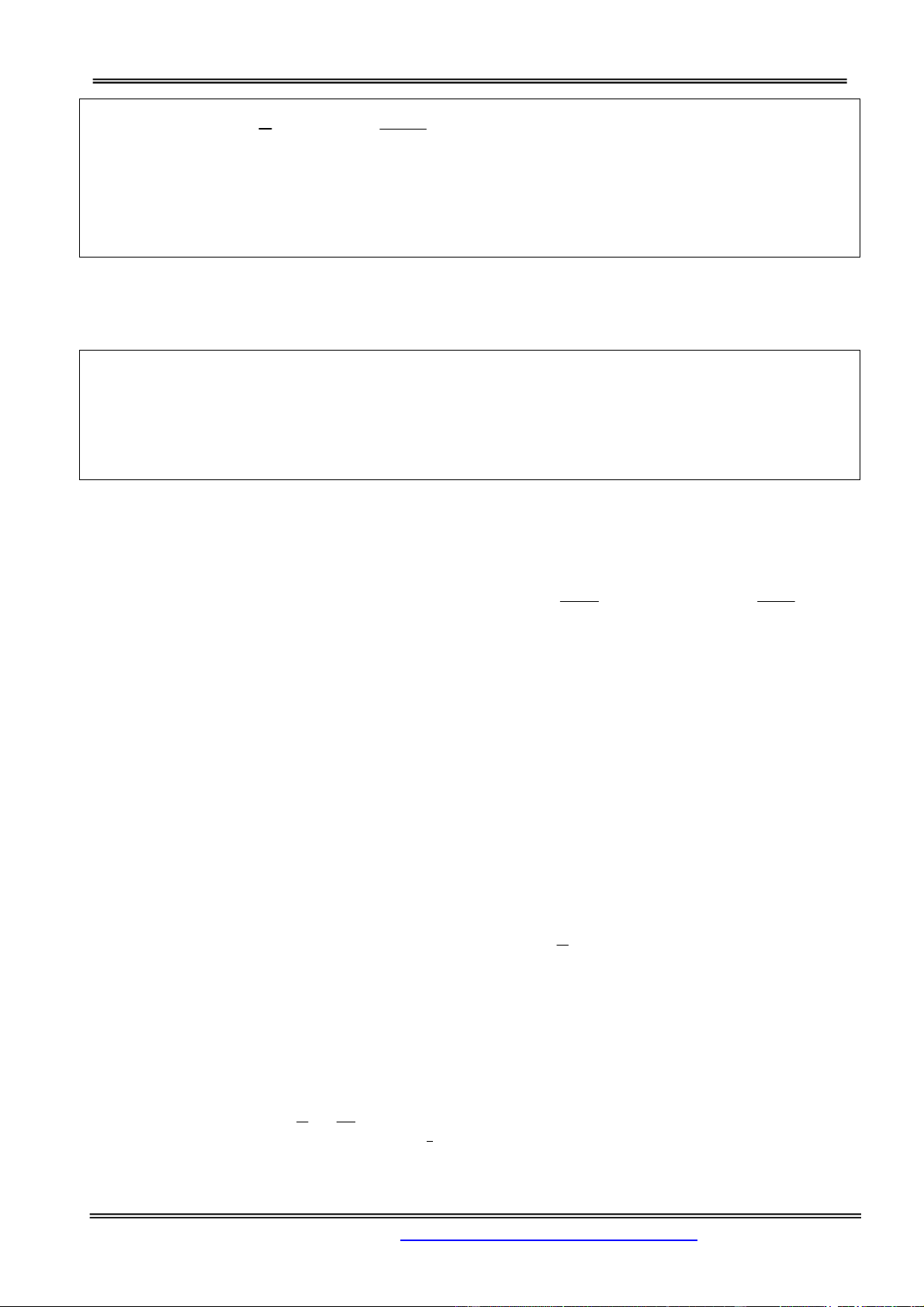
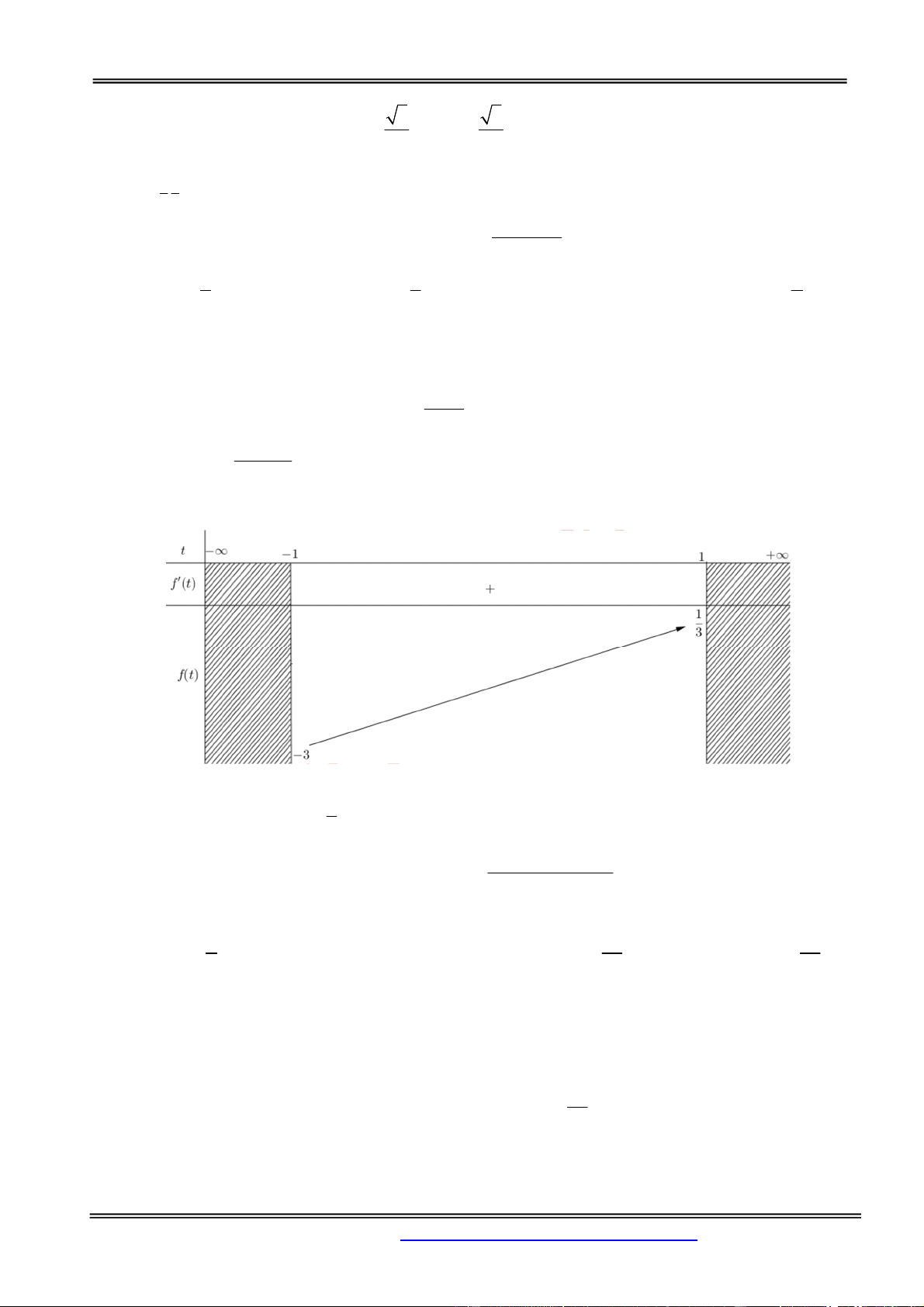
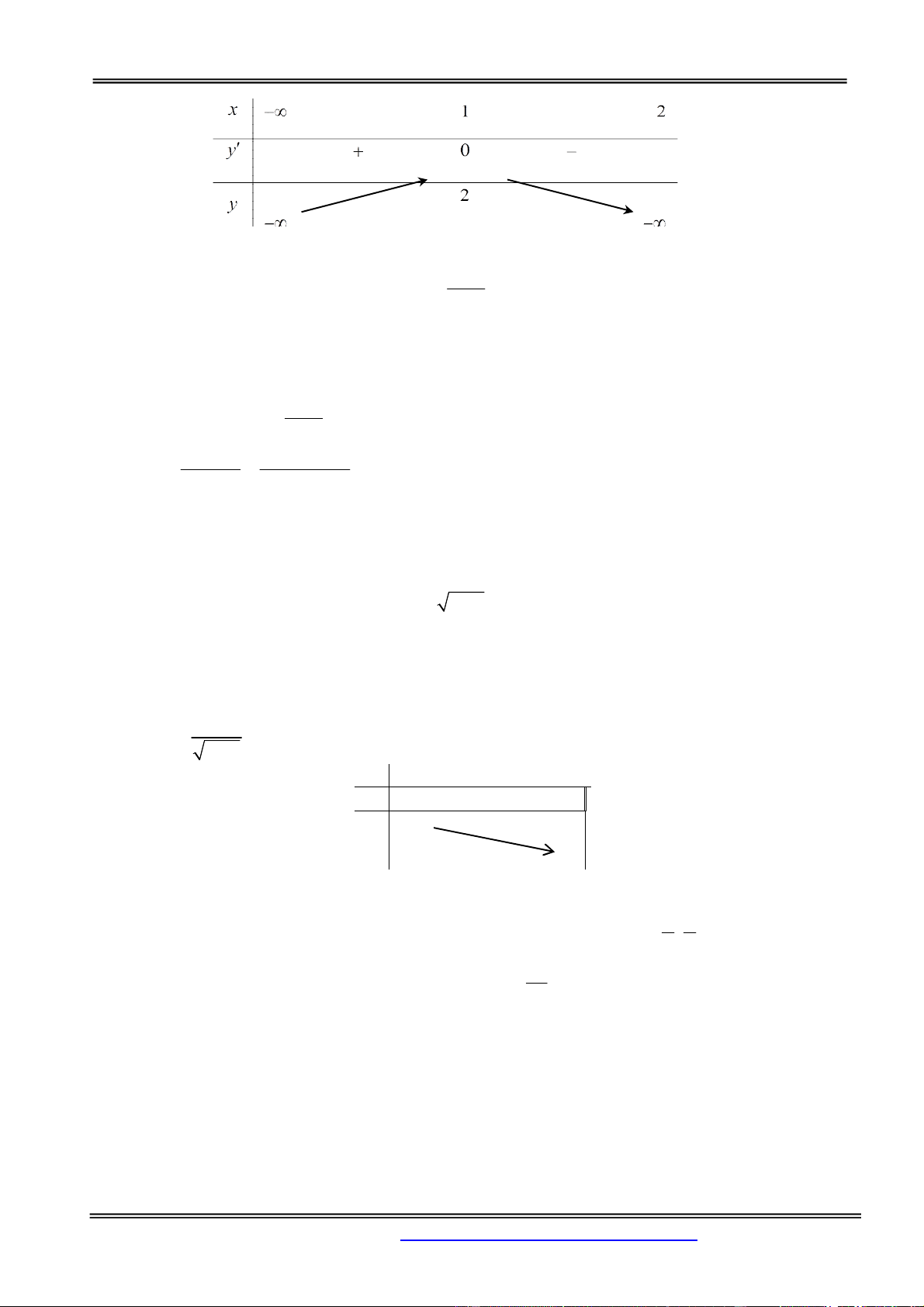
Câu 23. Cho hàm số y f x có đồ thị như hình bên. Tìm giá trị lớn nhất của hàm số y f x trên đoạn 1; 2. A. 1. B. 2. C. 5. D. 0. Hướng dẫn giải: Chọn đáp án C.
Trên đoạn 1; 2, giá trị lớn nhất của hàm số bằng 5 tại x  2 .
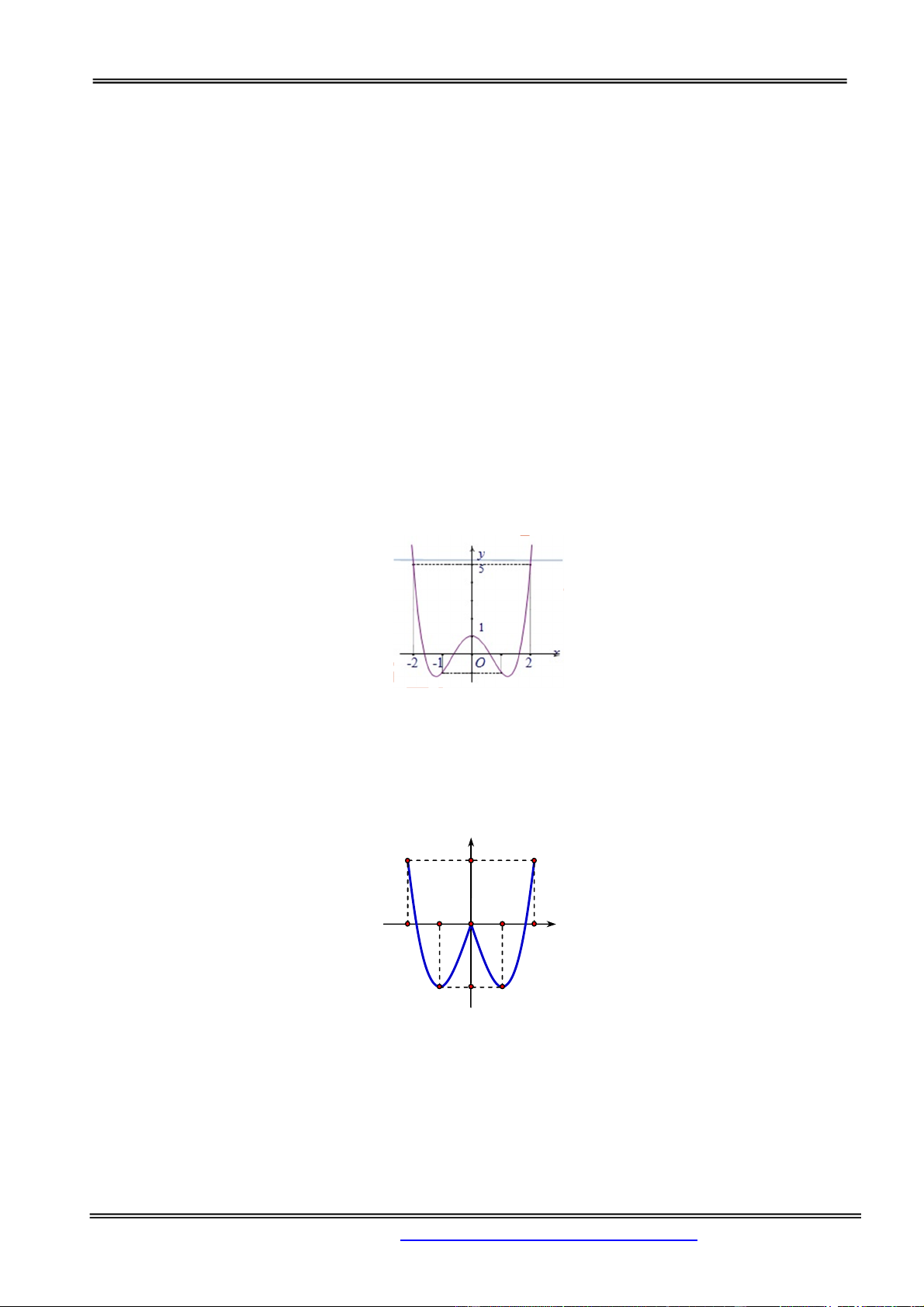
Câu 24. Cho hàm số y f x  liên tục trên đoạn  2;2     
 và có đồ thị trên đoạn 2;2   như sau:. y 2 1  O 1 2  2 x 2  .
Khẳng định nào sau đây là sai?
max f x  f  
max f x  f   A. 2 2  . B. . 2;2       2  ;2  
min f x  f  
min f x  f   C. 1 0  . D. . 2;2       2;2   Hướng dẫn giải: Chọn đáp án D.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
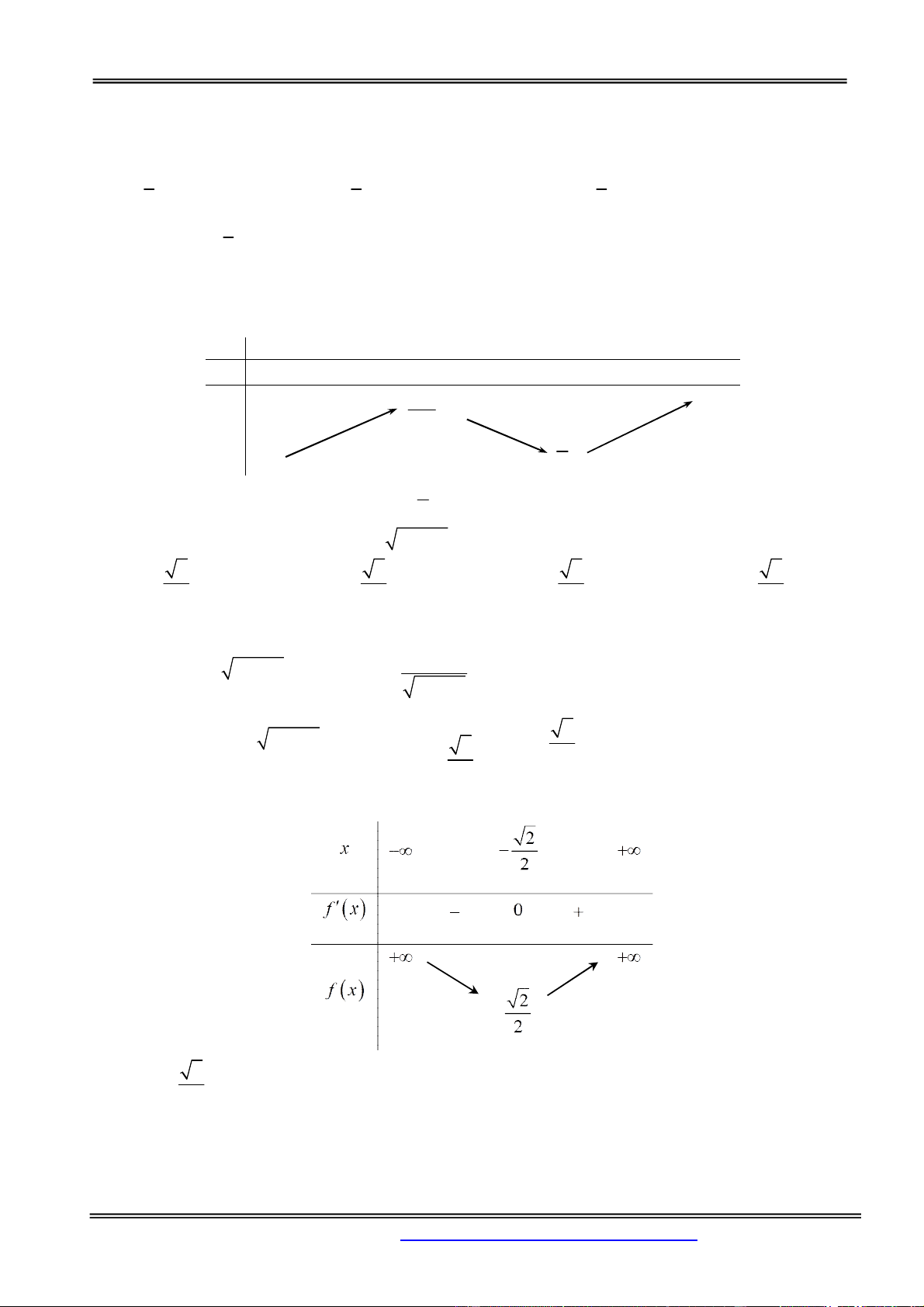
min f x  f   1  2;2   
Câu 25. Giá trị nhỏ nhất của hàm số 4 2
y x  4x  5 trên đoạn 1; 2 bằng? A. 1. B. 2 . C. 3 . D. 5 . Hướng dẫn giải: Chọn đáp án A. x  0 4 2
y x  4x  5 suy ra / 3
y  4x  8x . Ta có / y  0   . x   2  y  
1  2 , y 0  5 , y  2  1, y 2  5 . Vậy GTNN là 1. 3x 1
Câu 26. Tìm giá trị lớn nhất của hàm số y  trên đoạn 0;2 x  3 1 1 A.  . B. -5. C. 5. D. . 3 3 Hướng dẫn giải: Chọn đáp án D. 8 y   0,x  3.  x  32 1
Max y y 0  . 0; 2 3 4x 1
Câu 27. Xét hàm số y
trên đoạn [2 ;  1] . Hãy chọn khẳng định đúng x 9 A. max y  .
B. Hàm số không có giá trị nhỏ nhất. 2 ;   1 2 9
C. Hàm số không có giá trị lớn nhất. D. min y  . 2 ;   1 2 Hướng dẫn giải: Chọn đáp án D.
TXĐ: D   \   0 . 1 Ta có y   0 , x   0 . 2 x 9
Hàm số đồng biến trên  2  ;   1 và y  2    , y   1  5. 2 9 Vậy min y  . 2;  1 2 x 1
Câu 28.Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  trên đoạn 1;  3 là: 2x 1 2
A. GTNN bằng 1; GTLN bằng 3.
B. GTNN bằng 0; GTLN bằng . 7 2
C. GTNN bằng 0; GTLN bằng 1. D. GTNN bằng  ; GTLN bằng 0. 7 Hướng dẫn giải: Chọn đáp án B. 3 1 y   0, x    2x  2 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 10
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 y   1  0, y 3  . 7 2
Vậy GTNN bằng 0; GTLN bằng . 7 x 1
Câu 29. Cho hàm số y
. Chọn phương án đúng trong các phương án sau: 2x 1 2 A. min y  1.
B. max y  2 .
C. max y  0 . D. max y  . x   1;2 x   0;  1 x   1;  0 x   3;5 3 Hướng dẫn giải: Chọn đáp án C.
Hàm số không liên tục trên đoạn  1
 ; 2  Loại đáp án A.
Hàm số không liên tục trên đoạn 0  ;1  Loại đáp án B. 3  1 Ta có y   0 , x  
và max y y   1  0 . 2x  2 1 2 [1;0] 2x  1
Câu 30. Giá trị nhỏ nhất của hàm số y  trên đoạn 2;  3 bằng: 1  x 7 3 A.  . B. 5  C. 3 D. 2 4 Hướng dẫn giải: Chọn đáp án B.
+ TXĐ: D R \   1 . 3 + y ' 
 0x D  hàm số đồng biến trên các khoảng xác định 1 x2
 hàm số cũng đồng biến trên 2; 
3  Min y y 2  5  . 2;  3 3x 1
Câu 31. Tìm giá trị lớn nhất của hàm số y  trên đoạn 0; 2 x  3 1 1 A.  . B. 5 . C. 5 . D. . 3 3 Hướng dẫn giải: Chọn đáp án D. 8
y  x32 0 2 1
y 0  , y 2  5  3 Suy ra max y  5 . 0;2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 11
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  3 Câu 32. Kí hiệu ,
m M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y  trên đoạn 2x 1
[1;4]. Tính giá trị biểu thức d M  . m A. d  3. B. d  4. C. d  5. D. d  2. Hướng dẫn giải: Chọn đáp án A. 7 1 y   0 x  
. Suy ra hàm nghịch biến trên từng khoảng xác định, do đó hàm số 2x  2 1 2
nghịch biến trên đoạn [1;4]. Vậy m y 4  1; M y  
1  4  d M m  4 1  3. x  2
Câu 33. Gọi M , n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y f (x)  trên x  1
đoạn 0;2 . Hãy tính tích M .n . A. 2 . B. 0 . C. 1 . D. 1 . Hướng dẫn giải: Chọn đáp án B.
Hàm số f x xác định và liên tục trên 0;2 . 3
f  x   0 x  0; 2 . 2    x   1
f x đồng biến trên 0;2  M  max f x  f 2  0 , m  min f x  f 0  2  . 0;2 0;2
Vậy M .n  0 2 x 1
Câu 34.Gọi Q là giá trị lớn nhất và K là giá trị nhỏ nhất của hàm số y  trên đoạn 1;  2 . Khi x 1 24Q  27K
đó giá trị của biểu thức 1997 là: 2 3923 3925 3927 3929 A.  . B.  . C.  . D.  . 2 2 2 2 Hướng dẫn giải: Chọn đáp án C. 2 x  2x 1  x  1   2 y '   0   . 2 (x  1)  x  1   2 
K y(1)  1 
y ' đồng biến trên [1; 2] nên  . 5 Q y(2)    3 24Q  27K 3927 Suy ra 1997  . 2 2
Câu 35. Tìm tất cả các giá trị của tham số m để hàm số 3
y x   2 m  
1 x m 1 đạt GTNN bằng 5 trên 0  ;1 . A.   5 . B.   3 . C. 1;   2 . D.   4 . Hướng dẫn giải: Chọn đáp án C. 2
y  x   2 3 m   1  0, x    .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 12
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Hàm số đồng biến trên 0  ;1 .
max y  5 khi x  1 . 0;  1
Thay x  1, y  5 và hàm số ta được m  1; m  2  . mx 1
Câu 36. Giá trị của tham số thực m để giá trị lớn nhất của hàm số y
trên đoạn [1; 2] bằng 2 . x m là: A. m  3  .
B. m  3 .
C. m  1. D. Không tồn tại. Hướng dẫn giải: Chọn đáp án B. 2 m 1
Ta có: D   \   m và y   0, x   D .  x m2 mx 1
Do đó giá trị lớn nhất của hàm số y
trên đoạn [1; 2] bằng 2 khi và chỉ khi x m    y    m 1 1  2   2    1 mm  3 m 1; 2 
m  1 m  2  mx  1
Câu 37.Trên đoạn [2;4] hàm số y
đạt giá trị lớn nhất bằng 2. Khi đó : x m 7 3 A. m  . B. m  1 . C. m  2 . D. m  . 6 4 Hướng dẫn giải: Chọn đáp án D.
m x m 2  mx 1 m 1 Ta có: y '  
 0 với mọi x m . x m2  x m2
Vậy hàm số nghịch biến trên mỗi khoảng xác định của nó.
Do đó trên đoạn 2; 4 hàm số nghịch biến. Suy ra f 2  f 4 . 2m  1
Giá trị lớn nhất của hàm số trên đoạn 2; 4 là f 2  . 2  m 2m 1 3 
 2  2m 1  4  2m m  . 2  m 4
Lưu ý. Nếu m  2;4 thì hàm số không có giá trị lớn nhất. x m
Câu 38. Tìm tất cả giá trị của m để giá trị nhỏ nhất của hàm số f x  2 1  trên đoạn 1  ;2 x  1   bằng 1 A. m  1 . B. m  2 . C. m  3 . D. m  0 . Hướng dẫn giải: Chọn đáp án A.   f xm 3 '  2 (x  1) Nếu m
  3  0  m  3
thì hàm số đồng biến trên các khoảng xác định của nó, do đó GTNN m  1 của hàm số trên đoạn 1  ;2 f (1)   1  m  1  3  là    2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 13
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Nếu m
  3  0  m  3 thì hàm số nghịch biến trên các khoảng xác định của nó, do đó GTNN m  3 của hàm số trên đoạn 1  ;2 f (2)   1  m  0  3  là    3 Vậy m  1 2
x m m
Câu 39. Giá trị tham số m để giá trị nhỏ nhất của hàm số y  trên đoạn0;  1 bằng  2 là: x  1 1  21 1  21
A. m  1,m  2 . B. m  ,m  . 2 2
C. Không có giá trị m D. m  1  , m  2 Hướng dẫn giải: Chọn đáp án D.
+ D R \   1 . 2 1 1 3  1  3 2 m m   m   2 2. m m 1      2  4 + 2 4 4 y '   
 0x D hàm số đồng biến trên các  x  2 1  x  2 1  x  2 1
khoảng xác định  hàm số đồng biến trên 0; 
1  Min y y 0 2  m  . m 0;  1 m  1
+ Theo yêu cầu đề bài ta có: 2 2 Min y  2
  m m  2
  m m  2  0  .  0;  1 m  2  mx  5
Câu 40. Tìm m để hàm số f x 
đạt giá trị nhỏ nhất trên đoạn 0;  1 bằng 7. x m A. m  2 . B. m  0 . C. m  1. D. m  5 . Hướng dẫn giải: Chọn đáp án A. 2 mx  5 m(x  ) m mx  5 m  5 f x '   f (x)    0 x   . m x mx m2  x m2
Nên giá trị nhỏ nhất của hàm số trên đoạn 0;  1 là m  5 f (1)   7   m  2. 1  m 2 x m
Câu 41. Giá trị nhỏ nhất của hàm số y  trên 1; 0 bằng: x 1 2 m 1 2 1 m A. . B. 2 m  . C. . D. 2 m 2 2 Hướng dẫn giải: Chọn đáp án B. 2 x m 2 1   m Hàm số y  có y ' 
 0 x  1 nên hàm số nghịch biến trên 1;0 . x 1  x  2 1 Vậy: 2
min f (x)  f (0)  m . [1;0] 2mx 1 1
Câu 42. Giá trị lớn nhất của hàm số y  trên đoạn 2;  3 là 
khi m nhận giá trị m x 3 A. 0. B. 1. C. 5. D. 2. Hướng dẫn giải: Chọn đáp án A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 14
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2m 1 Ta có: y   0, m
  hàm số đồng biến trên 2;  3 m x2 6m  1 6m 1 1
 max y y 3      m  0 . 2;  3 m  3 m  3 3 1
Câu 43. Cho hàm số y x
, giá trị nhỏ nhất m của hàm số trên  1  , 2 là x  2 9 1 A. m  . B. m  . C. m  2 . D. m  0 . 4 2 Hướng dẫn giải: Chọn đáp án D. 2 1 1  x  2 1
Xét hàm số y x  trên  1
 , 2 , ta có y  1  . x  2  x  22  x  22
x  3 1, 2 2  
y  0   x  2 1  0  x  1 1  , 2  9 Mà y  
1  0 và y 2  . Do đó min y  0 . Vậy m  0 . 4 1,2 4
Câu 44. Tính giá trị nhỏ nhất của hàm số y x
trên đoạn 0; 4 . x 1   24
A. min y  4 . B. min y  .
C. min y  5 min y 3 . D.  . 0;4 5   0;4   0;4   0;4   Hướng dẫn giải: Chọn đáp án D. 4 x   1  x  3 4  y x   y  1  . x 1  2 2 x   1 x   1
x  3 0;4   y  0   . x  1 0; 4    24
y 0  4 , y   1  3 , y 4  . 5 Vậy min y  3 . 0;4   1
Câu 45. Giá trị nhỏ nhất của hàm số y  2x 1 trên đoạn 1;  2 bằng 2x 1 26 10 14 24 A. . B. . C. . D. . 5 3 3 5 Hướng dẫn giải: Chọn đáp án B. 1
Hàm số y  2x 1
liên tục trên đoạn 1;  2 . 2x 1  x  0  1; 2 2 2   Ta có y  2 
y  0  2x 1  1   . 2   2x   1  x  1  1;2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 15
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 10 26 10 Do y   1  ; y 2  nên min y  . 3 5 1;2 3 2 x  5
Câu 46. Tìm giá trị nhỏ nhất của hàm số y  trên đoạn 0;2 x  3 1 5 A. min y   . B. min y   . C. min y  2  . D. min y  10 . x   0;2 3 x   0;2 3 x   0;2 x   0;2 Hướng dẫn giải: Chọn đáp án D.
2x x  3   2 x  5 2 x  6x  5 Ta có: y    x  32  x  32 x  1 Suy ra : y  0 2
x  6x  5  0  x  5  5 1
Do đó ta có: f   1  2
 , f 0   , f  5    1
 0 , f 2   3 5 Vậy min y  10 . x   0;2 2 x  3
Câu 47. Tìm giá trị nhỏ nhất của hàm số y  trên đoạn 2;  4 . x 1 19 A. min y  .
B. min y  3 .
C. min y  2 .
D. min y  6 . [2;4 ] 3 [2;4 ] [2;4 ] [2;4] Hướng dẫn giải: Chọn đáp án D. 2x x   1   2 x   2 3 x  2x  3 Ta có : y   .  x  2 1  x  2 1
x  12;4 y  0   . x  32;4  19
y 2  7; y 4  ; y 3  6 . 3  min y  6 . [2;4 ] 2 x  3x  3  1 
Câu 48. Giá trị lớn nhất của hàm số y  trên đoạn  ;1 là: x 1  2    13 7 A. . B. 3. C. . D. – 1. 2 2 Hướng dẫn giải: Chọn đáp án C. 2 x  2x 2 x  2xx  0  1  Ta có y  . Cho y  0   0  
. Do x   ;1 nên x  0 .  2   x  2 1  x   1 x  2   2   1  7 7 7 y  
, y 0  3, y   1    . Vậy max y  .  2  2 2  1   ;1 2  2    2 x  4x
Câu 49. Tìm giá trị nhỏ nhất của hàm số y  trên đoạn 0; 3 . 2x  1  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 16
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 miny  0 3 min y  4  miny  1  A.  miny   0;3 . B. . C. . D. .         0;3 0;3 0;3        7   Hướng dẫn giải: Chọn đáp án D. 2 2x  2x  4 2 2x  2x  4 x  1 y  y 0 0        ;  2x  2 1   2 x  2 2 1  L x   y 0  0  ; y   1  1 ;y   3 3  7 2 x  3x
Câu 50. Hàm số y
giá trị lớn nhất trên đoạn 0;  3 là: x 1 A. 1. B. 3 . C. 2 . D. 0 . Hướng dẫn giải: Chọn đáp án D. 2 x  3x
Xét hàm số y x 1 2 2 x  2x  3 x  2x  3  x  1(n) Ta có: y '  . y '  0   0    x  2 1  x  2 1 x  3(l) 
y(0)  0, y(3)  0, y(1)  1. Vậy: max y  0 . [0;3] 2 x  2x  3
Câu 51.Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  trên đoạn 2;4 là: x 1 11
A. min f (x)  2; max f (x)  .
B. min f (x)  2 2; max f (x)  3 . 2;4 2;4 3 2;4 2;4 11
C. min f (x)  2; max f (x)  3 . D.
min f (x)  2 2; max f (x)  . 2;4 2;4 2;4 2;4 3 Hướng dẫn giải: Chọn đáp án D. 2 2 x  2x  3 x  2x 1  x  1 2 y   y   0   . x 1  x  2 1  x  1 2  11
f 2  3; f 4 
; f 1 2   2 2. 3 11
min f ( x)  2 2; max f (x)  . 2;4 2;4 3 2 x  3x 1
Câu 51.Giá trị lớn nhất của hàm số f x  trên đoạn  2  ; 0 x  2   là: 1 3 A. 2. B. 1. C. . D. . 2 4 Hướng dẫn giải: Chọn đáp án B.
2x  3 x  2   2 x  3x   2 1 x  4x  5 y    x  22  x  22
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 17
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  1  y  0  
x  5loai   3 1 y  2
   , y 0  , y   1  1 . 4 2 Vậy Maxy =1 . x   2;0
Câu 52. Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y
x x ?
A. Có giá trị lớn nhất và có giá trị nhỏ nhất.
B. Có giá trị nhỏ nhất và không có giá trị lớn nhất.
C. Có giá trị lớn nhất và không có giá trị nhỏ nhất.
D. Không có giá trị lớn nhất và giá trị nhỏ nhất. Hướng dẫn giải: Chọn đáp án A.
Tập xác định D  0  ;1 .
Hàm số đã cho liên tục trên 0 
;1 nên luôn có giá trị lớn nhất và giá trị nhỏ nhất trên 0  ;1 . Vậy min y  7 .  4  ; 2  
Câu 53. Giá trị nhỏ nhất và giá trị lớn nhất của hàm số 2 y  3
  4  x lần lượt là A. –3 và 0 . B. –3 và 1  . C. 0 và 2 . D. –2 và 2 . Hướng dẫn giải: Chọn đáp án B. Điều kiện 2   x  2. x 2 ' y  3
  4  x y   0  x  0. 2 4  x f (0)  1 
f (2)  f (2)  3.
Câu 54. Giá trị nhỏ nhất của hàm số y  6  x x  4 đạt tại x , tìm x ? 0 0
A. x   10 . B. x  4  . C. x  6 .
D. x  10 . 0 0 0 0 Hướng dẫn giải: Chọn đáp án B. TXD: 4   x  6 . 1  1 Ta có y    0,  x  4
 ; 6 , do đó hàm số đạt giá trị nhỏ nhất tại x  6 . 0 2 6  x 2 x  4
Câu 55. Giá trị lớn nhất của hàm số 2 y
x  4x là: A. 4. B. 0. C. 2. D. 2. Hướng dẫn giải: Chọn đáp án D.
+ TXD: D  0;  4 . x  2 + y ' 
, y '  0   x  2  0  x  2. 2 x  4x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 18
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 y 0  0 
+ Ta có:  y 4  0  y  2. max  y 2  2 
Câu 56. Tìm giá trị nhỏ nhất của hàm số 2
y  5x  4 trên đoạn  3   ;1
A. min y  3 .
B. min y  7 .
C. min y  2 .
D. min y  0 . 3;  1 3;  1 3;  1 3;  1 Hướng dẫn giải: Chọn đáp án C. Cách 1: 2 y  5x  4
Hàm số xác định và liên tục trên đoạn  3   ;1 . 5x y 
, y  0  x  0 3;  1 . 2 5x  4  y 3  7 
Ta có:  y 0  2 . Vậy min y  2 . 3;  1  y  1  3 
Cách 2: Sử dụng tabe MTCT
Câu 57. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x  2x  4 6  x
trên đoạn 3; 6. Tổng M m có giá trị là: A. 18 . B. 6  . C. 12 . D. 4 . Hướng dẫn giải: Chọn đáp án B.
Xét: f x  2x  4 6  x 1 6  x 1
Ta có: f ' x  2  2  2.
. f ' x vô nghiệm trên 3; 6. 6  x 6  x f ( 3  )  1  8, f (6)  12.
Vậy: M m  6.
Câu 58. Tìm giá trị lớn nhất của hàm số y
x 1  3  x trên đoạn [1;3]
A. max y  2 . B. max y  2 . [1;3] [1;3]
C. max y   2 . D. max y  2  . [1;3] [1;3] Hướng dẫn giải: Chọn đáp án A.
 3 x x 1 1 1 
Ta có hàm số đã cho xác đinh trên đoạn 1;  3 . y    2 x 1 2 3  x
2 x 1. 3  x
y  0  3  x x 1  0  3  x
x 1  x  2 1;  3 Khi đó. y  
1  y 3  2 ; y 2  2 . Vậy max y  2 . x   1;  3
Câu 59.Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y
x  6x  5 trên đoạn 1;  5 lần lượt là: A. 2 và 0 . B. 4 và 0 . C. 3 và 0 . D. 0 và 2 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 19
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: Chọn đáp án A. x  3 Ta có y 
nên y  0  x  3 1;5 . 2
x  6x  5 Vì y  
1  y 5  0 và y  
3  2 nên giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn 1;  5 lần lượt là 2 và 0 .
Câu 60. Cho hàm số y  5 3  x . Tìm giá trị nhỏ nhất của hàm số A. 3. B. 2 C. 0. D. 5 . Hướng dẫn giải: Chọn đáp án C.
TXD: x  3. Xét hàm số liên tục y  5 3  x trên  ;   3 ta có : 5  y   0, x  ; 
3 từ đó suy ra giá trị nhỏ nhất của hàm số là Min y f 3  0 . 2 3  x
Câu 61. Hàm số y  2
x x   x  2 4 2 3 2
x đạt giá trị lớn nhất tại hai giá trị x , x x x 1 2 . Tính 1 2 . A. 2 . B. 1 . C. 0 . D. 1 . Hướng dẫn giải: Chọn đáp án D.
Tập xác định D   . 2  x   2  x  
1 2  x  2x  3 4 2 2  Ta có y   2  2x  2 2 2 x  2x  3 x  2x  3
x  1, y  1 4 2  x  1 
y  0   x   1  2
2  x  2x  3   0  
 x  1 2, y  7 . 2
x  2x  3  2 
x 1 2, y  7  Bảng biến thiên x  1 2 1 1 2  y  0  0  0  7 7 y  1 4 2 
Suy ra hàm số đạt giá trị lớn nhất tại x  1 2, x  1 2 . Do đó, x x  1 . 1 2 1 2
Câu 62. Giá trị nhỏ nhất của hàm số y  5sin x  cos 2x là: A. 6  . B. 7  . C. 4  . D. 3 . Hướng dẫn giải: Chọn đáp án C.
Tập xác định D   . Ta có: 2
y  5sin x  cos 2x  5sin x 1  2 sin x .
Đặt t  sin x , 1   t  1.
Khi đó bài toán trở thành tìm giá trị nhỏ nhất của hàm số : g t  2
 2t  5t 1trên 1  ;  1 . 5
g '(t)  4t  5 ; g '(t)  0  4t  5  0  t   L . 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 20
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 g   1  4  ; g   1  6 ;.
Vậy giá trị nhỏ nhất của hàm số là 4  .
Câu 63. Tìm giá trị nhỏ nhất của hàm số . 2
y  2 cos x  4 cos x
A. min y  5 . B. min y  2  .
C. min y  7 .
D. min y  8 .     Hướng dẫn giải: Chọn đáp án B. Ta có : 2
y  2 cos x  4 cos x   x  2 2 cos 1  2 . Vì 1
  cos x  1  0  cos x 1  2    x  2 0 cos 1  4 . Do đó : 2   y  6 .
Suy ra giá trị nhỏ nhất của hàm số là y  2 khi cos x  1 .
Câu 64. Tìm giá trị lớn nhất của hàm số y  cos2x  4 cos x  1 .
A. min y  5 .
B. max y  6 .
C. min y  7 .
D. min y  8 .     Hướng dẫn giải: Chọn đáp án B. 2
y  cos 2x  4 cos x  1  2 cos x  4 cos . x
Đặt t  cos x  1   t   1 . . Khi đó  f (1)  2
  min f (t)  min f (x) [-1;1] y f t  2   
 2t  4t f '(t)  4t  4  0  t  1   .
f (1)  6  max f (t)  max f (x)  [-1;1]   9 1
Câu 65. Giá trị nhỏ nhất của hàm số 3 2
y  2 cos x
cos x  3cos x  là: 2 2 A. 1. B. 24 . C. 12 . D. 9  . Hướng dẫn giải: Chọn đáp án D.
Tập xác định D  . 9 1
Đặt t  cos x, t  1   ;1 . Hàm số trở thành 3 2 y  2t t  3t  . 2 2 t  1 Ta có 2
y  6t  9t  3, y 0     . 1 t   2  1  9 y   1  1 , y   1  9  , y     2  8
Vậy giá trị nhỏ nhất là 9.
Câu 66. Cho hàm số y  3cos x  4sin x  8 với x 0; 2 . Gọi M , m lần lượt là giá trị lớn nhất và
giá trị nhỏ nhất của hàm số. Khi đó tổng M m bằng bao nhiêu? A. 8 2 . B. 7 3 . C. 8 3 . D. 16. Hướng dẫn giải: Chọn đáp án D.
Ta có y  3cos x  4sin x  8  5sin x  8  5sin x  8, x  0; 2
Do 3  5sin x  8  13  3  y  13, x  0; 2
Vậy M m  16
Câu 67. Tìm giá trị lớn nhất f x 2
x  cos x trên đoạn 0;  . 2   
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 21
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. . B. 0 . C. . D. . 2 4 Hướng dẫn giải: Chọn đáp án C.
Hàm số f x trên 0;  . 2    
f  x   x x x x x x   x x2 2 2 1 2 sin cos sin cos 2 sin cos sin cos  0 x  0;  2      
f x đồng biến trên 0; 
. Vậy max f x  f    . 2      0;  2  2  2   
Câu 68. Tìm M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y x  2 cos x trên đoạn   0;  2    A. M   1; m  2 . B. M  ; m  2 .
C. M  1; m  0 . D. M  2; m  1 . 4 2 Hướng dẫn giải: Chọn đáp án A.
Xét hàm số y f x  x  2 cos x trên 0; 
, f ' x  1 2 sin x 2     x   k 2 1  4
Cho f ' x  0  1 2 sin x  0  sin x    k  2 3x   k 2  4  Vì x  0;  x   2    4 
Ta có: f 0  2, f  1, f       4  4  2  2
Vậy hàm số đạt giá trị lớn nhất M  max 
1, đạt giá trị nhỏ nhất min  2 .     0; 4  0; 2       2    
Câu 69. Tìm giá trị lớn nhất của hàm số 3
y  3sin x  4 sin x trên đoạn  ;  bằng: 2 2    A. 1 . B. 1. C. 3. D. 7. Hướng dẫn giải: Chọn đáp án C.
Đặt t  sin x, 1  t  1 ; Ta có: 3
y  3t  4t ;  t  0  3 3 y 0 3t 4t 0        t   (nhận cả 3 nghiệm)  2  3 t   2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 22
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  3   3  y  
1  1; y  
1  1; y 0  0; y   0; y  0     ; 2 2     Vậy max y  1.      ;  2 2    2 sin x 1
Câu 70.Tìm GTLN và GTNN của các hàm số sau: y  là: sin x  2 1 1 1 A. max y  .
B. max y   . C. min y  3  . D. min y  . 3 3 2 Hướng dẫn giải: Chọn đáp án A. - TXĐ: . 2t 1
- Đặt: t  sin x t  1;1 . Khi đó: y   f t .     t  2 5
- Ta có: f ' t
 0,t  1;1 .     t  22
- Ta có bảng biến thiên hàm số f t trên [1; 1]:
- Từ bảng biến thiên ta suy ra: 1
 max y  max f t  f   1  .
 min y  min f t f 1  3.      1  1 ;  3   11 ;   
2 sin x  cos x 1
Câu 71.Tìm GTLN và GTNN của các hàm số sau: y  là:
sin x  2 cos x  3 max y  2 max y  1 max y  2  max y  2   A.  . B.  . C.  . D. 1 1   1.  min y   min y  1  min y   min y    2  2  2 Hướng dẫn giải: Chọn đáp án D.
- TXĐ: sin x  2 cos x  3  0  x  .
- Khi đó: y sin x  2 cos x  3  2sin x  cos x 1  y  2sin x  2y  
1 cos x  1 3y (*) 2 2 1 
- Để (*) có nghiệm thì: 1 3y   y  2  2y   2 1    y  2.   2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 23
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 max y  2   Từ đây suy ra:  1.  min y    2 ln x
Câu 72. Giá trị lớn nhất của hàm số f x  trên đoạn 1;  3 là: x 1 ln 3 A. . B. e . C. . D. 24, 2 . e 3 Hướng dẫn giải: Chọn đáp án A. 1 .x ln x Ta có: 1 ln x . '   x f x
f ' x  0  1 ln x  0  x  . e 2 2   x x
Với x 1; e thì f ' x  0  hàm số đồng biến trên nửa khoảng 1;e . Với x   ; e
3 thì f 'x  0  hàm số nghịch biến trên nửa khoảng  ; e  3 . 1
Vậy giá trị lớn nhất của hàm số trên đoạn 1; 
3 là f e  . e
Câu 73.Giá trị nhỏ nhất của hàm số f x  x 2  ln x trên 2;  3 là A. 1. B. 4  2ln 2 . C. e . D. 2   2 ln 2 . Hướng dẫn giải: Chọn đáp án B.
Xét hàm số liên tục và xác định trên 2;  3 .
Ta có f  x  1 ln x , f  x  0  x e 2;  3 .
y 2  22  ln 2 , y 3  32  ln 3 , y e  e .
Vậy min y y 2  2 2  ln 2 . 2;  3
Câu 74. Tìm giá trị nhỏ nhất của hàm số y  2x  ln 1 2x trên  1  ; 0
A. min  2  ln 3 . B. min  0 . C. min  1  .
D. min  2  ln 3 . x   1;0 x   1;0 x   1;0 x   1;0 Hướng dẫn giải: Chọn đáp án A.
Xét f x  y  2x  ln 1 2x  1  TXĐ: D  ,    2  2
f ' x  2  1 2x 2 1 2x  2
Cho f ' x  0   0  4
x  0  x  0 1;0 1 2xf    1  2  ln 3 Ta có:  f  0  0  Vậy min  2   ln 3 . 1;0  1 
Câu 75. Tính giá trị lớn nhất của hàm số y x  ln x trên ; e  . 2   
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 24
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
A. max y e 1 . B. max y  1.
C. max y e . D.  1  1   1  x ;ex ;e x ;e 2         2   2  1 max y   ln 2 .  1  x ;e 2  2    Hướng dẫn giải: Chọn đáp án A.  1 
Hàm số y x  ln x liên tục trên đoạn ; e  . 2    1  1  Ta có y  1 
y  0  x  1 ; e . x  2     1  1 Do y   ln 2  
; y e  e 1; y  
1  1 nên max y e 1 .  2  2  1  x ;e  2   
Câu 76. Tìm GTLN và GTNN của hàm số f x 2
x  4ln x trên đoạn 1;e là: A. 2 e  4 và 1 B. 2
e  4 và 2  2 ln 2 2 2
C. e  4 và 1
D. e  4 và 22ln2 Hướng dẫn giải: Chọn đáp án C. 9 Xét hàm số trên 1; 
4 ; f '(x)  1 2 x x
 1;4  f '(x)  0  x  3 25
f (1)  10; f (3)  6; f (4)  4
Vậy: max f x  10 tại x = 1, min f (x)  6 tại x = 3.  1;4 1;4 Câu 77. 2 2x
Tìm GTLN và GTNN của hàm số f(x)  (x  2).e trên đoạn [–1; 2] là: 1 1 A. 4 2e và 2 e 4 4 2 4 B. 2e và 
C. 4e và e D. 4e và  2 e 2 e Hướng dẫn giải: Chọn đáp án A. 2 2x
Hàm số f(x) liên tục trên đoạn [–1; 2], f '(x)  2(x  x  2)e 2 f '(x)  0  x  x  2  0     x  1 x  (1; 2)  x  ( 1  ; 2)  2 1 4 f (1)  e , f ( 1  )  , f (2)  2e . 2 e 2 ln x m
Câu 78. Biết rằng giá trị lớn nhất của hàm số y  trên đoạn 3 1  ; e M
trong đó m, n là x   là , n e các số tự nhiên. Tính 2 3
S m  2n . A. S  13 . 5 . B. S  2 . 4 . C. S  2 . 2 . D. S  3 . 2 . Hướng dẫn giải: Chọn đáp án C. 2 2ln x  ln x ln x  0  x  1 y  , y  0   . 2   2 x ln x  2  x e
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 25
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 4 9 4 y   1  0 , y  2 e   , y  3 e   . Suy ra 2 3 M
m  4, n  2  S  4  2.2  32. 2 e 3 e 2 e
Câu 79. Tìm tập hợp tất cả các giá trị của tham số m sao cho bất phương trình sau có nghiệm:
x  5  4  x m . A.  ;   3 . B.  ;  3 2  . C. 3 2; . D. ;3 2  .  Hướng dẫn giải: Chọn đáp án B.
Đặt f x  x  5  4  x, x 5; 4. 1 1 1
f  x  
; f  x  0  x  5  4  x x   . 2 x  5 2 4  x 2 Bảng biến thiên: 1 x 5   4 2 f (  x)  + 3 2 f (x) 3 3
Yêu cầu bài toán  m  3 2 . 2
Câu 80. Với giá trị nào của tham số m thì phương trình x  4  x m có nghiệm
A. 2  m  2 .
B. 2  m  2 2 . C. 2   m  2 2 . D. 2   m  2 . Hướng dẫn giải: Chọn đáp án C.
Tập xác định D   2  ; 2 Phương trình 2
x  4  x m có nghiệm khi đường thẳng y m cắt đồ thị của hàm số 2
y x  4  x C  Xét hàm số 2
y x  4  x trên D   2  ; 2 x Ta có y  1 2 4  x xx  0 Cho 2 y  0  1
 0  4  x x    x  2 2 2 2 4  x 4  x   x Bảng biến thiên: x 2  2 2  y  0  2 2 y 2
Từ bảng biến thiên ta thấy đường thẳng y m cắt đồ thị hàm số C  khi 2   m  2 2 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 26
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 81. Cho x , y là các số thực thỏa mãn x y x 1  2 y  2 . Gọi M , m lần lượt là giá trị
lớn nhất và giá trị nhỏ nhất của 2 2
P x y  2 x   1  y  
1  8 4  x y . Khi đó, giá trị của M m bằng A. 44 . B. 41 . C. 43 . D. 42 . Hướng dẫn giải: Chọn đáp án C.
Ta có :  x y   x   y  2 2 1 2. 1
 1 2. x   1   y  
1   3. x y
Do đó : 0   x y  3. 2
Theo bài ra : P   x y  2 x y  2  8. 4   x y
Đặt t x y . Đk : 0  t  3 .
Xét : P f t  2
t  2t  2  8 4  t trên 0;  3 . 4
Có f t  2t  2  . 4  t 4 2
Đặt g t   f t   2t  2 
g 't   f t   2   0 với t  0;  3 . 4  t 4  t3
Do đó : hàm số g t  đồng biến trên 0;  3 .
Khi đó : g t   g 0  f t   f 0  0 . Suy ra hàm số f t  đồng biến trên 0;  3 . M f  3  25  
. Vì vậy : M m  43 . m f  0 18 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 27
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
DẠNG 2: GTLN, GTNN TRÊN MỘT KHOẢNG, NỬA KHOẢNG
Phương pháp: Xét khoảng hoặc nửa khoảng D
- Tính f ' x , giải phương trình f ' x  0 tìm nghiệm trên D.
- Lập BBT cho hàm số trên D.
- Dựa vào BBT và định nghĩa từ đó suy ra GTLN, GTNN.
Câu 1.Trên khoảng (0; +) thì hàm số 3
y  x  3x  1
A. Có giá trị nhỏ nhất là min y  3 .
B. Có giá trị lớn nhất là max y  1  .
C. Có giá trị nhỏ nhất là min y  1  .
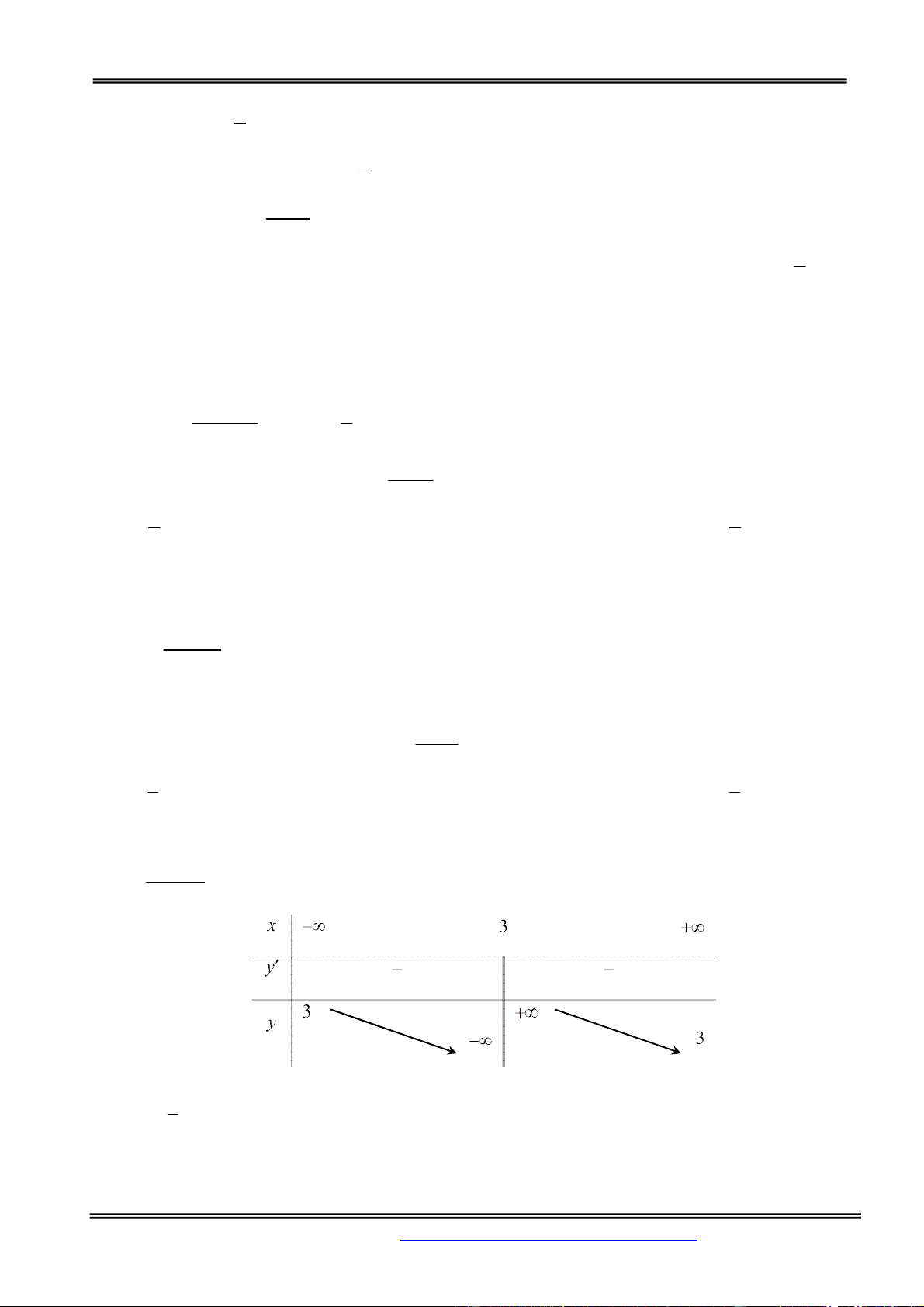
D. Có giá trị lớn nhất là max y  3 . Hướng dẫn giải: Chọn đáp án D.
Xét hàm số đã cho trên D  0,  .
x  1 0,  Ta có 2 y  3  x  3 , 2 y  0  3
x  3  0   . x  1  0,   Bảng biến thiên x 0 1  y  0  3 y 1 
Do đó, max y  3 và không tồn tại min y . 4
Câu 2. Tìm giá trị nhỏ nhất của hàm số y x
trên khoảng 0;  . x A. 4 . B. 2 . C. 2 . D. 4 . Hướng dẫn giải: Chọn đáp án A. Cách 1: 4
Vì hàm số xác định trên khoảng 0; nên ta có x  0 và  0 . x 4 4 4
Áp dụng bất đẳng thức Cô-si cho hai số x và ta có x   2 . x  4 . x x x
Vậy hàm số đạt giá trị nhỏ nhất bằng 4 , dấu bằng xảy ra khi x  2 . Cách 2:
TXĐ: D  0;  . 4 4 2 x  4 x  2 Ta có y  1 , y  0  1  0   0  . 2  x 2 x 2 x x  2   Bảng biến thiên. x 0 3   y   0    y   4 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 28
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Dựa vào bảng biên thiên ta có giá trị nhỏ nhất của hàm số là 4 . 1
Câu 3. Hàm số y
có bảng biến thiên như hình vẽ. Xét trên tập xác định của hàm số. Hãy 2 x 1
chọn khẳng định đúng ?
A. Hàm số có giá trị lớn nhất bằng 1 và giá trị nhỏ nhất bằng 0.
B. Hàm số có giá trị lớn nhất bằng 0.
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
D. Hàm số có giá trị lớn nhất bằng 1. Hướng dẫn giải: Chọn đáp án D.
Hàm số đạt giá trị lớn nhất bằng 1 khi x  0 nhưng hàm số không đạt giá trị nhỏ nhất tại 0 vì không tồn tại
giá trị nào của x thỏa mãn. 4
Câu 4. Hàm số y
có bảng biến thiên như hình vẽ. 2 x 1 x  0  y  0  y 4 0 0
Xét trên tập xác định của hàm số. Hãy chọn khẳng định đúng?
A. Hàm số có giá trị lớn nhất bằng 4 và giá trị nhỏ nhất bằng 0 .
B. Hàm số có giá trị lớn nhất bằng 0 .
C. Không tồn tại giá trị lớn nhất và giá trị nhỏ nhất của hàm số.
D. Hàm số có giá trị lớn nhất bằng 4 . Hướng dẫn giải: Chọn đáp án D. 2 x  3
Câu 5.Tìm giá trị lớn nhất của hàm số y  trên khoảng  ;  2 . x  2 A. max y  4 B. max y  3 C. max y  1
D. max y  2 . ;2 ;2 ;2 ;2 Hướng dẫn giải: Chọn đáp án D. 2 x  4x  3  x  1  ;  2 Ta có y 
nên y  0   .  x  22
x  3   ;  2  Ta có bảng biến thiên
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 29
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Nên max y  2 . ;2 1
Câu 6.Tìm giá trị nhỏ nhất của hàm số y  x  3  trên nửa khoảng  4  ; 2   . x  2
A. min y  5 .
B. min y  6 .
C. min y  4 .
D. min y  7 .  4  ; 2    4  ; 2    4  ; 2    4  ; 2   Hướng dẫn giải: Chọn đáp án D. 1
Xét hàm số y  x  3  trên nửa khoảng  4  ; 2   x  2 2 1
x  4x  3 y  1   x  22  x  22  x  1  4; 2   2
y  0  x  4x  3  0    x  3   4  ; 2    Bảng biến thiên
Câu 7. Tìm giá trị nhỏ nhất y
của hàm số y  2 3  x. min A. y  0 . B. y  6 . C. y  3 . D. y  2 . min min min min Hướng dẫn giải: Chọn đáp án A.
Tập xác định: D  ( ;  3]. 1  Ta có: y   0,x   ;
 3. Hàm số nghịch biến trên khoảng ;3. 3  x x  3 y –  y 0
Vậy min y y 3  0. (;3]    
Câu 8. Giá trị nhỏ nhất của hàm số 3
y  sin x  cos 2x  sin x  2 trên khoảng  ;   bằng:  2 2  23 A. 1. B. 6. C. . D. 1. 27 Hướng dẫn giải: Chọn đáp án C. Ta có 3 2
y  sin x  2 sin x  sin x 1 .
Đặt t  sin x  1  
;1 thì hàm số trở thành 3 2
y t  2t t 1,t  1   ;1 . Ta có 2
y  3t  4t 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 30
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 t  1(l)  1  23 y 0     1
Miny y   .    t   (n)  3  27  3 3 x    
Câu 9. Giá trị lớn nhất của hàm số 2 y  
x 1 trên khoảng  ;   bằng: 3  2 2  A. 3. B. 7. C. 1. D. -1. Hướng dẫn giải: Chọn đáp án C. 2
y  3cos x 12 sin x cos x .   x   k  2   cos x 0   x    k 2  2 6 y 0
3cos x 12sin x cos x 0         k   . 1 . sin x   5  x   k 2 2    6  7  x   k 2  6      Do x   ;  x     .  2 2  6           Ta có f  1   , f   1  
nên GTLN của hàm số trên khoảng  ;   bằng 1 .  6   6   2 2 
Câu 10. Tìm m để phương trình 5 3
x x  1 x m  0 có nghiệm trên   ;1 . A. m  2 . B. m  2  . C. m  2  . D. m  2 . Hướng dẫn giải: Chọn đáp án C. 5 3 5 3
x x  1 x m  0  x x  1 x  m . Xét hàm số 5 3
y x x  1 x trên   ;1 . 1 4 2
y  5x  3x   0, x  ;   1 . 2 1 x Bảng biến thiên x  1 y  2 y 
Ycbt  m  2  m  2  . 9
Câu 11. Cho hàm số f (x) 
x . Tính giá trị lớn nhất của hàm số f x trên (; 0) x A. 3. B. 6  . C. 9  D. 3  . Hướng dẫn giải: Chọn đáp án B. 9
Ta có : f   x  1 . 2 x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 31
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  3
Khi đó f  x  0   . x  3   Vì x   ;
 0 nên ta lấy x  3  , loại x  3 .
Ta có bảng biến thiên như sau x  3  0 y '  0  6  y  
Từ bảng biến thiên ta có giá trị lớn nhất của hàm số trên ;0 là 6  .
Câu 12. Tìm tất cả giá trị của m để phương trình 4 2
x 1  x m có nghiệm A. 0  ;1 . B. ;0 . C. 1; . D. 0  ;1 . Hướng dẫn giải: Chọn đáp án D. ĐK: x  0
Xét hàm số f x 4 2  x 1  x
x x  x  3 2 4 1 f ' x 
, f x   x x   x  3 2 4 2 4 ' 0 1
 3x  3x 1  0(VN ) 2  x  3 2 4 1 . x
f ' x  0  hàm số nghịch biến trên 0;  , f (0)  1, lim f x  0 x Vậy m 0  ;1 .
Câu 13. Tìm tất cả các giá trị thực của tham số m để phương trình 2
m 2  tan x m  tan x có ít nhất một nghiệm thực.
A.  2  m  2 . B. 1   m  1 .
C.  2  m  2 . D. 1   m  1 . Hướng dẫn giải: Chọn đáp án C. tan x pt m  2 2  tan x 1 t
Đặt tan x t m  2 2  t 1 2 t 2  2  t
Xét hàm số f t 
f 't    0  t   2 2  t 1
2  t . 2  t  2 2 2 2 1
Lập BBT với lim f t   1, lim f t   1
 , f  2   2, f  2   2  m   2; 2 . t  t   
Câu 14. Cho x, y là hai số không âm thỏa mãn x y  2 . Tìm giá trị nhỏ nhất của biểu thức 1 3 2 2 P
x x y x 1 3 7 17 115 A. min P  5 . B. min P  . C. min P  . D. min P  . 3 3 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 32
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: Chọn đáp án B.
Ta có x y  2  y  2  x 1 1 1 3 2 2 P
x x y x 1  P
x x  2  x2 3 2  x 1 3 2  P
x  2x  5x  5 3 3 3 1 Xét hàm số 3 2 y
x  2x  5x  5 trên 0;  3  x  1 2
y  x  4x  5 . Cho 2
y  0  x  4x  5  0   x  5  Bảng biến thiên: x  5  1  y  0  0  115  y 3 7  3 7
Từ bảng biến thiên ta thấy min P  . 3
Câu 15.Giá trị của m để phương trình 2
x  2x 1  m có nghiệm là: 2 2 2 2 A. m  . B. m  . C. m  . D. m  . 2 2 2 2 Hướng dẫn giải: Chọn đáp án A. 2x Đặt 2
f (x)  x  2x 1  f  x  1 2 2x 1 x  0  2
Ta có: f  x 2  0 
2x 1  2x   2  x   x   2  2 Bảng biến thiên 2 Vậy, m  . 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 33
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
DẠNG 3: ỨNG DỤNG GTLN, GTNN VÀO GIẢI TOÁN THỰC TẾ
Câu 1: Hình chữ nhật có chu vi không đổi là 8 m. Diện tích lớn nhất của hình chữ nhật đó là: A. 4m2. B. 8m2 C. 16m2. D. 2m2. Hướng dẫn giải: Chọn đáp án A.
Gọi 2 kích thước của hình chữ nhật là a,b a b  4. 2  a b S  . a b   4  
. Vậy diện tích lớn nhất của hình chữ nhật bằng 2 4m .  2 
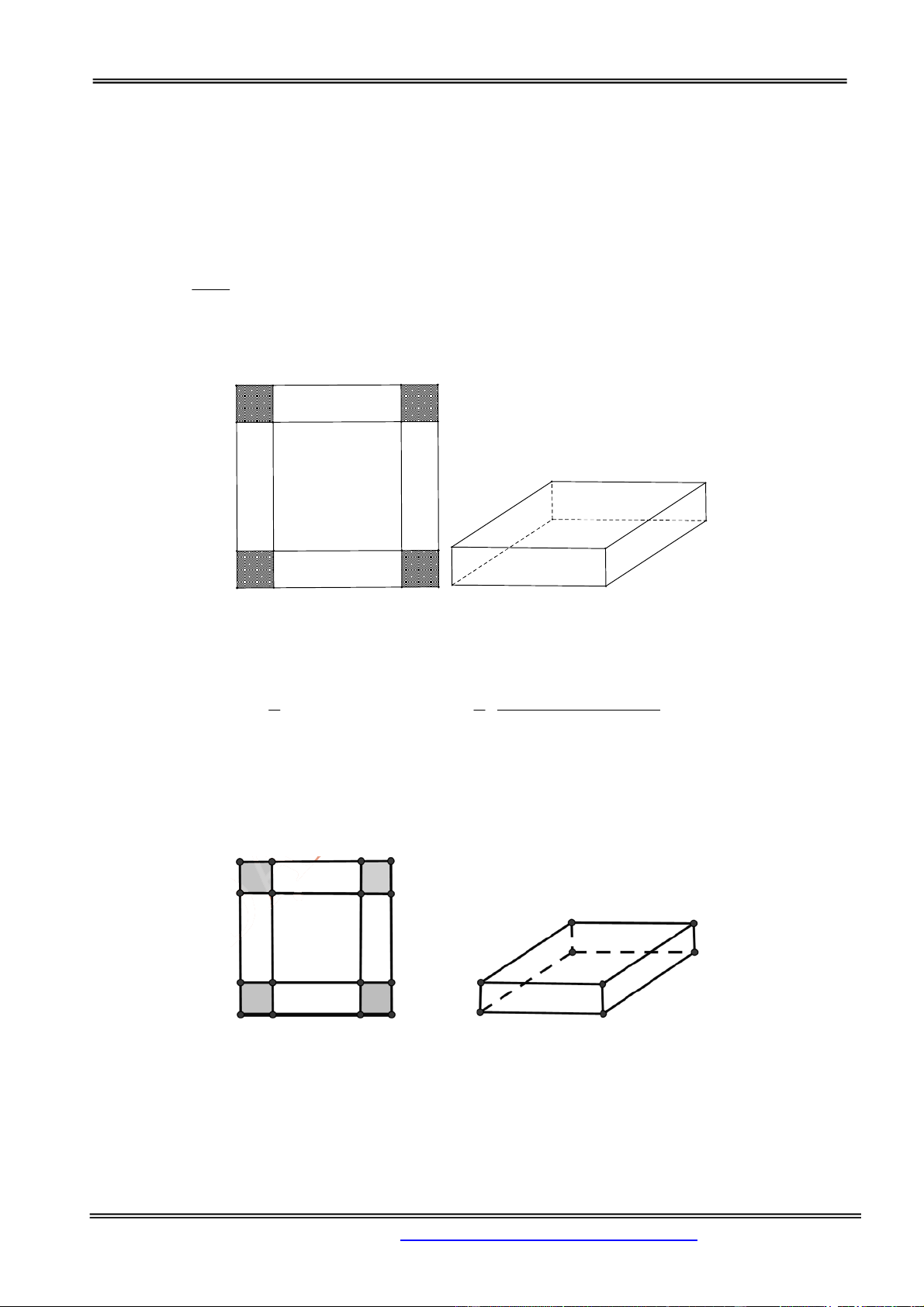
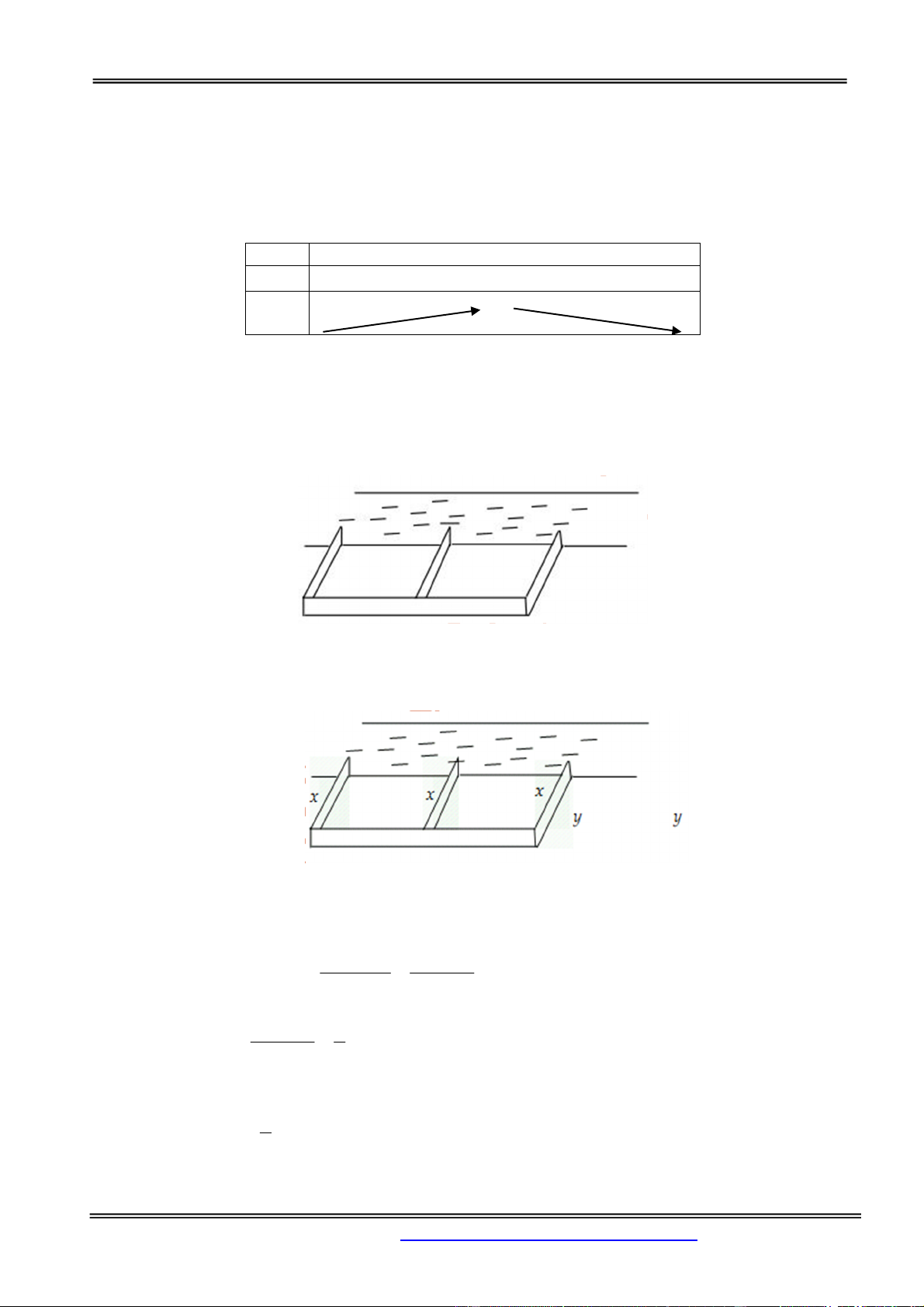
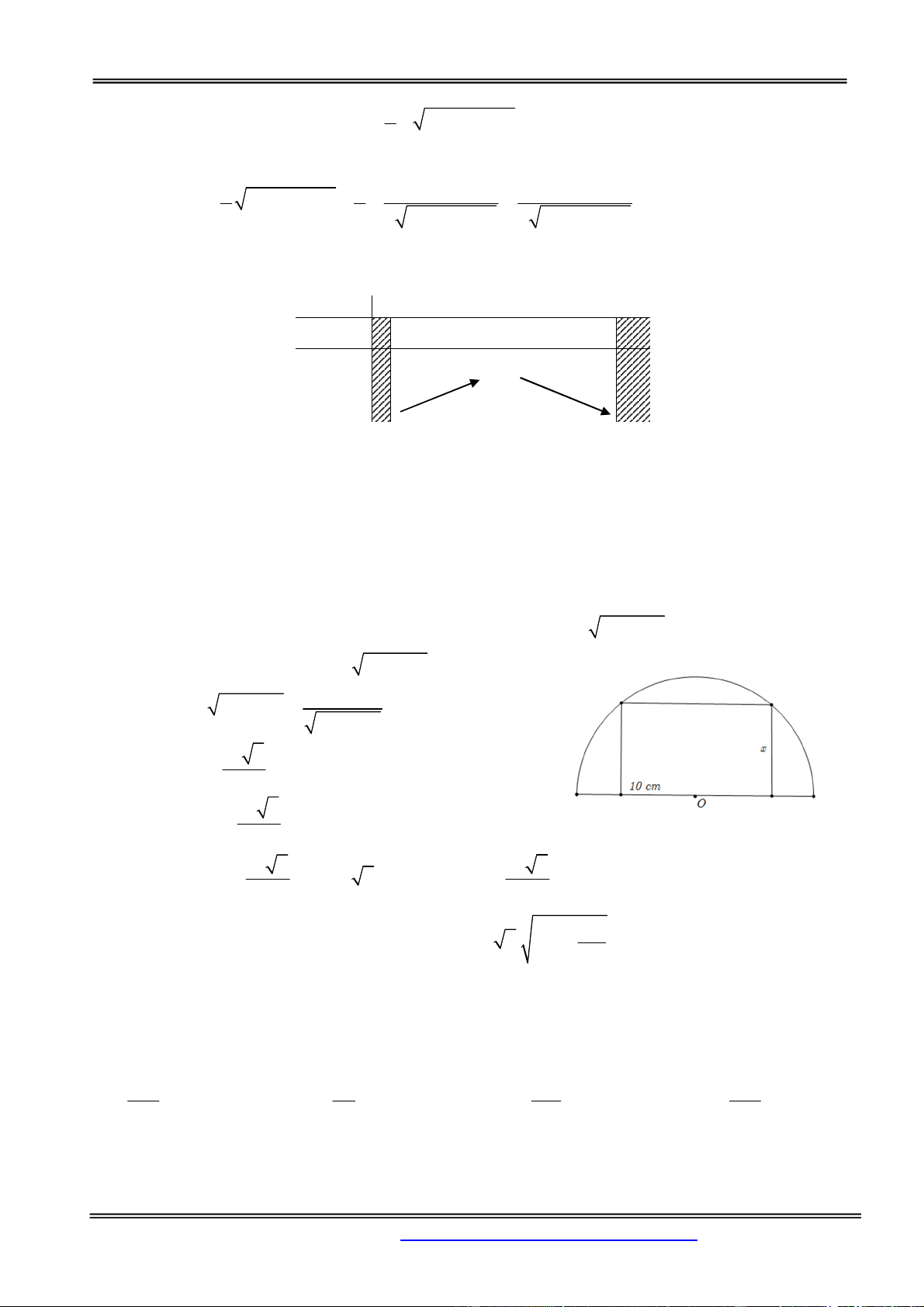
Câu 2: Cho một tấm nhôm hình vuông cạnh 18 cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn
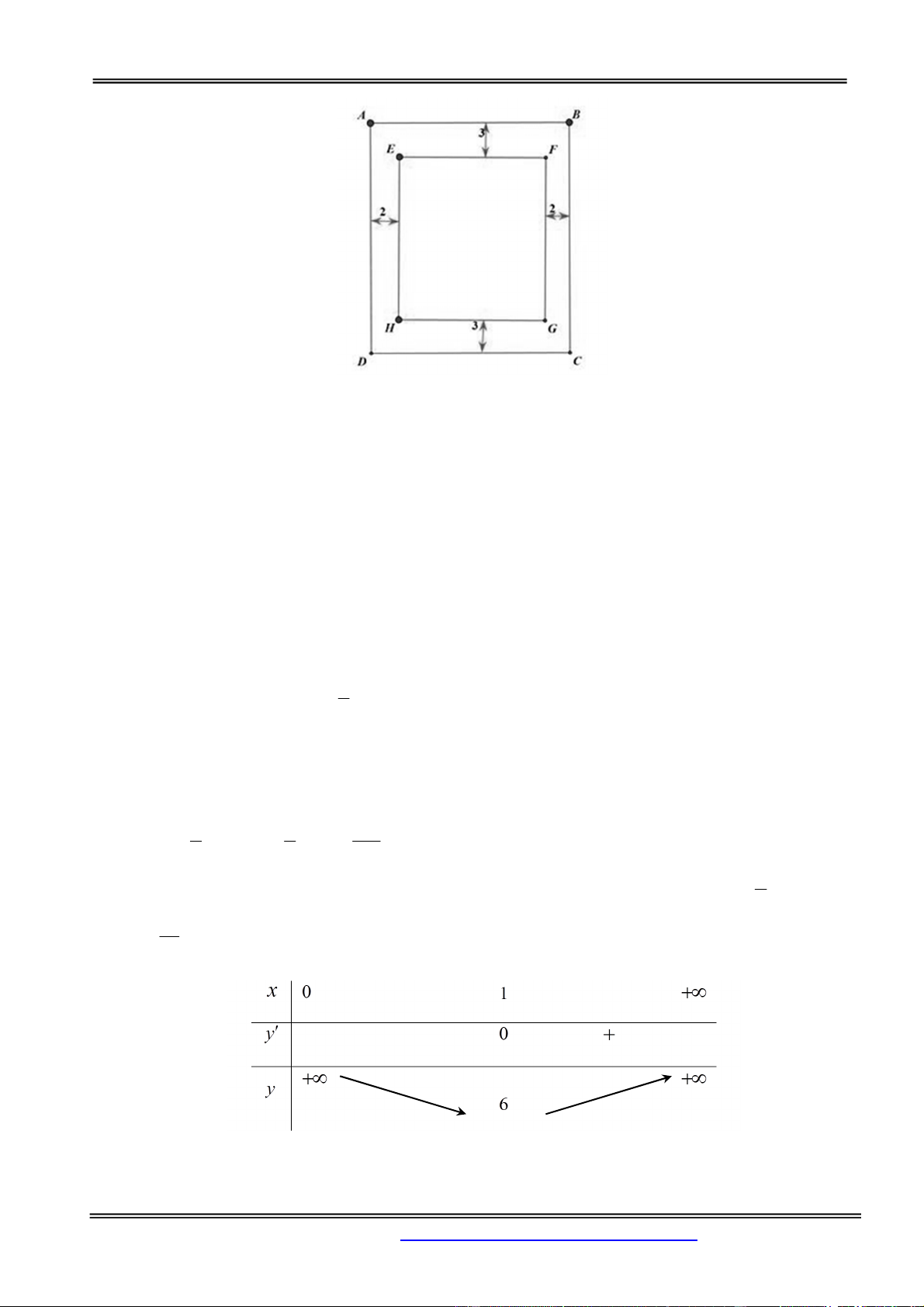
hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x cm , rồi gấp tấm nhôm lại như hình vẽ dưới
đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. x  2 . B. x  4 . C. x  6 .
D. x  3 . Hướng dẫn giải: Chọn đáp án C.
Khối hộp có đáy là hình vuông với độ dài cạnh là 18  2x và độ dài chiều cao là x nên có thể tích 3 2 1
1  4x 18  2x 18  2x
là V x 18  2x  .4 .
x 18  2x.18  2x   432   . 4 4  3 
Đẳng thức xảy ra khi và chỉ khi x  18  2x x  6 .
Vậy maxV  432  x  6 .
Câu 3: Cho một tấm nhôm hình vuông cạnh 24cm . Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông cạnh bằng nhau, mỗi hình vuông có cạnh bằng x (cm) rồi gập tấm nhôm lại như hình vẽ dưới
đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. x  6 . B. x  4 . C. x  2 . D. x  8 . Hướng dẫn giải: Chọn đáp án B.
Cạnh đáy của hộp là 24  2x .
Khi đó thể tích của hộp : V    x2 24 2
x f x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 34
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3
 24  2x  24  2x  4x
Có 4V  24  2x 24  2x 3 4x   16    3 
Dấu  xảy ra khi và chỉ khi 24  2x  4x x  4 .
Câu 4: Cho hình vẽ. .
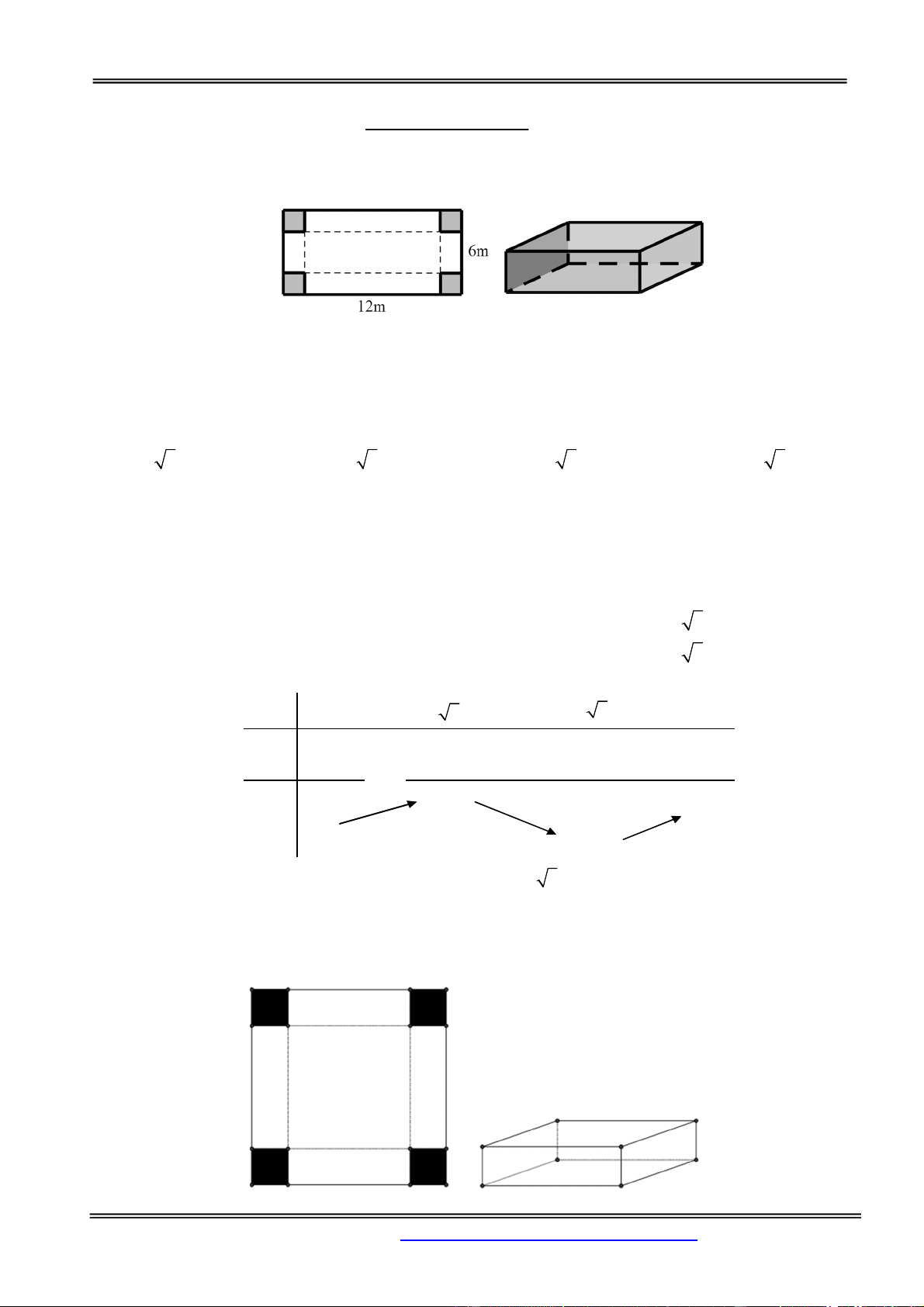
Bạn An có một tấm nhôm hình chữ nhật có chiều dài 12m , chiều rộng 6m . Bạn nhờ bác thợ hàn cắt ở
bốn góc bốn hình vuông bằng nhau và gập tấm nhôm lại (như hình trên) để được một cái hộp không nắp
dùng để đựng nước. Hỏi bác thợ hàn phải cắt cạnh hình vuông bằng bao nhiêu sao cho khối hộp chứa được nhiều nước nhất ? A. 24 3(m) . B. 3  3(m) . C. 3  3(m) . D. 24  3(m) . Hướng dẫn giải: Chọn đáp án B.
Gọi x là độ dài cạnh hình vuông bị cắt, khi đó ta có 0  x  6 .
Thể tích của khối hộp là V x  x12  2x6  2x  4x3  36x2  72x .
Ta cần tìm x sao cho V x lớn nhất với 0  x  6 .  x  3  3
Ta có V  x 2
12x  72x  72 , V x  0 2
 12x  72x  72  0   .  x  3  3  Bảng biến thiên. x 0 3  3 3  3 6 V   x   0  0  41, 57 V x  0 0 41, 57 .
Dựa vào bảng biên thiên ta có V x lớn nhất khi x  3  3 .
Câu 5: Cho một tấm nhôm hình vuông cạnh 18 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình
vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để
được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất. A. x  6 . B. x  3 . C. x  2 . D. x  4 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 35
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: Chọn đáp án B.
Theo đề bài ta có V h S x   x2 3 2 . . 18 2
 4x  72x  324 . x Xét f x 3 2
 4x  72x  324x liên tục trên 0;9.
Ta có f   x 2
 12x 144x  324. x  3
f  x  0  .  x  9  Bảng biến thiên x 0 3 9 f  x + 0  0 f x 432 0 0
Vậy thể tích lớn nhất khi x  3.
Câu 6: Một trang chữ của một quyển sách tham khảo Văn học cần diện tích 2
384 cm . Biết rằng trang giấy được canh lề trái là 2 cm , lề phải là 2 cm , lề trên
Trên không, vài con cò về tổ trễ đập nhanh
đôi cánh trắng phau rồi khuất trong lùm cây rậm 3 cm
lá. Những đám mây trắng đá ngả màu ngà, bầu
và lề dưới là 3 cm . Tìm chiều dài và chiều rộng của trang sách để trang sách
trời xanh cũng đã ngả sang màu sậm đưa đến
màu đen. Đâu đó có tiếng chim lẻ bạn, tiếng dơi
muỗi lào xào lẫn trong tiếng gió nhẹ lay cành.
có diện tích nhỏ nhất
Dưới bến sông, con nước ròng lên đầy mé đã
A. Chiều dài: 32 cm và chiều rộng: 12 cm .
đứng lại không lùa được những đợt lục bình lờ
lững giữa dòng ra sông cái. Dòng nước xanh chìm
đi trong màu xám sậm và những bóng cây bên bờ
B. Chiều dài: 24 cm và chiều rộng: 16 cm .
kia ngả xuống dòng càng lúc càng hiện rõ lù lù
thành hàng trong bóng nước.
C. Chiều dài: 40 cm và chiều rộng: 20 cm .
D. Chiều dài: 30 cm và chiều rộng: 20 cm . Hướng dẫn giải: Chọn đáp án B.
Gọi x , y là chiều dài và chiều rộng của trang chữ.
Theo đề bài ta có: xy  384 . Ta cần tìm x , y sao cho  x  4  y  6 đạt giá trị nhỏ nhất. 384
Ta có hàm f x  xy  6x  4 y  24  408  6x  4. x 1536  6x
 408  2 6.1536  408  192 x 1536
Dấu “=” xảy ra khi 6x
x  16 và y  24 x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 36
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 7: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày
xuất hiện bệnh nhân đầu tiên đến ngày thứ t là f t 2 3
 45t t (kết quả khảo sát được trong tháng 8
vừa qua). Nếu xem f t là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Hỏi tốc độ truyền bệnh sẽ
lớn nhất vào ngày thứ mấy? A. 12. B. 15. C. 20. D. 30. Hướng dẫn giải: Chọn đáp án B.
Ta có : f t  t  2 ' 90
3t .Cần tính giá trị lớn nhất của hàm số g t  f 't
Khi đó : g 't   f ' t   90  6t. g 't   0  t  15 .
Câu 8: [2D1-3]Khi xây nhà, chủ nhà cần làm một bồn nước bằng gạch và xi măng có dạng hình hộp
đứng đáy là hình chữ nhật có chiều rộng là x m, chiều dài gấp 2 lần chiều rộng và không nắp, có 4 3
chiều cao là h m , có thể tích là m . Tìm chiều rộng của đáy hình chữ nhật để chi phí xây dựng là 3 thấp nhất
A. x  1,5m.
B. x  2m.
C. x  1m.
D. x  2,5 m. Hướng dẫn giải: Chọn đáp án C. 4 4 2 Ta có 2 V   2x h   h  2 3 3 3x 4
Diện tích xung quang của bồn nước ( không nắp). S  2  xh  2xh 2 2 2
 2x  6xh  2x   2x x 4 S    4 ;
x S  0  x  1 2 x BBT –
Để chi phí xây dựng là thấp nhất thì S phải nhỏ nhất. Ta có MinS  6 khi x  1.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 37
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 9: Một chất điểm chuyển động theo phương trình 3 2 S  2
t 18t  2t 1, trong đó t tính bằng
giây  s và S tính bằng mét m . Thời gian vận tốc chất điểm đạt giá trị lớn nhất là
A. t  5s .
B. t  6s .
C. t  3s .
D. t  1s . Hướng dẫn giải: Chọn đáp án C.
Ta có v t   S t    t t    t  2 2 ' 6 36 2 6 3  56  56, t  .
Suy ra v t  lớn nhất bằng 56m / s khi t  3s .
Câu 10: Độ giảm huyết áp của một bệnh nhân được xác định bởi công thức G x 2
 0, 024x 30  x ,
trong đó x là liều lượng thuốc tiêm cho bệnh nhân cao huyết áp ( x được tính bằng mg). Tìm lượng
thuốc để tiêm cho bệnh nhân cao huyết áp để huyết áp giảm nhiều nhất A. 20 mg. B. 0, 5 mg. C. 2,8 mg. D. 15 mg. Hướng dẫn giải: Chọn đáp án A. x  0 L Gx  , 0 024 2
x 30  x  G'x  0 , 0 2  4 60x  3 2 x    
 0   x  20
Lập BBT  x  20mg là giá trị cần tìm.
Câu 11: Một công ty muốn làm đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn
đảo. Hòn đảo cách bờ biển 6 km . Giá để xây đường ống trên bờ là 50000 USD mỗi km , và
130000 USD mỗi km để xây dưới nước. B là điểm trên bờ biển sao cho BB vuông góc với bờ biển.
Khoảng cách từ A đến B là 9 km . Vị trí C trên đoạn AB sao cho khi nối ống theo ACB thì số tiền
ít nhất. Khi đó C cách A một đoạn bằng bao nhiêu ? A. 6, 5 km B. 6 km C. 0 km D. 9 km
Hướng dẫn giải:: Chọn đáp án A.
Theo hình vẽ, số tiền để xây dựng đường ống từ A đến B là: f x    x 2 50000. 9
 130000 36  x , 0  x  9 . x
f '  x  50000  130000. , f  x 2 5
 0  50000 36  x  130000x x  . 2 x  36 2  5 
f 0  1230000 , f  1170000  
, f 9  1170000 17 .  2   5 
 min f x  f   . 0;9  2 
Vậy C cách A 6, 5 km .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 38
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
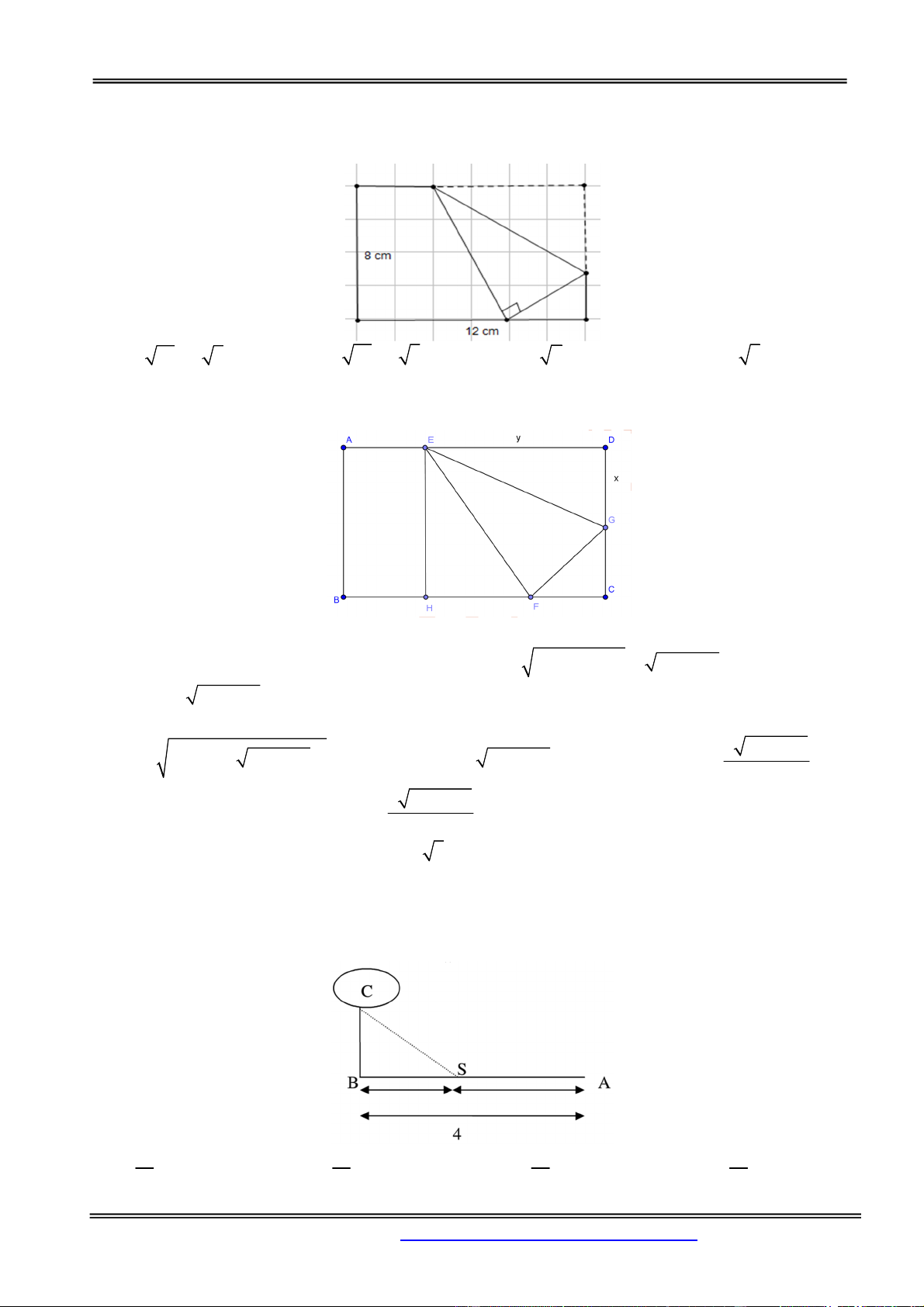
Câu 12: Cho một tờ giấy hình chữ nhật với chiều dài 12 cm và chiều rộng 8 cm. Gấp góc bên phải
của tờ giấy sao cho góc ở đỉnh của nó chạm với đáy như hình vẽ. Khi độ dài nếp gấp là nhỏ nhất thì giá
trị nhỏ nhất đó là bao nhiêu. A. 6 15  6 3 . B. 6 15  6 3 . C. 8 2 . D. 6 3 . Hướng dẫn giải: Chọn đáp án D.
Đặt DG FG x , ED HC EF y . Khi đó FC
x    x 2 2 8  16x  64 ,
HF y  16x  64 . Ta có: x
EF  8   y  16x  64 2 8 16 64 2 2 2
y  64  y  2 y 16x  64  16x  64  y y x 8 16x  64
Độ dài nếp gấp là f x  x y x  với 0  x  8 . x
Thay lần lượt các đáp án ta thấy với x  6 3 thì f (x) nhỏ nhất.
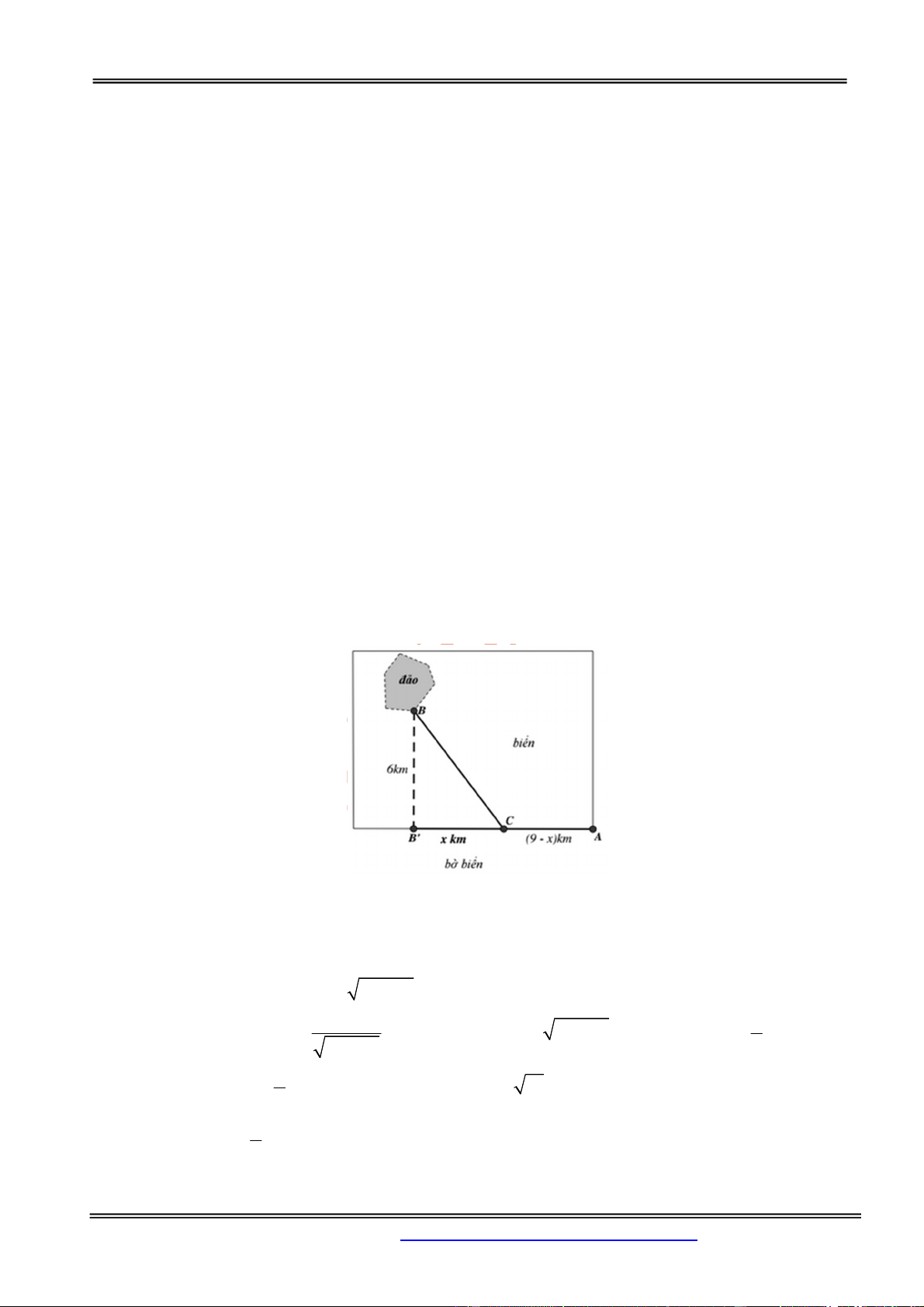
Câu 13: Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C khoảng cách
ngắn nhất từ C đến B là 1 km . Khoảng cách từ B đến A là 4 . Mỗi km dây điện đặt dưới nước là
mất 5000 USD , còn đặt dưới đất mất 3000 USD . Hỏi điểm S trên bờ cách A bao nhiêu để khi mắc
dây điện từ A qua S rồi đến C là ít tốn kém nhất? 15 13 10 19 A. km . B. km . C. km . D. km . 4 4 4 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 39
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: Chọn đáp án B.
Gọi x là khoảng cách từ A đến S ( 0  x  4 ), ta có BS  4  x , CS    x2 2 4 1 
x  8x 17 .
Chi phí cho đường dây diện là 2
y  3000x  5000 x  8x 17 .
Muốn ít tốn kém chi phí nhất ta cần tìm x để y . min Xét hàm số 2
y  3000x  5000 x  8x 17 với x 0, 4 . 2  x  
1000 3 x 8x 17  5x  20 5000 2 8 
Ta có y  3000   . 2 2 2 x  8x 17 x  8x 17 2
y  0  3 x  8x 17  20  5xx  4  19 x  4 x  4  x  loai        2 2 2 4
9x  72x 153  400  200x  25x
16x 128x  247  0     13   x  nhan   4  13 
Mà y 0  5000 17 , y 4  17000 , y  16000   .  4  13
Suy ra min y  16000 khi x  km . 0,4 4
Lập bảng xét dấu ta có x  2 2 thì khối chóp đạt giá trị lớn nhất.
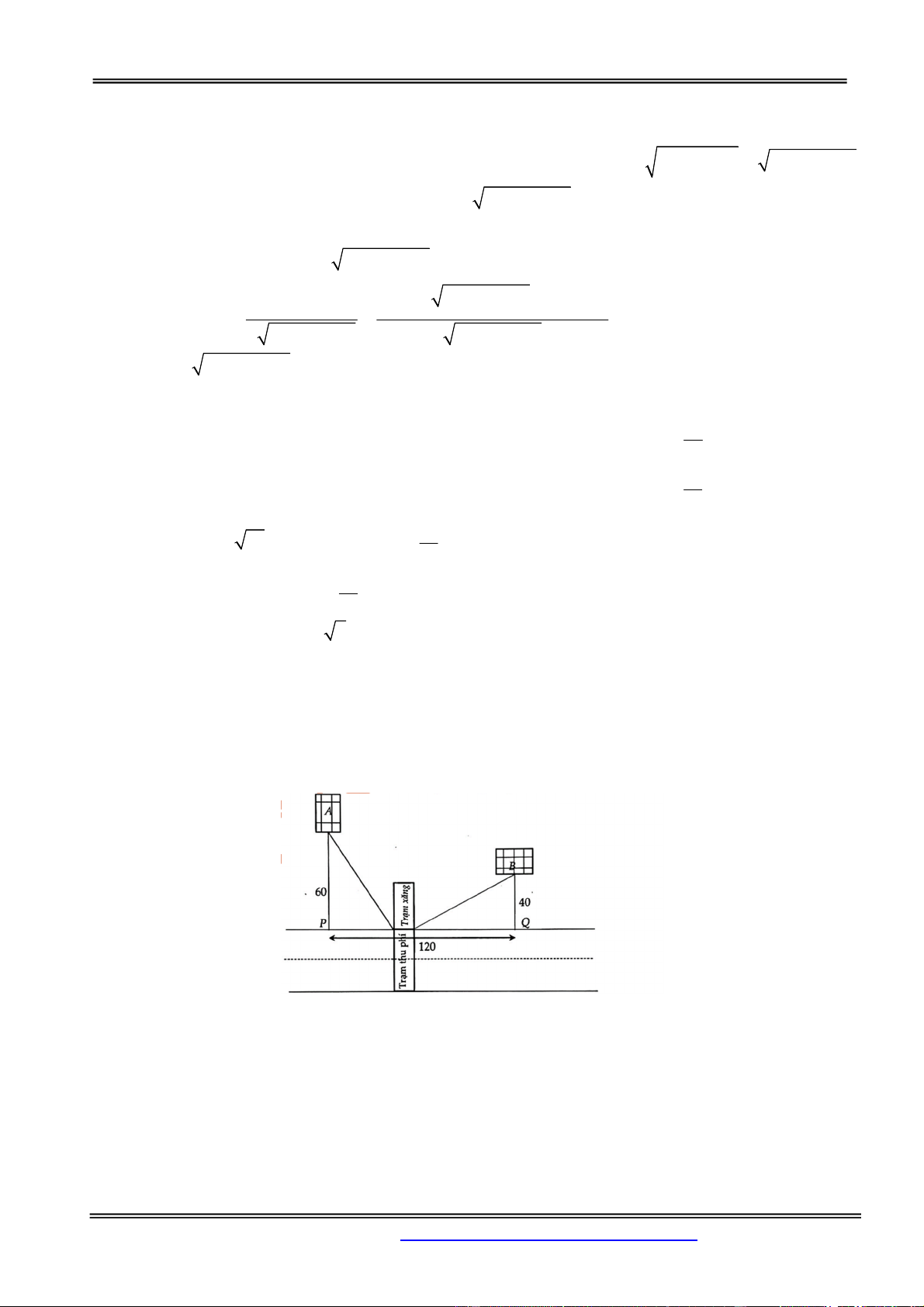
Câu 14: Đường cao tốc mới xây nối hai thành phố A và B, hai thành phố này muốn xây một trạm thu
phí và trạm xăng ở trên đường cao tốc như hình vẽ. Để tiết kiệm chi phí đi lại, hai thành phố này quyết
định toán xem xây trạm thu phí ở vị trí nào để tổng khoảng cách từ hai trung tâm thành phố đến trạm là
ngắn nhất, biết khoảng cách từ trung tâm thành phố A, B đến đường cao tốc lần lượt là 60km và 40km
và khoảng cách giữa hai trung tâm thành phố là 120km (được tính theo khoảng cách của hình chiếu
vuông góc của hai trung tâm thành phố lên đường cao tốc, tức là PQ kí hiệu như hình vẽ). Tìm vị trí
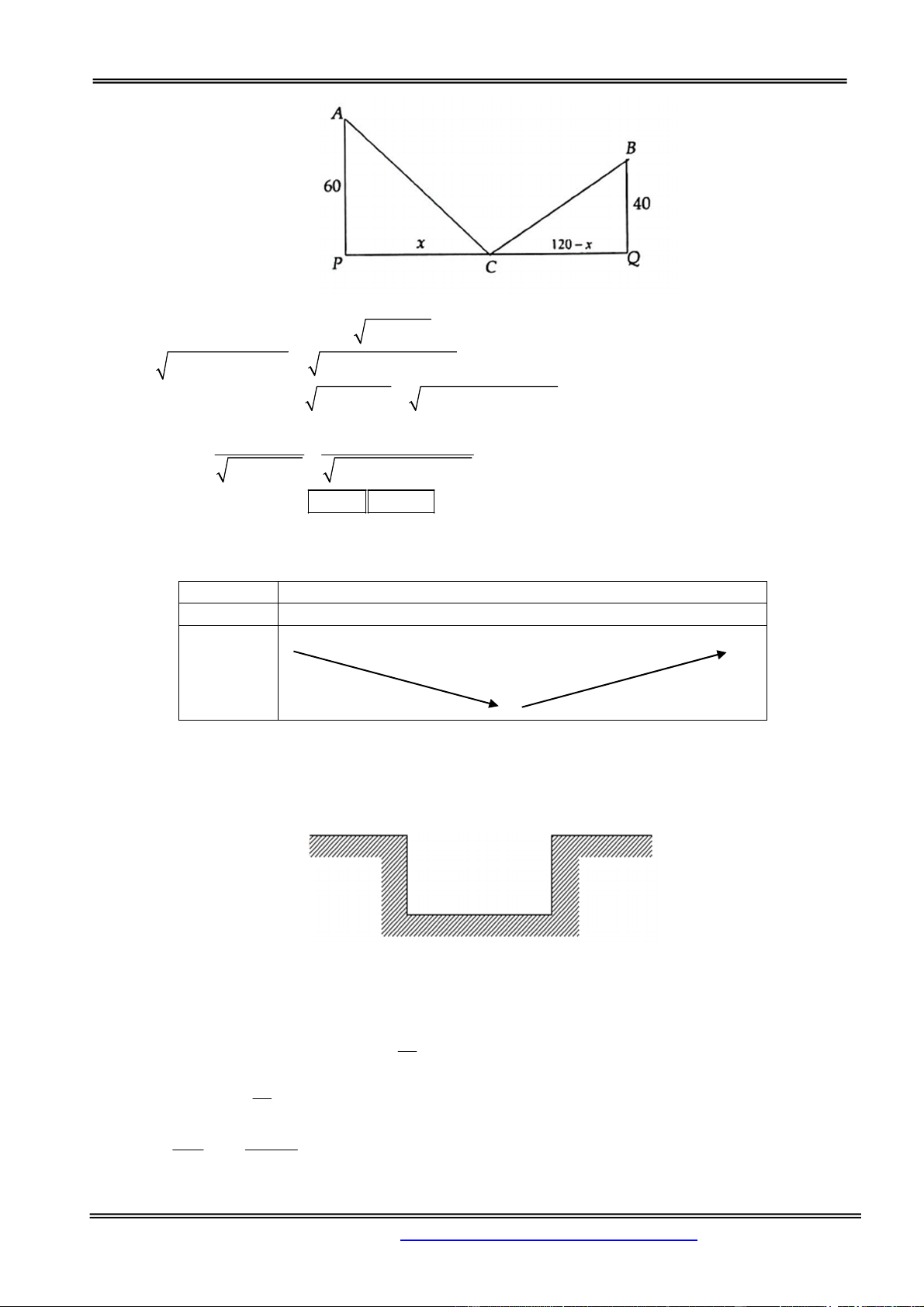
của trạm thu phí và trạm xăng? (Giả sử chiều rộng của trạm thu phí không đáng kể). A. 72km kể từ P B. 42km kể từ Q C. 48km kể từ P D. tại P Hướng dẫn giải: Chọn đáp án A.
Vẽ lại hình vẽ thì ta có hình vẽ đơn giản hóa như sau:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 40
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Thực chất bài toàn trở thành tìm x để AC+BC nhỏ nhất.
Theo định lý Pytago ta có 2 2 AC  60  x ; 2 2 2 BC  (120  x )  40  x  240x 16000 Khi đó 2 2 f (x)  AC  BC 
x  3600  x  240x 16000 . Ta cần tìm Min f (x) . (0;12) x x 120 Ta có f '(x)  
; khi bấm máy tính nhẩm bằng cách nhập vào màn 2 2 x  3600 x  240x 16000
hình biểu thức f’(x) và ấn SHIFT SLOVE và chọn một số nằm trong khoảng (0;120) để dò nghiệm,
như tôi nhập 2 máy nhanh chóng hiện nghiệm là 72.
Bấm máy tính sử dụng nút TABLE ta nhận thấy phương trình có duy nhất một nghiệm này do f’(x) chỉ
đổi dấu qua 72. Khi đó ta có BBT sau: x 0 72 120 f’(x) - 0 + f(x) Min
Vậy từ đó ta có thể kết luận CP=72.
Câu 15: Người ta cần xây dựng mương nước có dạng như hình vẽ, với diện tích tiết diện ngang của mương là 2
8m . Gọi l là độ dài đường biên giới hạn của tiết diện này. Để l đạt giá trị nhỏ nhất thì các
kích thước của mương là A. 4m và 1m. B. 2m và 1m. C. 4m và 2m. D. 3m và 2m. Hướng dẫn giải: Chọn đáp án C.
Gọi x, y lần lượt là chiều rộng và chiều cao của mương. 16 Theo bài ra ta có 8  .
x y , l  2 y x   x . x 16
Xét hàm số l x   x x 2 16 x 16 l ' x  1  2 2 x x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 41
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
x  4n
Cho l ' x  0   x  4  l   Lập bảng biến thiên
Ta được l đạt giá trị nhỏ nhất thì các kích thước của mương là x  4m, y  2m
Câu 16: Một người thợ xây cần xây một bể chứa 3
108m nước có dạng hình hộp chữ nhật với đáy là
hình vuông và không có nắp. Hỏi chiều dài cạnh đáy và chiều cao của lòng bể bằng bao nhiêu để số
viên gạch dùng xây bể là ít nhất? Biết thành bể và đáy bể đều được xây bằng gạch, độ dày của thành bể
và đáy là như nhau, các viên gạch có kích thước như nhau và số viên gạch trên một đơn vị diện tích là bằng nhau A. 3 3 108 ; m 108m . B. 6 ; m 3m .
C. 3m ;12m . D. 2 ; m 27m . Hướng dẫn giải: Chọn đáp án B.
Gọi x , h tương ứng là độ dài cạnh đáy và đường cao của hình hộp chữ nhật. 108 Ta có: 2 V  .
h x  108  h  . 2 x 432 216 216 2 2 2
S  4S S  4xh x   x    x . xq d x x x
Áp dụng bất đẳng thức AM – GM ta được 3 2 S  3 216 . 216 108
Dấu đẳng thức xảy ra khi 2
x x  6  h   3 . x 2 6
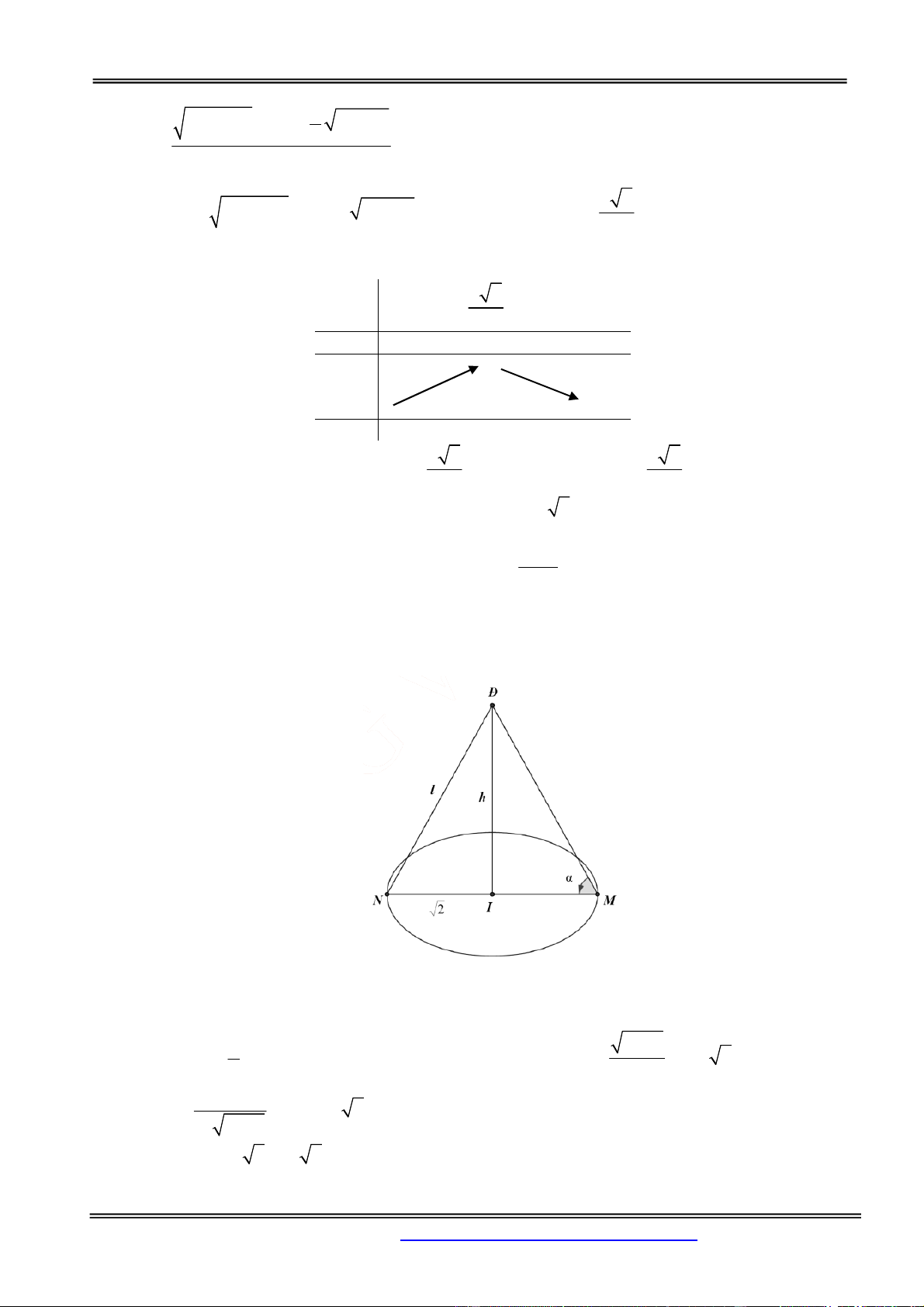
Câu 17: Cho một tấm gỗ hình vuông cạnh 200cm . Người ta cắt một tấm gỗ có hình một tam giác
vuông ABC từ tấm gỗ hình vuông đã cho như hình vẽ sau. Biết AB x 0  x  60cm là một cạnh
góc vuông của tam giác ABC và tổng độ dài cạnh góc vuông AB với cạnh huyền BC bằng 120cm .
Tìm x để tam giác ABC có diện tích lớn nhất.
A. x  40cm .
B. x  50cm .
C. x  30cm .
D. x  20cm . Hướng dẫn giải: Chọn đáp án A.
Ta có độ dài cạnh AC
BC AB    x2 2 2 2 120
x  14400  240x . 1 1
Diện tích tam giác ABC là: S A . B AC
x 14400  240x . 2 2
Xét hàm số f x  x 14400  240x với 0  x  60 . 120x 14400  360x
Ta có: f  x  14400  240x   ;. 14400  240x 14400  240x
f  x  0  x  400;60 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 42
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Bảng biến thiên: . Vậy Sf xx  40 . max  max
Câu 18: Cho một tấm bìa hình vuông cạnh 5 dm . Để làm một mô hình kim tự tháp Ai Cập, người ta
cắt bỏ bốn tam giác cân bằng nhau có cạnh đáy chính là cạnh của hình vuông rồi gấp lên, ghép lại
thành một hình chóp tứ giác đều. Để mô hình có thể tích lớn nhất thì cạnh đáy của mô hình là: 3 2 5 5 2 A. . B. . C. . D. 2 2 . 2 2 2 Hướng dẫn giải: A I B Chọn đáp án D.
Gọi x là chiêu dài cạnh đáy ( 0  x  5 2 ), ta có 2 2 M 5  x 2 25
25 10 2x  2x
25  5 2x x x 2 MI  , AM    2 4 4 2 2 2
25  5 2x x x 25  5 2x
Đường cao hình chóp là h    2 2 2 1 25  5 2x 1
Thể tích của khối chóp là 2 2 V xV   4 5 25x  5 2x  3 2 18 Xét hàm số 4 5
y  25x  5 2x trên khoảng 0;5 2  3 4 3
y  25.4x  25 2x  25x 4  2x  x  0
y  0  x  2 2  x 0 2 2 5 2 y  0  y 320
Suy ra max y  320 tại x  2 2 . Suy ra 0;5 2 Vx  2 2 . max
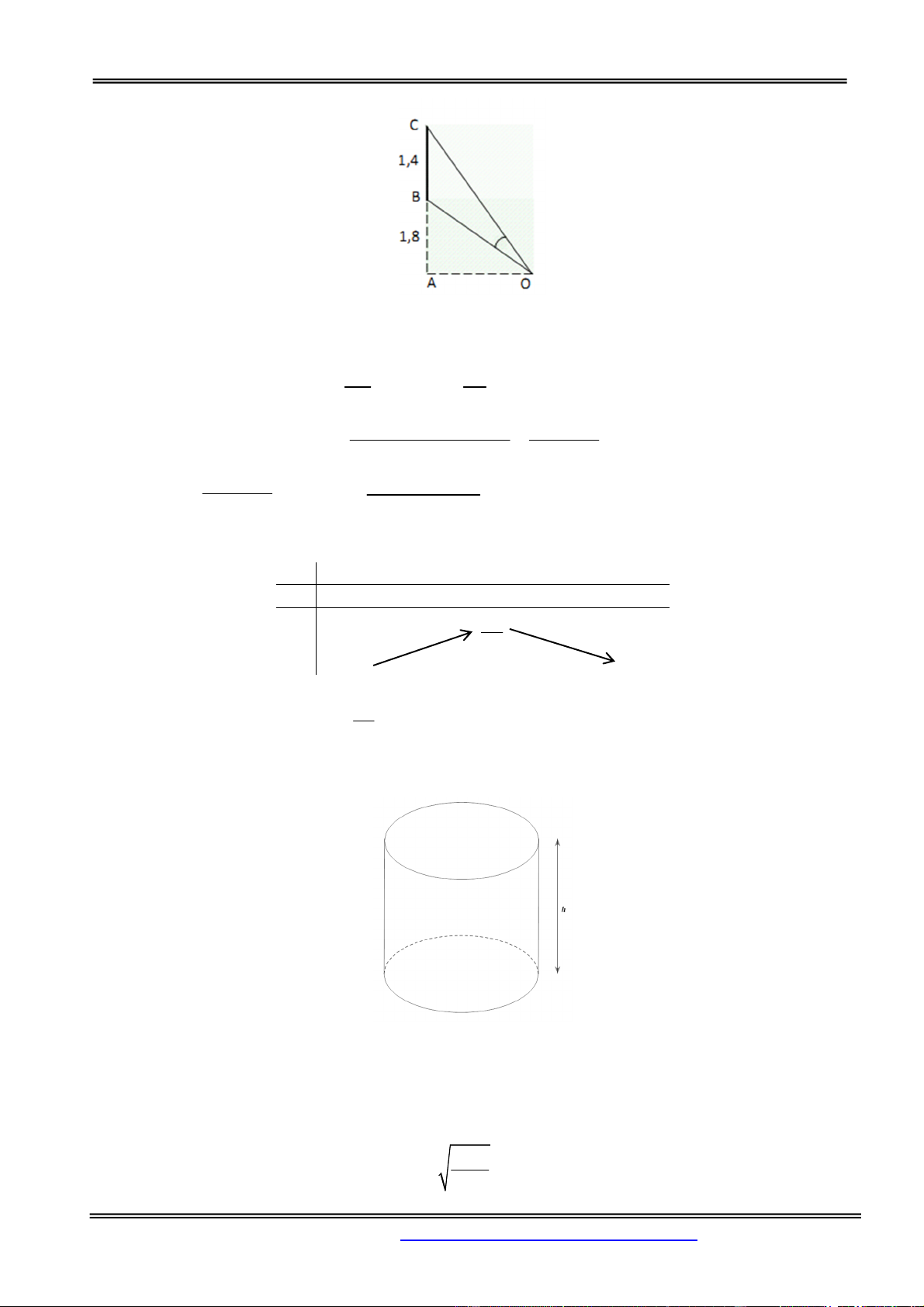
Câu 19: Một màn ảnh chữ nhật cao 1,4 mét được đặt ở độ cao 1,8 mét so với tầm mắt (tính từ đầu mép
dưới của màn hình). Để nhìn rõ nhất phải xác định vị trí đứng O sao cho góc nhìn lớn nhất. Hãy xác 
định vị trí điểm O ( BOC gọi là góc nhìn).
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 43
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
A. AO  2, 4m .
B. AO  2m .
C. AO  2, 6m .
D. AO  3m . Hướng dẫn giải: Chọn đáp án A. 3, 2 1,8 Đặ   t OA  .
x Ta có: tan AOC  , tan AOB  . x x       BOC
AOC AOB tan AOC tan AOB 1, 4x tan tan     . 2 1 tan AO . C tan AOB x  5, 76 1, 4x 2 1  , 4x  8, 064
Đặt f x 
f  x  . 2 x  5, 76 x  5,762 2 f  x 2
 0  x  5, 76  x  2, 4. x 0 2,4  y 0  0  y 7 24 0 0 7
Dựa vào BBT trên: max f x 
khi x  2, 4 m . 0; 24
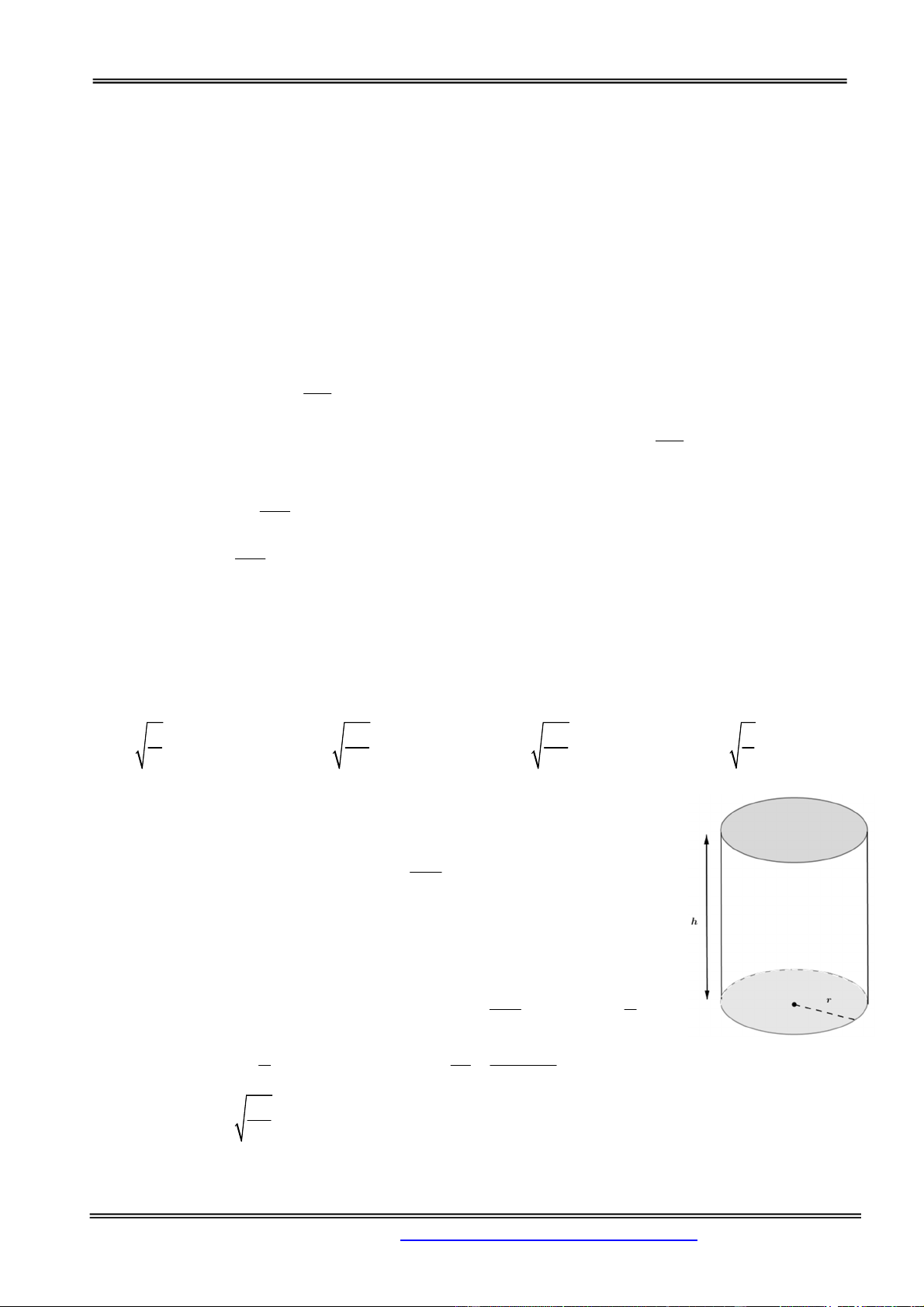
Câu 20: Muốn làm một bồn chứa 1000 lít hình trụ có nắp đậy, để ít tốn vật liệu nhất thì chiều cao
h dm của bồn phải gần nhất với giá trị nào sau đây? A. 10,84 . B. 10,83 . C. 10,85 . D. 10,86 . Hướng dẫn giải: Chọn đáp án A.
Để ít tốn vật liệu nhất thì diện tích toàn phần bồn nước phải nhỏ nhất. Tức là: 2
S  2 R  2 Rh nhỏ nhất. (với R là bán kính đường tròn đáy. tp 1000 Thể tích bồn nước 2
V  R h  1000  R  h
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 44
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1000 1000 2000 S  2.  2 .h   4000 h . tp  h  h h 2000 2000 4000 S    , 2 3 S  0 
4000 h  h h   10,84 . tp 2 h tp 4000 h
Sử dụng bảng biến thiên, ta tìm được S nhỏ nhất khi h  10,84 . tp
Câu 21: Khi nuôi cá trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của
mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng: P n  480  20n (gam). Hỏi
phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất. A. n  8. B. n  12. C. n  20. D. n  24. Hướng dẫn giải: Chọn đáp án B.
Cân nặng của n con cá là: 2 f ( ) n  .
n P(n)  480n  20n Ta có: 2 2 f ( )
n  480n  20n  2880  20(12  n)  2880
Vậy nhiều cá nhất khi n = 12
Câu 22: Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá
2 000 000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn
hộ thêm 50 000 đồng một tháng thì có thêm một căn hộ bị bỏ trống. Công ty đã tìm ra phương án cho
thuê đạt lợi nhuận lớn nhất. Hỏi thu nhập cao nhất công ty có thể đạt được trong một tháng là bao nhiêu? A. 115 250 000 . B. 101 250 000 . C. 100 000 000 . D. 100 250 000 . Hướng dẫn giải: Chọn đáp án B.
Gọi n là số lần tăng giá ( n là số tự nhiên). Khi đó số căn hộ bị bỏ trống cũng là n . Do đó số tiền
thu được khi cho thuê 50  n căn hộ là A  2.106  5.104.n50  n  5.104 n2  5.105 n 108 , điều kiện n  50 .
Xét hàm số f x  5.104 x2  5.105 x 108 , với 0  x  50 .
Ta có f   x  105 x  5.105 ; f  x  0  x  5 . max f
Lập bảng biến thiên, suy ra
x  f 5  101 250 000 . [ 0;50)
Vậy thu nhập cao nhất công ty có thể đạt được trong một tháng là 101 250 000 .
Câu 23: Doanh nghiệp Alibaba cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai
máy A và B. Máy A làm việc trong x ngày và cho số tiền lãi là x3  2x (triệu đồng), máy B làm việc
trong y ngày và cho số tiền lãi là 326 y  27 y2 (triệu đồng). Hỏi doanh nghiệp Alibaba cần sử dụng
máy A làm việc trong bao nhiêu ngày sao cho số tiền lãi là nhiều nhất? (Biết rằng hai máy A và B
không đồng thời làm việc, máy B làm việc không quá 6 ngày) A. 6 . B. 5 . C. 4 . D. 7 . Hướng dẫn giải: Chọn đáp án A.
Ta có x y  10  y  10  x (1)
Và 0  y  6  4  x  10 .
Số tiền lãi f x 3 2 3
x  2x  326y  27 y x  2x  326 10  x  2710  x2 (thay (1) vào).  f x 3 2
x  27x  216x  560 với x 4;10 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 45
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Ta có f   x 2
 3x  54x  216 . f   x 2
 0  3x  54x  216  0  x  6  x  12 .
Chỉ có x  6 4;10 . Vậy máy A làm việc trong 6 ngày.
Câu 24: Một người thợ xây cần xây một bể chứa 108 3
m nước có dạng hình hộp chữ nhật với đáy là
hình vuông và không có nắp. Hỏi chiều cao của lòng bể bằng bao nhiêu để số viên gạch dùng xây bể là
ít nhất. Biết thành bể và đáy bể đều được xây bằng gạch, độ dày thành bể và đáy bể là như nhau, các
viên gạch có kích thước như nhau và số viên gạch trên một đơn vị diện tích là bằng nhau. A. 9 m B. 3 m . C. 2 m . D. 6 m . . Hướng dẫn giải: Chọn đáp án B.
Gọi độ dài cạnh đáy bằng x m , chiều cao bằng h m  x  0;h  0 . 108 Khi đó 2 .
h x  108  h  . 2 x 108
Tổng diện tích xung quanh và diện tích phần đáy bể là 2 S  4. . x h x 2  4.  x x
Để số gạch dùng xây bể là ít nhất thì S nhỏ nhất. 432
Xét hàm số f x 2 
x trên khoảng 0;  x 432
Ta có f ' x  
 2x ; f ' x  0  x  6 2 x
Lập bảng biến thiên và suy ra S nhỏ nhất khi x  6 . Khi đó h  3 .
Câu 25: Ông An dự định làm một cái bể chứa nước hình trụ bằng inốc có nắp đậy với thể tích là k m3
( k  0 ). Chi phí mỗi m2 đáy là 600 nghìn đồng, mỗi m2 nắp là 200 nghìn đồng và mỗi m2 mặt bên
là 400 nghìn đồng. Hỏi ông An cần chọn bán kính đáy của bể là bao nhiêu để chi phí làm bể là ít
nhất? (Biết bề dày vỏ inốc không đáng kể) k 2 k k A. 3 . B. 3 . C. 3 . D. 3 . k 2 2 Hướng dẫn giải: Chọn đáp án C.
Gọi r, h r  0, h  0 lần lượt là bán kính đáy và chiều cao của hình trụ. k + Thể tích khối trụ 2
V  r h k h  . 2  r
+ Diện tích đáy và nắp là 2
Sđ Sn  r ; diện tích xung quanh là S  2 r . xq h
+ Khi đó chi phí làm bể là kk C  600  200 2 2 2
 r  400.2 rh  800 r  800 r  800  r  2    rr  3 k k 2 r k + Đặt 2
f (r)   r
, r  0  f (
r)  2 r   ; 2 2 r r r k 3 f (
r)  0  r  , (k  0) . 2 + Bảng biến thiên:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 46
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 k r 3  0 2 f (  r)  0  f (r) min f (r) (0;)
Vậy: Chi phí làm bể ít nhất  f (r) đạt giá trị k nhỏ nhất 3  r  . 2
Câu 26: Doanh nghiệp Alibaba cần sản xuất một mặt hàng trong đúng 10 ngày và phải sử dụng hai
máy A và B. Máy A làm việc trong x ngày và cho số tiền lãi là x3  2x (triệu đồng), máy B làm việc
trong y ngày và cho số tiền lãi là 326 y  27 y2 (triệu đồng). Hỏi doanh nghiệp Alibaba cần sử dụng
máy A làm việc trong bao nhiêu ngày sao cho số tiền lãi là nhiều nhất? (Biết rằng hai máy A và B
không đồng thời làm việc, máy B làm việc không quá 6 ngày) A. 6 . B. 5 . C. 4 . D. 7 . Hướng dẫn giải: Chọn đáp án A.
Ta có x y  10  y  10  x (1)
Và 0  y  6  4  x  10 .
Số tiền lãi f x  x3  2x  326y  27 y2  x3  2x  32610  x  27 10  x2 (thay (1) vào).
f x  x3  27x2  216x  560 với x 4;10 .
Ta có f   x  3x2  54x  216 . f   x  0  3x2  54x  216  0  x  6  x  12 .
Chỉ có x  6 4;10 . Vậy máy A làm việc trong 6 ngày.
Câu 27: Một con cá hồi bơi ngược dòng để vượt một khoảng cách là 400km . Vận tốc dòng nước là
10km/h . Nếu vận tốc bơi của cá khi nước đứng yên là v (km/h) thì năng lượng tiêu hao của cá trong
t giờ được cho bởi công thức E(v)  cv3t , trong đó c là hằng số, E được tính bằng jun. Tìm vận tốc
của cá khi nước đứng yên để năng lượng tiêu hao là ít nhất. A. 12 (km/h) . B. 15 (km/h) . C. 18 (km/h) . D. 20 (km/h) . Hướng dẫn giải: Chọn đáp án B. 400
Ta có vận tốc cá bơi ngược dòng là v 10km/h , thời gian cá bơi hết 400km là t  . v 10 400 400
Năng lượng tiêu hao của cá trong t
(giờ) được cho bởi công thức 3
E(v)  cv . với v 10 v 10 v  10 . v 15 v  0
Ta có E v 2  800 . c v , Ev 2  0  800 .
c v v 15  0   . v 102 v  15  Bảng biến thiên.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 47
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 v 1 0 1 5   E  v   0      E v E 1 5  .
Dựa vào bảng biến thiên vận tốc của cá khi nước đứng yên để năng lượng tiêu hao ít nhất là 15 km/h.
Câu 28: Từ một khúc gỗ tròn hình trụ có đường kính bằng 40 cm , cần xả thành một chiếc xà có tiết
diện ngang là hình vuông và bốn miếng phụ được tô màu xám như hình vẽ
dưới đây. Tìm chiều rộng x của miếng phụ để diện tích sử dụng theo tiết
diện ngang là lớn nhất. 3 34 17 2 3 34 19 2 A. x  cm . B. x  cm . 2 2 5 34 15 2 5 34 13 2 C. x  cm . D. x  cm . 2 2 Hướng dẫn giải: Chọn đáp án C.
Gọi x, y lần lượt là chiều rộng và dài của miếng phụ.
Diện tích sử dụng theo tiết diện ngang là S S  4xy . MNPQ MP 40
Cạnh hình vuông MN    20 2 cm . 2 2  S   2 20 2
 4xy  800  4xy (1).
Ta có 2x AB MN AB  20 2  BD  20 2  40  20 2 .
 0  x  20 10 2 .
Lại có AB AD BD    x  2 2 2 2 2 2 40 2 20 2  y  1600 . 2 2 2
y  800  80x 2  4x y  800  80x 2  4x . Thế vào   2 2 3 4
1  S  800  4x 800  80 x 2  4x  800  4 800x  80 x 2  4x .
Xét hàm số f x 2 3 4  800x  80x
2  4x , với x  0; 20 10 2  có. f  x  2 3  x xx x  2 1600 240 2 16 16
100 15x 2  x  .       x x   0;2010 2 0; 20 10 2  5 34 15 2 Ta có     x  .
f  x   x   2  xx  2 0 16 100 15 2  0  5 34 15 2 Khi đó x
chính là giá trị thỏa mãn bài toán. 2
Câu 29: Một đoàn tàu chuyển động thẳng khởi hành từ một nhà ga. Quãng đường s mét  đi được của
đoàn tàu là một hàm số của thời gian t phút  , hàm số đó là 2 3
s  6t – t . Thời điểm t giây mà tại
đó vận tốc v m / s của chuyển động đạt giá trị lớn nhất là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 48
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
A. t  4s .
B. t  2s .
C. t  6s .
D. t  8s . Hướng dẫn giải: Chọn đáp án B. Ta có: 2 3 2
s  6t – t v(t)  12t  3t .
v '(t)  12 6t v '(t)  0  t  2.
Bảng biến thiên của v(t) là: t 0 2  v '(t) + 0 - 12 v(t)
Vậy: Thời điểm 2  giây thì vận tốc v m / s của chuyển động đạt giá trị lớn nhất.
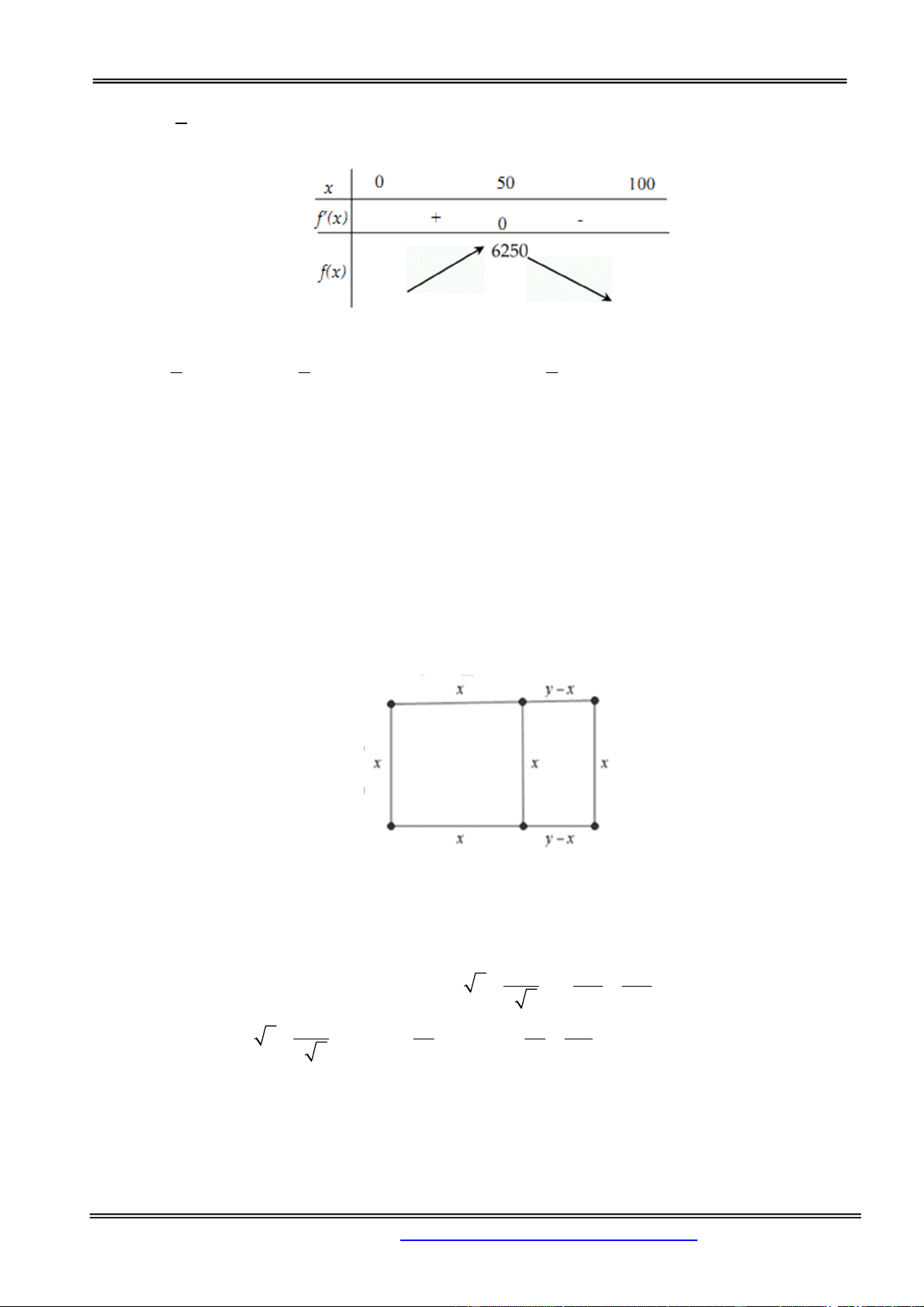
Câu 30: Một người nông dân có 15 000 000 đồng để làm một cái hàng rào hình chữ E dọc theo một
con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào
song song với bờ sông thì chi phí nguyên vật liệu là 60 000 đồng là một mét, còn đối với ba mặt hàng
rào song song nhau thì chi phí nguyên vật liệu là 50 000 đồng một mét. Tìm diện tích lớn nhất của đất rào thu được. A. 6250 2 m B. 1250 2 m C. 3125 2 m . D. 50 2 m Hướng dẫn giải: Chọn đáp án A.
Phân tích ta đặt các kích thước của hàng rào như hình vẽ
Từ đề bài ban đầu ta có được mối quan hệ sau:
Do bác nông dân trả 15 000 000 đồng để chi trả cho nguyên vật liệu và đã biết giá thành từng mặt nên ta có mối quan hệ: 3 . x 50000  2 . y 60000  15000000 150 15x 500  5x
 15x 12 y  1500  y   12 4
Diện tích của khu vườn sau khi đã rào được tính bằng công thức: 500  5x 1
f x  2. . x y  2 . x   2
5x  500x  4 2
Đến đây ta có hai cách để tìm giá trị lớn nhất của diện tích:
Cách 1: Xét hàm số trên một khoảng, vẽ BBT và kết luận GTLN: 1
Xét hàm số f x   2 5
x  500x trên 0;100 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 49
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1
f ' x   1
 0x  500, f ' x  0  x  50 2 Ta có BBT
Cách 2: Nhẩm nhanh như sau: Ta biết rằng 2
A g x  A với mọi x, nên ta có thể nhẩm nhanh được: 5 5 5
f x   2
x 100x   2
x  2.50.x  2500  2500  .2500   x  52   6250 2 2 2  
Hoặc bấm máy tính phần giải phương trình bậc hai và ấn bằng nhiều lần máy sẽ hiện như sau:
Câu 31: Kỳ thi THPT Quốc gia năm 2016 vừa kết thúc, Nam đỗ vào trường Đại học Bách Khoa Hà
Nội. Kỳ I của năm nhất gần qua, kỳ II sắp đến. Hoàn cảnh không được tốt nên gia đình rất lo lắng về
việc đóng học phí cho Nam, kỳ I đã khó khăn, kỳ II càng khó khăn hơn. Gia đình đã quyết định bán
một phần mảnh đất hình chữ nhật có chu vi 50 m, lấy tiền lo cho việc học của Nam cũng như tương lai
của em. Mảnh đất còn lại sau khi bán là một hình vuông cạnh bằng chiều rộng của mảnh đất hình chữ
nhật ban đầu. Tìm số tiền lớn nhất mà gia đình Nam nhận được khi bán đất, biết giá tiền 1m2 đất khi bán là 1500000 VN đồng.
A. 112687500 VN đồng.
B. 114187500 VN đồng.
C. 115687500 VN đồng.
D. 117187500 VN đồng. Hướng dẫn giải: Chọn đáp án D.
Diện tích đất bán ra càng lớn thì số tiền bán được càng cao
Gọi chiều rộng và chiều dài của mảnh đất hình chữ nhật ban đầu lần lượt là x, y m, x, y  0
Chu vi mảnh đất hình chữ nhật ban đầu bằng 50m  2  x y  50  y  25  x
Bài ra, ta có ngay mảnh đất được bán là một hình chữ nhật có diện tích là 2  25  625 625
S x y x  x 25  x x 2
 25x  2x   x 2     78,125    2 2  8 8 25 25 25 175
Dấu "=" xả ra  x 2   0  x   y  25   2 2 8 8 8
Như vậy, diện tích đất nước được bán ra lớn nhất 78,125 m2.
Khi đó số tiền lớn nhất mà gia đình Nam nhận được khi bán đất là 78,125.1500000  117187500
Câu 32: Chiều dài bé nhất của cái thang AB để nó có thể tựa vào tường AC và mặt đất BC, ngang qua
cột đỡ DH cao 4m, song song và cách tường CH=0,5m là:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 50
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. Xấp xỉ 5,602 B. Xấp xỉ 6,5902 C. Xấp xỉ 5,4902 D. Xấp xỉ 5,5902 Hướng dẫn giải: Chọn đáp án D.
Đặt BH x x  0 . Ta có 2 2 2 BD DH BH x 16 Vì DH / / AC nên 2 DA HC D . B HC x 16   DA   DB HB HB 2x 2 x 16 2  AB x 16  2x 2 x 16
Xét hàm số f x 2  x 16 
trên 0; . Ta có f(x) 2x
liên tục trên 0; và x 2
.2x  2 x 16 3 2 x x 16 x 8 x  8 f ' x      2 2 2 2 2 2 2 4 16 x x x 16 x x 16 x x 16
f ' x  0  x  2; f ' x  0  x  2; f ' x  0  0  x  2 5 5
Suy ra min AB  min f x  f 2   5, 5902mx   0; 2
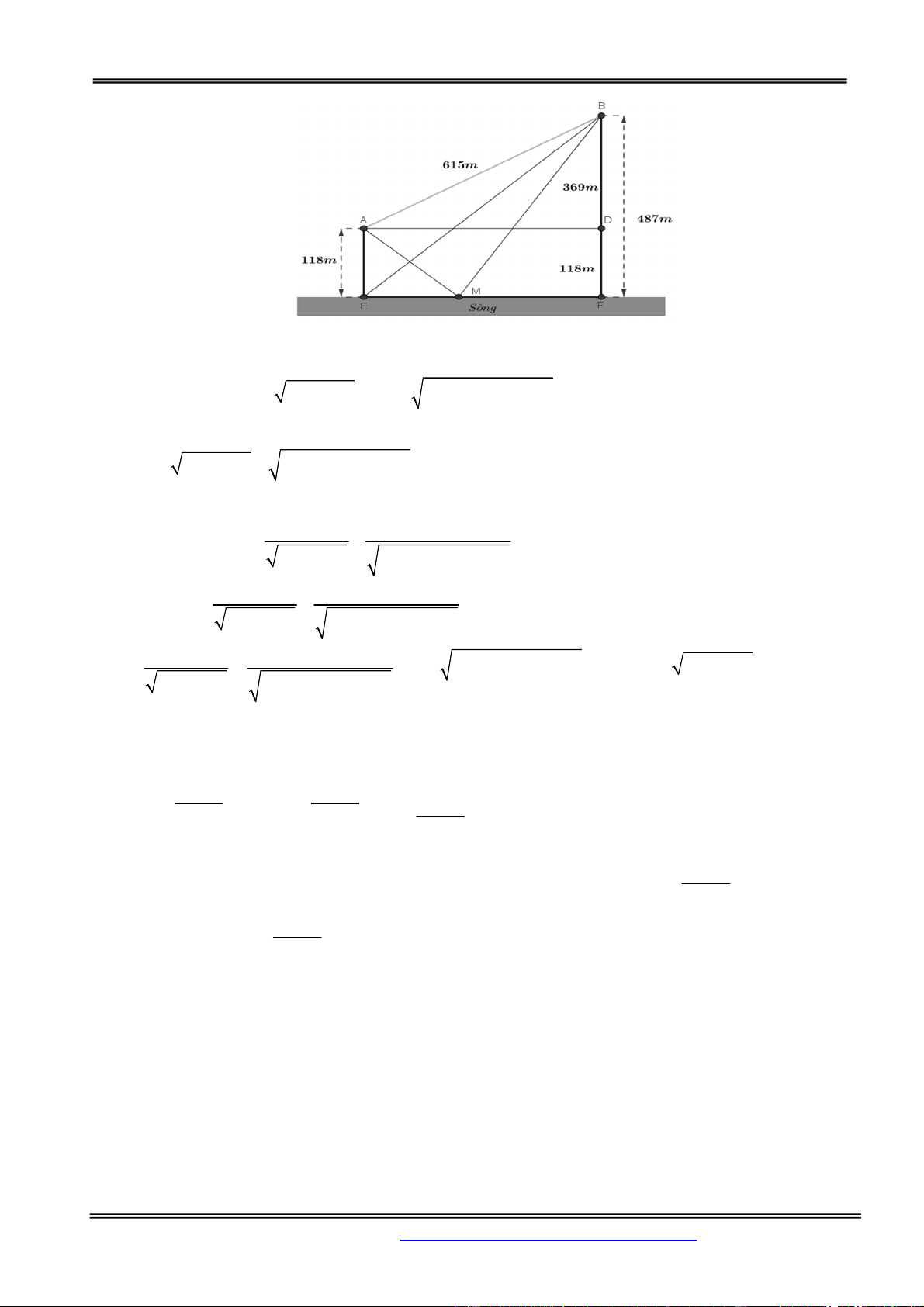
Câu 33: Cho hai vị trí A , B cách nhau 615m , cùng nằm về một phía bờ sông như hình vẽ. Khoảng
cách từ A và từ B đến bờ sông lần lượt là 118m và 487m Một người đi từ A đến bờ sông để lấy
nước mang về B . Đoạn đường ngắn nhất mà người đó có thể đi là: A. 596, 5m B. 671, 4m C. 779, 8m D. 741,2m Hướng dẫn giải: Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 51
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Giả sử người đó đi từ A đến M để lấy nước và đi từ M về B.
dễ dàng tính được BD  369, EF  492. Ta đặt EM x, khi đó ta được: MF   x AM x BM    x2 2 2 2 492 , 118 , 492  487 .
Như vậy ta có hàm số f x được xác định bằng tổng quãng đường AM và MB:
f x  x     x2 2 2 2 118 492
 487 với x 0; 492
Ta cần tìm giá trị nhỏ nhất của f x để có được quãng đường ngắn nhất và từ đó xác định được vị x 492  x
trí điểm M. f ' x   . 2 2 x 118 492  x2 2  487 x 492  x
f ' x  0    0 2 2 x 118 492  x2 2  487 x 492  x 2    x   x 2     x 2 2 492 487 492 x 118 2 2 x 118 492  x2 2  487   2 2 xx2       x2 2 2  2 2 492 487 492 x 118    
487x  58056 118x     0  x  492  0  x  492   58056 58056 x hay x   58056   605 369  x  605 0  x  492   58056 
Hàm số f x liên tục trên đoạn 0; 492 . So sánh các giá trị của f (0) , f
 , f 492 ta có  605   58056 
giá trị nhỏ nhất là f  779,8   m  605 
Khi đó quãng đường đi ngắn nhất là xấp xỉ 779,8m.
Câu 34: Một công ty bất động sản có 50 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá
2.000.000 đồng một tháng thì mọi căn hộ đều có người thuê và cứ tăng thêm giá cho thuê mỗi căn hộ
100.000 đồng một tháng thì sẽ có 2 căn hộ bị bỏ trống. Hỏi muốn có thu nhập cao nhất thì công ty đó
phải cho thuê mỗi căn hộ với giá bao nhiêu một tháng. A. 2.225.000. B. 2.100.000 C. 2.200.000 D. 2.250.000 Hướng dẫn giải: Chọn đáp án D.
Gọi x (đồng/tháng) là số tiền tăng thêm của giá cho thuê mỗi căn hộ. ( x  0 )
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 52
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2x
Khi đó số căn hộ bị bỏ trống là: (căn hộ). 100 000
Khi đó, số tiền công ti thu được là:     2 x      2 x  2x T x 2 000 000 5  0  
  100 000 000  10x  (đồng/tháng).  100 000   100 000
Khảo sát hàm số T x  trên 0;  .  4x
T 'x  10  . 100 000
T 'x  0  1000 000  4x  0  x  250 000. Bảng biến thiên x 0 250 000  T’  0  T 2 250 000
Do đó maxT x   T 250 00  0 x 0  = 2.250.000 .
Câu 35: Một cửa hàng bán lẻ bán 2500 cái ti vi mỗi năm. Chi phí gửi trong kho là 10$ một cái mỗi
năm. Để đặt hàng chi phí cố định cho mỗi lần đặt là 20$ cộng thêm 9$ mỗi cái. Cửa hàng nên đặt hàng
bao nhiêu lần trong mỗi năm và mỗi lần bao nhiêu cái để chi phí hàng tồn kho là nhỏ nhất ?
A. Đặt hàng 25 lần, mỗi lần 100 cái ti vi.
B. Đặt hàng 20 lần, mỗi lần 100 cái ti vi.
C. Đặt hàng 25 lần, mỗi lần 90 cái ti vi.
D. Đặt hàng 20 lần, mỗi lần 90 cái ti vi. Hướng dẫn giải: Chọn đáp án A.
Gọi x là số ti vi mà cừa hàng đặt mỗi lần ( x 1;2500 , đơn vị cái) x x
Số lượng ti vi trung bình gửi trong kho là
nên chi phí lưu kho tương ứng là 10.  5x 2 2 2500 2500
Số lần đặt hàng mỗi năm là
và chi phí đặt hàng là: 20  9x x x 2500 50000
Khi đó chi phí mà cửa hàng phải trả là: C  x 
20  9x  5x  5x   22500 x x
Lập bảng biến thiên ta được: C  C 100  23500 min  
Kết luận: đặt hàng 25 lần, mỗi lần 100 cái tivi.
Câu 36: Có một tấm gỗ hình vuông cạnh 200 cm. Cắt một tấm gỗ có hình tam giác vuông, có tổng của
một cạnh góc vuông và cạnh huyền bằng hằng số 120cm từ tấm gỗ trên sao cho tấm gỗ hình tam giác
vuông có diện tích lớn nhất. Hỏi cạnh huyền của tấm gỗ này là bao nhiêu?
A. 40cm .
B. 40 3cm .
C. 80cm .
D. 40 2cm . Hướng dẫn giải: Chọn đáp án C.
Kí hiệu cạnh góc vuông AB x,0  x  60
Khi đó cạnh huyền BC  120  x , cạnh góc vuông kia là 2 2 2 AC
BC AB  120  240x
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 53
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1
Diện tích tam giác ABC là: S x 2  .
x 120  240x . Ta tìm giá trị lớn nhất của hàm số này trên 2 khoảng 0;60 1 1 240 14400  360x
Ta có S, x 2  120  240x  . x
S ' x  0  x  40 2 2 2 2 2 120  240x 2 120  240x Lập bảng biến thiên:
Lập bảng biến thiên ta có: x 0 40 60 S'  x   0  S 40 S x
Tam giác ABC có diện tích lớn nhất khi BC  80
Câu 37: Tìm diện tích lớn nhất của hình chữ nhật nội tiếp trong nửa đường tròn bán kính 10cm , biết
một cạnh của hình chữ nhật nằm dọc trên đường kính của đường tròn. A. 2 80cm B. 2 100cm C. 2 160cm D. 2 200cm Hướng dẫn giải: Chọn đáp án B.
Gọi x (cm) là độ dài cạnh hình chữ nhật không nằm dọc theo đường kính đường tròn 0  x 10.
Khi đó độ dài cạnh hình chữ nhật nằm dọc trên đường tròn là: 2 2
2 10  x cm.
Diện tích hình chữ nhật: 2 2
S  2x 10  x 2 2x Ta có 2 2 2 2
S   2 10  x   2.10  4x 2 2 10  x  x  10 2  tho  ûa S    2 0  x 10 2  khoâng tho  ûa  2 1  0 2  10 2
S   8x S    40 2  0   . Suy ra x
là điểm cực đại của hàm S x .  2  2 2 10
Vậy diện tích lớn nhất của hình chữ nhật là: 2 S  10 2. 10   100  2 cm  2
Câu 38: Trong bài thực hành của môn huấn luyện quân sự có tình huống chiến sĩ phải bơi qua một con
sông để tấn công một mục tiêu ở phía bờ bên kia sông. Biết rằng lòng sông rộng 100m và vận tốc bơi
của chiến sĩ bằng một nửa vận tốc chạy trên bộ. Bạn hãy cho biết chiến sĩ phải bơi bao nhiêu mét để
đến được mục tiêu nhanh nhất, nếu như dòng sông là thẳng, mục tiêu ở cách chiến sĩ 1km theo đường chim bay. 400 40 100 200 A. B. C. D. 3 33 3 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 54
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 l m Hướng dẫn giải: Chọn đáp án A.
Vấn đề là chọn thời gian bơi và thời gian đi bộ sao cho “tối ưu”. Giả sử độ dài đoạn bơi là l và tốc
độ bơi của chiến sĩ là v . Ký hiệu m là độ dài đoạn sông kể từ người chiến sĩ đến đồn địch, khi ấy 2 2 l m l 100
tổng thời gian bơi và chạy bộ của người chiến sĩ là t   . v 2v 2 2 2 2 l l 100 2l l 100
Do m, v là cố định nên thời gian đạt cực tiểu khi hàm số f (l)    v 2v 2v
đạt cực tiểu, và cũng tức là khi hàm 2 2
g(l)  2l l 100 đạt cực tiểu. Điều này xảy ra khi l 2   0 , hay 2
l  2 l 100 , tức là l  400 / 3  133, 333333 (met). 2 2 l 100
Câu 39: Cần phải đặt một ngọn điện ở phía trên và chính giữa một cái bàn hình tròn có bán kính a. Hỏi
phải treo ở độ cao bao nhiêu để mép bàn được nhiều ánh sáng nhất. Biết rằng cường độ sáng C được sin 
biểu thị bởi công thức C  k
(  là góc nghiêng giữa tia sáng và mép bàn, k là hằng số tỷ lệ chỉ 2 r
phụ thuộc vào nguồn sáng). 3a a 2 a a 3 A. h  B. h  C. h  D. h  2 2 2 2 Hướng dẫn giải: Chọn đáp án B. Ta có: 2 2
r  a  h (Định lý Py- ta- go) h h sin  h sin     C  k.  k 2 2 R 2 a  h 2 2 R a  h  2 2 a  h  h Xét hàm f h  h  0 , ta có: 3    2 2 a  h 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 55
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3  3 2 2 a  h  2 2 2  2h . a  h   2 f ' h  a  h 3 2 2 3 a 2      2 2   2 2 2 f ' h 0 h a  3.h . a  h 2 2 2  h  a  3h  h  2 Bảng biến thiên: h a 2 0  2 f '(h) + - f(h) a 2 a 2
Từ bảng biến thiên suy ra: f h  h   C  k.f h   h  max max 2 2
Câu 40: Nhà Nam có một chiếc bàn tròn có bán kính bằng
2 m. Nam muốn mắc một bóng điện ở
phía trên và chính giữa chiếc bàn sao cho mép bàn nhận được nhiều ánh sáng nhất. Biết rằng cường độ sin
sáng C của bóng điện được biểu thị bởi công thức C c
(  là góc tạo bởi tia sáng tới mép bàn 2 l
và mặt bàn, c - hằng số tỷ lệ chỉ phụ thuộc vào nguồn sáng, l khoảng cách từ mép bàn tới bóng điện).
Khoảng cách nam cần treo bóng điện tính từ mặt bàn là A. 1m B. 1,2m C. 1.5 m D. 2m Hướng dẫn giải: Chọn đáp án D.
Gọi h là độ cao của bóng điện so với mặt bàn (h > 0); Đ là bóng điện; I là hình chiếu của Đ lên
mặt bàn. MN là đường kính của mặt bàn. ( như hình vẽ) h 2 l  2 Ta có sin  và 2 2
h l  2 , suy ra cường độ sáng là: C(l)  c (l  2) . l 3 l 2 6  l C 'l  . c  0 l   2 4 2   l . l  2
C 'l   0  l  6 l  2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 56
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Lập bảng biến thiên ta thu được kết quả C lớn nhất khi l  6 , khi đó h  2
Câu 41: Nhà của 3 bạn A, B, C nằm ở 3 vị trí tạo thành một tam giác vuông tại B ( như hình vẽ), AB =
10 km; BC = 25 km và 3 bạn tổ chức họp mặt ở nhà bạn C. Bạn B hẹn chở bạn A tại vị trí M trên đoạn
đường BC. Từ nhà, bạn A đi xe buýt đến điểm hẹn M với tốc độ 30km/h và từ M hai bạn A, B di
chuyển đến nhà bạn C bằng xe máy với tốc độ 50km/h. Hỏi điểm hẹn M cách nhà bạn B bao nhiêu km
để bạn A đến nhà bạn C nhanh nhất ? A B C M A. 5 km B. 7,5 km C. 10 km D. 12,5 km Hướng dẫn giải: Chọn đáp án B.
Đặt BM = x (km), x  0 2 100  x 25  x
Thời gian để bạn A di chuyển từ A đến M rồi đến nhà C là: t(x)   (h) 30 50 23 15
Lập bảng biến thiên, ta tìm được giá trị nhỏ nhất của t(x) là khi x  30 2
Câu 42: Một sợi dây có chiều dài là 6 m, được chia thành 2 phần. Phần thứ nhất được uốn thành hình
tam giác đều, phầm thứ hai uốn thành hình vuông. Hỏi độ dài của cạnh hình tam giác đều bằng bao
nhiêu để diện tích 2 hình thu được là nhỏ nhất? 18 36 3 12 18 3 A. (m) B. (m) C. (m) D. (m) 9  4 3 4  3 4  3 4  3 Hướng dẫn giải: Chọn đáp án A. 6  3x
Gọi độ dài cạnh hình tam giác đều là x (m) khi đó độ dài cạnh hình vuông là 4
Tổng diện tích khi đó là: 2 3  6  3x  1 2 S x    
9  4 3 2x  36x  36 4  4  16 Diện tích nhỏ nhất khi b 18 x    2a 9  4 3 18
Vậy diện tích Min khi x  9  4 3
Hoặc đến đây ta có thể bấm máy tính giải phương trình    2 9
4 3 x  36x  36 ấn bằng và hiện giá trị.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 57
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 43: Một khách sạn có 50 phòng. Hiện tại mỗi phòng cho thuê với giá 400 ngàn đồng một ngày thì
toàn bộ phòng được thuê hết. Biết rằng cứ mỗi lần tăng giá thêm 20 ngàn đồng thì có thêm 2 phòng
trống. Giám đốc phải chọn giá phòng mới là bao nhiêu để thu nhập của khách sạn trong ngày là lớn nhất. A. 480 ngàn. B. 50 ngàn. C. 450 ngàn. D. 80 ngàn. Hướng dẫn giải: Chọn đáp án C.
Gọi x (ngàn đồng) là giá phòng khách sạn cần đặt ra, x  400 (đơn vị: ngàn đồng).
Giá chênh lệch sau khi tăng x  400 .
x  400  2 x  400
Số phòng cho thuê giảm nếu giá là x :  . 20 10 x  400 x
Số phòng cho thuê với giá x là 50   90  . 10 10 2  x x
Tổng doanh thu trong ngày là: f (x)  x 90     90   x .  10  10 x f (
x)    90 . f (
x)  0  x  450 . 5 Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy f (x) đạt giá trị lớn nhất khi x  450 .
Vậy nếu cho thuê với giá 450 ngàn đồng thì sẽ có doanh thu cao nhất trong ngày là 2.025.000 đồng.
Câu 44: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện
tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng P n  480  20n (gam).
Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất ? A. 10 B. 12 C. 16 D. 24 Hướng dẫn giải: Chọn đáp án B.
Gọi n là số con cá trên một đơn vị diện tích hồ n  0 . Khi đó:
Cân nặng của một con cá là: P n  480  20n gam
Cân nặng của n con cá là:   2
n.P n  480n  20n gam Xét hàm số:   2
f n  480n  20n , n 0; .
Ta có: f 'n  480  40n , cho f 'n  0  n  12
Lập bảng biến thiên ta thấy số cá phải thả trên một đơn vị diện tích hồ để có thu hoạch nhiều nhất là 12 con.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 58
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 45: Hai con chuồn chuồn bay trên hai quỹ đạo khác nhau tại cùng một thời điểm. Một con bay
trên quỹ đạo đường thẳng từ điểm A0;0 đến điểm B 0;100 với vận tốc 5m / s . Con còn lại bay trên
quỹ đạo đường thẳng từ C 60;80 về A với vận tốc10m / s . Hỏi trong quá trình bay, thì khoảng cách
ngắn nhất mà hai con đạt được là bao nhiêu? A. 20(m) B. 50(m) C. 20 10( ) m D. 20 5( ) m Hướng dẫn giải: Chọn đáp án D. Xét ở thời điểm t
Tọa độ của con chuồn chuồn bay từ B về A là 0;100  5t  . 4
Do con chuồn chuồn bay từ C về A trên đường thẳng AC có hệ số góc k  tan  nên tọa độ của 3 con chuồn chuồn này là:  3
x  60 10t.cos 60 10t.  60  6t  5
y  80 10sin 80  8t
Như vậy ở thời điểm t khoảng cách giữa 2 con chuồn chuồn sẽ là: d  (60  6t)2  (20  3t)2
Khoảng cách giữa 2 con chuồn chuồn nhỏ nhất khi và chỉ khi (60  6t)2  (20  3t)2 đạt giá trị nhỏ
nhất với t 0;10
Xét f (t)  (60  6t)2  (20  3t)2 trên 0;10 20 Ta có: f (
t)  90t  600  0  t  3  20 
 min f (t)  f  2000    3 
 khoảng cách ngắn nhất giữa 2 con chuồn chuồn trong quá trình bay là 2000  20 5( ) m
Nhận xét: Đây là một bài toán cần khả năng tư duy thật nhanh khi làm bài thi trắc nghiệm. Và bài toán
này cũng cần khả năng tính toán rất cẩn thận vì số liệu khá lớn. Ở bước xử lí đạo hàm của hàm số f (t)
nếu tính toán sai rất có thể các bạn sẽ chọn min ở 2 đầu của đoạn0;1 
0 nên sẽ chọn đáp án B hoặc C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 59
Facebook: https://www.facebook.com/dongpay