Hướng dẫn giải các dạng toán sự tương giao của đồ thị hàm số – Đặng Việt Đông Toán 12

Hướng dẫn giải các dạng toán sự tương giao của đồ thị hàm số – Đặng Việt Đông Toán 12 được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn học sinh cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!

115 58 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số

Môn: Toán 12

Thông tin:

53 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
SỰ TƯƠNG GIAO CỦA ĐỒ THỊ HÀM SỐ
DẠNG 1: TỌA ĐỘ GIAO ĐIỂM CỦA HAI ĐỒ THỊ HÀM SỐ:
Câu 1: Số giao điểm của đường cong
3 2
2 2 1
y x x x
và đường thẳng
1
y x
bằng
A. 1. B. 2. C. 3. D. 0.
Hướng dẫn giải:
Chọn đáp án A.
Xét phương trình hoành độ giao điểm:
3 2 3 2
2 2 1 1 2 3 0 0.
x x x x x x x x
Vậy đường cong và đường thẳng có 1 giao điểm.
Câu 2: Tìm số giao điểm của đồ thị
C
:
3
2
y x x
và đường thẳng
1
y x
.
A.
2
. B.
3
. C.
0
. D.
1
.
Hướng dẫn giải:
Chọn đáp án D.
Phương trình hoành độ giao điểm:
3 3
2 1 1 1
x x x x x
.
Vậy
C
và đường thẳng
1
y x
chỉ có
1
giao điểm.
Câu 3: Tìm số giao điểm của đồ thị hàm số
4 2
4 1
y x x
và đường thẳng
3.
y
A.
0
. B.
2
. C.
3
. D.
4.
.
Hướng dẫn giải:
Chọn đáp án B.
Phươngtrìnhhoànhđộgiaođiểm:
4 2 4 2 2
4 1 3 4 4 0 2 2
x x x x x x
.
Câu 4: Tung độ giao điểm của đồ thị các hàm số
3 2
3 2, 2 8
y x x y x
là :
A. 2. B. 4. D. 0. D. 6.
Hướng dẫn giải:
Chọn đáp án A.
Xét phương trình hoành dộ giao điểm:
3 2
3 2 2 8
x x x
3 2
3 2 6 0
x x x
2 2
3 2 3 0 3 2 0 3
x x x x x x
2.3 8 2
y y
.
Câu 5: Tọa độ giao điểm của hai đồ thị hàm số
2
2 3
2
x x
y
x
và đường thẳng
3
y x
là
A.
3; 0
. B.
2; 3
. C.
1;0
. D.
3;1
.
Hướng dẫn giải:
Chọn đáp án A.
Phương trình hoành độ giao điểm
2
2 3
3 2
2
x x
x x
x
3; 0
x y
.
Phương pháp:
Cho 2 hàm số có đồ thị lần lượt là (C) và (C’).
+) Lập phương trình hoành độ giao điểm của (C) và (C’):
+) Giải phương trình tìm x từ đó suy ra y và tọa độ giao điểm.
+) Số nghiệm của (*) là số giao điểm của (C) và (C’).
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
Tọa độ giao điểm là
3; 0
.
Câu 6: Tung độ giao điểm của đồ thị hàm số
2x 3
3
y
x
và đường thẳng
1
y x
là:
A.
0
. B.
3
. C.
1
. D.
3
.
Hướng dẫn giải:
Chọn đáp án C.
Phương trình hoành độ giao điểm là:
2
2 3
1 0 0
3
x
x x x
x
. Do đó
1
y
.
Câu 7: Đường thẳng
d
1
y x
cắt đồ thị
C
của hàm số
2 5
1
x
y
x
tại hai điểm phân biệt. Tìm
các hoành độ giao điểm của
d
và
C
.
A.
1; 2
x x
. B.
0; 1
x x
. C.
1
x
. D.
2
x
.
Hướng dẫn giải:
Chọn đáp án D.
Xét phương trình hoành độ giao điểm của
d
và
C
:
2
2
2 5
1 4
2
1
x
x
x x
x
x
.
Câu 8: Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường
3 1
:
1
x
C y
x
và đường thẳng
: 1
d y x
là:
A.
0; 1
A
.
B.
0;1
A
.
C.
1;2
A
.
D.
2;7
A
.
Hướng dẫn giải:
Chọn đáp án B.
Hoành độ giao điểm của
C
và
d
là nghiệm của phương trình
3 1
1
1
x
x
x
(
1
x
)
2
0
3 1 1
3
x
x x
x
(thỏa mãn điều kiện).
Hoành độ nhỏ hơn 1 nên ta chọn
0 1
x y
. Vậy tọa độ điểm cần tìm là
0;1
A
.
Câu 9: Cho hàm số
4 2
4 2
y x x
có đồ thị
C
và đồ thị
2
: 1
P y x
. Số giao điểm của
P
và
đồ thị
C
là
A. 2. B. 1. C. 3. D. 4.
Hướng dẫn giải:
Chọn đáp án A.
Phương trình hoành độ giao điểm:
4 2 2 4 2
4 2 1 3 3 0
x x x x x
2
2
3 21
3 21
0
2
2
3 21
3 21
0
2
2
x
x
x
x
.
Câu 10: Tìm tọa độ giao điểm của đồ thị hàm số
2 3
1
x
y
x
với trục tung
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
A.
3
;0 .
2
B.
0;3 .
C.
3
;0 .
2
D.
0; 3 .
Hướng dẫn giải:
Chọn đáp án D.
Đồ thị cắt
0
Oy x
, thay
0
x
vào hàm số
2 3
1
x
y
x
, ta được
3
y
.
Câu 11: Số giao điểm của đồ thị hàm số
4 2
y x 7x 6
và
3
y x 13x
là
A.
1
. B.
2
. C.
3
. D.
4
.
Hướng dẫn giải:
Chọn đáp án C.
Phương trình hoành độ giao điểm của hai đồ thị là:
4 2 3
x 7x 6 x 13x
2
4 3 2
x 1
x x 7x 13x 6 0 x 1 x 2 x 3 0 x 2
x 3
.
Câu 12: Cho hàm số
2 1
1
x
y C
x
Trong các phát biểu sau, phát biểu nào sai ?
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng .
B. Hàm số luôn đồng biến trên từng khoảng của tập xác định của nó.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng .
D. Đồ thị hàm số
C
có giao điểm với
Oy
tại điểm .
Hướng dẫn giải:
Chọn đáp án D.
Giao điểm của đồ thị hàm số
C
với
Oy
là điểm
0; 1
.
Câu 13: Tìm số giao điểm
n
của đồ thị hàm số
2 2
3
y x x
và đường thẳng
2.
y
A.
6.
n
B.
8.
n
C.
2.
n
D.
4.
n
Hướng dẫn giải:
Chọn đáp án A.
Vẽ đồ thị hàm số
3
22
xxy
bằng cách suy ra từ đồ thị
24
3: xxyC
bằng cách
- Giữ nguyên đồ thị (C) phần phía trên trục hoành.
- Lấy đối xứng đồ thị (C) phần dưới trục hoành qua trục hoành.
Khi đó đt y =2 cắt đồ thị hàm số
3
22
xxy
tại 6 điểm phân biệt.
Câu 14: Tìm tọa độ giao điểm của đồ thị
2 1
1
x
y
x
với đường thẳng
1 3
y x
?
A.
2;5 , 1; 1
A B
. B.
2;5 , 0;1
A B . C.
2;5 , 0; 1
A B
. D.
2;5 , 0; 1
A B
.
Hướng dẫn giải:
Chọn đáp án D.
TXD:
1
x
.
Ta có phương trình hoành độ giao điểm của đồ thị và đường thẳng là :
2
0
2 1
3 1 2 1 1 3 1 3 6 0 2;5 ; 0; 1
2
1
x
x
x x x x x x A B
x
x
.
Câu 15: Đồ thị hàm số
2
7 5
y x x
và đồ thị hàm số
2
8 9 11
1
x x
y
x
có bao nhiêu điểm chung?
x 1
y 2
1
;0
2
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
A.
0.
B.
2.
C.
1.
D.
3.
Hướng dẫn giải:
Chọn đáp án D.
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho :
2
2
8 9 11
7 5
1
x x
x x
x
3 2 2 2
7 7 5 5 8 9 11
1
x x x x x x x
x
3
7 6 0
1
x x
x
3
2
1
x
x
x
Vì phương trình hoành độ giao điểm có 3 nghiệm phân biệt nên hai đồ thị đã cho có 3 giao điểm
phân biệt.
Câu 16: Đồ thị của hàm số
4 2
4 2 1
y x x
và đồ thị của hàm số
2
1
y
x
x
có tất cả bao
nhiêu điểm chung?
A.
3
. B.
1
. C.
2
. D.
4
.
Hướng dẫn giải:
Chọn đáp án A.
Phương trình hoành độ giao điểm :
4 2 2 4 2
0
1 4 3 0
3
2
4 2 1
x
x x xx
x
x x
Vậy hai đồ thị có 3 điểm chung.
Câu 17: Đồ thị của hàm số
23
3
2 1
x x
y x
và đồ thị của hàm số
2
2 1
3
x x
y
có tất cả
bao nhiêu điểm chung ?
A.
1
.
B.
3
.
C.
2
.
D.
0
.
Hướng dẫn giải:
Chọn đáp án B.
Số điểm chung là số nghiệm phân biệt của phương trình hoành độ:
3 2 2 3
3 2 1 3 2 1 4 0 0; 2
x x x x x x x x x
Phương trình có 3 nghiệm phân biệt nên số điểm chung là 3.
Câu 18: Gọi
,
M N
là giao điểm của đường thẳng
1
y x
và đường cong
2 4
1
x
y
x
. Hoành độ
trung điểm
I
của đoạn thẳng
MN
bằng:
A.
5
2
. B.
1
. C.
2
. D.
5
2
.
Hướng dẫn giải:
Chọn đáp án B.
Hoành độ giao điểm của đường thẳng
1
y x
và đường cong
2 4
1
x
y
x
là nghiệm của phương
trình
1
x
2 4
1
x
x
,
1
x
2
2 5 0
x x
.
Ta thấy phương trình có 2 nghiệm phân biệt
1 2
,
x x
khác
1
và
1 2
1
2
x x
. Do đó
1
I
x
.
Câu 19: Đồ thị hàm số
2 1
5
x
y
x
và đường thẳng
1
y x
cắt nhau tại hai điểm phân biệt
,
A B
.
Tìm hoành độ trung điểm
I
của đoạn thẳng
AB
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
A.
1
I
x
. B.
2
I
x
. C.
2
I
x
. D.
1
I
x
.
Hướng dẫn giải:
Chọn đáp án D.
Phương trình hoành độ giao điểm
2 1
1 5 .
5
x
x x
x
2
1,2
2 1 ( 1)( 5) 5 .
2 4 0 1 .
' 5 0.
1 5.
x x x x
x x
x
Đồ thị và đường cắt nhau tại hai điểm
1 5; 2 5 ; 1 5; 2 5
A B .
Có
I
là trung điểm của
AB
.
( 1; 2)
I
.
Câu 20: Biết rằng đồ thị hàm số
4 2
3 5
y x x
và đường thẳng
9
y
cắt nhau tại hai điểm phân
biệt
1 1
;
A x y
,
2 2
;
B x y
. Tính
1 2
x x
A.
1 2
3
x x
. B.
1 2
0
x x
. C.
1 2
18
x x
. D.
1 2
5
x x
.
Hướng dẫn giải:
Chọn đáp án B.
Phương trình hoành độ giao điểm là:
4 2 4 2
2
3 5 9 3 4 0
2
x
x x x x
x
Vậy tổng hai nghiệm là
1 2
0
x x
Câu 21: Biết đường thẳng
3 4
y x
cắt đồ thị hàm số
4 2
1
x
y
x
tại hai điểm phân biệt có tung
độ là
1
y
và
2
y
. Tính
1 2
y y
A.
1 2
10
y y
. B.
1 2
11
y y
. C.
1 2
9
y y
. D.
1 2
1
y y
.
Hướng dẫn giải:
Chọn đáp án B.
Phương trình hoành độ giao:
2
4 2
3 4 3 3 6 0
1
x
x x x
x
1
x
1
2
1 1
2 10
x y
x y
Vậy
1 2
11
y y
.
Câu 22: Đồ thị
C
của hàm số
2 8
x
y
x
cắt đường thẳng :
y x
tại hai điểm phân biệt
A
và
B
. Tìm tọa độ trung điểm
I
của đoạn thẳng
AB
A.
1;1
I
. B.
2;2
I
. C.
3; 3
I
. D.
6; 6
I
.
Hướng dẫn giải:
Chọn đáp án A.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
Ta có: phương trình hoành độ giao điểm của
( )
C
và
:
2 8
( 0)
x
x x
x
.
2 2
2 2
2 8 2 8 0
4 4
x y
x x x x
x y
.
Gọi
( ; )
I I
I x y
là trung điểm đoạn thẳng
AB
.
Suy ra :
4 2
1
2
2 4
1
2
I
I
x
y
( 1;1)
I
.
Câu 23: Đồ thị hàm số
3 2
3 2 1
y x x x
cắt đồ thị hàm số
2
3 1
y x x
tại hai điểm phân biệt
, .
A B
Tính độ dài đoạn
AB
A.
3
AB
. B.
2 2
AB . C.
2
AB
. D.
1
AB
.
Hướng dẫn giải:
Chọn đáp án D.
Ta có phương trình hoành độ giao điểm
3 2 2
3 2 1 3 1
x x x x x
3 2
4 5 2 0
x x x
1
2
1
2
x
x
1
2
1
1
y
y
Suy ra
1; 1 , 2; 1
A B
Vậy
2 2
2 1 1 1 1
AB
.
Câu 24: Tìm số giao điểm của đồ thị hàm số
1
x
y
x
và đường thẳng
y x
A.
3
. B.
1
. C.
2
. D.
0
.
Hướng dẫn giải:
Chọn đáp án C.
Phương trình hoành độ giao điểm
2 2
: 1
1
0
2 0
2
x
x DK x
x
x
x x x x x
x
Câu 25: Cho hàm số
3
2
y x x
có đồ thị
C
. Tìm tọa độ giao điểm của
C
và trục tung
A.
(0; 2)
. B.
(1;0)
. C.
( 2;0)
. D.
(0;1)
.
Hướng dẫn giải:
Chọn đáp án A.
Gọi
;
M x y
là giao điểm của đồ thị
C
với trục tung.
Khi đó ta có
0
x
2
y
.
Vậy
0; 2
M
.
Câu 26: Tìm số giao điểm của đồ thị hàm số
4 2
2
y x x
và đồ thị hàm số
2
2
y x
.
A.
4
. B.
2
. C.
3
. D.
1
.
Hướng dẫn giải:
Chọn đáp án A.
Phương trình hoành độ giao điểm là
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
4 2 2 4 2
2
2
2 2 3 2 0
1
1
x
x
x x x x x
x
x
Vậy có 4 giao điểm của hai đồ thị.
Câu 27: Cho hàm số
2 1
1
x
y
x
. Khẳng định nào sau đây là khẳng định sai ?
A. Đồ thị hàm số cắt
Oy
tại điểm
0;2
. B. Đồ thị hàm số có tâm đối xứng
1;2
I
.
C. Đồ thị hàm số có tiệm cận đứng
1
x
. D. Đồ thị hàm số có tiệm cận ngang
2
y
.
Hướng dẫn giải:
Chọn đáp án A.
Ta có:
2 1
1
x
y
x
.
Khi
0 1
x y
suy ra đồ thị hàm số cắt
Oy
tại điểm
(0; 1)
.
Câu 28: Biết rằng đồ thị hàm số
3
1
x
y
x
và đường thẳng.
2
y x
cắt nhau tại hai điểm phân biệt
;
A A
A x y
và.
;
B B
B x y
. Tính
A B
y y
A.
2
A B
y y
. B.
2
A B
y y
. C.
4
A B
y y
. D.
0
A B
y y
.
Hướng dẫn giải:
Chọn đáp án D.
Xét phương trình hoành độ giao điểm
2
2 5
3
2 2 1 0
1
2 5
x
x
x x x
x
x
Giả sử
2 5; 5 ; 2 5; 5
A B
0.
A B
y y
Câu 29: Biết đường thẳng
2
y x
cắt đồ thị
2 1
1
x
y
x
tại hai điểm phân biệt A, B có hoành độ lần
lượt
,
A B
x x
hãy tính tổng
A B
x x
A.
2
A B
x x
. B.
1
A B
x x
. C.
5
A B
x x
. D.
3
A B
x x
.
Hướng dẫn giải:
Chọn đáp án C.
Pt hoành độ giao điểm:
2
5 1 0
2 1
2 5.
1
1
A B
x x
x
x x x
x
x
Câu 30: Biết rằng đồ thị hàm số
3
1
x
y
x
và đường thẳng
2
y x
cắt nhau tại hai điểm phân biệt
;
A A
A x y
,
;
B B
B x y
. Khi đó
A B
x x
bằng
A. 4. B.
4
. C.
2 5
. D.
2.
Hướng dẫn giải:
Chọn đáp án A.
TXD:
1
x
.
Ta có phương trình hoành độ giao điểm của đồ thị và đường thẳng là :
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
2 2
2 3
3
2 3 1 2 3 2 3 4 1
1
2 3
x
x
x x x x x x x x x
x
x
.
Khi đó ta có
;
A A
A x y
,
;
B B
B x y
4
A B
x x
.
Câu 31: Đường thẳng
1
y x
cắt đồ thị hàm số
2 2
1
x
y
x
tại hai điểm phân biệt
1 1
;
A x y
và
2 2
;
B x y
. Khi đó tổng
1 2
y y
bằng
A. 1. B. 4. C. 3. D. 0.
Hướng dẫn giải:
Chọn đáp án B.
Phương trình hoành độ giao điểm
2 2
2 2
1( : 1)
1
3 4
2 2 1 2 3 0
1 0
x
x DK x
x
x y
x x x x
x y
Vậy
1 2
4
y y
Câu 32: Đồ thị hàm số
3
3
y x x
cắt
A. Đường thẳng
3
y
tại hai điểm. B. Đường thẳng
4
y
tại hai điểm.
C. Đường thẳng
5
3
y
tại ba điểm. D. Trục hoành tại một điểm.
Hướng dẫn giải:
Chọn đáp án C.
Lần lượt xét các phương trình hoành độ giao điểm
A.
3 3
3 3 3 3 0x x x x
, phương trình này chỉ có 1 nghiệm thực (sử dụng máy tính bỏ túi
kiểm tra). Loại A.
B.
3 3
3 4 3 4 0x x x x
, phương trình này chỉ có 1 nghiệm thực (sử dụng máy tính bỏ túi
kiểm tra). Loại B.
C.
3 3
5 5
3 3 0
3 3
x x x x
, phương trình này chỉ có 3 nghiệm thực (sử dụng máy tính bỏ túi
kiểm tra). Chọn C.
D.
3
0
3 0 3
3
x
x x x
x
, phương trình này chỉ có 3 nghiệm thực. Loại D.
Câu 33: Cho hàm số
2 2
2 1
y x mx m
có đồ thị
C
và đường thẳng
: 1
d y x
. Tìm tất cả giá
trị thực của tham số
m
để đồ thị hàm số
C
và đường thẳng
d
có giao điểm nằm trên trục hoành.
A.
2
m
. B.
2
m
. C.
0
m
. D.
0;2
m .
Hướng dẫn giải:
Chọn đáp án D.
Gọi
,
A x y
là giao điểm của
d
và
Ox
Phương trình hoành độ giao điểm của
d
và trục hoành là
1 0 1
x x
Suy ra
1;0
A
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 10
Facebook: https://www.facebook.com/dongpay
Theo YCBT ta có
1;0
A C
2 2 2
0
0 1 2 .1 1 2 0
2
m
m m m m
m
Câu 34: Cho hàm số
2 2 2
( ) ( 1)( 4)( 9)
y f x x x x x
. Hỏi đồ thị hàm số
(x)
y f
cắt trục hoành
tại bao nhiêu điểm phân biệt ?
A.
3.
B.
5.
C.
6.
D.
4.
Hướng dẫn giải:
Chọn đáp án C.
Đồ thị hàm số
(x)
y f
cắt trục hoành
6 4 2
'( ) 0 7 70 147 36 0.
f x x x x
Đặt
2
( 0)
x t t
. Phương trình trở thành:
3 2
7 70 147 36 0 1
t t t
Đặt
3 2
( ) 7 70 147 36
g t t t t
Có:
(0). (1) 0
(2). (7) 0
(7). (8) 0
g g
g g
g g
Phương trình
(1)
có 3 nghiệm nằm trong
(0;1);(2;7);(7;8).
Phương trình
(1)
có 3 nghiệm dương phân biệt. Suy ra phương trình
(x) 0
f
có 6 nghiệm phân
biệt. Hay đồ thị hàm số
(x)
y f
cắt trục hoành tại 6 điểm phân biệt.
Câu 35: Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số
2
2 3
1
x x
y
x
hợp với hai trục tọa
độ một tam giác có diện tích
S
bằng:
A.
1,5
S
. B.
2
S
. C.
3
S
. D.
1
S
.
Hướng dẫn giải:
Chọn đáp án D.
Cách 1: Ta có
2
2
2 1
1
x x
y
x
nên
0 1 2
y x
, do đó đồ thì hàm số có 2 điểm cực trị là
1 2;2 2
A
và
1 2; 2 2
B
.
Khi đó đường thẳng qua hai cực trị có vtcp
2 2; 4 2 2 2 1;2
u AB
nên có phương
trình là
2 1 2 2 2 0 2 2
x y y x d
.
Vì
d
cắt các trục tọa độ tại
0; 2
M
và
1;0
N nên diện tích là
1
. 1
2
S OM ON
.
Cách 2: Áp dụng tính chất cực trị của đồ thị hàm số
u x
y
v x
là đường thẳng
u x
y
v x
ta được
đường thẳng qua hai điểm cực trị là
: 2 2
d y x
.
Vì
d
cắt các trục tọa độ tại
0; 2
M
và
1;0
N nên diện tích là
1
. 1
2
S OM ON
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 11
Facebook: https://www.facebook.com/dongpay
DẠNG 2: SỰ TƯƠNG GIAO PHƯƠNG PHÁP BẢNG BIẾN THIÊN
VÀ ĐỒ THỊ HÀM SỐ
SỰ TƯƠNG GIAO BẰNG PHƯƠNG PHÁP BẢNG BIẾN THIÊN
Câu 1. Tìm
m
để phương trình
3
3 0
x x m
có 3 nghiệm thực phân biệt
A.
2 2
m
. B.
2 2
m
. C.
2 ; 2
m m
. D.
1 1
m
.
Hướng dẫn giải:
Chọn đáp án B.
Ta có
3 3
3 0 3 1
x x m m x x .
Xét hàm số
3
3
f x x x
có
2
3 3
f x x
;
1
0
1
x
f x
x
.
Bảng biến thiên:
.
Số nghiệm của phương trình
1
là số giao điểm của hai đồ thị
3
3
y x x
và
y m
.
Do đó
1
có ba nghiệm phân biệt
2 2
m
.
Câu 2. Tìm tất cả các giá trị
m
để phương trình
3
3 2
x x m
có
3
nghiệm phân biệt
A.
2 2.
m
B.
1 1.
m
C.
2 2.
m
D.
1 1.
m
Hướng dẫn giải:
Chọn đáp án B.
Xét hàm số
3
3
f x x x
trên
.
2
' 3 3
f x x
.
1
' 0
1
x
f x
x
.
Phương pháp 1: Bảng biến thiên
+) Lập phương trình hoành độ giao điểm dạng (phương trình ẩn x tham số m)
+) Cô lập m đưa phương trình về dạng
+) Lập BBT cho hàm số .
+) Dựa và giả thiết và BBT từ đó suy ra m.
Phương pháp 2: Đồ thị hàm số
+) Cô lập m hoặc đưa về hàm hằng là đường thẳng vuông góc với trục
+) Từ đồ thị hàm số tìm cực đại, cực tiểu của hàm số (nếu có)
+) Dựa vào số giao điểm của hai đồ thị hàm số ta tìm được giá trị của m theo yêu cầu của bài
toán.
*) Chú ý: Sử dụng PP bảng biến thiên và đồ thị hàm số khi m độc lập với x.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 12
Facebook: https://www.facebook.com/dongpay
Ta có
1 2; 1 2
f f
.
Bảng biến thiên
Vậy để phương trình có ba nghiệm phân biệt thì
2 2 2 1 1
m m
.
Câu 3. Tìm m để phương trình
3
3 2 0
x x m
có 3 nghiệm phân biệt
A.
4 4
m
. B.
4 0
m
. C.
4 2
m
. D.
16 16
m
.
Hướng dẫn giải:
Chọn đáp án B.
3 3
3 2 1
3 2 0 x mx x m x .
Đặt
3
3 2
f x x x
ta có
2
3 3
f x x
.
0 1
f x x
.
Bảng biến thiên
x

1
1
y
+
0
0
+
y

0
4
Từ bảng biến thiên ta có
4 0
m
.
Câu 4. Phương trình
3 2
3
x x m m
có 3 nghiệm phân biệt khi :
A.
2 1
m
B.
1 2
m
C.
1
m
D.
2
1
m
m
Hướng dẫn giải:
Chọn đáp án A.
Xét hàm số:
3
3
y x x
ta có:
+ TXĐ:
.
D R
+
2
' 3 3.
y x
+
2
' 0 3 3 0 1.
y x x
+ Bảng biến thiên.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 13
Facebook: https://www.facebook.com/dongpay
+ Dựa vào bảng biến thiên ta thấy, phương trình đã cho có 3 nghiệm phân biệt khi
2 2
2 2
2 2 0
2 1.
2 2 0
m m m m
m
m m m m
Câu 5. Phương trình
3
12 2 0
x x m
có 3 nghiệm phân biệt khi
A.
4 4
m
. B.
18 14
m
. C.
14 18
m
. D.
16 16
m
.
Hướng dẫn giải:
Chọn đáp án C.
3 3
12 2 0 12 2 1
x x m x x m .
Xét hàm số
3
12
y x x
. Ta có
2
3 12
y x
.
2 16
0
2 16
x y
y
x y
.
Bảng biến thiên
Để phương trình
1
có 3 nghiệm khi và chỉ khi đường thẳng 2
y m
cắt đồ thị hàm số
3
12
y x x
tại 3 điểm phân biệt
16 2 16 14 18.
m m
Câu 6. Với giá trị nào của m thì phương trình
3 2
3 0
x x m
có hai nghiệm phân biệt
A.
4 0
m m
. B.
4 0
m m
. C.
4 4
m m
. D. Kết quả khác.
Hướng dẫn giải:
Chọn đáp án A.
Xét hàm số
3 2
3
y x x
2
3 6
y x x
0; 0
0
2; 4
x y
y
x y
Số nghiệm của phương trình
3 2
3 0
x x m
là số giao điểm của đồ thị hàm số
3 2
3
y x x
và đường
thẳng
y m
.
x
0 2
y
0 0
0
4
x
y
y

2

16
2

0
0

16
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 14
Facebook: https://www.facebook.com/dongpay
Phương trình có 2 nghiệm phân biệt khi
0 0
4 4
m m
m m
.
Câu 7. Tìm các giá trị thực của m để phương trình
3 2
3 4 0
x x m
có ba nghiệm phân biệt.
A.
4 8
m
. B.
0
m
. C.
0 4
m
. D.
8 4
m
.
Hướng dẫn giải:
Chọn đáp án D.
Ta có:
3 2 3 2
3 4 0 3 4 .
x x m x x m
Đặt
3 2 2
1 2 1
3 4; 3 6 .
y x x y m y x x
Ta có BBT của
3 2
1
3 4.
y x x
x

0
2

1
y
+ 0 - 0 +
1
y
4


8
Từ BBT ta suy ra phương trình có ba nghiệm phân biệt khi
8 4.
m
Câu 8. Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
3
3 2
y x x
tại 3 điểm phân biệt
A.
0 2.
m
B.
0 4.
m
C.
0 4.
m
D.
2 4.
m
Hướng dẫn giải:
Chọn đáp án C.
2
3 3,
y x
1
0
1
x
y
x
x

1
1

y
0
0
.
y
.

4
0

Đường thẳng
y m
cắt đồ thị hàm số
3
3 2
y x x
tại 3 điểm phân biệt khi.
0 4.
m
Câu 9. Cho hàm số
3 2
y f x ax bx cx d
có bảng biến thiên như sau:
Khi đó
f x m
có bốn nghiệm phân biệt
1 2 3 4
1
2
x x x x
khi và chỉ khi
+
+
+
0
1
00
10
+
y
y
'
x
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 15
Facebook: https://www.facebook.com/dongpay
A.
1
1
2
m
. B.
1
1
2
m
.
C.
0 1
m
. D.
0 1
m
.
Hướng dẫn giải:
Chọn đáp án A.
Đồ thị
:
C y f x
được vẽ bằng cách:
Phần 1: Giữ nguyên phần đồ thị
:
C y f x
nằm bên trên trục hoành.
Phần 2: Lấy đối xứng phần đồ thị
:
C y f x
nằm dưới trục hoành qua trục hoành.
Đồ thị hàm số có tọa độ điểm uốn
1 1
;
2 2
I , nên phương trình đó
f x m
có bốn nghiệm phân
biệt
1 2 3 4
1
2
x x x x
khi
1
1
2
m
.
Câu 10. Đường thẳng y = m cắt đồ thị hàm số
3
3 2
y x x
tại 3 điểm phân biệt khi :
A.
0 4
m
B.
0 4
m
C.
0 4
m
D.
4
m
Hướng dẫn giải:
Chọn đáp án A.
Tập xác định:
D
Ta có:
3 2
1
3 2 ' 3 3 ' 0
1
x
y x x y x y
x
Bảng biên thiên:
Từ bảng biến thiên ta có
0 4
m
thì phương trình đã cho có ba nghiệm phân biệt
Câu 11. Tìm m để phương trình
3 2
2 3 12 13
x x x m
có đúng hai nghiệm
A.
13, 4
m m
. B.
13, 0
m m
. C.
20, 5
m m
. D.
20, 7
m m
.
Hướng dẫn giải:
Chọn đáp án C.
Xét hàm số:
3 2
2 3 12 13
y x x x
.
2
6 6 12
y x x
.
1
0
2
x
y
x
.
BBT
x

2
1

y
0
0
.
y
.

7
20

-1
4
0
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 16
Facebook: https://www.facebook.com/dongpay
Phương trình
3 2
2 3 12 13x x x m
có đúng hai nghiệm khi 20, 7m m .
Câu 12. Tìm m để phương trình
3 2
2x 3x 12x 13 m
có đúng 2 nghiệm.
A.
13; 4.m m
B.
.
C.
.
D.
.
Hướng dẫn giải:
Chọn đáp án D.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số
3 2
2 3 12 13y x x x
và đường thẳng
.y m
Lập bảng biến thiên của hàm số
3 2
2 3 12 13. y x x x
Nhìn vào BBT ta thấy để phương trình
3 2
2 3 12 13x x x m có đúng 2 nghiệm
thì đường thẳng
y m
phải cắt đồ thị hàm số
3 2
2 3 12 13y x x x
tại đúng 2 điểm
20
.
7
m
m
Vậy đáp án D thỏa mãn.
Câu 13. Cho hàm số ( )y f x liên tục trên và có bảng biến thiên như hình vẽ..
.
Với
1;3
m
thì phương trình ( )
f x m
có bao nhiêu nghiệm?
A. 4. B. 3. C. 2. D. 5.
Hướng dẫn giải:
Chọn đáp án A.
Dựa vào bảng biến thiên vẽ đồ thị hàm số ( ).y f x
Phần 1: Giữ nguyên đồ thị hàm số ( ).y f x
Phần 2: Lấy đối xứng phần đồ thị hàm số
( )
y f x
phía dưới trục hoành qua trục hoành.
Dựa vào đồ thị hàm số và với
1;3m thì phương trình
f x m
có 4 nghiệm
Câu 14.Tìm tất cả các giá trị thực k để phương trình
3 2
3 1
2 3 1
2 2 2
k
x x x có đúng 4 nghiệm
phân biệt
A.
19
;5 .
4
k
B. .k
C.
19
2; 1 1; .
4
k
D.
3 19
2; ;6 .
4 4
k
0; 13
m m
20; 5
m m
20; 7
m m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 17
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn đáp án D.
Ta có :
2
1
1
' 6 3 3. ' 0
2
x
y x x y
x
Bảng biến thiên đồ thị hàm số
3 2
3 1
2 3
2 2
y x x x
.
Với
3 2
1
3 1
2 3 0
7 33
2 2
8
x
x x x
x
x

7 33
8
1
7 33
8
1
2
1

'
y
0
0
y

11
8
0
0
0
2

Từ đó, suy ra bảng biến thiên của đồ thị hàm số
3 2
3 1
2 3
2 2
y x x x
x

7 33
8
1
7 33
8
1
2
1

y


2
11
8
0
0
0
Từ bảng biến thiên, nhận thấy: ycbt
19
6
11
4
1 2
3
8 2
2
4
k
k
k
.
Câu 15. Phương trình
4 2
2 2
x x m
có bốn nghiệm phân biệt khi:
A.
3 2
m
.
B.
3; 2.
m m
C.
3 2
m
.
D.
3.
m
Hướng dẫn giải:
Chọn đáp án A.
Xét hàm số
4 2
2 2
f x x x
xác định trên
. Có
3
' 4 4 .
f x x x
0
' 0 .
1
x
f x
x
Bảng biến thiên:
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 18
Facebook: https://www.facebook.com/dongpay
Dựa vào bảng biến thiên, để phương trình
4 2
2 2
x x m
có 4 nghiệm phân biệt thì
3 2
m
.
Câu 16. Xác định
m
để đường thẳng
4
y m
cắt đồ thị hàm số
4 2
2x 4
y x
tại 3 điểm phân biệt ?
A.
1
m
. B.
4
m
. C.
3 4
m
. D.
3
m
.
Hướng dẫn giải:
Chọn đáp án A.
3
4 4
y x x
0; 4
0
1; 3
x y
y
x y
.
Ycbt
max
4 4 1
m y m
.
Câu 17. Tìm
m
để đường thẳng
4
y m
cắt đồ thị hàm số
C
:
4 2
8 3
y x x
tại
4
phân biệt:
A.
13 3
.
4 4
m
B.
3
4
m
C.
13
4
m
. D.
13 3
.
4 4
m
.
Hướng dẫn giải:
Chọn đáp án A.
3
0
' 4 16 ' 0
2
x
y x x y
x
Bảng biến thiên
x

2
0 2

y
0 + 0
0 +
y

13
3
13

Câu 18. Tìm m để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại 4 điểm phân biệt.
A.
1 2.
m
B.
2.
m
C.
2 3.
m
D.
2.
m
Hướng dẫn giải:
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 19
Facebook: https://www.facebook.com/dongpay
Chọn đáp án A.
Xét hàm số
4 2
2 2
y x x
ta có.
+ TXĐ:
.
D R
+
3
' 4 4 .
y x x
+
3
0
' 0 4 4 0 .
1
x
y x x
x
+ Bảng biến thiên.
+ Dựa vào bảng biến thiên ta thấy đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại 4 điểm phân
biệt khi và chỉ khi
1 2.
m
Câu 19. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
4 2
: 1
m
C y x mx m
cắt trục hoành
tại bốn điểm phân biệt
A.
1
m
. B.
1
2
m
m
. C. không có
m
. D.
2
m
.
Hướng dẫn giải:
Chọn đáp án B.
Cách 2:
Ta có:
4 2
1
y x mx m
.
Tập xác định:
D
.
3
' 4 2
y x mx
.
3
2
0.
' 0 4 2 0
.
2
x
y x mx
m
x
.
Đồ thị hàm số cắt trục hoành tai bốn điểm phân biệt
0
m
.
Ta có:
2
2
0 1.
( 0) 1.
2 4
x y m
m m
x m y m
.
Bảng biến thiên
x
2
m
0
.
2
m
y
0
0
0
y
.
.
2
1
4
m
m
1
m
.
2
1
4
m
m
.
.
Yêu cầu bài toán
2
1 0
1.
2.
1 0
4
m
m
m
m
m
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 20
Facebook: https://www.facebook.com/dongpay
Câu 20.Số giao điểm nhiều nhất của đồ thị hàm số
4 2
2 1
y x x
với đường thẳng
y m
(với
m
là
tham số ) là bao nhiêu ?
A. 0. B. 2. C. 4. D. 3.
Hướng dẫn giải:
Chọn đáp án C.
Xét phương trình :
4 2
2 1 1
x x m
Xét đồ thị
4 2
2 1
y x x
Ta có : +)
3
' 4 4
y x x
3
0
' 0 4 4 0
1
x
y x x
x
+) Bảng biến thiên :
x

-
1 0 1
y
0 + 0
0 +
y
1

0 0
Dựa bảng biến thiên
đường thẳng
y m
cắt đồ thị
4 2
2 1
y x x
nhiều nhất là 4 điểm
Câu 21. Tìm
m
để phương trình
4 2
8 3 4 0
x x m
có 4 nghiệm thực phân biệt.
A.
13 3
4 4
m
. B.
13
4
m
. C.
3
4
m
. D.
13 3
4 4
m
.
Hướng dẫn giải:
Chọn đáp án D.
Cách 2:
Phương trình đã cho tương đương
4 2
4 8 3
m x x f x
.
Xét hàm số
f x
.
Tập xác định
D
.
3
4 16
y x x
,
0
0
2
x
y
x
.
Ta có bảng biến thiên:
x

2
0
2
y
0
0
0
y
Dựa vào Bảng biến thiên, để
1
có
4
nghiệm phân biệt thì
13 3
13 4 3
4 4
m m
.
Câu 22.Gọi
m
C
là đồ thị hàm số
4 2
2 2017
y x x m . Tìm
m
để
m
C
có đúng 3 điểm chung phân
biệt với trục hoành, ta có kết quả:
A.
2017
m
. B.
2016 2017
m
. C.
2017
m
. D.
2017
m
.
13
13
3
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 21
Facebook: https://www.facebook.com/dongpay
Hướng dẫn giải:
Chọn đáp án A.
Phương trình hoành độ giao điểm :
4 2
2 2017 0
x x m
4 2
2 2017
m x x
Số nghiệm của phương trình trên là số giao điểm của 2 đồ thị
4 2
2 2017
y m
y x x
Ta có :
3
4 4
y x x
. Cho
0
0
1
x
y
x
Dựa vào bảng biến thiên, ta thấy phương trình có 3 nghiệm khi và chỉ khi
2017
m
.
Câu 23. [2D1-2] Tìm
m
để đường thẳng
4
y m
cắt đồ thị hàm số
4 2
: 8 3
C y x x
tại
4
phân
biệt
A.
13 3
4 4
m
. B.
3
4
m
. C.
13
4
m
. D.
13 3
4 4
m
.
Hướng dẫn giải:
Chọn đáp án A.
Xét hàm số
4 2
8 3
y x x
trên
D
. Ta có
3
4 16
y x x
,
3
0, 3
0 4 16 0 2, 13
2, 13
x y
y x x x y
x y
Bảng biến thiên
x
2
0
2
y
0
0
0
y
13
3
13
Đường thẳng
4
y m
cắt
C
tại
4
điểm phân biệt khi chỉ khi
13 3
13 4 3
4 4
m m
.
Câu 24. Cho hàm số
( )
y f x
liên tục trên
và có bảng biến thiên như hình vẽ. Tìm tất cả các giá trị thực
của
m
để phương trình
( ) 2
f x m
có đúng hai nghiệm phân biệt.
x
-
1
0
1
y
+
0
-
0 +
0
-
y
.
0
.
-3
0
.
A.
0
3
m
m
. B.
3
m
. C.
0
3
2
m
m
. D.
3
2
m
.
Hướng dẫn giải:
x
–
∞
0
+∞
y
–
0
+
0
–
0
+
y
+∞
2016 2016
+∞
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 22
Facebook: https://www.facebook.com/dongpay
Chọn đáp án C.
Dựa vào BBT ta thấy để phương trình
( ) 2
f x m
có đúng hai nghiệm phân biệt thì
0
2 0
3
2 3
2
m
m
m
m
Câu 25. Cho hàm số
y f x
có bảng biến thiên như hình bên. Khi đó tất cả các giá trị của
m
để phương
trình
1
f x m
có ba nghiệm thực là
A.
3;5
m . B.
4;6
m .
C.
;3 5;m
. D.
4;6
m .
Hướng dẫn giải:
Chọn đáp án B.
Phương trình
1
f x m
có ba nghiệm thực khi và chỉ khi
3 1 5
m
4 6
m
.
Câu 26.Cho hàm số
( )
y f x
có bảng biến thiên sau :
x

-1 0 1
y
0 + 0
0 +
y
1
1
1
Với giá trị nào của
m
thì phương trình ( ) 1
f x m
có đúng 2 nghiệm ?
A.
1
m
. B.
1
m
.
C.
1
m
hoặc
2
m
. D.
1
m
hoặc
2
m
.
Hướng dẫn giải:
Chọn đáp án C.
+) Ta có
( ) 1 ( ) 1
f x m f x m
Dựa bảng biến thiên để phương trình (1) có đúng hai nghiệm
1 0
1 1
m
m
1
2
m
m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 23
Facebook: https://www.facebook.com/dongpay
Câu 27. Cho hàm số
( )
y f x
liên tục trên
và có bảng biến thiên như hình vẽ. Tìm tất cả các giá trị thực
của
m
để phương trình
( ) 2
f x m
có đúng hai nghiệm phân biệt.
x
-1 0 1
y
+ 0 - 0 + 0 -
y
.
0
.
-3
0
.
A.
0
3
m
m
. B.
3
m
. C.
0
3
2
m
m
. D.
3
2
m
.
Hướng dẫn giải:
Chọn đáp án C.
Dựa vào BBT ta thấy để phương trình
( ) 2
f x m
có đúng hai nghiệm phân biệt thì
0
2 0
3
2 3
2
m
m
m
m
Câu 28. Cho hàm số
( )
y f x
xác định trên
\ 1
, liên tục trên mỗi khoảng xác định và có bảng
biến thiên như sau:
Tìm tập hợp tất cả các giá trị của
m
sao cho phương trình ( )
f x m
có hai ngiệm thực phân biệt.
A.
; 1 .

B.
;2 .
 C.
( 1;2)
D.
;1 .

Hướng dẫn giải:
Chọn đáp án A.
Dễ dàng nhận thấy khi
1
m
thì phương trình
f x m
có hai nghiệm phân biệt.
Câu 29. Cho hàm số
y f x
xác định trên
\ 1
, liên tục trên từng khoảng xác định và có bảng biến
thiên như dưới đây:.
2
-∞
1
+∞
f '(x)
f(x)
x
-∞
+
-
-1
-∞
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 24
Facebook: https://www.facebook.com/dongpay
.
Tìm tập hợp tất các giá trị thực của
m
để phương trình
f x m
có nghiệm thực duy nhất
A.
0; .

. B.
2; .

. C.
2; .

. D.
0; .

Hướng dẫn giải:
Chọn đáp án B.
Số nghiệm thực của phương trình
f x m
bằng số giao điểm của đường thẳng
y m
và đồ thị hàm số
y f x
. Để phương trình
f x m
có nghiệm thực duy nhất thì
2
m
Câu 30. Giả sử tồn tại hàm số
y f x
xác định trên
\ 1 ,
liên tục trên mỗi khoảng xác định và
có bảng biến thiên như sau:.
.
Tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
f x m
có bốn nghiệm thực phân biệt là
A.
2;0 1
.
B.
2;0 1
.
C.
2;0
.
D.
2;0
.
Hướng dẫn giải:
Chọn đáp án D.
Câu 31. Cho hàm số
( )
y f x
xác định trên
\ 1;1
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như sau:.
.
Tìm tập hợp tất cả các giá trị của thàm số
m
sao cho phương trình
f x m
có ba nghiệm thực phân biệt
A.
2;2
. B.
2;2
. C.
;
 
. D.
2;

.
Hướng dẫn giải:
Chọn đáp án A.
Từ bảng biến thiên suy ra phương trình
f x m
có ba nghiệm thực phân biệt khi
2 2
m
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 25
Facebook: https://www.facebook.com/dongpay
Câu 32. Cho hàm số
y f x xác định trên
0; ,
liên tục trên khoảng
0; và có bảng biến thiên
như sau.
Tìm tập hợp tất cả các giá trị thực của tham số sao cho phương trình
f x m có hai nghiệm
1 2
,x x
thỏa mãn
1
0;2x và
2
2; .x
A.
2;0 . B.
2; 1 . C.
1;0 . D.
3; 1 .
Hướng dẫn giải:
Chọn đáp án B.
Nghiệm của phương trình là hoành độ giao điểm của đồ thị hàm số và đường thẳng
y m
Dựa vào BBT ta có kết luận
2; 1m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 26
Facebook: https://www.facebook.com/dongpay
SỰ TƯƠNG GIAO PHƯƠNG PHÁP ĐỒ THỊ HÀM SỐ
Câu 1.Cho hàm số
3 2
3 2y x x có đồ thị như hình vẽ.
Với giá trị nào của m thì phương trình
3 2
3 1 0x x m
có ba nghiệm phân biệt?
A. 1 3m . B. 3 1m . C. 3 1m . D. 1m .
Hướng dẫn giải:
Chọn đáp án C.
Ta có số nghiệm của phương trình
3 2 3 2
3 1 0 3 2 1
x x m x x m
là số giao điểm của đồ
thị hàm số
3 2
3 2y x x và đường thẳng 1y m .
Từ đồ thị ta thấy hàm số có 2
CĐ
y và 2
CT
y nên phương trình
3 2
3 1 0x x m
có ba nghiệm
phân biệt 2 1 2 3 1m m .
Câu 2.Đồ thị hình bên là của hàm số
3 2
3 4y x x
. Tìm tất cả giá trị của m để phương trình
3 2
3 0x x m có hai nghiệm phân biệt? Chọn một khẳng định ĐÚNG
A. 4m hoặc 0m . B. 4m . C. 0 4m . D. 0m .
Hướng dẫn giải:
Chọn đáp án A.
3 2 3 2
3 0 3 4 4x x m x x m
Phương trình có 2 nghiệm phân biệt khi
4 0 4
4 4 0
m m
m m
Câu 3. Cho hàm số
3 2
6 9 ,y x x x m C với m là tham số. Giả sử đồ thị
C cắt trục hoành tại 3
điểm phân biệt có hoành độ thỏa mãn
1 2 3
.x x x
Khẳng định nào sau đây đúng?
A.
1 2 3
1 3 4x x x
.
B.
1 2 3
0 1 3 4x x x
.
C.
1 2 3
0 1 3 4x x x
.
D.
1 2 3
1 3 4x x x
.
Hướng dẫn giải:
O
x
2
1
2
y
2
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 27
Facebook: https://www.facebook.com/dongpay
Chọn đáp án B.
3
1
09123'
2
x
x
xxy
Lập BBT có (C) cắt trục hoành tại 3 điểm phân biệt khi
40103 mmyy
Căn cứ vào BBT tvà điều kiện trên ta có
1 2 3
0 1 3 4x x x
.
Cách khác
Phương trình hoành độ giao điểm:
3 2 3 2
6 9 0 1 6 9x x x m x x x m
Gọi
3 2
: 6 9C y x x x
.
Số nghiệm của phương trình
1 là số giao điểm của đồ thị
C
và đường thẳng
:d y m .
Dựa vào đồ thị, ta thấy đường thẳng
d cắt
C
tại 3 điểm thỏa
1 2 3
0 1 3 4x x x
.
Câu 4. Cho hàm số
y f x có đồ thị là hình sau. Tìm tất cả các giá trị thực của tham số m để phương trình
( ) 1f x m có 4 nghiệm thực phân biệt
A. 4 hay 0.m m B. 4 0.m C. 0 4.m D. 1 3.m
Hướng dẫn giải:
Chọn đáp án D.
Ta có số nghiệm của phương trình ( ) 1f x m là số giao điểm
của hàm
y f x và 1y m .
Vậy để phương trình ( ) 1f x m có 4 nghiệm phân biệt
0 1 4m 1 3m .
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 28
Facebook: https://www.facebook.com/dongpay
Câu 5. Hình vẽ bên là đồ thị
C của hàm số
3
3 1y x x . Giá trị của m để phương trình
3
3 1x x m
có 3 nghiệm đôi một khác nhau là.
A. 0m . B. 1 3m . C. 3 1m . D. 0m , 3m .
Hướng dẫn giải:
Chọn đáp án D.
Đồ thị
3
: 3 1C y x x
được vẽ bằng cách:
Phần 1: Giữ nguyên phần đồ thị
3
: 3 1C y x x nằm bên trên trục hoành.
Phần 2: Lấy đối xứng phần đồ thị
3
: 3 1C y x x nằm dưới trục hoành qua trục hoành
Dựa vào đồ thị, phương trình
3
3 1
x x m
có 3 nghiệm đôi một khác nhau khi 0m , 3m .
Câu 6. Đồ thị sau đây là của hàm số
3
3 1y x x
. Với giá trị nào của m thì phương trình
03
3
mxx
có ba nghiệm phân biệt.
.
A. 31 m . B. . C. 22 m . D. 32 m .
Hướng dẫn giải:
Câu 7. Cho phương trình
3 2
3 1 0x x m
với m là tham số thực. Tìm tất cả các giá trị của m để phương
trình đã cho có 3 nghiệm thực phân biệt.
A. 1 5m . B. 0 4m . C. 5m . D. 1m .
Hướng dẫn giải:
Chọn đáp án A.
3 2
3 1 0x x m
(1)
Ta có:
3 2 3 2
3 1 0 3 1 . x x m x x m
Để phương trình (1) có 3 nghiệm phân biệt khi và chỉ khi đồ thị hàm số
3 2
3 1 y x x
và đường thẳng
y m
cắt nhau tại 3 điểm phân biệt. Dựa vào đồ thị, suy ra 1 5m .
22
m
Chọn đáp án B.
Ta có x
3
3x m 0 x
3
3x 1 m 1
1
.
Số nghiệm của phương trình
1
là số giao điểm của hai đồ thị
y x
3
3x 1
và y m 1.
Do đó
1
có ba nghiệm phân biệt 1 m 1 3 2 m 2.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 29
Facebook: https://www.facebook.com/dongpay
Câu 8. Cho hàm số y = f (x) có đồ thị hàm số đường cong trong hình vẽ bên. Tìm tất cả các giá trị
thực của tham số m để phương trình
f x m
có 4 nghiệm phân biệt.
A.
0 2.m
B.
0 4.m
C.
1 4.m
D.
Không có giá trị
nào của
m
.
Hướng dẫn giải:
Chọn đáp án B.
( ) ( ) 0
( )
( ) ( ) 0
f x khi f x
f x
f x khi f x
Suy ra, đồ thị hàm số
( )y f x
bao gồm 2 phần:
Phần 1: Giữ nguyên phần đồ thị hàm số
( )y f x
ở phía trên trục Ox.
Phần 2: Lấy đối xứng phần đồ thị phía dưới Ox của
( )y f x
qua Ox.
Số nghiệm của phương trình
( )f x m
là số giao điểm của đồ thị hàm số
( )y f x
và đường thẳng
.y m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 30
Facebook: https://www.facebook.com/dongpay
Dựa vào đồ thị hàm số ta kết luận, phương trình có 4 nghiệm phân biệt khi 0 4. m
Câu 9. Cho hàm số
y f x
liên tục trên đoạn
2;2 và có đồ thị là đường cong như hình vẽ bên.
Tìm số nghiệm của phương trình
1f x trên đoạn
2;2 .
A.
4
.
B.
5.
C.
3.
D.
6 .
Hướng dẫn giải:
Chọn đáp án D.
Từ đồ thị của hàm số
( )y f x
ta suy ra đồ thị của hàm số
y f x
như sau: Giữ nguyên phần đồ thị
nằm phía trên trục hoành của hàm số đã cho; Lấy đối xứng phần đồ thị nằm bên dưới trục hoành qua trục
hoành.
Số nghiệm của phương trình
1f x
là số giao điểm của đồ thị hàm số
y f x
và đường thẳng
1.y
Căn cứ vào đồ thị, ta thấy có sáu giao điểm. Vậy phương trình
1f x
có 6 nghiệm phân biệt.
Câu 10.Cho hàm số
3 2
3 2f x x x có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị
thực của tham số m đề phương trình
3
2
3 2x x m
có nhiều nghiệm thực nhất.
A.
2 2m ..
B.
0 2m .
C.
2 2m .
D.
0 2m .
Hướng dẫn giải:
Chọn đáp án C.
Câu 11. Đồ thị trong hình bên dưới là đồ thị của hàm số
4 2
4y x x . Dựa vào đồ thị bên hãy tìm
tất cả các giá trị thực của tham số m sao cho phương trình
4 2
4 2 0x x m
có đúng hai nghiệm
thực phân biệt?
1
x
2
x
O
2
2
2
x
y
4
2
4
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 31
Facebook: https://www.facebook.com/dongpay
A. 0, 4m m . B. 0m . C. 2; 6m m . D. 2m .
Hướng dẫn giải:
Chọn đáp án C.
Phương trình
4 2 4 2
4 2 0 2 4x x m m x x
Dựa vào đồ thị để phương trình
4 2
4 2 0
x x m
có đúng hai nghiệm thực phân biệt thì đường thẳng
2y m cắt đồ thị đã cho tại đúng hai điểm phân biệt. Tức là:
2 0 2
2 4 6
m m
m m
Câu 12. Cho hàm số
4 2
1
2
4
y x x có đồ thị
C
như hình vẽ sau. Dựa vào đồ thị
C
, tìm tất cả các giá
trị thực của tham số m để phương trình
4 2 2
8 2 0
m
x x
có bốn nghiệm phân biệt.
A. 2m . B. 0 2m . C. 0 4m . D. 0m .
Hướng dẫn giải:
Chọn đáp án A.
Phương trình
4 2 2 4 2 4 2
1 1
8 2 0 2 2 0 2 2
4 4
m m m
x x x x x x
.
Suy ra số nghiệm của phương trình
4 2 2
8 2 0
m
x x
là số giao điểm của đường thẳng
2
m
y
và đồ thị
hàm số
4 2
1
( ): 2
4
C y x x .
Yêu cầu bài toán
0 2 4 2
m
m
.
Câu 13. Tìm m để phương trình
4 2
2
5 4 logx x m
có 8 nghiệm phân biệt:
A.
4
9
0 2m
.
B.
Không có giá trị của m.
C.
4
9
1 2m . D.
4 4
9 9
2 2m .
Hướng dẫn giải:
Chọn đáp án C.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 32
Facebook: https://www.facebook.com/dongpay
Ta có
4 2
4 2
4 2
5 4, 2; 1 1;2
5 4
5 4, ; 2 1;1 2;
x x x
x x
x x x
 
.
Do đó đồ thị hàm số là phần bên trên trục hoành của đồ thị hàm số
4 2
5 4
y x x
và phần đối xứng bên
dưới trục hoành của đồ thị qua trục hoành. Từ đồ thị ta thấy để phương trình có 8 nghiệm phân biệt thì
4
9
2
9
0 log 1 2
4
m m .
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 33
Facebook: https://www.facebook.com/dongpay
DẠNG 3: TƯƠNG GIAO VỚI HÀM BẬC BA
Phương pháp 1: Nhẩm nghiệm – tam thức bậc 2.
+) Lập phương trình hoành độ giao điểm
F x,m 0
+) Nhẩm nghiệm: (Khử tham số). Giả sử
0
x x
là 1 nghiệm của phương trình.
+) Phân tích:
0
0
x x
F x,m 0 x x .g x 0
g x 0
(là
g x 0 là phương trình bậc
2 ẩn x tham số m ).
+) Dựa vào yêu cầu bài toán đi xử lý phương trình bậc 2
g x 0 .
Phương pháp 2: Cực trị
*) Nhận dạng: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm.
*) Quy tắc:
+) Lập phương trình hoành độ giao điểm
F x,m 0 (1). Xét hàm số
y F x,m
+) Đ
ể
(1) có đúng 1 nghi
ệ
m thì
đ
ồ
th
ị
y F x,m cắt trục hoành tại đúng 1 điểm.
(2TH)
- Hoặc hàm số luôn đơn điệu trên R
hàm số
không có cực trị
y' 0
hoặc vô nghiệm
hoặc có nghiệm kép
y'
0
- Hoặc hàm số có CĐ, CT và
cd ct
y .y 0
(hình
vẽ)
+) Đ
ể
(1) có đúng 3 nghi
ệ
m thì
đ
ồ
th
ị
y F x,m cắt trục hoành tại 3 điểm phân
biệt
Hàm số có cực đại, cực tiểu và
cd ct
y .y 0
cd ct
Bài toán: Tìm m để đồ thị hàm bậc 3 cắt trục hoành tại 3 điểm lập thành 1 cấp số cộng:
1. Định lí vi ét:
*) Cho bậc 2: Cho phương trình
2
ax bx c 0
có 2 nghiệm
1 2
x ,x
thì ta có:
1 2 1 2
b c
x x ,x x
a a
*) Cho bậc 3: Cho phương trình
3 2
ax bx cx d 0
có 3 nghiệm
1 2 3
x ,x ,x
thì ta có:
+) Để (1) có đúng 2 nghiệm thì đồ thị
y F
x,m
cắt trục hoành tại 2 điểm phân
biệt
Hàm số có cực đại, cực tiểu và
y .y 0
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 34
Facebook: https://www.facebook.com/dongpay
1 2 3 1 2 2 3 3 1 1 2 3
b c d
x x x , x x x x x x ,x x x
a a a
2.Tính chất của cấp số cộng:
+) Cho 3 số
a,b,c
theo thứ tự đó lập thành 1 cấp số cộng thì:
a c 2b
3. Phương pháp giải toán:
+) Điều kiện cần: là 1 nghiệm của phương trình. Từ đó thay vào phương trình để tìm m.
+) Điều kiện đủ: Thay m tìm được vào phương trình và kiểm tra.
Câu 1: Tìm số giao điểm của đồ thị hàm số
2
( 2)( 1)
y x x x
và trục hoành.
A.
1
. B.
0
. C.
2
. D.
3
.
Hướng dẫn giải:
Chọn A.
Ta có phương trình hoành độ giao điểm là
2
2
2 0
( 2)( 1) 2
1 0
x
y x x x x
x x
nên số giao
điểm là
1
.
Câu 2: Tìm
m
để phương trình
3 2
3 1 0
x x m
có ba nghiệm thực phân biệt
A.
1 5
m
. B.
1 5
m
. C.
5 1
m
. D.
1 5
m
.
Hướng dẫn giải:
Chọn B.
3 2 3 2
3 1 0 3 1
x x m x x m
Xét hàm số
3 2
3 1
xy x
ta có
2
0 1
6 03 ,
2 5
x y
x x y
x y
y
A.
3 1
m
. B.
2 0
m
. C.
3 1
m
. D.
3 0
m
.
A.
3
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Hướng dẫn giải:
Chọn A.
Xét phương trình hoành độ giao điểm :
3
1 3 1
mx x x
3
3 0
x x mx
2
3 0
x x m
0
3
b
x
a
Số nghiệm của phương trình
x
3
3x
2
m 1 0
là số giao điểm của đồ thị hàm số y x
3
3x
2
1 và đường
thẳng
y m
Phương trình
x
3
3x
2
m 1 0
có ba nghiệm thực phân biệt
5 m 1 1 m 5
.
Câu 3: Cho hàm số
y x
3
3x
2
1
có đồ thị
C
. Với giá trị nào của
m
thì phương trình
x
3
3x
2
m 2
có 3 nghiệm phân biệt trong đó có 2 nghiệm lớn hơn 1
Hướng dẫn giải:
Chọn B.
Dùng chức năng giải phương trình của máy tính. Chọn các giá trị m đại diện cho các phương án. Ta thay vào
phương trình và kiểm tra.
Phương án A. Lấy m 0,5 để thử. Loại A
Phương án C. Lấy m 2,5 để thử. Loại C, D
Vậy chọn B
Câu 4: Biết đường thẳng
y mx1
cắt đồ thị hàm số y x
3
3x 1 tại ba điểm phân biệt. Tất cả các
giá trị thực của tham số
m
là
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 35
Facebook: https://www.facebook.com/dongpay
2
0
3 1
x
x m
Để đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt thì
1
phải có 2 nghiệm phân biệt khác 0
3 0
m
3
m
.
Câu 5: Tìm m để phương trình
3 2
– 3 – 0
x x m
có ba nghiệm thực phân biệt
A.
4 0
m m
. B.
– 4 0 .
m
C.
4 0
m m
. D.
4 0.
m
Hướng dẫn giải:
Chọn D.
Xét
3 2
3
y x x m
Ta có
2
3 6
y x x
. Khi đó :
0
0
2
x
y
x
A.
2
2
m
m
. B.
2
m
. C.
2 2
m
. D.
2 2
m
.
Hướng dẫn giải:
Chọn D.
Ta có:
2
1 4 2
' 6 6 ' 0
1 4 2
x y m
y x y
x y m
Do hệ số
2 0
a
nên điểm cực đại
1; 4 2
m
và cực tiểu
1; 4 2
m
Để đồ thị của hàm số
3
2 6 2
y x x m
cắt trục hoành tại ít nhất 2 điểm phân biệt thì
. 0 4 2 . 4 2 0
CD CT
y y m m
A.
2 3
2
m
. B.
1 3
2
m
. C.
2 5
2
m
. D.
2 3
3
m
.
Hướng dẫn giải:
Chọn A.
2
3 3
y x m
.
Hàm số có cực đại cực tiểu
0
y
có hai nghiệm phân biệt
0
m
.
Khi đó đường thẳng qua hai điểm cực trị là
:2 2 0
mx y
.
2
2 1
, 1
4 1
m
d I R
m
(Do
luôn cắt đường tròn tại 2 điểm phân biệt)
Với
1
2
m
. Có
2
1 1 1
. . .sin
2 2 2
IAB
S IA IB AIB R
.
Để phương trình bài ra có 3 nghiệm thực phân biệt y
0
.y
2
0
m
.
m 4
0 4 m 0.
Câu 6: Điều kiện của tham số m để đồ thị của hàm số y 2x
3
6x 2m cắt trục hoành tại ít nhất
hai điểm phân biệt là
2 m 2.
Câu 7: Đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số y x
3
3mx 2 cắt đường tròn tâm
I
1;1
, bán kính bằng
1
tại
2
điểm phân biệt
A, B
sao cho diện tích tam giác
IAB
đạt giá trị lớn nhất khi m
có giá trị là
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 36
Facebook: https://www.facebook.com/dongpay
Do đó
0
max
1 2 2
1 90 ,
2 2 2
R
S SinAIB AIB d I .
Suy ra
2
2 2
2
2 1
2
2 2 1 4 1 4 8 1 0
2
4 1
m
m m m m
m
2 3
2
2 3
2
m n
m n
.
Câu 8: Cho hàm số
3
3 2
y x x
có đồ thị
C
. Gọi
d
là đường thẳng đi qua
3;20
A và có hệ số
góc
m
. Giá trị của
m
để đường thẳng d cắt
C
tại
3
điểm phân biệt là
A.
15
4
m
. B.
15
, 24
4
m m
. C.
15
, 24
4
m m
. D.
15
4
m
.
Hướng dẫn giải:
Chọn B.
Đường thẳng (d) đi qua
3;20
A có phương trình là:
3 20
y m x
.
Phương trình hoành độ giao điểm:
3
3 2 3 20
x x m x
3
( 3) 3 18 0
x m x m
2
2
( 3)( 3 6) 0
3
3 6 0 (*)
x x x m
x
x x m
Đặt:
2
( ) 3 6
g x x x m
Đường thẳng (d) cắt đồ thị
( )
m
C
tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt
khác 3.
15
9 4(6 ) 0
4
(3) 24 0
24
m
m
g m
m
Vậy, giá trị cần tìm là:
15
; 24
4
m m
Câu 9: Cho hàm số
3 2
( 3) (2 1) 3( 1)
y x m x m x m
. Tập hợp tất cả giá trị m để đồ thị hàm số
đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là
A.
B.
2;2 .
C.
; 4 .
D.
1; \ 2 .

.
Hướng dẫn giải:
Chọn A
Phương trình hoành độ giao điểm của đồ thị và trục hoành là :
3 2 2
( 3) (2 1) 3( 1) 0 1 4 3( 1) 0
x m x m x m x x m x m
ycbt
2
4 3( 1) 0
x m x m
có hai nghiệm âm phân biệt khác -1
2
2
2 0
2
4 0
4
1
3 1 0
2
1 4 1 3( 1) 0
m
b
m
m
m
a
m
c m
m
m
a
m m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 37
Facebook: https://www.facebook.com/dongpay
Câu 10: Tìm
m
để đồ thị hàm số
3 2
3 2
y x x
cắt đường thẳng
1
y m x
tại ba điểm phân
biệt có hoành độ
1 2 3
, ,
x x x
thỏa mãn
2 2 2
1 2 3
5.
x x x
A.
2.
m
B.
3.
m
C.
3.
m
D.
2.
m
Hướng dẫn giải:
Chọn
A
.
Phương trình hoành động giao điểm
3 2 2
3 2 1 1 2 2 0
x x m x x x x m
1
2
1
2 2 0 2
x
x x m
Để hai đồ thị hàm số cắt nhau tại
3
điểm phân biệt thì phương trình
1
có ba nghiệm phân biệt
phương trình
2
có hai nghiệm phân biệt khác
1
.
1 2 0
3
1 2 2 0
m
m
m
.
Gọi
1 2 3
1, ,
x x x
lần lượt là nghiệm của phương trình
1
2 3 2 3
2; . 2
x x x x m
.
Ta có:
2
2 2 2
1 2 3 2 3 2 3
5 2 4 4 2. 2 4 2
x x x x x x x m m
.
Câu 11: Cho hàm số
3 2
2 (1 ) (1)
y x x m x m . Tìm
m
để đồ thị hàm số (1) cắt trục hoành tại
3 điểm phân biệt có hoành độ
1 2 3
, ,
x x x
thỏa mãn điều kiện
2 2 2
1 2 3
4
x x x
A.
1
1
3
m
và
0
m
. B.
1
2
4
m
và
0
m
.
C.
1
1
4
m
. D.
1
1
4
m
và
0
m
.
Hướng dẫn giải:
Chọn D.
Xét phương trình
3 2 2
2
1
2 1 0 (1) 1 0
0 ( ) (2)
x
x x m x m x x x m
x x m g x
Để hàm số cắt trục hoành tại 3 điểm phân biệt
phương trình (2) phải có hai nghiệm phân
biệt khác 1
1
( ) 0 1 4 0
(*)
4
(1) 0 0
0
g x m
m
g m
m
Mặt khác
2 2 2
1 2 3
4
x x x
(
1 2 3
1 , ,
x x x
là hai nghiệm phương trình (2) )
2 2
2 3
3
x x
2
1 2 1 2
2 3
x x x x
1 2 3
m
1 2 3 1 (**)
m m
Từ (*) và (**) , ta có :
1
1
4
m
và
0
m
.
Câu 12: Cho hàm số
3 2
3 2
y x x
có đồ thị là
C
. Hỏi có tất cả bao nhiêu giá trị của tham số m
để đường thẳng
2
y mx
cắt đồ thị (C) tại ba điểm phân biệt có hoành độ
1 2 3
, ,
x x x
thỏa mãn điều
kiện
1 2 3 1 2 2 3 3 1
( ) 4
x x x x x x x x x
?
A.
3
. B.
2
. C.
0
. D.
1
.
Hướng dẫn giải:
Chọn D.
Phương trình hoành độ giao điểm của đồ thị
C
và đường thẳng
d
là
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 38
Facebook: https://www.facebook.com/dongpay
3 2
3 2
2
3 2 2
3 0
0
3 0 *
x x mx
x x mx
x
x x m
Đường thẳng
d
cắt đồ thị
C
tại
3
điểm phân biệt
phương trình
*
có hai nghiệm phân biệt khác
0
.
9
9 4 0
4
0
0
m
m
m
m
Không mất tính tổng quát gọi
3
0
x
,
1 2
,
x x
là nghiệm của phương trình
*
.
1 2 3 1 2 2 3 3 1 1 2 1 2
( ) 4 4
3 4 1
x x x x x x x x x x x x x
m m tm
Câu 13: Cho hàm số
3
3 2
y x x
có đồ thị
C
. Gọi
d
là đường thẳng đi qua
3;20
A và có hệ số góc
m
. Giá trị của
m
để đường thẳng
d
cắt
C
tại 3 điểm phân biệt là
A.
15
4
m
B.
15
, 24
4
m m
C.
15
, 24
4
m m
D.
15
4
m
.
Hướng dẫn giải:
Chọn C.
+ Đường thẳng
d
qua
3;20
A và có hệ số góc
m
có dạng:
20 3 3 20.
y m x y mx m
+Phương trình hoành độ giao điểm của
d
và
C
là:
3
3 2 3 20.
x x mx m
3 2
2
3
3 3 18 0 3 3 6 0 .
3 6 0 *
x
x m x m x x x m
x x m
+
d
cắt
C
tại 3 điểm phân biệt
*
có 2 nghiệm phân biệt
3
15
4 15 0
.
4
9 9 6 0
24
m
m
m
m
Câu 14: Tìm
m
để đường thẳng
: 1 1
d y m x cắt đồ thị
C
hàm số
3
3 1
y x x
tại ba điểm
phân biệt
1;1
A ,
B
,
C
.
A.
0
m
. B.
9
4
m .
C.
9
0
4
m . D.
0
m
hoặc
9
4
m .
Hướng dẫn giải:
Chọn C
Phương trình hoành độ giao điểm là
3 2
3 1 1 1 1 2 0
x x m x x x x m
2
1
2 0
x
f x x x m
. Để đường thẳng
d
cắt đồ thị
C
tại hai điểm phân biệt thì phương trình
0
f x
có hai nghiệm phân biệt khác
1
, khi đó ta có
1 0
9
; 0
49 0
\
4
f
f m
m
m

.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 39
Facebook: https://www.facebook.com/dongpay
Câu 15: Tìm
m
để đồ thị
C
của
3 2
3 4
y x x
và đường thẳng
y mx m
cắt nhau tại
3
điểm phân
biệt
1;0 , ,
A B C
sao cho
OBC
có diện tích bằng
8
A.
3
m
. B.
1
m
. C.
4
m
. D.
2
m
.
Hướng dẫn giải:
Chọn C
Phương trình hoành độ giao điểm:
3 2 2
2
3 4 1 4 4 0
1
4 4 0
x x mx m x x x m
x
x x m
Đường thẳng
y mx m
cắt
C
tại ba điểm phân biệt khi và chỉ khi phương trình
2
4 4 0
x x m
(1) có
hai nghiệm phân biệt khác
1
. Điều này tương đương với
0 0
9 9
m
m m
.
Gọi
,
B C
x x
là hai nghiệm phân biệt của (1). Theo định lý Viet, ta có
4
. 4
B C
B C
x x
x x m
Ta có phương trình đường thẳng
BC
:
0
y mx m mx y m
d
Mặt khác
2 2
2
2 2 2
2
2 2
2
1 1
. ; . . .
2 2
1
1 1
. . . . 1
2 2
1 1
1 1
. . 4 . . 4 .
2 2
OBC B C B C
B C B C B C
B C B C
m
S d O BC BC x x y y
m
m m
x x mx mx m x x
m m
m x x x x m m m m
Giả thiết
8
OBC
S
suy ra
. 8 4
m m m
.
Câu 16: Cho hàm số
3 2
3 4
y x x có đồ thị
C
. Gọi
d
là đường thẳng đi qua
1;0
A và có hệ số
góc
k
. Tìm
m
để đường thẳng
d
cắt đổ thị
C
tại
3
điểm phân biệt
, ,
A B C
sao cho diện tích tam giác
OBC
bằng
1
.
A.
2
k
. B.
1
k
. C.
1
k
. D.
2
k
.
Hướng dẫn giải:
Chọn B
Phương trình đường thẳng
:
d y kx k
.
PTHĐGĐ của
C
và
d
là:
3 2 2
3 4 0 1 4 4 0
x x kx k x x x k
2
1
4 4 0
x
x x k
Đường thẳng
d
cắt đổ thị
C
tại
3
điểm phân biệt khi phương trình
2
4 4 0
g x x x k
có hai
nghiệm phân biệt khác
1
.
0
0
1
1 0
g
k
k
g
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 40
Facebook: https://www.facebook.com/dongpay
2
1 ; . 2 . 2
1
OBC
k
S d O d BC BC
k
trong đó
, ,C ,
B B C C
B x y x y
là tọa độ giao điểm của
C
và
d
,
,
B C
x x
là nghiệm của phương trình
0
g x
.
; ;
C B C B C B C B
BC x x y y x x k x x
2
2 2 2
1 1 . 4 1 . 4
C B C B B C
BC k x x k x x x x k k
Khi đó:
. 1 1
k k k
.
Câu 17: Đường thẳng
: 4
d y x
cắt đồ thị hàm số
3 2
2 3 4
y x mx m x
tại 3 điểm phân biệt
0;4 ,
A B
và
C
sao cho diện tích tam giác
MBC
bằng 4, với
1;3 .
M Tìm tất cả các giá trị của
m
thỏa
mãn yêu cầu bài toán.
A.
2
m
hoặc
3.
m
B.
2
m
hoặc
3.
m
C.
3.
m
D.
2
m
hoặc
3.
m
Hướng dẫn giải:
Chọn C
Phương trình hoành độ giao điểm
3 2
2 2 0
x mx m x
2
0
2 2 0 *
x
x mx m
Để
d
cắt đồ thị hàm số tại 3 điểm phân biệt thì (*) có 2 nghiệm phân biệt khác
0
.
2
0
1 2
3 2 0
2
0 0 2 0
g
m m
m
m
g m
.
Gọi
1 2
,
x x
là nghiệm của phương trình (*)
Có
1 1 2 2
, 4 , , 4
B x x C x x
2 2
2
2 1 1 2 1 2
2 2 8 8 2
BC x x x x x x m m
Có
4
MBC
S
1
, . 4
2
d M d BC
2
2. 8 2 8
m m
2
3
6 0
2 ( )
m
m m
m L
.
Câu 18: Cho hàm số
3
3 2
y x x
có đồ thị
C
. Gọi
d
là đường thẳng đi qua điểm
3;20
A và có hệ số
góc là
m
. Với giá trị nào của
m
thì
d
cắt
C
tại 3 điểm phân biệt?
A.
1
5
0
m
m
. B.
15
4
24
m
m
. C.
15
4
24
m
m
. D.
1
5
1
m
m
.
Hướng dẫn giải:
Chọn B.
Phương trình của
: ( 3) 20
d y m x
.
Phương trình hoành độ giao điểm của
d
và
C
:
3
3 2 ( 3) 20
x x m x
2
3 3 6 0
x x x m
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 41
Facebook: https://www.facebook.com/dongpay
d
và
C
cắt nhau tại 3 điểm phân biệt
phương trình
2
3 6 0
x x m
có 2 nghiệm phân biệt khác 3
9 4 6 0
3 24 0
m
f m
15
4
24.
m
m
Câu 19: Hàm số
3 2
3 2
y x x mx m
. Đồ thị của hàm số cắt trục
Ox
tại 3 điểm phân biệt khi:
A.
2
m
. B.
3
m
. C.
3
m
. D.
3
m
.
Hướng dẫn giải:
Chọn B.
Xét phương trình hoành độ giao điểm ta có
3 2 2
3 2 0 1 2 2 0
x x mx m x x x m
2
1
2 2 0 *
x
x x m
.
Để đồ thị hàm số cắt trục
Ox
tại 3 điểm phân biệt khi phương trình
*
có 2 nghiệm phân biệt
1
x
.
1 2 0
3
3
3
1 2 2 0
m
m
m
m
m
.
Câu 20: Để đường thẳng
:
d y mx m
cắt đồ thị hàm số
3 2
3 4
y x x
tại
3
điểm phân biệt
1;0 , ,
M A B
sao cho
2
AB MB
khi:
A.
9
.
4
m
B.
0
.
9
m
m
C.
0
.
9
m
m
D.
0
.
9
m
m
Hướng dẫn giải:
Chọn A.
Phương trình hoành độ giao điểm của đường thẳng
d
và đồ thị hàm số
3 2
3 4
x mx m
x
3 2
3 4 0
x x mx m
2
1
4 4 0(*)
x
x x m
Để đường thẳng
d
cắt đồ thị tại 3 điểm phân biệt thì phương trình
*
có hai nghiệm phân biệt khác
1
' 0 0
9 9
m m
m m
Gọi
1 1
;A x mx
m
,
2 2
;B x mx
m
(
1 2
;
x
x
là nghiệm phương trình
*
)
2 2 2
2 2
2 1 2 1 2 1
1x mAB x mx m
x
xx
2
2 2
2 2 2 2
2 2
1 1 1 1
M x xmB m x
2 2
4
AB MB
2 2
2 1 2
4 1
xx x
Mà
2
2
2 1
4 4
x Sx
P m
2
2
1
m x
Mà
1 2 1 2 2 2
4, 4 4
4x x x mx x x m
2
2 2 2
4
1 4
x x x
2
1
2
x
9
4
m
(nhận).
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 42
Facebook: https://www.facebook.com/dongpay
DẠNG 4: TƯƠNG GIAO CỦA HÀM SỐ PHÂN THỨC
Phương pháp
Cho hàm số
ax b
y C
cx d
và đường thẳng
d : y px q
. Phương trình hoành độ giao điểm của (C) và (d):
ax b
px q F x,m 0
cx d
(phương trình bậc 2 ẩn x tham số m).
*) Các câu hỏi thường gặp:
1. Tìm m để d cắt (C) tại 2 điểm phân biệt
1
có 2 nghiệm phân biệt khác
d
c
.
2. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh phải của (C)
1
có 2 nghiệm phân biệt
1 2
x ,x
và thỏa mãn
1 2
d
: x x
c
.
3. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh trái của (C)
1
có 2 nghiệm phân biệt
1 2
x ,x
và thỏa mãn
1 2
d
x x
c
.
4. Tìm m để d cắt (C) tại 2 điểm phân biệt thuộc 2 nhánh của (C)
1
có 2 nghiệm phân biệt
1 2
x ,x
và thỏa
mãn
1 2
d
x x
c
.
5. Tìm m để d cắt (C) tại 2 điểm phân biệt A và B thỏa mãn điều kiện hình học cho trước:
+) Đoạn thẳng
AB k
+) Tam giác
ABC
vuông.
+) Tam giác ABC có diện tích
0
S
* Quy tắc:
+) Tìm điều kiện tồn tại A, B
(1) có 2 nghiệm phân biệt.
+) Xác định tọa độ của A và B (chú ý Vi ét)
+) Dựa vào giả thiết xác lập phương trình ẩn m. Từ đó suy ra m.
*) Chú ý: Công thức khoảng cách:
+)
B
2
2
A A B B B A A
A x ;y ,B x ;y :AB x x y y
+)
0 00 0
2 2
0 0
Ax By C
M x ;y
d M,
:Ax By C 0
A B
BÀI TẬP:
Câu 1: Cho hàm số
2 3
1
x
y
x
. Đồ thị hàm số cắt đường thẳng
y x m
tại 2 giao điểm khi
A.
1; 3
m m
. B.
1; 3
m m
. C.
1 3
m
. D.
1; 7
m m
.
Hướng dẫn giải:
Chọn A
Phương trình hoành độ giao điểm
2 3
1
x
x m
x
2
3 3 0
x m x m
Ycbt
0
2
2 3 0 1 3
m m m m
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 43
Facebook: https://www.facebook.com/dongpay
Câu 2: Cho hàm số
1
x
y
x
có đồ thị
C
. Tìm
m
để đường thẳng :
d y x m
cắt đồ thị
C
tại hai điểm phân biệt ?
A.
1 4
m
.
B.
0
m
hoặc
2
m
.
C.
0
m
hoặc
4
m
.
D.
1
m
hoặc
4
m
.
Hướng dẫn giải:
Chọn C.
Xét phương trình hoành độ giao điểm 2 đồ thị hàm số:
1
2
0 *
1
x
x
x m x mx m
x
.
Hai đồ thị hàm số cắt nhau tại 2 điểm phân biệt
*
có 2 nghiệm phân biệt khác 1
2
0
4
4 0
1 0
0
1 0
m
m m
f
m
m m
.
Câu 3: Tìm tham số
m
để đường thẳng cắt đồ thị hàm số
2 1
:
1
x
C y
x
tại hai điểm phân
biệt
A.
3 2 3;3 2 3
m
. B.
;3 2 3 3 2 3;m
 
.
C.
2;2
m
. D.
;1 1;m
.
Hướng dẫn giải:
Chọn B.
Phương trình hoành độ giao điểm của
C
và
d
là.
1 2 1
2 1
1
1
x x m x
x
x m
x
x
.
2
1 1 0 1
1
x m x m
x
.
C
và
d
cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình
1
có 2 nghiệm phân biệt khác
1
2
0
6 3 0 3 2 3 3 2 3
1 1 1 0
m m m m
m m
.
Câu 4: Tìm tập hợp tất cả các giá trị của tham số
m
sao cho đường thẳng
1
y mx
cắt đồ thị của hàm số
3
1
x
y
x
tại hai điểm phân biệt.
A.
;0 16;
 
. B.
;0 16;

. C.
16;

. D.
;0
 .
Hướng dẫn giải:
Chọn B.
Phương trình hoành độ giao điểm:
3
1
1
x
mx
x
2
4 0 *
mx mx ,
1
x
.
:
d y x m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 44
Facebook: https://www.facebook.com/dongpay
Yêu cầu bài toán
phương trình
*
có hai nghiệm phân biệt khác
1
2
2
16 0
1 1 4 0
m m
m m
;0 16;
4 0
m

;0 16;m

.
Câu 5: Cho hàm số
2
1
mx
y
x
m
C
. Tìm
m
để giao điểm của hai tiệm cận của
m
C
trùng với tọa độ đỉnh
của Parabol
2
: 2 3
P y x x
.
A.
2
m
. B.
1
m
. C.
0
m
. D.
2
m
.
Hướng dẫn giải:
Chọn A.
Giao điểm hai tiệm cận
mI ;1
Tọa độ đỉnh của (P):
2;1J
. Vậy 2
m .
Câu 6: Biết rằng đường thẳng : 3
d y x m
cắt đồ thị
2 1
:
1
x
C y
x
tại 2 điểm phân biệt
A
và
B
sao
cho trọng tâm của tam giác
OAB
thuộc đồ thị
,
C
với
0;0
O là gốc tọa độ. Khi đó giá trị của tham số
m
thuộc tập hợp nào sau đây ?
A.
; 3 .

B.
;18
.
C.
18;2
.
D.
5; 2 .
Hướng dẫn giải:
Chọn C.
Phương trình hoành độ giao điểm:
10113
1
12
3
2
xmxmxxf
x
x
mx
(*)
Đường thẳng cắt đồ thị tại hai điểm phân biệt khi pt (*) phải có hai nghiệm phân biệt khác 1
11
1
01
0
m
m
f
Gọi hai giao điểm là
mxxBmxxA
2211
3;,3;
G là trọng tâm tam giác OAB
3
1
3
23
9
1
3
21
21
mmxx
y
mxx
x
G
G
G thuộc đồ thị hàm số khi
.
2
13515
02515
1
9
1
1
9
1
.2
3
1
2
mmm
m
m
m
Câu 7: Những giá trị của
m
để đường thẳng
1
y x m
cắt đồ thị hàm số
2 1
1
x
y
x
tại hai điểm phân biệt
,
A B
sao cho
2 3
AB là
A.
4 10
m . B.
4 3
m . C.
2 3
m . D.
2 10
m .
Hướng dẫn giải:
Chọn A.
Phương trình hoành độ giao điểm
2 1
1
1
x
x m
x
2
2 2 0, 1
g x x m x m x
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 45
Facebook: https://www.facebook.com/dongpay
Đồ thị hai hàm số có hai giao điểm khi và chỉ khi
0
g x
có hai nghiệm phân biệt khác
1
.
0
2
1 0
6
m
g
m
Khi đó
1 1 2 2
; 1 , ; 1
A x x m B x x m
và
2 2
2 1
2 2 8 12
AB x x m m .
Theo giả thiết
2
2 3 2 8 12 12 4 10
AB m m m (thoả điều kiện).
Câu 8:Cho hàm số
2 1
1
x
y
x
có đồ thị
( )
C
. Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
1 ( )
y x m d
cắt đồ thị tại hai điểm phân biệt sao cho
2 10
AB
?
A.
1
.
B.
.
1;3
C.
.
1;1
D.
1;

Hướng dẫn giải:
Chọn D.
Phương trình hoành độ giao điểm của đồ thì và đường thẳng:
2 2
2 1
1 1 2 2 1
1 2 0
1
x
x m x x xmx x m xm x m
x
.
Đường thẳng
d
và đồ thị cắt nhau tại 2 điểm phân biệt thì phương trình
1
có hai nghiệm phân biệt khác
1
.
Khi đó ta có
0
6
2 6 0
2
1 0 1 0
m
m m
m
f
.
Gọi
1 2
;
x x
là nghiệm của
1
. Ta có
1 2
1 2
2
2
x x m
x x m
.
Ta đặt
1 1 2 2
; 1 ;B ; 1
A x x m x x m
. Ta có :
2 2
2
1 2 1 2 1 2
2 10 2 2 3 4 12 4 4 4 8 6
AB x x x x x x m m m
2
4 10
8 6 0
4 10
m
m m
m
. Kết hợp điều kiện ta có
4 10
4 10
m
m
.
Câu 9: Tìm tất cả các giá trị của tham số m để đường thẳng
:
d y x m
cắt đồ thị hàm số
2 1
1
x
y
x
tại hai điểm A, B sao cho
2 2
AB
A.
1, 2
m m
. B.
1, 7
m m
. C.
7, 5
m m
. D.
1, 1
m m
.
Hướng dẫn giải:
Chọn B
Phương trình hoành độ giao điểm của đồ thị và đường thẳng d là :
2 2
2
2
2 1
2 1 1 1 0
1
1 4 1 6 3
x
x m x x mx x m x m x m
x
m m m m
Đồ thị cắt đường thẳng d tại hai điểm
2
0 6 3 0
m m
(*)
Khi đó tọa độ giao điểm lần lượt là :
2 2 2 2
1 6 3 1 6 3 1 6 3 1 6 3
; , ;
2 2 2 2
m m m m m m m m m m m m
A B
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 46
Facebook: https://www.facebook.com/dongpay
2 2 2
6 3; 6 3 2 6 3
AB m m m m AB m m
Theo đề :
2 2
1
2 2 6 3 2 6 7 0
7
m
AB m m m m
m
( thỏa (*)).
Câu 10:Cho hàm số
2 1
1
x
y
x
có đồ thị
C
. Tìm tất cả giá trị của m để đường thẳng
: 1
d y x m
cắt
C
tại 2 điểm phân biệt A, B sao cho
2 3
AB
A.
4 3
m . B.
4 10
m . C.
2 3
m . D.
2 10
m .
Hướng dẫn giải:
Chọn D.
Phương trình hoành độ giao điểm:
1022
1
12
1
2
xmxmxxf
x
x
mx
(*)
Đường thẳng cắt đồ thị tại hai điểm phân biệt khi pt (*) phải có hai nghiệm phân biệt khác -1
6
2
01
0
m
m
f
Gọi hai giao điểm là
1;,1;
2211
mxxBmxxA
.1020624232
2
mmmAB
Câu 11: Tìm tất cả các giá trị của tham số m sao cho đường thẳng :
d y x m
cắt đồ thị hàm số
2 1
( ):
1
x
C y
x
tại hai điểm phân biệt
,
M N
sao cho diện tích tam giác
IMN
bằng
4
với
I
là tâm đối xứng
của
( )
C
A.
3; 1
m m
. B.
3; 5
m m
. C.
3; 3
m m
. D.
3; 1
m m
.
Hướng dẫn giải:
Chọn A.
Đồ thị hàm số có tiện cận đứng
1
x
.
Đồ thị hàm số có tiện cận ngang
2.
y
Tâm đối xứng của đồ thị có tọa độ
1;2
I
;
1
: 0
2
I d
m
d y x m x y m d
Xét phương trình hoành độ giao điểm
2
2 1
3 1 0 1
1
x
x m x m x m
x
Gọi
1 2
;
x x
là nghiệm phương trình
1
. Theo Viet ta có :
1 2
1 2
3
1
x x m
x x m
Giả sử
1 1 2 2
; ; ;
M x x m N x x m
2 2 2
2
2 1 2 1 1 2
2 2 8 2 3 8 8 2 4 26
MN x x x x x x m m m m
Diện tích tam giác
IMN
là:
2
2
1 1 2 13
1
2 4 26 4
2 2
2
m m m m
m m
2
2 2
2
1 4
1 1 12 64
1 16
m
m m
m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 47
Facebook: https://www.facebook.com/dongpay
Do
2 2
3
1 0 1 4 .
1
m
m m
m
Câu 12: Xác định tất cả giá trị
m
để đồ thị hàm số
2
2 4
1
x x
y
x
cắt đường thẳng
4
y m x
tại hai
điểm phân biệt.
A.
2
2, , 1
3
m m m
. B.
1
m
.
C.
m
. D.
2
–2 , 0
3
m m
.
Hướng dẫn giải:
Chọn A.
TXD:
1
x
.
Ta có phương trình hoành độ giao điểm của đồ thị và đường thẳng là :
2
2 2
2 4
4 2 4 4 1 1 2 5 4 4 0 1
1
x x
m x x x m x x m x m x m
x
.
Để đồ thị cắt đường thẳng tai hai điểm phân biệt thì
2
1
1
1 0
2
0 3 4 4 0
2
3 0
1 0
3
m
m
m
m
m m
m
f
.
Câu 13:Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
2
3
3
x mx
y
x
cắt đường thẳng
7
y mx
tại 2 điểm phân biệt?
A.
19
2
m B.
19
1
2
m vàm
C.
19
2
m
. D.
19
1
2
m vàm
Hướng dẫn giải:
Chọn B
2
2 22
3
7 3 7 3 21 1 07
3
21 1
x mx
mx x mx x mxm m xx x
x
Ycbt
1
có 2 nghiệm phân biệt
1
1
19
49 84 1 0
12
m
m
m
m
Câu 14:Cho hàm số
2 1
2
x
y
x
có đồ thị là
C
. Tìm tất cả các giá trị của
m
để đường thẳng
d
đi qua
0;2
A có hệ số góc
m
cắt đồ thị
C
tại 2 điểm thuộc 2 nhánh của đồ thị
A.
0
m
. B.
0
m
. C.
5
m
. D.
0
m
hoặc
5
m
.
Hướng dẫn giải:
Chọn B
Phương trình đường thẳng
d
đi qua
0;2
A và có hệ số góc
m
có dạng:
2
y mx
.
Xét phương trình hoành độ giao điểm
2 1
2, 2 .
2
x
mx x
x
2 2
2 2 4 2 1 2 5 0 1
mx x mx x mx mx
Mặt khác đồ thị hàm số có tiệm cận đứng là đường thẳng
2
x
nên
Để
d
cắt
C
tại hai điểm phân biệt nằm về hai nhánh của đồ thị thì khi và chỉ khi phương trình
1
có hai
nghiệm phân biệt
1 2
,
x x
sao cho
1 2
2
x x
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 48
Facebook: https://www.facebook.com/dongpay
Đặt
2
t x
khi đó phương trình
1
trở thành
2
2
2 2 2 5 0 2 5 0 2
m t m t mt mt
Khi đó Ycbt tương đương với phương trình
2
có hai nghiệm trái dấu
. 0 . 5 0 0
a c m m
. Vậy
0
m
thì thỏa Ycbt.
Câu 15: Tìm tất các giá trị thực của tham số
m
để đồ thị
C
của hàm số
2 3
1
x
y
x
cắt đường thẳng
:
y x m
tại hai điểm phân biệt
A
và
B
sao cho tam giác
OAB
vuông tại
O
A.
6
m
. B.
3
m
. C.
5
m
. D.
1
m
.
Hướng dẫn giải:
Chọn A.
Ta có: phương trình hoành độ giao điểm của
( )
C
2 3
1
x
y
x
và đường thẳng :
y x m
:.
2 3
( 1)
1
x
x m x
x
.
2 2
2 3 ( )( 1) 2 3 ( 3) 3 0.
x x m x x x x mx m x m x m .
2 2 2
( 3) 4( 3) 2 21 ( 1) 20 0m m m m m m
.
Suy ra:
luôn cắt
( )
C
tại hai điểm phân biệt.
Gọi
( ; ); ( ; )
A A B B
A x y B x y
là hai giao điểm của
và
( )
C
.
Mặt khác: Tam giác
OAB
vuông tại
O
. 0
OA OB

.
2
2
. ( )( ) 0 2 . ( ) 0
( 3) 2( 3) 0 6.
A B A B A B A B
x x x m x m x x m x x m
m m m m m
.
Câu 16: Tập hợp tất cả các giá trị của tham số thực
m
sao cho phương trình
2
1
x
m
x
có đúng hai
nghiệm phân biệt là
A.
0;2
.
B.
1;2
.
C.
1;2 0
.
D.
1;2 0
.
Hướng dẫn giải:
Chọn D.
Hàm số
2
( )
1
x
y f x
x
được suy từ hàm số
2
1
x
y
x
bằng cách sau.
+ Giữ nguyên phần đồ thị hàm số
( )
y f x
ở phía phải trục Oy.
+ Lấy đối xứng phần đồ thị vừa giữ lại của
( )
y f x
qua Oy.
+ Giữ nguyên phần đồ thị hàm số
( )
y f x
ở phía trên trục Ox.
+ Lấy đối xứng phần đồ thị phía dưới Ox của
( )
y f x
qua Ox.
Số nghiệm của phương trình
(| |)
f x m
là số giao điểm của đồ thị hàm số
(| |)
y f x
và đường thẳng
.
y m
Ta kết luận, phương trình có 2 nghiệm phân biệt khi
1;2 0 .
m
Câu 17: Biết rằng đường thẳng
:
d y x m
luôn cắt đường cong
2 1
:
2
x
C y
x
tại hai điểm phân
biệt
A
,
B
. Độ dài đoạn
AB
đạt giá trị nhỏ nhất bằng bao nhiêu?
A. 4. B.
6
. C.
3 6
. D.
2 6
.
Hướng dẫn giải:
Chọn D.
Phương trình hoành độ giao điểm:
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 49
Facebook: https://www.facebook.com/dongpay
2
2
2 1
2
2
4 1 2 0 1
12 0,
x
x m x
x
x m x m
m m
Phương trình
1
luôn có 2 nghiệm phân biệt
,
A B
x x
tức đường thẳng
d
luôn cắt
C
tại hai điểm phân biệt
1 1 2 2
; , ;
A x y B x y
. Ta có:
2 2 2 2
2 1 2 1 2 1 2 1
2
2
2
2 1
2 2 2 12
AB x x y y x x x x
x x m
AB
đạt giá trị nhỏ nhất bằng
2 6
khi
0.
m
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 50
Facebook: https://www.facebook.com/dongpay
DẠNG 5: SỰ TƯƠNG GIAO CỦA HÀM SỐ BẬC 4
NGHIỆM CỦA PHƯƠNG TRÌNH BẬC 4 TRÙNG PHƯƠNG:
4 2
ax bx c 0
(1)
1. Nhẩm nghiệm:
- Nhẩm nghiệm: Giả sử
0
x x
là một nghiệm của phương trình.
- Khi đó ta phân tích:
0
2 2
0
x x
f x,m x x g x 0
g x 0
- Dựa vào giả thiết xử lý phương trình bậc hai
g x 0
2. Ẩn phụ - tam thức bậc 2:
- Đặt
2
t x , t 0
. Phương trình:
2
at bt c 0
(2).
- Để (1) có đúng 1 nghiệm thì (2) có nghiệm
1 2
t ,t
thỏa mãn:
1 2
1 2
t 0 t
t t 0
- Để (1) có đúng 2 nghiệm thì (2) có nghiệm
1 2
t ,t
thỏa mãn:
1 2
1 2
t 0 t
0 t t
- Để (1) có đúng 3 nghiệm thì (2) có nghiệm
1 2
t ,t
thỏa mãn:
1 2
0 t t
- Để (1) có đúng 4 nghiệm thì (2) có nghiệm
1 2
t ,t
thỏa mãn:
1 2
0 t t
3. Bài toán: Tìm m để (C):
4 2
y ax bx c 1
cắt (Ox) tại 4 điểm có hoành độ lập thành cấp số cộng.
- Đặt
2
t x , t 0
. Phương trình:
2
at bt c 0
(2).
- Để (1) cắt (Ox) tại 4 điểm phân biệt thì (2) phải có 2 nghiệm dương
1 2 1 2
t ,t t t
thỏa mãn
2 1
t 9t
.
- Kết hợp
2 1
t 9t
vơi định lý vi ét tìm được m.
BÀI TẬP:
Câu 1: Số giao điểm của trục hoành và đồ thị hàm số
4 2
2 3
y x x
là:
A. 1. B. 3. C. 2. D. 4.
Hướng dẫn giải:
Chọn C.
Phương trình hoành độ giao điểm:
4 2
2 3 0 3
x x x
.
Vậy có hai giao điểm.
Câu 2:Hàm số
4 2
y x x
, có số giao điểm với trục hoành là:
A.
1
. B.
2
. C.
3
. D.
4
.
Hướng dẫn giải:
Chọn C.
Xét phương trình hoành độ giao điểm
4 2
0
x x
2 2
1 0
x x
0
1
x
x
.
Câu 3:Cho hàm số
4 2
2 1
y x x
. Tìm số giao điểm của đồ thị hàm số với trục
Ox
:
A. 1. B. 3. C. 4. D. 2.
Hướng dẫn giải:
Chọn D.
Xét phương trình
2
4 2
2
1 2
0 2 1 0 (1)
1 2
x
y x x
x
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 51
Facebook: https://www.facebook.com/dongpay
2
1 2
x
1 2
x
Phương trình (1) có hai nghiệm
số giao điểm của đồ thị với trục
Ox
là 2
Câu 4: Tìm tất cả các giá trị thực của tham số
m
để đồ thị hàm số
4 2
: 1
m
C y x mx m
cắt trục hoành
tại bốn điểm phân biệt
A.
1
m
. B.
1
2
m
m
. C. không có
m
. D.
2
m
.
Hướng dẫn giải:
Chọn B.
Xét phương trình hoành độ giao điểm
4 2
1 0
x mx m
.
Đặt
2
, 0
t x t
ta được phương trình
2
1 0
t mt m
.
Để đồ thị hàm số
4 2
: 1
m
C y x mx m
cắt trục hoành tại bốn điểm phân biệt thì phương trình
2
1 0
t mt m
phải cóhai nghiệm dương phân biệt.
2
0 4 4 0
2
0 1 0
1
0 0
m m
m
P m
m
S m
.
Cách 1:
Phương trình hoành độ giao điểm của
( )
m
C
và trục hoành:
4 2
1 0.
x mx m
Đặt
2
0
t x
, phương trình trên thành:
2
1 0 (*)
t mt m
.
( )
m
C
cắt trục hoành tại 4 điểm phân biệt.
phương trình
(*)
có 2 nghiệm dương phân biệt.
2
( 2) 0
0 1 0 1 2.
0 0
m
P m m
S m
.
Câu 5: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số
4 2
: 1
m
C y x mx m
cắt trục hoành
tại bốn điểm phân biệt
A.
1
m
. B.
1
2
m
m
. C. không có
m
. D.
2
m
.
Hướng dẫn giải:
Chọn B.
Cách 1:
Phương trình hoành độ giao điểm của
( )
m
C
và trục hoành:
4 2
1 0.
x mx m
Đặt
2
0
t x
, phương trình trên thành:
2
1 0 (*)
t mt m
.
( )
m
C
cắt trục hoành tại 4 điểm phân biệt.
phương trình
(*)
có 2 nghiệm dương phân biệt.
2
( 2) 0
0 1 0 1 2.
0 0
m
P m m
S m
.
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 52
Facebook: https://www.facebook.com/dongpay
Cách 2:
Ta có:
4 2
1
y x mx m
.
Tập xác định:
D
.
3
' 4 2
y x mx
.
3
2
0.
' 0 4 2 0
.
2
x
y x mx
m
x
.
Đồ thị hàm số cắt trục hoành tai bốn điểm phân biệt
0
m
.
Ta có:
2
2
0 1.
( 0) 1.
2 4
x y m
m m
x m y m
.
Bảng biến thiên
x
2
m
0
.
2
m
y
0
0
0
y
. .
2
1
4
m
m
1
m
.
2
1
4
m
m
.
.
Yêu cầu bài toán
2
1 0
1.
2.
1 0
4
m
m
m
m
m
.
Câu 6:Tìm tất cả các giá trị của tham số
m
để đồ thị hàm số
4 2
2
y x x m
cắt trục hoành tại đúng hai
điểm
A.
1.
m
B.
0;m 1.
m
C.
0.
m
D.
3.
m
TH1:
2
có nghiệm kép dương
1 0
1
1 0
m
m
t
TH2:
2
có hai nghiệm trái dấu
0 0
ac m
Giá trị m cần tìm
0
1
m
m
.
Hướng dẫn giải:
Chọn B
TX Đ:
Để đồ thị
hàm số
y x
4
2x
2
m
cắt trục hoành tại đúng hai điểm thì phương trình sau có hai
nghiệm:
x
4
2x
2
m 0
1
Đặt x
2
t
t 0
. Khi đó phương trình
1
trở thành:
.
t
2
2t m 0
2
1
có hai nghiệm khi
2
có một nghiệm dương:
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 53
Facebook: https://www.facebook.com/dongpay
Câu 7:Tìm tập hợp tất cả giá trị thực m để đồ thị
m
C
của hàm số
4 2
2 3
y x mx m
có 4 giao
điểm với đường thẳng
1
y
, có hoành độ nhỏ hơn 3
A.
2;11 \ 4 .
m B.
2;11 .
m
C.
2; \ 4 .
m
D.
2;5 .
m
.
Hướng dẫn giải:
Chọn A
Phương trình hoành độ giao điểm của đồ thị
m
C
với đường thẳng
1
y
là :
4 2 4 2
2 3 1 2 4 0
x mx m x mx m
(phương trình trùng phương *)
2
2
4 2 4 4 0
m m m
Phương trình (*) có 4 nghiệm phân biệt
0
4
0 0 2; \ 4
2
2 4 0
m
b
m m m
a
m
c
m
a

(1)
Khi đó , ta có :
2
2
2
4
2 2
2
2
2
m m
x m x m
x
x
x
Vì hoành độ giao điểm nhỏ hơn 3 nên
2 3 11
m m
(2)
Từ (1), (2) suy ra
2;11 \ 4
m thỏa ycbt.
| 1/53
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 1
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
SỰ TƯƠNG GIAO CỦA ĐỒ THỊ HÀM SỐ
DẠNG 1: TỌA ĐỘ GIAO ĐIỂM CỦA HAI ĐỒ THỊ HÀM SỐ: Phương pháp: Cho 2 hàm số
có đồ thị lần lượt là (C) và (C’).
+) Lập phương trình hoành độ giao điểm của (C) và (C’):
+) Giải phương trình tìm x từ đó suy ra y và tọa độ giao điểm.
+) Số nghiệm của (*) là số giao điểm của (C) và (C’).
Câu 1: Số giao điểm của đường cong 3 2
y x  2x  2x 1 và đường thẳng y  1 x bằng A. 1. B. 2. C. 3. D. 0. Hướng dẫn giải: Chọn đáp án A.
Xét phương trình hoành độ giao điểm: 3 2 3 2
x  2x  2x  1  1 x x  2x  3x  0  x  0.
Vậy đường cong và đường thẳng có 1 giao điểm.
Câu 2: Tìm số giao điểm của đồ thị C  : 3
y x x  2 và đường thẳng y x  1 . A. 2 . B. 3 . C. 0 . D. 1 . Hướng dẫn giải: Chọn đáp án D.
Phương trình hoành độ giao điểm: 3 3
x x  2  x  1  x  1  x  1.
Vậy C  và đường thẳng y x 1 chỉ có 1 giao điểm.
Câu 3: Tìm số giao điểm của đồ thị hàm số 4 2
y x  4x  1 và đường thẳng y  3  . A. 0 . B. 2 . C. 3 . D. 4. . Hướng dẫn giải: Chọn đáp án B.
Phươngtrìnhhoànhđộgiaođiểm: 4 2 4 2 2
x  4x 1  3  x  4x  4  0  x  2  x   2 .
Câu 4: Tung độ giao điểm của đồ thị các hàm số 3 2
y x  3x  2, y  2
x  8 là : A. 2. B. 4. D. 0. D. 6. Hướng dẫn giải: Chọn đáp án A.
Xét phương trình hoành dộ giao điểm: 3 2
x  3x  2  2x  8 3 2
x  3x  2x  6  0 2
x x     x      x   2 3 2 3 0 3
x  2  0  x  3  y  2
 .3  8  y  2 . 2 x  2x  3
Câu 5: Tọa độ giao điểm của hai đồ thị hàm số y
và đường thẳng y x  3 là x  2 A. 3; 0 . B. 2;3 . C.  1  ;0 . D.  3   ;1 . Hướng dẫn giải: Chọn đáp án A. 2 x  2x  3
Phương trình hoành độ giao điểm
x  3  x  2 x  2
x  3; y  0 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 2
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Tọa độ giao điểm là 3; 0 . 2x  3
Câu 6: Tung độ giao điểm của đồ thị hàm số y
và đường thẳng y x 1 là: x  3 A. 0 . B. 3 . C. 1. D. 3  . Hướng dẫn giải: Chọn đáp án C. 2x  3
Phương trình hoành độ giao điểm là: 2
x 1  x  0  x  0 . Do đó y  1  . x  3 2x  5
Câu 7: Đường thẳng d y x 1 cắt đồ thị C  của hàm số y
tại hai điểm phân biệt. Tìm x  1
các hoành độ giao điểm của d  và C  .
A. x  1; x  2 .
B. x  0; x  1 .
C. x  1 . D. x  2 . Hướng dẫn giải: Chọn đáp án D. 2x  5  x  2
Xét phương trình hoành độ giao điểm của d  và C  : 2
x 1  x  4   . x  1 x  2   3x 1
Câu 8: Tọa độ giao điểm có hoành độ nhỏ hơn 1 của đường C  : y  và đường thẳng x 1
d  : y x 1 là: A. A0;  1 . B. A0;  1 .
C. A1; 2 . D. A 2  ;7 . Hướng dẫn giải: Chọn đáp án B.
Hoành độ giao điểm của C  và d  là nghiệm của phương trình
3x 1  x 1 ( x 1) x 1 x  0 2
 3x 1  x 1  
(thỏa mãn điều kiện). x  3 
Hoành độ nhỏ hơn 1 nên ta chọn x  0  y  1. Vậy tọa độ điểm cần tìm là A0;  1 . Câu 9: Cho hàm số 4 2
y x  4x  2 có đồ thị C  và đồ thị  P 2
: y  1 x . Số giao điểm của  P và
đồ thị C  là A. 2. B. 1. C. 3. D. 4. Hướng dẫn giải: Chọn đáp án A.
Phương trình hoành độ giao điểm: 3  21   3  21 2  x   0 x  4 2 2 4 2 2  2
x  4x  2  1 x x  3x  3  0    .   3  21 2 3  21  x   0 x    2  2 2x  3
Câu 10: Tìm tọa độ giao điểm của đồ thị hàm số y  với trục tung x 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 3
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  3   3  A. ;0 .   B. 0;3. C.  ;0 .   D. 0;  3 .  2   2  Hướng dẫn giải: Chọn đáp án D. 2x  3
Đồ thị cắt Oy x  0 , thay x  0 vào hàm số y
, ta được y  3 . x 1
Câu 11: Số giao điểm của đồ thị hàm số 4 2 y  x  7x  6 và 3 y  x 13x là A. 1. B. 2 . C. 3 . D. 4 . Hướng dẫn giải: Chọn đáp án C.
Phương trình hoành độ giao điểm của hai đồ thị là: 4 2 3 x  7x  6  x 13x  x  1 2  4 3 2
 x  x  7x 13x  6  0  x  
1  x  2 x  3  0  x  2 .  x  3   2x 1
Câu 12: Cho hàm số y
C  Trong các phát biểu sau, phát biểu nào sai ? x 1
A. Đồ thị hàm số có tiệm cận đứng là đường thẳng x  1  .
B. Hàm số luôn đồng biến trên từng khoảng của tập xác định của nó.
C. Đồ thị hàm số có tiệm cận ngang là đường thẳng y  2 .  1 
D. Đồ thị hàm số C  có giao điểm với Oy tại điểm ; 0 .    2  Hướng dẫn giải: Chọn đáp án D.
Giao điểm của đồ thị hàm số C  với Oy là điểm 0;  1 .
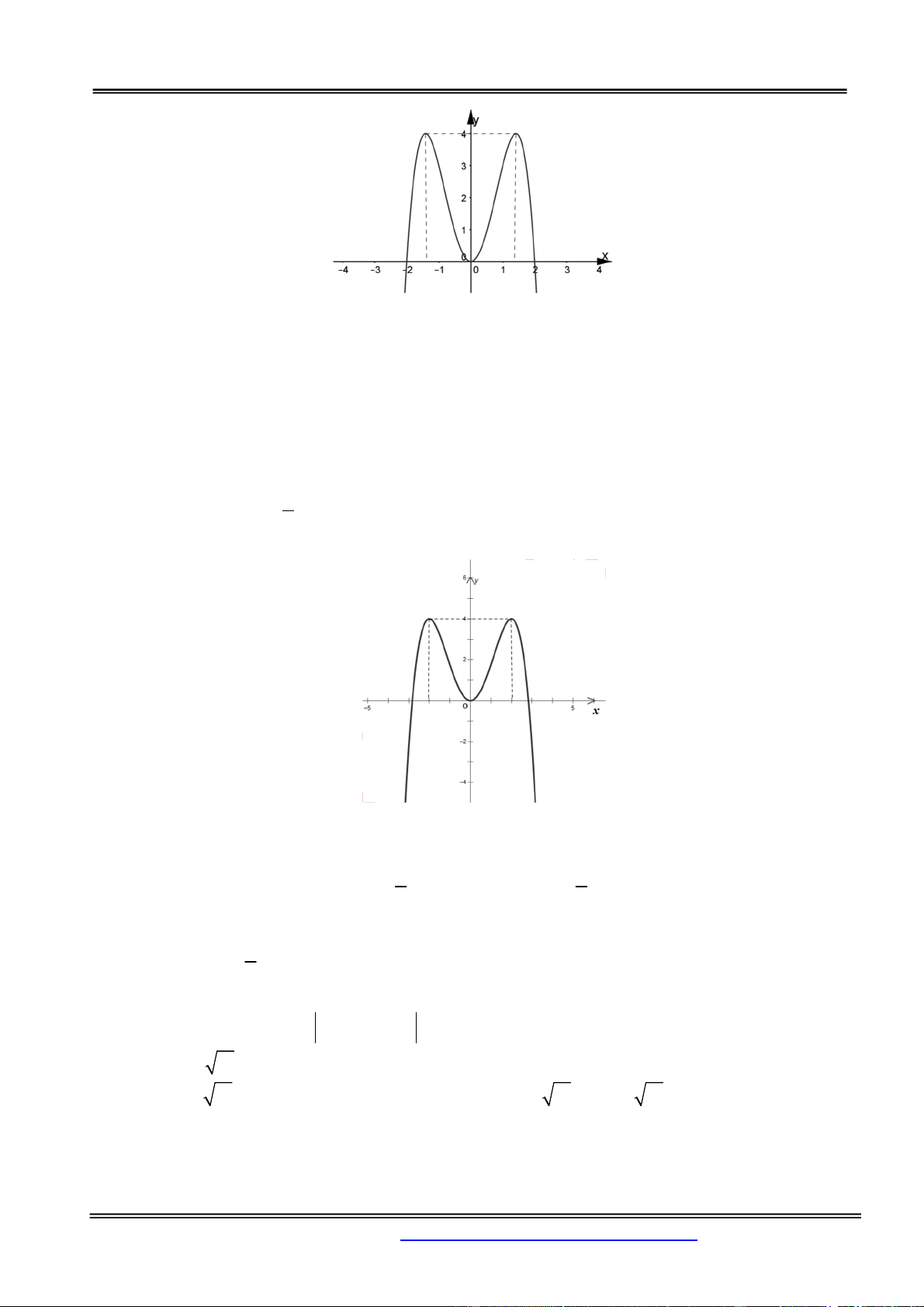
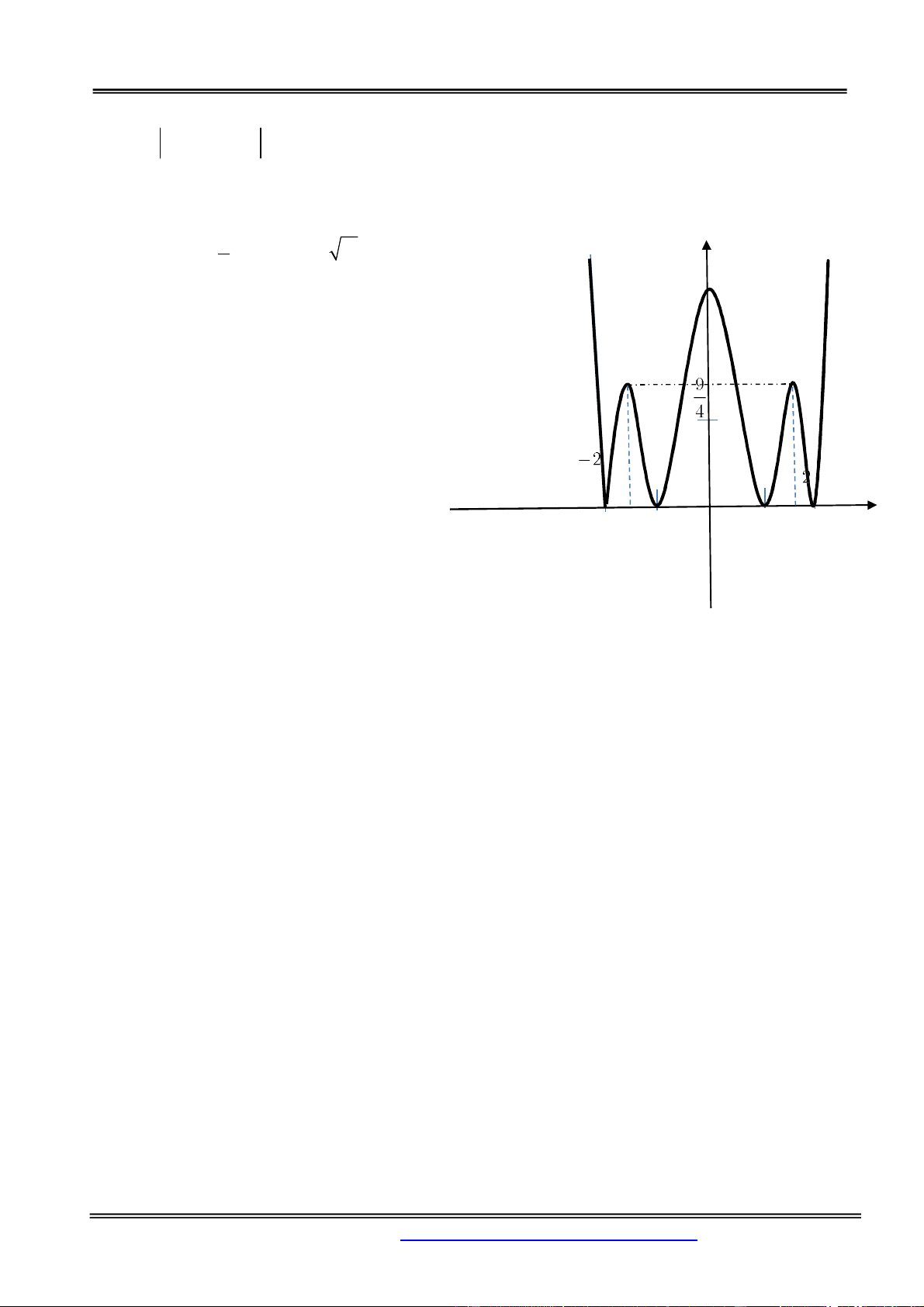
Câu 13: Tìm số giao điểm n của đồ thị hàm số 2 2
y x x  3 và đường thẳng y  2. A. n  6. B. n  8. C. n  2. D. n  4. Hướng dẫn giải: Chọn đáp án A.
Vẽ đồ thị hàm số 2 2
y x x  3 bằng cách suy ra từ đồ thị C 4 2
: y x  3x bằng cách
- Giữ nguyên đồ thị (C) phần phía trên trục hoành.
- Lấy đối xứng đồ thị (C) phần dưới trục hoành qua trục hoành.
Khi đó đt y =2 cắt đồ thị hàm số 2 2
y x x  3 tại 6 điểm phân biệt. 2x 1
Câu 14: Tìm tọa độ giao điểm của đồ thị y
với đường thẳng y  1   3x ? 1 x A. A 2
 ;5, B 1;  1 . B. A 2  ;5, B 0  ;1 .
C. A2;5, B 0;  1 . D. A 2
 ;5, B 0;   1 . Hướng dẫn giải: Chọn đáp án D. TXD: x  1 .
Ta có phương trình hoành độ giao điểm của đồ thị và đường thẳng là : 2x 1  x  0
 3x 1  2x 1   x   1  3  x   2
1  3x  6x  0   A 2  ;5; B 0;    1 . x 1 x  2  2 8x  9x 11
Câu 15: Đồ thị hàm số 2
y x  7x  5 và đồ thị hàm số y
có bao nhiêu điểm chung? x 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 4
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. 0. B. 2. C. 1. D. 3. Hướng dẫn giải: Chọn đáp án D.
Xét phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho : 2 8x  9x 11 3 2 2 2
x x  7x  7x  5x  5  8x  9x 11 2
x  7x  5    x 1 x  1  x  3 3
x  7x  6  0     x  2 x  1    x  1 
Vì phương trình hoành độ giao điểm có 3 nghiệm phân biệt nên hai đồ thị đã cho có 3 giao điểm phân biệt.
Câu 16: Đồ thị của hàm số 4 2
y  4x  2x  1 và đồ thị của hàm số 2
y x x  1 có tất cả bao nhiêu điểm chung? A. 3 . B. 1 . C. 2 . D. 4 . Hướng dẫn giải: Chọn đáp án A. x   0 
Phương trình hoành độ giao điểm : 4 2 2 4 2
4x  2x  1  x x  1  4x  3x  0   3 x     2
Vậy hai đồ thị có 3 điểm chung.
Câu 17: Đồ thị của hàm số 3 2
y  x  3x  2x 1 và đồ thị của hàm số 2
y  3x  2x 1 có tất cả
bao nhiêu điểm chung ? A. 1. B. 3 . C. 2 . D. 0 . Hướng dẫn giải: Chọn đáp án B.
Số điểm chung là số nghiệm phân biệt của phương trình hoành độ: 3 2 2 3
x  3x  2x 1  3x  2x 1 x  4x  0  x  0; x  2 
Phương trình có 3 nghiệm phân biệt nên số điểm chung là 3. 2x  4
Câu 18: Gọi M , N là giao điểm của đường thẳng y x 1 và đường cong y  . Hoành độ x 1
trung điểm I của đoạn thẳng MN bằng: 5 5 A.  . B. 1. C. 2 . D. . 2 2 Hướng dẫn giải: Chọn đáp án B. 2x  4
Hoành độ giao điểm của đường thẳng y x 1 và đường cong y  là nghiệm của phương x 1 2x  4 trình x 1  ,  x   1 x 1 2
x  2x  5  0 . x x
Ta thấy phương trình có 2 nghiệm phân biệt x , x khác 1 và 1
2  1. Do đó x  1. 1 2 I 2 2x  1
Câu 19: Đồ thị hàm số y
và đường thẳng y x  1 cắt nhau tại hai điểm phân biệt , A B . x  5
Tìm hoành độ trung điểm I của đoạn thẳng AB
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 5
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 A. x  1 . B. x  2  . C. x  2 . D. x  1  . I I I I Hướng dẫn giải: Chọn đáp án D. 2x  1
Phương trình hoành độ giao điểm
x  1 x  5. x  5
2x  1  (x  1)(x  5) x    5 . 2
x  2x  4  0  1.  '  5  0.  x  1  5. 1,2
Đồ thị và đường cắt nhau tại hai điểm A1  5; 2  5; B 1 5; 2  5.
Có I là trung điểm của AB .  I (1;2).
Câu 20: Biết rằng đồ thị hàm số 4 2
y x  3x  5 và đường thẳng y  9 cắt nhau tại hai điểm phân
biệt Ax ;y , B x ;y . Tính x x 2 2  1 1  1 2
A. x x  3 .
B. x x  0 .
C. x x  18 .
D. x x  5 . 1 2 1 2 1 2 1 2 Hướng dẫn giải: Chọn đáp án B. x  2 
Phương trình hoành độ giao điểm là: 4 2 4 2
x  3x  5  9  x  3x  4  0  x  2  
Vậy tổng hai nghiệm là x x  0 1 2 4x  2
Câu 21: Biết đường thẳng y  3x  4 cắt đồ thị hàm số y
tại hai điểm phân biệt có tung x 1
độ là y và y . Tính y y 1 2 1 2
A. y y  10 .
B. y y  11 .
C. y y  9 .
D. y y  1 . 1 2 1 2 1 2 1 2 Hướng dẫn giải: Chọn đáp án B. 4x  2
Phương trình hoành độ giao: 2 3x  4 
 3x  3x  6  0 x  1 x  1
x  1  y  1  1
 x  2  y  10  2  y y  11 Vậy 1 2 . 2x  8
Câu 22: Đồ thị C của hàm số y
cắt đường thẳng  : y  x tại hai điểm phân biệt A và x
B . Tìm tọa độ trung điểm I của đoạn thẳng AB A. I  1  ;  1 . B. I  2  ; 2 .
C. I 3;  3 . D. I 6; 6   . Hướng dẫn giải: Chọn đáp án A.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 6
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2x  8
Ta có: phương trình hoành độ giao điểm của (C ) và  :
 x (x  0) . x
x  2  y  2  2 2
 2x  8  x x  2x  8  0   .
x  4  y  4 
Gọi I (x ; y ) là trung điểm đoạn thẳng AB . I I  4  2 x   1 I   2 Suy ra :   I ( 1  ;1) . 2  4  y   1 I   2
Câu 23: Đồ thị hàm số 3 2
y x  3x  2x 1 cắt đồ thị hàm số 2
y x  3x 1 tại hai điểm phân biệt ,
A B. Tính độ dài đoạn AB A. AB  3 . B. AB  2 2 . C. AB  2 . D. AB  1. Hướng dẫn giải: Chọn đáp án D.
Ta có phương trình hoành độ giao điểm x  1  y  1  3 2 2
x  3x  2x 1  x  3x 1 3 2
x  4x  5x  2  0 1  1    x  2  y  1  2  2 Suy ra A1;   1 , B 2;   1 2 2
Vậy AB  2   1   1    1 1. x
Câu 24: Tìm số giao điểm của đồ thị hàm số y
và đường thẳng y   x x  1 A. 3 . B. 1. C. 2 . D. 0 . Hướng dẫn giải: Chọn đáp án C.
Phương trình hoành độ giao điểm x
 x DK : x    1 x 1  x  0 2 2
x  x x x  2x  0  x  2  
Câu 25: Cho hàm số 3
y x x  2 có đồ thị C . Tìm tọa độ giao điểm của C và trục tung A. (0; 2) . B. (1; 0) . C. (2; 0) . D. (0;1) . Hướng dẫn giải: Chọn đáp án A. Gọi M  ;
x y là giao điểm của đồ thị C với trục tung.
Khi đó ta có x  0  y  2  . Vậy M 0; 2   .
Câu 26: Tìm số giao điểm của đồ thị hàm số 4 2
y x  2x và đồ thị hàm số 2
y x  2 . A. 4 . B. 2 . C. 3 . D. 1. Hướng dẫn giải: Chọn đáp án A.
Phương trình hoành độ giao điểm là
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 7
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x   2  4 2 2 4 2  x  2
x  2x x  2  x  3x  2  0  x  1    x  1 
Vậy có 4 giao điểm của hai đồ thị. 2x 1
Câu 27: Cho hàm số y
. Khẳng định nào sau đây là khẳng định sai ? x 1
A. Đồ thị hàm số cắt Oy tại điểm 0; 2 .
B. Đồ thị hàm số có tâm đối xứng I 1;2 .
C. Đồ thị hàm số có tiệm cận đứng x  1 .
D. Đồ thị hàm số có tiệm cận ngang y  2 . Hướng dẫn giải: Chọn đáp án A. 2x 1 Ta có: y  . x 1
Khi x  0  y  1
 suy ra đồ thị hàm số cắt Oy tại điểm (0; 1  ) . x  3
Câu 28: Biết rằng đồ thị hàm số y
và đường thẳng. y x  2 cắt nhau tại hai điểm phân biệt x 1
Ax ; y và. B x ; y
. Tính y y . B B A A A B
A. y y  2  .
B. y y  2 .
C. y y  4 .
D. y y  0 . A B A B A B A B Hướng dẫn giải: Chọn đáp án D. x  3 x  2  5
Xét phương trình hoành độ giao điểm 2
x  2  x  2x 1  0   x 1 x  2  5 
Giả sử A2  5; 5; B 2  5; 5  y y  0. A B 2x 1
Câu 29: Biết đường thẳng y x  2 cắt đồ thị y
tại hai điểm phân biệt A, B có hoành độ lần x 1
lượt x , x hãy tính tổng x x A B A B
A. x x  2 .
B. x x  1 .
C. x x  5 .
D. x x  3 . A B A B A B A B Hướng dẫn giải: Chọn đáp án C. 2 2x 1
x  5x 1  0 Pt hoành độ giao điểm:  x  2  
x x  5. x 1 A B x  1  x  3
Câu 30: Biết rằng đồ thị hàm số y
và đường thẳng y x  2 cắt nhau tại hai điểm phân biệt x 1
Ax ; y , B x ; y
. Khi đó x x bằng B B A A A B A. 4. B. 4 . C. 2 5 . D. 2. Hướng dẫn giải: Chọn đáp án A. TXD: x  1  .
Ta có phương trình hoành độ giao điểm của đồ thị và đường thẳng là :
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 8
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  3  x  2  3
x  2  x  3   x   1  x  2 2 2
x  3x  2  x  3  x  4x 1   . x 1  x  2  3 
Khi đó ta có Ax ; y , B x ; y
x x  4 . B B A A A B 2x  2
Câu 31: Đường thẳng y x 1 cắt đồ thị hàm số y
tại hai điểm phân biệt Ax ; y và 1 1  x 1
B x ; y . Khi đó tổng y y bằng 2 2  1 2 A. 1. B. 4. C. 3. D. 0. Hướng dẫn giải: Chọn đáp án B.
Phương trình hoành độ giao điểm
2x  2  x 1(DK : x 1) x 1
x  3  y  4 2 2
 2x  2  x 1  x  2x  3  0  x  1   y  0 
Vậy y y  4 1 2
Câu 32: Đồ thị hàm số 3
y x  3x cắt
A. Đường thẳng y  3 tại hai điểm.
B. Đường thẳng y  4 tại hai điểm. 5
C. Đường thẳng y  tại ba điểm.
D. Trục hoành tại một điểm. 3 Hướng dẫn giải: Chọn đáp án C.
Lần lượt xét các phương trình hoành độ giao điểm A. 3 3
x  3x  3  x  3x  3  0 , phương trình này chỉ có 1 nghiệm thực (sử dụng máy tính bỏ túi kiểm tra). Loại A. B. 3 3 x  3x  4
  x  3x  4  0 , phương trình này chỉ có 1 nghiệm thực (sử dụng máy tính bỏ túi kiểm tra). Loại B. 5 5 C. 3 3 x  3x   x  3x
 0 , phương trình này chỉ có 3 nghiệm thực (sử dụng máy tính bỏ túi 3 3 kiểm tra). Chọn C.  x  0  D. 3
x  3x  0  x  3 
, phương trình này chỉ có 3 nghiệm thực. Loại D.  x   3 
Câu 33: Cho hàm số 2 2
y x  2mx m 1 có đồ thị C  và đường thẳng d : y x 1. Tìm tất cả giá
trị thực của tham số m để đồ thị hàm số C  và đường thẳng d có giao điểm nằm trên trục hoành. A. m  2 . B. m  2 . C. m  0 .
D. m 0;  2 . Hướng dẫn giải: Chọn đáp án D. Gọi A ,
x y là giao điểm của d và Ox
Phương trình hoành độ giao điểm của d và trục hoành là x 1  0  x  1 Suy ra A1;0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com Trang 9
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 m  0
Theo YCBT ta có A1;0 C  2 2 2  0  1 2 .
m 1  m 1  m  2m  0  m  2  Câu 34: Cho hàm số 2 2 2
y f (x)  x(x 1)(x  4)(x  9) . Hỏi đồ thị hàm số y f (x) cắt trục hoành
tại bao nhiêu điểm phân biệt ? A. 3. B. 5. C. 6. D. 4. Hướng dẫn giải: Chọn đáp án C.
Đồ thị hàm số y f (  x) cắt trục hoành 6 4 2
f '(x)  0  7x  70x 147x  36  0. Đặt 2
x t(t  0) . Phương trình trở thành: 3 2
7t  70t 147t  36  0   1 Đặt 3 2
g(t)  7t  70t  147t  36
g(0).g(1)  0 
Có: g(2).g(7)  0  Phương trình (1) có 3 nghiệm nằm trong (0;1);(2;7);(7;8).
g(7).g(8)  0 
Phương trình (1) có 3 nghiệm dương phân biệt. Suy ra phương trình f (
 x)  0 có 6 nghiệm phân
biệt. Hay đồ thị hàm số y f (x) cắt trục hoành tại 6 điểm phân biệt. 2 x  2x  3
Câu 35: Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y  hợp với hai trục tọa x  1
độ một tam giác có diện tích S bằng:
A. S  1,5 .
B. S  2 .
C. S  3.
D. S  1. Hướng dẫn giải: Chọn đáp án D. 2 x  2x  1
Cách 1: Ta có y 
nên y  0  x  1  2 , do đó đồ thì hàm số có 2 điểm cực trị là  x  2 1
A1 2;2 2 và B 1 2;2 2 .  
Khi đó đường thẳng qua hai cực trị có vtcp u AB  2 2; 4 
2   2 2 1;2 nên có phương
trình là 2  x 1 2   y  2 2  0  y  2x  2d  . 1
Vì d  cắt các trục tọa độ tại M 0; 2
  và N 1;0 nên diện tích là S OM .ON  1. 2 u xu x
Cách 2: Áp dụng tính chất cực trị của đồ thị hàm số y
là đường thẳng y  ta được v xv x
đường thẳng qua hai điểm cực trị là d  : y  2x  2 . 1
Vì d  cắt các trục tọa độ tại M 0; 2
  và N 1;0 nên diện tích là S OM .ON  1. 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 10
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
DẠNG 2: SỰ TƯƠNG GIAO PHƯƠNG PHÁP BẢNG BIẾN THIÊN
VÀ ĐỒ THỊ HÀM SỐ
Phương pháp 1: Bảng biến thiên
+) Lập phương trình hoành độ giao điểm dạng
(phương trình ẩn x tham số m)
+) Cô lập m đưa phương trình về dạng +) Lập BBT cho hàm số .
+) Dựa và giả thiết và BBT từ đó suy ra m.
Phương pháp 2: Đồ thị hàm số
+) Cô lập m hoặc đưa về hàm hằng
là đường thẳng vuông góc với trục
+) Từ đồ thị hàm số tìm cực đại, cực tiểu của hàm số (nếu có)
+) Dựa vào số giao điểm của hai đồ thị hàm số ta tìm được giá trị của m theo yêu cầu của bài toán.
*) Chú ý: Sử dụng PP bảng biến thiên và đồ thị hàm số khi m độc lập với x.
SỰ TƯƠNG GIAO BẰNG PHƯƠNG PHÁP BẢNG BIẾN THIÊN
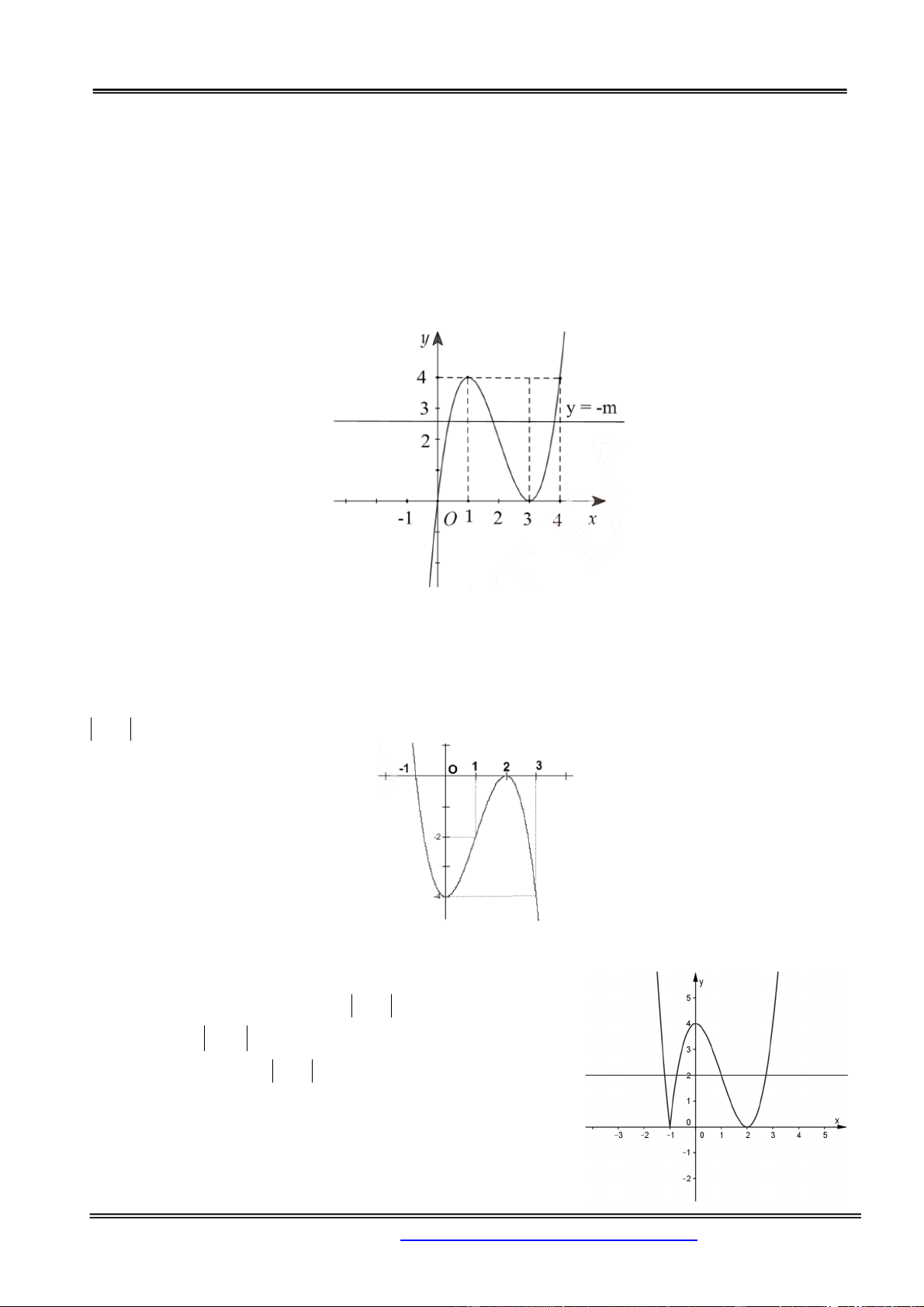
Câu 1. Tìm m để phương trình 3
x  3x m  0 có 3 nghiệm thực phân biệt A. 2   m  2 . B. 2   m  2 . C. 2   ; m m  2 . D. 1   m  1 . Hướng dẫn giải: Chọn đáp án B. Ta có 3 3
x  3x m  0  m  3x x   1 .  x  1
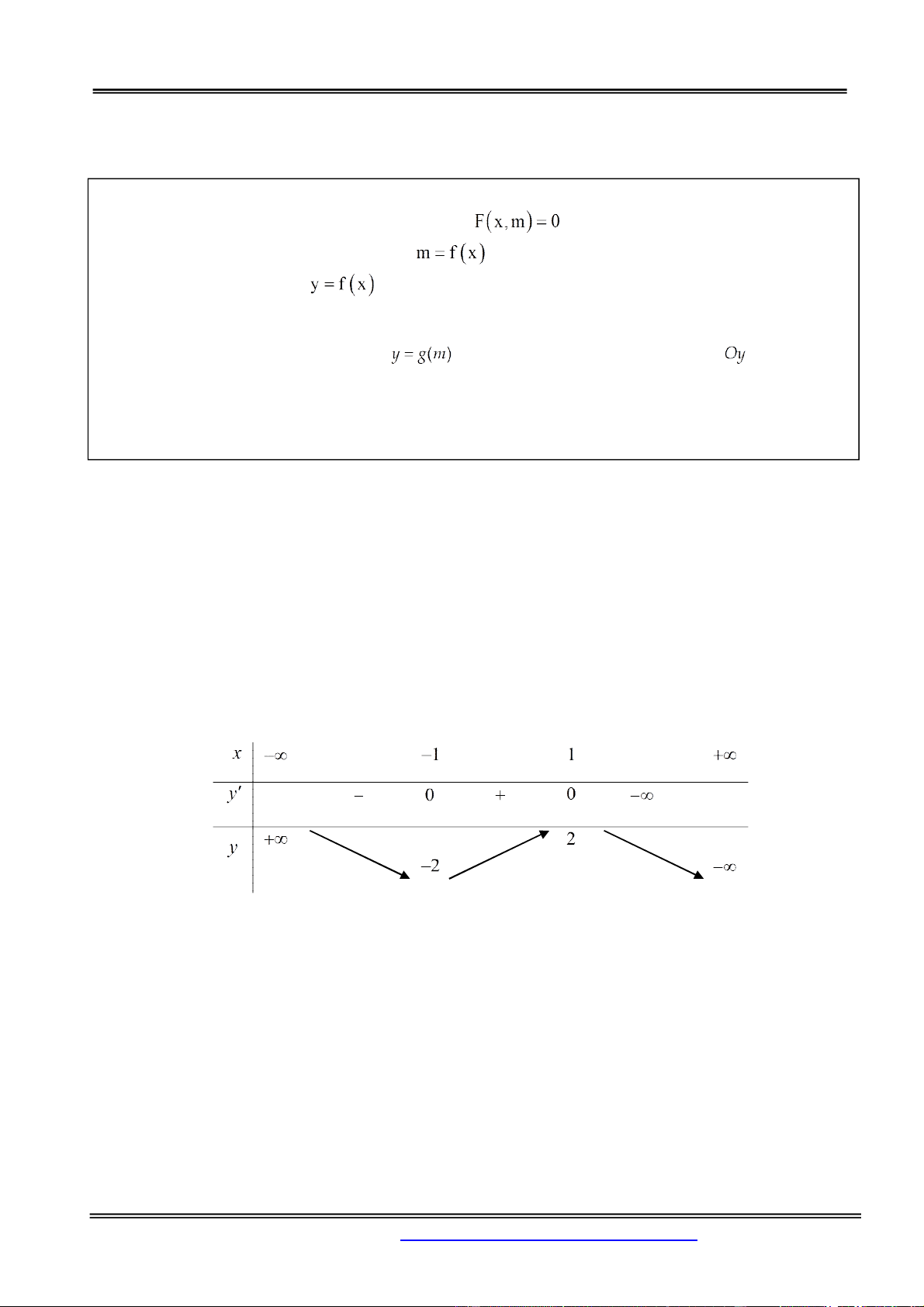
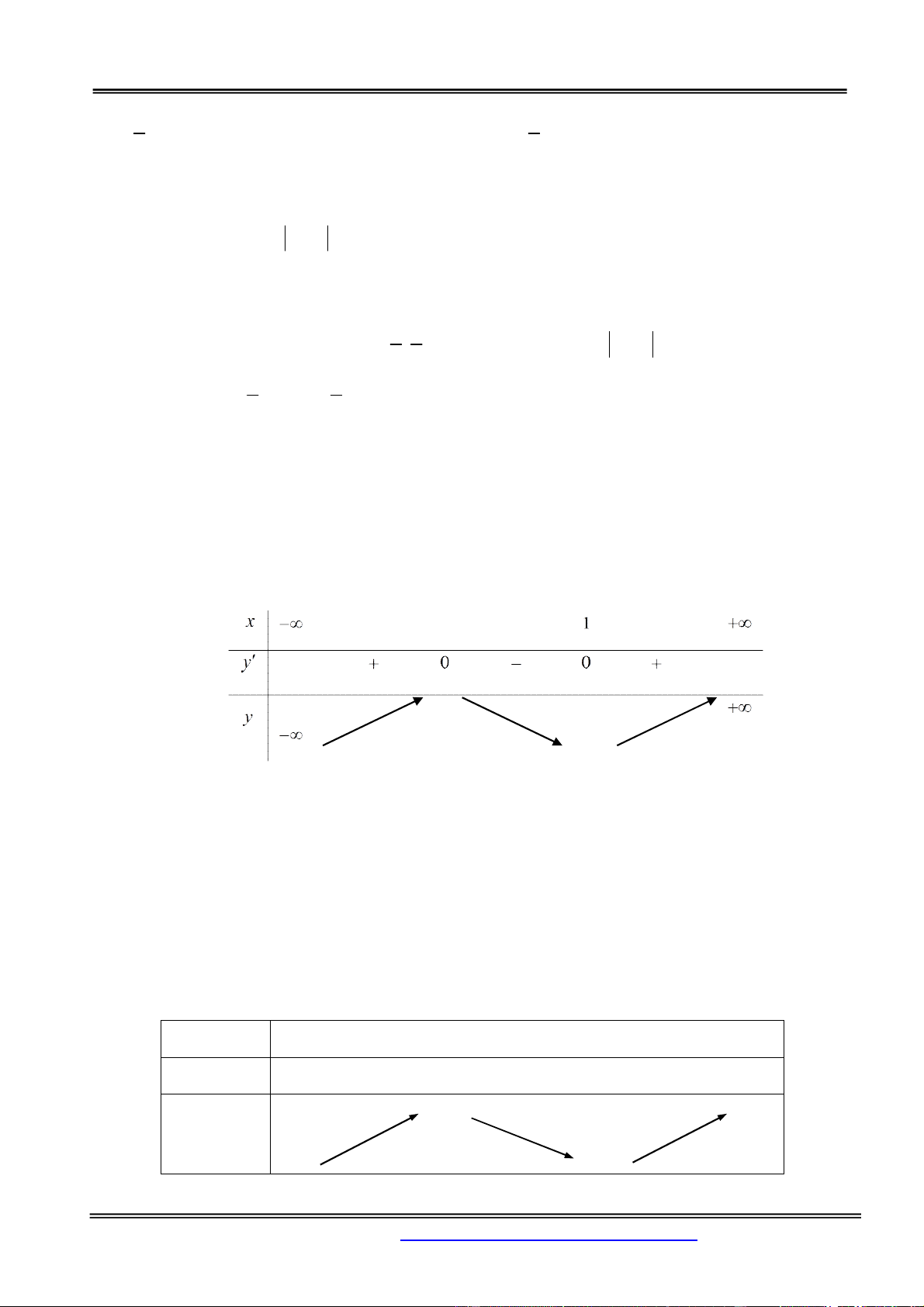
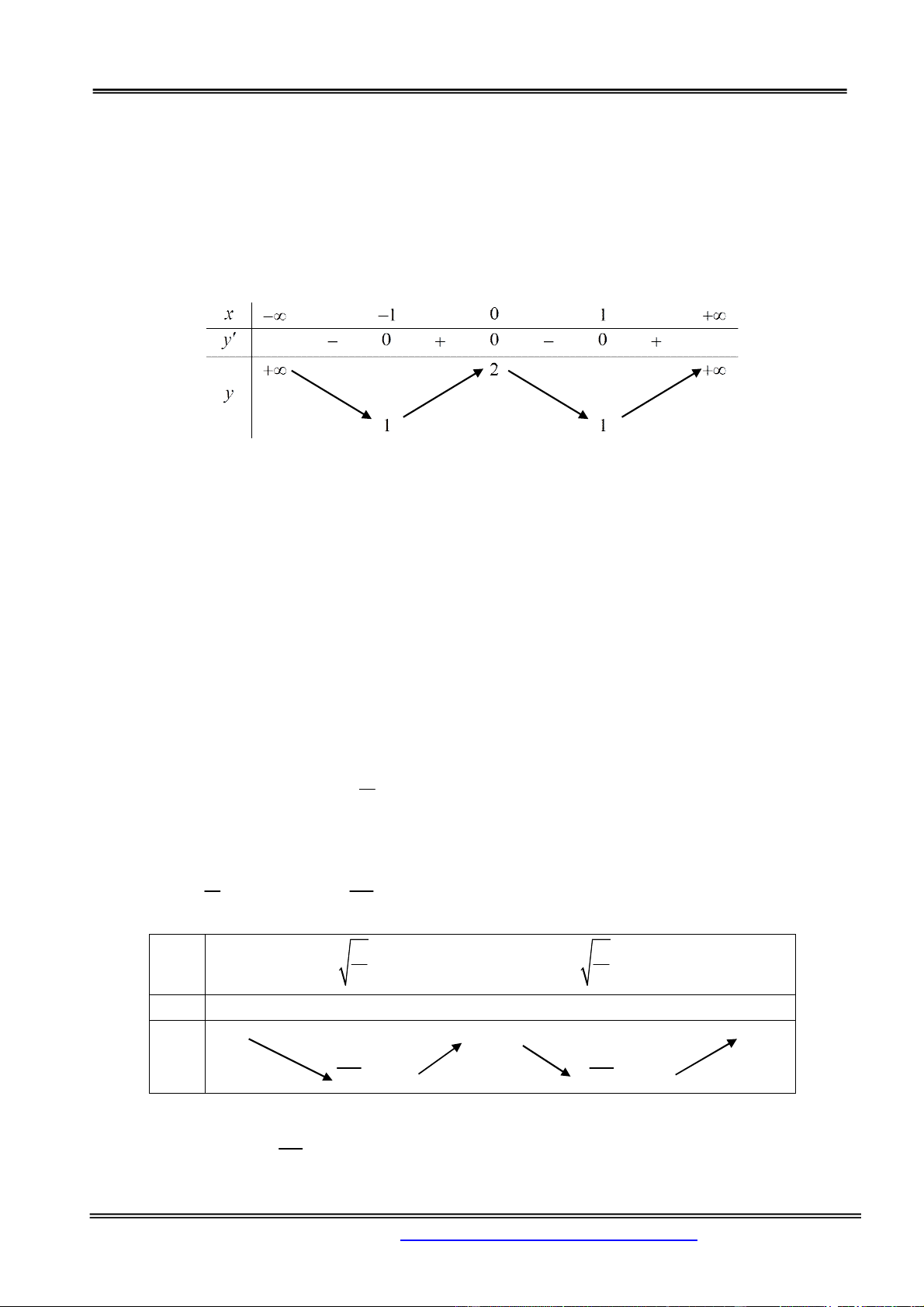
Xét hàm số f x 3
 3x x có f  x 2
 3  3x ; f  x  0   . x  1   Bảng biến thiên: .
Số nghiệm của phương trình  
1 là số giao điểm của hai đồ thị 3
y  3x x và y m . Do đó  
1 có ba nghiệm phân biệt  2  m  2 . Câu 2. 3
Tìm tất cả các giá trị m để phương trình x  3x  2m có 3 nghiệm phân biệt
A. 2  m  2.
B. 1  m  1.
C. 2  m  2.
D. 1  m  1. Hướng dẫn giải: Chọn đáp án B.
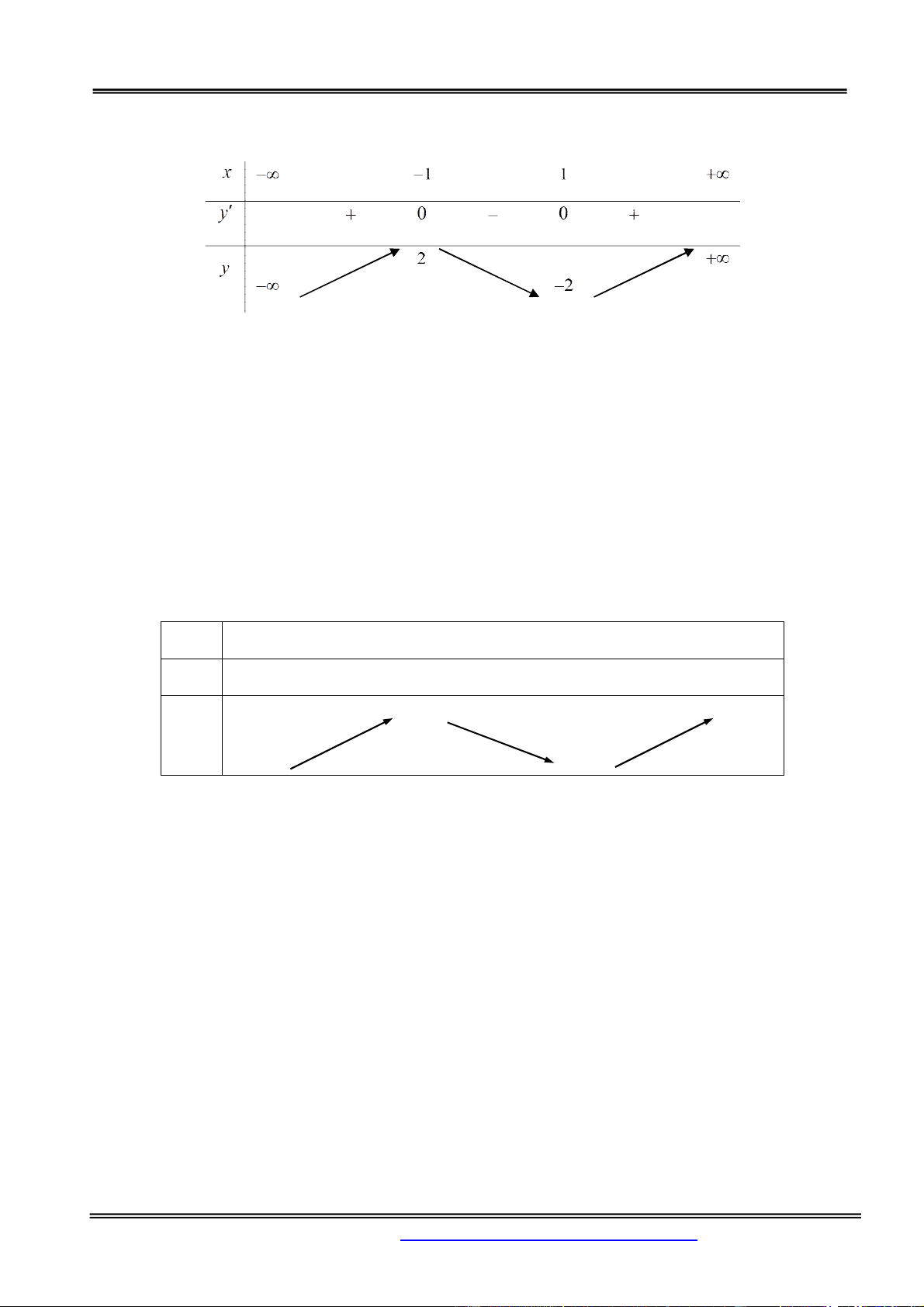
Xét hàm số f x 3
x  3x trên . f x 2 '  3x  3 .  x  1
f ' x  0   . x  1 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 11
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Ta có f  
1  2; f   1  2 . Bảng biến thiên
Vậy để phương trình có ba nghiệm phân biệt thì 2   2m  2  1   m  1.
Câu 3. Tìm m để phương trình 3
x  3x m  2  0 có 3 nghiệm phân biệt A. 4   m  4 . B. 4   m  0 . C. 4   m  2 . D. 1  6  m  16 . Hướng dẫn giải: Chọn đáp án B. 3 3
x  3x m  2  0  x  3x  2  m   1 .
Đặt f x 3
x  3x  2 ta có f  x 2  3x  3 .
f  x  0  x  1  . Bảng biến thiên x  1  1  y + 0  0 + 0  y  4 
Từ bảng biến thiên ta có 4   m  0 .
Câu 4. Phương trình 3 2
x  3x m m có 3 nghiệm phân biệt khi : m  2
A. 2  m  1
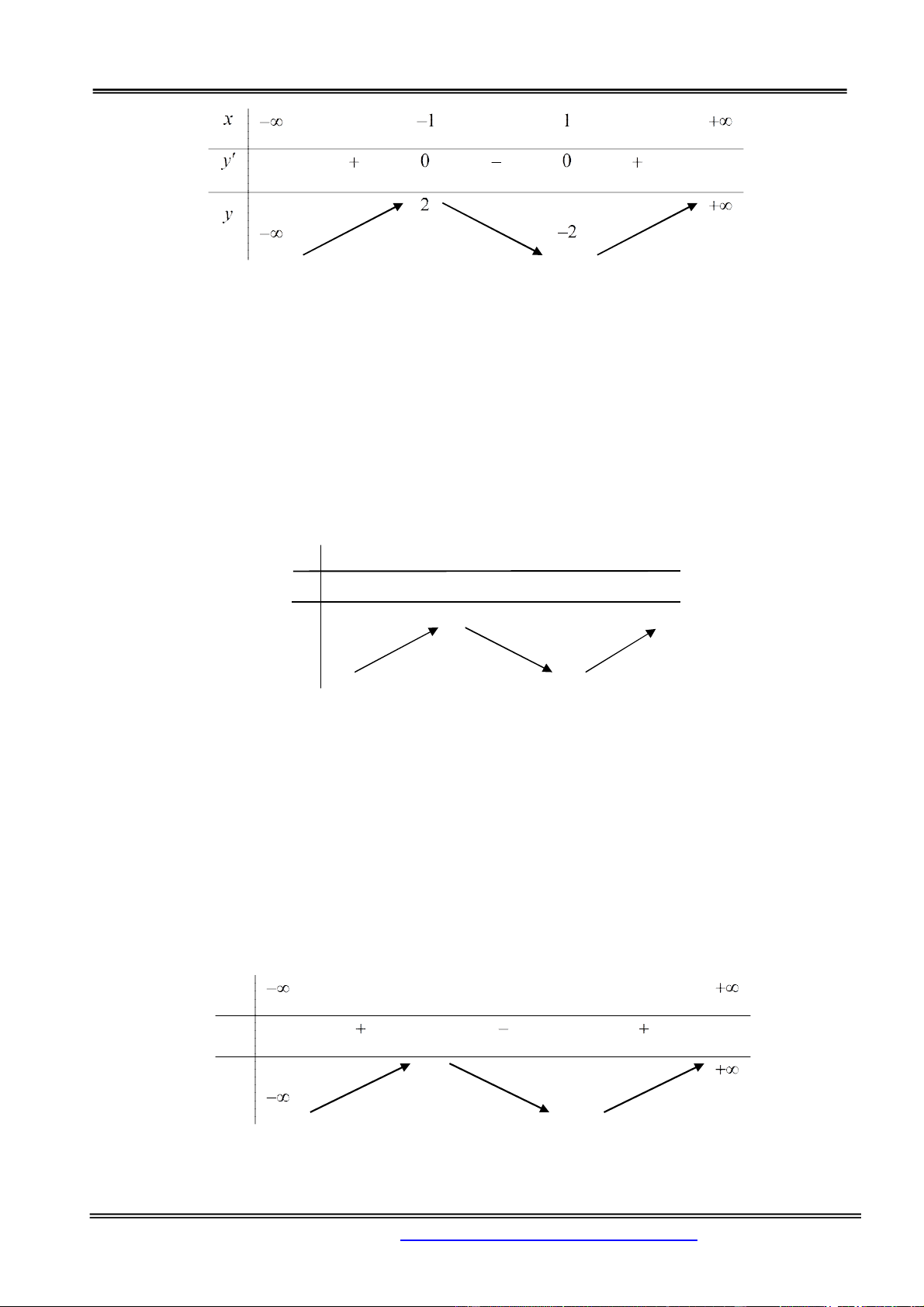
B. 1  m  2 C. m  1 D. m  1  Hướng dẫn giải: Chọn đáp án A. Xét hàm số: 3
y x  3x ta có: + TXĐ: D  . R + 2
y '  3x  3. + 2
y '  0  3x  3  0  x  1  . + Bảng biến thiên.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 12
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
+ Dựa vào bảng biến thiên ta thấy, phương trình đã cho
có 3 nghiệm phân biệt khi 2 2 
m m  2 
m m  2  0     2   m  1. 2 2 m m  2 
m m  2  0 
Câu 5. Phương trình 3
x 12x m  2  0 có 3 nghiệm phân biệt khi A. 4   m  4 . B. 1  8  m  14 . C. 1  4  m  18 . D. 1  6  m  16 . Hướng dẫn giải: Chọn đáp án C. 3 3
x 12x m  2  0  x 12x  2  m   1 .
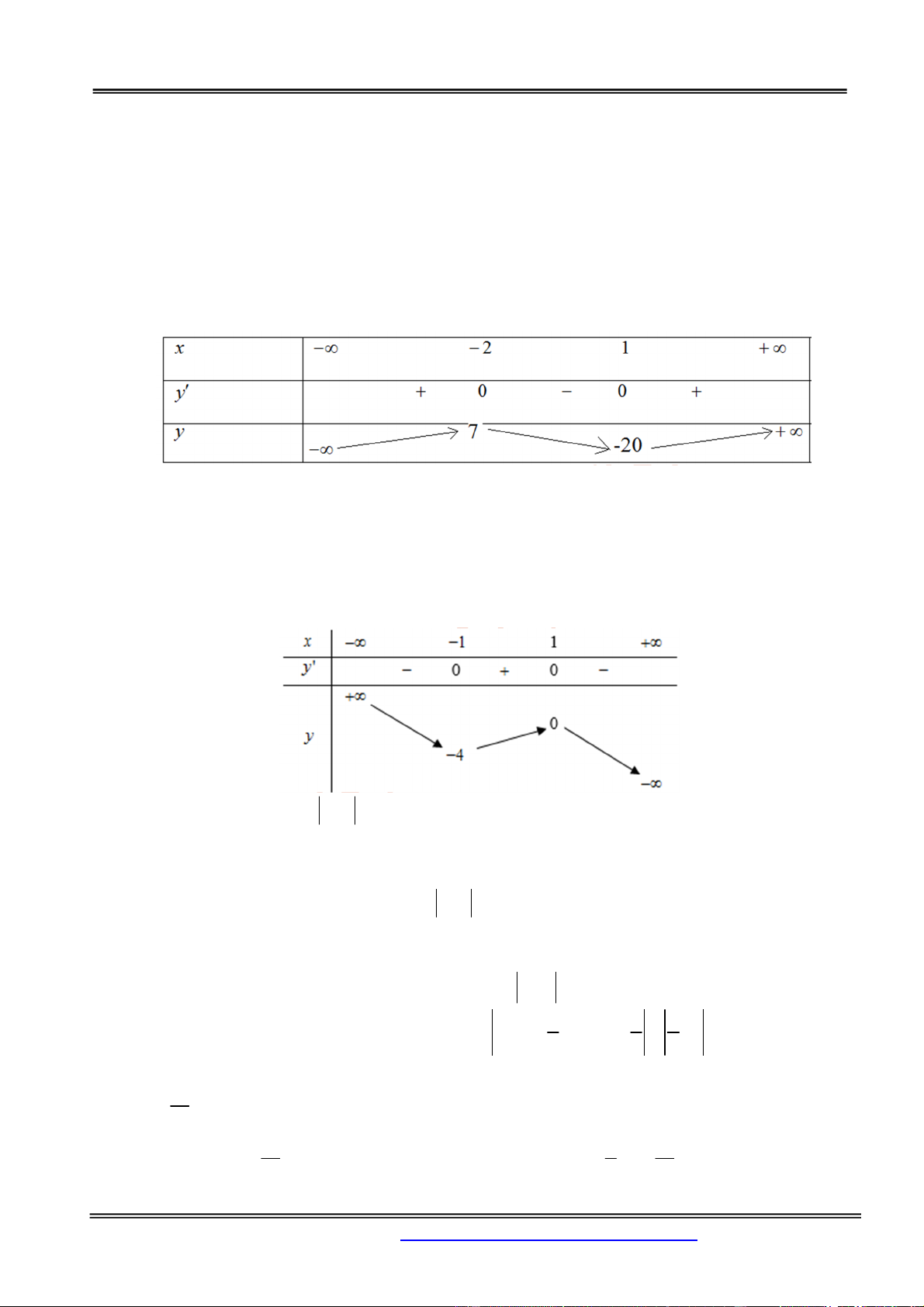
x  2  y  16  Xét hàm số 3
y x 12x . Ta có 2
y  3x 12 . y  0   . x  2   y  16  Bảng biến thiên x  2  2  y  0  0  16  y  1  6 Để phương trình  
1 có 3 nghiệm khi và chỉ khi đường thẳng y  2  m cắt đồ thị hàm số 3
y x 12x tại 3 điểm phân biệt  16  2  m  16  1  4  m  18.
Câu 6. Với giá trị nào của m thì phương trình 3 2
x  3x m  0 có hai nghiệm phân biệt
A. m  4  m  0 .
B. m  4  m  0 .
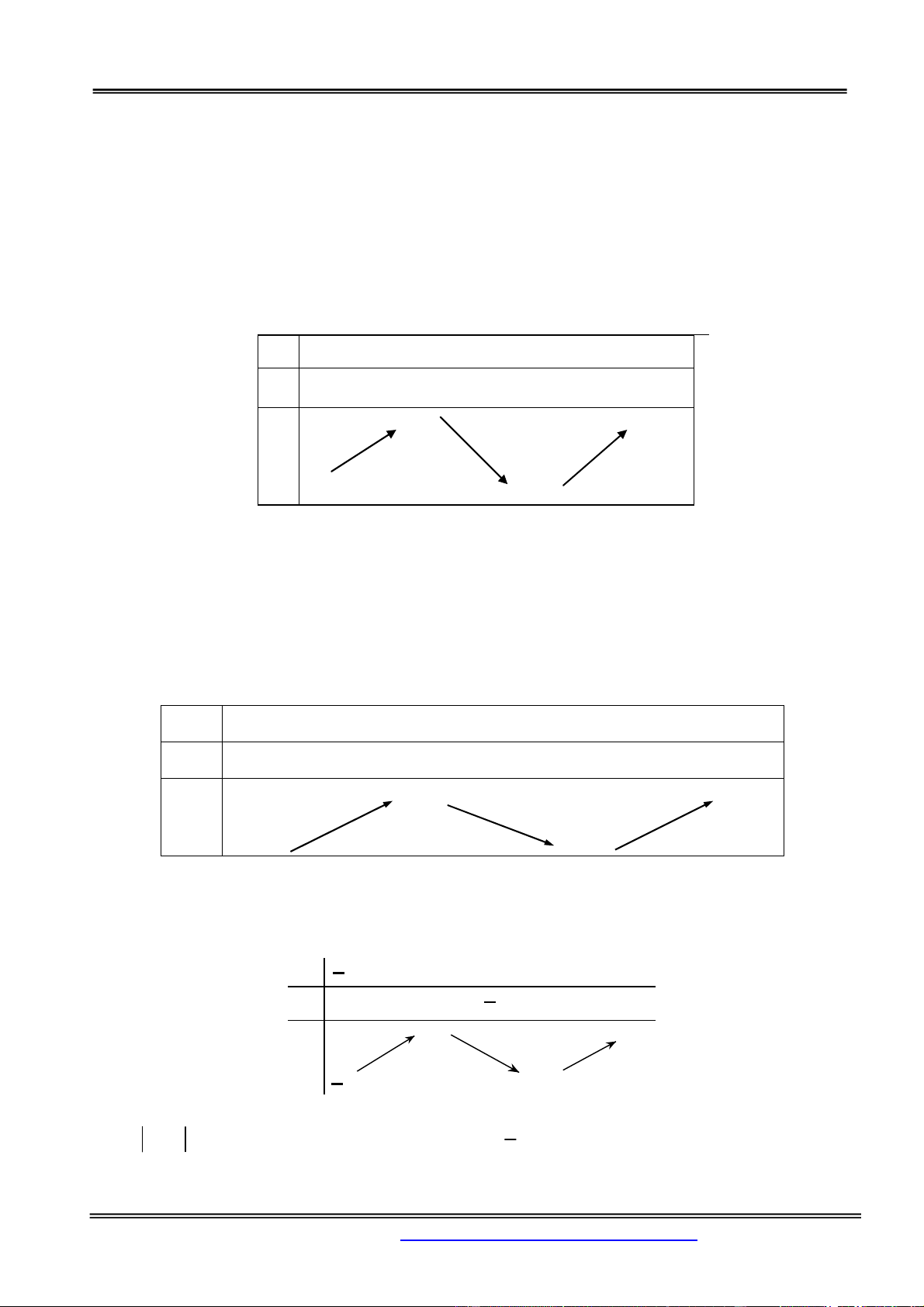
C. m  4  m  4 . D. Kết quả khác. Hướng dẫn giải: Chọn đáp án A. Xét hàm số 3 2
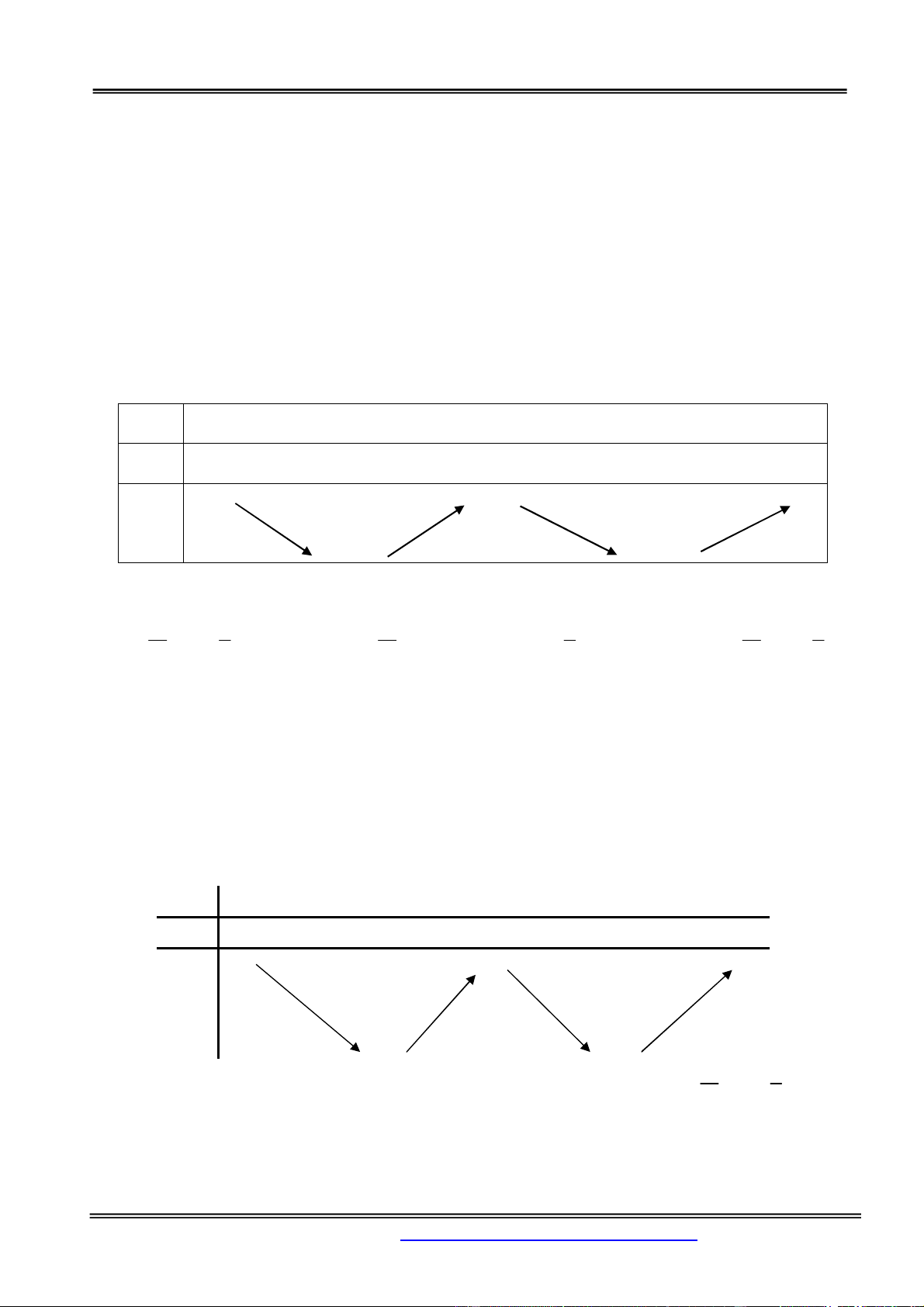
y x  3x 2
y  3x  6x
x  0; y  0
y  0  x  2; y  4   x 0 2 y 0 0 0 4
Số nghiệm của phương trình 3 2
x  3x m  0 là số giao điểm của đồ thị hàm số 3 2
y x  3x và đường
thẳng y  m .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 13
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 m  0 m  0
Phương trình có 2 nghiệm phân biệt khi    . m  4 m  4  
Câu 7. Tìm các giá trị thực của m để phương trình 3 2
x  3x m  4  0 có ba nghiệm phân biệt.
A. 4  m  8 . B. m  0 .
C. 0  m  4 .
D. 8  m  4 . Hướng dẫn giải: Chọn đáp án D. Ta có: 3 2 3 2
x  3x m  4  0  x  3x  4  . m Đặt 3 2 2
y x  3x  4; y m y  3x  6x. 1 2 1 Ta có BBT của 3 2
y x  3x  4. 1 x  0 2  y + 0 - 0 + 1 y 4  1  8
Từ BBT ta suy ra phương trình có ba nghiệm phân biệt khi 8  m  4.
Câu 8. Tìm m để đường thẳng y m cắt đồ thị hàm số 3
y x  3x  2 tại 3 điểm phân biệt
A. 0  m  2.
B. 0  m  4.
C. 0  m  4.
D. 2  m  4. Hướng dẫn giải: Chọn đáp án C. x  1 2
y  3x  3, y  0  x  1   x  1  1  y  0  0  . 4  y .  0
Đường thẳng y m cắt đồ thị hàm số 3
y x  3x  2 tại 3 điểm phân biệt khi. 0  m  4.
Câu 9. Cho hàm số y f x 3 2 
ax bx cx d có bảng biến thiên như sau: x  0 1 + y' + 0 0 + 1 + y 0  1
Khi đó f x  m có bốn nghiệm phân biệt x x x
x khi và chỉ khi 1 2 3 4 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 14
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1 1 A.m  1 . B.m  1 . 2 2
C. 0  m  1 .
D. 0  m  1 . Hướng dẫn giải: Chọn đáp án A.
Đồ thị C : y f x được vẽ bằng cách:
Phần 1: Giữ nguyên phần đồ thị C  : y f x nằm bên trên trục hoành.
Phần 2: Lấy đối xứng phần đồ thị C  : y f x nằm dưới trục hoành qua trục hoành.  1 1 
Đồ thị hàm số có tọa độ điểm uốn I ; 
 , nên phương trình đó f x   m có bốn nghiệm phân  2 2  1 1
biệt x x x   x khi  m  1 . 1 2 3 4 2 2
Câu 10. Đường thẳng y = m cắt đồ thị hàm số 3
y x  3x  2 tại 3 điểm phân biệt khi : A. 0  m  4 B. 0  m  4 C. 0  m  4 D. m  4 Hướng dẫn giải: Chọn đáp án A.
Tập xác định: D    x  1 Ta có: 3 2
y x  3x  2  y '  3x  3  y '  0  x 1  Bảng biên thiên: -1 4 0
Từ bảng biến thiên ta có 0  m  4 thì phương trình đã cho có ba nghiệm phân biệt
Câu 11. Tìm m để phương trình 3 2
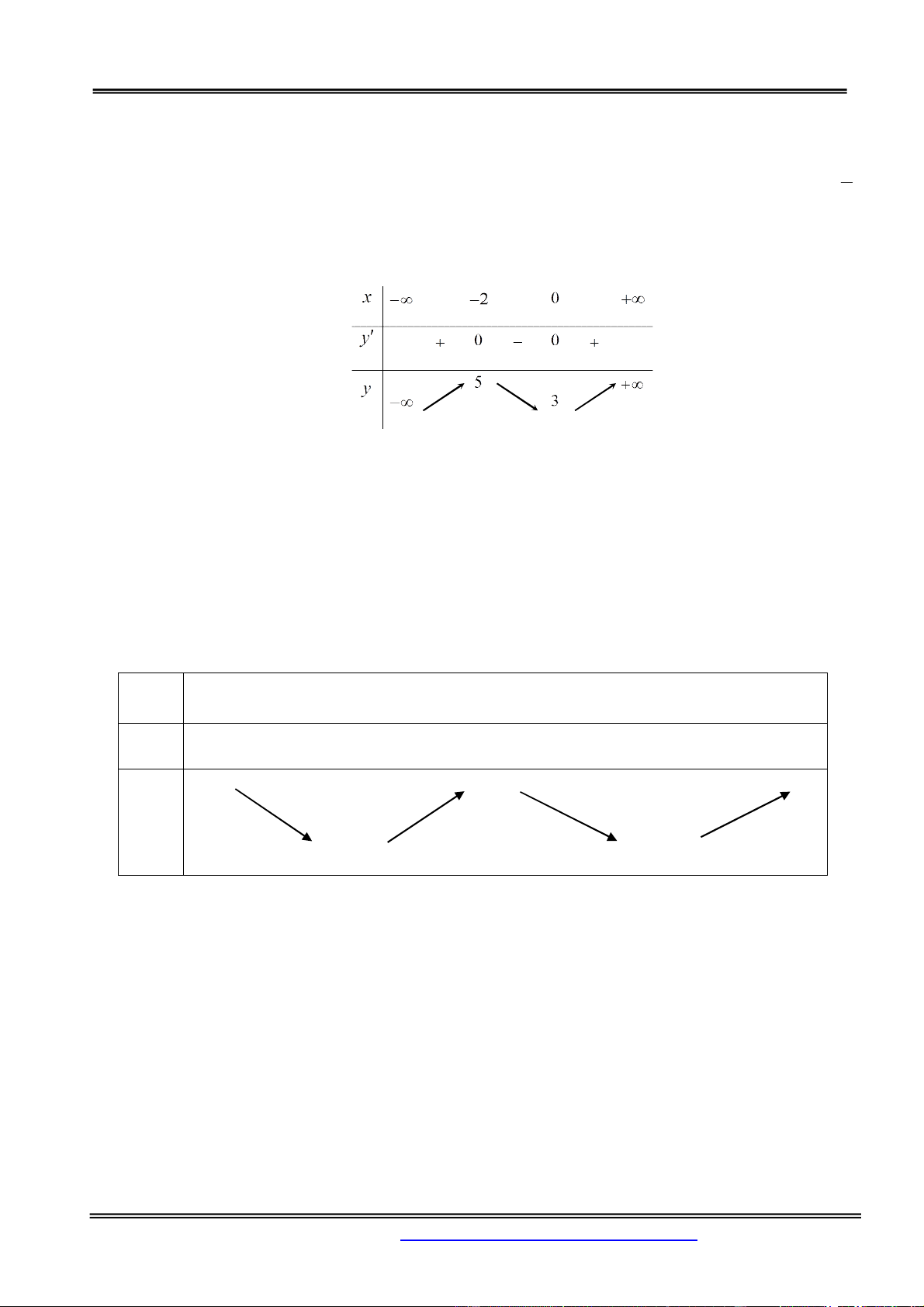
2x  3x 12x 13  m có đúng hai nghiệm A. m  1  3, m  4 . B. m  1  3, m  0 . C. m  2  0, m  5 . D. m  2  0, m  7 . Hướng dẫn giải: Chọn đáp án C. Xét hàm số: 3 2
y  2x  3x 12x 13. 2
y  6x  6x 12 .  x  1 y  0   . x  2   BBT x  2  1  y  0  0  . 7  y .  2  0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 15
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Phương trình 3 2
2x  3x 12x 13  m có đúng hai nghiệm khi m  2
 0, m  7 .
Câu 12. Tìm m để phương trình 3 2
2x  3x 12x 13  m có đúng 2 nghiệm. A. m  1
 3; m  4.
B. m  0; m  1  3 .
C. m  20; m  5 .
D. m  20; m  7 . Hướng dẫn giải: Chọn đáp án D.
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số 3 2
y  2x  3x 12x 13 và đường thẳng y  . m
Lập bảng biến thiên của hàm số 3 2
y  2x  3x 12x 13. 3 2
Nhìn vào BBT ta thấy để phương trình 2x  3x 12x 13  m có đúng 2 nghiệm
thì đường thẳng y m phải cắt đồ thị hàm số 3 2
y  2x  3x 12x 13 tại đúng 2 điểm m  20  .  m  7 
Vậy đáp án D thỏa mãn.
Câu 13. Cho hàm số y f (x ) liên tục trên và có bảng biến thiên như hình vẽ.. .
Với m  1;3 thì phương trình f (x)  m có bao nhiêu nghiệm? A. 4. B. 3. C. 2. D. 5. Hướng dẫn giải: Chọn đáp án A.
Dựa vào bảng biến thiên vẽ đồ thị hàm số y f (x) .
Phần 1: Giữ nguyên đồ thị hàm số y f (x).
Phần 2: Lấy đối xứng phần đồ thị hàm số y f (x ) phía dưới trục hoành qua trục hoành.
Dựa vào đồ thị hàm số và với m  1;3 thì phương trình f x   m có 4 nghiệm 3 1 k
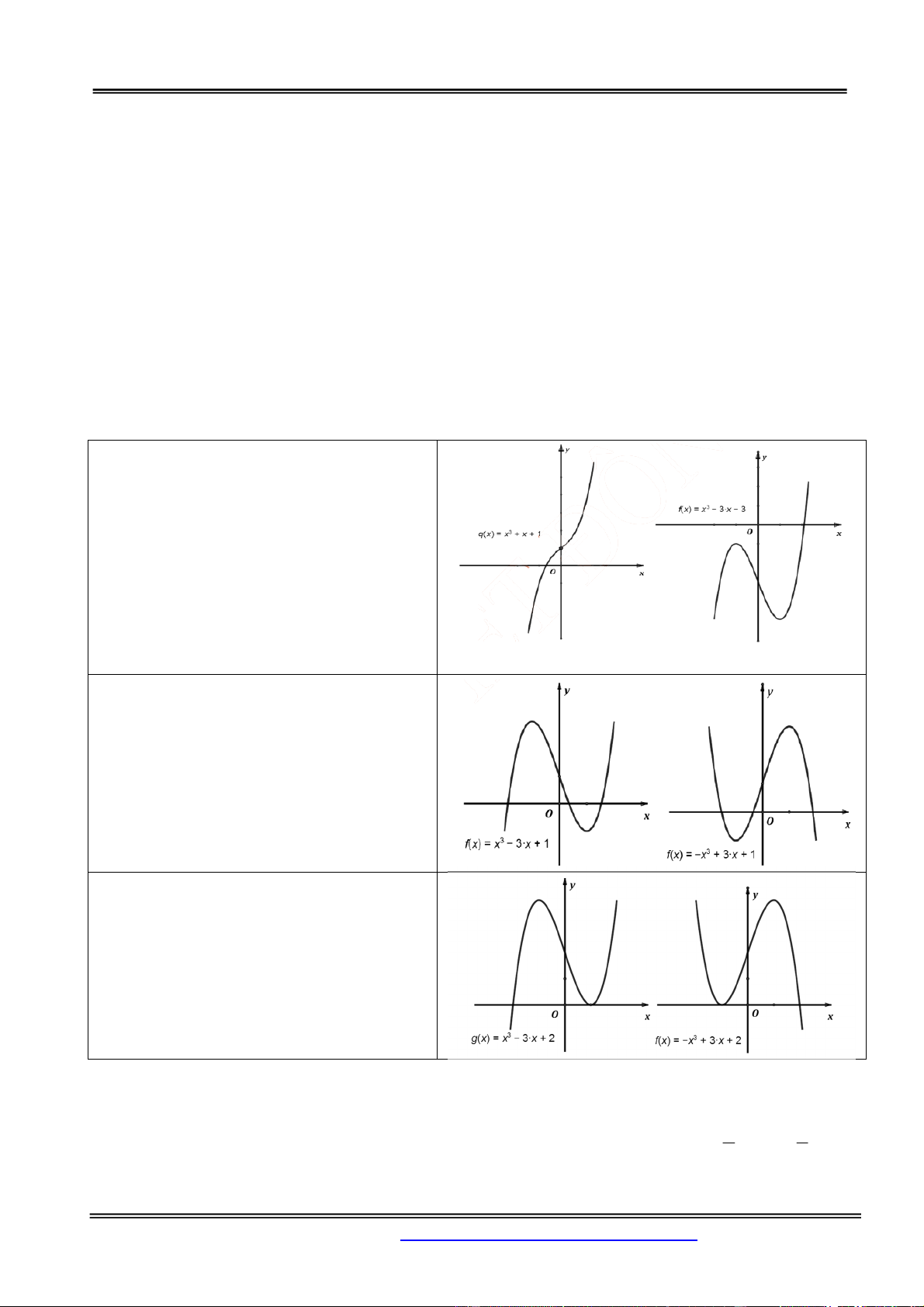
Câu 14.Tìm tất cả các giá trị thực k để phương trình 3 2 2  x x  3x   1 có đúng 4 nghiệm 2 2 2 phân biệt  19  A. k  ;5 .   B. k  .   4   19   3   19  C. k   2  ;   1  1; .   D. k  2  ;   ;6 .      4   4   4 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 16
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
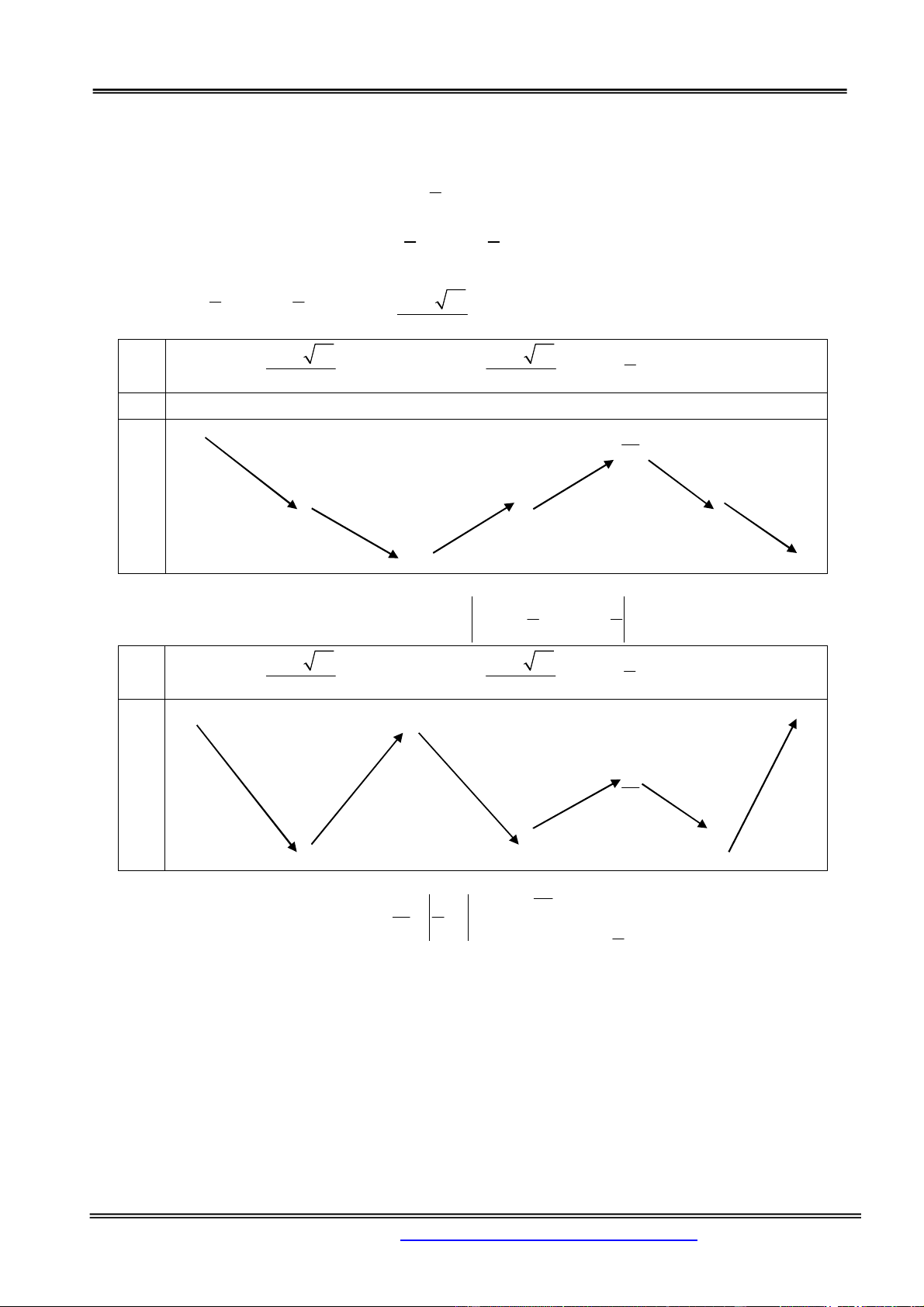
Phần Hàm số - Giải tích 12 Hướng dẫn giải: Chọn đáp án D. x  1  Ta có : 2 y '  6
x  3x  3. y '  0   1 x   2 3 1
Bảng biến thiên đồ thị hàm số 3 2 y  2  x x  3x  . 2 2 x  1 3 1 Với 3 2 2  x x  3x   0   7   33 2 2 x   8 7  33 7  33 1  x  1  8 8 2 1 y '  0  0   11 y 8 0 0 0 2   3 1
Từ đó, suy ra bảng biến thiên của đồ thị hàm số 3 2 y  2  x x  3x  2 2 7  33 7  33 1  x  1  8 8 2 1   2 y 11 8 0 0 0 19  k  6 11 k
Từ bảng biến thiên, nhận thấy: ycbt 4   1  2   . 3 8 2 2  k    4
Câu 15. Phương trình 4 2
x  2x  2  m có bốn nghiệm phân biệt khi: A. 3   m  2  . B. m  3  ; m  2. C. 3   m  2  . D. m  3. Hướng dẫn giải: Chọn đáp án A.
Xét hàm số f x 4 2
x  2x  2 xác định trên  . Có f x 3 '  4x  4 . xx  0
f ' x  0  .  x  1  Bảng biến thiên:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 17
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Dựa vào bảng biến thiên, để phương trình 4 2 x  2 x  2 
m có 4 nghiệm phân biệt thì 3   m  2  .
Câu 16. Xác định m để đường thẳng y  4m cắt đồ thị hàm số 4 2
y x  2x  4 tại 3 điểm phân biệt ? A. m  1. B. m  4 .
C. 3  m  4 . D. m  3 . Hướng dẫn giải: Chọn đáp án A. 3
y  4x  4x
x  0; y  4 y  0   .
x  1; y  3 
Ycbt  4m y  4  m  1 . max
Câu 17. Tìm m để đường thẳng y  4m cắt đồ thị hàm số C: 4 2
y x  8x  3 tại 4 phân biệt: 13 3 3 13 13 3 A.   m  . B. m  . C. m   . D.   m  . . 4 4 4 4 4 4 Hướng dẫn giải: Chọn đáp án A. x  0 3
y '  4x  16x y '  0  x  2  Bảng biến thiên x  2 0 2  y  0 + 0  0 + y  3  1  3 1  3
Câu 18. Tìm m để đường thẳng y m cắt đồ thị hàm số 4 2
y x  2x  2 tại 4 điểm phân biệt.
A. 1  m  2. B. m  2.
C. 2  m  3. D. m  2. Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 18
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án A. Xét hàm số 4 2
y x  2x  2 ta có. + TXĐ: D  . R + 3
y '  4x  4 . xx  0 + 3
y '  0  4x  4x  0  .  x  1   + Bảng biến thiên.
+ Dựa vào bảng biến thiên ta thấy đường thẳng y m cắt đồ thị hàm số 4 2
y x  2x  2 tại 4 điểm phân
biệt khi và chỉ khi 1  m  2.
Câu 19. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C  4 2
: y x mx m 1 cắt trục hoành m
tại bốn điểm phân biệt m   1 A. m  1. B.  .
C. không có m . D. m  2 . m  2  Hướng dẫn giải: Chọn đáp án B. Cách 2: Ta có: 4 2
y x mx m  1 .
Tập xác định: D   . 3
y '  4x  2mx .  x  0. 3 y ' 0 4x 2mx 0       m . 2  x  .  2
Đồ thị hàm số cắt trục hoành tai bốn điểm phân biệt  m  0 .
x  0  y m 1. Ta có:  2 m m . 2  x
(m  0)  y    m 1.  2 4 Bảng biến thiên x  m 0 . m   2 2 y '  0  0  0  y  . . m 1 . .  . 2 m 2 m   m 1   m 1 4 4 m 1  0  m  1. Yêu cầu bài toán 2   m   .   m 1  0 m  2.    4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 19
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 20.Số giao điểm nhiều nhất của đồ thị hàm số 4 2
y x  2x 1 với đường thẳng y m (với m là tham số ) là bao nhiêu ? A. 0. B. 2. C. 4. D. 3. Hướng dẫn giải: Chọn đáp án C. Xét phương trình : 4 2
x  2x 1  m   1 Xét đồ thị 4 2
y x  2x 1 Ta có : +) 3
y '  4x  4x x  0 3
y '  0  4x  4x  0  x  1   +) Bảng biến thiên : x  -1 0 1  y '  0 + 0  0 + y  1  0 0
Dựa bảng biến thiên  đường thẳng y m cắt đồ thị 4 2
y x  2x 1 nhiều nhất là 4 điểm
Câu 21. Tìm m để phương trình 4 2
x  8x  3  4m  0 có 4 nghiệm thực phân biệt. 13 3 13 3 13 3 A.   m  . B. m   . C. m  . D.   m  . 4 4 4 4 4 4 Hướng dẫn giải: Chọn đáp án D. Cách 2:
Phương trình đã cho tương đương 4 2
4m x  8x  3  f x .
Xét hàm số f x .
Tập xác định D   .  x  0 3
y  4x  16x , y  0   . x  2  Ta có bảng biến thiên: x  2 0 2  y  0  0  0   3   y 1  3 1  3 13 3
Dựa vào Bảng biến thiên, để  
1 có 4 nghiệm phân biệt thì 1
 3  4m  3    m  . 4 4
Câu 22.Gọi C là đồ thị hàm số 4 2
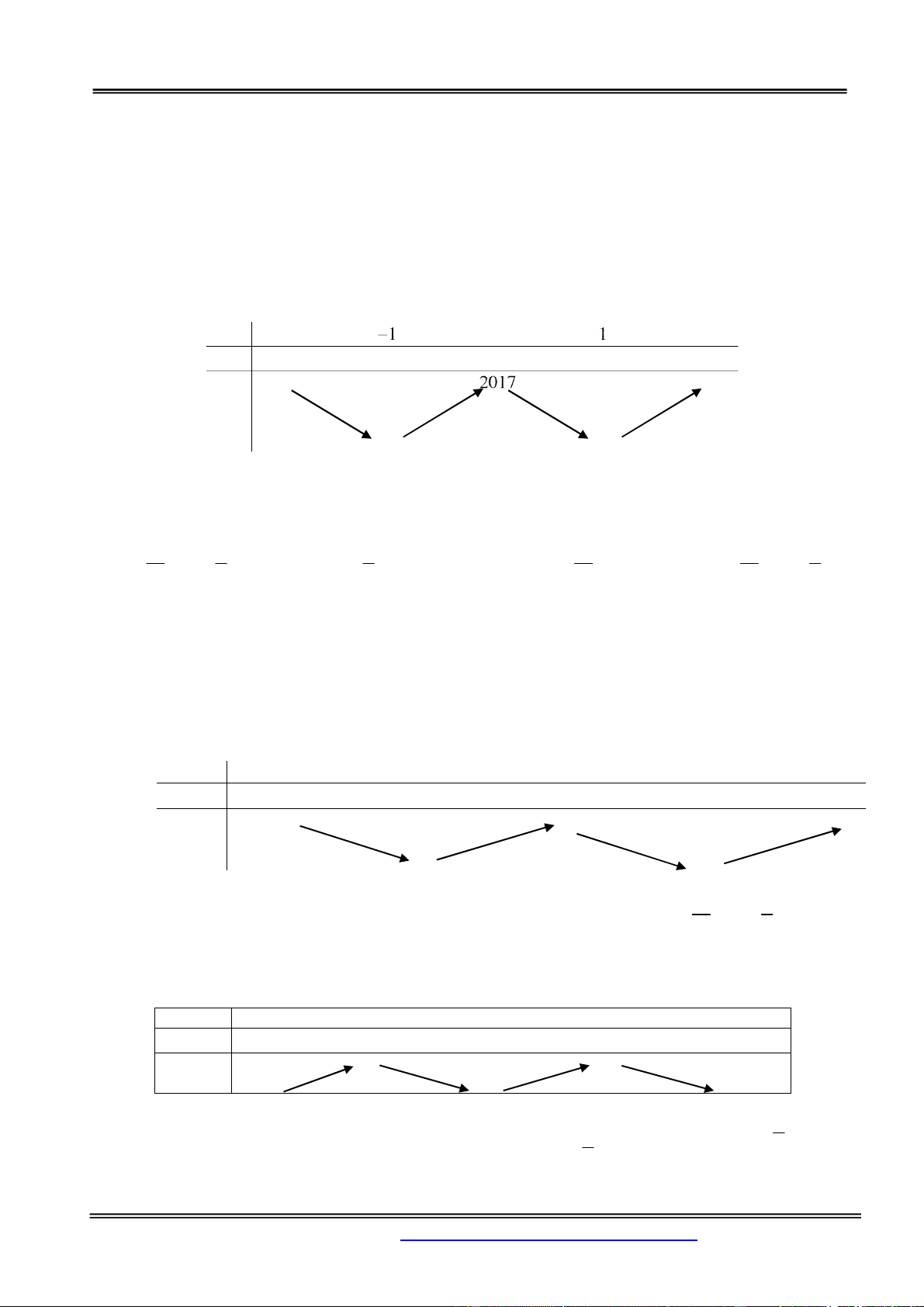
y x  2x m  2017 . Tìm m để C
có đúng 3 điểm chung phân m m
biệt với trục hoành, ta có kết quả: A. m  2017 .
B. 2016  m  2017 . C. m  2017 . D. m  2017 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 20
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Hướng dẫn giải: Chọn đáp án A.
Phương trình hoành độ giao điểm : 4 2
x  2x m  2017  0 4 2
m x  2x  2017
Số nghiệm của phương trình trên là số giao điểm của 2 đồ thị y m 4 2
y x  2x  2017  x  0 Ta có : 3
y  4x  4x . Cho y  0  x  1   x –∞ 0 +∞ y – 0 + 0 – 0 + +∞ +∞ y 2016 2016
Dựa vào bảng biến thiên, ta thấy phương trình có 3 nghiệm khi và chỉ khi m  2017 . Câu 23.
[2D1-2] Tìm m để đường thẳng y  4m cắt đồ thị hàm số C  4 2
: y x  8x  3 tại 4 phân biệt 13 3 3 13 13 3 A.   m  . B. m  . C. m   . D.   m  . 4 4 4 4 4 4 Hướng dẫn giải: Chọn đáp án A. Xét hàm số 4 2
y x  8x  3 trên D   . Ta có 3
y  4x 16x ,
x  0, y  3 3 
y  0  4x 16x  0  x  2, y  13   x  2  , y  1  3  Bảng biến thiên x  2 0 2  y  0  0  0   3  y 1  3 1  3 13 3
Đường thẳng y  4m cắt C  tại 4 điểm phân biệt khi chỉ khi 1
 3  4m  3    m  . 4 4
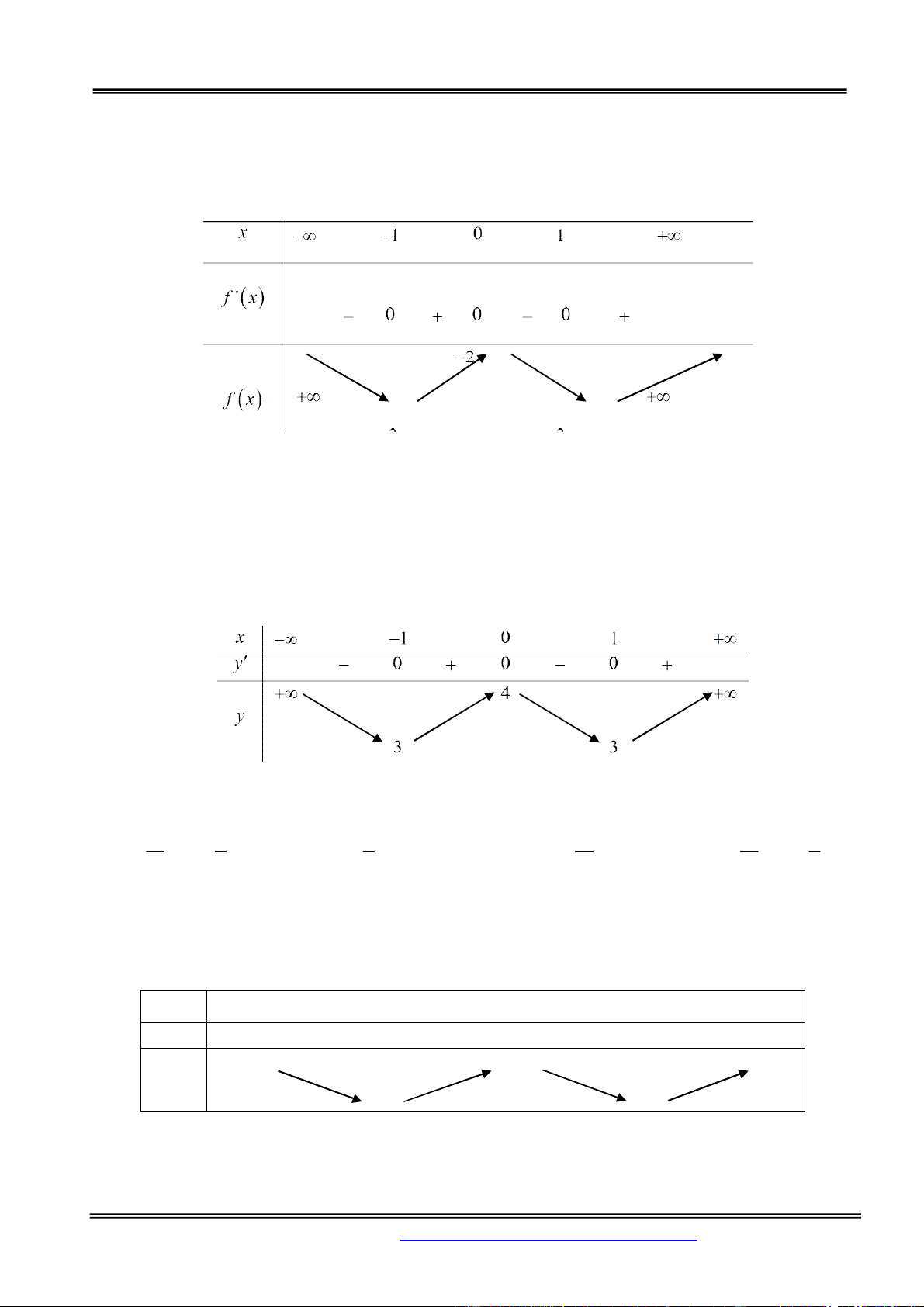
Câu 24. Cho hàm số y f (x) liên tục trên  và có bảng biến thiên như hình vẽ. Tìm tất cả các giá trị thực
của m để phương trình f ( x)  2m có đúng hai nghiệm phân biệt. x  -1 0 1  y ' + 0 - 0 + 0 - y . 0 . 0 .  -3  m  0 m  0 3 A.   . B. m  3  . C. 3 . D. m   . m  3   m   2  2 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 21
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án C. m  0 2m  0
Dựa vào BBT ta thấy để phương trình f ( x)  2m có đúng hai nghiệm phân biệt thì    3 2m  3   m    2
Câu 25. Cho hàm số y f x có bảng biến thiên như hình bên. Khi đó tất cả các giá trị của m để phương
trình f x  m 1 có ba nghiệm thực là
A. m  3; 5 .
B. m  4;6 .
C. m   ;
 3  5;   .
D. m 4;6 . Hướng dẫn giải: Chọn đáp án B.
Phương trình f x  m 1 có ba nghiệm thực khi và chỉ khi 3  m 1  5  4  m  6 .
Câu 26.Cho hàm số y f (x) có bảng biến thiên sau : x  -1 0 1  y '  0 + 0  0 + y  1  1 1
Với giá trị nào của m thì phương trình f (x) 1  m có đúng 2 nghiệm ? A. m  1. B. m  1  .
C. m  1 hoặc m  2  . D. m  1  hoặc m  2  . Hướng dẫn giải: Chọn đáp án C.
+) Ta có f (x) 1  m f (x)  m 1
Dựa bảng biến thiên để phương trình (1) có đúng hai nghiệm m 1  0 m  1      m 1  1  m  2  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 22
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 27. Cho hàm số y f (x) liên tục trên  và có bảng biến thiên như hình vẽ. Tìm tất cả các giá trị thực
của m để phương trình f ( x)  2m có đúng hai nghiệm phân biệt. x  -1 0 1  y ' + 0 - 0 + 0 - y . 0 . 0 .  -3  m  0 m  0 3 A.   . B. m  3  . C. 3 . D. m   . m  3   m   2  2 Hướng dẫn giải: Chọn đáp án C.
Dựa vào BBT ta thấy để phương trình f (x)  2m có đúng hai nghiệm phân biệt thì m  0 2m  0    3 2m  3   m    2
Câu 28. Cho hàm số y f (x) xác định trên  \  
1 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: x -∞ 1 +∞ f '(x) - + 2 -1 f(x) -∞ -∞
Tìm tập hợp tất cả các giá trị của m sao cho phương trình f (x)  m có hai ngiệm thực phân biệt. A.  ;    1 . B.  ;  2. C. (1;2) D.  ;   1 . Hướng dẫn giải: Chọn đáp án A.
Dễ dàng nhận thấy khi m  1
 thì phương trình f x  m có hai nghiệm phân biệt.
Câu 29. Cho hàm số y f x  xác định trên  \  
1 , liên tục trên từng khoảng xác định và có bảng biến thiên như dưới đây:.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 23
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 .
Tìm tập hợp tất các giá trị thực của m để phương trình f x   m có nghiệm thực duy nhất A. 0;.. B. 2;.. C. 2;   .   . D. 0;   .  Hướng dẫn giải: Chọn đáp án B.
Số nghiệm thực của phương trình f x   m bằng số giao điểm của đường thẳng y m và đồ thị hàm số
y f x . Để phương trình f x  m có nghiệm thực duy nhất thì m  2
Câu 30. Giả sử tồn tại hàm số y f x xác định trên  \  
1 , liên tục trên mỗi khoảng xác định và
có bảng biến thiên như sau:. .
Tập hợp tất cả các giá trị của tham số thực m sao cho phương trình f x  m có bốn nghiệm thực phân biệt là A.  2  ; 0   1 . B.  2  ; 0   1 . C.  2  ; 0 . D.  2  ;0 . Hướng dẫn giải: Chọn đáp án D.
Câu 31. Cho hàm số y f (x ) xác định trên  \ 1; 
1 , liên tục trên mỗi khoảng xác định và có
bảng biến thiên như sau:. .
Tìm tập hợp tất cả các giá trị của thàm số m sao cho phương trình f x   m có ba nghiệm thực phân biệt A.  2; 2    . B. 2;2 . C.  ;  . D. 2;. Hướng dẫn giải: Chọn đáp án A.
Từ bảng biến thiên suy ra phương trình f x   m có ba nghiệm thực phân biệt khi 2   m  2 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 24
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
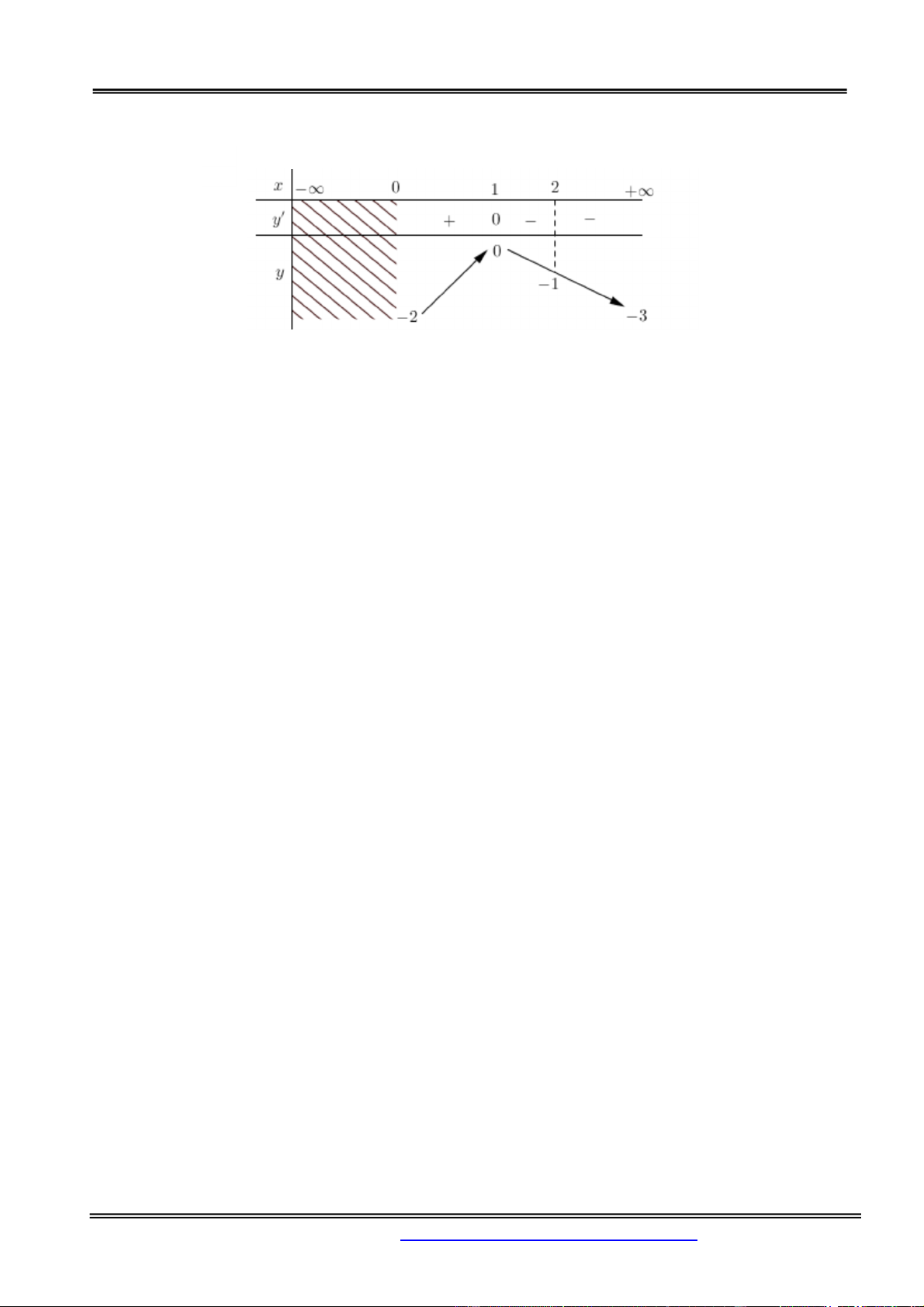
Câu 32. Cho hàm số y f x  xác định trên 0;    ,  
liên tục trên khoảng 0;
 và có bảng biến thiên như sau.
Tìm tập hợp tất cả các giá trị thực của tham số sao cho phương trình f x   m có hai nghiệm x ,x thỏa mãn 1 2
x  0;2 và x  2;  . 2   1   A.  2  ;  0 . B.  2  ;  1 . C.  1  ;  0 . D.  3  ;  1 . Hướng dẫn giải: Chọn đáp án B.
Nghiệm của phương trình là hoành độ giao điểm của đồ thị hàm số và đường thẳng y m
Dựa vào BBT ta có kết luận m   2  ;  1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 25
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
SỰ TƯƠNG GIAO PHƯƠNG PHÁP ĐỒ THỊ HÀM SỐ Câu 1.Cho hàm số 3 2
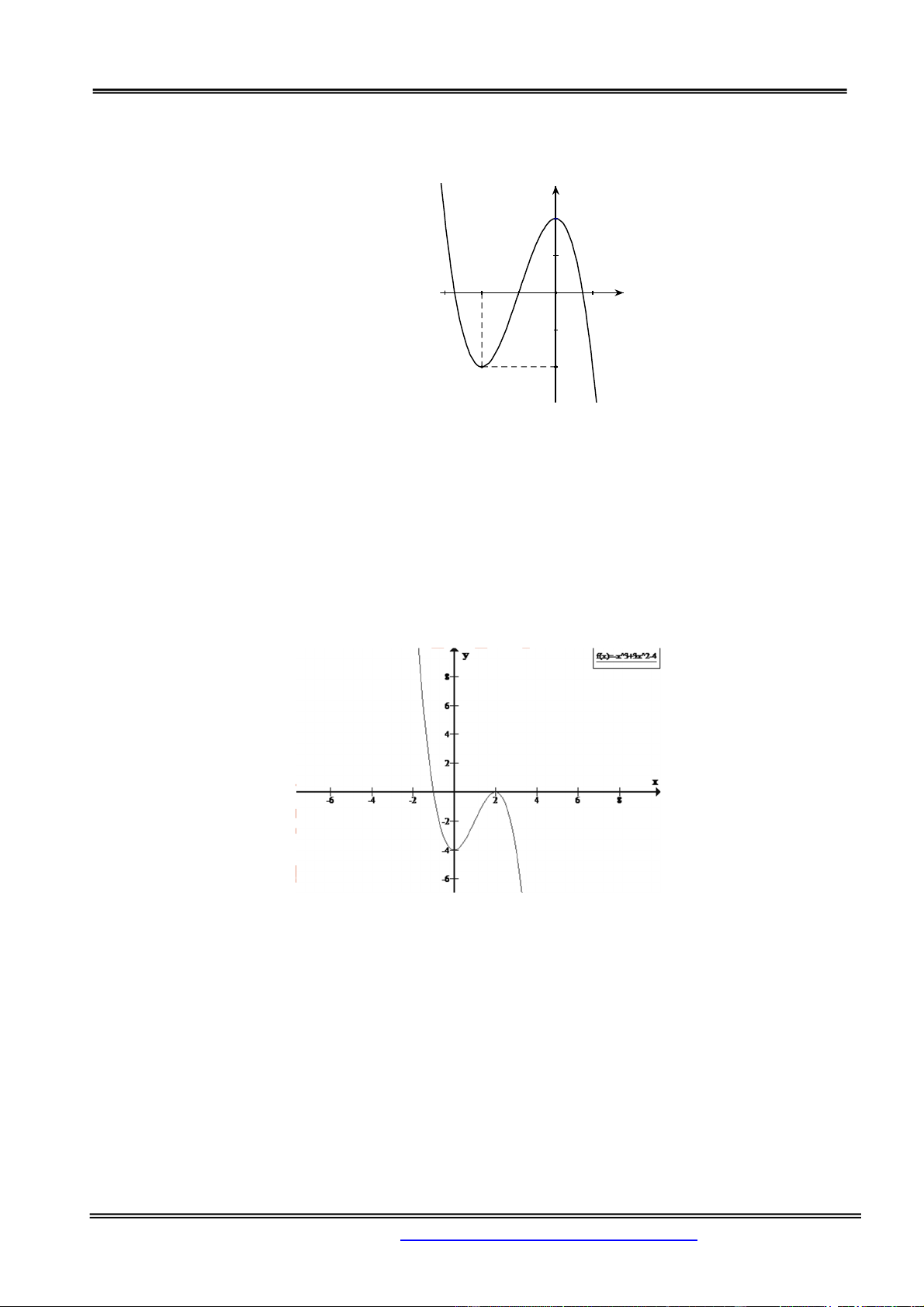
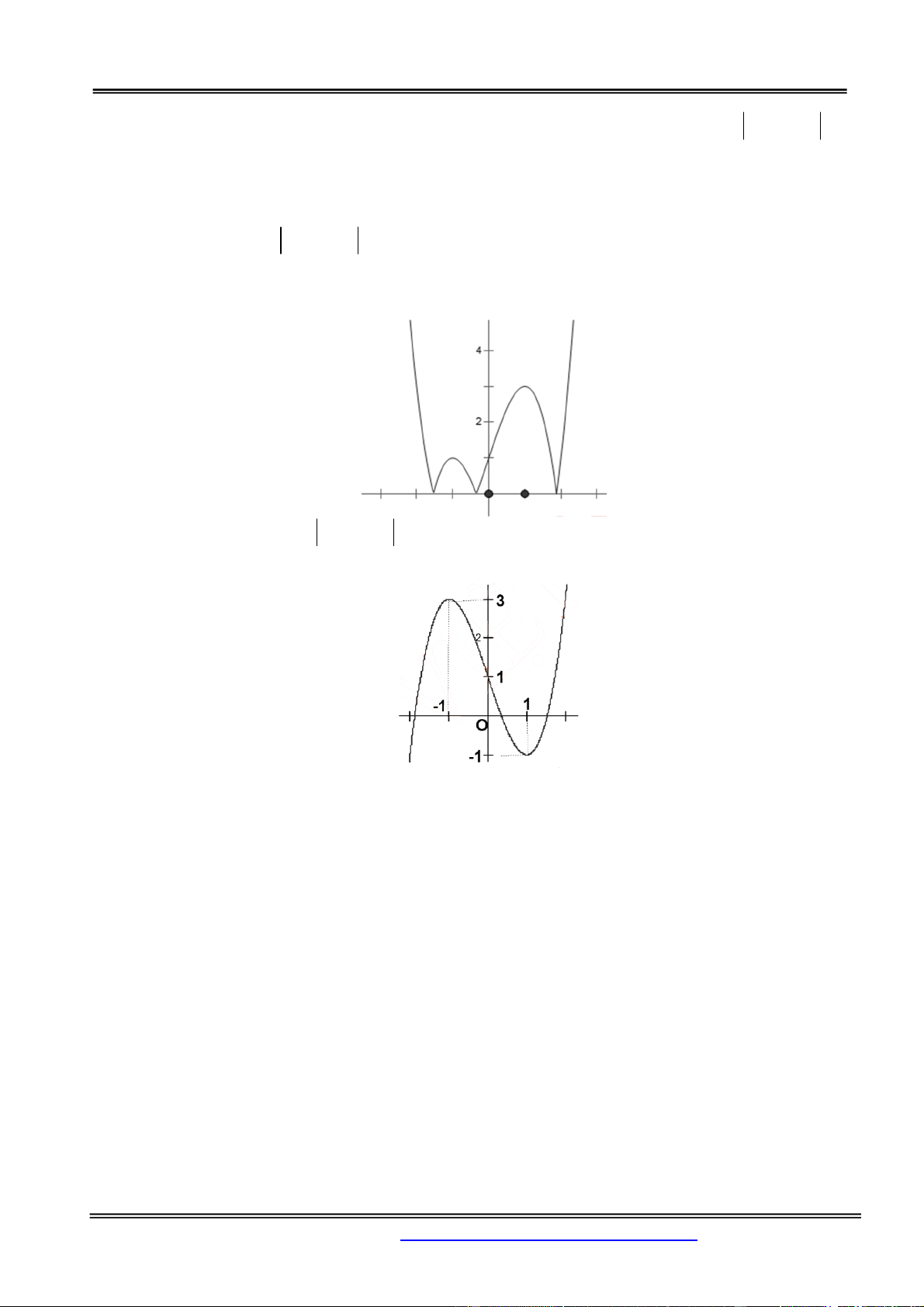
y   x  3x  2 có đồ thị như hình vẽ. y 2 2  1 O x 2 
Với giá trị nào của m thì phương trình 3 2
x  3x  1  m  0 có ba nghiệm phân biệt? A. 1
  m  3 . B. 3
  m  1 . C. 3
  m  1 .
D. m  1 . Hướng dẫn giải: Chọn đáp án C.
Ta có số nghiệm của phương trình 3 2 3 2
x  3x  1  m  0   x  3x  2  m  1 là số giao điểm của đồ thị hàm số 3 2
y   x  3x  2 và đường thẳng y m  1.
Từ đồ thị ta thấy hàm số có y  2 và y  2  nên phương trình 3 2
x  3x  1  m  0 CĐ CT có ba nghiệm phân biệt 2
  m  1  2  3
  m  1 .
Câu 2.Đồ thị hình bên là của hàm số 3 2 y x
  3x  4 . Tìm tất cả giá trị của m để phương trình 3 2
x  3x m  0 có hai nghiệm phân biệt? Chọn một khẳng định ĐÚNG
A. m  4 hoặc m  0 . B. m  4 .
C. 0  m  4 . D. m  0 . Hướng dẫn giải: Chọn đáp án A. 3 2 3 2
x  3x m  0  x
  3x  4  m  4 m  4 0 m     4    m  4 4 m      0  
Phương trình có 2 nghiệm phân biệt khi  Câu 3. Cho hàm số 3 2
y x  6x  9x m C , với m là tham số. Giả sử đồ thị C  cắt trục hoành tại 3
điểm phân biệt có hoành độ thỏa mãn x x x . Khẳng định nào sau đây đúng? 1 2 3
A. 1  x x  3  x  4 .
0  x 1  x  3  x  4 . 1 2 3 B. 1 2 3
C. x  0  1  x  3  x  4 .
1  x  3  x  4  x . 1 2 3 D. 1 2 3 Hướng dẫn giải:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 26
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Chọn đáp án B. x  1 y'  3 2
x  12x  9  0  x  3
Lập BBT có (C) cắt trục hoành tại 3 điểm phân biệt khi y  3  0  y 
1  m  0  m  4
Căn cứ vào BBT tvà điều kiện trên ta có 0  x  1  x  3  x  4 . 1 2 3 Cách khác
Phương trình hoành độ giao điểm: 3 2
x x x m    3 2 6 9
0 1  x  6x  9x  m Gọi C 3 2
: y x  6x  9x .
Số nghiệm của phương trình  
1 là số giao điểm của đồ thị C và đường thẳng d  : y  m .
Dựa vào đồ thị, ta thấy đường thẳng d  cắt C tại 3 điểm thỏa 0  x  1  x  3  x  4 . 1 2 3
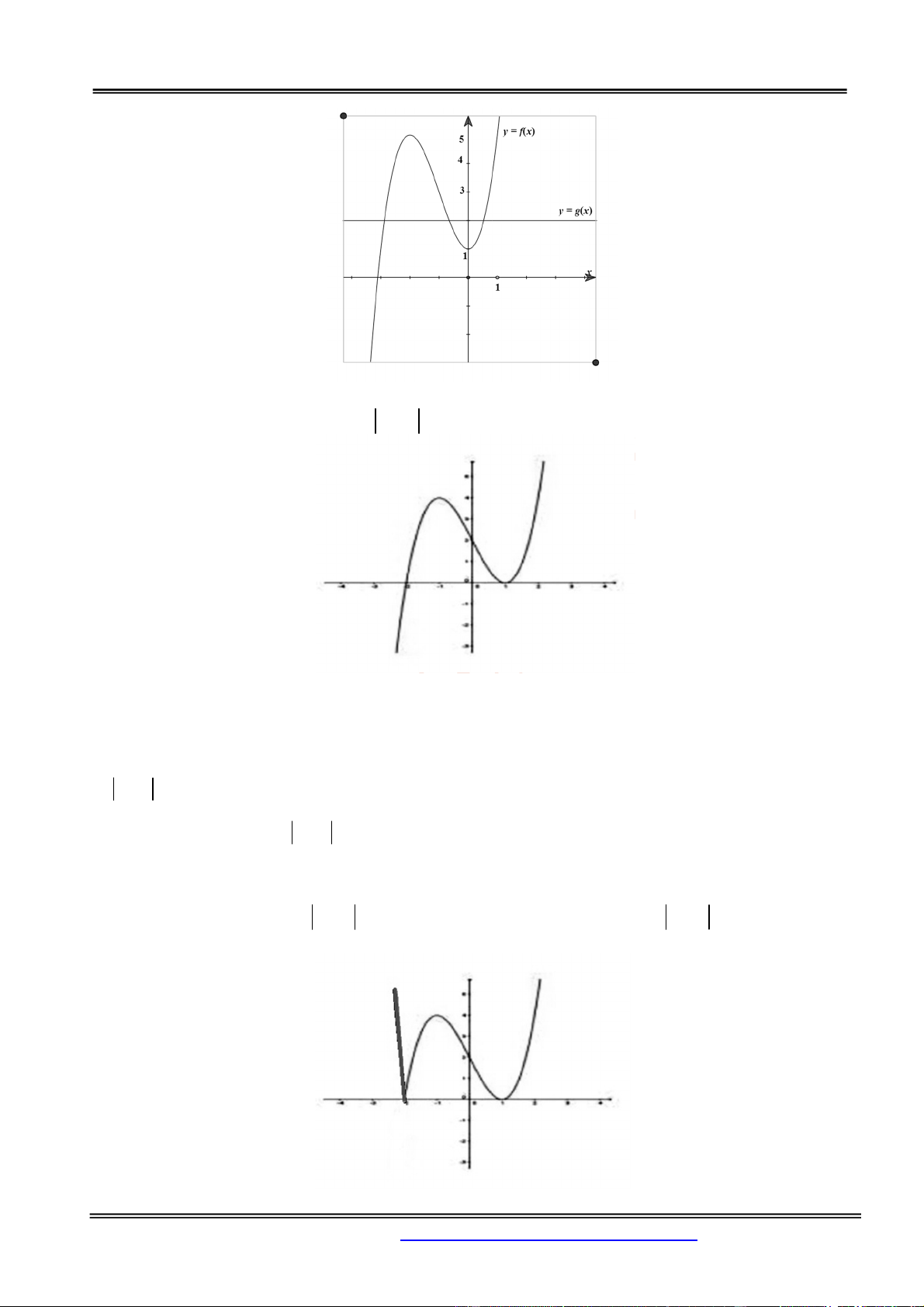
Câu 4. Cho hàm số y f x có đồ thị là hình sau. Tìm tất cả các giá trị thực của tham số m để phương trình
f (x)  m 1 có 4 nghiệm thực phân biệt A. m  4  hay m  0. B. 4   m  0.
C. 0  m  4. D. 1   m  3. Hướng dẫn giải: Chọn đáp án D.
Ta có số nghiệm của phương trình f (x)  m  1 là số giao điểm
của hàm y f x và y m 1.
Vậy để phương trình f (x)  m 1 có 4 nghiệm phân biệt
 0  m 1  4  1   m  3 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 27
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 5. Hình vẽ bên là đồ thị C  của hàm số 3
y x  3x 1. Giá trị của m để phương trình 3
x  3x 1  m
có 3 nghiệm đôi một khác nhau là. A. m  0 .
B. 1  m  3 . C. 3   m  1.
D. m  0 , m  3 . Hướng dẫn giải: Chọn đáp án D. Đồ thị C 3
: y x  3x 1 được vẽ bằng cách:
Phần 1: Giữ nguyên phần đồ thị C  3
: y x  3x 1 nằm bên trên trục hoành.
Phần 2: Lấy đối xứng phần đồ thị C  3
: y x  3x 1 nằm dưới trục hoành qua trục hoành
Dựa vào đồ thị, phương trình 3
x  3x 1  m có 3 nghiệm đôi một khác nhau khi m  0 , m  3 .
Câu 6. Đồ thị sau đây là của hàm số 3
y x  3x 1. Với giá trị nào của m thì phương trình 3
x  3x m  0 có ba nghiệm phân biệt. .
A.  1  m  3 .
B.  2  m  2 .
C.  2  m  2 .
D.  2  m  3 . Hướng dẫn giải: Chọn đáp án B.
Ta có x3  3x m  0  x3  3x  1  m 1 1 .
Số nghiệm của phương trình 1 là số giao điểm của hai đồ thị y x3  3x 1 và y m 1.
Do đó 1 có ba nghiệm phân biệt  1  m 1  3  2  m  2 .
Câu 7. Cho phương trình 3 2
x  3x m 1  0 với m là tham số thực. Tìm tất cả các giá trị của m để phương
trình đã cho có 3 nghiệm thực phân biệt.
A. 1  m  5 .
B. 0  m  4 . C. m  5 . D. m  1. Hướng dẫn giải: Chọn đáp án A. 3 2
x  3x m 1  0 (1) Ta có: 3 2 3 2
x  3x m 1  0  x  3x 1  . m
Để phương trình (1) có 3 nghiệm phân biệt khi và chỉ khi đồ thị hàm số 3 2
y x  3x 1 và đường thẳng
y m cắt nhau tại 3 điểm phân biệt. Dựa vào đồ thị, suy ra 1  m  5 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 28
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 8. Cho hàm số y = f (x) có đồ thị hàm số đường cong trong hình vẽ bên. Tìm tất cả các giá trị
thực của tham số m để phương trình f x  m có 4 nghiệm phân biệt.
A. 0  m  2.
B. 0  m  4.
C. 1  m  4.
D. Không có giá trị nào của m . Hướng dẫn giải: Chọn đáp án B.
f (x) khi f (x)  0
f (x)   f (x) khi f (x)  0 
Suy ra, đồ thị hàm số y f (x) bao gồm 2 phần:
Phần 1: Giữ nguyên phần đồ thị hàm số y f (x) ở phía trên trục Ox.
Phần 2: Lấy đối xứng phần đồ thị phía dưới Ox của y f (x) qua Ox.
Số nghiệm của phương trình f (x)  m là số giao điểm của đồ thị hàm số y f (x) và đường thẳng y  . m
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 29
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Dựa vào đồ thị hàm số ta kết luận, phương trình có 4 nghiệm phân biệt khi 0  m  4.
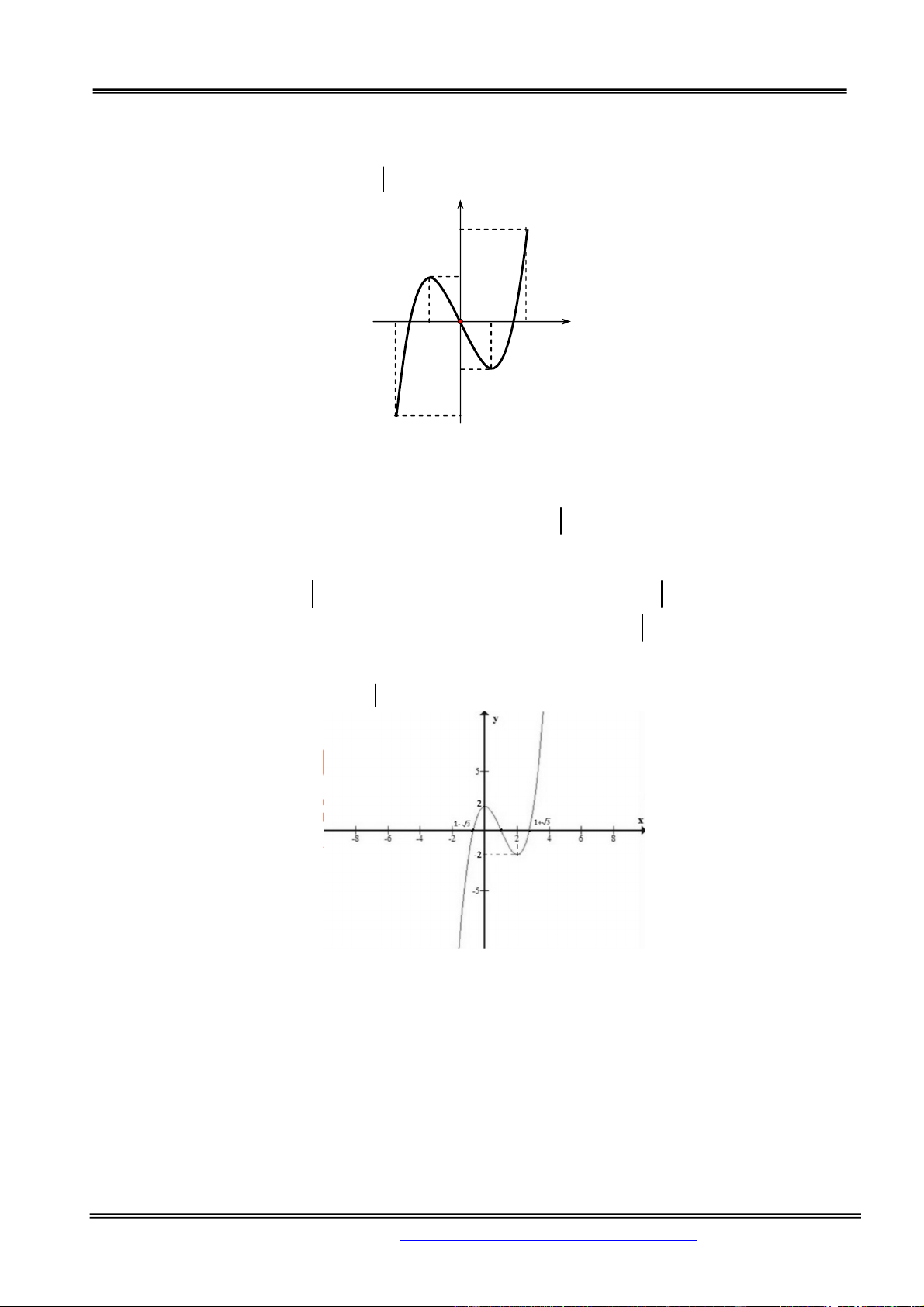
Câu 9. Cho hàm số y f x liên tục trên đoạn 2;2 và có đồ thị là đường cong như hình vẽ bên.
Tìm số nghiệm của phương trình f x  1 trên đoạn 2;2 . y 4 2 x 2  2 x O 2 x 1 2  4  A. 4 . B. 5 . C. 3 . D. 6 . Hướng dẫn giải: Chọn đáp án D.
Từ đồ thị của hàm số y f (x) ta suy ra đồ thị của hàm số y f x như sau: Giữ nguyên phần đồ thị
nằm phía trên trục hoành của hàm số đã cho; Lấy đối xứng phần đồ thị nằm bên dưới trục hoành qua trục hoành.
Số nghiệm của phương trình f x  1 là số giao điểm của đồ thị hàm số y f x và đường thẳng
y  1. Căn cứ vào đồ thị, ta thấy có sáu giao điểm. Vậy phương trình f x  1 có 6 nghiệm phân biệt.
Câu 10.Cho hàm số f x 3 2
x  3x  2 có đồ thị là đường cong trong hình bên. Tìm tất cả các giá trị 3 2
thực của tham số m đề phương trình x  3x  2  m có nhiều nghiệm thực nhất. A. 2   m  2 ..
B. 0  m  2 . C. 2   m  2 .
D. 0  m  2 . Hướng dẫn giải: Chọn đáp án C.
Câu 11. Đồ thị trong hình bên dưới là đồ thị của hàm số 4 2
y  x  4x . Dựa vào đồ thị bên hãy tìm
tất cả các giá trị thực của tham số m sao cho phương trình 4 2
x  4x m  2  0 có đúng hai nghiệm thực phân biệt?
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 30
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
A. m  0, m  4 . B. m  0 .
C. m  2; m  6 . D. m  2 . Hướng dẫn giải: Chọn đáp án C. Phương trình 4 2 4 2
x  4x m  2  0  m  2   x  4x
Dựa vào đồ thị để phương trình 4 2
x  4x m  2  0 có đúng hai nghiệm thực phân biệt thì đường thẳng
y m  2 cắt đồ thị đã cho tại đúng hai điểm phân biệt. Tức là: m  2  0 m  2  m 2 4    m  6   1 Câu 12. Cho hàm số 4 2 y  
x  2x có đồ thị C như hình vẽ sau. Dựa vào đồ thị C , tìm tất cả các giá 4
trị thực của tham số m để phương trình 4 2 m2
x  8x  2
 0 có bốn nghiệm phân biệt. A. m  2 .
B. 0  m  2 .
C. 0  m  4 . D. m  0 . Hướng dẫn giải: Chọn đáp án A. m 1 m 1 Phương trình 4 2 2 4 2 4 2   8  2  0    2  2  0    2  2m x x x x x x . 4 4
Suy ra số nghiệm của phương trình 4 2 m2
x  8x  2
 0 là số giao điểm của đường thẳng 2m y  và đồ thị 1 hàm số 4 2 (C) : y   x  2x . 4
Yêu cầu bài toán  0  2m  4  m  2 . 4 2
Câu 13. Tìm m để phương trình x  5x  4  log m có 8 nghiệm phân biệt: 2 A. 4 9 0  m  2 .
B. Không có giá trị của m. 4 9 4 9 4 9 C. 1  m  2 .
D.  2  m  2 . Hướng dẫn giải: Chọn đáp án C.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 31
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  4 2  x
  5x  4,x 2;1  1  ;2 4 2     
Ta có x  5x  4   . 4 2 x
  5x  4,x   ;    2  1;  1  2;    4 2
Do đó đồ thị hàm số là phần bên trên trục hoành của đồ thị hàm số y x  5x  4 và phần đối xứng bên
dưới trục hoành của đồ thị qua trục hoành. Từ đồ thị ta thấy để phương trình có 8 nghiệm phân biệt thì 9 4 9 0  log m
 1  m  2 . 2 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 32
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
DẠNG 3: TƯƠNG GIAO VỚI HÀM BẬC BA
Phương pháp 1: Nhẩm nghiệm – tam thức bậc 2.
+) Lập phương trình hoành độ giao điểm F x, m  0
+) Nhẩm nghiệm: (Khử tham số). Giả sử x  x là 1 nghiệm của phương trình. 0 x  x0
+) Phân tích: Fx, m  0  x  x .g x  0 
(là g  x  0 là phương trình bậc 0    gx  0  2 ẩn x tham số m ).
+) Dựa vào yêu cầu bài toán đi xử lý phương trình bậc 2 g  x  0 .
Phương pháp 2: Cực trị
*) Nhận dạng: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm. *) Quy tắc:
+) Lập phương trình hoành độ giao điểm F x, m  0 (1). Xét hàm số y  Fx, m
+) Để (1) có đúng 1 nghiệm thì đồ thị
y  Fx, m cắt trục hoành tại đúng 1 điểm. (2TH)
- Hoặc hàm số luôn đơn điệu trên R  hàm số
không có cực trị  y '  0 hoặc vô nghiệm
hoặc có nghiệm kép    0 y'
- Hoặc hàm số có CĐ, CT và y .y  0 (hình cd ct vẽ)
+) Để (1) có đúng 3 nghiệm thì đồ thị
y  Fx, m cắt trục hoành tại 3 điểm phân
biệt  Hàm số có cực đại, cực tiểu và y .y  0 cd ct
+) Để (1) có đúng 2 nghiệm thì đồ thị
y  Fx, m cắt trục hoành tại 2 điểm phân
biệt  Hàm số có cực đại, cực tiểu và y .y  0 cd ct
Bài toán: Tìm m để đồ thị hàm bậc 3 cắt trục hoành tại 3 điểm lập thành 1 cấp số cộng: 1. Định lí vi ét: b c
*) Cho bậc 2: Cho phương trình 2
ax  bx  c  0 có 2 nghiệm x , x thì ta có: x  x   , x x  1 2 1 2 1 2 a a
*) Cho bậc 3: Cho phương trình 3 2
ax  bx  cx  d  0 có 3 nghiệm x , x , x thì ta có: 1 2 3
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 33
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 b c d x  x  x   , x x  x x  x x  , x x x   1 2 3 1 2 2 3 3 1 1 2 3 a a a
2.Tính chất của cấp số cộng:
+) Cho 3 số a, b, c theo thứ tự đó lập thành 1 cấp số cộng thì: a  c  2b
3. Phương pháp giải toán: b
+) Điều kiện cần: x  
là 1 nghiệm của phương trình. Từ đó thay vào phương trình để tìm m. 0 3a
+) Điều kiện đủ: Thay m tìm được vào phương trình và kiểm tra.
Câu 1: Tìm số giao điểm của đồ thị hàm số 2
y  (x  2)(x x  1) và trục hoành. A. 1 . B. 0 . C. 2 . D. 3 . Hướng dẫn giải: Chọn A. x  2  0
Ta có phương trình hoành độ giao điểm là 2
y  (x  2)(x x  1)   x  2  nên số giao 2
x x 1  0  điểm là 1 .
Câu 2: Tìm m để phương trình 3 2
x  3x m 1  0 có ba nghiệm thực phân biệt
A. 1  m  5 .
B. 1  m  5 . C. 5   m  1.
D. 1  m  5 . Hướng dẫn giải: Chọn B. 3 2 3 2
x  3x m 1  0  x  3x 1  m Xét hàm số 3 2
y x  3x 1 ta có
x  0  y  1  2
y  3x  6x, y  0  x  2  y  5  
Số nghiệm của phương trình x3  3x2  m 1  0 là số giao điểm của đồ thị hàm số y x3  3x2 1 và đường
thẳng y m
Phương trình x3  3x2  m 1  0 có ba nghiệm thực phân biệt  5  m  1  1  m  5 .
Câu 3: Cho hàm số y x3  3x2 1 có đồ thị C  . Với giá trị nào của m thì phương trình x3  3x2  m  2
có 3 nghiệm phân biệt trong đó có 2 nghiệm lớn hơn 1 A. 3   m  1. B. 2   m  0 . C. 3   m  1  . D. 3   m  0 . Hướng dẫn giải: Chọn B.
Dùng chức năng giải phương trình của máy tính. Chọn các giá trị m đại diện cho các phương án. Ta thay vào
phương trình và kiểm tra.
Phương án A. Lấy m  0, 5 để thử. Loại A
Phương án C. Lấy m  2, 5 để thử. Loại C, D Vậy chọn B
Câu 4: Biết đường thẳng y mx 1 cắt đồ thị hàm số y x3  3x 1 tại ba điểm phân biệt. Tất cả các
giá trị thực của tham số m là
A. m  3 .
B. m  3 . C. m  3  .
D. m  3 . Hướng dẫn giải: Chọn A.
Xét phương trình hoành độ giao điểm : 3
mx 1  x  3x 1 3
x  3x mx  0  x  2
x  3  m  0
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 34
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x  0   2
x m  3  1 
Để đường thẳng cắt đồ thị hàm số tại 3 điểm phân biệt thì  
1 phải có 2 nghiệm phân biệt khác 0  m  3  0  m  3  .
Câu 5: Tìm m để phương trình 3 2
x – 3x – m  0 có ba nghiệm thực phân biệt A. m  4
  m  0 .
B. – 4  m  0 . C. m  4
  m  0 . D. 4   m  0. Hướng dẫn giải: Chọn D. Xét 3 2
y x  3x mx  0 Ta có 2
y  3x  6x . Khi đó : y  0  x  2 
Để phương trình bài ra có 3 nghiệm thực phân biệt  y 0.y 2  0
 m.m  4  0  4  m  0 .
Câu 6: Điều kiện của tham số m để đồ thị của hàm số y  2x3  6x  2m cắt trục hoành tại ít nhất
hai điểm phân biệt là m  2  A.  . B. m  2  . C. 2   m  2 . D. 2   m  2 . m  2  Hướng dẫn giải: Chọn D. Ta có:  x  1
y   4  2m 2
y '  6x  6  y '  0  x  1
  y  4  2m
Do hệ số a  2  0 nên điểm cực đại và cực tiểu 1; 4  2m 1; 4  2m
Để đồ thị của hàm số 3
y  2x  6x  2m cắt trục hoành tại ít nhất 2 điểm phân biệt thì y .y
 0   4  2m. 4  2m  0 CD CT  2  m  2 .
Câu 7: Đường thẳng đi qua điểm cực đại, cực tiểu của đồ thị hàm số y x3  3mx  2 cắt đường tròn tâm
I 1;1, bán kính bằng 1 tại 2 điểm phân biệt A, B sao cho diện tích tam giác IAB đạt giá trị lớn nhất khi m có giá trị là 2  3 1 3 2  5 2  3 A. m  . B. m  . C. m  . D. m  . 2 2 2 3 Hướng dẫn giải: Chọn A. 2
y  3x  3m .
Hàm số có cực đại cực tiểu  y  0 có hai nghiệm phân biệt  m  0 .
Khi đó đường thẳng qua hai điểm cực trị là  : 2mx y  2  0 . 2m 1
d I ,  
R  1 (Do  luôn cắt đường tròn tại 2 điểm phân biệt) 2 4m  1 1 1  1 1 Với m  . Có 2 S  .I . A I . B sin AIB R  . 2 IAB 2 2 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 35
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 1   R 2 2 Do đó 0 S
Sin AIB  1  AIB  90  d I ,    . max   2 2 2  2  3 m   n 2m 1 2 2 Suy ra   2 2m  2 2 2 1
 4m 1  4m  8m 1  0   . 2 2 4m 1  2  3 m  n  2 Câu 8: Cho hàm số 3
y x  3x  2 có đồ thị C  . Gọi d là đường thẳng đi qua A3; 20 và có hệ số
góc m . Giá trị của m để đường thẳng d cắt C  tại 3 điểm phân biệt là 15 15 15 15 A. m  . B. m  , m  24 . C. m  , m  24 . D. m  . 4 4 4 4 Hướng dẫn giải: Chọn B.
Đường thẳng (d) đi qua A3; 20 có phương trình là: y m x   3  20 .
Phương trình hoành độ giao điểm: 3
x  3x  2  m x   3  20 3
x  (m  3)x  3m  18  0  (x  2
3)(x  3x m  6)  0  x  3   2
x  3x m  6   0 (*) Đặ 2 t: (
g x)  x  3x m  6
Đường thẳng (d) cắt đồ thị (C ) tại 3 điểm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm phân biệt m khác 3.  15
  9  4(6  m)  0 m      4 (3
g )  m  24   0 m   24 15
Vậy, giá trị cần tìm là: m  ; m  24 4 Câu 9: Cho hàm số 3 2
y x  (m  3)x  (2m 1)x  3(m 1) . Tập hợp tất cả giá trị m để đồ thị hàm số
đã cho cắt trục hoành tại ba điểm phân biệt có hoành độ âm là A. .  B. 2  ;  2 . C.  ;  4  . D.  1  ;  \  2 . . Hướng dẫn giải: Chọn A
Phương trình hoành độ giao điểm của đồ thị và trục hoành là : 3 2 x m x m x m     x   2 ( 3) (2 1) 3( 1) 0
1 x  m  4 x  3(m 1)  0   ycbt 2
x  m  4 x  3(m 1)  0 có hai nghiệm âm phân biệt khác -1
  m  22  0  bm  2   m  4  0  m  4 a      m   c m  1    3m   1  0 m  2 a     2
1  m  4   1  3(m 1)  0 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 36
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 10: Tìm m để đồ thị hàm số 3 2
y x  3x  2 cắt đường thẳng y m x   1 tại ba điểm phân
biệt có hoành độ x , x , x thỏa mãn 2 2 2
x x x  5. 1 2 3 1 2 3 A. m  2. B. m  3. C. m  3. D. m  2  . Hướng dẫn giải: Chọn A .
Phương trình hoành động giao điểm 3 2 x x
m x     x    2 3 2 1
1 x  2x  2  m  0   1  x  1   2
x  2x  2  m  0 2 
Để hai đồ thị hàm số cắt nhau tại 3 điểm phân biệt thì phương trình  
1 có ba nghiệm phân biệt 
phương trình 2 có hai nghiệm phân biệt khác 1 .
  1  2  m  0    m  3  .
1  2  2  m  0 
Gọi x  1, x , x lần lượt là nghiệm của phương trình  
1  x x  2; x .x  2  m . 1 2 3 2 3 2 3 2 Ta có: 2 2 2
x x x  5  x x
 2x x  4  4  2. 2  m  4  m  2  . 1 2 3  2 3  2 3   Câu 11: Cho hàm số 3 2
y x  2x  (1 )
m x m (1) . Tìm m để đồ thị hàm số (1) cắt trục hoành tại
3 điểm phân biệt có hoành độ x , x , x thỏa mãn điều kiện 2 2 2
x x x  4 1 2 3 1 2 3 1 1 A.
m  1 và m  0 . B.
m  2 và m  0 . 3 4 1 1 C.   m  1. D.
m  1 và m  0 . 4 4 Hướng dẫn giải: Chọn D. Xét phương trình  x  1 3 2
x  2x  1 mx m  0 (1)   x   1  2
x x m  0   2
x x m  0  g(x) (2) 
Để hàm số cắt trục hoành tại 3 điểm phân biệt  phương trình (2) phải có hai nghiệm phân  1   g  (x)  0 1   4m  0 m  biệt khác 1       4 (*) g(1)  0 m  0   m  0  Mặt khác 2 2 2
x x x  4 ( x  1 , x , x là hai nghiệm phương trình (2) ) 1 2 3 1 2 3 2 2
x x  3   x x
 2x x  3  1 2 m  3 1 2 2 2 3 1 2
 1 2m  3  m  1 (**) 1
Từ (*) và (**) , ta có : 
m  1 và m  0 . 4 Câu 12: Cho hàm số 3 2
y x  3x  2 có đồ thị là C  . Hỏi có tất cả bao nhiêu giá trị của tham số m
để đường thẳng y mx  2 cắt đồ thị (C) tại ba điểm phân biệt có hoành độ x , x , x thỏa mãn điều 1 2 3
kiện x x x  (x x x x x x )  4 ? 1 2 3 1 2 2 3 3 1 A. 3 . B. 2 . C. 0 . D. 1. Hướng dẫn giải: Chọn D.
Phương trình hoành độ giao điểm của đồ thị C  và đường thẳng d là
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 37
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 3 2
x  3x  2  mx  2 3 2
x  3x mx  0  x  0   2
x  3x m  0 * 
Đường thẳng d cắt đồ thị C  tại 3 điểm phân biệt  phương trình  
* có hai nghiệm phân biệt khác 0 .  9 9  4m  0 m       4 m  0  m  0 
Không mất tính tổng quát gọi x  0 , x , x là nghiệm của phương trình   * . 3 1 2
x x x  (x x x x x x )  4  x x x x  4 1 2 3 1 2 2 3 3 1 1 2 1 2
 3  m  4  m  1tmCâu 13: Cho hàm số 3
y x  3x  2 có đồ thị C  . Gọi d  là đường thẳng đi qua A3;20 và có hệ số góc
m . Giá trị của m để đường thẳng d  cắt C  tại 3 điểm phân biệt là 15 15 15 15 A. m B. m  , m  24 C. m  , m  24 D. m  . 4 4 4 4 Hướng dẫn giải: Chọn C.
+ Đường thẳng d  qua A3;20 và có hệ số góc m có dạng: y  20  m x  
3  y mx  3m  20.
+Phương trình hoành độ giao điểm của d  và C  là: 3
x  3x  2  mx  3m  20. x  3 3
x  m  
3 x  3m  18  0  x   3  2
x  3x m  6  0  .  2
x  3x m  6  0   *   15
  4m  15  0 m
+ d  cắt C  tại 3 điểm phân biệt   
* có 2 nghiệm phân biệt  3     4 .
9  9  m  6  0  m  24 
Câu 14: Tìm m để đường thẳng d : y m x  
1 1 cắt đồ thị C  hàm số 3
y  x  3x 1 tại ba điểm phân biệt A1;  1 , B , C . 9 A. m  0 . B. m  . 4 9 9 C. 0  m  .
D. m  0 hoặc m  . 4 4 Hướng dẫn giải: Chọn C
Phương trình hoành độ giao điểm là 3
x x   m x      x    2 3 1 1 1
1 x x m  2  0 x  1  
. Để đường thẳng d cắt đồ thị C  tại hai điểm phân biệt thì phương trình f x 2
x x m  2  0   f    1  m  0  9 
f x  0 có hai nghiệm phân biệt khác 1, khi đó ta có   m   ;  \     0 .   9  4m  0   4 f  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 38
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 15: Tìm m để đồ thị C  của 3 2
y x  3x  4 và đường thẳng y mx m cắt nhau tại 3 điểm phân biệt A 1
 ; 0 , B, C sao cho OBC có diện tích bằng 8 A. m  3 . B. m  1. C. m  4 . D. m  2 . Hướng dẫn giải: Chọn C
Phương trình hoành độ giao điểm: 3 2
x  3x  4  mx m   x   1  2
x  4x  4  m  0  x  1    2
x  4x  4  m  0 
Đường thẳng y mx m cắt C  tại ba điểm phân biệt khi và chỉ khi phương trình 2
x  4x  4  m  0 (1) có   0 m  0
hai nghiệm phân biệt khác 1
 . Điều này tương đương với    . m  9 m  9  
Gọi x , x là hai nghiệm phân biệt của (1). Theo định lý Viet, ta có B C
x x  4 B C
x .x  4  mB C
Ta có phương trình đường thẳng BC : y mx m mx y m  0 d  Mặt khác 1 1 m S  .d O BC BC x xy y OBC  ; . . .  B C 2  B C 2 2 2 2 m 1 1 m 2 2 1 m 2  . .  x xmx mxm x x B C   B C  2 . . 1  B C  2 2 2 2 m 1 m 1 1 1 
. m .  x xx x m m m m B C 2 4 . . 4 . 2 B C 2 Giả thiết S
 8 suy ra m . m  8  m  4 . OBC Câu 16: Cho hàm số 3 2
y x  3x  4 có đồ thị C  . Gọi d  là đường thẳng đi qua A 1  ; 0 và có hệ số
góc k . Tìm m để đường thẳng d  cắt đổ thị C  tại 3 điểm phân biệt ,
A B, C sao cho diện tích tam giác OBC bằng 1. A. k  2 . B. k  1 . C. k  1  . D. k  2  . Hướng dẫn giải: Chọn B
Phương trình đường thẳng d  : y kx k .
PTHĐGĐ của C  và d  là: 3 2
x x kx   k    x   2 3 4 0
1 x  4x  4  k   0  x  1    2
x  4x  4  k  0 
Đường thẳng d  cắt đổ thị C  tại 3 điểm phân biệt khi phương trình g x 2
x  4x  4  k  0 có hai
nghiệm phân biệt khác 1.   0  gk  0     . g   1  0 k  1  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 39
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 k S  1  d O d BC   BC
trong đó B x , y  , C x , y
là tọa độ giao điểm của B B C C OBC  ; . 2 . 2 2 1 k
C  và d  , x , x là nghiệm của phương trình g x  0 . B C 
BC   x x ; y y    x x ; k x x C B C B C BC B   BC
k x x   kx x 2 2 2 2 1 1 .
 4x x  1 k . 4k C B C B B C
Khi đó: k . k  1  k  1 .
Câu 17: Đường thẳng d : y x  4 cắt đồ thị hàm số 3 2
y x  2mx  m  3 x  4 tại 3 điểm phân biệt
A0;4, B và C sao cho diện tích tam giác MBC bằng 4, với M 1; 
3 . Tìm tất cả các giá trị của m thỏa
mãn yêu cầu bài toán.
A. m  2 hoặc m  3. B. m  2  hoặc m  3. C. m  3. D. m  2  hoặc m  3  . Hướng dẫn giải: Chọn C
Phương trình hoành độ giao điểm 3 2
x  2mx  m  2 x  0 x  0   2
x  2mx m  2  0   * 
Để d cắt đồ thị hàm số tại 3 điểm phân biệt thì (*) có 2 nghiệm phân biệt khác 0 . 2   0  gm  3  2  0 m  1   m  2       . g  0  0 m  2  0 m  2   
Gọi x , x là nghiệm của phương trình (*) 1 2
Có B x , x  4 , C x , x  4 1 1   2 2  BC
2 x x 2  2 x x 2  8x x  8 2 m m  2 2 1 1 2 1 2  1 Có S  4 
d M , d .BC  4   2
2. 8 m m  2  8 MBC 2 m  3 2
m m  6  0   . m  2  (L)  Câu 18: Cho hàm số 3
y x  3x  2 có đồ thị C  . Gọi d là đường thẳng đi qua điểm A3; 20 và có hệ số
góc là m . Với giá trị nào của m thì d cắt C  tại 3 điểm phân biệt?  1  15  15  1 m  m  m  m A.  5 . B.  4 . C.  4 . D.  5 . m  0     m  24  m  24  m  1  Hướng dẫn giải: Chọn B.
Phương trình của d : y m(x  3)  20 .
Phương trình hoành độ giao điểm của d và C  : 3
x  3x  2  m(x  3)  20   x    2 3
x  3x  6  m  0 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 40
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
d và C  cắt nhau tại 3 điểm phân biệt  phương trình 2
x  3x  6  m  0 có 2 nghiệm phân biệt khác 3  15   9  4  6  m  0 m      4 f
 3  24  m  0  m  24.  Câu 19: Hàm số 3 2
y x  3x mx m  2 . Đồ thị của hàm số cắt trục Ox tại 3 điểm phân biệt khi: A. m  2 . B. m  3 . C. m  3 . D. m  3 . Hướng dẫn giải: Chọn B.
Xét phương trình hoành độ giao điểm ta có 3 2
x x mx m     x   2 3 2 0
1 x  2x m  2  0 x  1    . 2
x  2x m  2  0   * 
Để đồ thị hàm số cắt trục Ox tại 3 điểm phân biệt khi phương trình * có 2 nghiệm phân biệt x  1 .  
  1  m  2  0 m  3     m  3 . 1
  2  m  2  0 m  3  
Câu 20: Để đường thẳng d  : y mx m cắt đồ thị hàm số 3 2
y  x  3x  4 tại 3 điểm phân biệt M  1  ;0, ,
A B sao cho AB  2MB khi: 9 m  0 m  0 m  0 A. m   . B.  . C.  . D.  . 4 m  9  m  9  m  9  Hướng dẫn giải: Chọn A.
Phương trình hoành độ giao điểm của đường thẳng d  và đồ thị hàm số  x  1  3 2
x  3x  4  mx m 3 2
 x  3x mx m  4  0   2
x  4x m  4  0 (*) 
Để đường thẳng d  cắt đồ thị tại 3 điểm phân biệt thì phương trình * có hai nghiệm phân biệt khác 1   '  m  0 m  0     m  9  m  9   
Gọi Ax ; mx m , B x ; mx m ( x ; x là nghiệm phương trình * ) 2 2  1 1  1 2
AB   x x 2  mx mx 2  m  
1  x x 2 2 2 2 1 2 1 2 1 2
MB   x  2
1  m x   1  m   1  x  2 2 2 2 2 1 2 2 2 2 2 2
AB  4MB   x x  4 x 1 2 1   2 
Mà  x x 2 2
S  4P  4
m m    x 1 2 2 2 1
Mà x x  4, x x m  4  4  x x m  4 1 2 1 2  2  2 1 9
 4  x x   x  2 1  4  x   m   (nhận). 2 2 2 2 2 4
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 41
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
DẠNG 4: TƯƠNG GIAO CỦA HÀM SỐ PHÂN THỨC Phương pháp ax  b Cho hàm số y 
C và đường thẳng d : y  px  q . Phương trình hoành độ giao điểm của (C) và (d): cx  d
ax  b  px  q  Fx,m  0 (phương trình bậc 2 ẩn x tham số m). cx  d
*) Các câu hỏi thường gặp: d
1. Tìm m để d cắt (C) tại 2 điểm phân biệt   
1 có 2 nghiệm phân biệt khác  . c
2. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh phải của (C)   
1 có 2 nghiệm phân biệt x , x 1 2 d và thỏa mãn :   x  x . 1 2 c
3. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh trái của (C)   
1 có 2 nghiệm phân biệt x , x 1 2 d
và thỏa mãn x  x   . 1 2 c
4. Tìm m để d cắt (C) tại 2 điểm phân biệt thuộc 2 nhánh của (C)   
1 có 2 nghiệm phân biệt x , x và thỏa 1 2 d mãn x    x . 1 2 c
5. Tìm m để d cắt (C) tại 2 điểm phân biệt A và B thỏa mãn điều kiện hình học cho trước: +) Đoạn thẳng AB  k +) Tam giác ABC vuông.
+) Tam giác ABC có diện tích S 0 * Quy tắc:
+) Tìm điều kiện tồn tại A, B  (1) có 2 nghiệm phân biệt.
+) Xác định tọa độ của A và B (chú ý Vi ét)
+) Dựa vào giả thiết xác lập phương trình ẩn m. Từ đó suy ra m.
*) Chú ý: Công thức khoảng cách: 2 2 +) A x ; y , B x ; y : AB  x  x  y  y A A   B B   B A   B A  M  x ; y Ax  By  C 0 0  +)  d M,  0 0   2 2  : Ax  By  C  0  0 0 A  B BÀI TẬP: 2x  3
Câu 1: Cho hàm số y
. Đồ thị hàm số cắt đường thẳng y x m tại 2 giao điểm khi x 1 A. m  1  ; m  3 . B. m  1  ; m  3 . C. 1
  m  3 .
D. m  1; m  7 . Hướng dẫn giải: Chọn A 2x  3
Phương trình hoành độ giao điểm  x m x 1 2
x  m  3 x m  3  0 Ycbt    0 2
m  2m  3  0  m  1 m  3 .
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 42
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 x
Câu 2: Cho hàm số y
có đồ thị C  . Tìm m để đường thẳng d : y  x m cắt đồ thị C x 1
tại hai điểm phân biệt ?
A. 1  m  4 .
B. m  0 hoặc m  2 .
C. m  0 hoặc m  4 .
D. m  1 hoặc m  4 . Hướng dẫn giải: Chọn C.
Xét phương trình hoành độ giao điểm 2 đồ thị hàm số: x 1  x 2
 x m x mx m  0 * . x 1
Hai đồ thị hàm số cắt nhau tại 2 điểm phân biệt   
* có 2 nghiệm phân biệt khác 1 2   0 
m  4m  0 m  4       . f    1  0
1  m m  0 m  0    2x 1
Câu 3: Tìm tham số m để đường thẳng d : y   x m cắt đồ thị hàm số C  : y  tại hai điểm phân x 1 biệt
A. m  3 2 3;3 2 3 .
B. m   ;
 3  2 3  3  2 3; . C. m 2  ; 2 . D. m ;   1 1; . Hướng dẫn giải: Chọn B.
Phương trình hoành độ giao điểm của C và d là. 2x 1    x  
1 x m  2x 1 x m    x 1 . x  1  2 
x  m  
1 x m 1  0   1   . x  1 
C và d cắt nhau tại hai điểm phân biệt khi và chỉ khi phương trình  
1 có 2 nghiệm phân biệt khác 1   0  2  
m  6m  3  0  m  3  2 3  m  3  2 3 . 1  m   1  m 1  0 
Câu 4: Tìm tập hợp tất cả các giá trị của tham số m sao cho đường thẳng y mx 1 cắt đồ thị của hàm số x  3 y
tại hai điểm phân biệt. x 1
A. ;0 16; . B.  ;
 0  16; . C. 16;  . D. ;0 . Hướng dẫn giải: Chọn B. x  3
Phương trình hoành độ giao điểm:  mx 1 2
mx mx  4  0   * ,  x    1 . x 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 43
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2
  m 16m  0 
Yêu cầu bài toán  phương trình  
* có hai nghiệm phân biệt khác 1   m   2 1  m   1  4  0   m   ;  0  16;    
m ;0  16;   . 4  0  mx  2
Câu 5: Cho hàm số y
C . Tìm m để giao điểm của hai tiệm cận của C trùng với tọa độ đỉnh m m x 1 của Parabol  P 2
: y x  2x  3 . A. m  2 . B. m  1. C. m  0 . D. m  2  . Hướng dẫn giải: Chọn A.
Giao điểm hai tiệm cận I  ; 1 m
Tọa độ đỉnh của (P): J  ; 1 2. Vậy m  2 . 2x 1
Câu 6: Biết rằng đường thẳng d : y  3x m cắt đồ thị C  : y
tại 2 điểm phân biệt A và B sao x 1
cho trọng tâm của tam giác OAB thuộc đồ thị C , với O 0; 0 là gốc tọa độ. Khi đó giá trị của tham số m
thuộc tập hợp nào sau đây ? A.  ;   3 . B. 1 ; 8  . C.  1 ; 2  8 . D.  5  ; 2. Hướng dẫn giải: Chọn C.
Phương trình hoành độ giao điểm: 2x  1  3x m
f x  3 2
x  1  mx m  1  0x   1 (*) x  1
Đường thẳng cắt đồ thị tại hai điểm phân biệt khi pt (*) phải có hai nghiệm phân biệt khác 1    0 m  1    f     1  0  m  11 Gọi hai giao điểm là 
A x ;3x m, Bx ;3x m 1 1 2 2  x x 1  m x  1 2  G
G là trọng tâm tam giác OAB   3 9    3 x x m m 1 2   2 1  y    G 3 3 1  m . 2  1 m 1  2 15 5 13
G thuộc đồ thị hàm số khi 9 
m  15m  25  0  m  . 3 1 m 2  1 9 2x 1
Câu 7: Những giá trị của m để đường thẳng y x m 1 cắt đồ thị hàm số y
tại hai điểm phân biệt x  1 ,
A B sao cho AB  2 3 là
A. m  4  10 .
B. m  4  3 .
C. m  2  3 .
D. m  2  10 . Hướng dẫn giải: Chọn A.
Phương trình hoành độ giao điểm
2x 1  x m 1  g x 2
x  m  2 x m  2  0, x  1. x 1
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 44
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Đồ thị hai hàm số có hai giao điểm khi và chỉ khi g x  0 có hai nghiệm phân biệt khác 1  .   0  m  2    g   1 0    m  6  
Khi đó Ax ; x m 1 , B x ; x m 1 và 2
AB  2 x x   2  2
m  8m 12 . 2 1  1 1   2 2 
Theo giả thiết AB    2 2 3
2 m  8m  12  12  m  4  10 (thoả điều kiện). 2x  1
Câu 8:Cho hàm sốy
có đồ thị (C ) . Tìm tất cả các giá trị thực của tham số m để đường thẳng x  1
y x m  1 (d) cắt đồ thị tại hai điểm phân biệt sao choAB  2 10 ? A. 1 . B.. 1;  3 C..  1  ;  1 D. 1;  Hướng dẫn giải: Chọn D.
Phương trình hoành độ giao điểm của đồ thì và đường thẳng: 2x  1 2 2
x m 1  x mx x x m  1  2x  1  x  m  2x m 2  0   1 . x  1
Đường thẳng d và đồ thị cắt nhau tại 2 điểm phân biệt thì phương trình  
1 có hai nghiệm phân biệt khác 1 .   0  m 2  m 6 0 m   6  Khi đó ta có     . f    1  0 1  0 m     2       x
  x  2 m  1 2
Gọi x ;x là nghiệm của   1 . Ta có  . 1 2 x
x m  2  1 2 
Ta đặt Ax ;x m  1 ;B x ;x m  1 . Ta có : 1 1   2 2 
AB  2 10  2x x 2  2 3  x x 2 2
 4x x  12  m  4m  4  4m  8  6 1 2 1 2 1 2 m   4  10 m   4  10 2   
m  8m  6  0  
. Kết hợp điều kiện ta có  . m   4  10     m 4 10 
Câu 9: Tìm tất cả các giá trị của tham số m để đường thẳng d : y  x m cắt đồ thị hàm số 2  x  1 y
tại hai điểm A, B sao cho AB  2 2 x 1
A. m  1, m  2  .
B. m  1, m  7 . C. m  7  ,m  5 .
D. m  1, m  1  . Hướng dẫn giải: Chọn B
Phương trình hoành độ giao điểm của đồ thị và đường thẳng d là :
2x 1  x m  2x 1  2
x mx x m  2
x  m  
1 x m 1  0 x 1 2   m   1  4m   1  2 m  6m  3
Đồ thị cắt đường thẳng d tại hai điểm 2
   0  m  6m  3  0 (*)
Khi đó tọa độ giao điểm lần lượt là : 2 2 2 2  m 1 m 6m 3 m 1 m 6m 3   m 1 m 6m 3 m 1 m 6m 3                  A ;  , B  ;   2 2   2 2     
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 45
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12  AB   2 2 m m
m m    AB   2 6 3; 6 3
2 m  6m  3 m  Theo đề : 2 2 1 AB  2 2 
m  6m  3  2  m  6m  7  0  ( thỏa (*)). m  7   2x 1
Câu 10:Cho hàm số y
có đồ thị C  . Tìm tất cả giá trị của m để đường thẳng d  : y x m 1 cắt x  1
C  tại 2 điểm phân biệt A, B sao cho AB  2 3
A. m  4  3 .
B. m  4  10 .
C. m  2  3 .
D. m  2  10 . Hướng dẫn giải: Chọn D.
Phương trình hoành độ giao điểm: 2x  1 x m 1   f x 2
x  m  2x m  2   0 x    1 (*) x  1
Đường thẳng cắt đồ thị tại hai điểm phân biệt khi pt (*) phải có hai nghiệm phân biệt khác -1    0 m  2    f     1  0 m  6 Gọi hai giao điểm là 
A x ; x m  
1 , Bx ; x m   1 1 1 2 2
AB  2 3  m  22  
4 m  2  6  0  m  2  10.
Câu 11: Tìm tất cả các giá trị của tham số m sao cho đường thẳng d : y x m cắt đồ thị hàm số 2x 1 (C) : y
tại hai điểm phân biệt M , N sao cho diện tích tam giác IMN bằng 4 với I là tâm đối xứng x 1 của (C)
A. m  3; m  1  .
B. m  3; m  5  .
C. m  3; m  3  . D. m  3  ; m  1  . Hướng dẫn giải: Chọn A.
Đồ thị hàm số có tiện cận đứng x  1 .
Đồ thị hàm số có tiện cận ngang y  2.
Tâm đối xứng của đồ thị có tọa độ I 1; 2 m 1
d : y x m x y m  0  d   I ;d  2 2x 1
Xét phương trình hoành độ giao điểm 2
x m x  m  3 x m 1  0   1 x 1
x x  3  m 1 2
Gọi x ; x là nghiệm phương trình   1 . Theo Viet ta có : 1 2
x x  m 1  1 2
Giả sử M x ; x m ; N x ; x m 1 1   2 2  MN
2  x x 2  2 x x 2  8x x  23  m2 2
 8m  8  2m  4m  26 2 1 2 1 1 2 2 1 m 1
m 1 m  2m 13
Diện tích tam giác IMN là: 2
2m  4m  26   4 2 2 2  m 1  4 2 2  2  m   1 m   1 12  64     m  2 1  16 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 46
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2 2 m  3 Do m   1  0  m   1  4  .  m  1  2 x  2x  4
Câu 12: Xác định tất cả giá trị m để đồ thị hàm số y
cắt đường thẳng y m x  4 tại hai x 1 điểm phân biệt. 2
A. m  2, m  , m  1.
B. m  1. 3 2 C. m.
D. –2  m  , m  0 . 3 Hướng dẫn giải: Chọn A. TXD: x  1 .
Ta có phương trình hoành độ giao điểm của đồ thị và đường thẳng là : 2
x  2x  4  mx4 2
x  2x  4  mx  4  x   1  m   2
1 x  2  5mx  4m  4  0   1 . x 1 m  1 m 1  0 m  1    m  2 
Để đồ thị cắt đường thẳng tai hai điểm phân biệt thì 2   0  3
m  4m  4  0   . 2  f   1  0  3   0 m      3 2 x  3mx
Câu 13:Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y
cắt đường thẳng y mx  7 x  3
tại 2 điểm phân biệt? 19 19 19 19 A. m  . B. m
và m  1 C. m . D. m
và m  1 2 2 2 2 Hướng dẫn giải: Chọn B 2 x  3mx 2 2
mx  7  x  3mx mx  7x  3mx  21  m   2
1 x  7x  21  0   1 x  3 m  1 m  1   Ycbt   
1 có 2 nghiệm phân biệt        m   19 49 84 1  0 m     12 2x 1
Câu 14:Cho hàm số y
có đồ thị là C  . Tìm tất cả các giá trị của m để đường thẳng d  đi qua x  2
A0; 2 có hệ số góc m cắt đồ thị C  tại 2 điểm thuộc 2 nhánh của đồ thị A. m  0 . B. m  0 . C. m  5 .
D. m  0 hoặc m  5  . Hướng dẫn giải: Chọn B
Phương trình đường thẳng d đi qua A0; 2 và có hệ số góc m có dạng: y mx  2 . 2x 1
Xét phương trình hoành độ giao điểm
mx  2,  x  2. x  2 2 2
mx  2x  2mx  4  2x 1  mx  2mx  5  0   1
Mặt khác đồ thị hàm số có tiệm cận đứng là đường thẳng x  2 nên
Để d cắt C  tại hai điểm phân biệt nằm về hai nhánh của đồ thị thì khi và chỉ khi phương trình   1 có hai
nghiệm phân biệt x , x sao cho x  2  x . 1 2 1 2
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 47
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2
Đặt t x  2 khi đó phương trình  
1 trở thành m t    m t   2 2 2
2  5  0  mt  2mt  5  0 2
Khi đó Ycbt tương đương với phương trình 2 có hai nghiệm trái dấu  . a c  0  . m  5
   0  m  0 . Vậy m  0 thì thỏa Ycbt. 2x  3
Câu 15: Tìm tất các giá trị thực của tham số m để đồ thị C của hàm số y  cắt đường thẳng x 1
 : y x m tại hai điểm phân biệt A và B sao cho tam giác OAB vuông tại O A. m  6 . B. m  3  . C. m  5 . D. m  1. Hướng dẫn giải: Chọn A. 2x  3
Ta có: phương trình hoành độ giao điểm của (C ) y
và đường thẳng  : y x m :. x 1
2x  3  x m(x 1). x 1 2 2
 2x  3  (x m)(x 1)  2x  3  x x mx m x  (m  3)x m  3  0. . 2 2 2
  (m  3)  4(m  3)  m  2m  21  (m 1)  20  0 m   .
Suy ra:  luôn cắt (C ) tại hai điểm phân biệt. Gọi (
A x ; y ); B(x ; y ) là hai giao điểm của  và (C ) . A A B B  
Mặt khác: Tam giác OAB vuông tại O O . A OB  0 . 2
x .x  (x m)(x  )
m  0  2x .x m(x x )  m  0 A B A B A B A B . 2
m m(m  3)  2(m  3)  0  m  6. x  2
Câu 16: Tập hợp tất cả các giá trị của tham số thực m sao cho phương trình  m có đúng hai x 1
nghiệm phân biệt là A. 0; 2 . B. 1; 2 .
C. 1; 2   0 .
D. 1; 2   0 . Hướng dẫn giải: Chọn D. x  2 x  2
Hàm số y f ( x ) 
được suy từ hàm số y  bằng cách sau. x  1 x  1
+ Giữ nguyên phần đồ thị hàm số y f (x) ở phía phải trục Oy.
+ Lấy đối xứng phần đồ thị vừa giữ lại của y f (x) qua Oy.
+ Giữ nguyên phần đồ thị hàm số y f (x) ở phía trên trục Ox.
+ Lấy đối xứng phần đồ thị phía dưới Ox của y f (x) qua Ox.
Số nghiệm của phương trình f (| x |)  m là số giao điểm của đồ thị hàm số y f (| x |) và đường thẳng y  . m
Ta kết luận, phương trình có 2 nghiệm phân biệt khi m 1; 2   0 . x
Câu 17: Biết rằng đường thẳng d : y x
  m luôn cắt đường cong C  2 1 : y  tại hai điểm phân x  2
biệt A , B . Độ dài đoạn AB đạt giá trị nhỏ nhất bằng bao nhiêu? A. 4. B. 6 . C. 3 6 . D. 2 6 . Hướng dẫn giải: Chọn D.
Phương trình hoành độ giao điểm:
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 48
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2x  1  x
  m x    2 x  2 2
x  4 mx  1 2m  0   1 2
  12  m  0, m Phương trình  
1 luôn có 2 nghiệm phân biệt x ,x tức đường thẳng d luôn cắt C  tại hai điểm phân biệt A B
Ax ;y ,B x ;y . Ta có: 1 1  2 2
AB  x x 2  y y 2  x x 2  x x 2 2 1 2 1 2 1 2 1
 2 x x   2  2 2 2  2 12  m 2 1
AB đạt giá trị nhỏ nhất bằng 2 6 khi m  0.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 49
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
DẠNG 5: SỰ TƯƠNG GIAO CỦA HÀM SỐ BẬC 4 4 2
NGHIỆM CỦA PHƯƠNG TRÌNH BẬC 4 TRÙNG PHƯƠNG: ax  bx  c  0 (1) 1. Nhẩm nghiệm:
- Nhẩm nghiệm: Giả sử x  x là một nghiệm của phương trình. 0 x  x0
- Khi đó ta phân tích: f x, m   2 2 x  x g x  0  0    gx  0 
- Dựa vào giả thiết xử lý phương trình bậc hai g  x  0
2. Ẩn phụ - tam thức bậc 2: - Đặt 2
t  x ,t  0 . Phương trình: 2 at  bt  c  0 (2). t  0  t
- Để (1) có đúng 1 nghiệm thì (2) có nghiệm t , t thỏa mãn: 1 2 1 2 t  t  0  1 2 t  0  t
- Để (1) có đúng 2 nghiệm thì (2) có nghiệm t , t thỏa mãn: 1 2 1 2 0  t  t  1 2
- Để (1) có đúng 3 nghiệm thì (2) có nghiệm t , t thỏa mãn: 0  t  t 1 2 1 2
- Để (1) có đúng 4 nghiệm thì (2) có nghiệm t , t thỏa mãn: 0  t  t 1 2 1 2
3. Bài toán: Tìm m để (C): 4 2 y  ax  bx  c  
1 cắt (Ox) tại 4 điểm có hoành độ lập thành cấp số cộng. - Đặt 2
t  x ,t  0 . Phương trình: 2 at  bt  c  0 (2).
- Để (1) cắt (Ox) tại 4 điểm phân biệt thì (2) phải có 2 nghiệm dương t , t t  t thỏa mãn t  9t . 1 2  1 2  2 1
- Kết hợp t  9t vơi định lý vi ét tìm được m. 2 1 BÀI TẬP:
Câu 1: Số giao điểm của trục hoành và đồ thị hàm số 4 2
y   x  2x  3 là: A. 1. B. 3. C. 2. D. 4. Hướng dẫn giải: Chọn C.
Phương trình hoành độ giao điểm: 4 2
x  2x  3  0  x   3 . Vậy có hai giao điểm. Câu 2:Hàm số 4 2
y  x x , có số giao điểm với trục hoành là: A. 1. B. 2 . C. 3 . D. 4 . Hướng dẫn giải: Chọn C. x  0
Xét phương trình hoành độ giao điểm 4 2 x x  0 2  x  2 x   1  0   . x  1   Câu 3:Cho hàm số 4 2
y x  2x 1. Tìm số giao điểm của đồ thị hàm số với trục Ox : A. 1. B. 3. C. 4. D. 2. Hướng dẫn giải: Chọn D. 2 x  1 2 Xét phương trình 4 2
y  0  x  2x 1  0 (1)   2 x  1 2 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 50
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 2  x  1 2  x   1 2
Phương trình (1) có hai nghiệm  số giao điểm của đồ thị với trục Ox là 2
Câu 4: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C  4 2
: y x mx m 1 cắt trục hoành m
tại bốn điểm phân biệt m   1 A. m  1. B.  .
C. không có m . D. m  2 . m  2  Hướng dẫn giải: Chọn B.
Xét phương trình hoành độ giao điểm 4 2
x mx m 1  0 . Đặt 2
t x , t  0 ta được phương trình 2
t mt m 1  0 .
Để đồ thị hàm số C  4 2
: y x mx m 1 cắt trục hoành tại bốn điểm phân biệt thì phương trình m 2
t mt m 1  0 phải cóhai nghiệm dương phân biệt. 2   0
m  4m  4  0   m  2
 P  0  m 1  0   . m  1    S  0 m  0   Cách 1:
Phương trình hoành độ giao điểm của (C ) và trục hoành: 4 2
x mx m 1  0. m Đặt 2
t x  0 , phương trình trên thành: 2
t mt m  1  0 (*) .
(C ) cắt trục hoành tại 4 điểm phân biệt. m
 phương trình (*) có 2 nghiệm dương phân biệt. 2   (m  2)  0  
 P  0  m 1  0  1  m  2. . S 0   m  0  
Câu 5: Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số C  4 2
: y x mx m 1 cắt trục hoành m
tại bốn điểm phân biệt m   1 A. m  1. B.  .
C. không có m . D. m  2 . m  2  Hướng dẫn giải: Chọn B. Cách 1:
Phương trình hoành độ giao điểm của (C ) và trục hoành: 4 2
x mx m 1  0. m Đặt 2
t x  0 , phương trình trên thành: 2
t mt m  1  0 (*) .
(C ) cắt trục hoành tại 4 điểm phân biệt. m
 phương trình (*) có 2 nghiệm dương phân biệt. 2   (m  2)  0  
 P  0  m 1  0  1  m  2. . S 0   m  0  
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 51
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12 Cách 2: Ta có: 4 2
y x mx m  1 .
Tập xác định: D   . 3
y '  4x  2mx .  x  0. 3 y ' 0 4x 2mx 0       m . 2  x  .  2
Đồ thị hàm số cắt trục hoành tai bốn điểm phân biệt  m  0 .
x  0  y m 1. Ta có:  2 m m . 2  x
(m  0)  y    m 1.  2 4 Bảng biến thiên x  m 0 . m   2 2 y '  0  0  0  y  . . m 1 . .  . 2 m 2 m   m 1   m 1 4 4 m 1  0  m  1. Yêu cầu bài toán 2   m   .   m 1  0 m  2.    4
Câu 6:Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4 2
y x  2x m cắt trục hoành tại đúng hai điểm A. m  1.
B. m  0; m  1. C. m  0. D. m  3. Hướng dẫn giải: Chọn B TX Đ: 
Để đồ thị hàm số y x4  2x2  m cắt trục hoành tại đúng hai điểm thì phương trình sau có hai
nghiệm: x4  2x2  m  01
Đặt x2  t t  0 . Khi đó phương trình 1 trở thành:. t2  2t m  02
1 có hai nghiệm khi 2 có một nghiệm dương:
  1 m  0
TH1: 2 có nghiệm kép dương    m  1 t  1  0 
TH2: 2 có hai nghiệm trái dấu  ac  0  m  0 m  0
Giá trị m cần tìm m  1 . 
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 52
Facebook: https://www.facebook.com/dongpay
ST và BS: Th.S Đặng Việt Đông Trường THPT Nho Quan A
Phần Hàm số - Giải tích 12
Câu 7:Tìm tập hợp tất cả giá trị thực m để đồ thị C của hàm số 4 2
y x mx  2m  3 có 4 giao m
điểm với đường thẳng y 1, có hoành độ nhỏ hơn 3
A. m  2;1  1 \   4 .
B. m  2;1  1 .
C. m  2;   \   4 .
D. m  2;5. . Hướng dẫn giải: Chọn A
Phương trình hoành độ giao điểm của đồ thị C
với đường thẳng y 1 là : m  4 2 4 2
x mx  2m  3 1  x mx  2m  4  0 (phương trình trùng phương *)
  m   m    m  2 2 4 2 4 4  0    0 m  4  b
Phương trình (*) có 4 nghiệm phân biệt    m  0
 m  0  m  2; \   4 (1) a  m  2 c    2m  4  0  a 2 m m  4
x m  2
x   m  2 Khi đó , ta có : 2 x    2   2 x  2  x   2 
Vì hoành độ giao điểm nhỏ hơn 3 nên m  2  3  m  11 (2)
Từ (1), (2) suy ra m 2;1  1 \   4 thỏa ycbt.
File Word liên hệ: 0978064165 - Email: dangvietdong.bacgiang.vn@gmail.com
Trang 53
Facebook: https://www.facebook.com/dongpay