Khối đa diện được bao bởi? Đặc điểm, tính chất về khối đa diện

Khối đa diện được bao bởi? Đặc điểm, tính chất về khối đa diện 1. Khối đa diện là gì?
Khối đa diện được xác định là không gian miền trong của mỗi hình đa điện
tạo thành. Nghĩa là mỗi hình đa diện sẽ có một khối đa diện tương ứng.
1.1. Hình đa diện là gì?
Hình đa diện là hình học gồm các đa giác phẳng thỏa mãn các tính chất sau:
- Hai đa giác phân biệt chỉ có thể không có điểm chung, hoặc chỉ có một cạnh
chung, hoặc chỉ có một đỉnh chung. Có nghĩa là hình mà 2 đa giác không
thuộc các trường hợp trên hoặc có nhiều hơn một trường hợp trong các
trường hợp trên đều không có hình đa diện.
- Mỗi cạnhh của mọi đa giác đều là cạnh chung của đúng 2 đa giác.
1.2. Đặc điểm, tính chất về khối đa diện
Tính chất 1: Cho một khối đa diện đều, ta có:
- Đỉnh của một khối tứ diện đều khác là trọng tâm của các mặt
- Trung điểm của mọi cạnh chính là các đỉnh của khối bát diện đều.
Tính chất 2: Cho khối lập phương, tâm các mặt của nó sẽ tạo thành 1 khối bát diện đều.
TÍnh chất 3: Cho khối bát diện đều, tâm các mặt của nó sẽ tạo thành một khối lập phương.
Tính chất 4: Hai đỉnh của một khối bát diện đều được gọi là hai đỉnh đối diện
nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh
đối diện gọi là đường chéo của khối bát diện đều. Khi đó:
- Ba đường chéo giao nhau tại vị trí trung điểm của mỗi đường
- Ba đường chéo vuông góc với nhau theo từng đôi một.
- Ba đường chéo bằng nhau.
Tính chất 5: Một khối đa diện phải có tối thiểu 4 mặt.
Tính chất 6: Hình đa điện có tối thiểu 6 cạnh
Tính chất 7: Không tồn tại đa diện có 7 cạnh
1.3. Ví dụ về các khối đa diện
Một số khối đa diện thường gặp Khối Số đỉnh Số cạnh Số mặt
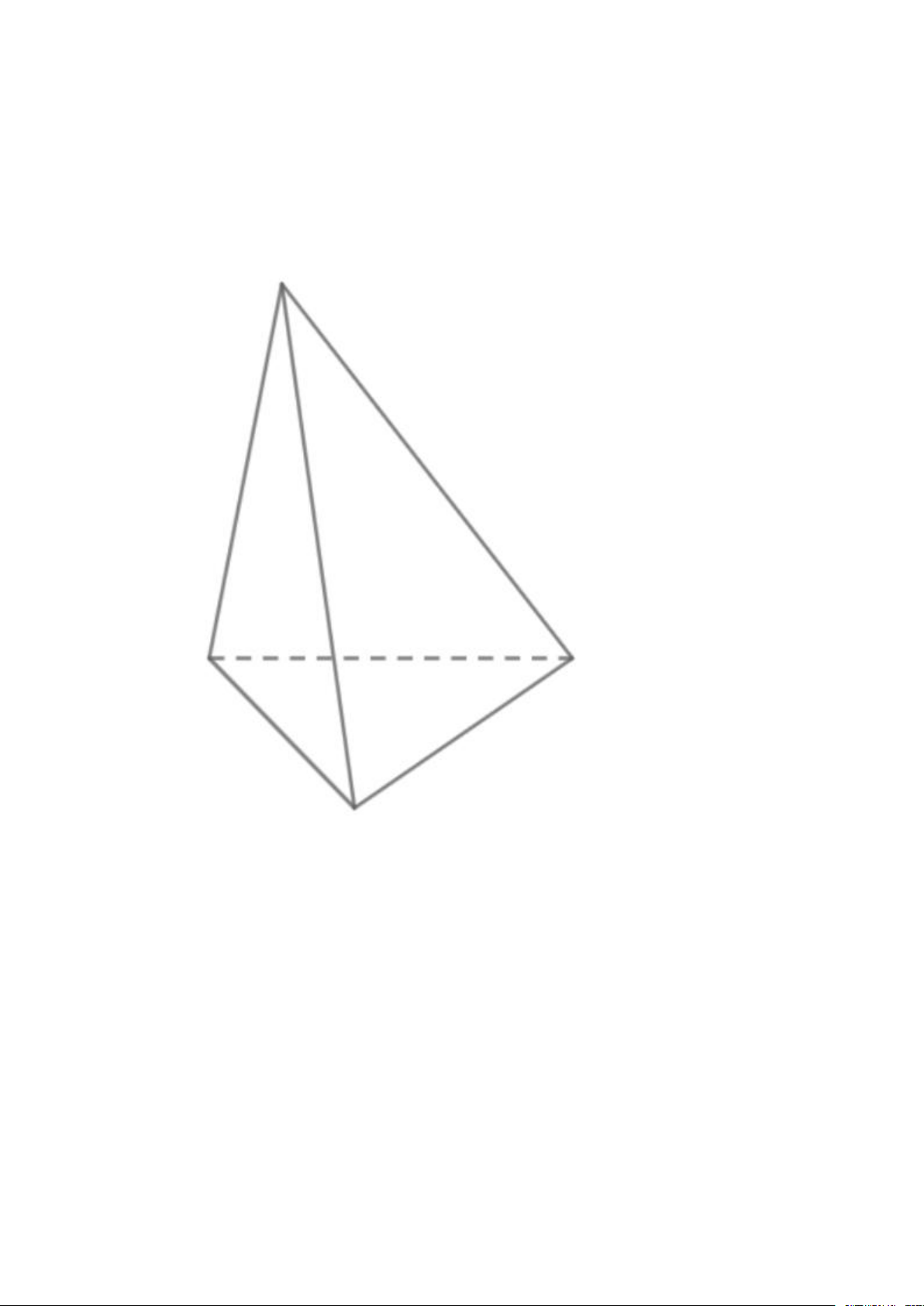
Mặt bên Mặt đáy Hình minh họa Khối chóp Hình tam giác 4 6 4 Hình tam giác tam giác Khối chóp Hình tứ tứ giác 5 8 5 Hình tam giác giác Khối
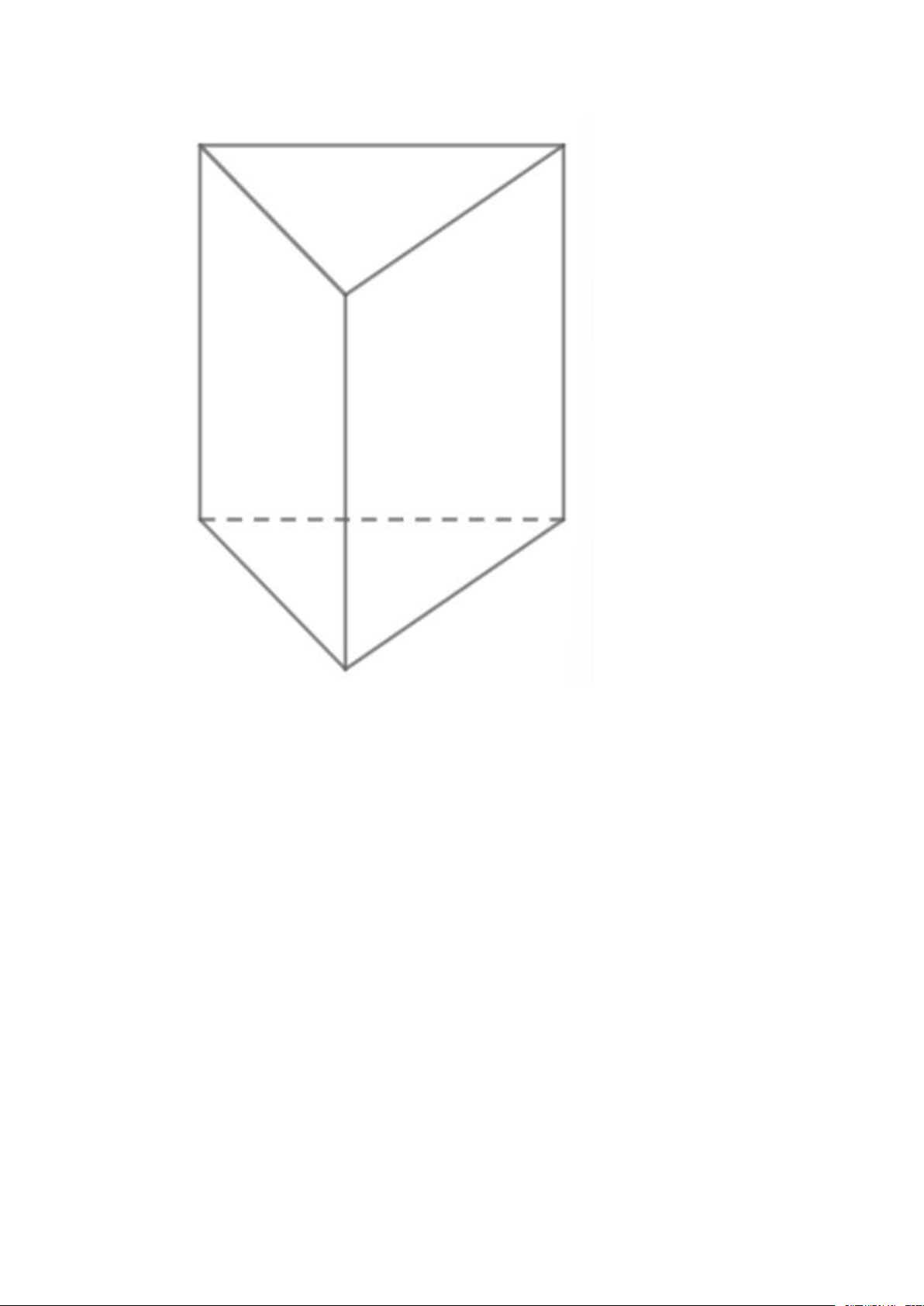
chóp 2 lần số đỉnh 3 lần số cạnh Số cạnh đa Hình cụt của đa giác giác đáy thêm đáy đa giác đáy 2 thang Đa giác Khối hộp 8 12 6 Hình bình Hình tứ hành giác Khối lăng trụ Hình tam giác 6 9 5 Hình bình hành tam giác
2. Khối đa diện lồi là gì?
Khối đa diện lồi được xác định bằng đoạn thẳng nối 2 điểm bất kì thuộc khối
đa diện. Nếu đoạn thẳng đó nằm hoàn toàn trên khối đa diện thì đó là đa diện lồi.
Ví dụ như khối lăng trụ, khối chóp là các đa diện lồi:
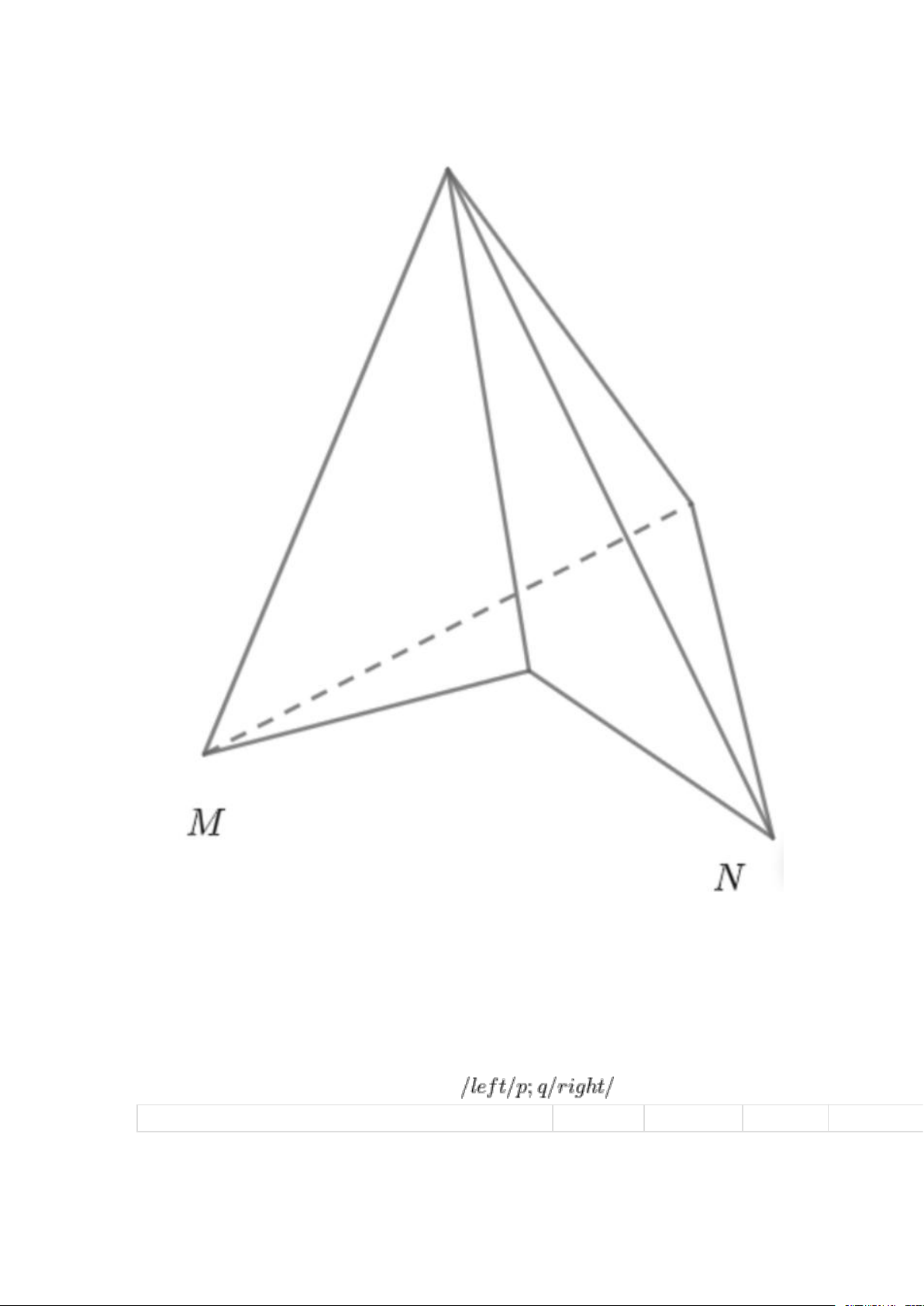
Ngược lại trường hợp hình sau đây không phải đa diện lồi vì đoạn MN không thuộc trong khối đa diện: 3. Khối đa diện đều
Khối đa diện đều là trường hợp đa diện đặc biệt trong số các khối đa diện lồi.
Để xác định khối đa diện đều cần thỏa mãn 2 điều kiện sau:
- Mỗi mặt của khối đa diện là đa giác đều có p cạnh
- Mỗi đỉnh đều là đỉnh chung của q mặt.
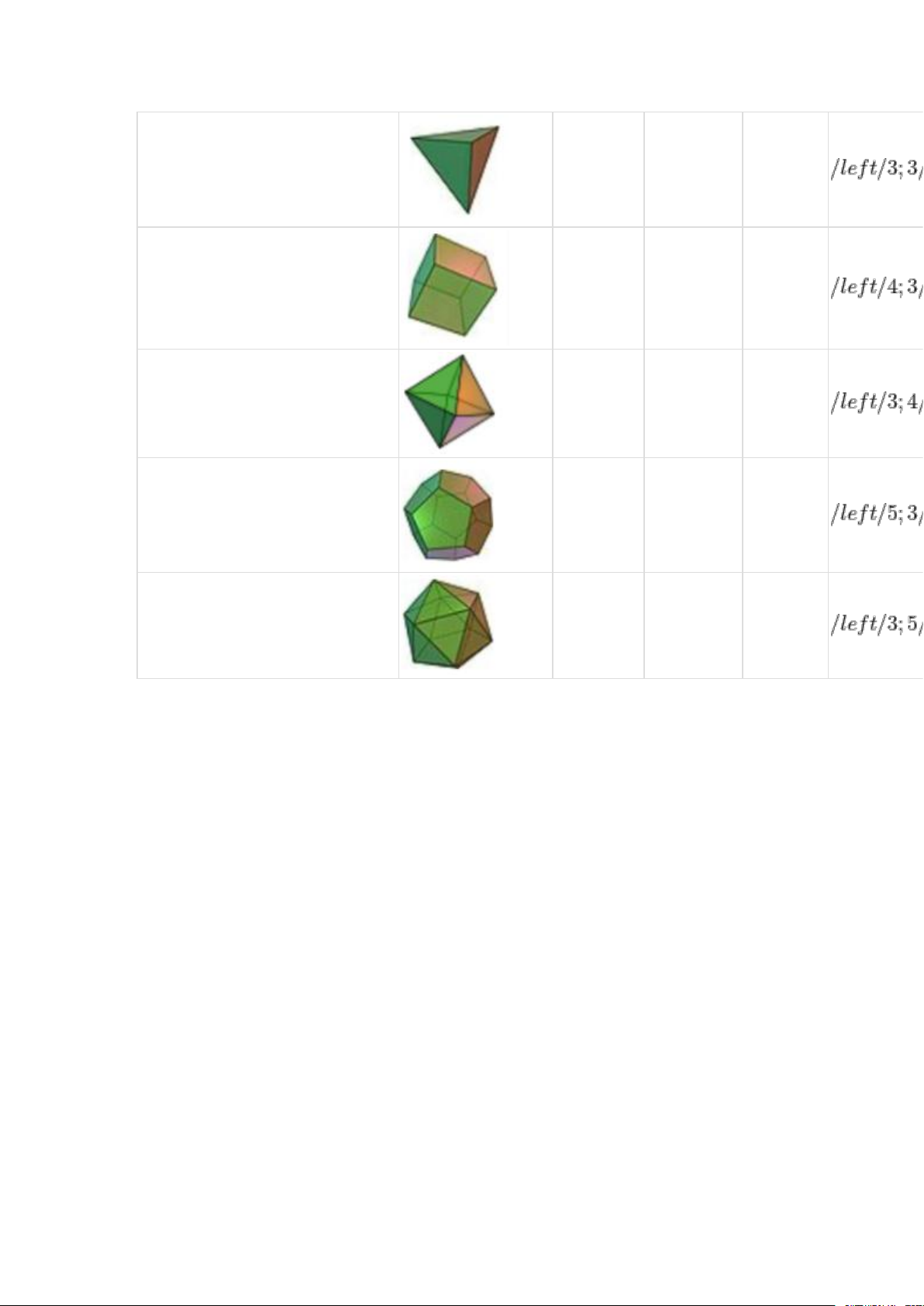
Như vậy ta được khối đa diện đều loại Khối đa diện đều Số đỉnh Số cạnh Số mặt Loại Khối tứ diện đều 4 6 4 Khối lập phương 8 12 6 Khối bát diện đều 6 12 8
Khối mười hai mặt đều 20 30 12 Khối hai mươi mặt đều 12 30 20
4. Khối đa diện được bao bởi gì?
Khối đa diện được bao bởi các hình đa giác phẳng. Bởi :
Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác phẳng thỏa mãn hai tính chất sau:
- Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoăc chỉ có một
đỉnh chung, hoặc chỉ có một cạnh chung.
- Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả
hình đa diện đó. Những điểm không thuộc khối đa diện được gọi là điểm
ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc
hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.
Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được
gọi là miền ngoài của khối da diện.
Mỗi khối đa diện được xác định bởi một hình đa diện ứng với nó. Ta cũng gọi
đỉnh, cạnh, mặt trong, điểm ngoài,.. của một khối đa diện theo thứ tự là đỉnh,
cạnh, mặt, điểm trong, điểm ngoài của hình đa diện tương ứng. 5. Hai hình bằng nhau
5.1. Phép dời hình trong không gian
- không gian, quy tắc đặt tương ứng mỗi điểm M với điểm M' xác định duy
nhất được gọi là phép biến hình trong không gian.
- Phép biến hình trong không gian được gọi là phép dời hình nếu nó bảo toàn
khoảng cách giữa hai điểm tùy ý.
- Phép tịnh tiến, phép đối xứng tâm, phép đối xứng trục, phép đối xứng qua mặt phẳng.
- Thực hiện liên tiếp các phép dời hình sẽ được một phép dời hình.
- Phép dời hình biến đa diện ( H ) thành đa diện ( H ' ), biên đỉnh, cạnh, mặt
của ( H ) thành đỉnh, cạnh, mặt tương ứng của ( H ' ). 5.2. Hai hình bằng nhau
Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
6. Thể tích các khối đa diện
1. Thể tích của khối hộp chữ nhật: V = a. b. c với a, b, c là ba kích thước của khối hộp chữ nhật
2. Thể tích của khối lập phương: V = a với aa là cạnh của hình lập phương
3. Thể tích của khối chóp:
với S là diện tích đáy, h là chiều cao của khối chóp
4. Thể tích của khối lăng trụ: V = S. h với S là diện tích đáy. h là chiều cao của khối hình trụ
5. Một số phương pháp tính thể tích khối đa diện
a, Tính thể tích bằng công thức 
Tính các yếu tố cần thiết: độ dài cạnh, diện tích đáy, chiều cao,... 
Sử dụng công thức để tính thể tích
b, Tính thể tích bằng cách chia nhỏ
Ta chia khối đa diện thành nhiều khối đa diện nhỏ mà có thể dễ dàng tính
được thể tích của chúng. Sau đó cộng các kết quả ta được thể tích của khối đa diện cần tính.
c, Tính thể tích bằng cách bổ sung
Ta có thể ghép thêm vào khối đa diện một khối đa diện khác sao cho khối đa
diện thêm vào và khối đa diện mới tạo thành có thể dễ dàng tính được thể tích.
d, Tính thể tích công thức tỉ số thể tích
Ta có thể vận dụng tính chất sau:
Cho ba tia Ox, Oy, Oz không đồng phẳng. Với bất kì các điểm A, A' trên Ox; B,
B' trên Oy; C, C' trên Oz ta đều có: 7. Bài tập ứng dụng
Bài 1: Cho hình chóp S. ABC có mặt bên SBC là tam giác đều cạnh a,
cạnh bên SA vuông góc với mặt phẳng đáy. Biết góc BAC = 120 °, tính
thể tích của khối chóp S. ABC theo a
Bài 2: Cho hình chóp S.ABCD có đáy ABCD có hình vuông cạnh a, cạnh
bên SA vuông góc với mặt phẳng đáy, góc giữa mặt phẳng ( SBD ) và
mặt phẳng đáy bằng 60 °. Tính thể tích của khối chóp S.ABCD theo a.
Bài 3: Cho hình chóp S. ABCD có đáy ABCD là hình thang vuông tại A
và D với AD = CD = a, AB = 3a. Cạnh bên SA vuông góc với mặt phẳng
đáy và cạnh bên SC tạo với mặt đáy một góc bằng 45 °. Tính thể tích của khối chóp S. ABCD theo a.
Bài 4: Cho hình lăng trụ đứng ABC. A'B'C' có đáy ABC là tam giác vuông
tại b và BA = BC = a. Góc giữa đường thẳng A'B với mặt phẳng ( ABC) =
60°. Tính thể tích khối lăng trụ ABC . A'B'C' theo a.
Bài 5: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh
bên SA vuông góc với mặt phẳng đáy. Đường thẳng SD tạo với mặt
phẳng (SAB) một góc 30 °. Tính thể tích khối chóp S. ABCD theo a.
Document Outline

• Khối đa diện được bao bởi? Đặc điểm, tính chất về
  • 1. Khối đa diện là gì?
    • 1.1. Hình đa diện là gì?
    • 1.2. Đặc điểm, tính chất về khối đa diện
    • 1.3. Ví dụ về các khối đa diện
  • 2. Khối đa diện lồi là gì?
  • 3. Khối đa diện đều
  • 4. Khối đa diện được bao bởi gì?
  • 5. Hai hình bằng nhau
    • 5.1. Phép dời hình trong không gian
    • 5.2. Hai hình bằng nhau
  • 6. Thể tích các khối đa diện
  • 7. Bài tập ứng dụng