Kinh tế Vi mô - Đường Cầu và Lợi Ích Người Tiêu Dùng | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

Nội dung buổi 3 Kinh tế Vi mô *Lưu ý
1. Đường cầu càng dốc thì cầu càng ít co giãn
2. Ở trên một đường cầu, độ dốc sẽ không đổi nhưng độ co giãn có thay đổi (giảm từ trên xuống dưới)
3. Đường cầu ít co giãn hơn đường cung thì người tiêu dùng chịu nhiều thuế hơn người sx
Đường cung ít co giãn hơn đường cầu thì người sx sẽ chịu nhiều thuế hơn
 Càng ít co giãn thì càng phải chịu nhiều thuế.
Ví dụ: Giá bột giặt là 35.000 đồng/kg. Khi Chính phủ đánh thuế 3.000 đồng/kg thì giá
trên thị trường là 38.000/kg. Vậy tính chất co giãn cầu theo giá của bột giặt là A. Co giãn nhiều B. Co giãn hoàn toán C. Co giãn ít D. Hoàn toàn không co giãn
Chương IV: Lý thuyết hành vi người tiêu dùng
1.Lý thuyết lợi ích
− Tiêu dùng: LÀ hành động nhằm thỏa mãn những nguyện vọng, trí tưởng tượng và nhu
cầu về tinh thần và vật chất của cá nhân hoặc hộ gia đình thông qua việc mua sắm và sử dụng hàng hóa dịch vụ
− Mục đích của người tiêu dùng: đạt được sự thỏa mãn tối đa với ràng buộc về ngân sách
− Lợi ích (U): biểu diễn mức độ thỏa mãn nhu cầu của người tiêu dùng khi tiêu dùng hàng hóa và dịch vụ.
*Giả thiết lợi ích có thể đo được
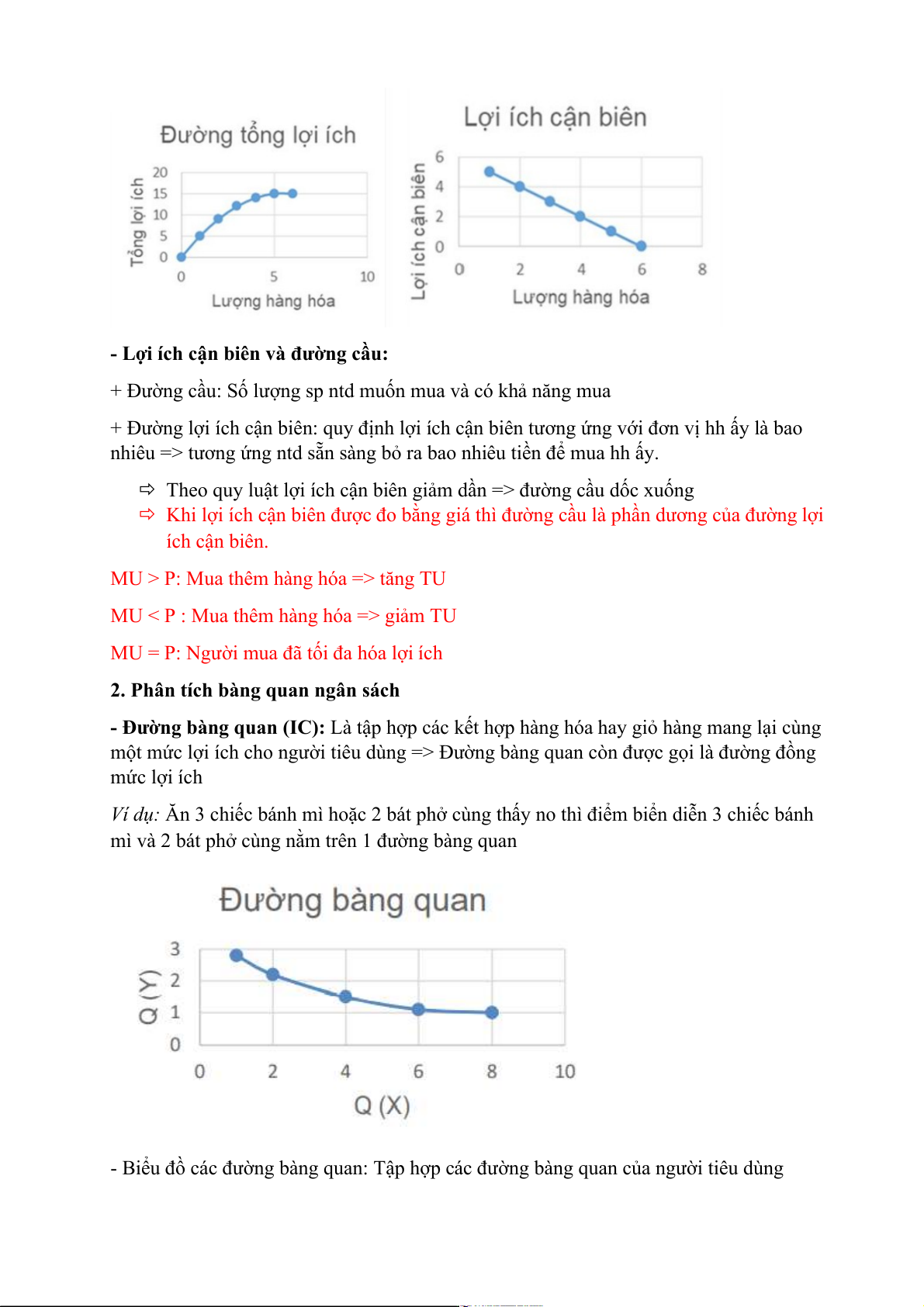
− Tổng lợi ích (TU): là toàn bộ sự thỏa mãn và hài lòng từ việc tiêu dùng hàng hóa dịch vụ nhất định.
− Lợi ích cận biên (MU): Là mức thay đổi của tổng lợi ích do việc tiêu dùng thêm 1 đơn
vị hàng hóa mang lại, với điều kiện giữ nguyên mức tiêu dùng các hàng hóa khác.
TU = TU + MU MU= ∆ TU = (TU)’ 1 0 1 ∆ Q
*Xét lợi ích tiêu dùng 1 hàng hóa duy nhất
- Quy luật lợi ích cận biên giảm dần: Lợi ích cận biên của 1 đơn vị hàng hóa có xu
hướng giảm xuống ở 1 điểm nào đó khi hàng hóa đó được tiêu dùng nhiều hơn trong một
khoảng thời gian nhất định với điều kiện giữ nguyên tiêu dùng các hàng hóa khác. Lượng tiêu Tổng lợi ích Lợi ích cận
Sự thay đổi TU và MU dùng (Q) (TU) biên (MU) 0 0 - MU > 0: Tăng Q thì TU tăng 1 5 5 2 9 4 3 12 3 4 14 2 5 15 1 6 15 0 MU = 0: TU max nên dừng lại 7 14 -1 MU < 0 : Tăng Q thì TU sẽ giảm.
- Lợi ích cận biên và đường cầu:
+ Đường cầu: Số lượng sp ntd muốn mua và có khả năng mua
+ Đường lợi ích cận biên: quy định lợi ích cận biên tương ứng với đơn vị hh ấy là bao
nhiêu => tương ứng ntd sẵn sàng bỏ ra bao nhiêu tiền để mua hh ấy.
 Theo quy luật lợi ích cận biên giảm dần => đường cầu dốc xuống
 Khi lợi ích cận biên được đo bằng giá thì đường cầu là phần dương của đường lợi ích cận biên.
MU > P: Mua thêm hàng hóa => tăng TU
MU < P : Mua thêm hàng hóa => giảm TU
MU = P: Người mua đã tối đa hóa lợi ích
2. Phân tích bàng quan ngân sách
- Đường bàng quan (IC): Là tập hợp các kết hợp hàng hóa hay giỏ hàng mang lại cùng
một mức lợi ích cho người tiêu dùng => Đường bàng quan còn được gọi là đường đồng mức lợi ích
Ví dụ: Ăn 3 chiếc bánh mì hoặc 2 bát phở cùng thấy no thì điểm biển diễn 3 chiếc bánh
mì và 2 bát phở cùng nằm trên 1 đường bàng quan
- Biểu đồ các đường bàng quan: Tập hợp các đường bàng quan của người tiêu dùng *Đặc điểm:
- Các đường bàng quan có độ dốc âm
- Các đường bàng quan càng xa gốc tọa độ thì biểu diễn mức lợi ích càng lớn
- Các đường bàng quan không cắt nhau
- Các đường bàng quan lồi so với gốc tọa độ A B C D
Ban đầu ở điểm A: 15 kẹo mút và 2 bim bim
Điểm B: 9 kẹo và 3 bim bim
=>để tăng từ 2 bim bim lên 3 bim bim thì mình giảm 6 kẹo mút Điểm C: 5 kẹo 5 bim bim
Điểm D: 4 kẹo và 6 bim bim
 Để tăng từ 5 bim bim lên 6 bim bim thì giảm 1 kẹo mút
Đi từ trái => phải đường bàng quan ngày càng thoải tức là độ dốc ngày càng giảm 6 MRS = −∆ Y = = 6 ∆ X 1 1 MRS = −∆ Y = = 1 ∆ X 1
- Tỉ lệ thay thế cận biên (MRS): tỷ lệ thay thế cận biên của hàng hóa X cho hàng hóa Y
là số đơn vị hh Y giảm đi khi tăng tiêu dùng 1 đơn vị hàng hóa X để giữ nguyên mức lợi ích ban đầu.
=> Tỷ lệ thay thế cận biên giảm dần MU
MRS= −∆ Y =
X (độ dốc của đường bàng quan) ∆ X MUY
X tăng lên 1 lượng ∆ X thì lợi ích từ việc tiêu dùng X tăng lên MU x X ∆ X
Y giảm đi 1 lượng là ∆ Y thì lợi ích từ việc tiêu dùng Y tăng lên MU x Y ∆ Y
Lượng lợi ích thay đổi: MU x x X ∆ X =−MU ∆ Y Y
- Đường bàng quan đặc biệt:
Đường bàng quan 2 hh thay thế hoàn hảo
Đường bàng quang 2 hh bổ sung
- Đường ngân sách: P .X + P .Y = I x Y
Ví dụ: Giả sử một người tiêu dùng có thu nhập bằng tiền I = $60 dùng để mua hai hàng
hóa X và Y với giá tương ứng Px = 3$ và Py = 1$. Lập phương trình đường ngân sách 2 hh X và Y? 3X + Y = 60
+ Thay đổi giá: Giá X giảm thì lượng hàng hóa X tăng làm đường ngân sách dịch sang phải + Thay đổi thu nhập:
 Thu nhập tăng: Đường ngân sách dịch phải song song với đường ban đầu
 Thu nhập giảm: Đường ngân sách dịch trái, song song với đường ban đầu
Ví dụ 1: Khi giá hàng hóa được biểu diễn trên trục hoành thay đổi sẽ làm thay đổi
phương trình ngân sách như thế nào?
A. Độ dốc và điểm cắt của đường ngân sách với trục tung thay đổi
B. Độ dốc và điểm cắt của đường ngân sách với trục hoành thay đổi
C. Điểm cắt của đường ngân sách với trục tung và trục hoành thay đổi nhưng không thay đổi độ dốc
D. Chỉ làm thay đổi độ dốc
Ví dụ 2: Nếu thu nhập tăng, đường ngân sách sẽ:
A. Dịch chuyển sang trái và dốc hơn
B. Dịch chuyển sang trái và song song với đường ban đầu
C. Dịch chuyển sang phải và song song với đường ngân sách ban đầu
D. Dịch chuyển song song nhưng sang trái hay sang phải phụ thuộc hàng hóa là thông thường hay cấp thấp.
Ví dụ 3: Bảo tiêu dùng táo và chuối, giả sử thu nhập của Bảo tăng gấp đôi và giá của táo
và chuối cũng tăng gấp đôi thì đường ngân sách của Bảo sẽ: P .X + P .Y = I x Y
A. Dịch sang phải và không thay đổi độ dốc
B. Dịch sang phải và dốc hơn
C. Dịch sang phải và thoải hơn D. Không thay đổi
- Lựa chọn tối ưu của người tiêu dùng
MUx = MUy MUx  = Px Px Py MUy Py
Ví dụ 1: Giả sử một người tiêu dùng có thu nhập bằng tiền là I bằng 1000000đ dùng để
mua hai hàng hóa X và Y với giá tương ứng là Px = 20000đ và Py = 5000đ, cho biết hàm
tổng lợi ích của việc tiêu dùng hai hàng hóa là TU = (X – 2)Y. Để lợi ích thu được là lớn
nhất thì lượng hàng hóa X, Y mà người tiêu dùng mua là bao nhiêu? Tính lợi ích lớn nhất khi đó.
Phương trình đường ngân sách: 20. X + 5. Y = 1000 (*) MU = TU ' = Y x X
MU = TU ' = X - 2 y Y Y = X−2 (**) 20 5
Kết hợp (*) và (**) => X= 26, Y = 96 TU = (X – 2)Y = 2304
Ví dụ 2: Một cá nhân có số tiền là 90$ dùng để tiêu dùng hai hàng hóa X và Y, Px = 10$; Py = 20$. Thông tin cho: Q (X, Y) 1 2 3 4 5 TU 15 25 35 40 43 X MUx 15 10 10 5 3 TU 40 70 90 105 109 Y MUy 40 30 20 15 4
Để lợi ích thu được là lớn nhất thì lượng hàng hóa X, Y mà người tiêu dùng mua là bao nhiêu? Px. X + Py. Y = I X + 2Y = 9 
MUx = MUy MUx  = MUy Px Py 1 2 X= 3, Y =3 X= 1, Y=2 X= 2, Y= 3
Kết hợp vs pt đường ngân sách => X= 3, Y= 3
TU= TU + TU = 35 + 90 = 125 X y