Kinh Tế Vi Mô: Sản Xuất, Chi Phí và Lợi Nhuận | Microeconomics | Trường Đại học Quốc tế, Đại học Quốc gia Thành phố Hồ Chí Minh

Nội dung buổi 4 Kinh tế Vi mô
Chương 5: Sản xuất, chi phí và lợi nhuận
1. Lý thuyết sản xuất
1.1: Hàm sản xuất
- Hàm sản xuất: là mối quan hệ kỹ thuật biểu thị lượng hàng hóa tối đa mà doanh nghiệp
có thể sản xuất được từ các tập hợp khác nhau của các yếu tố đầu vào với một trình độ
công nghệ nhất định và trong một khoảng thời gian nhất định. Q= f(X1, X2, X3,….)
X1, X2, X3 là số lượng các yếu tố đầu vào
Q là số lượng hàng hóa có thể sản xuất
Hàm sản xuất được gọi là hiệu quả khi sản lượng sản xuất ra là lớn nhất. Giả định rằng:
1) Các yếu tố đầu vào là đồng nhất
2) Mục tiêu của các hãng là tối đa hóa lợi nhuận
- Giả định chỉ có hai yếu tố sản xuất là tư bản – vốn (K) và lao động (L): Q = f (K, L)
* Hàm sản xuất Cobb – douglass:
Q= a.Kα.Lβ Ta chứng minh được:
α là hệ số co giãn của Q theo K : E = Q ' . K = K
α. Khi K tăng 1% thì Q tăng α % Q
β là hệ số co giãn của Q theo L. Khi L tăng 1 % thì Q tăng β%
=> khi cả K và L đều tăng 1 % thì Q tăng (α + β )%
- Hiệu suất theo quy mô : đề cập tới sự thay đổi của sản lượng đầu ra khi tất cả đầu vào tăng theo 1 tỷ lệ.
+ Khi các yếu tố đầu vào cùng tăng lên t lần, Q tăng ít hơn t lần =>Hiệu suất giảm theo quy mô
+ Khi các yếu tố đầu vào cùng tăng lên t lần, Q tăng t lần => Hiệu suất không đổi theo quy mô.
+ Khi các yếu tố đầu vào tăng t lần, Q tăng nhiều hơn t lần => Hiệu suất tăng theo quy mô.
Ví dụ 1: Cho hàm sản xuất f(K, L) = 2K + L (t>1)
Giả sử các yếu tố K và L cùng tăng lên t lần
f(tK, tL)= 2. (tK) + tL = t (2K + L) =t .f(K, L)
 Hiệu suất không đổi theo quy mô
Ví dụ 2: Cho hàm sản xuất 𝒇(𝑲, 𝑳) = 1 1 K /2 + L /2
Giả sử K và L đều tăng t lần
f(tK, tL) = (tK )1/2 + ¿= 1 1 1 1
t /2(K /2 + L /2)= t /2. 𝒇(𝑲, 𝑳)
 Hàm hiệu suất giảm theo quy mô
*Đặc biệt với hàm Cobb – Douglass: Q= a.Kα .Lβ
khi cả K và L đều tăng 1 % thì Q tăng (α + β )%
+ (α + β ¿<1 => Hiệu suất giảm theo quy mô
+ α + β = 1 => Hiệu suất không đổi theo quy mô
+ α + β>1 => Hiệu suất tăng theo quy mô
Ví dụ: Cho hàm sản xuất f (K, L) = 2. 1 K /2. 2 L
α + β = ½ + 2= 5/2 >1 => Hiệu suất tăng theo quy mô.
- Ngắn hạn và dài hạn
+ Ngắn hạn: là khoảng thời gian có ít nhất 1 yếu tố đầu vào cố định.
+ Dài hạn: khoảng thời gian tất cả các yếu tố đầu vào thay đổi.
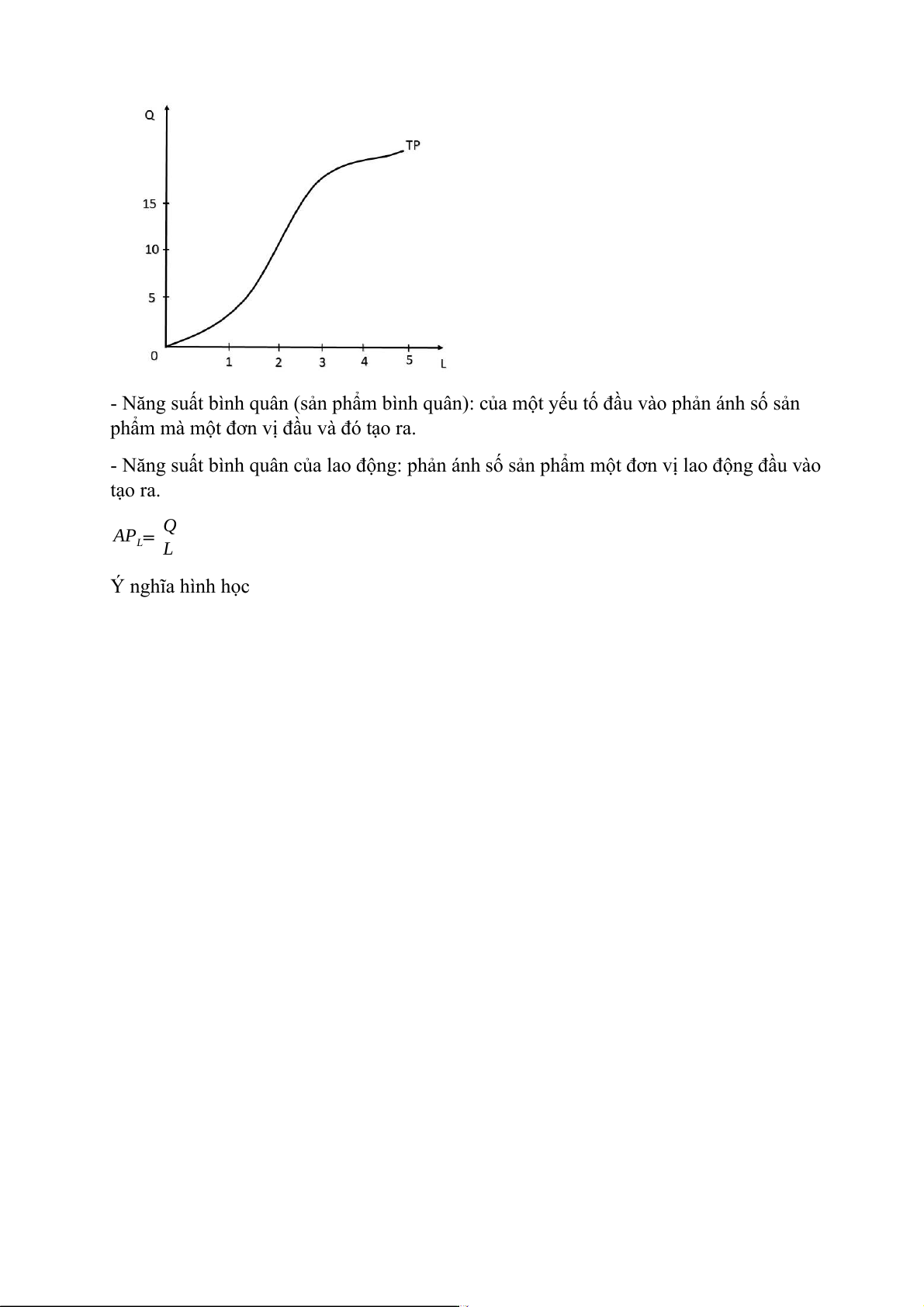
- Sản xuất với một đầu vào biến đổi: Hàm sản xuất trong ngắn hạn, giả sử vốn không đổi
(K ko đổi), doanh nghiệp thì chỉ có thể tăng giảm sảm lượng bằng cách thay đổi L.
Q = f(K, L) => Q= f(L) Số lượng lao Sản lượng Năng suất Năng suất động (L) đầu ra (Q) bình quân cận biên 0 0 0 0 1 4 4 4 2 10 5 6 3 13 4.3 3 4 15 3.75 2 5 16 3.2 1
- Năng suất bình quân (sản phẩm bình quân): của một yếu tố đầu vào phản ánh số sản
phẩm mà một đơn vị đầu và đó tạo ra.
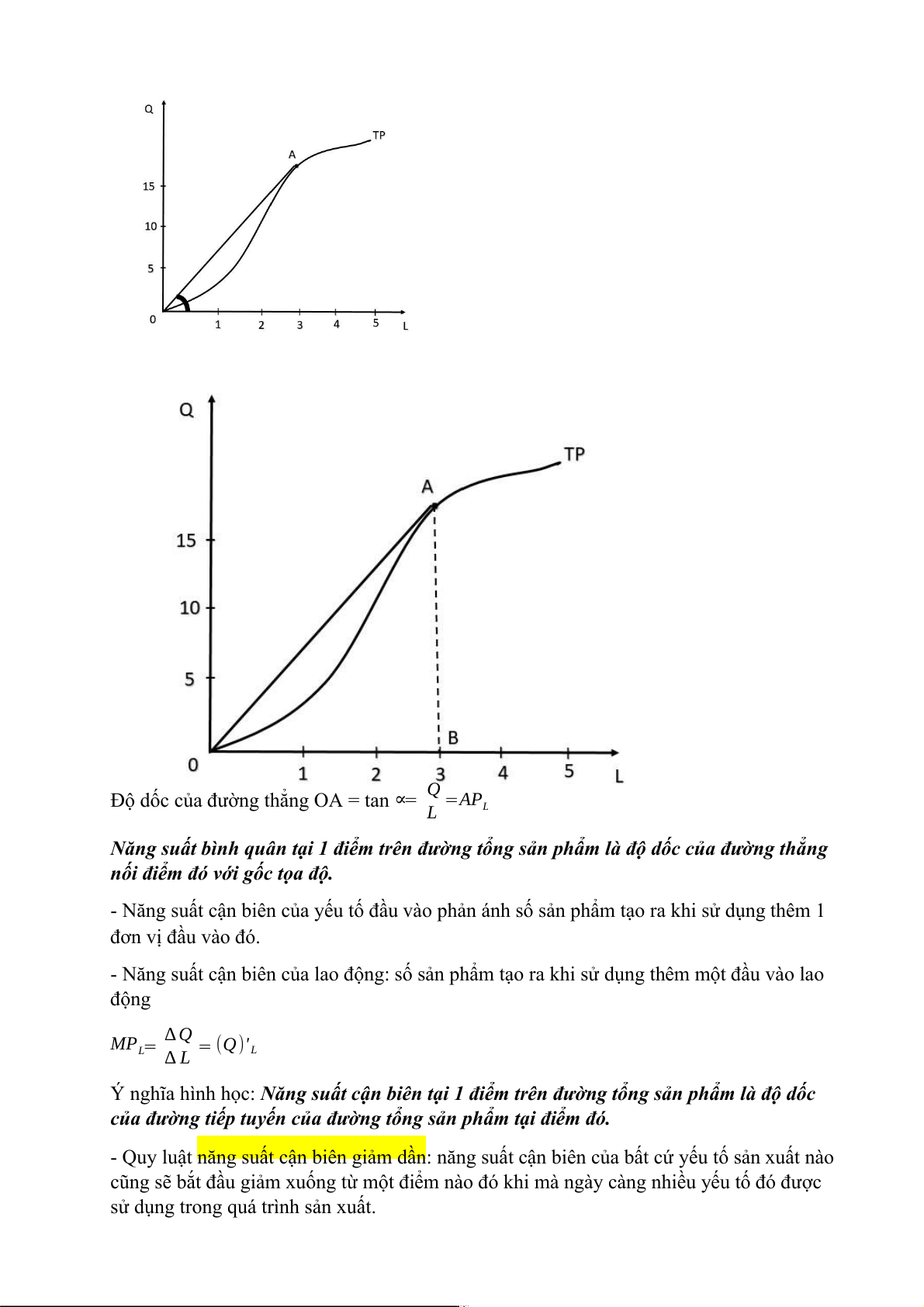
- Năng suất bình quân của lao động: phản ánh số sản phẩm một đơn vị lao động đầu vào tạo ra. AP = Q L L Ý nghĩa hình học
Độ dốc của đường thẳng OA = tan ∝= Q =AP L L
Năng suất bình quân tại 1 điểm trên đường tổng sản phẩm là độ dốc của đường thẳng
nối điểm đó với gốc tọa độ.
- Năng suất cận biên của yếu tố đầu vào phản ánh số sản phẩm tạo ra khi sử dụng thêm 1 đơn vị đầu vào đó.
- Năng suất cận biên của lao động: số sản phẩm tạo ra khi sử dụng thêm một đầu vào lao động
MPL= ∆ Q = (Q)' ∆ L L
Ý nghĩa hình học: Năng suất cận biên tại 1 điểm trên đường tổng sản phẩm là độ dốc
của đường tiếp tuyến của đường tổng sản phẩm tại điểm đó.
- Quy luật năng suất cận biên giảm dần: năng suất cận biên của bất cứ yếu tố sản xuất nào
cũng sẽ bắt đầu giảm xuống từ một điểm nào đó khi mà ngày càng nhiều yếu tố đó được
sử dụng trong quá trình sản xuất.
Ví dụ: Năng suất cận biên của lao động sẽ bắt đầu giảm xuất từ một điểm nào đó khi mà
ngày càng nhiều lao động được sử dụng trong quá trình sản xuất, trong điều kiện các yếu tố khác ko đổi.
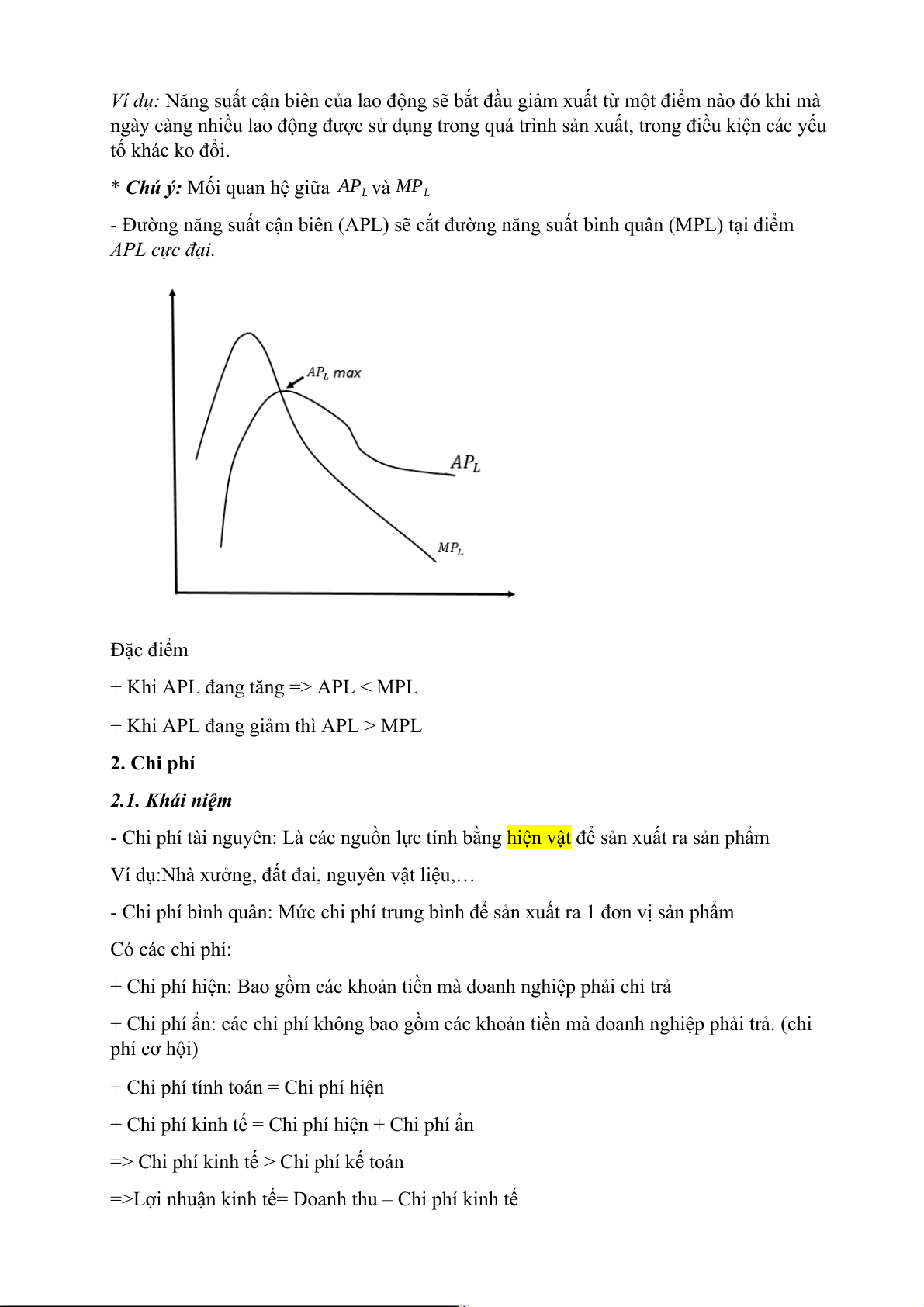
* Chú ý: Mối quan hệ giữa AP và MP L L
- Đường năng suất cận biên (APL) sẽ cắt đường năng suất bình quân (MPL) tại điểm APL cực đại. Đặc điểm
+ Khi APL đang tăng => APL < MPL
+ Khi APL đang giảm thì APL > MPL 2. Chi phí
2.1. Khái niệm
- Chi phí tài nguyên: Là các nguồn lực tính bằng hiện vật để sản xuất ra sản phẩm
Ví dụ:Nhà xưởng, đất đai, nguyên vật liệu,…
- Chi phí bình quân: Mức chi phí trung bình để sản xuất ra 1 đơn vị sản phẩm Có các chi phí:
+ Chi phí hiện: Bao gồm các khoản tiền mà doanh nghiệp phải chi trả
+ Chi phí ẩn: các chi phí không bao gồm các khoản tiền mà doanh nghiệp phải trả. (chi phí cơ hội)
+ Chi phí tính toán = Chi phí hiện
+ Chi phí kinh tế = Chi phí hiện + Chi phí ẩn
=> Chi phí kinh tế > Chi phí kế toán
=>Lợi nhuận kinh tế= Doanh thu – Chi phí kinh tế
Lợi nhuận kế toán = Doanh thu – Chi phí kế toán
 Lợi nhuận kinh tế < Lợi nhuận kế toán
Ví dụ: Tỷ lệ lãi suất là 10%/năm. Bạn đầu tư 150 triệu đồng khoản tiền riêng của mình
vào một công việc kinh doanh và kiếm được lợi nhuận tính toán là 40 triệu đồng sau một
năm. Giả sử các yếu tố khác không đổi, lợi nhuận kinh tế mà bạn thu được là: A. 15 triệu B. 25 triệu C. 4 triệu đồng D. 20 triệu đồng
Lợi nhuận kế toán = 40tr
Chi phí ẩn = 150tr x 10% = 15tr
Lợi nhuận kinh tế = (Doanh thu – Chi phí kế toán)- Chi phí ẩn = Lợi nhuận kế toán – Chi phía ẩn= 40 – 15 = 25 tr
Chú ý: - Chi phí bình quân và cận biện của lđ có đồ thị hình chữ U (nghịch đảo của năng suất)
- Do quy luật năng suất cận biên giảm dần, chi phí cận bên tăng dần
- Chi phí cơ hội = Chi phí kinh tế
2.2. Các chi phí ngắn hạn
- Tổng chi phí (TC): là toàn bộ giá trị của các yếu tố đầu vào mà doanh nghiệp sử dụng
để sản xuất một số lượng sản phẩm nhất định.
- Chi phí cố định (FC): Là những chi phí không thay đổi khi sản lượng thay đổi, nó
không phụ thuộc và số lượng sản phẩm.
Ví dụ: chi phí đầu tư nhà xưởng, máy móc
- Chi phí biến đổi (VC): là toàn bộ các chi phí phụ thuộc vào các mức sản lượng, tăng khi
sản lượng tăng, giảm khi sản lượng giảm
Ví dụ: nguyên vật liệu đầu vào TC = VC + FC - Chi phí bình quân:
- Tổng chi phí bình quân (ATC): Tổng chi phí tính trên một đơn vị sản phẩm ATC = TC Q
- Chi phí biến đổi bình quân: (AVC): tổng chi phí biến đổi trên một đơn vị sản phẩm AVC = VC Q
- Chi phí cố định bình quân (AFC): Tổng chi phí cố định trên một đơn vị sản phẩm AFC = FC Q TC = VC + FC
AVC + AFC = VC + FC = TC = ATC Q Q Q
- Chi phí cận biên (MC) : mức chi phí tăng thêm để sản xuất 1 đơn vị sản phẩm
MC = ∆ TC = (TC)’= (VC + FC)’= (VC)’ ∆ Q TC = TC + MC n n−1 n
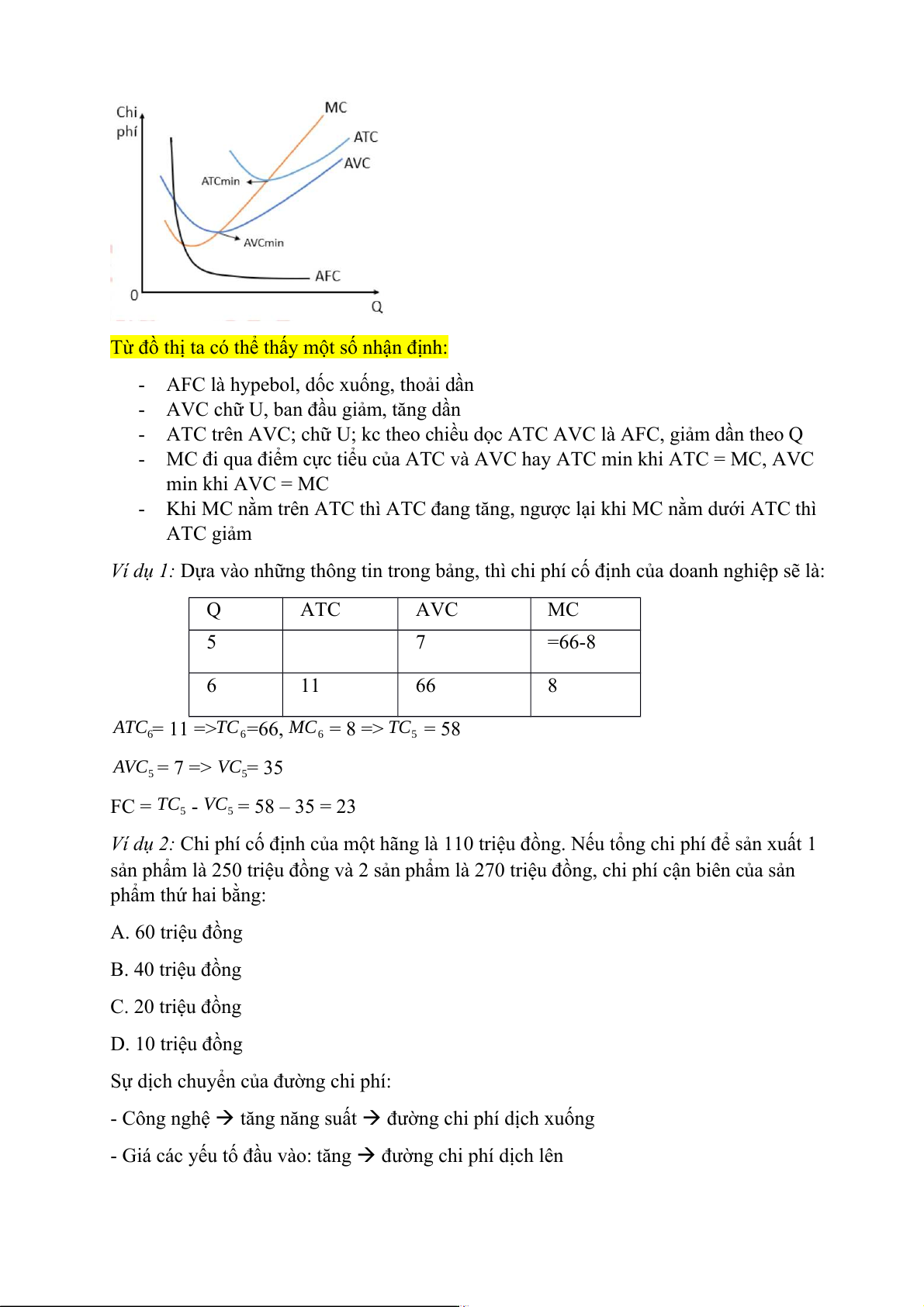
Từ đồ thị ta có thể thấy một số nhận định:
- AFC là hypebol, dốc xuống, thoải dần
- AVC chữ U, ban đầu giảm, tăng dần
- ATC trên AVC; chữ U; kc theo chiều dọc ATC AVC là AFC, giảm dần theo Q
- MC đi qua điểm cực tiểu của ATC và AVC hay ATC min khi ATC = MC, AVC min khi AVC = MC
- Khi MC nằm trên ATC thì ATC đang tăng, ngược lại khi MC nằm dưới ATC thì ATC giảm
Ví dụ 1: Dựa vào những thông tin trong bảng, thì chi phí cố định của doanh nghiệp sẽ là: Q ATC AVC MC 5 7 =66-8 6 11 66 8
ATC = 11 =>TC =66, MC = 8 => TC = 58 6 6 6 5
AVC = 7 => VC = 35 5 5
FC = TC - VC = 58 – 35 = 23 5 5
Ví dụ 2: Chi phí cố định của một hãng là 110 triệu đồng. Nếu tổng chi phí để sản xuất 1
sản phẩm là 250 triệu đồng và 2 sản phẩm là 270 triệu đồng, chi phí cận biên của sản phẩm thứ hai bằng: A. 60 triệu đồng B. 40 triệu đồng C. 20 triệu đồng D. 10 triệu đồng
Sự dịch chuyển của đường chi phí:
- Công nghệ  tăng năng suất đường chi phí dịch xuống 
- Giá các yếu tố đầu vào: tăng đường chi phí dịch lên 
+ Giá của đầu vào cố định (thuế đất, khẩu hao máy móc,…)  ảnh hưởng đến FC, AFC, ATC
+ giá của đầu vào biển đổi ảnh hưởng đến VC  - Thuế:
+ thuế sản lượng (quantity tax): tiền thuế phải nộp phụ thuộc vào lượng hàng bán ra
+ thuế khoán (lump sum): thuế cố định
2.3: Chi phí dài hạn
-Hàm tổng chi phí: TC = rK + wL r:giá của tư bản (K) w: giá của lao động (L) Đường đồng phí
- Đường đồng lượng: các kết hợp yếu tố đầu vào cho ra cùng một mức sản lượng − MP
- Tỷ lệ thay thế kĩ thuật cận biên: MRST = ∆ K =
L (Độ dốc của đường đồng lượng) ∆ L MPK - Điểm tối ưu MPL = MPK w r
* Mối quan hệ giữa năng suất lao động cận biên với chi phí cận biên, năng suất lao động
bình quân với tổng chi phí bình quân:
Năng suất lao động cận biên với chi phí cận biên MC = w MPL
Ví dụ: Khi MC tăng thì MPL như nào
Năng suất lao động bình quân với chi phí biến đổi bình quân: AVC = w APL 3. Lợi nhuận
- Lợi nhuận: là phần chênh lệch tổng doanh thu và tổng chi phí π = TR – TC π max (
 π ¿' = 0 (TR – TC)= 0  TR’ = TC’  MR = MC +
Ví dụ: Một doanh nghiệp sản xuất hàng hóa có hàm tổng chi phí như sau: TC = 2
Q + 12Q + 2500 =VC + FC
a. Xác định các hàm số FC, VC, ATC, AVC, AFC, MC
b. Khi hàm cầu của thị trường có dạng P = -2Q + 200, tìm sản lượng tối ưu (sản lượng để lợi nhuận lớn nhất).
TR = P.Q = (-2Q + 200). Q= -2 2
Q + 200Q => MR = TR’= -4Q + 200
Lợi nhuận tối đa khi: MR = MC -4Q + 200 = 2Q + 12   Q= 31.3
 Doanh nghiệp tối đa hóa lợi nhuận tại mức sản lượng Q = 31.3 Giải: a. FC= 2500 VC= 2 Q + 12Q 2500 ATC= TC/Q = Q + 12 + Q AVC = Q + 12 2500 AFC = Q MC = TC’ = 2Q + 12
Ví dụ 2: Một doanh nghiệp nếu bán sản phẩm với giá P = 20 nghìn đồng, thì bán được Q
= 100 nghìn đvsp, biết hệ số có dãn của cầu tại thời điểm này EDP = 0,2.
a. Hãy xác định phương trình đường cầu của doanh nghiệp.
b. Có số liệu hàm TC = Q + 40Q +50, xác định MC, AC, AVC 2
c. Để tối đa hóa lợi nhuận thì DN này sẽ lựa chọn sản xuất bao nhiêu sp và bán với giá nào?
d. Xác định giá bán và sản lượng để DN đạt mục tiêu tối đa hóa doanh thu
TR max  TR’=0 MR = 0 => Q?  Giải
a. Pt đường cầu: Q = a – bP 20 EDP= Q’ x P = -b. Q 100  b=? => a?
Ví dụ 3: Hàm sản xuất của một DN có dạng: Q = 2. K. L1/2.
Biết Pk = 20 USD, PL = 12 USD.
a. Giả sử DN đầu tư 14.400 USD. Hãy cho biết với mức đầu tư đó thì DN sẽ lựa chọn K
và L tối ưu như thế nào, mức sản lượng tối đa đạt được là bao nhiêu?
b. Doanh nghiệp mở rộng quy mô thì hiệu suất tăng hay giảm?