


















Preview text:
Lecture 3 PERCENTAGES, QUANTITATIVE POWERS METHODS AND SIMPLIFICATION Lecture 3 LEARNING OBJECTIVES Calculate percentages.
Understand an advanced operation, power, which can be positive,
negative, an integer and a fraction.
Simplify expressions using expansion and factorisation.
Understand the fundamental concept of present value. Lecture 3 INTRODUCTION
A company employs 100 people of whom 25 are women, this could be expressed as:
• Women make up one-quarter of the labour force (fraction)
• Women make up 0.25 of the labour force (decimal)
• Women make up 25% of the labour force (percentage)
The literal meaning of “percent” is per hundred (“centum” meant one
hundred in Latin; “cent” is French for a hundred, “cento” is Italian for a
hundred, “a century” is a hundred years in English). Lecture 3 1. PERCENTAGES CALCULATINGPERCENTAGES
• When we speak of 5% of 235, we mean: 235 11.75
• When we say the number A increases by 𝑥%, then:
The increase in the number A is: The increased number is: 𝐴 𝐴 𝐴 1 𝐴 Lecture 3 1. PERCENTAGES CALCULATINGPERCENTAGES
• Example 1: A salary of £55,240 is to be increased by 12%. Calculate: The increase (in pounds): 12 55,240 6,628.8 100 The new salary (in pounds): 12 100 55,240 61,868.8 100 Lecture 3 1. PERCENTAGES CALCULATINGPERCENTAGES
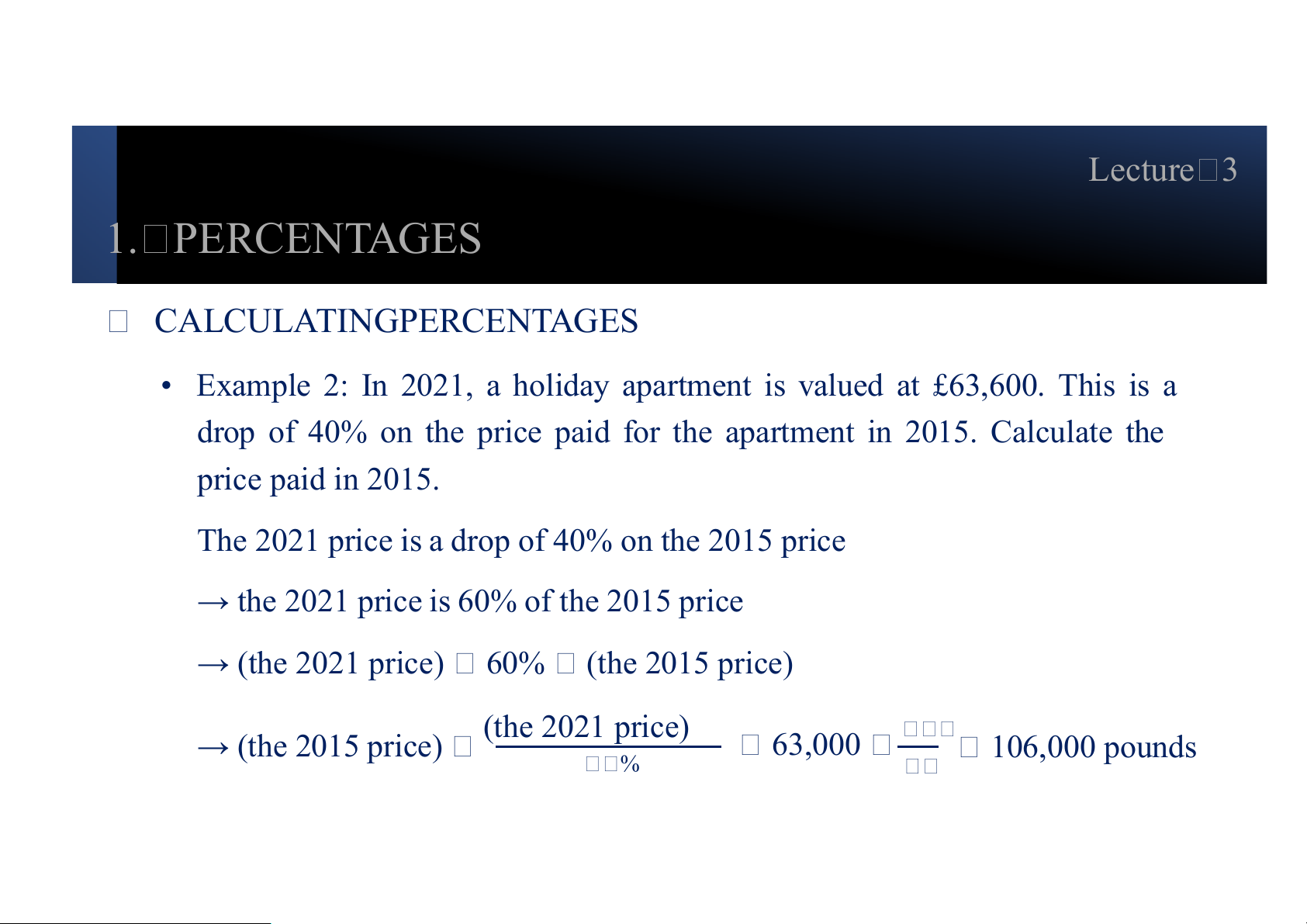
• Example 2: In 2021, a holiday apartment is valued at £63,600. This is a
drop of 40% on the price paid for the apartment in 2015. Calculate the price paid in 2015.
The 2021 price is a drop of 40% on the 2015 price
→ the 2021 price is 60% of the 2015 price → (the 2021 price) 60% (the 2015 price) (the 2021 price) → (the 2015 price) 63,000 106,000 pounds % Lecture 3 1. PERCENTAGES CALCULATINGPERCENTAGES
• Example 3: A bookshop gets £20 for every copy of a particular book
sold, 70% of which is paid to the publisher. The publisher pays 10%
of the 70% they get to the writer of the book. If the book sells 270
copies, how much will the writer get? The bookshop gets: 270 20 5400 pounds The publisher gets: 5400 70% 3780 pounds The writer gets: 3780 10% 378 pounds Lecture 3 2. POWERS DEFINITION
• Originally, powersare invented to provide a shorthand way of
representing repeated multiplications.
• Example: 2 is called “2 to the power of 7” and means 2 multiplied by itself 7 times: 2 2 2 2 2 2 2 2 128.
• In particular, if the power is 2, then it is called squared; if the
power is 3, then it is called cubed. Lecture 3 2. POWERS DEFINITION
• In a general expression 𝑥 (“𝑥 tothepowerof𝑛”), 𝑥 is called base
and 𝑛 is called poweror exponent.
• Review: in scientific notations, the powers of 10 or E have the same meaning: 2300 2.3 10 or 2.3𝐸3.
• The power 𝑛 can be positive, negative, an integer and a fraction. Lecture 3 2. POWERS INTEGERPOWERS
• A number to a positivepower is defined as repeated multiplication: 2 , 2 , , 0 .
• A number to a negativepoweris defined as the reciprocalof the corresponding positive power: 2 , 2 .
• A number to a zeropoweris defined to be equal to 1. Notice: 0 0 if 𝑛 0; 0 does not exist if 𝑛 0. Lecture 3 2. POWERS LAWSOFPOWERS
• Multiplying Powers: 𝑥 𝑥 • Dividing Powers: • Powers of a Power: 𝑥
• Powers of a Product/Quotient: 𝑥𝑦 𝑦 ; • Warning 1: 𝑥 𝑥 ; 𝑦 .
• Warning 2: Power has priority over ( ; ): 2 1 2 2 . Lecture 3 2. POWERS FRACTIONALPOWERS
• In general, the power can be defined for any fraction (or its decimal
counterpart), and the result can be interpreted as the 𝒏thprincipalroot: 𝑥
𝑥 (“the𝑛throotof𝑥”) 𝑥 𝑥 or 𝑥
Notice: ∎ or ∎ is an arithmetic operator returning the “principal root” of
∎. It is different from solving for an equation 𝑥 ∎ (there are 𝑛 roots). Lecture 3 2. POWERS FRACTIONALPOWERS • Examples: 9 9 . 9
3 (there are actually two square roots of 9, i.e. 3). 8 8 .
8 2 (there are actually three cube roots of 8, one real root 8 2, and two complex roots). 8 8 2; 16 16 . 16 2
Notice: 𝑥 denotes the real 𝑛th root if 𝑛 is odd; the positive 𝑛th root if 𝑛 is even and 𝑥 is positive. Lecture 3 2. POWERS REVIEW:ORDERSOFOPERATIONS
• Brackets (from inner to outer) • Powers •
and (from left to right if more than one ; ) •
and (from left to right if more than one ; ) Examples: 2 4 8 15 5 ? 2 3 3 ? Lecture 3 2. POWERS APPLICATION:PRESENTVALUE
• If you have an amount of 𝐴 and decide to keep it in a bank with the
annualised interest rate 𝑟, then you have: After 1 year: 𝐵 𝑟𝐴 1 After 2 years: 𝐵 1 𝐴 1 … After 𝑡 years: 𝐵 1 𝐴 1
𝐴 is called the presentvalueof your money, 𝐵 is called the future valueof 𝐴 after 𝑡 years. Lecture 3 2. POWERS APPLICATION:PRESENTVALUE
• In general, we can symbolise the relationship between the present
value (PV) and future value (FV) in any period ahead: 𝑃𝑉 1 𝑉
where: 𝑟 is the compound interest rate (interest generates interest).
𝑡 is the number of periods (can be years, months or days).
• To calculate the PVof any future cash flow FV, we can use the formula (derived from above): 𝑃𝑉 (1) Lecture 3 2. POWERS APPLICATION:PRESENTVALUE
• Since PVis generally less than FV, this process is also called “discounting”
the FVto PV, the interest rate is also called “discount rate”, and ≡ 𝐷
is called “discount factor”. Notice1: If 𝑡 0, then 𝑃𝑉
𝐹𝑉, implying that the PVis just the FV.
Notice2: If the interest compounds 𝑛 times a year and 𝑟 is the annualised
interest rate, then we need to use: 𝑃𝑉 (2) Lecture 3 2. POWERS APPLICATION:PRESENTVALUE
• Example 1: find the present value of £1,000 in 3 years’ time if the
interest rate is 8% compounded or payable annually. 794 𝐹𝑉 𝑃𝑉 1
• Example 2: find the present value of £2,500 in 2 years’ time if the
interest rate is 7% compounded twice a year. 2179 𝐹𝑉 𝑃𝑉 1 𝑟 𝑛 Lecture 3 2. POWERS APPLICATION:PRESENTVALUE
• Example 3: An investment project requires a current cost of 100
million VND and will bring in 150 million VND after 3 years. With
the current annualised interest rate of 8%, should you take the
project or not? (Canyousolvethisproblemin 2ways?)
Project = 150 - 100x(1 - 8%)^3 = 24
Bank = 100 - 100x(1 - 8%)^3 =26 Lecture 3 3. SIMPLIFICATION PURPOSE
• With the help of symbols, we can use variables and parameters to build a
model to express some general relationships between quantities.
• Both numbers and symbols follow the same set of rules and laws, by which
we can transform an expression from one to another equivalent form.
• When we transform an expression, some forms are preferred to others,
because they are simple and informative – that is the ultimate purpose of simplification.
• Simplification using expansionand factorisationcan help understanding
complicated models more easily.




