Analytical Chemistry 1 Lecture'9 Precipitationtitration Instructor:*Nguyen*ThaoTrang Producing'Soluble'Complexes
Complexation reactions involve a metal ion M reacting
witha ligandL toforma complexML. M+ L ML
Complexation reactionsoccurin a stepwise fashion,and
the reaction above is often followed by additional reactions: ML+L ML2 ML2 +L ML3 …... MLn-1+L MLn Producing Soluble Complexes
• The equilibrium constants for complex formation
reactions are generally written as formation constants.
• The overall formation constants are products of the
stepwiseformationconstantsfortheindividualsteps leadingto theproduct. Forming'Insoluble'Species
• Additionofligandstoa metalionmayresultininsoluble species.
• Inmanycases,theintermediateunchargedcomplexesin
thestepwiseformationschememaybesparinglysoluble,
whereastheadditionofmoreligandmoleculesmay result insolublespecies.
• Ex. AgCl is insoluble, but addition of large excess of Cl- producessolubleAgCl - 2- 3- 2 , AgCl3 , andAgCl4 . Forming'Insoluble'Species
In contrastto complexation equilibria, which are most
oftentreatedasformationreactions,solubilityequilibria
areusuallytreatedasdissociationreactions MxAy(s) xMy+(aq)+yAx-(aq) Ksp= [My+]x[Ax- y ]
where, Ksp = solubility product. Hence, for BiI3, the solubilityproductiswrittenK 3+ - sp= [Bi ][I ]3.
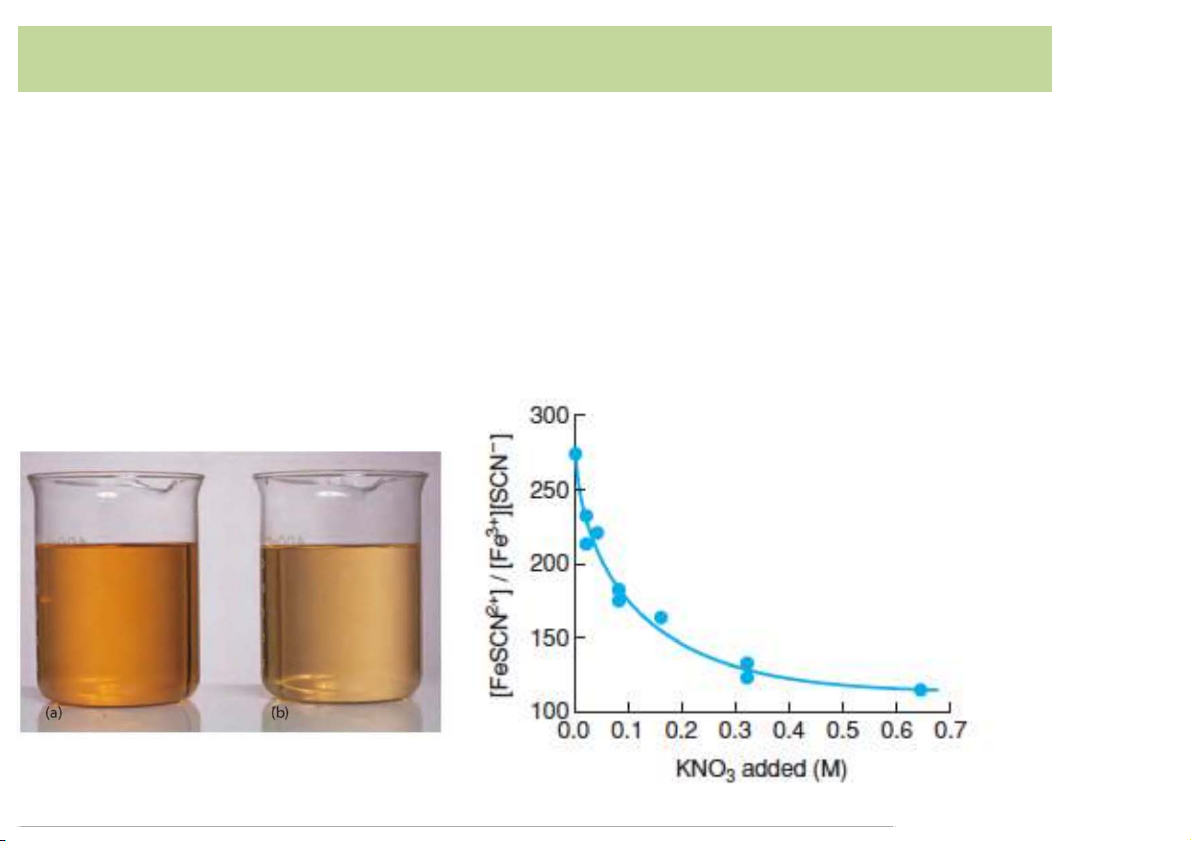
EffectQofQionicQstrengthQonQsaltQsolubility • Fe3+ + SCN- ⇌ Fe(SCN)2+ Pale yellow colorless Red K 2+ 3+ - eq = [Fe(SCN) ]/( F [ e ].[SCN ])
àdecreases with adding the “inert salt” KNO3 à not really a constant! with added KNO3 6
EffectQofQionicQstrengthQonQsaltQsolubility • CaSO 2- 4 (s) ⇌ Ca2+ + SO4 K 2- sp = [Ca2+][SO4 ] = 2.4 x10-5
Adding KNO3, more CaSO4 dissolves
à increase the solubility of CaSO4 7 Ionic strength
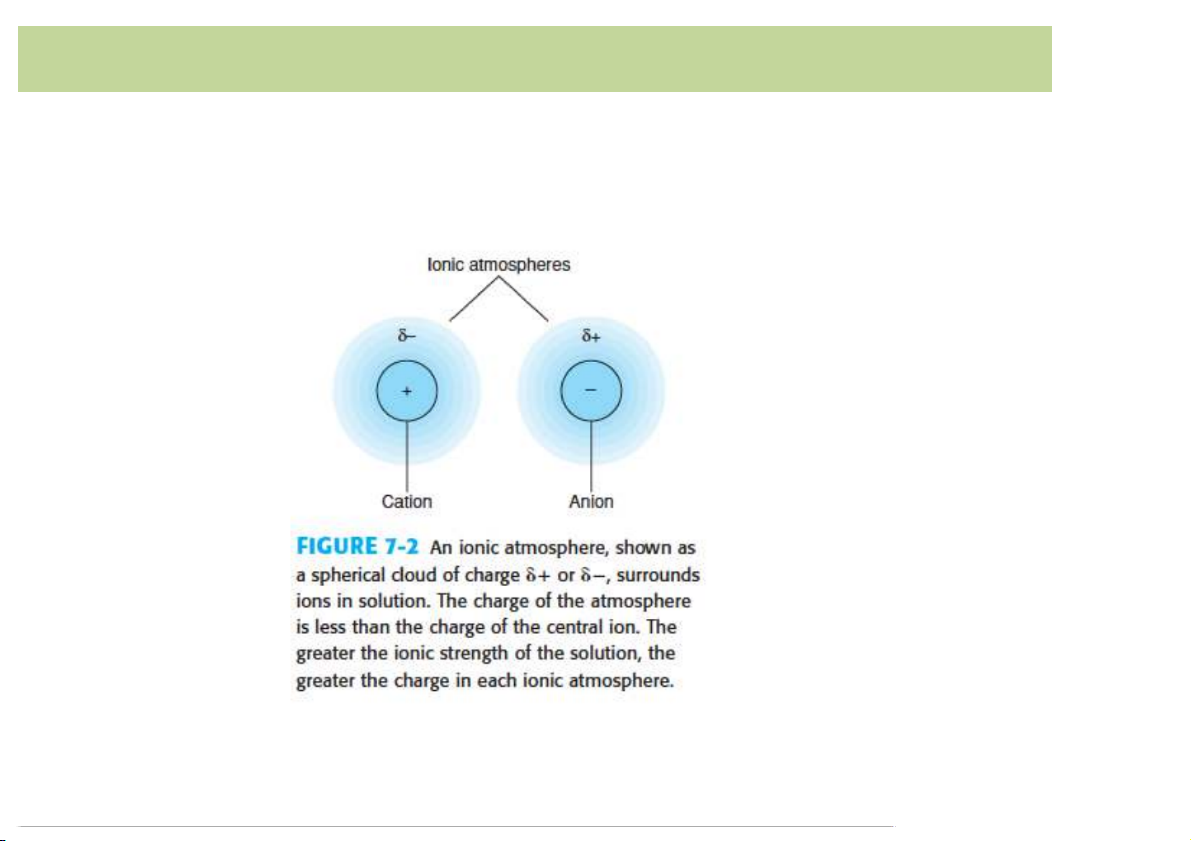
Cation is surrounded by excess anions.
Anion is surrounded by excess cations 8 Ionic strength
Adding salt to the solution, the ionic strength increases. • Thus Ca2+ , SO 2- 4
are surrounded by charged ionic
atmospheres that partially screen the ions from each
other. The formation of CaSO4 requires the disruption of
the ionic atmospheres surrounding the Ca2+ and SO 2- 4 ions.
• Increasing the concentrations of ions in solution, by
adding KNO3, increases the size of these ionic atmospheres.
• Since more energy is now required to disrupt the ionic
atmospheres, there is a decrease in the formation of
CaSO4, and an apparent increase in the equilibrium constant. 9 Ionic strength
• A measure of total concentration of ions in solution.
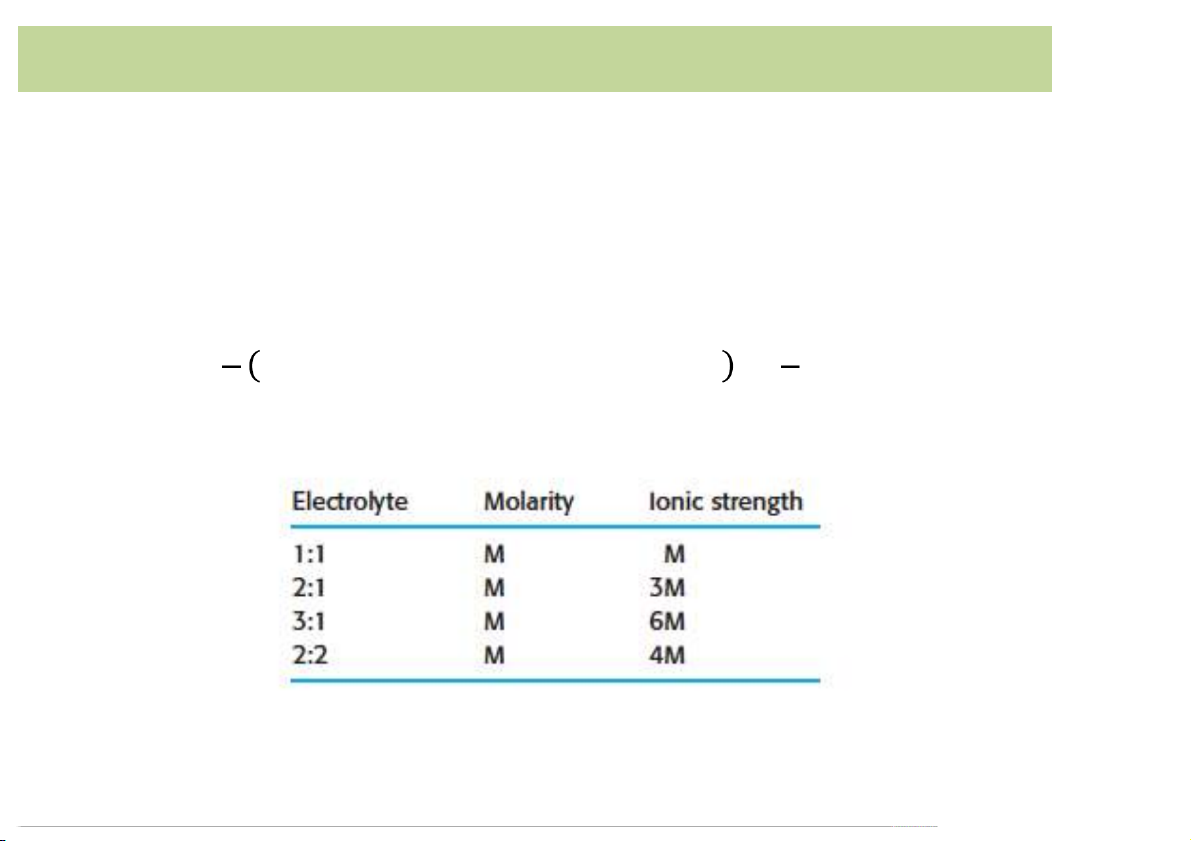
• The more highly the ion is charged, the more it is counted. . 1 1 𝜇 = c ( + c ( + c ( ++… . +c ( = / c ( 2 &z& (z( *z* .z. 2 0z0 01& 10 Ionic strength 11 Activity Coefficient
• TheQtrueQthermodynamicQequilibriumQconstantQisQaQfunction
activityQratherQthanQconcentration.
• TheQactivityQofQaQspecies,QaA ,QisQdefinedQasQtheQproductQ
molarQconcentration,Q[A],QandQaQsolution-dependentQactivityQ coefficient,Q𝛾A . aA ='[A].𝛾A • Ca(SO 2- 4)2 (s) ⇌ Ca2+ + SO4 • K 2+ 2- 2- 2+ 2- sp = aCa
. aSO4 = [Ca2+][SO4 ]. 𝛾Ca . 𝛾SO4 12 Activity Coefficient
• For gases, pure liquids, pure solids, nonionic solutes, the
activity coefficients are unity à the difference between
concentration and activity can be negligibl . e
• For ionic solutes, the activity coefficients can be
calculated by the extended Debye Huckel theory:
𝒍𝒐𝒈𝜸= + 7𝟎.𝟓𝟏𝒛𝟐 𝝁
𝟏>(𝜶 𝝁/𝟑𝟎𝟓)
where 𝛼 is the effective diameter of hydrated ion in pm at 25oC
- Debye Huckel is valid when 𝜇 ≤ 0.1 M, beyond not very accurate in predicting γ 13 Activity Coefficient 14 pH revisit
• 𝑝𝐻 =−logAMN =−log{ H> .𝛾MN} 15 pH revisit
• 𝑝𝐻 =−logAMN =−log{ H> .𝛾MN} 16 Precipitation titration
• Precipitation titration, which is based on reactions that
yieldioniccompoundsoflimitedsolubility.
• Theslowrateofformationofmostprecipitates,however,
limitsthenumberofprecipitatingagentsthatcanbeused intitrations toa handful.
• The most widely used and important precipitating
reagent, silver nitrate AgNO3, which is used for the
determination of the halogens, the halogen-like anions.
Titrations with silver nitrate are sometimes called argentometrictitrations. Precipitation titration
• ConsiderQtheQtitrationQofQ25.00QmLQofQ0.1000QMQ 0.05000QMQAg+.
Ag+(aq)Q+QI-(aq)Qà AgIQ(s)Q(1)
TheQdissociationQreactionQofQtheQprecipitation: AgI(s)QßàAg+(aq)Q+QI-(aq); K -17 sp=[Ag+][I-]Q=Q8.3Qx 10
KQ=Q1/Ksp=Q1.2x 1016Qà theQtitrationQgoesQtoQ completion! 18 Precipitation titration
• At equivalence point: Ve volume of Ag+ required
to react completely with all I- present. 19 Precipitation titration
• Before the equivalence point:VAg+ = 10.00 mL 20 Precipitation titration
• Before the equivalence point: repeat the
calculation of pAg+ based on [I-] remained.
• Or can apply streamlined calculation base on
fraction remaining of the analyte and dilution: 21 Precipitation titration • At the equivalence point: AgI(s) ßàAg+(aq) + I-(aq); x x
àThe pAg is independent on the original concentrations and volumes! 22 Precipitation titration
• After the equivalence point:VAg+ = 52.00 mL
àthe volume of Ag+ excess the equivalence point: 2.00 mL. 23
The shape of Precipitation titration
• Titrationcurvesforprecipitationreactionsarederivedin
a completelyanalogouswayto themethodsdescribedfor
titrationsinvolvingstrongacids andstrongbases.
• Most indicators for argentometric titrations respond to
changes in the concentration of silver ions. As a
consequence, titration curves for precipitation reactions
usuallyconsistofa plotofpAg+ versus volumeofAgNO3.
The shape of Precipitation titration • Higher [Ag+], larger pAg+ change at the equivalence point.
• Lower [I-], the larger volume
of the titrant required at the equivalence point, the less accurate the determination of the end point. • TheQsmallerQKsp,QtheQ greaterQchangeQinQpAgQ atQtheQequivalenceQ point. • IonsQformingQ precipitatesQwithQKsp>Q 10-10doQnotQyieldQ satisfyingQendpoints.
Endpoint of Precipitation titration
Colorchangeortheappearanceordisappearanceof turbidity. Therequirementsare:
• (1) the color change should occur over a limited rangeinthep-function,and
• (2) the color change should take place within the
steepportionofthetitration curve.
Formation of a Colored Precipitate The'Mohr'Method
• Sodium chromate can serve as an indicator for the
argentometric determination of Cl-, Br-, and CN- by
reacting with Ag+ to form a brick-red silver chromate
(Ag2CrO4) precipitateintheequivalence-pointregion.
• The reactions involved in the determination of chloride andbromide(X-) are titrationreaction: Ag+ +X- AgX(s) [white]
indicatorreaction: 2Ag+ + CrO 2- 4 Ag C 2 rO4(s) [red]
The solubilityofsilverchromateis several timesgreater
than thatofsilverchlorideorsilverbromide.
FigureQ1.QBeforeQtheQadditionQofQanyQsilverQ
nitrateQtheQchromateQindicatorQgivesQtheQclearQ solutionQaQlemon-yellowQcolor.
FigureQ2.QCloudyQprecipitateQofQAgClrearQth
endpointQ(left)QandQlightQred-brownQAg2CrO4
formedQwithQslightlyQ excessQAg+QjustQoverQtheQ endpointQ(right). 29
The Volhard Method (Colored Complex)
• ThemostimportantapplicationoftheVolhardmethod
isfortheindirectdeterminationofhalideions.
• A measuredexcessofstandardsilvernitratesolutionis
added to the sample, and the excess silver ion is
determined by back-titration with a standard thiocyanatesolution.
The'VolhardMethod'(Colored'Complex)
In the Volhard method, excess silver ions are titrated
witha standard solutionofthiocyanateion: Ag+ + SCN- AgSCN(s)
Iron(III)serves astheindicator. Thesolutionturnsred
withthefirstslightexcessofthiocyanateion: Fe3++ SCN- Fe(SCN)2+ [FeS(CN ) 2] + 3 red Kf = [ - 3+ = . 10 × 5 1 0 Fe ] [ SCN ]
The titration mustbe carried out in acidic solution to
preventprecipitation ofiron(III)asthehydratedoxide.
FigureQ2.QafterQtheQendpoint,QtheQredQQ FigureQ1.QBeforeQtheQendpoint Fe(SCN)2+ 32
Adsorption'Indicators:'The'FajansMethod
• An adsorption indicator is an organic compound that
tends to be adsorbed onto the surface ofthe solid in a
precipitationtitration. Ideally,theadsorptionoccursnear
the equivalence point and results not only in a color
changebutalsoina transferofcolorfromthesolutionto thesolid(orthereverse).
• Fluoresceinisa typicaladsorptionindicatorusefulforthe titrationofCl- withAgNO3.
– In aqueous solution, fluorescein partially dissociates into
hydroniumionsandnegativelychargedfluoresceinateionthat areyellow-green.
– Thefluoresceinateionformsanintenselyredsilversalt.
• Titrations involving adsorption indicators are rapid, accurate,and reliable.